0 引言
绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)是当前中、大、超大电力电子装置中应用最广泛的全控型电力电子器件。随着装备技术的飞速发展,各领域对IGBT器件的设计制造工艺及可靠性要求也越来越高[1-2]。有限元法(Finite Element Method, FEM)是一种基于结构与材料的数值解法,在具体操作上非常灵活,可以克服实验条件的局限性,已经成为在IGBT的仿真建模、结构优化设计以及可靠性分析等问题的研究中被普遍应用的一种方法[3-4]。FEM仿真软件对电场问题的求解方式普遍符合欧姆定律,而IGBT作为一种半导体器件,其电气特性本质上区别于纯导体,芯片的电导率也不等同于芯片材料的电导率,这给基于FEM的仿真带来了不便。此外,考虑到在实际应用中IGBT的工作环境较为复杂,其外部载荷(如电流、电压等)经常处于不断变化的状态。因此,有必要构建一种能对电流连续变化下的IGBT电气特性进行准确表征,同时在算法上适用于FEM仿真的电气模型。
在基于FEM的IGBT电气模型建模方面,国内外学者已进行了较多研究。文献[5]将IGBT的功率损耗进行了平均化处理,将其表示为电流、电压以及频率的函数。而温度是影响IGBT饱和压降以及开关频率的重要因素,因此文献[6]在对功率损耗的分析中进一步考虑了温度反馈的影响。但此种处理方法只能对IGBT的功率损耗进行粗略估计,不能用于基于FEM的电场仿真。文献[7-8]基于温度线性化的假设对IGBT的V-I特性曲线进行了拟合,将IGBT的电导率表示为对温度的线性函数,并进一步构建了基于FEM的IGBT的电-热-力多场耦合模型,但上述处理只是对单一恒定电流下的拟合,不适合对电流连续变化的工况进行仿真。文献[9]基于TCAD有限元仿真获得了IGBT在不同温度下的V-I特性,并通过构建查表的方法建立了IGBT的电气行为模型。这种处理方式可明显提高仿真效率,但V-I特性查表的获取依赖于复杂的TCAD模型,且由于查表数据量有限,在电流连续变化的条件下难以保证模型依旧具备良好的精度。文献[10]对某逆变器装置中IGBT器件的电流及饱和压降进行了在线提取,通过递归最小二乘法对测量数据进行了线性化处理,同时也考虑了温度对IGBT饱和压降的影响,但因其对V-I特性的线性化处理方法过于理想化,因此更适用于装置级、大数据下的在线监测,而对模块级的FEM建模而言会带来较大误差。
针对现有建模方法存在的问题,为构建通用性强,且能对电流连续变化下IGBT的电热特性进行精确表征的FEM模型,本文根据行为模型的构建思想,首先通过最小二乘法对IGBT数据手册提供的V-I特性曲线进行了分段线性化拟合,综合考虑了IGBT结温(Tj)、导通压降(VCE)以及电流(IC)的相互影响,并定义了IGBT等效电阻的概念。通过函数转换得到了在计算方法上符合欧姆定律的IGBT等效电阻数学表达式,并在FEM软件中构建了IGBT的电热耦合模型,最后通过仿真分析与实验验证,证明了所建模型的准确性。
1 IGBT等效电阻模型的构建
以斯达某型1 200V/50A模块为例,数据手册中给出了IGBT在典型温度下的V-I特性曲线,如图1所示。IGBT作为一种功率半导体器件,其V-I特性区别于纯导体,即其导通电流与压降并不满足正比关系。此外,IGBT的饱和压降VCE不仅与导通电流IC有关,同时也受结温Tj的影响。图1中标注的拐点A是IGBT器件的V-I特性随温度变化的共同特征,A点以上的部分表现为与温度呈正相关,A点以下的部分则表现为与温度负相关。同时,在温度一定时,A点以上部分的VCE与IC具有相对较好的线性关系[10-11]。
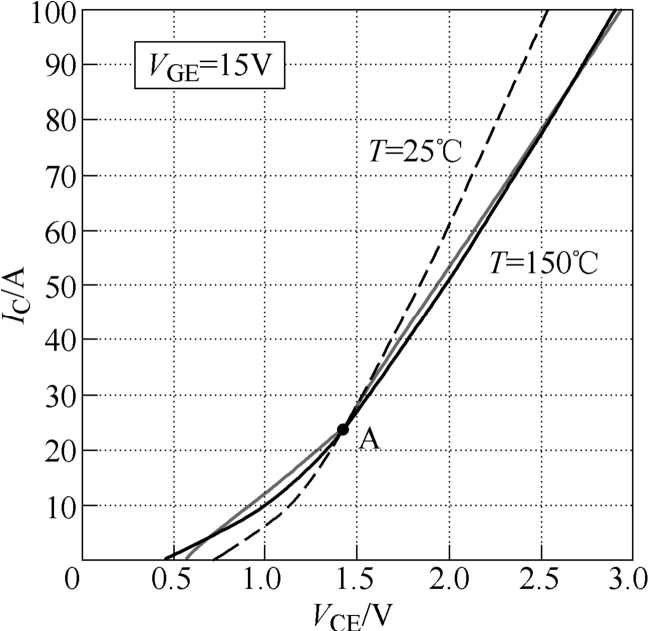
图1 待测IGBT模块的V-I特性曲线
Fig.1 Output characteristics curves of the studied IGBT
文献[10]表明,IGBT的电阻RCE是温度的函数,可通过IGBT V-I特性曲线的斜率dVCE/dIC进行表示。文献[12]通过实验对不同电流IC下IGBT的V-I特性进行了测试,研究表明:在IC一定时,dVCE/dIC与温度呈现出良好的线性关系,即有
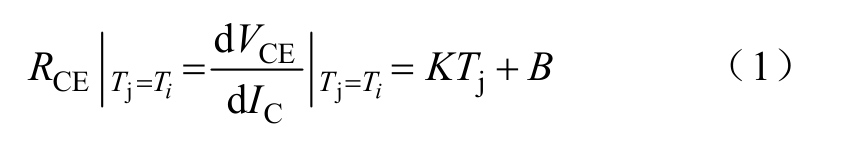
式中,K、B分别为拟合系数。
为兼顾模型的仿真精度与效率,本文以图1中的A点为界,对IGBT V-I特性曲线的正、负温度特性区分别进行线性化拟合。同时为了减小拟合误差,通过最小二乘法对数据手册中V-I特性曲线的数据进行处理。以150℃下的V-I曲线为例,线性化处理后的V-I特性可表示为
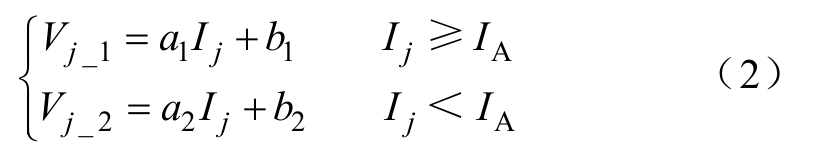
式中,Vj_1、Vj_2分别表示对图1中拐点A以上以及以下部分的拟合曲线;a1、a2、b1、b2为待定系数;IA为拐点A对应的电流值(A);(Ii, Vi)为V-I曲线的坐标,分别对应分段线性化处理后的坐标(Ij, Vj)。基于最小二乘法的目标优化函数为
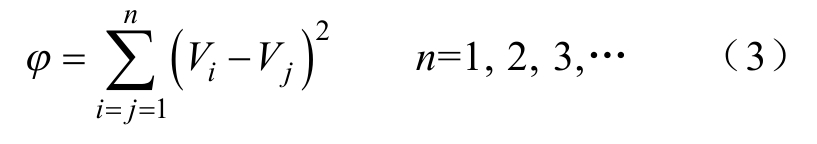
要使线性化拟合的误差最小,应保证目标函数φ 取最小值。此外,考虑到分段线性化处理后的模型收敛性问题,需保证分段函数的连续性,因此还需增加边界条件
将式(1)代入式(2),可得线性化后V-I曲线在任意温度下的VCE与Tj、IC之间的关系为
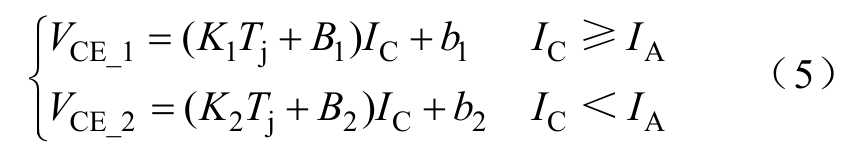
拟合曲线的函数转化示意图如图2所示。拟合后的V-I曲线在任意温度下为连续的分段线性函数,可见实线所体现的电压与电流的关系为一般线性关系,并不符合欧姆定律的正比关系。对于实线上的任意一点,将其与原点进行连线,如图2中虚线所示。其中,虚线与实线的交点体现了IGBT实际的静态特性,而虚线同时可使VCE与IC满足正比关系,即符合欧姆定律的基本算法。定义图2中所有虚线斜率倒数(VCE/IC)的集合为RCE_equ,即IGBT的等效电阻,根据式(5)则有

式中,当IC≥IA时,i=1;反之i=2。
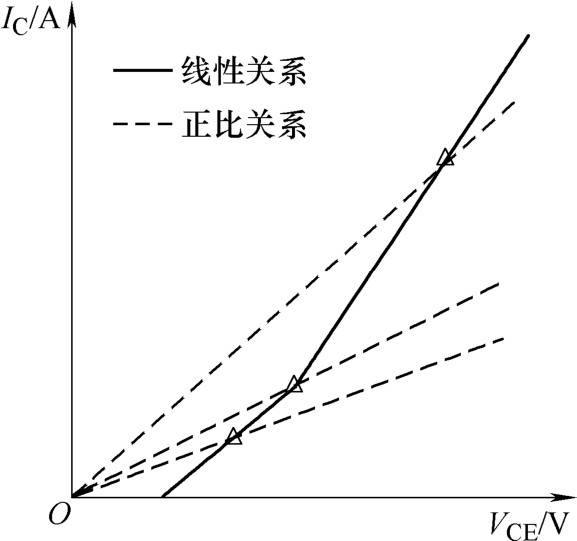
图2 拟合曲线的函数转化示意图
Fig.2 Function transformation of the fitted curves
需要说明的是,IGBT的V-I曲线是通过测量功率端子两端的VCE得到的,因此上述得到的RCE_equ并非是IGBT芯片的等效电阻。IGBT模块的电阻 RCE由功率端子电阻Rcu_p、覆铜层电阻Rcu_m、键丝电阻Rwire、接触电阻Rdie_att以及芯片电阻Rchip五部分组成,当IGBT模块未发生疲劳退化时接触电阻Rdie_att可以忽略[10,13]。同时文献[13]指出,芯片电阻与键丝电阻为非退化IGBT模块总电阻的主要组成部分。本文暂不考虑封装疲劳问题,仅对理想状态下IGBT芯片的等效电阻进行表征,并近似认为IGBT模块的电阻由Rwire与Rchip两部分组成。因此,IGBT芯片的等效电阻Rchip_equ最终可表示为
式中,Rwire为与IGBT芯片互连键丝的总电阻(Ω)。本文所研究的IGBT模块的数据手册中给出了该参数的典型值为0.75mΩ。此外,在对IGBT模块进行三维实体建模后,也可通过FEM[14]对回路中的电阻参数进行提取。
在栅压一定的条件下,式(7)体现了IGBT等效电阻Rchip_equ与导通电流IC以及芯片结温Tj之间的定量关系,符合IGBT实际的静态特性。由于Rchip_equ在数值计算上等于导通压降与导通电流之比,符合欧姆定律的基本算法,因此可应用于FEM仿真。以所研究的斯达1 200V/50A模块为例,图3对式(7)进行了可视化表征。
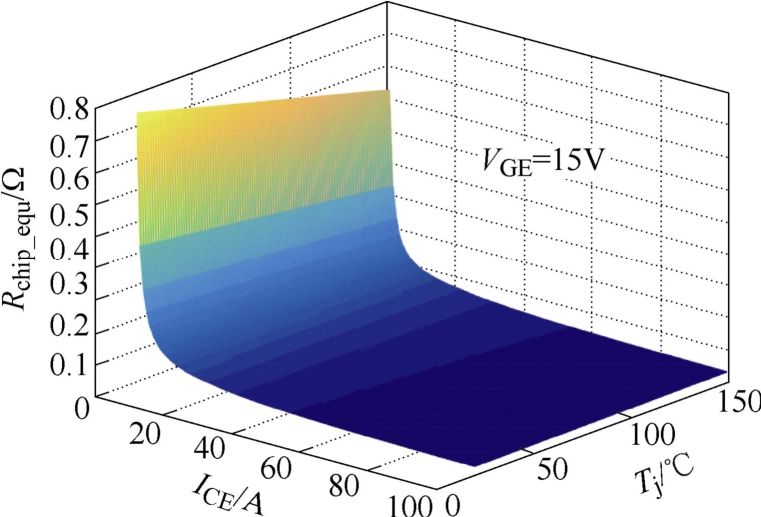
图3 Rchip_equ与Tj、ICE的相互关系
Fig.3 The relationship between Rchip_equ, Tj and ICE
需要说明的是,通过上述方式所建立的等效电阻模型能够对IGBT的静态特性进行较为精确的表征,但却无法表征开关暂态特性。因此,所建立的模型更适用于开关频率较低以及导通损耗占比总损耗较大的工况,如s级的功率循环工况。此外,由图1可知,IGBT正负温度特性拐点以下的部分表现出了明显的非线性化特征,对该区域仅进行单次的线性化拟合将不可避免地带来计算误差。因此,对于需要重点关注拐点电流以下区域的小电流工况而言,可通过连续多段线性化拟合的方式对该区域进行处理,从而减小拟合误差。
2 IGBT电热耦合模型的构建
2.1 待测IGBT模块概述
本文所研究的斯达某型1 200V/50A模块为典型的焊接式封装结构,其内部结构如图4所示。该模块为半桥结构,包括两支IGBT芯片和两支二极管芯片。模块在纵向上有7层结构组成,分别为芯片层、芯片焊料层、上铜层、陶瓷层、下铜层、衬底焊料层以及基板。其中芯片层上表面镀有铝金属薄层;上下铜层通过“直接键合”覆盖在陶瓷层表面;键丝通过超声波焊接与芯片层及上铜层相连。该型模块的主要性能参数见表1。

图4 待测IGBT模块的内部结构
Fig.4 Internal structure of the studied IGBT module
表1 待测IGBT模块的主要性能参数
Tab.1 Main specifications of the studied IGBT module

参 数 数 值 阻断电压VCES/V 1 200 TC=25℃ 100 集电极电流IC/A TC=100℃ 50 栅-发射极电压VGES/V ±20 最高结温Tjmax/℃ 175
2.2 电热耦合模型
IGBT在导通电流时会产生功率损耗,在焦耳热作用下模块的温度会升高,整体上表现为横向及纵向上的温度分布不均衡[15]。材料特性(如热导率、热容等)受温度影响较大,从而会影响温度场的计算。与此同时,用不断更新的温度重新计算芯片的等效电导率,进而得到实时变化的损耗参数,应用FEM对IGBT的电热耦合效应进行求解的基本原理如图5所示。由此可见,IGBT的电气特性与温度有很强的依赖关系,因此只有同时求解传热问题和电问题才能精确求解温度分布与电流分布。

图5 IGBT电热耦合作用机理
Fig.5 Electro-thermal coupling mechanism of IGBT module
将式(7)得到的IGBT芯片等效电阻代入式(8),可得到FEM仿真所需的IGBT芯片等效电导率σ。在FEM仿真中,首先通过给定的初始条件对电流场进行求解,得到IGBT的功率损耗Qj,如式(9)所示[7]。在考虑内热源的影响时,可进一步通过式(10)所示的偏微分方程求解温度分布问题[16]。
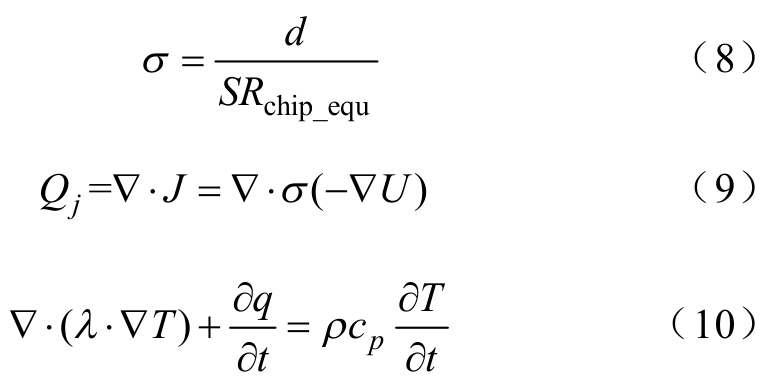
式中,J为电流密度(A/m2);U为电动势(V);ρ 为密度(kg/m3);q为热流量(W/m2);cp为比热容(J/(kg·℃));λ 为热导率(W/(m·K));d、S分别为IGBT芯片的厚度(m)与面积(m2)。
处于稳态下的温度分布是一种理想情况,IGBT更多工作在外部电载荷不断变化的工况中,此时对温度的求解也是一个动态求解问题,这依旧可以通过FEM得到解决,但是会对仿真的收敛性和效率产生明显影响[16]。为了兼顾仿真计算的精度与效率,对模型进行合理的简化是十分必要的,因此本文在构建IGBT的等效电阻时并未进行过于复杂的分段线性化处理,同时在对IGBT的三维实体建模时也忽略了一些诸如倒角、边弧等对结果影响较小的 细节。
FEM是一种基于材料与结构的数值解法,模型的结构与材料参数对仿真的精确计算非常重要[17]。为保证模型结构参数的准确性,本文通过扫描电子显微镜(Scanning Electron Microscope, SEM)对纵向解剖后的IGBT模块各层厚度参数进行了精确提取,如图6所示。待测模块的各层材料及厚度参数见表2。同时,在材料属性定义时,考虑了硅、铝、铜等材料热导率及热容的温度敏感性[18]。

图6 通过SEM提取IGBT的各层厚度参数
Fig.6 Extraction of thickness parameters for the IGBT through SEM
表2 待测IGBT模块的材料及厚度参数
Tab.2 Layer composition and thickness of the studied IGBT module
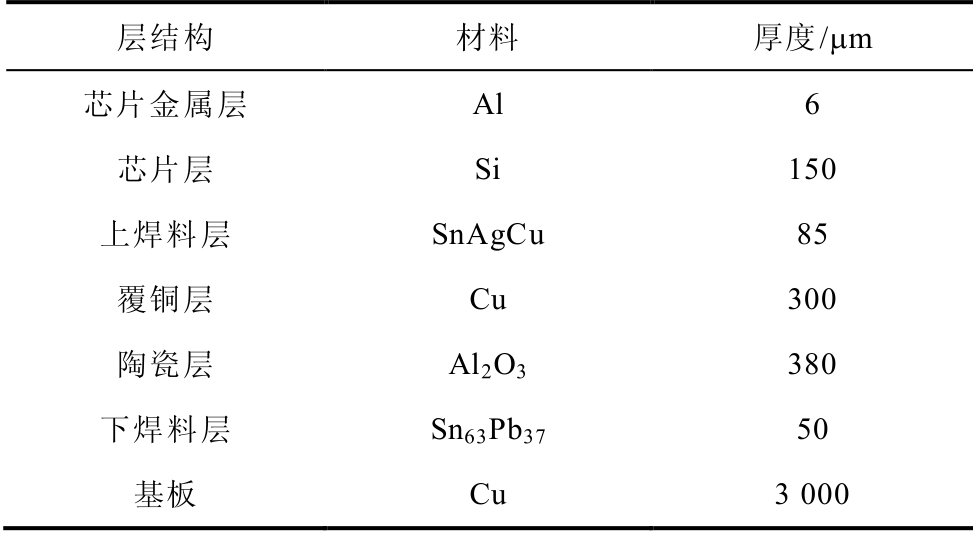
层结构 材料 厚度/μm 芯片金属层 Al 6 芯片层 Si 150 上焊料层 SnAgCu 85 覆铜层 Cu 300 陶瓷层 Al2O3 380 下焊料层 Sn63Pb37 50 基板 Cu 3 000
为验证上文所述建模方法的有效性,通过有限元仿真软件COMSOL Multiphysics构建了待测IGBT模块的电热耦合模型,网格划分及仿真条件如图7所示。设置IGBT模型的集电极端子为电流终端,用于表征注入电流信号。设置发射极端子为接地。仿真的电流载荷为持续时间为10ms的变电流,通过实验进行采集。

图7 电热耦合仿真条件设置
Fig.7 Conditions setting for electro-thermal coupling simulation
为便于对待测IGBT的结温变化进行实时观测,对后续实验所用的IGBT模块进行了拆封,并去除了模块上表面附着的硅胶。为保证仿真与实验的一致性,通过换热系数h模拟芯片与空气的对流传热[8]。在实际运行中,通常需要在IGBT模块的基板处均匀涂抹导热硅脂并连接散热器,进而提高器件的散热能力。在有限元仿真中可通过设置换热系数对散热器进行等效处理,可通过开展稳态实验对该参数进行标定[19]。需要说明的是,在本文仿真与实验的时间尺度(10ms)内,散热器对IGBT结温变化的影响较小,因此对基板下表面设置的热边界条件为恒定室温(26.5℃)。
3 仿真分析与实验验证
为了对所提出的建模方法进行验证,同时检验所建模型对电流载荷动态变化的响应能力,设计了电流变化的单脉冲实验,实验装置如图8所示。实验电路为如图9所示的半桥逆变单元,其中Ls为回路杂散电感,R为感性负载。实验在室温下进行。在被测IGBT器件(DUT)的栅-发射极接入+15V的电压,通过栅极驱动信号控制DUT的导通时间。通过FLIR SC7700型高速红外热像仪与罗氏线圈分 别对IGBT的结温与导通电流进行实时采集与记录。为减小热辐射引起的成像误差,通过哑光黑漆对IGBT模块的表面发射率进行了统一,并将红外摄像仪的表面发射率对应设置为0.97,同时将采样频率设置为1 000Hz。为满足红外热像仪的采样要求,将驱动信号的脉宽设置为10ms。

图8 实验测试装置
Fig.8 Experimental testing setup
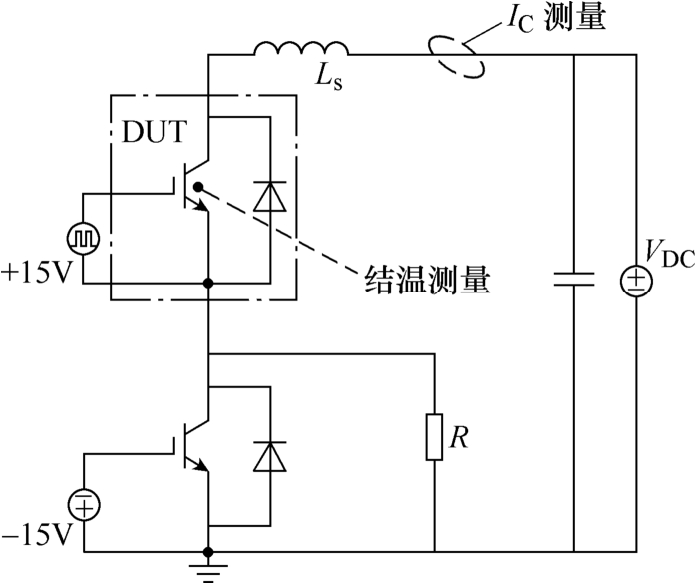
图9 实验测试电路
Fig.9 Schematic of the experimental circuit
实验测试结果如图10所示,在预设的实验工况下,IGBT的导通电流实时变化,最高峰值为196A,约为额定电流的4倍。由于DUT为0电流开通,因此不会产生开通损耗,而相对于10ms的导通时间而言,关断损耗并不会对IGBT的结温变化产生过大的影响。需要说明的是,VCE的在线实时监测需要测量设备同时满足量程以及响应速度的要求,并且需要实现对数据的实时存储。由于实验室测量手段的限制,未能对IGBT导通阶段内的饱和压降进行有效采集。因此,本文通过IGBT的结温变化对所建立的模型进行了验证。

图10 实验结果
Fig.10 Results of the experiment
为保证仿真与实验条件的一致性,将实验测量得到的电流数据作为电热耦合仿真的输入载荷,按上文所述的设置进行了瞬态电热耦合仿真。图11为IGBT在变电流载荷下的饱和压降仿真结果。图12为IGBT导通第7ms时芯片上表面温度分布的仿真与实验对比。同时,以IGBT芯片上表面几何中心位置处的温度为参量,将仿真与实验得到的芯片温升情况进行了比较,如图13所示。
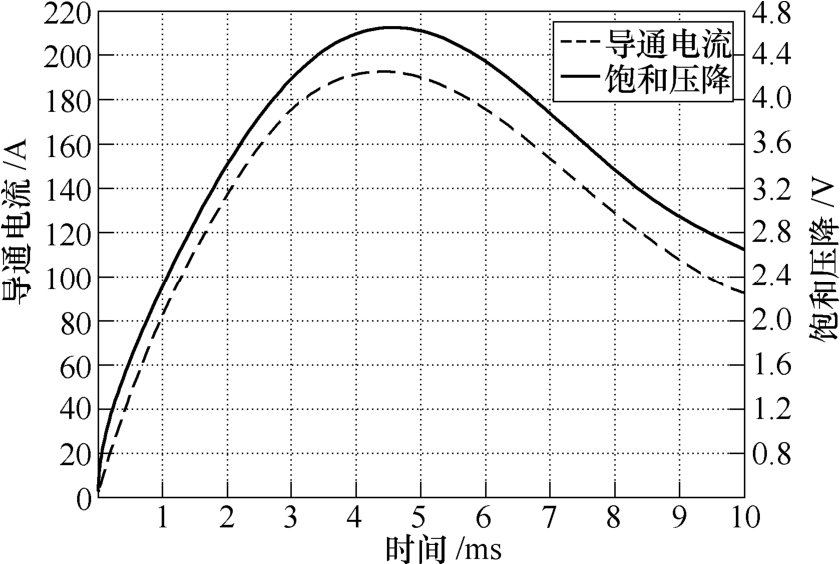
图11 仿真的导通电流与饱和压降变化曲线
Fig.11 The curves of IC and VCE in the electro-thermal simulation

图12 仿真与实验的温度分布对比(t =7ms)
Fig.12 Temperature distribution comparison between simulation and experiment (t =7ms)

图13 IGBT芯片上表面几何中心处的结温变化曲线
Fig.13 Temperature variation curves at surface geometric center on IGBT chip
由图11可知,IGBT在导通时刻的饱和压降初始值为0.817V,导通后电流迅速增大并进入V-I曲线的正温特性区。总体上IGBT的饱和压降与导通电流呈现了类似的变化趋势,而变化趋势的差异主要是由温度导致的,这种差异会随着电流的增大而变得愈加明显。仿真的结果符合IGBT实际的电气特性。
由图12的温度分布结果可知,在IGBT导通第7ms时,高温区主要集中在IGBT芯片的有源区,且有源区边缘位置处温度梯度较大。对键丝而言,除了与芯片互连的焊点外,键丝起拱处的温度要明显低于芯片温度。整体看来IGBT呈现出了明显的 温度分布不均衡。这是由于在导通时间为10ms的时间尺度内,功率损耗产生的热量并未得到有效的向外传递,此时的温升主要由芯片与键丝的自热导致,而相比于芯片而言,键丝电阻较小,因此焦耳热效应不明显。在第7ms时,实验测量与仿真模拟得到的芯片上表面几何中心处的结温分别为81℃与78.6℃,误差约为2.96%。
图13的温升对比结果也体现了仿真与实验具有良好一致性。这表明所建立的电热模型能对电流载荷动态变化下的IGBT的动态温度分布特性进行准确表征。同时,由图11与图13的结果可以发现,芯片温度的变化相对电流和饱和压降存在2ms左右的延迟,这是由于温度采集点位于IGBT芯片上表面,而相比于电的时间尺度,热的时间尺度较大(ms级),两者在时间上的延迟也较好反映了电与热在时间尺度上的差异。
4 结论
本文开展的工作:通过最小二乘法对IGBT的V-I特性曲线进行了分段线性化拟合,提出了IGBT等效电阻的概念。将建立的IGBT等效电阻模型应用于有限元仿真,进一步构建了IGBT的电热耦合模型,最后通过变电流的单脉冲实验证明了建模方法的有效性与准确性。所提出的等效电阻建模方法可以定量、准确地表征IGBT的V-I特性,并应用于电流连续变化的工况。另外,由于符合欧姆定律,该等效电阻模型还适用于COMSOL、ANSYS等有限元软件的电流场计算。
未来将要开展的工作:由于实验测量手段的限制,本文并未实现对变电流工况下IGBT导通压降VCE的有效采集,因此在实验验证时采用了通过结温变化进行间接验证的方式。针对此问题,后续将进一步设计相应的VCE数据采集系统,以完善对所提建模方法的验证。
[1]马伟明. 电力电子在舰船电力系统中的典型应用[J]. 电工技术学报, 2011, 26(5): 1-7. Ma Weiming. Typical applications of power elec- tronics in naval ship power system[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 1-7.
[2]唐勇, 汪波, 陈明, 等. 高温下的IGBT可靠性与在线评估[J]. 电工技术学报, 2014, 29(6): 17-23. Tang Yong, Wang Bo, Chen Ming, et al. Reliability and on-line evaluation of IGBT modules under high temperature[J]. Transactions of China Electro- technical Society, 2014, 29(6): 17-23.
[3]刘宾礼, 罗毅飞, 肖飞, 等. 基于传热动力学作用特征的IGBT结温预测数学模型[J]. 电工技术学报, 2017, 32(12): 79-87. Liu Binli, Luo Yifei, Xiao Fei, et al. Investigation into a junction temperature prediction mathematical model of IGBT based on the characteristics of thermal dynamics[J]. Transactions of China Elec- trotechnical Society, 2017, 32(12): 79-87.
[4]Gao Bing, Yang Fan, Chen Minyou, et al. Thermal lifetime estimation method of IGBT module considering solder fatigue damage feedback loop[J]. Microelectronics Reliability, 2018, 82(6): 51-61.
[5]Patel A, Joshi S, Chandwani H, et al. Estimation of junction temperature and power loss of an IGBT used in VVVF inverter using numerical solution from data sheet parameter[J]. International Journal of Computer Communication and Information System, 2010, 26(2): 17-22.
[6]Deng Erping, Zhao Zhibin, Lin Zhongkang, et al. Influence of temperature on the pressure distribution within press pack IGBTs[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 6048-6059.
[7]Gao Bing, Yang Fan, Chen Minyou, et al. A temper- ature gradient-based potential defects identification method for IGBT module[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2227-2242.
[8]Özkol E, Hartmann S, Pâques G. Improving the power cycling performance of the emitter contact of IGBT modules: implementation and evaluation of stitch bond layouts[J]. Microelectronics Reliability, 2014, 54(12): 2796-2800.
[9]Riccio M, Falco G D, Maresca L, et al. 3D electro- thermal simulations of wide area power devices operating in avalanche condition[J]. Microelectronics Reliability, 2012, 52(9-10): 2385-2390.
[10]Eleffendi M A, Johnson C M. In-service diagnostics for wire-bond lift-off and solder fatigue of power semiconductor packages[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 7187-7198.
[11]Singh A, Anurag A, Anand S. Evaluation of Vce at inflection point for monitoring bond wire degradation in discrete packaged IGBTs[J]. IEEE Transactions on Power Electronics, 2016: 1-1.
[12]罗毅飞, 汪波, 刘宾礼, 等. 基于电压对电流变化率的IGBT结温变化机理及监测方法[J]. 高电压技术, 2017, 43(1): 38-43. Luo Yifei, Wang Bo, Liu Binli, et al. Junction temperature variation mechanism and monitoring method of IGBTs based on derivative of voltage to current[J]. High Voltage Engineering, 2017, 43(1): 38-43.
[13]Pedersen K B, Kristensen P K, Popok V, et al. Degradation assessment in IGBT modules using four-point probing approach[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2405-2412.
[14]Wu Rui, Reigosa P D, Iannuzzo F, et al. A comprehensive investigation on the short circuit performance of MW-level IGBT power modules[C]// European Conference on Power Electronics & Applications, Geneva, 2015: 1-6.
[15]Wu Rui, Iannuzzo F, Wang H, et al. Electro-thermal modeling of high power IGBT module short-circuits with experimental validation[C]//Annual Reliability and Maintainability Symposium (RAMS), Palm Harbor, 2015: 1-7.
[16]Pedersen K B, Pedersen K. Dynamic modeling method of electro-thermo-mechanical degradation in IGBT modules[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 975-986.
[17]Ghimire P, Pedersen K B, Vega A R D, et al. A real time measurement of junction temperature variation in high power IGBT modules for wind power converter application[C]//8th International Con- ference on Integrated Power Systems, Nurembery, 2014: 1-6.
[18]Lutz J, Schlangenotto H, Scheyermann U, et al. Semiconductor power devices, physics, characteri- stics, reliability[M]. Springer-Verlag, Berlin Heidelberg, 2011.
[19]Hartmann S, Bayer M, Schneider D, et al. Obser- vation of chip solder degradation by electrical measurements during power cycling[C]//Inter- national Conference on Integrated Power Electronics Systems, 2010: 1-6.