0 引言
簧片式继电器广泛应用于铁路信号系统和船舶电力控制系统。在应用中，继电器将不可避免地受到外界环境的振动和冲击干扰。尤其是当外界振动频率与系统固有频率相近时，系统会产生共振，造成触点误动作甚至使其机械结构疲劳损坏[1]。因此，研究簧片式继电器的固有振动特性具有重要意义。
此前，国内外对继电器及相关开关电器的振动特性已进行了广泛研究，对振动问题的分析方法也不断完善。在初期研究阶段，许多学者将开关电器的触簧系统进行等效简化，利用单自由度振动理论进行计算分析，得到了振动极限加速度等基本的抗振性能指标[2-3]。随着多领域的相互融合，从材料力学角度将触簧振动问题类比为梁弯曲问题，为振动分析提供了新的思路[4-6]。计算机技术的发展开拓了振动计算方法，应用有限元法对开关设备振动问题进行研究，进一步完善了设计基础和理论依据[7-9]。但在现有文献中，大多以频域的分析方法来处理振动问题，且通常使用线性弹簧单元来等效触点接触，缺少用较新的非线性算法对簧片式继电器的固有振动特性进行深入研究。
本文充分考虑簧片式继电器的结构特点，根据梁弯曲理论建立了触簧系统的振动分析模型。利用有限元仿真软件选择了较新的Bathe复合时间积分算法对簧片式继电器的固有振动特性进行了定频时域计算分析，最后通过振动试验结果与仿真数据相对比，验证了本文分析方法的有效性。
1 触簧系统数学模型
1.1 物理模型分析
本文以某型号的铁路信号继电器为研究对象，三维实物如图1所示。
图1 铁路信号继电器
Fig.1 Railway signal relay
簧片式继电器由于触簧系统具有刚柔耦合的特点，易于发生共振，其中又以常闭触点的抗振性最弱。继电器几何模型如图2所示。
图2 继电器几何模型
Fig.2 Geometry model of relay
继电器工作在释放状态时，常闭触点在反力弹簧提供的接触压力下发生接触。在本文中，采用推动力来替代反力弹簧作用，使常闭触点闭合。之后通过在底座施加激励来完成振动仿真过程。
1.2 簧片弯曲分析
在继电器底座受到振动影响时，继电器簧片会随之发生弯曲。由图2可见，簧片底部固定在底座，上部可以在一定区域内自由摆动，根据振动力学中梁弯曲理论[10]，有两种典型结构：铁木辛柯梁和欧拉-伯努利梁。对于梁的长度和宽度比值较小的铁木辛柯梁来说，簧片的剪切变形和转动惯量对弯曲的分析计算结果影响很大，不能忽略这两个变量对计算结果的影响。而簧片式继电器的长度和宽度比值较大，所以铁木辛柯梁结构并不适用。因此，本文将采用欧拉-伯努利梁结构对簧片的弯曲变形进行建模研究。
以动簧片为例，考虑实际工作状态的簧片计算模型如图3所示。选取簧片x点处截面的一段微分单元dx，设簧片密度为ρ，横截面面积为A。
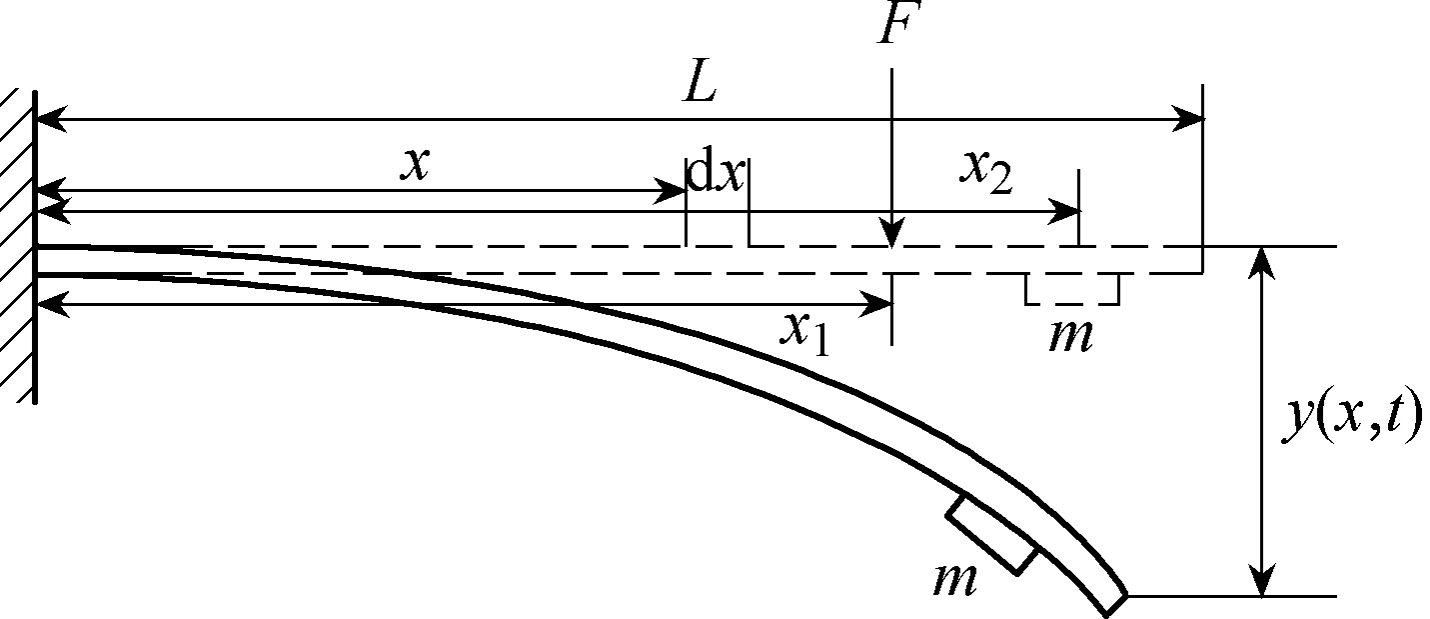
图3 簧片计算模型
Fig.3 Calculation model of reeds
当弯曲至平衡状态时，微元在竖直方向上受力平衡，可得
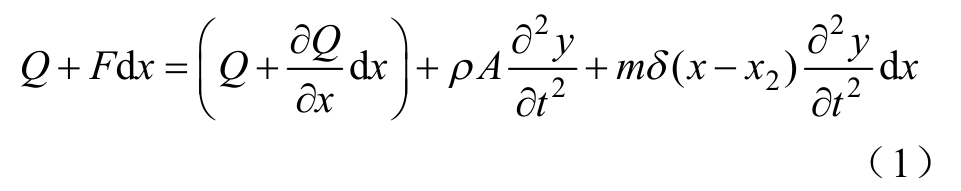
式中，Q为固定端剪切力；M为弯矩；F为推动力；m为触头质量；δ 为狄拉克函数。
微元力矩平衡方程可表达为
考虑截面挠度与弯矩的关系[11]，并将式（2）代入到式（1）中，得到簧片弯曲状态方程
式中，E为簧片材料弹性模量；I为簧片截面对中性轴的惯性矩。
本文簧片式继电器中的簧片为等截面结构，则由式（3）可得簧片动力学方程为
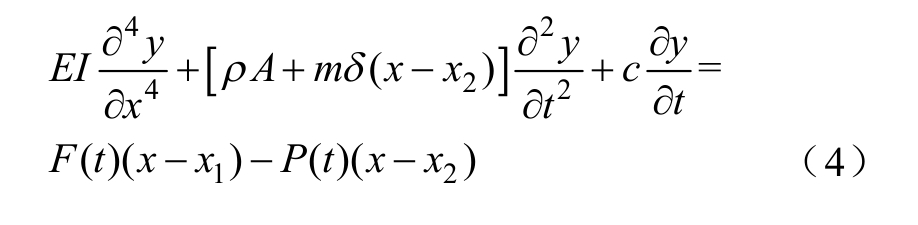
式中，P(t)为触点间接触力。
1.3 固有振动参数计算
固有振动频率只与系统结构有关，不考虑外力作用和簧片结构阻尼系数，则式（4）可转化为
将空间与时间解耦，令 y(x,t)=Y(x)b sin(ω t+φ)，其中 ()Yx为振型函数，将 (,)yxt代入式（5）中得
令
则特征方程为
求解特征方程，将 Y(x)函数的通解代入y(x,t)中得
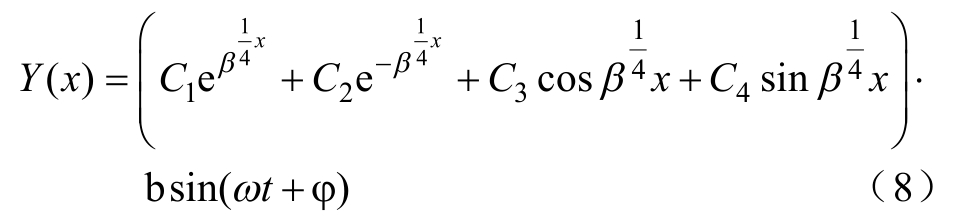
式中，C（ii=1,2,3,4）及ω由边界条件和振型条件确定；常数b、φ 由初始化条件确定。
在触簧系统中，底座与簧片的连接处为固定端，即在x=0时，Y(x)=Y ′(x)=0。
图2中，簧片右端为自由端，即在x=L时，
为限位片开口宽度。
1.4 触点接触分析
簧片式继电器的触点材料为AgCdO，接触面光滑，可忽略摩擦力，只传递法向压力。两触点表面形状为圆形抛物面，接触形式是点接触或面接触，在受到微小作用力后，它们会在最初的接触面附近形成一个有限的接触区域，且刚体接触的两物体互不穿透[12-13]。通过以上分析可知，该继电器触点接触力P(t)可以采用赫兹接触理论进行分析。
由于外部振动的作用，P(t)必将随之变化。因此，可用接触力P(t)的值表征触点间的接触状态[14]。当 P(t)≤ 0时，可认为触点处于断开或抖断状态。
相对于动触点来说，静触点只承受动触点传递的接触力，则静触点运动方程可写为
式中，y2、c2、k2和m2分别是静触点的位移、阻尼、刚度和质量。根据赫兹接触模型，由文献[15]可知， 接触刚度
P0为初始接触压力，k0为 与材料、尺寸相关的系数。
1.5 非线性求解算法选择
振动非线性动力学微分方程为
式中，M为质量矩阵；C为系统阻尼矩阵；K为刚度矩阵；u(t)为系统位移矢量；
为对象速度值；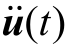
为对象加速度值；F为外界作用力[16]。
继电器受到外部机械振动时，振动激励F会通过底座传递到簧片使其发生形变，触点接触力随着簧片形变而不断变化。因此，继电器触簧系统具有高度的非线性，可采用隐式直接时间积分法。目前常用的隐式直接时间积分法有Newmark法、HHT法和Bathe复合积分法[17]。Bathe复合时间积分算法对求解非线性动力接触问题具有较高的稳定性和可靠性。因此，本文采用Bathe复合时间积分算法求解触簧系统的固有振动特性，算法流程如图4所示。
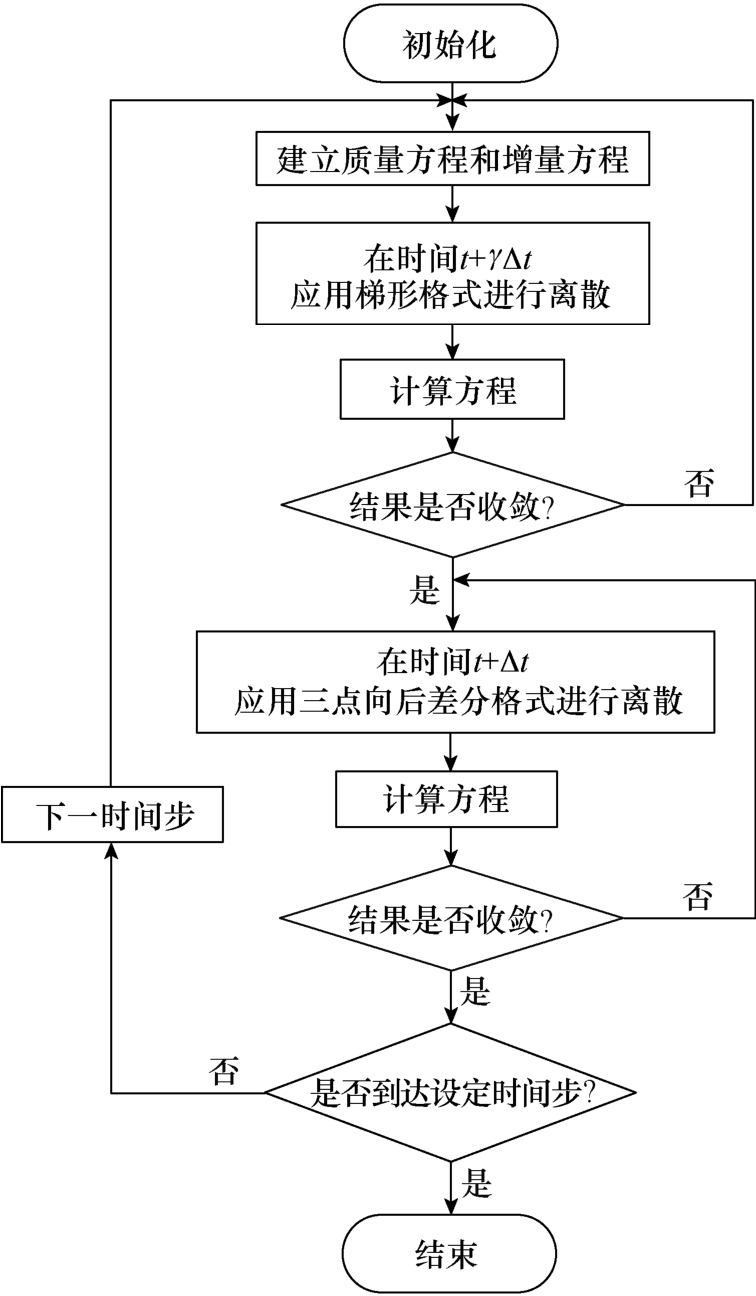
图4 Bathe求解流程
Fig.4 Solving flow chart of Bathe
2 振动仿真分析
2.1 模态仿真结果
几何模型作为求解的边界条件之一，建模的准确与否直接关系到仿真结果的准确度[18]，对几何模型进行模态分析可以得到系统基本的振动特性，如系统的固有频率和振型等，这有利于在后续的动力学分析中设置合理的仿真参数。
由于继电器触簧系统具有高度非线性的特性，因此采用六面体网格进行划分和求解计算。六面体网格单元对于接触非线性的有限元计算有良好的收敛性。
为了计算簧片式继电器触簧系统的固有频率和模态振型，需先对模型进行前处理，如设定材料属性等参数[19]。之后将静力学分析步添加到分析模块中，在动簧片上施加预紧力使触点发生初始接触，利用静力分析结果的接触状态导入至模态分析步中。得到触簧系统的前2阶固有频率和振型分布，见表1和图5、图6所示。
表1 模态分析
Tab.1 Modal analysis
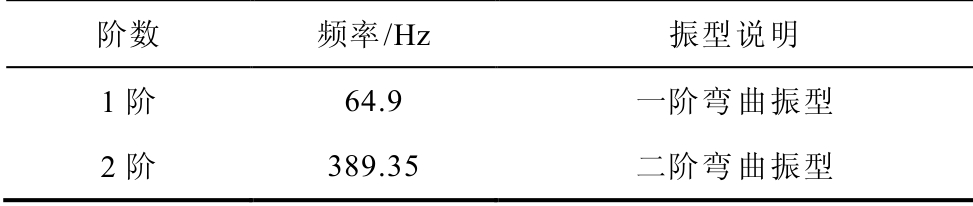
阶数 频率/Hz 振型说明 1阶 64.9 一阶弯曲振型 2阶 389.35 二阶弯曲振型
图5 触簧系统一阶模态振型
Fig.5 First order mode shape of spring system
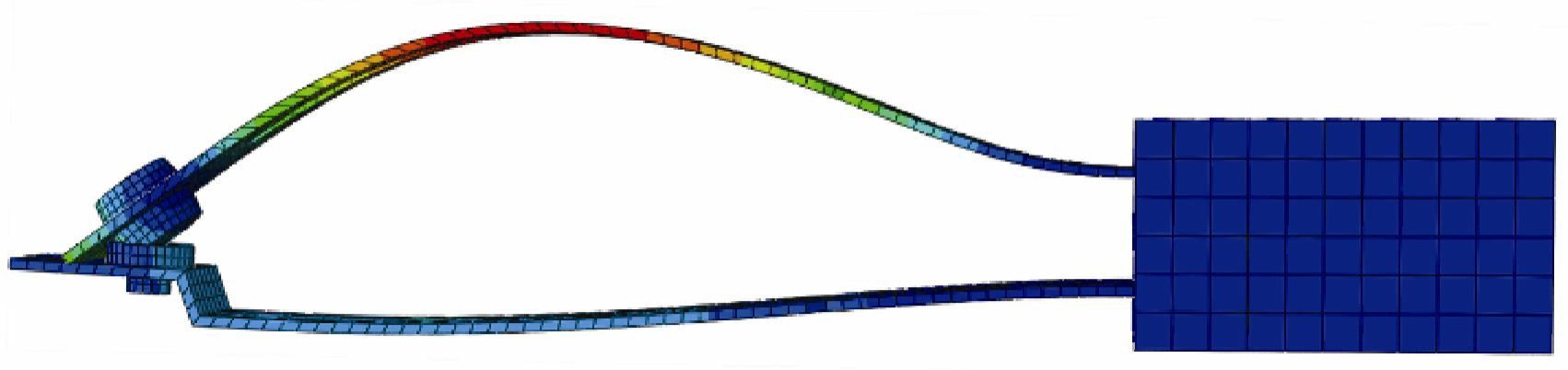
图6 触簧系统二阶模态振型
Fig.6 Second order mode shape of spring system
2.2 限位条件下振动仿真
在簧片式继电器实际产品中，大部分产品都会对簧片进行位移限制。本文模型根据限位片实际开口宽度和动簧片运动行程，采用四个小方块等效限制两根簧片的运动范围，限制方式示意图如图7 所示。
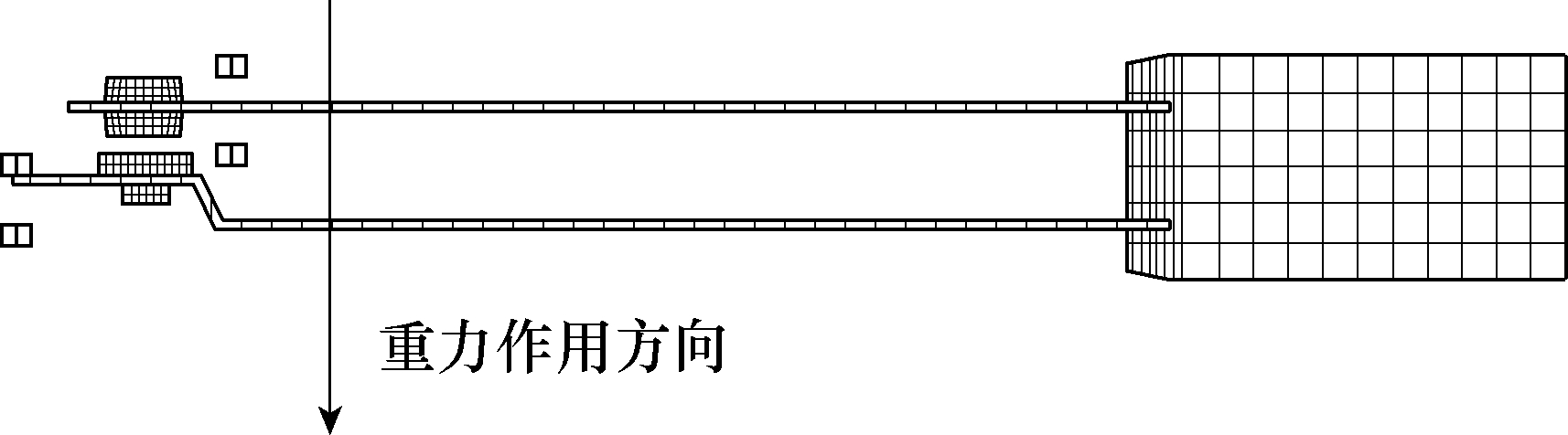
图7 簧片位移等效限制
Fig.7 Equivalent restriction of reed displacement
簧片式继电器的簧片较长，当继电器安装方向与簧片动作方向相同时，触点质量对簧片的力矩也应该在考虑范围。因此，在此方向上分析固有振动时需考虑重力的影响。在充分考虑实际固有振动条件后设置振动频率为64.9Hz（一阶固有频率），对加速度分别为0.5g、2g、4g（g=10m/s2）的三种工况进行瞬态动力学分析。
2.3 接触力响应分析
在动力学分析步中，选择动静触点间接触力为历程输出，得到在3个工况下的触簧系统接触力曲线如图8和图9所示。
图8 工况1（0.5g）触点接触力曲线
Fig.8 Contact force curve of condition 1 (0.5g)
图9 工况2(2g)、工况3(4g)触点接触力曲线
Fig.9 Contact force curves of condition 2 (2g) and 3 (4g)
由图8可知，在一阶固有频率下，工况1的最大接触力为0.135mN，最小接触力为0.074mN。接触力波形具有明显的下波峰，这是因限位片对簧片的限制作用导致，此时动簧片运动受限，而静簧片仍可摆动一小段距离。逐步提高振动加速度，使最小接触力刚好为零时，可得一阶固有频率下触簧系统的振动加速度极限为1.2g。由图9可知，由于工况2和工况3加速度已超过振动极限，触点接触力产生抖断并呈现一定规律性，两种工况下的抖断周期约为0.015s。
2.4 静簧片位移响应分析
在振动过程中，簧片的位置也将随之不断地发生变化。在有限元软件中，设置静簧片顶端下表面一节点位移与最下方限位块上表面一节点的位移值为输出参数，并将两位移值求差，得到静簧片与下限位块的相对位移曲线如图10所示。
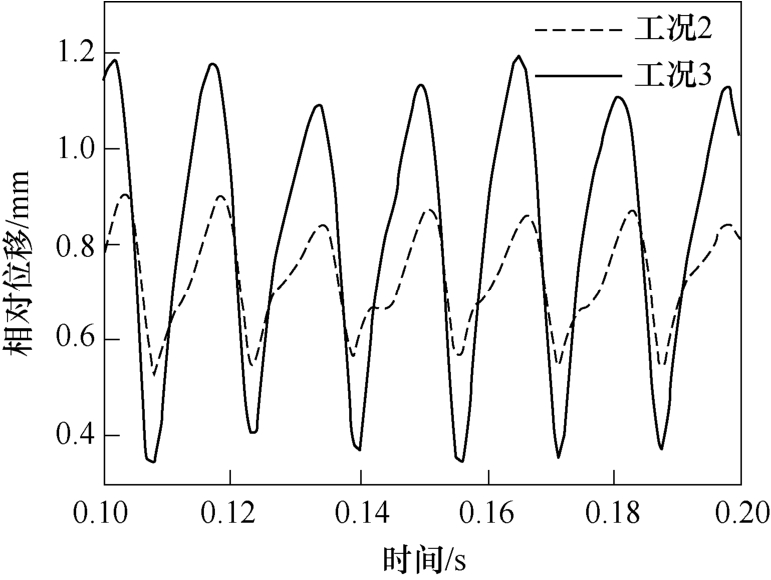
图10 有重力静簧片位移曲线
Fig.10 Displacement curves of static reed with gravity
不考虑重力的影响作用，得到在工况2和工况3时无重力因素下的静簧片相对位移曲线如图11所示。
图11 无重力静簧片位移曲线
Fig.11 Displacement curves of static reed without gravity
提取图10和图11中曲线的特性参数，见表2。
表2 曲线特性参数
Tab.2 Parameters of curve characteristic（单位: s）
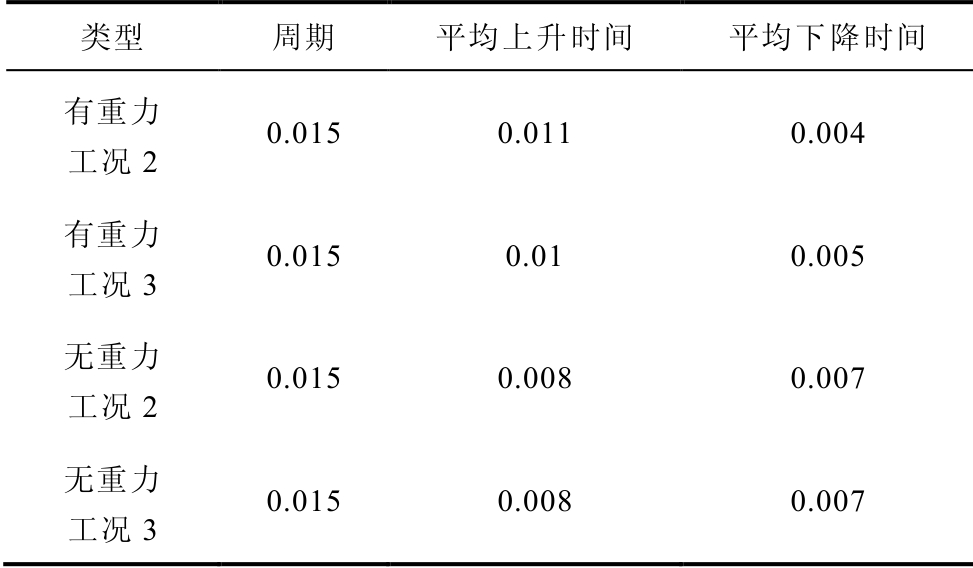
类型 周期 平均上升时间 平均下降时间 有重力 工况2 0.015 0.011 0.004 有重力 工况3 0.015 0.01 0.005 无重力 工况2 0.015 0.008 0.007 无重力 工况3 0.015 0.008 0.007
由表2可知，由于触簧系统受到重力作用的影响，静簧片位移曲线的平均上升时间与无重力状态相比有所增加，平均下降时间减少，静簧片的恢复速度加快。
2.5 簧片应力响应分析
触簧系统在预紧力加载完成时刻的应力场分布如图12所示。模型的最大应力曲线需要先编写脚本文件，再将模型中每一帧的最大应力值提取出来，得到簧片最大应力曲线，如图13所示。
图12 预紧力作用下的应力分布云图
Fig.12 Nephogram of stress distribution with preload
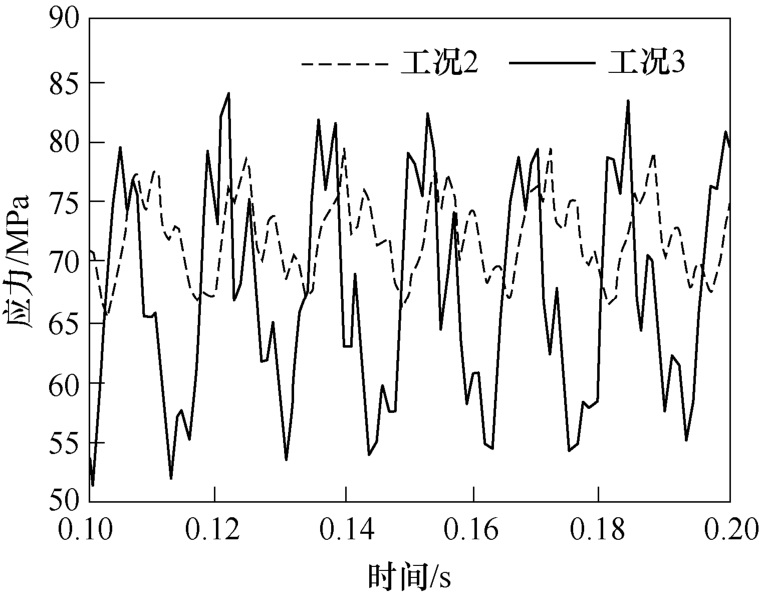
图13 簧片最大应力曲线
Fig.13 Maximum stress curves of reed
由图12可知，当预紧力加载结束，且簧片未受到振动作用时，在动簧片下端开口处为最大应力位置。通过图13可知，在工况2和工况3中的等效应力最大值分别为77.91MPa和84.3MPa，小于簧片材料的屈服极限为193MPa。
3 振动试验分析
3.1 试验设备
试验采用航天希尔G系列振动台，振动台正弦推力为9 800N；频率范围为2～5 000Hz，持续位移为51mm，最大加速度为981m/s2。根据振动试验标准进行试验设计，并使用高速相机和传感器对振动过程进行拍照和采集振动信息[20]。试验设备如图14所示。
图14 试验设备
Fig.14 Test equipments
3.2 固有频率测量
首先对继电器触簧系统进行一阶固有频率测量试验，设置振动台参数为2g加速度，扫频范围为5～100Hz，振动方向为继电器触簧系统运动方向。试验中使用监测设备实时监测触点接触状态和接触压降，扫频过程中八组常闭触点接触压降数据如图15所示。
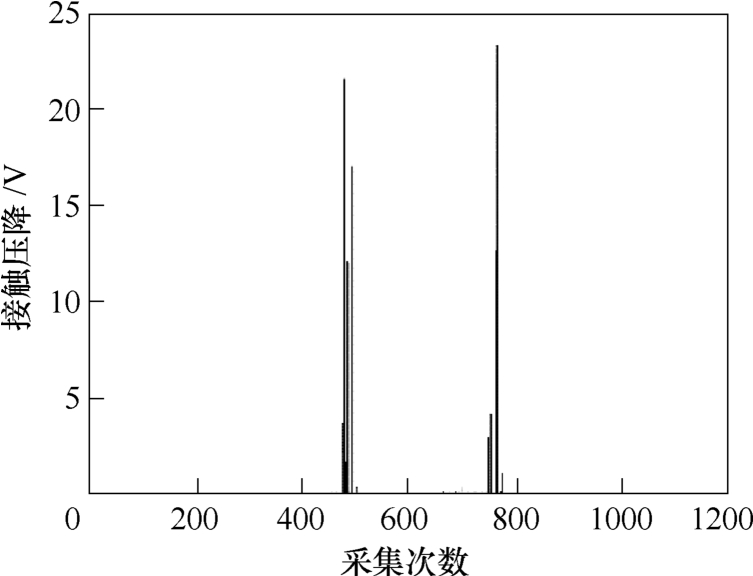
图15 常闭触点接触压降
Fig.15 Contact voltage of closed contacts
由图15可知，在扫频周期中触点发生两次抖断。逐渐缩小扫频范围，最终测得继电器触簧系统一阶固有频率为68Hz，二阶固有频率为340Hz。仿真数据与试验结果相比，一阶频率较为接近，而由于有限元模型为理想边界条件，刚度比实际高，且在高频下更为明显，因此仿真结果的二阶固有频率偏大。
3.3 定频振动分析
测量到继电器触簧系统的固有频率后，在68Hz频率下进行定频振动试验，加速度分别设置为2g和4g，得到触点接触压降曲线，如图16所示。
由图16可知，簧片在2g加速度下振动剧烈，触点接触不良，发生严重抖断使触点间电压抖升，4g加速度下抖断更为严重。通过逐帧分析高速相机拍摄的视频，试验振型结果与仿真振型结果基本一致，振动过程截图画面如图17所示。
3.4 静簧片行程测量
图16 2g和4g工况下的常闭触点接触压降
Fig.16 Contact voltage of closed contacts under 2g、4g
图17 振动过程视频截图
Fig.17 Video captures of vibration process
继电器振动过程中直接测量簧片的运动行程较 为困难。簧片式继电器的簧片较长，宽度较窄，使用传感器的方式不仅难以安装，又会对系统质量产生影响，因此本文采用间接测量方式。
测量之前需要对测量系统进行坐标标定，并计算图像与实际距离的换算关系。之后在稳定振动过程中，使用高速相机拍摄继电器簧片的振动视频[21]。视频处理后得到继电器常闭触点中静簧片时间-相对位移曲线，如图18所示。
由于在测量过程中振动台带动试件运动，拍摄的角度也随之变化，测量结果与实际值存在一定误差，现阶段只能对静簧片的大致位移规律进行分析。由图18可知，在2g和4g振动加速度下，静簧片振动周期均约为0.015s，2g加速度下平均上升时间约 为0.011s，4g加速度下平均上升时间约为0.01s。静簧片相对位移曲线的试验结果与仿真数据的运动规律基本相同，近似为正弦，且运动周期和平均上升时间、平均下降时间基本一致。
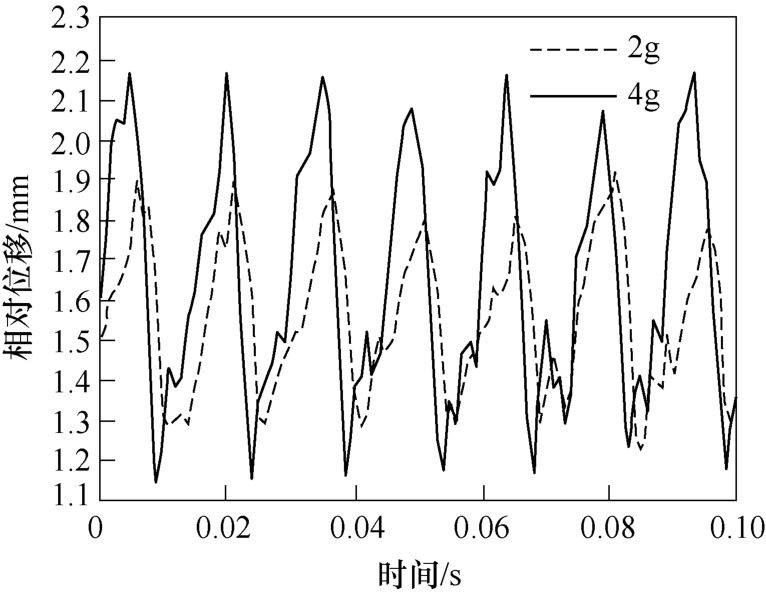
图18 静簧片时间-相对位移曲线
Fig.18 Time travel curves of static reed
4 结论
通过对簧片式继电器的固有振动特性进行仿真和试验分析，结论如下。
1）本文首先基于梁弯曲理论建立了簧片式继电器触簧系统振动分析模型。之后通过有限元软件进行了振动仿真计算，得到了触簧系统的一、二阶固有频率和一阶共振频率下的静簧片时程曲线。仿真数据与试验结果证明了本文分析方法的正确性。
2）仿真和试验表明，簧片式继电器一阶共振时的静簧片时程曲线呈近似正弦的形式，且因重力作用，静簧片恢复速度加快。因此，在继电器的实际应用中，也应考虑其安装方向对抗振性能的影响。
3）限位片限制了簧片的摆动，使触簧系统可以减缓共振的幅值。并且由于动静簧片限位位置不同，当静簧片停止运动时，动簧片依旧可以进行一定程度的摆动，产生接触力突变。
4）在固有频率下，虽会产生严重的抖断，但由于限位作用，簧片摆动程度可控制在一定范围内，簧片所承受的应力低于屈服极限，簧片不会产生塑性形变。
[1]孙宏杰, 曹云东, 刘炜, 等. 铁路信号继电器触簧系统振动特性的仿真研究[J]. 电器与能效管理技术, 2015(6): 15-19. Sun Hongjie, Cao Yundong, Liu Wei, et al. The vibration characteristic simulation study of contact spring system for the railway signal relay[J]. Electriacal & Energy Management Technology, 2015(6): 15-19.
[2]Chambega D J. Qualitative analysis on the effect of external vibrations on the performance of relays[C]// Proceedings 1996 4th IEEE AFRICON Conference Part2, Stellenbosch, South Africa, 1996: 1035-1039.
[3]任万滨, 陈英华, 康云志, 等. 电磁继电器振动极限加速度分析方法[J]. 电工技术学报, 2011, 26(1): 63-67. Ren Wanbin, Chen Yinghua, Kang Yunzhi, et al. The analyzing method of limit vibration acceleration for the electromagnetic relays[J]. Transactions of China Electrotechnical Society, 2011, 26(1): 63-67.
[4]翟国富, 陈英华, 任万滨. 一种含赫兹接触的梁结构冲击特性分析方法[J]. 振动与冲击, 2009, 28(9): 82-85. Zhai Guofu, Chen Yinghua, Ren Wanbin. A shock characteristics analysis method of beam structures with Hertzian contact[J]. Journal of Vibration and Shock, 2009, 28(9): 82-85.
[5]张凡, 汲胜昌, 师愉航, 等. 电力变压器绕组振动及传播特性研究[J]. 中国电机工程学报, 2018, 38(9): 2790-2798. Zhang Fan, Ji Shengchang, Shi Yuhang, et al. Reserch on transformer winding vibration and pro- pagation characteristics[J]. Proceedings of the CSEE, 2018, 38(9): 2790-2798.
[6]Ren Wanbin, Zhai Guofu, Cui Li. Contact vibration characteristic of electromagnetic relay[J]. IEICE Transactions on Electronics, 2006, E89-C(8): 1177- 1181.
[7]刘建强, 陈爱峰, 闫一凡, 等. 高速列车电磁接触器可靠性评估方法[J]. 电工技术学报, 2018, 33(增刊2): 461-471. Liu Jianqiang, Chen Aifeng, Yan Yifan, et al. Reliability evaluation method of electromagnetic contactor used in high-speed train[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 461-471.
[8]闫明, 刘栋, 张磊, 等. 舰艇电气设备中簧片式触点开关冲击响应分析[J]. 振动与冲击, 2016, 35(1): 183-187. Yan Ming, Liu Dong, Zhang Lei, et al. Shock response analysis for reed contact switches in naval ships’ electrical equipment[J]. Journal of Vibration and Shock, 2016, 35(1): 183-187.
[9]Wattiaux D, Verlinden O. Modeling of the dynamic behavior of electromechanical relays for the analysis of sensitivity to shocks and vibrations[J]. Experi- mental Mechanics, 2011, 51(9): 1459-1472.
[10]倪振华. 振动力学[M]. 西安: 西安交通大学出版社, 1988.
[11]单辉祖. 材料力学[M]. 北京: 高等教育出版社, 2000.
[12]黄梓嫄, 韩邦成, 周银锋. 非线性接触下磁悬浮电机柔性转子系统模态分析[J]. 中国电机工程学报，2014, 34(15): 2438-2444. Huang Ziyuan, Han Bangcheng, Zhou Yinfeng. Modal analysis of the flexible rotor system of magnetic levitation motors under nonlinear contact[J]. Proceedings of the CSEE, 2014, 34(15): 2438-2444.
[13]纽春萍, 陈德桂, 李兴文, 等. 交流接触器触头弹跳的仿真及影响因素[J]. 电工技术学报, 2007, 22(10): 85-90. Niu Chunping, Chen Degui, Li Xingwen, et al. Simulation of contact bounce of AC contactor and study of its influence factors[J]. Transactions of China Electrotechnical Society, 2007, 22(10): 85-90.
[14]李汾. 继电器接点簧片的振动分析[J]. 机电元件, 1981(4): 1-7. Li Fen. Vibration analysis of relay contact spring[J]. Electromechanical Components, 1981(4): 1-7.
[15]蒋玲莉, 卜忠颉, 韩清凯, 等. 双列深沟球轴承刚柔耦合多体接触建模与振动特性研究[J]. 大连理工大学学报, 2017, 57(4): 360-366. Jiang Lingli, Pu Zhongji, Han Qingkai, et al. Research on rigid-flexible coupling multi-body contact modeling and vibration characteristics of double-row deep-groove ball bearing[J]. Journal of Dalian University of Technology, 2007, 57(4): 360-366.
[16]张鹏宁, 李琳, 程志光, 等. 并联电抗器与变压器模型铁心振动仿真与试验对比[J]. 电工技术学报, 2018, 33(10): 1-9. Zhang Pengning, Li Lin, Cheng Zhiguang, et al. Vibration simulation and experiment comparison of shunt reactor and transformer model core[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 1-9.
[17]闫明, 刘栋, 张磊, 等. 舰艇电气设备中簧片式触点开关冲击响应分析[J]. 振动与冲击, 2016, 35(1): 183-187. Yan Ming, Liu Dong, Zhang Lei, et al. Shock response analysis for reed contact switches in naval ship’s electrical equipment[J]. Vibration and Shock, 2016, 35(1): 183-187.
[18]李丹, 张代润, 杨林. 电磁继电器温升特性的仿真研究[J]. 电气技术, 2018, 19(3): 26-30. Li Dan, Zhang Dairun, Yang Lin. Simulationresearch on thermal analysis of electromagnetic relays[J]. Electrical Engineering, 2018, 19(3): 26-30.
[19]董华军, 司明月, 郭英杰, 等. 触头片结构对新型带铁心的杯状纵磁真空灭弧室磁场影响仿真[J]. 电工技术学报, 2018, 33(11): 2448-2455. Dong Huajun, Si Mingyue, Guo Yingjie, et al. Influence of contact plate structure on magnetic field strength of a new type of cup-shaped axial magnetic field vacuum interrupter with iron core[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(11): 2448-2455.
[20]李中, 宋天慧, 郭通, 等. 不同负载电流下变压器表面三维振动信号特征分析[J]. 电力系统保护与控制, 2017, 45(12): 29-34. Li Zhong, Song Tianhui, Guo Tong, et al. Characteri- stics analysis on three-dimensional surface vibration signals of transformer under different load current[J]. Power System Protection and Control, 2017, 45(12): 29-34.
[21]李俊峰, 苏秀苹, 郑新芳, 等. 基于触头动态接触压力的触头弹跳分析[J]. 电工技术学报, 2015, 30(9): 138-144. Li Junfeng, Su Xiuping, Zheng Xinfang, et al. Analysis of contact bounce based on dynamic contact pressure of contacts[J]. Transactions of China Electrotechnical Society, 2015, 30(9): 138-144.