0 引言
开关功率放大器作为磁悬浮轴承控制系统的执行部件,其性能直接影响磁悬浮轴承系统的特性。磁悬浮轴承开关功放的主电路拓扑有单臂式、半桥式、单相全桥式、多桥臂式等多种结构[1]。永磁偏置磁悬浮轴承要求开关功放能够提供双向电流[2-3],因此,必须采用全桥结构[4]。单相全桥拓扑能够提供双向电流,并且比多桥臂拓扑具有较高的可靠性[5-8],因此在永磁偏置磁悬浮轴承开关功放中应用广泛。该拓扑结构共有九种工作模态,输出电压有三态,能够实现三电平调制,相比于两电平调制[9],能获得更小的电流纹波和更快的电流响应速度[10]。
磁悬浮轴承控制系统主要有两种拓扑:采用电流型功放的电流控制模式和采用电压型功放的电压控制模式。由于磁悬浮轴承线圈为感性负载,会阻碍电流突变,从而影响系统的总体动态性能。因此,需要对线圈电流进行反馈控制。若采用电压型功放,整个控制系统的拓扑会较为复杂,因此,目前用于旋转机械的大多数磁悬浮轴承系统均采用基于电流型功放的电流控制模式[11]。
目前磁悬浮轴承开关功放常用的控制策略包括电流滞环(Current Hysteresis, CH)控制、采样-保持(Sample-Hold, SH)控制、最大电流误差控制、空间矢量脉宽调制(Space Vector Pulse Width Modu- lation, SVPWM)控制、比例-积分-微分(Proportion- Integral-Derivative, PID)控制等。其中,电流滞环控制、采样-保持控制、最大电流误差控制等方案在模拟控制中实现简单、有较高的控制精度,但在数字控制中效果不理想[12];SVPWM适用于多桥臂的主电路拓扑[13];PID控制存在最优参数整定困难、可能出现混沌现象等缺点[14]。
单周期控制(One-cycle Control, OC)技术由美国学者Smedley KM和Cuk S提出[15],是一种非线性大信号PWM控制算法,通过对控制量在一个周期内的值进行积分,控制其在该周期内的均值等于基准值,算法简单,易实现,控制精度高,响应速度快,适用于开关功放的控制[15-16]。单周期控制可以分为模拟控制和数字控制两类。在功率因数校正(Power Factor Correction, PFC)变换器[17]、三相三电平Vienna整流器[18-19]、双输入Buck变换器[20]、Sepic逆变器[21]中均有单周期模拟控制的应用。然而,模拟控制电路往往较为复杂,体积庞大,参数调整不便。相较于模拟控制,单周期数字控制具有易实现、参数调节方便的优点。文献[22-27]均采用单周期数字控制的方法。单周期算法的控制对象可以是电压量,也可以是电流量。目前,单周期算法广泛应用于电压型功放中,以输出电压为控制量,但也可以用于对电流量的控制,文献[17, 20, 23]中均对电流量进行了单周期控制。其中,文献[23]提出了电流型开关功放数字单周期控制的方法,获得了良好的控制效果。文献[24]将数字单周期算法应用到五相六桥臂开关功率放大器中,同样获得了良好的控制效果。文献[25-26]对双极性和单极性两类单周期算法进行了控制效果的比较,得出单极性控制效果更好的结论。文献[27]针对单周期控制中的延时,提出了一种相位滞后补偿方法。
然而,传统的数字单周期控制算法中,开关管开关次数不均衡,造成开关管发热不均,同时影响其利用率和使用寿命。并且,占空比数学模型的建立和开关周期的状态切换均没有考虑线圈电阻的影响,从而导致了实际电流的失真。
本文分析了单相全桥主电路的九种工作模态,并在此基础上重新确定了数字单周期控制的开关逻辑;在全周期考虑线圈电阻压降的前提下,推导改进型单周期算法的原理,优化了充放电周期的判断准则,建立更精确的算法模型。最后,进行仿真分析与实验验证,通过改进前后算法控制效果的比较,验证了改进型单周期算法的优越性。
1 全桥开关功放的工作原理
本文的控制对象为混合型磁悬浮轴承的电流型开关功率放大器,要求开关功放主电路稳定性高、能够提供双向电流。因此,本文选取单相全桥开关功放主电路拓扑,拓扑结构如图1所示。其中,Udc为直流母线电压,Lm和Rm分别为线圈的等效电感与电阻,Q为开关管,VD为续流二极管。假设开关器件均为理想器件,单相全桥负载为磁悬浮轴承 每一自由度的控制线圈,图中箭头方向为线圈电流的参考正方向。

图1 单相全桥开关功率放大器拓扑
Fig.1 Single phase full bridge switching power amplifier
图2为单相全桥主电路九种开关状态下的线圈电流回路。其中,以1表示开关管导通,0表示开关管关断,以Q1Q2Q3Q4四位数表示开关状态。
由图2可知,若线圈电流为正向,当开关状态为1001时,电流正向增大;开关状态为1000、0001、1010、0101时,电流正向续流;开关状态为0100、0010、0110、0000时,电流正向减小;若线圈电流为反向,当开关状态为0110时,电流反向增大;开关状态为0100、0010、1010、0101时,电流反向续流;开关状态为1000、0001、1001、0000时,电流反向减小。

图2 九种开关状态下的线圈电流
Fig.2 Coil current in nine switching states
2 改进型数字单周期控制算法的原理
单周期控制可以分为双极性控制和单极性控制两类。与双极性控制相比,单极性控制下,线圈两端电压具有三态,电流纹波较小,且跟踪精度与响应速度之间不存在矛盾[24-25],因此,本文将以性能较好的单极性单周期控制方式为例进行分析。
2.1 优化的开关逻辑
单极性单周期数字控制算法下,线圈电流存在正向增长、正向减小和续流三种状态。在一个开关周期内,可能存在续流态和上升态或是续流态和下降态。传统开关逻辑下,Q3、Q4开关频率极低,开关次数少;而Q1、Q2开关频率高,开关次数多,开关管发热严重不均,影响了功率器件的利用率和使用寿命。其次,各个开关周期之间必然存在开关状态的切换,开关次数较多。最后,电流上升态位于开关周期首尾,系统硬件延时对控制精度的影响较明显。为了解决上述问题,本文对单周期控制的开关逻辑进行了优化。
(1)为了避免判断电流极性,造成算法复杂度增加,以及采样延时及控制延时造成的极性判断不准确,本文选取0101或1010作为续流态开关状态,选取1001作为电流上升态的开关状态,选择0110作为电流下降态的开关状态,则无论电流极性如何,均能实现续流、电流上升与电流下降。
(2)为了减少开关次数,无论该周期为充电还是放电,均采用统一的续流态,且续流态的作用时间在开关周期首尾,则两个周期之间不需要开关状态的切换,开关次数减少,控制精度受系统延时影响小。考虑到具体的硬件电路实现,选取0101作为每一周期的续流态。
2.2 改进的数学模型
传统的单周期算法数学模型,通常忽略磁轴承线圈电阻压降,导致实际电流存在一定的失真。因此,本文在全开关周期考虑电阻压降的情况下,重新推导了单周期算法的数学模型。单极性单周期控制算法模型要求对正向充电周期和正向放电周期分别进行分析。
2.2.1 正向充电周期
若开关周期内线圈正向充电,改进型单周期算法控制下的波形如图3所示,由上至下分别为开关周期的触发脉冲、交叠三角波、占空比波形、线圈中的电流波形。图中,Ts为数字单周期控制的开关周期,Toff为每个周期非续流态持续的时间,d为线圈续流状态的占空比,cnt为交叠三角波的峰值,i为磁悬浮轴承控制线圈中的电流。

图3 数字单周期控制原理(充电周期)
Fig.3 Schematic diagrams of digital one-cycle control (charge cycle)
1)当t0<t<t1时,占空比波形为1,线圈处在续流态,开关管Q2、Q4导通,Q1、Q3关断,开关状态为0101。线圈电流的状态方程为

式中,L为磁悬浮轴承线圈电感;R为磁悬浮轴承线圈电阻;i(t)为磁悬浮轴承线圈电流。
通过求解状态方程,可得线圈电流的时域表达式
则有
由洛必达法则可知
由图3可得
将式(5)代入式(1),并结合式(4)可得

则t0~t1时间段内的电流变化量为

2)当t1<t<t2时,占空比波形为0,线圈处在充电状态,开关管Q1、Q4导通,Q2、Q3关断,开关状态为1001。线圈电流的状态方程为
可得线圈电流的时域表达式为

t1~t2时间段内的电流变化量为
3)当t2<t<t3时,工作状态与t0<t<t1时间段一致,状态方程与式(1)相同,同理可得该时间段内的电流变化量为

因此,当开关周期为正向充电周期时,一个周期内的线圈电流变化量为

假设以终值跟踪为目标,则要求每个开关周期结束时刻的实际电流值,能准确跟踪上该周期的电流给定,则一个开关周期内的实际电流变化量为
由于电流内环的时间常数远小于位移外环的时间常数,因此可以认为i(t0)、i(t1)、i(t2)近似等于一个开关周期内的电流平均值,即
将式(13)和式(14)代入式(12),可以解得占空比d为

2.2.2 正向放电周期
若开关周期内线圈正向放电,改进型单周期算法控制下的波形如图4所示。

图4 数字单周期控制原理(放电周期)
Fig.4 Schematic diagram of digital one-cycle control (discharge cycle)
1)当t0<t<t1时,占空比波形为1,线圈处在续流态,开关管Q2、Q4导通,Q1、Q3关断,开关状态为0101。线圈电流的状态方程为
通过求解状态方程,可得线圈电流的时域表达式为
则t0~t1时间段内的电流变化量为
2)当t1<t<t2时,占空比波形为0,线圈处在放电状态,开关管Q2、Q3导通,Q1、Q4关断,开关状态为0110。线圈电流的状态方程为

则得线圈电流的时域表达式为
t1~t2时间段内的电流变化量为
3)当t2<t<t3时,工作状态与t0<t<t1时间段一致,状态方程与式(1)相同,同理可得该时间段内的电流变化量为
因此,当开关周期为正向充电周期时,一个周期内的线圈电流变化量为

假设以终值跟踪为目标,则要求每个开关周期结束时刻的实际电流值,能准确跟踪上该周期的电流给定,则可以解得占空比d为

2.3 改进的状态切换准则
单周期数字控制算法下,需要在一个开关周期的起始时刻确定该周期为充电周期还是放电周期,从而确定该周期非续流态的开关管状态以及占空比的数学模型。假设电流给定值为iref,周期开始时刻的电流实际值为i(t0),在传统的单周期数字控制算法中,以电流误差的极性作为判断该周期充放电的依据,即在开关周期起始时刻,若iref -i(t0)>0,则该周期为充电周期;若iref -i(t0)<0,则该周期为放电周期;若iref -i(t0)=0,则该周期始终续流。实际上,由于控制线圈电阻的影响,在以下两种工作情形下,采用传统的控制方式,无法实现跟踪目标,会导致实际电流失真。
1)工作情形一如图5所示,iL为实际电流,iref为给定电流,Δi0为周期开始时刻的电流误差。当周期开始时刻实际电流i(t0)与给定电流iref满足
若按照传统算法,判断该周期为充电周期,由于


图5 工作情形一
Fig.5 Working situation one
则整个开关周期都处于续流状态,仍不能实现跟踪上iref的目标。
2)工作情形二如图6所示,当周期开始时刻实际电流i(t0)与给定电流iref满足

图6 工作情形二
Fig.6 Working situation two
若按照传统算法,判断该周期为放电周期,由于

则整个开关周期都处于续流状态,同样也不能实现跟踪上iref的目标。
实际上,考虑到线圈电阻压降,在判断充放电周期时,应考虑续流带来的电流变化量。若iref>i(t0),但充电周期占空比dch>1,即全周期续流电流变化量仍过大,则采用放电模型;若iref<i(t0),但放电周期占空比ddisch>1,则采用充电模型。
因此,本文提出的改进型单周期数字控制算法中,判断开关周期充放电的依据如下。
若满足

该周期采用充电模型;否则采用放电模型。采用该判断准则,能有效避免电流误差较小的情况下,开关周期充放电状态判断不准确的问题。
综上所述,改进型单周期数字控制算法的数学模型可以表示为

其中

3 仿真与实验
为了验证改进型单周期数字控制算法的可行性和优越性,本文利用Matlab搭建了仿真模型,进行了仿真分析,并在基于FPGA的数字控制系统平台上进行了相关实验验证。仿真与实验中,为了模拟一台永磁偏置磁轴承绕组,采用L=2mH,R=3Ω 的电感线圈作为负载。仿真与实验条件设定:母线电压Udc=50V,开关频率fc=50kHz。
3.1 仿真分析
为了验证改进型单周期数字控制算法的可行性,分别给定幅值为2A的阶跃信号和幅值为3A、频率为500Hz的正弦信号,进行了仿真,仿真结果如图7、图8所示。图中,iref表示给定电流波形,ifeed表示反馈电流波形。由仿真结果可见,在改进型单周期数字控制算法下,电流给定为阶跃信号和正弦信号时,实际电流均能准确、快速地跟踪上给定,响应速度快,跟踪精度高,没有超调,不存在稳态误差。

图7 阶跃信号跟踪波形
Fig.7 Tracking waveforms of step signal
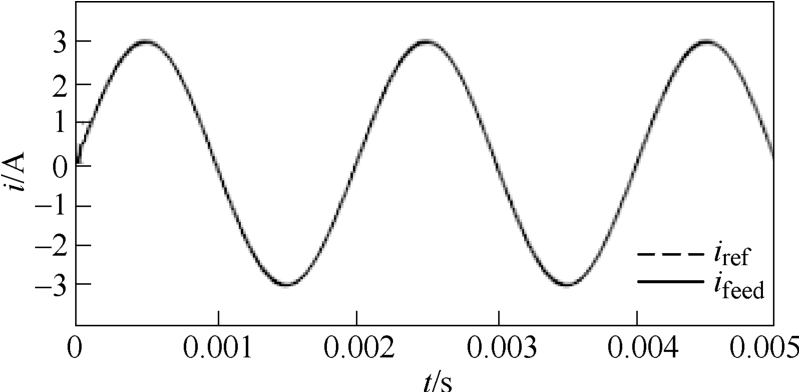
图8 正弦信号跟踪波形
Fig.8 Tracking waveforms of sine signal
为了进一步验证改进型单周期数字控制算法相比于传统型算法的优越性,本文对改进前后单周期数字控制算法的性能进行了对比分析。图9为改进前后单周期算法控制下,跟踪正弦信号时的开关管波形。其中,Q1与Q2互补导通,Q3与Q4互补导通,因此选取Q1、Q3波形进行对比分析。由图9可见,传统单周期算法控制下,Q1、Q2开关频率很高,而Q3、Q4开关频率很低,开关管发热严重不均,影响了其利用率和使用寿命;而改进型单周期控制下,各开关管开关次数较为均衡。

图9 开关信号波形
Fig.9 Simulation waveforms of switching signal
为了验证改进型单周期控制数学模型引入电阻对跟踪效果的影响,分别给定几组正弦信号,改进前后的单周期数字控制算法下,实际电流的基波幅值仿真对比见表1。定义实际电流与给定电流基波幅值的差值与给定幅值的比值为幅值失真率,可以看出,在传统型单周期数字控制算法下,基波幅值有较明显的失真,幅值失真率在3%左右,而改进型的单周期算法下,基波幅值几乎没有失真,幅值失真仅为传统型的1%左右,电流跟踪精度更高。
表1 仿真对比
Tab.1 Comparison of simulation

给定正弦信号 基波幅值/A 改进型 传统型 序号 幅值/A 频率/Hz 1 2 1 000 1.999 1.940 2 2 500 2.000 1.941 3 4 500 3.999 3.882
为了验证优化开关周期判断准则对单周期算法控制效果的影响,分别给定幅值3A,频率500Hz的正弦信号,图10a为优化前电流误差的方均根(RMS)值,图10b为优化后电流误差的RMS值。由仿真结果可见,传统的开关周期判断准则下,由于部分开关周期无法实现跟踪目标,电流误差存在明显的尖峰,电流误差RMS峰值达到0.15A;而改进后的算法控制下,电流误差的RMS值始终较小,不存在明显尖峰,电流失真小,跟踪精度更高。

图10 电流误差RMS值
Fig.10 RMS of current error
3.2 实验验证
为了进一步验证改进型单周期算法的可行性和优越性,本文利用基于FPGA的硬件平台,对改进前后的单周期算法进行了实验比较。实验平台如图11所示。采用信号发生器产生的信号经过ADC采样,作为电流环的给定信号。采用电感线圈负载模拟磁悬浮轴承线圈,线圈参数L=2mH,R=3Ω,为磁悬浮轴承线圈实测值。FPGA芯片采用Altera公司的Cyclone ⅣCE40F23I7。电流环控制频率为50kHz。

图11 电流闭环实验平台
Fig.11 Test rig of current-loop controller
图12为传统型和改进型单周期算法在500Hz、3A正弦给定信号下的电流跟踪波形。实验结果表明,改进型单周期算法控制下,实际电流能够快速准确地跟踪给定,控制精度高,动态性能好,相较于传统型,不存在明显的幅值失真。

图12 电流跟踪实验波形
Fig.12 Experiment waveforms of current tracking
图13分别为改进前后单周期控制下的开关信号波形。其中,UGS表示开关管的栅源极电压。实验波形表明,改进型单周期算法控制下,4个开关管的开关次数均衡,验证了理论仿真的结果。

图13 开关信号波形
Fig.13 Experiment waveforms of switching signal
图14分别为改进前后单周期控制下实际电流的傅里叶分解波形。实验结果表明,相比传统型单周期,改进型单周期算法控制下,电流谐波含量 更少。


图14 傅里叶分解波形
Fig.14 Experiment waveforms of Fourier transform
表2为几组给定信号下,改进前后单周期算法控制下的实际电流幅值。实验结果表明,改进型单周期算法的数学模型更精确,实际电流幅值失真更小,与仿真结果一致。
表2 实际电流幅值实验对比
Tab.2 Experiment comparison of actual current amplitude

给定正弦信号 基波幅值/A 序号 幅值/A 频率/Hz 改进型 传统型 1 2 1 000 1.94 1.88 2 2 500 1.92 1.84 3 4 500 3.92 3.80
4 结论
本文对传统的单周期数字控制算法进行了优化,分析了九种开关状态下的线圈电流,在此基础上优化了单周期控制下的开关逻辑。其次,全周期考虑线圈电阻影响,重新建立了占空比的数学模型,优化了开关周期充放电的判断依据。仿真和实验表明,与传统型单周期数字控制算法相比,改进型的单周期算法具有以下优点:
1)单相全桥的4个开关管开关次数更均衡,有利于提高开关管的利用率和使用寿命。
2)实际电流几乎没有幅值失真。
3)每个周期均能实现跟踪目标,不会出现电流误差的尖峰。
4)电流谐波含量少,控制精度高。
[1]臧晓敏. 磁轴承开关型功率放大器的研究[D]. 南京: 南京航空航天大学, 2004.
[2]赵旭升, 邓智泉, 王晓琳, 等. 永磁偏置磁轴承的研究现状及其发展[J]. 电工技术学报, 2009, 24(9): 9-20. Zhao Xusheng, Deng Zhiquan, Wang Xiaolin, et al. Research status and development of permanent magnet biased magnetic bearings[J]. Transactions of China Electrotechnical Society, 2009, 24(9): 9-20.
[3]Zhang Weiyu, Ruan Ying, Ji Shanghua, et al. Variable stiffness coefficient analysis and control system study for radial AC hybrid magnetic bearing[C]// 2011 30th Chinese Control Conference (CCC), Yantai, China, 2011: 3494-3499.
[4]Zhang Li, Liu Kun, Chen Xiaofei. FPGA implent- ation of a three-level power amplifier for magnetic bearings[C]//9th International Conference on Elec- tronic Measurement & Instruments, Beijing, China, 2009: 1455-1460.
[5]阮新波, 严仰光. 四桥臂三相逆变器的控制策略[J]. 电工技术学报, 2000, 15(1): 61-64. Ruan Xinbo, Yan Yangguang. The control strategy for three-phase Inverter with four bridge legs[J]. Transactions of China Electrotechnical Society, 2000, 15(1): 61-64.
[6]费清照, 邓智泉, 王晓琳, 等. 适用于磁悬浮轴承的新型五相六桥臂开关功放控制策略[J]. 中国电机工程学报, 2012, 32(9): 124-131. Fei Qingzhao, Deng Zhiquan, Wang Xiaolin, et al. A control strategy of novel five-phase six-leg switching power amplifiers applied in magnetic levitation bearing systems[J]. Proceedings of the CSEE, 2012, 32(9): 124-131.
[7]孙驰, 毕增军, 魏光辉. 一种新颖的三相四桥臂逆变器解耦控制的建模与仿真[J]. 中国电机工程学报, 2004, 24(1): 124-130. Sun Chi, Bi Zengjun, Wei Guanghui. Modeling and simulation of a three-phase four-leg inverter based on a novel decoupled control technique[J]. Proceedings of the CSEE, 2004, 24(1): 124-130.
[8]Li Xiangsheng, Deng Zhiquan, Chen Zhida, et al. Analysis and simplification of three-dimensional space vector PWM for three-phase four-leg inver- ters[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 450-464.
[9]余忠磊, 祝长生. 二电平电流型开关功率放大器稳定性分析[J]. 电工技术学报, 2019, 34(2): 306-315. Yu Zhonglei, Zhu Changshen. Analysis on the stability of two-level current mode switching power amplifiers[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 306-315.
[10]臧晓敏, 王晓琳, 仇志坚, 等. 磁轴承开关功放中电流三态调制技术的研究[J]. 中国电机工程学报, 2004, 24(9): 167-172. Zang Xiaomin, Wang Xiaolin, Qiu Zhijian, et al. Research on current mode tri-state modulation technology in switching power amplifier for magnetic bearings[J]. Proceedings of the CSEE, 2004, 24(9): 167-172.
[11]Schweitzer G, 等. 磁悬浮轴承: 理论、设计及旋转机械应用[M]. 北京: 机械工业出版社, 2012.
[12]费清照. 磁悬浮轴承开关功率放大器控制策略研究[D]. 南京: 南京航空航天大学, 2012.
[13]韩辅君, 房建成, 刘刚. SVPWM方法在磁轴承开关功放中的设计及应用[J]. 电工技术学报, 2009, 24(5): 119-124. Han Fujun, Fang Jiancheng, Liu Gang. Design and implementation of SVPWM switching power ampli- fiers for active magnetic bearing[J]. Transactions of China Electrotechnical Society, 2009, 24(5): 119- 124.
[14]范友鹏, 刘淑琴, 代燕杰. 磁轴承中三电平全桥变换器的混沌现象分析[J]. 电机与控制学报, 2013, 17(3): 34-39. Fan Youpeng, Liu Shuqin, Dai Yanjie. Analysis of chaos phenomenon in three-level full bridge con- verter[J]. Electric Machines and Control, 2013, 17(3): 34-39.
[15]Smedley K M, Cuk S. One-cycle control of switching converters[J]. IEEE Transactions on Power Electro- nics, 1995, 10(6): 525-633.
[16]Bento A A D M, Vieira P K P, Silva E R C D. Application of the one-cycle control technique to a three-phase three-level NPC rectifier[J]. IEEE Transactions on Industry Applications, 2014, 50(2): 1177-1184.
[17]江涛, 毛鹏, 谢少军. 单周期控制PFC变换器的输入电流畸变研究[J]. 中国电机工程学报, 2011, 31(12): 51-57. Jiang Tao, Mao Peng, Xie Shaojun. Distortion issue on input current of OCCPFC converter and its solution[J]. Proceedings of the CSEE, 2011, 31(12): 51-57.
[18]韦徵, 陈新, 樊轶, 等. 单周期控制的三相三电平VIENNA整流器输出中点电位分析及控制方法研究[J]. 中国电机工程学报, 2013, 33(15): 29-37. Wei Zheng, Chen Xin, Fan Yi, et al. Study and analysis of neutral-point potential and control methods for one-cycle controlled three-phase three- level VIENNA rectifiers[J]. Proceedings of the CSEE, 2013, 33(15): 29-37.
[19]邹甲, 王聪, 程红, 等. 三相线电压级联VIENNA变换器调制及直流侧电压控制[J]. 电工技术学报, 2018, 33(16): 3835-3844. Zou Jia, Wang Cong, Cheng Hong, et al. Research on modulation strategy and balance control for DC-link voltages in triple line-voltage cascaded VIENNA converter[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3835-3844.
[20]杨东升, 杨敏, 阮新波. 双输入Buck变换器的单周期控制[J]. 电工技术学报, 2012, 27(1): 162-171. Yang Dongsheng, Yang Min, Ruan Xinbo. One-cyle control for double-input Buck converter[J]. Transa- ctions of China Electrotechnical Society, 2012, 27(1): 162-171.
[21]王立乔, 祝百年, 孙孝峰. 一种单级隔离型Sepic逆变器[J]. 电工技术学报, 2016, 31(18): 75-82. Wang Liqiao, Zhu Bainian, Sun Xiaofeng. A single- stage isolated Sepic inverter[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 75-82.
[22]周雒维, 龚伟, 苏向丰. 一种改进的单周控制的开关功率放大器[J]. 电工技术学报, 2004, 19(5): 106- 110. Zhou Luowei, Gong Wei, Su Xiangfeng. An improved switching power amplifier with one cycle control[J]. Transactions of China Electrotechnical Society, 2004, 19(5): 106-110.
[23]刘程子, 邓智泉, 曹鑫, 等. 混合型磁悬浮轴承开关功放的单周期数字控制[J]. 中国电机工程学报, 2015, 35(22): 5899-5907. Liu Chengzi, Deng Zhiquan, Cao Xin, et al. An one- cycle control digital control strategy for switching power amplifiers in hybrid magnetic levitation bearing systems[J]. Proceedings of the CSEE, 2015, 35(22): 5899-5907.
[24]刘程子, 邓智泉, 曹鑫, 等. 一种新型的磁悬浮轴承五相六桥臂开关功率放大器控制策略[J]. 电工技术学报, 2016, 31(9): 112-119. Liu Chengzi, Deng Zhiquan, Cao Xin, et al. A novel control of five-phase six-leg switching power amplifier in magnetic levitating bearing system[J]. Transactions of China Electrotechnical Society, 2016, 31(9): 112-119.
[25]陆超, 袁静. 一种基于单周期数字控制的三相逆变器的研究[J]. 电源技术, 2013, 47(2): 70-71. Lu Chao, Yuan Jing. Research on digital one-cycle control for single-phase inverter[J]. Chinese Journal of Power Sources, 2013, 47(2): 70-71.
[26]刘程子. 适用于高速电机的混合型磁悬浮轴承设计及控制策略的研究[D]. 南京: 南京航空航天大学, 2015.
[27]周杰, 邓智泉, 李克翔, 等. 具有延时补偿的磁悬浮轴承开关功率放大器数字单周期控制[J]. 电工技术学报, 2017, 31(9): 112-119. Zhou Jie, Deng Zhiquan, Li Kexiang, et al. Digital one-cycle control algorithm with compensation of time delay for switching power amplifier in magnetic suspension bearings[J]. Transactions of China Elec- trotechnical Society, 2017, 31(9): 112-119.