0 引言
与传统的“旋转电机+滚珠丝杠”相比，永磁直线同步电动机（Permanent Magnet Linear Synchronous Motor, PMLSM）省去了中间传动装置，因此避免了齿侧间隙和刚性不足等缺点[1-2]。由于高速度、高精度、动态响应快、结构简单和推力大等优点，PMLSM已广泛应用于工业机器人、半导体制造系统和机床加工等领域中[3]。
然而PMLSM伺服系统易受参数变化、外部扰动和摩擦力等不确定性因素影响，因此为提高控制精度，引入了反推控制方法[4]。反推控制是一种鲁棒性强的非线性控制方法，利用Lyapunov稳定性理论对高阶系统的每一阶子系统设计虚拟控制律，实现全局调节和跟踪[5-6]。文献[7]针对永磁同步电机设计了反推控制器，使其速度控制具有良好的瞬态特性，提高了系统稳定性，但设计中忽略了系统本身参数变化对系统性能的影响。文献[8]将模糊神经网络和自适应反推控制相结合以实现位置跟踪，但模糊规则的执行需要大量的选择，控制精度也相对较低。文献[9]采用基于径向基神经网络的反推控制对系统进行无传感器位置跟踪，但该神经网络为静态前向网络，利用静态网络对系统进行辨识会引起收敛速度变慢，同时系统会对外部扰动更敏感。因此，文献[10]提出了基于动态神经网络——Elman神经网络对PMLSM进行无位置传感器控制，但Elman神经网络仅限于一阶系统的辨识，用于高阶系统时计算复杂。而改进Elman神经网络能适用高阶系统，且具有更高的精度、更好的性能和动态鲁棒性[11]。
因此，本文采用了积分反推控制和自适应改进Elman神经网络相结合的方法控制PMLSM伺服系统。利用积分反推控制方法选择适当的状态变量函数作为整个系统中每个子系统的虚拟控制输入，每个反推阶段利用上一阶段的控制律产生新的虚拟控制律，通过计算与每个设计阶段相关的Lyapunov函数得到最终控制律，实现期望的设计目标，利用自适应改进Elman神经网络来估计不确定性以进一步提高系统的鲁棒性能。最后，通过实验验证了该方法的有效性。
1 PMLSM数学模型
PMLSM的运动方程为
式中，Fe为电磁推力；m为动子质量；vr为动子速度；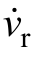
为动子加速度；B为黏滞摩擦系数；fL为外 部扰动；kf为推力系数；iq为动子q轴电流。
由于实际的PMLSM伺服系统受参数变化、外部负载扰动和摩擦力的影响，式（1）可改写为
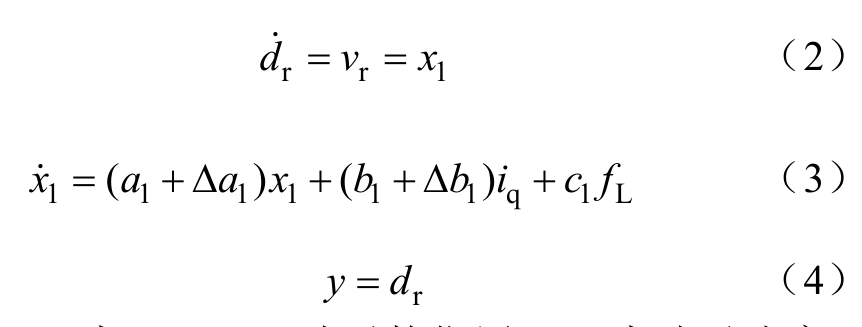
式中，dr为PMLSM动子的位置；x1为动子速度；
和 Δa2表示由参数m和B引入的不确定性。
式（3）改写为
式中，总不确定性l1为
总不确定性l1的值可利用自适应Elman神经网络估计得到。
2 自适应改进Elman神经网络积分反推控制系统
2.1 积分反推控制器的设计
积分反推控制系统框图如图1所示。PMLSM伺服系统的控制目的是使系统的输出 y(t)渐近地跟踪参考轨迹 yd(t)，即 dm。其步骤如下。
图1 积分反推控制系统框图
Fig.1 Block diagram of the integral backstepping control system
为实现位置跟踪，定义跟踪误差
定义函数
式中，k1和k2为正常数
为积分作用，保证跟踪误差收敛到零。
定义虚拟跟踪误差
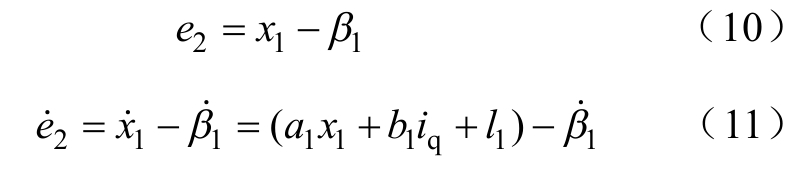
设总不确定性l1是有界的，即
为额定条件下的值。定义Lyaounov函数为
对V1求导并将式（8）和式（11）代入式（12）得
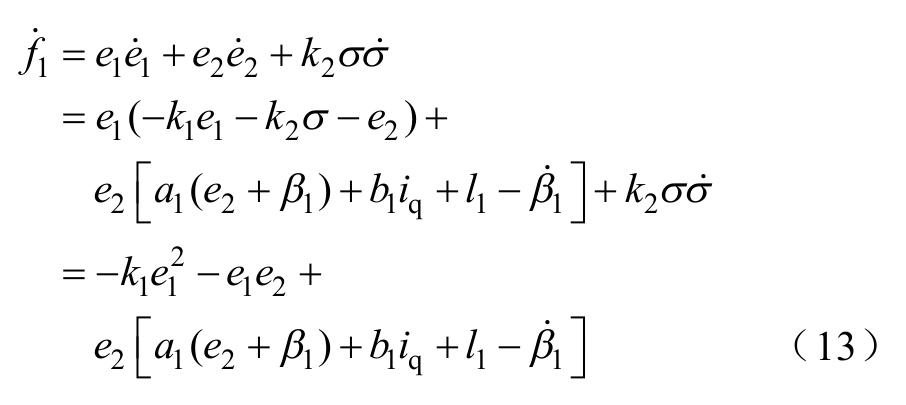
根据式（13），设计积分反推控制律为
式中，k3是正常数。将式（14）代入式（13）得
定义
则
由于 
有界， 
非增且有界，则
另外，
有界，则 ε(t)连续。
根据Barbalat引理，可得
时，e1和 e2将收敛到零。另外， 
因此，积分反推控制系统渐近稳定，即可以保证积分反推控制系统的稳定性。
2.2 自适应改进Elman神经网络积分反推控制器的设计
由于总不确定性l1在实际应用中未知，所以l1的值很难确定，因此采用改进Elman神经网络来估计总不确定性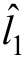
的值。四层的改进Elman神经网络的结构如图2所示，其中包括输入层（i层）、隐含层（j层）、承接层（k层）和输出层（o层）。
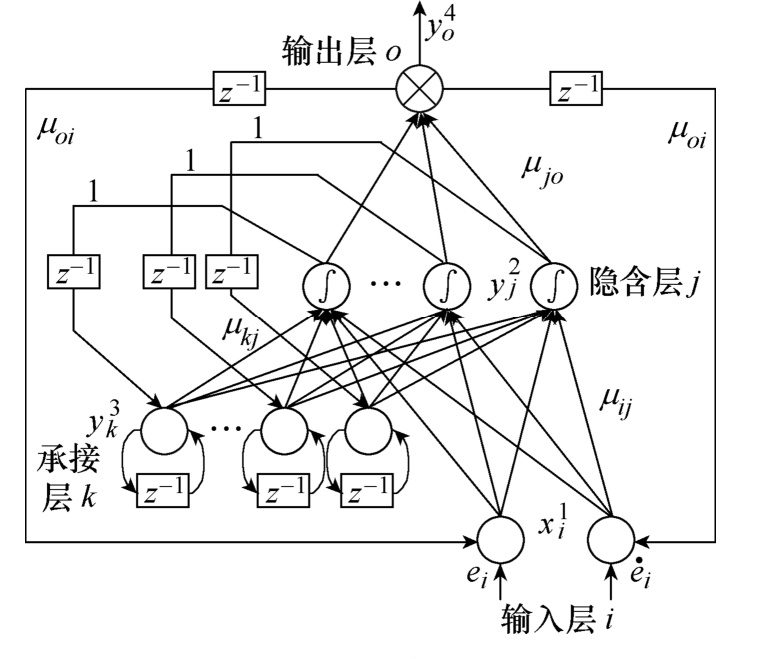
图2 改进Elman神经网络的结构
Fig.2 Structure of the modified Elman neural network
各层的信号传递和激活函数如下。
第一层：输入层i。对于该层的节点i，网络的输入和输出表示为
式中， 
为输入层节点的第i个输入；N为迭代次数；e1为改进Elman神经网络的输入；z-1为时间延迟；μoi为输出层和输入层的回归权重； 
为改进Elman神经网络的输出；
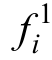为激活函数。
第二层：隐含层j。对于该层的节点j，输入和输出表示为
式中，μkj为承接层和隐含层的连接权重；μij为输入层和隐含层的连接权重；m为隐含层中节点个数；
为激活函数，即 
为输入层节点第i个输出；
为承接层节点第k个 输入。
第三层：承接层k。在承接层中，节点的输入和输出表示为
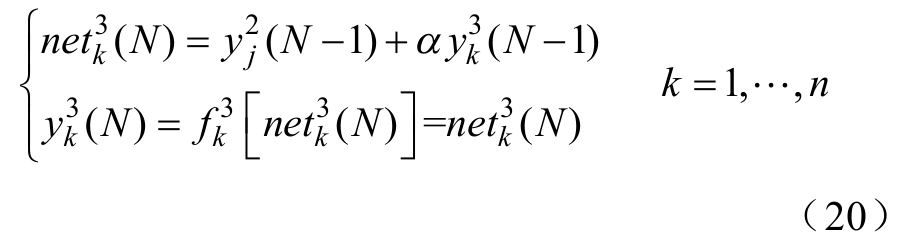
式中，
为隐含层节点的第j个输出；
代表承接层节点的第k个输出；n表示承接层神经元 的个数；0≤ α ≤1是承接层的自连接反馈增益。
第四层：输出层o。输入和输出表示为
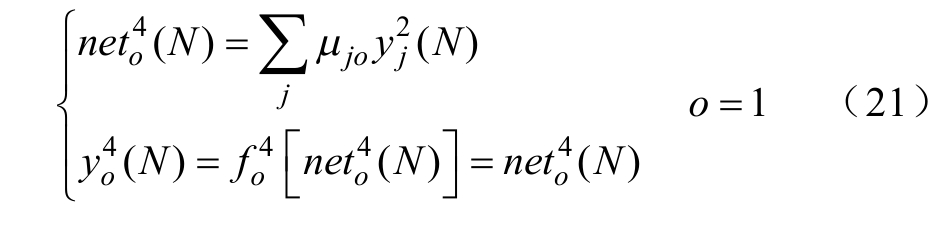
式中，μjo为隐含层和输出层之间的连接权重；
为激活函数；
为输出层节点的第j个输入。改进Elman神经网络的输出改为
式中， 
为改进Elman神经网络可调参数的集合；
其中
由S函数确定且
。
为得到改进Elman神经网络的自适应律，定义最小重构误差δ为
式中，Ω*是实现最小重构误差的最优权重向量，假设
为正常数。
选择Lyapunov函数
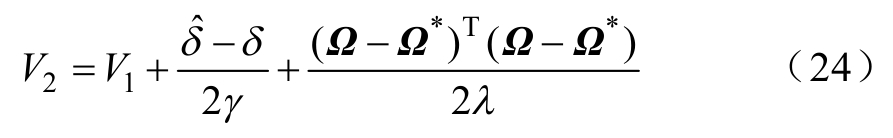
式中，γ和λ为正常数；
为δ的估计值。
对V2求导得
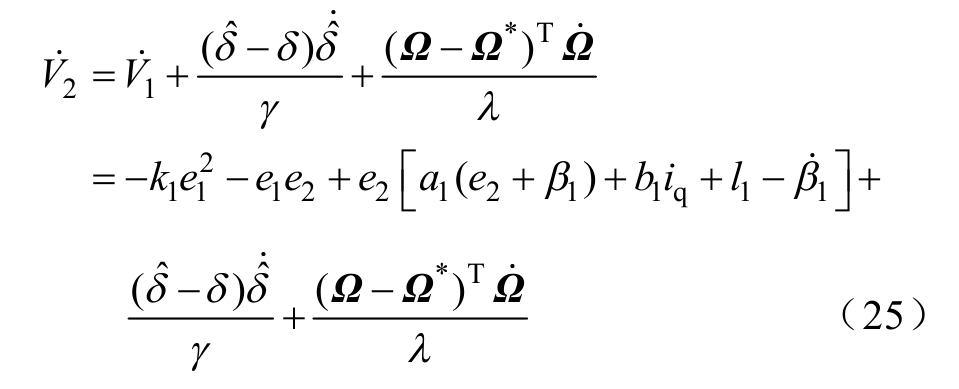
根据式（25），提出自适应改进Elman神经网 络反推控制律
为
将式（26）代入式（25），得
设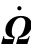
和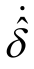
的自适应律为
将式（28）代入式（27）得
根据Barbalat引理，可得当t→∞时，-ε(t)→0，e1和e2收敛到零。因此，保证了图3所示的自适应改进Elman神经网络积分反推控制系统的稳定性。另外，跟踪误差收敛到零并不意味着总不确定性的估计值会收敛到不确定性的实际值。为了使估计值收敛到理论值，应满足持续的激励条件。
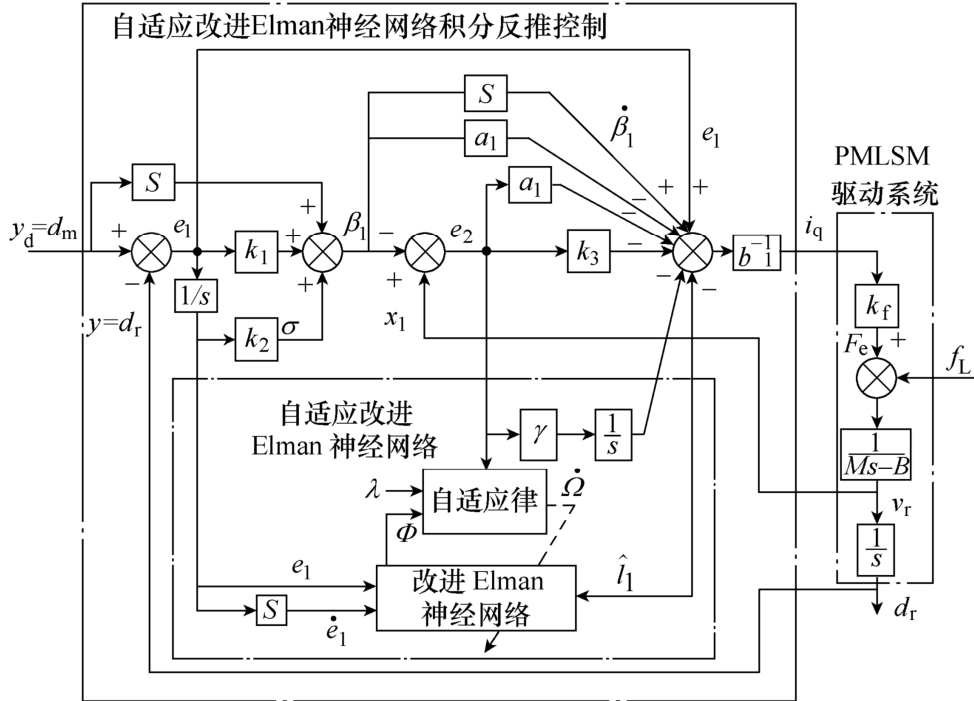
图3 自适应改进Elman神经网络积分反推控制 系统框图
Fig.3 Block diagram of the adaptive modified Elman neural network integral backstepping control system
为了有效地训练改进Elman神经网络，可以使用Lyapunov稳定定理的自适应律
推导出在线参数训练方法。自适应律 
可以通过梯度下降法和反向传播算法来计算。输出层和隐含层的连接权重μjo更新为
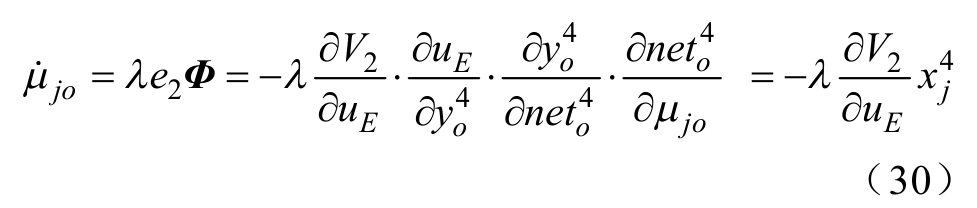
系统的雅克比矩阵可改写为 
计算误差项为
承接层和隐含层的连接权重kμj更新为
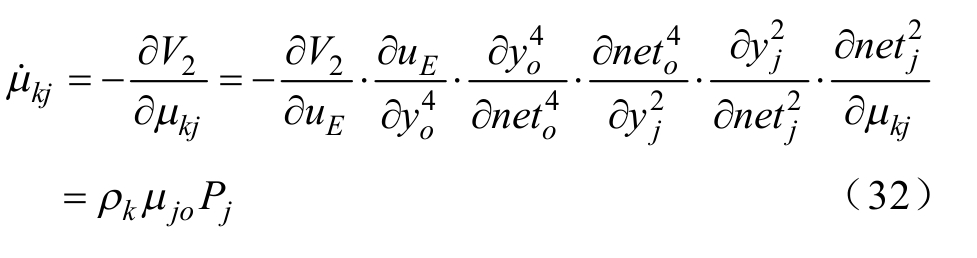
式中， 
隐含层和输入层的连接权重可更新为
式中，
输出层和输入层之间的回归权重 
更新为
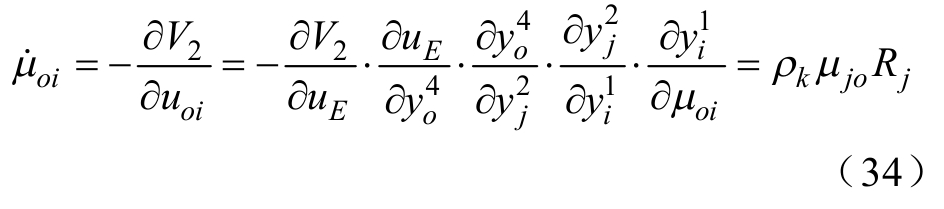
式中， 
3 系统仿真实验分析
首先，为验证自适应改进Elman神经网络积分反推控制方案的有效性，对系统进行仿真分析。给定两种输入信号：梯形信号和周期性正弦信号。电机和自适应改进Elman神经网络积分反推控制器参数如下：m=16.4kg ，B= 8.0N·s/m ，τ= 16mm ，kf= 50N/A，Rs=2.1Ω，Ld=Lq =41.4mH，k1=9，k2=4，k3=4，γ= 0.2，λ= 0.1。另外，神经网络的输入 层、隐含层、承接层和输出层神经元个数分别为2、6、6和1。
当输入图4所示的梯形信号并施加图5所示的负载时，积分反推控制和自适应改进Elman神经网络积分反推控制系统跟踪误差曲线如图6和图7所示。对比图6和图7，在转折处两种方法都会出现超调，其中图6在两个周期的误差区间依次为-3.9～3.9μm和-6.8～6.8μm，而图7的误差依次为-1.3～1.2μm和-2.6～2.8μm；在突加负载和负载改变时，图6的误差约为2μm，而图7的误差约为0.15μm；此外，图6的超调持续时间约为0.3s，而图7几乎在瞬间恢复稳定状态。
图4 输入信号曲线（一）
Fig.4 Signal curve of input (1)
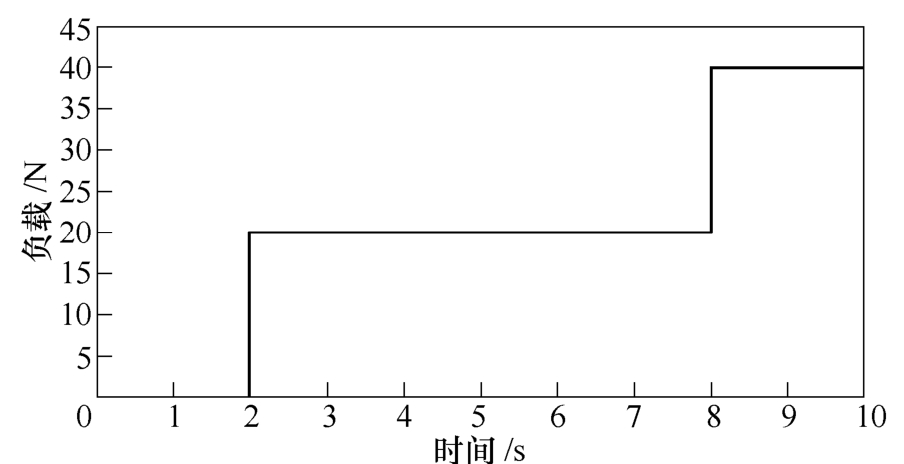
图5 负载信号曲线
Fig.5 Signal curve of load
图6 积分反推控制系统跟踪误差曲线（一）
Fig.6 Tracking error curve of integral backstepping control system (1)
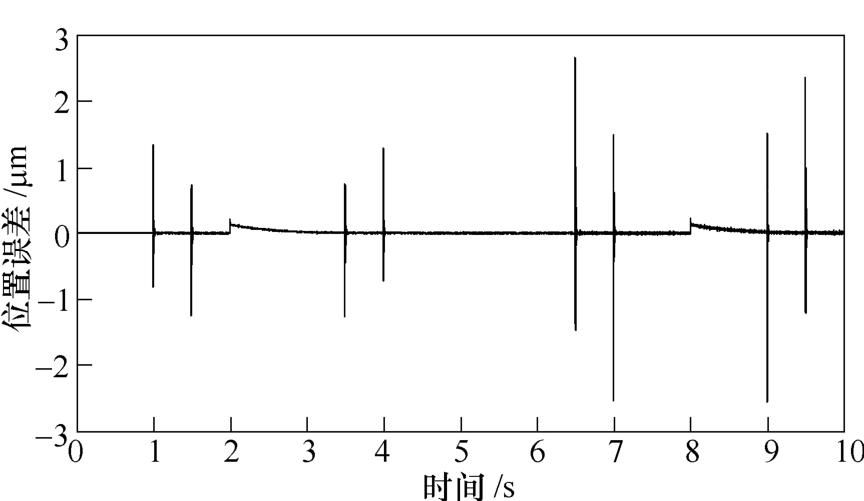
图7 自适应改进Elman神经网络积分反推控制系统 跟踪误差（一）
Fig.7 Tracking error curve of the adaptive modified Elman neural network integral backstepping control system (1)
当系统输入图8所示的正弦信号时，系统跟踪曲线如图9和图10所示。在系统响应初期，图9波动较大，最大误差约为-25μm，在正负转折处误差在-5～5μm波动；而图10在响应初期最大误差约为-2.8μm且迅速变平缓，正负转折处的误差在-2.2～2.2μm波动；同时图9比图10的超调持续时间更久，恢复稳定更慢。由此可知，自适应改进Elman神经网络积分反推控制具有更好的跟踪精度和鲁棒性能。
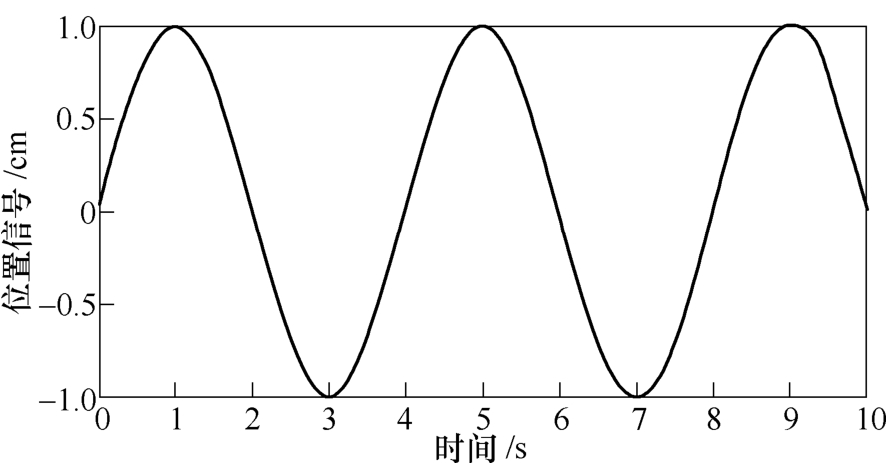
图8 输入信号曲线（二）
Fig.8 Signal curve of input (2)
图9 积分反推控制系统跟踪误差曲线（二）
Fig.9 Tracking error curve of integral backstepping control system (2)
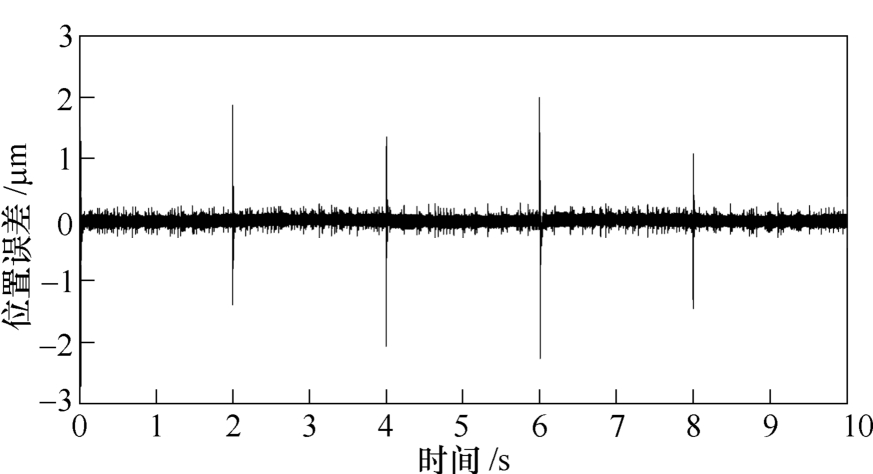
图10 自适应改进Elman神经网络积分反推控制系统 跟踪误差曲线（二）
Fig.10 Tracking error curve of the adaptive modified Elman neural network integral backstepping control system (2)
在相同条件下，对两种控制方案进行实验对比分析。采用DSP TMS320F2812A作为执行单元，基于DSP的PMLSM控制系统结构如图11所示，主要包括整流器、IPM（interior permanent magnet）、PMLSM、直线光栅尺、电流传感器和DSP控制单元等。在位置输入曲线转折处，两种控制方案都出现了一定程度的超调。图12a的超调持续时间约为0.5s，而图13a的超调仅存在于转折瞬间；在两个周期内，图12a的误差区间依次为-4.5～5.5μm和-9～9.5μm，而图13a的误差区间依次为-3.1～3.6μm和-6.5～6.5μm；在2s和8s加入负载时，图12a的超调约为5.9μm，而图13a的超调约为1μm。综上所述，自适应改进Elman神经网络具有更好的控制精度和鲁棒性。
图11 基于DSP的PMLSM控制系统结构
Fig.11 Structure diagram of PMLSM control system based on DSP
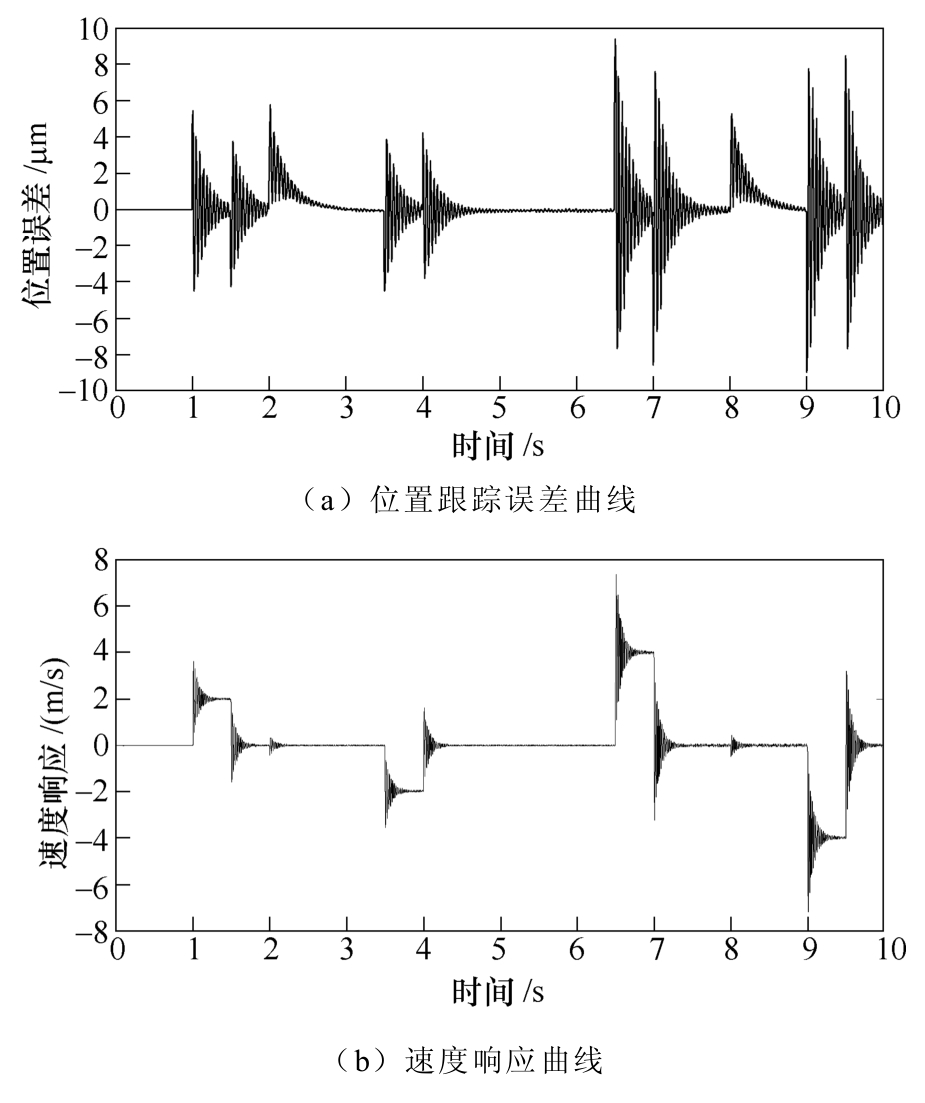
图12 积分反推控制系统响应曲线（一）
Fig.12 Response curves of integral backstepping control system (1)
图13 自适应改进Elman神经网络积分反推控制系统 响应曲线（一）
Fig.13 Response curves of the adaptive modified Elman neural network integral backstepping control system (1)
对比速度响应曲线，在转折处两种控制方案都有超调，图12b的超调时间约为0.3s，而图13b的超调时间几乎为零；在2s和8s加入负载时，图12b的速度在-0.2～0.2m/s波动，而图13b在负载变化时刻几乎无波动。可以看出，无论是运行状态还是负载的改变，自适应改进Elman神经网络积分反推控制都具有更好的鲁棒性。
当系统输入为正弦信号时，两种控制方案的系统响应曲线如图14和图15所示。首先，对比位置跟踪误差曲线。在电机起动初期和运行方向改变时，图14a都经历了0.3s的超调时间，而图15a则在瞬间恢复稳定跟踪状态；在电机起动瞬间，图14a的跟踪误差区间约为-32～33μm，而图15a的误差区 间约为-3～2.1μm；在转折处引起的超调，图14a的误差区间约为-17～19μm，而图15a的误差区间约为-7～7μm。对比可得，自适应改进Elman神经网络具有更好的控制精度和鲁棒性。
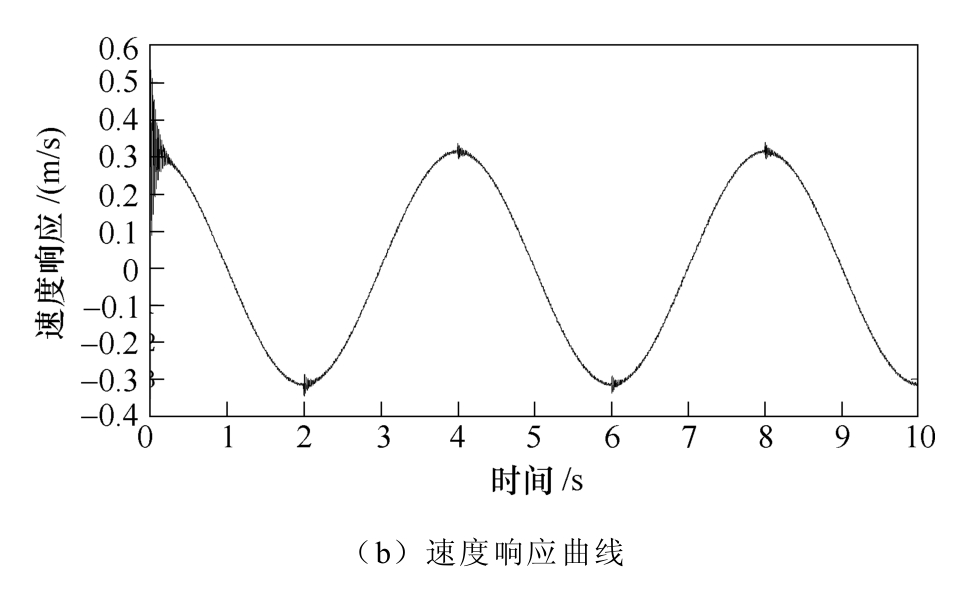
图14 积分反推控制系统响应曲线（二）
Fig.14 Response curves of integral backstepping control system (2)
图15 自适应改进Elman神经网络积分反推控制系统 响应曲线（二）
Fig.15 Response curves of the adaptive modified Elman neural network integral backstepping control system (2)
对速度响应曲线进行比较。从宏观上来看，图15b的速度输出曲线更平滑，且超调较少；从数值上来看，在电机起动瞬间和运行方向改变时，图14b都经过了0.3s恢复稳定速度运行，而图15b则在超调的瞬间恢复到稳定运行状态；对比可得，自适应改进Elman神经网络积分反推控制具有更好的快速性。
4 结论
本文采用一种基于自适应改进Elman神经网络积分反推控制方法来控制PMLSM伺服系统跟踪参考轨迹。首先利用积分反推控制方法使系统获得了良好的稳定性能；然后采用精度高、鲁棒性好的自适应改进Elman神经网络来估计存在的不确定性；最后通过仿真和实验得到位置跟踪曲线和速度响应曲线，对比可知自适应改进Elman神经网络积分反推控制具有更好的跟踪性能、鲁棒性能和稳定性能。
[1]Panah P G, Ataei M, Mirzaeian B, et al. A robust adaptive sliding mode control for PMLSM with variable velocity profile over wide range[J]. Research Journal of Applied Sciences Engineering & Technology, 2015, 10(9): 997-1006.
[2]王丽梅, 张宗雪. H型精密运动平台交叉耦合模糊PID同步控制[J]. 沈阳工业大学学报, 2018, 40(1): 1-5. Wang Limai, Zhang Zongxue. Cross-coupled fuzzy PID synchronous control for H-type precision motion platform[J]. Journal of Shenyang University of Technology, 2018, 40(1): 1-5.
[3]朱国昕, 雷鸣凯, 赵希梅. 永磁同步电机伺服系统自适应迭代学习控制[J].沈阳工业大学学报, 2018, 40(1): 6-11. Zhu Guoxin, Lei Mingkai, Zhao Ximei. Adaptive iterative learning control for permanent magnet synchronous motor servo system[J]. Journal of Shenyang University of Technology, 2018, 40(1): 6-11.
[4]赵希梅, 吴勇慷. 基于多阶段速度规划的PMLSM自适应反推滑模控制[J]. 电工技术学报, 2018, 33(3): 662-669. Zhao Ximei, Wu Yongkang. Adaptive backstepping siding mode control for PMLSM based on multi- segment velocity planning[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 662-669.
[5]Hocine A, Benalia A. Sensorless fault tolerant control for induction motors using: backstepping strategy and sliding mode observer[C]//8th International Con- ference on Modelling, Identification and Control, Algiers, 2017: 1020-1028.
[6]余洋, 郭旭东, 郑晓明, 等. 基于反推控制的机械弹性储能永磁同步电机最大转矩电流比控制[J]. 电工技术学报, 2017, 32(22): 82-90. Yu Yang, Guo Xudong, Zheng Xiaoming, et al. Back- stepping control based maximum torque per ampere control of permanent magnet synchronous motor for mechanical elastic energy storage[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 82-90.
[7]Lin Chih-Hong, Lin Chih-Peng. Integral backstepping control for a permanent magnet synchronous motor using adaptive recurrent neural network uncertainty observer[J]. International Journal of Engineering & Technology Innovation, 2012, 1(1): 777-780.
[8]Shao Mingling, Yu Haisheng, Yu Jinpeng, et al. Position control of permanent magnet synchronous motor speed sensorless servo system via back- stepping[C]//27th Chinese Control and Decision Conference, Qingdao, 2015: 4089-4094.
[9]Yu Jinpeng, Shi Peng, Dong Wenjie, et al. Neural network-based adaptive dynamic surface control for permanent magnet synchronous motors[J]. IEEE Transactions on Neural Networks & Learning Systems, 2015, 26(3): 640-645.
[10]Wang Limei, Li Xiaobin. Position sensorless control for PMLSM using Elman neural network[C]//Inter- national Conference on Information Engineering and Computer Science, Wuhan, 2009: 1-4.
[11]Lin Chih-Hong. Dynamic control of V-belt con- tinuously variable transmission-driven electric scooter using hybrid modified recurrent legendre neural network control system[J]. Nonlinear Dynamics, 2015, 79(2): 787-808.