0 引言
学者早在20世纪20年代初期就提出了同步磁阻电机（Synchronous Reluctance Motor, SynRM）的概念[1]。文献[1]提出的同步磁阻电机结构凸极比低，转矩脉动大，难以正常运行。文献[2]提出了块状转子式的同步磁阻电机结构，凸极比有所增加，但需要较大励磁电流以建立磁场，导致电机效率、功率因数均较低，难以推广使用。目前，广泛应用的同步磁阻电机转子无永磁体或绕组，结构简单，成本低，耐高温性能好[3]，成为了近年来的研究热 点[4]。但同步磁阻电机的运行性能受磁路饱和程度影响很大，且功率因数较低[5]，为了进一步提高同步磁阻电机的性能，除优化设计电机结构外，还需要高性能的控制策略。
同步磁阻电机高性能控制策略的研究从20世纪90年代开始兴起[6]。现行使用较多的控制方法为矢量控制（Vector Control, VC）与直接转矩控制（Direct Torque Control, DTC）。同步磁阻电机的矢量控制策略研究较为成熟，通过调整d、q轴电流大小，可方便地实现多种控制方式，如最大转矩电流比（Maximum Torque Per-Ampere, MTPA）控制，最大功率因数控制（Maximum Power Factor Control, MPFC）、最大效率控制（Maximum Efficiency Control, MEC）等[7-9]。矢量控制策略控制精度较高，但转矩响应与转速响应较慢。
直接转矩控制策略直接对电机的磁链和转矩进行控制，可大幅提高电机转矩响应速度[10]。文献[11]论述了直接转矩控制应用于异步电机、永磁同步电机与同步磁阻电机上的异同，提出了同步磁阻电机直接转矩控制面临的问题，并对四极轴向叠片式转子电机进行实验，验证了同步磁阻电机在直接转矩控制下具有较高的抗扰动能力和快速的动态响应能力。另外，同步磁阻电机优秀的弱磁性能可在直接转矩控制中得到良好的体现。文献[12-13]在直接转矩控制的基础上对电机进行弱磁控制，使电机运行转速范围进一步扩大。
将MTPA算法应用于直接转矩控制，可以降低电机运行时的损耗，文献[14]在磁链给定环节加入MTPA算法，但未考虑磁路饱和的影响。同步磁阻电机依靠高凸极比产生磁阻转矩运行，电机常运行在饱和或深度饱和状态下，若不计及饱和的影响，则控制性能难以提高。
同时，上述文献均使用了传统直接转矩控制策略，虽然实现简单，但在一个控制周期内逆变器只输出8个基本电压空间矢量之一，磁链轨迹不光滑，转矩和磁链脉动较大，静态性能不理想，需要大幅增大驱动器开关频率以抑制转矩脉动[15]。为解决上述问题，文献[16-17]以磁链矢量方向为x轴，建立x-y坐标系，重新对磁链、电流进行坐标变换，增设两个PI控制器，对磁链、电流进行闭环控制，形成了直接磁链电流矢量控制，再利用空间矢量调制（Space Vector Modulation, SVM）技术输出电压，减小了电机的转矩脉动。但对磁链与电流进行PI控制在一定程度上损失了直接转矩控制的转矩快速响应性能，且PI控制器数量较多，难以整定参数。
为在保证快速转矩响应的基础上改进电机的运行性能，本文将SVM技术引入传统直接转矩控制，实现磁链轨迹圆化，减小电机转矩脉动。同时，利用MTPA算法降低了电机运行损耗，并在考虑电机磁路影响的情况下建立控制模型，对电机进行精确控制。
1 同步磁阻电机模型
1.1 同步磁阻电机数学模型
图1展示了同步磁阻电机静止坐标系α-β、旋转坐标系d-q及其相对位置角θ。ds轴为定子磁链矢量轴，与定子磁链矢量λs方向一致。γ 为定子电流与d轴夹角，称为电流角。δ 为定子磁链与d轴夹角，称为磁链角。θs为磁链矢量与α 轴夹角，称为磁链矢量位置角。通常，同步磁阻电机的数学模型建立在d-q轴坐标系中，其电压方程为
式中，vd、vq分别为定子电压矢量在d-q轴上的分量；id、iq分别为定子电流矢量在d-q轴上的分量；λd、λq分别为定子磁链矢量在d-q轴上的分量；ωe为电角速度；Rs为定子电阻。
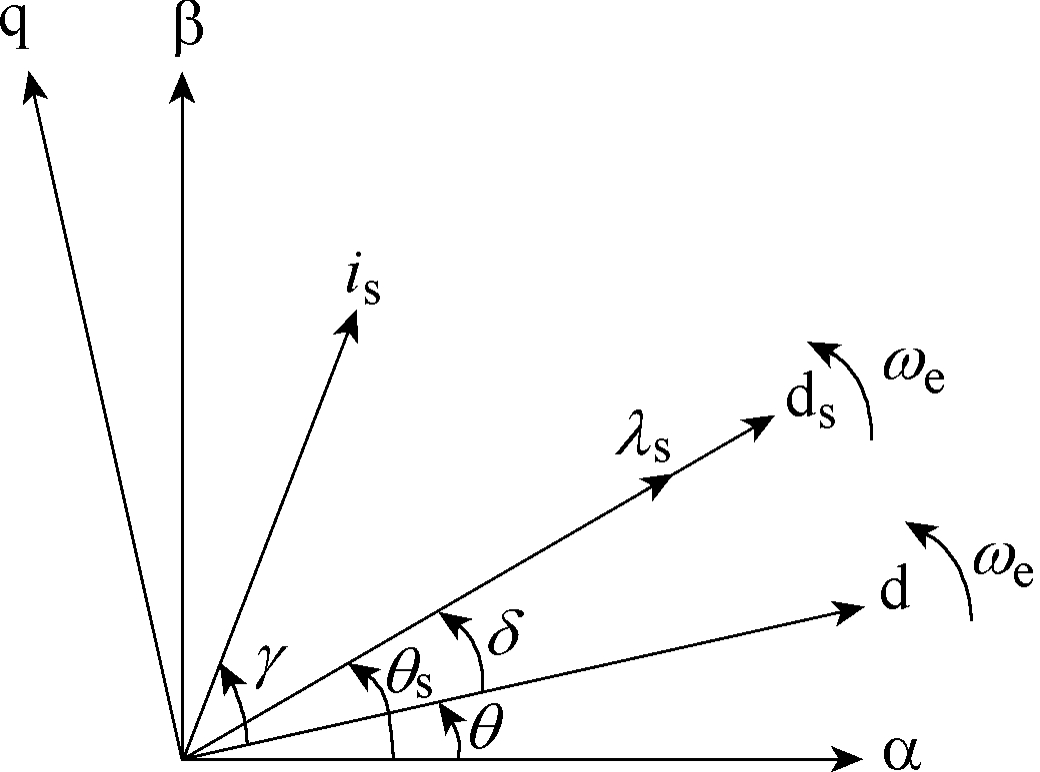
图1 参考坐标系与定子磁链矢量轴
Fig.1 Reference coordinate and axis of stator flux vector
同步磁阻电机依靠磁阻转矩运行，其电磁转矩可表示为
式中，p为电机极对数。
电机定子磁链可表示为
式中，Ld、Lq分别为d、q轴电感。
定子磁链在d、q轴上的分量可表示为
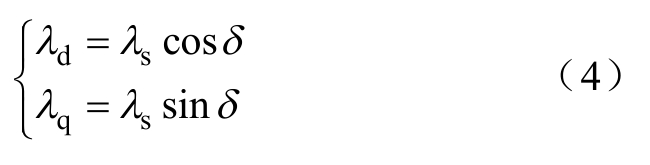
式中，λs为定子磁链幅值。将式（3）和式（4）代入式（2），则电机电磁转矩也可表示为
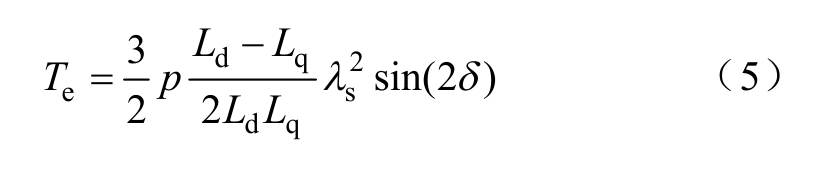
1.2 同步磁阻电机饱和与交叉饱和现象
为利用同步磁阻电机的高凸极比产生额定的转矩，电机在工作时多处于饱和或深度饱和状态。图2展示了d、q轴电感与d、q轴电流的关系曲面，其中，电感值由有限元计算得到。可见同步磁阻电机d轴电感受饱和影响很大，q轴电感受饱和影响较小，但在电流较小时，其值明显随电流变化而变化。
另外，由图3可见，λq(0, iq) 与λq(9, iq) 两条曲线不重合，即当电流iq值相同、id值不同时，λq值明显不同，可知电机q轴电感受交叉饱和影响很大。同理可知，d轴电感在中度饱和时也明显受到交叉饱和的影响。
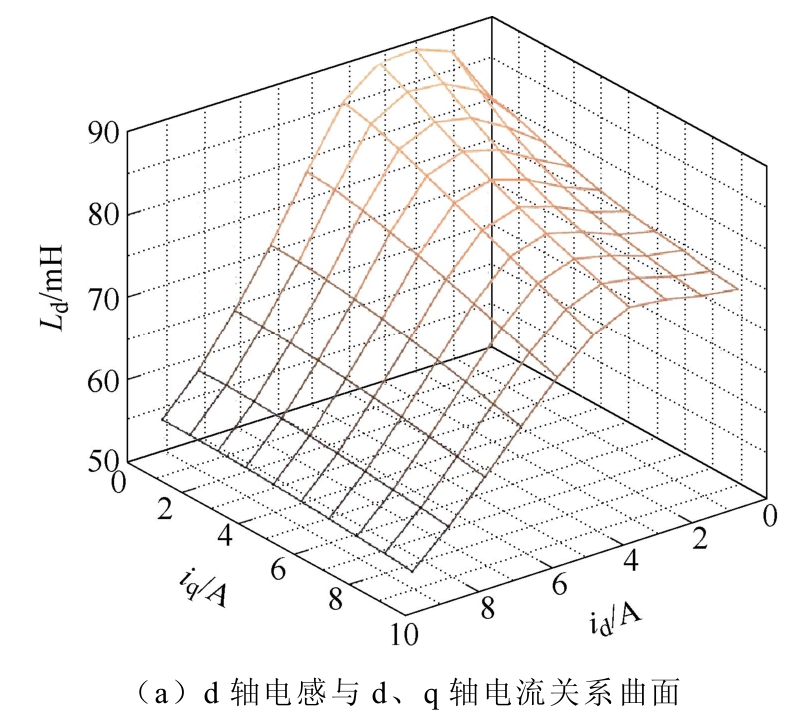
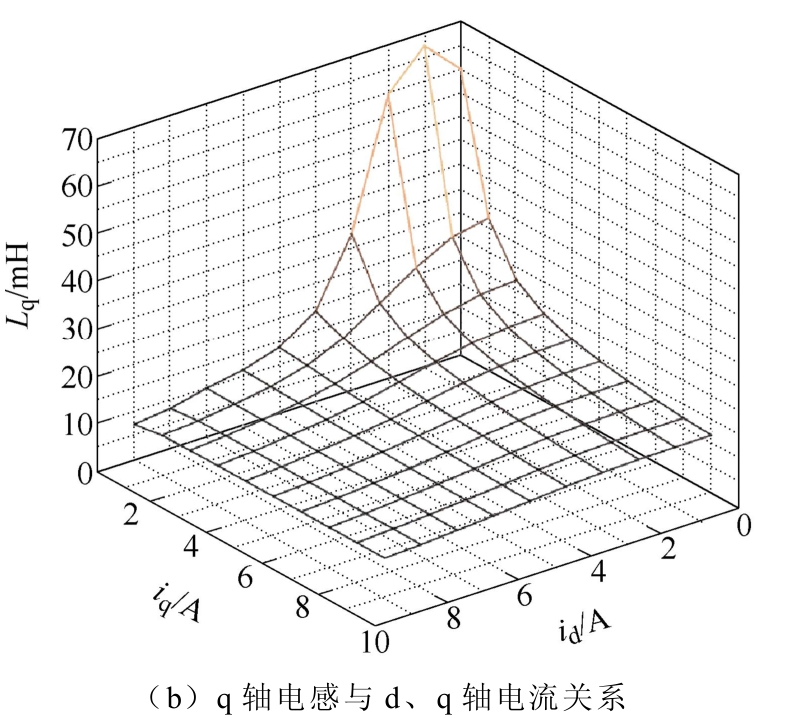
图2 d、q轴电感与d、q轴电流关系
Fig.2 Inductance and current relation of d-axis and q-axis
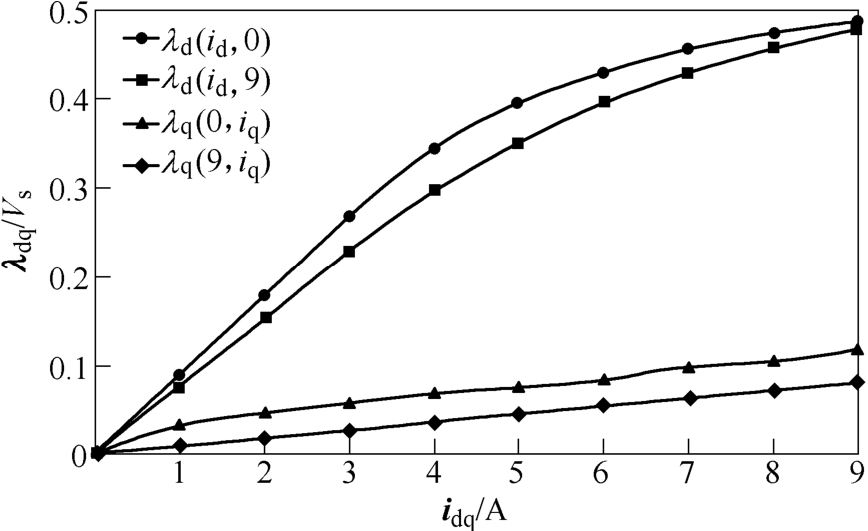
图3 同步磁阻电机磁链电流关系曲线
Fig.3 Flux linkage and current relation curves of SynRM
因此，若忽略磁路饱和的影响，认为d、q轴电感为恒值，则无法得到最优的控制效果。式（3）应改写为
考虑饱和与交叉饱和后，利用查表法得到准确Ld、Lq数值后用于计算。
2 基于MTPA的同步磁阻电机DTC-SVM控制原理
2.1 控制流程
本文提出的基于MTPA的DTC-SVM控制策略流程如图4所示。通过对转速误差进行PI计算可得 到转矩给定
磁链幅值给定 
由转矩给定通过MTPA算法查表得到。磁链变化角给定Δδ*由转矩 误差经PI计算得到。参考电压计算模块代替了传统DTC控制中的滞环比较环节，通过磁链变化角给定Δδ*，结合电机当前的磁链幅值λs、磁链位置角θs等信息，利用转矩、磁链误差计算出所需的电压矢量。随后通过SVM技术[18]，利用基础电压空间矢量调制输出所需的任意电压空间矢量，代替了传统DTC中的电压矢量查表输出，可减小转矩、磁链脉动，并固定逆变器的开关频率。同时，整个控制流程中仅需2个PI控制器，便于参数整定。另外，磁链转矩观测器可观测实时转矩、磁链幅值与磁链矢量位置，用于转矩、磁链的闭环控制。可见，本控制策略改进了传统DTC策略，在改进的转矩、磁链闭环控制的基础上，又融入了MTPA策略与SVM方法。
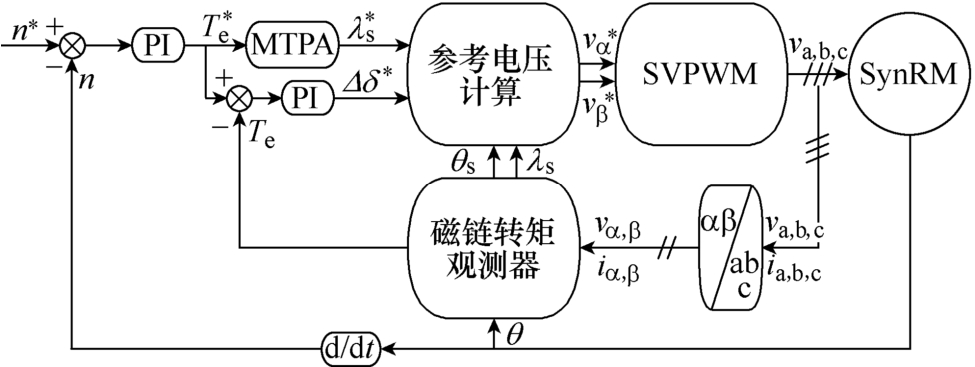
图4 基于MTPA的DTC-SVM控制流程
Fig.4 The DTC-SVM control flow diagram based on MTPA
2.2 考虑饱和的MTPA磁链给定算法
由于同步磁阻电机转子铁耗很小，故当电机运行于低速或中低速（通常为10 000r/min以下）时，铜耗为主要损耗。在传统DTC中，磁链给定为常数，一般与额定工况下磁链幅值一致，但此时电机电流幅值并非最小值，铜耗较大。MTPA算法能使电机铜耗最小化，是同步磁阻电机高性能控制策略的首选。然而，为减少计算量，简化控制，文献[19-20]忽略了电机饱和影响，认为d、q轴电感恒定，将MTPA简化为恒电流角控制，即取电流角γ 为45°，则根据式（5），电机的转矩-磁链关系式为
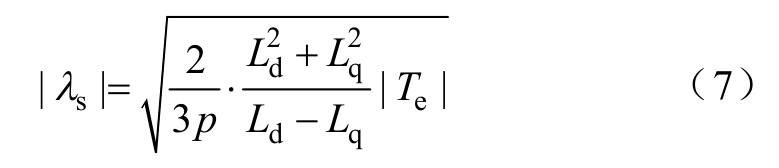
但同步磁阻电机常运行在饱和或深度饱和状态，d、q轴电感受电流影响很大，考虑饱和的MTPA才能够使电机铜耗最小化。故而本文由有限元分析结果，得到不同定子电流下的转矩与电感值，进而根据考虑磁路饱和的MTPA算法[21]，得到电机真实的MTPA曲线，如图5a所示，再根据式（2）和式（3）计算得到转矩-磁链关系曲线，如图5b所示。可见，考虑磁路饱和的转矩-磁链关系曲线与不考虑饱和（取电流角为45°）时的曲线存在一定的差距。控制时，磁链幅值给定应由转矩给定通过考虑饱和的转矩-磁链关系曲线查表得到。
图5 考虑饱和的转矩-磁链关系曲线
Fig.5 The torque-flux trajectory considering the saturation
2.3 参考电压计算
同步磁阻电机定子磁链公式为
式中，vs为定子电压矢量；is为定子电流矢量。通过输出不同方向与大小的电压空间矢量，可调节定子磁链位置与幅值大小。由式（5）可知，在磁链幅值保持不变的情况下，改变磁链角δ（即改变磁链矢量位置角θs）可快速调节转矩。由图6可知，
式中，Δδ*由转矩误差eT经PI计算得到，其计算公式为 Δδ*=KpeT+KiΣeT，其中，Ki、Kp分别为PI调节中的积分调节系数与比例调节系数。
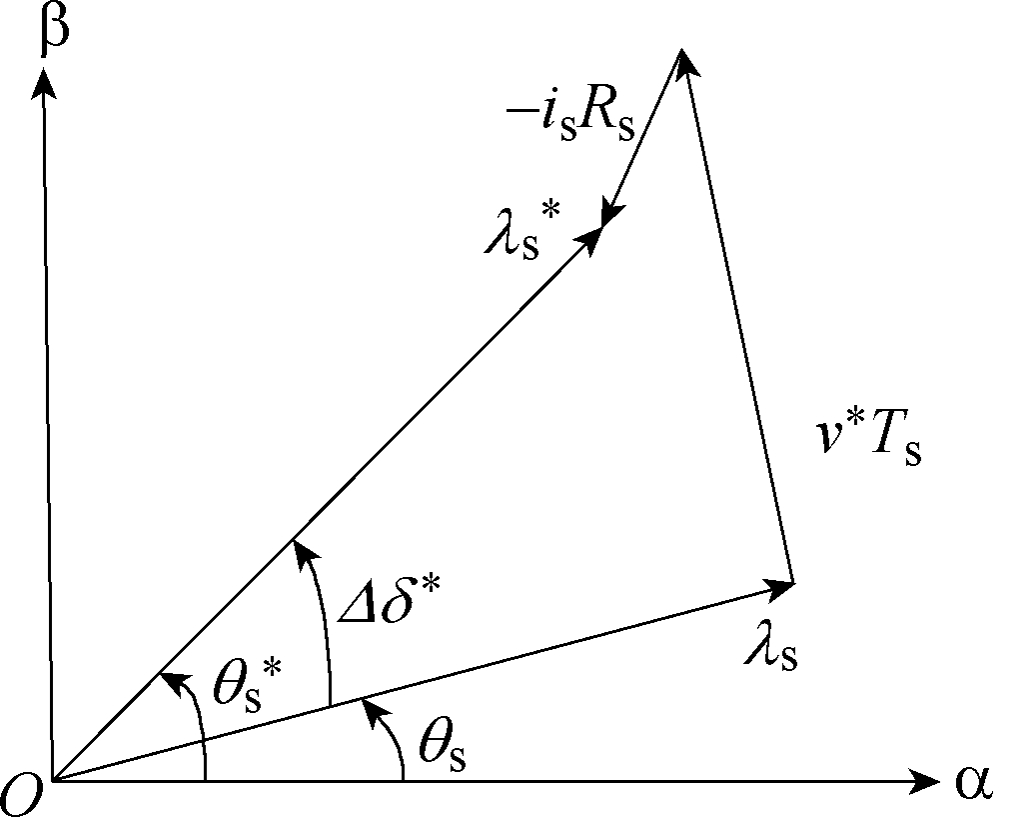
图6 定子电压、电流与磁链矢量
Fig.6 Vector diagram of the stator voltage, current and flux linkage
最终，参考电压在α-β 轴上的分量vα、vβ 由磁链幅值给定以及当前磁链幅值的误差在α-β 轴上的分量计算得到：
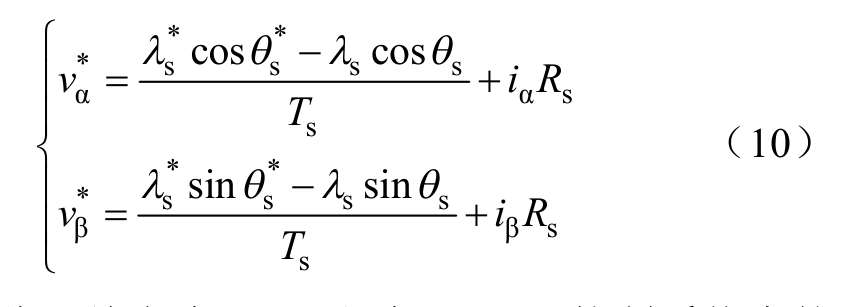
因此，结合式（9）和式（10），控制系统中的参考电压由转矩、磁链误差计算得到，实现了转矩、磁链闭环控制。
2.4 磁链转矩观测
本文使用的定子磁链观测器由磁链的反电动势模型式（8）与电流模型式（6）共同构成，如图7所示，其传递函数为
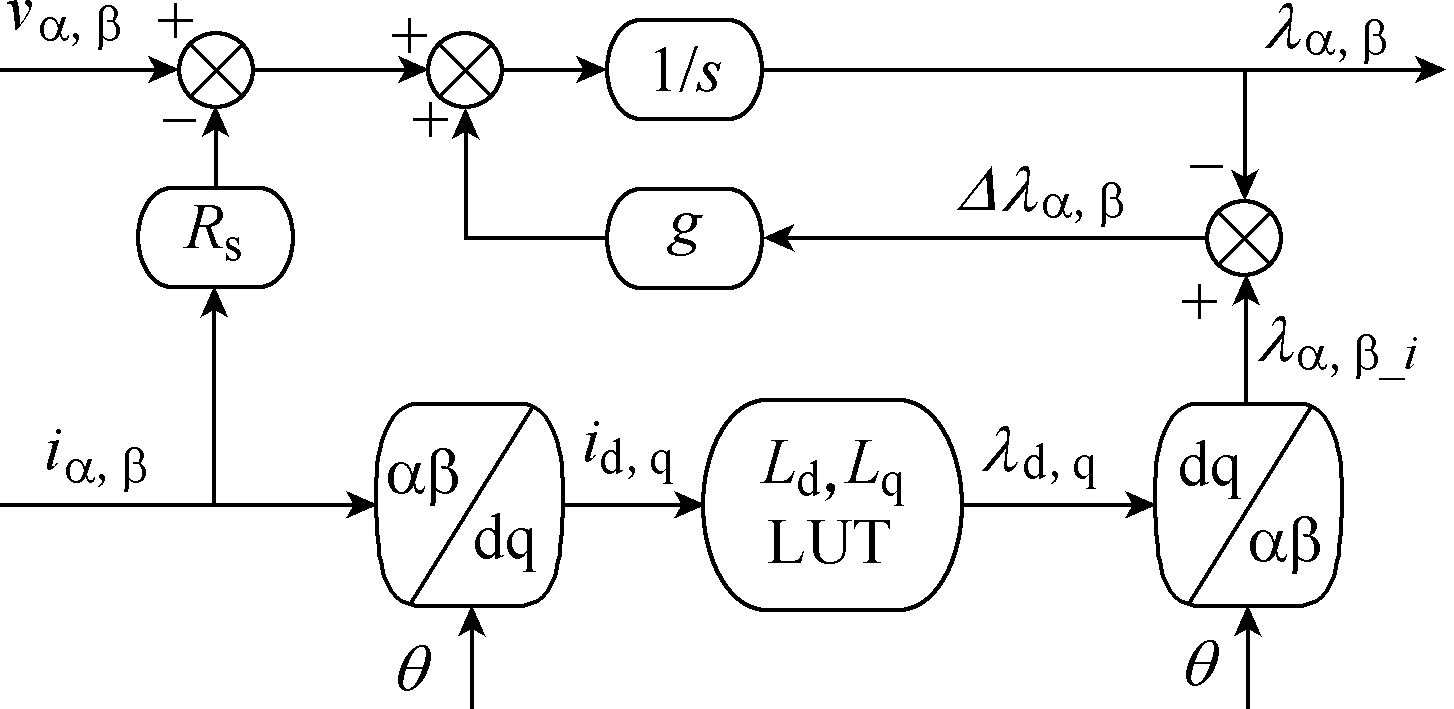
图7 定子磁链观测器
Fig.7 Stator flux linkage observer
当电机电角速度ωe＜g时，磁链主要由电流模型计算得到，避免了电机在低速时反电动势小，电压模型计算不准确的问题。当电机电角速度ωe＞g时，磁链主要由电压模型计算得到，避免了高速时磁链受铁心损耗等的影响[22]。磁链幅值、相位、转矩计算式为
3 仿真验证
为验证本文提出的控制策略的可行性，本节在在Matlab/Simulink中搭建了仿真模型。仿真模型与图4原理一致，表1给出了仿真模型中的控制参数。仿真中使用的电机模型与下文实验验证中使用的电机参数一致，见表2。
表1 仿真模型中的控制参数
Tab.1 Control parameters in simulation model
控制模块 参 数 数 值 Kp 0.07 转速PI模块 Ki 0.046 Kp 0.03 转矩PI模块 Ki 0.03 磁链转矩观测模块 g 120
表2 同步磁阻电机参数
Tab.2 Parameters of SynRM
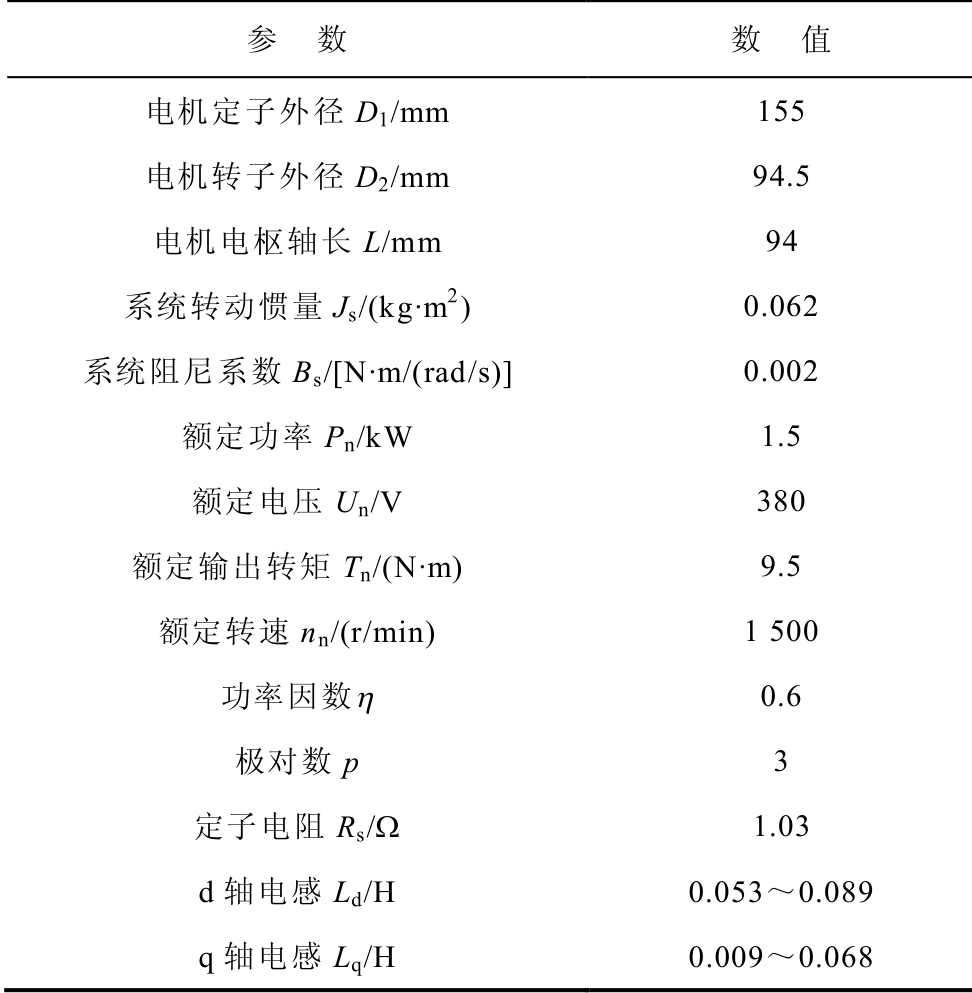
参 数 数 值 电机定子外径D1/mm 155 电机转子外径D2/mm 94.5 电机电枢轴长L/mm 94 系统转动惯量Js/(kg·m2) 0.062 系统阻尼系数Bs/[N·m/(rad/s)]0.002 额定功率Pn/kW 1.5 额定电压Un/V 380 额定输出转矩Tn/(N·m) 9.5 额定转速nn/(r/min) 1 500 功率因数η 0.6 极对数p 3 定子电阻Rs/Ω 1.03 d轴电感Ld/H 0.053～0.089 q轴电感Lq/H 0.009～0.068
恒负载起动与变速仿真结果如图8所示，起动转速阶跃给定为500r/min，负载给定为5N·m。起动时，电机转矩响应快，以较大起动转矩起动，速度响应也较快，当转速稳定在500r/min后，转矩可稳定在5N·m。4s时将转速给定阶跃增大至1 000r/min，可见电机以较大转矩加速，转矩、转速响应较快，当转速稳定在1 000r/min后，转矩依然稳定在5N·m。
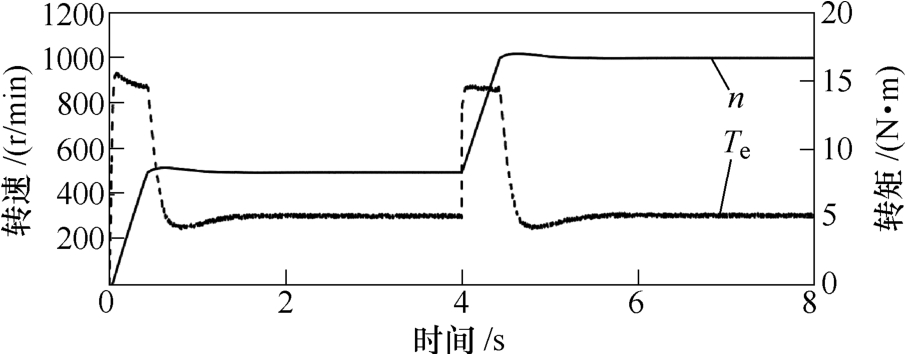
图8 恒负载（5N·m）起动与变速（500r/min→1 000r/min）实验仿真结果
Fig.8 Simulation results of starting and variable speed (500r/min→1 000r/min) experiment with constant torque (5N·m)
图9显示了恒速变负载实验结果。如图9a所示，初始时电机转速为1 000r/min，负载为6N·m。2s时，负载转矩突增至8N·m；6s时负载转矩突降至7N·m。可见，在变负载的过程中，电机转速略有跌落或超调，但可很快恢复至给定转速。电机电磁转矩可良好地跟随负载转矩，稳态运转时，转矩脉动不超过±0.2N·m（6.7%）。图9b展示了电机稳态运行时三相定子线电流曲线，可见在SVM方法控制下，电机三相电流基本成正弦。本文提出的控制策略可行，性能良好。
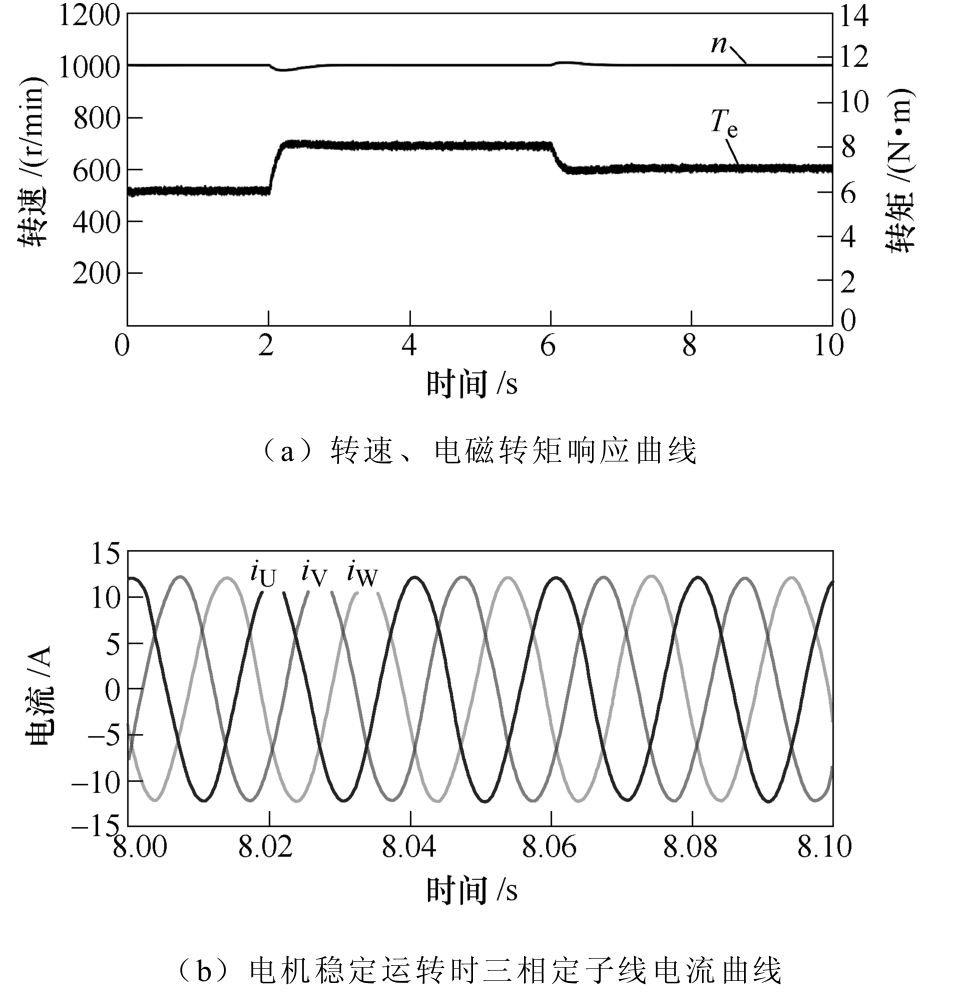
图9 恒速（1 000r/min）变负载（6N·m→8N·m→7N·m）仿真结果
Fig.9 Simulation results of variable load (6N·m→8N·m→7N·m) experiment with constant speed (1 000r/min)
4 实验结果与分析
实验所用同步磁阻电机绕组为三角形连接，其参数见表2。图10展示了实验装置实物图。直流电源A为逆变器提供直流母线电压，主控板使用STM32F407芯片作为微处理器芯片，其中运行的控制程序接受电机电流、电压、转子位置等信号，依据本文提出的控制方法进行计算，输出开关信号控制逆变器运行，从而驱动同步磁阻电机运行。光电编码器、转矩传感器、负载与电机同轴相连，其分别具有检测转子位置、检测电机稳态转矩、提供稳定负载等功能，直流电源B为转矩传感器供电。实验中，PWM控制频率为10kHz。实验中的控制参数见表3。
表3 实验中的控制参数
Tab.3 Control parameters in experiments
控制模块 参 数 数 值 Kp 0.04 转速PI模块 Ki 0.022 Kp 0.07 转矩PI模块 Ki 0.075 磁链转矩观测模块 g 120
图10 同步磁阻电机驱动控制实验装置实物图
Fig.10 Physical charts of synchronous reluctance motor drive and control experimental device
4.1 空载实验
空载实验中，负载转矩为零，起动转速阶跃给定为500r/min，如图11所示，电机起动时，转速可在0.3s之内达到500r/min，随后产生10r/min（2%）的转速超调，经过闭环调节后，转速可在1s之内稳定在500r/min，稳定后，转速波动为±2r/min（0.8%）。随后，3.6s左右时将转速给定突增至1 000r/min，此时，电机转速可在0.2s内增至1 000r/min，但后续存在10r/min（1%）的转速超调，经1s闭环调节后，转速可稳定在1 000r/min。由空载实验可见，同步磁阻电机在本文提出的控制策略下，转速响应很快，转速跟随性较好，且转速波动很小。
图11 空载变速（500r/min→1 000r/min）实验结果
Fig.11 Experimental results of variable speed (500r/min→1 000r/min) with no-load
4.2 负载实验
为验证本控制策略的带负载能力与MTPA策略的有效性，本节样机进行了负载实验分析。
如图12a～图12c所示，0～8s内，电机给定转速1 000r/min，给定负载6.5N·m，此时电机输出转矩稳定在6.5N·m，转矩脉动在±0.2N·m（6%）以内，转速波动在±2r/min（0.4%）以内，电机定子磁链可以很好地跟随MTPA给定，保持为0.38Vs，磁链波动小于±0.01Vs（5.3%）。
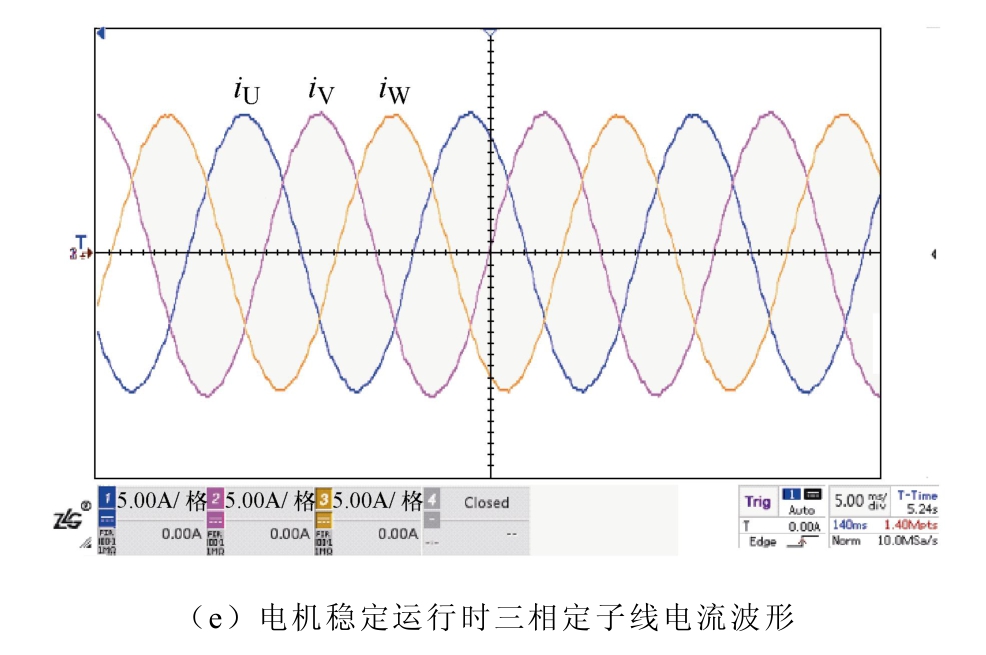
图12 恒速（1 000r/min）变负载（6.5N·m→7.7N·m→7.0N·m）实验结果
Fig.12 Experimental results of content speed (1 000r/min) with variable load (6.5N·m→7.7N·m→7.0N·m)
8s时，负载突加至7.7N·m，此时电机转矩响应很快，可在0.5s内达到7.7N·m并保持稳定。根据MTPA曲线，此时磁链给定增至0.4Vs，电机定子磁链也可快速跟随给定变化，在0.5s内达到给定值。突加负载时，转速跌落约12r/min（1.2%），但经过转速环调节后，可在1s内恢复至1 000r/min。
9～15s内，电机稳定运行于1 000r/min，转速波动范围在±2r/min（0.4%）以内，转矩脉动小于±0.3N·m（7.7%），磁链波动范围约为±0.01Vs（5%）。
15s时负载突减至7N·m，电机转矩响应较快，可在0.4s内跟随负载变化并保持稳定。此时，根据MTPA曲线，磁链给定为0.39Vs，电机定子磁链可在0.4s内跟随给定并保持稳定。突减负载时，转速超调约9r/min（0.9%），可在1s内恢复并保持稳定。
16s～20s内，电机稳定运行于1 000r/min，转速波动范围约为±2r/min（0.4%），转矩脉动小于±0.2N·m（5.7%），磁链波动在±0.01Vs（5.1%） 以内。
图12d展示了上述过程中电机三相线电流波形。可见，随着负载增减，电流幅值动态响应过程也较快。图12e展示了电机在后续稳态运行（1 000r/min，7N·m）时的三相定子线电流波形，电流波形基本正弦。可见，在本控制策略下，同步磁阻电机负载性能良好，动态响应较快，且稳态运行时，电机转速稳定，转矩脉动较小。
由图12c可见，当负载变化时，电机定子磁链也可跟随转矩-磁链关系曲线运行。为进一步验证实验中MTPA策略的有效性，本文在同样的负载状态下进行了使用和不使用MTPA策略的对照实验，在不使用MTPA策略时，磁链给定与电机额定工况下磁链幅值一致。图13绘制出电机负载（5N·m→6.2N·m→7.7N·m）时，在MTPA策略与非MTPA策略控制下的定子线电流幅值曲线。可见，电机在MTPA控制下的定子线电流幅值（is_MTPA）明显小于非MTPA控制下的定子线电流幅值（is），随着负载接近额定值，两者差距减小。可见，电机在MTPA控制下，电流幅值较小，从而降低了电机绕组铜耗。
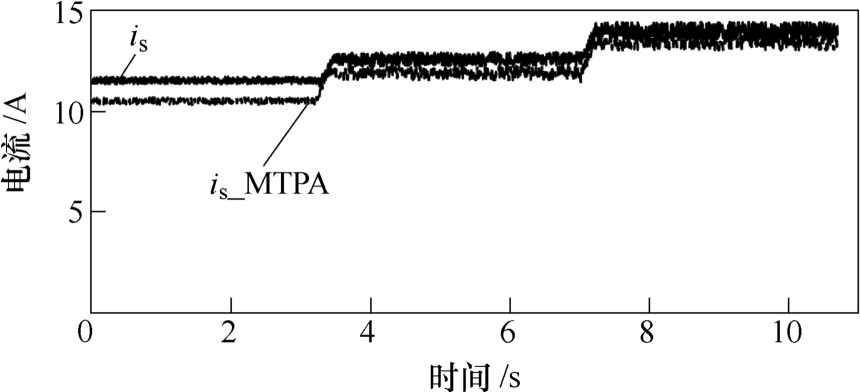
图13 恒速（1 000r/min）变负载（5N·m→6.2N·m→7.7N·m）时定子线电流幅值曲线
Fig.13 Amplitude of stator current of content speed (1 000r/min) with variable load (5N·m→6.2N·m→7.7N·m)
图14绘制了当电机转速为1 000r/min，负载为5N·m时的α-β 轴磁链轨迹曲线，可见，在SVM技术下，逆变器可实时斩波输出所需电压矢量，电机α-β 轴磁链轨迹光滑，圆度较好。
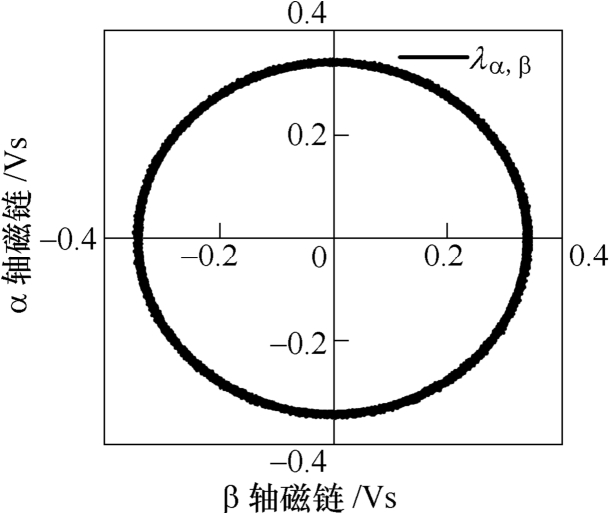
图14 α-β 轴磁链轨迹曲线 （转速1 000r/min，负载5N·m）
Fig.14 Flux linkage trajectory curve on the α-β axis
5 结论
为提高同步磁阻电机的转矩响应速度，并进一步提高电机运行性能，本文在传统直接转矩控制策略中，引入SVM技术，降低电机磁链和转矩脉动，实现了磁链轨迹圆化。同时，为了降低电机损耗，本文将MTPA控制思想引入直接转矩控制，并在考虑电机饱和的情况下，对电机进行精确控制，使电机输出给定转矩时的电流幅值最小，从而降低了电机铜耗。
经过仿真分析与实验验证，本文提出的控制策略具有较好的静态性能与动态性能，实验结果表明，电机转速、转矩响应较快，稳态运行时脉动小，抗干扰能力强，磁链轨迹光滑，且电机能够运行在MTPA曲线上，定子电流幅值较小，电机铜耗较小。
[1]Kostko J K. Polyphase reaction synchronous motors[J]. Journal of the American Institute of Electrical Engineers, 1923, 42(11): 1162-1168.
[2]Lawrenson P J, Agu L A. Theory and performance of polyphase reluctance machines[J]. Proceedings of the Institution of Electrical Engineers, 1964, 111(8): 1435-1445.
[3]沈建新, 蔡顺, 袁赛赛. 同步磁阻电机分析与设计(连载之一)概述[J]. 微电机, 2016(10): 72-79. Shen Jianxin, Cai Shun, Yuan Saisai. Analysis and design of synchronous reluctance machines Part I: an overview[J]. Micromotors, 2016(10): 72-79.
[4]赵争鸣. 新型同步磁阻永磁电机发展及现状[J]. 电工电能新技术, 1998(3): 22-25. Zhao Zhengming. Review for the development of a novel synchronous reluctance and permanent magnet machine[J]. Advanced Technology of Electrical Engineering and Energy, 1998(3): 22-25.
[5]Cai Shun, Jin Mengjia, Hao He, et al. Comparative study on synchronous reluctance and PM machines[J]. Compel International Journal of Computations & Mathe- matics in Electrical, 2016, 35(2): 607-623.
[6]Betz R E. Theoretical aspects of control of synchronous reluctance machines[J]. IEE Proceedings B-Electric Power Applications, 1992, 139(4): 355-364.
[7]Betz R E, Lagerquist R, Jovanovic M, et al. Control of synchronous reluctance machines[J]. IEEE Transa- ctions on Industry Applications, 1993, 29(6): 1110- 1122.
[8]Kang S J, Sul S K. Efficiency optimized vector control of synchronous reluctance motor[C]//Industry Applications Conference, San Diego, USA, 1996: 117-121.
[9]Singh B, Varshney A. Maximum power factor based vector control approach for synchronous reluctance motor driven solar PV array fed water pumping system[C]//IEEE Power India International Confer- ence, Delhi, India, 2016: 1-6.
[10]Takahashi I, Noguchi T. A new quick-response and high-efficiency control strategy of an induction motor[J]. IEEE Transactions on Industry Appli- cations, 1986, 22(5): 820-827.
[11]周立求. ALA转子同步磁阻电机直接转矩控制系统研究[D]. 武汉: 华中科技大学, 2005.
[12]Zhang Xinan, Foo G H B. A robust field-weakening algorithm based on duty ratio regulation for direct torque controlled synchronous reluctance motor[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(2): 765-773.
[13]Foo G H B, Zhang Xinan. Robust direct torque control of synchronous reluctance motor drives in the field-weakening region[J]. IEEE Transactions on Power Electronics, 2016, 32(2): 1289-1298.
[14]Foo G H B, Zhang Xinan. Robust constant switching frequency-based field-weakening algorithm for direct torque controlled reluctance synchronous motors[J]. IEEE Transactions on Industrial Informatics, 2016, 12(4): 1462-1473.
[15]Wiedemann S, Dziechciarz A. Comparative evaluation of DTC strategies for the Synchronous Reluctance machine[C]//Tenth International Conference on Ecological Vehicles and Renewable Energies, Monte- Carlo, Monaco, 2015: 1-5.
[16]Yousefi-Talouki A, Pellegrino G. Sensorless direct flux vector control of synchronous reluctance motor drives in a wide speed range including standstill[C]// Xxii International Conference on Electrical Machines, Lausanne, Switzerland, 2016: 1167-1173.
[17]解良, 刘思贝, 姚文熙, 等. 基于空间矢量的同步磁阻电机直接转矩控制[J]. 机电工程, 2017(10): 1156-1161. Jie Liang, Liu Sibei, Yao Wenxi, et al. Direct torque control for synchronous reluctance motor based on space vector modulation[J]. Journal of Mechanical & Electrical Engineering, 2017(10): 1156-1161.
[18]杜佳星. 同步磁阻电机的矢量控制研究[D]. 武汉:华中科技大学, 2006.
[19]Zhang Xinan, Foo G H B, Vilathgamuwa D M, et al. An improved robust field-weakeaning algorithm for direct-torque-controlled synchronous-reluctance-motor drives[J]. IEEE Transactions on Industrial Electro- nics, 2015, 62(5): 3255-3264.
[20]Inoue Y, Morimoto S, Sanada M. A novel control scheme for maximum power operation of synchronous reluctance motors including maximum torque per flux control[J]. IEEE Transactions on Industry Appli- cations, 2009, 47(1): 115-121.
[21]谭泳涛. 铁氧体永磁同步电动机的优化设计和矢量控制策略研究[D]. 杭州: 浙江大学, 2018.
[22]Vagati A, Pastorelli M, Franceschini G, et al. Flux- observer-based high-performance control of synchronous reluctance motors by including cross saturation[J]. IEEE Transactions on Industry Applications, 2002, 35(3): 597-605.