0 引言
普通同步电机转子上只有一套励磁绕组,这决定了其静态稳定极限功角不能超过90°,限制了发电机的稳定运行范围。双轴励磁同步电机(以下简称“双励机”)在转子直轴和交轴均设有励磁绕组,能够通过调节两相励磁绕组的励磁电流使合成励磁磁动势处于转子任意位置,大大提高了发电机的稳定运行范围[1-4]。然而,双励机转子具有一套两相励磁绕组,使得其转子绕组及磁路结构与普通同步电机存在明显差异,在电机运行特性分析中主要体现在磁场分布和同步电抗的不同。因此,研究双励机与普通同步电机同步电抗的差异及其在不同运行工况下的变化规律对于进一步研究双励机的运行特性及稳定运行能力具有重要意义。
普通同步电机的同步电抗通常采用电磁计算公式获得,再利用空载特性曲线对其进行修正,从而得到电抗的饱和值。该方法能够较好地反映空载情况下的同步电抗,但是无法反映负载变化对同步电抗的影响[5]。文献[6]指出同步电机负载条件下的磁场饱和及畸变与空载时存在明显差别,导致负载时的同步电抗与空载时不同。为了研究负载变化对同步电抗的影响,通常采用有限元法来计算同步电抗,该方法不仅可以充分考虑同步电机运行过程中的各种非线性因素,还能通过固定磁导率法对不同运行工况下的同步电抗进行计算[7-10]。文献[11]采用有限元法计算了发电机同步电抗并与设计值进行了对比,发现两者存在明显差别。文献[12]提出采用随转子角变化的定子电感矩阵特征值来间接获取同步电机的同步电抗,计算结果与直接采用有限元方法的计算结果非常接近。目前,对双励机的研究主要集中在励磁控制方法的研究[13-14],而在双励机磁场分布、同步电抗等运行特性和参数方面的研究则较少。
为了研究双励机同步电抗与普通同步电机的差异,以及双励机同步电抗随运行工况的变化规律。本文基于文献[15]建立了双励机的时步有限元模型,对双励机不同励磁方式下的磁场分布及饱和特性进行了研究,并与普通同步发电机进行了对比。采用两种不同的方法对双励机的同步电抗进行了计算,对比分析了双励机同步电抗与普通同步发电机的差异。在此基础上,研究了单轴励磁和双轴励磁时同步电抗随双励机功角变化的规律,分析了双轴励磁时,直轴分别位于励磁绕组轴线和合成磁动势位置时,双励机同步电抗随功角的变化规律。研究结果可为双励机的运行特性及稳定性分析提供理论基础。
1 双励机转子绕组结构及有限元模型
1.1 双励机转子绕组结构
本文采用的普通同步电机和双励机如图1所示。双励机的定子结构与普通发电机完全相同,而转子结构则不同,转子绕组采用双层短距分布的叠绕组结构,两相励磁绕组(分别为d绕组和q绕组)的轴线相互垂直。双励机的励磁方式有两种:①仅有一相励磁绕组作用,称为单轴励磁方式;②两相励磁绕组均作用,称为双轴励磁方式。普通同步电机与双励机的转子结构参数的差异见表1。普通同步电机与双励机的外特性对比如图2所示,可以看出,普通同步电机的外特性与双励机的外特性存在一定差别,普通同步电机的电压降落更加明显。

图1 普通同步电机与双励机的二维截面图
Fig.1 The 2D-section of the TSG and the DESG
1.2 双励机有限元模型
对于双励机直线部分,采用二维平面场进行计算。根据麦克斯韦方程组可得到双励机电磁场方程 的边值[16-17]形式为
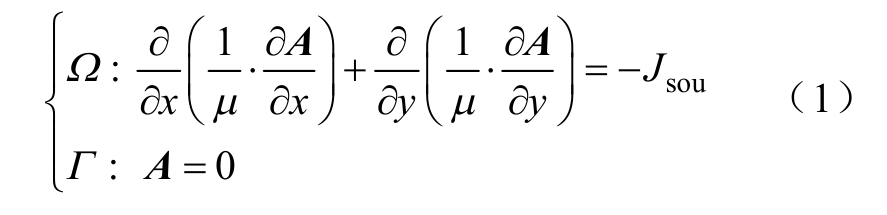
表1 普通同步电机和双励机的参数
Tab.1 The parameters of the TSG and the DESG

同步电机 双励机 额定功率/MW 300 300 额定电压/kV 20 20 额定电流/kA 10.18 10.18 额定功率因数 0.85 0.85 额定转速/(r/min) 3 000 3 000 极对数p 2 2 转子绕组相数 1 2 转子槽数Z1 32 48 转子极距τ — 24 转子节距y1 — 20 转子每极每相槽数 — 12
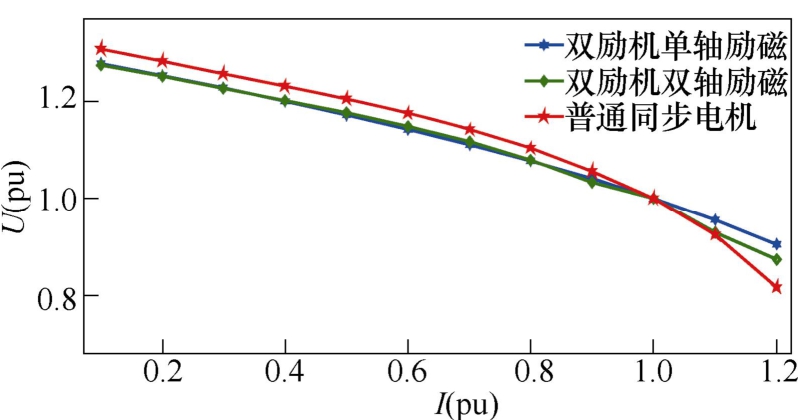
图2 普通同步电机与双励机的外特性对比
Fig.2 The external characteristics of the TSG and the DESG
式中,A为矢量磁位;μ 为磁导率;Jsou为源电流密度,包括定子电流密度与励磁电流密度。
采用有限元计算时,双励机定子绕组Js和励磁绕组Jfd、Jfq的电流密度可表示为
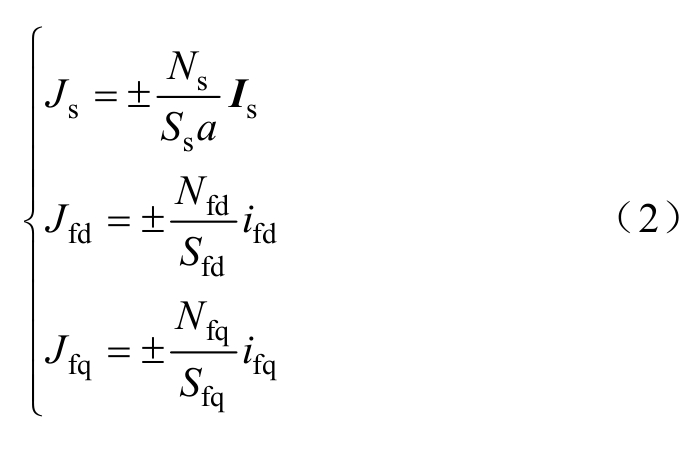
式中,“+”号对应电流流出端;“-”号对应电流流入端;Is为定子电流矩阵;ifd和ifq分别为d、q轴励磁电流;Ns为定子绕组匝数;Ss为线圈截面积;a为定子绕组并联支路数;Nfd和Nfq分别为d、q轴励磁绕组匝数;Sfd和Sfq分别为d、q轴励磁绕组截面积。
将式(2)代入磁场方程式(1)中,并根据加权余量法对其进行有限元离散,可得双励机的磁场方程为
式中,K为刚度矩阵;Cs为定子电流的关联矩阵;Cfd和Cfq分别为d、q轴励磁电流的关联矩阵。
2 双励机不同运行工况下的磁场分析
2.1 双励机空载运行
双励机转子槽均匀分布在转子铁心表面,使得双励机的磁路与普通同步电机明显不同。图3给出了普通同步电机与双励机空载运行时的磁力线分布。由于双励机转子没有大齿,其等效磁路的磁阻较大,且磁场在转子齿部更容易饱和,因此从图4所示的空载特性曲线可以看出,双励机更易饱和,在饱和阶段产生相同感应电动势时,双励机所需的励磁电流更大。

图3 普通同步电机与双励机的空载磁力线
Fig.3 The magnetic line of force of the TSG and the DESG
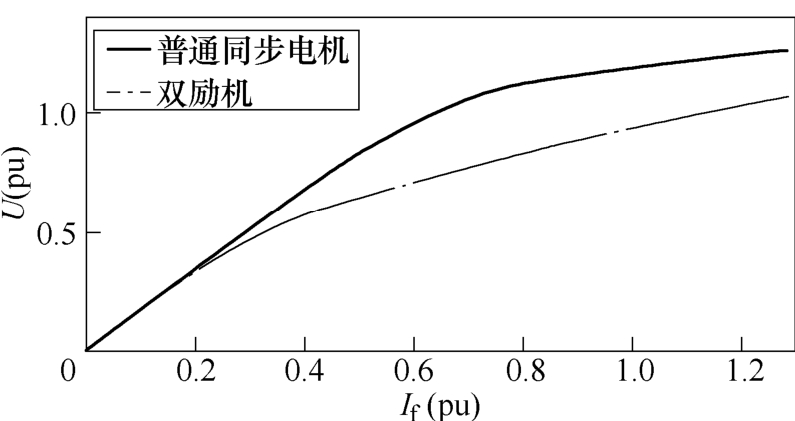
图4 普通同步电机与双励机空载特性对比
Fig.4 The no-load characteristics of TSG and DESG
图5给出了空载运行时,普通同步电机与双励机单轴及双轴励磁条件下的磁通密度分布。由图可见,普通同步电机定子铁心最大磁通密度为1.86T,而转子铁心的磁通密度可达2.33T。单轴和双轴励磁时,双励机的定子铁心最大磁通密度分别为1.74T与1.91T,而转子则分别可达到2.70T与2.87T。可见,与普通同步电机相比,双励机转子铁心的饱和程度更为严重。
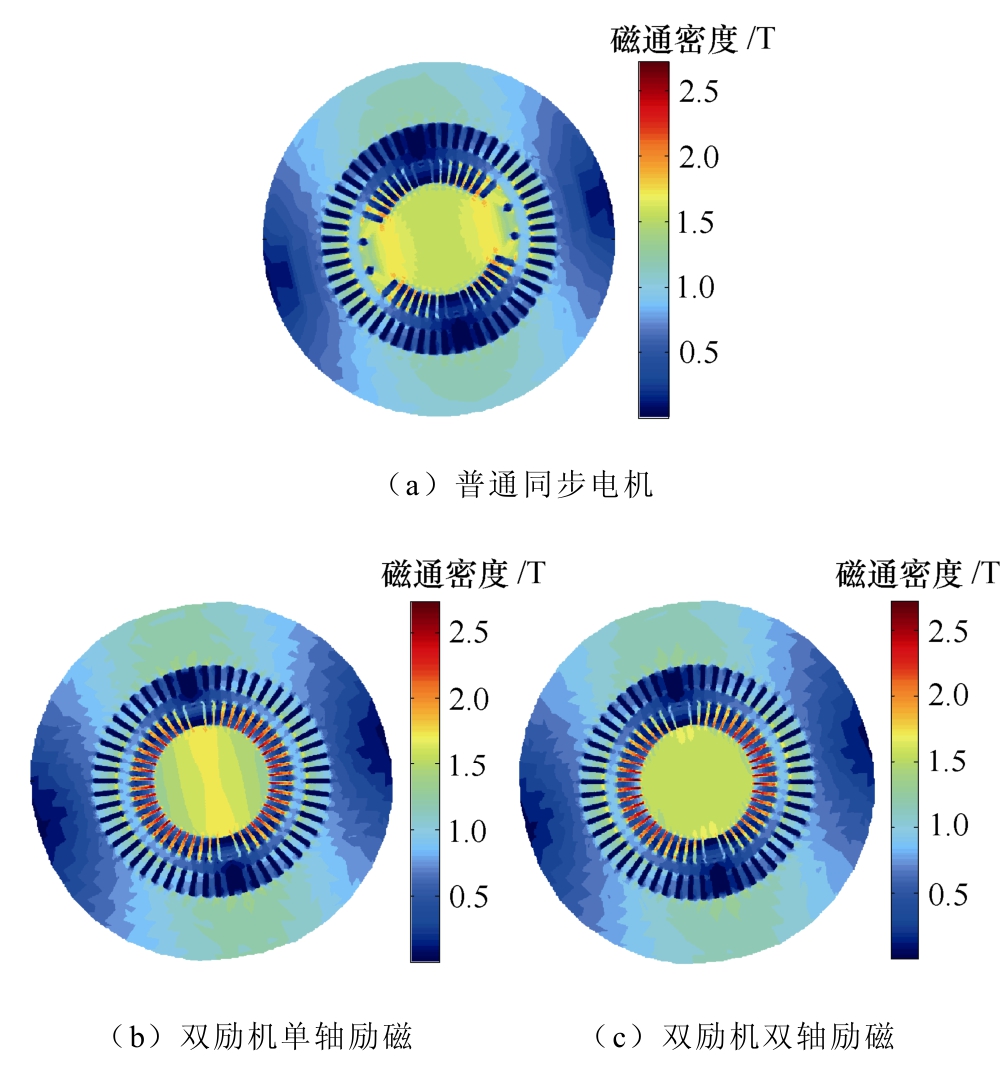
图5 空载运行时的磁通密度分布
Fig.5 The flux density distribution of DESG with no-load condition
2.2 双励机负载运行
根据文献[18]中的负载条件下非线性特性的计算方法,计算了双励机功角δ 为30°时的非线性特性曲线,并与双励机空载时的饱和特性曲线进行了对比,结果如图6所示。由于双励机在q轴增加了一相励磁绕组,因此图6横坐标所示的合成电流IΣ由d、q轴励磁电流及d、q轴定子电流Id、Iq共同构成,其表达式为![]() 由图6可见,功角30°时的非线性特性曲线与空载特性曲线存在明显差别,说明负载情况下双励机气隙磁场的饱和程度与空载时不同。
由图6可见,功角30°时的非线性特性曲线与空载特性曲线存在明显差别,说明负载情况下双励机气隙磁场的饱和程度与空载时不同。
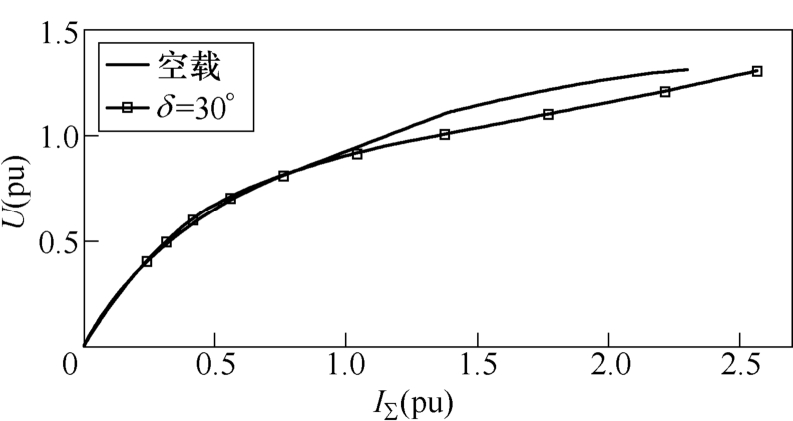
图6 双励机空载与负载工况下的饱和曲线对比
Fig.6 The saturated curves of TSG with no-load and on-load

图7 负载运行时的磁通密度分布
Fig.7 The flux density distribution of DESG with on-load
图7给出了负载运行时,普通同步电机与双励机两种励磁方式下的磁场分布。由图可见,普通同步电机定子铁心最大磁通密度为2.1T,而转子铁心 的磁通密度可达2.7T。双励机单双轴励磁时的定子最大磁通密度均为2.1T,转子最大磁通密度分别达到2.8T和3.0T。负载工况下,双励机转子齿槽的饱和情况较空载时更为严重。不同运行工况下,双励机不同的饱和程度会对同步电抗的大小产生重要影响。
3 双励机不同励磁方式下的同步电抗对比
3.1 双励机同步电抗的计算方法
3.1.1 合成电流法(方法1)
在定子三相绕组中分别施加大小为iA=Im和iB= iC=-Im/2的电流,Im为电流幅值,当转子直轴与A相绕组轴线重合时,交链A相绕组的磁链ψβ[19]为
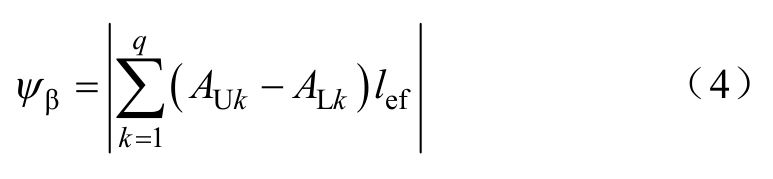
式中,AUk、ALk为A相第k个线圈上、下层的磁位;lef为定子铁心有效长度;q为定子每极每相槽数。
根据磁链与电流的关系,并计及定子端部漏磁,可得到直轴同步电抗的标幺值[19]为
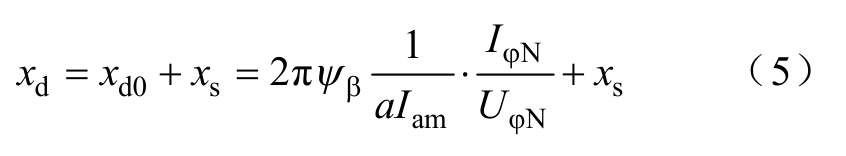
式中, ψβ 为定子每相串联的相带数;a为定子绕组支路数;Iam为A相支路电流幅值;IφN和UφN分别为额定相电流和额定相电压;xs为端部漏电抗标幺值。
采用相同方法计算出转子直轴绕组轴线分别与B、C两相绕组轴线重合时的电抗,取三相平均值作为xd的实际值。采用电磁计算公式可计算出定子端部漏电抗标幺值[19]为
式中,Ks为定子绕组槽漏抗系数;Kws为定子绕组系数;Di为定子铁心内径。
同理,分别将转子交轴与定子A、B、C三相绕组的轴线重合的电抗取平均值可得到交轴同步电抗xq。
3.1.2 坐标变换法(方法2)
根据Park变换可以得到dqo坐标系下直轴、交轴同步电抗参数[20]为
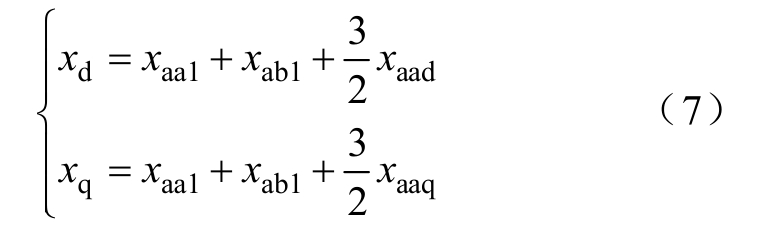
式中,xaad、xaaq分别为直轴、交轴与+A轴重合时A相绕组的电抗;xaa1为定子A相绕组的自漏抗;xab1为定子A、B两相绕组的互漏抗。
当直轴与+A轴重合时,在定子A相绕组通入幅值为Im的电流,在A相绕组感应的电动势与A相电流之比,即为电抗xaad;同理,当交轴与+A轴重合时,可以得到xaaq。当直轴与+A轴重合时,将转子铁心磁导率赋为空气磁导率,令励磁绕组和阻尼绕组开路,在定子A相绕组通入幅值为Im电流,在A相绕组感应的电动势与A相电流之比,即为A相绕组的自漏抗xaa1;此时,在B相绕组感应的电动势与A相绕组电流之比,即为A、B两相绕组的互漏抗xab1。
3.2 双励机与普通同步电机的同步电抗对比
为了研究双励机与普通同步电机同步电抗的差异,采用两种方法对同步电抗进行计算,方法1基于磁链与电流的关系计算同步电抗,方法2基于Park变换就计算同步电抗,计算结果见表2。
表2 双励机与普通同步电机同步电抗对比
Tab.2 Comparison of synchronous reactance between TSG and DESG
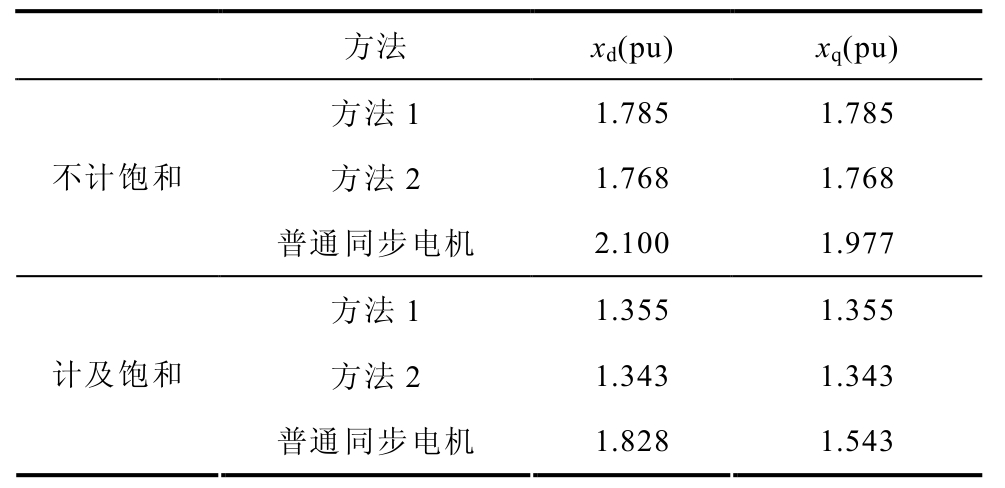
方法 xd(pu) xq(pu) 方法1 1.785 1.785 方法2 1.768 1.768 不计饱和 普通同步电机 2.100 1.977 方法1 1.355 1.355 方法2 1.343 1.343 计及饱和 普通同步电机 1.828 1.543
由表2可见,两种方法计算的同步电抗存在差异,不计饱和时两者相差1.0%,计及饱和时两者相差0.7%,差异不大。由于双励机直轴和交轴的磁路结构相同,因此双励机的直交轴同步电抗相同,而普通同步发电机在直轴和交轴的磁路不对称,因此传统同步电机的直交轴同步电抗不同,且双励机的同步电抗明显小于普通同步发电机。以方法1为例,不计饱和时,两种电机的xd相差15.0%,xq相差9.7%,计及饱和时,两种电机的xd相差23.9%,xq相差12.2%。双励机的定子结构与普通同步电机相同,而转子结构则相差较大。双励机转子上没有大齿会导致磁路的磁阻明显大于普通同步电机的磁阻,从而使得两种电机的同步电抗存在明显差异。
3.3 双励机不同励磁方式下的同步电抗及其随功角的变化规律
3.3.1 单轴励磁方式
双励机运行工况的变化会导致其内部的磁路饱和、磁场畸变等非线性因素发生变化,从而使得双励机的同步电抗表现出随运行工况变化的时变特性。双励机处于不同功角下稳态运行时,电枢反应的作用使得气隙磁场发生扭斜,从而造成直交轴磁路磁阻发生变化,影响同步电抗的数值。图8给出了双励机空载和60°功角时的磁力线,从图中可以看出,两种情况下的磁力线存在明显差别。功角为 60°时,气隙合成磁场偏离励磁d绕组轴线,使得双励机直轴方向磁阻与空载时存在较大差别,导致两种情况下的同步电抗存在差异。
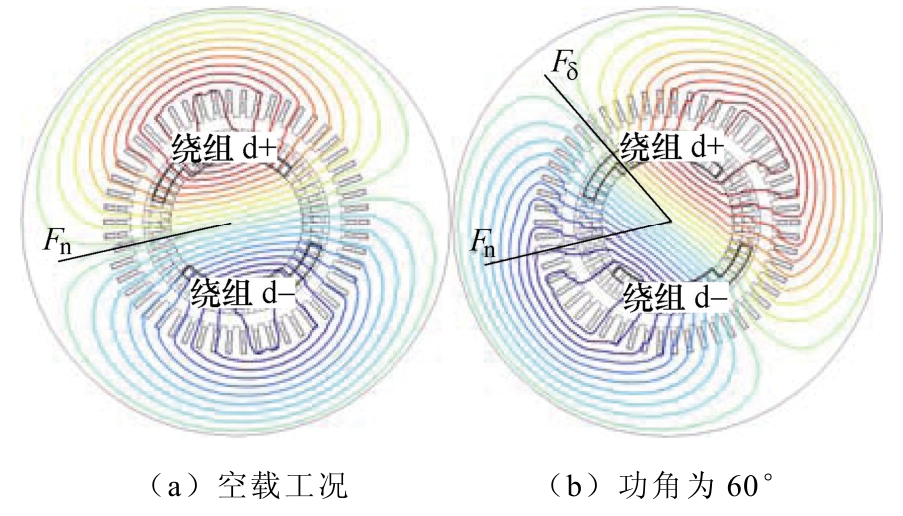
图8 双励机空载及60°功角下的磁力线对比
Fig.8 The magnetic line of force of DESG under no-load condition and 60° power angle condition
基于冻结磁导率法,计算了双励机单轴励磁时不同功角下的直交轴同步电抗,结果如图9所示。从图9中可以看出,随着电机功角的增大,xd逐渐增大,而xq逐渐减小。由表3可见,两种方法计算的同步电抗相差不大,相对于表2中双励机的饱和电抗,不同功角下两种方法计算的xd最大变化了25%和22%,xq最大变化了11%和9%。随着功角的逐渐增大,气隙合成磁场逐渐偏离直轴轴线,偏向交轴轴线,则直轴方向的饱和程度会随功角增加逐渐减小,而交轴方向的饱和程度会逐渐上升。因此,随着功角的增加,直轴同步电抗逐渐增大而交轴同步电抗逐渐减小。
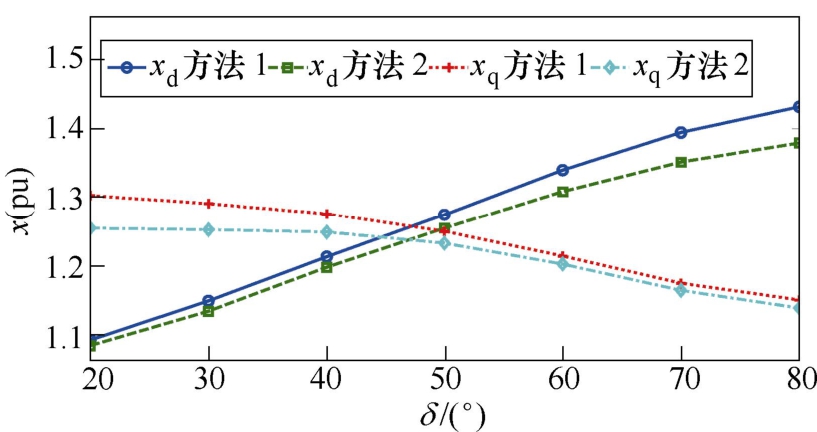
图9 单轴励磁时同步电抗随功角变化曲线
Fig.9 The variation law of synchronous reactance along with power angle under single excitation
表3 单轴励磁时不同功角下的同步电抗
Tab.3 Synchronous reactance with different power angle under single excitation
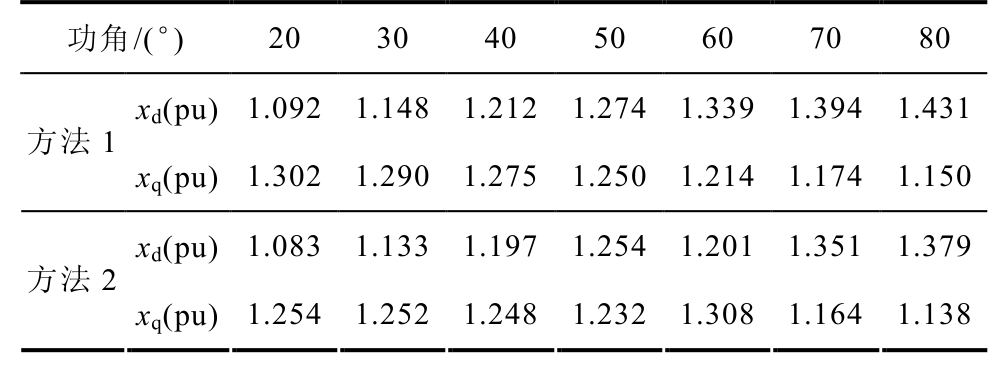
功角/(°) 20 30 40 50 60 70 80 xd(pu) 1.092 1.148 1.212 1.274 1.339 1.394 1.431 方法1 xq(pu) 1.302 1.290 1.275 1.250 1.214 1.174 1.150 xd(pu) 1.083 1.133 1.197 1.254 1.201 1.351 1.379 方法2 xq(pu) 1.254 1.252 1.248 1.232 1.308 1.164 1.138
3.3.2 双轴励磁方式
双励机单轴励磁时励磁磁动势只能位于励磁绕组轴线上,而双轴励磁时则可通过调节励磁电流的大小,改变励磁合成磁动势的大小及其相对转子上的位置,如图10所示。由图可见,当两相励磁绕组均通入相同电流时,励磁d绕组的轴线与励磁合成磁场的位置并不重合。双励机动态过程中,通常需控制励磁合成磁场保持同步速以使得定转子之间产 生单向力矩,减小系统的振荡时间,而转子转速则会偏离同步速运行。双轴励磁时直轴既可位于励磁绕组轴线采用dqo坐标系,也可位于合成磁动势位置采用同步坐标系。

图10 双轴励磁时,两种不同的直轴选取
Fig.10 The two kinds of direct axis selection under dual-excitation mode
当两相励磁绕组通入相同励磁电流时,励磁合成磁动势与励磁d绕组轴线相差45°。本节计算了直轴位于励磁绕组轴线和励磁合成磁动势位置时,双励机同步电抗随功角的变化规律,对比分析了两种方法计算同步电抗时的差异,同步电抗随功角的变化曲线如图11所示,计算结果见表4和表5。由图11可见,选取不同的直轴时,同步电抗随功角变化的趋势都存在明显差异。由表4和表5可得出如下结论。
(1)当选取励磁合成磁动势位置为直轴时,随着功角的增大,直轴同步电抗逐渐增大,而交轴同步电抗逐渐减小;当选取励磁d绕组轴线为直轴时, 随着功角的增大,直轴同步电抗先减小后增大,交轴同步电抗先增大后减小。

图11 双轴励磁时同步电抗随功角变化规律
Fig.11 The variation law of synchronous reactance along with power angle under dual excitation
表4 选取励磁合成磁动势位置为直轴
Tab.4 The direct-axis located at the synthetic excitation MMF
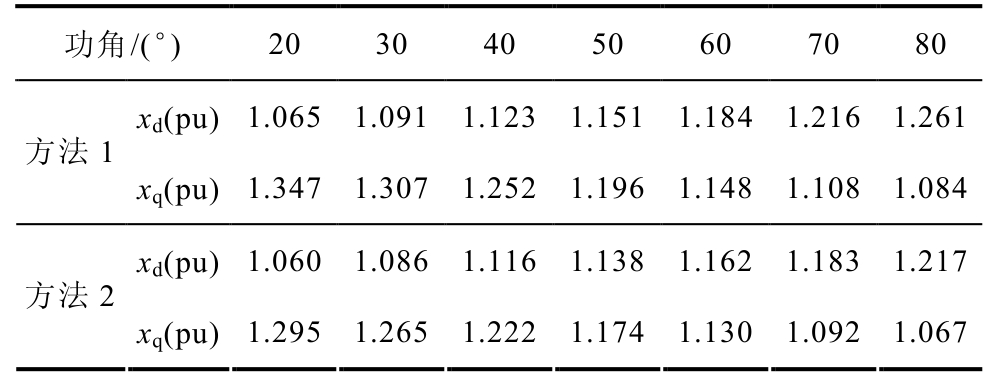
功角/(°) 20 30 40 50 60 70 80 xd(pu) 1.065 1.091 1.123 1.151 1.184 1.216 1.261 方法1 xq(pu) 1.347 1.307 1.252 1.196 1.148 1.108 1.084 xd(pu) 1.060 1.086 1.116 1.138 1.162 1.183 1.217 方法2 xq(pu) 1.295 1.265 1.222 1.174 1.130 1.092 1.067
表5 选取励磁d绕组轴线为直轴
Tab.5 The direct-axis located at the axis of excitation- winding d
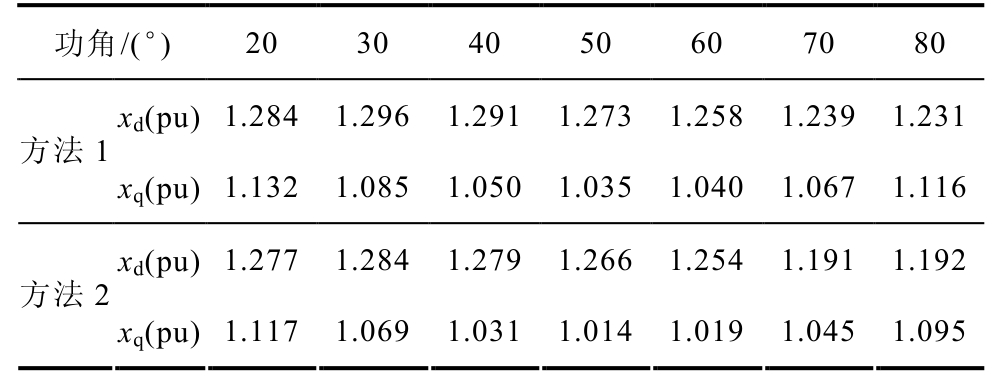
功角/(°) 20 30 40 50 60 70 80 xd(pu) 1.284 1.296 1.291 1.273 1.258 1.239 1.231 方法1 xq(pu) 1.132 1.085 1.050 1.035 1.040 1.067 1.116 xd(pu) 1.277 1.284 1.279 1.266 1.254 1.191 1.192 方法2 xq(pu) 1.117 1.069 1.031 1.014 1.019 1.045 1.095
(2)当选取励磁合成磁动势位置为直轴时,不同功角下两种方法计算的直轴同步电抗最大变化了14%和12%,交轴同步电抗最大变化了20%和17%;当选取励磁绕组轴线为直轴时,不同功角下两种方法计算的直轴同步电抗最大变化了7%和8%,交轴同步电抗最大变化了5%和7%。从结果可以看出,选取励磁合成磁动势位置为直轴时,同步电抗的波动较大。
(3)当选取励磁d绕组轴线作为直轴时,随着功角的增大,气隙合成磁场逐渐偏向交轴,导致直轴方向饱和程度下降,而交轴方向饱和程度上升,如图12a所示;而功角δ >45°后,气隙合成磁场会偏离交轴,偏向直轴的反方向,导致直轴方向饱和程度上升,交轴方向饱和程度下降,如图12b所示。因此,随着功角的增加,直轴方向饱和程度先减小后增大,而交轴方向饱和程度先增大后减小,直轴同步电抗相应先增大后减小,而交轴同步电抗先减小后增大。
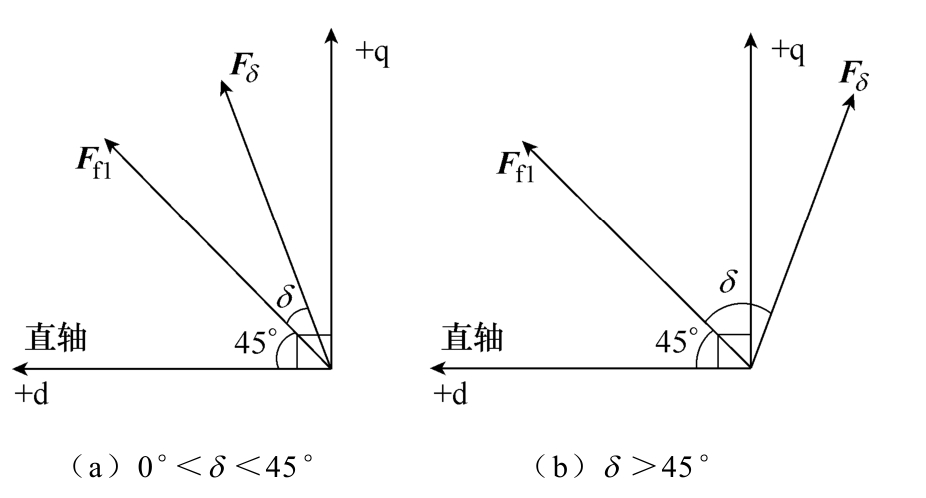
图12 选取励磁d绕组轴线为直轴时的矢量图
Fig.12 The vector diagram after choosing excitation-winding d as direct axis
4 实验验证
4.1 感应电动势的仿真与实测对比
为了验证计算结果的正确性,在300MW大功率双励机的基础上,研制了一台10kW双励机,参数见表6,结构及样机如图13所示。
表6 普通同步电机动模机与双励机动模机的参数
Tab.6 The parameters of the TSG model machine and the DESG model machine
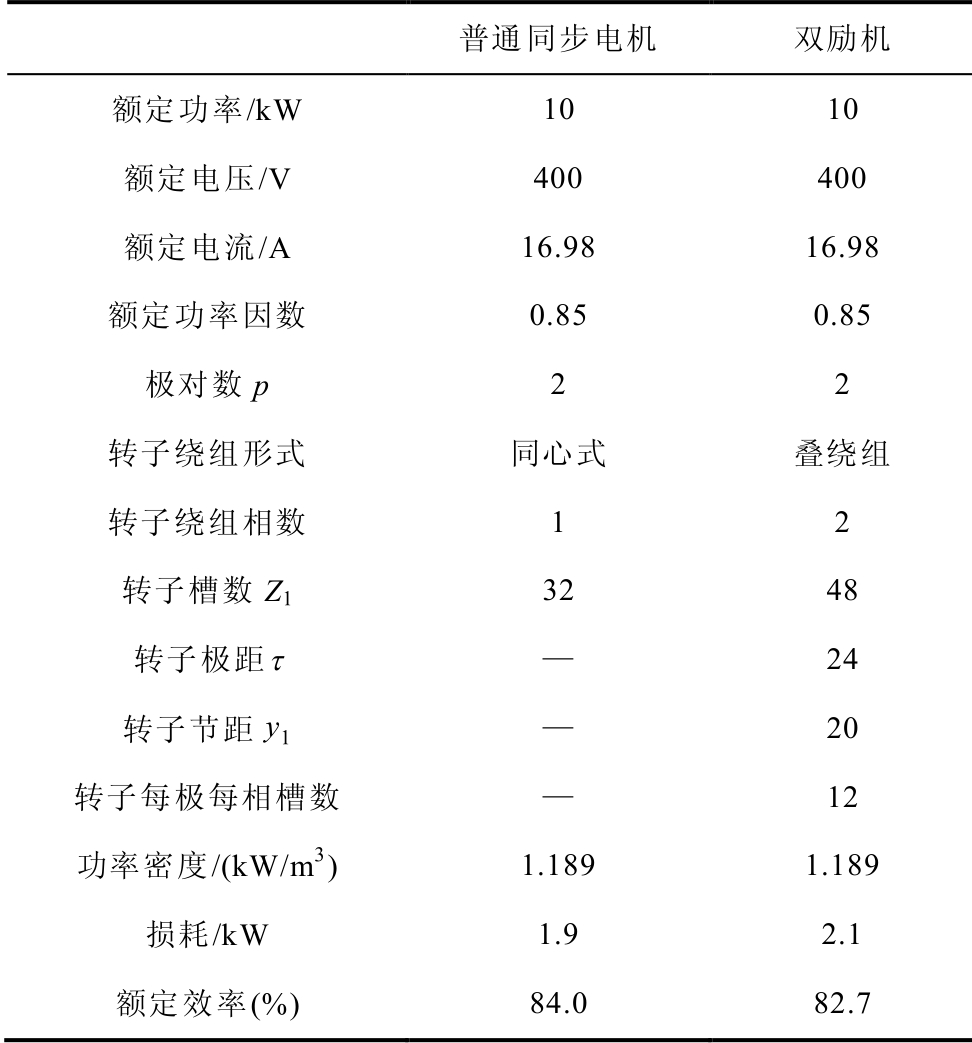
普通同步电机 双励机 额定功率/kW 10 10 额定电压/V 400 400 额定电流/A 16.98 16.98 额定功率因数 0.85 0.85 极对数p 2 2 转子绕组形式 同心式 叠绕组 转子绕组相数 1 2 转子槽数Z1 32 48 转子极距τ — 24 转子节距y1 — 20 转子每极每相槽数 — 12 功率密度/(kW/m3) 1.189 1.189 损耗/kW 1.9 2.1 额定效率(%) 84.0 82.7

图13 10kW双励机模型机
Fig.13 10kW DESG model machine
在模型机上进行了两组实验,第一组实验是在励磁d绕组施加直流电流,此时q绕组开路,电机在同步速下空载运行;第二组实验是励磁d、q绕组中均通入相同的直流电流,电机在同步速下空载运行。将测试结果与仿真结果进行对比,如图14所示,可以看出两种结果非常吻合。
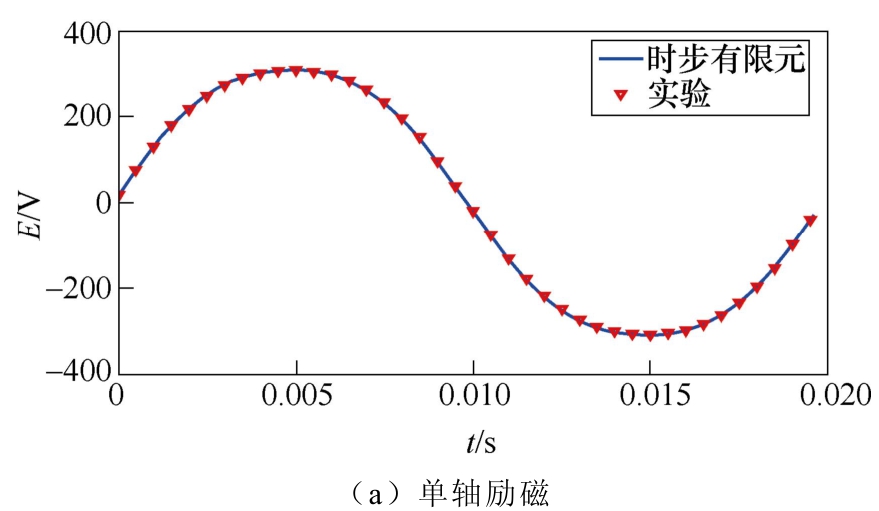
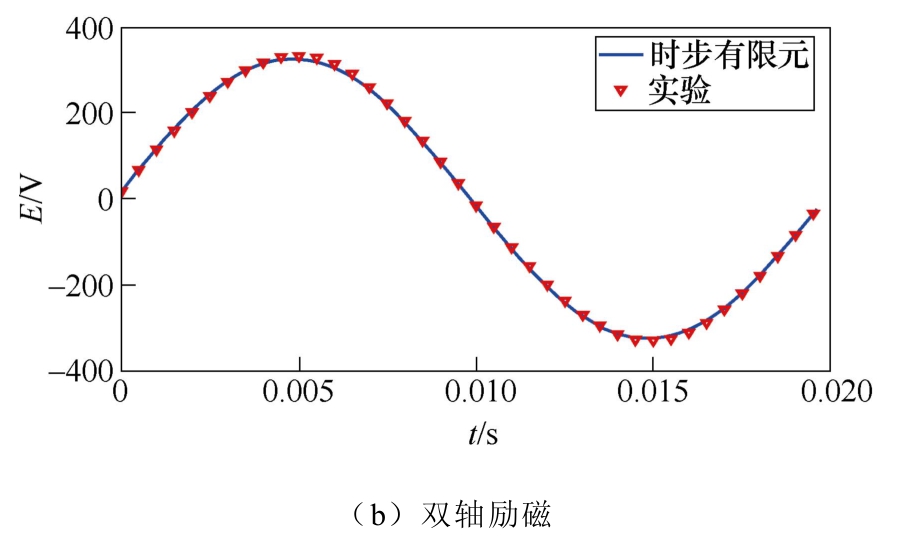
图14 感应电动势实验与时步有限元仿真对比
Fig.14 Comparison of EMF between test and T-S FEM
4.2 同步电抗的仿真与实测结果对比
通过模型机的空载特性与稳态短路特性可以求得双励机的直轴同步电抗,将其与两种参数计算方法的结果进行对比来验证仿真结果的正确性。图15给出了模型机的空载特性曲线与稳态短路特性曲线。通过计算得出仿真和实验得到的直轴同步电抗见表7。
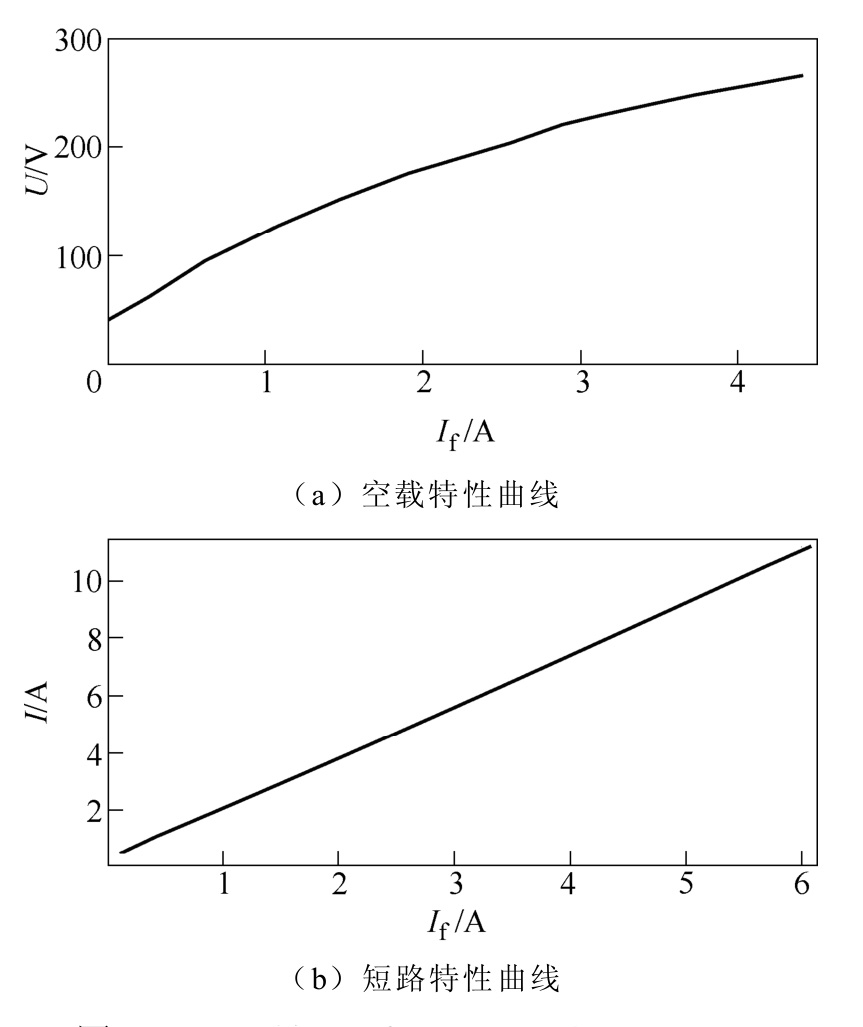
图15 模型机空载和短路特性实验结果
Fig.15 The no-load characteristic and short circuit characteristic test of model machine
表7 实验与仿真同步电抗结果对比
Tab.7 The comparison of synchronous reactance by test and simulation

计算方式 实验结果 方法1 方法2 xd(pu) 1.542 1.487 1.529
由表7可见,两种方法计出的同步电抗与实验结果非常接近,方法1计算结果与实验相差3.5%,方法2计算结果与实验相差0.84%。实测结果验证了仿真计算的正确性。
5 结论
1)双励机转子上具有两相对称励磁绕组,其转子槽均匀分布在转子表面,主磁路磁阻明显大于普通同步电机,且磁场更容易饱和,因此双励机的饱和同步电抗明显小于普通同步电机。
2)双励机单轴励磁时,d轴同步电抗随功角的增大而增大,而q轴同步电抗则随功角的增加而减小,这是因为随着功角的增大,气隙合成磁场逐渐偏离d轴轴线,d轴饱和程度逐渐减小,而q轴饱和逐渐增加。
3)双励机双轴励磁时,当选取合成励磁磁动势位置为直轴时,同步电抗随功角的变化规律与单轴励磁时相同;而选取转子d绕组轴线作为直轴时,随着功角的增加,xd先增大后减小而xq则先减小后增大。这是因为随着功角的增加,直轴方向饱和程度先减小后增大,而交轴方向饱和程度先增大后减小。
[1]Shakaryan Y, Sokur P. Experience in the development and operation of asynchronized turbogenerators and condensers in the russian power system[J]. Archives of Electrical Engineering, 2015, 64(1): 7-15.
[2]Kuzmin V V, Shpatenko T V. Experience in deve- lopment and use of asynchronized turbogenerators made by elektrotyazhmash[J]. Russian Electrical Engineering, 2010, 81(N2): 54-57.
[3]Agarwal H C, Kapoor S C. Power system dynamic studies for improved stability and minimum rotor heating via graph-theoretic modelling of a dual- excited synchronous generator[J]. IEEE Transactions on Power Apparatus & Systems, 2006, 94(2): 177- 186.
[4]Antonyuk O V, Kadi-Ogly I A, Pinchuk N D, et al. Asynchronized turbogenerators projected and released by a power machine company[J]. Russian Electrical Engineering, 2010, 2(81): 67-72.
[5]梁艳萍. 汽轮发电机饱和同步电抗的波动[J]. 电机与控制学报, 1998, 2(3): 40-42. Liang Yanping. Oscillation of saturated synchronous reactance of turbo generator[J]. Transactions of China Electro Technical Society, 1998, 2(3): 40-42.
[6]刘晓芳, 蒙亮, 罗应立, 等. 同步发电机d-q轴饱和特性曲线族[J]. 中国电机工程学报, 2002, 22(2): 69-73. Liu Xiaofang, Meng Liang, Luo Yingli, et al. The saturation curve series of synchronous generators[J]. Proceedings of the CSEE, 2002, 22(2): 69-73.
[7]戈宝军, 殷继伟, 陶大军, 等. 基于励磁与调速控制的单机无穷大系统场-路-网时步有限元建模[J]. 电工技术学报, 2017, 32(3): 139-148. Ge Baojun, Yin Jiwei, Tao Dajun, et al. Modeling of field-circuit-network coupled time- stepping finite element for one machine infinite bus system based on excitation and speed control[J]. Transactions of China Electro Technical Society, 2017, 32(3): 139-148.
[8]薛易, 李伟力, 王立坤. 转子导磁导电槽楔材料对汽轮发电机参数和转子表面损耗影响的研究[J]. 中国电机工程学报, 2015, 35(7): 1768-1774. Xue Yi, Li Weili, Wang Likun. Study on influences of magnetic and electric conductive slot wedges on parameters of turbo-generators and losses on rotor surface[J]. Proceedings of the CSEE, 2015, 35(7): 1768-1774.
[9]李桂芬, 戈宝军, 李金香, 等. 大型发电机机网动态分析的机-场-路-网耦合时步有限元方法建模[J]. 中国电机工程学报, 2014, 34(36): 6476-6484. Li Guifen, Ge Baojun, Li Jinxiang, et al. Modeling of mechanical shaft-field-circuit-network coupled time- step finite element method for dynamic analysis of large machine and power network[J]. Proceedings of the CSEE, 2014, 34(36): 6476-6484.
[10]李和明, 张健, 刘明基, 等. 基于时步有限元的永磁同步电机稳态参数改进计算方法[J]. 电工技术学报, 2012, 27(4): 35-41. Li Heming, Zhang Jian, Liu Mingji, et al. An improved calculation method for steady-state parameters of PMSM with T-S FEM[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 35-41.
[11]王伟华, 王红宇, 许国瑞, 等. 基于时步有限元的抽水蓄能电机瞬态参数计算方法的对比[J]. 电工技术学报, 2015, 30(1): 89-97. Wang Weihua, Wang Hongyu, Xu Guorui, et al. Research on operation of turbine generator con- sidering saturation and magnetic field distortion[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 89-97.
[12]康锦萍, 徐英辉, 刘晓芳, 等. 计及双因素非线性影响的汽轮发电机同步电抗的计算方法[J]. 中国电机工程学报, 2014, 34(33): 5941-5947. Kang Jinping, Xu Yinghui, Liu Xiaofang, et al. A calculation method for synchronousreactances of turbine generators considering two factors affecting nonlinear characteristics[J]. Proceedings of the CSEE, 2014, 34(33): 5941-5947.
[13]应黎明, 陈允平, 陈明榜. 异步化同步发电机转子励磁的模糊PID控制[J]. 中国电机工程学报, 2006,26(17): 163-168. Ying Liming, Chen Yunping, Chen Mingbang. Fuzzy PID control of rotor current excitation in an asynchronized synchronous generator[J]. Proceedings of the CSEE, 2006, 26(17): 163-168.
[14]季海波, 陈欢, 王冰, 等. 双轴励磁同步发电机非线性鲁棒自适应控制[J]. 电机与控制学报, 2005, 9(1): 20-24. Ji Haibo, Chen Huan, Wang Bing, et al. Robust adaptive control of dual-excited synchronous gener- ator[J]. Electric Machines and Control, 2005, 9(1): 20-24.
[15]Xu Guorui, Hu Yiping, Hao Xiajing. The relationship of magneto motive force under different excitation modes of dual-excited synchronous generator[J]. IEEE Transactions on Magnetics, 2018, 54(3), 8200704.
[16]许国瑞, 汤涌, 刘晓芳, 等. 汽轮发电机不同模型小扰动特性[J]. 电工技术学报, 2013, 28(9): 302- 309. Xu Guorui, Tang Yong, Liu Xiaofang, et al. Small disturbance characteristics of the different turbine generator models[J]. Transactions of China Electro- technical Society, 2013, 28(9): 302-309.
[17]许国瑞, 王红宇, 刘晓芳, 等. 同步发电机不同实用模型的大扰动特性对比研究[J]. 中国电机工程学报, 2012, 32(24): 67-73, 12. Xu Guorui, Wang Hongyu, Liu Xiaofang, et al. Comparison of large disturbance characteristics of different generator practical models[J]. Proceedings of the CSEE, 2012, 32(24): 67-73, 12.
[18]康锦萍, 刘晓芳, 罗应立, 等. 不同容量汽轮发电机负载非线性特性的对比研究[J]. 中国电机工程学报, 2009, 29(24): 73-77. Kang Jinping, Liu Xiaofang, Luo Yingli, et al. Research on the nonlinear load characteristics of different capacity turbine generators[J]. Proceedings of the CSEE, 2009, 29(24): 73-77.
[19]梁艳萍, 侯宇. 转子磁路结构对汽轮发电机同步电抗的影响[J]. 电机与控制学报, 2013, 17(7): 34-39. Liang Yanping, Hou Yu. Influence of rotor magnetic circuit structure on synchronous reactance of turbo- generator[J]. Electric Machines and Control, 2013, 17(7): 34-39.
[20]汤蕴璆, 张奕黄, 范瑜. 交流电机动态分析[M]. 北京: 机械工业出版社, 2008.