0 引言
磁耦合无线电能传输（Magnetic Coupling Wireless Power Transfer, MC-WPT）是指利用磁场耦合原理实现电能从电源端到用电设备端的无电气连接传输。自2007年美国麻省理工学院Marin Soljacic教授所在的科研小组在《Science》期刊上发文提出“磁共振无线电能传输”技术实现2m范围内60W无线电能传输以来[1-2]，该技术得到了国内外研究学者的高度关注。经过近十来年的飞速发展，目前该技术已成功应用于消费电子[3-4]、家用电器[5-6]和电动汽车[7-10]等领域。
目前MC-WPT系统大多都是基于美国麻省理工学院（MIT）提出的“共振耦合”原理：将MC-WPT系统中各振荡电路的固有频率设置为同一频率，并通过整定磁场激励频率使得其等于设置的电路固有频率以此实现系统“共振”来获取最大能量传输[11-14]。据MIT描述，基于该“共振耦合”原理的MC-WPT系统能够在一定范围内实现“无方向”能量传输[1-2]。但随着研究的深入发现，该传输模式普遍存在一种称之为“频率分裂”的物理现象：在一定参数条件下，MC-WPT系统存在多个功率峰值点，对应的频率都偏离设置的各振荡电路环节的固有频率，系统工作在设置的电路固有环节点反而使其功率下降，且传输功率表现出“随传输距离减小能效反而降低”以及“传输方向极度敏感”等特性[15-19]。该现象极大程度上限制了MC-WPT系统的能效性。
针对频率分裂现象，目前已提出多种技术方案，如频率跟踪控制[17, 20]、增加阻抗匹配网络[21-22]、调节耦合强度[23-24]等。但这些方案都只针对频率分裂现象采用的能效补偿措施。频率分裂现象的存在表明，至少在某些参数条件下，传统的传输模型并非处于共振状态，设计的电路固有频率并非系统的共振频率。MC-WPT系统存在多个共振点，其个数和位置会随系统参数变化而变化[25-26]。构建MC-WPT系统共振点与系统电参数之间的数学关系，研究其随电参数的分布特性，不仅可快速、准确地得到任意参数条件下系统的共振点，还可解释频率分裂现象的物理涵义，揭示MC-WPT系统的共振机理，为系统工作在共振状态提供理论指导。同时构建解析表达式也可为后续共振点的优化设计提供理论基 础[15, 19, 27]，如对电参数进行优化设计，使得共振点的能效更大，或优化设计参数使得系统共振在给定的频段。众所周知，随着MC-WPT系统应用推广，各产业联盟都在制定相应的标准，包括频标。该要求下需要系统工作在给定的频段。
鉴于MC-WPT系统的实质为一个多自由度振荡系统[18, 26]，其内在机理及外部响应能够完全由该系统的固有参数表征，因此本文基于复模态分析法，对四线圈结构MC-WPT系统进行共振机理建模，进而建立MC-WPT系统共振频率及共振点功率的解析表达式。在此基础上，深入分析MC-WPT系统共振频率及其功率随距离及电阻变化的分布特性，以此解释频率分裂等复杂动力学行为的物理原理，为进一步研究共振点的优化及控制提供了相应的理论基础。
1 理论分析
1.1 MC-WPT系统状态空间模型
四线圈结构MC-WPT系统一般等效电路如图1所示。系统包含四个线圈，每个线圈连接一个补偿电容以此形成一个振荡回路。
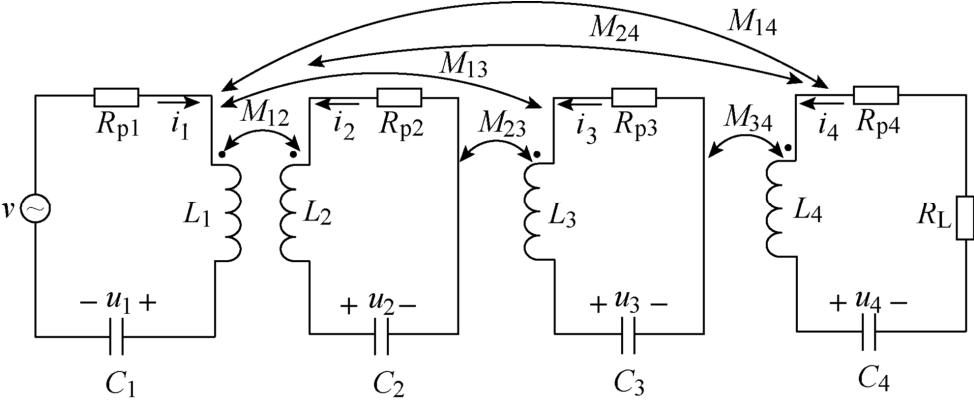
图1 四线圈结构MC-WPT系统一般等效电路
Fig.1 The generalized equivalent circuit diagram of four-coil MC-WPT systems
在图1中，下标m表示第m个振荡回路，Lm和Rpm分别表示第m个线圈的电感和内阻，Mmj表示第m个线圈和第j个线圈之间的互感，Cm表示第m个回路的补偿电容，um表示补偿电容Cm两端的电压，im表示第m个回路的电流，v表示电源电压，RL表示负载，m=1, 2, 3, 4。基于基尔霍夫电压定律，该系统的数学模型可表示为
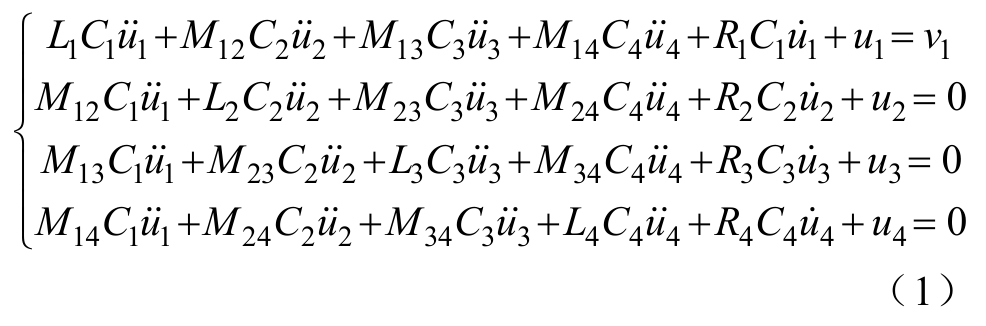
定义矢量 
分别为系统的电源电压矢量、 电流矢量、电容电压矢量，矩阵L、C和R分别为系统的电感矩阵、电容矩阵和电阻矩阵，表示为
式中，R1=Rp1；R2=Rp2；R3=Rp3；R4=Rp4+RL。
令
和
分别为系 统的状态矢量和输入矢量，则系统的状态空间模型可建立为
其中
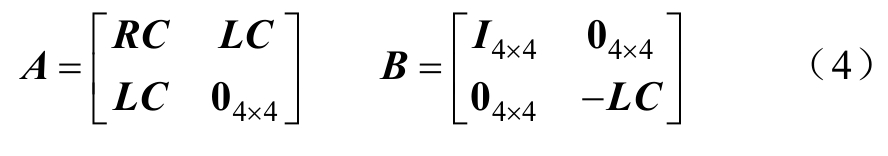
式中，In×m和0n×m分别表示n×m阶的单位矩阵和零矩阵。将式（3）所示的状态空间模型进行标准化变换，可得
式中，S为系统的系统矩阵，即
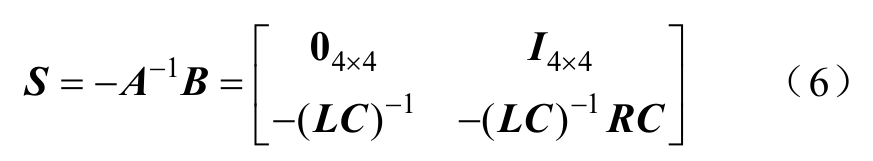
1.2 MC-WPT系统共振响应分析
基于振动学相关理论可知[28]，共振是指当系统外部激励频率等于某些特定值时，整个系统的能量出现激增的现象。这些特定的外部激励频率则为该系统的共振频率。式（3）表明，MC-WPT系统实质是一个由多个振荡环节（振荡电路）通过相互耦合的方式共同组成的多自由度振荡系统，系统的自由度即为系统中振荡环节的个数。基于此，可定义MC-WPT的共振为当磁场激励频率（外部电源频率）等于某些特定值时，整个系统能量出现激增时的现象。系统能量激增时对应的磁场激励频率（电源频率）定义为MC-WPT系统的共振频率。为了和系统中各振荡环节的固有频率进行区分，将系统中各振荡回路的固有频率称之为电路固有频率。
对MC-WPT系统而言，整个系统的能量与系统中各振荡回路电流幅值呈正相关。因此根据上述定义可知，当MC-WPT系统各回路电流幅值同时出现激增时，系统处于共振状态，此时对应的磁场激励频率（外部电源频率）即为该系统的共振频率。 基于矩阵理论可知，存在非奇异矩阵Φ=(φij)8×8，使得式（7）成立。
式中，算子 diag[·]表示以括号内的元素为对角元素生产对角矩阵；λq和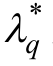
互为共轭复数，q=1, 2, 3, 4。
鉴于一个实际物理系统的特征值实数部分通常 为一个绝对值很小的负数，因此 λq和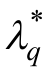
表示为 λq= -αq+jωr,q 和
其中，αq和 ωr,q为正实数，且αq很小。值得注意，本文中的下标q和下标m表征不同的物理涵义，下标m表示系统中第m个 振荡回路相关的参数，下标q则表示特征值的位置。 令 y=Φ-1x，联立式（7），则式（5）所示的状态空间模型可解耦成
通过频谱变换，即i(t)↔ I(jω)，u(t)↔ U (jω)，x ( t)↔X (jω)，y(t)↔Y (jω)，vin(t)↔Vin (jω)，式（8）可变换为
将Y=Φ - 1X代入式（9），可得
令
则式（10）可写为
根据 
以及电容电压与电流的关系i=Cu˙，可得 
和 I=jωCU。将其代入式（12）可得
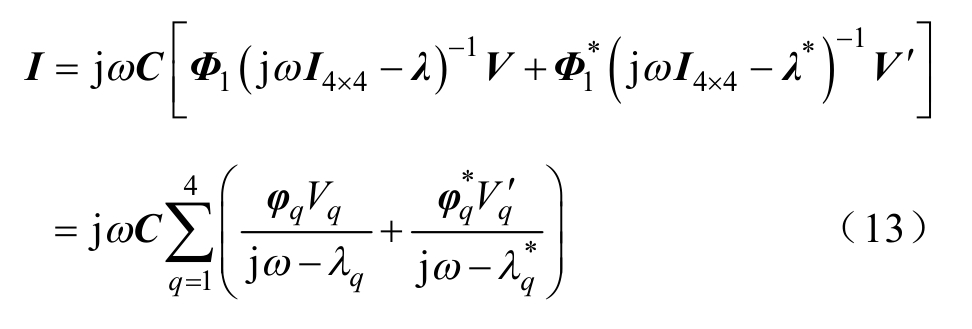
即系统中第m个回路的电流相量可表示为
其中
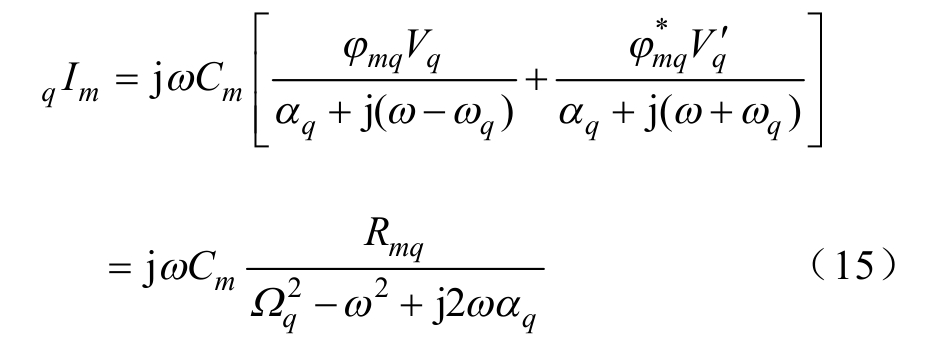
其中
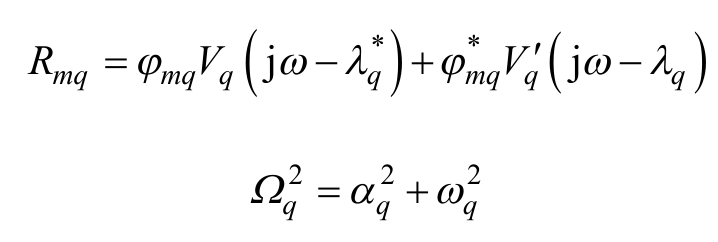
当电源频率ω = Ωq时，
取最大值
其中
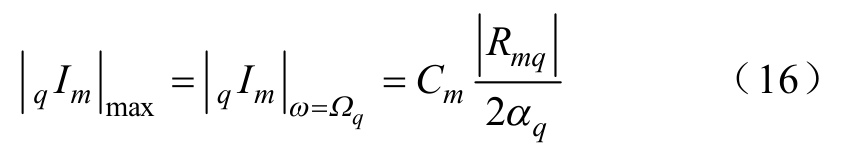
由于αq通常很小，因此当电源频率ω = Ωq时，
通常都很大，由此可知：如果 Ω1、 Ω2、Ω3、Ω4彼此相隔较远，当电源频率ω = Ωq 时，
将会远远大于其他项
此时 
即当电源频率ω = Ωq时，电流幅值
取极大值，系统 处于共振状态；反之，如果存在两个或者多个 Ωq相隔 很近，不妨假设 Ωp和 Ωq相隔很近。当电源频率ω = Ωq时，
都将增大，则有
此时电流幅值
的极值点将在 Ωp和 Ωq之间。不过 Ωp和 Ωq相隔很近，因而 Ωp和极值点将更为接近，则可认为 Ωp是系统的共振频率。综上分析可知，四线圈结构MC-WPT系统存在四个共振频率 ωr,q （ q= 1,2,3,4），其值为系统矩阵S的特征值的模，即
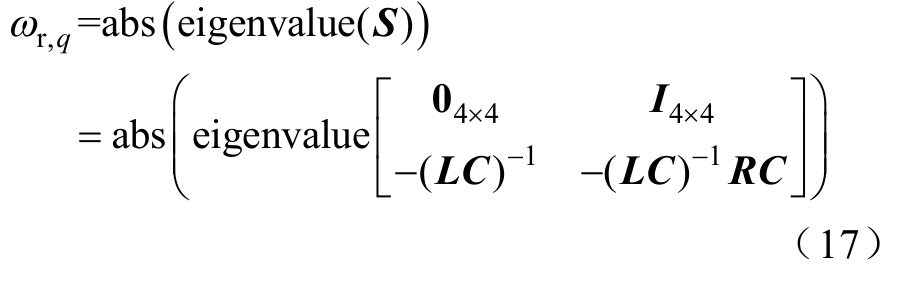
基于式（17）可快速得到MC-WPT系统的共振频率。将其代入至式（14），可得系统共振下的输出功率以及效率表达式分别为
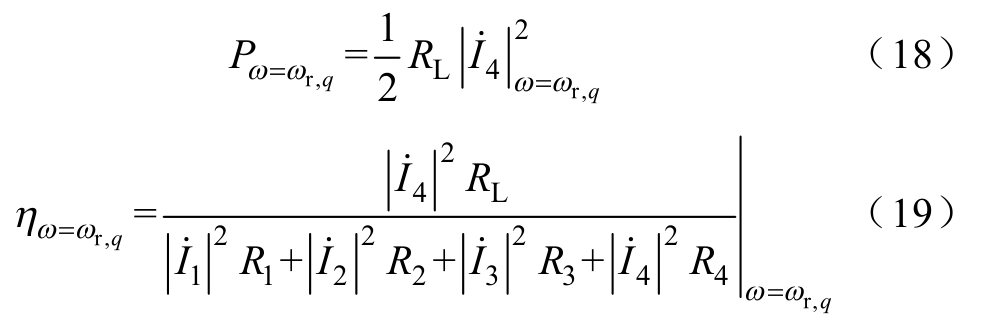
运用式（17）～式（19），可快速、准确地得到MC-WPT系统所有共振点的频率及能效，因此可根据实际需要选取相应的共振频率作为工作频率。
此外，基于理论推导过程可知，只需要改变相应矢量及矩阵的维度，该方法就可推广应用到其他线圈架构系统中。
2 共振点分布特性研究
由式（17）可知，MC-WPT系统的共振频率并不等于各回路的电路固有频率，而是由系统中各回路的电路固有频率、互感以及电阻共同决定的。在实际系统中，线圈参数及各回路补偿电容一经设定后一般都保持不变，传输距离、传输方位及负载值是MC-WPT系统常见的易变参数。鉴于线圈参数给定，传输距离和传输方位影响的实质就只是互感，因此本节将对MC-WPT系统共振点随传输距离（互感）和负载变化的分布特性进行深入研究，以此揭示频率分裂等复杂动力学行为过程的内在物理 原理。
2.1 距离（互感）特性分析
为了深入分析MC-WPT系统共振点分布的距离特性，4个平面螺旋线圈同心共轴放置，其结构如图2所示，其中dmj为线圈m和线圈j之间的距离。4个线圈参数设置完全相同，内半径为0.03m，匝数为18匝，匝间距为0.01m。
图2 MC-WPT系统线圈结构
Fig.2 Coil’s structure of the MC-WPT system
基于COMSOL实物仿真，该几何结构下线圈的自感为57μH，内阻为0.13Ω。四个线圈的补偿电容设置为61.5nF，则基于电路固有频率公式 
可知，每个振荡回路的电路固有频率为 85kHz。在本节中，负载电阻RL固定为5Ω，距离d12和d34固定为0.05m，传输距离d23从0.05m开始以0.05m的步长变化到0.3m。不同传输距离下线圈间的互感[29]为
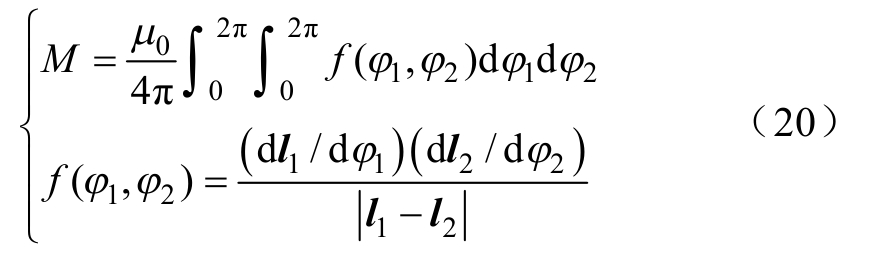
将上述给定的参数代入式（17）和式（18）中，可得不同传输距离下系统所有的共振频率及共振点的功率的分布，共振频率随传输距离变化的分布（理论值）如图3所示，共振点功率随传输距离变化的分布（理论值）如图4所示。为了验证共振频率及共振点功率理论计算的正确性，以给定参数为基准，运用COMSOL搭建MC-WPT系统实物仿真模型。当传输距离为0.05m，0.15m及0.35m时，系统仿真功率随电源频率变化曲线如图5所示。 从图3可知，当传输距离d23较小时（d23＜0.15m），系统存在4个彼此远离的共振点，此时4个共振点的功率都相差不大，但远大于电路固有频率点（85kHz）的功率，如图4所示。对应至图5中的传输距离为0.05m的功率曲线所示，系统存在4个峰值功率点，其对应的频率和功率与图3中计算的理论共振频率以及图4计算得到的理论共振点的功率完全一致，由此证明本文推导得到了共振频率及共振点功率解析表达式是正确的。
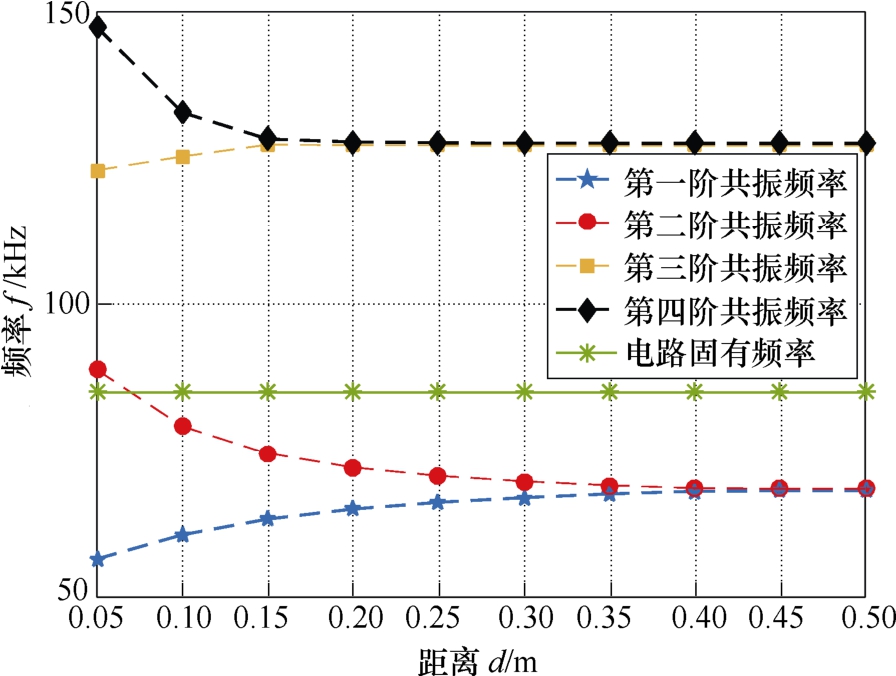
图3 共振频率随传输距离变化的分布（理论值）
Fig.3 The distribution of resonant frequencies versus the transfer distance (theoretical value)
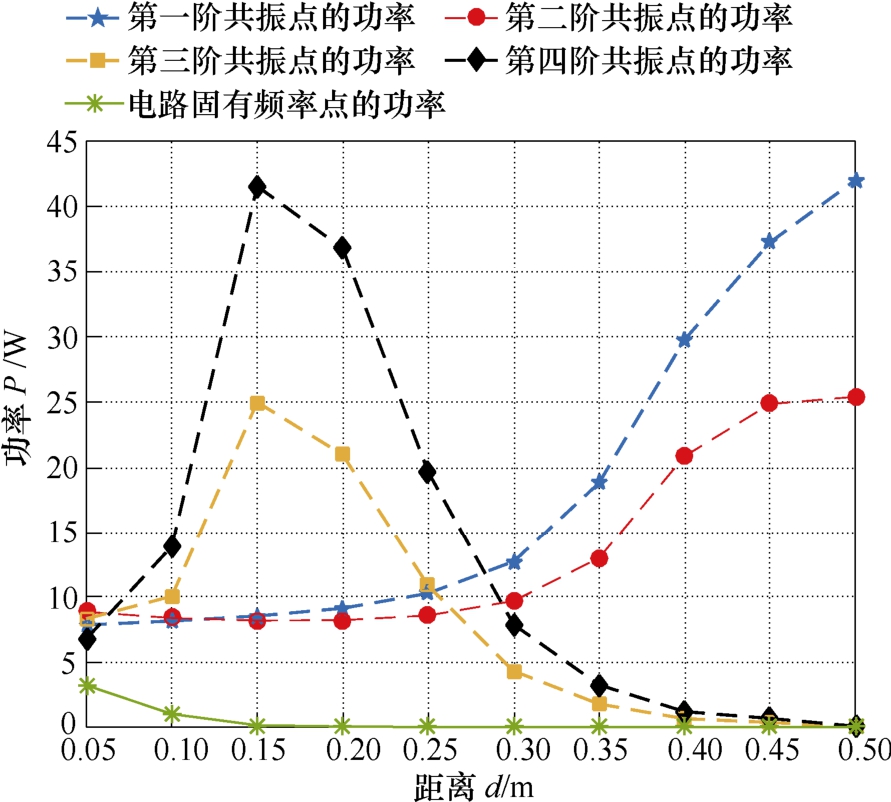
图4 共振点功率随传输距离变化的分布（理论值）
Fig.4 The distribution of powers of resonant points versus the transfer distance (theoretical value)
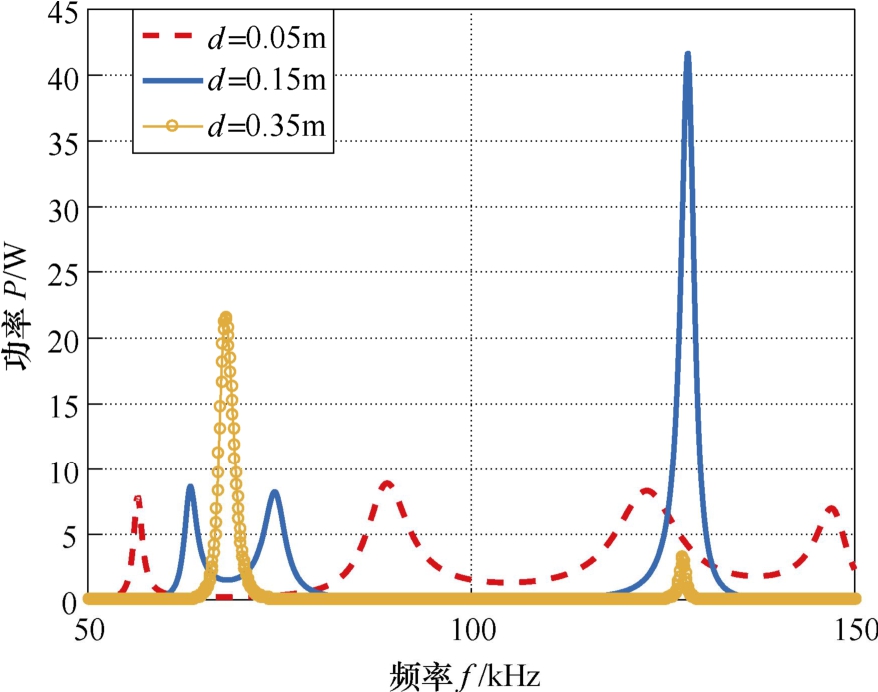
图5 传输距离为0.05m、0.15m和0.35m时，系统传输功率随电源频率变化曲线（仿真值）
Fig.5 For a distance of 0.05m, 0.15m and 0.35m,the simulated power versus the operating frequency
随着距离进一步增大（0.15m＜d23＜0.35m），如图3所示，此时第三阶共振频率和第四阶共振频率相互重合，系统只存在3个彼此分离的共振频率。对应图5中距离为0.15m的功率曲线，此时系统功率随频率变化曲线只存在3个峰值功率点，峰值功率点的频率与理论计算得到的共振频率完全一致。同时由图4可知，该距离范围内，第一阶共振点和第二阶共振点的功率基本保持不变，第三阶和第四阶重叠后的功率先逐步增大再减小，但都远远大于电路固有频率点的功率。同时重叠共振点的功率鲁棒性非常差，如图4所示，重叠共振点频率附近，频率小幅度变化时，功率变化幅度非常大。
当传输距离d23＞0.35m时，如图3所示，此时第一阶共振频率和第二阶共振频率也相互重叠，系统只存在两个相互分离的共振点。由图4可知，此时第三阶和第四阶共振点的功率特别小，第一阶和第二阶重叠的共振点的功率较大，但鲁棒性差（第一阶和第二阶频率十分接近，但功率却相差很远）。对应如图5中距离为0.35m的功率曲线，曲线只有两个峰值功率点，其对应的频率和计算得到的共振频率完全一致，且第一个峰值点的鲁棒性差，第二个峰值点的功率十分小。
2.2 电阻特性分析
在本节中，各线圈之间的距离固定为0.05m，负载从1Ω 的步长逐渐增大到50Ω，其余参数与2.1节中系统的参数保持不变。运用式（17）和式（18），计算不同负载下系统共振频率及共振点功率的分布曲线，分别如图6和图7所示。同样地，为了验证不同负载电阻下系统共振点及共振点功率分布的正确性，以给定参数为基准，运用COMSOL搭建MC- WPT系统实物仿真模型。当负载电阻为1Ω、10Ω、50Ω 时，系统仿真功率随电源频率变化曲线如图8所示。
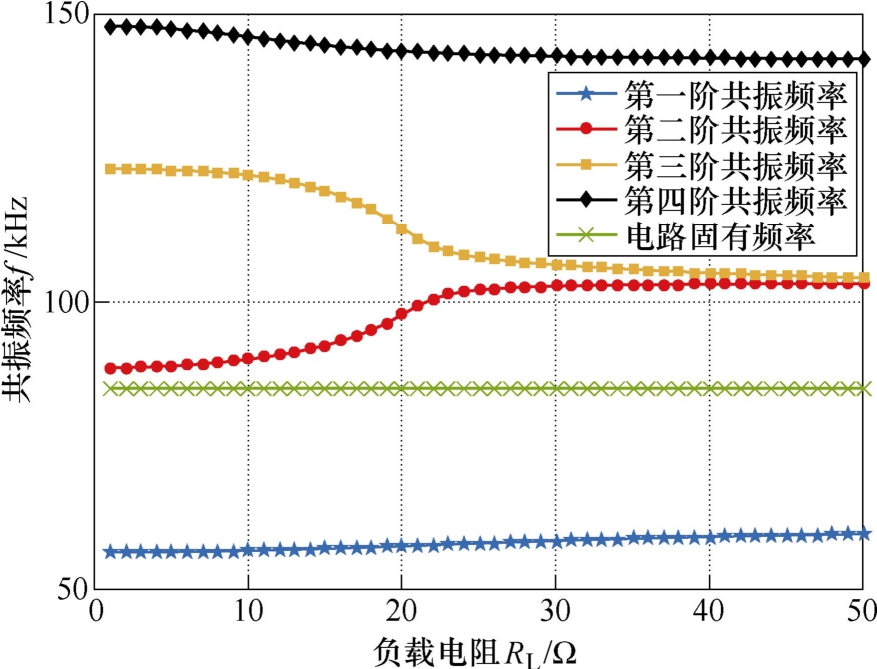
图6 共振频率随负载电阻变化的分布（理论值）
Fig.6 The distribution of resonant frequencies versus the load resistance (theoretical value)
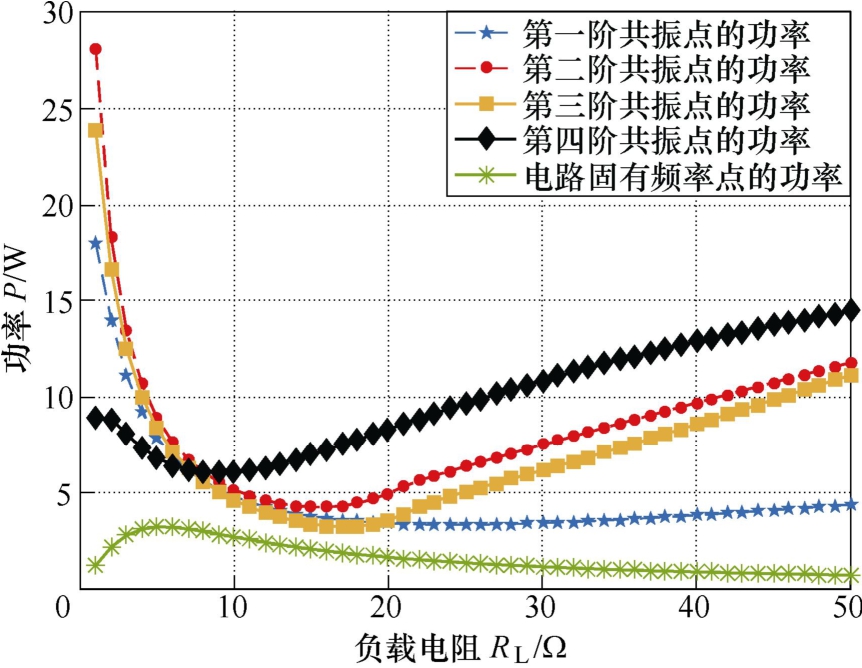
图7 共振点功率随负载电阻变化的分布（理论值）
Fig.7 The distribution of powers of resonant points versus the load resistance (theoretical value)
图8 电阻为1Ω、10Ω 和50Ω 时，系统传输功率随 电源频率变化曲线（仿真值）
Fig.8 For a resistance of 1Ω, 10Ω and 50Ω, the simulated power versus the operating frequency
由图6可知，当负载阻值较小的时候，系统存在 4个彼此分离的共振频率点。且在一定范围内（RL＜ 10Ω)，系统的共振频率基本保持不变。对应到图8中的负载为1Ω 和10Ω 的功率曲线，此时功率随电源频率变化曲线存在4个峰值功率点，峰值点的频率及功率和图3及图4中计算得到的共振频率及共振点功率完全一致。
当负载进一步增大时，系统第二阶共振频率和第三阶共振频率逐渐靠近，最终重叠在一起，即此时系统只有3个彼此分离的共振点。对应至图8中负载为50Ω 的功率曲线，此时功率随频率变化曲线只存在3个峰值点，其对应的频率和计算得到的系统固有频率完全吻合。同时由图3和图4可知，不论负载怎么变化，系统的共振点都不会和系统中电路固有频率点重合，共振点的功率均大于电路固有频率点的功率。该现象表明在某些参数条件下，系统不存在传统的临界耦合值。
综合2.1小节可得：①理论计算得到的共振频率及相应的功率和实物仿真结果十分吻合，表明本文推导得出的共振频率及相应共振点的功率解析表达式是正确的；②MC-WPT系统共振频率和系统中电路固有频率并不是同一个概念；③频率分裂现象的本质原因是系统存在彼此分离的共振频率；④不论是强耦合还是弱耦合、强阻尼还是弱阻尼，不需要确定参数边界条件，运用式（17）、式（18）可快速准确地得到MC-WPT系统所有的共振频率以及对应共振点的功率，因而能够快速确定合适的工作频率使得系统处于共振状态。
3 实验验证
3.1 平台搭建
为了验证本文提出的理论模型的正确性，搭建了如图9所示的实验装置。实验平台主要由直流电源、全桥逆变电路、耦合线圈组成。4个耦合线圈几何参数完全相同，内半径为0.03m，匝数为18匝，匝间距为0.01m。4个线圈平行共轴放置，相邻线圈间的传输距离设置为0.05m。实验平台中的相关电参数通过数字电桥测量所得，系统实测电参数见表1。直流电源电压设置为18V，负载电阻设置为5Ω，各回路补偿电容设置为63nF。同时，以实测所得电参数，搭建了对应的Simulink仿真模型。
图9 实验装置
Fig.9 The setup of the experiment
表1 系统实测电参数
Tab.1 The measured electrical parameters of the system
参 数 数 值 L1, L2, L3, L4/μH 58 Rp1, Rp2, Rp3, Rp4/Ω 0.13 M12, M23, M34/μH 28.31 M13, M24/μH 14.59 M14/μH 8.27
3.2 模型验证
基于给定的电参数，运用固有频率公式
可得系统中各振荡回路的电路固有频率为83kHz。运用式（17）～式（19）可快速得到系统的共振频率以及共振点的功率和效率，具体数值见表2。
表2 共振频率及相应共振点的输出功率理论值
Tab.2 The theoretical value of the resonant frequencies and corresponding powers
共振频率/kHz 输出功率/W 传输效率(%) 58 51.74 87.85 85 58.62 93.34 112 55.07 91.17 132 47.08 78.46
在实验中，采用4个高精度电流探头记录各振荡回路的电流波形。为了验证理论模型以及共振点分布的正确性，电源频率从50kHz以1kHz的步长变化至180kHz，理论、仿真及实测功率随电源频率变化曲线如图10所示。
图10 理论、仿真、实测功率随电源频率变化曲线
Fig.10 The theoretical, simulated and measured output power versus the operating frequency
由图10所示，各频率点的理论值和仿真值完全吻合，表明本文基于复模态分析建立的理论模型是合理有效的。实测值和理论值存在一定的偏差主要是由于系统中实测电参数的误差引起的。同时从图10可知，系统存在四个功率极大值，其对应的频率和理论计算得到的共振频率完全一致，都偏离设置的电路固有频率（83kHz），由此证实本文推导得到的共振频率解析表达式是完全正确的，即MC-WPT系统的共振频率为系统矩阵特征值的模。
4个共振点的实测电流波形如图11所示，其中I1为第1个线圈回路的电流波形，I2为第2个线圈回路的电流波形，I3为第3个线圈回路的电流波形，I4为第4个线圈回路的电流波形。
图11 共振点实测电流波形
Fig.11 The measured current waveforms of resonant states
由图11可以看出，系统处于共振状态时，各回路电流相位接近于同相或者反相，表明系统中各振荡回路并非处于纯阻性状态，证实系统的共振频率不等于系统中各振荡回路的电路固有频率。同时基于图11，可得4个共振点（58kHz、86kHz、112kHz和133kHz）的实测效率依次为90.1%、94.6%、92.5%和82.5%，和理论值十分接近。实测值都略微大于理论值的原因主要是由于测量误差引起的。但从理论值和实测结果可知，尽管共振点等价于系统的功率极大值点，但共振状态下的效率都不低，即系统工作在共振状态下能够较好的兼顾功率和效率。
4 结论
针对MC-WPT系统各电参数对系统共振点的分布影响问题，本文综合考虑系统中各电路固有频率、互感及电阻等参数，基于复模态分析理论对MC-WPT系统进行共振机理建模，得到了MC-WPT系统共振频率及共振点功率的解析表达式，并深入分析了MC-WPT系统的共振频率及共振点功率随传输距离及负载电阻变化的分布特性，证实：
1）MC-WPT系统共振频率和系统中电路固有频率并不是同一个概念。MC-WPT系统共振频率是MC-WPT系统的系统矩阵特征值的模。
2）频率分裂现象的本质原因是系统存在彼此分离的共振频率。
3）在某些参数条件下，不论距离或者互感如何变化，系统共振点可能永远不会和系统中电路固有频率点重合，即不存在传统的临界耦合值。共振点的功率会随系统参数变化有所改变，但都明显大于电路固有频率点的功率。
4）不论是强耦合还是弱耦合、强阻尼还是弱阻尼，均不需要确定参数边界条件，运用本文推导得到的式（17）～式（19）可快速准确地得到MC-WPT系统所有的共振频率以及共振状态下的功率和效率。
[1]Kurs A, Karalis A, Moffatt R, et al. Wireless power transfer via strongly coupled magnetic resonances[J]. Science, 2007, 317(5834): 83-86.
[2]Karalis A, Joannopoulos J D, Soljačić M. Efficient wireless non-radiative mid-range energy transfer[J]. Annals of Physics, 2008, 323(1): 34-48.
[3]Diao Yinliang, Shen Yuanmao, Gao Yougang. Design of coil structure achieving uniform magnetic field distribution for wireless charging platform[C]//2011 4th International Conference on Power Electronics Systems and Applications, Hong Kong, China, 2011: 1-5.
[4]Kim N Y, Kim K Y, Ryu Y H, et al. Automated adaptive frequency tracking system for efficient mid- range wireless power transfer via magnetic resonanc coupling[C]//2012 42nd European Microwave Con- ference, Amsterdam, Netherlands, 2012: 221-224.
[5]Chen Jiming, Li Songyuan, Chen Shuo, et al. Q-charge: a quadcopter-based wireless charging platform for large-scale sensing applications[J]. IEEE Network, 2017, 31(6): 56-61.
[6]Nguyen D T, Lee E S, Choi B, et al. Optimal shaped dipole-coil design and experimental verification of inductive power transfer system for home appli- cations[C]//2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Beach, California, 2016: 1773- 1779.
[7]Hu Chao, Sun Yue, Lü Xiao, et al. Magnetic coupler design procedure for IPT system and its application to EVs' wireless charging[J]. International Journal of Applied Electromagnetics and Mechanics, 2015, 47(3): 861-873.
[8]赵锦波, 蔡涛, 段善旭, 等. 适用于分段式动态无线充电的T型抗偏移补偿拓扑[J]. 电工技术学报, 2017, 32(18): 36-43. Zhao Jinbo, Cai Tao, Duan Shanxu, et al. A T-type high misalignment tolerant compensated topology for sectional track-based dynamic wireless power trans- mission system[J]. Transactions of China Electro- technical Society, 2017, 32(18): 36-43.
[9]陈琛, 黄学良, 谭林林, 等. 电动汽车无线充电时的电磁环境及安全评估[J]. 电工技术学报, 2015, 30(19): 61-67. Chen Chen, Huang Xueliang, Tan Linlin, et al. Electromagnetic environment and security evaluation for wireless charging of electric vehicles[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(19): 61-67
[10]宋凯, 朱春波, 李阳, 等. 用于电动汽车动态供电的多初级绕组并联无线电能传输技术[J]. 中国电机工程学报, 2015, 35(17): 4445-4453. Song Kai, Zhu Chunbo, Li Yang, et al. Wireless power transfer technology for electric vehicle dynamic charging using multi-parallel primary coils[J]. Proceedings of the CSEE, 2015, 35(17): 4445-4453.
[11]Zhang Yiming, Lu Ting, Zhao Zhengming, et al. Selective wireless power transfer to multiple loads using receivers of different resonant frequencies[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6001-6005.
[12]Ye Zhaohong, Sun Yue, Dai Xin, et al. Energy efficiency analysis of u-coil wireless power transfer system[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4809-4817.
[13]Zhang Wei, Wong Siuchung, Tse C K, et al. Design for efficiency optimization and voltage controllability of series-series compensated inductive power transfer systems[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 191-200.
[14]Zhong Wenxin, Zhang Cheng, Liu Xun, et al. A methodology for making a three-coil wireless power transfer system more energy efficient than a two-coil counterpart for extended transfer distance[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 933- 942.
[15]杨庆新, 章鹏程, 祝丽花, 等. 无线电能传输技术的关键基础与技术瓶颈问题[J]. 电工技术学报, 2015, 30(5): 1-8. Yang Qingxin, Zhang Pengcheng, Zhu Lihua, et al. Key fundamental problems and technical bottlenecks of the wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 1-8.
[16]赵争鸣, 张艺明, 陈凯楠. 磁耦合谐振式无线电能传输技术新进展[J]. 中国电机工程学报, 2013, 33(3): 1-13. Zhao Zhengming, Zhang Yiming, Chen Kainan. New progress of magnetically-coupled resonant wireless power transfer technology[J]. Proceedings of the CSEE, 2013, 33(3): 1-13.
[17]Sample A, Meyer D, Smith J. Analysis, experimental results, and range adaptation of magnetically coupled resonators for wireless power transfer[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 544-554.
[18]孙跃, 廖志娟, 叶兆虹, 等. 基于振动理论的MCR- WPT系统频率分裂特性研究[J]. 电工技术学报, 2018, 33(13): 3140-3148. Sun Yue, Liao Zhijuan, Ye Zhaohong, et al. Research on frequency splitting characteristic of MCR-WPT systems based on vibration theory[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3140- 3148.
[19]黄学良, 谭林林, 陈中, 等. 无线电能传输技术研究与应用综述[J]. 电工技术学报, 2013, 28(10): 1-11. Huang Xueliang, Tan Linlin, Chen Zhong, et al. Review and research progress on wireless power transfer technology[J]. Transactions of China Elec- trotechnical Society, 2013, 28(10): 1-11.
[20]刘帼巾, 李义鑫, 崔玉龙, 等. 基于FPGA的磁耦合谐振式无线电能传输频率跟踪控制[J]. 电工技术学报, 2018, 33(14): 3185-3193. Liu Guojin, Li Yixin, Cui Yulong, et al. Frequency tracking control of wireless power transfer via magnetic resonance coupling based on FPGA[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3185-3193.
[21]Beh T, Kato M, Imura T, et al. Automated impedance matching system for robust wireless power transfer via magnetic resonance coupling[J]. IEEE Transa- ctions on Industrial Electronics, 2013, 60(9): 3689- 3698.
[22]李阳, 董维豪, 杨庆新, 等. 过耦合无线电能传输功率降低机理与提高方法[J]. 电工技术学报, 2018, 33(14): 3176-3184. Li Yang, Dong Weihao, Yang Qingxin, et al. Mechanism of power decreasing and improvement method for wireless power transfer system in over coupled regime[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3176-3184.
[23]李阳, 杨庆新, 闫卓, 等. 磁耦合谐振式无线电能传输方向性分析与验证[J]. 电工技术学报, 2014, 29(2): 197-203. Li Yang, Yang Qingxin, Yan Zhuo, et al. Analysis and validation on characteristic of orientation in wireless power transfer system via coupled magnetic resonances[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 197-203.
[24]Zhang Yiming, Zhao Zhengming, Chen Kainan. Frequency-splitting analysis of four-coil resonant wireless power transfer[J]. IEEE Transactions on Industry Applications, 2014, 50(4): 2436-2445.
[25]Nguyen H, Agbinya J. Splitting frequency diversity in wireless power transmission[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6088-6096.
[26]Sun Yun, Liao Zhijuan, Ye Zhaohong, et al. Deter- mining the maximum power transfer points for MC-WPT systems with arbitrary number of coils[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9734-9743.
[27]张波, 黄润鸿, 丘东元. 磁谐振中距离无线电能传输及关键科学问题[J]. 电源学报, 2015, 13(4): 1-7. Zhang Bo, Huang Runhong, Qiu Dongyuan. Key problems of midrange wireless power transfer via magnetic resonances[J]. Journal of Power Supply, 2015, 13(4): 1-7.
[28]陈奎孚. 机械振动教材[M]. 北京: 中国农业大学出版社, 2014.
[29]Ye Zhaohong, Liao Zhijuan, Sun Yue, et al. Study on optimal design of WPT resonators based on genetic algorithm[C]//2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 2016: 1-3.