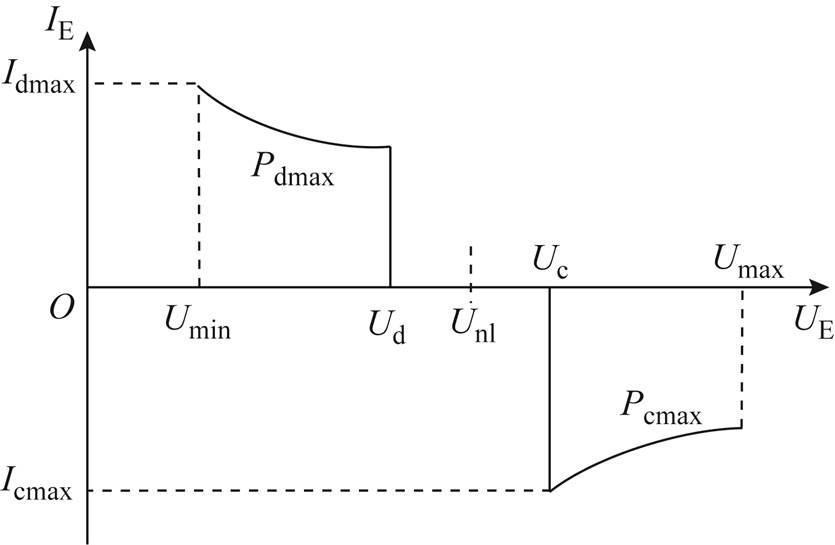
图1 储能装置U-I特性
Fig.1 U-I characteristic curve of energy storage device
摘要 地面储能装置在城市轨道交通牵引供电系统中有较为广阔的应用前景。该文建立了地面储能装置的通用计算模型,提出一种基于滞环算法的变电所多状态切换策略,给出不同工作状态下等效电路的求解方法,并分析了储能装置与整流机组协同输出时的电流分配关系。在此基础上设计的直流牵引供电计算双层迭代算法具有迭代速度快的特点。该文提出一组评估储能装置节能稳压效果的指标,针对广州某地铁线路进行不同发车间隔下的算例研究。全线安装储能后牵引网电压有明显改善,再生制动能量回收率从56.4%提升到95%以上,全线牵引变电所节能率可达12.1%。仿真结果表明,储能装置在地铁牵引供电系统中具有良好的节能、稳压效果。
关键词:城市轨道交通 储能装置 再生制动 直流牵引供电系统
城市轨道交通运营具有车站间距离短、车辆运行密度高等特点,列车在频繁起动与制动的过程中会产生数量可观的制动能量[1],但也随之引起牵引网电压剧烈波动,若电压提升过高,甚至会导致再生制动失效,危害行车安全[2]。
目前常见的再生制动能量处理方式主要包括电阻式、逆变回馈式和储能式三种[3]。电阻式制动将电能转换为热能耗散,与节能环保的要求相悖,且装置温升可能提高环控成本;逆变回馈装置仅在车辆制动时动作,回馈的制动能量对电网造成冲击,可能会产生谐波与环流等问题,且不能在车辆加速起动中提供辅助电能;储能装置在列车制动时吸收多余再生制动能量,并在列车牵引时与整流机组协同输出功率。因此,为提高再生能量利用率,改善牵引网电压,在轨道交通牵引供电系统中配置储能装置是一种综合效果较好的方案[4-5]。储能装置根据安装方式可分为车载式与地面式两种[6],由于列车空间有限,且增加车重会提高牵引能耗,采用地面式储能装置代替车载储能装置是一种较好的方案。
近年来国内外学者对于储能装置的研究主要集中于控制策略与优化配置两方面,在建模时往往针对某一类特定的储能装置进行。清华大学的刘学对飞轮储能装置充电过程采用恒转矩与恒功率联合控制、放电过程采用弱磁控制,飞轮工作模式切换迅速,全功率范围内直流母线电压稳定[7]。中国科学院的刘文军提出了一种基于改进型滑模观测器的飞轮储能系统控制方法,在飞轮充电和能量保持时采用速度外环、电流内环的双闭环控制策略;在飞轮放电时采用电压外环、电流内环的双闭环控制策略,并通过实验验证了控制策略的有效性[8]。
文献[9]在Matlab环境下建立了适用于城轨交通的地面超级电容储能系统仿真平台,并用于讨论储能装置的容量优化配置。文献[10]对供电系统参数与储能装置容量配置进行综合优化,有效提高了储能系统的节能率。文献[11]建立了基于列车运行图和牵引供电系统负荷潮流的仿真算法,用于验证飞轮储能系统的节能稳压效果,但文中提出的飞轮储能装置状态切换算法较为简单,实际计算过程中状态控制量可能会在切换阈值附近波动,导致状态切换出现重复。文献[12]将储能装置作为电流源进行建模,分析了储能装置应用于城市轨道中的节能潜力,并提出了一种评估线路能耗的方案,但未考虑储能装置与整流机组协同放电时的能量分配关系。
目前已有的储能装置主要包括超级电容、飞轮、蓄电池等,相应的控制策略也较多,在前期供电计算与设计时不必针对各种情况——建立模型。因此,本文建立了一种适用于多种类型储能装置的黑盒模型,并设计相应的直流牵引供电系统仿真算法。
本文在前人工作的基础上,首先给出含储能装置的牵引供电系统模型,包括储能装置黑盒模型;然后设计基于Bang-Bang算法的变电所多状态切换策略,优化状态迭代过程中的收敛性问题;接着给出每种状态对应的等效电路的求解方法,并分析储能装置与整流机组协同放电的能量分配关系,建立含储能装置的城市轨道交通直流牵引供电系统计算算法;最后给出一套评估储能装置节能稳压效果的指标,并针对广州某一地铁线路进行不同发车间隔下的全线仿真分析。
储能装置的建模主要包括内部电路建模与外特性建模两种方式[13],后者更适用于直流牵引供电系统计算。IEEE Std 1887—2017[14]中定义了储能装置的黑盒模型。考虑能量流动情况,地面式储能装置可分为充电、放电与关断三种基本工作状态。
储能装置U-I特性曲线如图1所示。其中,Unl为牵引变电所整流机组空载电压;UE为储能装置电压;IE为储能装置电流;Uc为储能装置充电阈值电压;Ud为储能装置放电阈值电压;Pcmax为储能装置最大充电功率;Pdmax为储能装置最大放电功率;Umax为储能装置最大工作电压;Umin为储能装置最小工作电压;Icmax为储能装置最大充电电流;Idmax为储能装置最大放电电流。

图1 储能装置U-I特性
Fig.1 U-I characteristic curve of energy storage device
对充电过程而言,当列车进行再生制动时,牵引网电压升高,若电压高于充电阈值,储能装置进入恒压充电模式,且UE=Uc,充电电流可调,以维持牵引网电压稳定。随着再生制动能量的增大,储能装置响应电流增大,充电功率上升,当功率超过Pcmax时,储能装置切换至最大功率充电模式,等效为功率源,其功率PE =Pcmax。放电过程储能装置模型与此类似。
为模拟实际运行中的充放电能量损耗,可引入能量转换效率η,如式(1)所示。
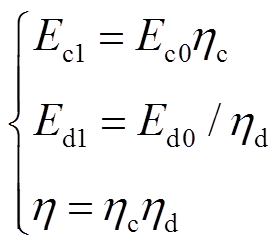 (1)
(1)
式中,Ec0为充电过程牵引网提供给储能装置的能量;Ec1为储能装置实际储存的能量;Ed0为放电过程牵引网需要储能装置提供的能量;Ed1为储能装置实际释放的能量;ηc为储能装置充电效率;ηd为储能装置放电效率。
直流牵引供电系统主要由整流变压器、整流机组、牵引网和列车等部分组成。
整流机组有两种模型,即恒压源-内阻模型与多折线外特性模型[15],考虑到算法求解速度与精度,前者已可满足要求,且不考虑短路计算情况下,多折线外特性模型只会用到前两段特性曲线,因此整流机组按照恒压源-内阻模型进行建模。
牵引网包括接触网、钢轨、埋地金属和地四个部分。因为杂散电流分析非本文研究重点,因此可忽略埋地金属,建立三层等效地网模型,简化直流侧节点导纳矩阵,加快算法求解速度[16]。
列车电流源模型误差较大,因此采用功率源进行建模,根据迭代过程中计算得到的牵引网压对列车电流进行实时修正。
列车制动时,为保证行车安全,可通过车载制动电阻吸收多余再生制动能量。
当列车网压Utrain高于车载制动电阻启动电压Urb时,车载制动电阻启动,消耗部分再生能量;当网压高于最大限制电压Urbmax时,全部制动能量消耗在车载制动电阻上[10]。车载制动电阻启动后,列车剩余制动功率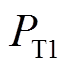 为
为
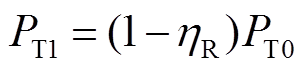 (2)
(2)式中,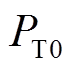 为车载制动电阻启动前,列车的再生制动功率;ηR为车载制动电阻启动占空比。
为车载制动电阻启动前,列车的再生制动功率;ηR为车载制动电阻启动占空比。
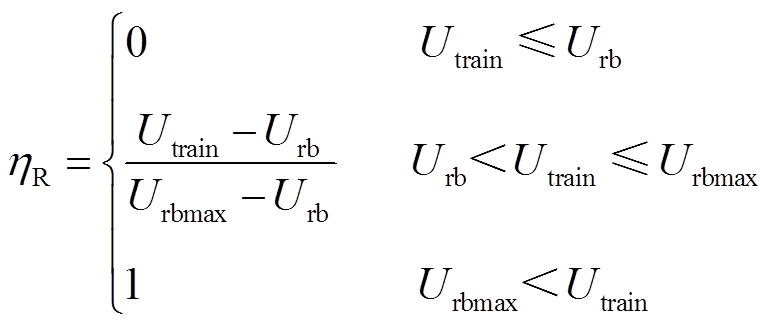 (3)
(3)
含储能装置的直流牵引供电仿真算法可分为内外两层循环。外层循环完成状态切换和计算模型调整,包含牵引变电所多状态切换过程;内层循环完成直流供电网络单次求解计算,包含储能装置与列车的功率源迭代过程。
考虑储能装置数学模型及其与整流机组的协同工作方式,可将变电所划分为六种工作状态:保持状态(TOFF)、整流状态(REC)、恒压充电状态(ECU)、最大功率充电状态(ECP)、恒压放电状态(EDU)、最大功率放电状态(EDP)。
TOFF状态下,储能装置与整流机组均不工作;REC状态下,整流机组单独工作;ECU与ECP状态下,储能装置单独工作;EDU与EDP状态下,储能装置与整流机组协同工作。
影响储能装置工作状态的参数主要有充放电阈值电压、充放电峰值功率、荷电状态(State of Charge, SOC)条件、最大/最小工作电压限制,据此,可设计相应的储能装置状态切换策略,如图2所示。图中,US为变电所处牵引网电压;SOCmax和SOCmin分别为储能装置荷电状态上、下限;Umax和Umin分别为储能装置允许工作电压最大值和最小值。
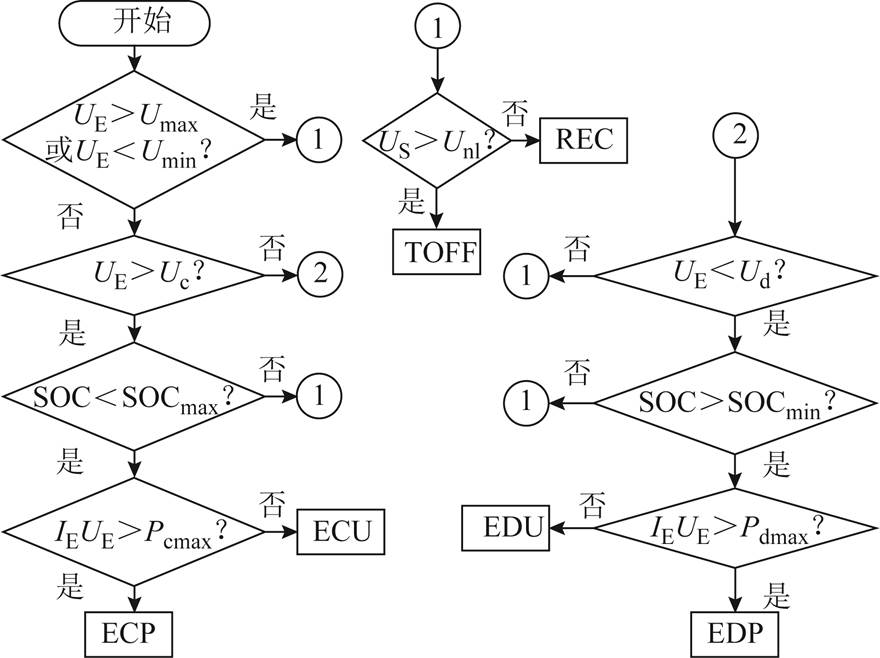
图2 储能装置状态切换策略
Fig.2 State-switch strategy of energy storage device
实际算法中,为避免各状态间的重复切换,在上述策略的基础上引入Bang-Bang控制(Bang-Bang Control, BBC)算法,对各控制量进行滞环比较,如式(4)所示。
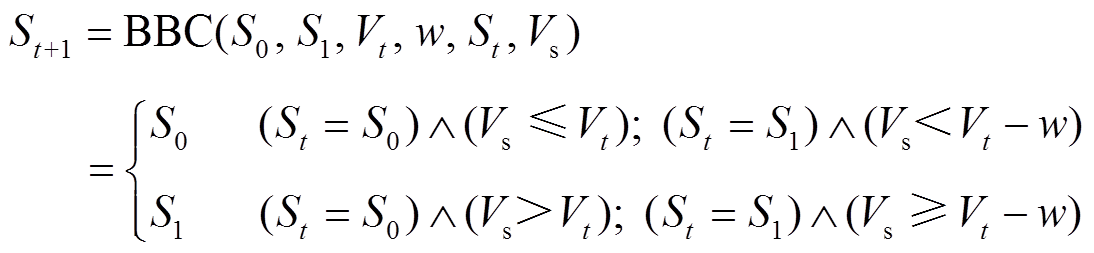 (4)
(4)式中,St为切换前变电所状态;St+1为切换后变电所状态;S0和S1分别为两种不同的状态;Vt为两种状态之间的切换阈值,如Uc;Vs为状态控制变量,如UE;w为滞环宽度。
BBC算法削弱了UE或IE位于切换阈值附近时算法的敏感性,限制了系统状态在相邻状态区间的频繁切换。据此可设计基于BBC的变电所多状态切换算法,见表1。
表1 基于BBC的多状态切换算法
Tab.1 Multi-state-switch algorithm based on BBC

输入:St,w,UE,IE,Us,Unl,Uc,Ud,Umax,Umin,Pcmax, Pdmax,SOCmax,SOCmin输出:St+1 1 根据初始状态St,执行相应步骤:EDP→2;EDU→3;REC→4;TOFF→5;ECU→6;ECP→7。2 St+1 = BBC (REC, EDP, Umin, w, EDP, UE)若St+1 = St, St+1 = BBC (EDU, EDP, Pdmax, w, EDP, IEUE)进入8。3 St+1 = BBC (EDU, EDP, Pdmax, w, EDU, IEUE)若St+1 = St, St+1 = BBC (EDU, REC, 0, w, EDU, IE)进入8。4 St+1 = BBC (EDU, REC, Ud, w, REC, UE)若St+1 = St, St+1 = BBC (REC, TOFF, Unl, w, REC, US)进入8。5 St+1 = BBC (REC, TOFF, Unl, w, TOFF, US)若St+1 = St, St+1 = BBC (TOFF, ECU, Uc, w, TOFF, UE)进入8。6 St+1 = BBC (ECU, TOFF, 0, w, ECU, -IE)若St+1 = St, St+1 = BBC (ECU, ECP, Pcmax, w, ECU, IEUE)进入8。7 St+1 = BBC (ECP, TOFF, Umax, w, ECP, UE)若St+1 = St, St+1 = BBC (ECU, ECP, Pcmax, w, ECP, IEUE)进入8。8 条件1:(St+1 = ECU) 或 (St+1 = ECP) 且(SOC≥SOCmax)条件2:(St+1 = EDU) 或 (St+1 = EDP) 且(SOC≤SOCmin)以上条件满足任意一个则进入9,否则进入109 St+1 = BBC (REC, TOFF, Unl, w, REC, US)10 输出St+1
考虑2.1节中提出的变电所六种工作状态,可得含储能装置的直流牵引供电系统等效电路,如图3所示。为便于求解,图中整流机组根据诺顿定理等效为电流源并联电阻的形式,功率源模型的求解可通过电流源迭代计算实现。
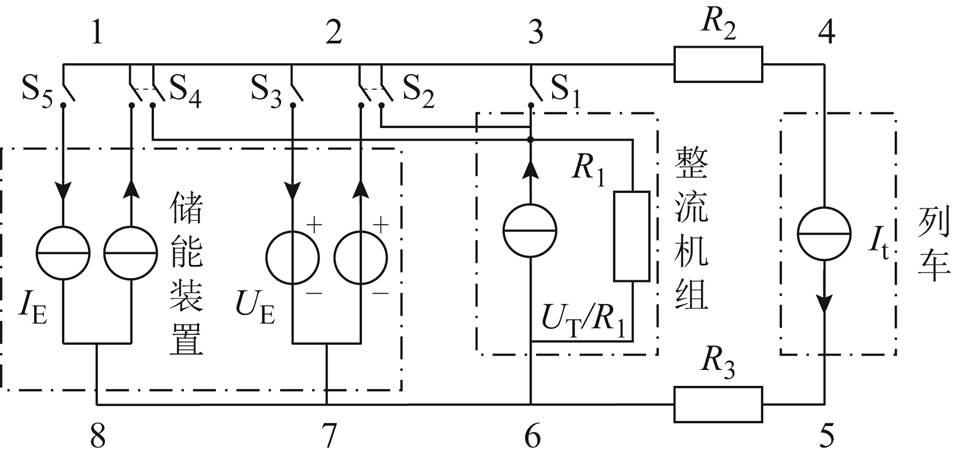
图3 含储能装置的直流牵引供电系统等效电路
Fig.3 Circuit of DC traction power supply system including energy storage device
设Sk=1表示开关闭合,Sk=0表示开关断开(其中k=1,2,3,4,5),则全部开关的状态可用数组S=(S1S2S3S4S5)表示,数组中元素的可能取值只有六种。
S=(00000)对应状态TOFF。S=(10000)对应状态REC,此时整流机组单独工作,可等效为理想电压源串电阻,或依据诺顿定理变形为电流源并电阻,等效电路可根据节点电压法求解。
S=(01000)与S=(00100)对应状态EDU与ECU,此时储能装置等效为独立电压源,且UE=Ud或UE=Uc。对于EDU状态而言,储能装置与整流机组协同工作。根据修改节点电压法[14],为每一个独立电压源支路引入一个独立电流量,可得到矩阵为
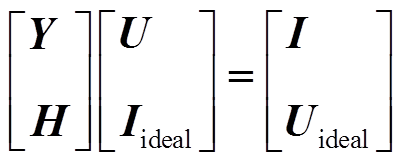 (5)
(5)式中,Y与H为节点导纳矩阵;U为节点电压矩阵;Iideal为理想电压源支路电流矩阵;I为节点注入电流矩阵;Uideal为理想电压源电压矩阵。
Iideal与U为待求解的量,其余量均为已知量,只要求出Iideal与U,即可通过进一步的计算得到储能装置的能量响应信息。
S=(00010)与S=(00001)对应状态EDP与ECP,此时储能装置等效为恒功率源,且PE=Pdmax或PE=Pcmax。由于功率源无法线性求解,因此可用电流源迭代算法求解如下:
1)若判断变电所进入EDP或ECP状态,令迭代次数k=0,根据此时牵引网压初始化储能装置电压。
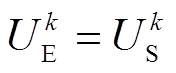 (6)
(6)
2)根据电压与功率更新储能装置电流。
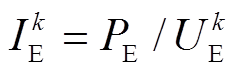 (7)
(7)
3)根据式(5)重新计算各节点电压,包括储能装置电压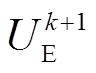 。
。
4)依据式(8)检查各节点电压是否收敛。
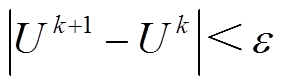 (8)
(8)
式中,ε为允许收敛误差。若满足式(8),则计算收敛,否则转入步骤2)继续迭代计算。
根据2.2节的分析可知,当变电所工作在EDU或EDP状态时,储能装置与整流机组协同工作,此时计算得到的节点流出电流为牵引负荷总电流,且满足
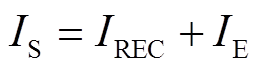 (9)
(9)
式中,IS为牵引负荷总电流;IREC为整流机组电流。为明确整流机组和储能装置各自的出力,有必要研究此时二者的能量分配情况。
对EDP状态而言,此时储能装置响应功率确定,网压可根据等效电路求解,其电流可由式(7)得到,整流机组电流可由式(9)计算得到。
对EDU状态而言,其网压等于储能装置等效的恒压源电压。根据整流机组外特性,如式(10)、式(11),可得其输出电流,如式(12)。
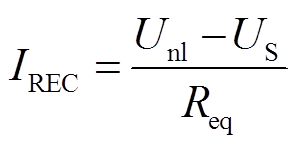 (10)
(10)
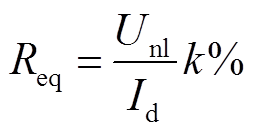 (11)
(11)
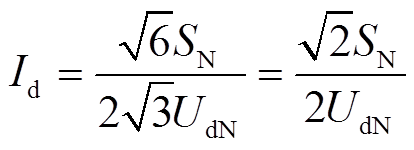 (12)
(12)式中,Req为整流机组等效电阻;Id为整流机组额定电流;UdN为整流机组阀侧额定电压;k为直流电压调整率;SN为整流机组额定容量。
根据式(10)~式(12),消去Req与Id可得
 (13)
(13)同理,储能装置的电流IE可根据式(9)求得。
根据前文分析,设计直流牵引供电系统双层迭代算法见表2。
表2 直流牵引供电系统双层迭代算法
Tab.2 Two-loops iterative algorithm of DC traction power supply system

输入:列车运行图;列车牵引计算信息;系统参数;储能装置参数;整流机组参数等输出:整流机组与储能装置的电流、电压、功率、能量;储能装置SOC;列车节点处电压、电流等 1 扫描列车运行图,读取当前时刻t列车位置信息,初始化系统参数2 全线牵引所初始状态置为REC3 扫描全线元件,建立节点-支路矩阵,根据式(5)求解等效电路,更新各节点信息4 根据求解得到的新的支路电流与节点电压数据和当前整流机组与储能装置的工作状态St,由表1重新判断下一时刻工作状态St+1。若St+1≠St,则修改储能装置模型;若St+1=St,状态迭代收敛,执行步骤55 判断是否出现全部整流机组与储能装置关断的情况,此情况下等效电路不可解。若出现全关断,说明再生制动能量无法被完全吸收,此时削减制动列车功率,返回步骤3;否则执行步骤66 判断各列车节点电压是否超过车载制动电阻启动阈值,若超过则按照式(2)、式(3)削减列车制动功率7 更新储能装置SOC。生成详细计算结果。若仿真未到达终点,则t=t+1,返回步骤1;否则仿真结束
为进一步量化储能装置的节能稳压效果,定义以下评估指标:
1)牵引网电压最大/最小值f1H、f1L。
用于评估储能装置投入后对牵引网压的支撑效果。
 (14)
(14)式中,t1, ,tn为仿真开始到结束的每一个扫描时间断面;s1,
,tn为仿真开始到结束的每一个扫描时间断面;s1, ,sm为线路始端到末端的每一个牵引网节点。
,sm为线路始端到末端的每一个牵引网节点。
2)再生制动能量回收率f2。
用于评估安装储能装置后全线再生制动能量回收效果。若忽略牵引网网损,根据能量守恒,列车再生制动时线路上的能量分配满足
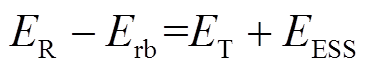 (15)
(15)式中,ER为全线列车再生制动总能量;Erb为车载制动电阻消耗总能量;ET为邻近牵引工况列车吸收的再生制动能量;EESS为储能装置回收的再生制动能量。ET与EESS之和即为全线被有效回收的再生制动能量,但ET难以统计,因此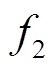 可定义为
可定义为
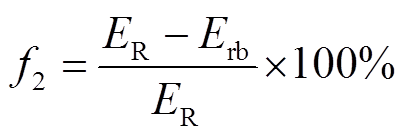 (16)
(16)
3)牵引变电所节能率f3。
用于评估储能装置放电过程牵引变电所的节能效果。
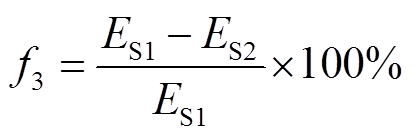 (17)
(17)式中,ES2为投入储能装置后全线整流机组的输出总能量;ES1为参考系统全线整流机组的输出总能量。
以广州地铁某运营线路作为供电计算实例,线路长度为25.442km,全线共设置车站9个,牵引变电所10个,其中2个为区间所。各牵引变电所与车站位置分布如图4所示。车辆参数见表3。通过实测得到上下行列车的速度-位置与功率-位置曲线,如图5所示,列车最高运行速度为115km/h,最大牵引功率与最大制动功率均为4MW。

图4 牵引变电所与车站位置
Fig.4 Location of substations and stations
表3 车辆参数设置
Tab.3 Parameters of vehicles
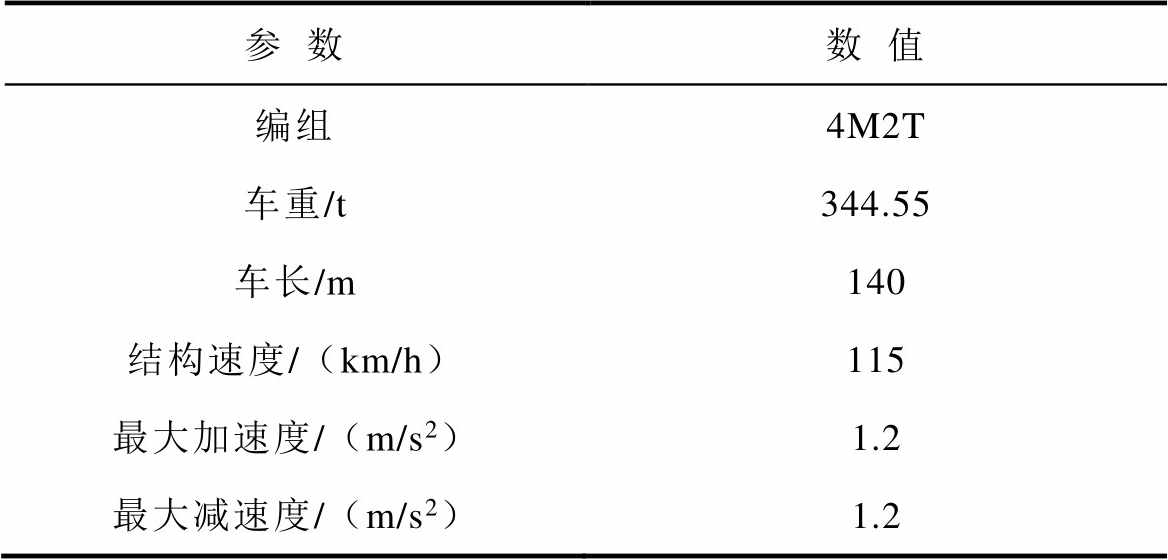
参数数值 编组4M2T 车重/t344.55 车长/m140 结构速度/(km/h)115 最大加速度/(m/s2)1.2 最大减速度/(m/s2)1.2
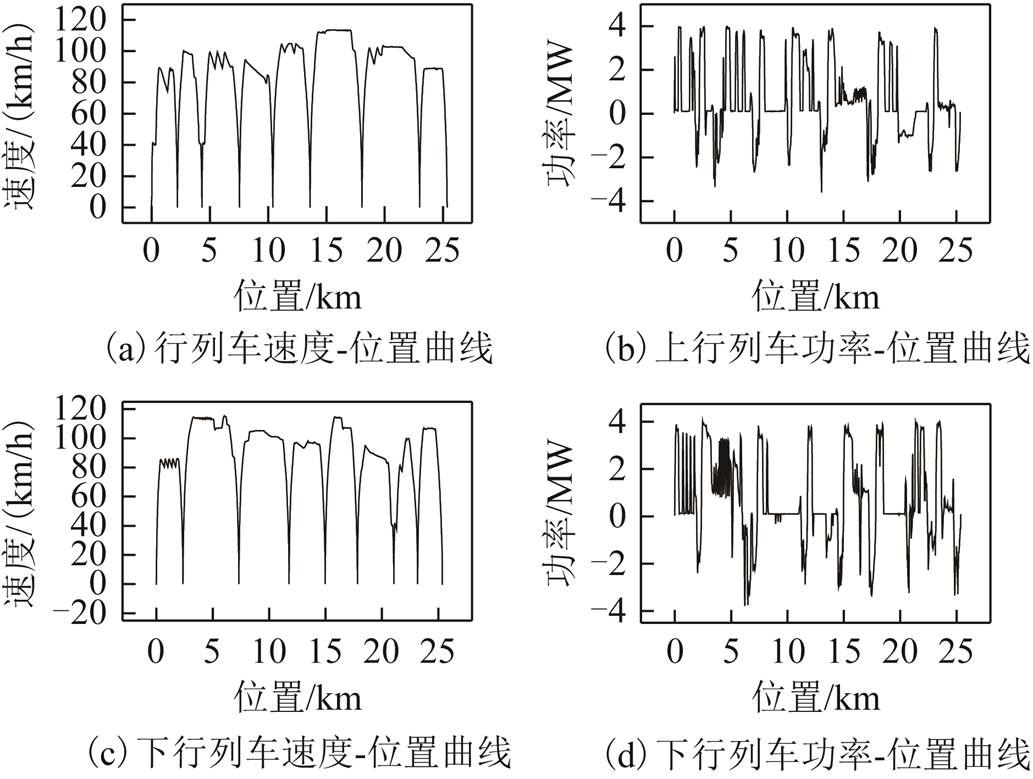
图5 上下行列车运行曲线
Fig.5 Operation curve of up train and down train
为验证直流牵引供电系统计算算法的有效性,设置收敛精度为ε=10-3。考虑以下情形:①全所均不安装储能装置(参考系统);②全所安装储能装置。
任意选取列车某一运行时刻,比较情景①和情景②在同一时刻下的变电所整流机组输出功率、牵引网电压。设置发车间隔为525s,列车从t=0s开始运行,考察t=290s时的运行情况。表4为供电系统参数设置;表5为储能装置系统参数设置。情景①与情景②的计算收敛次数均为3。
比较两种不同系统的牵引网电压,如图6所示。从图中可见,t=290s时,情景①最高牵引网压为1 781.85V,最低牵引网压为1 583.95V;情景②最高牵引网压为1 712.07V,最低牵引网压为1 602.74V。情景②的牵引网电压波动相比情景①而言明显降低。
表4 供电系统参数设置
Tab.4 Parameters of power supply system
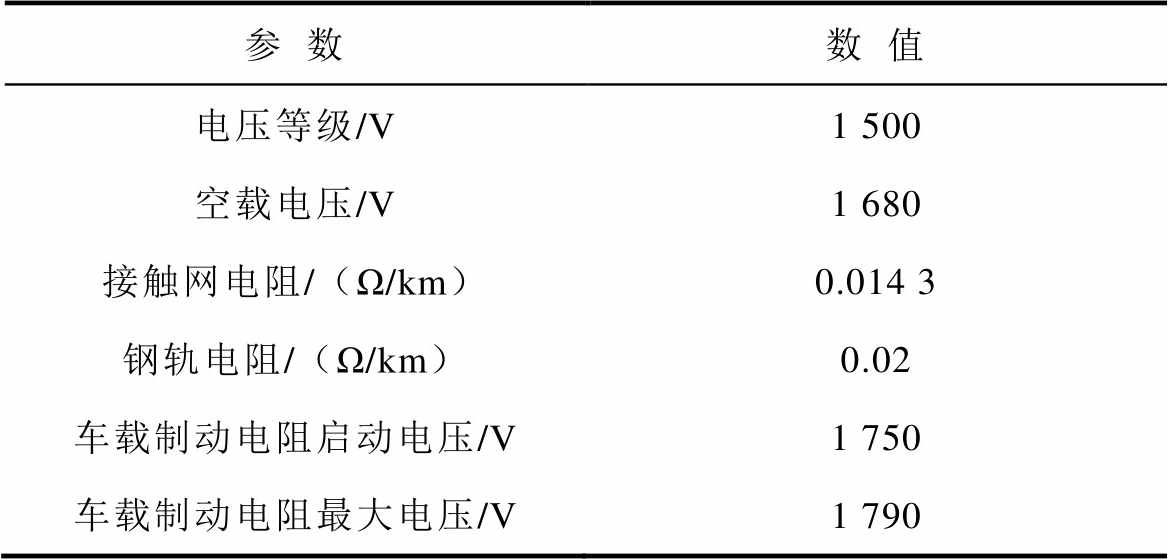
参数数值 电压等级/V1 500 空载电压/V1 680 接触网电阻/(Ω/km)0.014 3 钢轨电阻/(Ω/km)0.02 车载制动电阻启动电压/V1 750 车载制动电阻最大电压/V1 790
表5 储能装置参数设置
Tab.5 Parameters of energy storage devices

参数数值 容量/(kW·h)10 Uc/V1 700 Ud/V1 670 Umax/V1 800 Umin/V1 000 Pcmax/kW2 000 Pdmax/kW2 000 η0.9 SOCinit0.2 SOCmax0.9 SOCmin0.2
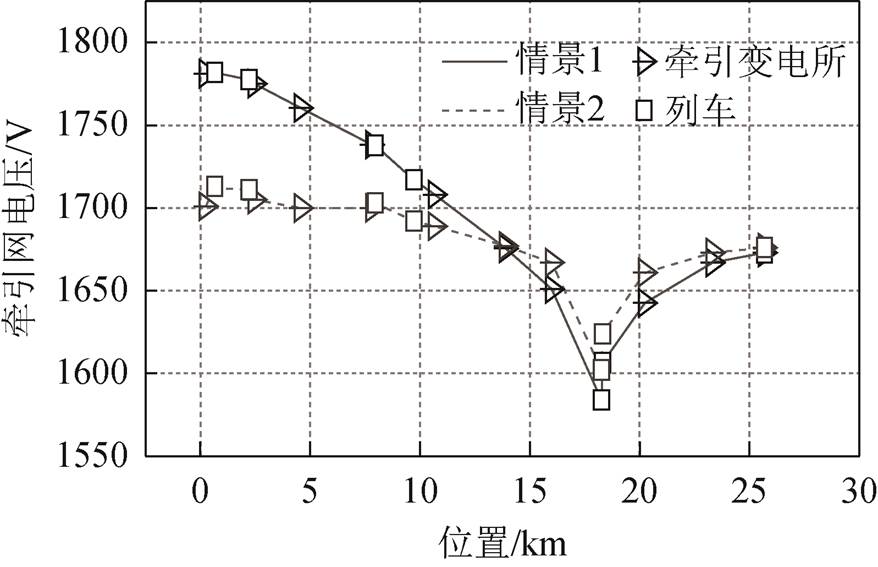
图6 系统牵引网电压
Fig.6 Traction network voltage of system
为验证引入储能装置后牵引变电所的节能效果,统计比较情景①与情景②在t=290s时全线牵引变电所整流机组与储能装置瞬时功率响应如图7所示。
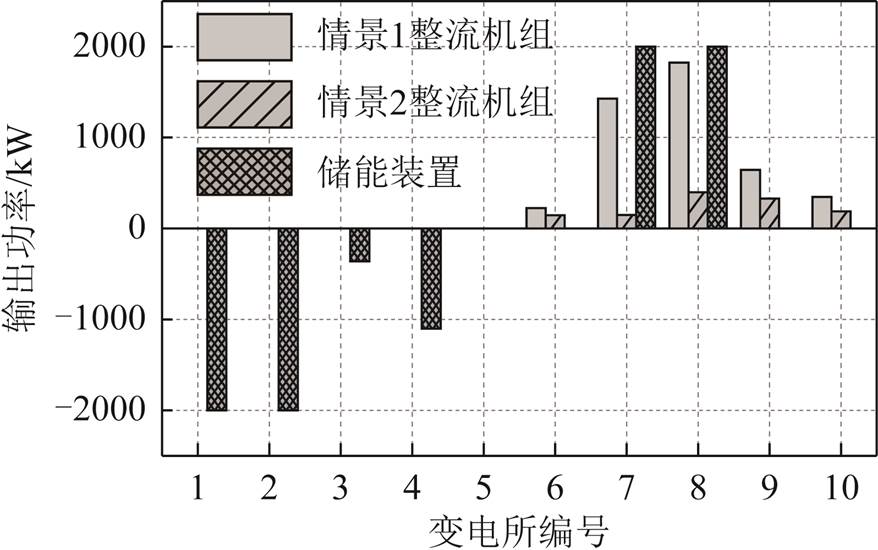
图7 系统瞬时输出功率 Fig.7 Instantaneous output power of system
可见,引入储能装置后,1号与2号牵引变电所储能装置满功率充电,7号与8号牵引所储能装置满功率放电,整流机组的瞬时输出功率明显降低,且某一牵引变电所内安装的储能装置对邻近所的整流机组输出也有一定的功率支撑作用。
分别针对情景①和情景②进行全周期动态仿真。设置各牵引变电所初始状态为REC,列车发车间隔为525s,其余参数设置同4.1节。进行全线仿真并统计结果。
仿真可得情景①和情景②牵引所3的牵引网电压波形对比,如图8所示,整流机组输出功率如图9所示。
分析图8可知,安装储能装置后,变电所电压更为稳定,大部分电压波峰被削低,波谷被抬升。且电压峰值限制在储能装置充电阈值附近,电压谷值限制在储能装置放电阈值附近。安装储能装置前,由于考虑车载制动电阻,牵引网电压被限制在车载制动电阻最大功率电压1 790V附近,电阻启动频繁。安装储能装置后,牵引网电压低于车载制动电阻启动电压1 750V,车载制动电阻启动频率降低。
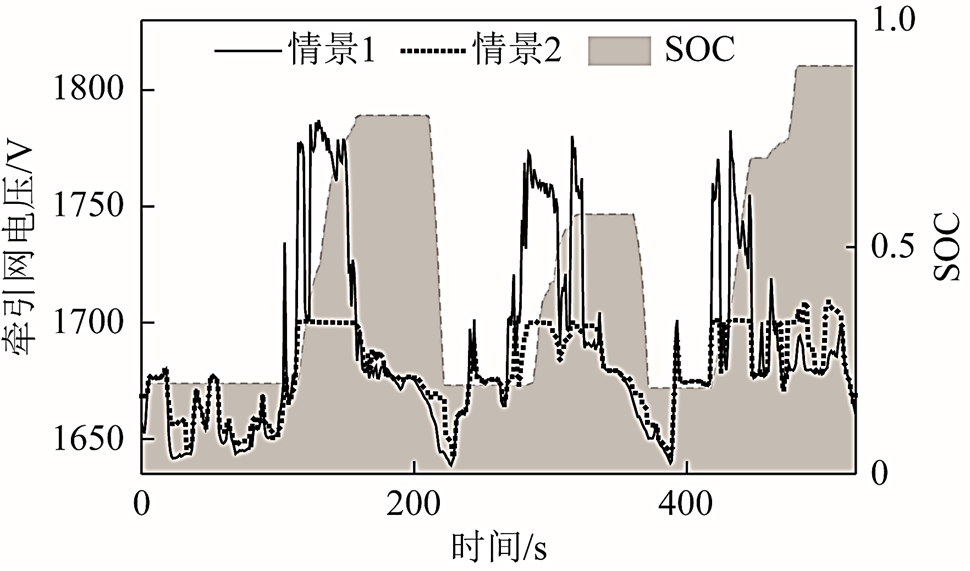
图8 牵引所3牵引网电压 Fig.8 Traction network voltage of ST-3
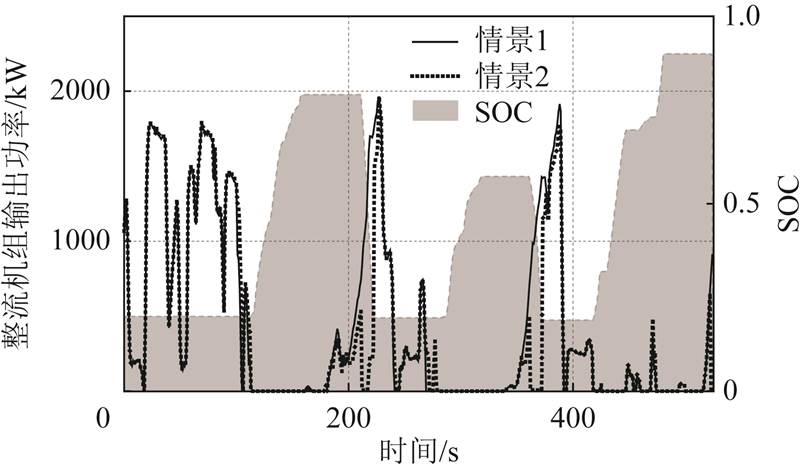
图9 牵引所3整流机组输出功率 Fig.9 Output power of rectifier in ST-3
分析图9可知,装设储能装置后,由于放电时储能装置可与整流机组协同运行,分担功率输出,变电所整流机组输出功率明显降低。部分时段整流机组输出功率并未降低,从SOC曲线可知,此时储能装置能量耗尽,无法继续工作在放电状态,可考虑改变储能装置的安装容量或放电电压以改善这一状况。
考察发车间隔为150s、300s、450s、600s、750s和900s条件下全线安装储能装置的节能稳压效果,参数设置同4.1节,仿真统计不同发车间隔下的算法收敛情况见表6,系统节能稳压指标如图10~图12所示。
表6 不同发车间隔算法收敛次数
Tab.6 Convergence times for different departure time
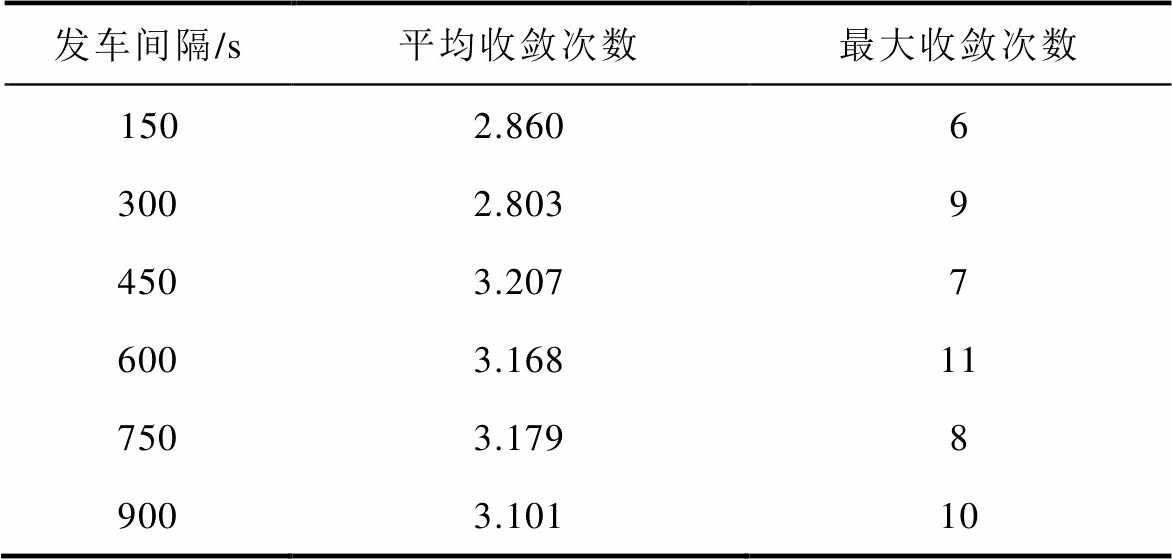
发车间隔/s平均收敛次数最大收敛次数 1502.8606 3002.8039 4503.2077 6003.16811 7503.1798 9003.10110
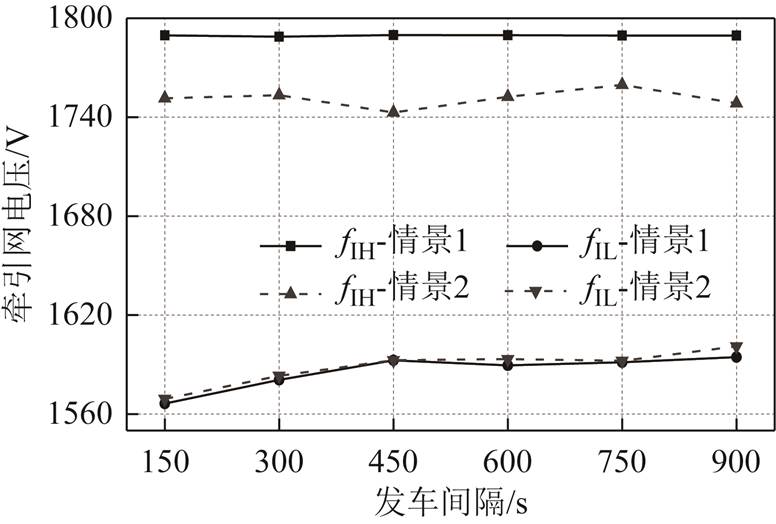
图10 系统稳压指标
Fig.10 Voltage stablization indexes of system
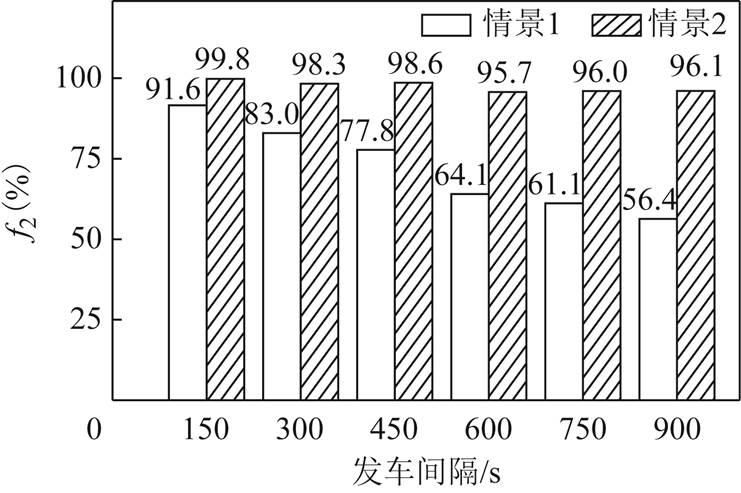
图11 再生制动能量回收率
Fig.11 Recovery rate of regenerative braking enegy
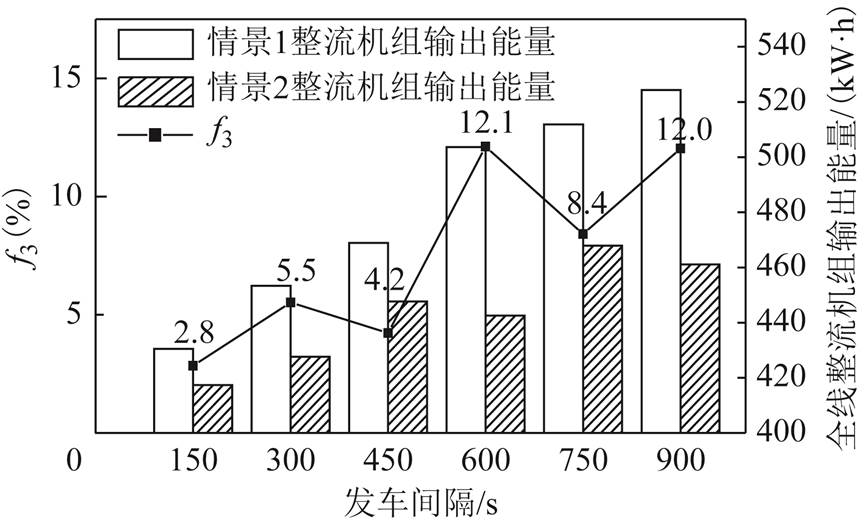
图12 牵引变电所节能率
Fig.12 Energy saving rate of substations
由图10可见,对情景①而言,六种发车间隔下的牵引网最高电压均达到车载制动电阻最大功率启动值1 790V;而引入储能装置后,情景②的牵引网最高电压降低至1 740~1 760V。同时,由于网压较低时储能装置与整流机组协同工作,牵引网最低电压也有所抬升。考虑到储能装置充电完毕后应尽快释放电能,以满足下一次响应列车制动能量的能力,保证再生制动安全有效,储能装置的放电电压阈值设得较高,从图8可看出,这会导致列车牵引时储能装置响应过早,牵引高峰时刻无法继续放电,导致牵引网最低电压改善不大。要在二者之间取得最优结果,还需结合仿真与工程实际进一步讨论。
由图11可知,对情景①而言,发车间隔越高,再生制动能量回收率越低,当发车间隔为900s时,再生制动能量回收率仅为56.4%,未被回收的再生制动能量比例高达43.6%。对情景②而言,全线安装储能装置后,六种发车间隔下的再生制动能量回收率均为95%以上,再生制动能量几乎被完全回收。
由图12可知,随着发车间隔的减小,引入储能装置后的牵引变电所节能率呈下降趋势。当发车间隔为150s时,牵引变电所节能率仅为2.8%;而发车间隔为600s时,牵引变电所节能率可达12.1%。因此,对于郊区、城际等发车间隔较大的线路,安装储能装置有较大的节能潜力;对于发车间隔较小的线路,则可考虑在充分利用邻车吸收能力的前提下,针对再生制动能量较高或牵引网电压较高的区间与车站进行选择性安装。
本文建立了地面式储能装置的黑盒模型,并设计了一种基于BBC的储能装置多状态切换策略,提出了一种求解直流牵引供电系统的双层迭代算法,通过仿真研究得出结论如下:
1)本文提出的含地面式储能装置的直流牵引供电双层迭代算法收敛速度快,且考虑到整流机组与储能装置协同输出时的能量分配情况,可针对地铁工程全线快速求解,满足工程应用需要。
2)通过仿真分析,某线路全线安装地面储能装置后,牵引网电压改善效果明显。再生制动能量回收率提升到95%以上,车载制动电阻启动明显减少,全线牵引变电所节能率最高可达12.1%。
3)储能装置的配置设计与线路发车间隔关系密切,对于不安装储能的系统,发车间隔为150s时,再生制动能量回收率高达91.6%;发车间隔为900s时,再生制动能量回收率仅为56.4%。因此,对于发车间隔较高的线路,全线安装储能装置可取得较好的节能效果;对于发车间隔较低的线路,可针对再生制动能量回收潜力较高的区间进行选择性安装。
参考文献
[1] 杨俭, 李发扬, 宋瑞刚, 等. 城市轨道交通车辆制动能量回收技术现状及研究进展[J]. 铁道学报, 2011, 33(2): 26-32. Yang Jian, Li Fayang, Song Ruigang, et al. Review of the utilization of vehicular braking energy in urban railway transportation[J]. Journal of the China Railway Society, 2011, 33(2): 26-32.
[2] 许爱国, 谢少军, 姚远, 等. 基于超级电容的城市轨道交通车辆再生制动能量吸收系统[J]. 电工技术学报, 2010, 25(3): 117-123. Xu Aiguo, Xie Shaojun, Yao Yuan, et al. Regenerating energy storage system based on ultra-capacitor for urban railway vehicles[J]. Transactions of China Electrotechnical Society, 2010, 25(3): 117-123.
[3] 刘炜, 娄颖, 张戬, 等. 计及城市轨道逆变回馈装置的交直流统一供电计算[J]. 电工技术学报, 2019, 34(20): 4381-4391. Liu Wei, Lou Ying, Zhang Jian, et al. Unified AC/DC power supply calculation taking into account urban rail inverter feedback devices[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4381-4391.
[4] Zhang Gang, Tian Zhongbei, Pietro T. Inverter operating characteristics optimization for DC traction power supply systems[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3400-3410.
[5] 胡婧娴, 林仕立, 宋文吉, 等. 城市轨道交通储能系统及其应用进展[J]. 储能科学与技术, 2014, 3(2): 106-116. Hu Jingxian, Lin Shili, Song Wenji, et al. Energy storage for urban rail transportation[J]. Energy Storage Science and Technology, 2014, 3(2): 106-116.
[6] 韦绍远, 姜久春, 程龙, 等. 储能式有轨电车车地一体化配置模型[J]. 电工技术学报, 2019, 34(2): 427-436.Wei Shaoyuan, Jiang Jiuchun, Cheng Long, et al. Optimal sizing model of the energy storage type tranway considering the integration of on-board energy storage and off-board energy supply[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 427-436.
[7] 刘学, 姜新建, 张超平, 等. 大容量飞轮储能系统优化控制策略[J]. 电工技术学报, 2014, 29(3): 75-82. Liu Xue, Jiang Xinjian, Zhang Chaoping, et al. Optimization control strategies of large capacity flywheel energy storage system[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 75-82.
[8] 刘文军, 周龙, 唐西胜, 等. 基于改进型滑模观测器的飞轮储能系统控制方法[J]. 中国电机工程学报, 2014, 34(1): 71-78. Liu Wenjun, Zhou Long, Tang Xisheng, et al. Research on FESS control based on the improved sliding-mode observer[J]. Proceeding of the CSEE, 2014, 34(1): 71-78.
[9] 秦强强, 郭婷婷, 林飞, 等. 基于能量转移的城轨交通电池储能系统能量管理和容量配置优化[J]. 电工技术学报, 2019, 34(增刊1): 414-423. Qin Qiangqiang, Guo Tingting, Lin Fei, et al. Optimal research for energy management and configuration of battery ESS in urban rail transit based on energy transfer[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 414-423.
[10] 褚斐琴, 杨中平, 林飞, 等. 城轨交通牵引供电系统参数与储能系统容量配置综合优化[J]. 电工技术学报, 2019, 34(3): 579-588. Chu Feiqin, Yang Zhongping, Lin Fei, et al. Synthetic optimization of traction power parameters and energy storage systems in urban rail transit[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 579-588.
[11] Gee A M , Dunn R W. Analysis of trackside flywheel energy storage in light rail systems[J]. IEEE Transactions on Vehicular Technology, 2015, 64(9): 3858-3869.
[12] Luisa A, Luigi B, Mario P. Impact on railway infrastructure of wayside energy storage systems for regenerative braking management: a case study on a real Italian railway infrastructure[J]. IET Electrical Systems in Transportation, 2019, 9(3): 140-149.
[13] 葛维春, 孙恺, 葛延峰, 等. 计及大规模全钒液流电池储能系统外特性建模与仿真[J]. 电力系统保护与控制, 2019, 47(17): 171-179. Ge Weichun, Sun Kai, Ge Yanfeng, et al. Modelling and simulation considering external characteristics of large scale VFB energy storage system[J]. Power System Protection and Control, 2019, 47(17): 171-179.
[14] IEEE 1887-2017 IEEE Guide for Wayside Energy Storage Systems for DC Traction Applications[S]. 2017.
[15] 刘炜, 李群湛, 李良威. 基于多折线外特性模型的直流牵引供电系统稳态短路计算[J]. 机车电传动, 2008(1): 61-64. Liu Wei, Li Qunzhan, Li Liangwei. Steady-state short-circuit calculation of DC traction supply system based on polygonal external characteristic[J]. Electric Drive for Locomotives, 2008(1): 61-64.
[16] 郑侃, 刘炜, 李群湛. 考虑混合储能系统的城市轨道交通供电系统仿真研究[J]. 电气应用, 2014, 33(12): 36-42. Zhen Kan, Liu Wei, Li Qunzhan. Simulation of urban railway transit power supply system including hybrid energy storage system[J]. Electrotechnical Application, 2014, 33(12): 36-42.
Modeling and Simulation of Way-Side Energy Storage Devices in DC Traction Power Supply System
Abstract Way-side energy storage system (ESS) has a broad application prospect in urban railway power supply system. The black-box model of ESS was built in this paper, which can be controlled by a multi-state switching strategy for traction substation with ESS based on BBC algorithm. The solving solutions of equivalent circuits in different states were given, into which the current distribution relationship between ESS and rectifier during discharging condition were took. The 2-loops iterative algorithm of DC traction power supply system proposed in this paper has high iteration speed. Three indexes were defined to evaluate the voltage stabilizing and energy saving effect of ESS under different departure interval. Case study for different departure time based on a certain metro line in Guangzhou was analyzed. The traction network voltage is improved a lot after installing ESS in each substation. The recovery rate of regenerative braking energy is raised from 56.4% to 95%. The output energy saving rate of substations can be as high as 12.1%. The result of simulation indicates that the voltage stabilizing and energy saving effect of ESS is obvious.
keywords:Urban railway, energy storage device, regenerative braking, DC traction power supply system
中图分类号:TM922
刘 炜 男,1982年生,副教授,博士生导师,研究方向为牵引供电系统设计仿真,再生制动能量利用,杂散电流。E-mail:liuwei_8208@swjtu.cn(通信作者)
吴拓剑 男,1996年生,硕士研究生,研究方向为牵引供电系统仿真及再生制动能量利用。E-mail:wutuojian@foxmail.com
国家自然科学基金资助项目(51607148)。
收稿日期2019-10-11
改稿日期 2019-12-02
(编辑 赫蕾)