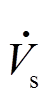 为外施电压,Rs和Xs分别为定子电阻、电抗,Rr和Xr分别为转子电阻、电抗,Xm为励磁电抗,其中转子侧的参数已归算到定子侧。此外,X为转子开路电抗,X=Xs+Xm;
为外施电压,Rs和Xs分别为定子电阻、电抗,Rr和Xr分别为转子电阻、电抗,Xm为励磁电抗,其中转子侧的参数已归算到定子侧。此外,X为转子开路电抗,X=Xs+Xm;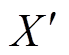 为转子短路电抗,
为转子短路电抗,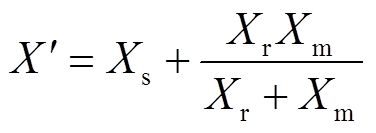 ;
;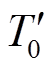 为定子开路、转子回路暂态时间常数,
为定子开路、转子回路暂态时间常数,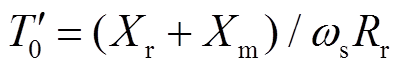 ;ωs为感应电动机同步转速。
;ωs为感应电动机同步转速。摘要 感应电动机负荷的动态特性对电力系统电压稳定性有重要的影响。为快速评估不对称故障后感应电动机的动态响应特性并避免繁琐的时域仿真计算,基于电路和电机分析理论,提出一种计算电力系统不对称故障电压跌落下感应电动机动态特性的快速解析算法。该解析算法先求解转子一阶机械暂态方程,得到扰动后转子的转速和转差率变化。在此基础上,求解转子相量形式的暂态电动势微分方程,得到暂态电动势的变化。最后,准确获得扰动后感应电动机的电流和功率响应。该解析算法在感应电动机负荷三阶机电暂态模型基础上稍加修改即可实现。将解析算法计算结果与PSCAD/EMTDC电磁暂态仿真结果进行比较,证明了该解析算法的有效性。将解析算法应用于求解电力系统综合负荷的动态响应特性,表明其具有应用于电力系统稳定性分析的潜力。
关键词:感应电动机 动态特性 不对称故障 电压跌落 解析算法
随着电网的快速发展,电源构成多元化、网架结构复杂化、负荷成分多样化,电网安全稳定运行压力逐渐增大,对仿真模型准确性的要求越来越高,其中负荷模型尤其是动态负荷模型的选取,对系统稳定计算结果的可信度具有重要影响[1-10]。受端系统负荷重、感应电动机负荷比例高,电网发生故障及恢复过程中,感应电动机由于电磁转矩下降,转差率增大,常会吸收大量的动态功率,导致系统暂态电压难以恢复[11-16]。学者们注意到研究感应电动机动态特性与电压跌落相互影响的重要性,提出试验法[17-19]、时域仿真法[20-23]与解析法[24-27]三类研究方法。
试验法借助电压跌落发生器产生各种类别的电压跌落波形,记录电动机的输出响应。
时域仿真法借助电力系统电磁暂态或机电暂态仿真程序,考虑较为精确的电动机动态模型,通过数值计算对问题进行探讨。两者的优点在于结果真实可信,但为揭示某一因素的影响,常需进行多次试验或仿真。除了繁琐、费时之外,在分析和解释试验和仿真现象时,都显得力所不及。
解析法借助电路和电机分析理论,显式求解感应电动机动态响应和系统电压间的交互作用,是最根本、最透彻的研究方法,但难度较大。文献[25]提出计算感应电动机临界切除时间的解析算法。文献[28]对感应电动机一阶机械暂态模型进行解析计算,在求得感应电动机的暂态转差变化后,利用感应电动机稳态等效电路计算暂态电流和暂态功率。
文献[20]指出感应电动机的一阶机械暂态模型有功功率计算精度较高,但无功功率计算精度很低,这表明文献[28]所提算法在原理上存在缺陷,本文的仿真结果也证实了这一点。在电力系统与感应电动机的相互作用中,电力系统主要通过其电压水平影响电动机的动态响应,而电动机则主要通过其功率特性影响电力系统的电压及运行,文献[28]所提解析算法的计算结果精度是难以接受的。到目前为止,解析法尚未取得突破性进展,还不能准确求得受扰后电动机的全部运行和状态变量。在机电暂态仿真中,由于无法详细模拟感应电动机定子绕组的暂态过程,截至目前,仍采用基于三相对称正序电压推导出的感应电动机三阶暂态模型作为其仿真模型[29]。三阶机电暂态模型无法准确模拟感应电动机负荷动态特性,也无法准确判断感应电动机负荷失稳发生的条件,在实际仿真中只是根据工程经验将正序电压或三阶机电暂态方程计算出的转子转差率作为判据,因而在发生不对称故障时其计算精度不高。
为了弥补机电暂态仿真在电动机负荷动态特性评估方面的不足,同时又能适用于大规模电网的仿真分析,近年来机电-电磁暂态混合仿真方法得到大力发展,并取得一系列研究成果[30-31]。由于混合仿真中电磁暂态仿真部分的规模及其初始化问题尚未得到彻底解决,以及混合仿真速度慢、计算内存需求大等方面的原因,尚不能满足目前电网大量运行方式计算应用的要求。
基于目前提高机电暂态仿真中感应电动机动态特性评估的准确性仍有很高的实用价值,本文在将外部网络等效为简单两节点系统的基础上,提出不对称故障电压跌落下精确计算感应电动机动态响应的解析算法,多场景下的算例证明了该方法的可行性和准确性。
感应电动机数学模型是电力系统计算分析软件模型库的重要组成部分,其稳态等效电路如图1所示[23]。在图1中,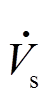 为外施电压,Rs和Xs分别为定子电阻、电抗,Rr和Xr分别为转子电阻、电抗,Xm为励磁电抗,其中转子侧的参数已归算到定子侧。此外,X为转子开路电抗,X=Xs+Xm;
为外施电压,Rs和Xs分别为定子电阻、电抗,Rr和Xr分别为转子电阻、电抗,Xm为励磁电抗,其中转子侧的参数已归算到定子侧。此外,X为转子开路电抗,X=Xs+Xm;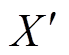 为转子短路电抗,
为转子短路电抗,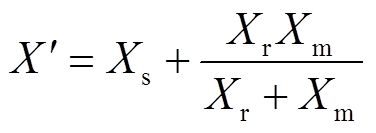 ;
;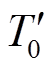 为定子开路、转子回路暂态时间常数,
为定子开路、转子回路暂态时间常数,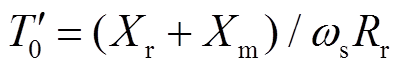 ;ωs为感应电动机同步转速。
;ωs为感应电动机同步转速。

图1 感应电动机稳态等效电路
Fig.1 The steady state equivalent circuit of induction motor
根据不同的应用领域和计算分析的目的,已经提出了多种感应电机动态仿真模型。其中,计算精度最高的是五阶电磁暂态模型。该模型考虑定子绕组、转子绕组的电磁暂态特性以及转子的机械暂态特性,精度高,计算量大,一般仅用于等值系统的暂态稳定性研究中[15]。当忽略定子绕组的电磁暂态特性时,则得到感应电动机三阶机电暂态模型如式(1),对应的电动机暂态等效电路如图2所示[24]。该三阶机电暂态模型在电力系统稳定性分析中得到了最为广泛的应用。
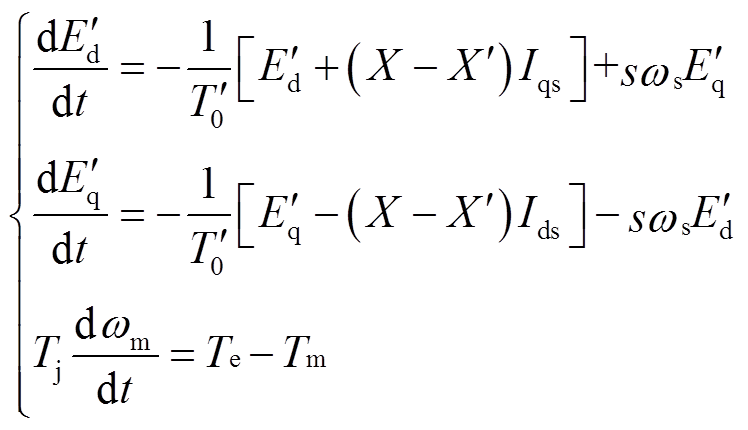 (1)
(1)式中,Tj为电动机惯性时间常数;ωm为电动机转速;s为转子转差率,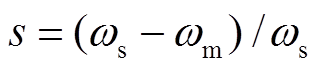 ;Te和Tm分别为电磁转矩和机械负载转矩,本研究中Tm考虑为常数;
;Te和Tm分别为电磁转矩和机械负载转矩,本研究中Tm考虑为常数;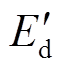 和
和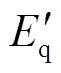 分别为转子暂态电动势
分别为转子暂态电动势 的d轴和q轴分量;Vds和Vqs分别为外施定子电压
的d轴和q轴分量;Vds和Vqs分别为外施定子电压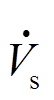 的d轴和q轴分量;Ids和Iqs分别为定子电流
的d轴和q轴分量;Ids和Iqs分别为定子电流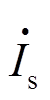 的d轴和q轴分量,表达式为
的d轴和q轴分量,表达式为
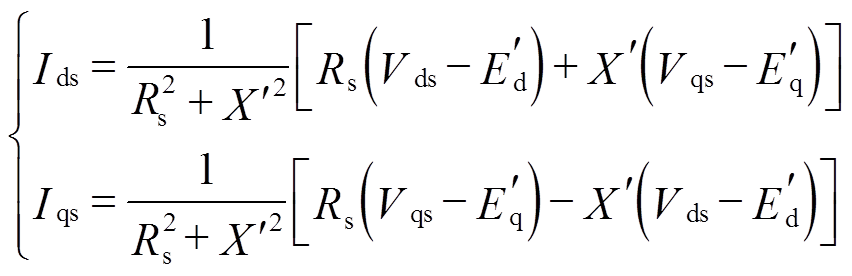 (2)
(2)
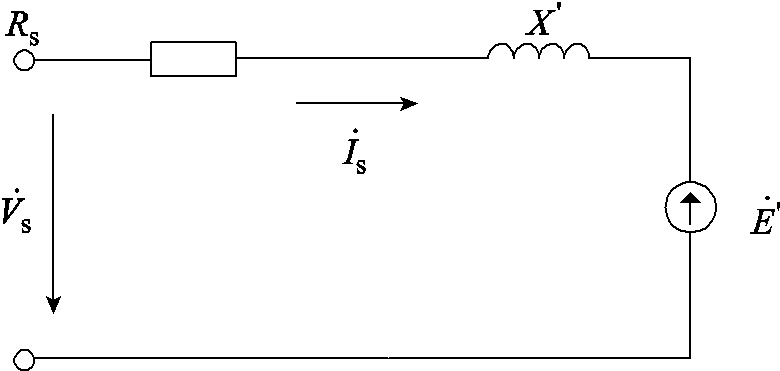
图2 感应电动机暂态等效电路
Fig.2 The transient state equivalent circuit of induction motor
如果进一步忽略转子绕组的电磁暂态特性,仅保留式(1)中第三个公式,就得到感应电动机一阶机械暂态模型。为了适应电力系统暂态电压稳定性分析,还有学者提出一阶电压暂态模型[20]。
考虑图3所示供电系统,电源通过阻抗为Zeq=Req+jXeq的供电网络向感应电动机IM供电。
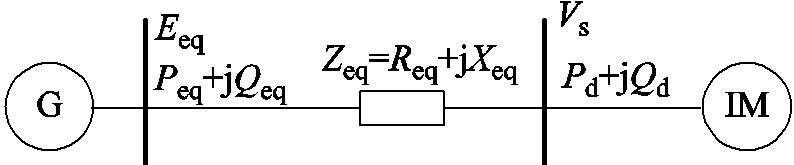
图3 单机带感应电动机供电系统
Fig.3 The single machine-induction motors power system
本文首先参考文献[28],求解电源发生对称或不对称故障电压跌落时感应电动机的转速和转差变化。感应电动机的正序等效电路即为图1,负序等效电路如图4所示[32]。
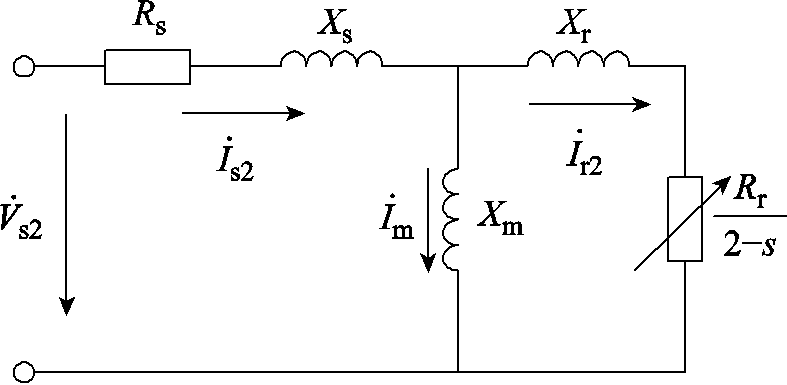
图4 感应电动机负序等效电路
Fig.4 The negative sequence equivalent circuit of induction motor
应用对称分量法将电源电势分量分解为三组对称的正、负、零序分量,其计算式为
 (3)
(3)式中,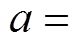
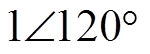 ;
;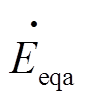 、
、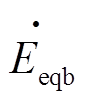 、
、 分别为电源三相电压;下标“1”、“2”分别表示正、负序分量;
分别为电源三相电压;下标“1”、“2”分别表示正、负序分量;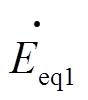 、
、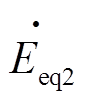 、
、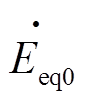 分别为电源正序、负序、零序电压。
分别为电源正序、负序、零序电压。
感应电动机一般不接中性线,则无零序电流,因此只需分析正序和负序电压分量对感应电动机的影响[29]。图3中,送端发电机功率Peq+jQeq与受端电动机功率Pd+jQd满足
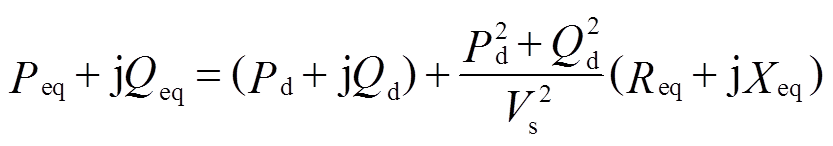 (4)
(4)电动机端正、负序电压计算如式(5)。
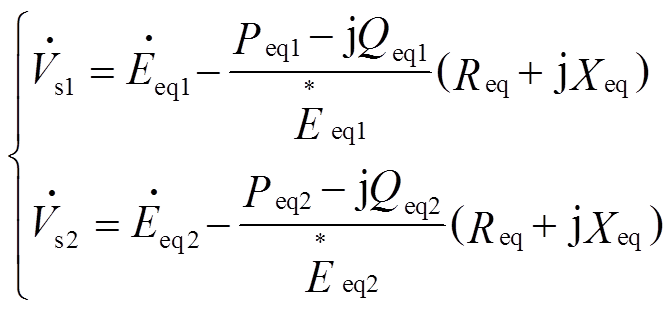 (5)
(5)
式中,上标*表示共轭值。
忽略励磁电抗Xm的影响,并考虑到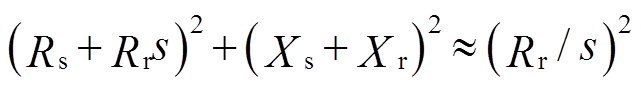 ,
,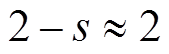 ,有
,有
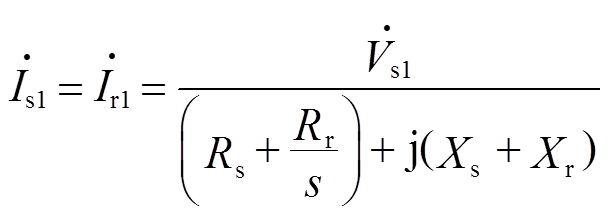 (6)
(6)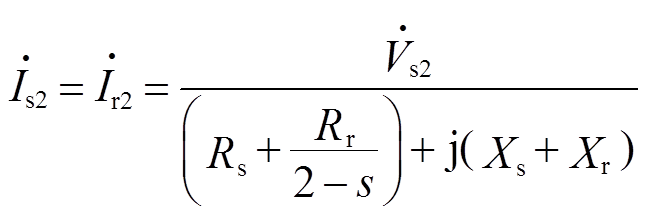 (7)
(7)
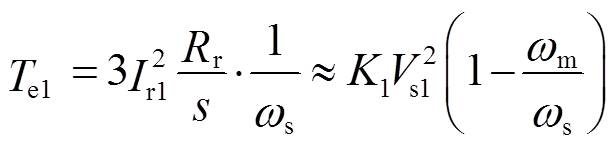 (8)
(8)
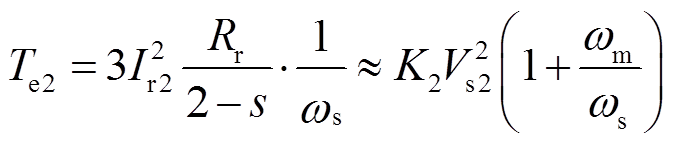 (9)
(9)式中,K1、K2为常数,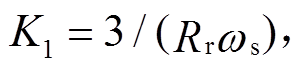
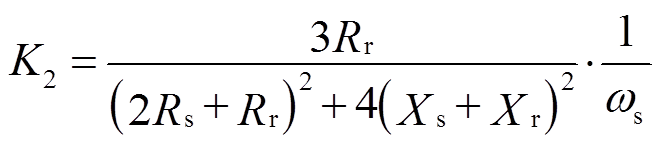 。不对称故障电压跌落期间,感应电动机的转子运动方程为
。不对称故障电压跌落期间,感应电动机的转子运动方程为
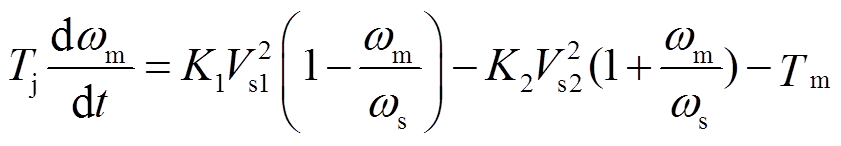 (10)
(10)
电压跌落清除后,定子电压中不含负序电压分量,转子运动方程也不再含负序电磁转矩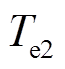 ,有
,有
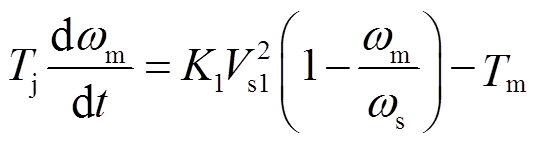 (11)
(11)上级供电网络发生故障导致电压跌落时,感应电动机的转子角速度变化如图5所示。
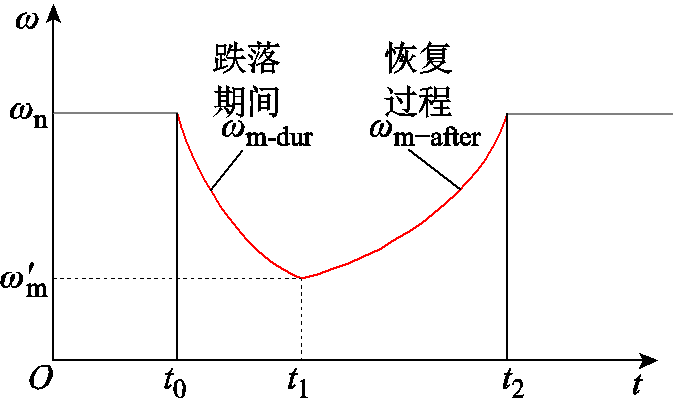
图5 电压跌落时感应电动机转子角速度变化
Fig.5 The variation of induction motor speed subjected to voltage sag after power system fault
感应电动机的初始角速度为wn,从电压跌落发生时刻t0开始不断下降,到故障清除时刻t1,感应电动机角速度降至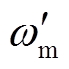 。求解式(10),可得故障期间感应电动机角速度wm-dur的近似解析表达式为
。求解式(10),可得故障期间感应电动机角速度wm-dur的近似解析表达式为
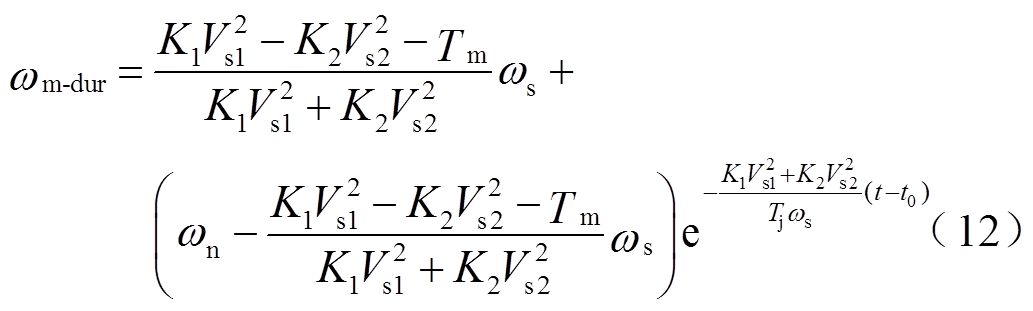
电压跌落清除后,经过一段时间,感应电动机的转子角速度才恢复。通过求解式(11),可得故障清除后感应电动机角速度wm-after的近似解析表达式为
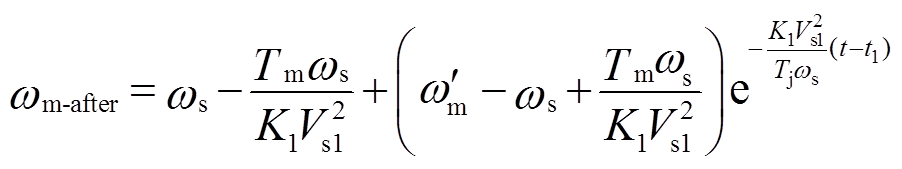 (13)
(13)
根据式(12)和式(13),可以求出任意类型不对称故障电压跌落发生后感应电动机角速度的变化,进而求出转差率s。文献[28]将转差率s代入图1电动机的稳态等效电路,求得扰动后电动机的暂态电流和功率,其中无功功率和电流的计算结果不准确,本文计算方法见2.2节。
当感应电动机定子端施加正序电压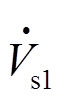 时,将式(1)前两式写成相量形式,可得
时,将式(1)前两式写成相量形式,可得
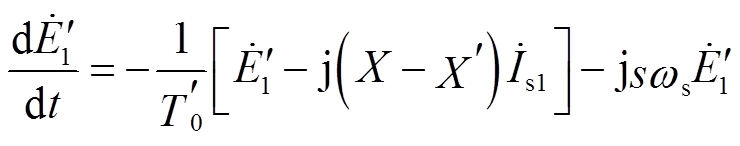 (14)
(14)式中,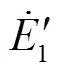 和
和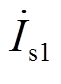 分别为转子正序暂态电动势和定子正序电流相量。
分别为转子正序暂态电动势和定子正序电流相量。
再由式(2)易得,定子电流的相量形式为
 (15)
(15)
由式(14)和式(15),易得式(16),即转子正序暂态电动势微分方程的相量形式。
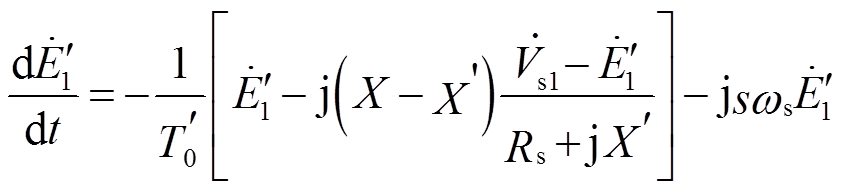 (16)
(16)当感应电动机定子端施加负序电压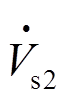 时,流过负序电流
时,流过负序电流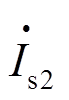 ,建立负向旋转磁场,它与转子旋转方向相反,负序转差率为2-s。转子负序暂态电动势微分方程的相量形式为
,建立负向旋转磁场,它与转子旋转方向相反,负序转差率为2-s。转子负序暂态电动势微分方程的相量形式为
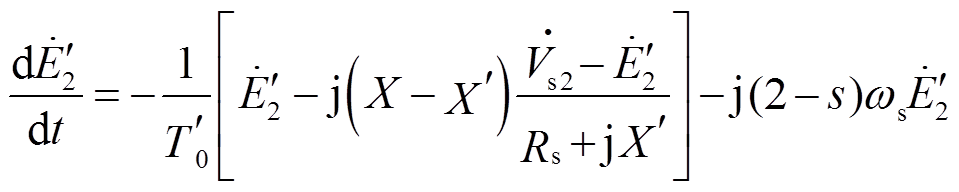 (17)
(17)
式中,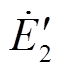 为转子负序暂态电动势。
为转子负序暂态电动势。
整理式(16)和式(17)后,得
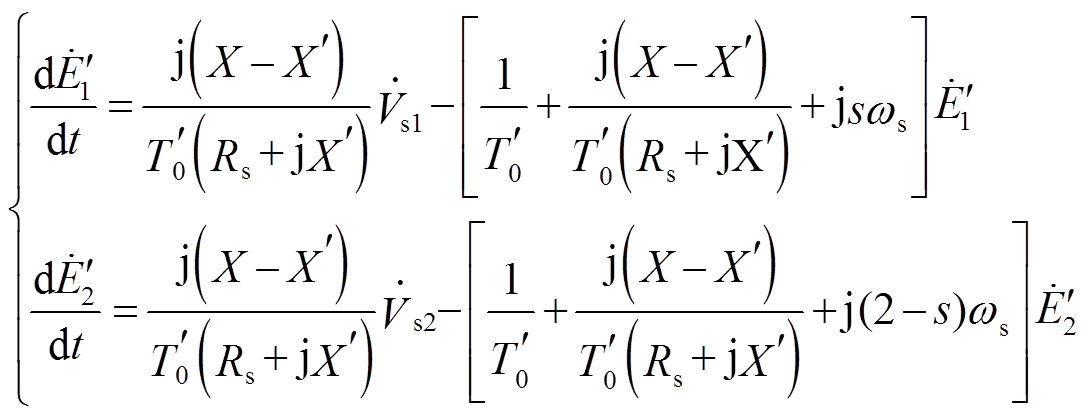 (18)
(18)令
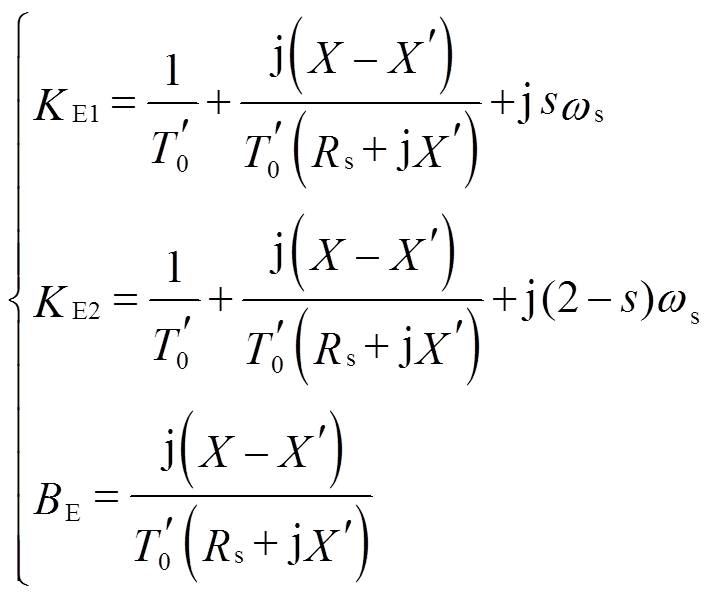 (19)
(19)
式(19)中,转差率s取2.1节的计算结果,则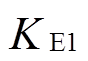 、
、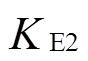 和
和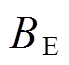 均为已知量。式(18)简化为
均为已知量。式(18)简化为
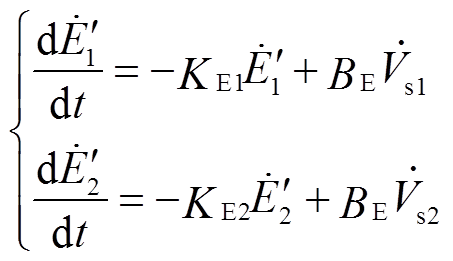 (20)
(20)求解式(20),可得不对称故障期间感应电动机转子暂态电动势的解析表达式为
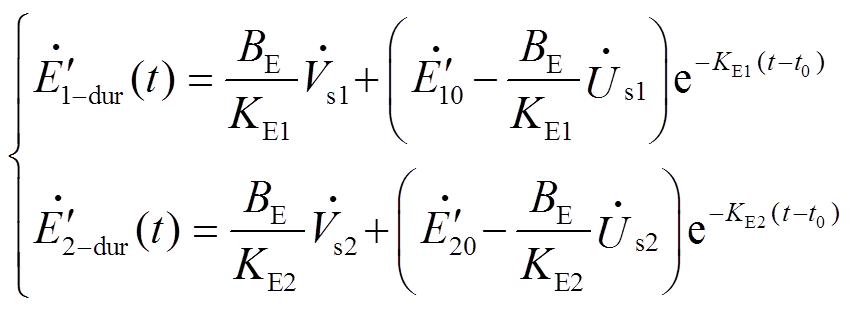 (21)
(21)
式中,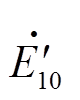 和
和 分别为感应电动机正、负序暂态电动势初值,其计算表达式分别为
分别为感应电动机正、负序暂态电动势初值,其计算表达式分别为
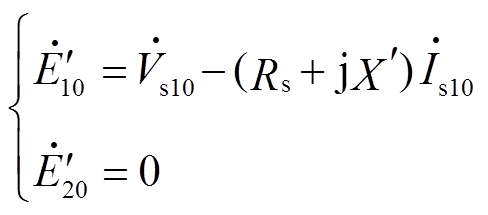 (22)
(22)式中,下标“0”表示变量的初值。
电压跌落清除后恢复过程中,定子电压中不含负序电压分量,感应电动机的暂态电动势仅含正序分量,其解析表达式为
 (23)
(23)式中,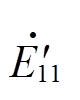 为电压跌落清除时刻感应电动机的正序暂态电动势。
为电压跌落清除时刻感应电动机的正序暂态电动势。
将式(21)计算得到的故障期间电动机转子暂态电动势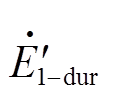 和
和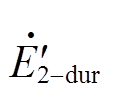 的d轴分量
的d轴分量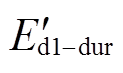 、
、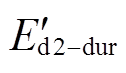 及q轴分量
及q轴分量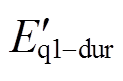 、
、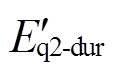 分别代入式(2),可得电压跌落期间电动机d、q轴的正序定子电流
分别代入式(2),可得电压跌落期间电动机d、q轴的正序定子电流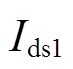 、
、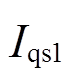 和负序定子电流
和负序定子电流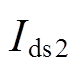 、
、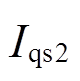 。电压跌落期间,电动机消耗的有功功率
。电压跌落期间,电动机消耗的有功功率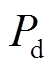 和无功功率
和无功功率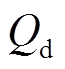 分别为
分别为
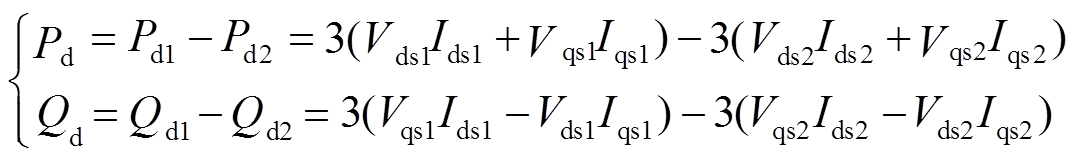 (24)
(24)式中,Pd1、Pd2分别为正、负序有功功率; 、
、 分别为正、负序无功功率。负序电流产生的功率与正序电流产生的功率方向相反,起制动作用。
分别为正、负序无功功率。负序电流产生的功率与正序电流产生的功率方向相反,起制动作用。
电压跌落清除后,定子电压中不再含负序电压分量。将式(23)计算得到的暂态电动势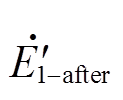 的d轴分量
的d轴分量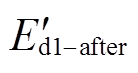 和q轴分量
和q轴分量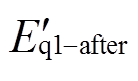 分别代入式(2),可得电压跌落期间电动机d、q轴的正序定子电流
分别代入式(2),可得电压跌落期间电动机d、q轴的正序定子电流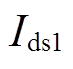 、
、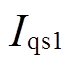 。电动机消耗的有功功率Pd和无功功率
。电动机消耗的有功功率Pd和无功功率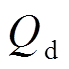 分别为
分别为
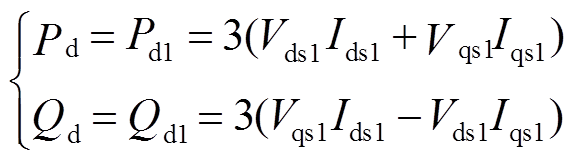 (25)
(25)求得电动机的功率消耗Pd+jQd后,定子电流正序分量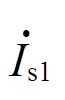 、负序分量
、负序分量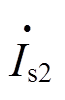 分别为
分别为
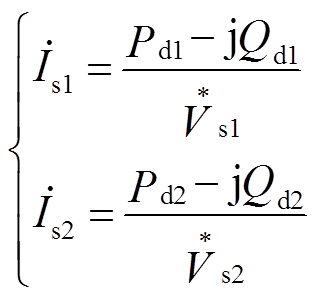 (26)
(26)
再由对称分量法易得各相电流。以上算法可在Matlab环境下编程实现。
时域仿真是研究电力系统动态特性的重要手段,负荷模型对电力系统稳定性分析结果有十分重要的影响。电力系统电压稳定性分析中,常采用感应电动机并联静态ZIP模型的方法来模拟电力系统综合负荷。但电力系统负荷节点很多,大量采用上述综合负荷动态仿真模型,对电力系统仿真速度要求很高。
以PSCAD/EMTDC为代表的电力系统电磁暂态仿真软件采用五阶感应电动机模型,能够准确计算对称和不对称故障电压跌落下电动机的动态响应,但计算繁琐。
以PSD/BPA为代表的电力系统机电暂态仿真软件采用三阶感应电动机模型,计算速度较电磁暂态仿真提高很多,但在不对称故障电压跌落下忽略了负序分量对感应电动机的影响。由于感应电动机运行时转子转差率s很小,但即使很小的负序电压,也会产生较大的负序电流和负序转矩,因而机电暂态仿真在不对称故障下的结果是不准确的[20,33]。
文献[28]所述解析法实现了感应电动机一阶机械暂态模型的解析计算,但对无功和电流的计算精度较低。
本文在文献[28]的基础上,利用转子暂态电动势微分方程的相量形式,实现了感应电动机三阶机电暂态模型的联立解析求解,可以较为精确地求得对称和不对称故障电压跌落下感应电动机的暂态转差、电动势、功率和电流。所提出的解析法具有以下优点:①计算模型均为代数表达式,与电力系统机电和电磁暂态仿真联立求解微分-代数方程组相比,在计算速度上具有明显优势;②计入了不对称故障时负序分量对电动机动态响应的影响,计算精度高于只考虑正序基波分量的机电暂态仿真;③显式计算电动机机械和电气参量,易于分析和解释结果与现象。解析法的不足在于仅能考虑恒转矩机械负载,这会造成电压稳定性分析结果偏悲观。从电网运行的安全性考虑是可以接受的。
为了验证本文提出的感应电动机动态特性解析算法对于不同故障类型和不同电动机参数的适应性,采用表1中电动机参数,在电磁暂态仿真程序PSCAD/EMTDC搭建图3所示10kV供电系统的仿真模型,进行了以下两种情形的比较:①设置电源在0.2s时发生持续时间为0.2s的不对称故障
电压跌落。电压跌落前:Eeqa,pre=1.0∠0o (pu),Eeqb,pre= 1.0∠-120o (pu),Eeqc,pre= 1.0∠120o (pu);电压跌落期间:Eeqa,dur=0.0∠10o (pu),Eeqb,dur=1.0∠-130o (pu),Eeqc,dur= 1.0∠130o (pu)。采用表1中容量为1.4MW的电动机。②设置电源在0.2s时发生持续时间为0.2s的对称故障电压跌落。电压跌落前:Eeqa,pre=1.0∠0o(pu),Eeqb,pre=1.0∠-120o(pu),Eeqc,pre=1.0∠120o(pu);电压跌落期间:Eeqa,dur=0.6∠0o(pu),Eeqb,dur=0.6∠-120o(pu),Eeqc,dur=0.6∠120o(pu)。采用表1中容量为1MW的感应电动机。算例中感应电动机均带额定负载运行,负载转矩Tm取1.0(pu),系统等值阻抗Zeq=(1.3+ j3.8)Ω,PSCAD/EMTDC仿真步长为100μs,解析算法计算步长为0.01s,计算结果如图6和图7所示。在图6和图7中,实线、虚线和点线分别为本文方法、文献[28]所述解析法和PSCAD/EMTDC的计算结果,图中依次标记为“本文方法”“解析法2”和“PSCAD”。
表1 感应电动机负荷模型参数
Tab.1 The parameters of induction motors load model

电动机类型Un/kVRs(pu)Xs(pu)Rr(pu)Xr(pu)Xm(pu)Tj/s 1.4MW100.029 40.141 10.004 30.025 32.635 38.9 1MW100.031 90.160 40.004 20.009 82.638 78.6 IEEE 21100.0130.0670.0090.1703.803
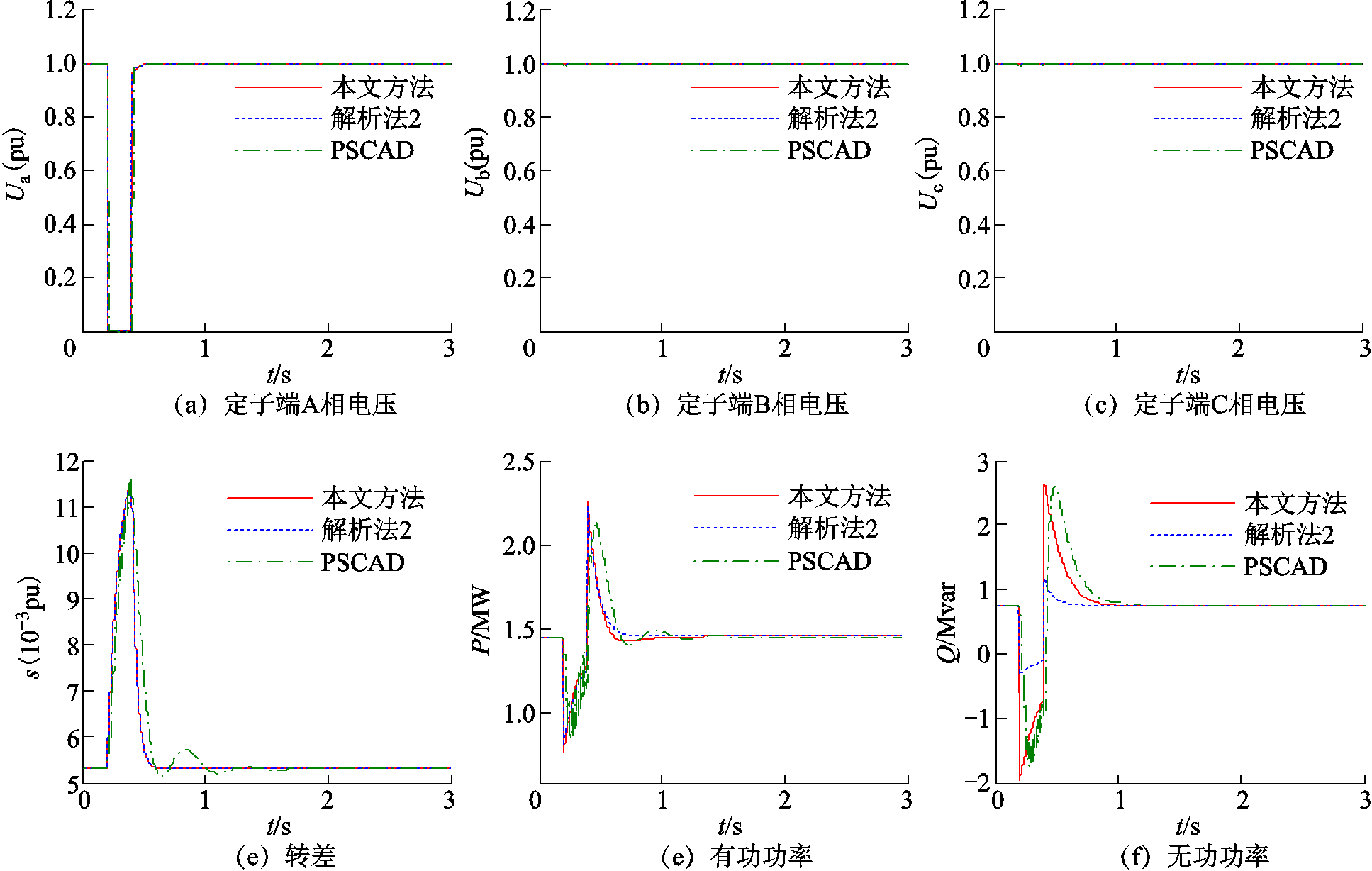
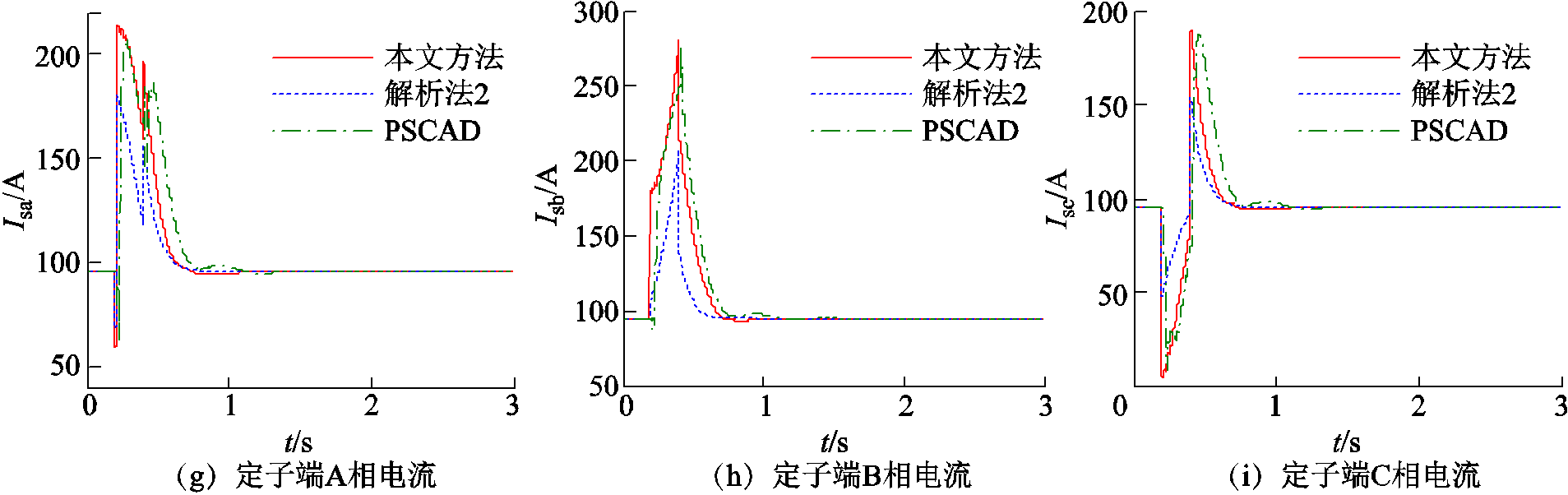
图6 不对称电压跌落时电动机的动态响应
Fig.6 Induction motor's dynamic response subjected to asymmetrical voltage sag
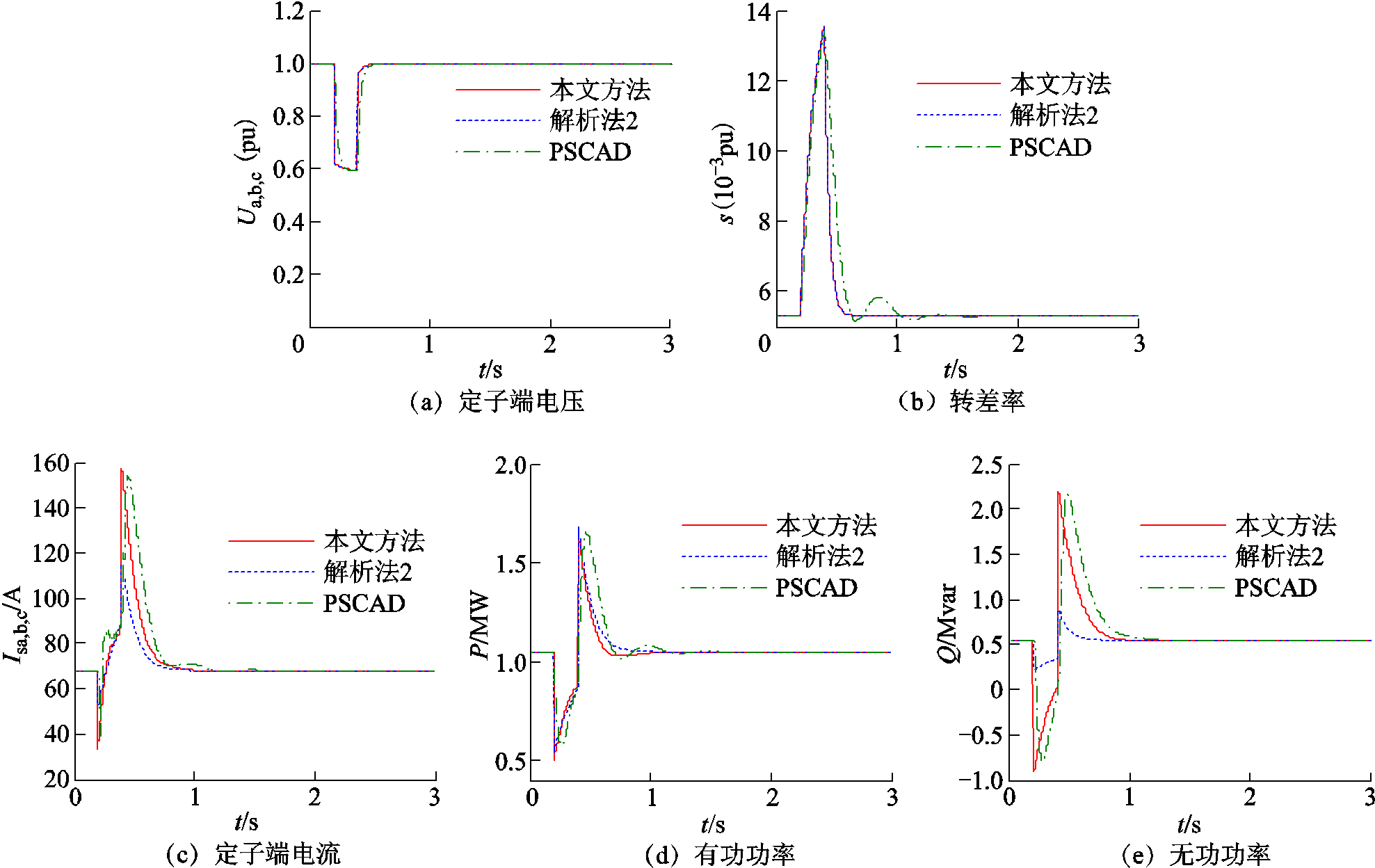
图7 对称电压跌落时电动机的动态响应
Fig.7 Induction motor's dynamic response subjected to symmetrical voltage sag
文献[28]所述解析法没有考虑电动机暂态电动势的变化,得到的动态无功和定子电流误差较大。本文方法计算的各项动态特性均与PSCAD/EMTDC仿真结果吻合良好,表明了本文算法的有效性和准确性。值得一提的是在电压跌落发生和清除的瞬间,解析法的计算结果会发生突变,而PSCAD/EMTDC
不会。产生这种差异的主要原因在于解析法没有计及定子绕组的电磁暂态过程,即认为定子绕组的各电气量是可以突变的。
为进一步验证本文提出的感应电动机动态特性解析算法应用于大电网时域仿真计算中的可行性,本文采用PSD/BPA和PSCAD/EMTDC搭建如图8所示110kV单机带综合负荷供电系统仿真模型。系统等值阻抗Zeq=(1.6+j7.2)Ω,综合负荷功率为PL0+ jQL0=(50+j20) MV·A,感应电动机负荷占比50%。采用表1中IEEE 2型工业电动机模型参数,PSD/BPA仿真步长为0.01s,PSCAD/EMTDC仿真步长为100μs,解析算法计算步长为0.01s。感应电动机负载转矩Tm取1.0(pu),负荷其余部分考虑为恒阻抗负荷模型。进行了以下情形的计算:0.2s时负荷母线发生BC两相接地短路,0.4s时故障清除。
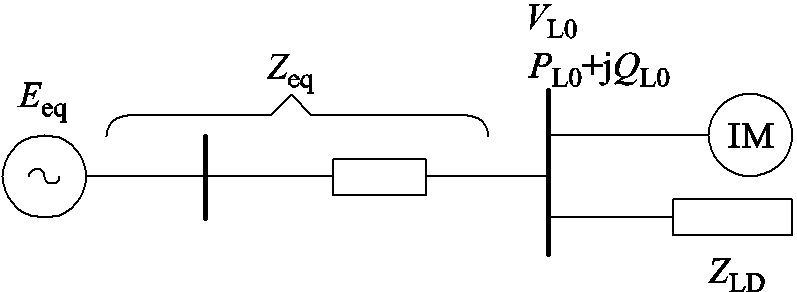
图8 单机带电动机综合负荷供电系统仿真模型
Fig.8 The single machine-IM Synthesis load power system
单机带综合负荷供电系统算例中电压跌落发生位置与前文设定的情形不同,根据电力系统短路计算理论,求得负荷母线各序电压分量即可按照第2节的方法进行计算。综合负荷初始化计算参照文献[34]完成。本文方法、BPA和PSCAD的计算结果曲线比较如图9所示。
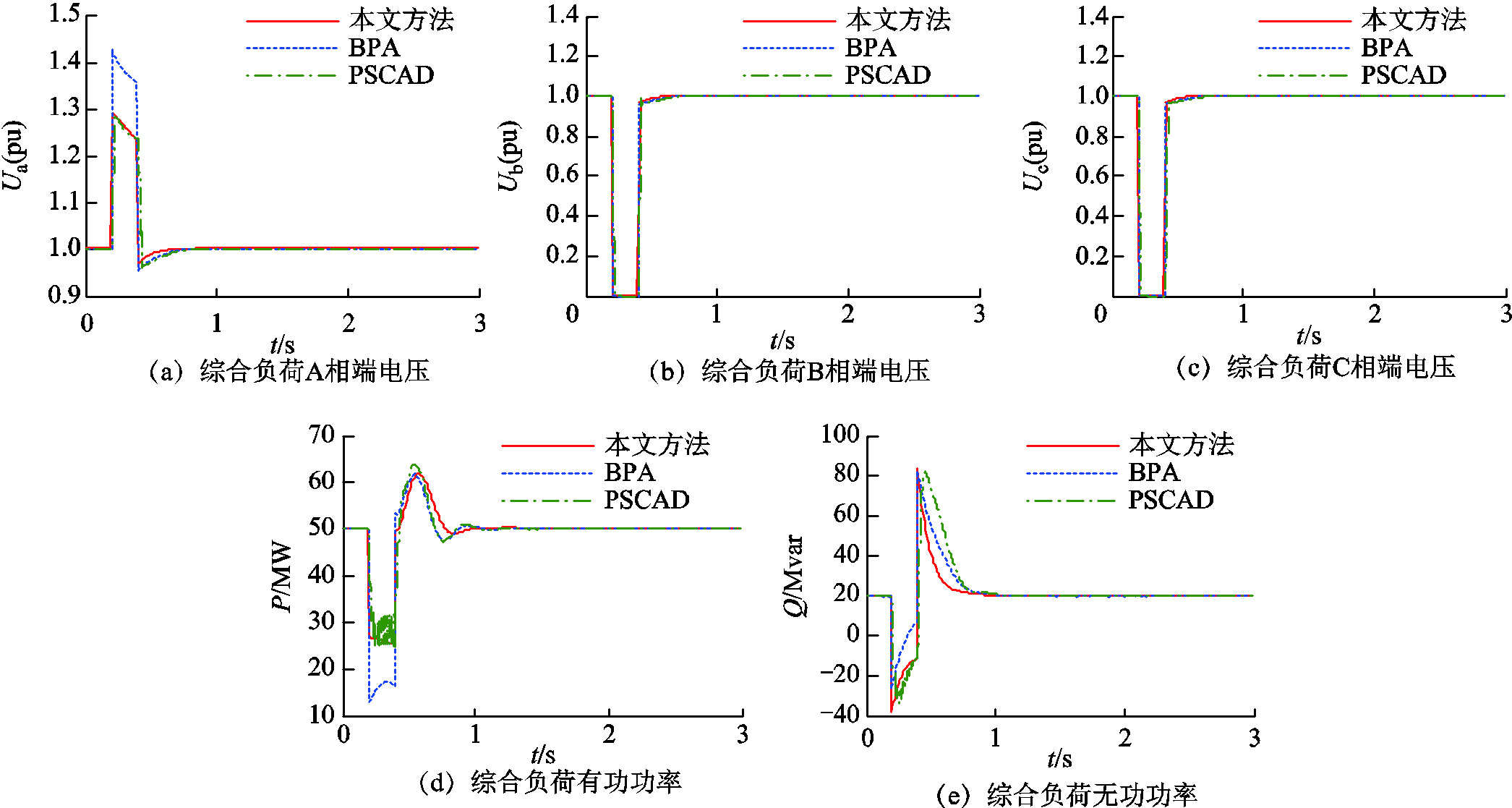
图9 含50%IEEE 2型感应电动机的综合负荷动态响应
Fig.9 Dynamic response of composite load with 50% IEEE 2 induction motor
由图9可见,BPA机电暂态仿真软件在不对称故障期间忽略了负序电压的影响,计算精度欠佳。当大量负荷节点均采用综合负荷动态模型时,误差的影响值得评估。本文方法与PSCAD的计算结果吻合良好,表明所提方法有潜力应用于电力系统稳定性分析计算。
感应电动机负荷是电力系统最主要的动态负荷,其动态响应特性对电力系统稳定性分析结果有重要的影响。为快速评估系统故障电压跌落后感应电动机的动态响应特性,同时避免繁琐的时域仿真计算高阶微分方程组,本文提出一种快速计算电力系统对称和不对称故障电压跌落下感应电动机负荷动态特性的解析算法,通过感应电动机负荷微分方程的理论分析,先求出扰动后感应电动机转子的转速和转差率变化,再计算暂态电动势的变化,从而准确求得扰动后感应电动机的转速、电流、电动势和功率响应。将所提解析算法与仿真结果进行比较,验证了该解析算法的有效性,得到以下结论:
1)采用本文所提的感应电动机负荷动态特性的解析算法,克服了时域仿真求解高阶微分方程组耗费大量时间的不足,可有效提升电力系统电磁暂态仿真的计算速度。
2)本文所提出的解析算法考虑了不对称故障电压跌落情况下产生的负序电压分量对感应电动机负荷动态特性的影响,提高了感应电动机三阶机电暂态仿真模型的计算精度,体现了解析算法在不对称故障电压跌落下的计算准确性优势。
3)解析算法显式给出了电力系统故障后感应电动机动态负荷各机械、电气参量的计算表达式,除可用于快速评估感应电动机负荷与电压跌落的相互影响外,也有应用于电力系统稳定性分析计算的潜力。
4)本文对带恒机械转矩负载的感应电动机及综合负荷动态功率特性进行了解析计算,应用所提的解析算法对感应电动机负荷模型参数与动态响应特性的解析灵敏度分析是下一步研究的方向。
参考文献
[1] 梁涛, 周宁, 卢天琪, 等. 感应电动机负荷暂态模型的参数填补方法及典型参数分析[J]. 电力系统自动化, 2020, 44(1): 74-82. Liang Tao, Zhou Ning, Lu Tianqi, et al. Parameter imputation methods and typical parameter analysis of load transient model of induction motor[J]. Automation of Electric Power Systems, 2020, 44(1): 74-82.
[2] 程佩芬, 李崇涛, 傅闯, 等. 基于状态空间法的高压直流输电系统电磁暂态简化模型的解析算法[J]. 电工技术学报, 2019, 34(6): 1230-1239. Cheng Peifen, Li Chongtao, Fu Chuang, et al. An analytic solution for simplified electromagnetic transient model of HVDC transmission system based on state space method[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1230-1239.
[3] 邵鹏飞, 李勇, 肖华. 新型HVDC换流变压器绕组振动抑制研究[J].电机与控制学报, 2019, 23(7): 87-97. Shao Pengfei, Li Yong, Xiao Hua. Study on winding vibration suppression of new HVDC converter transformer [J]. Electric Machines and Control, 2019, 23(7): 87-97.
[4] 金涛, 许立彬, 高伟, 等. 一种基于LCD-Hilbert变换和奇异谱熵的配电网暂时过电压类型识别方法[J]. 电机与控制学报, 2018, 22(11): 26-36. Jin Tao, Xu Libin, Gao Wei, et al. Temporary overvoltage classification and recognition method of distribution network based on LCD-Hilbert transform and singular- spectrum entropy[J]. Electric Machines and Control, 2018, 22(11):26-36.
[5] 陈鹏远, 黎灿兵, 周斌, 等. 异步互联电网柔性直流输电紧急功率支援与动态区域控制偏差协调控制策略[J]. 电工技术学报, 2019, 34(14): 3025-3034. Chen Pengyuan, Li Canbing, Zhou Bin, et al. VSC-HVDC emergency power support and dynamic area control error coordinated control strategy for improving the stability of asynchronous interconnected power grids[J]. Transactions of China Electrotechnical Society, 2019, 34 (14): 3025-3034.
[6] 邵冰冰, 赵书强, 高本锋, 等. 连接弱交流电网的VSC-HVDC失稳机理及判据研究[J]. 电工技术学报, 2019, 34(18): 3884-3996. Shao Bingbing, Zhao Shuqiang, Gao Benfeng, et al. Instability mechanism and criterion analysis of VSC-HVDC connected to the weak AC power grid[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3884-3996.
[7] 郑超, 汤涌, 马世英, 等. 网源稳态调压对暂态无功支撑能力的影响研究[J]. 中国电机工程学报, 2014, 34(1): 115-122. Zheng Chao, Tang Yong, Ma Shiying, et al. Study on the influence of steady-state voltage regulation schemes on transient reactive power supporting capability[J]. Proceedings of the CSEE, 2014, 34(1): 115-122.
[8] 郭挺, 谢敏, 刘明波. 模型预测暂态电压稳定紧急控制的简化空间算法[J]. 中国电机工程学报, 2012, 32(16): 53-61. Guo Ting, Xie Min, Liu Mingbo. Reduced space algorithm for model predictive transient voltage stability emergency control[J]. Proceedings of the CSEE, 2012, 32(16): 53-61.
[9] 林泽坤 , 彭显刚, 武小梅, 等. 基于交叠概率的含风电的地区电网暂态电压稳定评估的特征选择[J]. 电网技术, 2014, 38(2): 484-488. Lin Zekun, Peng Xiangang, Wu Xiaomei, et al. Overlapped probability based feature selection for assessment on transient voltage stability of regional power system containing wind farms [J]. Power System Technology, 2014, 38(2): 484-488.
[10] 侯建兰, 刘育权, 谢小荣, 等. 一种量化评估暂态电压稳定性的指标与方法[J]. 电力自动化设备, 2015, 35(10): 151-156. Hou Jianlan, Liu Yuquan, Xie Xiaorong, et al. Quantitative assessment index and method of transient voltage stability[J]. Electric Power Automation Equipment, 2015, 35(10): 151-156.
[11] 张曦, 张宁, 龙飞, 等. 分布式电源接入配网对其静态电压稳定性影响多角度研究[J]. 电力系统保护与控制, 2017, 45(6): 120-125. Zhang Xi, Zhang Ning, Long Fei, et al. Research of the impacts on static voltage stability of distribution networks with distributed generation from different aspects[J]. Power System Protection and Control, 2017, 45(6): 120-125.
[12] 初壮, 孙陶然, 雷振伍, 等. 考虑带泵类负载感应电动机影响的静态电压稳定性分析[J]. 电力系统保护与控制, 2019, 47(1): 51-58. Chu Zhuang, Sun Taoran, Lei Zhenwu, et al. Static voltage stability analysis considering the influence of pump loads induction motor[J]. Power System Protection and Control, 2019, 47(1): 51-58.
[13] 朱永强, 刘光晔, 廖庭坚, 等. 计及负荷电压静态特性的电力系统最小负荷裕度的快速评估[J]. 电力系统保护与控制, 2016, 44(6): 23-28. Zhu Yongqiang, Liu Guangye, Liao Tingjian, et al. Rapid assessment of power system minimum load margin considering load voltage static characteristics[J]. Power System Protection and Control, 2016, 44(6): 23-28.
[14] 顾卓远, 汤涌, 易俊, 等. 电力系统功角失稳与局部感应电动机失稳相互影响机理分析[J]. 电网技术, 2017, 41(8): 2499-2505. Gu Zhuoyuan, Tang Yong, Yi Jun, et al. Study on mechanism of interrelationship between power system angle stability and induction motor stability[J]. Power System Technology, 2017, 41(8): 2499-2505.
[15] 张文朝, 张博, 潘捷, 等. 基于感应电动机网荷互馈特性的暂态电压失稳机理探析[J]. 电力系统自动化, 2017, 41(7): 8-14. Zhang Wenchao, Zhang Bo, Pan Jie, et al. Mechanism analysis for transient voltage instability based on crossfeed characteristics between power network and load of induction motor[J]. Automation of Electric Power Systems, 2017, 41(7): 8-14.
[16] 张嫣, 林涌艺, 邵振国. 电压暂降可观约束下的定位监测点多目标优化配置[J]. 电工技术学报, 2019, 34(11): 2375-2383. Zhang Yan, Lin Yongyi, Shao Zhenguo. Multi-objective optimal allocation of monitors for voltage sag location under observability constraint[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2375-2383.
[17] 马一鸣, 周理兵, 王晋, 等. 基于直流阶跃电压试验与NSGAⅡ算法的同步电机动态参数辨识方法[J]. 电工技术学报, 2019, 34(23): 4890-4900. Ma Yiming, Zhou Libing, Wang Jin, et al. A method for synchronous machine dynamic parameters identification based on DC step voltage test and NSGAⅡalgorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4890-4900.
[18] Hirotsuka I, Tsuboi K, Ueda F. Experimental transient characteristics of a threephase squirrelcage induction motor under unbalanced voltage condition[C]//The 11th International Conference on Electrical Machines and Systems, Wuhan, China, 2008: 57-60.
[19] Hardi S, Hs S, Hafizi M, et al. Induction motors performance under symmetrical voltage sags and interruptiontest result[C]//Proceedings of the IEEE 7th International Power Engineering and Optimization Conference, Langkawi Island, Malaysia, 2013: 630-635.
[20] 鞠平, 潘学萍, 韩敬东. 3种感应电动机综合负荷模型的比较[J]. 电力系统自动化, 1999, 23(19): 41-43. Ju Ping, Pan Xueping, Han Jingdong. Comparison of three composite induction motor load models[J]. Automation of Electric Power Systems, 1999, 23(19): 41-43.
[21] 汤涌, 侯俊贤, 刘文焯, 等. 电力系统数字仿真负荷模型中配电网络及无功补偿与感应电动机的模拟[J]. 中国电机工程学报, 2005, 25(3): 8-12. Tang Yong, Hou Junxian, Liu Wenzhou, et al. The modeling of distribution network and VAR compensator and induction motor in the load model for power system digital simulation[J]. Proceedings of the CSEE, 2005, 25(3): 8-12.
[22] Pedra J, Candela I, Sainz L. Modelling of squirrelcage induction motors for electromagnetic transient programs[J]. IET Electric Power Applications, 2009, 3(2): 111-122.
[23] Aree P. Effects of large induction motors on voltage sag[C]//IEEE PES AsiaPacific Power and Energy Engineering Conference, 2012: 1-4.
[24] 何笠, 李兴源, 徐梅梅. 考虑动态负荷机械转矩参数的节点暂态电压评估[J]. 电力系统自动化, 2010, 34(19): 11-15. He Li, Li Xingyuan, Xu Meimei. Assessment of transient voltage stability of load bus considering mechanical torque of dynamic load[J]. Automation of Electric Power Systems, 2010, 34(19): 11-15.
[25] 王志军, 朱珂, 王小宇. 感应电动机对称电压跌落临界清除时间解析算法[J]. 电网技术, 2014, 38(2): 509-514. Wang Zhijun, Zhu Ke, Wang Xiaoyu. An analytical method to calculate critical clearance time of symmetrical voltage sags for induction motors[J]. Power System Technology, 2014, 38(2): 509-514.
[26] 李立理, 陆超, 黄志刚. 计及感应电动机的负荷节点暂态电压稳定解析评估方法[J]. 电力系统自动化, 2009, 33(7): 1-5. Li Lili, Lu Chao, Huang Zhigang. Analytical assessment of transient voltage stability of load bus considering induction motors[J]. Automation of Electric Power Systems, 2009, 33(7): 1-5.
[27] 焦石, 兰志勇, 王琳. 基于解析法的表贴式永磁同步电动机电磁场与齿槽转矩的分析[J]. 电气技术, 2019, 20(4): 7-11. Jiao Shi, Lan Zhiyong, Wang Lin. Analysis of electromagnetic field and cogging torque of surface mounted permanent magnet synchronous motor based on analytic method[J]. Electrical Engineering, 2019, 20(4): 7-11.
[28] Milanović J V, Aung M T, Vegunta S C. The influence of induction motors on voltage sag propagation—part I: accounting for the change in sag characteristics[J]. IEEE Transactions on Power Delivery, 2008, 23(2): 1063-1071.
[29] Kundur P. Power system stability and control[M]. 北京: 中国电力出版社, 2001.
[30] 岳程燕, 田芳, 周孝信, 等. 电力系统电磁暂态-机电暂态混合仿真接口原理[J]. 电网技术, 2006, 30(4): 6-10. Yue Chengyan, Tian Fang, Zhou Xiaoxin, et al. Principle of interfaces for hybrid simulation of power system electromagnetic-electromechanical transient process[J]. Power System Technology, 2006, 30(4): 6-10.
[31] 刘文焯, 侯俊贤, 汤涌, 等. 考虑不对称故障的机电暂态-电磁暂态混合仿真方法[J]. 中国电机工程学报, 2010, 30(13): 8-15. Liu Wenzhuo, Hou Junxian, Tang Yong, et al. Electromechanical transient/electromagnetic transient hybrid simulation method considering asymmetric faults[J]. Proceedings of the CSEE, 2010, 30(13): 8-15.
[32] 胡虔生, 胡敏强. 电机学[M]. 北京: 中国电力出版社, 2012.
[33] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[34] 汤涌, 卜广全, 侯俊贤, 等. PSD-BPA暂态稳定程序用户手册(中国版4.15)[Z]. 2010, 6: 258-261.
Fast Analytical Method for Calculating the Dynamic Performance of Induction-Motor Loads Considering the Effect of Asymmetrical Fault
Abstract The dynamic performance of induction motor loads has an important influence on power system voltage stability. To assess their post-asymmetrical fault transient response quickly and avoid tedious time-domain simulation, fast analytical method to calculate the dynamic performance of induction motors following power system voltage sag after asymmetrical and symmetrical fault is proposed based on circuit and machine analysis theory. Firstly, the first-order mechanical transient equation of the rotor is solved and the rotor’s speed and slip variations after disturbance are obtained. Based on this, the rotor’s phasor-form transient electric potential differential- equation is solved, and the change of the transient potential is attained. In the end, the current and the power response of the perturbed motor are acquired. This analytical method can easily be used in the Third-order electromechanical transient model of induction motor loads. Compared with PSCAD/EMTDC electromagnetic transient simulation results, the effectiveness of the algorithm is proved. Application of the proposed method to calculate the dynamic response of power system composite load demonstrates its utilization potential in power system stability studies.
keywords:Induction motor, dynamic performance, asymmetrical fault, voltage sag, analytical method
中图分类号:TM744
DOI:10.19595/j.cnki.1000-6753.tces.191207
廖卫平 男, 1990年生,硕士,工程师,研究方向为电力系统规划与运行控制,智能配电网自动化技术。E-mail:1071672259@qq.com(通信作者)
张 艳 女,1982年生,硕士,高级工程师,研究方向为电力系统规划与运行控制。E-mail:14137416@qq.com
收稿日期 2019-09-24
改稿日期 2020-03-31
(编辑 赫蕾)