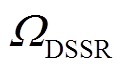表示为[28]摘要 该文进行了配电网安全域（DSSR）的全维直接观测。首先，总结了现有观测方法。其次，提出DSSR的全维直接观测方法。对两供一备和柔性两供一备接线的全维直接观测发现：两供一备的安全域是凹多面体，由一个“域核”和多个“域角”构成；域表面有“山脊”和“山谷”，“山谷”形成了域凹陷。柔性两供一备的安全域是凸多面体，不存在“山谷”，填补了传统两供一备的域凹陷。可见，全维直接观测清楚地展现了不同电网结构体现在安全域上的不同几何特征。该文还进一步给出了“域核”、“域角”、“山脊”、“山谷”的物理意义和形成原因。最后，将该方法与其他安全域观测方法进行对比和总结。
关键词：配电网安全域 全维直接观测 域核 域角 山脊 山谷
“域”方法源于输电系统，描述了电力系统整体安全运行的区域[1]。文献[2]提出了配电网安全域（Distribution System Security Region, DSSR）的概念，DSSR是满足一定安全准则的所有工作点（系统状态）的集合[3]。文献[3]给出了DSSR的严格数学定义，指出安全域需要具备封闭的边界，边界内的工作点全部安全，边界外的工作点全部不安全。文献[4-5]从仿真观测、实验证明了DSSR的存在性。
安全域观测（可视化）在电力系统监控、安全评估中扮演着重要角色[6]。输电系统安全域的可视化已有大量研究，一般将高维安全域进行降维或局部观测，得到二维或三维可视化视图，进而评估系统的安全性。文献[7-9]研究了割集功率空间上的静态电压稳定域（Static Voltage Stability Region Cut. set Space, CVSR）可视化问题并开发出配套软件。文献[10-11]对CVSR的局部可视化方法进行了研究。文献[12]的优化模型实现了二维/三维空间中静态电压稳定域（SVSR）的边界搜索。文献[13]解决了实用动态安全域（PDSR）降维和可视化问题，该方法在研究跳闸、重合闸对动态安全域的影响中得到了应用[14-15]。文献[16]开发了PDSR可视化系统。进一步，文献[17]对含双馈风机的动态安全域进行了三维投影观测。文献[18]对断面热稳定安全域进行了三维可视化。
对于配电网安全域，在状态空间中观测也是研究DSSR的最基本手段，能够帮助人们了解DSSR的形态特征，对比不同配电网的DSSR形态差异。现有研究观测发现，DSSR由安全边界切割状态空间形成，DSSR的边界由状态空间边界和安全边界两类构成，依据临界性的不同，安全边界又分为严格安全边界和非严格安全边界[19]。观测还发现，配电网安全边界是一系列近似线性、紧致、且不会“打结”的超平面[4,20]。
现有DSSR的观测方法主要包括二维投影直接观测法和基于安全距离的间接全维观测法。二维投影直接观测法对高维DSSR进行降维处理，得到二维投影图像。文献[21]将可能的二维投影图像总结形成了DSSR的二维图谱。二维投影法只能观测安全域的局部，为克服这一不足，文献[22]提出了DSSR的全维间接观测方法，计算原点到各个边界的安全距离，再形成完整观测DSSR所有维度的形状视图和边界凹陷视图，该方法在文献[23]的规划模型中得到了应用。此外，供电能力曲线反映了DSSR中严格边界的效率[24]，DSSR体积反映出了DSSR的大小[25]，二者也可视为对DSSR的观测。
上述方法各自存在一些局限性，二维投影法是直接观察，但很难反映安全域的全维信息，后面三种方法虽能反映全维信息，但都是间接观察。
接线模式是构成配电网网架结构的基本单元，其维度一般不高，有条件进行安全域的全维直接观测。本文选择南方电网公司常用的两供一备接线开展了安全域的全维直接观测，并与目前受到关注的采用电力电子软开关的柔性配电网（Flexible Distribution Network, FDN）[26]接线进行对比。
配电网安全域（DSSR）定义为配电网中所有满足N-1安全准则的工作点W的集合[27]。对于有n个节点负荷的配电系统，其安全域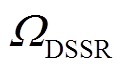表示为[28]
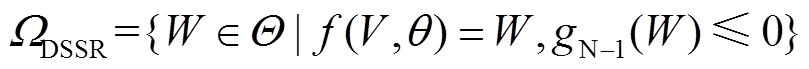（1）式中，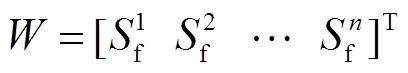
，
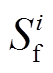为节点负荷视在功率；
为状态空间；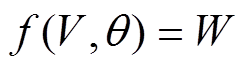
为潮流方程，
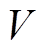和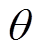
分别为节点电压和节点相角；
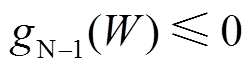为系统N-1的安全约束，包括容量约束和电压约束。文献[28]发现对于城市配电网，直流潮流DSSR模型相对于交流潮流DSSR模型的误差很小，为了观测方便，本文采用大多数DSSR研究采用的直流潮流模型[29]。
实际配电网的规模大，DSSR是由高维超平面围成。DSSR的二维投影观测选择某工作点中的两个观测变量，而其他变量保持不变，将整个域投影到观测变量构成的二维坐标系上进行观测[4,20]。此外，还可以进行三维投影观测。
文献[22]的DSSR全维观测首先得到DSSR所有边界对应的等效半径，再对安全域进行可视化观察，能得到全维的域形状视图（雷达图）和凹陷视图（折线图）。文献[22]还定义了形状畸变指标（Shape Distortion Index, SDI）、凹陷边界数（Concavity Boundary Number, CBN）来定量描述域的圆润程度和凹陷程度。该方法不能直接观测到安全域，而是基于边界等效半径间的间接观测。
供电能力曲线通过抽样生成有限个能代表完整边界的边界点样本，按其边界点的供电能力（Boundary Supply Capability, BSC）从小到大进行排序，得到供电能力曲线[24]。除观测供电能力曲线的形状外，还可以得到平均供电能力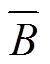
、BSC最小值Bmin及BSC最大值（Total Supply Capability, TSC[30-31]）三个指标，综合地反映了满足安全约束下的配电网效率。
配电网安全域体积定义为安全域的大小[25]。n维DSSR体积可以由n重积分表示为
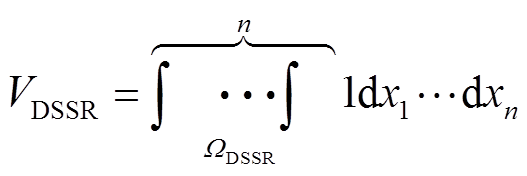（2）式中，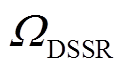
为积分区域，即配电网安全域；xi为第i回馈线在高维空间对应的坐标轴；1作为被积函数求DSSR的体积。
对于典型接线模式，当互联的几回馈线的总段数不大于3时，安全域表达式的约束变量个数不超过三个。其安全域由多个三维平面围成，通过等式和不等式约束，能够在三维坐标系中画出立体几何的形状，因此，可以直接展现出DSSR的全貌。
观察DSSR的三维图形，分析域形状的凸性和凹性，并将凹性域拆分成若干凸多面体，进而分析域的构成、特征。通过分析三维图形外表面以及棱的走势、位置，可以得到DSSR边界上供电能力的变化情况，进而了解边界的特征，从而判断安全域是否存在凹陷，并分析凹陷的成因。
综上，DSSR全维直接观测的步骤为：①根据N-1准则列写安全域表达式；②画出安全域三维图形；③观察三维图形的构成；④分析每个面供电能力变化和边界特征；⑤判断安全域凹陷并分析成因。
两供一备接线模式如图1所示，其结构对称，每回馈线末端都有一个常开联络开关，出口处都有一个常闭馈线开关。为便于比较计算结果，设馈线容量均为1MV∙A，类似于标幺值。
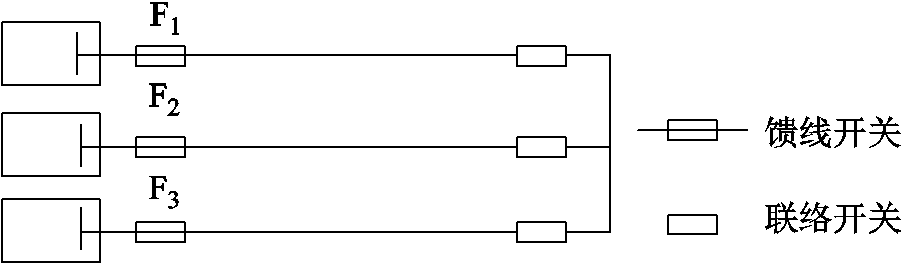
图1 两供一备接线
Fig.1 Two-supply-one-backup wiring
两供一备接线N-1后有四种转带模式：模式1~3采用一回馈线同时做另两回馈线的备用，该馈线和其中一回馈线互为备用；而模式4的三回馈线互为备用，一回馈线只单独做另一回馈线的备用。四种模式的安全约束以及对应的转带关系见表1。其中，SLi指馈线Fi所带负荷。
表1 两供一备四种转带模式的表达式
Tab.1 Four transfer modes’ expressions of two-supply-one-backup
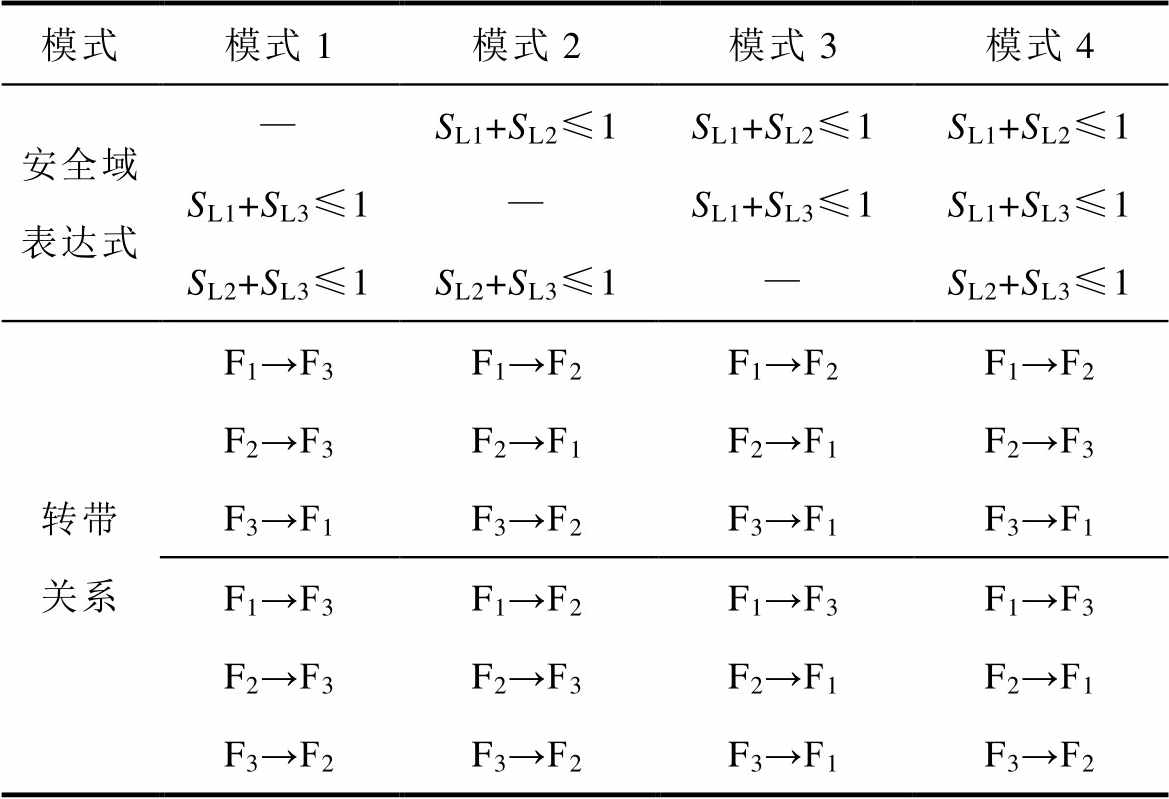
模式模式1模式2模式3模式4 安全域表达式—SL1+SL2≤1SL1+SL2≤1SL1+SL2≤1 SL1+SL3≤1—SL1+SL3≤1SL1+SL3≤1 SL2+SL3≤1SL2+SL3≤1—SL2+SL3≤1 转带关系F1→F3F2→F3F3→F1F1→F2F2→F1F3→F2F1→F2F2→F1F3→F1F1→F2F2→F3F3→F1 F1→F3F2→F3F3→F2F1→F2F2→F3F3→F2F1→F3F2→F1F3→F1F1→F3F2→F1F3→F2
注：“→”表示一回馈线发生N-1后，负荷转带给另一回馈线。
模式1~3的安全约束含有两个“≤”不等式，而模式4含有三个“≤”不等式。两供一备的安全域表达式为模式1~4安全域表达式的并集。特别地，模式4的安全约束是模式1、2、3的交集。
2.3.1 域核和域角
两供一备的安全域如图2a所示，它是一个凹多面体。为便于分析，将凹多面体切割成小凸多面体。因为模式4的约束是四种模式的交集，其对应的域也是四种模式的公共部分，因此将模式4的三个安全约束表达式中的“≤”换成“≥”，便形成了三个切割平面，这三个平面将安全域切割成P0、P1、P2、P3 共四个小凸多面体，如图2b所示。
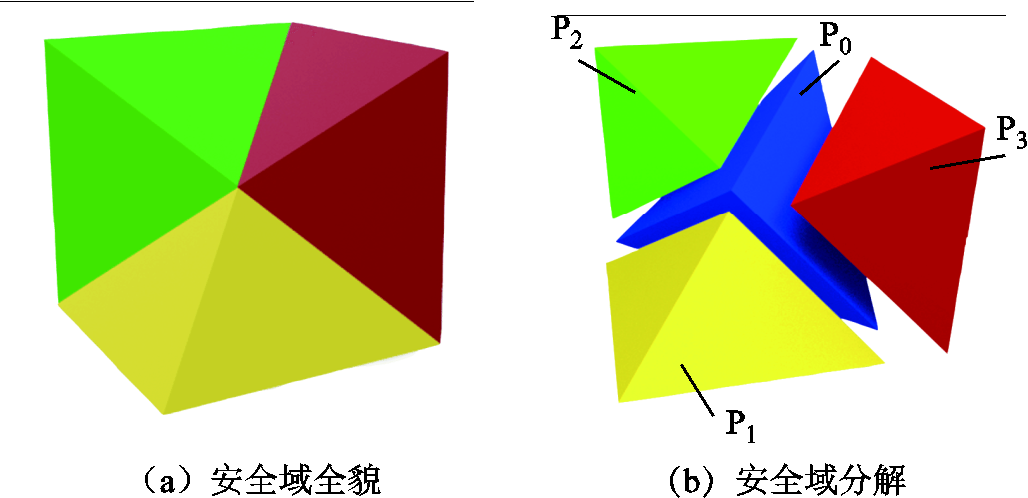
图2 两供一备安全域
Fig.2 Security region of two-supply-one-backup wiring
按转带模式将凹安全域凸分解后，两供一备的整个安全域表示为
DSSR = P0+P1+P2+P3 （3）
四个小凸多面体的类型、表达式、转带模式及图形见表2。
表2 小凸多面体的表达式
Tab.2 The expressions of the small convex polyhedrons
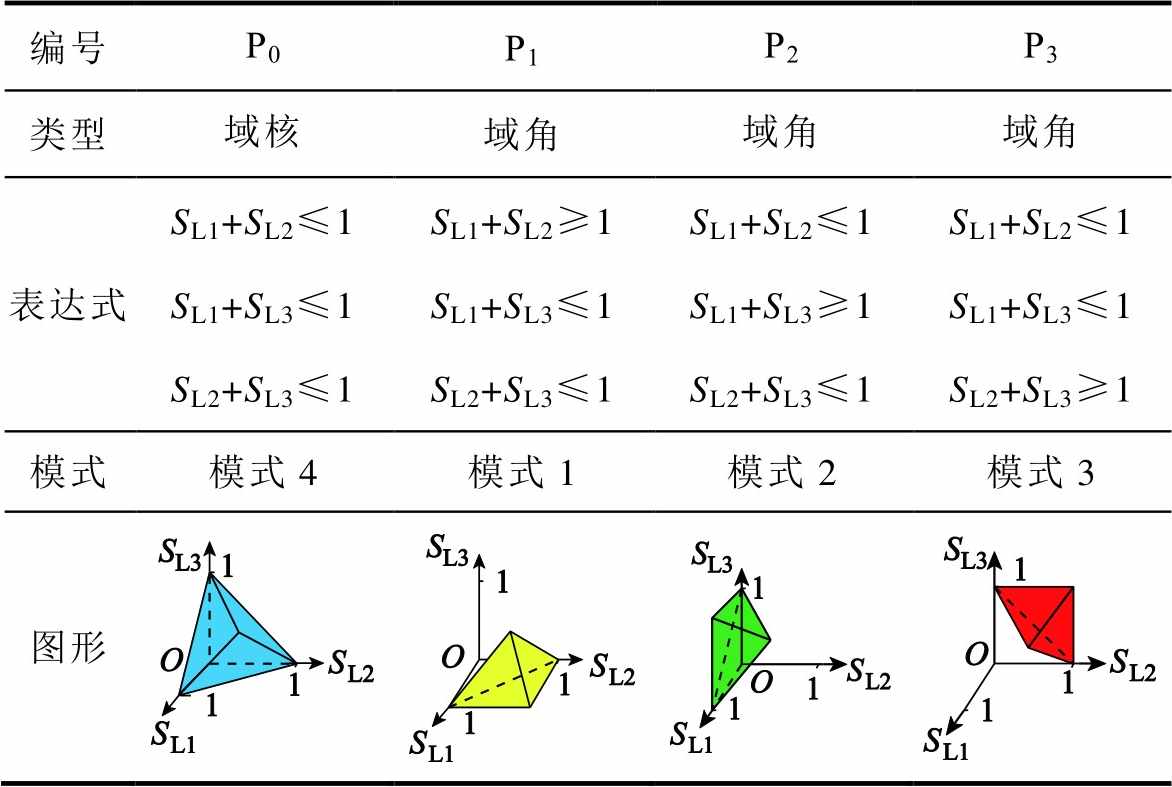
编号P0P1P2P3 类型域核域角域角域角 表达式SL1+SL2≤1SL1+SL2≥1SL1+SL2≤1SL1+SL2≤1 SL1+SL3≤1SL1+SL3≤1SL1+SL3≥1SL1+SL3≤1 SL2+SL3≤1SL2+SL3≤1SL2+SL3≤1SL2+SL3≥1 模式模式4模式1模式2模式3 图形
在表2中，P0与模式4对应，本文将其称为“域核（region core）”。P1、P2、P3三个小三棱锥分别是模式1~3对应的域比P0凸出的部分，本文称其为“域角（region angle）”。
2.3.2 域核和域角的物理意义
“域核”和“域角”的概念具有一般性，适用于具有多种转带模式的配电网。假设配电网有n种转带模式，每种转带模式下的安全域分别为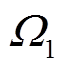
,
, 
,
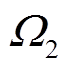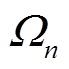，则域核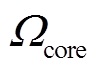
定义为多种转带模式下安全域的交集，即
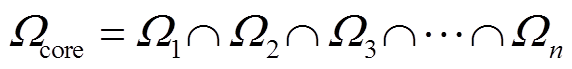（4）第i个域角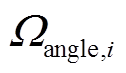
定义为第i个转带模式的安全域（非域核）比域核多出的部分，即
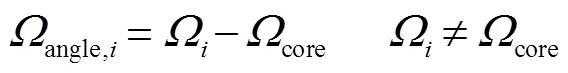（5）
域核和域角具有明确的物理意义：
1）三个域角是模式1~3的独有域空间，当工作点处于域角时，N-1后只能通过特定的转带模式转移负荷。
2）域核是模式1~3的公共域空间，当工作点处于域核时，N-1后可以由多种转带模式的任意一种转移负荷，即域核区域的N-1转带模式更灵活。
2.4.1 山脊和山谷
图3显示了安全域表面的特征。
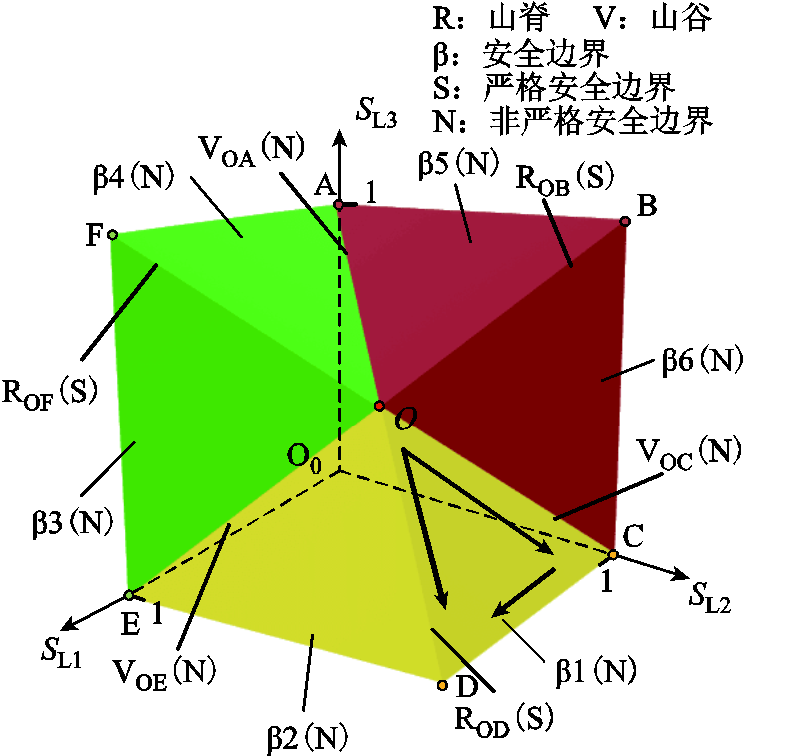
图3 两供一备安全域表面
Fig.3 Security region surface of two-supply-one-backup
从图3看出，OB、OD、OF为凸出来的三个“山脊（Ridge）”，记为ROB、ROD、ROF。OA、OC、OE为凹进去的三个“山谷（Valley）”，记为VOA、VOC、VOE。
山谷为安全域最凹陷的区域，从山谷到山脊，供电能力逐步增大。山脊上的点是供电能力曲线点，即BSC点，山谷上的点是非BSC点。例如，在边界β1上，VOC整体供电能力最低，ROD整体供电能力最高，沿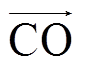
和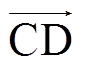
方向供电能力增大。山脊ROD上的O点供电能力最小，为Bmin，D点供电能力最大，为TSC，沿
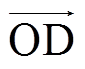方向边界供电能力逐步增大。
在整个域表面，仅山脊是严格边界，其他边界（包括山谷）均为非严格边界。山脊属于相交型严格安全边界[19]，山谷属于相交型非严格安全边界。依据文献[19]定义，严格边界为所有具有严格临界性工作点的集合，非严格边界为所有具有非严格临界性工作点的集合。一般情况下，相交型严格/非严格边界均由两个非严格边界相交形成[19]。
山谷和山脊的物理意义为：当工作点处在山谷时，为非严格临界安全状态，可以沿域表面继续朝着某一方向增加供电能力；而当工作点处在山脊时，为严格临界安全状态，无法朝着任何一个方向增加供电能力。
为验证上述观测结论的一般性，采用具有两供一备接线和单联络接线两种接线模式的IEEE_RBTS扩展算例进行三维投影直接观测，发现其局部三维域空间也是凹的，具有域核和域角，并且存在山谷和山脊两种边界，详细结果和数据见附录。
2.4.2 山脊和山谷的成因
从两供一备的转带关系和备用关系入手，分析山脊、山谷以及凹陷的成因。如表1所示,两供一备在N-1故障后，具有四种转带模式，由于模式1和模式2、3类似，为进一步分析，取模式1和模式4做对比。假设模式1下的备用关系为：馈线F1和F2的备用都是F3，而F3的备用为F1；模式4下的备用关系为：F1的备用为F2，F2的备用为F3，F3的备用为F1。它们的表达式和图形见表3。
表3 模式1和模式4对比
Tab.3 Comparison of mode 1 and mode 4
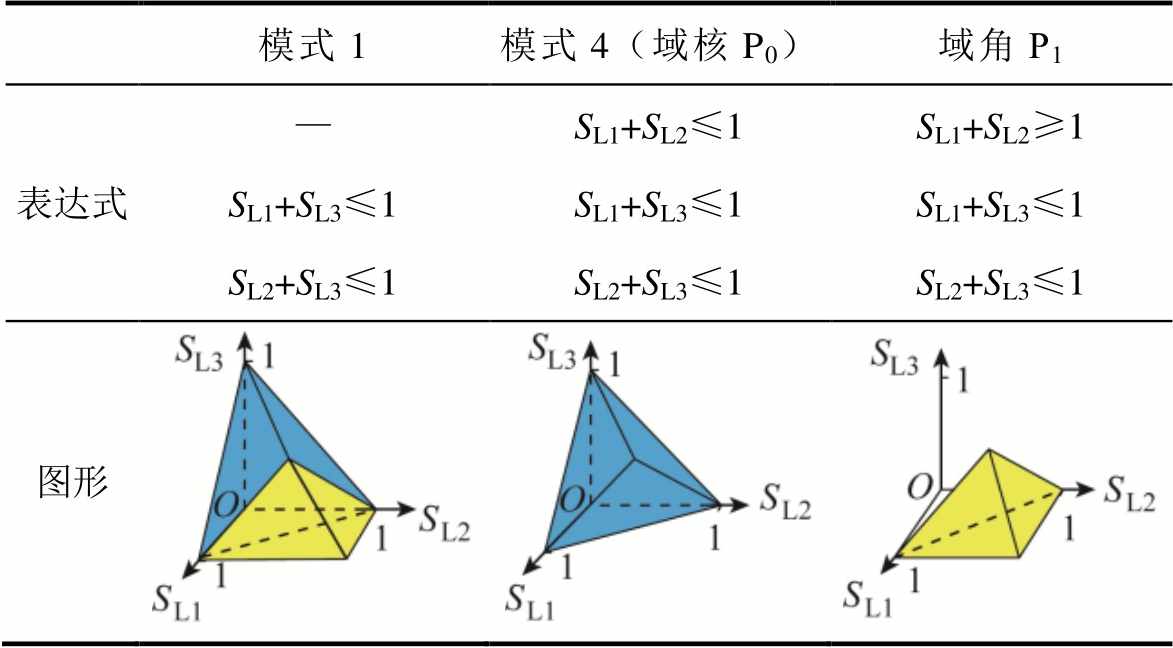
模式1模式4（域核P0）域角P1 表达式—SL1+SL2≤1SL1+SL2≥1 SL1+SL3≤1SL1+SL3≤1SL1+SL3≤1 SL2+SL3≤1SL2+SL3≤1SL2+SL3≤1 图形
单独考虑模式4下的安全域，其有三个严格安全边界，即VOA、VOC、VOE，O点的供电能力最高，为1.5MV·A。模式1突破了SL1+SL2≤1的限制，使得安全域在模式4基础上延伸出域角P1，形成了山脊ROD，ROD的供电能力在O点的基础上不断提高，一直达到供电能力最高的D点，为2MV∙A。同时，域角P1使得VOC、VOE由原来模式4下的严格边界变成了模式1的非严格安全边界，即VOC、VOE不再具有严格的安全临界性，可以沿着某一方向继续增大供电能力，从而变成了山谷。可见，发生这种变化的根本原因是不同恢复方案下的转带关系发生了变化，例如两供一备，由三回馈线互为备用转换成了一回馈线同时做其他两回馈线的备用。F1的备用馈线由F2转换成了F3，因此F1和F2之间减少了直接的限制，在更大的范围内也能保证N-1安全。进而考虑模式2、3，VOA、VOC、VOE最终都变成了非严格安全边界，成为了山谷，形成了凹陷。
柔性配电网（FDN）两供一备接线模式如图4所示。柔性接线以柔性互联装置代替两供一备接线的三个联络开关，三回馈线之间通过柔性互联装置相互连通，每回馈线出口处也有一个常闭馈线开关，正常情况下柔性闭环运行，可以双向连续调控潮流。为便于与两供一备接线对比，假设柔性两供一备每回馈线的容量均为1MV·A，柔性互联装置端口容量为1MV·A。
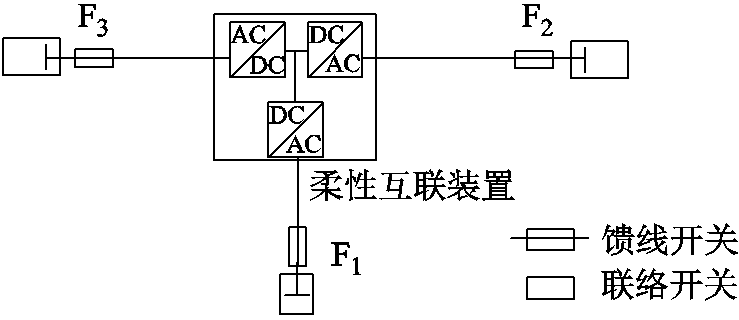
图4 柔性两供一备接线
Fig.4 Flexible two-supply-one-backup wiring
柔性两供一备的安全域表达式见表4。柔性两供一备在N-1后只有1种转带模式，因此，其安全域表达式不是两供一备的并集形式。
表4 柔性两供一备安全域表达式
Tab.4 Security region expressions of FDN
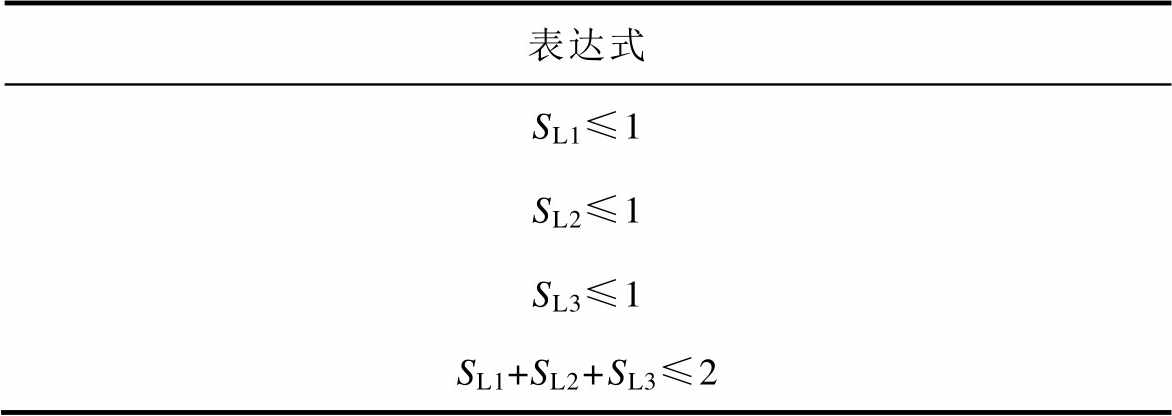
表达式 SL1≤1 SL2≤1 SL3≤1 SL1+SL2+SL3≤2
柔性两供一备的安全域如图5a所示，它是一个凸多面体。
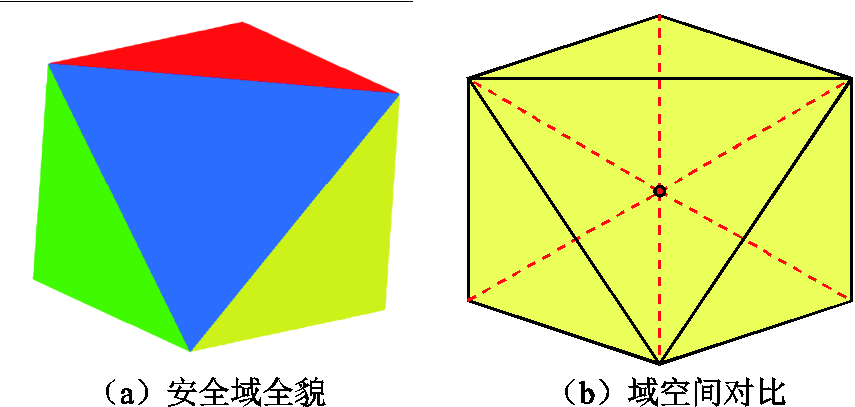
图5 柔性两供一备安全域图形
Fig.5 Security region diagtam of FDN
由图5b所示，实线为柔性两供一备安全域的轮廓，虚线为两供一备安全域的轮廓。柔性两供一备的安全域在两供一备凹域的基础上扩大，填补了部分凹陷，形成了饱满的凸域，工作点运行空间更大。
图6显示了安全域表面的特征。从图6看出，BF、BD、DF是凸出来的山脊，记为RBF、RBD、RDF，三个山脊围成“山顶”β4，其为独立型严格安全边界。不同于两供一备，柔性接线的三个山脊均由非严格安全边界和“山顶”相交形成，为相交型严格边界。柔性两供一备安全域没有山谷。在整个域表面，山脊和山顶是严格安全边界，其他都为非严格安全边界。山脊和山顶边界点都为BSC点，它们的供电能力相同，都能达到TSC。
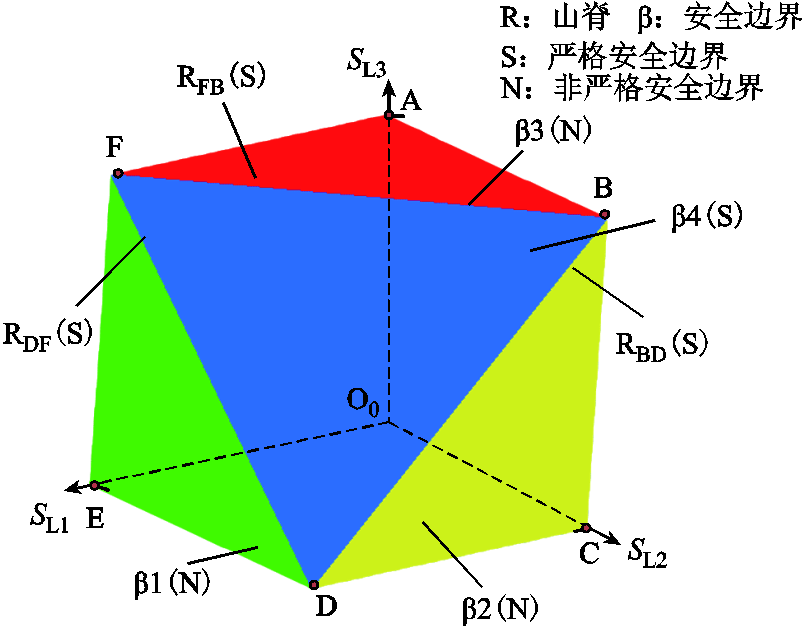
图6 柔性两供一备安全域表面
Fig.6 Security region surface of flexible two-supply-one-backup
与两供一备相比，柔性接线的安全域在安全边界β1、β2、β3、β4下的空间饱满，补平了两供一备安全域的“山谷”区域，填补了部分凹陷。由于运行方式约束SL1+SL2+SL3≤2的存在，山顶β4是工作点运行的极限状态，不能做到在整个状态空间安全。尽管如此，柔性化改造后在运行范围上仍有很大的优势。但在配电网规划实践中决定是否实施柔性化改造，还须综合考虑电力电子设备造价、可靠性等诸多因素[32-33]。
文献[34]采用了二维投影直接观测法，选取SL1和SL2为观测变量，保持SL3为均衡工作点不变，将安全域投影在以SL1和SL2构成的二维坐标系上得到二维视图，观测了传统配电网（Traditional Distribution Network, TDN）和柔性配电网的多联络电缆网的DSSR，观测结果见表5。进一步，下文分别采用供电能力曲线、全维间接观测和DSSR体积三种方法对两种接线模式的安全域进行观测，并和全维直接观测结果进行对比。记两供一备为算例1，记柔性两供一备为算例2。
根据文献[24]的供电能力曲线观测法，求取两种接线模式的BSC抽样分布，作出供电能力曲线，算出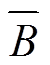
、Bmin等指标；根据文献[22]的安全域全维间接观测方法，选取“山脊”和“山谷”边界为观测对象，采用最小平均曼哈顿距离求两种接线模式的半径，进而作出雷达图、折线图，求出指标SDI、CBN；根据文献[25]求安全域体积的方法求出两种接线安全域的体积。观测结果见表5。
表5 本文方法与其他观测方法结果对比
Tab.5 Comparison of the results of this paper with other observation methods
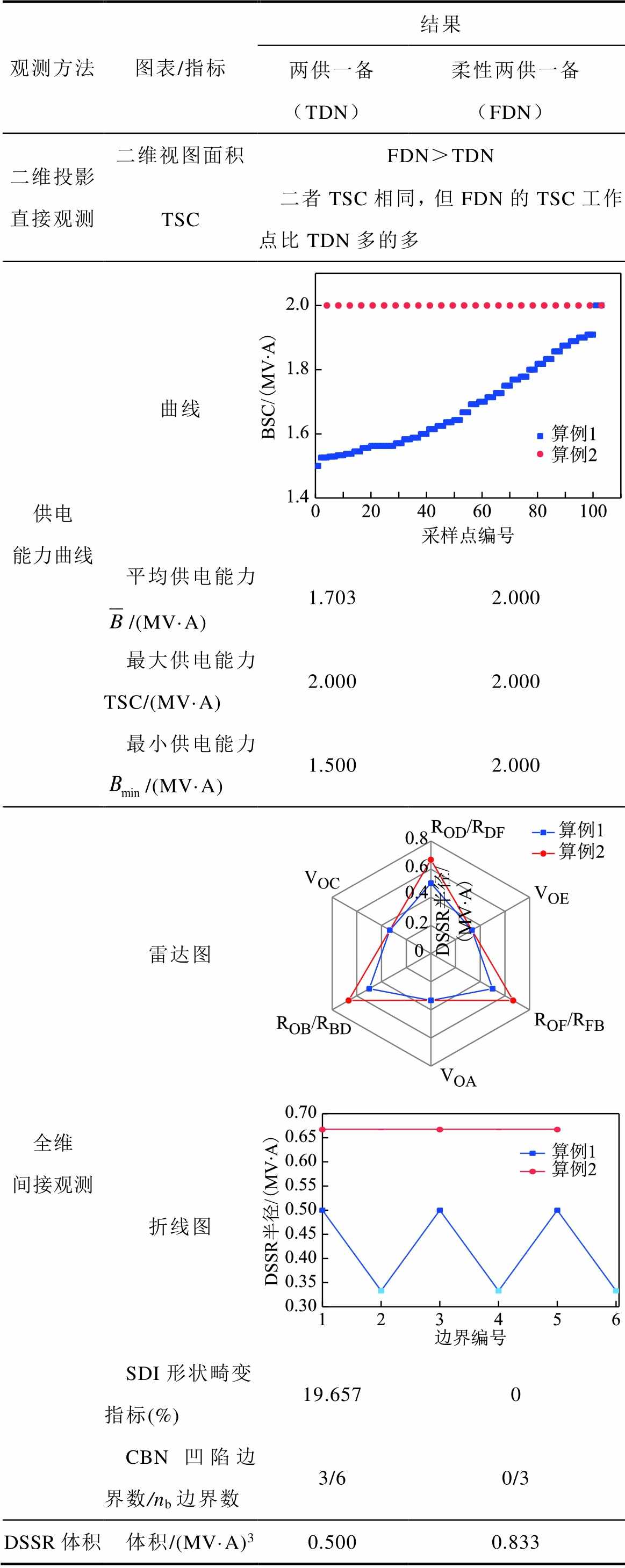
观测方法图表/指标结果 两供一备（TDN）柔性两供一备（FDN） 二维投影直接观测二维视图面积FDN＞TDN TSC二者TSC相同，但FDN的TSC工作点比TDN多的多 供电能力曲线曲线 平均供电能力/(MV·A)1.7032.000 最大供电能力TSC/(MV·A)2.0002.000 最小供电能力/(MV·A)1.5002.000 全维间接观测雷达图 折线图 SDI形状畸变指标(%)19.6570 CBN凹陷边界数/nb边界数3/60/3 DSSR体积体积/(MV·A)30.5000.833
二维投影直接观测和全维直接观测得到的结论相同，但二维投影观测法只能反映出SL1和SL2两个变量的工作区域及边界，若要观察SL1、SL2、SL3三者的共同作用，则需不断改变SL3的取值，得到一系列二维视图，视图数量成倍增加的同时其形状也有可能发生变化，增大了该方法的观测难度。而全维直接观测扩展了观测的范围和维度，通过一次观测便能观察出所有工作点，全面反映TSC和BSC的分布：FDN的BSC均能达到TSC，而TDN的BSC小于等于TSC，仅有少量有限个TSC工作点。
全维直接观测与供电能力曲线观测均能发现两供一备和柔性两供一备安全域的BSC数值变化规律，即二者的TSC均为2MV∙A，柔性两供一备的BSC大于等于两供一备，柔性两供一备的所有BSC均能达到TSC，而两供一备仅在个别BSC点达到TSC。两种方法各有所长，供电能力曲线能够直观地显示出这两种接线模式的BSC分布情况：柔性两供一备的供电能力曲线位于两供一备上方，大部分BSC明显高于两供一备，说明柔性两供一备的供电能力更强；而全维直接观测可以发现BSC点在DSSR的分布位置及变化规律，即在哪个边界上存在BSC点以及沿着边界BSC值是变大还是变小，这就克服了供电能力曲线通过排序后只能反映数量大小而不能在安全域上定位BSC点的局限性。
全维直接观测和全维间接观测均能观测出柔性两供一备比两供一备的安全域大，体现在全维直接观测上则发现柔性两供一备的形状比两供一备大，全维间接观测发现柔性两供一备的等效半径比两供一备大。全维间接观测得到两供一备的等效半径雷达图结构对称，验证了全维直接观测发现两供一备安全边界对称的结论。同时，全维间接观测发现了两供一备存在三个较小的半径，它们对应了山谷，说明山谷的存在导致安全域的凹陷；而柔性两供一备不存在山谷，因此没有凹陷区域，并填补了两供一备安全域的部分凹陷，充分证明了全维直接观测的结论。
DSSR体积法发现柔性两供一备安全域的体积比两供一备增大了66.7%，验证了全维直接观测的结论。另外，全维直接观测不仅能观测出安全域的大小，还能观测出安全域的形状构成以及凹陷区域，大大地扩展了DSSR体积观测的范围。
针对上文的观测结果，表6总结了全部观测方法的优缺点及适用场合。全维直接观测方法的用途虽有局限，但是也有价值。该方法的局限为必须在低维模式下使用，所以仅能用于接线模式的安全域观测；但接线模式是构建整个网架的基本结构，接线模式的全维直接观测结果能帮助理解配电网的安全与效率特征。
表6 安全域观测方法总结
Tab.6 Summary of observation methods of DSSR
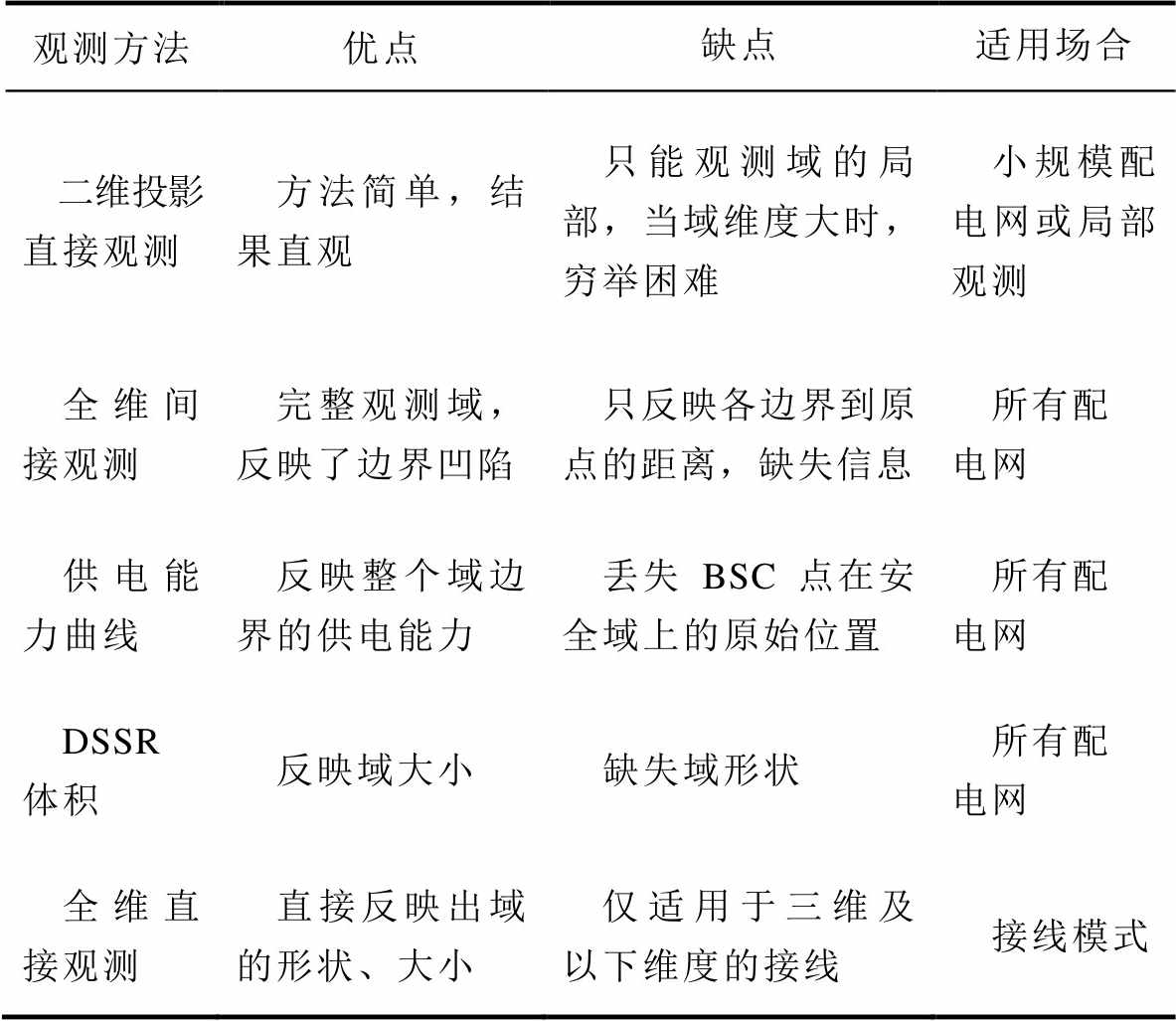
观测方法优点缺点适用场合 二维投影直接观测方法简单，结果直观只能观测域的局部，当域维度大时，穷举困难小规模配电网或局部观测 全维间接观测完整观测域，反映了边界凹陷只反映各边界到原点的距离，缺失信息所有配电网 供电能力曲线反映整个域边界的供电能力丢失BSC点在安全域上的原始位置所有配电网 DSSR体积反映域大小缺失域形状所有配电网 全维直接观测直接反映出域的形状、大小仅适用于三维及以下维度的接线接线模式
本文进行了配电网安全域DSSR的全维直接观测。与现有DSSR观测手段对比表明，本文方法能直接反映域的全貌。两供一备和柔性两供一备接线模式的全维直接观测结论如下：
1）两供一备的安全域是凹多面体；柔性两供一备的安全域为凸多面体。
2）配电网凹型安全域具有多种负荷转带模式，由域核和域角构成，域核最安全，N-1时可选择任一模式灵活转移负荷；而域角工作点N-1时只能由一种特定模式转移负荷。
3）域表面存在“山脊”和“山谷”两种边界。山脊是相交型严格边界，普遍存在；山谷是相交型非严格边界，仅存在于凹型域中，导致域的凹陷。多转带方案下的备用关系转换是形成山谷的原因。
4）两供一备的严格安全边界均是“山脊”；而柔性两供一备除了“山脊”外，还包括三个“山脊”围成的“山顶”，“山顶”是独立型严格边界。
5）柔性接线补平了传统接线的“山谷”，域更饱满，域的变化直接反映了柔性化改造的效果。
目前对配电网凹型安全域的研究尚处于起步阶段，未来将对凹型安全域的性质、机理，具有多种负荷转移方案的DSSR安全边界表达式等进行进一步研究。
附 录
1.复杂接线配电网三维投影直接观测方法
对于复杂接线（维数＞3）配电网，其超出了全维直接观测的适用范围，但仍可采用三维投影法对其进行直接观测，步骤如下：①列写安全域表达式，将其化为最简式；②选取三个观测变量，如馈线Fi、Fi-1、Fi+1，其他变量保持不变；③在三维空间画出Fi、Fi-1、Fi+1构成的局部域空间；④对域空间进行观测。
2.IEEE_RBTS扩展算例简介
算例网络结构如附图1所示，共6台主变、16回馈线，主变压器容量为16MV·A，馈线容量为6MV·A。图中虚线框区域为四组两供一备接线，其他区域采用单联络接线。对于单联络接线，当一回馈线N-1后只能向与其互联的另一回馈线转带负荷；而对于两供一备接线，当一回馈线N-1后，可以选择与其互联的两回馈线中的任意一回转带负荷。
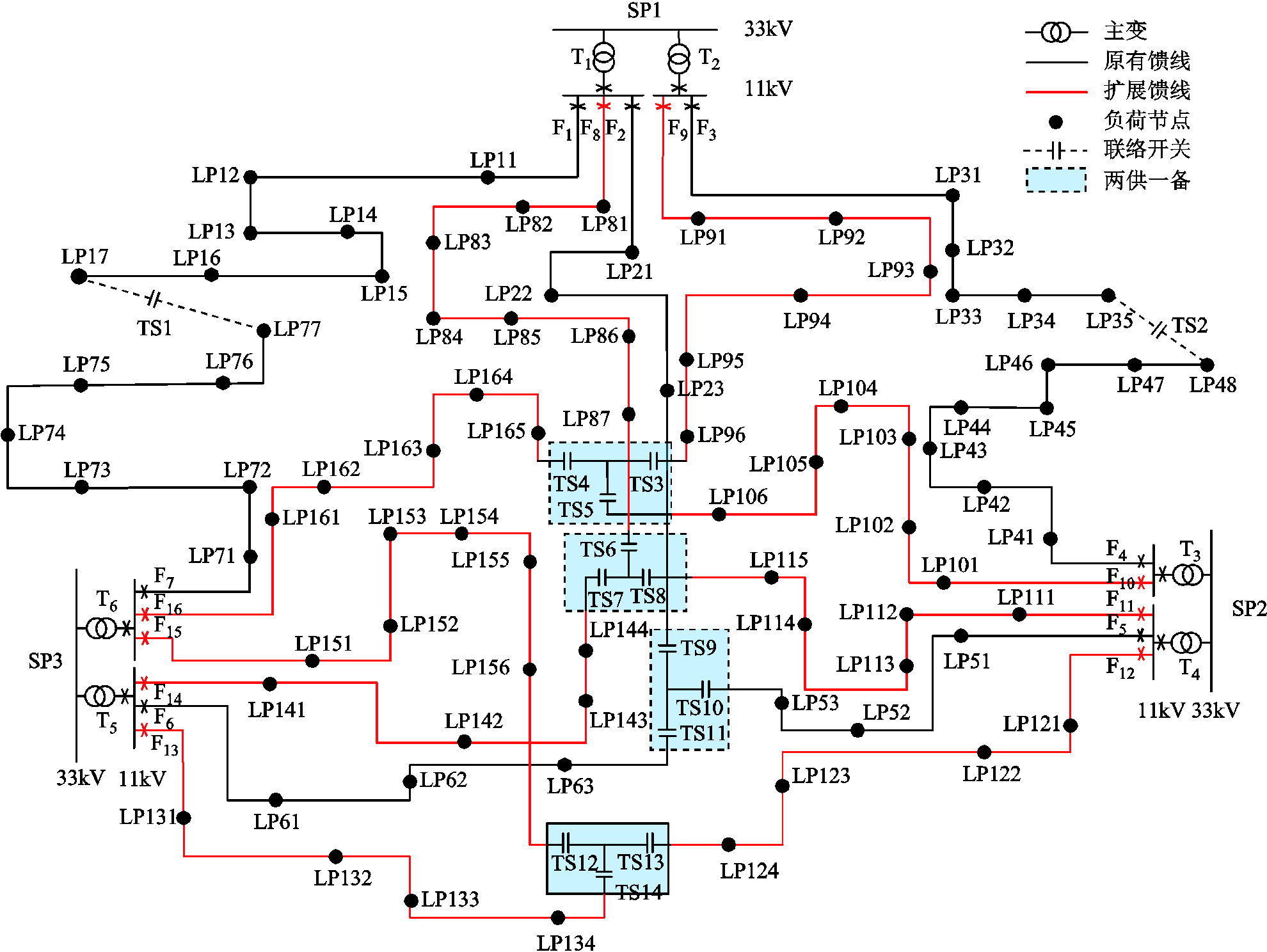
附图1 IEEE_RBTS扩展算例
App.Fig.1 IEEE_RBTS expanded case
3.安全域表达式
列写IEEE_RBTS扩展算例安全域表达式，并将其化简，最终结果见附表1。
4.三维投影直接观测结果-域空间几何特征
选取馈线F2、F5和F6进行观测，化简该算例的安全域表达式为
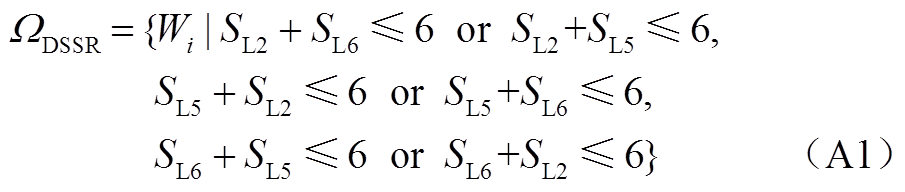
由式（A1）绘制三维投影观测视图，如附图2所示。
由附图2a可知，IEEE_RBTS扩展算例DSSR的三维投影观测视图和两供一备接线的全维观测视图（正文图2）相似，也是一个凹多面体。因此，IEEE_RBTS扩展算例局部三维域空间拥有和两供一备接线DSSR相似的性质和机理，采用2.3.1节的方法对其进行域切割，如附图2b所示，其也由域核P0和三个域角P1、P2、P3构成。
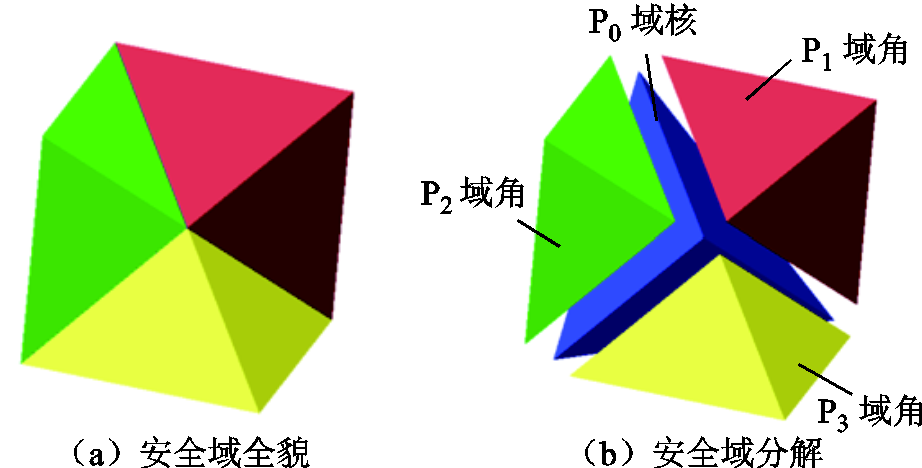
附图2 IEEE_RBTS扩展算例安全域三维观测视图
App.Fig.2 3D observation view of IEEE_RBTS expanded case’s DSSR
附表1 IEEE_RBTS扩展算例安全域表达式
App.Tab.1 DSSR expressions of IEEE_RBTS expanded case
编号安全约束表达式 1SL1+SL7≤6; SL1+SL7+SL15+SL16≤16 2(SL2+SL5≤6; SL2+SL5+SL11+SL12≤16) or (SL2+SL6≤6; SL2+SL6+SL13+SL14≤16) 3SL3+SL4≤6; SL3+SL4+SL10≤16 4SL3+SL4+SL9≤16 5(SL2+SL5≤6; SL1+SL2+SL5+SL8≤16) or (SL5+SL6≤6; SL5+SL6+SL13+SL14≤16) 6(SL2+SL6≤6; SL1+SL2+SL6+SL8≤16) or (SL5+SL6≤6; SL5+SL6+SL11+SL12≤16) 7SL1+SL2+SL7+SL8≤16 8(SL8+SL11≤6; SL5+SL8+SL11+SL12≤16) or (SL8+SL14≤6; SL6+SL8+SL13+SL14≤16) 9(SL9+SL10≤6; SL4+SL9+SL10≤16) or (SL9+SL16≤6; SL7+SL9+SL15+SL16≤16) 10(SL9+SL10≤6; SL3+SL9+SL10≤16) or (SL10+SL16≤6; SL7+SL10+SL15+SL16≤16) 11(SL8+SL11≤6; SL1+SL2+SL8+SL11≤16) or (SL11+SL14≤6; SL6+SL11+SL13+SL14≤16) 12(SL12+SL13≤6; SL6+SL12+SL13+SL14≤16) or (SL12+SL15≤6; SL7+SL12+SL15+SL16≤16) 13(SL12+SL13≤6; SL5+SL11+SL12+SL13≤16) or (SL13+SL15≤6; SL7+SL13+SL15+SL16≤16) 14(SL8+SL14≤6; SL1+SL2+SL8+SL14≤16) or (SL11+SL14≤6; SL5 +SL11+SL12+SL14≤16) 15(SL12+SL15≤6; SL5+SL11+SL12+SL15≤16) or (SL13+SL15≤6; SL6+SL13+SL14+SL15≤16) 16(SL9+SL16≤6; SL3+SL9+SL16≤16) or (SL10+SL16≤6; SL4+SL10+SL16≤16)
5.三维投影直接观测结果-域表面几何特征
附图3反映了IEEE_RBTS扩展算例局部三维域空间的表面几何特征，其拥有ROB、ROD、ROF三条“山脊”边界，以及VOA、VOC、VOE三条“山谷”边界。
如附图3所示，在边界β1上，E点供电能力最低，为6MV·A，并且VOE整体供电能力最低。β1表面沿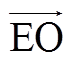
和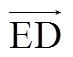
方向供电能力增大。山脊ROD上的O点供电能力最小，为9MV·A（Bmin），D点供电能力最大，为12MV·A（TSC），沿
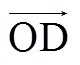方向边界供电能力逐步增大，但是无法沿着ROD两侧的域表面继续提升供电能力。因此，ROD的整体供电能力最高。综上，山谷为安全域最凹陷的区域，从山谷到山脊，供电能力逐步增大。
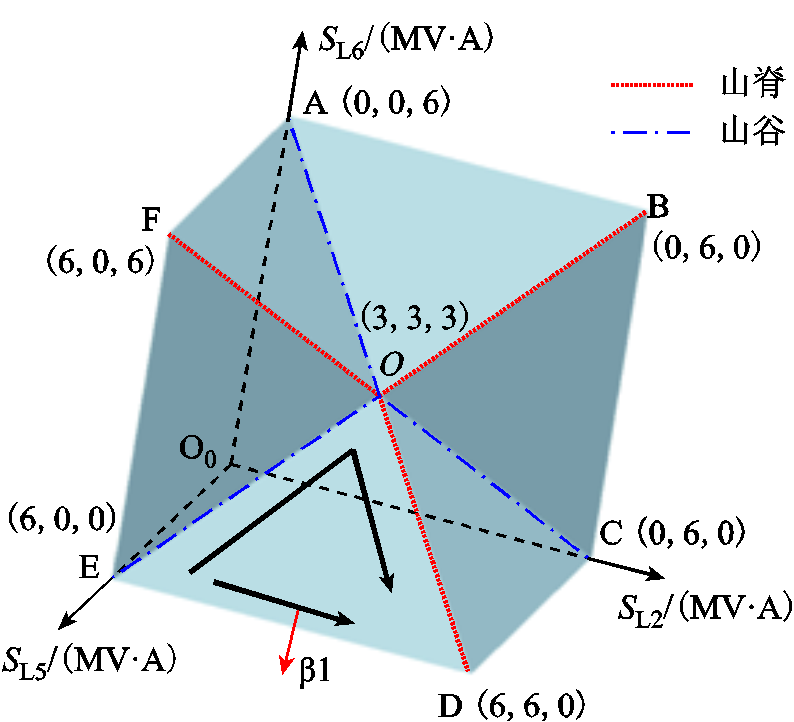
附图3 IEEE_RBTS扩展算例局部3维域空间表面
App.Fig.3 Local 3D DSSR’s surface of IEEE_RBTS expanded case
参考文献
[1] 余贻鑫. 安全域的方法学及实用性结果[J]. 天津大学学报, 2003, 36(5): 525-528. Yu Yixin. Methodology of security region and practical results[J]. Journal of Tianjin Univerisity, 2003, 36(5): 525-528.
[2] Xiao Jun, Gu Wenzhuo, Wang Chengshan, et al. Distribution system security region: definition, model and security assessment[J]. IET Generation, Transmission & Distribution, 2012, 6(10): 1029-1035.
[3] 肖峻, 祖国强, 白冠男, 等. 配电系统安全域的数学定义与存在性证明[J]. 中国电机工程学报, 2016, 36(18): 4828-4836. Xiao Jun, Zu Guoqiang, Bai Guannan, et al. Mathematical definition and existence proof of distribution system security region[J]. Proceedings of the CSEE, 2016, 36(18): 4828-4836.
[4] Xiao Jun, Zu Guoqiang, Gong Xiaoxu, et al. Observation of security region boundary for smart distribution system[J]. IEEE Transactions on Smart Grid, 2017, 8(4): 1731-1738.
[5] 肖峻, 祖国强, 贺琪博, 等. 配电网安全域的实证分析[J]. 电力系统自动化, 2017, 41(3): 153-160. Xiao Jun, Zu Guoqiang, He Qibo, et al. Empirical analysis in distribution system security region[J]. Automation of Electric Power Systems, 2017, 41(3): 153-160.
[6] 余贻鑫. 电力系统安全域方法研究述评[J]. 天津大学学报, 2008, 41(6): 635-646. Yu Yixin. A review of research on power system security region methods[J]. Journal of Tianjin University, 2008, 41(6): 635-646.
[7] 赵金利. 电压稳定域的可视化及其应用[D]. 天津:天津大学, 2004.
[8] 赵金利, 余贻鑫, 贾宏杰, 等. 电力系统割集空间静态电压稳定域的可视化及实现[J]. 电力系统自动化, 2005, 29(5): 56-61. Zhao Jinli, Yu Yixin, Jia Hongjie, et al. Visualization and implementation of static voltage stability region in power system cut set space[J]. Automation of Electric Power Systems, 2005, 29(5): 56-61.
[9] 牛犇, 余贻鑫, 贾宏杰, 等. 静态电压稳定域的三维可视化技术[J]. 电网技术, 2005, 29(7): 56-59. Niu Ben, Yu Yixin, Jia Hongjie, et al. Three- dimensional visualization technology of static voltage stability region[J]. Power System Technology, 2005, 29(7): 56-59.
[10] 王成山, 许晓菲, 余贻鑫, 等. 电力系统电压稳定域的局部可视化描述及其应用[J]. 中国电机工程学报,2004, 24(3): 6-10. Wang Chengshan, Xu Xiaofei, Yu Yixin, et al. Local visualization description of power system voltage stability region and its application[J]. Proceedings of the CSEE, 2004, 24(3): 6-10.
[11] 王成山, 许晓菲, 余贻鑫, 等. 基于割集功率空间上的静态电压稳定域局部可视化方法[J]. 中国电机工程学报, 2004, 24(9): 17-22. Wang Chengshan, Xu Xiaofei, Yu Yixin, et al. Local visualization method of static voltage stability region based on cut set power space[J]. Proceedings of the CSEE, 2004, 24(9): 17-22.
[12] 姜涛, 张明宇, 崔晓丹, 等. 电力系统静态电压稳定域边界快速搜索的优化模型[J]. 电工技术学报, 2018, 33(17): 4167-4179. Jiang Tao, Zhang Mingyu, Cui Xiaodan, et al. An optimization model for fast search of static voltage stability region boundary in power system[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4167-4179.
[13] 杨延滨, 余贻鑫, 曾沅, 等. 实用动态安全域降维可视化方法[J]. 电力系统自动化, 2005, 29(12): 44-48. Yang Yanbin, Yu Yixin, Zeng Yuan, et al. Visualization method of dimensionality reduction in practical dynamic security region[J]. Automation of Electric Power Systems, 2005, 29(12): 44-48.
[14] 刘怀东, 方伟, 王锦桥, 等. 线路两端不同时跳闸对动态安全域的影响[J]. 电工技术学报, 2018, 33(13): 3034-3040. Liu Huaidong, Fang Wei, Wang Jinqiao, et al. Influence of tripping at differentends of the line on dynamic safety region[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3034-3040.
[15] 刘怀东, 王锦桥, 冯志强, 等. 重合闸时刻对动态安全域的影响及最优重合时刻实用算法[J]. 电工技术学报,2018, 33(8):1854-1862. Liu Huaidong, Wang Jinqiao, Feng Zhiqiang, et al. Influence of reclosing time on dynamic security region and the practical algorithm of optimal coincidence time[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1854-1862.
[16] 单莹. 网络化的实用动态安全域可视化系统[D]. 天津: 天津大学,2007.
[17] 秦超, 刘艳丽, 余贻鑫, 等. 含双馈风机电力系统的动态安全域[J]. 电工技术学报, 2015, 30(18): 157- 163. Qin Chao, Liu Yanli, Yu Yixin, et al. Dynamic safety region of power system with doubly-fed wind turbines[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 157-163.
[18] 赵金利, 张继楠, 贾宏杰, 等. 计及N-1约束的多维空间断面热稳定安全域边界快速计算[J]. 电力系统自动化, 2016, 40(4): 128-135. Zhao Jinli, Zhang Jinan, Jia Hongjie, et al. Fast calculation of multi-dimensional spatial section thermal stability safety region boundary considering N-1 constraints[J]. Automation of Electric Power Systems, 2016, 40(4): 128-135.
[19] 肖峻, 肖居承, 张黎元, 等. 配电网的严格与非严格安全边界[J]. 电工技术学报, 2019, 34(12): 2637-2648. Xiao Jun, Xiao Jucheng, Zhang Liyuan, et al. Strict and non-strict security boundary of distribution system[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2637-2648.
[20] 肖峻, 贡晓旭, 贺琪博, 等. 智能配电网N-1安全边界拓扑性质及边界算法[J]. 中国电机工程学报, 2014, 34(4): 545-554. Xiao Jun, Gong Xiaoxu, He Qibo, et al. Topological characteristics and algorithm of N-1 security boundary for smart distribution system[J]. Proceedings of the CSEE, 2014, 34(4): 545-554.
[21] 肖峻, 周欢, 祖国强. 配电网安全域的二维图谱[J]. 电力系统自动化, 2019, 43(24): 96-117. Xiao Jun, Zhou Huan, Zu Guoqiang. Two-dimensional map of distribution system security region[J]. Automation of Electric Power Systems, 2019, 43(24): 96-117.
[22] 肖峻, 张宝强, 邵经鹏, 等. 配电网安全域的全维观测[J]. 电力系统自动化, 2018, 42(16): 73-79. Xiao Jun, Zhang Baoqiang, Shao Jingpeng, et al. Full-dimensional observation of distribution system security region[J]. Automation of Electric Power Systems, 2018, 42(16): 73-79.
[23] 江钧, 成乐祥, 孙国强,等. 考虑安全域的配电网重构二阶锥双层规划模型[J]. 电力系统保护与控制, 2019, 47(4): 9-16. Jiang Jun, Cheng Lexiang, Sun Guoqiang, et al. Second-order cone bilevel programming model for distribution network reconstruction considering security region[J]. Power System Protection and Control, 2019, 47(4): 9-16.
[24] 肖峻, 张苗苗, 司超然, 等. 配电网的供电能力分布[J]. 电网技术, 2017, 41(10): 3326-3332. Xiao Jun, Zhang Miaomiao, Si Chaoran, et al. Supply capability distribution of distribution systems[J]. Power System Technology, 2017, 41(10): 3326-3332.
[25] 肖峻, 张苗苗, 祖国强, 等. 配电系统安全域的体积[J]. 中国电机工程学报, 2017, 37(8): 2222-2231. Xiao Jun, Zhang Miaomiao, Zu Guoqiang, et al. Volume of distribution system security region[J]. Proceedings of the CSEE, 2017, 37(8): 2222-2231.
[26] 肖峻, 刚发运, 黄仁乐, 等. 柔性配电网的最大供电能力模型[J]. 电力系统自动化, 2017, 41(5): 30-38. Xiao Jun, Gang Fayun, Huang Renle, et al. Model of total supply capability for flexible distribution system[J]. Automation of Electric Power Systems 2017, 41(5): 30-38.
[27] 肖峻, 谷文卓, 王成山. 面向智能配电系统的安全域模型[J]. 电力系统自动化, 2013, 37(8): 14-19. Xiao Jun, Gu Wenzhuo, Wang Chengshan. A security region model for smart distribution system[J]. Automation of Electric Power Systems, 2013, 37(8): 14-19.
[28] 肖峻, 左磊, 祖国强, 等. 基于潮流计算的配电系统安全域模型[J]. 中国电机工程学报, 2017, 37(17): 4941-4949. Xiao Jun, Zuo Lei, Zu Guoqiang, et al. Safety region model of power distribution system based on power flow calculation [J]. Proceedings of the CSEE, 2017, 37 (17): 4941-4949.
[29] 肖峻, 苏步芸, 贡晓旭, 等. 基于馈线互联关系的配电网安全域模型[J]. 电力系统保护与控制, 2015, 43(20): 36-44. Xiao Jun, Su Buyun, Gong Xiaoxu, et al. Security region model of distribution system based on feeder interconnection [J]. Power System Protection and Control, 2015, 43(20): 36-44.
[30] 肖峻, 佘步鑫. 配电网接线模式的综合效率评价[J]. 电网技术, 2019, 43(10): 3769-3781. Xiao Jun, She Buxin. Comprehensive efficiency evaluation of distribution mode of distribution system[J]. Power System Technology, 2019, 43(10): 3769-3781.
[31] 肖晗, 叶志浩, 纪锋, 等. 考虑电动机起动的舰船直流区域配电系统预防控制方法[J]. 电工技术学报, 2018, 33(2): 413-422. Xiao Han, Ye Zhihao, Ji Feng, et al. Prevention and control method of ship DC area power distribution system considering motor starting[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 413-422.
[32] 杨欢, 蔡云旖, 邓焰, 等. 配电网柔性开关设备关键技术及其发展趋势[J]. 电力系统自动化, 2018, 42(7): 153-165. Yang Huan, Cai Yunyi, Deng Yan, et al. Key technologies and development trends of flexible switchgear in distribution networks[J]. Automation of Electric Power Systems, 2018, 42(7): 153-165.
[33] 王成山, 宋关羽, 李鹏, 等. 基于智能软开关的智能配电网柔性互联技术及展望[J]. 电力系统自动化, 2016, 40(22): 168-175. Wang Chengshan, Song Guanyu, Li Peng, et al. Flexible interconnection technology and prospect of intelligent distribution network based on intelligent soft switch[J]. Automation of Electric Power Systems, 2016, 40(22): 168-175.
[34] 肖峻, 刚发运, 邓伟民, 等. 柔性配电网的安全域模型[J]. 电网技术, 2017, 41(12): 3764-3774. Xiao Jun, Gang Fayun, Deng Weimin, et al. Security region model for flexible distribution system[J]. Grid Technology, 2017, 41(12): 3764-3774.
Full-Dimensional Direct Observation of Distribution System Security Region
Abstract Full-dimensional direct observation of distribution system security region (DSSR) is carried out in this paper. Firstly, the existing observation methods are summarized. Secondly, a full-dimensional direct observation method of DSSR is proposed. The full-dimensional direct observation of two-supply-one-standby and flexible two-supply-one-standby connections shows that the security domain of two-supply-one-standby is a concave polyhedron, which is composed of a“domain core” and multiple“domain corners”; The surface of its security region has “ridges” and “valleys”, and “valleys” form domain depression. The security domain of flxible two-supply-one-backup wiring is a convex polyhedron, and there is no “valley”, which fills the traditional depression of two supplies and one backup It can be seen that the full-dimensional direct observation clearly shows the different geometric characteristics of different power grid structures embodied in the security region. This paper further gives the physical meanings and formation reasons of “region core”,“region angle”,“ridge” and“valley”. Finally, the method of this paper is compared and summarized with other security domain observation methods.
keywords：Distribution system security region, full-dimensional direct observation, region core, region angle, ridge, valley
中图分类号：TM711
DOI:10.19595/j.cnki.1000-6753.tces.191038
肖 峻 男，1971年生，博士，教授，研究方向为配电系统规划评估，智能配电系统运行和分布式电源与微网。E-mail：xiaojun@tju.edu.cn（通信作者）
曹 严 男，1997年生，硕士研究生，研究方向为配电系统规划和智能配电系统运行。E-mail：yan221@tju.edu.cn
国家重点研发计划（2016YFB0900100）和国家自然科学基金（51877144）资助项目。
收稿日期 2019-08-18
改稿日期 2020-06-12
（编辑 赫蕾）