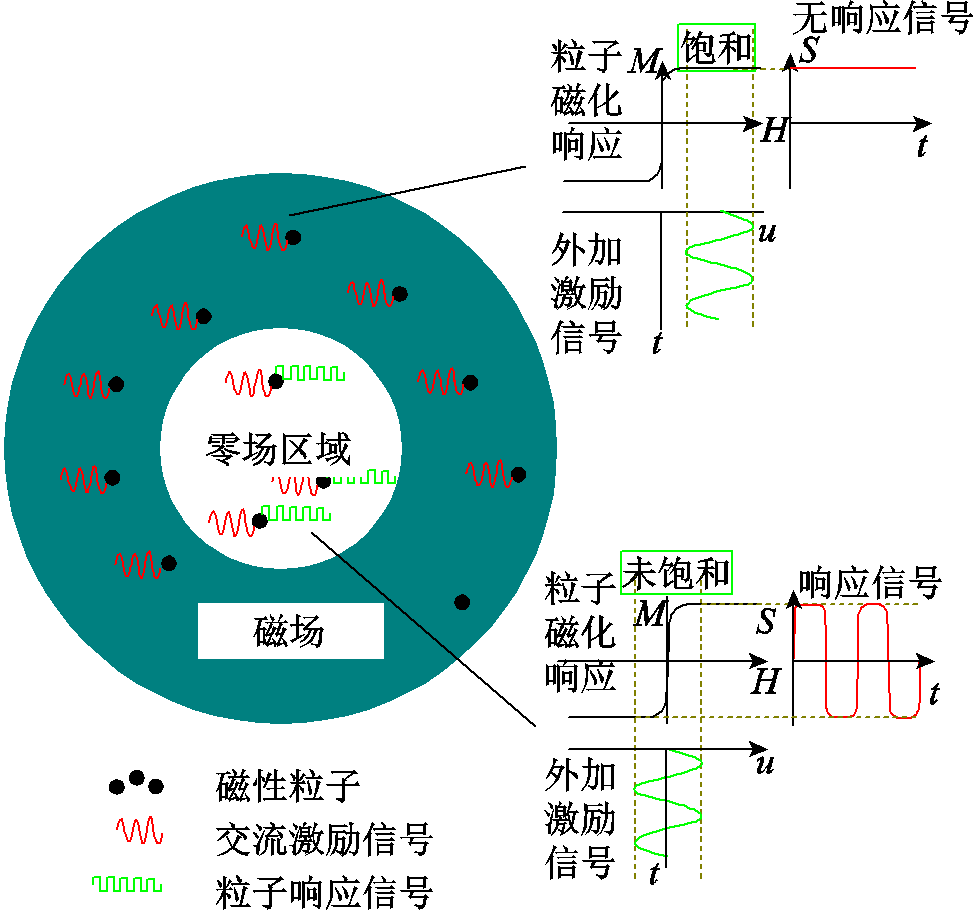
图1 MPI检测原理
Fig.1 Detection principle of MPI
摘要 磁性纳米粒子成像（MPI）是近年来兴起的一种医学成像方法，具有无电离辐射、毫秒级检测速度、亚毫米级成像精度的优势，其中线型零磁场扫描可实现被测物内部磁性纳米粒子分布的图像，在高精度成像、快速检测及动态监测方面具有重要的研究意义。针对磁性纳米粒子成像存在的系统检测孔径和检测精度问题，该文设计了一种开放式磁性纳米粒子断层线成像方法。开放式的系统结构扩大系统检测孔径，提出磁场线圈的电气驱动完成断层成像中零场线全周旋转，实现系统精准扫描。仿真计算和实验分析结果表明，该文设计的系统结构形成高度为200mm侧面开放的检测孔径，提出的电气驱动旋转零场线的方法形成的旋转角度误差小于0.025 9°，用于扫描的线型零磁场宽度不超过0.95mm，单次扫描时间为3.6ms。因此，该文设计的开放式磁性纳米粒子断层成像系统可以有效扩大检测孔径，同时实现亚毫米级精度成像及毫秒级检测速度。
关键词：磁性纳米粒子断层成像 线型零磁场 零场线旋转 开放式
磁性纳米粒子成像（Magnetic Particle Imaging，MPI）是一种新型成像技术[1]，将交变磁场下的超顺磁氧化铁纳米粒子作为示踪剂，利用其非线性磁化特性检测粒子浓度的时空分布图像。由于磁性纳米粒子对生物体具有无损伤特性，该技术具有多种潜在的医学用途，如血管造影[2-6]、干细胞跟踪[7-8]和肿瘤检测[9]等。最早利用磁性纳米粒子成像的是B.Gleich和J.Weizenecker[1]，他们于2005年建立了第一台MPI扫描设备并进行粒子浓度成像实验。之后P. W. Goodwill等于2010年提出了基于X-space投影的MPI重建方法[10-12]，使磁性粒子断层成像成为可能，该研究组使用钕铁硼磁铁产生零场线，建立基于零场线的三维MPI成像系统。该系统通过机械旋转的方式旋转被测物实现扫描并生成3D图像，获得单个投影图像的时间为3.15s[13]。J.Weizenecker等利用多个线圈产生旋转的零场线[14]，并利用驱动线圈使其沿垂直于零场线的方向移动。之后该研究小组对扫描仪结构进行改进[15-16]，提高了扫描仪的工作效率。改进后的扫描仪可产生旋转零场线，旋转角度误差为1.251°，零场线从0°旋转到180°所需时间为3.2ms[17]。因此，与机械旋转方式相比，通电线圈驱动零场线旋转可以提高数据采集效率，但基于该种方式采集数据的MPI系统多为封闭式系统，检测区域直径在3~12cm之间[18]，只能进行小型物体的检测。与此同时，T. F. Sattel[19]和A. Tonyushkin等建立了基于零场点扫描的单边的MPI 扫描器，该系统有效地扩大了检测区域的范围，可对待测物体进行多维成像[20]。但是这种单边的MPI 扫描仪与最初的封闭式扫描器设计相比，其空间分辨率表现出强烈的非均匀性。
因此，本文针对MPI系统检测孔径小，以及扩大检测孔径后带来的检测精度低等问题，提出一种开放式线型旋转零磁场磁性粒子检测系统，围绕磁性粒子断层成像，设计了线型零磁场的产生及旋转驱动方法。利用两组平行放置的麦克斯韦线圈生成零场线，形成开放式线型零磁场设计结构，有效地扩大了检测区域的范围。针对线型零磁场的旋转扫描问题，提出电气驱动旋转，精准控制线型旋转零磁场，实现高精度快速检测。
磁性纳米粒子在磁场环境下，根据磁场的分布具有明显的磁化特性表征，根据磁性纳米粒子的非线性磁化响应，可获得其分布图像。
磁性纳米粒子在磁场内的磁化特性如图1所示[1]，当外部磁场强度H为零（零场区域）时，磁性纳米粒子随外加正弦激励信号产生交变的响应信号，可被接收装置获得；当外部磁场为非零状态时，粒子磁化强度M为稳定状态，则接收装置无响应信号。将含有磁性纳米粒子的待测物放置在磁场区域中，可通过零磁场区域的响应信号S获得该点的粒子量，改变零磁场区域的位置可获得被测物成像平面内所有粒子浓度分布，进而获得携带磁性纳米粒子的被测物特性图像。
图1 MPI检测原理
Fig.1 Detection principle of MPI
完成磁性纳米粒子成像过程，首先系统要产生零场线。由毕奥-萨伐尔定律可知，如图2a所示的单个通电圆形线圈，在空间内任意一点P的磁场分布可用式（1）和式（2）表示[21-22]。磁场B可以分解为两个正交方向，Ba和Br分别为
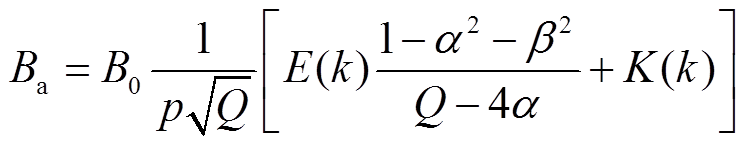（1）
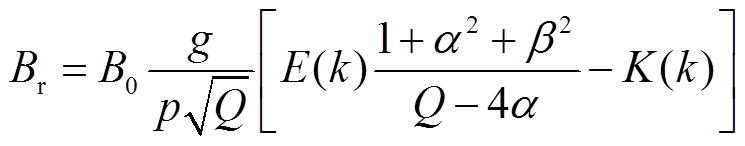（2）
其中
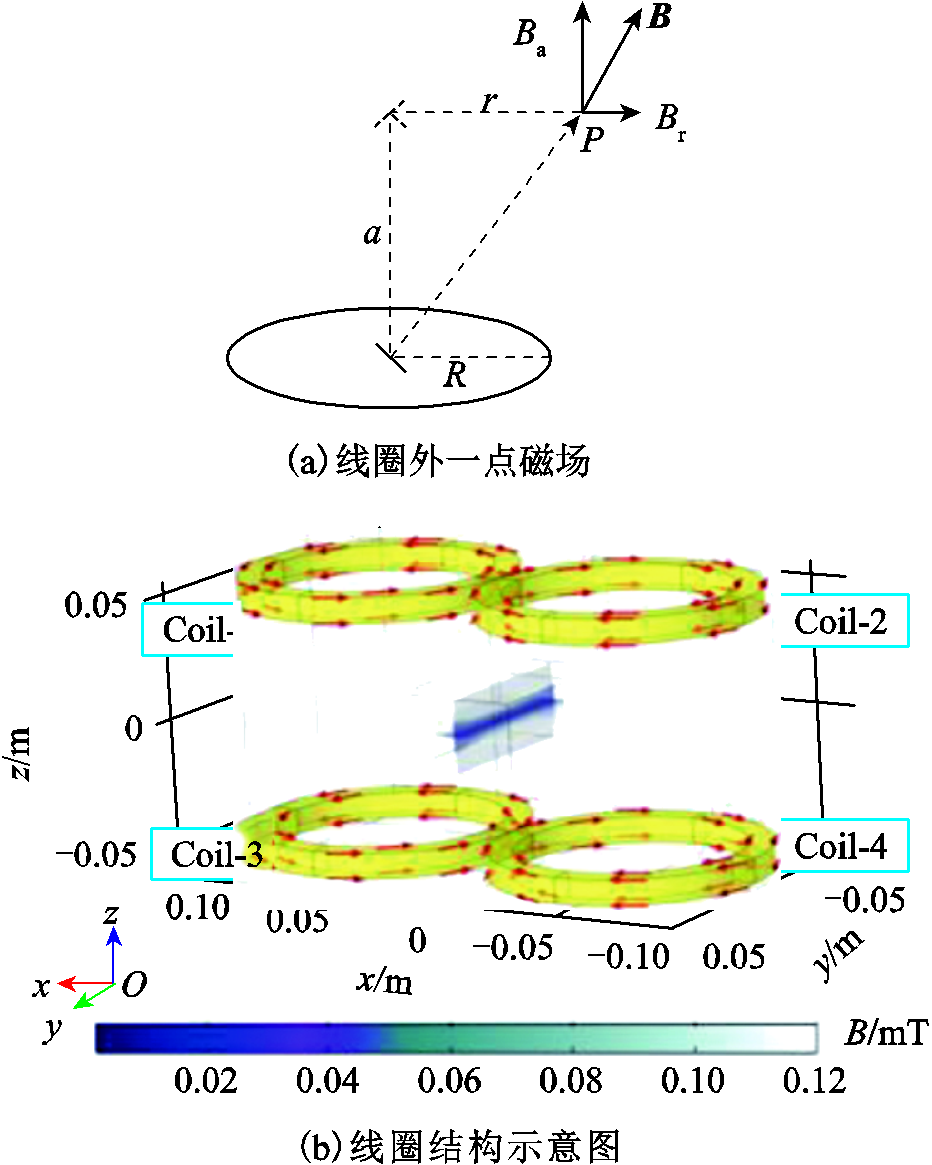
图2 选择场线圈结构
Fig.2 The structure of selection field coil
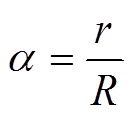
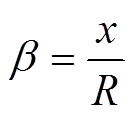
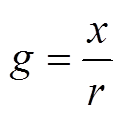Q=(1+α)2+β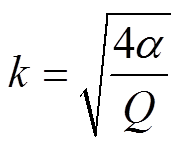
式中，Ba是磁场沿线圈轴向的分量；Br是与Ba垂直的半径方向的分量；E和K分别为椭圆积分的第一解和第二解；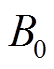
为线圈中心位置磁感应强度；p为常数，
。
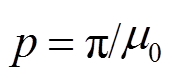四个圆形线圈按照如图2b的方式排布，Coil-1~Coil-4的线圈中心分别为（0.05, 0, 0.05），（-0.05, 0, 0.05），（0.05, 0, -0.05）和（-0.05, 0, -0.05），各线圈电流幅值相同，其中，Coil-1与Coil-3的电流方向相同，为逆时针方向，Coil-2与Coil-4方向相同，为顺时针方向。电流方向如图2b所示。线圈i在空间内一点P处的磁场B可以分解成3个正交分量Bi,a、Bi,rx、Bi,ry，其中，Bi,a是磁场沿线圈轴向的分量，Bi,rx是磁场沿x方向的分量，Bi,ry是磁场沿y方向的分量。因此，图2b所示的各线圈在y轴上的磁场分布有关系。
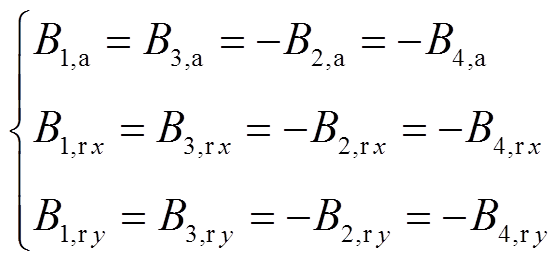（3）由上述关系可知，在y轴上的磁场B的所有分量之和为零。因此，该线圈结构在y轴上产生零场线，该线圈结构为选择场线圈。选择场线圈在x-y平面磁场分布表达式为
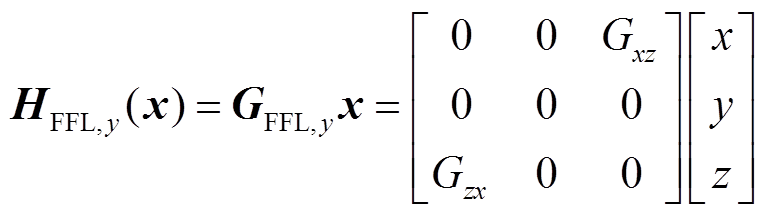（4）
式中，x为位置向量；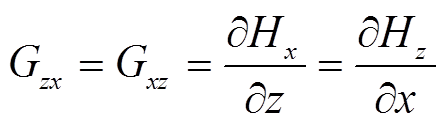
。
图3所示为圆形选择场线圈结构在空间内的磁场分布情况，图3a为x-z平面内的磁场分布，图3b为x-y平面内的磁场分布。由磁场分布结果可知，圆形线圈结构会在y轴方向产生零场线，但x-y平面上磁感应强度沿y方向随着距原点的距离增大而减小，导致零场线方向上磁场梯度非均匀变化，使得线型零磁场内粒子分布的检测精度降低。
图3 圆形选择场线圈的磁场分布
Fig.3 Magnetic field distribution of circular selection field coil
矩形线圈的边相当于四条直导线，与导线垂直距离相等位置的磁场大小相同，在一定范围内矩形线圈在与之平行的轴上产生的磁场强度不变。因此，本文提出用矩形线圈代替圆形线圈，改进零场线的精度和均匀性，结果如图4所示，图4a为改进后的生成零场线的线圈，图4b为x-y平面（z=0）产生的磁场分布。
矩形线圈产生的线型零磁场均匀度优于圆形线圈，设计矩形线圈作为开放式磁性纳米粒子成像系统中的选择场线圈，即Coil-y。
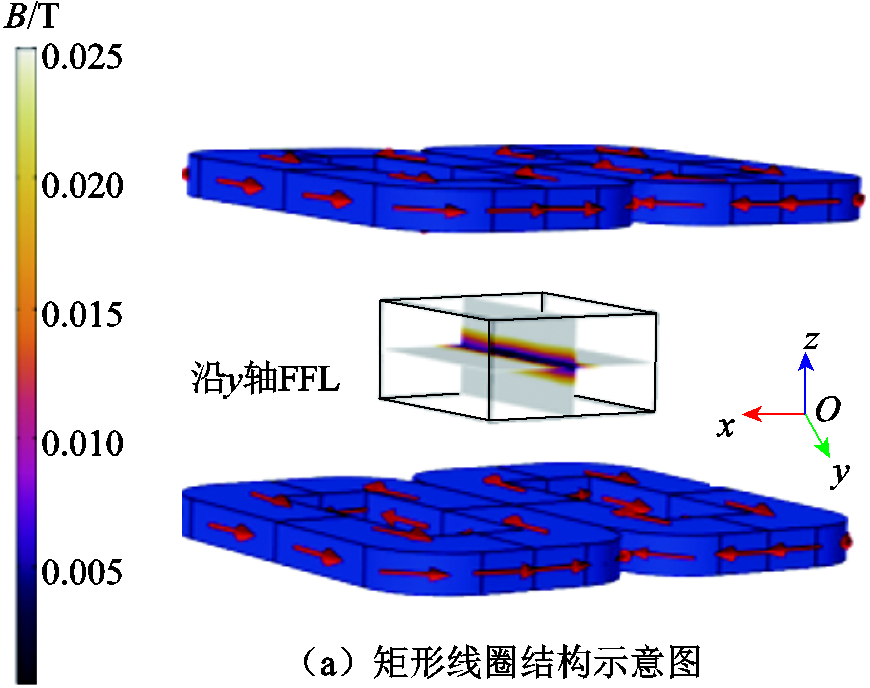
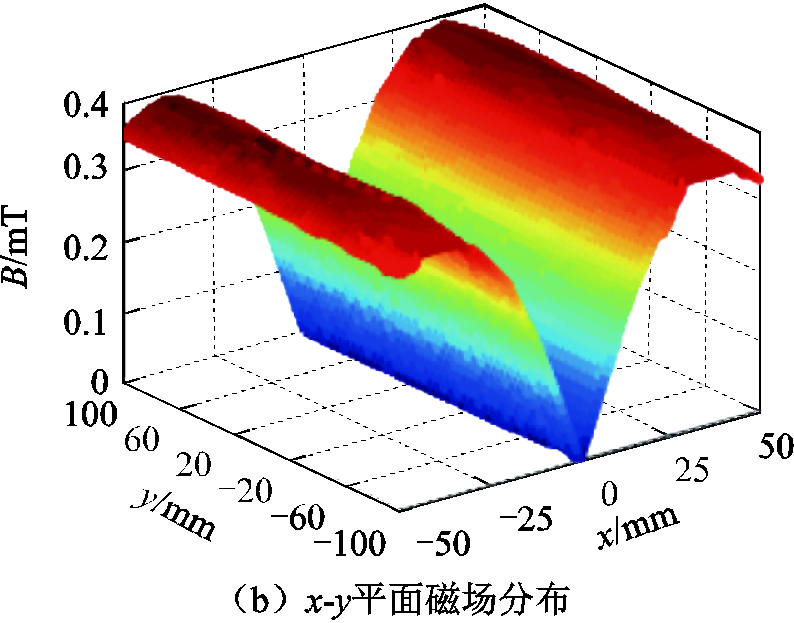
图4 Coil-y生成零场线结果图
Fig.4 Coil-y generates the result graph of field-free line
选择场线圈在x-y平面上磁场分布为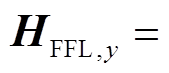
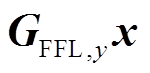。为获得全周各角度零场线上的磁性纳米粒子检测信号，设计磁场旋转方法如式（5）所示。
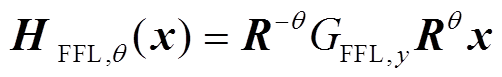（5）其中
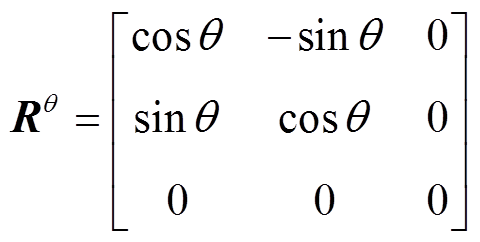
式中，Rq为x-y平面上的旋转矩阵；q为零场线与y轴形成的旋转角度。整理式（5），可得
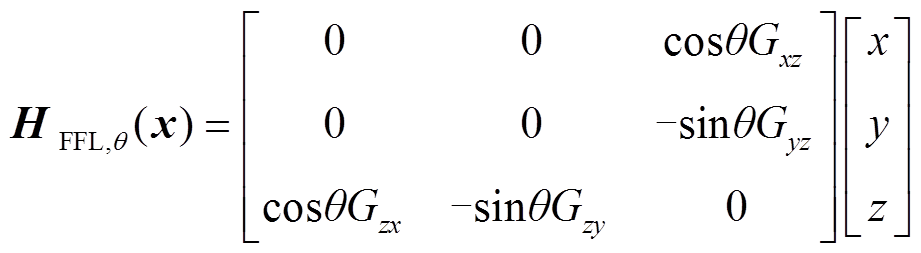（6）线型旋转零磁场HFFL,θ可表示为
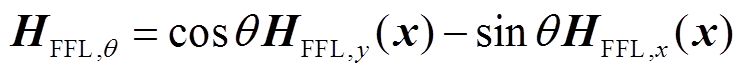（7）
式中，HFFL,y(x)和HFFL,x(x)分别为生成沿y轴和x轴方向零场线时x-y面的磁场分布。
因此，在x方向加入一组双平面梯度线圈Coil-x，产生沿x轴方向的零场线，对原有沿y轴的零磁场进行拉动。Coil-x与Coil-y相互垂直放置，通过激励电流的控制改变x-y平面的磁场分布，实现零磁场在x-y平面内旋转，开放式磁性粒子断层成像系统的整体结构如图5所示。
该结构对磁场的拉动效果如图6所示，图6a和图6b分别为Coil-x和Coil-y单独作用时x-y平面的磁通密度分布，图6c为Coil-x和Coil-y共同作用时x-y平面的磁通密度分布。从结果得出，该结构可实现线型零磁场在x-y平面内电气驱动旋转。
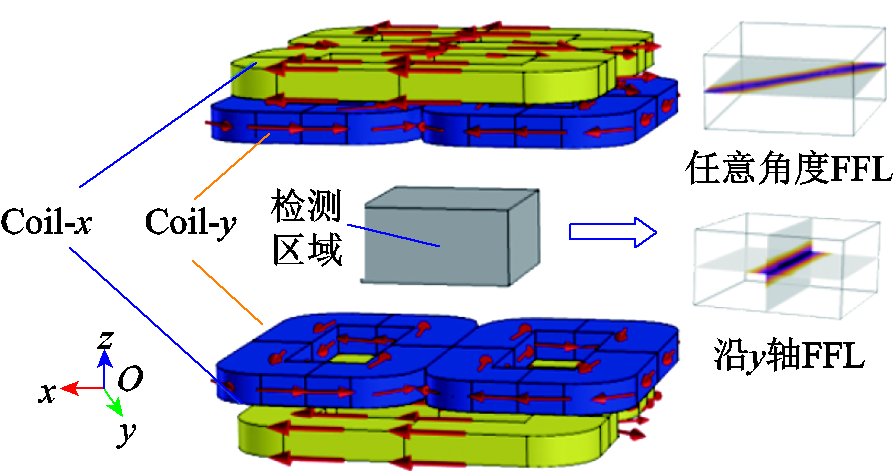
图5 开放式磁性粒子断层成像系统旋转结构
Fig.5 Open bore magnetic particle tomography system rotating structure
图6 x-y平面磁通密度分布变化
Fig.6 x-y plane magnetic flux density distribution change
在Coil-x、Coil-y中分别通入Ix(θ)=-Ix0 sinθ和Iy(θ)=Iy0 cosθ时会在x-y平面内形成多角度线型零磁场，Ix0和Iy0为两组线圈电流的幅值。通过控制线圈中的电流实现线型零磁场在x-y平面内的连续旋转，获得多角度零磁场上的磁性纳米粒子信号。
线圈中电流的幅值影响x-y平面磁场的梯度，从而影响系统检测精度。在磁性粒子检测中，用式（8）表示磁场梯度与检测精度之间的关系[23]。
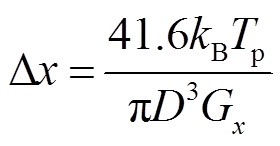（8）
式中，kB为玻耳兹曼常数，kB=1.38×10-23；Tp为粒子温度，一般取305K。当磁性纳米粒子的粒径一定时，系统的检测精度仅与磁场梯度Gx相关。选取磁性纳米粒子的粒径为40nm，磁场梯度与检测精度的关系为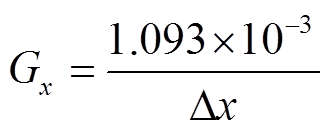
。因此，若要实现Dx≤1mm的亚毫米级检测，需要磁场梯度Gx≥1.093T/m。
由于Coil-x、Coil-y与x-y平面的距离不同，为准确控制零场线的旋转角度，需要Coil-x与Coil-y分别激励时在x-y平面内产生的磁场梯度相同。探究两组线圈分别激励时，产生的磁场梯度（Gxz与Gyz）与电流的关系如图7所示。
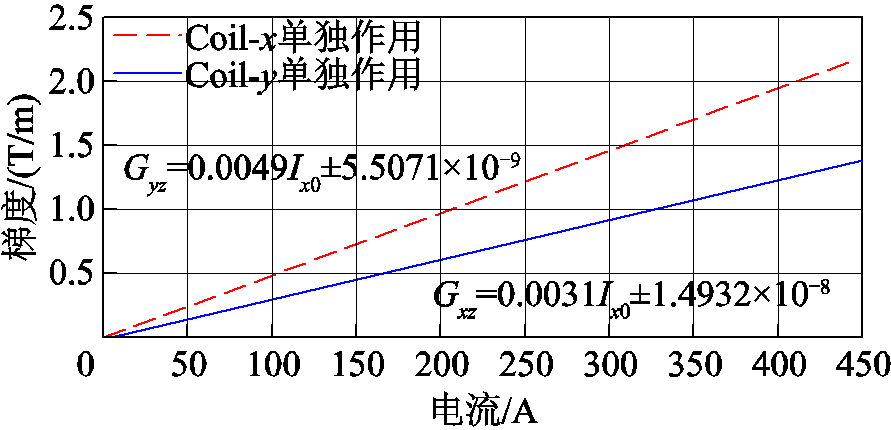
图7 x-y平面的磁场梯度与电流之间关系
Fig.7 Relationship between magnetic field gradient and current in x-y plane
磁场梯度与线圈通入电流呈线性关系，由于Coil-y距离x-y平面距离更近，在相同电流下产生的磁场梯度Gyz更大。当Gxz=Gyz=1.093T/m时，Coil-y中峰值电流应为223.06A，Coil-x中峰值电流应为352.58A，即Ix0=352.58A和Iy0=223.06A。
建立旋转角度与采集时间的关系，令θ=2πfst，通过调整激励电流频率与采集时间间隔，实现全周多角度零磁场上磁性粒子信号的采集。因此，Coil-x和 Coil-y通入图8所示电流。其中
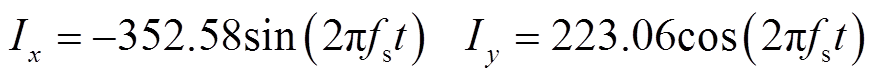
按照上述激励方式两组线圈在40mm×40mm的x-y平面内形成的磁场模分布如图9所示。
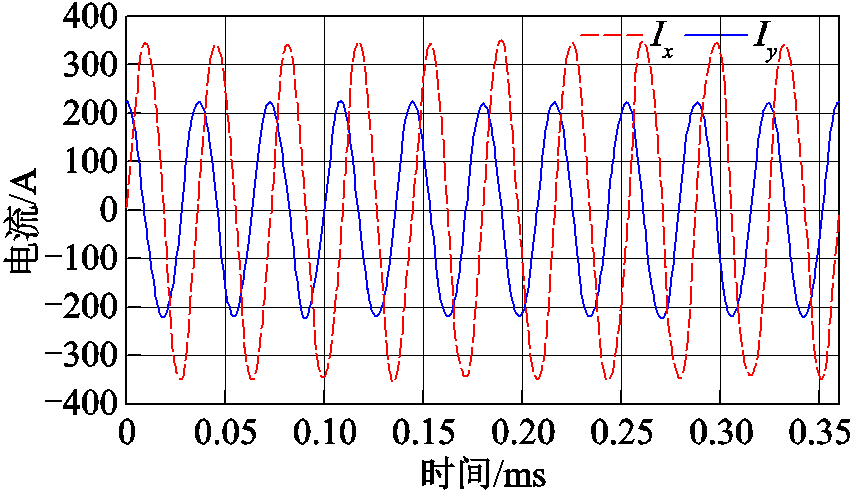
图8 线圈电流
Fig.8 Coil current
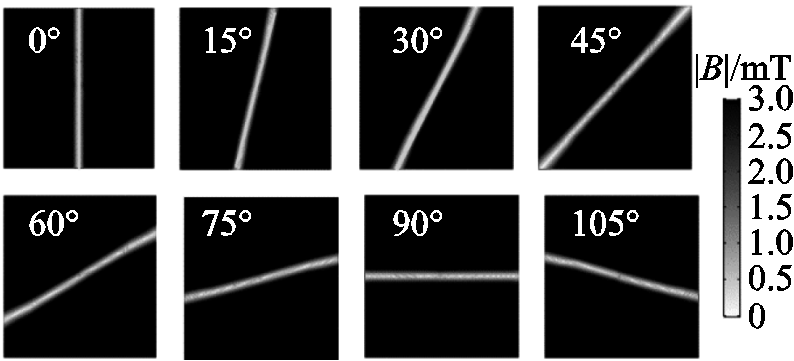
图9 零场线旋转结果
Fig. 9 Results of the FFL field rotation
由结果可知，上述激励方式在x-y平面内形成多角度零场线，实现零场线在平面内的旋转扫描。
利用图10所示的线型零磁场旋转结构进行仿真分析，系统各线圈参数值见表1。系统整体外部尺寸为280mm×240mm×285mm，检测区域大小为240mm×240mm×200mm。
表1 开放式检测系统线圈参数值
Tab.1 Coil properties for open bore magnetic particle tomography system
线圈名称匝数外部尺寸(x×y)/mm 截面尺寸(水平×竖直)/mm Coil-x148240×14045×20 Coil-y125280×12045×20
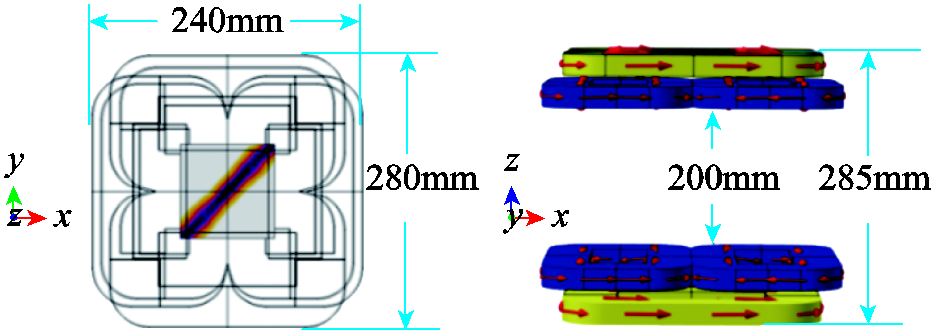
图10 开放式MPI系统整体结构
Fig.10 Coil geometry and dimensions for open bore magnetic particle tomography system
线圈Coil-x与Coil-y通入图8所示电流，其中，θ=2πfst，令fs=2500/9Hz，可实现0.01ms零场线旋转1º。因此，设计数据采集时间间隔为0.01ms，全周采集时间为3.6ms。开放式MPI系统所有线圈结构都平行放置，侧面为开放式，因此，系统增加检测线圈等其他结构后不会影响系统的开放性。
3.2.1 旋转角度误差
投影重建为多个角度的投影图像相叠加后形成的图像，因此线型零磁场旋转角度的准确性影响投影重建的精度。定义旋转角误差为零场线与y轴所成的旋转角θ和预期旋转角度θideal之间差值，即：Δθ=θ-θideal。计算0°~90°的旋转角度误差，结果如图11所示。
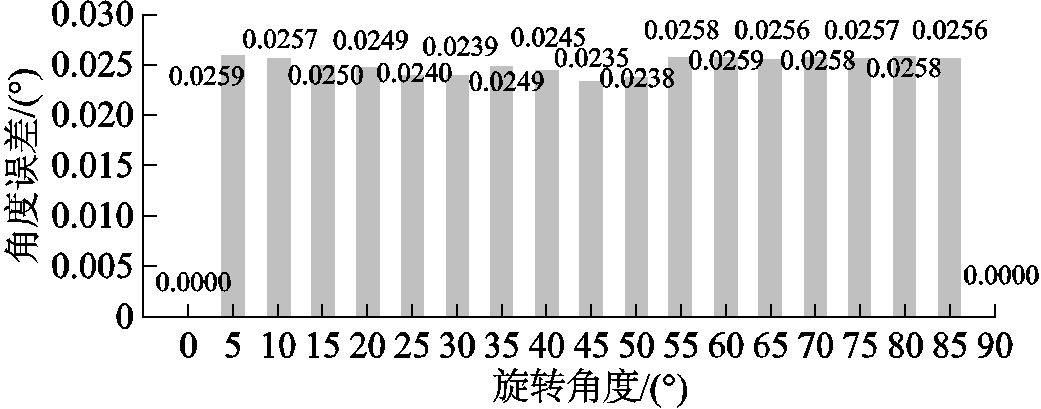
图11 零场线的旋转角度误差
Fig.11 FFL rotation angle error
由结果可知，电气驱动线型零磁场旋转形成的角度误差最大值为0.025 9°，数据采集的间隔为1°，形成的误差为10-2量级，可以通过重建算法进行校正，因此，提出的电气驱动零场线旋转的方式可以实现零场线准确旋转。
3.2.2 零场线平均偏差
磁性纳米粒子成像中，在激励场作用下只有处于非饱和状态的磁性纳米粒子才会产生响应信号。磁性纳米粒子的饱和磁场强度定义为粒子磁化强度达到最大值的90%时的磁场强度[17]，即
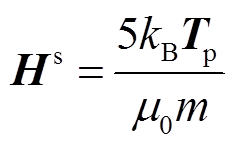（9）
式中，μ0为真空磁导率，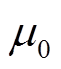
=4π×10-7H/m；m为粒子磁矩，m=VMs，V为粒子体积等于πD3/6，D为粒子直径，Ms为粒子核饱和磁化强度，
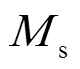=0.6T/μ0[26]。因此，磁性纳米粒子的粒径为40nm时，粒子达到饱和的磁场强度为1 046.69A/m。
利用基于零场线扫描的磁性粒子动态成像中磁场质量的评价方法[17]，使用零场线平均偏差εFFL(θ)对生成线型旋转零磁场的质量进行评价。
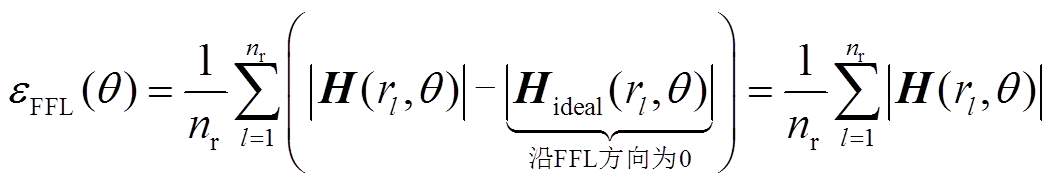（10）式中，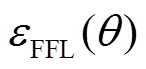
为磁场强度沿零场线方向在特定空间位置的绝对值大小的平均值；r为该位置距扫描仪中心位置的距离；θ为零场线与y轴形成的旋转角。x-y平面40mm×40mm范围内的各角度零磁场平均偏差计算结果如图12所示。
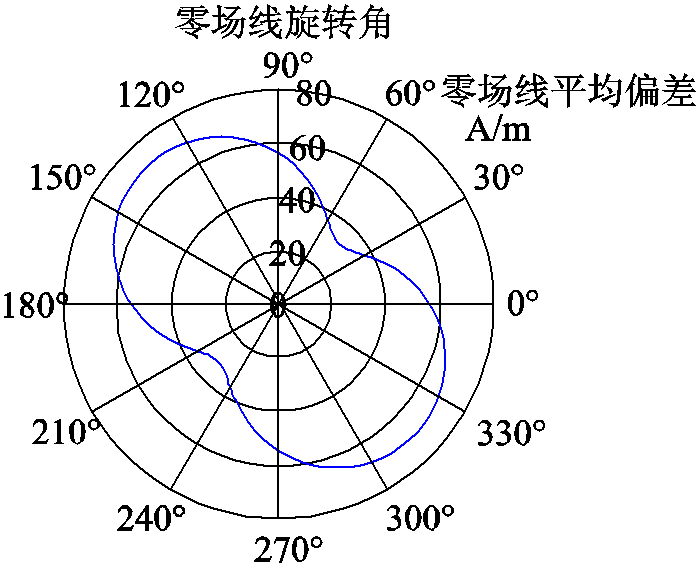
图12 各角度的零场线平均偏差
Fig.12 Mean FFL deviation for each rotation angle
零场线平均偏差关于原点中心对称，旋转角度为135°和315°时出现最大值，但最大值不超过70.422 5A/m，远小于磁性纳米粒子饱和所需的磁场强度。因此，在线型零磁场区域的磁性纳米粒子能有效产生响应信号，设计的旋转零磁场满足磁性纳米粒子成像的需求。
3.2.3 线型旋转零磁场精细度评价
线型旋转零磁场的精细程度决定了系统的检测精度，因此讨论各旋转角度下线型零磁场的宽度，确定线型旋转零磁场可达到的检测精度。线型零磁场宽度定义为垂直于零场线方向且磁场强度小于1 046.69A/m的范围，如图13所示。
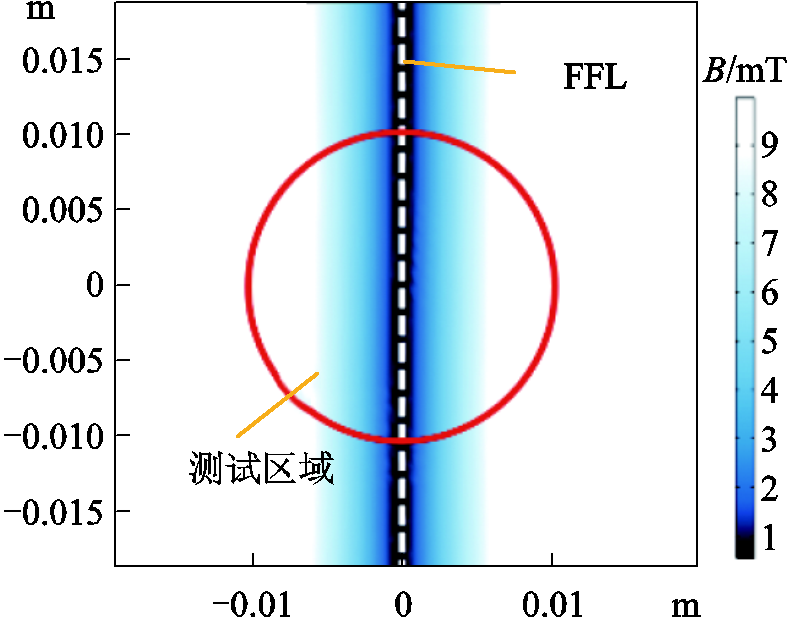
图13 线型旋转零磁场宽度评价示意图
Fig.13 Schematic diagram of linear rotating FFL’s width evaluation
检测各旋转角度下测试区域内的磁场强度，确定测试区域内各角度线型零磁场对应的线型零磁场宽度的平均值，结果如图14所示。
由结果可以得出，本文设计的线型旋转零磁场宽度的最大值为0.948 6mm，可分辨直径小于1mm的被测目标。因此，所设计的线型旋转零磁场可达到亚毫米级的检测精度。
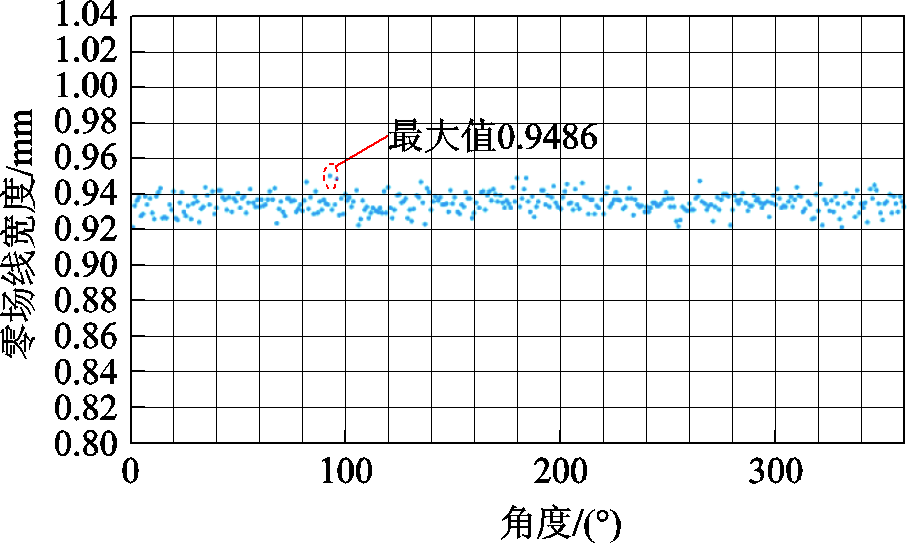
图14 各角度零场线宽度的平均值
Fig.14 Average of the FFL width of each rotation angle
建立如图15的开放式MPI结构，图15a为线型零磁场生成系统，图15b为线圈结构，图15c为测量平面中心位置的测量点示意图。考虑到实际情况，本文利用线径为0.1mm、1 500股的利兹线制作线圈，匝数为72匝，上、下选择场线圈间距离为100mm。
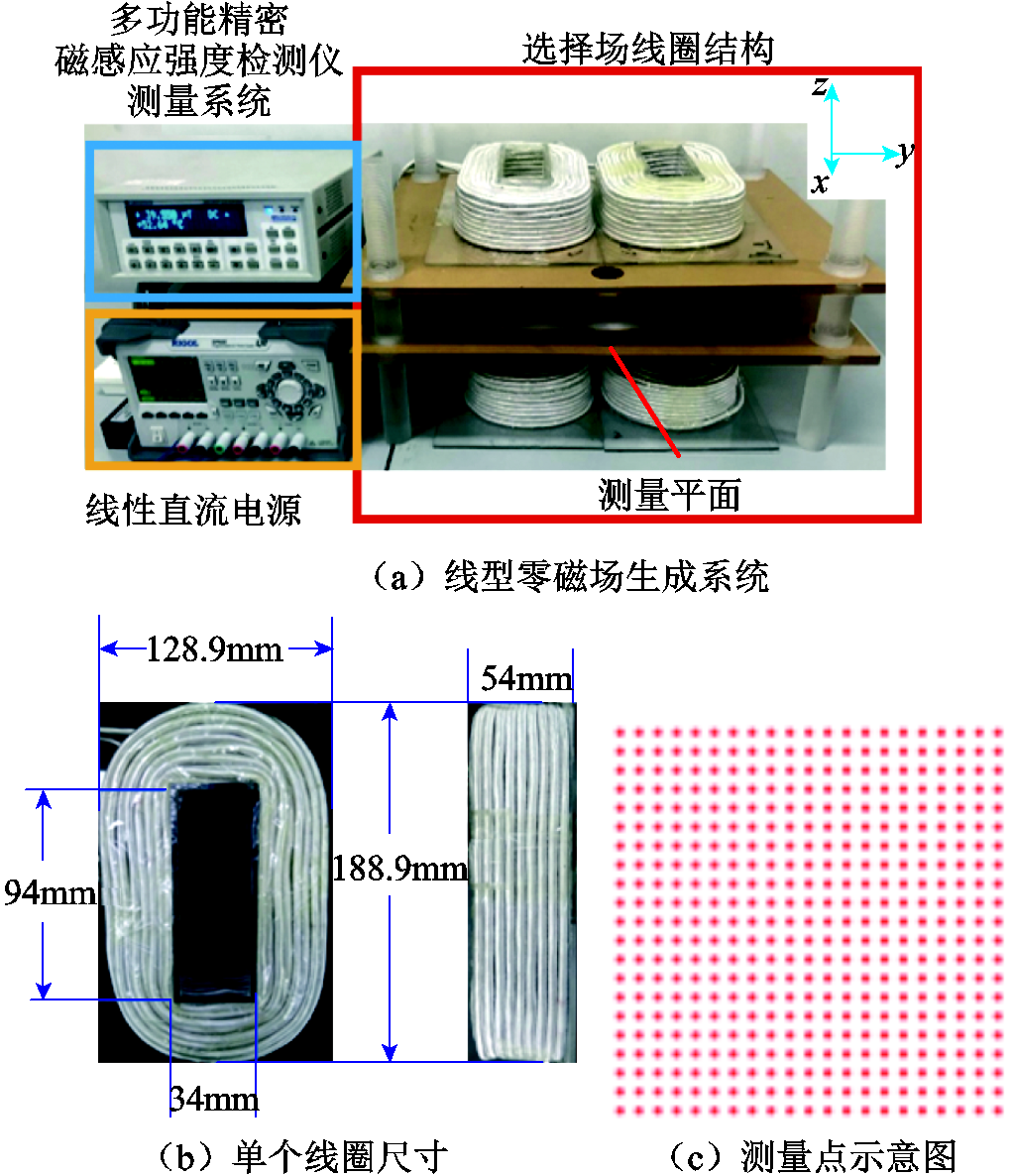
图15 开放式MPI磁场系统结构
Fig.15 Open bore MPI system
ROGOL DP832 可编程线性直流电源作为系统电源为选择场线圈提供电流。上述线圈中通入3A电流，利用多功能精密磁感应强度检测仪测量系统产生的磁场分布。选取测量平面中心位置150mm× 150mm的范围作为检测区域，以平面中心为原点建立直角坐标系，x、y的坐标范围为-75~75mm。磁感应强度的部分测量结果见表2，利用x-y平面磁感应强度测量值绘制二维磁感应强度分布图像，结果如图16所示。
表2 x-y平面磁感应强度
Tab.2 x-y plane magnetic induction （单位：mT）
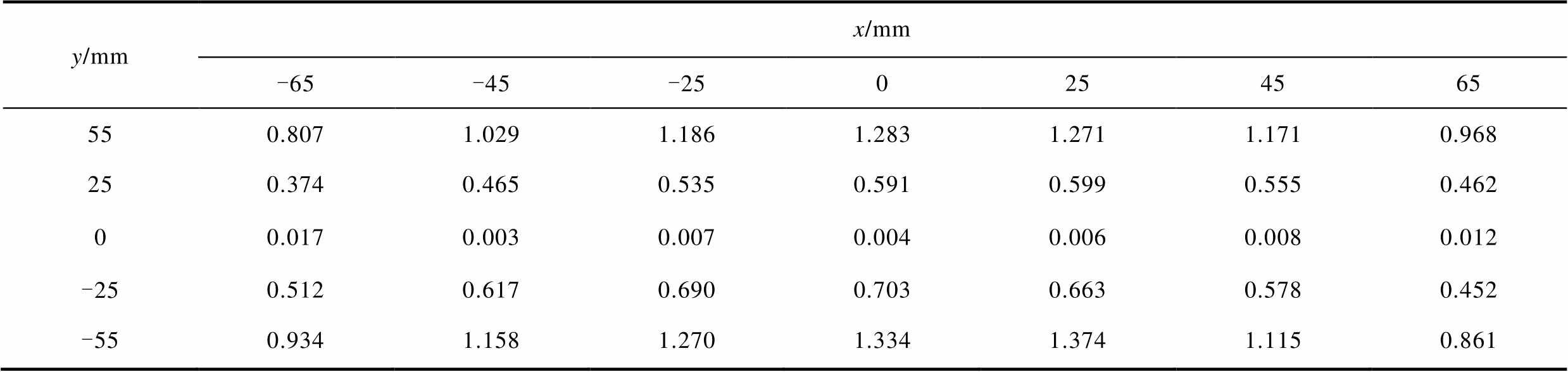
y/mmx/mm -65-45-250254565 550.8071.0291.1861.2831.2711.1710.968 250.3740.4650.5350.5910.5990.5550.462 00.0170.0030.0070.0040.0060.0080.012 -250.5120.6170.6900.7030.6630.5780.452 -550.9341.1581.2701.3341.3741.1150.861
图16 x-y平面磁场分布
Fig.16 x-y plane magnetic field distribution
根据测量结果可以看出，设计的开放式MPI系统的选择场线圈结构可以在x-y平面产生零场线。计算零场线方向的磁场梯度，研究零场线均匀性，结果如图17所示。
系统选择场线圈产生的零场线在中心区域的均匀性较好，有效长度可达到75mm，因此，系统的成像区域可达到75mm×75mm。由于实际测量时的线圈电流仅为3A，使形成的磁场梯度较小，但磁场梯度与电流之间呈线性关系，因此，通过增大线圈电流即可提高磁场梯度。
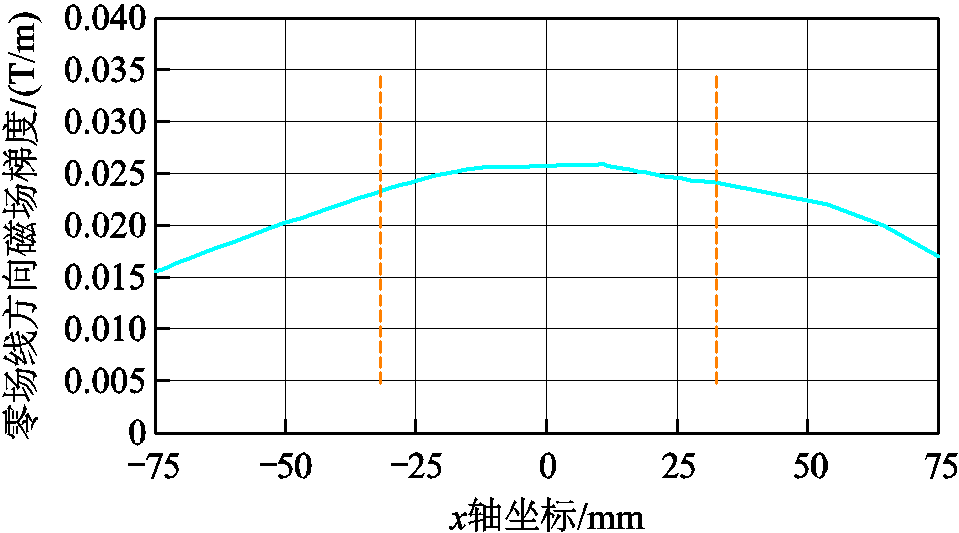
图17 磁场梯度变化
Fig.17 Magnetic gradient variation
利用建立的开放式磁性纳米粒子磁体系统，并结合仿真进行成像实验。
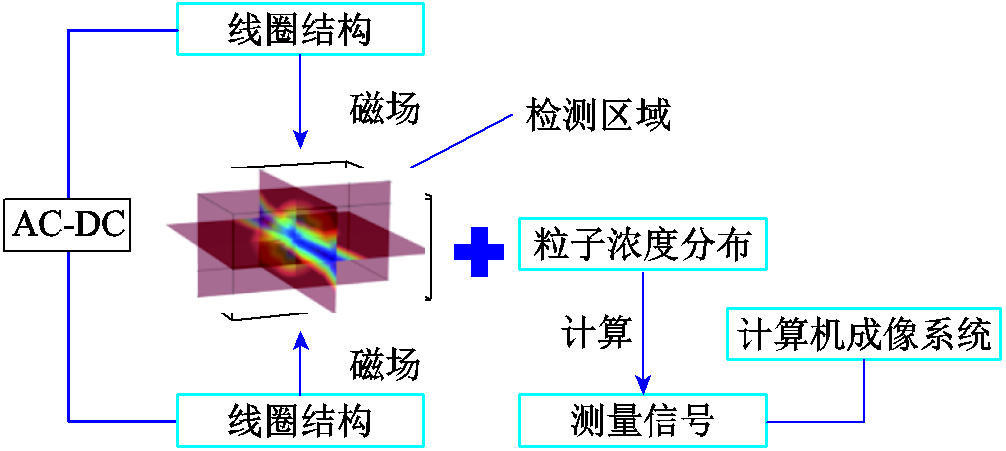
图18 成像过程示意图
Fig.18 Schematic diagram of the imaging process
实验过程如下：首先，建立三维开放式磁性纳米粒子成像系统模型，选定成像区域，利用有限元法计算出该区域内各时刻的磁场强度[24-25]；然后，建立粒子浓度分布模型，通过式（11）计算得到粒子信号；最后，利用粒子信号进行图像重建。
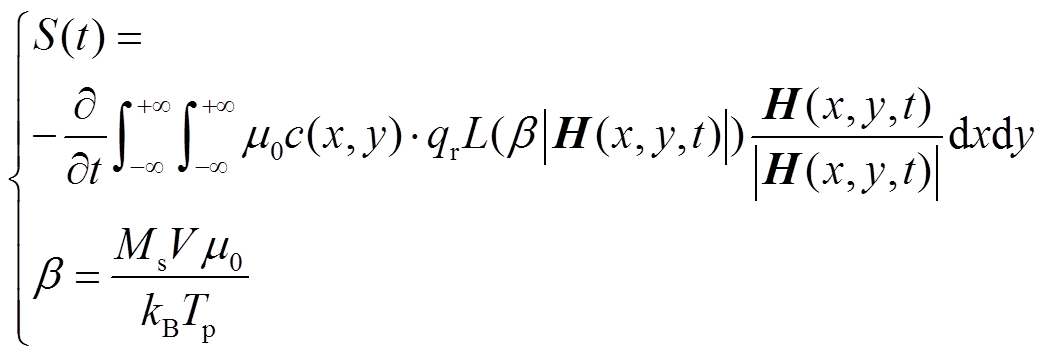（11）式中，μ0为真空磁导率；c(x, y) 为磁性粒子的浓度分布；L(·)是郎之万函数；H(x,y,t) 为磁场强度；Ms为饱和磁化强度，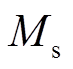
=0.6T/μ0[26]；V为磁性粒子体积；qr为线圈灵敏度。本文中粒子直径为40nm。
根据仿真实验得到的粒子信号，利用投影重建算法分别对不同大小、不同位置的磁性粒子浓度模型，以及多个目标的粒子浓度模型进行成像。单目标粒子浓度模型的成像结果见表3。
表3 单目标磁性粒子浓度模型成像结果
Tab.3 x-y plane magnetic induction
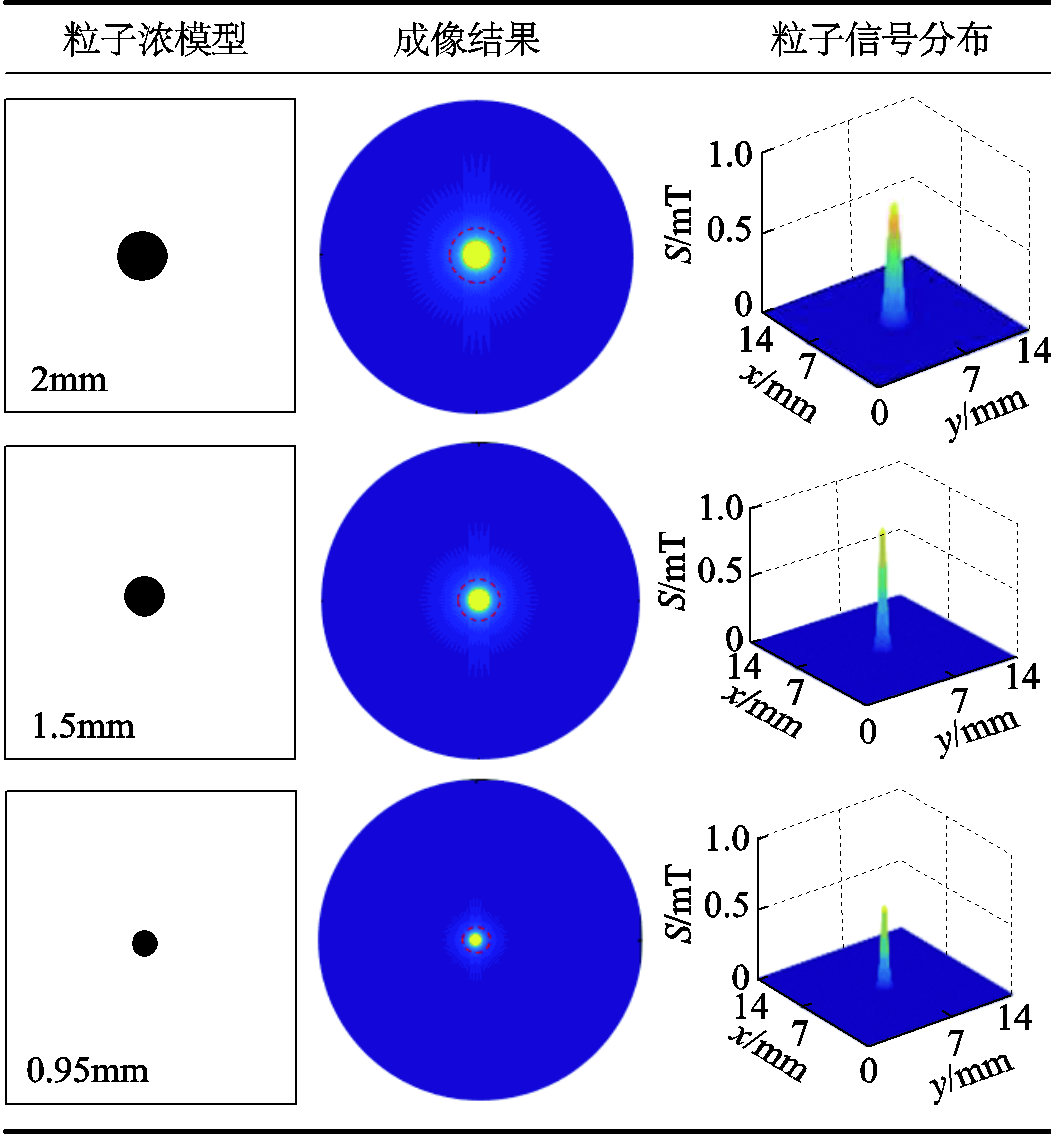
由成像结果可以得出，本文建立的开放式磁性纳米粒子成像系统可以分辨出不同大小的粒子浓度模型，对于0.95mm的被测物可以清楚分辨。粒子信号能量集中在中心区域，大小与粒子浓度正相关。
研究系统对不同大小、不同位置的多个目标的粒子浓度模型的分辨能力，系统成像结果如图19所示。
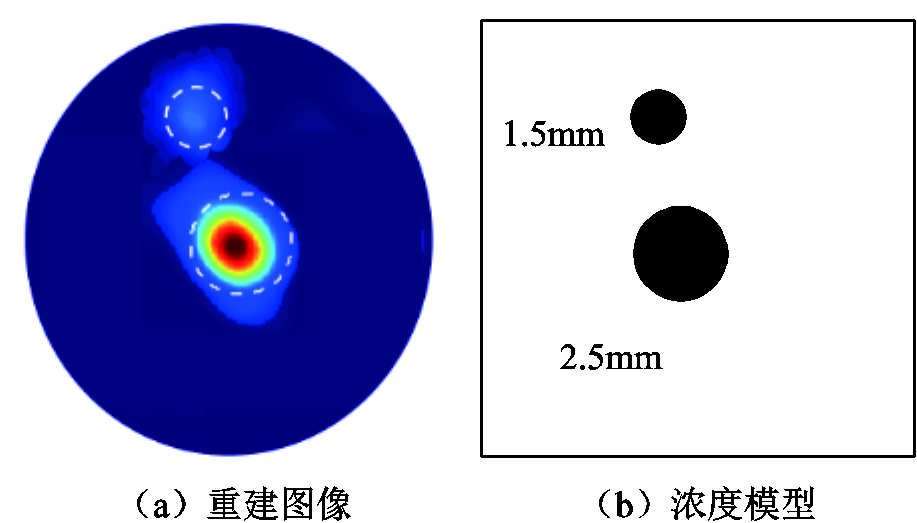
图19 多目标磁性粒子浓度模型成像结果
Fig.19 Multi-target magnetic particle concentration model imaging results
本文建立的开放式磁性纳米粒子成像系统可以分辨出不同大小、不同位置的成像目标。处于成像区域中心位置的粒子更容易被分辨，伪影较少，中心成像区域的成像分辨率可以达到0.95mm，处于边缘位置的粒子重建后的图像边缘模糊。
本文设计了开放式磁性粒子断层成像所需的线型旋转零磁场，将所有线圈结构平行放置，设计开放式系统结构，扩大系统检测孔径，设计磁场线圈的电气驱动方式完成断层成像中全周旋转扫描，并完成部分系统的搭建与磁场测量。仿真计算和实验结果表明，在零场线上的磁性纳米粒子能有效产生响应信号，线型零磁场旋转形成的角度误差在10-2数量级，可实现零场线的精准扫描。同时该系统可以分辨不同大小、不同形状、不同位置的被测物，对于0.95mm大小的被测物图像边缘清晰。因此，本文设计的线型旋转零磁场可以满足磁性粒子断层成像需求，提出的开放式线圈结构可用于磁性纳米粒子断层成像。
参考文献
[1] Gleich B, Weizenecker J. Tomographic imaging using the nonlinear response of magnetic particles[J]. Nature, 2005, 435(7046): 1214-1217.
[2] Gleich B, Weizenecker J, Rahmer J, et al. Three-dimensional real-time in vivo magnetic particle imaging[J]. Physics in Medicine and Biology, 2009, 54(5): L1- L10.
[3] Haegele J, Rahmer J, Gleich B, et al. Magnetic particle imaging: visualization of instruments for cardiovascular intervention[J]. Radiology, 2012, 265(3): 933-938.
[4] Rahmer J, Wirtz D, Bontus C, et al. Interactive magnetic catheter steering with 3D real-time feedback using multi-color magnetic particle imaging[J]. IEEE Transactions on Medical Imaging, 2017, 36(7): 1449-1456.
[5] Vaalma S, Rahmer J, Panagiotopoulos N, et al. Magnetic particle imaging: experimental quantification of vascular stenosis using stationary stenosis phantoms[J]. Plos One, 2017, 12(1): e0168902.
[6] Salamon J, Hofmann M, Jung C, et al. Magnetic particle magnetic resonance imaging: in-vitro MPI-guided real time catheter tracking and 4D angioplasty using a road map and blood pool tracer approach[J]. Plos One, 2016, 11(6): e0156899.
[7] Zheng Bo, See M P V, Yu E, et al. Quantitative magnetic particle imaging monitors the transplantation, bio-distribution, and clearance of stem cells in vivo[J]. Theranostics, 2016, 6(3): 291-301.
[8] Them K, Salamon J, Szwargulski P, et al. Increasing the sensitivity for stem cell monitoring in system-function based magnetic particle imaging[J]. Physics in Medicine and Biology, 2016, 61(9): 3279-3290.
[9] Yu E Y, Bishop M, Zheng Bo, et al. Magnetic particle imaging: a novel in vivo imaging platform for cancer detection[J]. Nano Letters. 2017, 17(3): 1648-1654.
[10] Goodwill P W, Conolly S M. The X-space formulation of the magnetic particle imaging process:1-D signal, resolution, bandwidth, SNR, and magneto stimulation[J]. IEEE Transactions on Medical Imaging, 2010, 29(11) : 1851-1859．
[11] Goodwill P W, Conolly S M. Multidimensional X-space magnetic particle imaging[J]. IEEE Transactions on Medical Imaging, 2011, 30(9): 1581-1590.
[12] Goodwill P W, Konkle J J, Zheng B, et al. Projection x-space magnetic particle imaging[J]. IEEE Transactions on Medical Imaging. 2012, 31(5): 1076-1085.
[13] Konkle J J, Goodwill P W, Saritas E U, et al. Twenty-fold acceleration of 3D projection reconstruction MPI[J]. Biomed Tech (Berl), 2013, 58(6): 565-576.
[14] Weizenecker J, Gleich B, Borgert．Magnetic particle imaging using a field free line[J]. Journal of Physics D: Applied Physics, 2008, 41(10) : 105009.
[15] Knopp T, Erbe M, Biederer S, et al. Efficient generation of a magnetic field-free line[J]. Medical Physics, 2010, 37(7): 3538-3540.
[16] Erbe M, Knopp T, Sattel T F, et al. Experimental generation of an arbitrarily rotated field-free line for the use in magnetic particle imaging[J]. Medical Physics, 2011, 38(9): 5200.
[17] Erbe M. Field free line magnetic particle imaging[M]. Südost: Springer Fachmedien Wiesbaden, 2014.
[18] Knopp T, Gdaniec, N, Möddel M, et al. Magnetic particle imaging: from proof of principle to preclinical applications[J]. Physics in Medicine and Biology, 2017, 62(14): R124-R178.
[19] Sattel T F, Knopp T, Biederer S, et al．Single-sided device for magnetic particle imaging[J]. Journal of Physics D: Applied Physics, 2009, 42(1): 1-5．
[20] Tonyushkin A. Single-sided field-free line generator magnet for multi-dimensional magnetic particle imaging[J]. IEEE Transactions on Magnetics, 2017, 53(9): 5300506.
[21] Lü Xing, Wang Zheng, Yang Wenhui. Field free line generation for magnetic particle imaging based on the mirror rule[C]//IEEE International Conference on Biomedical Engineering & Informatics, Hangzhou, 2014, DOI: 110.1109/BMEI.2013.6746904.
[22] 雷银照. 用坐标变换方法求解倾斜圆环线圈时谐电磁场的解析解[J]. 电工技术学报, 2010, 25(4): 15-18.Lei Yinzhao. Analytical solution to time-harmonic electromagnetic field of tilted circular coil by the coordinate transformation method[J]. Transactions of China Electrotechnical Society, 2010, 25(4): 15-18.
[23] Knopp T, Buzug T M. Magnetic particle imaging[M]. Südost: Springer Fachmedien Wiesbaden, 2012.
[24] 陈德智, 姜贺, 张哲, 等. 有限元法的一种数据结构[J]. 电工技术学报, 2015, 30(1): 1-7. Chen Dezhi, Jiang He, Zhang Zhe, et al. A data structure for finite element method[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 1-7.
[25] 王泽忠, 石雨鑫. 三维电场多极子曲面边界元方法研究[J]. 电工技术学报, 2018, 33(24): 5797-5804. Wang Zezhong, Shi Yuxin. Fast multipole curved boundary element method for 3D electrostatic field[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5797-5804.
[26] Rahmer J, Weizenecker J, Gleich B, et al. Signal encoding in magnetic particle imaging: properties of the system function[J]. BMC Medical Imaging, 2009, 9(1): 1-21.
Electronically Rotated Field-Free Line Generation for Open Bore Magnetic Particle Tomography Imaging
Abstract Magnetic nanoparticle imaging (MPI) is a new detection technology. It has the advantages of safety, fast detection and high accuracy in imaging. Field-free line scanning can image the magnetic nanoparticles distribution inside the measured object, which has important research significance. Due to small detection area and accuracy in the MPI, here an open bore MPI method is proposed. The field-free line (FFL) and its rotation mode for open magnetic particle tomography are studied. The way of the electric drive is designed to realize the rotation of FFL under the open structure. The simulation results show that the detection aperture of the system structure is 200mm high and leaving sides open，the rotation angle error of field-free line is less than 0.025 9°, the width of FFL is less than 0.95mm, single scan time is 3.6ms. The open bore MPI system designed in this paper effectively expands the detection aperture and fitting the submillimeter precision to image the magnetic particle distribution and millisecond detection speed.
keywords：Magnetic nanoparticles tomography, field-free line, field-free line rotation, open bore
中图分类号：TM153
DOI：10.19595/j.cnki.1000-6753.tces.191226
祖婉妮 女，1994年生，博士研究生，研究方向为医学电磁工程。E-mail：1193136339@qq.com
柯 丽 女，1979年生，教授，博士生导师，研究方向为生物电磁成像。E-mail：keli@aut.edu.com（通信作者）
国家自然科学基金（51377109）和辽宁省自然科学基金（2019-ZD-0204）资助项目。
收稿日期2019-09-27
改稿日期 2019-11-18
（编辑 郭丽军）