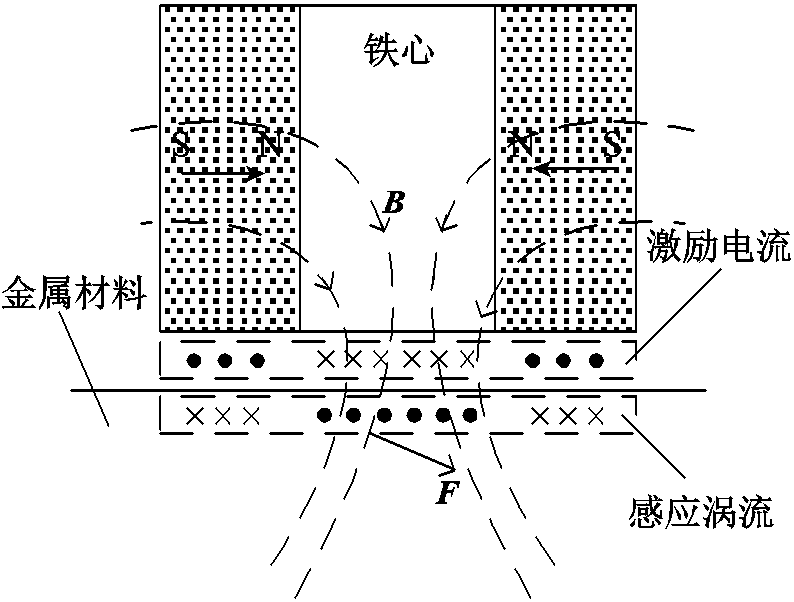
图1 电磁加载原理示意图
Fig.1 Schematic diagram of electromagnetic loading
摘要 基于临界折射纵波对金属材料进行应力无损检测具有广泛的应用前景，该检测技术中金属材料声弹性系数的标定尤为重要。目前金属材料声弹性系数标定方法主要是采用机械加载方式对金属材料进行拉伸测试，这种方法不适用于一些在役金属构件的声弹性系数的测量。针对上述问题，该文基于洛仑兹力的产生机理设计了一种用于铝板声弹性系数标定的电磁加载装置。采用二维仿真模型对装置进行了尺寸参数分析与选择，建立三维有限元仿真模型计算铝板轴向电磁加载力。搭建了电磁加载实验平台，测量电磁加载状态下铝板中临界折射纵波的传播时间并计算铝板中轴向应力平均值，实验结果与仿真结果基本一致，验证了电磁加载装置的可行性。
关键词：声弹性系数 电磁加载装置 尺寸选择 临界折射纵波
金属材料在加工制造或冷却过程中，例如轧制、挤压、焊接和金属切削等，其内部若发生非线性变形或者金属相变，将导致金属材料中存在残余应力[1]。金属材料存在残余应力，尤其是拉伸应力，将会导致金属材料在服役期间容易腐蚀、出现裂纹甚至断裂失效，极大地缩短了金属材料的使用寿命[2-3]。因此，检测金属构件内部残余应力的分布状况可以有效监测金属材料结构的健康状态。
在金属材料应力检测技术中，采用声弹性理论对金属材料进行超声应力无损检测受到广泛关注[4]。超声法测应力主要有表面波法、临界折射纵波法和激光超声法等[5]。表面波法仅适用于表征金属材料表面和次表面的应力分布状况[6]。激光超声法易实现高精度测量，具有较高的时间和空间分辨率，但是其渗透深度小，而且激光能量值高，对金属材料表面可能带来损伤[7-8]。临界折射纵波对应力敏感度最高，其渗透深度与超声波频率有关，一般低频超声渗透深度大，并且临界折射纵波激发装置简单易实现，因此采用临界折射纵波检测金属材料应力分布具有独特的优势[9-10]。然而，临界折射纵波法测应力需要对金属材料的声弹性系数进行标定。现有金属材料声弹性系数的标定方法主要是采用万能试验机对金属材料进行拉伸测试，测量不同应力下金属材料内部临界折射纵波波速，拟合波速与应力之间的线性关系[11]。这种机械拉伸方式测量声弹性系数的方法存在一些问题。首先，为了获取被测金属材料的声弹性系数，一般需要从被测金属材料中切割一部分用作声弹性系数的标定试件，这不是真正意义上的无损检测；或者采用与被测金属构件近似材料属性的替代材料作为声弹性系数的标定试件。其次，文献[12-13]表明在役金属构件的工作环境对声弹性效应有较大影响，倘若采用替代材料的声弹性系数进行应力计算将不可避免地给应力测量结果带来误差。
针对上述在役金属结构声弹性系数的标定问题，以1060铝板为研究对象，以洛仑兹力为主要电磁加载力[14-15]，本文采用电磁加载装置对铝板施加轴向应力，基于该电磁加载装置表征在役金属板的声弹性效应。由于电磁加载装置以洛仑兹力产生机理为主，该装置的偏置磁场强度和激励线圈在铝板中感应涡流的大小将决定铝板中电磁加载力的大小，因此合理选择电磁加载装置尺寸参数将在很大程度上提升铝板中的电磁加载效应。单个永磁体在铝板中的剩余磁通密度较小，为了增强偏置磁场的磁感应强度，广泛采用带铁心的永磁体阵列[16-17]，而使该装置中偏置磁场的剩余磁通密度最大化的尺寸设计将是本文的重点之一。本文设计的电磁加载装置主要是给铝板施加单方向的电磁加载力，因此激励线圈的绕制方式选择较为单一，主要选用两个跑道型线圈并列摆放，但是对跑道型线圈宽度以及匝数的选择则是本文工作的另一个重要部分，通过选择合适的线圈宽度和匝数将有利于提高铝板中的电磁加载力。
为实现电磁加载装置的尺寸参数设计，本文基于COMSOL Multiphysics 5.4有限元仿真软件建立电磁加载装置的二维仿真模型，以确定永磁体、铁心以及激励线圈的合理尺寸，建立三维仿真模型计算电磁加载装置施加在铝板中的电磁加载力的大小。搭建电磁加载实验平台，对铝板施加不同大小的电磁加载力，测量不同电磁加载状况下铝板中临界折射纵波波速，并根据声弹性原理计算轴向应力值。
电磁加载原理示意图如图1所示，电磁加载装置由偏置磁场和激励电流两部分构成。偏置磁场是通过两个永磁体的同极性面相对排列，两个永磁体之间放置一个导磁材料（铁心），两永磁体产生相互排斥的磁力线，在导磁材料的作用下产生向下的磁感应强度B。永磁体正下方是两个并列排放的线圈，当分别流过大小相等方向相反的激励电流时，激励线圈将在金属材料中感应出如图1中所示的涡流，根据电磁感应定理，感应涡流在偏置磁场的作用下将产生洛仑兹力F[18-19]。本文则通过改变激励电流大小，给金属材料施加不同大小的电磁加载力，进而实现金属材料声弹性系数的标定。
图1 电磁加载原理示意图
Fig.1 Schematic diagram of electromagnetic loading
金属材料中洛仑兹力F的计算公式为
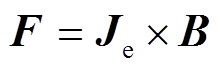（1）
式中，Je为激励电流在金属材料中的感应涡流密度；B为偏置磁场强度，其主要由永磁体提供。因此，在有限元仿真计算中对磁场强度分布以及金属材料中感应涡流密度分布的计算是求解金属材料所受电磁加载力的关键所在。
磁场强度H与剩余磁通密度B之间的关系式为
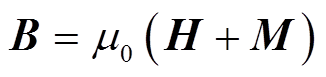（2）式中，M为磁化强度矢量；μ0为真空磁导率。磁化强度矢量M的表达式为
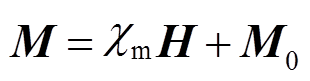（3）
式中，M0为剩余磁化强度；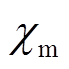
为磁化率。对于永磁体，其剩余磁通密度Br可表示为
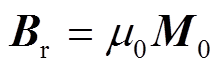（4）
对于永磁体产生的静态磁场，有关系式
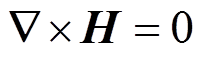（5）
因此，标量磁势Vm可以定义为
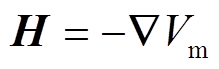（6）
此外，由麦克斯韦电磁场理论可知
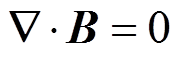（7）
那么将式（3）和式（6）代入式（7）可以得到[20-21]
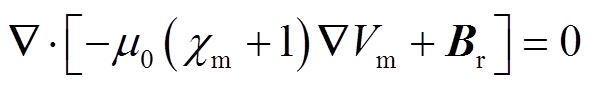（8）式（8）即可用于有限元仿真求解模型中偏置磁场的磁场强度分布，一般采用稳态求解域求解。
对于激励线圈中通过电流i，在不考虑线圈趋肤效应和邻近效应的情形下，激励线圈中的平均电流密度分布JS为
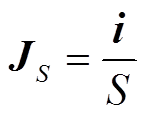（9）
式中，S为激励线圈导体的截面积。
在涡流动态磁场中，引入矢量磁位A，其满足关系式
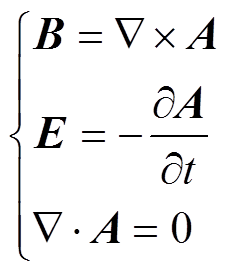（10）
那么金属材料中感应涡流密度Je可表示为
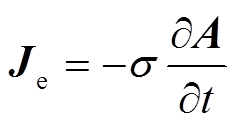（11）
式中，σ为金属材料的电导率。
因此，对于低频激励电流可忽略位移电流的影响，那么可建立近似微分方程[22-24]为
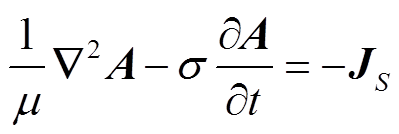（12）式（12）建立了感应涡流密度与激励电流之间的关系式，其可用于计算金属材料中的涡流密度分布。
本文设计的单个电磁加载装置如图2所示，在铁心四周均对称放置磁力线方向如图所示的永磁体以增强偏置磁场强度，单个永磁体的磁感应强度为0.5T。激励线圈绕制方式则采用类似于蝴蝶状的两个并列摆放的跑道型线圈。四个对称放置的电磁加载装置截面图如图3所示。以1060铝板为研究对象，为了给铝板施加轴向电磁加载力，本文设计了四个对称放置的电磁加载装置。左右对称结构可以提高轴向电磁加载力大小；上下对称结构则不仅可以提高电磁加载效果，而且还可以通过永磁体的相互吸引力避免竖直方向上的洛仑兹力分量使铝板发生竖直方向上的位移。
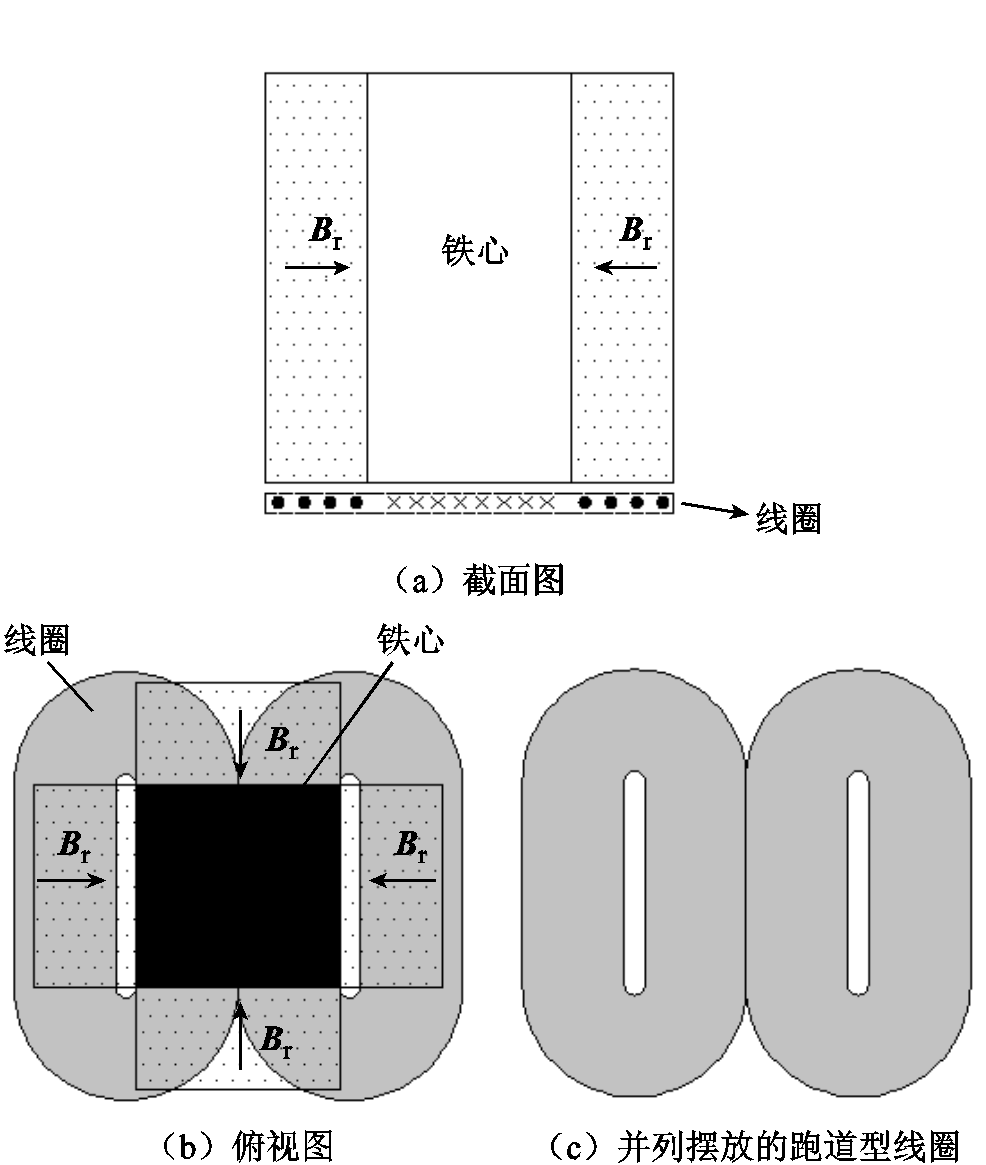
图2 单个电磁加载装置示意图
Fig.2 Schematic diagram of a single electromagnetic loading device
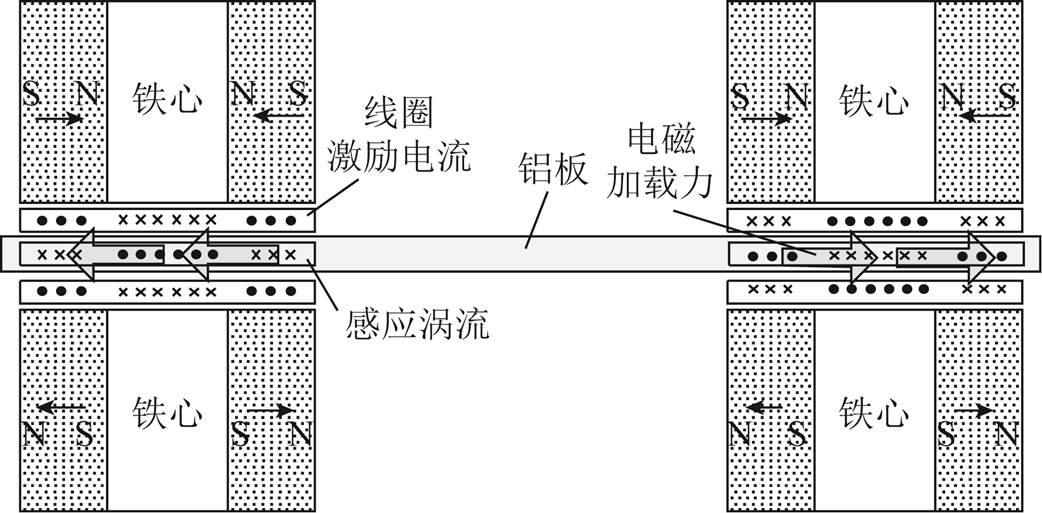
图3 四个对称放置的电磁加载装置截面图
Fig.3 Section of four symmetrical electromagnetic loading devices
本文设计了一个如图4所示充放电电路用于给激励线圈提供激励电流。电容组C的容量为2 800μF，耐压值为1 200V。实验中所用激励线圈的电阻值R1为0.239 6Ω，电感值L1为291.380 6μH。充放电电路工作原理是：使用STC89C52型号的单片机控制晶闸管VT1导通，VT2截止，稳压源E给电容C充电至预设值UC；然后通过单片机控制晶闸管VT1截止，VT2导通，电容给激励线圈放电，该放电电路为二阶零输入响应电路。
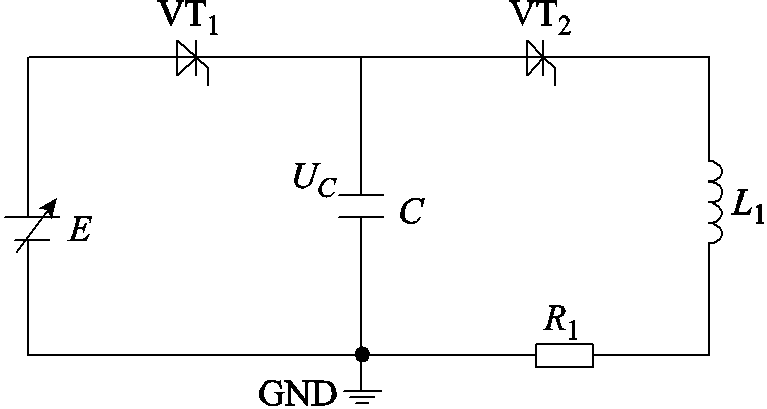
图4 充放电电路
Fig.4 Charge and discharge circuit
针对上述电磁加载装置设计方案，为了使电磁加载装置给铝板施加的电磁加载力最大，下面分析该装置各部分尺寸参数与电磁加载力之间的关系，综合考虑各方面影响因素，合理选择装置各部分尺寸。
图3设计的电磁加载装置是一个轴对称结构，因此为了节省仿真模型计算时间，在COMSOL Multiphysics 5.4仿真软件中采用轴对称组件建立电磁加载装置的右半部分仿真模型。该二维仿真模型与实际电磁加载装置最大差异在于永磁体建模无法反映图2b所示的永磁体阵列，但是该模型仅剩余磁通密度大小与实际电磁加载装置有所差异，其静磁场分布状况与实际静磁场分布基本一致，对于该部分内容的讨论将在三维建模中进一步分析。首先比较单个永磁体与带铁心的永磁体阵列产生的磁感应强度，其中永磁体磁感应强度均为0.5T。不同静磁场结构的剩余磁通密度分布如图5所示。仿真结果表明带铁心的永磁体阵列产生的磁感应强度最大值超过了1T，铝板上的剩余磁通密度约为0.42T；而单个永磁体产生的磁感应强度最高不超过0.5T，在铝板上的剩余磁通密度则低于0.3T，所以本文选用带铁心的永磁体阵列来构建偏置磁场。
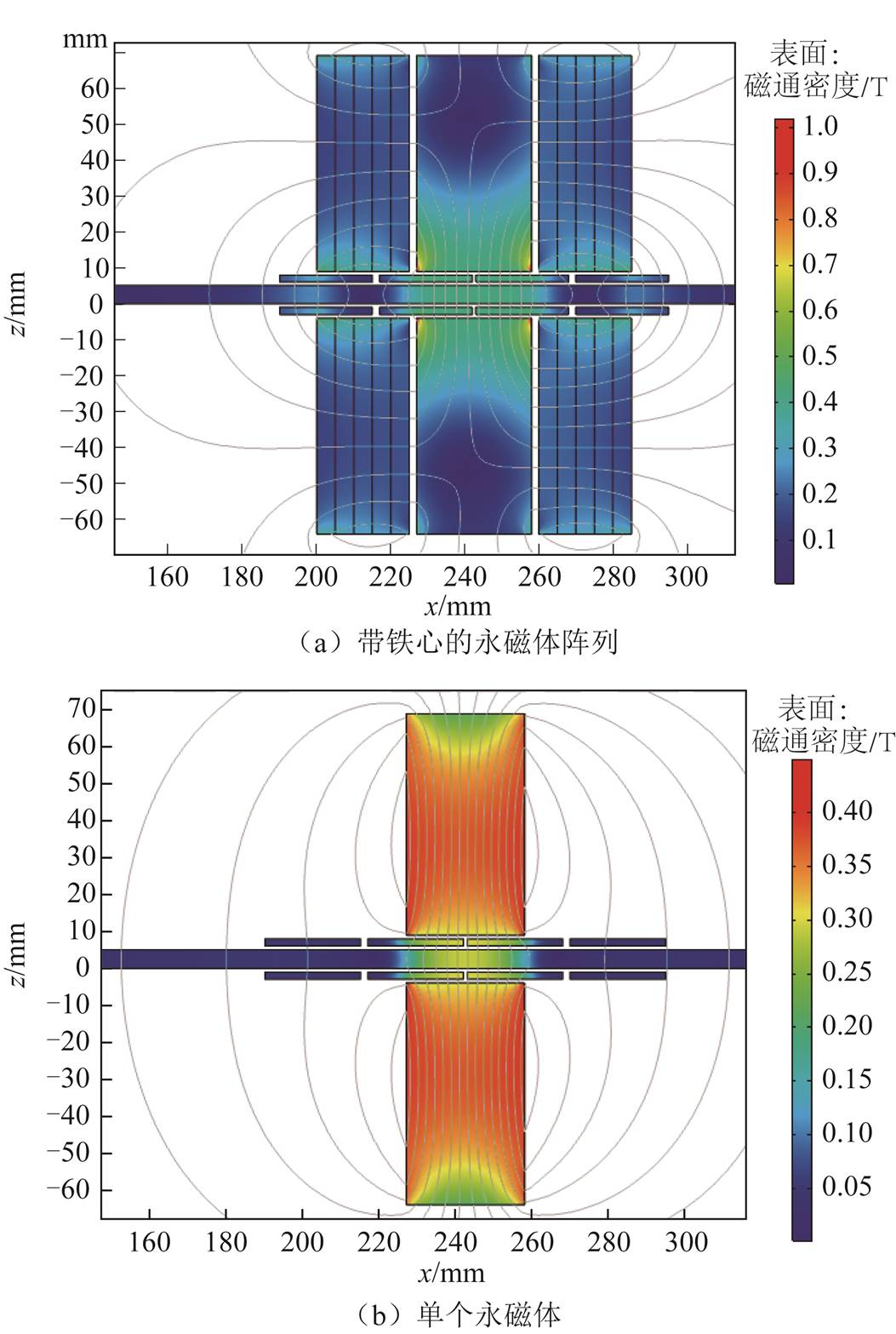
图5 不同静磁场结构的剩余磁通密度分布
Fig.5 Residual flux density distribution of different static magnetic field structures
计算二维轴对称电磁加载仿真模型。图6a所示为铝板轴向应力分布图，从仿真结果可以看出铝板中间部分的应力分布较为均匀。二维轴对称电磁加载仿真模型计算结果如图6b所示，选取铝板仿真模型中对称轴中心点为研究对象，计算该点所受轴向应力值与时间的关系曲线，也给出了激励线圈中电流密度随时间的变化曲线，曲线表明铝板中轴向应力峰值时刻大约在1.18ms时刻，实验中则采用单片机延时程序控制临界折射纵波的激发和接收时刻，从而仅采集铝板应力峰值时刻的波形信号。因此下文仅讨论峰值时刻铝板中的轴向应力分布。
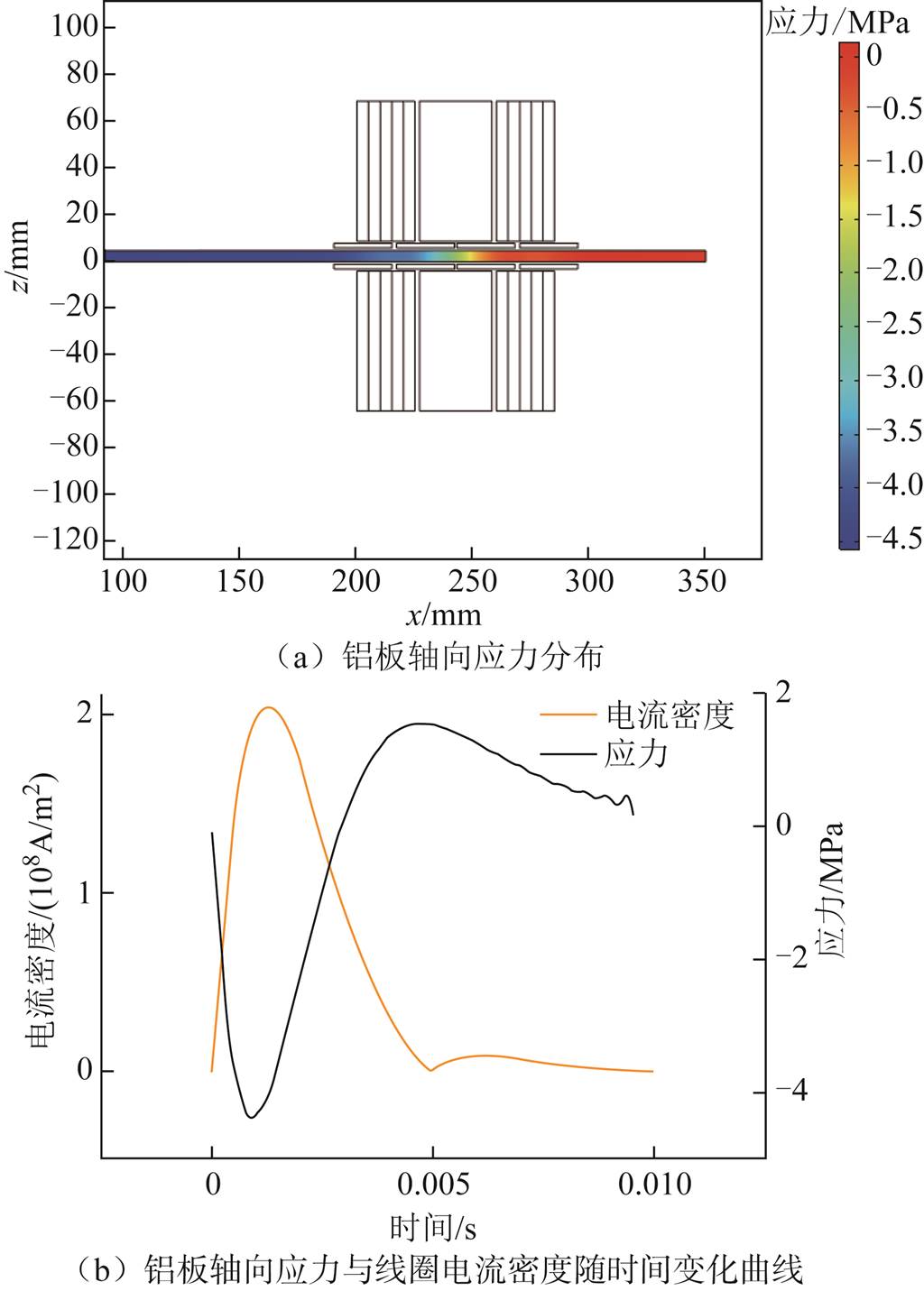
图6 二维轴对称电磁加载仿真模型计算结果
Fig.6 Calculation results of two-dimensional axisymmetric electromagnetic loading simulation model
为了选择永磁体高度，以10mm为间距分别改变二维轴对称电磁加载仿真模型中永磁体高度，计算永磁体高度为10～100mm之间铝板所受轴向应力分布，仿真模型保持铁心高度与永磁体高度一致。不同永磁体高度下应力分布仿真结果如图7所示。由图7a可知，由于本文选用临界折射纵波的激发频率为5MHz，其渗透深度为1mm左右，所以截取距离铝板表面1mm厚度下水平方向上的应力分布。从仿真结果可以看出，对于不同永磁体高度，铝板受到的应力分布趋势大致相同，仅应力值大小不同。采用临界折射纵波对金属材料的应力检测结果作为波形传播路径上的应力平均值，对于本文设计的电磁加载装置，实验中只能在电磁加载装置之间放置压电探头用于发射和接收临界折射纵波，那么检测的应力值应为水平方向电磁加载装置之间的铝板应力平均值。由图7a可知，水平方向0～150mm之间的应力分布较为均匀，有利于提高铝板声弹性系数的检测精度，因此可以通过计算并比较每条曲线水平方向0～150mm之间的平均应力值来选择永磁体高度的最佳尺寸。图7b所示的应力-永磁体高度曲线，随着永磁体高度的增加，铝板所受应力值大小也单调递增，然而当永磁体高度增加至60mm时，铝板所受应力值大小增加速率明显下降，因此综合考虑现有永磁体高度尺寸规格等因素，本文选用的永磁体高度为60mm。
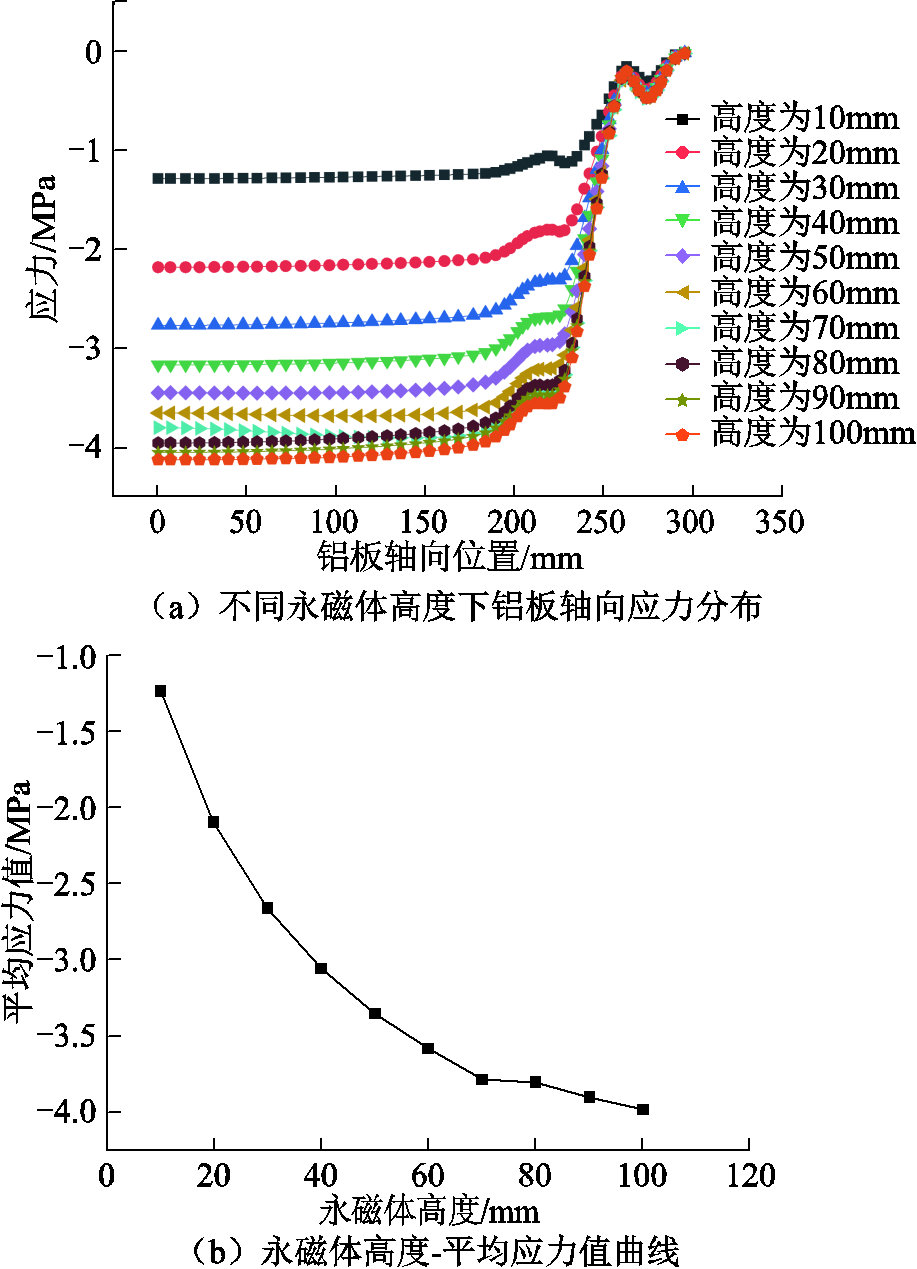
图7 不同永磁体高度下应力分布仿真结果
Fig.7 Simulation results of stress distribution under different permanent magnet heights
保持仿真模型中永磁体高度为60mm不变，以10mm为梯度计算铁心高度为10～100mm之间铝板所受轴向平均应力大小。不同铁心高度下应力分布仿真结果如图8所示。由图8可知，当铁心高度达到40mm时，铝板所受平均应力值最大，此时永磁体高度与铁心高度之比为3:2。为了进一步验证此结论，当永磁体高度为90mm固定不变时，改变铁心高度，在图8中绘制铝板所受应力大小与铁心高度之间的关系曲线，该曲线变化规律同样满足大约永磁体高度与铁心高度之比为3:2时铝板中平均应力值最大。因此，本文定制的铁心高度为40mm。
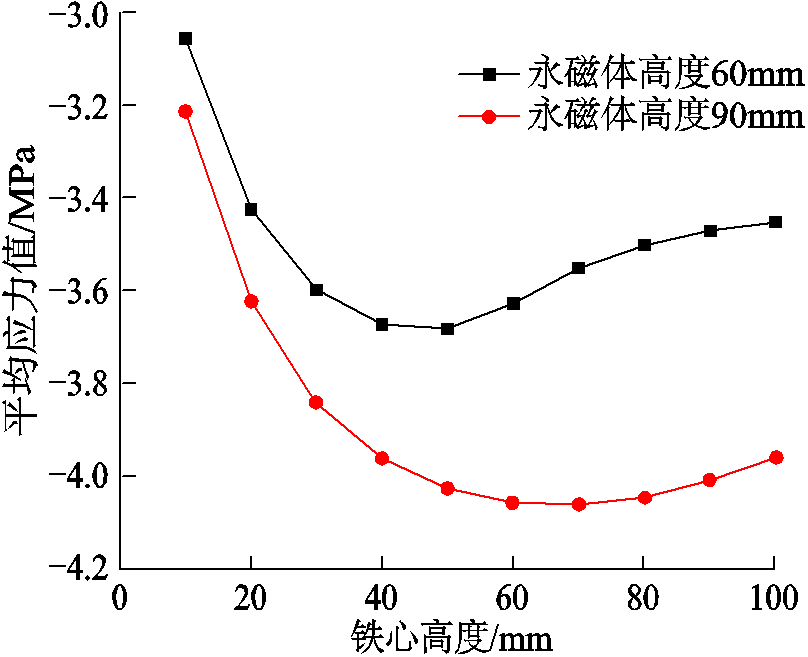
图8 不同铁心高度下应力分布仿真结果
Fig.8 Simulation results of stress distribution under different core heights
根据充放电电路激励线圈中电流大小，本文选用线径为0.8mm的激励线圈，当激励线圈宽度（跑道型线圈环形宽度）不变时，线圈匝数将决定线圈的厚度。不同线圈匝数下应力分布仿真结果如图9所示。由图9可知，激励线圈匝数越大，铝板所受轴向应力值越大，但当激励线圈匝数大于250匝时，增加激励线圈匝数，应力值增加较为缓慢，因此激励线圈匝数选择250匝。
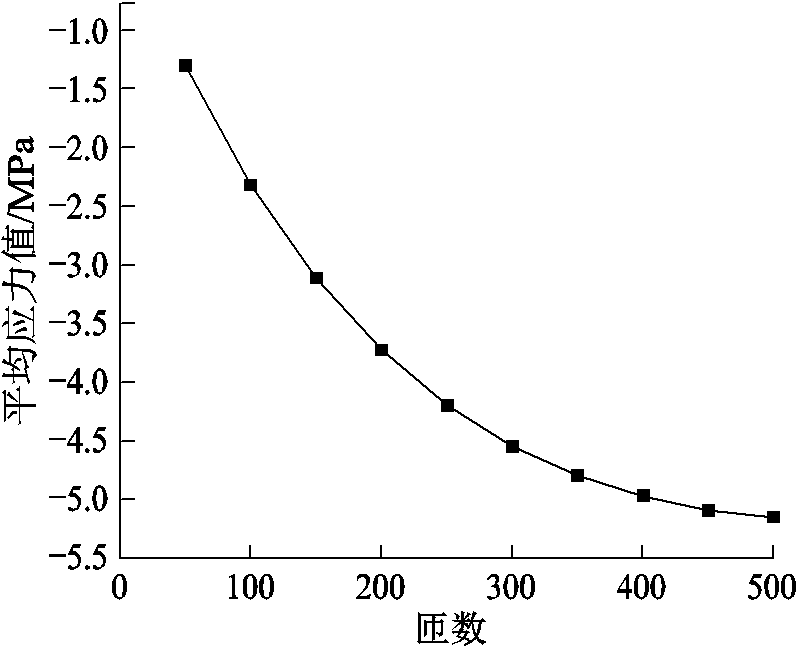
图9 不同线圈匝数下应力分布仿真结果
Fig.9 Simulation results of stress distribution under different coil turns
在确定铁心和永磁体高度之后，分别探究永磁体宽度、铁心宽度以及激励线圈宽度对铝板轴向应力大小的影响。图10a、图10b、图10c三个曲线图分别表示永磁体宽度、铁心宽度和激励线圈宽度与铝板中平均应力值之间的关系。当铁心宽度为40mm、激励线圈宽度为20mm时，永磁体宽度值越大，铝板应力值越大，但是当宽度值达到20mm时，应力值增长坡度放缓；当永磁体宽度和激励线圈宽度均为20mm固定不变时，铁心宽度与铝板应力值近似呈线性关系；当铁心宽度为40mm、永磁体宽度为20mm时，改变激励线圈宽度，可以发现其值为25mm时铝板所受平均应力值为极大值点。永磁体宽度的改变仅影响铁心下方通过铝板的剩余磁通密度值，所以本文选择宽度为20mm的永磁体；而铁心宽度以及激励线圈宽度的改变则相应地不仅影响磁感应强度大小和涡流密度大小，同时也影响磁通密度以及涡流密度的分布，因此在选择铁心宽度与激励线圈宽度时需综合考虑这两个方面因素对铝板应力值的影响。本文通过仿真计算当永磁体宽度为20mm不变时，不同铁心宽度和激励线圈宽度下铝板的平均应力值，绘制了如图10d所示的三维曲面图。该曲面图表明，当线圈宽度为25mm、铁心宽度为30mm时，铝板所受的轴向应力最大。综上所述，本文将选择永磁体、铁心以及激励线圈的宽度分别为20mm、30mm和25mm。
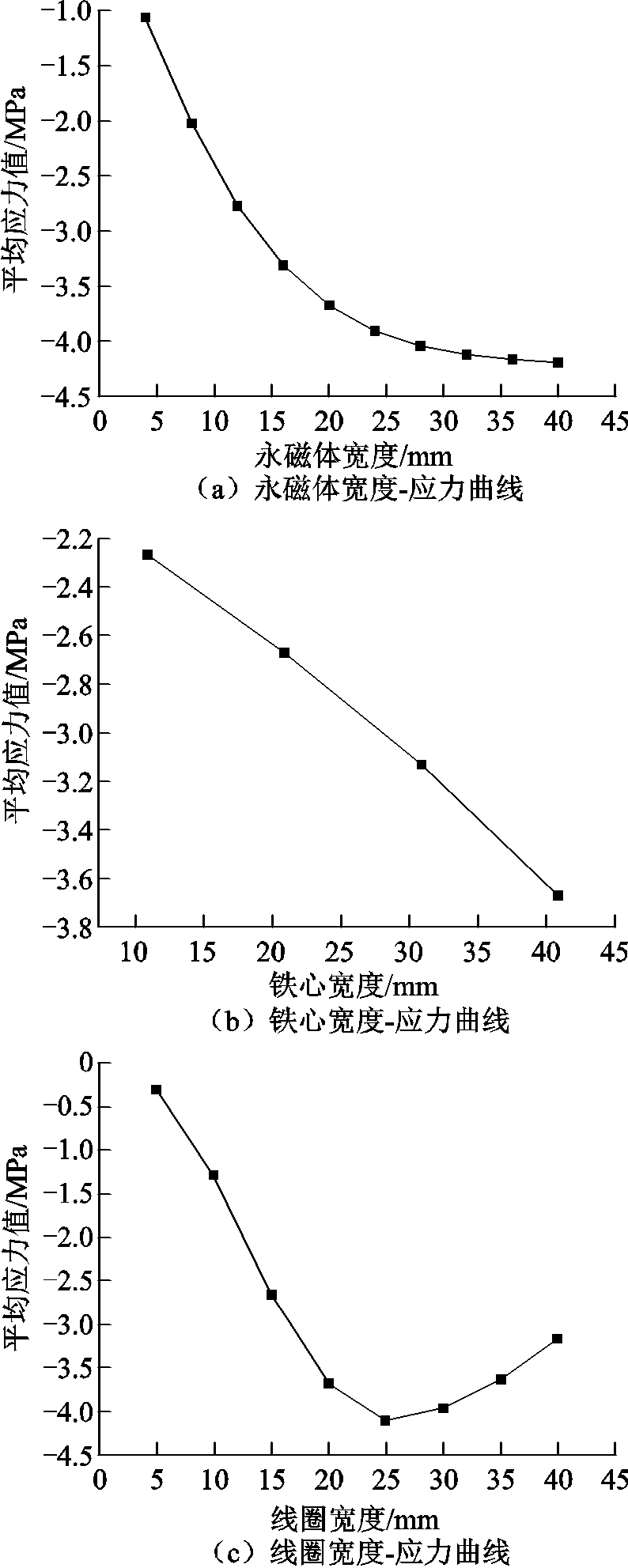
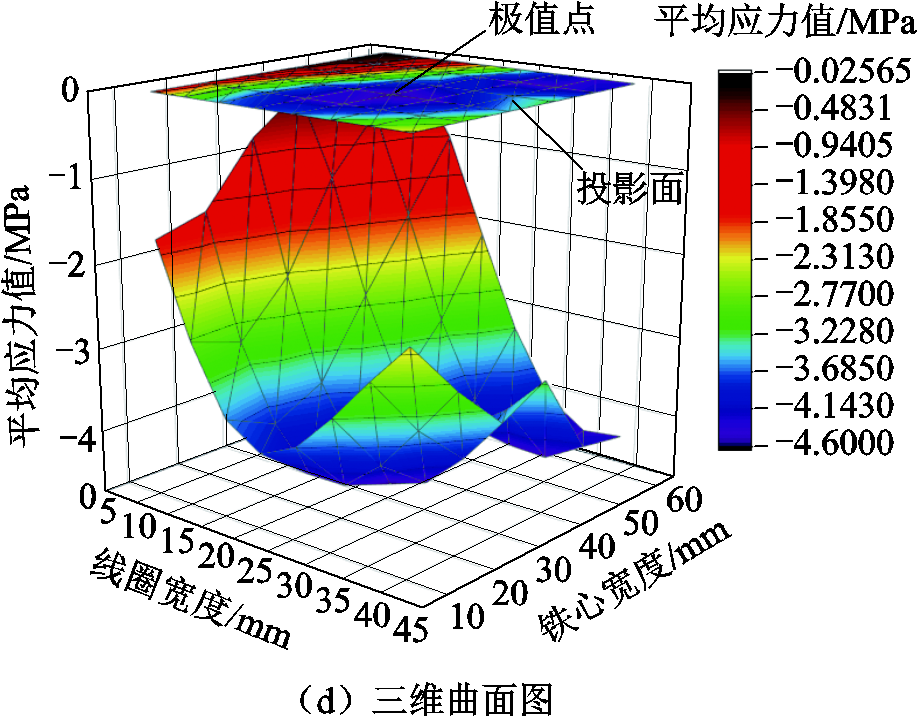
图10 永磁体宽度、铁心宽度以及激励线圈宽度对铝板轴向应力大小的影响
Fig.10 Effect of permanent magnet width, core width and excitation coil width on axial stress of aluminum plate
电磁加载装置的提离距离对铝板中轴向应力的影响也不容忽视。基于上述确定的电磁加载装置尺寸参数建立仿真模型，以0.5mm为梯度，仿真求解了提离距离为0.5～4mm下的铝板应力分布。不同提离距离下应力分布仿真结果如图11所示。由图11可知提离距离与铝板中的平均应力值近似呈线性关系，提离距离越小，铝板中的应力值越大，因此应尽可能降低电磁加载装置的提离距离，但是实际电磁加载装置由于线圈绝缘层以及外在固定装置的存在等因素使得提离距离的存在不可避免，本文实际搭建的电磁加载装置提离距离大约4mm。
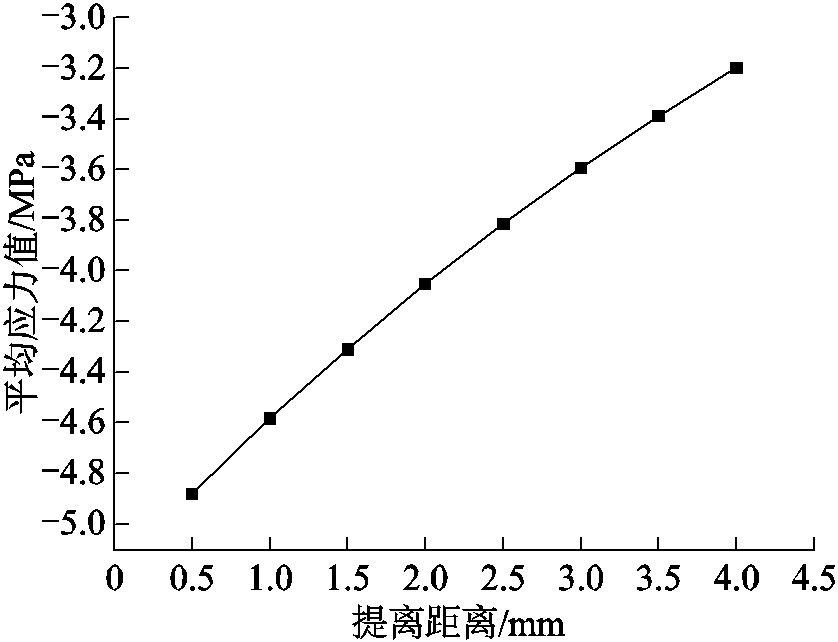
图11 不同提离距离下应力分布仿真结果
Fig.11 Simulation results of stress distribution under different lift-off distances
上述电磁加载装置二维轴对称模型由于其模型简单、仿真计算时间短，仅用作电磁加载装置的尺寸参数选择，该模型只能反映电磁加载装置如图3所示截面的剩余磁通密度、铝板上涡流密度以及铝板轴向应力的分布状况。对于实际电磁加载装置的偏置磁场分布以及在铝板中感应的涡流分布和轴向应力分布则需要通过建立三维仿真模型来反映。本文按照2.1节确定的电磁加载装置最佳尺寸建立如图12所示的三维电磁加载装置仿真模型。考虑到电磁加载装置的对称性，为缩短模型的计算时间，本文仅建立装置的左半部分模型。此外，由于仿真软件对线圈几何形状的限制，模型采用环状线圈代替跑道型线圈。
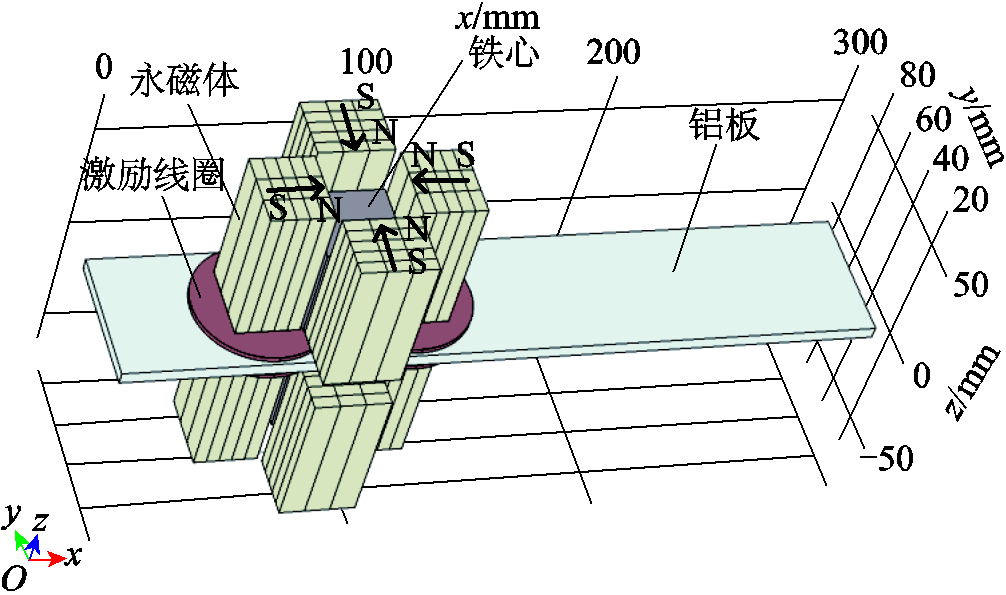
图12 三维电磁加载装置仿真模型
Fig.12 3D simulation model of electromagnetic loading device
三维模型仿真结果如图13所示。图13a为铝板上的剩余磁通密度分布，铁心下方部位的磁感应强度大约0.55T；图13b为电磁加载装置x-z截面上的偏置磁场磁感应强度分布图，图中磁感应强度分布与图5a中二维模型磁感应强度分布基本一致，验证了本文采用二维建模对装置进行尺寸参数分析的可行性；图13c为铝板y轴方向上的涡流密度分布；图13d为铝板轴向应力分布，可以观察到整个铝板中间区域的应力分布较为均匀。不同放电电压下铝板中应力大小如图14所示，改变电容的放电电压，仿真计算不同激励电压下铝板中轴向应力平均值，坐标系中每个点的应力值取铝板三维模型中高度4mm，x轴方向150～300mm截面的应力平均值，由曲线图可知，放电电压与铝板轴向平均应力成正比。
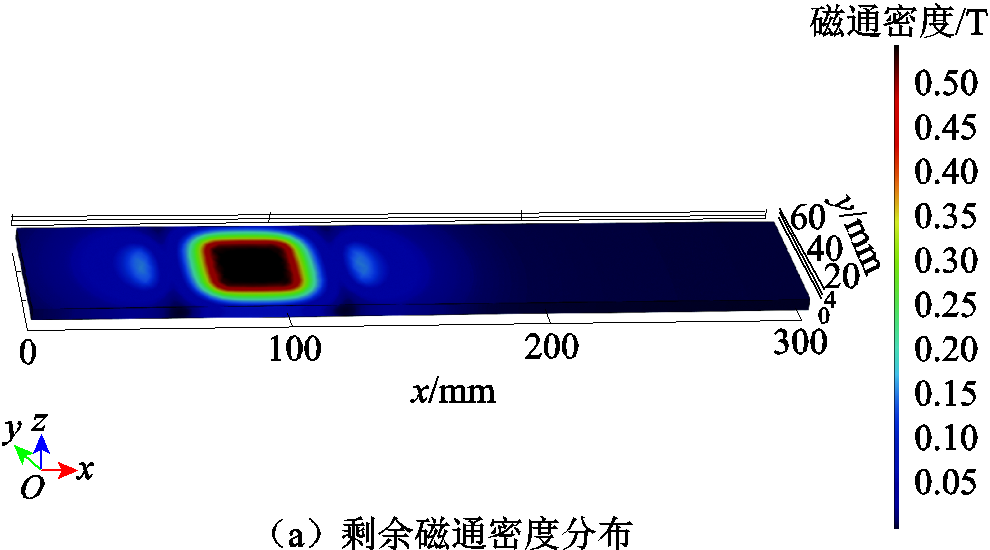
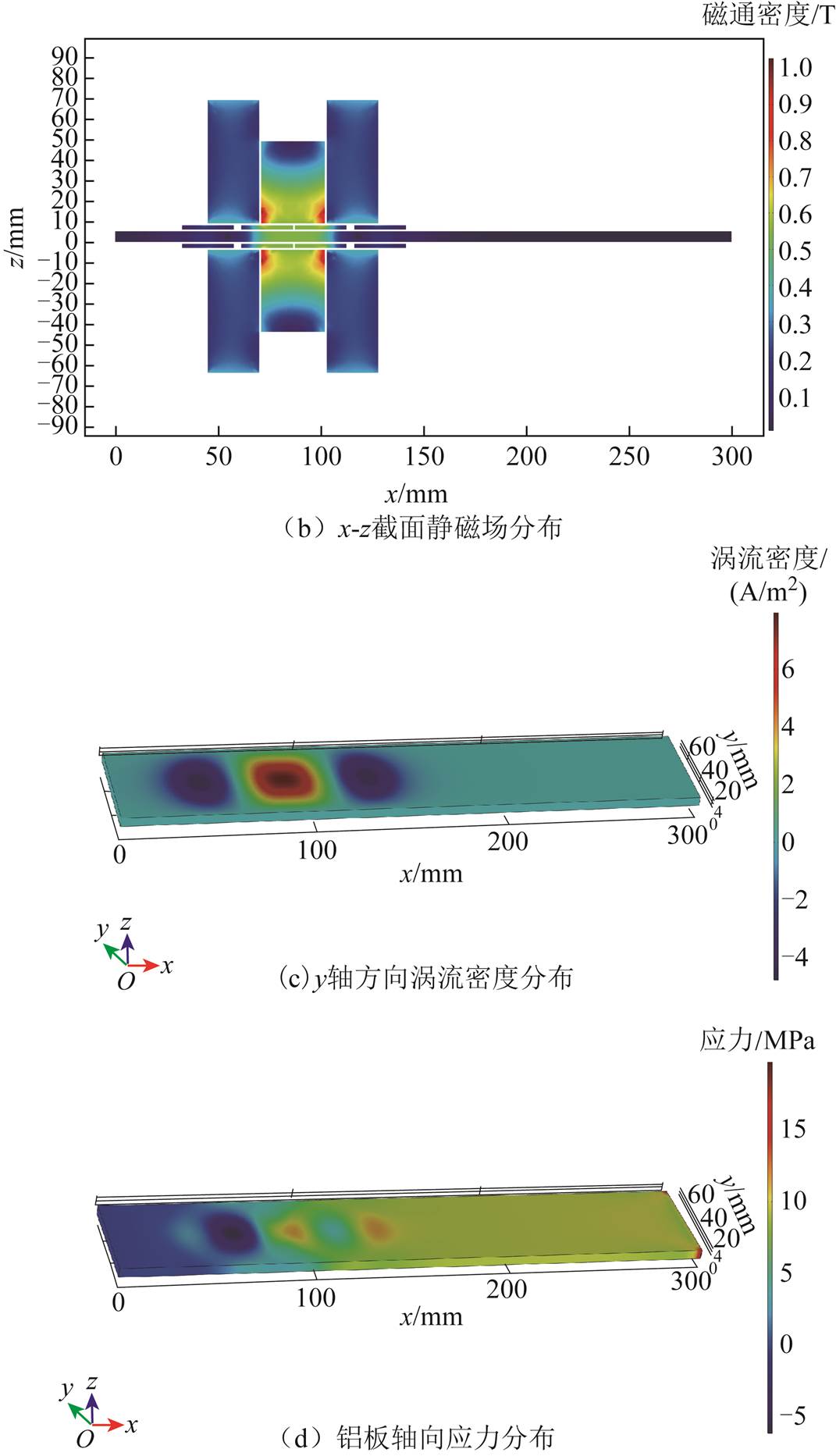
图13 三维模型仿真结果
Fig.13 3D-model simulation results
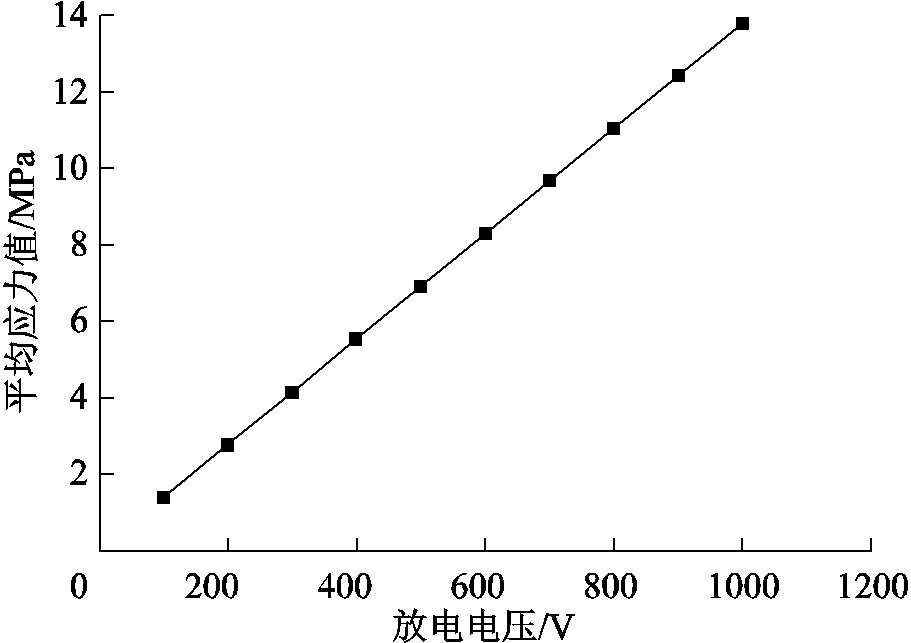
图14 不同放电电压下铝板中应力大小
Fig.14 Stress in aluminum plate under different discharge voltages
基于上述确定的电磁加载装置尺寸参数制作了如图15a所示的电磁加载装置。以1060铝板为实验样本，铝板尺寸为650mm×55mm×5mm，本文搭建了如图15b所示的电磁加载装置实验平台。电磁加载装置施加给铝板轴向电磁加载力的同时，由于作用力与反作用力的关系，电磁加载装置自身也将受到反向的力，因此为了避免电磁加载装置发生位移，实验中给电磁加载装置添加了一个固定模具。实验平台主要由三部分组成：充放电电路、临界折射纵波信号激励和接收装置以及电磁加载装置。实验首先通过稳压源给电容器组充电至预设电压值，采用STC89C52型号的单片机控制晶闸管的通断，使电容器组给激励线圈放电。为了捕捉铝板在受到最大电磁加载力时刻临界折射纵波的传播速度，单片机设置延时触发程序控制信号发生器在电容器放电后的1.18ms时刻触发压电探头，压电探头发射和接收临界折射纵波（可调节度的压电探头根据Snell定理设置压电片的倾斜角度）。
图15 电磁加载装置及实验平台
Fig.15 Electromagnetic loading device experimental platform
临界折射纵波信号如图16所示，分别采集铝板不受电磁加载力时（实验所用铝板为自由状态，即铝板中应力近似为0MPa）和电容器组放电电压为400V时临界折射纵波在铝板中的传播波形信号。实验中中压探头间距为10mm固定不变，临界折射纵波波速最大，其波形如图中虚线圈中的波包所示。其中放电电压为0V时，临界折射纵波波形达到时刻为22.792μs；放电电压为400V时，波形到达时刻为22.932μs。
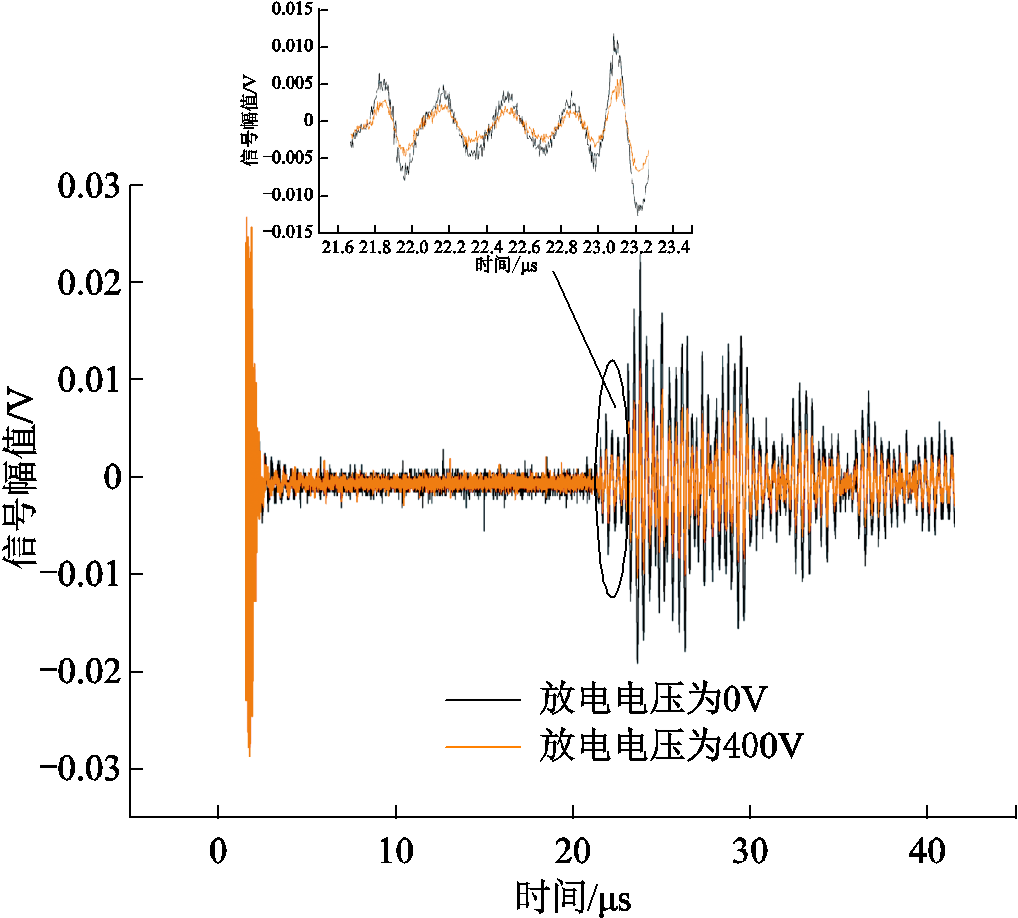
图16 临界折射纵波信号
Fig.16 Critical refracting longitudinal wave signal
由临界折射纵波的声弹性效应可知，铝板中应力σ与临界折射纵波波速v之间的关系式为
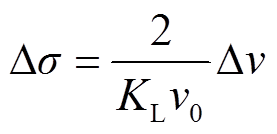（13）
式中，KL为铝板的声弹性系数；v0为铝板在自由状态下临界折射纵波波速；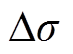
、
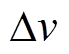分别为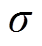
和v的变化量。
采用传统机械加载方法标定实验样本的声弹性系数为-1.083 9×10-4MPa-1，实验测得自由状态下铝板中临界折射纵波波速为6 458.3m/s，因此通过式（13）可以计算出当电容预设电压为400V时，电容给激励线圈放电，电磁加载装置给铝板施加的轴向平均应力值大约为7.65MPa。放电电压-应力散点图如图17所示，测量不同放电电压下的铝板轴向应力值，实验中铝板所受的应力值比仿真结果大，但是变化趋势基本一致。因此，可以利用本文设计的电磁加载装置给铝板施加轴向应力，通过改变电容放电电压，测量不同轴向电磁加载力下铝板中临界折射纵波波速，进而可实现铝板的声弹性系数的标定。需要注意的是，在役金属板的声弹性系数未知，因此可通过对金属板施加大小相等方向相反的电磁加载力，并测量临界折射纵波到达时刻，同时考虑电磁加载状态下金属板弹性形变的影响，根据声弹性效应理论建立轴向应力求解方程，进而实现金属板声弹性系数的在线测量[25]。
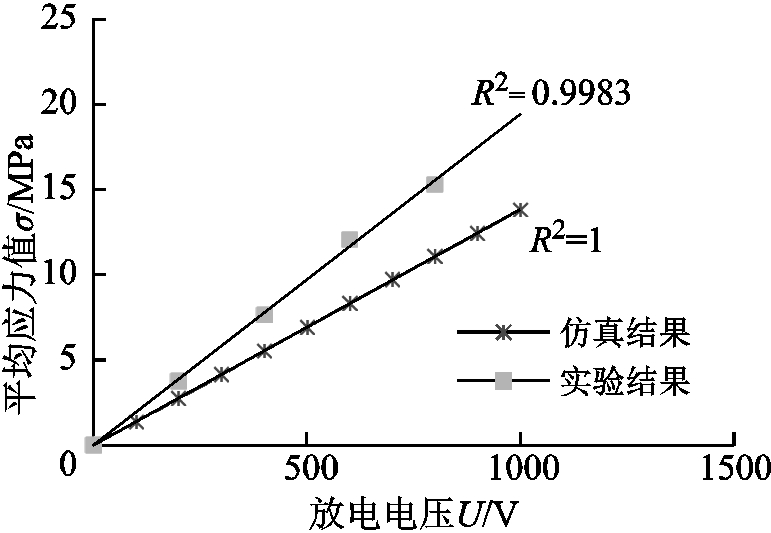
图17 放电电压-应力散点图
Fig.17 Discharge voltage-stress scatter plot
在役金属材料的声弹性系数受在役环境影响较大，采用现有机械拉伸方式对在役金属材料声弹性系数进行标定，其测量结果误差较大，这将影响金属材料的应力检测精度。鉴于上述问题，本文设计了一个用于铝板声弹性系数标定的电磁加载装置。基于COMSOL Multiphysics 5.4有限元仿真软件建立电磁加载装置二维仿真模型，仿真分析了电磁加载装置各个尺寸参数对电磁加载力的影响，依据分析结果确定了电磁加载装置永磁体、铁心以及激励线圈等的尺寸，然后进行三维仿真建模，仿真计算模型静磁场分布、感应涡流分布以及铝板轴向应力分布。搭建了电磁加载实验平台，测量不同放电电压下铝板中的临界折射纵波波速，计算了铝板中的轴向电磁加载应力平均值。实验结果表明，本文设计的电磁加载装置可作为在役金属板材的声弹性系数标定装置。
参考文献
[1] Goswami G, Qadri S B, Feng C R, et al. Residual stress and localized lattice rotation under fatigue loading[J]. Materials Science and Engineering: A, 2019, 763: 138113.
[2] Umapathi A, Swaroop S. Measurement of residual stresses in titanium alloys using synchrotron radiation[J]. Measurement, 2019, 140: 518-525.
[3] 胡兴, 戴培元, 张超华, 等. 合并焊道法对 SUS304不锈钢平板对接接头焊接残余应力计算精度和效率的影响[J]. 机械工程学报, 2019, 55(12): 72-82. Hu Xing, Dai Peiyuan, Zhang Chaohua, et al. Influence of lumped-pass method on calculation accuracy and efficiency of welding residual stress in SUS304 stainless steel butt joints[J]. Journal of Mechanical Engineering, 2019, 55(12):72-82.
[4] 贾雪. 基于声弹性效应的螺栓轴向应力检测系统研究[D]. 成都: 西南交通大学, 2018.
[5] 邵营. 超声表面波应力无损检测技术研究[D].徐州: 中国矿业大学, 2016.
[6] Chen Yue, Man Chi-Sing, Tanuma K, et al. Monitoring near-surface depth profile of residual stress in weakly anisotropic media by rayleigh-wave dispersion[J]. Wave Motion, 2018, 77: 119-138.
[7] Zhan Yu, Liu Chen, Zhang Junjian, et al. Measurement of residual stress in laser additive manufacturing TC4 titanium alloy with the laser ultrasonic technique[J]. Materials Science and Engineering: A, 2019, 762: 138093.
[8] 薛茂盛. 基于激光超声的金属表面残余应力无损检测研究[D]. 杭州: 浙江大学, 2018.
[9] Li Yapeng, Liu Haibo, Liu Yankun, et al. In-plane elastic anisotropic constants (IEACs) measurement of rolling aluminum plate at different depth using ultrasonic LCR wave[J]. Applied Acoustics, 2019, 149: 59-67.
[10] Mohammadi M, Fesharaki J J. Determination of acoustoelastic/acoustoplastic constants to measure stress in elastic/plastic limits by using LCR wave[J]. NDT & E International, 2019, 104: 69-76
[11] 全国无损检测标准化技术委员会. GB/T32073—2015无损检测残余应力超声临界折射纵波检测方法[S]. 北京: 中国标准出版社, 2016.
[12] 朱其猛. 临界折射纵波(LCR)应力测试修正方法与机理研究[D]. 成都: 西南交通大学, 2017.
[13] Liu Haibo, Li Yapeng, Li Te, et al. Influence factors analysis and accuracy improvement for stress measurement using ultrasonic longitudinal critically refracted(LCR) wave[J]. Applied Acoustics, 2018, 141: 178-187.
[14] 孙文秀, 刘国强, 夏慧, 等. 非铁磁材料的电磁超声接收过程数值模拟及实验研究[J]. 电工技术学报, 2018, 33(19): 4443-4449. Sun Wenxiu, Liu Guoqing, Xia Hui, et al. Numerical simulation and experimental study on electromagnetic ultrasonic receiving process of non-ferromagnetic materials[J]. Journal of Electrical Technology, 2018, 33(19): 4443-4449.
[15] 刘素贞, 董硕, 张闯, 等. 电磁超声加载方式对Lamb波模态的影响[J]. 电工技术学报, 2018, 33(19): 12-19. Liu Suzhen, Dong Shuo, Zhang Chuang, et al. The influence of electromagnetic acoustic transducer loading way on the mode of Lamb wave[J]. Journal of Electrical Technology, 2018, 33(19): 12-19.
[16] Isla J, Cegla F. Optimisation of the bias magnetic field of shear wave EMATs[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2016: 2558467.
[17] 杨晨, 白保东, 陈德志, 等. 可变磁通永磁辅助同步磁阻电机设计与性能分析[J]. 电工技术学报, 2019, 34(3): 45-52. Yang Chen, Bai Baodong, Chen Dezhi, et al. Design and analysis of a variable flux permanent magnet assisted synchronous motor[J]. Journal of Electrical Technology, 2019, 34(3):45-52.
[18] 邱立, 余一杰, 聂小鹏, 等. 管件电磁胀形过程中的材料变形性能问题与电磁力加载方案[J]. 电工技术学报, 2019, 34(2): 14-20. Qiu Li, Yu Yijie, Nie Xiaopeng, et al. Study on material deformation performance and electromagn-etic force loading in electromagnetic tube expansion process[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 14-20.
[19] Hyeong L G , Reyoung K H . Numerical analysis of the electromagnetic force for design optimization of a rectangular DC electromagnetic pump[J]. Nuclear Engineering and Technology, 2018, 50(6): 869-876.
[20] 朱武兵, 庄劲武, 赵文春, 等. 载体感应磁场的改进积分方程法[J]. 国防科技大学学报, 2018, 40(3): 101-106. Zhu Wubing, Zhuang Jinwu, Zhao Wenchun, et al. Modified integral equation method for carrier's induced magnetic field solving[J]. Journal of National University of Defense Technology, 2018, 50(6):101-106.
[21] 李湘平, 鲁军勇, 李玉, 等. 电磁发射弹丸膛内磁场分布特性的三维数值分析[J]. 电机与控制学报, 2018, 22(8): 34-40. Li Xiangping, Lu Junyong, Li Yu, et al. 3-D numerical analysis of distribution characteristics of electromagnetic launcher projectile in-bore magnetic field[J]. Electric Machines and Control, 2018, 22(8):34-40.
[22] Sun Hongyu, Huang Songling, Wang Qing, et al. Improvement of unidirectional focusing periodic permanent magnet shear-horizontal wave electromag-netic acoustic transducer by oblique bias magnetic field[J]. Sensors and Actuators A: Physical, 2019, 290: 36-47.
[23] 赵小军, 关大伟, 钟玉廷, 等. 应用于非线性涡流问题的定点谐波平衡改进算法[J]. 电工技术学报, 2017, 32(1): 214-221. Zhao Xiaojun, Guan Dawei, Zhong Yuting, et al. The improved fixed-point harmonic-balanced method for the nonlinear eddy current problems[J]. Journal of Electrical Technology, 2017, 32(1): 214-221.
[24] 朱二夯, 黄浩, 边旭, 等. 大型同步调相机定子压圈涡流损耗计算及降损方法[J]. 电机与控制学报, 2019, 23(10): 33-40. Zhu Erhang, Huang Hao, Bian Xu, et al. Research on calculation and decrease of eddy current losses in stator clamping ring for a large synchronous condenser[J]. Electric Machines and Control, 2019, 23(10): 33-40.
[25] 张闯, 王标, 刘素贞, 等. 基于电磁加载的铝板残余应力在线检测方法研究[J]. 中国电机工程学报, 2019, 39(24): 7429-7435.Zhang Chuang, Wang Biao, Liu Suzhen, et al. research on on-line detection method of residual stress of aluminum plate based on electromagnetic loading[J]. Proceedings of the CSEE, 2019, 39(24): 7429-7435.
Electromagnetic Loading Device Design for Acoustoelastic Coefficient Calibration of Aluminum Plates
Abstract The non-destructive testing of stress in metallic materials based on critical refracting longitudinal waves has broad application prospects. The calibration of metal materials' acoustoelastic coefficient is particularly important. At present, the calibration method for acoustoelastic coefficient of metal materials is to perform tensile testing on metal materials by mechanical loading, which is not suitable for in-service metal components. Aiming at the above problems, based on the Lorentz force generation mechanism, this paper designed an electromagnetic loading device to calibrate acoustoelastic coefficient of aluminum plates. The two-dimensional simulation model was used to analyze and select the dimensional parameters of the device, and the three-dimensional finite element simulation model was established to calculate the axial electromagnetic loading force of aluminum plate. An electromagnetic loading test platform was built to measure the propagation time of critical refracting longitudinal waves in aluminum plates under electromagnetic loading and the average axial stress in the aluminum plates was calculated. The experimental results were basically consistent with the simulation results, which verified the feasibility of the electromagnetic loading device.
keywords：Acoustoelastic coefficient, electromagnetic loading device, size selection, critical refracting longitudinal waves
中图分类号：TM15
DOI：10.19595/j.cnki.1000-6753.tces.191222
张 闯 男，1982年生，博士，教授，研究方向为电磁无损检测与评估。E-mail：czhang@hebut.edu.cn（通信作者）
王 标 男，1995年生，硕士研究生，研究方向为现代工程电磁技术及应用。E-mail：1552970543@qq.com
国家自然科学基金（51777052, 51977058）、新能源电力系统国家重点实验室开放课题（LAPS20018）和河北省高校科研重点项目（ZD2018214）资助。
收稿日期2019-09-27
改稿日期 2019-12-26
（编辑 郭丽军）