图1 单片测量系统
Fig.1 MST measurement system
摘要 硅钢片的磁致伸缩效应是变压器等电力装备本体振动噪声的主要原因。为了准确地建立取向硅钢磁致伸缩模型，依据硅钢磁畴旋转特性，引入磁畴旋转相关参数k1，对J-A模型进行改进；在此基础上，结合二次畴转模型建立取向硅钢的磁致伸缩模型，并用粒子群优化算法（PSO）提取模型中的多个参数。考虑电力变压器服役环境的影响，该文分别在理想正弦，含谐波、直流偏磁不同条件下开展了取向硅钢磁致伸缩特性分析。结果表明在三种不同状态下，建立的模型计算结果与实验测量的磁致伸缩特性结果具有较好的一致性。该文建立的磁致伸缩模型可应用于取向硅钢在服役条件下磁致伸缩特性模拟。
关键词：J-A模型 取向硅钢 磁致伸缩模型 服役条件 粒子群优化算法
磁致伸缩是引起电力变压器等电工装备振动噪声的主要原因，已引起国内外学者广泛研究。关于硅钢磁致伸缩特性的测量较为困难，目前只见国际电工委员会（IEC）关于单片磁致伸缩测量的技术指导，缺少国家与国际统一标准。大多是从磁畴理论、现象学理论、热力学与弹性力学四个角度对磁致伸缩进行建模及理论相关研究[1]。根据能量最小化原理，D.C.Jiles推导出磁致伸缩λ关于M2与M4的线性组合[2]。同时，计及磁滞影响的磁致伸缩模型表达式被提出，具有明确的物理基础，但磁致伸缩λ的推导过程也较为复杂，仅适用于简单的情形[3]。利用Preisach模型推导得到的磁致伸缩模型涉及微分及积分，运算较为复杂[4-5]。张黎等根据取向硅钢的磁致伸缩物理机制，得到了综合考虑磁场和预应力对磁致伸缩影响，但仍存在部分参数获取较为复杂的问题[6]。基于Maxwell方程与能量守恒定律，通过弹性力学推导出来的磁致伸缩的函数虽有较强的物理意义，但误差较大，且时变性能较弱[7-9]。T. Hilgert介绍了正弦激励下的磁致伸缩的动态描述，但是该模型对于实验数据的数量以及精度有很高的要求[10]，实现较为困难。通过实验结果与相关拟合公式相结合，推导得到磁致伸缩的多项式本构关系[11]，但缺乏物理意义。因此，对铁磁材料的磁致伸缩仍需要进一步深入的研究。
本文考虑硅钢磁畴的旋转因素，改进J-A模型，并将其与二次畴转模型结合，建立服役条件下描述取向硅钢磁致伸缩特性的模型。为验证模型的准确性和适用性，采用模型分别对不同工作状态下取向硅钢的磁致伸缩特性进行计算，并与测量结果进行对比分析。
本文采用磁致伸缩特性单片测试仪MST500对不同激励条件下取向硅钢片磁特性进行测量，其中样片磁化部分符合IEC 404—3规定，磁致伸缩测量采用激光实现，原理方法参照IEC 62531。MST 500的样片尺寸为500mm×100mm×0.28mm，该装置测取的硅钢磁致伸缩方向平行于样片磁通密度方向，其测量系统如图1所示。
选取首钢型号为18221955047的取向硅钢片作为试验样片，在正弦激励下的磁滞回线和磁致伸缩回线的测量结果如图2所示。
图1 单片测量系统
Fig.1 MST measurement system
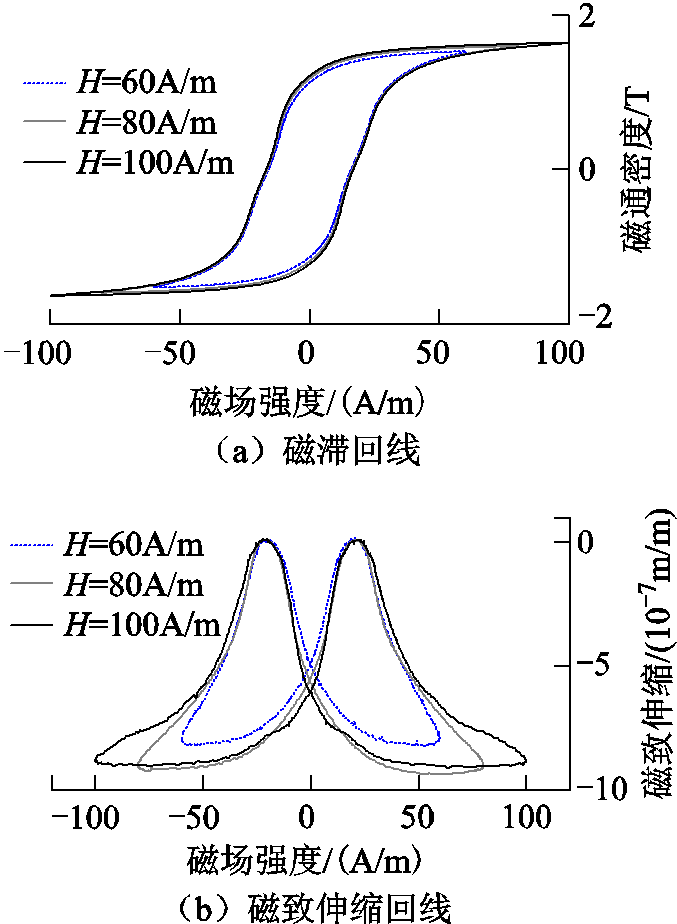
图2 正弦激励下磁滞回线与磁致伸缩回线
Fig.2 Hysteresis loop and magnetostrictive loop under sinusoidal excitation
磁化过程会引起磁畴的微观变化，磁滞特性与磁致伸缩特性同时产生。因此对磁化机理的研究十分重要。磁化过程如图3所示。O~b：从去磁状态到部分磁化；b~c：从磁化曲线的部分磁化到膝点；c~d：从磁化曲线的膝点到磁化饱和。
根据磁畴理论[12]，即使在磁性材料的去磁状态，原子磁矩也是有序的。因此，去磁状态与磁化之间的差异要归因于磁畴的状态。当施加外磁场时，磁畴的状态决定了磁性材料的外在表现。以90°磁畴为例进行说明。
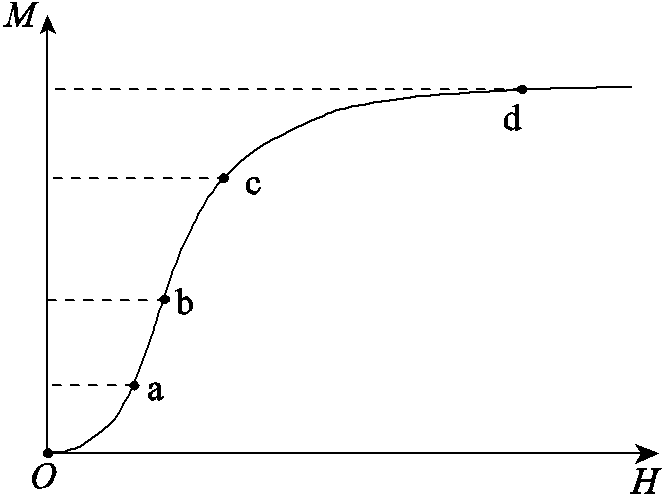
图3 磁化曲线
Fig.3 Magnetization curve
在图4中，从去磁状态（图4a）到部分磁化（图4c）是由于畴壁的移动，磁矩方向向接近磁场方向的磁畴增长。其中，图4b是畴壁的可逆运动，图4c是畴壁的不可逆运动。通过磁化过程中磁畴的不可逆旋转，磁性材料部分磁化（图4c）到磁化曲线的膝点（图4d），从磁化曲线的膝点（图4d）到磁化饱和（图4e）则是由磁畴的可逆旋转导致。
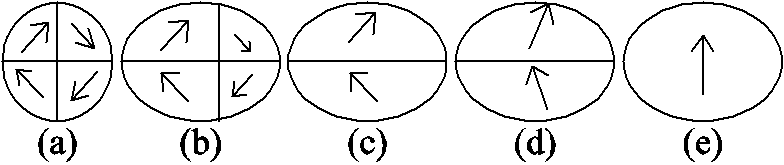
图4 磁化过程中磁畴的变化
Fig.4 Changes in magnetic domain during magnetization
磁致伸缩是硅钢材料一个重要的磁化特性，它是由于磁畴的重新排列产生磁性材料尺寸的变化。根据二次畴转模型[13]，磁致伸缩系数λ定义为
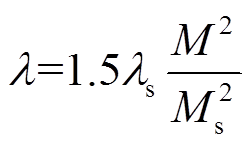（1）
式中，M为磁化强度；Ms为材料饱和磁化；λs为材料饱和磁致伸缩。
目前，描述磁滞现象的模型很多，其中J-A模型中的参数较其他模型求解简单，且对于表征磁特性也显示了很好的效果[14-16]。传统的J-A模型对于以磁畴平移作为主要磁化机制的磁化过程有很好的描述。但随着施加磁场逐渐增大，磁化机理主要与磁畴的旋转有关。仅仅将J-A模型与二次畴转模型结合得到模型与实验的对比结果发现：在磁致伸缩回线膝点至接近饱和的部分，模型计算结果与实验结果有很大的误差。一个合理的假设是与磁畴平移有关的参数k并不能很好地反映磁化的整个过程。
基于磁畴旋转理论，从部分磁化阶段到磁饱和的过程中，其磁化机制与磁畴的旋转相关。因此，参数k1被引入到J-A模型中，将J-A模型进行修改，推导出适用于取向硅钢的磁致伸缩模型。磁化过程中的能量平衡方程被修改为
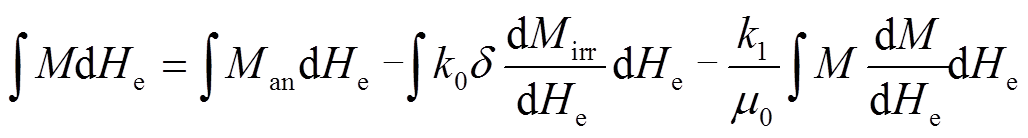（2）
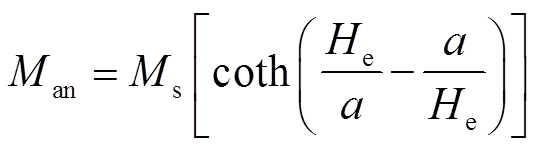（3）
式中，Man为无磁滞磁化强度；Mirr为不可逆磁化强度分量；μ0为真空磁导率；δ=sign(dH/dt)为没有物理意义的方向参数；a为无磁滞磁化的形状参数；He=H+αM表示有效磁场。式（2）包含k0的项与原始的J-A模型中k参数含义相同，表示钉扎效应；k1表示与磁畴矩旋转相关参数，包含参数k1的相关项表示使M偏离Man而消耗的能量，从而影响在磁致伸缩回线中从膝点到接近饱和的部分。通过结合式（1）与式（2）进行推导，最终得到磁致伸缩模型为
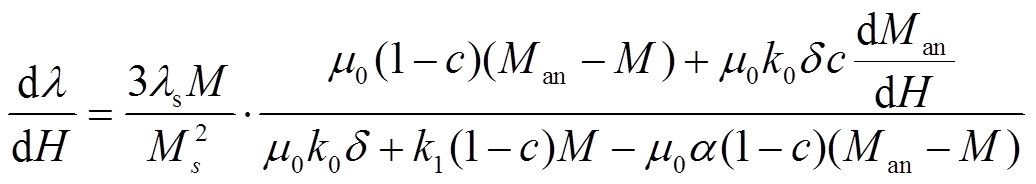（4）式中，c为与磁畴有关的弯曲系数；α为耦合参数。
J-A模型中的参数根据其物理意义[17]，直接从实验数据的特定参考点处进行近似计算。本文依据此理论探究模型中参数之间的关系，用于参数的定性分析。
所有的参数中，参数Ms可以通过对铁磁材料施加具体的激励磁场或通过查阅相关手册得到。由畴壁弯曲和可逆平移引起的可逆磁化分量Mrev在模型中由系数c确定。在初始磁化曲线的开始处，磁场较低，无磁滞磁化强度可以被近似地表示为
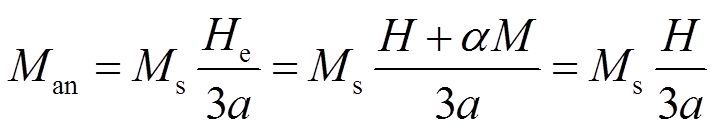（5）而参数c可以表示为
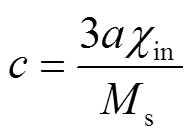（6）
假设参数a已知，且初始磁化率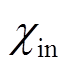
与饱和磁化强度Ms已经从实验数据中获得。参数k0可以在H=Hc，M=0处的磁化率确定，即
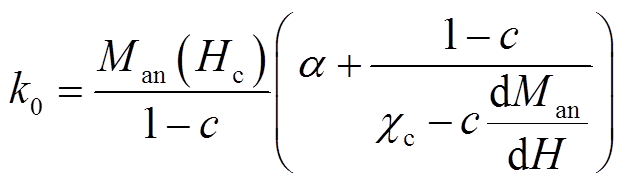（7）式中，Hc为矫顽力；
为矫顽点处的磁化率。在参数α、a、c已知的情况下，参数k0可以被计算出来。在剩余磁化强度Mr处得到参数α。此时δ=-1，并且磁场强度为零。
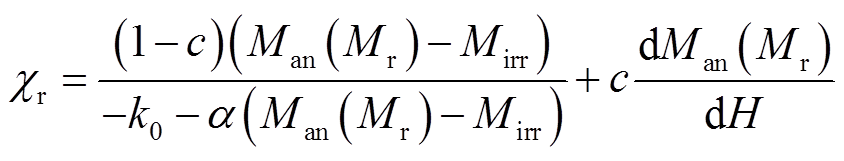（8）
式中，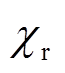
为剩磁点磁化率。参数a是从磁滞回线尖端的数据中得到的，假设在高饱和磁化水平时，磁滞与非磁滞相等。参数a的计算可由式（9）得到。
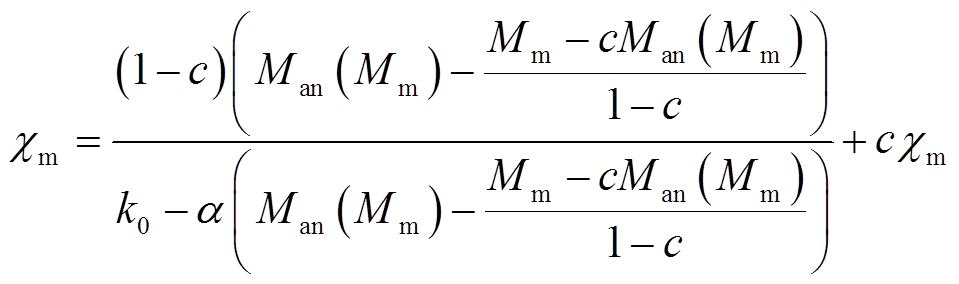（9）式中，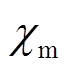
为饱和点磁化率；(Hm, Mm)是饱和点对应的磁场强度和磁化强度坐标。
同样，在磁滞回线尖端的数据中推导得到参数k1的表达式，在这个点上，δ=1，H=Hm，M=Mm，磁滞与非磁滞情况是等效的。
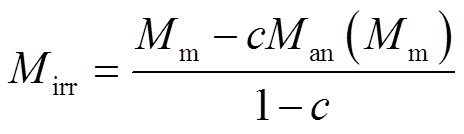（10）
（11）
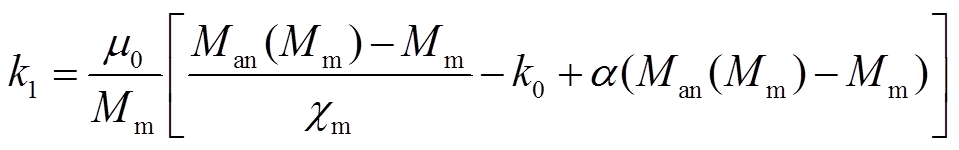（12）
式（12）表明参数k1与参数a、c、α、k0有关。
粒子群优化（Particle Swarm Optimization, PSO）算法是由J. Kennedy和R. C. Eberhart提出的一种进化算法[18-19]。本文采用粒子群优化算法对模型中多参数进行求解，优化的目标是模型计算结果与实验测量结果之间相差最少，建立的目标函数为
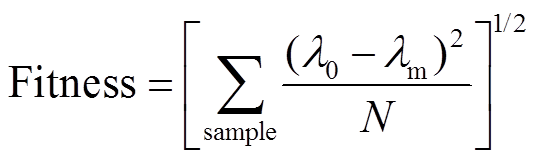（13）式中，N、λe和λm分别代表选取点的数量、磁致伸缩测量值以及模型计算值。求解目标函数的过程实际上是求解七个参数的最佳组合使目标函数最小。图5所示为求解过程的流程。
用粒子群算法优化分别得到取向硅钢样片18221955047在激励磁场强度最大值为80A/m（Hmax= 80A/m）与B27R085在Hmax=40A/m激励下，不同工作条件下的参数见表1~表3。
在正弦激励理想工作状态下，提取的磁滞回线与磁致伸缩回线的参数见表1。对于硅钢样片18221955047，当H线性增加10A/m，参数Ms增加0.001×106A/m，λs增加0.3×10-7m/m。在磁滞回线中参数k0=18.180 6，而磁致伸缩回线中k0=22.180 6，数值上相差4。对于硅钢样片B27R085，当H线性增加，参数Ms与λs也有同样的规律，而k0在数值上相差1。
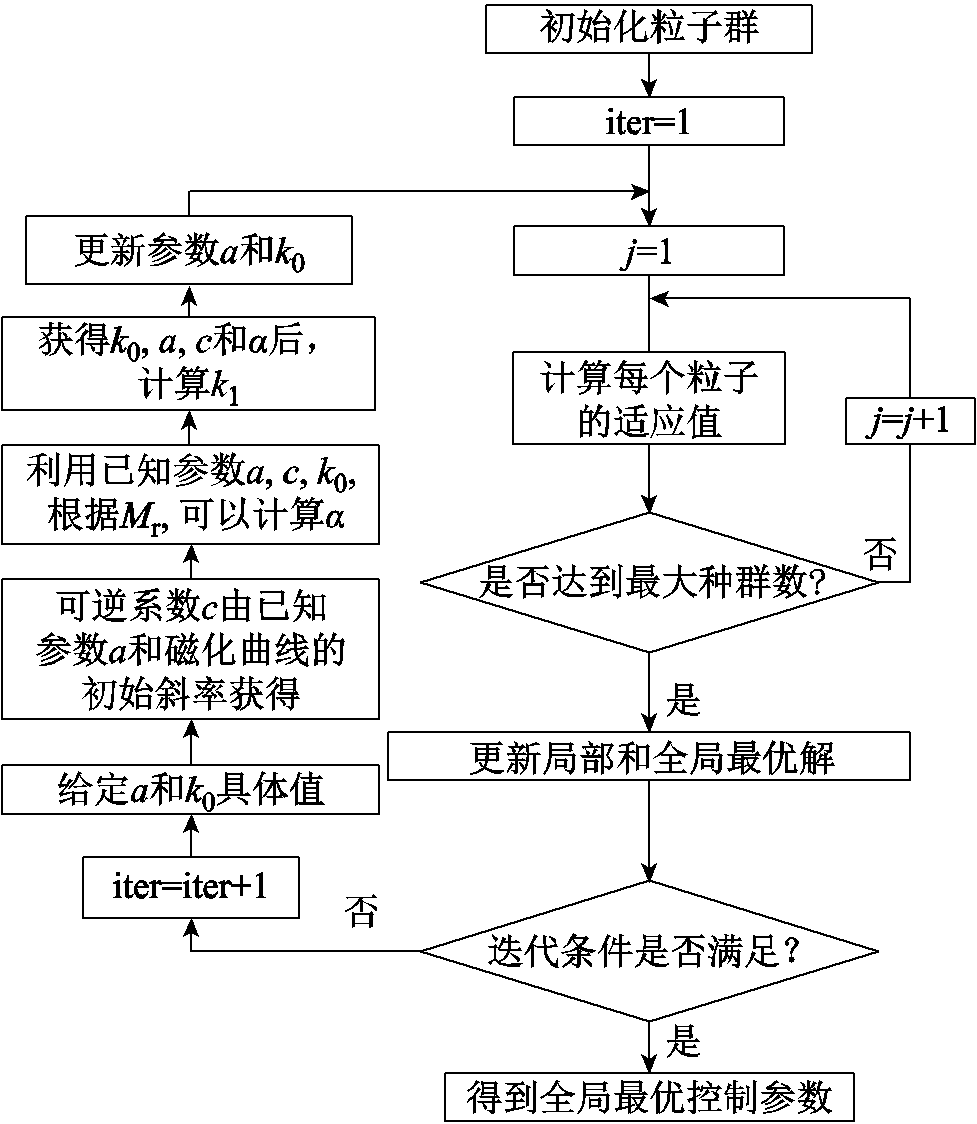
图5 粒子群优化算法流程
Fig.5 Flowchart of PSO algorithm
表1 正弦激励下取向硅钢参数表
Tab.1 Parameters of oriented silicon steel under sinusoidal excitation
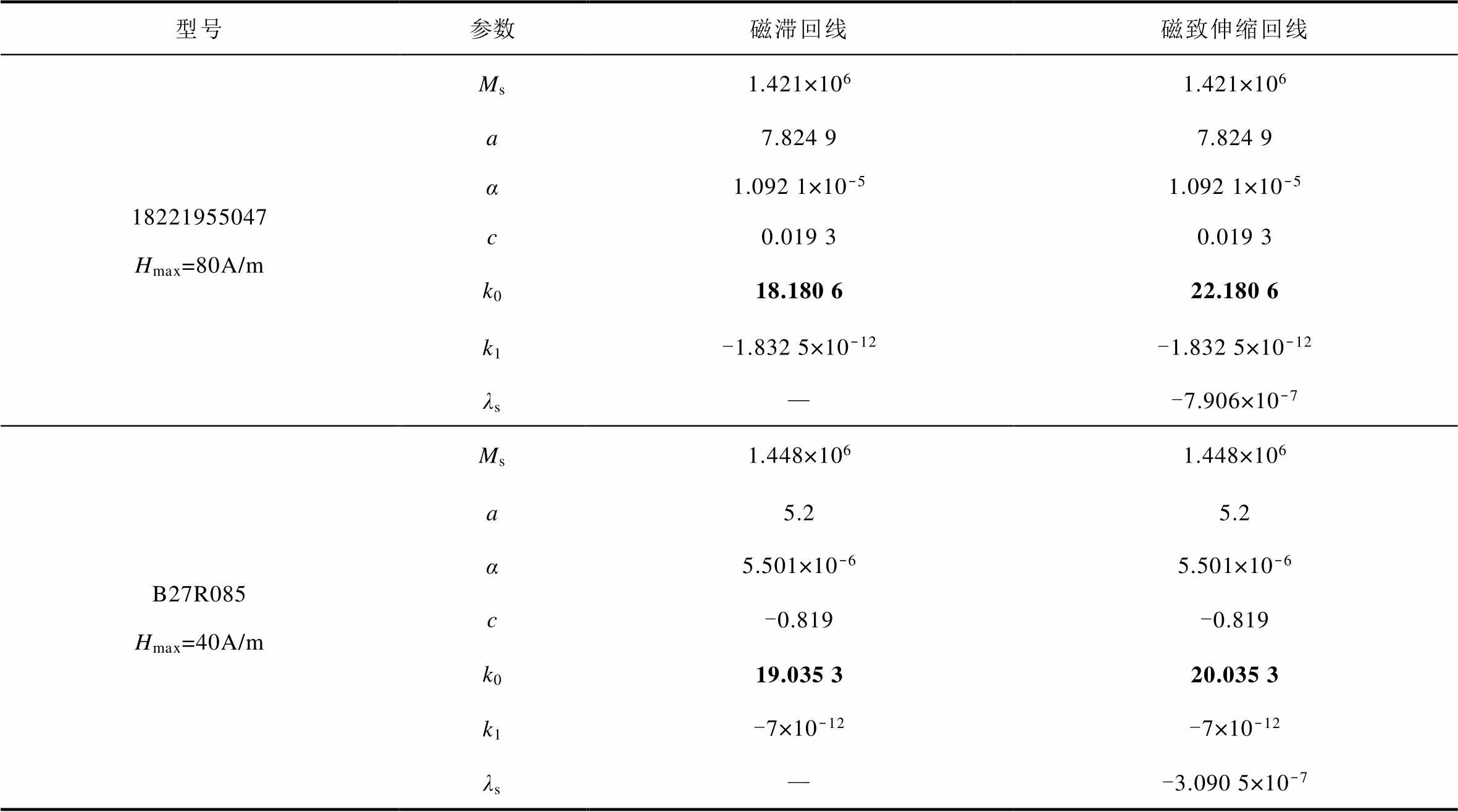
型号参数磁滞回线磁致伸缩回线 18221955047Hmax=80A/mMs1.421×1061.421×106 a7.824 97.824 9 α1.092 1×10-51.092 1×10-5 c0.019 30.019 3 k018.180 622.180 6 k1-1.832 5×10-12-1.832 5×10-12 λs—-7.906×10-7 B27R085Hmax=40A/mMs1.448×1061.448×106 a5.25.2 α5.501×10-65.501×10-6 c-0.819-0.819 k019.035 320.035 3 k1-7×10-12-7×10-12 λs—-3.090 5×10-7
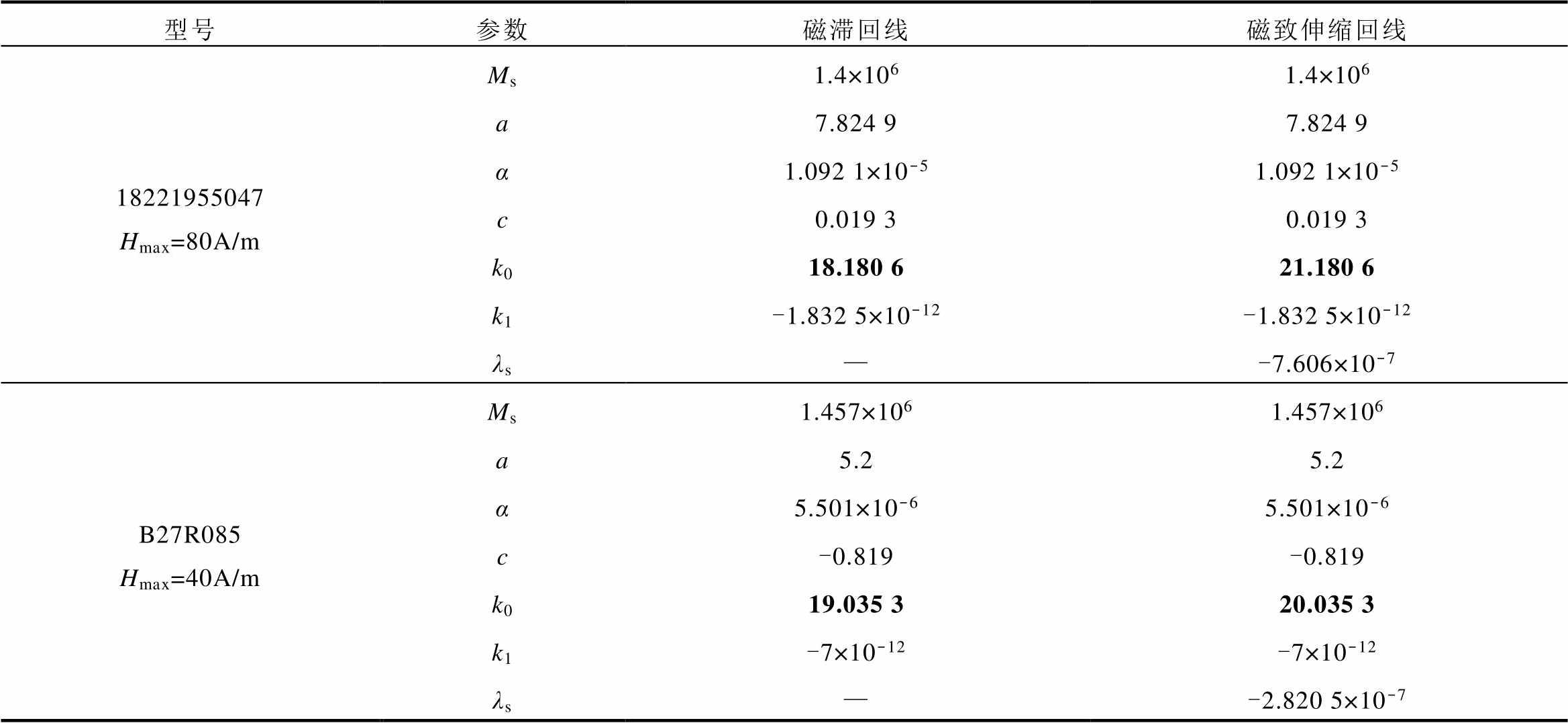
表2为在直流偏磁为1A条件下，当H以10A/m线性步长增加，硅钢片18221955047的参数Ms以0.01×106A/m增加；λs以0.05×10-7m/m增加，且磁滞回线与磁致伸缩回线中参数k0数值上相差为3。硅钢片B27R085的参数Ms增加0.001×106A/m；λs 增加0.03×10-7m/m，k0在数值上相差1。
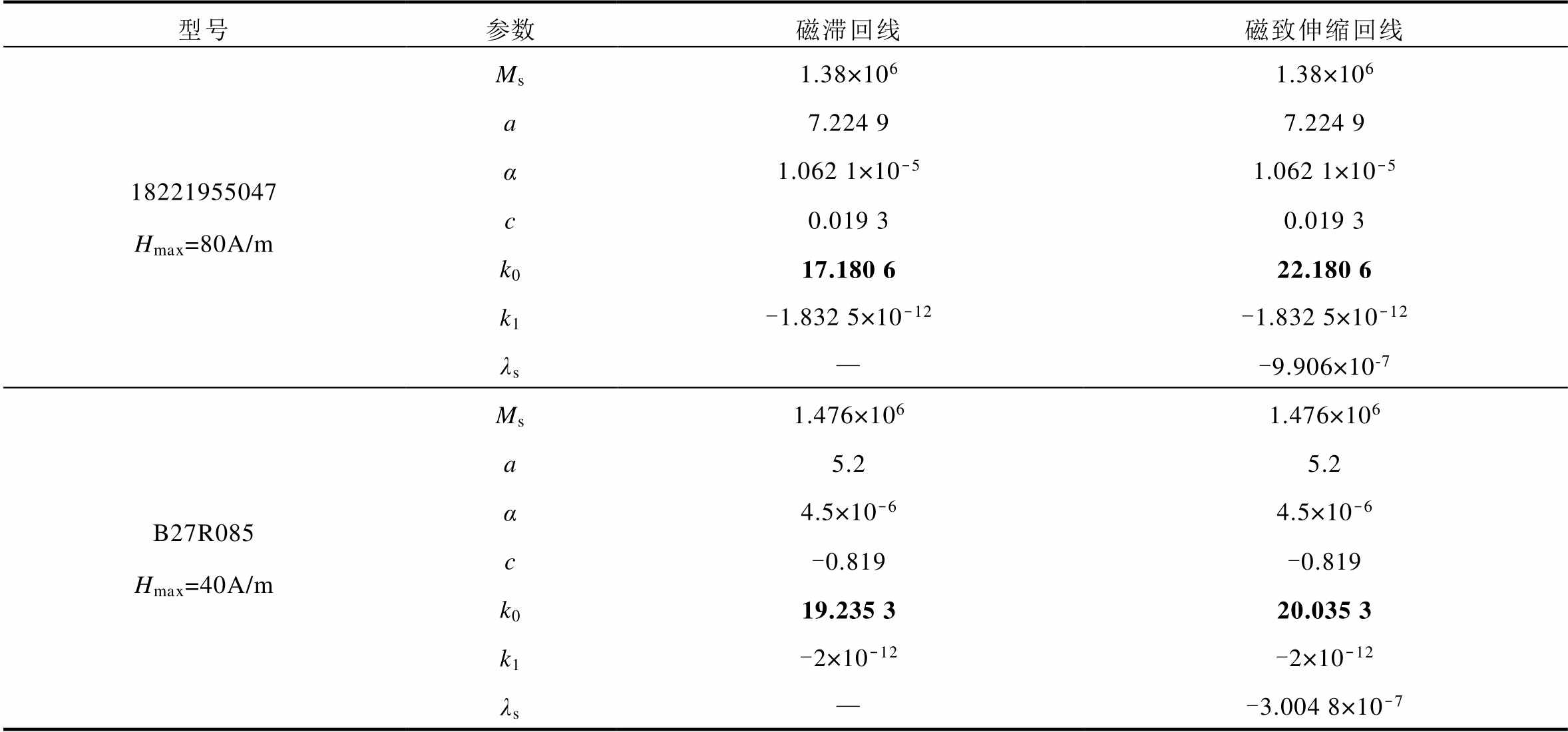
在占比为10%的3次谐波激励下，提取的磁滞回线与磁致伸缩回线的参数，见表3。当H增加10A/m，在硅钢片18221955047中，参数Ms增加0.005× 106A/m；λs以0.05×10-7m/m增加，在磁滞回线中参数k0=17.180 6，而磁致伸缩回线中k0=22.180 6，数值相差为5。而硅钢片B27R085的参数Ms增加0.001×106A/m；λs以0.01×10-7m/m增加，k0在数值上相差为1。
表2 直流偏磁影响下取向硅钢参数表
Tab.2 Parameters of oriented silicon steel under DC bias
型号参数磁滞回线磁致伸缩回线 18221955047Hmax=80A/mMs1.4×1061.4×106 a7.824 97.824 9 α1.092 1×10-51.092 1×10-5 c0.019 30.019 3 k018.180 621.180 6 k1-1.832 5×10-12-1.832 5×10-12 λs—-7.606×10-7 B27R085Hmax=40A/mMs1.457×1061.457×106 a5.25.2 α5.501×10-65.501×10-6 c-0.819-0.819 k019.035 320.035 3 k1-7×10-12-7×10-12 λs—-2.820 5×10-7
表3 三次谐波影响下取向硅钢参数表
Tab.3 Parameters of oriented silicon steel under third harmonic
型号参数磁滞回线磁致伸缩回线 18221955047Hmax=80A/mMs1.38×1061.38×106 a7.224 97.224 9 α1.062 1×10-51.062 1×10-5 c0.019 30.019 3 k017.180 622.180 6 k1-1.832 5×10-12-1.832 5×10-12 λs—-9.906×10-7 B27R085Hmax=40A/mMs1.476×1061.476×106 a5.25.2 α4.5×10-64.5×10-6 c-0.819-0.819 k019.235 320.035 3 k1-2×10-12-2×10-12 λs—-3.004 8×10-7
另外，结合取向硅钢的磁特性特点，随着激励磁场的变化，磁致伸缩曲线交点处位置会发生明显的变化。这与在剩磁点（0, Mr）处计算的参数α紧密相关。因此，以上三种情况下的参数显示：在正弦、直流偏磁和谐波等不同激励条件下，随着激励磁场的线性变化，参数α也发生规律性的变化。
将所获得的多参数代入模型中，得到模型的计算结果，并与实验结果进行对比，以在激励磁场峰值为80A/m时的硅钢片18221955047和在激励场峰值为40A/m时的硅钢片B27R085为例进行讨论。正弦激励、直流偏磁和谐波影响下对比结果及误差分析如图6~图8所示。
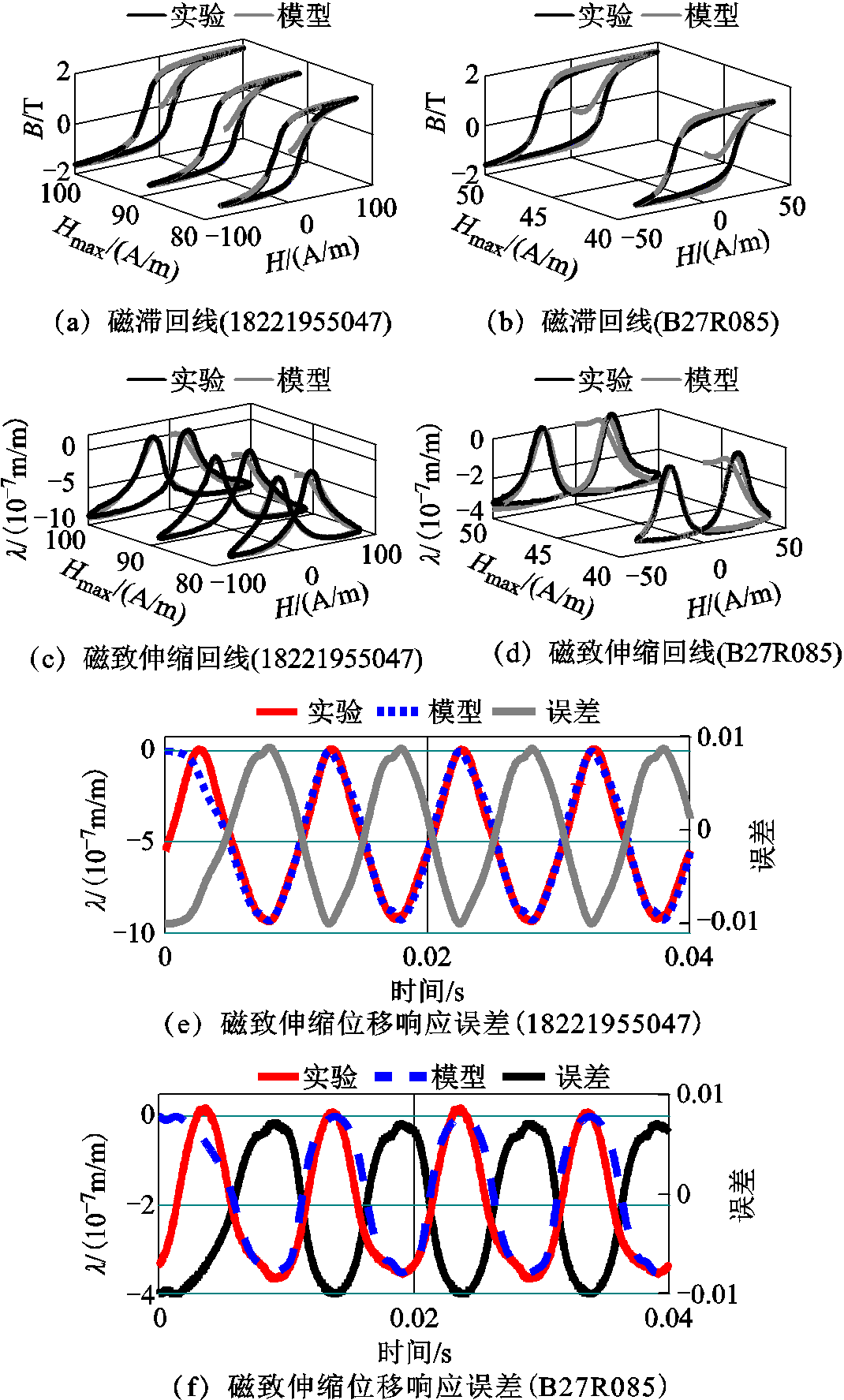
图6 正弦激励下对比结果及误差分析
Fig.6 Comparison and error analysis under sinusoidal excitation
为了进一步验证模型的准确性，用式（13）计算模型计算与实验测量之间的误差，磁致伸缩位移响应的平均误差定义为
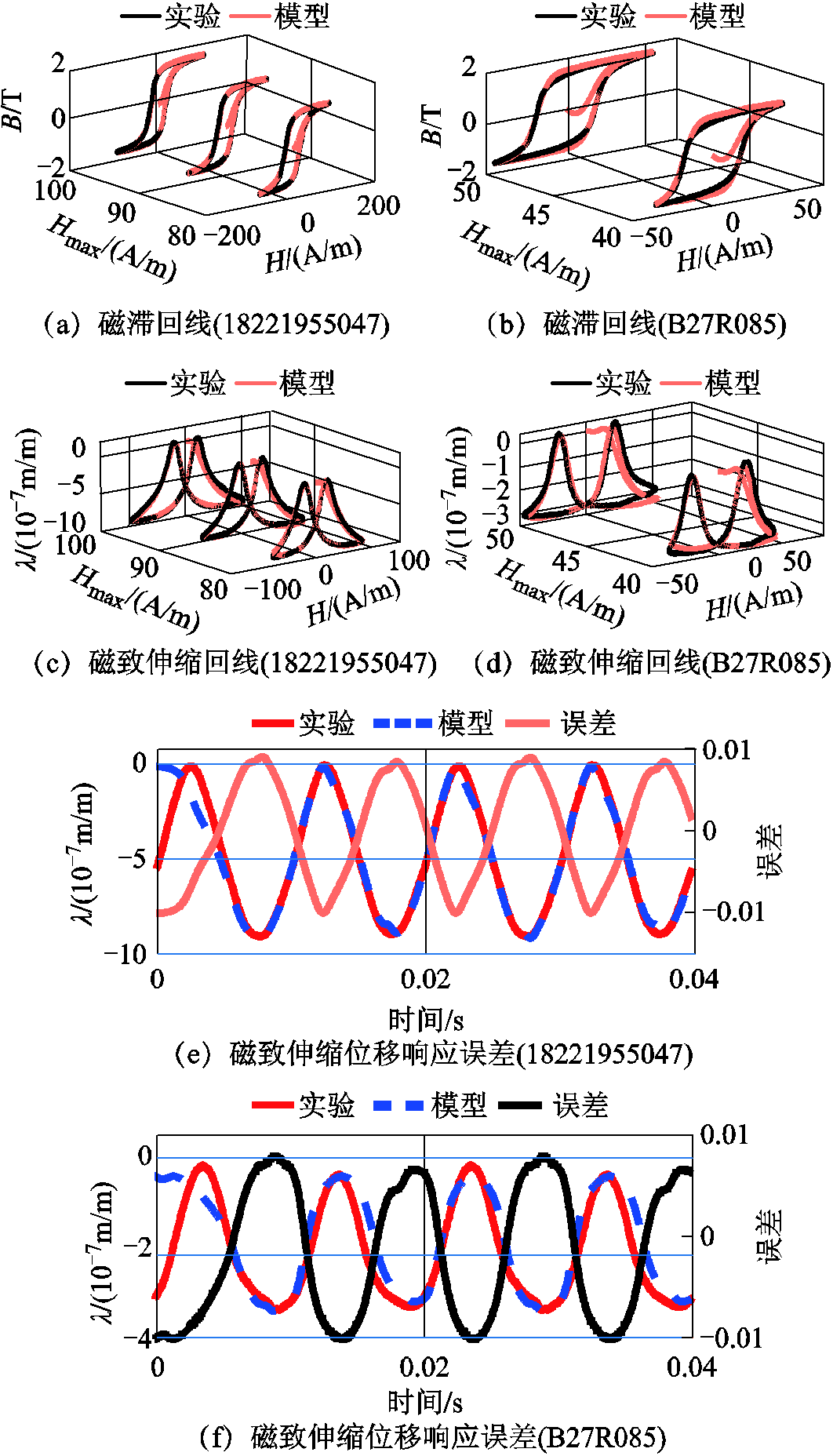
图7 直流偏磁影响下对比结果及误差分析
Fig.7 Comparison and error analysis under DC bias
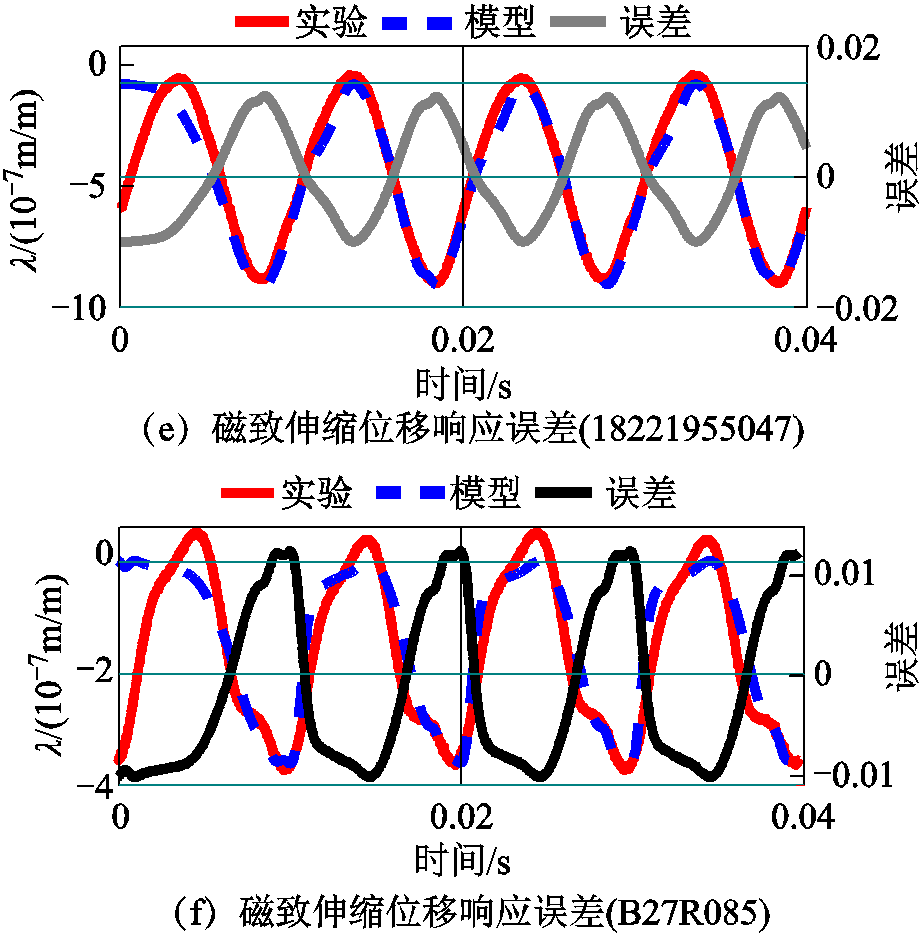
图8 谐波影响下对比结果及误差分析
Fig.8 Comparison and error analysis under harmonic
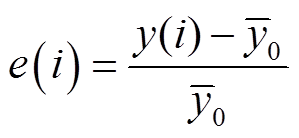（13）
式中，y(i)为模型计算得到的磁致伸缩位移响应；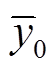
为实验中磁致伸缩位移响应的平均值。
在给定正弦激励条件下，利用模型计算与实验测量的磁特性结果对比如图6所示。结果表明磁滞回线和磁致伸缩回线计算和测量之间的吻合度很好，如图6a~图6d所示。为进一步表示两者误差，对其进行误差分析，如图6e和图6f所示。
通过对不同工作点下的磁致伸缩位移响应的定量分析，求解得到硅钢片18221955047的磁致伸缩结果与测量之间误差如图6e所示，其误差小于1%；图6f所示的硅钢片B27R085的误差则更小。
在直流偏磁为1A时得到的模型计算与实验测量的对比结果如图7所示。图7a和图7c是硅钢片18221955047的磁滞和磁致伸缩回线模型计算与测量的对比结果，图7b和图7d是硅钢片B27R085的对比结果。两者结果均表明实验测量与模型计算结果具有良好的一致性。在偏磁场1A/m情况下，以激励磁场强度Hmax=80A/m进行分析，如图7e所示，硅钢片18221955047模型计算的磁致伸缩与测量结果之间的误差约1%；硅钢片B27R085以激励磁场Hmax=40A/m为例，对应误差小于1%。结果表明建立的磁致伸缩模型适用于直流偏磁下的取向硅钢的磁致伸缩的计算。
在动态激励磁场下加入3次谐波，磁滞回线与磁致伸缩回线的实验测量与模型计算的对比分别如图8a~图8d所示。硅钢片18221955047激励磁场Hmax=80A/m时的误差分析如图8e所示，其磁致伸缩位移响应误差在2%以下；硅钢片B27R058激励磁场Hmax=40A/m为例，其磁致伸缩位移响应误差分析如图8f所示，误差在1.2%左右。结果表明模型对于谐波情况下的磁致伸缩特性仍具有适用性。
通过不同条件下进行对比分析，可以看出在谐波存在时磁致伸缩模型计算与测量误差较大于其他两种工况，这是由于谐波的存在会增加硅钢片的附加铁耗和铜耗，会使特性回线局部发生明显畸变。本文基于改进的J-A模型建立的磁致伸缩模型没有精确地考虑增加的这部分损耗。在不同服役条件下，通过PSO优化求解得到的参数代入磁致伸缩模型，在电工硅钢服役磁通范围内得到的计算结果与实验测量结果之间良好的一致性与较小的误差证明了建立模型的准确性。需要指出的是，本文建立的模型在较低磁场时具有局限性，误差较大，需要对模型进一步完善。文中建立的磁致伸缩模型可实现由磁滞特性预测磁致伸缩特性的目标，对于获取较难测量的磁致伸缩特性有较高的工程应用价值。
为研究建立硅钢磁致伸缩特性模型，本文在J-A模型的基础上引入与磁畴旋转有关的参数k1，结合改进的J-A模型和二次畴转模型，推导建立了适用于取向硅钢的磁致伸缩模型。用粒子群优化算法得到动态激励磁场下模型中多参数之间的关系，由磁滞回线的参数推及磁致伸缩模型参数，为在能够测取磁化特性但无法测量磁致伸缩时通过建立模型预测获得磁致伸缩特性奠定基础。
考虑硅钢铁心工作条件，本文分别在正弦、直流偏磁与谐波不同激励条件下，将建立的模型计算结果与实验测量结果进行对比分析，结果表明两者具有很高的吻合度，且对磁致伸缩位移误差进行定量分析，均控制在2%以内。本文的研究结果表明，建立的模型可用于在磁滞特性的基础上预测取向硅钢磁致伸缩特性，对研究电力变压器等电工装备的磁致振动具有重要意义。
参考文献
[1] 李长云, 郝爱东, 娄禹. 直流偏磁条件下电力变压器振动特性研究进展[J]. 电力自动化设备, 2018, 38(6): 215-223. Li Changyun, Hao Aidong, Lou Yu. Research progress on vibration characteristics of power transformers under DC bias conditions[J]. Electric Power Automation Equipment, 2018, 38(6): 215-223.
[2] Jiles D C. Theory of the magnetomechanical effect[J]. Journal of Physics D: Applied Physics, 1999, 28(8): 1537.
[3] Sablikm, Jiles D C. Coupled magnetoelastic theory of magnetic and magnetostrictive hysteresis[J]. IEEE Transactions on Magnetics, 1993, 29(3)：2113-2123.
[4] Hristoforou E. Magnetostrictive delay lines: engineering theory and sensing applications[J]. Measurement Science & Technology, 2003, 14(2): R15-R47.
[5] Adly A A , Mayergoyz I D , Bergqvist A . Preisach modeling of magnetostrictive hysteresis[J]. Journal of Applied Physics, 1991, 69(8): 5777-5779.
[6] 张黎, 王国政, 董攀婷, 等. 基于磁致伸缩本征特性的晶粒取向性变压器铁心振动模型[J]. 中国电机工程学报, 2016, 36(14): 3990-4000. Zhang Li, Wang Guozheng, Dong Panting, et al. Core-oriented transformer core vibration model based on magnetostrictive intrinsic property[J]. Proceedings of the CSEE, 2016, 36(14): 3990-4000.
[7] Foster S L, Reiplinger E. Charcteristics and control of transformer sound[J]. IEEE Transactions on Power Apparatus and Systems, 1981, PAS-100(3): 1072-1077.
[8] 顾晓安, 曾进, 沈荣瀛. 正弦电磁场中铁磁材料数学模型[J]. 应用数学和力学, 2004, 25(9): 974-982. Gu Xiaoan, Zeng Jin, Shen Rongying. Mathematical model of ferromagnetic materials in sinusoidal electromagnetic field[J]. Applied Mathematics and Mechanics, 2004, 25(9): 974-982.
[9] 祝丽花, 杨庆新, 闫荣格, 等. 考虑磁致伸缩效应电力变压器振动噪声的研究[J].电工技术学报, 2013, 28(4): 1-6,19. Zhu Lihua, Yang Qingxin, Yan Rongge, et al. Study on vibration and noise of power transformer considering magnetostrictive effect[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 1-6, 19.
[10] Hilgert T, Vandevelde L, Melkebeek J. Neural- network-based model for dynamic hysteresis in the magnetostriction of electrical steel under sinusoidal induction[J]. IEEE Transactions on Magnetics, 2007, 43(8): 3462-3466.
[11] Li Q, Wang X, Zhang L, et al. Modelling methodology for transformer core vibrations based on the magnetostrictive properties[J]. IET Electric Power Applications, 2012, 6(9): 604.
[12] Jiles David C. Introduction to magnetism and magnetic materials[M]. Boca Raton: CRC Pr I LIc, 1998.
[13] Lee E W. Magnetostriction and magnetomechanical effects[J]. Reports on Progress in Physics, 1955, DOI:10.1088/0034-4885/18/1/305.
[14] 李长云, 刘亚魁. 直流偏磁条件下变压器铁心磁化特性的Jiles-Atherton修正模型[J]. 电工技术学报, 2017, 32(19): 193-201. Li Changyun, Liu Yakui. Jiles-Atherton correction model of magnetization characteristics of transformer core under DC bias[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 193-201.
[15] 王旭, 张艳丽, 唐伟, 等.旋转磁化下逆矢量Jiles-Atherton磁滞模型改进[J]. 电工技术学报, 2018, 33(增刊2): 257-262. Wang Xu, Zhang Yanli, Tang Wei, et al. Improvement of inverse vector Jiles-Atherton hysteresis model under rotational magnetization[J]. Transactions of China Electrotechnical Society, 2018, 33 (S2): 257-262.
[16] Li Yang, Zhu Lihua, Zhu Jianguo. Core loss calculation based on finite-element method with Jiles-Atherton dynamic hysteresis model[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-5.
[17] Jiles D C, Thoelke J B, Devine M K. Numerical determination of hysteresis parameters for the modeling of magnetic properties using the theory of ferromagnetic hysteresis[J]. IEEE Transactions on Magnetics, 1992, 28(1): 27-35.
[18] 程声烽, 程小华, 杨露. 基于改进粒子群算法的小波神经网络在变压器故障诊断中的应用[J]. 电力系统保护与控制, 2014, 42(19): 37-42. Cheng Shengfeng, Cheng Xiaohua, Yang Lu. Application of wavelet neural network based on improved particle swarm optimization in transformer fault diagnosis[J]. Power System Protection and Control, 2014, 42(19): 37-42.
[19] 刘任, 李琳, 王亚琦, 等. 基于随机性与确定性混合优化算法的Jiles-Atherton磁滞模型参数提取[J]. 电工技术学报, 2019, 34(11): 2260-2268. Liu Ren, Li Lin, Wang Yaqi, et al. Parameter extraction of Jiles-Atherton hysteresis model based on hybrid optimization algorithm of randomness and determinism[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2260-2268.
Research on Magnetostrictive Model for Oriented Silicon Steel under Service Conditions
Abstract Magnetostrictive effect of silicon steel is the main source of vibration noise for power equipment such as transformers. In order to establish the magnetostrictive model for silicon steel, the magnetic domain rotation characteristics were considered and the related parameter k1 was added in the J-A model. Then, the magnetostrictive model of oriented silicon was established by combing the improvedJ-A model with the quadratic domain rotation model. The parameters in the model were extracted using the particle swarm optimization algorithm(PSO). Considering the working condition of power transformers, the magnetostrictive properties of oriented silicon steel were analyzed under ideal sine, harmonics and DC bias, respectively. The results showed that the magnetostrictive curves calculated by the model under the different conditions were in good agreement with the experimentally measured data. Therefore, the magnetostrictive model proposed in the paper can be used to simulate the magnetostrictive properties of oriented silicon steel under service conditions.
keywords：J-A model, oriented silicon steel, magnetostrictive model, service condition, particle swarm optimization algorithm(PSO)
DOI：10.19595/j.cnki.1000-6753.tces.191224
中图分类号：TM401+.1
祝丽花 女，1984年生，博士，副教授，研究方向为工程电磁场数值计算，电工装备减振降噪技术。E-mail：zhulihua@tjpu.edu.cn（通信作者）
李晶晶 女，1994年生，硕士研究生，研究方向为硅钢片磁致伸缩测量及模型的建立。E-mail：2475679932@qq.com
国家自然科学基金重大项目资助（51690181）。
收稿日期 2019-09-26
改稿日期 2019-12-16
（编辑 郭丽军）