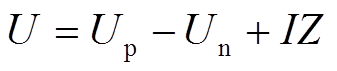 (1)
(1) 式中,U为端电压;Up、Un分别为正、负极电动势;I为电池电流,放电时为负值;Z为电池阻抗;角标p、n分别为正极和负极。
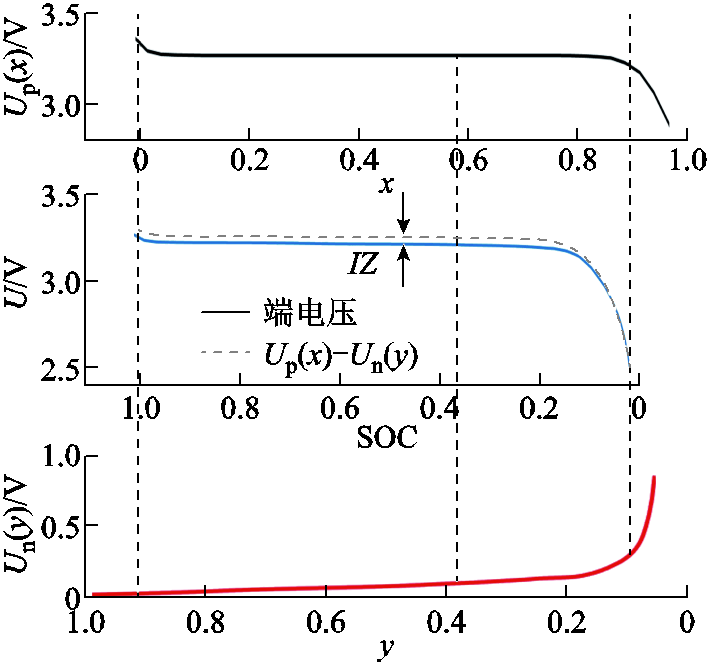
图1 正负极电势以及全电池电压曲线
Fig.1 Positive and negative potential and full battery voltage curves
摘要 商用锂离子电池包含正极和负极,这两个电极的老化速度一般不一致。以磷酸铁锂电池为例,该电池老化主要由负极贡献的。为了在不拆解全电池的情况下研究其老化问题,需要从其外特性中求取可反映老化现象的负极特征曲线,然后再从这段特征曲线中确定相关的老化信息。该项工作首先需要确定该曲线明显的荷电状态(SOC)区间段,称为负极特征区间。为此,该文首先提出电池基于分数阶模型的线性化电势变化模型;通过研究在不同SOC工作点处正负电极电势的变化特征,给出可以利用全电池阶跃电流激励仿真确定该负极特征区间的方法;最后分析了该区间与电池老化的关联性。该文采用三电极电池(含参比电极)验证了该负极特征区间的正确性,该方法对商用磷酸铁锂电池老化问题的在线观测具有指导意义。
关键词:磷酸铁锂 电池老化 分数阶模型 负极特征区间
锂离子电池具有能量密度和功率密度高、无记忆效应等优点,因此在电动汽车和混合动力汽车上具有广阔的应用前景[1-4]。在使用过程中,由于副反应因素的影响,锂离子电池内部正、负极和固体电解质相界面(Solid Electrolyte Interphase, SEI)膜等部分的形态和性质发生变化[5-6],导致电池出现老化现象。电池老化的宏观外特性通常表现为容量衰减和内阻升高[7-8],这使得电池管理系统对电池的有效控制与管理难度增加[9-11]。因此,老化问题除了应在电池设计与制造时充分考虑外,使用过程中需要依靠有效的模型和工程方法对其进行评估与预测。
商用锂离子电池为双电极结构,这两个电极的老化状态一般不一致。磷酸铁锂电池的老化主要归因于负极的老化。清华大学韩雪冰等利用双水箱模型对电池正、负极电极老化情况进行描述,基于充电曲线重构电池的衰减机理并定量分析几种商用电池电极正、负极容量和锂离子浓度随老化的变化[12]。韩雪冰等通过建立MPM(mechanistic and prognostic model)模型分析磷酸铁锂电池老化[13],指出磷酸铁锂电池老化主要发生的是负极容量变化以及锂离子浓度改变,而正极容量几乎不发生变化。锂离子电池的SEI膜形成主要发生在负极[14-16],首次或者前几次充电时会在石墨负极形成SEI膜。负极材料在锂离子嵌入和脱嵌的过程中,会发生体积变化,这会使SEI膜出现裂纹,从而在每次电池循环中不可避免地都会有富锂的石墨负极与电解液进行反应,消耗电解液与可用锂离子,导致电池可用容量持续减少,同时使SEI膜持续增厚。负极如何表征电池老化有待进一步研究。
电池电压响应包含正极和负极的电势响应。文献[17]基于锂离子电池单颗粒模型,结合固相扩散偏微分方程,对固相颗粒表面锂离子浓度与电流体密度的函数关系进行简化,得到了可以表征正负极动态响应过程的分数阶模型。
基于以上成果,为了在不拆解全电池的情况下在线研究电池老化问题,需要从全电池外特性中求出含有上述老化特性的负极特性曲线(如电势-电流或荷电状态(State of Charge,SOC)特性),并从这段特征曲线中求解相关的老化信息。因此,首先要的确定该曲线中负极特征明显的SOC区间段,本文称为负极特征区间。本文基于上述电池分数阶模型,首先分析了在不同SOC下两个电极电势的变化特征,线性化“负极电势变化-SOC”特性以便获取参数。然后,为了求解该负极特征区间,从电池获取一组基于阶跃激励的正、负极电势变化曲线,并从中找出在全寿命周期一直存在的负极电势随SOC变化剧烈而正极却相对稳定的特征区间。论文采用三电极实物实验和基于上述线性化模型的全电池实验确认方法的可行性和有效性。最后分析和验证电池老化前、后该负极特征区间的变化情况,以确定该区间随着电池老化的不变性。
锂离子电池的全电压响应包含正极和负极的电势响应。以磷酸铁锂电池为例,图1为磷酸铁锂电池正、负极电势和端电压曲线[13],图中横轴x、y分别为正、负极锂离子浓度,SOC为当前全电池荷电状态,电池端电压可以看成正、负极电势差和全电池阻抗引起的电压降,即
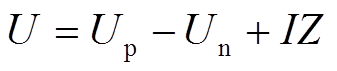 (1)
(1) 式中,U为端电压;Up、Un分别为正、负极电动势;I为电池电流,放电时为负值;Z为电池阻抗;角标p、n分别为正极和负极。

图1 正负极电势以及全电池电压曲线
Fig.1 Positive and negative potential and full battery voltage curves
对于式(1)的阻抗Z,公认的小幅值电流激励下的阻抗谱(Electrochemical Impedance Spectrum, EIS)如图2所示[17-18]。其高频部分为集流体与测试线导致的高频感抗;中频部分为电荷转移、传质、液相扩散等共同形成的半圆形阻抗Z中频;低频部分为固相扩散形成的倾斜直线,该区间内电池主要发生固相扩散反应。
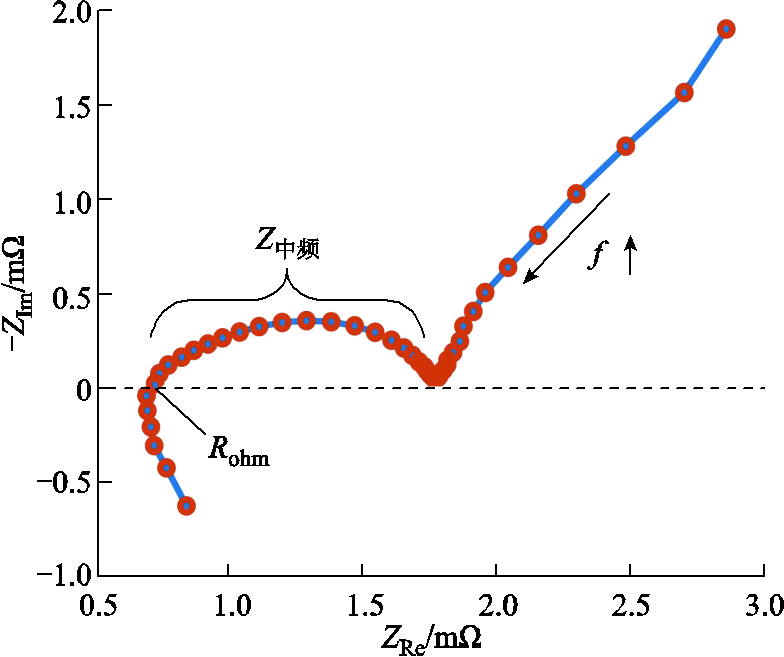
图2 典型阻抗谱
Fig.2 Typical impedance spectrum
进一步,文献[17]将图2阻抗Z分为欧姆内阻Rohm(一般认为Rohm是半圆与实轴交点)和中频阻抗Z中频(Z中频用来描述中频半圆阻抗)。固相扩散过程体现在引起正、负极电动势Up、Un的变化中。因此在SOC0处电池施加电流激励后端电压U的响应为
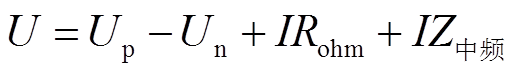 (2)
(2)正、负极电势Up、Un分别是三种荷电状态的函数,即SOC0为施加激励电流之前的SOC,SOCI为电流引起的SOC变化;SOCdiff为固相扩散引起的SOC变化,因此式(2)中
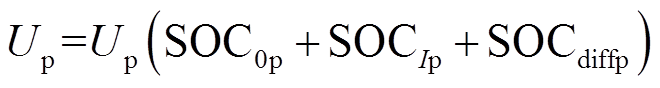 (3)
(3)
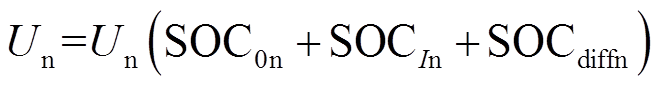 (4)
(4)文献[17]基于分数阶理论[19]对正、负极固相扩散进行建模,所建立的模型可以描述电池内部动态过程。得到正、负极扩散引起SOC变化以及电流引起SOC变化关系如式(5)~式(8)所示。
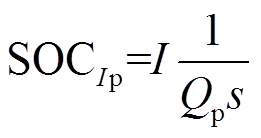 (5)
(5)
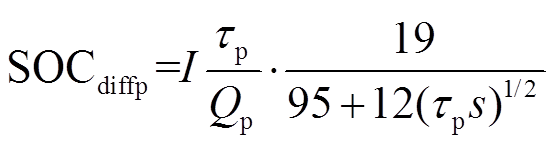 (6)
(6)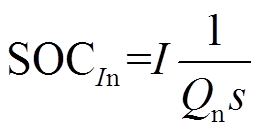 (7)
(7)
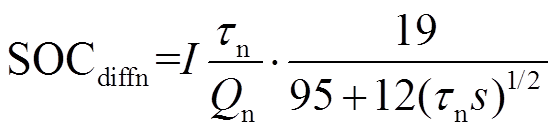 (8)
(8)
式中,Qp、Qn分别为正、负极容量;τp、τn分别为正、负极扩散时间常数。
由于式(2)~式(8)构成的模型非常复杂,难以通过对全电池施加简单的激励后从电池响应信号中辨识模型的参数。为此,以负极为例,首先研究负极电势变化的线性化模型。
为了便于说明,将图1重作于图3a。由上文可知,相对于磷酸铁锂电池负极电势而言,放电电流激励几乎不引起其正极电势的变化。在图3a某SOC0处施加阶跃放电电流激励,则图3b为对应的动态响应过程中负极SOC随时间的变化。对应地,在图3a中SOC0处负极电势变化为∆Un。本文采用线性函数对负极电势的变化∆Un建模。基于式(4),∆Un线性化模型如式(9)。
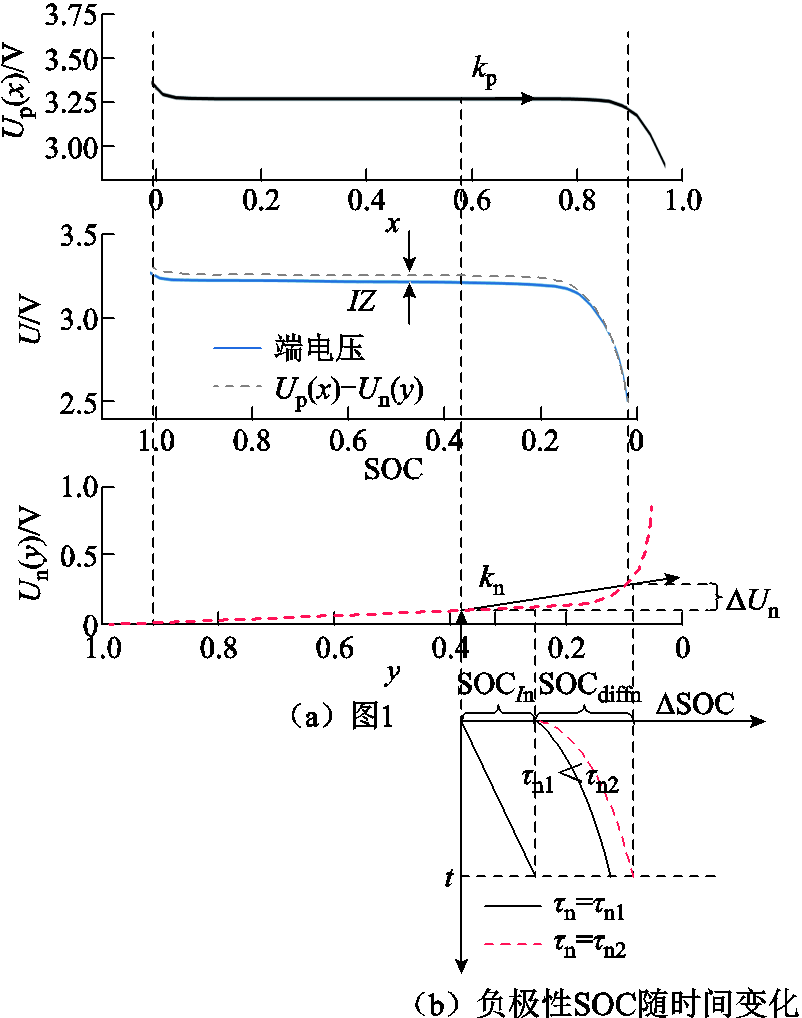
图3 SOC0处电池阶跃响应负极电势变化图
Fig.3 Negative potential change at SOC0
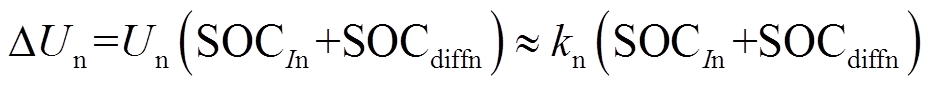 (9)
(9)式中,k为SOC0处电势曲线的斜率。由于电池在恒流放电的过程中,电流在正负极间通过,由放电电流引起的SOC变化大致相等,因此负极电势变化∆Un与负极的斜率kn、SOC diffn相关。由图3b所示,实线为τn=τn1时SOCn diff随时间的变化,虚线为τn=τn2时SOCn diff随时间的变化。在其他参数不变的条件下,当τn越大,引起的SOC变化越大,根据式(9),电势变化也越大。因此每个SOC点的阶跃响应电势变化∆Un与kn、负极固相扩散时间常数τn相关,τn越大、kn越大,电势变化越大。
实际工程中比较常见的是在电池上施加阶跃电流信号,因此本文选取的电池激励为电池阶跃电流激励。电池阶跃电流响应中,以电池静置后阶跃电流的电压响应最为基本[20-21]。下文如无特殊说明,电池阶跃响应均指静置后对应阶跃放电电流的电压响应。
于是,基于分数阶模型以及线性化电势变化模型,利用一组在SOC0处的阶跃响应即可得到电池正、负极电势变化。以下将讨论如何通过电池实验获取模型参数。
为了获取上述模型的实际参数,本节特制了电池实验的条件及工具,并介绍分数阶模型参数的获取方法。2.1节和2.2节基于同款磷酸铁锂电池实验获取分数阶模型参数,2.1节基于半电池实验获取电势曲线进而获取参数k,2.2节基于三电极电池实验获取扩散时间常数τ。2.3节为电池老化实验,用来分析τ随老化的变化,实验结果见4.2节。
分别取正负极材料做成纽扣半电池(负极为锂金属的单电极电池)在充满氩的手套箱进行实验。磷酸铁锂电极在3.5V(充电截止电势)和2.8V(放电截止电势)之间循环,石墨电极在1.8V和50mV之间循环,获得类似如图1所示的正、负极电势曲线以及正负极的开路电压(Open Circuit Voltage, OCV)数据,从而可以确定正、负极电势曲线,进而得到各SOC点的k值。
半电池只能用来求取正、负极充放电电势曲线,为求取正、负极分别的固相扩散时间常数,需要正负极分别进行EIS实验,因此需要利用三电极电池进行实验。
在磷酸铁锂软包电池中插入铜丝作参比电极做成三电极电池,在环境温度为25℃的条件下进行EIS实验,电池参数见表1。利用Bio-Logic公司的VMP3多通道恒电位器进行电化学测量。该恒电位器可同时测量电池正极-负极、正极-参比电极和负极-参比电极的阻抗。施加幅值1.5A的正弦变化的电流,频率范围为1mHz~10kHz。
表1 三电极实验用电池参数
Tab.1 Parameters of three-electrode experimentation

参数数值(型号) 电池型号WX123250 实测容量/(A·h)50 放电电流范围/A0~1.5 端电压范围/V2.0~3.6 工作温度/℃25
基于三电极EIS实验可辨识正负极固相扩散时间常数。以负极为例,由式(8)可知SOC变化量δSOCn相对电流的关系为
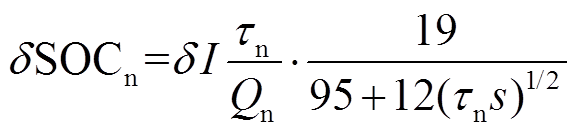 (10)
(10)而EIS测试为
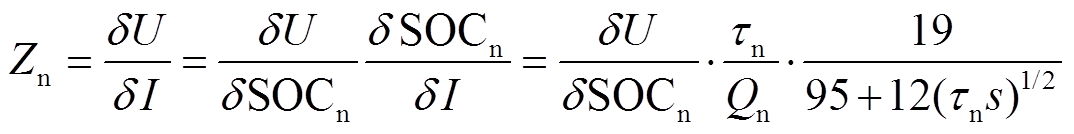 (11)
(11)
由式(10)和式(11)可以看到,EIS测试与SOC的关系差一个电压相对SOC的微分关系,该关系可通过电压微分(DVA)得到。在得到电压微分结果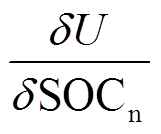 之后,即可求出负极固相扩散时间常数τn。
之后,即可求出负极固相扩散时间常数τn。
实验采用新威公司BTS-4系列电池测试台对某款磷酸铁锂电池进行充放电操作,并使用高低温实验箱来控制实验的环境温度,电池的具体参数见表2。具体实验步骤如下:
(1)先将电池根据电池厂商的标准以及电池特性充满电,在环境温度25℃下使用I=0.05C的电流恒流充电,当U=3.65V时开始恒压充电,当电流为0.02C时充电完成。
(2)对电池进行放电,放电电流I=0.05C,当U=2.0V时放电完成。
(3)将电池静置3h,使得电池内部的化学物理状态达到稳定状态(注:静置时间需要根据选用电池的体积以及形状等实际情况确定,比如大体积、不利于散热的电池需要的静置时间多,本次实验所用电池采用上述静置时间已足够)。
(4)将电池充满电,在环境温度25℃下使用I=1C的电流恒流充电,当U=3.65V时开始恒压充电,当电流为0.02C时充电完成。
(5)对电池进行放电,放电电流I=1C,当U=2.0V时放电完成。
(6)重复步骤(3)~(5)50次,该步骤是为了老化电池,采取步骤(1)和(2)进行电池测试(注:该步骤使得电池在每循环50次后进行1次低电流充放电,用来更新模型参数{Qp, Qn, y0, x0, Z})。
(7)重复步骤(1)~(6)至电池完全老化。
表2 老化实验用电池参数
Tab.2 Parameters of aging experimentation

参数数值(型号) 电池型号26650MP2-Fe 实测容量/(A·h)3.2 放电电流范围/A0~3 端电压范围/V2.0~3.6 工作温度/℃25
参数{Qp, Qn, y0, x0, Z}的求取方法详见文献[9],参数Z中频参考文献[17],本文不再赘述。
本节首先仿真得到新电池的负极特征区间,然后利用三电极EIS实验对得到的负极特征区间进行验证。
根据式(4),正负极阶跃响应电势变化由初始点SOC0、充放电电流引起的SOC变化以及固相扩散引起的SOC变化决定;全电池阶跃响应电压由正负极电势以及欧姆内阻和中频阻抗引起的电压降决定。阶跃响应负极电势变化框图如图4所示。同理,正极电势变化也有如图4所示关系,其中在SOC为100%时各模型参数见表3。根据图4在Matlab/ Simulink中搭建磷酸铁锂电池分数阶模型。
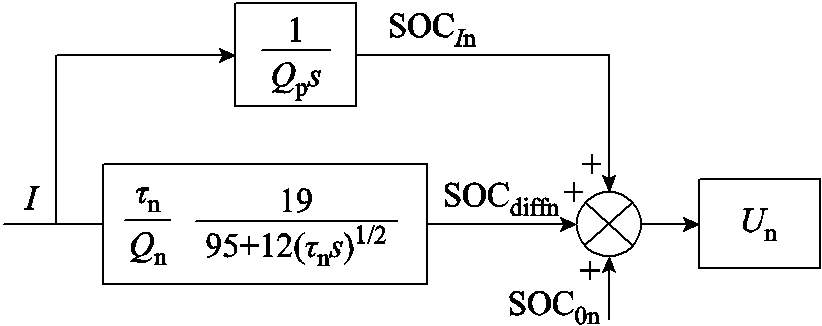
图4 阶跃响应负极电势变化框图
Fig.4 Negative potential change of step response
表3 模型参数
Tab.1 Model parameters

参数数值 Qp/(A·h)3.905 9 Qn/(A·h)3.635 3 τp1 616 τn253.3
利用图4搭建好的电池分数阶模型以及电池实验获取的模型参数,在SOC为100%、30%处施加1C阶跃放电电流,结果如图5和图6所示。图5、图6a为阶跃响应正极电势变化曲线,图6b为全电池阶跃响应电压变化曲线,图6c为阶跃响应负极电势变化曲线。可以看出,在SOC为100%时正极电势变化为0.05V,而负极电势变化约为0.005V,在SOC为30%时正极电势变化不到0.001V,负极电势变化约为0.02V。表明在SOC为100%的阶跃响应是正极特征更明显,SOC为30%的阶跃响应是负极特征更明显。
对足够多的SOC点进行阶跃响应仿真,正、负极电势变化如图7所示。横坐标表示电池SOC,纵坐标表示在相应SOC施加阶跃放电激励,正、负极电势变化。SOC在100%~90%区间,正极电势变化更大,SOC在90%~45%区间,正、负极均有变化更大的区域。而SOC在45%~10%区间,负极阶跃响应电势变化更大而正极电势几乎不变,但是10%~0%的SOC区间由于正、负极电势变化都很大但两者变化量差距不大,无法达到利用全电池数据提取负极特征的目的,因此负极SOC特征区间为10%~45%。
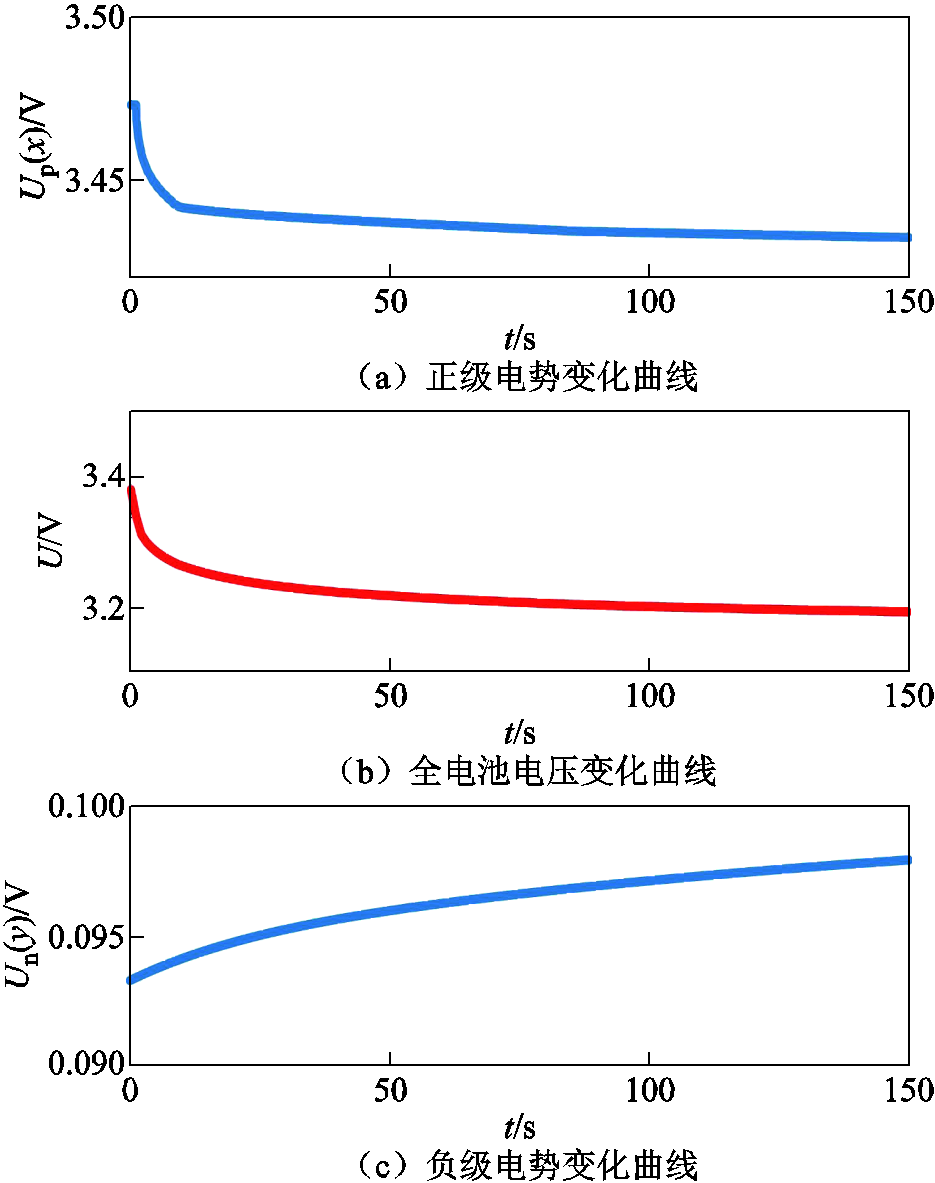
图5 SOC为100%时的点阶跃响应
Fig.5 Step response when SOC is 100%

图6 SOC为30%时的阶跃响应
Fig.6 Step response when SOC is 30%
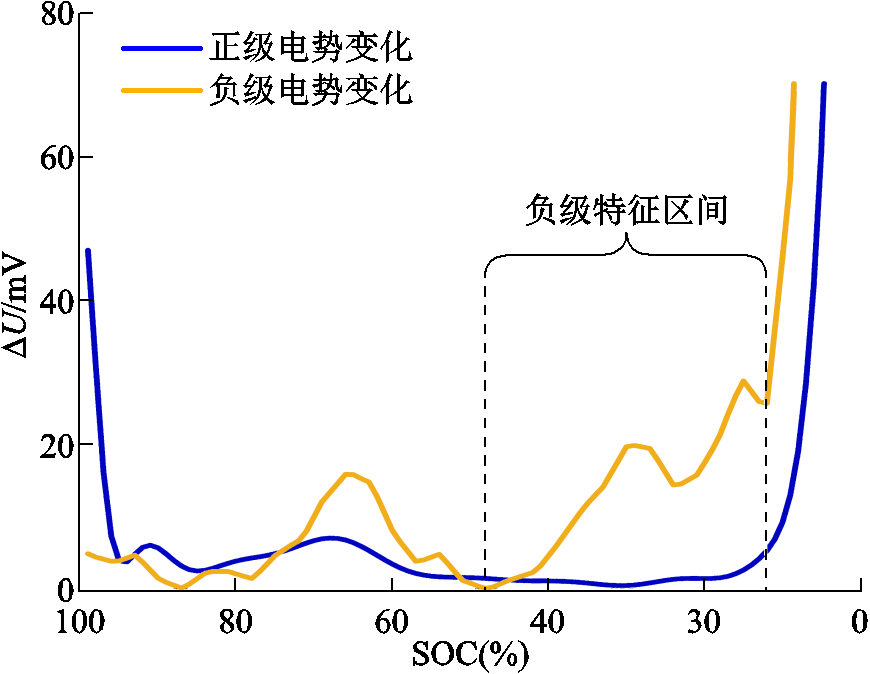
图7 在不同SOC点阶跃响应正负极电势变化
Fig.7 The positive and negative potential change at different SOCs
通过前文的分析可知,在负极的特征区间中,可以利用全电池数据来提取负极的特征。本节以位于负极SOC特征区间的30%和SOC区间外的100%为例,利用2.2节介绍的三电极电池实验求取负极固相扩散时间常数τn,并与利用全电池求取的负极固相扩散时间常数进行比较,从而验证负极特征区间的正确性。
在SOC为30%时进行三电极EIS实验,结果如图8所示。基于1.2节提到的求取固相扩散时间常数的方法,利用全电池EIS数据求得τ=746.11s,利用负极EIS数据求得的负极固相扩散时间常数τn=710.93s,误差为4.7%。
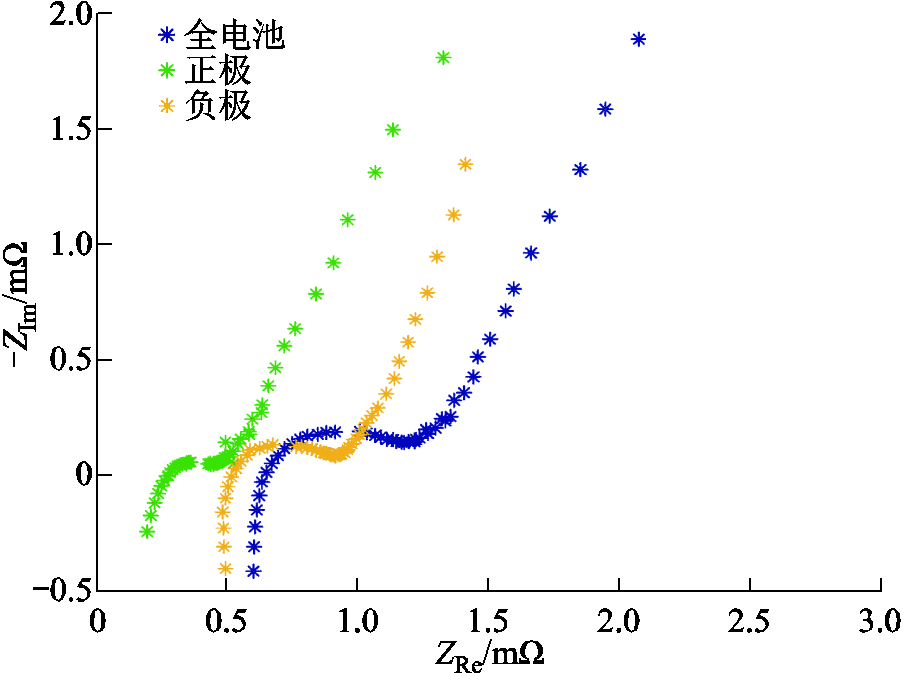
图8 30%SOC三电极EIS实验结果
Fig.8 EIS experiment results of three-electrode at 30%SOC
图9为SOC为100%时该电池的三电极EIS实验结果。同理,利用全电池EIS数据求得τ =1 664.5s,利用负极EIS数据求得τn=253.3s,误差为84.8%,反而利用正极EIS数据求得的τp=1 616s,与全电池求得的τ相比误差为2.96%。对比在SOC为30%和100%求取τn的结果,说明全电池SOC在30%主要包含负极的特征,而SOC在100%主要包含正极的特征。这证明利用新电池负极特征区间的有效性。
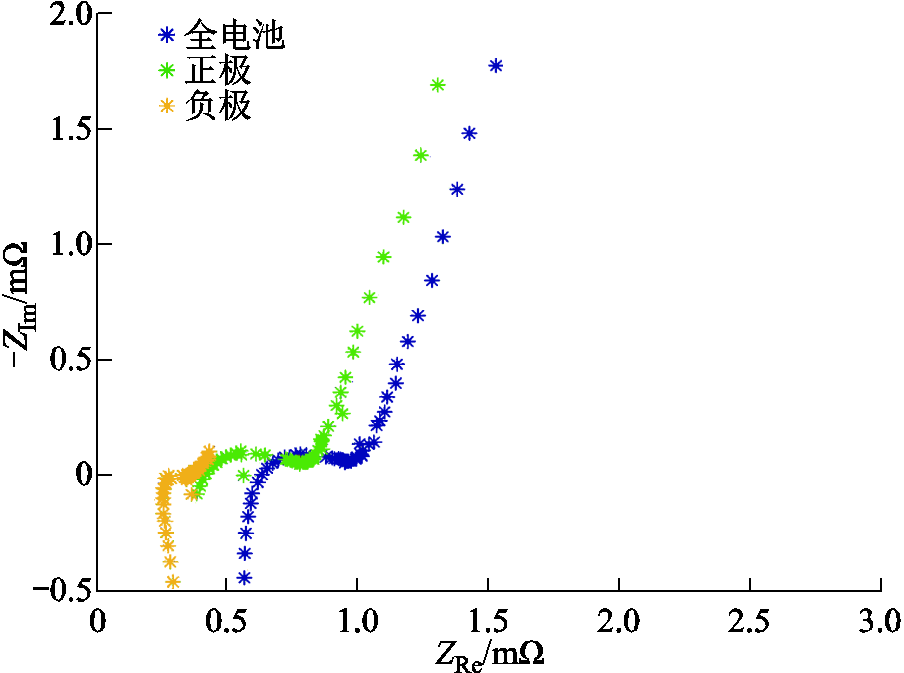
图9 SOC为100%时三电极EIS实验结果
Fig.9 EIS experiment results of three-electrode when SOC is 100%
本节研究老化对负极特征区间的影响,从而得到随着电池老化一直存在的负极特征区间,并且利用老化电池三电极EIS实验进行验证。
通过1.2节的分析可知,影响电池电势响应的两个参数为电势曲线斜率k、固相扩散时间常数τ。因此本节首先分析老化对这两个因素的影响,然后调整分数阶模型参数从而得到老化电池的负极特征区间,之后确定老化过程中一直存在的负极特征区间,最后基于老化电池的三电极实验进行验证。通过分析不同老化程度的电池试验数据,得到老化程度与两个参数为正相关关系,由于篇幅关系,在此处仅以老化程度为80%的电池进行说明。下文中老化电池均为该老化状态。
从文献[12-13]可知,磷酸铁锂电池老化过程中,内部正极容量Qp基本没有衰减,而其负极容量Qn稳定衰减,同时其内部可用锂离子的总量稳定减少,电池的内阻也有明显增加。电极容量减少,电势曲线会相应发生平移伸缩变化,而磷酸铁锂电池主要发生的是负极的老化。随着电池老化,负极电势曲线会发生伸缩平移,参数k随着电势曲线的变化而变化,将正极电势变化忽略,结果如图10所示。
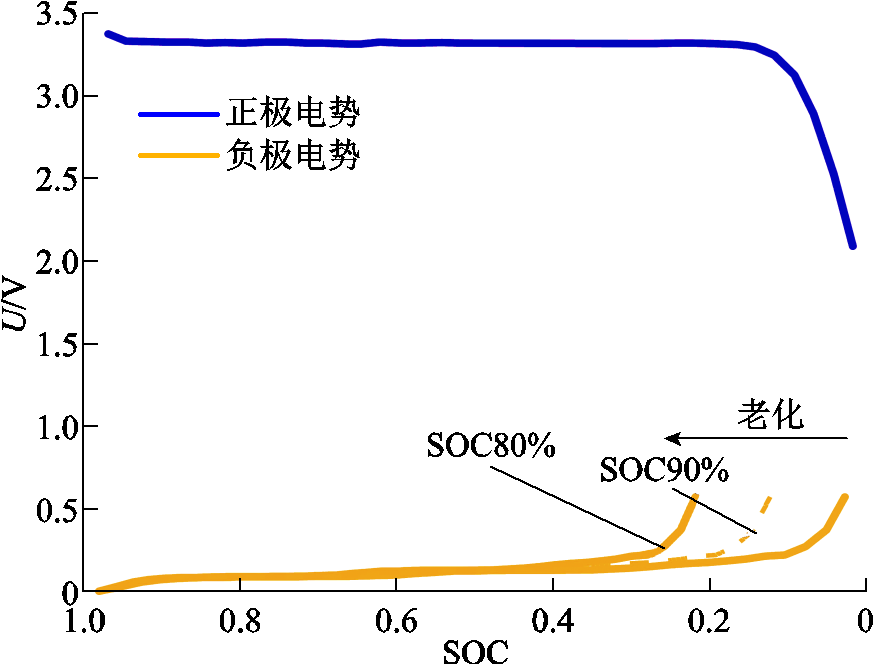
图10 电势曲线变化
Fig.10 The change of potential curve
目前精确求取固相扩散时间常数τ需要进行三电极电池实验,而该实验比较复杂,难以在每个老化状态进行。因此为了得到固相扩散时间常数随老化的变化规律,本文基于2.3节介绍的电池老化实验,在不同老化状态下对电池进行阶跃放电。随着电池老化,电池阶跃响应电压变化会增大,如图11所示。
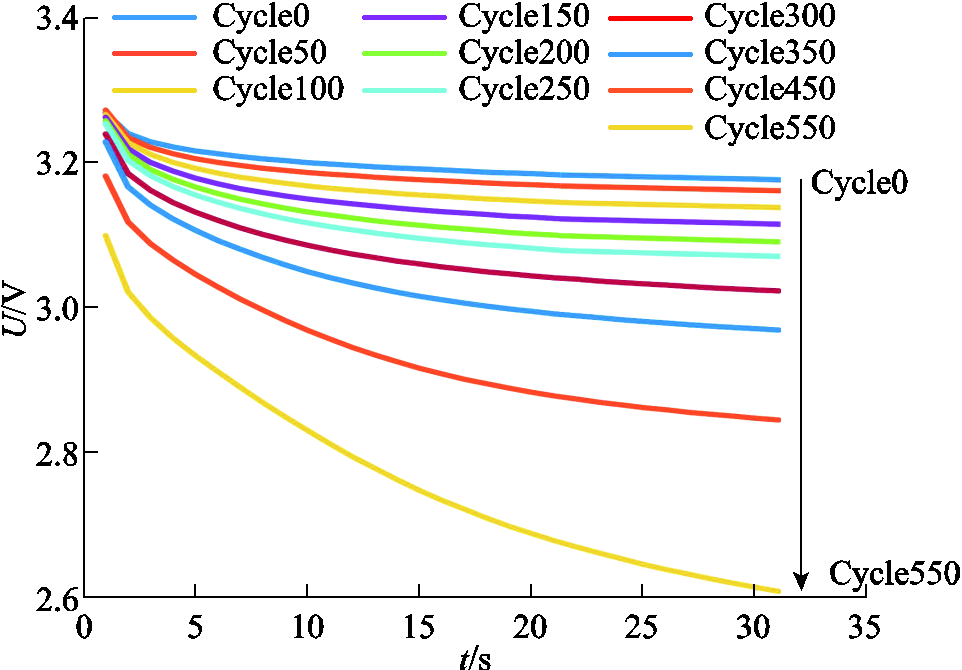
图11 阶跃响应电压变化
Fig.11 Voltage change of step response
由于正极基本不发生老化,正极的阶跃响应不受老化影响,因此电压随着老化的变化主要是由负极引起。根据式(9),负极固相扩散时间常数τn越大,电势变化越大,因此根据电池老化实验可知,随着电池老化,τn增大。在老化过程中假设正极的固相扩散时间常数不发生变化,即正极电势变化在老化过程中不发生变化,实验测得的∆U均由负极电势变化引起,结合实验数据,可以求出∆Un随着老化的变化,根据式(4)、式(9)即可求出τn的变化范围。
基于3.3节的分析得到影响电池正、负极电势响应的参数的变化,重新调整分数阶模型参数并基于Matlab/Simulink中搭建磷酸铁锂电池分数阶模型进行仿真,得到的结果如图12所示。
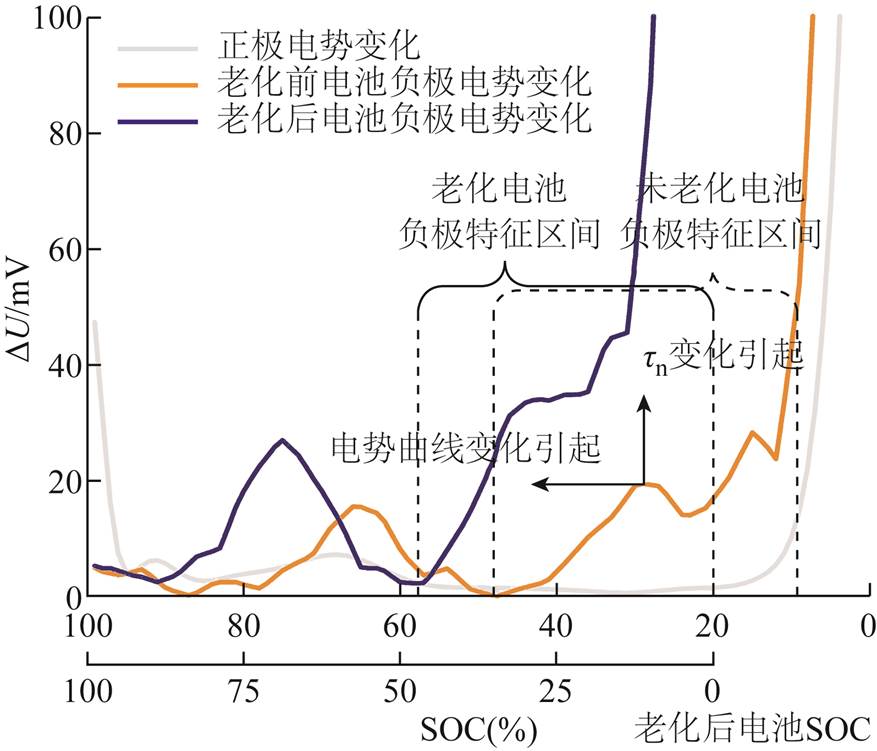
图12 老化前后电池特征区间对比图
Fig 12 Comparison of negative characteristic region before and after aging
从图12可以看出,电势曲线的变化主要引起负极特征区间的向左并向上平移。通过之前的分析可知,影响负极电势响应的两个参数是电势曲线斜率k和负极固相扩散时间常数τn,老化过程中,负极电势曲线伸缩平移。老化使得电池中锂离子浓度减少,因此如图10所示,负极电势曲线向左平移,所以在各个SOC点施加激励,负极电势变化曲线也会向左平移。并且老化过程中电池电极结构发生变化,使得固相扩散过程加剧,因此电极电势变化也加剧,所以老化后负极电势曲线也会向上平移。老化前负极SOC特征区间为10%~45%,老化使得负极特征区间平移扩张,老化后SOC特征区间为0%~55%,与老化前的负极特征区间取交集,得到电池的SOC在10%~45%为电池的负极特征区间。
与3.2节方法一致,对老化电池进行三电极EIS实验验证。基于2.2节提到的求取固相扩散时间常数的方法,在SOC为30%时利用全电池EIS数据求得τ=1 258.23s,利用负极EIS数据求得的τn= 1 184.12s,误差为5.9%。相比于新电池的负极固相扩散时间常数,老化电池的负极固相扩散时间常数增大,也表明2.2节分析的准确性。
同理,在SOC为100%时进行电池的三电极EIS实验,利用全电池EIS数据求得τ=2034.1s,利用负极EIS数据求得的τn=347.4s,误差为82.9%,对比在SOC为30%和100%求取τn的结果,证明老化电池负极特征区间的有效性。
磷酸铁锂电池的老化主要是负极的老化。为了今后从全电池外特性中提取负极老化信息,本文提出了具有这些信息的负极特征区间的确定方法。该方法主要结论如下。
1)分析了磷酸铁锂电池的分数阶模型,提出了阶跃电流激励下基于分数阶模型的电势变化线性模型,该组模型参数可通过电池实验数据获得。
2)提出了用于辨识负极特征的负极特征区间的求取方法。该区间基于对全电池的不同SOC0处的阶跃响应和电势变化线性模型确定,方法简单实用。
3)研究了该特征区间与电池老化的关系。由于老化使得新电池确定的负极特征区间扩张,因此新电池确定负极特征区间可保证进行电池老化后的参数获取。
4)该方法通过三电极电池实验进行了验证。分析和验证表明:磷酸铁锂新电池的负极SOC特征区间为10%~45%,老化使得负极特征区间平移扩张,老化后电池负极SOC特征区间为0%~55%。据此,确定了本文所用电池的负极特征区间为10%~45%。
下一步将研究老化对负极特征区间特征变化的机理。
参考文献
[1] 郭永芳, 黄凯, 李志刚. 基于短时搁置端电压压降的快速锂离子电池健康状态预测[J]. 电工技术学报, 2019, 34(19): 3968-3978. Guo Yongfang, Huang Kai, Li Zhigang. Fast state of health prediction of lithium-ion battery based on terminal voltage drop during rest for short time[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3968-3978.
[2] 谷苗, 夏超英, 田聪颖. 基于综合型卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2019, 34(2): 419-426. Gu Miao, Xia Chaoying, Tian Congying. Li-ion battery state of charge estimation based on comprehensive Kalman filter[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 419-426.
[3] 李晓宇, 徐佳宁, 胡泽徽, 等. 磷酸铁锂电池梯次利用健康特征参数提取方法[J]. 电工技术学报, 2018, 33(1): 9-16. Li Xiaoyu, Xu Jianing, Hu Zehui, et al. The health parameter estimation method for LiFePO4 battery echelon use[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 9-16.
[4] 刘伟, 吴海桑, 何志超, 等. 一种均衡考虑锂电池内部能量损耗和充电速度的多段恒流充电方法[J]. 电工技术学报, 2017, 32(9): 112-120. Liu Wei, Wu Haisang, He Zhichao, et al. A multistage current charging method for Li-ion battery considering balance of internal consumption and charging speed[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 112-120.
[5] 何志超. 锂离子动力电池的动态模型研究[D]. 北京: 清华大学, 2016.
[6] 何志超, 杨耕, 卢兰光, 等. 一种动力电池动态特性建模[J]. 电工技术学报, 2016, 31(11): 194-203. He Zhichao, Yang Geng, Lu Languang, et al. A modeling method for power battery dynamics[J]. Transactions of China Electrotechnical Society, 2016, 31(11): 194-203.
[7] Zhang Q, White R E. Calendar life study of Li-ion pouch cells[J]. Journal of Power Sources, 2007, 173(2): 990-997.
[8] Zhang Q, White R E. Calendar life study of Li-ion pouch cells: Part 2: simulation[J]. Journal of Power Sources, 2008, 179(2): 785-792.
[9] 陈英杰. 锂离子动力电池工程模型及其参数估计问题研究[D]: 北京: 清华大学, 2019.
[10] 陈英杰, 杨耕, 祖海鹏, 等. 基于恒流实验的锂离子电池开路电压与内阻估计方法[J]. 电工技术学报, 2018, 33(17): 3976-3988.Chen Yingjie, Yang Geng, Zu Haipeng, et al. An open circuit voltage and internal resistance estimation method of lithium-ion batteries with constant current tests[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 3976-3988.
[11] 卫志农, 原康康, 成乐祥, 等. 基于多新息最小二乘算法的锂电池参数辨识[J]. 电力系统自动化, 2019, 43(15): 139-145. Wei Zhinong, Yuan Kangkang, Cheng Lexiang, et al. Parameter identification of lithium-ion battery based on multi-innovation least squares algorithm[J]. Automation of Electric Power Systems, 2019, 43(15): 139-145.
[12] 韩雪冰. 车用锂离子电池机理模型与状态估计研究[D]. 北京: 清华大学, 2014.
[13] Han Xuebing, Ouyang Minggao, Lu Languang, et al. A comparative study of commercial lithium ion battery cycle life in electric vehicle: capacity loss estimation[J]. Journal of Power Sources, 2014, 268: 658-669.
[14] Aurbach D. Review of selected electrode–solution interactions which determine the performance of Li and Li ion batteries[J]. Journal of Power Sources, 2000, 89(2): 206-218.
[15] Pallavi V, Pascal M, Petr N. A review of the features and analyses of the solid electrolyte interphase in Li-ion batteries[J]. Electrochimica Acta, 2010, 55(22): 6332-6341.
[16] Aurbach D, Zinigrad E, Cohen Y, et al. A short review of failure mechanisms of lithium metal and lithiated graphite anodes in liquid electrolyte solutions[J]. Solid State Ionics, 2002, 148(3-4): 405-416.
[17] Guo Dongxu, Yang Geng, Feng Xuning. Physics-based fractional-order model with simplified solid phase diffusion of lithium-ion battery[J]. Journal of Energy Storage, 2020, 30: 101404.
[18] Maheshwari A, Heck M, Santarelli M, et al. Cycle aging studies of lithium nickel manganese cobalt oxide-based batteries using electrochemical impedance spectroscopy[J]. Electrochimica Acta, 2018, 273: 235-348.
[19] 孙国强, 任佳琦, 成乐祥, 等. 基于分数阶阻抗模型的磷酸铁锂电池荷电状态估计[J].电力系统自动化, 2018, 42(23): 57-63. Sun Guoqiang, Ren Jiaqi, Cheng Lexiang, et al. State of charge estimation of LiFePO4 battery based on fractional-order impedance model[J]. Automation of Electric Power Systems, 2018, 42(23): 57-63.
[20] 祖海鹏, 刘旭, 杨耕, 等. 锂离子电池静置下阶跃放电电流动态模型[J]. 电源学报, 2019, 17(2): 163-170.
[21] Liu Xu, Guo Dongxu, Chen Yingjie, et al. BP neural network model of lithium-ion phosphate battery based on step-discharge current response[C]// 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, 2018: 1-6.
A Method to Determine Characteristic Region of Negative Electrode with State of Charge for Lithium-Ion Battery
Abstract There are a positive and a negative electrode in a commercial lithium ion batteries. The aging rates of the two electrodes are generally inconsistent. Take lithium iron phosphate batteries as an example, the negative electrode dominates the degradation in this battery. It is considerable to distinguish the characteristics of the negative electrode from the external characteristics of the battery, and then to find the relevant aging information from this characteristic curve to study the aging problem of lithium iron phosphate batteries without dismantling them. As first step of the work, It is necessary to determine the obvious characteristics’ SOC region of the curve which is called negative characteristic region in this paper. Based on the fractional-order model and the linear model of different State of charge (SOC) working point, this paper analyzes potential change of two electrodes under different SOC, and give a method to determine the negative characteristic region. Finally, the correlation between the region and the aging of the battery were analyzed. These results are verified by the three-electrode experiment, which indicates that this method has guiding significance for the on-line observation of the aging problem of commercial lithium iron phosphate battery.
keywords:Lithium-ion phosphate, battery aging, fractional order model, negative characteristic region
中图分类号:TM912
DOI:10.19595/j.cnki.1000-6753.tces.200128
石琼林 男,1994年生,硕士研究生,研究方向为电池管理。E-mail:Shiqionglin@whut.edu.cn
杨 耕 男,1957年生,教授,博士生导师,研究方向为电力电子技术和新能源发电技术。E-mail:yanggeng@tsinghua.edu.cn(通信作者)
国家重点研发计划(2016YFB0900300)和国家自然科学基金(U1510208, 61273045, 51777146)资助项目。
收稿日期2020-02-11
改稿日期 2020-04-27
(编辑 郭丽军)