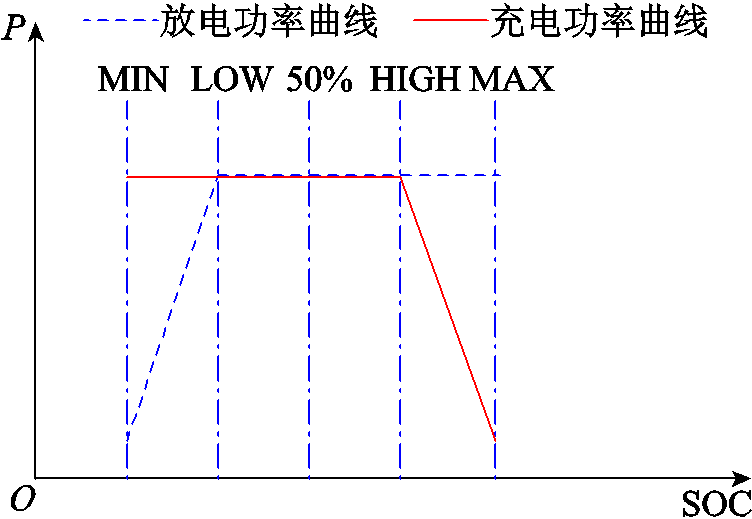
图1 一次函数式控制策略
Fig.1 First order functional control strategry
摘要 随着新能源技术的蓬勃发展,传统电网频率控制面临着日益严峻的考验,锂离子电池储能系统协助火电机组参与调频具有良好的发展空间。该文以锂离子电池储能系统辅助火电机组参与自动发电控制(AGC)辅助服务为应用场景,结合“两个细则”中的相关规定编写了AGC辅助服务的考评补偿算法。通过衰退实验搭建相对保守但可靠的电池能量衰退模型。在控制策略上,搭建基于Logistic函数的能量状态(SOE)趋中控制策略和基于评价指标的经济性策略,拟合出储能系统的每日调节模型。最后,针对项目的全寿命周期净收益、投资回收期和投资回报率进行项目经济性分析。该文通过评估投资回收期和投资回报率得到储能系统初始能量配置方案,并对可能产生的政策更新和市场变动进行敏感性分析。利用该经济模型能够得到较为严谨可靠、对政策和市场变化兼容性强的投资方案。
关键词:AGC辅助服务 锂离子电池 寿命衰退模型 趋中控制 Logistic函数 经济性分析
近年来,随着电力电子技术和可再生能源发电技术的发展,电网的源、网、荷三大环节均有较大变化,传统电网频率控制面临着日益严峻的考验。从发电端来看,现有的新能源发电机组在入网时通常含有一定的谐波和直流分量,以风电和光电为代表的电能不确定性与波动性增加了电网的频率控制难度[1-2]。在传输方面,高压直流输电技术的换流设备在换流过程中需要消耗大量的无功功率,易引发电网的频率浮动[3-4]。在负荷方面,新能源汽车的大力推广和普及带动了电动车充电桩市场的迅速增长。大量电动汽车集中在负荷高峰期充电时会加剧电网负荷峰谷差,对电网而言也是一种考验[5]。可见,电网的调频压力在发电、传输、负荷三个环节都有所加重。在此形势下,提升电网频率稳定性将越来越重要。
自动发电控制(Automatic Generation Control,AGC)是一种二次调频方式。在我国,火电机组一直是AGC调频的主力,但其调节过程中常出现延迟、超调、反调等现象[6]。锂离子电池储能系统协助火电机组参与调频可以弥补后者独立调频的不足[7],根据美国西北太平洋国家实验室在2008年给出的数据,在调频效果上储能系统可以达到水电机组的1.4倍、天然气机组的2.3倍以及燃煤机组的20倍以上[8]。因此,使用储能系统可以显著提升AGC调频的效果。
储能系统与火电机组执行相同的调频工况,极易导致电池能量耗尽或满充而丧失调节能力。因此国内的电池储能系统常与火电机组联合,提供一部分调频出力[9]。Xie Xiaorong等[10]以北京石景山热电厂投产的2MW磷酸铁锂电池储能系统(Battery Energy Storage System, BESS)示范项目为例,制定了储能系统的充放电控制策略,并通过现场实验研究其经济效益。文献[11]建立了风机与储能系统的联合模型,可以在降低风机输出波动性、提升风电利用率的同时承担二次调频服务,以增加两者联合体的经济效益。
控制策略方面,文献[12]中储能系统的输出功率不随荷电状态(State of Charge, SOC)变化而变化,这种控制策略可以称之为“满充满放式”,其容易导致电池过早进入充放电极限而失去调节能力。为了让储能系统更多地保持在高可用状态上,需要尽可能地让储能系统的SOC或能量状态(State of Energy, SOE)保持在居中的位置,以此获得最大的充放电能力,也就是丁冬等[13]所提出的SOE居中思想。I. Serban等[14]利用线性函数作为出力P与SOC的关系曲线,这种方法可以称为“一次函数式”,如图1所示。该方法的思路是通过一次函数限制电池SOC高位的充电功率和SOC低位的放电功率,对电池使用过程中出现的满充满放有一定的抑制作用,是一种较为简单的SOE居中策略。

图1 一次函数式控制策略
Fig.1 First order functional control strategry
电池的外特性不是一成不变的,其电压、内阻、可用容量、峰值电流等参数会随着使用时间的增长而逐渐衰退。有研究者评估了在简单的控制策略下电池的老化情况[15-17],也有一些针对环境因素的老化研究[18],然而大部分项目使用的老化模型比较简单,无法准确描述衰退过程[19]。
综上可知,国内外已有一些针对储能系统参与调频的研究,但针对我国电力市场的研究仍稍显薄弱,主要体现在相对简单的控制策略以及对寿命性能结合不够紧密,通常采用的还是较为简单的寿命衰退计算方式。此外,许多容量配置方法并不是以净效益最大为目标,且效益模型还不完善,比较单一[20]。因此,本文立足于国内华北地区的AGC辅助服务政策与山西省某调频机组工况,基于Logistic函数建立储能系统控制策略,在实现SOE趋中的同时尽可能释放储能出力,并结合真实数据得到的能量衰退模型和充分参考市场环境的经济性模型共同得出储能系统的能量配置模型和全寿命周期分析模型,为同类项目的设计提供参考。
AGC辅助服务的工作过程可以分为三部分:①发电侧或负载侧出现功率波动,频率偏离预设点;②AGC控制器算出需求后分配给各发电机;③发电机跟踪AGC指令,使电网频率恢复额定频率。
《华北区域发电厂并网运行管理实施细则(试行)》详细制定了包含AGC辅助服务在内的有偿辅助服务的考核标准、补偿原则和计算方法,并在此基础上进行经济补偿。Kp是衡量AGC调节效果的指标,D是调节深度指标。在每天的调节工作结束后,控制中心得到当天调节参数Kp和D的平均值,并得到每日补偿费用Iday为
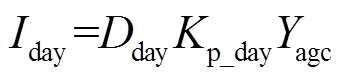 (1)
(1)式中,Yagc为AGC调节性能补偿指标;Kp_day、Dday分别为每日调节性能指标和调节深度的平均值。
1.2.1 调节性能指标
Kp是衡量AGC调节效果的指标,包含三个小的指标:调节速率指标K1、调节精度指标K2及响应时间指标K3,下面将给出这4个指标的定义、判断条件、计算公式与含义。
1)调节速率指标K1
调节速率vi是指调频机组响应AGC设点指令的速度,其计算的是从机组跨出响应死区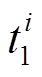 开始,到机组进入调节死区
开始,到机组进入调节死区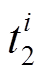 为止的机组出力变化速度,即
为止的机组出力变化速度,即
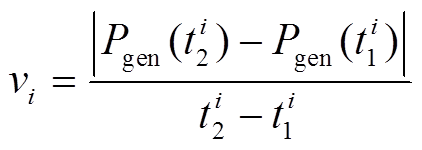 (2)
(2)调节速率与指标K1的关系式为
 (3)
(3)
式中,vN为调频机组的标准调节速率,根据机组类型取不同的值。
2)调节精度指标K2
调节精度指标用来衡量调频机组响应趋于稳定后,其实际出力围绕设点指令振荡幅度的大小。起点就是式(2)描述的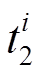 ,终点则是新的AGC指令下达时刻
,终点则是新的AGC指令下达时刻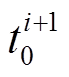 。将调频机组实际出力与AGC设点指令两者在此时段内差值的绝对值进行积分,再将得到的积分值除以积分时间,得到的结果就是本次调节的调节偏差量,即
。将调频机组实际出力与AGC设点指令两者在此时段内差值的绝对值进行积分,再将得到的积分值除以积分时间,得到的结果就是本次调节的调节偏差量,即
 (4)
(4)式中,Pgen(ti)为调频机组在有效区间内每时刻的实际出力;Pagc(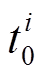 )为第i次调频AGC设点指令的值;∆Pi为本次调节的调节偏差量,MW。调节精度指标K2的计算公式为
)为第i次调频AGC设点指令的值;∆Pi为本次调节的调节偏差量,MW。调节精度指标K2的计算公式为
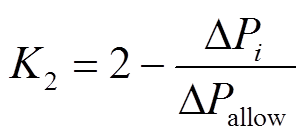 (5)
(5)
式中,∆Pallow为政策中规定的调节允许的偏差量,等于调频机组额定有功功率的1%。在计算过程中,当K2的计算值小于0.1时,取其值为0.1。
3)响应时间指标K3
响应时间∆ti是指调频机组收到AGC指令后更改出力直到可靠地跨出与调节方向一致的响应死区的时间。响应时间指标K3的计算公式为
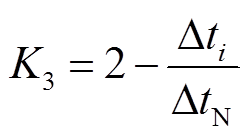 (6)
(6)
式中,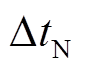 为规定的机组标准响应时间,火电机组的标准响应时间是1min。
为规定的机组标准响应时间,火电机组的标准响应时间是1min。
在实际计算中,如果K3的计算值小于0.1,同样取其值为0.1。
4)调节性能指标Kp
调节性能指标Kp是K1、K2和K3的乘积,即
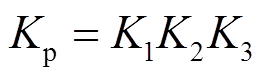 (7)
(7)
当K1、K2和K3中某项不满足计算规则但机组仍有调频贡献时,取Kp的值为1。
1.2.2 调节深度指标
调节深度用来衡量调频机组在一次AGC调节过程中实际做出贡献的出力变化量,因此涉及两个重要的评判标准:一是要对电网的频率稳定起到积极作用,即出力变化方向朝向AGC设点指令靠拢;二是要对这部分起积极作用的贡献做量化。针对不同的出力工况具体分析,才能得到较为准确的调节深度,实际计算方式如图2所示。需要注意的是,反调机组的调节深度为负数。
本文采用的基于Matlab程序的AGC辅助服务考评补偿算法,流程如图3所示,点画线框将算法分为两部分,分别根据AGC设点指令命令和机组实际出力值计算调节性能指标Kp和调节深度D。
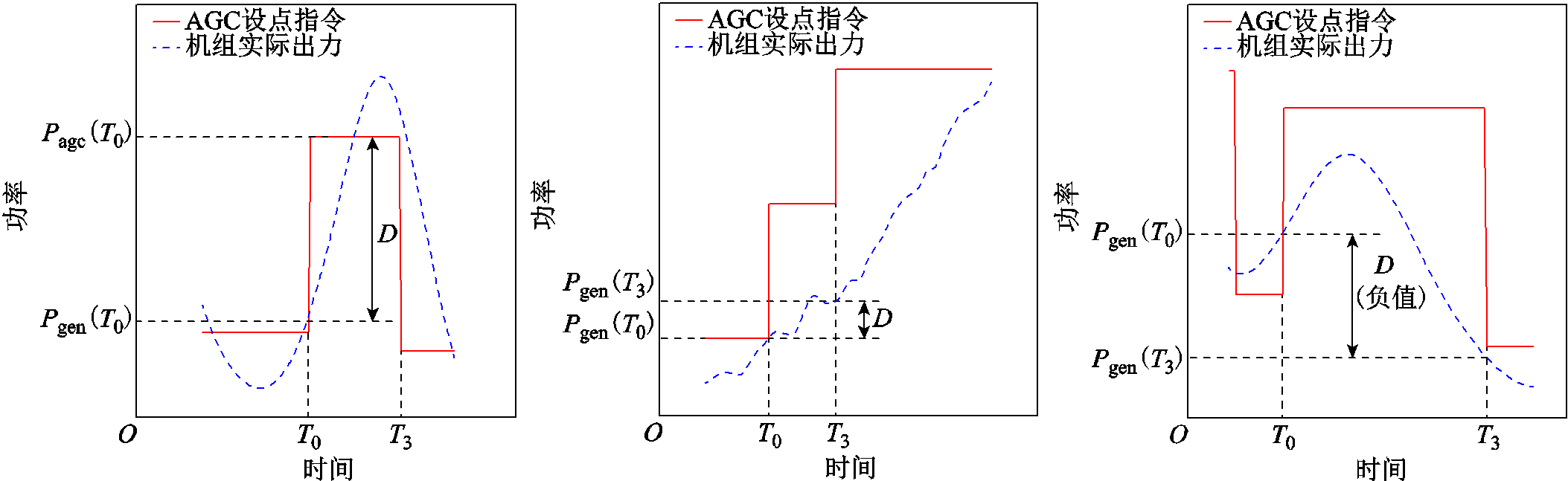
图2 AGC辅助服务常规、欠出力和反调工况的调节深度
Fig.2 Adjustment depth of normal working conditions, under-output conditions, reversed conditions in AGC auxiliary service
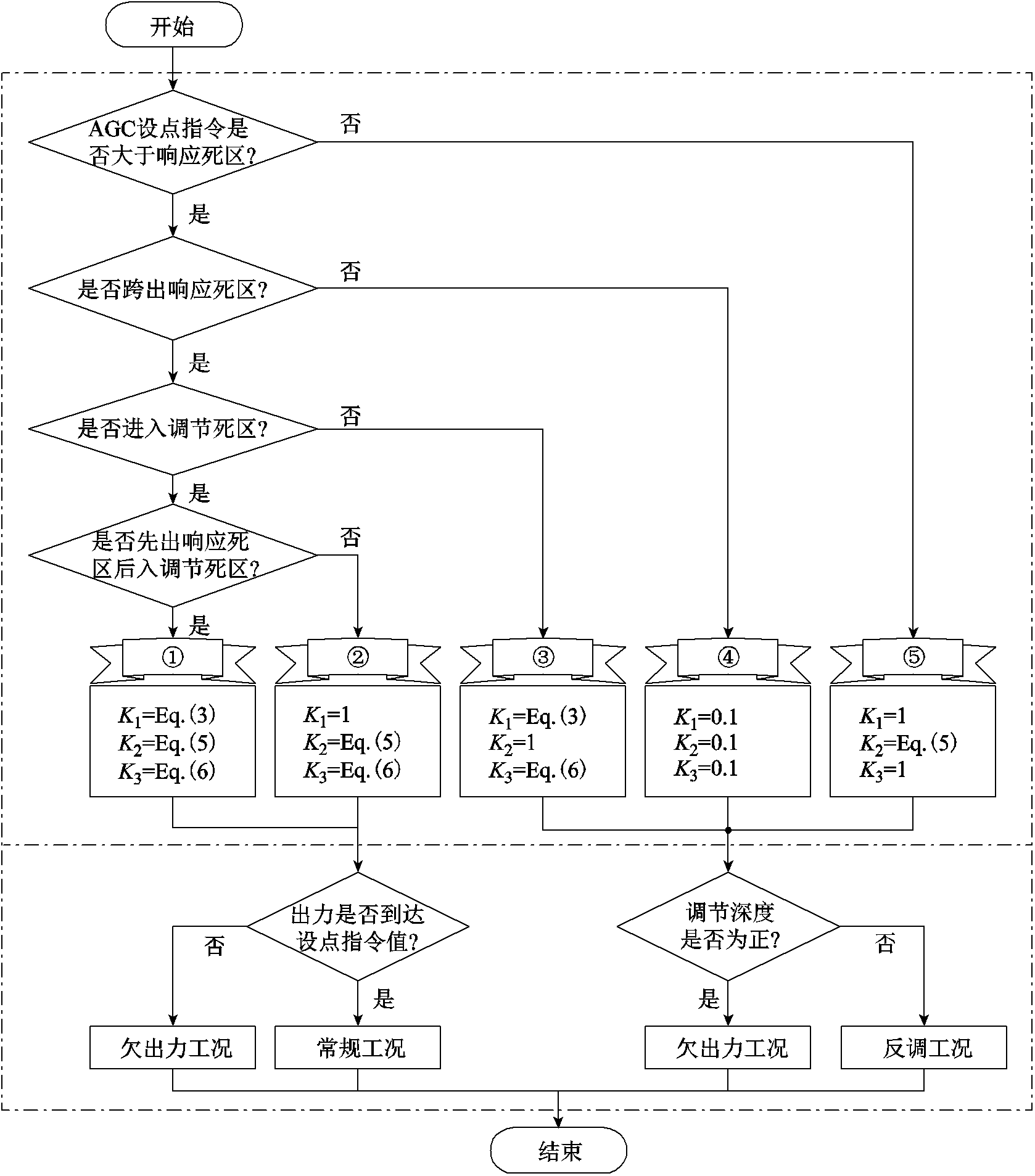
图3 AGC辅助服务考评补偿算法流程
Fig.3 The flow chart of AGC auxiliary service compensation evaluation algorithm
将AGC设点指令命令和机组实际出力值矩阵输入程序,在每次AGC调节开始时首先判断AGC设点指令是否超过设定的响应死区。如果未能超过响应死区,本次调节的调节速率指标和响应时间指标无法计算,但调节精度指标依然可以计算,因此按式(5)计算K2并按政策要求设置K1和K3的值为1,为后文方便叙述,该工况称为工况⑤;如果差值大于响应死区,再判断机组是否向正确的方向出力并跨出响应死区。如果机组没能跨出响应死区,那么此次调节没有贡献甚至可能是反调,因此三项指标均置为0.1,该工况称为工况④;如果机组跨出了响应死区,继续判断其是否进入调节死区。如果未能进入调节死区,则可能是欠出力或者是有贡献的反调,其调节精度指标K2无法计算置为1,其余两项指标分别按公式计算,该工况称为工况③;如果机组成功地进入了调节死区,在实际计算中,有时由于设点指令与机组原始出力过于接近,会出现尚未跨出响应死区就进入调节死区的情况,这会导致调节速率指标的计算公式无法正确识别。因此,如果机组进入调节死区前没有跨出响应死区,则将其调节速率指标置为1,其他两个指标用对应公式计算,该工况称为工况②;否则即为标准调节工况,其三个调节性能指标均可用对应公式计算。
计算完调节性能指标后即可进行调节深度的计算。对于工况①和②,只需要判断机组的出力是否到达设点指令值即可选择按照常规工况或欠出力工况计算;对于工况③、④、⑤而言,由于存在反调且均未到达设点指令值,因此需要判断其调节深度的符号后按照欠出力工况或反调工况计算。
电池使用寿命关系到储能系统的退役年限,影响到项目全寿命周期的盈利能力,需要在确保安全的前提下制定合适的使用区间,尽量延长电池的经济性。
2.1.1 使用区间
将全新三元材料电池两个一组,共分为三组,按照实际使用情况分为0%~100%、5%~95%和15%~95%三个不同的放电深度于25℃的温箱中进行循环衰退实验,实验结果如图4所示。可见0%~100%全区间循环的寿命衰退最快,5%~95%区间的DOD略大于15%~95%区间,但两者的等效循环衰退速度是近似一致的。
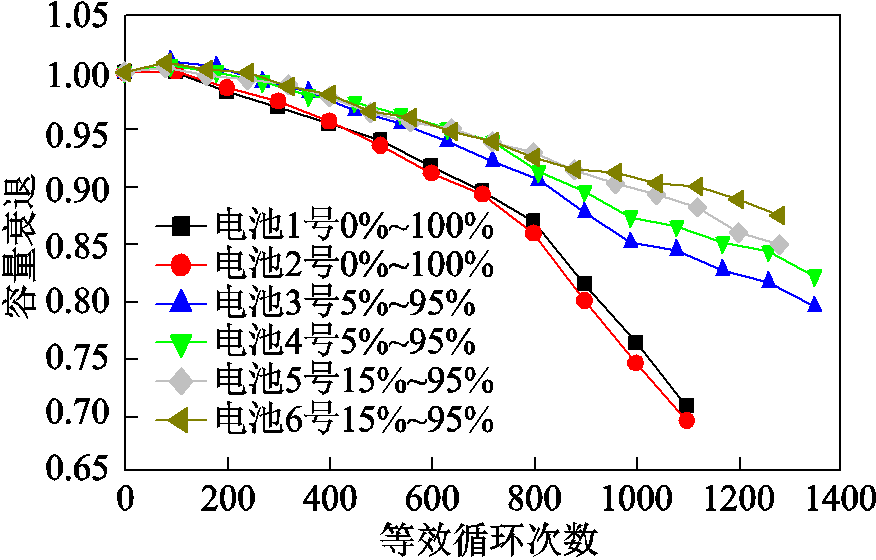
图4 不同DOD对电池容量衰退的影响
Fig.4 The effect of different DOD on battery capacity decline
2.1.2 储能系统状态参数
对于储能系统而言,采用能量而不是容量作为描述储能系统状态的参数能够明确其依照给定功率可以运作的时间,比容量指标更有意义。明确SOC与SOE的关系有助于使用SOE描述储能系统状态。
图5为电池放电过程中SOE与SOC的关系曲线,可见两者基本呈线性关系,且衰退前后几乎没有发生改变。根据本实验室的相关数据,该规律在三元材料电池和钛酸锂电池中亦有不同程度的体现,有一定的适用性。
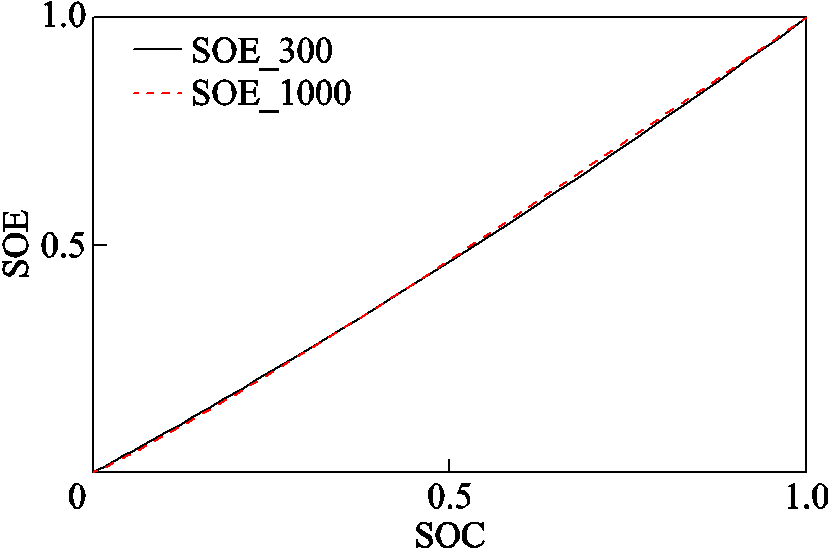
图5 SOC-SOE曲线
Fig.5 SOC-SOE curve compensation evaluation algorithm
2.1.3 全寿命周期能量吞吐量
本文制定了以下规则用于明确电池的退役时间:对工况中每一次充放过程取其功率对时间的积分,得到本次能量吞吐量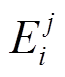 。当每日的调节任务结束后计算该日的能量吞吐量
。当每日的调节任务结束后计算该日的能量吞吐量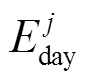 ,并求出机组运行至今
,并求出机组运行至今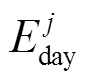 的累加和,与电池组的全寿命周期吞吐量Elife进行比较。当前者大于等于后者时,即视为电池退役。该过程可以用式(8)和式(9)描述。
的累加和,与电池组的全寿命周期吞吐量Elife进行比较。当前者大于等于后者时,即视为电池退役。该过程可以用式(8)和式(9)描述。
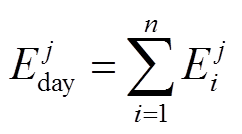 (8)
(8)
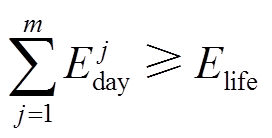 (9)
(9)
式中,j为AGC机组的第j个调频日;i为当日第i次调频;n为该日调频的总次数;m为AGC参与调频的天数。
对电池的寿命衰退进行分析,能够得出系统的全寿命周期能量吞吐量Elife。实验中电池的充放电能量衰退曲线略有不同,但两者均具有很强的线性特征,所以可以通过电池的额定能量和若干次循环衰退后的能量进行计算。考虑到该电池厂商给出的质量保证范围为1 000次循环内,因此保守计算将1 000次等效循环设定为电池的循环寿命终点,其计算公式为
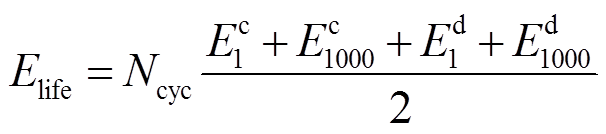 (10)
(10)式中, 和
和 分别为电池出厂时的充电能量和放电能量;
分别为电池出厂时的充电能量和放电能量;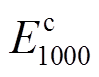 和
和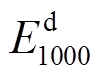 分别为1 000次等效循环后电池的充电能量和放电能量,4个参数均对应电池在本项目中的实际使用区间(5%~95%);Ncyc为电池的循环次数,在本项目中取1 000次。经计算,该电池的Elife达18 249.01W·h。
分别为1 000次等效循环后电池的充电能量和放电能量,4个参数均对应电池在本项目中的实际使用区间(5%~95%);Ncyc为电池的循环次数,在本项目中取1 000次。经计算,该电池的Elife达18 249.01W·h。
2.1.4 能量衰退模型
电池的老化会引起其容量、内阻等参数的衰退,并最终影响电池的使用。将运行第j天的累计放电能量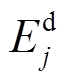 与额定能量
与额定能量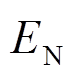 的比值定义为额定放电次数x。以额定放电次数为自变量,以放电能量保持率为因变量,可以得到一条描述电池放电能量衰退的曲线。利用Matlab对这条曲线进行公式拟合,得到的结果如图6所示,拟合公式如式(11)所示。需要指出的是,在已知电池累计充放电吞吐量求解能量衰退值时,应当先近似地换算成累计放电能量,再计算放电能量保持率,并将其作为电池最大可用能量的保持率,如式(12)所示。
的比值定义为额定放电次数x。以额定放电次数为自变量,以放电能量保持率为因变量,可以得到一条描述电池放电能量衰退的曲线。利用Matlab对这条曲线进行公式拟合,得到的结果如图6所示,拟合公式如式(11)所示。需要指出的是,在已知电池累计充放电吞吐量求解能量衰退值时,应当先近似地换算成累计放电能量,再计算放电能量保持率,并将其作为电池最大可用能量的保持率,如式(12)所示。
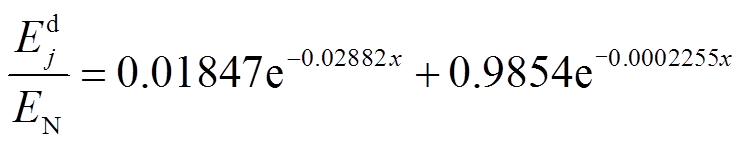 (11)
(11)
图6 衰退拟合曲线
Fig.6 Fitting curve of decline
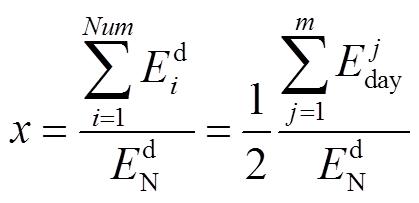 (12)
(12)式中,Num为电池的放电次数;m为储能系统的运行天数;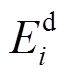 为第i次放电能量。
为第i次放电能量。
电池不同SOC点对应的最大出力功率是不同的,明确电池峰值功率特性对电池的安全使用与控制策略的制定具有至关重要的意义。将全新的三元材料电池进行容量测试后调整到不同的SOC点,并测试电池10s内充满或放空所能承受的最大电流。测试结果见表1。可以看出,在95% SOC点处电池仍能以近0.5C的电流持续放电10 s,这为后文仿真策略参数的设置提供了帮助。
表1 某三元材料单体电池峰值电流
Tab.1 The peak current of the ternary material battery

SOC(%)峰值充电电流/A峰值放电电流/A 515.718.34 1015.1113.35 1514.4417.56 2014.0720.98 3013.1124.75 4011.4226.24 509.9628.68 607.9032.54 705.8635.85 803.7638.69 901.9840.56 951.3041.31
为机组增设储能设备可以填补火电机组出力变化速度慢的劣势,并灵活吸收机组到达设点指令后的出力波动,进而提升调频效果,获得更好的经济效益。当机组出现欠出力或反调情况时,储能系统也能根据不同的策略填补输出差值或拉平机组出力。这就是储能系统辅助火电机组提升AGC调频效果的原理,如图7所示。
储能系统参与调频服务的优点是响应速度快、出力调整灵活;缺点是其能量有限,面对持续上坡和下坡工况时容易耗尽能量储备而停止工作。本文提出基于Logistic函数的SOE趋中策略,配合安全策略共同辅助储能系统。
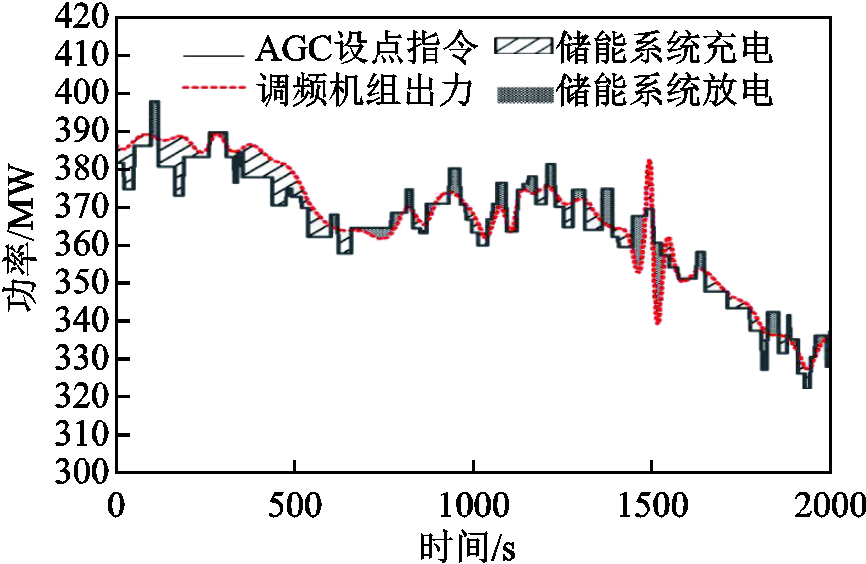
图7 AGC储能系统工作原理
Fig.7 Principle of energy storage system in AGC auxiliary service
3.1.1 安全策略
确保电池安全可靠运行需要诸多参数的限制,本文仅讨论策略所涉及的使用区间、充放电倍率等因素,温度等外界因素不在此列。5%~95%区间电池衰退速度较0%~100%更慢,而与15%~95%持平,因此被选为电池的实际使用区间。
在放电倍率方面,寿命衰退实验使用厂商给出的最优寿命工况0.5C充和1C放。实验证明,电池的寿命衰退依然存在一定的裕度。本文选取-1.5C~ +0.7C作为储能系统的最大出力限制。储能系统最大出力限制与最大可用能量Ex的关系为
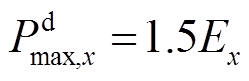 (13)
(13)
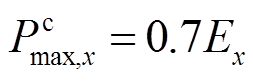 (14)
(14)
式中,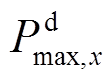 为最大放电功率;
为最大放电功率;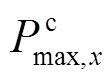 为最大充电功率。
为最大充电功率。
3.1.2 基于Logistic函数的SOE趋中策略
电池储能系统的劣势在于其可吸纳或放出的能量有限,尽量确保储能系统的SOE保持在50%为中心的区间可以让储能系统尽可能保有较大的充电和放电能力,以应对接下来的调节工况。
Logistic函数是一类常见的数学函数关系,常用来描述资源一定情况下的种群增长模型。李若等利用Logistic函数的变式作为一次调频中储能出力与SOC的关系曲线,可以在约束SOE的同时平滑储能的波动[21]。但由于其应用场景为小电网内的一次调频控制,因此对于出力的限制比较保守。对于SOE趋中的要求相对一次调频要宽松,原因在于储能主要用于填补火电机组出力与设点指令间的偏差,出力功率较小。因此,本文选取Logistic函数的变式作为最大输出功率与额定功率的比值。
下面以放电方向为例详细解释该策略。Logistic函数规定的放电策略出力最大值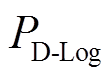 与最大放电功率
与最大放电功率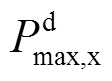 的比值
的比值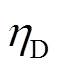 的计算公式为
的计算公式为
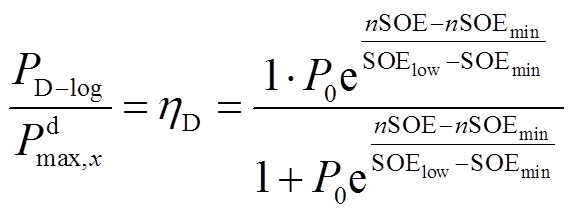 (15)
(15)式中,SOE为系统出力时的SOE值;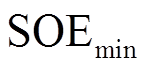 为系统可用区间的终点,设为0.05;
为系统可用区间的终点,设为0.05;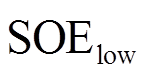 为设定好的低SOE区间,设为0.2;n、P0为Logistic函数的两个形状参数,经调整,n和P0分别取10和0.5。为了减轻电池管理系统的负担,将曲线部分以5%为一挡划分为4个平台,各平台参数选取规则如下:前三个平台取每挡对应Logistic函数值的平均数近似值作为参数值(0.6、0.8、0.95),第4个平台(全功率出力)参数值为1。因此得到放电方向的出力
为设定好的低SOE区间,设为0.2;n、P0为Logistic函数的两个形状参数,经调整,n和P0分别取10和0.5。为了减轻电池管理系统的负担,将曲线部分以5%为一挡划分为4个平台,各平台参数选取规则如下:前三个平台取每挡对应Logistic函数值的平均数近似值作为参数值(0.6、0.8、0.95),第4个平台(全功率出力)参数值为1。因此得到放电方向的出力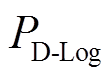 与SOE关系为
与SOE关系为
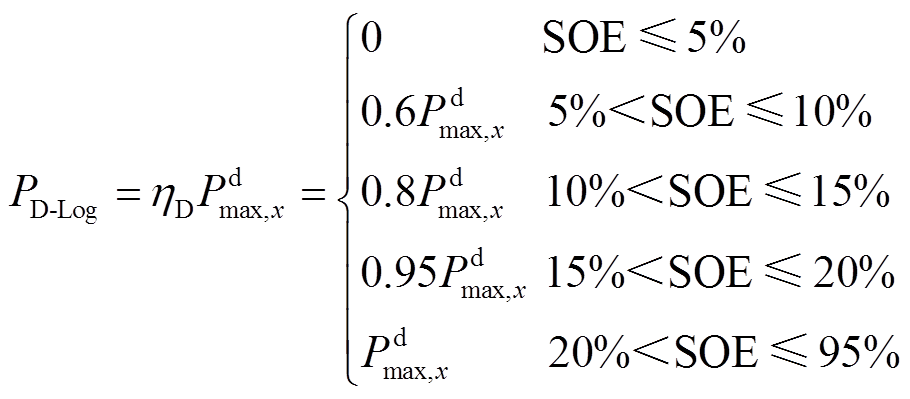 (16)
(16)
同理,充电方向的出力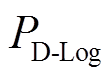 与SOE关系为
与SOE关系为
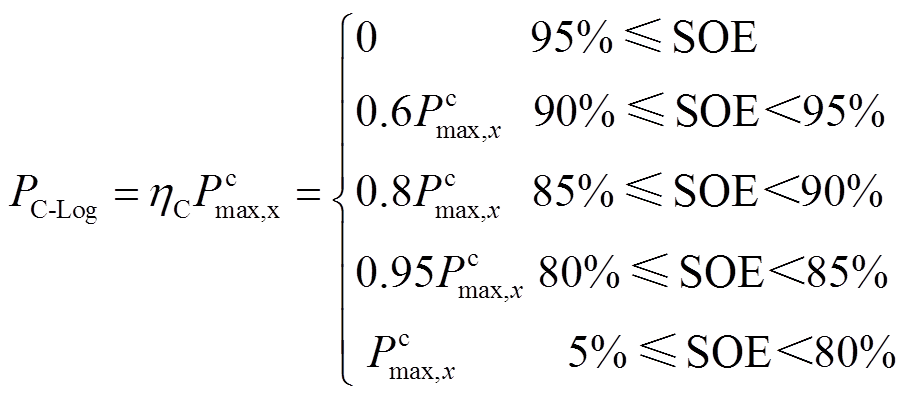 (17)
(17)本文采用基于Logistic函数的SOE趋中策略,与全功率控制策略相比可以增加SOE趋中的效果,并提升对特殊工况的调节能力,使用Logistic函数确定阈值比一次函数式更能释放电池的调节能力。
图8分别给出了配置容量与每日调节性能指标、每日调节深度指标和每日吞吐量的关系。拟合公式如式(18)所示,拟合结果见表2,这样在下文的经济性分析中,就不必每次代入常规工况求解这3个参数,可以提高仿真运行效率。
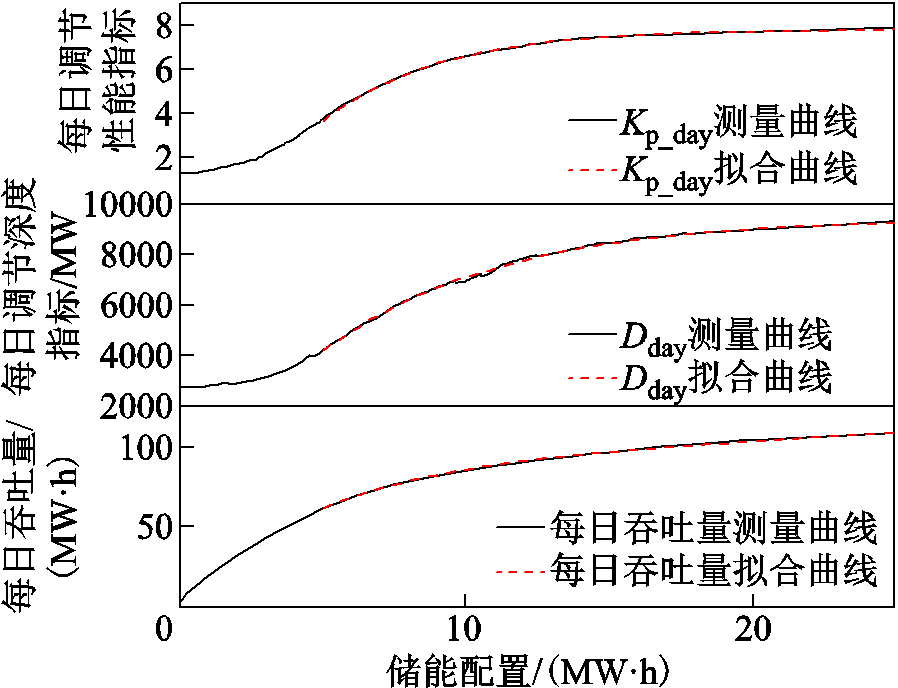
图8 基于Logistic函数的控制策略仿真结果
Fig.8 Simulation result with strategy based on Logistic function
 (18)
(18)表2 式(18)的参数
Tab.2 The performance of Eq.(18)
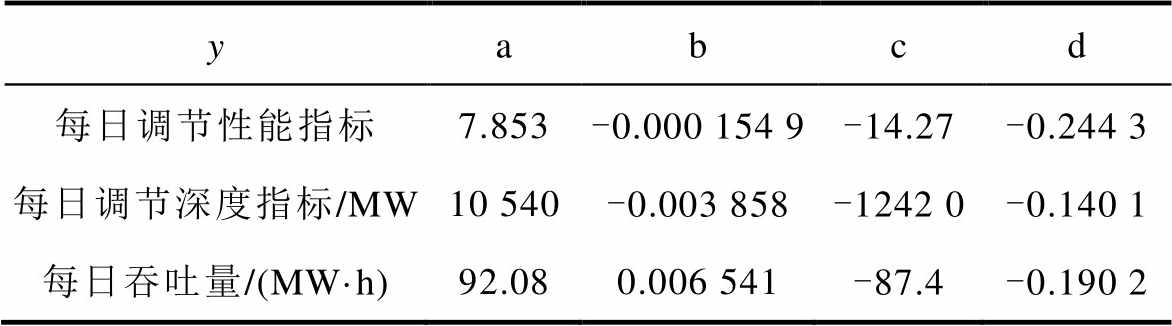
yabcd 每日调节性能指标7.853-0.000 154 9-14.27-0.244 3 每日调节深度指标/MW10 540-0.003 858-1242 0-0.140 1 每日吞吐量/(MW·h)92.080.006 541-87.4-0.190 2
在经济市场中,一个项目落地前需要对其经济性进行衡量,分析和估算其投入与产出情况。本文采用较为常用的成本-收益模型作为衡量项目经济性的方法,结合前文的电池寿命和控制策略进行联合仿真,进而搭建起一个较为准确的经济性模型,分析项目具体的经济回报。仿真从安装储能系统开始,当检测到系统能量衰减大于80%时认为系统需要退役,仿真结束。
4.1.1 成本模型
项目总成本主要由项目的投资建设成本和项目的运维成本组成,表达式为
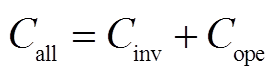 (19)
(19)
式中,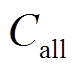 为项目总成本;
为项目总成本;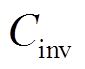 为项目的投资建设成本;
为项目的投资建设成本;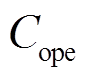 为项目的运维成本。
为项目的运维成本。
储能系统的投资建设成本主要由电池组成本、施工成本、电力转换设备成本及冷却与消防等辅助设备成本四部分组成。本项目使用的是能量密度很高的三元材料电池,因此可以采用集装箱式储能,安排在火电厂内的合适位置,其占地面积较小,因此不必额外计入占地成本。储能系统投资成本的计算公式为
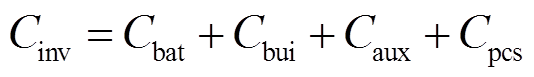 (20)
(20)式中,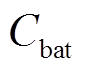 为电池组成本;
为电池组成本;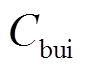 为施工成本;
为施工成本;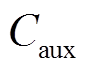 为辅助设备成本;
为辅助设备成本;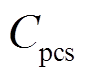 为电力转换设备成本。
为电力转换设备成本。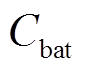 、
、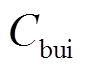 、
、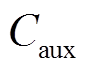 、
、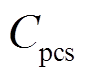 的计算公式分别为
的计算公式分别为
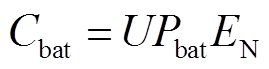 (21)
(21)
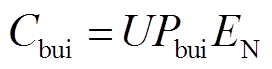 (22)
(22)
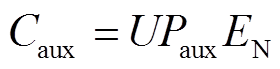 (23)
(23)
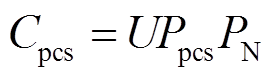 (24)
(24)
式中,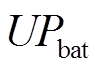 为电池组单位能量成本,元/MW·h;
为电池组单位能量成本,元/MW·h;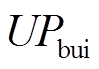 为施工单位能量成本,元/MW·h;
为施工单位能量成本,元/MW·h;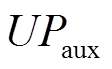 为辅助设备单位能量成本,元/MW·h;
为辅助设备单位能量成本,元/MW·h;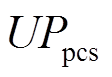 为电力转换设备单位能量成本,元/MW·h;
为电力转换设备单位能量成本,元/MW·h;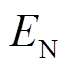 为额定能量配置,MW·h;
为额定能量配置,MW·h; 为额定功率,MW。由于三元材料电池的充放电功率不同,因此此处的额定功率取两者中较大的放电功率值。
为额定功率,MW。由于三元材料电池的充放电功率不同,因此此处的额定功率取两者中较大的放电功率值。
运维成本是指设备投产后每日运行产生的成本,主要包含参与人员的工资、设备的检修成本及相关设备的运行成本等。储能系统的用电功率与动辄十几兆瓦的输出功率相比微不足道,而且在实际工程中电网并不对参与调频的机组征收电费,因此电费可以免于考虑。在此给出储能系统的运维成本为
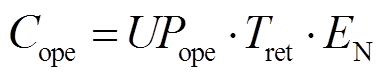 (25)
(25)式中, 为单位运维成本,(元/MW)/天;
为单位运维成本,(元/MW)/天;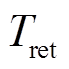 为储能系统运行天数。
为储能系统运行天数。
4.1.2 收益模型
由于机组和储能系统均有出力,因此补偿款需要分为两部分,即机组获得的补偿款和储能系统获得的补偿款。在本文中,通过计算火电机组添加储能系统前后的调频性能指标和调节深度指标,可分别得出机组应得的补偿款和两者共同得到的补偿款,储能系统应得的补偿款为
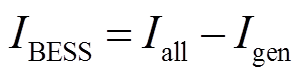 (26)
(26)式中,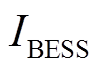 为储能系统应得的补偿款;
为储能系统应得的补偿款;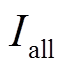 为两者共同得到的补偿款;
为两者共同得到的补偿款;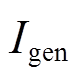 为机组应得的补偿款。
为机组应得的补偿款。
计算得到的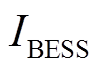 并不是储能系统当日的盈利,因为依然包含了每日的运营成本
并不是储能系统当日的盈利,因为依然包含了每日的运营成本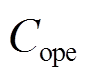 。因此,在计算每日的盈利时,需要在现值化之前扣除这部分支出。由于金融资本存在时间价值和不确定性,因此对于时间跨度较大的项目,需要将后续收入转换为投资当时的现值进行比较。常用的现值计算公式为
。因此,在计算每日的盈利时,需要在现值化之前扣除这部分支出。由于金融资本存在时间价值和不确定性,因此对于时间跨度较大的项目,需要将后续收入转换为投资当时的现值进行比较。常用的现值计算公式为
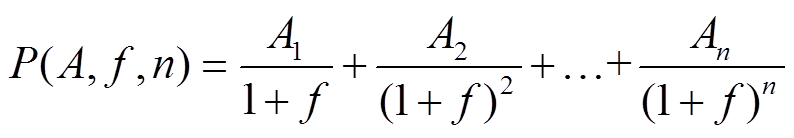 (27)
(27)式中,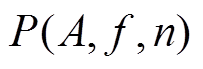 为折合成现值的总收益;
为折合成现值的总收益;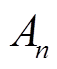 为第
为第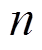 年的收益值;
年的收益值;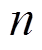 为寿命周期内的年数;
为寿命周期内的年数;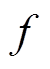 为折现率。
为折现率。
4.2.1 仿真思路
储能系统配合火电机组参与AGC辅助服务的经济性仿真思路流程如图9所示。首先,对于给定的储能系统能量配置,得到其参与每日调频的最大可用能量。根据每日调节模型可以快速得到每日调节的调节性能指标、调节深度及当日的调节吞吐量。在累计吞吐量到达寿命期限之前,借由吞吐量和最大可用能量衰退曲线计算出每日衰退后的最大可用能量,再开始新一轮的计算。当累计吞吐量到达寿命期限时,判定电池退役,此时的工作天数即储能系统的全寿命工作时间。得到寿命时间后,利用寿命期限内每日调节的调节指标按考评补偿算法计算项目的经济性。
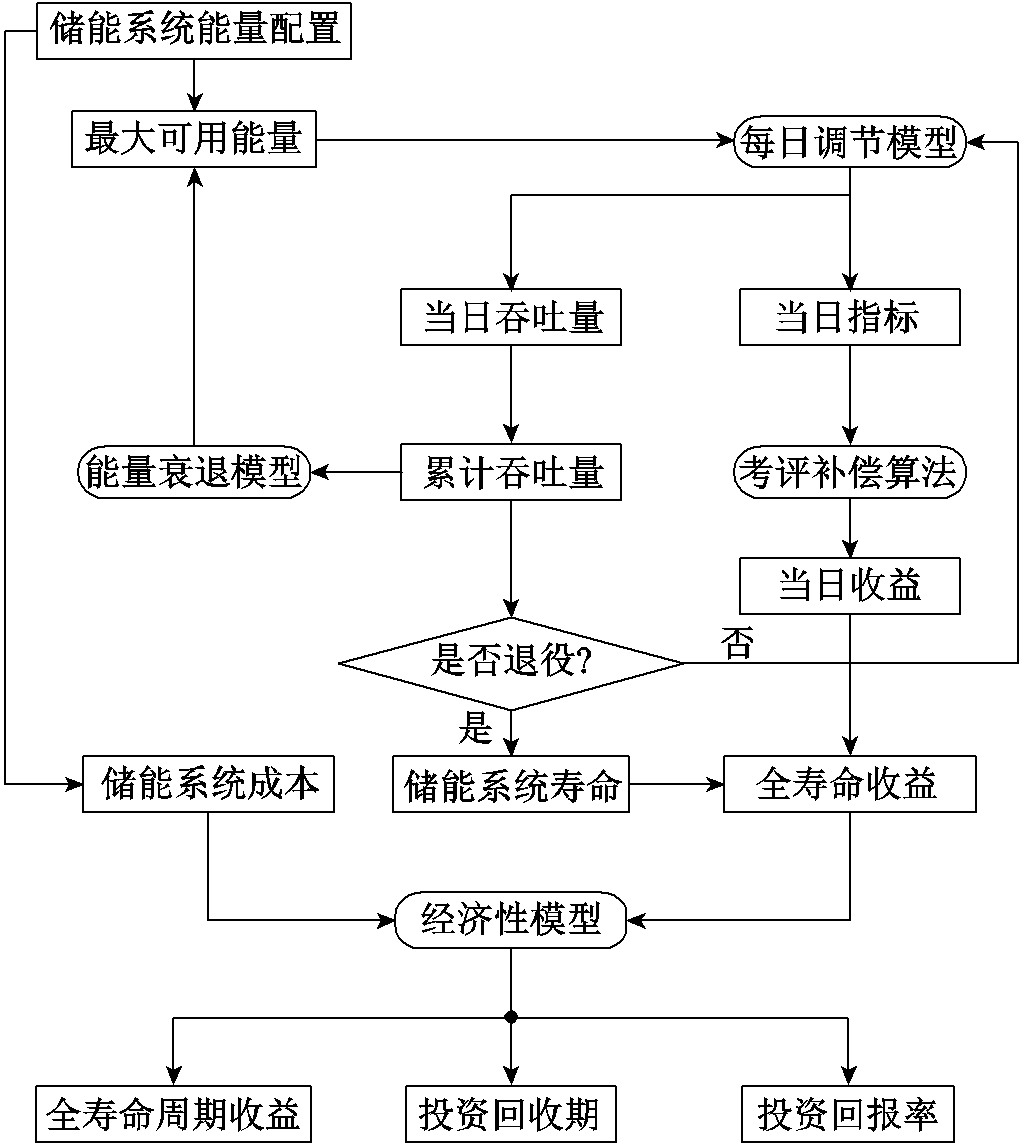
图9 经济性仿真思路流程
Fig.9 Flow chart of economic simulation
本文仿真中涉及的边界条件主要有以下几方面:
(1)首先是电池本身的充放电限制,不能过充过放,工作温度也要在受控范围内。
(2)其次是第2节研究电池寿命模型给出的电池寿命限制,即电池能量衰减到出厂值80%时认为其需要退役处理,仿真中使用额定能量吞吐量进行限制。此外,对电池的使用区间进行了规定,充电SOE不高于95%,放电SOE不低于5%,以尽可能延长电池寿命。
(3)最后是第3节对电池的充放电功率也做出了限制,综合电池峰值电流测试得到的结果,将电池的最大出力限制设定为-1.5C~+0.7C,并结合出力与SOE曲线得到不同SOE对应的出力限制(见式(16)、式(17))。
仿真中使用的各项参数见表3。储能系统的辅
助设备构成较为复杂,根据文献[22]从某公司得到的报价单,将该项数值定为100万元/(MW·h)。储能系统的运维价格包含了日常维护和运营的价格,参考2019年3月份河南电网100MW电池储能电站项目运维服务采购招标情况,国网河南综合能源服务公司以450万元/年的价格中标了10年的运维权,可以计算出运维单位能量成本为123.29元/(MW·h·天)。
表3 仿真参数
Tab.3 Economic simulation parameter table

仿真参数数值 三元材料电池模组单位能量成本/(元/W·h)0.9 储能系统施工单位能量成本/[万元/(MW·h)]30 储能系统辅助设备单位能量成本/[万元/(MW·h)]100 储能系统电力转换设备单位能量成本/(万元/MW)50 储能系统运维单位能量成本/[(元/(MW·h)/天]123.29 储能系统循环寿命(折合成额定能量的倍数)1 843.33 电池使用区间(%)5~95 AGC辅助服务单位补偿价格/元5 折现率(%)6
至此,参与仿真的参数已经介绍完毕。在本文中,主要用三个参数来描述储能系统的经济性,分别是全寿命周期收益、投资回收期和投资回报率。后文将通过这三个经济性指标完成储能系统的能量配置方案。
4.2.2 基于全寿命周期净收益现值的能量配置
储能电池在全寿命服役期间,获得的总收益的现值减去其成本,得到储能系统的全寿命周期收益现值。对于能量配置大于5MW·h的储能系统,使用图9的仿真方案,得到其全寿命周期收益与能量配置的关系如图10所示。
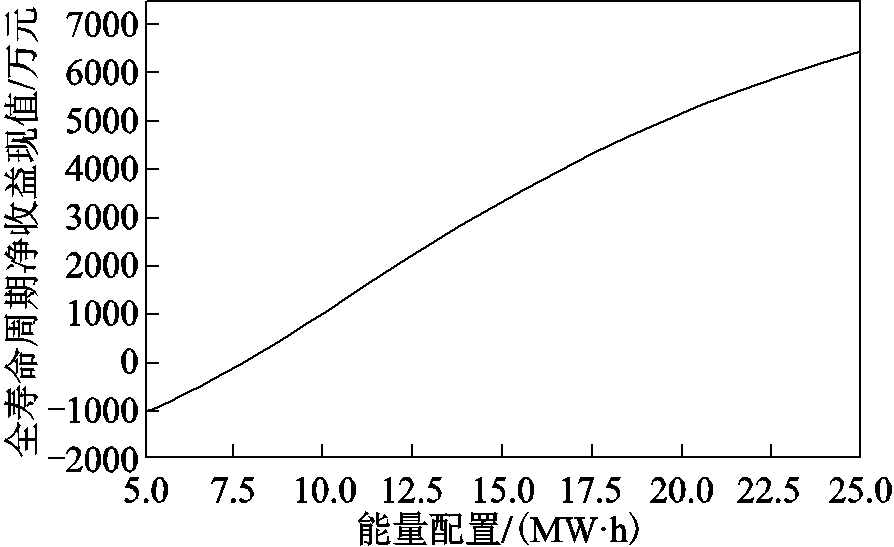
图10 全寿命周期净收益现值与能量配置的关系Fig.10 Relationship between present value of net life expectancy and energy allocation
可见,在能量配置从5MW·h增长到25MW·h的过程中,储能系统的全寿命周期净利润现值增长是相对线性的,即越大的储能配置能够获得更高额的净利润现值,这似乎成为了一个简单的“投资越大回报越大”的投资问题。因此,全寿命周期收益对于储能系统的能量配置而言参考价值十分有限。
4.2.3 基于投资回收期的能量配置
投资回收期是指项目收益超过项目投资的时间。当储能系统能量配置超过7.9MW·h时,其全寿命周期收益超过投资成本,即此时项目回收期等于项目的全寿命周期。图11为项目的资本回收期与储能系统能量配置之间的关系。

图11 资本回收期与储能系统能量配置之间的关系
Fig.11 Relationship between capital payback period and energy allocation
投资回收期对于储能系统调频这种成本敏感型的投资而言比较重要。根据仿真数据,当能量配置取11.4 ~12.6MW·h时,项目的投资期最短为149天。考虑到全寿命周期收益的线性增长特性,取12.6MW·h作为基于投资回收期得到的储能系统能量配置方案。
4.2.4 基于投资回报率的能量配置
投资回报率是指将投资得到收益的现值除以投资成本得到的百分数,用来衡量单位投资成本得到的收益值。
对本项目而言,将全寿命周期净利润现值和投资成本的比值作为因变量,同样将储能配置系统能量作为自变量,得到投资回报率与储能系统能量配置之间的关系如图12所示。可以看到,项目的投资回报率在储能能量配置增长的前期呈现较快的增长态势,在到达顶峰后开始降低。项目投资回报率的最高值是91.44%,对应的能量配置为21.5MW·h。
将山西某火电调频机组某日参与AGC辅助调频的工况进行详细分析。在增设储能设备辅助调频之前,火电机组的调频效果并不尽如人意。图13为只有火电机组参与调频时一天1 650次AGC调频的调节性能指标分布直方图,可见小于2的调节性

图12 投资回报率与储能系统能量配置之间的关系
Fig.12 Relationship between return on investment and energy allocation
能指标占比多达70.79%,而小于0.5的调节性能指标甚至达到了36.8%,原因是无法抑制反调工况,严重拖累了储能机组的日平均调节指标(反调工况的调节指标值是0.001)。调节前的性能指标平均值见表4。
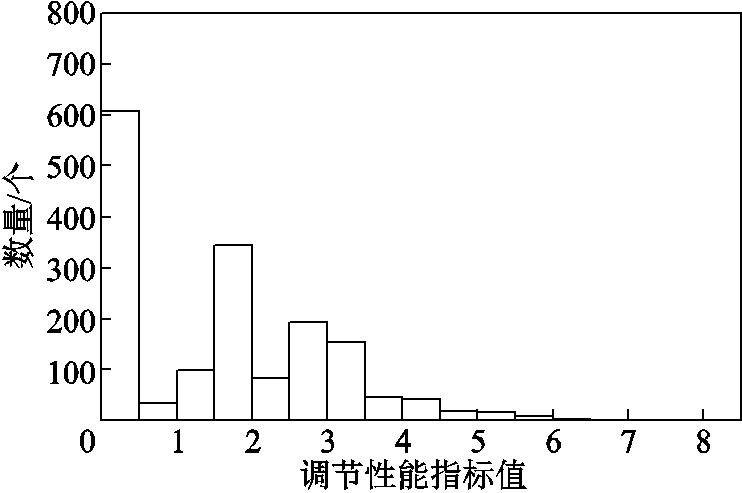
图13 无储能系统的日调节性能指标分布直方图
Fig.13 Histogram of daily adjustment performance index distribution without energy storage system
表4 火电机组调频日平均指标
Tab.4 Daily average indicator of thermal power frequency modulation unit

K1K2K3KpdayDday/MW 0.691.111.121.573 549.50
4.3.1 基于投资回收期最短的方案
将投资回收期最短作为储能配置的寻优目标时,意味着项目可以最短时间回收其成本,在具备较高盈利能力的同时对于投资过程中可能出现的风险也有着更强的应对能力。当储能系统的初始能量配置为12.6MW·h时,其首日参与AGC辅助服务的性能参数见表5,其充放电功率可以覆盖91.16%的工况需求。可以看到在储能系统的协助下,储能系统的日平均K1、K2和K3的值均有较大提升,也有效避免了机组被考核的情况。
图14为12.6MW·h储能系统的初始调节工况。可以很明显地看到储能系统的参与有效提升了联合系统对于AGC设点指令的响应程度。也正因为如此才能够取得表5中所示的良好经济性。
表5 12.6MW·h储能系统初始性能参数
Tab.5 Initial performance parameters with 12.6MW·h energy storage system

配置参数数值 储能能量配置/(MW·h)12.6 额定放电功率/MW18.9 额定充电功率/MW8.82 覆盖的工况需求(%)91.16 全寿命周期能量吞吐量/(MW·h)23 225.958 首日平均调节速率指标K11.83 首日平均调节精度指标K21.86 首日平均响应时间指标K31.89 首日平均调节性能指标Kp7.24 首日平均调节深度指标D/MW8 007.95 首日储能系统净收益/万元26.03 首日能量吞吐量/(MW·h)91.84
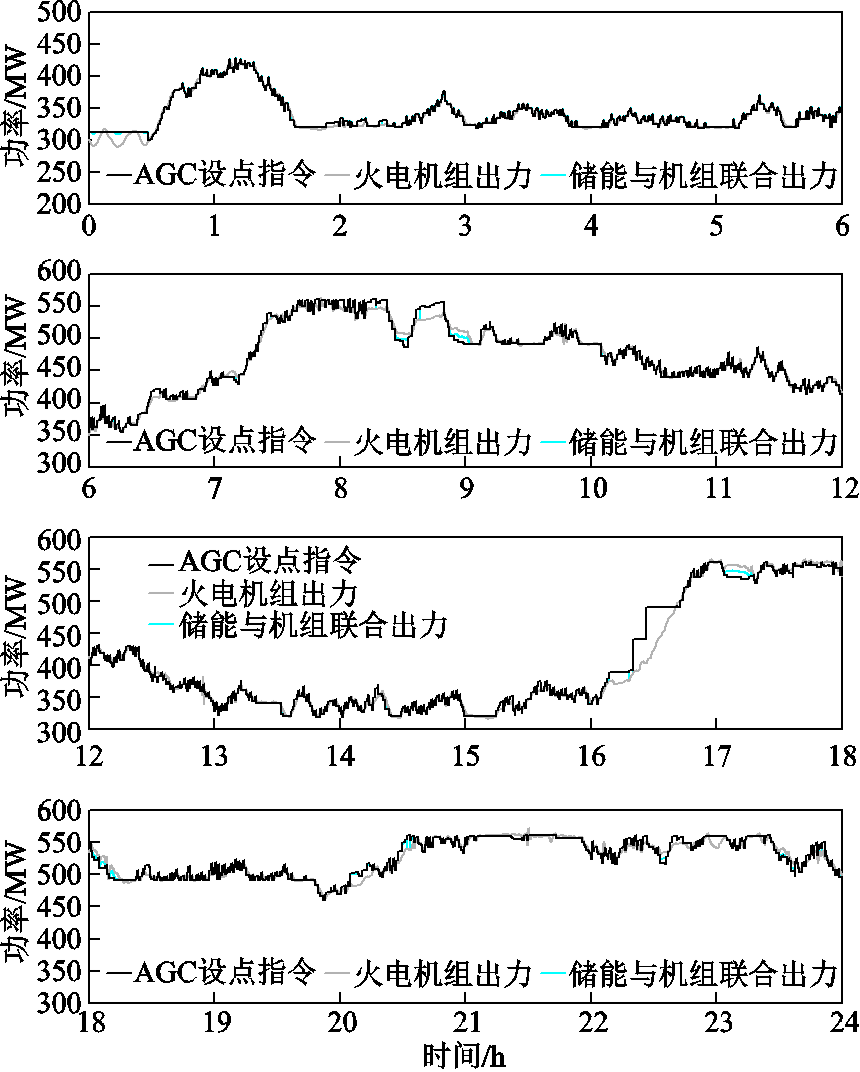
图14 配置12.6MW·h储能系统的首日调节工况
Fig.14 First day adjustment of the 12.6MW·h energy storage system
再来分析一下12.6MW·h储能系统在全寿命周期内的表现。表6为该储能系统循环性能参数,其全寿命周期共271天(按每天24h计算),在第149天收回全部投资成本。总投资成本为3 591万元,在系统退役后累计收益2 257.12万元。
表6 12.6MW·h储能系统循环性能参数
Tab.6 Cycle performance parameter with 12.6MW·h energy storage system

循环性能参数数值 投资回收期/天149 运行寿命/天271 投资成本/万元3591 全寿命周期净收益现值/万元2 257.12 投资回报率(%)62.85 平均调节性能指标6.89 平均调节深度指标D/MW7 486.38 平均日收益/万元22.87
4.3.2 基于投资回报率最大的方案
项目投资回报率最优时意味着其单位投资成本可以收到最大的投资收益现值,在相对稳定的投资环境中更为适用。表7中列出了21.5MW·h储能系统配置方案的初始性能参数。可见相比12.6MW·h的配置方案,在增加了近70%的储能系统配置后,日均调节性能指标的提升效果并不明显,对于日平均K1、K2和K3的提升在0.1左右,整体调节性能指标上升了0.49。但在调节深度上增加了近1 029.09,考虑到补偿公式计算的是日平均调节性能指标、日平均调节深度和补偿系数的乘积,因此首日储能系统的净收益从26.03万元增加到了34.66万元。
表7 21.5MW·h储能系统初始性能参数
Tab.7 Initial performance parameters with 21.5MW·h energy storage system
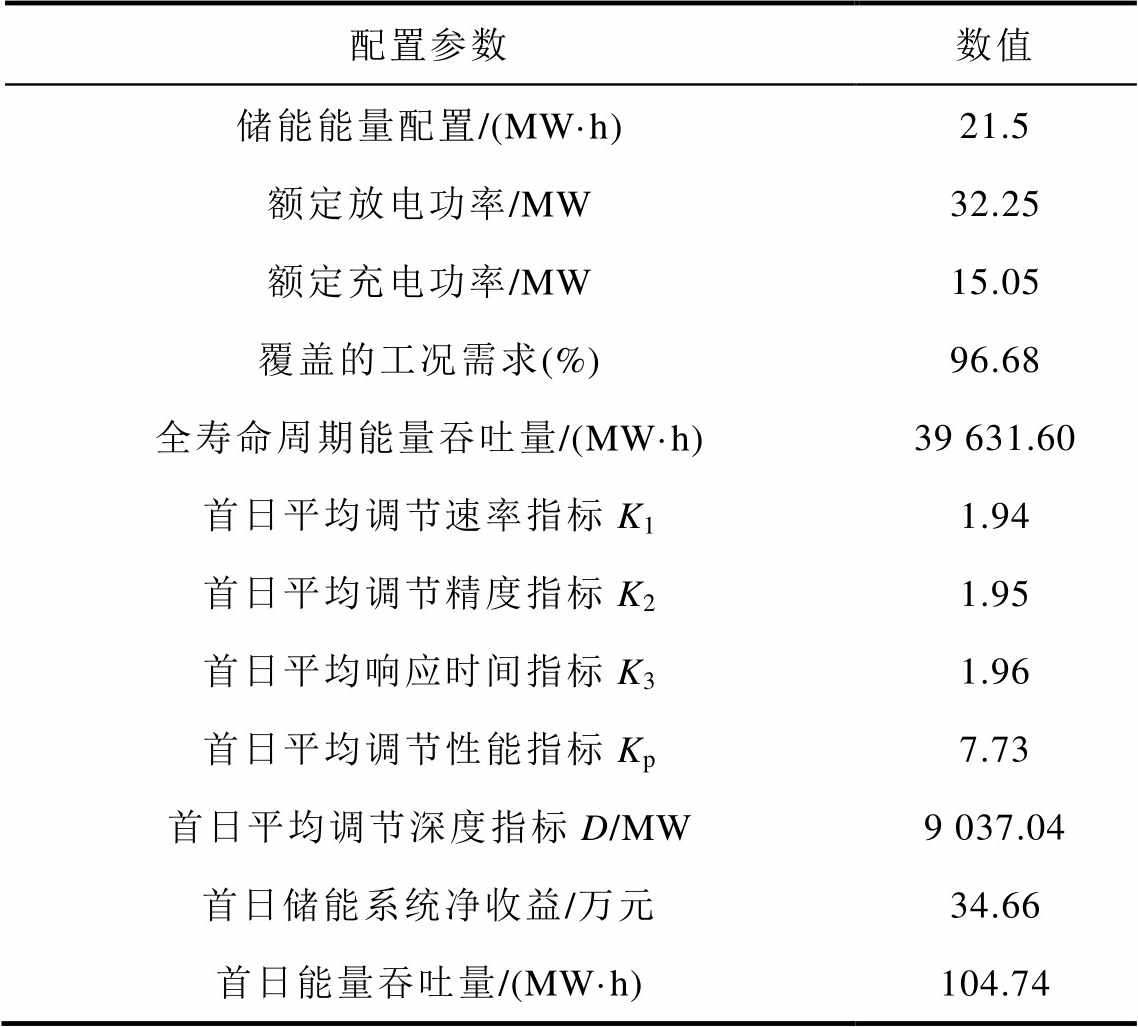
配置参数数值 储能能量配置/(MW·h)21.5 额定放电功率/MW32.25 额定充电功率/MW15.05 覆盖的工况需求(%)96.68 全寿命周期能量吞吐量/(MW·h)39 631.60 首日平均调节速率指标K11.94 首日平均调节精度指标K21.95 首日平均响应时间指标K31.96 首日平均调节性能指标Kp7.73 首日平均调节深度指标D/MW9 037.04 首日储能系统净收益/万元34.66 首日能量吞吐量/(MW·h)104.74
表8为21.5MW·h储能系统循环性能参数,由于采取了最大化投资回报率的策略,其投资回报率从62.85%增长到91.44%。
表8 21.5MW·h储能系统循环性能参数
Tab.8 Cycle performance parameter with 21.5MW·h energy storage system

循环性能参数数值 投资回收期/天192 运行寿命/天402 投资成本/万元6 127.50 全寿命周期净收益现值/万元5 602.81 投资回报率(%)91.44 平均调节性能指标7.69 平均调节深度指标D/MW8 921.48 平均日收益/万元31.24
本文立足于火电机组通过AGC辅助服务参与电网二次调频时暴露出来的调节效果差、出力灵活性低、经济效益低等问题,通过配置锂离子电池储能系统提升AGC辅助服务质量,并进行了建模与仿真,主要有以下结果:
1)分析比较国内外电力市场化改革的特点,尤其是针对储能系统参与AGC辅助调频服务的引导性政策和法规。梳理“两个细则”中指定的考核标准,编写了考评补偿算法,为储能系统控制策略的制定和经济性分析打下基础。
2)通过对锂离子电池不同区间应力下的循环衰退特性进行分析,选定荷电状态为5%~95%的区间为电池的最优使用区间,并建立了电池能量衰退模型,使项目的寿命周期预测更加真实可靠。采取基于Logistic函数的控制策略具有较好的SOE趋中效果,能有效地协助储能系统参与AGC辅助服务。
3)利用调频考评补偿算法、电池能量衰退模型、储能系统每日调节模型共同建立起储能系统参与AGC辅助服务的全寿命周期经济性模型。基于全寿命周期净收益现值、投资回收期和投资回报率寻找最优的能量配置方案,并最终根据后两者制定了12.6MW·h和21.5MW·h两种能量配置方案。两者的日平均收益分别是26.03万元和31.24万元,全寿命周期收益现值分别达到了2 257.12万元和 5 602.81万元。
可以预见,未来随着电池成本的进一步下降和电力市场改革的进一步深入,储能系统参与AGC辅助服务的市场经济表现将进一步加强,市场竞争也会日趋激烈。仿真度和准确度更高的分析模型可以为项目设计提供一定助力,控制策略的进步也能提升储能系统的表现,这方面的研究一定也会呈现百花齐放的局面。
参考文献
[1] 王俊, 顾尧.新能源电力接入对电网规划的影响思考[J]. 科技创新导报, 2018, 15(36): 220-222.Wang Jun, Gu Yao. The influence of new energy power access on grid planning[J]. Science and Technology Innovation Herald, 2018, 15(36): 220-222.
[2] 刘伟龙, 王丽芳, 廖承林, 等. 充电模态下电动汽车动力电池模型辨识[J]. 电工技术学报, 2017, 32(11): 198-207. Liu Weilong, Wang Lifang, Liao Chenglin, et al. Model identification of electric vehicle power battery in charging mode[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 198-207.
[3] Takasu N, Oshi T, Miyawaki F, et al. An experimental analysis of DC excitation of transformers by geomagnetically induced currents[J]. IEEE Transactions on Power Delivery, 1994, 9(2): 1173-1182.
[4] 李金蓉. 基于一致性理论的多端柔性直流输电系统频率控制研究[D]. 武汉: 武汉大学, 2018.
[5] 和敬涵, 谢毓毓, 张金国. 电动汽车充电负荷时空分布及其对配电网的影响[J]. 电力建设, 2015, 36(7): 83-88. He Jinghan, Xie Yuyu, Zhang Jinguo. Spatial and temporal distribution of EV charging load and its influence on distribution network[J]. Electric Power Construction, 2015, 36(7): 83-88.
[6] 张平. 火电与电储能联合调频方法的研究[J].通信电源技术, 2018, 35(10): 31-33. Zhang Ping. Research on combined frequency modulation method of thermal power and electric energy storage[J]. Telecom Power Technologies, 2018, 35(10): 31-33.
[7] 李欣然, 崔曦文, 黄际元, 等. 电池储能电源参与电网一次调频的自适应控制策略[J].电工技术学报, 2019, 34(18): 3897-3908. Li Xinran, Cui Xiwen, Huang Jiyuan, et al. The self-adaption control strategy of energy storage batteries participating in the primary frequency regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3897-3908.
[8] 张立, 牟法海, 周中锋, 等. 电池储能参与发电厂AGC调频技术与经济分析[J]. 电工技术, 2018(8): 76-78. Zhang Li, Mou Fahai, Zhou Zhongfeng, et al. Technology and economic analysis of AGC FM in power plant by battery energy storge[J]. Electrotechnics, 2018(8): 76-78.
[9] 李欣然, 黄际元, 陈远扬, 等. 基于灵敏度分析的储能电池参与二次调频控制策略[J]. 电工技术学报, 2017, 32(12): 224-233. Li Xinran, Huang Jiyuan, Chen Yuanyang, et al. Battery energy storage control strategy in secondary frequency regulation considering its action moment and depth[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 224-233.
[10] Xie Xiaorong, Guo Yonghong, Wang Bin, et al. Improving AGC performance of coal-fueled thermal generators using multi-MW scale BESS: a practical application[J]. IEEE Transactions on Smart Grid, 2018, 9(3): 1769-1777.
[11] 胡泽春, 夏睿, 吴林林, 等. 考虑储能参与调频的风储联合运行优化策略[J]. 电网技术, 2016, 40(8): 2251-2257. Hu Zechun, Xia Rui, Wu Linlin. Joint operation optimization of wind-storge union with energy storge participating frequency regulation[J]. Power System Technology, 2016, 40(8): 2251-2257.
[12] Thorbergsson E, Knap V, Swierczynski M, et al. Primary frequency regulation with li-ion battery based energy storage system-evaluation and comparison of different control strategies[C]// International Telecommunications Energy Conference, Smart Power and Efficiency, Hamburg, Germany, 2013: 1-6.
[13] 丁冬, 刘宗歧, 杨水丽, 等. 基于模糊控制的电池储能系统辅助AGC调频方法[J]. 电力系统保护与控制, 2015, 43(8): 81-87. Ding Dong, Liu Zongqi, Yang Shuili, et al. Battery energy storage aid automatic generation control for load frequency control based on fuzzy control[J]. Power System Protection and Control, 2015, 43(8): 81-87.
[14] Serban I, Teodorescu R, Marinescu C. Analysis and optimization of the battery energy storage systems for frequency control in autonomous microgrids, by means of hardware-in-the-loop simulations[C]//3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 2012: 374-379.
[15] Xu Bolun, Oudalov A, Poland J, et al. BESS control strategies for participating in grid frequency regulation[J]. IFAC Proceedings Volumes, 2014, 47(3): 4024-4029.
[16] Watson D, Hastie C, Rodgers M. Comparing different regulation offerings from a battery in a wind R&D park[J]. IEEE Transactions on Power Systems, 2018, 33(3): 2331-2338.
[17] Stroe D I, Swierczynski M, Stroe A I, et al. Degradation behaviour of Lithium-ion batteries based on field measured frequency regulation mission profile[C]//2015 IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 2015: 14-21.
[18] 孙丙香, 姜久春, 韩智强, 等. 基于不同衰退路径下的锂离子动力电池低温应力差异性[J]. 电工技术学报, 2016, 31(10): 159-167. Sun Bingxiang, Jiang Jiuchun, Han Zhiqiang, et al. The lithium-ion battery low temperature stress based on different degradation paths[J]. Transactions of China Electrotechnical Society, 2016, 31(10): 159-167.
[19] Cui Tiansong, Wang Yanzhi, Chen Shuang, et al. Optimal control of PEVs for energy cost minimization and frequency regulation in the smart grid accounting for battery state-of-health degradation[C]//52nd ACM/ EDAC/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 2015: 1-6.
[20] 汤杰, 李欣然, 黄际元, 等. 以净效益最大为目标的储能电池参与二次调频的容量配置方法[J]. 电工技术学报, 2019, 34(5): 963-972. Tang Jie, Li Xinran, Huang Jiyuan, et al. Capacity allocation of BESS in secondary frequency regulation with the goal of maximum net benefit[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 963-972.
[21] 李若, 李欣然, 谭庄熙, 等. 考虑储能电池参与二次调频的综合控制策略[J]. 电力系统自动化, 2018, 42(8): 74-82. Li Ruo, Li Xinran, Tan Zhuangxi, et al. Integrated control strategy considering energy storage battery participating in secondary frequency regultion[J]. Automation of Electric Power Systems, 2018, 42(8): 74-82.
[22] 杨洋. 参与AGC辅助服务的储能系统容量配置方法研究[D]. 北京: 北京交通大学, 2018.
Study on the Economy of Energy Storage System with Lithium-Ion Battery Participating in AGC Auxiliary Service
Abstract With the vigorous development of new energy technologies, the traditional grid frequency control is facing an increasingly severe test. There is good development space for the lithium-ion battery energy storage system helps the thermal power unit to participate in frequency adjustment. In this paper, the application scenario is the lithium-ion battery energy storage system assists the thermal power unit to participate in the automatic generation control (AGC) auxiliary service. And the evaluation compensation algorithm of the AGC auxiliary service is compiled according to the "two rules". A comparatively conservative but reliable battery energy decay model was established through the decay experiment. About the control strategy, the SOE trend control strategy based on Logistic function and the economic strategy based on evaluation index were built. Operating conditions is used to be simulated to fit the daily adjustment model of the energy storage system. Finally, a project economic analysis is conducted for the project's life cycle net income, investment payback period and return on investment. This paper obtains the initial energy allocation scheme of the energy storage system by evaluating the payback period and return on investment, and provides a sensitivity analysis of possible policy updates and market changes. We can obtain more rigorous and reliable investment solutions having strong compatibility with policy and market changes by using this economic model.
Keywords:Automatic generation control auxiliary service, lithium-ion battery, energy decline model, central control strategy, Logistic function, economic analysis
中图分类号:TM911
DOI: 10.19595/j.cnki.1000-6753.tces.191151
孙丙香 女,1979年生,副教授,博士生导师,研究方向为动力电池成组应用技术。E-mail:bxsun@bjtu.edu.cn(通信作者)
李旸熙 男,1995年生,硕士研究生,研究方向为动力电池成组应用技术。E-mail:lyxbsd@163.com
国家重点研发计划(2018YFB0905304)和国家自然科学基金(51907005, U1664255)资助项目。
收稿日期 2019-09-09
改稿日期 2019-11-22
(编辑 郭丽军)