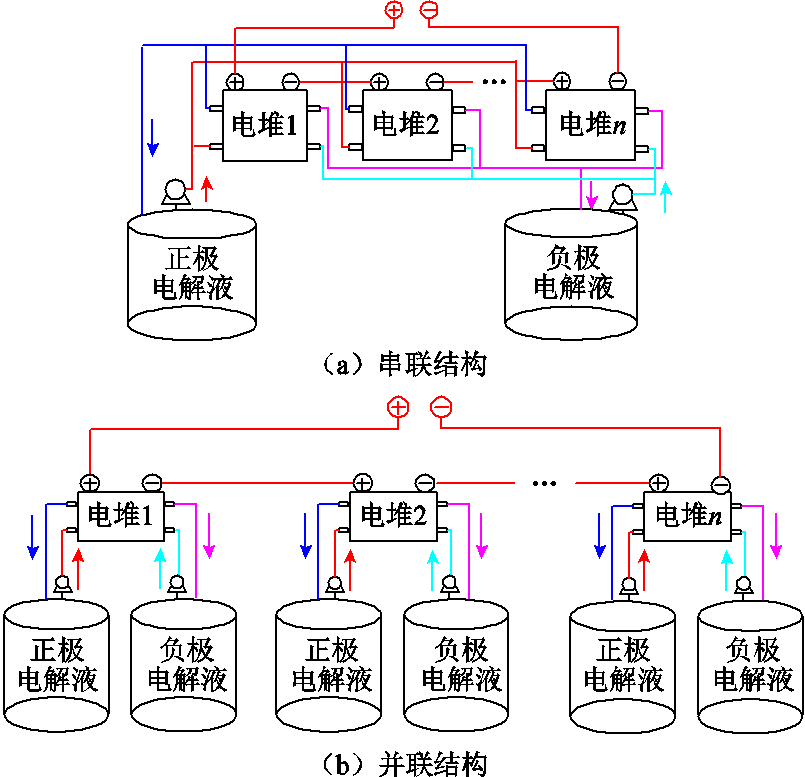
图1 大容量VRB储能系统基本拓扑结构
Fig.1 Basic topology of large-capacity VRB energy storage system
摘要 针对由多组全钒液流电池并联构成的大容量储能系统,给出计及损耗的系统功率优化分配策略。该策略首先建立计及损耗的功率分配模型,然后将系统损耗、荷电状态(SOC)均衡度作为目标优化函数,在满足功率需求、SOC上下限等约束条件下采用虚拟粒子-自适应差分进化算法(VP-ADE)寻求最优解,进而实现储能系统的功率优化分配;最后,基于Matlab对该文策略进行仿真,并与传统策略进行对比。仿真结果表明该策略能在分配功率过程中降低系统损耗,同时使各储能单元的SOC在充放电过程中逐渐趋于一致。
关键词:功率分配 全钒液流电池 损耗 荷电状态 差分进化算法
随着风能、光伏等可再生能源发电比例的日益提高,其本身所具有的波动性和间歇性给现有电力系统的运行带来了巨大挑战[1-3]。作为解决可再生能源大规模接入、传统电力系统削峰填谷及分布式区域能源系统负荷平衡的关键支撑,大容量储能技术在能源革命中发挥着重要作用[4-8]。全钒液流电池(Vanadium Redox Flow Battery,VRB)由于具有安全环保、寿命长、效率高、选址自由等特点,成为大容量高效储能技术的首选技术之一[9-10]。
由于单个储能单元电压低、容量有限,不能满足大型风电场等场景对储能的需求。出于电路成本和效率的原因,将电池串联到较高的电压、再并联扩大容量后进行整体管理和控制是通常采用的最为经济可靠的方案[11-12]。然而大容量储能系统内部的功率分配问题一直是困扰电池串并联成组使用的技术难点,同时随着储能系统的长期投入运行,储能单元内部损耗也会降低自身的充放电性能,从而制约整个储能系统运行效率和装置可用率。
针对大容量储能系统的功率分配问题,目前国内外研究可大致分为三类。第一类是传统的功率分配策略,即按照储能系统中各储能单元荷电状态(State of Charge,SOC)占整体比例进行功率分配[13-14],该策略原理简单且容易实现。第二类是基于电气结构的控制策略,如文献[15-17]以储能单元间SOC良好的均衡度为目的,提出基于SOC的改进下垂控制实现功率的协调控制;文献[19-21]在传统的P-f下垂控制中加入SOC平衡因子控制逆变器输出的有功功率。第三类是引入智能优化算法的控制策略,文献[22]建立以系统经济运行为目标的功率分配优化模型,在条件约束下使用遗传算法进行在线优化,从而协调系统充放电过程和功率分配;文献[23]使用模糊控制规则实时修正储能系统单元的充放电功率。但上述文献多数未考虑系统运行损耗,且控制对象多为混合储能系统。
为减少电池的能量损耗,从技术角度来讲,应在前期系统的规划与设计过程中考虑到多种因素,包括管道回路的设计与布局、材料选择、管径参数设计等,这样可以减少电解液因电堆管道摩擦、堆栈压力等因素造成的损耗[24]。从既定系统优化的角度来讲,如采用最佳流量控制可以降低泵损和提高系统效率[25-26];考虑能量损耗与功率损耗、充放电时间的关系,可将功率损耗作为电池组调度的优化目标。因此,本文在以上研究的基础上,以系统损耗最低、SOC均衡度最优为优化目标,给出了基于虚拟粒子-自适应差分进化算法(Virtual Particle-Adaptive Differential Evolution Algorithm, VP-ADE)的并联钒电池储能系统功率优化分配策略,搭建了考虑系统运行损耗的功率分配模型,利用VP-ADE算法对储能系统功率分配进行实时优化,并将所提出的功率分配方案与传统方案进行对比分析。
为满足大功率高容量储能系统的要求,大容量VRB储能系统常由多个VRB串联或并联构成,针对不同的控制策略或系统负载需求,其拓扑结构的设计存在多种形式。VRB串联的常见连接方式如图1a所示,该结构是将多个VRB电堆串联而成,在液体回路上共用一套电解液罐和动力系统,然而在这种结构中,某个单元出现故障将直接影响整个储能系统的工作效率,同时随着电池组规模的扩充,电堆间的管道网络将变得复杂。并联结构如图1b所示,在这种分布式拓扑结构中,每个VRB储能单元都可以实现独立控制,从而可以避免串联方式的弊端,提升系统整体的稳定性。

图1 大容量VRB储能系统基本拓扑结构
Fig.1 Basic topology of large-capacity VRB energy storage system
因此,本文选取的研究对象为直流微电网中并联拓扑结构的钒电池储能系统,其拓扑结构如图2所示,每个储能单元都是一套完整的VRB系统,并通过DC-DC变换器与直流母线相连接,在每个工作周期内由功率优化分配模块实现每个储能单元的独立控制及并联电池组灵活投切,及时、高效地分配各单元运行功率值,显著提高系统的耐久性与稳定性。
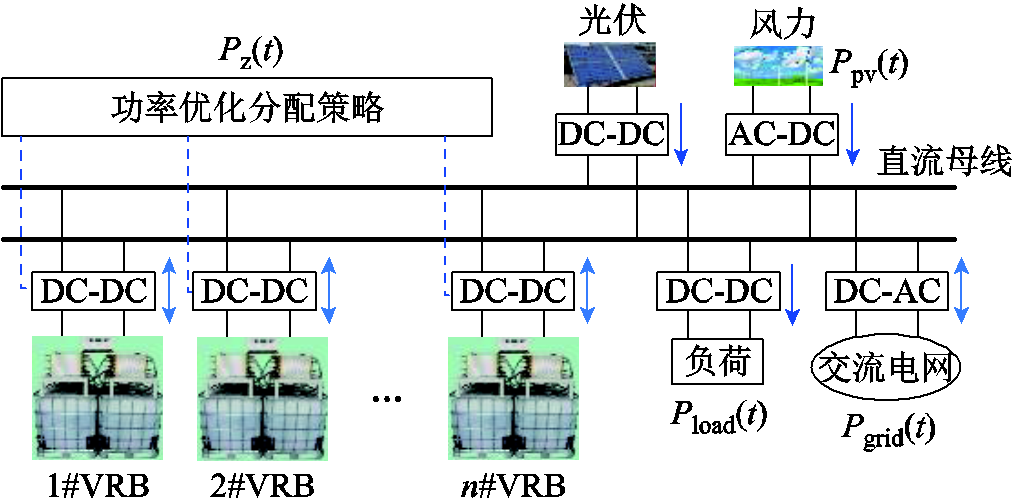
图2 直流微电网并联VRB储能系统拓扑结构
Fig.2 Parallel topology of VRB storage system in DC microgrid
定义可再生能源发电系统输出功率为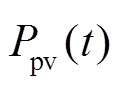 ,交流电网功率为
,交流电网功率为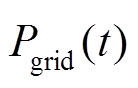 ,负荷功率为
,负荷功率为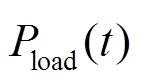 ,储能系统功率为
,储能系统功率为 ,设定充电方向为正方向。在任一时间周期t内,都需要满足直流微电网功率平衡,以储能系统充电为例,当
,设定充电方向为正方向。在任一时间周期t内,都需要满足直流微电网功率平衡,以储能系统充电为例,当 >0时,表明可再生能源发电系统输出的过剩功率通过储能系统充电进行消纳,输出功率
>0时,表明可再生能源发电系统输出的过剩功率通过储能系统充电进行消纳,输出功率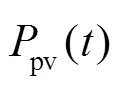 与负荷功率
与负荷功率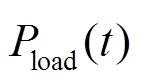 、电网功率
、电网功率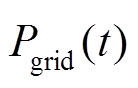 在第t时间段的功率差即为储能系统功率值
在第t时间段的功率差即为储能系统功率值 ,即
,即
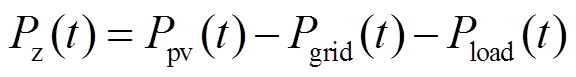 (1)
(1)基于VRB的工作原理建立其等效损耗电路模型[27-28],如图3所示,其中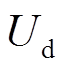 为VRB两端的端电压;
为VRB两端的端电压;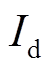 为电池充放电电流;
为电池充放电电流; 为VRB的电堆电压,因与SOC有关,故采用受控电压源表示;
为VRB的电堆电压,因与SOC有关,故采用受控电压源表示;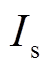 为电堆电流;
为电堆电流;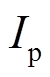 为泵损,采用恒流源表示;
为泵损,采用恒流源表示;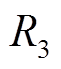 为寄生电阻;
为寄生电阻;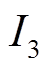 为流经寄生电阻的电流;
为流经寄生电阻的电流;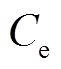 为电极电容,主要用来模拟电池的动态过程;
为电极电容,主要用来模拟电池的动态过程;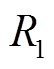 为由反应动力学引起的反应内阻;
为由反应动力学引起的反应内阻;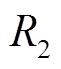 为由电极材料(离子交换膜、电极、双电极等)产生的欧姆内阻。实际运行中
为由电极材料(离子交换膜、电极、双电极等)产生的欧姆内阻。实际运行中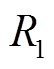 、
、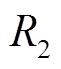 数值受SOC、单体电池串并联级数以及温度等因素影响而发生改变,但是当SOC处于20%~80%范围内时内阻变化幅度较小[29-32]。本文将内阻作为定值进行简化处理。
数值受SOC、单体电池串并联级数以及温度等因素影响而发生改变,但是当SOC处于20%~80%范围内时内阻变化幅度较小[29-32]。本文将内阻作为定值进行简化处理。
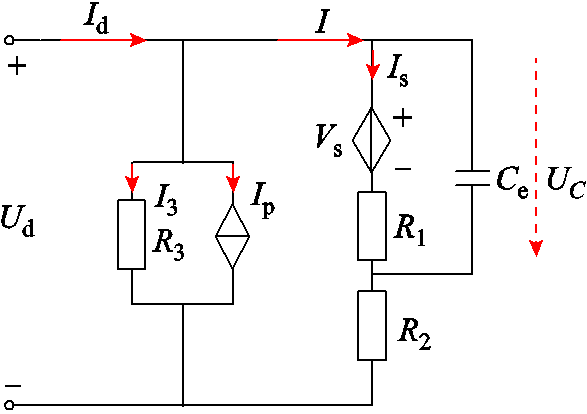
图3 VRB等效电路损耗模型
Fig.3 VRB equivalent circuit loss model
由图3中模型各变量间关系可得出VRB的状态空间模型,其中状态方程为
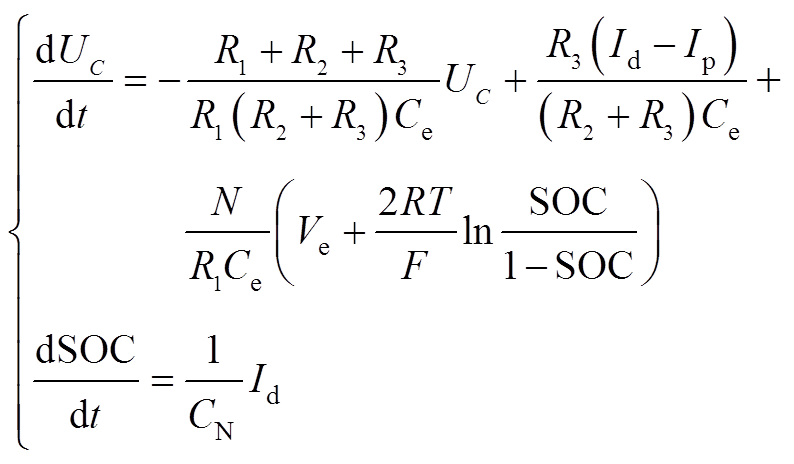 (2)
(2)输出方程为
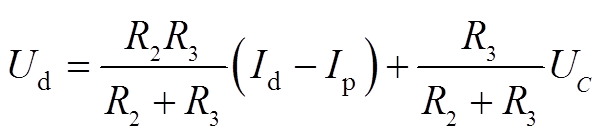 (3)
(3)
式中,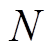 为VRB内部串联的单体电池个数;Ve为电池标准电极电动势;
为VRB内部串联的单体电池个数;Ve为电池标准电极电动势;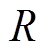 为气体常数;
为气体常数;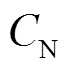 为电池额定容量,A·h;
为电池额定容量,A·h;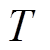 为温度,通常取298K(即25℃);
为温度,通常取298K(即25℃);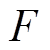 为法拉第常数。通过该数学模型能够体现出VRB的非线性、时变性等特点,方便对储能系统进行分析和控制。
为法拉第常数。通过该数学模型能够体现出VRB的非线性、时变性等特点,方便对储能系统进行分析和控制。
2.2.1 功率损耗最低
系统VRB储能系统的功率损耗主要包括VRB电池组损耗及DC-DC损耗。由2.1节建立的VRB等效电路损耗模型可知,VRB电池组损耗Pbat_loss包括内部电阻损耗Pbat_loss_R和寄生损耗(Ppump+Pfixd)两大部分,即
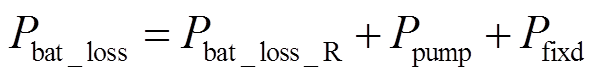 (4)
(4)其中,内部电阻损耗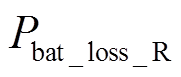 主要包括
主要包括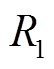 、
、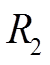 产生的损耗,即
产生的损耗,即
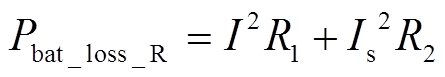 (5)
(5)
寄生损耗是由泵损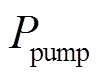 及寄生电阻
及寄生电阻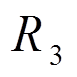 产生的损耗
产生的损耗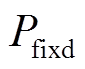 组成,二者分别为
组成,二者分别为
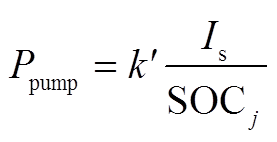 (6)
(6)
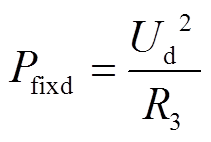 (7)
(7)
式中,k′为泵升损耗常数;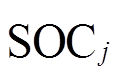 为第j个VRB储能单元的SOC。
为第j个VRB储能单元的SOC。
DC-DC损耗根据其工作状态分为工作损耗和待机损耗,即
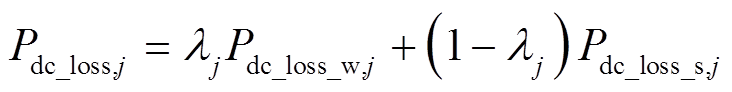 (8)
(8)式中,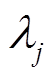 为第j个VRB储能单元的使能因子,
为第j个VRB储能单元的使能因子,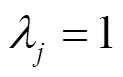 表示该储能单元处于开机状态,DC-DC产生工作损耗,如式(9)所示;
表示该储能单元处于开机状态,DC-DC产生工作损耗,如式(9)所示;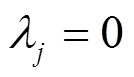 表示该储能单元未开机工作,DC-DC产生待机损耗,如式(10)所示。
表示该储能单元未开机工作,DC-DC产生待机损耗,如式(10)所示。
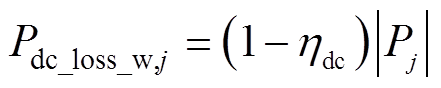 (9)
(9)
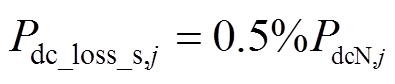 (10)
(10)式中,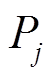 为第j个VRB储能单元的实际分配功率,
为第j个VRB储能单元的实际分配功率,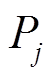 >0表示充电,
>0表示充电,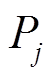 <0表示放电;
<0表示放电;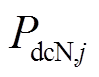 为DC-DC的额定功率;
为DC-DC的额定功率;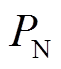 为VRB电池组额定功率;
为VRB电池组额定功率;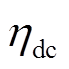 为DC-DC的工作效率,实际情况中DC-DC的工作效率会随着输出效率的改变而产生变化,在额定状态时效率最大,随着功率减小效率会降低,故取
为DC-DC的工作效率,实际情况中DC-DC的工作效率会随着输出效率的改变而产生变化,在额定状态时效率最大,随着功率减小效率会降低,故取
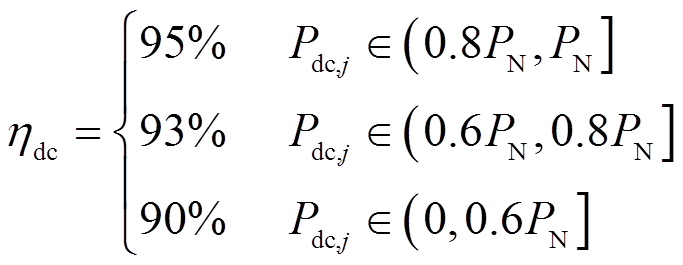 (11)
(11)
综上,VRB储能系统的总损耗为
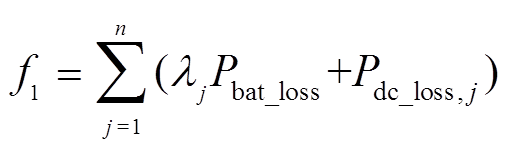 (12)
(12)式中,n为系统并联的储能单元数量。
2.2.2 SOC均衡度最优
VRB储能系统的SOC均衡度目标函数由各VRB储能单元的剩余荷电状态的方差表示,且在寻求SOC均值的基础上,将电池当前可充放电量引入目标函数(本文暂不考虑电池容量折损),从而加快均衡速度。目标函数为
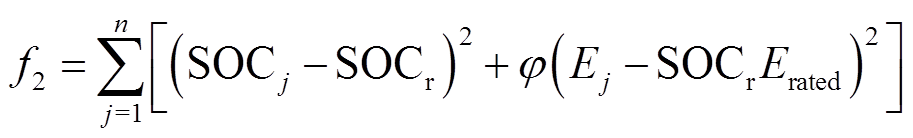 (13)
(13)式中,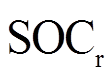 为VRB储能系统的SOC均值,表达式见式(14);
为VRB储能系统的SOC均值,表达式见式(14);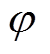 为权重系数;
为权重系数;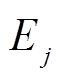 为第j个VRB储能单元当前可充放电量;
为第j个VRB储能单元当前可充放电量;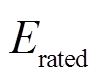 为储能单元额定电量。
为储能单元额定电量。
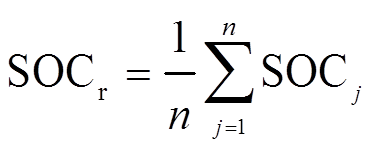 (14)
(14)
所有VRB储能单元的总出力约束
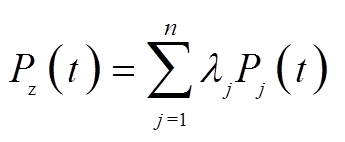 (15)
(15)VRB储能单元SOC约束
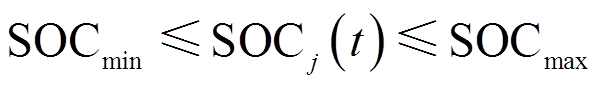 (16)
(16)
式中,SOCmax、SOCmin分别为SOC上、下限。
VRB储能单元能量约束
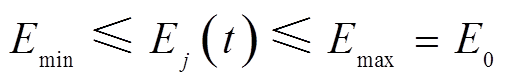 (17)
(17)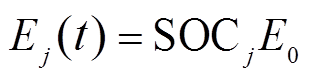 (18)
(18)
式中,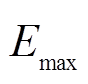 、
、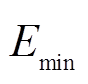 分别为储能单元剩余能量的上、下限;
分别为储能单元剩余能量的上、下限;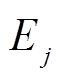 (t)为第j个VRB当前剩余能量;
(t)为第j个VRB当前剩余能量;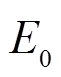 为储能单元额定能量。
为储能单元额定能量。
VRB储能单元出力约束
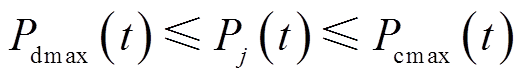 (19)
(19)其中,最大充电允许值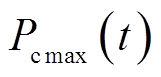 为
为
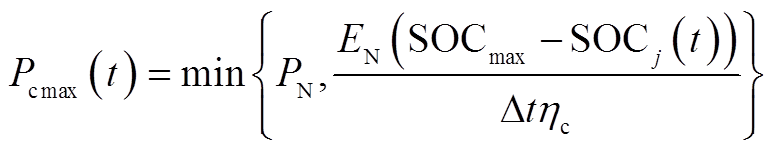
最大放电允许值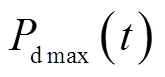 为
为
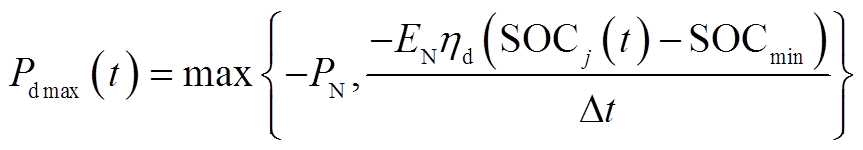
式中,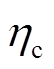 、
、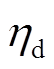 分别为电池的充电效率和放电效率。
分别为电池的充电效率和放电效率。
借鉴液流电池国际标准IEC62932—2020《固定式液流电池》及储能系统国家运行标准GBT36549—2018《电化学储能电站运行指标及评价》,定义如下评价指标。
1)VRB储能单元充放电状态切换次数
VRB储能有三种运行状态:充电、放电与待机,充放电交替出现时为一次充放电状态切换次数,如式(20)所示。该指标越大,表明储能单元放电状态切换越频繁,产生运行损耗越多。
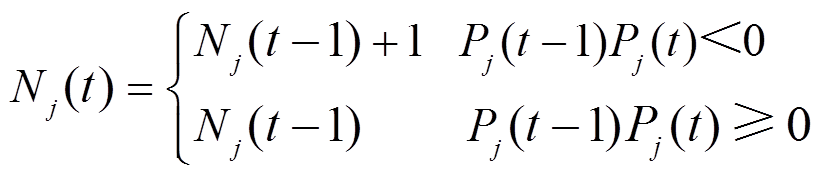 (20)
(20)2)VRB储能单元利用系数
VRB储能单元利用系数为评价周期内储能系统运行时间与统计时间的比值,即
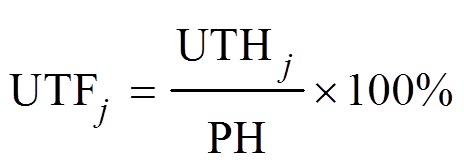 (21)
(21)式中, 为第j个VRB储能单元在评价周期内的实际运行小时数;PH为评价周期内总小时数。
为第j个VRB储能单元在评价周期内的实际运行小时数;PH为评价周期内总小时数。
为了避免复杂的比较,提高算法优化实时性,在此采用虚拟粒子法对目标函数进行预处理。虚拟粒子算法的基本原理如图4所示,该算法在目标函数解区域中构造一个虚拟的粒子P,P点坐标为两个单目标函数在其各自约束中的最优解,因不能同时实现,所以P是一个虚拟的点,而其他粒子通过与该粒子的几何平均距离来判断自身位置的优劣。
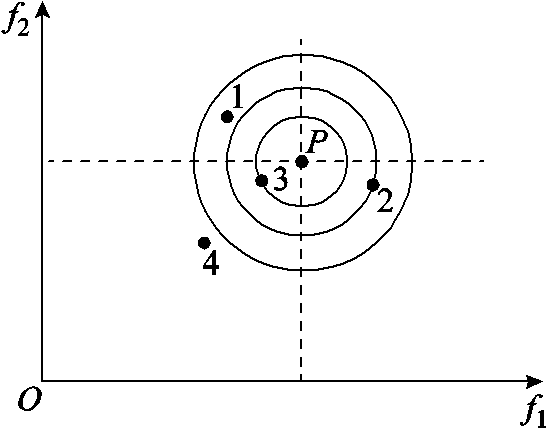
图4 虚拟粒子法基本原理
Fig.4 Basic principle of virtual particle method
由图4可以看出点3最优,也就是实际问题中最终要选取的折中解。考虑到中长期的SOC控制只需在一定范围,避免储能单元出现无法参与调节的情况出现即可,因此本文将SOC均衡运行目标进行条件性优化。基于虚拟理想粒子的功率优化分配总目标函数可构造为
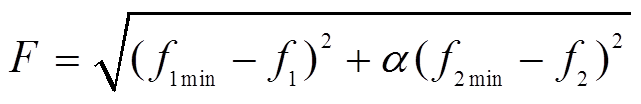 (22)
(22)式中,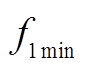 、
、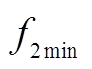 分别为功率损耗、SOC均衡度的目标最优解;
分别为功率损耗、SOC均衡度的目标最优解;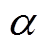 为对应目标的权重系数,当
为对应目标的权重系数,当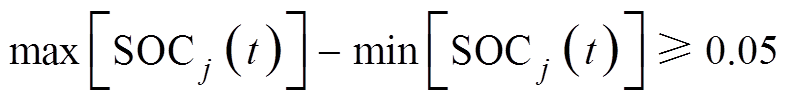 时,
时,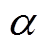 =1,其余情况
=1,其余情况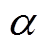 =0。
=0。
基于自适应差分进化算法的VRB储能系统功率优化分配策略流程如图5所示,具体步骤分为两大部分,本文以第t周期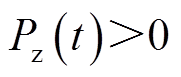 、储能系统需要进行充电为例进行说明。其中第一部分先读取当前周期
、储能系统需要进行充电为例进行说明。其中第一部分先读取当前周期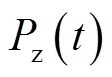 值,当
值,当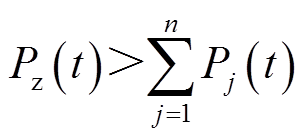 时,所有储能单元满功率运行;当
时,所有储能单元满功率运行;当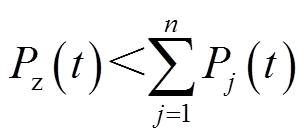 时,先根据每个VRB储能单元的SOC值进行升序排列,SOC越低的储能单元该周期选择充电的优先级越高,然后按当前周期总出力要求来判断并选定参与本次功率分配VRB储能单元组合,直至满足
时,先根据每个VRB储能单元的SOC值进行升序排列,SOC越低的储能单元该周期选择充电的优先级越高,然后按当前周期总出力要求来判断并选定参与本次功率分配VRB储能单元组合,直至满足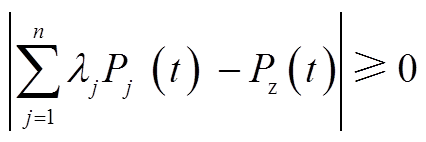 ,则可得到当前充电周期参加功率分配最优的m个VRB单元,反之同理。
,则可得到当前充电周期参加功率分配最优的m个VRB单元,反之同理。
第二部分是在选定的VRB单元组合内采用ADE进行功率优化分配,步骤如下。
(1)算法初始化。从给定边界约束内随机生成由NP个实数值组成的参数向量,见式(23),向量维数D=m-1,每个个体即代表一组储能单元的功率分配优化值。
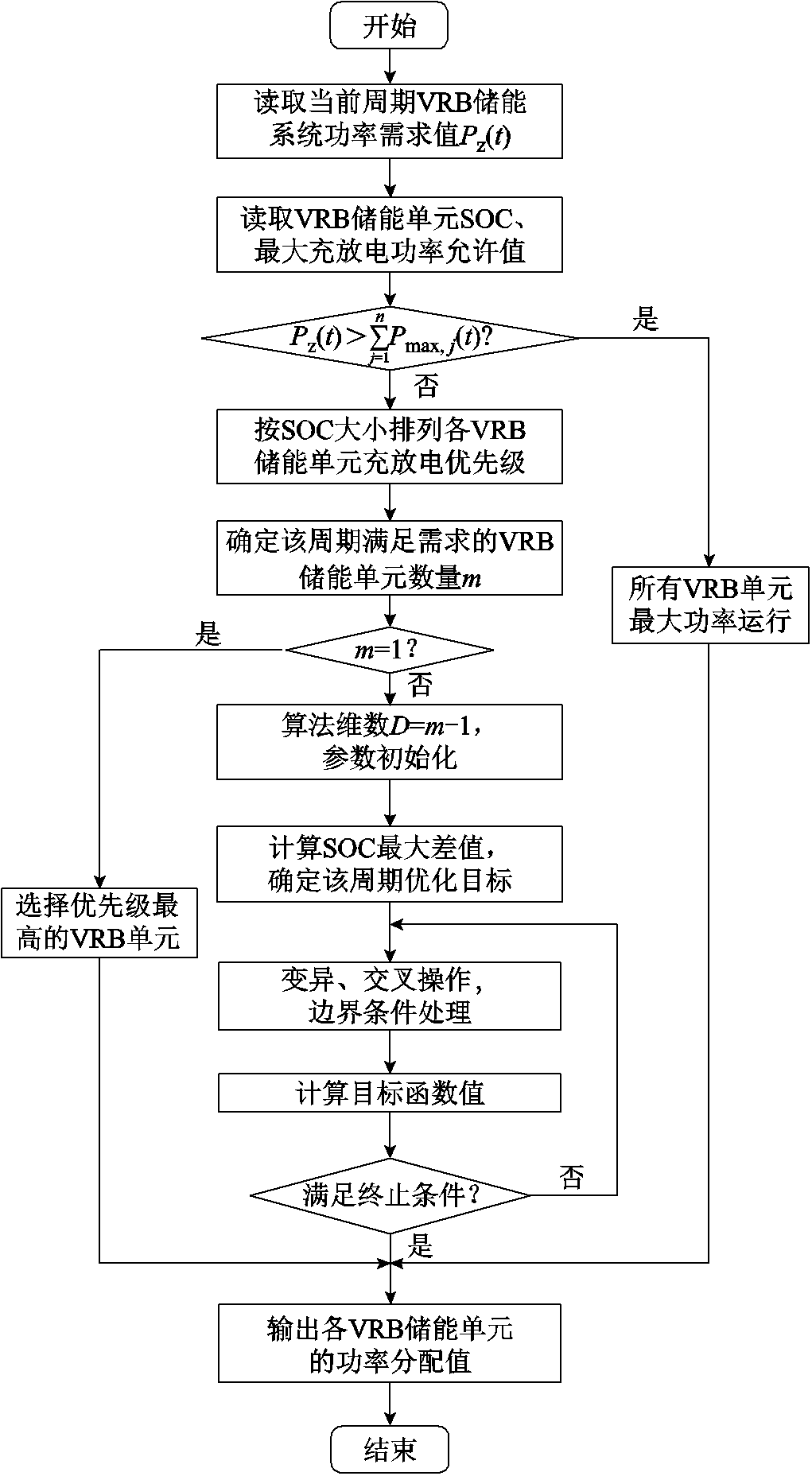
图5 功率优化分配策略流程
Fig.5 Power optimization allocation strategy flow chart
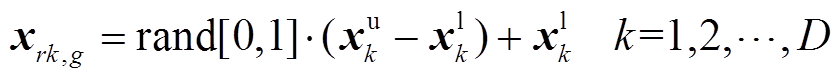 (23)
(23)式中,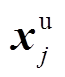 、
、 分别为参数变量的上、下限;r=1,2,
分别为参数变量的上、下限;r=1,2, ,NP,NP为种群规模;g为当前迭代次数,g=1,2,
,NP,NP为种群规模;g为当前迭代次数,g=1,2, ,G。
,G。
(2)计算此时储能单元的SOC最大差异值,确定该周期的算法优化目标。
(3)变异。从种群中随机选择三个互不相同的个体(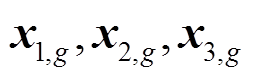 ),并且按式(24)产生变异向量V。
),并且按式(24)产生变异向量V。
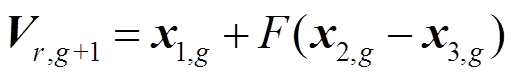 (24)
(24)式中,F为变异算子,取值范围为[0,2]。为保持种群多样性,避免算法早熟,在此设计具有自适应能力的变异算子为
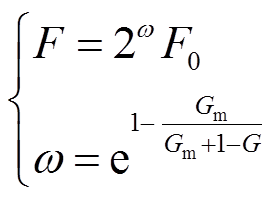 (25)
(25)
式中,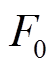 为初始变异算子;
为初始变异算子;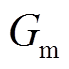 为最大迭代次数。
为最大迭代次数。
(4)交叉。变异向量V和目标向量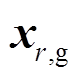 之间交叉操作,产生试验个体
之间交叉操作,产生试验个体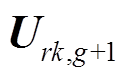 为
为
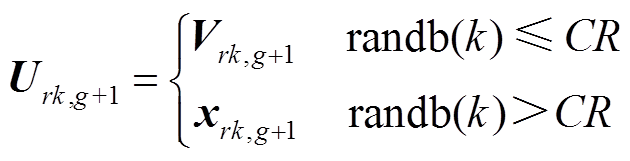 (26)
(26)式中,CR为交叉算子,取值范围为[0,1];randb(k)为产生[0,1]之间随机数发生器的第k个估计值。
(5)选择。根据式(27)选择试验个体U,如果目标个体的适应度函数值小于试验个体,则目标个体保留到下一个,否则试验个体保留到下一代。
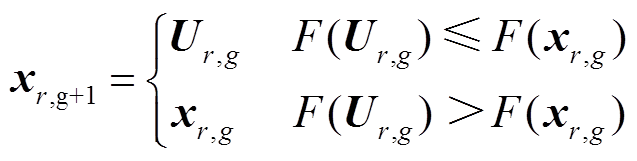 (27)
(27)(6)是否满足结束条件。若算法达到最大迭代次数或当目标函数值小于阈值,则输出最优解并停止运行,若未满足结束条件则转到步骤(3)。
4.1.1 储能系统参数说明
VRB储能系统的总需求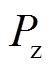 可来自平抑光伏或风电波动的数据,或者直接来自电网调度数据,本文采用湖南某光伏电站平抑光伏波动所需的储能功率作为输入值,如图6所示,共60个调度周期(5:00~ 20:00, 15h),时间间隔为15min。
可来自平抑光伏或风电波动的数据,或者直接来自电网调度数据,本文采用湖南某光伏电站平抑光伏波动所需的储能功率作为输入值,如图6所示,共60个调度周期(5:00~ 20:00, 15h),时间间隔为15min。
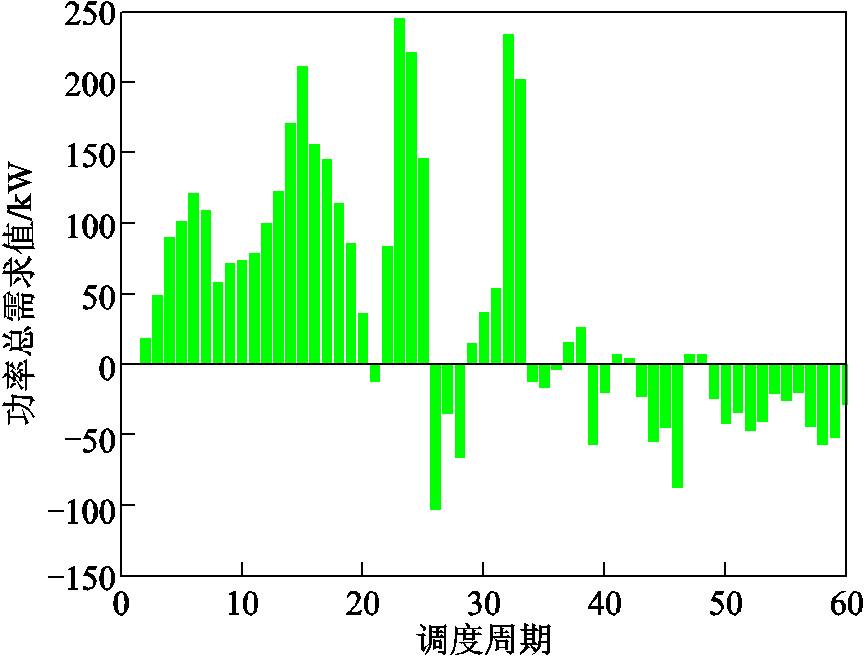
图6 储能系统功率需求值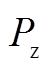 曲线
曲线
Fig.6 Energy storage system power demand is 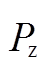 curve
curve
本文设定的大容量储能系统由四组VRB并联构成,每个储能单元额定容量为50kW,模型参数设置见表1。电池SOC介于0.2~0.8时,本文选用的VRB等效损耗模型能够真实地反映电池充放电特性[26],因此本文四组VRB初始SOC值依次设置为0.2、0.25、0.3和0.4。
表1 VRB等效损耗模型参数
Tab.1 VRB equivalent loss model parameter

参数数值 额定功率P/kW50 额定电压/V187 额定电流/A310 额定能量300 反应内阻R1/Ω0.22 欧姆电阻R2/Ω0.13 寄生电阻R3/Ω45.33 充放电效率,(%)80
4.1.2 VP-ADE算法参数设置
算法初始化,选取个体数目NP=50,最大迭代数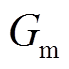 =200,初始变异算子F0=0.4,交叉算子CR=0.1,阈值为10-6,运行算法可得如图7所示的ADE算法目标函数进化曲线,该算法在迭代100次左右进入收敛状态,目标函数值趋于稳定,表明迭代次数选为200代较为合理。
=200,初始变异算子F0=0.4,交叉算子CR=0.1,阈值为10-6,运行算法可得如图7所示的ADE算法目标函数进化曲线,该算法在迭代100次左右进入收敛状态,目标函数值趋于稳定,表明迭代次数选为200代较为合理。
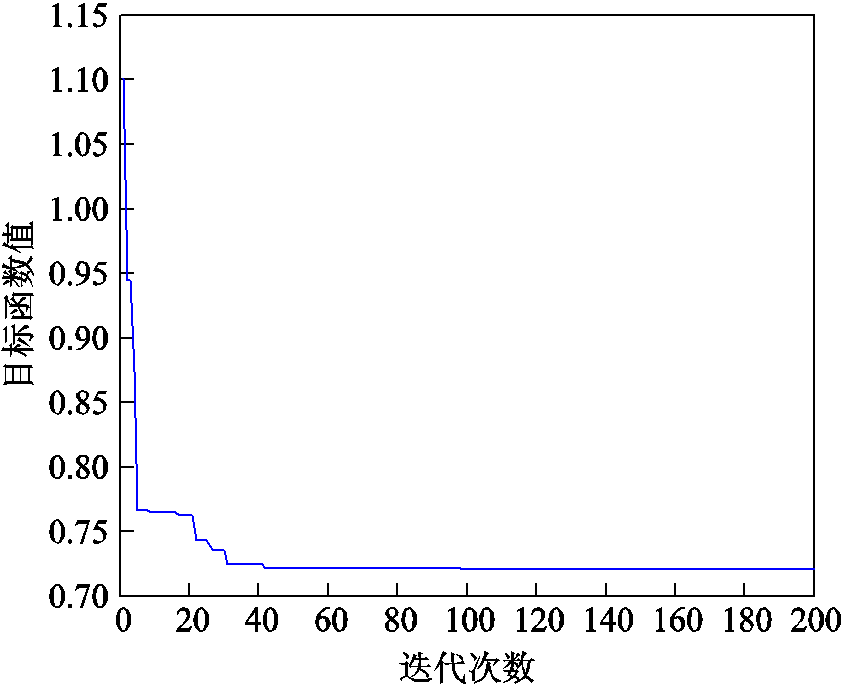
图7 ADE算法目标函数进化曲线
Fig.7 ADE algorithm objective function evolution curve
4.2.1 算例仿真
采用VP-ADE算法对图6所示的储能系统总功率进行功率分配,四组并联储能单元功率优化分配的结果如图8所示,储能单元的SOC曲线如图9所示。由图8可知,在第1个调度周期,储能总需求功率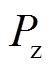 为18.5kW,按照本文策略只需将功率分给优先级最高的储能单元。由最初给定的各个VRB储能单元SOC初始值可知,4个VRB储能单元的优先级是1号VRB>3号VRB>2号VRB>4号VRB,故此时将功率分配给1号VRB,1号VRB储能单元开始充电,其他三个VRB储能单元处于待机状态。到了第2个调度周期,1号~4号VRB储能单元的SOC变为0.233、0.25、0.3、0.4,
为18.5kW,按照本文策略只需将功率分给优先级最高的储能单元。由最初给定的各个VRB储能单元SOC初始值可知,4个VRB储能单元的优先级是1号VRB>3号VRB>2号VRB>4号VRB,故此时将功率分配给1号VRB,1号VRB储能单元开始充电,其他三个VRB储能单元处于待机状态。到了第2个调度周期,1号~4号VRB储能单元的SOC变为0.233、0.25、0.3、0.4,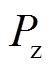 为48.58kW,该功率小于单个VRB的最大充电功率,则此时仍选用优先级最高的VRB储能单元,即给1号VRB。到了第3个调度周期,1号~4号VRB的SOC变为0.254、0.25、0.3、0.4,
为48.58kW,该功率小于单个VRB的最大充电功率,则此时仍选用优先级最高的VRB储能单元,即给1号VRB。到了第3个调度周期,1号~4号VRB的SOC变为0.254、0.25、0.3、0.4,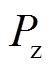 为89.88kW,该功率大于单个VRB的最大充电功率,则此时需要两个VRB储能单元。因1号和2号VRB优先级最高,故先选择这两个储能单元。然后再用VP-ADE算法进行组合内功率分配,而此时储能单元SOC最大差值为0.15,所以该周期优化目标函数为系统损耗与SOC均衡度,利用VP-ADE算法输出该周期组合内各储能单元的功率分配值。依此类推,直至完成整个调度周期。
为89.88kW,该功率大于单个VRB的最大充电功率,则此时需要两个VRB储能单元。因1号和2号VRB优先级最高,故先选择这两个储能单元。然后再用VP-ADE算法进行组合内功率分配,而此时储能单元SOC最大差值为0.15,所以该周期优化目标函数为系统损耗与SOC均衡度,利用VP-ADE算法输出该周期组合内各储能单元的功率分配值。依此类推,直至完成整个调度周期。
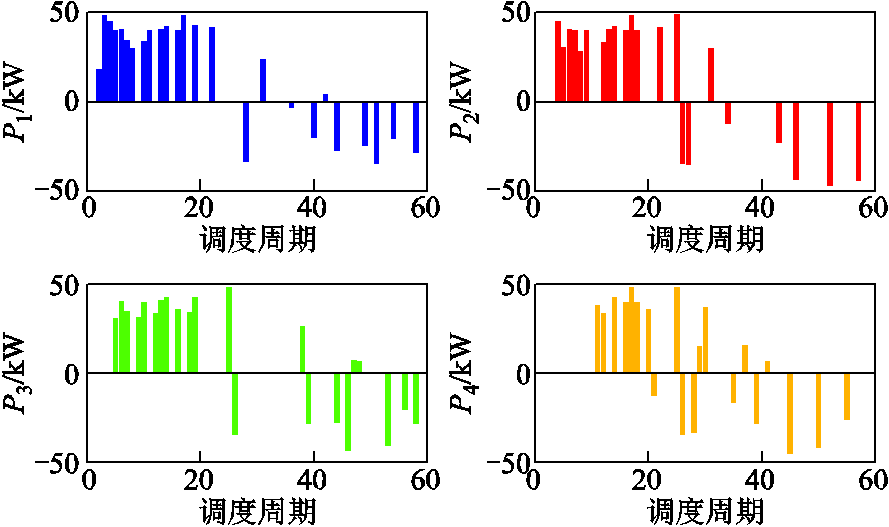
图8 VRB储能单元功率分配曲线
Fig.8 Power distribution curve of VRB energy storage unit
当图8中功率分配值显示为0时,表示当前周期该储能单元优先级较低,不参与此次功率分配,如4号储能单元直到第12周期,与其他单元SOC相近时才起动参与功率分配,从而实现储能单元从整体上减少充放电次数,降低损耗的目的。
通过本文策略进行功率分配后,虽然4个储能单元初始SOC值不同,但经过几个周期的功率优化分配之后,储能单元的SOC基本趋于一致,并能长期保持良好的均衡度。
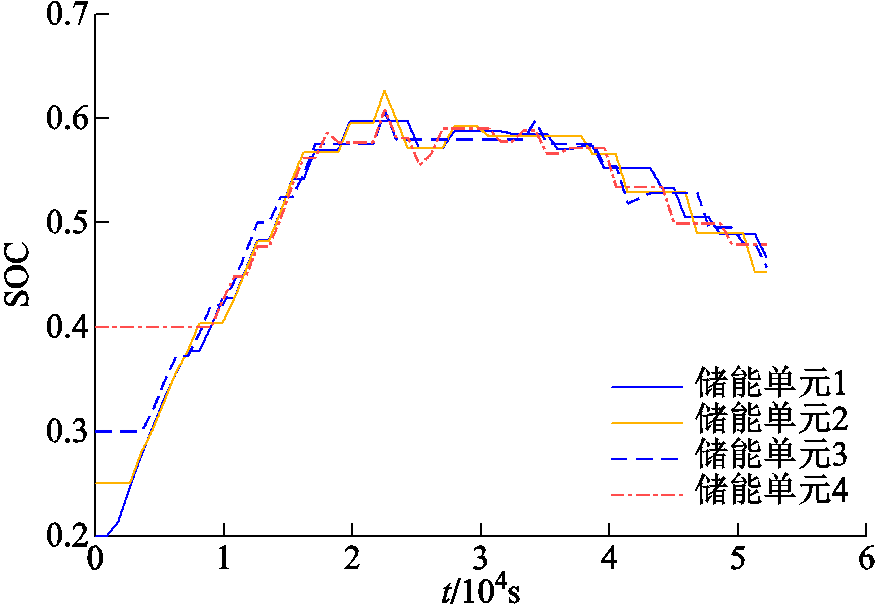
图9 VRB储能单元SOC曲线
Fig.9 SOC curves of VRB energy storage unit
4.2.2 与传统功率分配策略对比分析
传统储能系统功率分配策略指储能单元功率分配值按当前SOC大小进行分配[13],当系统充电时,即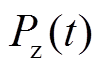 >0,各个VRB储能单元功率给定值为
>0,各个VRB储能单元功率给定值为
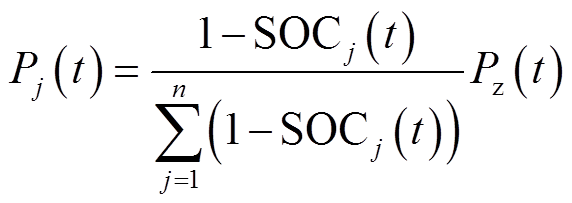 (28)
(28)当系统放电时,即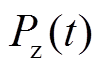 <0,各个VRB储能单元功率给定值为
<0,各个VRB储能单元功率给定值为
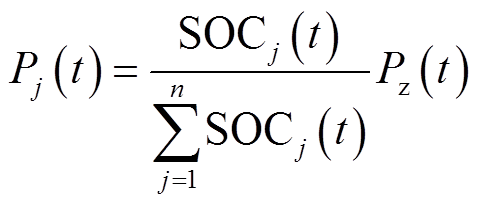 (29)
(29)
将传统功率分配策略应用于上文构建的VRB仿真模型,得出60个调度周期中各VRB储能单元的功率分配值如图10所示,SOC曲线如图11所示。
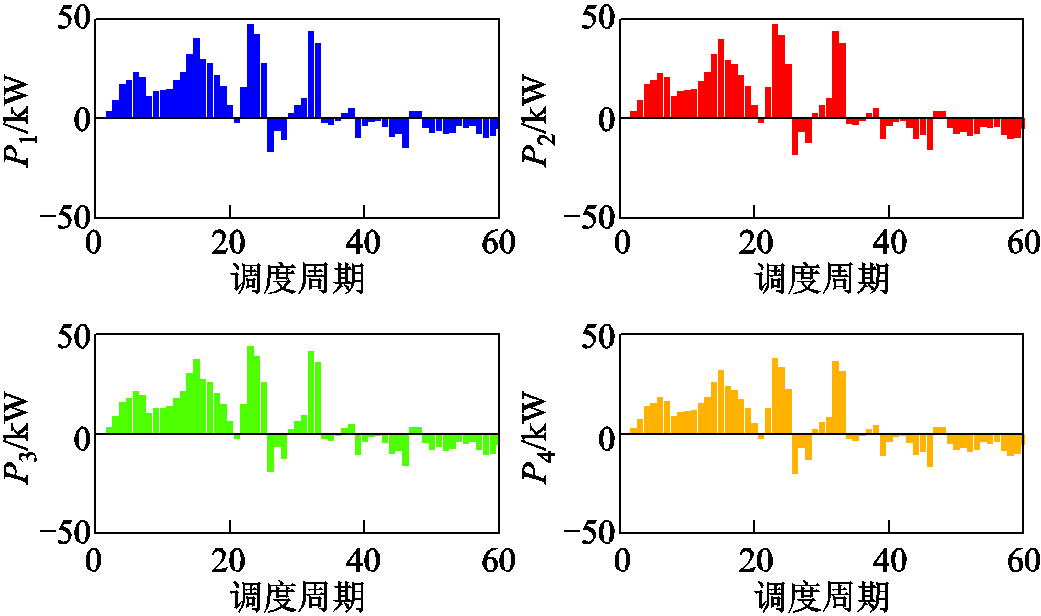
图10 传统策略下VRB储能单元功率分配曲线
Fig.10 Power distribution curve of VRB energy storage unit in traditional strategy
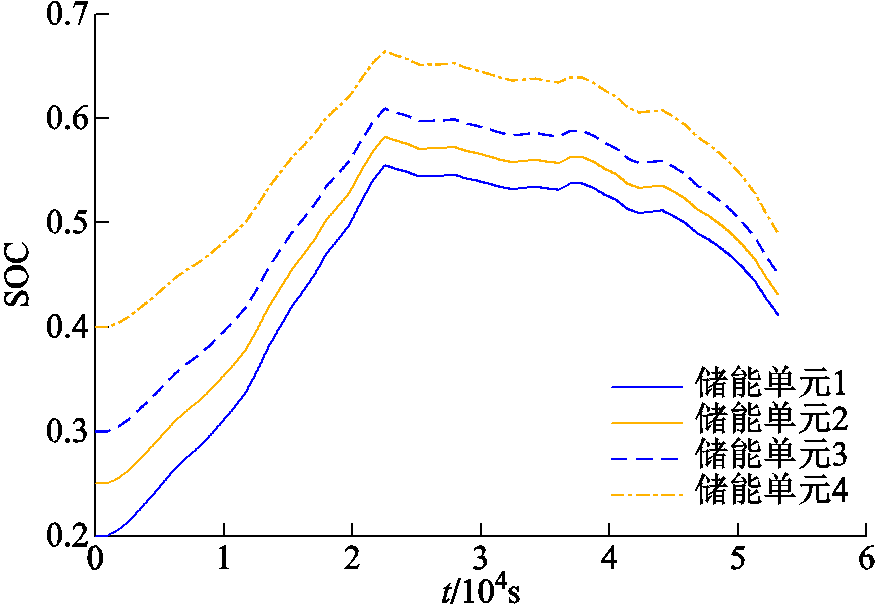
图11 传统策略下VRB储能单元的SOC曲线
Fig.11 SOC curve of VRB energy storage unit in traditional strategy
由图10和图11可知,传统功率分配策略根据SOC值的大小进行分配。在每个调度周期,所有VRB储能单元均参与工作,经过一定的调度周期后各个储能单元的SOC并没有明显趋于一致。
将由传统策略得到的各VRB储能单元的功率给定值加到本文策略中的损耗目标函数中进行计算,可得对比曲线如图12所示。由此可知,采用本文策略进行功率分配的目标函数适应度值比采用传统功率策略时低,可以降低系统损耗。
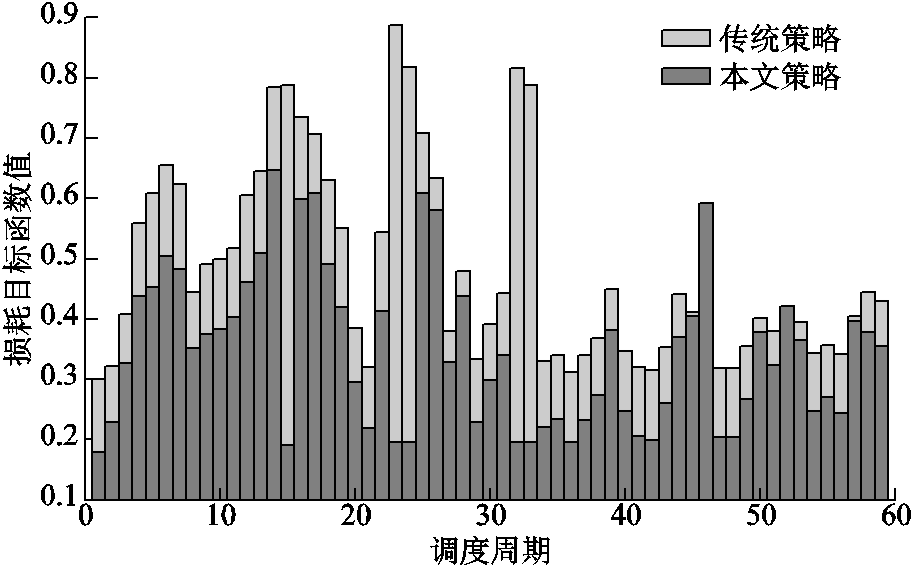
图12 两种策略的损耗目标函数值对比图
Fig.12 Comparison of the loss objective function values of the two strategies
本文策略与传统策略的评价指标对比见表2,由表2可知,采用本文策略进行VRB储能系统功率分配时,因其充、放电次数比采用传统策略时的少,整体上实现减少储能单元开启次数,延长系统寿命周期的目的;而利用系数比传统策略低,是因为本文策略采用的SOC充放电优先级原理,并不是每个VRB储能单元在所有调度周期都参与工作。
表2 两种策略的评价指标对比
Tab.2 Comparison of evaluation indicators of two strategies
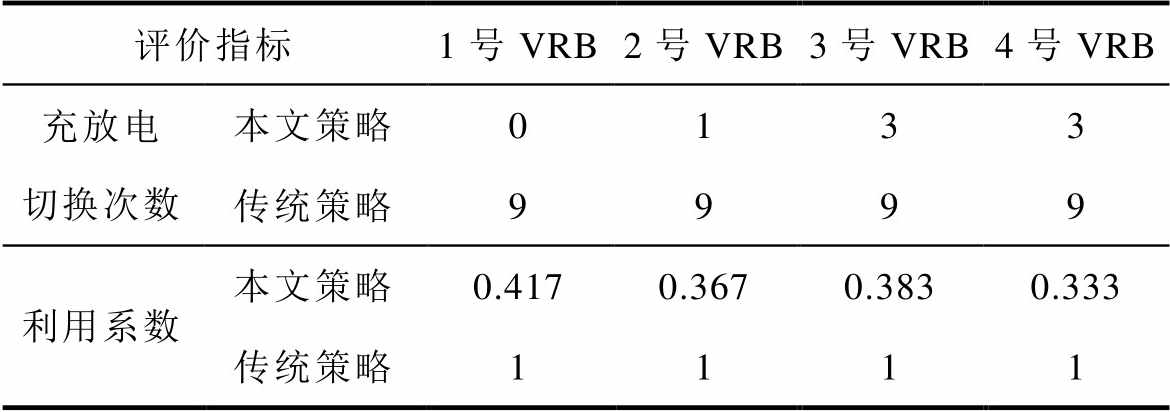
评价指标1号VRB2号VRB3号VRB4号VRB 充放电切换次数本文策略0133 传统策略9999 利用系数本文策略0.4170.367 0.383 0.333 传统策略111 1
针对并联钒电池储能系统的调度问题,本文给出了计及损耗的功率优化分配策略,通过算例仿真验证了所提方法的有效性,主要结论如下:
1)将功率运行损耗与SOC均衡度作为算法运行目标进行优化,相比传统策略,系统整体损耗约减少26%。同时储能单元在长时间调度之后SOC保持良好的均衡度。
2)将充放电优先级策略与优化算法相结合,电池充放电状态切换次数平均减少79%,利用率降低约61%,有利于提升储能系统运行寿命。
本文简化了SOC等因素对电池内部阻抗的影响,后续将深入研究考虑可变内阻损耗的功率分配策略,制定更为精细化的优化运行模型。
参考文献
[1] 李建林, 袁晓冬, 郁正纲, 等. 利用储能系统提升电网电能质量研究综述[J]. 电力系统自动化, 2019, 43(8): 15-24. Li Jianlin, Yuan Xiaodong, Yu Zhenggang, et al. Comments on power quality enhancement research for power grid by energy storage system[J]. Automation of Electric Power Systems, 2019, 43(8): 15-24.
[2] 赖昌伟, 黎静华, 陈博, 等. 光伏发电出力预测技术研究综述[J]. 电工技术学报, 2019, 34(6): 1201-1217. Lai Changwei, Li Jinghua, Chen Bo, et al. Review of research on photovoltaic power output prediction technology[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1201-1217.
[3] Vine E. Building a sustainable organizational energy evaluation system in the Asia Pacific[J]. Global Energy Interconnection, 2019, 2(5): 378-385.
[4] 李建林, 马会萌, 惠东. 储能技术融合分布式可再生能源的现状及发展趋势[J]. 电工技术学报, 2016, 31(14): 1-10, 20. Li Jianlin, Ma Huimeng, Hui Dong. Present development condition and trends of energy storage technology in the integration of distributed renewable energy[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 1-10, 20.
[5] 刘舒, 李正力, 王翼, 等. 含分布式发电的微电网中储能装置容量优化配置[J]. 电力系统保护与控制, 2016, 44(3): 78-84. Liu Shu, Li Zhengli, Wang Yi, et al. Optimal capacity allocation of energy storage in micro-grid with distributed generation[J]. Power System Protection and Control, 2016, 44(3): 78-84.
[6] 施云辉, 王橹裕, 陈玮, 等. 基于风电预测误差聚类的分布鲁棒含储能机组组合[J]. 电力系统自动化, 2019, 43(22): 3-12. Shi Yunhui, Wang Luyu, Chen Wei, et al. Distributed robust unit commitment with energy storage based on forecasting error clustering of wind power[J]. Automation of Electric Power Systems, 2019, 43(22): 3-12.
[7] 贾科, 宣振文, 林瑶琦, 等. 基于Adaboost算法的并网光伏发电系统的孤岛检测法[J]. 电工技术学报, 2018, 33(5): 1106-1113. Jia Ke, Xuan Zhenwen, Lin Yaoyi, et al. An islanding detection method for grid-connected photovoltaic power system based on Adaboost algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1106-1113.
[8] Benzahia A, Boualaga R, Moussi A, et al. A PV powered shunt active power filter for power quality improvement[J]. Global Energy Interconnection, 2019, 2(2): 143-149.
[9] 刘坚. 储能技术应用潜力与经济性研究[M]. 北京: 中国经济出版社, 2016.
[10] 胡国珍, 段善旭, 蔡涛, 等. 基于液流电池储能的光伏发电系统容量配置及成本分析[J]. 电工技术学报, 2012, 27(5): 260-267. Hu Guozhen, Duan Shanxu, Cai Tao, et al. Sizing andcost analysis of photovoltaic generation system based onvanadium redox battery[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 260-267.
[11] 凌志斌, 黄中, 田凯. 大容量电池储能系统技术现状与发展[J]. 供用电, 2018, 35(9): 3-8, 21. Ling Zhibin, Huang Zhong, Tian Kai. Current status and development of large capacity battery energy storage system technology[J]. Power Supply, 2018, 35(9): 3-8, 21.
[12] Lu Minghui, Duan Shanxu, Chen Changsong, et al. Coordinate control of parallel connected power conditioning system for battery energy storage system in microgrid[C]// IEEE Applied Power Electronics Conference and Exposition, Fort Worth, TX, USA, 2014: 707-711.
[13] Li Xiangjun, Hui Dong, Lai Xiaokang. Battery energy storage station (BESS)-based smoothing control of photovoltaic (PV) and wind power generation fluctuations[J]. IEEE Transactions on Sustainable Energy, 2013, 4(2): 464-473.
[14] Li Xiangjun, Yao Liangzhong, Hui Dong. Optimal control and management of a large-scale battery energy storage system to mitigate fluctuation and intermittence of renewable generations[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(4): 593-603.
[15] 唐芬, 姜久春, 吴丹, 等. 考虑电池储能系统荷电状态的有功功率协调控制[J]. 电力系统自动化, 2015, 39(22): 30-36. Tang Fen, Jiang Jiuchun, Wu Dan, et al. Active power coordinated control considering SOC of battery energy storage system[J]. Automation of Electric Power Systems, 2015, 39(22): 30-36.
[16] 刘忠, 杨陈, 蒋玮, 等. 基于一致性算法的直流微电网储能系统功率分配技术[J]. 电力系统自动化, 2020, 44(7): 61-75. Liu Zhong, Yang Chen, Jiang Wei, et al. Power distribution technology of DC microgrid energy storage system based on consensus algorithm[J]. Automation of Electric Power Systems, 2020, 44(7): 61-75.
[17] Wu Dan, Tang Fen, Dragicevic T, et al. Coordinated control based on bus-signaling and virtual inertia for islanded DC microgrids[J]. IEEE Transactions on Smart Grid, 2015, 6(6): 2627-2638.
[18] 毕恺韬, 孙力, 安群涛, 等. 基于模块化多电平直流变换器的储能系统分布式能量均衡控制策略[J]. 电工技术学报, 2018, 33(16): 3811-3821. Bi Kaitao, Sun Li, An Quntao, et al. Distributed energy balance control strategy of energy storage system based on modular multilevel DC converter [J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3811-3821.
[19] 吴青峰, 孙孝峰, 王雅楠, 等. 基于分布式下垂控制的微电网分布式储能系统SOC平衡策略[J]. 电工技术学报, 2018, 33(6): 1247-1256. Wu Qingfeng, Sun Xiaofeng, Wang Yanan, et al. SOC balancing strategy of microgrid distributed energy storage system based on distributed droop control[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1247-1256.
[20] 王炜信, 段建东, 张润松, 等. 孤岛电网中多储能设备SOC一致性优化策略[J]. 电工技术学报, 2015, 30(23): 126-135. Wang Weixin, Duan Jiandong, Zhang Runsong, et al. Optimal state-of-charge balancing control for paralleled battery energy storage devices in islanded microgrid[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 126-135.
[21] 张继元, 舒杰, 宁佳, 等. 考虑SOC自均衡的光储独立微电网协调控制[J]. 电工技术学报, 2018, 33(增刊2): 527-537.Zhang Jiyuan, Shu Jie, Ning Jia, et al. Coordinated control of optical storage independent microgrid considering SOC self-balance[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 527-537.
[22] 朱永强, 王甜婧, 许阔, 等. 基于动态规划-遗传算法的混合储能系统实时协调调度和经济运行[J]. 太阳能学报, 2019, 40(4): 1059-1066. Zhu Yongqiang, Wang Tianjing, Xu Kuo, et al. Real-time coordinated scheduling and economic operation of hybrid energy storage system based on dynamic programming-genetic algorithm[J]. Journal of Solar Energy, 2019, 40(4): 1059-1066.
[23] 李亚楠, 王倩, 宋文峰, 等. 混合储能系统平滑风电出力的变分模态分解-模糊控制策略[J]. 电力系统保护与控制, 2019, 47(7): 58-65. Li Yanan, Wang Qian, Song Wenfeng, et al. Variational mode decomposition and fuzzy control strategy of hybrid energy storage for smoothing wind power outputs[J]. Power System Protection and Control, 2019, 47(7): 58-65.
[24] 李蓓, 郭剑波, 陈继忠, 等. 液流储能电池系统支路电流的建模与仿真分析[J]. 中国电机工程学报, 2011, 31(27): 1-7. Li Bei, Guo Jianbo, Chen Jizhong, et al. Modeling and simulation analysis of branch current of liquid flow energy storage battery system[J]. Proceedings of the CSEE, 2011, 31(27): 1-7.
[25] 赵航飞, 刘承志, 刘湘东, 等. 液流电池的效率分析[J]. 电源技术, 2018, 42(12): 1872-1875. Zhao Hangfei, Liu Chengzhi, Liu Xiangdong, et al.Efficiency analysis of flow battery[J]. Power Technology, 2018, 42(12): 1872-1875.
[26] 迟晓妮, 朱敏刚, 吴秋轩. 基于等效模型的全钒液流电池运行优化控制研究[J]. 储能科学与技术, 2018, 7(3): 530-538. Chi Xiaoni, Zhu Mingang, Wu Qiuxuan. Research on optimal operation control based on the equivalent model of VRFB system[J]. Energy Storage Science and Technology, 2018, 7(3): 530-538.
[27] Wu Zhenwei, Jiang Xiaoping, Ma Huimeng, et al. Wavelet packet-fuzzy control of hybrid energy storage systems for PV power smoothing[J]. Proceedings of the CSEE, 2014, 34(3): 317-324.
[28] 邱亚, 李鑫, 魏达, 等. 全钒液流电池的柔性充放电控制[J]. 储能科学与技术, 2017, 6(1): 78-84. Qiu Ya, Li Xin, Wei Da, et al. Flexible charge-discharge control of vanadium redox battery[J]. Energy Storage Science and Technology, 2017, 6(1): 78-84.
[29] 尤东江, 张华民. 氧化还原电池组等效电路模型[J]. 电化学, 2014, 20(2): 156-163. You Dongjiang, Zhang Huamin. Equivalent circuit model of redox battery pack[J]. Electrochemistry, 2014, 20(2): 156-163.
[30] Chahwan J, Abbey C, Joos G, et al. VRB modelling for the study of output terminal voltages, internal losses and performance[C]//2007 IEEE Canada Electrical Power Conference, Montreal Que, Canada, 2007: 387-392.
[31] 王亚光, 王秋源, 陆继明, 等. 大容量液流电池系统数学模型与仿真[J]. 电力自动化设备, 2015, 35(8): 72-78. Wang Yaguang, Wang Qiuyuan, Lu Jiming, et al. Mathematical model and simulation of large-capacity flow battery system[J]. Electric Power Automation Equipment, 2015, 35(8): 72-78.
[32] 彭思敏, 施刚, 蔡旭, 等. 基于等效电路法的大容量蓄电池系统建模与仿真[J]. 中国电机工程学报, 2013, 33(7): 11-18. Peng Simin, Shi Gang, Cai Xu, et al. Modeling and simulation of large-capacity battery system based on equivalent circuit method[J]. Proceedings of the CSEE, 2013, 33(7): 11-18.
Power Optimization Allocation Strategy for Vanadium Battery Energy Storage System Considering Loss
Abstract For the large-capacity energy storage system composed of multiple sets of vanadium redox flow batteries connected in parallel, an optimized power allocation strategy considering the loss is given.This strategy first establishes a power allocation model that takes into account losses, and then takes the system loss and SOC balance as the objective optimization function.And the virtual particle-adaptive differential evolution algorithm (VP-ADE) is used to find the optimal solution under the constraints of meeting the power demand, state of charge (SOC) upper and lower limit, etc. Therefore, the optimal power distribution of the energy storage system is realized.Finally, the strategy of this paper is simulated and verified based on Matlab, and compared with the traditional strategy , the simulation results show that this the SOC of each energy storage unit gradually converge during charging and discharging.
keywords:Power distribution, vanadium redox flow battery, system loss, state of charge (SOC), differential evolution algorithm
中图分类号:TM316
DOI:10.19595/j.cnki.1000-6753.tces.200122
陈 薇 女,1981年生,副教授,硕士生导师,研究方向为非线性预测控制、复杂系统建模等。E-mail:windy02@hfut.edu.cn(通信作者)
侯杨成 男,1995年生,硕士研究生,研究方向为储能系统建模与优化控制。E-mail:1532449409@qq.com
国家重点研发计划(2017YFB0903502)和安徽省科技重大专项(17030701041)资助项目。
收稿日期2020-02-10
改稿日期 2020-07-22
(编辑 郭丽军)