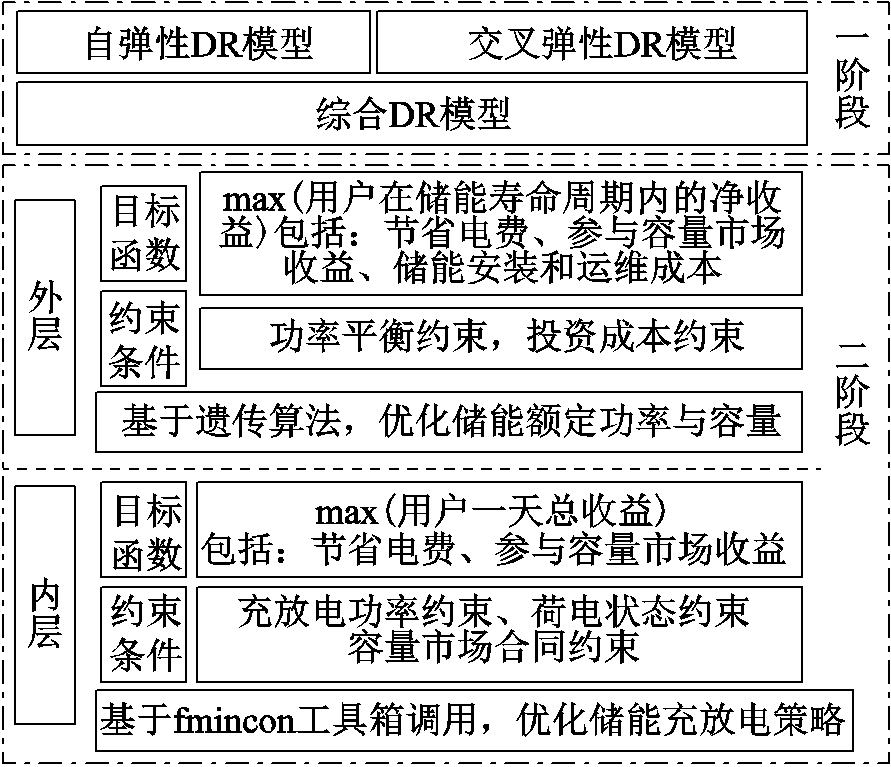
图1 DR-ESS优化模型架构
Fig.1 DR-ESS two-stage decision-making optimization model architecture diagram
摘要 容量市场能够为间歇性可再生能源的大规模并网提供灵活的容量支持,激励常规机组发电容量投资并保证峰荷时期备用容量充裕,在未来现货市场环境下建立相适应的容量市场机制是保障长期电力供给安全的有效方法,故储能作为用户侧的快速响应资源有望参与容量市场。该文结合容量市场,从用户对主能量市场实时电价进行响应后再利用储能充放电实现最优化用电的角度提出了一种用户需求响应-储能调节(DR-ESS)的优化模型。首先,基于容量市场合同构建用户实时电价需求响应模型;然后计及容量市场,建立储能定容双层优化配置模型,外层以用户在储能全寿命周期内净收益最大为目标优化储能功率及容量,内层以用户日收益最大化优化储能充放电策略。两层模型分别采用遗传算法与fmincon工具箱进行求解。以美国PJM市场下某大工业用户所在负荷节点数据进行算例分析,结果表明,采用DR-ESS优化模型在提升用户经济效益同时能够有效实现削峰填谷、降低电网尖峰负荷,减少电网投资成本,提高运行可靠性。
关键词:容量市场 储能系统 需求响应 双层优化
随着我国电力现货市场建设不断推进,建立适应我国电力发展的容量市场机制能够为间歇性可再生能源的大规模并网提供灵活的容量支持[1-6],激励常规机组发电容量投资并保证峰荷时期备用容量充裕[7-9],是保障我国长期电力供给安全的有效途径,故储能系统(Energy Storage System, ESS)作为用户侧的快速响应资源[10-13]有望参与容量市场。因此,在容量市场机制下,如何利用储能的合理配置,使用户在参与容量市场竞争的同时,实现在主能量市场下的优化用电,从而提升系统运营稳定性并促进可再生能源消纳,将成为研究的重点。
根据国外容量市场的发展以及相关学者对容量市场机制的研究,容量市场的供给方式包括发电容量和需求侧响应两种[7]。在需求侧,终端用户的需求响应(Demand Response, DR)资源可以通过负荷服务实体或削减服务提供商来参与容量市场中与发电资源共同竞争,以容量市场出清价格进行结算[14]。
在储能优化配置方面,已有大量学者进行了深入研究,但针对用户侧储能,考虑用户需求响应并结合容量市场的文献不多。文献[15-18]梳理分析了国外不同容量市场机制和DR资源参与容量市场的方式,建立了DR资源参与容量市场的模型,对本文研究具有一定借鉴意义,但对用户侧储能的优化配置研究不够深入;文献[19-20]分别针对风储、光储、风光储微网系统,从促进新能源消纳的角度出发,给出了电力市场环境下储能系统优化配置方法,但研究基于分时电价,对未来现货市场下电价的实时变动情况考虑不足;文献[21-23]在两部制分时电价背景下,考虑需量管理,以大工业用户利益分析为主体,分别构建了储能配置双层优化模型、储能月前和日内两阶段优化模型,但未考虑用户需求响应和储能参与电力市场;文献[24]兼顾系统的经济性与稳定性,探索储能作为独立运营商参与电力市场,从运行与规划的角度建立了储能系统的双层优化配置模型,但研究面向电网侧储能,且未考虑电价的实时变动。上述模型与方法均具有一定先进性,但对于用户侧储能的研究都是基于分时电价,未考虑现货市场下电价实时变动的情况,针对储能作为用户DR资源参与到容量市场的研究也未有涉及。
本文结合容量市场,提出了一种用户需求响应-储能调节(DR-ESS)的优化模型。首先,基于用户签订的容量市场合同,构建用户实时电价需求响应模型;然后计及容量市场,建立储能定容双层优化配置模型,外层以用户在储能全寿命周期内净收益最大为目标优化储能充放电功率及额定容量,内层以用户日收益最大化优化储能充放电策略。两层模型分别采用遗传算法与fmincon工具箱进行求解,以美国PJM市场下某大工业用户的负荷数据和负荷节点电价数据进行算例分析,验证了模型和方法的有效性。
根据容量市场机制,DR资源可以在容量市场中与发电资源共同竞争,以容量市场出清价格进行结算。用户在参与容量市场计划(Capacity Market Program, CAP)并签订合同后需要在容量交付年限提供相应的容量备用,否则将要支付罚金。本文提出DR-ESS优化模型,用户在签订容量市场合同后,同时利用DR资源参与主能量市场,在日内运行第一阶段利用对实时电价的需求响应实现负荷转移与义务负荷削减,在第二阶段利用储能运行调整实现最大化收益。模型架构如图1所示。

图1 DR-ESS优化模型架构
Fig.1 DR-ESS two-stage decision-making optimization model architecture diagram
第一阶段:将用户签订的容量市场合同数据引入传统需求响应分析模型,构建用户基于实时电价的DR模型。
第二阶段:以用户DR后的负荷曲线为数据基础,建立用户基于容量市场计划的储能双层决策优化配置模型。外层目标函数为用户在储能全寿命周期内的净收益最大化,包括节省电费、参与容量市场收益、储能的安装和运维成本,主要决策变量为储能功率容量配置、储能充放电策略以及用户容量市场合同的履行结果;内层模型主要决策变量为储能的充放电策略,目标函数为用户日收益最大化。
用户根据实时电价响应前后的用电负荷为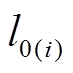 和
和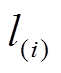 ,令
,令
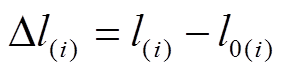 (1)
(1)
根据容量市场结算结果,用户签订合同在第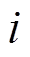 时刻每小时削减单位负荷获得的激励补贴价格为
时刻每小时削减单位负荷获得的激励补贴价格为 ,则用户在第
,则用户在第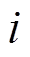 时刻通过需求响应获得的总补贴价格费用为
时刻通过需求响应获得的总补贴价格费用为
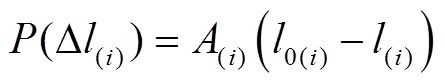 (2)
(2)如果用户没有按照合同要求的负荷削减量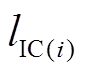 进行削减,相应第
进行削减,相应第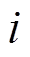 时刻未削减的单位负荷需要支付罚金
时刻未削减的单位负荷需要支付罚金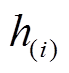 ,故第
,故第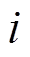 时刻需支付的总罚金
时刻需支付的总罚金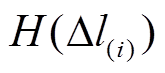 为
为
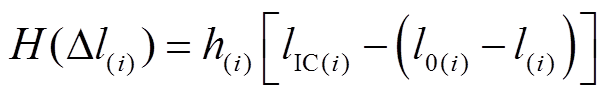 (3)
(3)
令用户在第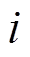 时刻的总收益为S,第
时刻的总收益为S,第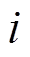 时刻的电价为
时刻的电价为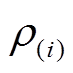 ,设用户消耗电能
,设用户消耗电能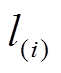 所获得的效益为
所获得的效益为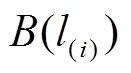 ,则用户在进行自弹性响应后的收益
,则用户在进行自弹性响应后的收益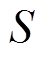 为
为
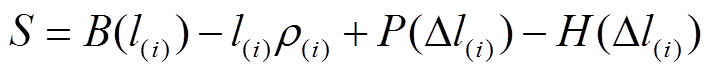 (4)
(4)对式(4)求偏导为零得
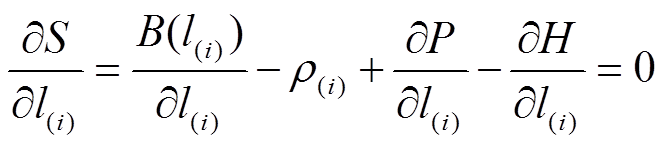 (5)
(5)
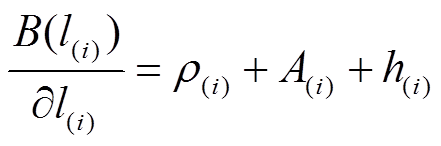 (6)
(6)效益函数中,最经典二次收益函数为
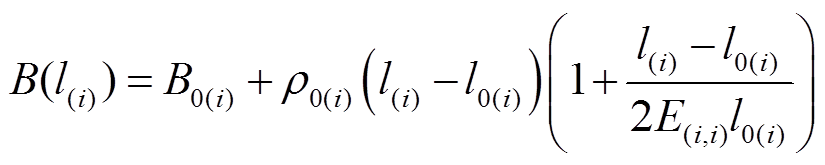 (7)
(7)
式中,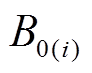 为用户进行需求响应前的消耗电能
为用户进行需求响应前的消耗电能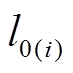 所获得的收益;
所获得的收益;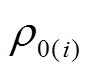 为用户所在节点第i时刻的日前实时电价;E为24h弹性矩阵,
为用户所在节点第i时刻的日前实时电价;E为24h弹性矩阵,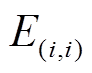 为矩阵E的元素。
为矩阵E的元素。
对效益函数求偏导并与前式联立得
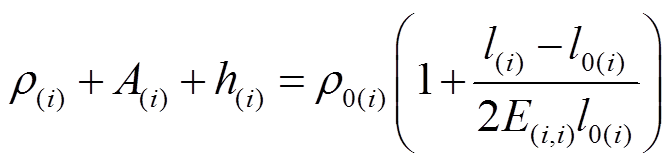 (8)
(8)因此,考虑自弹性后用户的用电负荷为
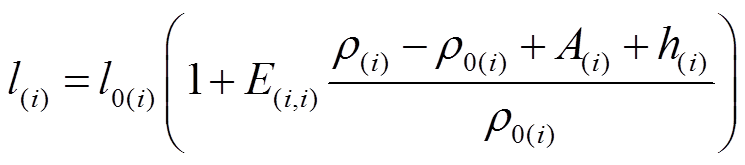 (9)
(9)
在式(9)中,如果电价没有变化且容量合同激励中和罚金为零,那么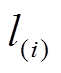 将与初始值
将与初始值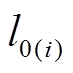 相同。
相同。
用户交叉弹性的定义为
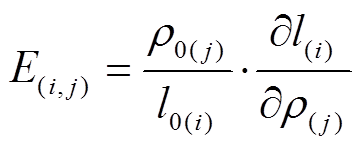 (10)
(10)假设需求函数为线性函数,则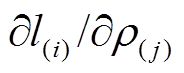 为常数,
为常数,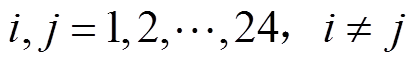 ,用户对实时电价进行响应后
,用户对实时电价进行响应后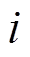 时段的用电需求为
时段的用电需求为
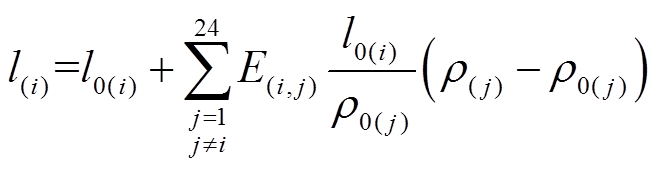 (11)
(11)
式(11)考虑了一天24h的情形,结合自弹性需求的推导,式中的价格变量若包含容量市场合同中的激励补贴与罚金,则基于容量市场合同的用户交叉弹性需求响应模型可表示为
 (12)
(12)结合式(9)与式(12),实时电价下用户计及容量市场合同的综合需求响应模型可表示为
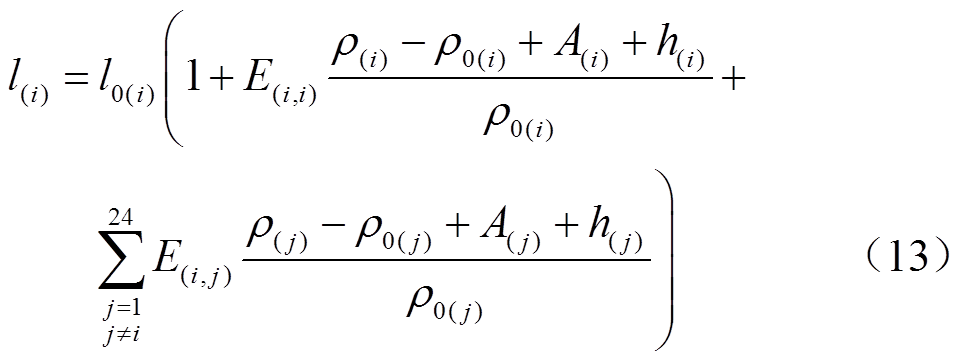
以上模型表示,在24h内用户基于容量市场合同仅通过需求响应获得最大效益后的用电需求。
3.1.1 外层优化模型目标函数
外层优化模型目标函数为储能全寿命周期内的净收益最大化。
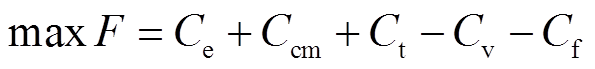 (14)
(14)式中,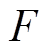 为储能全寿命周期内的净收益。考虑成本和收益两个方面,F由以下几个部分构成。
为储能全寿命周期内的净收益。考虑成本和收益两个方面,F由以下几个部分构成。
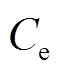 表示储能全寿命周期内,用户通过需求响应和储能的运行实现用电费用的减少,包括两个方面:①日时间尺度下用户电量电费
表示储能全寿命周期内,用户通过需求响应和储能的运行实现用电费用的减少,包括两个方面:①日时间尺度下用户电量电费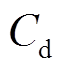 的减少;②月时间尺度下用户容量电费
的减少;②月时间尺度下用户容量电费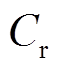 的减少。
的减少。
 (15)
(15)
其中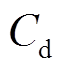 和
和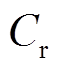 分别为
分别为
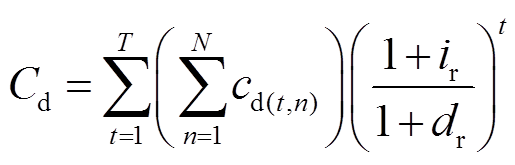 (16)
(16)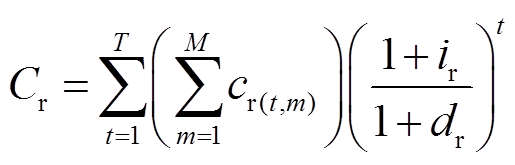 (17)
(17)
式中,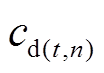 为用户第
为用户第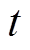 年
年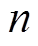 天减少的电量电费;
天减少的电量电费;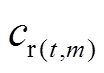 为用户第
为用户第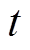 年
年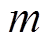 月减少的容量电费;
月减少的容量电费;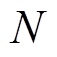 为年运行天数;
为年运行天数;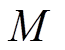 为年运行月数;
为年运行月数;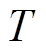 为储能的寿命;
为储能的寿命;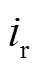 为贴现率;
为贴现率;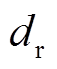 为通货膨胀率。
为通货膨胀率。
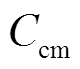 表示储能全寿命周期内,用户通过需求响应和储能参与容量市场,执行容量合同计划获得的净收益。
表示储能全寿命周期内,用户通过需求响应和储能参与容量市场,执行容量合同计划获得的净收益。
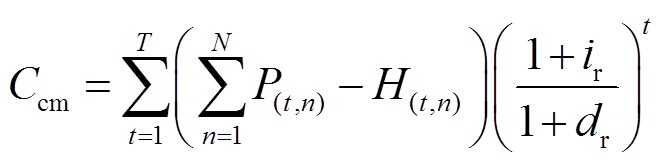 (18)
(18)
式中,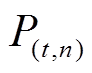 为用户第
为用户第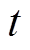 年
年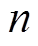 天执行合同要求削减相应负荷后获得的总收益;
天执行合同要求削减相应负荷后获得的总收益;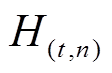 为用户第
为用户第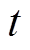 年
年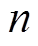 天违约不执行合同要求不削减负荷而支付的总罚金。
天违约不执行合同要求不削减负荷而支付的总罚金。
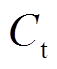 为储能全寿命周期内,年峰值负荷减少所降低的变压器成本,由于变压器与储能装置的寿命周期不同,考虑资金的时间性
为储能全寿命周期内,年峰值负荷减少所降低的变压器成本,由于变压器与储能装置的寿命周期不同,考虑资金的时间性
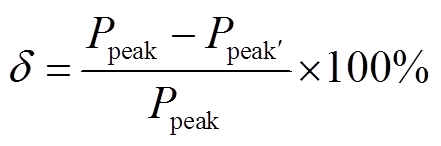 (19)
(19)
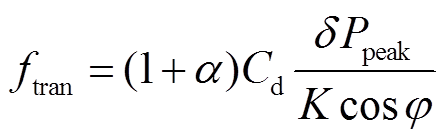 (20)
(20)
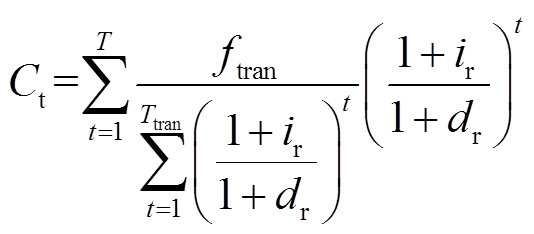 (21)
(21)式中,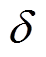 为年负荷削峰率;
为年负荷削峰率;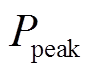 为用户原始年负荷最大值;
为用户原始年负荷最大值;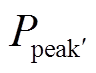 为用户参与需求响应与储能调节后的年负荷最大值;
为用户参与需求响应与储能调节后的年负荷最大值;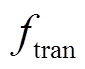 为用户年峰值负荷减少所降低的变压器成本;
为用户年峰值负荷减少所降低的变压器成本;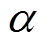 为变压器安装费用占设备造价比率;
为变压器安装费用占设备造价比率;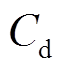 为工业用户侧变压器单位造价;
为工业用户侧变压器单位造价;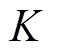 为变压器的负载率;
为变压器的负载率;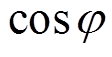 为功率因数;
为功率因数;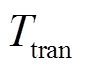 为变压器寿命周期。
为变压器寿命周期。
用户侧储能全寿命周期成本主要包括一次性固定投资成本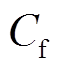 和运行维护成本
和运行维护成本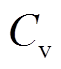 ,分别为
,分别为
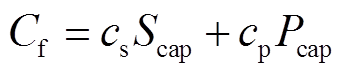 (22)
(22)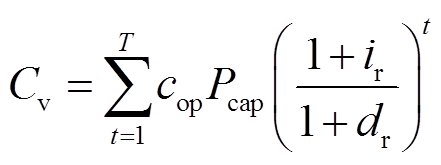 (23)
(23)
式子,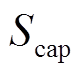 和
和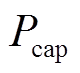 分别为储能系统的额定容量和额定充放电功率;
分别为储能系统的额定容量和额定充放电功率;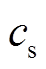 为储能单位容量造价;
为储能单位容量造价;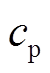 为储能单位充/放电功率造价;
为储能单位充/放电功率造价; 为储能系统单位充/放电功率的年运行维护成本。
为储能系统单位充/放电功率的年运行维护成本。
此外,为了充分考虑蓄电池充放电次数和充放电深度对储能循环寿命的影响,使储能优化配置的结果更具合理性,本文参考文献[24],其以锂离子电池为例,采用式(24)所示幂函数法对不同放电深度与电池循环寿命的对应关系进行拟合[25],得到的锂离子电池循环寿命曲线如图2所示。
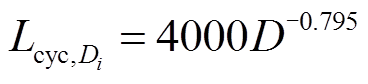 (24)
(24)式中,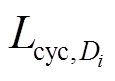 为第
为第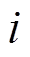 次充放电深度下蓄电池的循环寿命;
次充放电深度下蓄电池的循环寿命;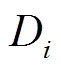 为蓄电池第
为蓄电池第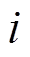 次充放电深度。
次充放电深度。
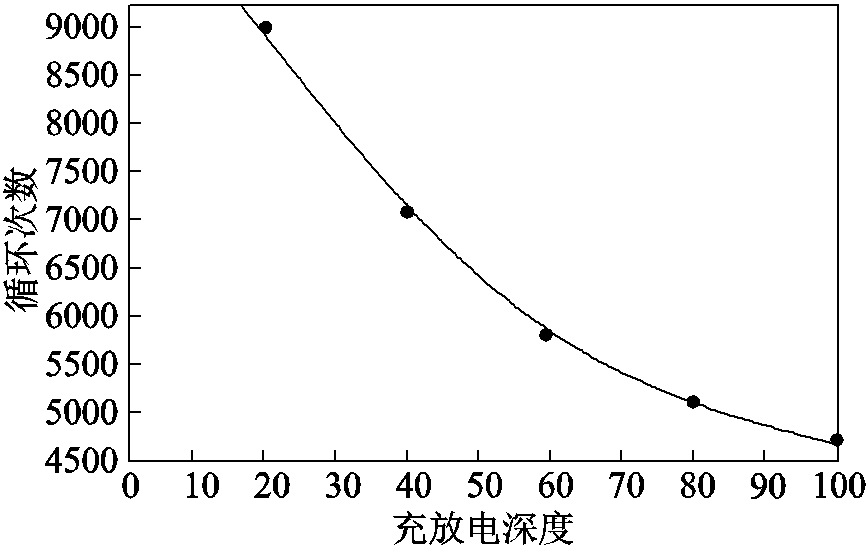
图2 锂离子电池循环寿命拟合曲线
Fig.2 Li-ion battery cycle life fitting curve
基于锂电池在每次充放电的过程中,内部会发生不可逆的电化学反应,导致容量下降的思想,储能系统的等效运行年限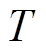 为
为
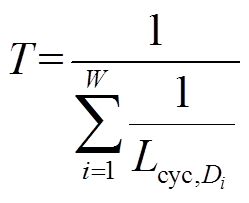 (25)
(25)
式中,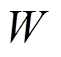 为储能系统一年的充放电次数。
为储能系统一年的充放电次数。
3.1.2 约束条件
1)功率平衡约束
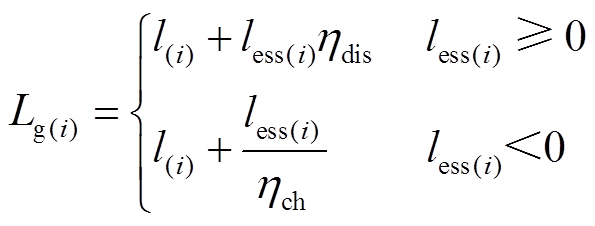 (26)
(26)式中,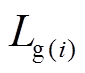 为用户第
为用户第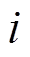 时刻与电网交换的功率;
时刻与电网交换的功率;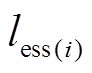 为第
为第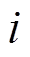 时刻储能系统的充放电功率,放电为正;
时刻储能系统的充放电功率,放电为正;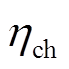 和
和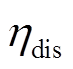 分别为蓄电池的充放电效率。
分别为蓄电池的充放电效率。
2)用户投资成本约束
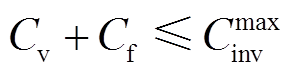 (27)
(27)
式中,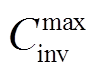 为用户投资成本最大值。
为用户投资成本最大值。
3.2.1 内层优化模型目标函数
内层模型目标函数为在需求响应实现负荷转移后用户利用储能的运行实现日收益最大化。
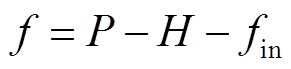 (28)
(28)
式中,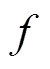 为用户在进行需求响应后,通过储能系统的运行实现的日最大收益;
为用户在进行需求响应后,通过储能系统的运行实现的日最大收益;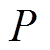 为一天中用户通过需求响应与储能执行容量市场合同获得的总收益;
为一天中用户通过需求响应与储能执行容量市场合同获得的总收益;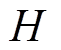 为一天中用户为未执行容量市场合同需要支付的总罚金;
为一天中用户为未执行容量市场合同需要支付的总罚金;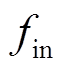 为一天中用户进行需求响应与储能运行后的总用电费用。
为一天中用户进行需求响应与储能运行后的总用电费用。
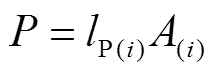 (29)
(29)
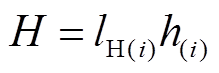 (30)
(30)
式中,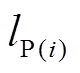 和
和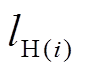 分别为
分别为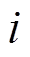 时刻用户执行容量合同削减的负荷和未完成执行容量市场合同的负荷。
时刻用户执行容量合同削减的负荷和未完成执行容量市场合同的负荷。
用户一天的电费由每个时段的电费累加得到,即
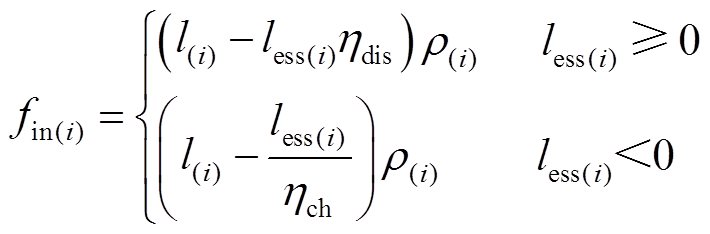 (31)
(31)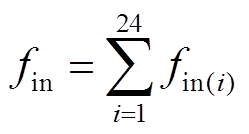 (32)
(32)
式中,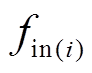 为第
为第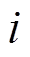 时刻的用电费用。
时刻的用电费用。
3.2.2 内层优化模型约束条件
1)蓄电池充放电功率约束
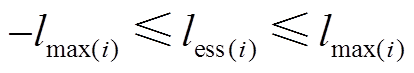 (33)
(33) 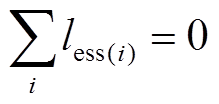 (34)
(34)
式中,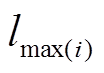 为储能在第
为储能在第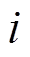 时刻的充放电功率最大值。式(34)表示储能系统一天充放电功率守恒。
时刻的充放电功率最大值。式(34)表示储能系统一天充放电功率守恒。
2)蓄电池荷电状态约束
储能系统在运行过程中,其剩余容量需要满足一定约束,在任一时刻,其荷电状态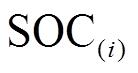 都必须维持在一定区间
都必须维持在一定区间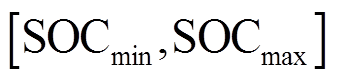 ,并且,为了保证连续运行,储能的荷电状态在一个调度周期的始末时刻要一致。
,并且,为了保证连续运行,储能的荷电状态在一个调度周期的始末时刻要一致。
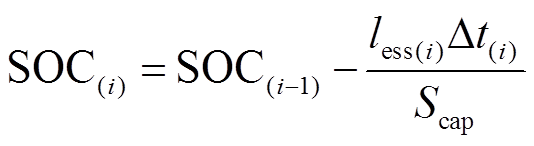 (35)
(35) (36)
(36)
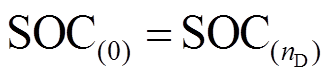 (37)
(37)
式中,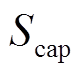 为储能系统的额定容量;
为储能系统的额定容量;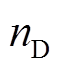 为储能一个调度周期的末时刻值,在本文中为24。
为储能一个调度周期的末时刻值,在本文中为24。
3)容量市场合同约束
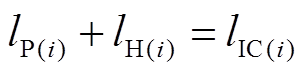 (38)
(38)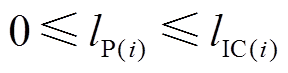 (39)
(39)
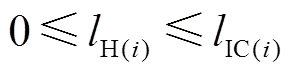 (40)
(40)
本文建立的储能优化配置模型属于非线性、混合整数问题。在求解外层模型时采用遗传算法,基于外层目标对储能的额定容量、额定充放电功率进行寻优。在求解内层模型时,采用有效集算法来求解,相比于内点法、信赖域反射算法,有效集算法适用于约束条件较多的二次规划问题,调用Matlab中的fmincon函数,以用户一天内的效益最大化为目标,优化储能在对应额定容量、额定功率下的最优充放电策略。经过一年的循环计算后将内层的储能的放电次数、每次充放电深度数据、年负荷削峰率以及容量市场合同执行数据返回给外层,外层计算目标函数值与适应度值,并进行寻优,最终得到最优解,求解流程如图3所示。
本文中用户签订的容量市场合同数据见表1。本文以锂电池储能系统为例,设备参数见表2。变压器设备参数及其他参数见表3。工业用户负荷采用美国宾夕法尼亚-新泽西-马里(Pennsylvania-New Jersey-Maryland, PJM)电力市场中某区域的大工业用户2018年6月1日~2019年5月31日一个容量交付年的负荷数据,电价数据为该用户对应节点的一年日前实时电价与当日的实时电价数据,相关数据皆来自美国PJM官网[26]。
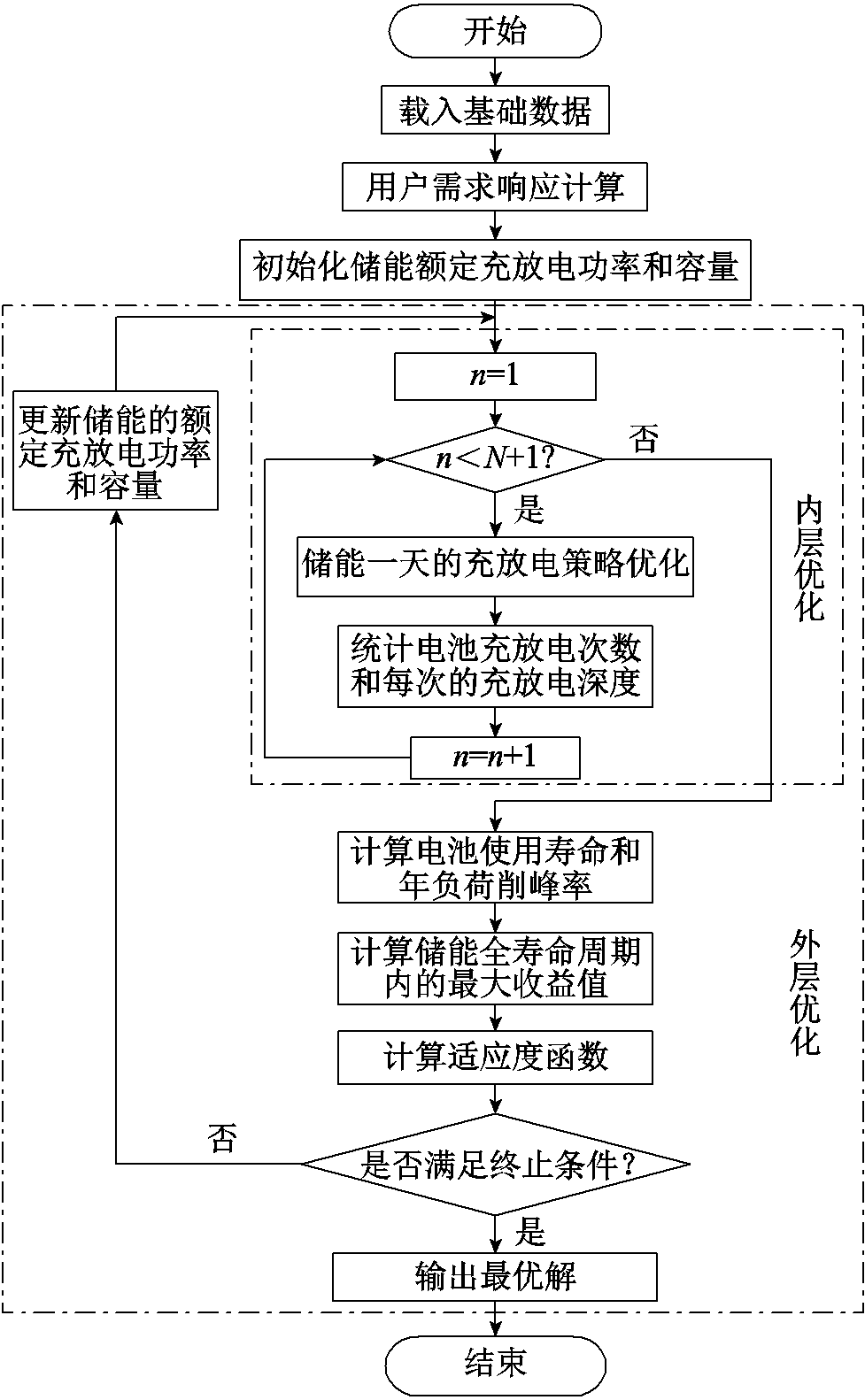
图3 储能优化配置求解流程
Fig.3 Energy storage optimization configuration solution flow chart
表1 容量市场合同数据
Tab.1 Capacity market contract data

参数数值 单位负荷削减补贴A(i)/($/kW)150 单位负荷违约罚金pen(i)/($/kW)75
表2 储能电池相关参数
Tab.2 Energy storage battery related parameters
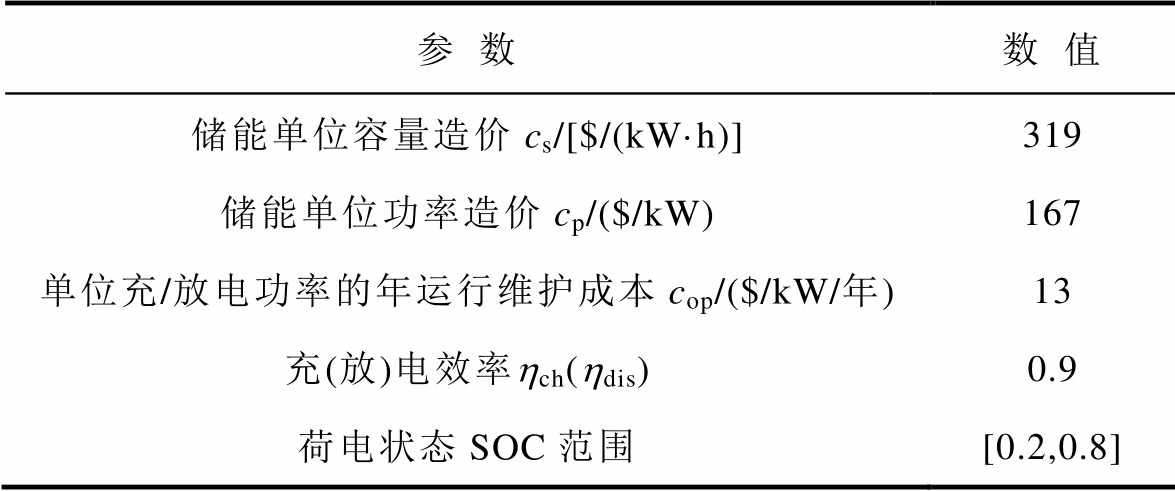
参数数值 储能单位容量造价cs/[$/(kW·h)]319 储能单位功率造价cp/($/kW)167 单位充/放电功率的年运行维护成本cop/($/kW/年)13 充(放)电效率hch(hdis)0.9 荷电状态SOC范围[0.2,0.8]
根据美国PJM容量市场机制,用户利用需求响应资源参与容量市场的次数是有限制的,故本文选取6月~12月中负荷最大的3天作为用户要求履行容量市场合同的日期,有效时间段为14:00~19:00,削减量为原始负荷10%。
表3 变压器设备参数
Tab.3 Transformer equipment parameters

参数数值 负载率K0.75 功率因数cosj0.85 单位造价Cd/[$/(kV·A)]500 安装费用占设备造价比率a0.3 寿命/年20
5.2.1 储能优化配置结果
用户储能优化配置结果见表4。通过对储能系统的额定功率和容量进行寻优,得到用户净收益最大时储能额定功率为5.3MW,额定容量为33MW·h,用户的年负荷削峰率为14.75%,蓄电池可用寿命仅为3.2年,这是由于在每次电池充放电过程中都充分地考虑了充放电次数与放电深度对电池的损耗,用户为了最大利益频繁地调用储能,故其寿命较标准寿命参数小。可以看出用户通过对实时电价的需求响应以及储能系统的优化运行,实现了年峰值负荷的有效削减并获得了经济效益。
表4 储能优化配置结果
Tab.4 Energy storage optimization configuration result

参数数值 Pcap/MW5.3 Scap/(MW·h)33 年负荷削峰率d(%)14.75 电池寿命/年3.2 用户收益/$106 578
在得出储能优化配置结果的基础上,进一步分析用户的净收益随储能额定功率和额定容量的变化情况。在仿真过程中,用户的净收益随储能额定功率与额定容量的变化应该是一个曲面图,但为便于分析并使表达清晰直观,根据额定容量的配置结果,以10为步长,另选取4个储能额定容量的值,在额定功率变化时分析用户净收益的变化情况,所得曲线如图4所示。
图4反映了用户的净收益随储能额定功率和额定容量的变化情况。从图4中可以看出,虽然用户收益曲面随着容量与功率的变化呈局部波动性的变化,但整体上有一定的趋向性。储能的额定容量一定时,用户的净收益随额定功率的增加先增加到最大值,然后开始减小,当额定功率过小或数值上接近额定容量数值时,用户净收益基本上都较小甚至为负数。随着储能额定容量的增加,用户在净收益最大时对应的额定功率也相应增加,如额定容量为13MW·h时,用户净收益最大时对应的额定功率为1.7MW,当额定容量分别为33MW·h与53MW·h时,用户净收益最大时对应的额定功率则分别增加到5.3MW与6.5MW。

图4 用户净收益随储能容量与功率变化曲线
Fig.4 User net income with energy storage capacity and power curve
由图4中还可以看出,用户的净收益最大值并不随额定容量的增加而一直增加,在额定容量小于33MW·h时,用户的净收益最大值随额定容量的增加而增加,在额定容量大于33MW·h时,用户的净收益最大值随额定容量的增加反而逐渐减少了。
从以上分析可以得出,储能额定功率和额定容量的配置皆不宜过小或过大。若用户安装了过小的额定功率和容量参数的储能系统,则其无法在用户参与需求响应或执行容量市场合同时发挥有效的作用,反而用户还要承担不菲的设备安装与运行维护费用;额定功率和额定容量过大,设备的安装成本则会过高,虽然储能可以在优化调度运行时满足用户各种需求,但储能资源会过剩且用户的收益无法抵消成本。
5.2.2 模型有效性验证
为了进一步验证本文所建立的用户基于容量市场计划的需求响应模型和储能优化配置模型的有效性,在得出最优储能系统额定功率和容量配置基础上,提取用户8月份峰负荷最大日的日负荷曲线与电价数据,如图5所示,并选取无容量市场合同(CAP)与有容量市场合同两种情景进行对比分析。
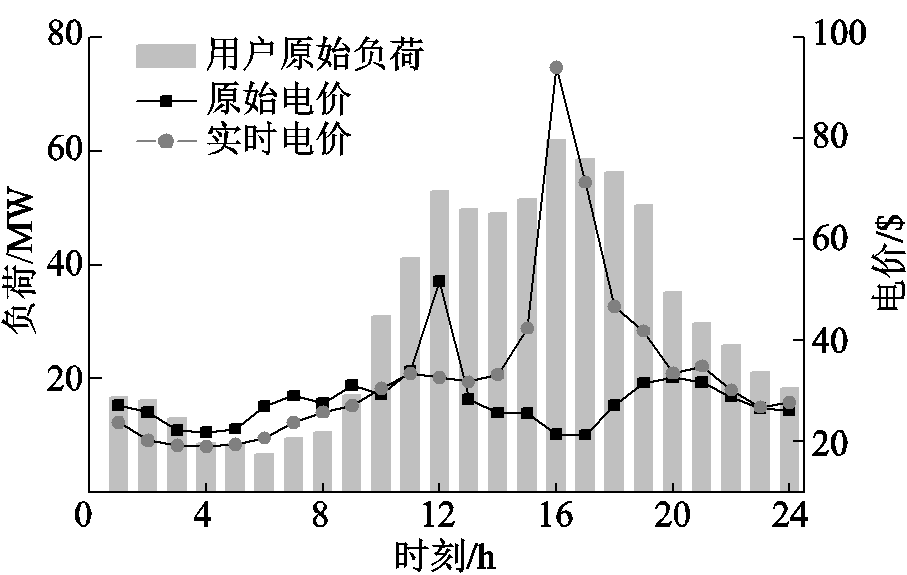
图5 现货市场下用户负荷曲线与实时电价
Fig.5 User net income with energy storage capacity and power curve
从图8中可以看出,日前实时电价在13:00~20:00时处于电价偏低的状态,而用户的用电高峰时段为12:00~19:00,实时电价在15:00~19:00时间段大幅度上升,与用户高峰用电时段大致吻合。说明在用户用电高峰时段,电网负荷过大,重载运行,容量资源紧缺,在缺电情况下实时电价出现激增,希望用户能进行需求响应减少用电负荷,或以发电机组增加出力来缓解电网压力,维持可靠运行。
用户在签订与未签订容量市场合同下的需求响应曲线和储能充放电策略如图6所示。
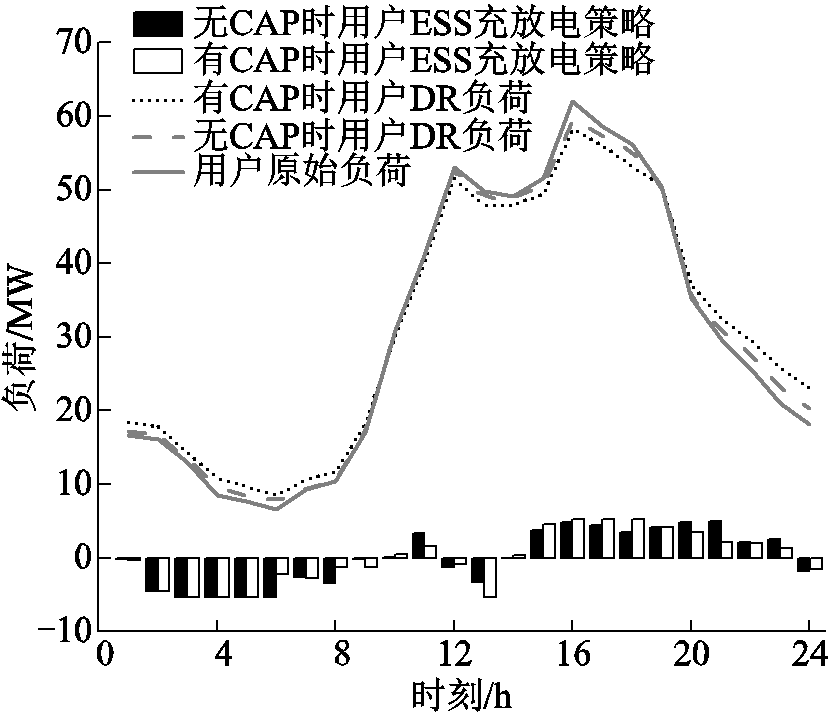
图6 两种场景下用户DR和储能运行的策略图
Fig.6 Strategy figure for user DR and energy storage operation in two scenarios
从图6三条曲线的对比分析可以看出,有CAP时用户需求响应实现的削峰填谷力度较无CAP时大,峰时段负荷减少更多,说明在原始的需求响应模型中增加容量市场合同因素的激励,能够促进用户对电价进一步响应,降低峰谷差。
图6还显示了用户在签订容量市场合同和未签订容量市场合同时的储能充放电策略。将二者进行对比分析,可以看出,整体上储能都是在实时电价较低时刻充电,在电价高峰时段放电。在放电时段中,15:00~18:00时,有CAP时的储能放电功率较无CAP时的放电功率大,在19:00二者持平,而在20:00~23:00,情况基本相反。这是由于14:00~19:00存在着容量市场的激励与惩罚机制,用户必须要在这个时间段内履行负荷削减义务,否则会受到罚款,因此其储能在这个时间段尽可能多放电,放电功率较无CAP时大。以上分析说明了用户储能的充放电策略不仅会受到电价变化的影响,同时放电时间段与放电功率也会受到容量市场合同的影响。
综上,在签订容量市场合同时,用户参与需求响应实现削峰填谷的效果较未签订容量市场合同情况下好,在配置储能系统后,用户皆可利用储能系统的优化运行实现进一步的削峰填谷。但签订容量市场合同下,储能会在履行合同的时间段放出大部分的电,未签订容量市场合同时储能主要根据电价高低进行放电,放电时间段受高峰电价的影响。
用户在两种情景下的净负荷曲线如图7所示,从图7中可以看出,用户签订容量市场合同情况后,经过需求响应和储能优化运行后的净负荷曲线较未签订时平缓。容量市场合同机制下用户的履约情况见表5,可以看出用户并没有在所有时间段完全实现义务量的负荷削减,但这部分未完成的量基本都是在实时电价的非高峰时刻,说明在储能充放电能力有限的情况下,用户的储能资源优先用在电价最高峰时段,以减少电费的支出并获得负荷削减补贴;而电价不高时,用户承担相应电费并支付违约罚金,实现日运行总效益的最大化。
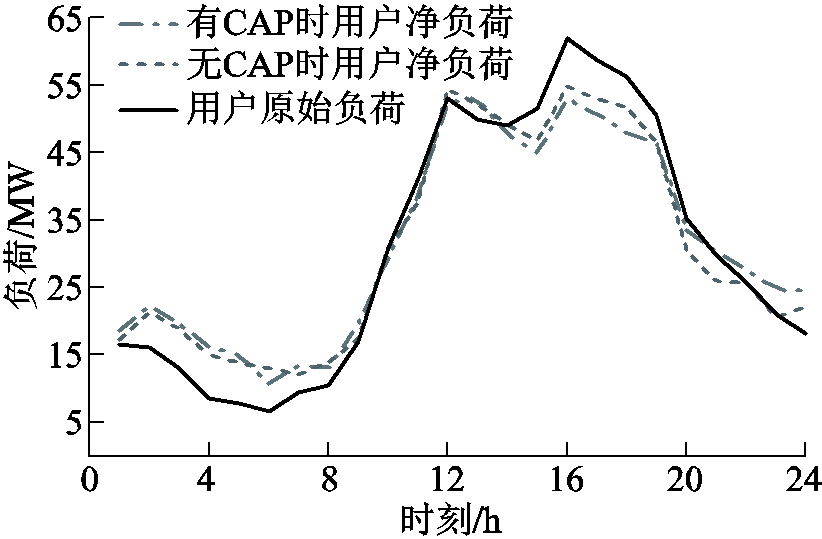
图7 两种场景下用户的净负荷曲线对比
Fig.7 User's net load curve comparison in two scenarios
表5 容量市场合同执行情况
Tab.5 Capacity market contract execution
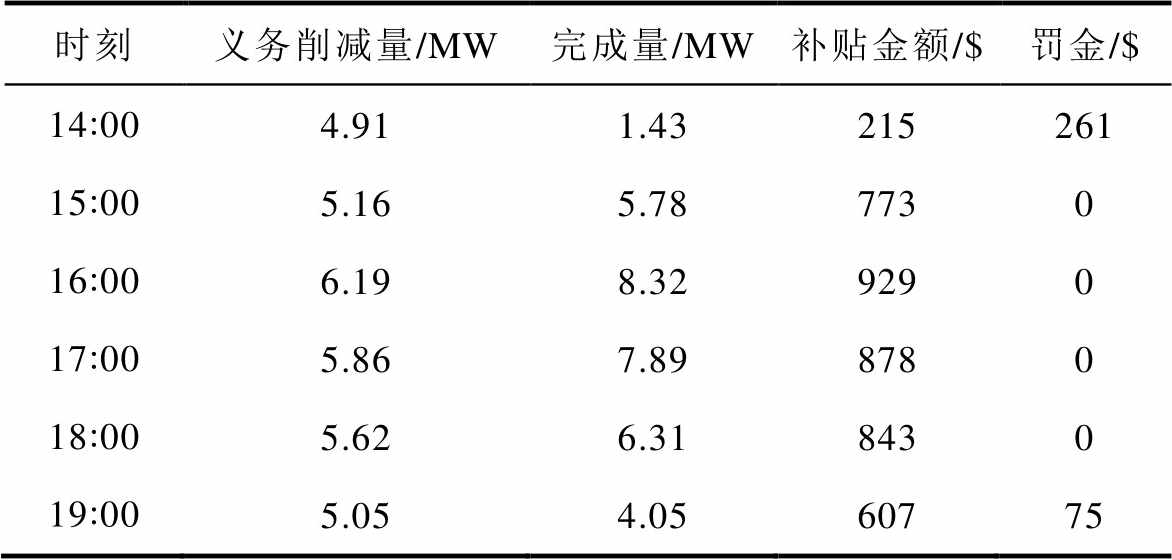
时刻义务削减量/MW完成量/MW补贴金额/$罚金/$ 14:004.911.43215261 15:005.165.787730 16:006.198.329290 17:005.867.898780 18:005.626.318430 19:005.054.0560775
结合以上分析得到两种场景下用户日运行效益情况,并基于《需求响应效果监测与综合效益效果评价导则》[27]计算在此情况下的峰负荷削减给电网侧所带来的可免容量成本,对比分析结果见表6。可以看出,在有容量市场合同时,用户的峰荷降低更多,总收益也较无容量市场合同时大。虽然全年内用户参与容量市场实现负荷削减需求响应的次数不多,但每次参与带来的效益却是巨大的,不论对用户还是电网都具有良好的经济性。
表6 两种情景下日运行效益对比
Tab.6 Comparison of daily operating benefits under two scenarios
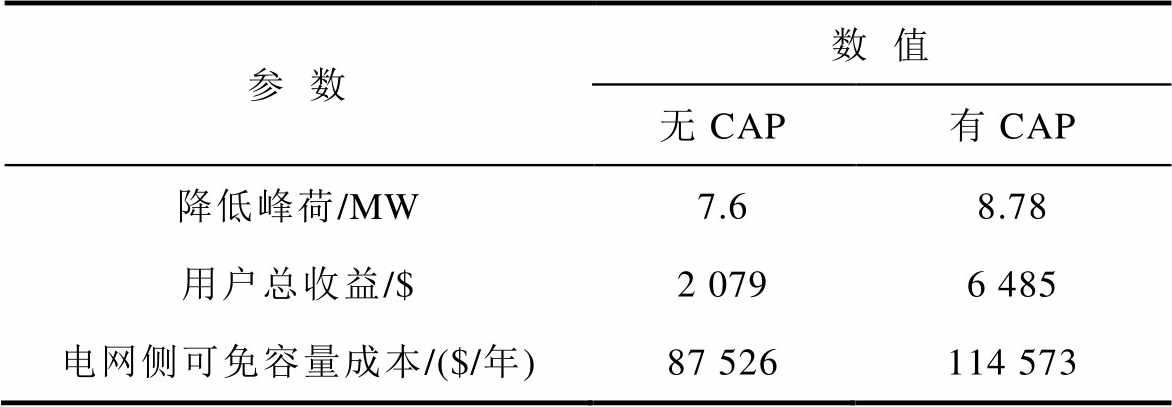
参数数值 无CAP有CAP 降低峰荷/MW7.68.78 用户总收益/$2 0796 485 电网侧可免容量成本/($/年)87 526114 573
储能可以作为用户便捷迅速的需求响应资源参与容量市场竞争,实现进一步应用推广。本文结合市场机制建立需求响应-储能调节(DR-ESS)优化模型进行储能优化配置。所得结论如下:
1)本文通过仿真分析得到用户净收益最大时的储能配置结果,额定功率为5.3MW,额定容量为33MW·h。随着额定功率或额定容量的增加,用户的净收益最大值均呈现先增加后减少的变化,因此储能额定功率和额定容量的配置皆不宜过小或过大。
2)在签订容量市场合同情况下,用户参与需求响应实现的削峰填谷效果较未签订容量市场合同情况下好,配置储能系统后,用户可利用储能系统的优化运行实现进一步的削峰填谷。但签订容量市场合同下,储能会在履行合同的时间段放出大部分的电,未签订容量市场合同时储能主要根据电价高低进行放电,放电时间段受高峰电价的变化而变化。
3)在用户侧储能中引入容量市场机制可提升用户经济效益,有效实现削峰填谷,降低电网尖峰负荷,减少电网投资成本并提高了运行可靠性,为在市场机制逐渐完善的情况下将储能纳入市场轨道,促进其进一步商业化推广应用提供了新思路。
本文研究基于美国PJM容量市场,但对用户DR资源参与基本拍卖市场与追加拍卖市场的竞价出清没有作深入探讨,结合我国电力市场发展形式,今后可以进一步研究,并可在本文研究基础上将研究拓展至发电侧储能与电网侧储能。
参考文献
[1] 朱彤. 我国可再生能源的发展阶段与面临挑战[J]. 中国国情国力, 2019(7): 8-12. Zhu Tong. The development stage and challenges of China's renewable energy[J]. China National Conditions and Strength, 2019(7): 8-12.
[2] 赖昌伟, 黎静华, 陈博, 等. 光伏发电出力预测技术研究综述[J]. 电工技术学报, 2019, 34(6): 1201-1217. Lai Changwei, Li Jinghua, Chen Bo, et al. A review of research on photovoltaic power generation prediction technology[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1201-1217.
[3] 鲁宗相, 李海波, 乔颖. 高比例可再生能源并网的电力系统灵活性评价与平衡机理[J]. 中国电机工程学报, 2017, 37(1): 9-20. Lu Zongxiang, Li Haibo, Qian Ying. Flexibility evaluation and supply demand balance principle of power system with high-penetration renewable electricity[J]. Proceedings of the CSEE, 2017, 37(1): 9-20.
[4] 盛万兴, 吴鸣, 季宇, 等. 分布式可再生能源发电集群并网消纳关键技术及工程实践[J]. 中国电机工程学报, 2019, 39(8): 2175-2186. Sheng Wanxing, Wu Ming, Ji Yu, et al. Key technologies and engineering practices for distributed renewable energy generation clusters connected to the grid[J]. Proceedings of the CSEE, 2019, 39(8): 2175-2186.
[5] 吴俊, 薛禹胜, 舒印彪, 等. 大规模可再生能源接入下的电力系统充裕性优化(一)旋转级备用的优化[J]. 电力系统自动化, 2019, 43(8): 101-110. Wu Jun, Xue Yusheng, Shu Yinbiao, et al. Adequacy Optimization for a large-scale renewable energy integrated power system part one spinning-grade reserve optimization[J]. Automation of Electric Power Systems, 2019, 43(8): 101-110.
[6] 邵庆祝, 杨畅, 谢民, 等. 基于RTDS的光伏接入配电网故障特征研究[J]. 电力系统保护与控制, 2019, 47(22): 1-8. Shao Qingzhu, Yang Chang, Xie Min, et al. Research on fault characteristics of photovoltaic access distribution network based on RTDS [J]. Power System Protection and Control, 2019, 47 (22): 1-8.
[7] 侯孚睿, 王秀丽, 锁涛, 等. 英国电力容量市场设计及对中国电力市场改革的启示[J]. 电力系统自动化, 2015, 39(24): 1-7. Hou Furui, Wang Xiuli, Suo Tao, et al. Design of UK power capacity market and its implications for China's power market reform[J]. Automation of Electric Power Systems, 2015, 39(24): 1-7.
[8] Feng Zhao, Zheng Tongxin, Litvinov E. Constructing demand curves in forward capacity market [J]. IEEE Transactions on Power Systems, 2018, 33(1): 525-535.
[9] Vatani B, Chowdhury B, Jeremy L. The role of demand response as an alternative transmission expansion solution in a capacity market[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 1039-1046.
[10] Liu Yingqi. Demand response and energy efficiency in the capacity resource procurement: case studies of forward capacity markets in ISO New England, PJM and Great Britain[J]. Energy Policy, 2017, 43(9): 271-282.
[11] Lynch M Á, Nolan S, Devine M T. The impacts of demand response participation in capacity markets[J]. Applied Energy, 2019, 39(12): 444-451.
[12] 熊连松, 修连成, 王慧敏, 等. 储能系统抑制电网功率振荡的机理研究[J]. 电工技术学报, 2019, 34(20): 4373-4380. Xiong Liansong, Xiu Liancheng, Wang Huimin, et al. Research on the mechanism of energy storage system suppressing power grid oscillations[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4373-4380.
[13] 吉斌, 谭建成, 曾雪彤. 电力市场环境下新能源产业园储能优化控制策略研究[J]. 电气技术, 2018, 19(8): 22-29. Ji Bin, Tan Jiancheng, Zeng Xuetong. Research on energy storage optimization control strategy of new energy industrial park in electricity market environment[J]. Electrical Engineering, 2018, 19(8), 22-29.
[14] 陈新仪, 严正, 魏学好, 等. PJM电网需求响应模式及其启示[J]. 中国电力, 2015, 48(4): 113-120. Chen Xinyi, Yan Zheng, Wei Xuehao, et al. PJM grid demand response model and its enlightenment[J]. China Electric Power, 2015, 48(4): 113-120.
[15] Walawalkar R, Fernands S, Thakur N, et al. Evolution and current status of demand response(DR) in electricity markets: insights from PJM and NYISO[J]. Energy, 2010, 45(21): 1553-1560.
[16] Aalami H A, Moghaddam M P, Yousefi G R. Demand response modeling considering Interruptible/ Curtailable loads and capacity market programs[J]. Applied Energy, 2010, 28(6): 243-250.
[17] Byers C, Levin T, Botterud A. Capacity market design and renewable energy: performance incentives, qualifying capacity, and demand curves[J]. The Electricity Journal, 2018, 31(6): 65-74.
[18] Hach D, Chyong C K, Spinler S. Capacity market design options: a danamic capacity investment model and a GB case study[J]. European Journal of Operational Research, 2016, 21(13): 691-705.
[19] 李佳琪, 陈健, 张文, 等. 高渗透率光伏配电网中电池储能系统综合运行控制策略[J]. 电工技术学报, 2019, 34(2): 437-446. Li Jiaqi, Chen Jian, Zhang Wen, et al. Comprehensive operation control strategy of battery energy storage system in high-permeability photovoltaic distribution network[J]. Transactions of China Electrotechnical Society, 2019, 34 (2): 437-446.
[20] 周楠, 樊伟, 刘念, 等. 基于需求响应的光伏微网储能系统多目标容量优化配置[J]. 电网技术, 2016, 40(6): 1709-1716. Zhou Nan, Fan Wei, Liu Nian, et al. Battery storage multi-objective optimization for capacity configuration of PV-based microgrid considering demand response[J]. Power System Technology, 2016, 40(6): 1709-1716.
[21] 李建林, 郭斌琪, 牛萌, 等. 风光储系统储能容量优化配置策略[J]. 电工技术学报, 2018, 33(6): 1189-1196. Li Jianlin, Guo Binqi, Niu Meng, et al. Optimal configuration strategy of energy storage capacity in wind/pv/storage hybrid system[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1189- 1196.
[22] 丁逸行, 徐青山, 吕亚娟, 等. 考虑需量管理的用户侧储能优化配置[J]. 电网技术, 2019, 43(4): 1179-1186. Ding Yixing, Xu Qingshan, Lü Yajuan, et al. Optimized configuration of user side energy storage considering demand management[J]. Power System Technology, 2019, 43(4): 1179-1186.
[23] 陈丽娟, 吴甜恬, 柳惠波, 等. 基于需量管理的两阶段大用户储能优化模型[J]. 电力系统自动化, 2019, 43(1): 262-271. Chen Lijuan, Wu Tiantian, Liu Huibo, et al. Two-stage large-user energy storage optimization model based on demand management[J]. Automation of Electric Power Systems, 2019, 43(1): 262-271.
[24] 姜欣, 郑雪媛, 胡国宝, 等. 市场机制下面向电网的储能系统优化配置[J]. 电工技术学报, 2019, 34(21): 4601-4610. Jiang Xin, Zheng Xueyuan, Hu Guobao, et al. Optimal allocation of energy storage systems to the power grid under the market mechanism[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4601-4610.
[25] Dubarry M, Liaw B Y. Identify capacity fading mechanism in a commercial LiFePO4 cell[J]. Journal of Power Sources, 2009, 194(1): 541-549.
[26] PJM. Data Directory [DB/OL]. [2019-07-09]. http:// www.pjm.com/markets-and-operations/data-dictionary.aspx.
[27] 中华人民共和国国家质量监督检验检疫总局. 需求响应效果监测与综合效益评价导则[EB/OL].[2016-05-01]. http://www.doc88.com/p-712 6385511983. html.
Research on User Side Energy Storage Optimization Configuration Considering Capacity Market
Abstract The capacity market can provide flexible capacity support for large-scale grid connection of intermittent renewable energy, stimulate the investment of conventional unit power generation capacity, and ensure sufficient reserve capacity during peak load period. In the future spot market environment, the establishment of a suitable capacity market mechanism can guarantee the long-term power supply security in China, so energy storage as a user-side rapid response resource is expected to participate in the capacity market. This paper combined the capacity market, and proposed a user demand response-reservoir regulation (DR-ESS) optimization model from the perspective of users responding to the real-time electricity price of the main energy market and then using the energy storage to achieve optimal power consumption. Firstly, based on the capacity market contract, the user real-time electricity price demand response model is constructed; then the capacity market is considered, the energy storage double-layer optimization configuration model is established, the outer layer optimized the energy storage capacity and capacity, and the inner layer optimized the energy storage charge and discharge strategy. The two-layer model was solved by genetic algorithm and fmincon toolbox respectively. The analysis of a large industrial user data in the PJM market shows that the DR-ESS optimization model can effectively improve the user's economic benefits, realize peak clipping and valley filling, reduce grid investment costs and increase operational reliability.
keywords:Capacity market, energy storage system, demand response, double layer optimization
中图分类号:TM714
DOI:10.19595/j.cnki.1000-6753.tces.191526
麻秀范 女,1970年生,博士,副教授,研究方向为配电网规划与运行、电动汽车规划与运行。E-mail:xfmhbdll@vip.sina.com
陈 静 女,1995年生,硕士研究生,研究方向为储能优化配置。E-mail:charris@126.com(通信作者)
收稿日期 2019-11-20
改稿日期 2020-04-29
(编辑 赫蕾)