 需要根据观测结果
需要根据观测结果 进行更新估计。在最小方均误差准则下,系统状态最优估计为后验概率密度分布函数
进行更新估计。在最小方均误差准则下,系统状态最优估计为后验概率密度分布函数 的条件期望值
的条件期望值 ,可表示为
,可表示为摘要 针对标准粒子滤波算法在锂离子电池剩余使用寿命预测方面出现的估计精度不高、算法不稳定及计算效率低等问题,该文提出一种改进粒子滤波算法的状态跟踪与剩余使用寿命预测估计方法。选取电池容量衰退经验物理模型为基础,通过贝叶斯理论对历史样本进行状态跟踪建模,优化训练算法辨识物理模型参数与重采样策略。采用状态跟踪训练优化后最新量测信息取代序贯重要性采样过程中未考虑观测噪声的量测信息,指导产生新的提议分布更新粒子重要性权值计算的方法来改善粒子退化现象,同时基于马尔科夫链-蒙特卡洛(MCMC)方法中的M-H(Metropolis-Hastings)抽样算法丰富采样粒子多样性,改良重采样策略来解决由其引起的粒子枯竭问题,并通过仿真揭示出不同跟踪集S和粒子数M等模型参数对预测结果的影响规律,继而构建实时更新提议分布、MCMC方法与粒子滤波算法优化融合的状态跟踪与剩余使用寿命预测模型——基于MCMC的更新改进粒子滤波融合算法模型。仿真实验结果表明,该文提出的改进算法具有状态跟踪拟合度好、预测精度高及计算效率性能优良等特点,并通过设计出不同类型电池容量和算法模型等多种组合方案的仿真,验证了改进算法较强的稳定鲁棒性、泛化适应性和通用有效性。
关键词:改进粒子滤波算法 马尔科夫链-蒙特卡洛方法 锂离子电池 状态跟踪 剩余使用寿命预测
锂离子电池以输出功率大、能量密度高、充放电速度快、自放电率低、无记忆效应、绿色环保等优点成为理想的储能装置,被广泛应用在航空航天、汽车、军事装备及消费类产品等众多领域[1]。然而锂离子电池在循环使用过程中,由于电极活性材料的不可逆溶解、钝化膜的形成生长、电解液的分解以及进而引起的电池内部晶体结构变异破坏,都会导致其性能逐渐衰退,最终会间接引起用电系统(设备)的功能下降或故障。因此,快速准确地估计电池健康状态[2-3]并实现实时在线预测其荷电容量与剩余使用寿命等参数信息,对提高锂离子电池和用电系统(设备)的安全性和可靠性具有重要意义。
锂离子电池的剩余使用寿命(Remaining Useful Life, RUL)是指在一定的充放电条件下,电池性能或健康状态退化到不能满足设备继续工作或规定值(失效阈值)之前所经历的充放电循环次数。近年来,针对电池剩余使用寿命的估计理论及预测算法研究深受国内外专家学者的高度重视。目前基于电池机理模型的研究已较为成熟,且基于模型[4]方法实现RUL预测成为可能,该方法依托电池的退化机理、负载条件及电极材料属性并结合失效机制对RUL进行预测,以对象模型架构确定为应用前提,精度取决于模型建立的完善准确程度。K. Darcovich等在准确架构电池模型的前提下,提出耦合数值算法预测电动汽车的锂离子电池剩余寿命[5]。G. Ning等运用计算物理学中第一性原理建立充放电仿真模型,模拟验证电池循环工作性能变化[6]。R. E. White等将电池衰减过程分为三个阶段,利用单粒子物理机理性能模型仿真分析其寿命循环衰减过程[7]。
以上方法单纯利用经验退化模型来模拟预测电池充放电衰退过程,具有一定的应用局限性。粒子滤波(Particle Filter, PF)算法[8]是目前应用较为广泛的一类基于模型的电池RUL预测方法,该算法主要以贝叶斯理论和蒙特卡洛方法近似得到目标系统的真实状态最小方差估计。然而,由于标准PF算法中重要性采样选用先验概率代替重要性函数,且等效条件假设的原因造成算法的自身缺陷(粒子退化、枯竭及收敛性),从而影响算法的应用和推广。
为解决算法自身不足,国内外学者提出了很多改进算法,如B. Saha等提出PF与相关向量机(Relevance Vector Machine, RVM)结合,采用RVM回归估计模型状态方程,运用自适应算法优化RVM参数,建立衰减模型跟踪其退化趋势,利用外推法预测电池RUL[9]。J. H. Kotecha和P. M. Djuric等提出高斯PF模型,将状态估计后验概率密度函数假设为高斯分布,延缓粒子退化频率,弱化重采样过程,使计算量明显减少且预测精度提高,但有一定的应用局限性[10]。谢长君等提出无迹卡尔曼滤波(Unscented Kalman Filter, UKF)方法与PF算法相结合,将UKF计算结果作为PF算法的建议密度,同时将最新的量测值引入状态预测过程,提高了PF算法的滤波性能,但计算量增大、时效性降低[11]。毕晓君等构造出萤火虫优化PF算法,将混沌扰动搜索策略引入寻优过程,有效地提高了算法对非线性系统状态估计的精度和速度[12]。虽然以上研究已取得一定进展,但改善方法大多依靠相关算法的相互补充融合,同时受到电池本身性能、负载条件与使用环境的影响[13],改进算法在锂离子电池RUL预测方面仍存在诸多问题,如预测精度、鲁棒性、时效性等。
基于此,本文以电池容量衰退经验模型为核心,建立锂离子电池状态跟踪与容量预测估计模型。首先,针对电池容量历史样本创建状态跟踪训练贝叶斯模型,优化拟合算法辨识衰退模型参数,以此搭建标准PF算法预测模型;其次,采用状态跟踪训练更新后的量测信息完善提议分布,指导重要性采样过程的方法解决粒子退化问题,同时基于马尔科夫链-蒙特卡洛(Markov Chain Monte Carlo, MCMC)方法中的M-H(Metropolis-Hastings)抽样算法改善粒子枯竭现象,继而构建基于MCMC的更新改进PF算法RUL预测模型;最后,设计不同容量和算法模型的组合仿真方案,以证明本文提出的改进PF算法的预测精度、计算效率及适应性、稳定性和有效性等可靠性特征。
粒子滤波是一种基于蒙特卡洛(Monte Carlo, MC)理论仿真的贝叶斯估计算法,其核心思想是采用大量离散随机采样点来近似系统随机变量的概率密度函数(Probability Density Function, PDF),以样本均值代替积分运算,从而获得系统真实状态的最小方差估计。
在贝叶斯估计理论[14-15]下,k时刻的系统状态 需要根据观测结果
需要根据观测结果 进行更新估计。在最小方均误差准则下,系统状态最优估计为后验概率密度分布函数
进行更新估计。在最小方均误差准则下,系统状态最优估计为后验概率密度分布函数 的条件期望值
的条件期望值 ,可表示为
,可表示为
 (1)
(1)由此得出最优估计涉及构建后验概率密度函数 ,需同时引入最新量测信息并通过更新与递归预测计算得出。
,需同时引入最新量测信息并通过更新与递归预测计算得出。
在量测信息 未知和状态变量遵循一阶马尔科夫过程的前提下,运用状态方程计算出
未知和状态变量遵循一阶马尔科夫过程的前提下,运用状态方程计算出 的先验值
的先验值 。同时结合k-1时刻的后验概率密度函数
。同时结合k-1时刻的后验概率密度函数 ,通过运用Chapman-Kolmogorov理论公式计算得到状态k时刻的先验概率密度函数,即
,通过运用Chapman-Kolmogorov理论公式计算得到状态k时刻的先验概率密度函数,即
 (2)
(2)利用k时刻量测信息 的概率密度函数
的概率密度函数 更新先验概率分布,进而得到
更新先验概率分布,进而得到 后验概率密度函数,即
后验概率密度函数,即
 (3)
(3)
其中,归一化常数为
 (4)
(4)为了解决最优贝叶斯滤波算法中积分复杂的问题,引入蒙特卡洛采样方法代替计算后验概率。其方法核心思想是:利用一系列关联随机样本的加权和来表示所需系统概率密度,并用计算样本期望值来近似状态的估计值。由于系统后验概率密度函数未知,通常选取一个重要性概率密度函数 来近似抽样,并获取粒子
来近似抽样,并获取粒子 ,进而可以得到后验概率密度为
,进而可以得到后验概率密度为
 (5)
(5)
式中, 为近似后验概率密度N个抽样样本归一化后的权值;
为近似后验概率密度N个抽样样本归一化后的权值; (*)为狄克拉函数。
(*)为狄克拉函数。
假定重要性概率密度函数 代表过去所有时刻状态的后验估计,同时状态和量测信息变量遵循一阶马尔科夫过程,那么序贯重要性采样粒子权重可转换为
代表过去所有时刻状态的后验估计,同时状态和量测信息变量遵循一阶马尔科夫过程,那么序贯重要性采样粒子权重可转换为
 (6)
(6)序贯重要性采样经过若干次迭代后,部分粒子的权值可能小到近似忽略不计,这种退化现象因算法本身缺陷而无法避免。因此,为了降低粒子退化现象的影响,引入重要性重采样。
重要性重采样[16]的本质是增加粒子的多样性,保留并复制权值大的样本点以适应系统动态过程建模,从而抑制退化现象,图1给出PF算法粒子重采样过程示意图。解决粒子退化现象采取重采样方法,通常需要测定有效采样尺度,即
 (7)
(7)式中,var(·)为方差求解; 为粒子权重;
为粒子权重; 为衡量粒子权值的退化程度,该值越大代表粒子权重之间的差距越大,表明权值退化越严重。
为衡量粒子权值的退化程度,该值越大代表粒子权重之间的差距越大,表明权值退化越严重。

图1 PF算法粒子重采样过程示意图
Fig.1 Process diagram of particle resampling in the PF algorithm
标准粒子滤波算法在序贯重要性采样过程中会出现粒子退化现象[17],即粒子权值方差会随着算法迭代次数的增加而不断累积,大多数粒子对应的重要性权值随之趋于零,导致计算资源的严重浪费,同时也使得状态估计不能准确地表达真实的后验分布,进而难以保证电池RUL的预测精度水平。针对粒子退化问题,本文将开展以下三种解决措施研究:
1)增加采样粒子数M
增加采样粒子数[11]是克服序贯重要性采样权值退化问题最直接、简便的方法。随着粒子数目的增加,采样概率密度函数会逐渐逼近真实状态的概率分布情况,在达到延缓退化效果的同时,又能提高最优贝叶斯估计的精度,但计算时间也随之大幅增加,严重影响算法的时效性。因此在增加粒子数目减缓退化问题上要充分考虑算法的时效性,后续章节将针对本文研究对象验证采样粒子数目对预测精度的影响,并对其进行最优选择。
2)选择合理的提议分布
目前设计粒子滤波器的关键是选择合理的提议分布。标准PF算法中的选取分布是先验概率密度,显然这种方式选择舍弃k时刻的量测值,使得状态估计精度严重依赖模型。若量测噪声在某状态下突然发生变化,上述提议分布便不能有效地涵盖真实分布,造成序贯重要性采样计算权重时未计入系统的量测噪声,影响最终的滤波效果。本文采用更新提议分布方法解决算法本身缺陷造成粒子退化问题,提出状态跟踪最优训练模型计算得出的新量测信息取代重要性采样中未考虑观测噪声的量测值,更新粒子的重要性权重计算,利用更新量测信息指导产生新的提议分布,进而提升状态估计精度。
3)改进重采样策略
重采样方法是解决粒子退化问题的重要有效手段,通过对重要性采样得到的离散近似后验概率密度进行再采样,在粒子总数保持不变的情况下,权值较大的样本在粒子运动和前一状态的分布指导下被多次复制,使得有效粒子数目增加,进而达到抑制退化的目的。目前重采样方法众多,本文研究算例采用随机重采样(Random resampling, Ran)、系统重采样(System resampling, Sys)、多项式重采样(Multinomial resampling, Mul)和残差重采样(Residual resampling, Res)四种策略进行仿真,通过对比算法性能确定最优重采样策略。
与此同时,重采样过程中很可能造成大部分权值较低粒子的丢失,这样使得重采样后的粒子过早地远离真实状态,出现样本枯竭问题[18],最终导致状态估计方差变大且滤波性能下降。本文拟采用马尔科夫链-蒙特卡洛理论中M-H抽样方法[19]改善重采样后出现的样本枯竭问题,该算法以构造马尔科夫链为核心,经过状态转移矩阵迭代计算以产生接近目标分布的新粒子集,并通过接受-拒绝规则来缩小状态空间分布,有效地增加了粒子多样性,缓解样本枯竭程度,提高精度。
基于以上分析,本文在采用贝叶斯状态跟踪训练更新提议分布方法来改善粒子退化现象的基础上,结合MCMC算法丰富采样粒子多样性以解决重采样枯竭问题的优势特征,提出并创建一种基于MCMC的更新改进PF算法的锂离子电池状态跟踪与RUL预测估计研究模型。在电池容量衰退模型参数辨识前提下,利用状态跟踪训练更新后的量测信息作为提议分布指导标准PF算法中的重要性采样,以此创建基于实时更新提议分布的PF(Updating PF, UPPF)算法模型,达到以更新模型补偿量测信息增量消除粒子退化影响的目的。继而在UPPF算法模型基础上采用马尔科夫链-蒙特卡洛(MCMC)理论中的M-H抽样方法改良重采样策略,构建基于MCMC方法的更新改进PF融合(UPPF Based on MCMC, MCUPPF)算法解决粒子枯竭问题。图2给出算法具体搭建与实施流程,同时可概括为以下步骤:
(1)提取电池容量数据集OX,对数据进行预处理。由于人为或设备的噪声干扰,容量集可能会出现少量异常数据,故对其进行筛选剔除;同时为提高算法时效,应进行数据精简(每隔N个点取一点,N在不影响衰退趋势前提下视效果而定)。

图2 基于MCUPPF算法的锂离子电池状态跟踪与RUL预测方法
Fig.2 State tracking and RUL prediction method for lithium-ion batteries based on MCUPPF algorithm
(2)设定跟踪集TS和参数初值。在实验数据部分已知前提下,应选取较大规模历史样本作为跟踪集以确保预测算法精度和实效性;以参考样本电池非线性最小二乘法拟合系数作为跟踪初值。
(3)基于双指数物理模型与贝叶斯理论对历史样本进行跟踪训练,寻优选定未知噪声分布信息,判定识别最优参数以此更新构建状态空间模型。
(4)运用标准PF算法建立锂离子电池RUL预测模型,结合状态跟踪最优量测信息修正提议分布指导序贯重要性采样,更新粒子权重计算。
(5)权重判定。选择最佳重采样策略,引入MCMC理论中M-H抽样方法,依据接受-拒绝规则对粒子状态估计集合进行再抽样,进而得到电池容量的最终状态估计值Capout。
(6)按顺序重复执行上述步骤,根据状态跟踪训练最优参数辨识进行迭代更新,判断Capout是否达到电池失效阈值,若满足条件,则预测算法终止,并输出最终估计结果。
本文所研究的锂离子电池剩余使用寿命是以容量衰退信息作为电池健康状态的直接表征参量,因此对其容量数据进行研究分析。在我国,锂离子电池的性能测试规范[20-21]中认定当工作温度在(20±2)℃以下,且范围在20%~100%的荷电状态(State of Charge, SOC)之间进行恒流充放电循环至其实际容量低于额定容量的80%时认定失效。基于此,本文将电池额定容量的80%作为寿命终结的失效阈值。
依照容量状态跟踪训练参数识别与电池RUL预测算法流程对电池容量数据集进行仿真。充放电周期在Scycle(预测仿真起始充放电周期次数)之前进行状态跟踪参数辨识,即估计出能最大限度地减少算法预测值与实验真实值之间误差的最优模型参数,整个方法由数据集提取及预处理、模型参数初始化及设定样本训练集、状态跟踪训练建模优化及噪声多特征寻优等三部分构成;Scycle之后执行MCUPPF算法预测电池容量值,并判断是否达到失效阈值。仿真中设计算法分为三部分:①标准PF(PF)算法;②基于更新提议分布PF(UPPF)算法;③基于MCMC改进PF(MCUPPF)算法。所用仿真计算机CPU为Inter(R) Core(TM) i7-7500U2.70GHz,内存为8GB,所用工具为Matlab R2016a。
本文改进PF算法预测电池RUL的精度严重依赖容量衰退物理模型,而模型的开发需要通过已知的系统物理知识来获取,通常选用从传感器测量设备中提取特征信息,包括电压、电流、功率、电化学阻抗谱、频率和温度等电池参数,捕获其内在联系并以此搭建能表征电池容量退化趋势等信息的等效电路模型[9]如图3所示。图3中,CDL为双层电容,VC为双层电容电压,RCT为电荷转移电阻,RW为Warburg阻抗,IR为极化电流,RE为电解液电阻,IL为负载电流,VL为端电压,OCV为开路电压。
结合电路模型且依托其电化学特征衰减机理得出指数函数之和,其可模拟电池阻抗随时间增加而增加的现象,借助容量衰退与电池内部阻抗之间的关系,通过实验数据的统计学理论回归分析,构建含有电池特征参数的容量衰退经验物理模型,模型需保持较强稳定性,以便能够适应并满足电池容量衰退的强非线性变化趋势。进而利用已知历史实验样本数据,基于贝叶斯理论的跟踪训练能力对经验退化模型参数进行实时估计及噪声多特征寻优,其优劣直接影响经验物理模型精准表征电池容量衰退信息的程度,从而构建RUL预测环节中所使用的状态空间模型[21]。同时由于不同类型电池不同阶段的退化趋势各不相同,通过合理选定模型参数初值和跟踪训练集(多特征寻优的噪声分布),根据贝叶斯理论对特定电池和阶段进行模型参数优化辨识,辨识后物理模型可以有效地收敛到电池真实衰退的渐变趋势状态,以此建立基于PF算法的状态跟踪与RUL预测模型。

图3 电池等效电路模型
Fig.3 Battery equivalent circuit model
根据以上理论分析,本文针对锂离子电池RUL预测问题研究主要包含三个方面:①依托电池负载条件、材料属性及退化机理,结合电池失效机制建立电池容量衰退模型(状态空间模型);②利用贝叶斯理论对电池容量历史样本数据进行跟踪训练,优化拟合算法辨识衰退模型参数(噪声多特征分布);③针对PF算法实现电池RUL预测功能的固有缺陷(粒子退化和枯竭现象),构建基于更新提议分布和改良重采样策略的MCUPPF算法模型实现锂离子电池的RUL预测。基于此,使用统计和机器学习技术方法跟踪电池退化(故障)趋势并估计其隐含机理,建立依托于表征系统递推规律的状态转移方程(电池系统物理模型)和将系统隐含信息转化为可见输出的观测方程(数据特征量测方程)所组成的状态空间模型。结合系统状态空间模型与实际观测输出信息,融入电池表征物理特性,依据上一时刻的状态预测结果以及转移方程给出当前时刻的状态估计,利用当前时刻的实际量测信息(噪声干扰)与估计观测值之间的误差,生成带有权重的修正项来实现状态的更新过程,从而构成一个实时预测系统并得出可信度较高的状态估计,最终实现锂离子电池状态跟踪与RUL预测评估等过程。
基于上述电池机理基础分析和理论支撑,针对锂离子电池健康状态评估问题,在衰退物理模型精准架构和科学辨识其参数前提下,合理选取状态跟踪训练集(噪声分布)和初始参数,在状态跟踪历史样本充分获取衰退信息的基础上,结合本文提出的改进PF算法针对非线性系统状态高精度预测估计的优势特点,可实现锂离子电池非线性剩余寿命周期衰减特征过程的状态跟踪与RUL预测功能,跟踪预测结果精度较好。由此可确保,本文提出改进PF算法的状态跟踪与RUL预测模型,面对不同电池类型及多种使用工况具有一定普适性。
本文研究对象锂离子电池的容量衰退原始数据(Battery_Capacity.dat)来源于美国马里兰大学先进寿命周期工程中心(Center for Advanced Life Cycle Engineering, CALCE)的开源实验数据。从原始测试集中提取出相同类型电池的四组数据为 、
、 、
、 和
和 ,图4为电池容量数据集随充放电周期变化曲线。
,图4为电池容量数据集随充放电周期变化曲线。

图4 四种电池的容量衰退曲线
Fig.4 Capacity degradation curves of the four batteries
容量衰退物理经验模型是制约电池RUL预测精度的关键因素,常采取已知的系统物理知识来获取,通过保持模型稳定特性以便能够适应并满足电池容量衰退的强非线性变化趋势特征要求。结合电池等效电路模型[9],并依据电化学特征机理对实验数据进行回归分析,发现双指数衰退经验模型[22-23]能够精准表征电池容量衰退趋势,经验退化方程为
Cap (8)
(8)
式中,Cap为锂离子电池容量(A·h);k为循环周期次数;未知模型参数a和c与电池阻抗有关,b和d与容量衰退速率有关。
本文所研究的MCUPPF算法是以实时更新提议分布与改进重采样策略为基础的优化方法,而目前重采样方法种类较多,建立基于MCUPPF算法RUL预测模型以评价不同重采样方法的性能优劣,选择合理重采样策略,进而构建最优MCUPPF算法。在相同参数设定下将四种重采样方法(随机、系统、多项式和残差重采样)构成的MCUPPF算法对锂离子电池RUL进行预测,仿真共进行50次运算,表1给出四种重采样算法仿真50次后的RUL预测结果对比情况,图5和图6分别给出四种算法RUL预测结果的方均根误差和计算时间对比曲线。
表1 四种重采样策略RUL预测结果对比(50次)
Tab.1 Comparison of RUL prediction results of four resampling strategies (50 times)
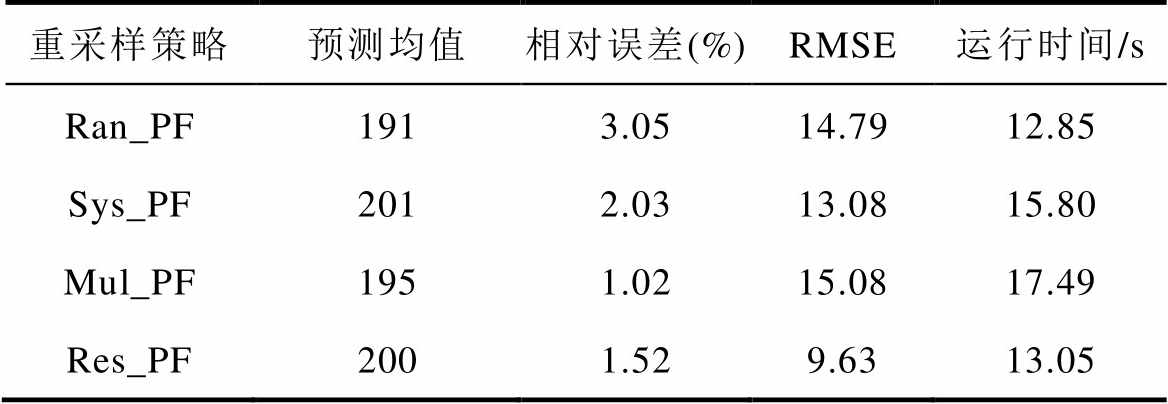
重采样策略预测均值相对误差(%)RMSE运行时间/s Ran_PF1913.0514.7912.85 Sys_PF2012.0313.0815.80 Mul_PF1951.0215.0817.49 Res_PF2001.529.6313.05

图5 四种重采样策略RUL预测方均根误差对比(50次)
Fig.5 RMSE comparison of RUL prediction of four resampling strategies (50 times)

图6 四种重采样策略RUL预测计算时间对比(50次)
Fig.6 Comparisons of RUL prediction computing time of four resampling strategies (50 times)
由表1、图5和图6可知,从预测精度方面分析,多项式重采样算法预测精度最高,残差重采样次之,随机重采样算法精度最低;从计算时间角度分析,随机重采样算法耗时最短,残差重采样算法次之,多项式重采样算法最长,其中以上三种重采样算法计算时间随仿真次数的增加均趋于稳定;从样本多样性角度分析,残差重采样算法较其他三种算法的方均根误差最小,且方均根误差曲线随着仿真次数的增加而趋于稳定。
基于以上分析,从精度、计算时间及样本多样性方面综合考虑,残差重采样算法性能均优于其他重采样策略。当然,针对不同复杂系统不同应用对象的故障检测和健康管理预测问题,不同的重采样算法可能具有不同的应用精度和适用性。而针对本文电池RUL预测问题研究,通过对比结果分析得出残差重采样算法性能最优。
状态跟踪集S与抽样粒子数M是决定MCUPPF算法在电池RUL预测精度、稳定性及时效性的两个重要参数。特此进行不同状态跟踪集S和粒子数M条件下的仿真证明,其中状态跟踪集规模S随机选取82、100和121次(约为容量数量集OX的4/10、5/10和6/10),抽样粒子数数目随机选取5 000、10 000和15 000,呈递增阶梯分布,共计九种不同验证方案。通过对比实验得出两个重要算法参数对RUL预测结果的影响规律,结合多特征噪声分布寻优,依据跟踪效果最终确定最优参数。
基于MCUPPF算法对上述九种方案进行仿真分析,运行计算次数为50次。图7给出单次运行预测算法的状态跟踪与RUL预测结果,可直观地判断并对比不同跟踪集S的预测效果。为了全面展示两个重要参数对MCUPPF算法性能的影响规律,表2给出每种方案下进行50次仿真得到预测结果的量化对比情况,包括RUL预测均值、相对误差、方均根误差及运行时间等预测效果评价指标。图8和图9分别给出不同方案下所对应的预测结果方均根误差和运行时间随仿真次数的变化曲线,以此来验证两个重要参数对MCUPPF算法在不同算例方案下的稳定性与时效性。

图7 基于MCUPPF算法的不同跟踪集S方案下锂离子电池状态跟踪与RUL预测结果(M=15 000)
Fig.7 State tracking and RUL prediction result for lithium-ion batteries based on MCUPPF algorithm under schemes of different tracking set S (M=15 000)
表2 基于MCUPPF算法的不同跟踪集S和粒子数M方案下RUL预测结果对比(50次)
Tab.2 Comparison of RUL prediction results based on MCUPPF algorithms under different schemes of tracking set S and particle number M (50 times)
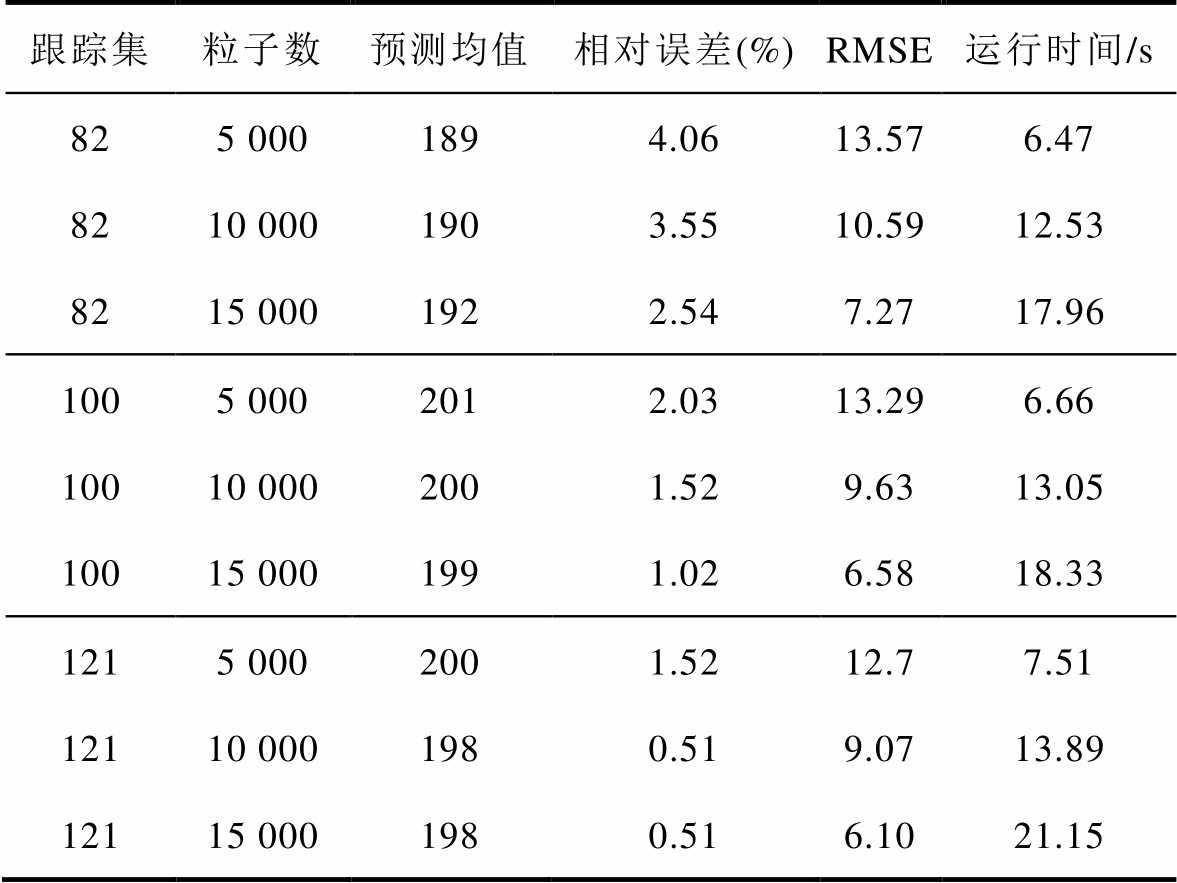
跟踪集粒子数预测均值相对误差(%)RMSE运行时间/s 825 0001894.0613.576.47 8210 0001903.5510.5912.53 8215 0001922.547.2717.96 1005 0002012.0313.296.66 10010 0002001.529.6313.05 10015 0001991.026.5818.33 1215 0002001.5212.77.51 12110 0001980.519.0713.89 12115 0001980.516.1021.15


图8 基于MCUPPF算法的不同跟踪集S和粒子数M方案下RUL预测结果的方均根误差对比(50次)
Fig.8 RMSE comparison of RUL prediction results based on MCUPPF algorithms under different schemes of tracking set S and particle number M(50 times)


图9 基于MCUPPF算法的不同跟踪集S和粒子数M方案下RUL预测计算时间对比(50次)
Fig.9 Comparison of RUL prediction computing time based on MCUPPF algorithms under different schemes of tracking set S and particle number M (50 times)
由图7可知,在粒子数选取M=15 000时,不同规模跟踪集S所对应的状态跟踪训练效果良好,单次仿真的预测失效阈值依次为190、195和198次,相对误差分别提高到3.55%、1.02%和0.51%,三种规模跟踪集S预测结果概率密度函数分布带宽区间依次为51、43和34次,且区域均涵盖实验失效阈值。当跟踪集规模S=121时,RUL预测结果PDF分布中心点距离实验失效阈值点较跟踪集规模S=82和S=100两种方案更近,且分布带宽区间最小,峰值最高,这表征预测真实结果状态的粒子集合离散程度最小,不确定性表达的精度最高。
由表2可知,九种方案下RUL预测结果均值与实验失效阈值的相对误差皆维持在5%以内,精度高且完全满足实际工程要求。在跟踪集S规模已知的前提下,预测结果相对误差(精度)随粒子数M的增加呈递减(上升)趋势,但当粒子数M增加到一定程度时,下降趋势不明显;同样在粒子数M不变的前提下,预测结果相对误差(精度)随跟踪集S规模的扩大而呈下降(上升)趋势。
结合表2,由图8可知,九种方案下RUL预测结果方均根误差(RMSE)范围维持在6.1~13.6以内;在相同跟踪集S规模下,RMSE随粒子数M增加而递减,且在粒子数M三个方案下递减程度约为3个单位,同时在运算次数达到25次之后随仿真次数的增加一致趋近于稳定值;同样在粒子数M不变的前提下,RMSE随跟踪集S规模的扩大而呈下降趋势。
结合表2,由图9可知,九种方案下RUL预测运行计算时间在6.47~21.15s;在跟踪集S规模确定下,运行时间随粒子数M的增加呈上升趋势,且在粒子数M三个方案下增加程度约为倍数关系,同时随仿真次数的增加基本趋近于稳定数值;同样在粒子数M不变的前提下,运行时间随跟踪集S规模的扩大而呈上升趋势。
通过以上仿真计算结果及评价指标可总结以下规律:随着跟踪集S和粒子数M的增加,即状态跟踪训练规模越大、抽样粒子数目越多,RUL预测结果均值越接近失效阈值,精度越高,且相对误差和方均根误差(RMSE)越小,但计算运行时间更长,同时粒子数M增加到一定范围时,预测精度上升不明显;通过对比观察不同规模跟踪集S的状态训练与RUL预测结果,PDF分布区域均涵盖实验失效阈值,且随着跟踪集S规模的增大,表征结果状态估计的离散程度越小,不确定性表达的预测精度越高;通过对比九种不同方案预测结果评价指标可得出,RMSE和运行时间随仿真次数变化的曲线波动不大,并在达到一定仿真次数(25次)后均趋于稳定。因此,通过以上性能分析,并综合考虑比较精度参数和运行时间等评价因素,得出在跟踪集S规模一定,粒子数选取M=10 000时算法性能最优,同时也从侧面反映出该MCUPPF算法具有较高的预测精度和有效的鲁棒稳定性。
通过以上分析,训练数据(状态跟踪)作用的实质是辨识出状态空间模型与真实容量数据的最小方差参数估计,为预测数据(物理退化经验模型)的准确度估计提供前提条件。由电池机理角度分析预测数据与训练数据之间的理论关系可知,运用等效电路方法建立能精准表征电池退化趋势的容量物理模型,以跟踪训练优化辨识状态模型参数为基础,通过多种组合方案验证改进PF方法预测RUL非线性问题均具有可行性和较好的精度保证,即电池在剩余寿命周期前段训练部分所体现的机理与后段预测部分的机理保持相同性质有较好的保障依据。同时综合考虑比较精度参数和运行时间等评价因素,针对特定型号电池和确定的评价指标(精度、计算速度等),必然存在一组固定的最优参数组合(确定数量的粒子数M和规模跟踪集S)。
为验证本文提出的MCUPPF算法可靠性程度,现从适应性、稳定性与有效性三方面出发进行仿真证明,采用马里兰大学CALCE研发中心的M5、M8和M12三种电池容量数据预测RUL来验证算法的适应性,而每种电池容量数据采用PF、UpPF和MCUPPF三种算法对RUL进行预测来验证算法的稳定性,该验证实验共有九种不同方案;此外参考现有文献著作(彭喜元[21]和张凝[24]等学者)的PF相关改进算法预测电池RUL模型,同时基于本文MCUPPF算法在电池容量数据集(NASA PCoE)同一选择和相同参数设定的前提下建立仿真模型,得出预测状态估计值,并参照以上两位学者算法结果进行横向对比证明其有效性。表3给出两类不同数据集的参数和实验工况,表3中,CALCE研发中心的三组测试集以标准恒流0.5C充电直至电压达到4.2V,随后转为恒压充电直至电流衰减为0.05A,放电循环中电压降为2.7V,即为一个充放电周期;NASA PCoE(B18)数据集实验过程同上。
表3 CALCE和NASA两类数据集的参数和实验工况
Tab.3 Parameters and experimental conditions of two kinds of data sets about CALCE and NASA
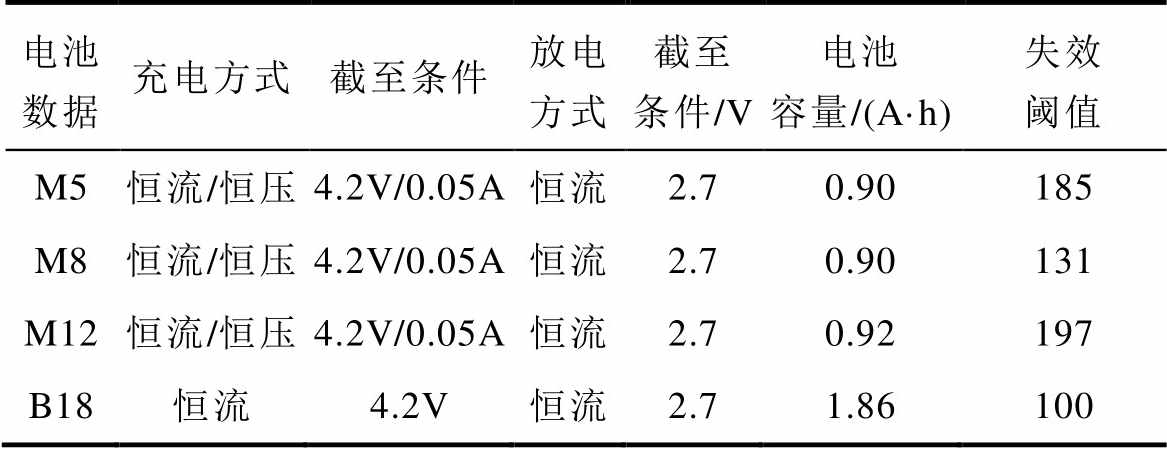
电池数据充电方式截至条件放电方式截至条件/V电池容量/(A·h)失效阈值 M5恒流/恒压4.2V/0.05A恒流2.70.90185 M8恒流/恒压4.2V/0.05A恒流2.70.90131 M12恒流/恒压4.2V/0.05A恒流2.70.92197 B18恒流4.2V恒流2.71.86100
基于PF、UpPF和MCUPPF三种不同算法对上述适应性和稳定性九种方案进行仿真分析,选计算运行次数为50。图10~图12分别给出PF、UPPF、MCUPPF三种算法在不同电池容量条件下进行单次状态跟踪与RUL预测仿真实验结果,可直接主观判断分析跟踪训练拟合度与预测精度效果。为了更全面准确地验证MCUPPF算法的适应性、稳定性以及对比预测性能优劣水平,表4给出不同算法的不同容量电池进行50次仿真实验的量化评价指标数据。图13给出不同容量电池三种算法预测结果RMSE对比曲线,进一步验证了本文提出的MCUPPF算法在不同实验条件下的适应性与稳定性。


图10 基于PF、UPPF和MCUPPF算法的M5电池状态跟踪与RUL预测结果(单次)
Fig.10 State tracking and RUL prediction result for batteries M5 based on PF, UPPF and MCUPPF (single time)


图11 基于PF、UPPF和MCUPPF算法的M8电池状态跟踪与RUL预测结果(单次)
Fig.11 State tracking and RUL prediction result for batteries M8 based on PF, UPPF and MCUPPF (single time)


图12 基于PF、UPPF和MCUPPF算法的M12电池状态跟踪与RUL预测结果(单次)
Fig.12 State tracking and RUL prediction result for batteries M12 based on PF, UPPF and MCUPPF (single time)
通过仿真结果及评价指标数据可概括规律如下:
(1)由图10~图12可知,不同算法针对不同电池容量的状态训练跟踪拟合良好,MCUPPF算法预测RUL结果精度明显优于PF和UpPF两种算法,预测趋势相对更接近真实容量衰退曲线,预测结果PDF分布带宽区间较其余两种算法最小、峰值最高,分布中心点距离实验失效阈值点最近,且区域均涵盖实验失效阈值。
表4 基于PF、UPPF和MCUPPF算法的不同电池容量方案下RUL预测结果对比(50次)
Tab.4 Comparison of RUL prediction results based on PF, UPPF and MCUPPF algorithms under different schemes of battery capacity (50 times)
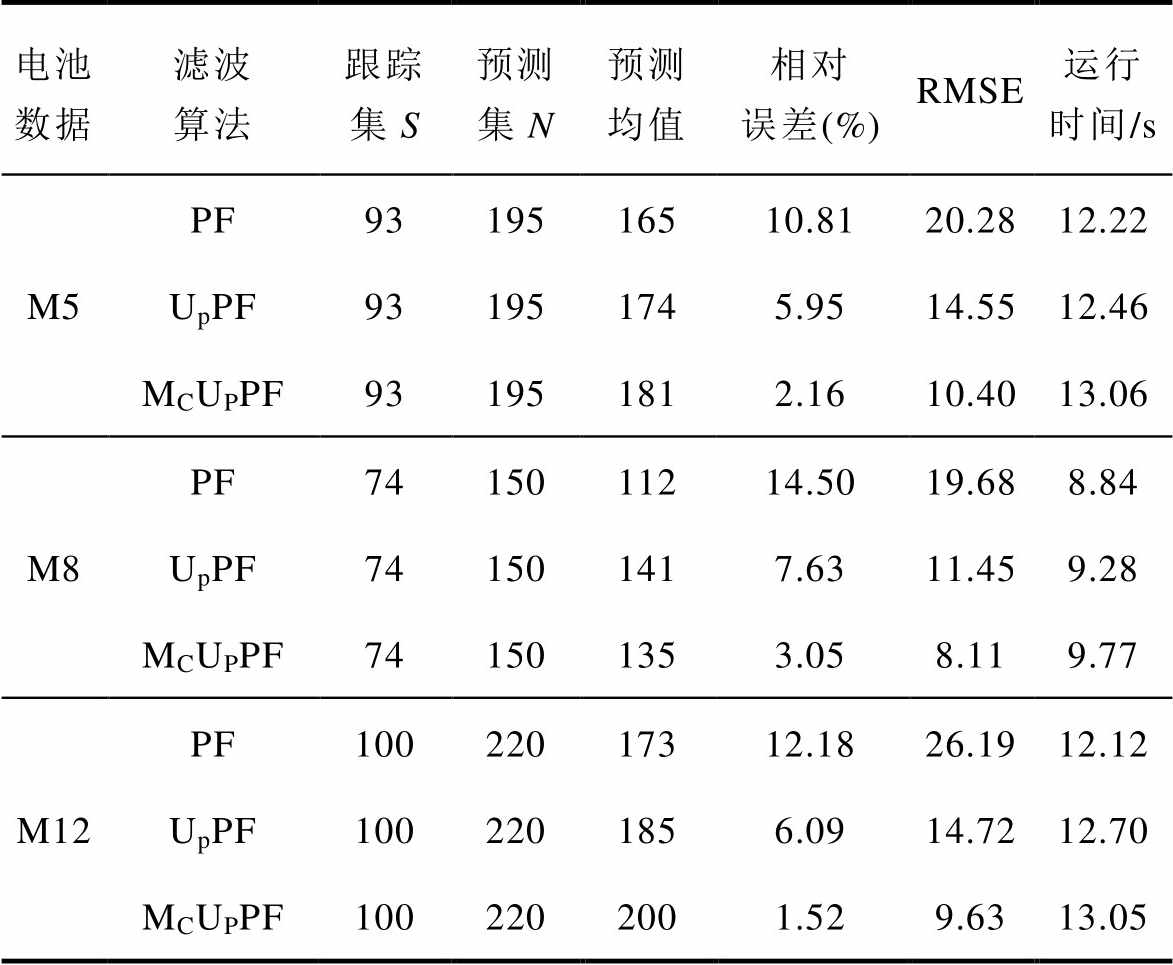
电池数据滤波算法跟踪集S预测集N预测均值相对误差(%)RMSE运行时间/s M5PF9319516510.8120.2812.22 UpPF931951745.9514.5512.46 MCUPPF931951812.1610.4013.06 M8PF7415011214.5019.688.84 UpPF741501417.6311.459.28 MCUPPF741501353.058.119.77 M12PF10022017312.1826.1912.12 UpPF1002201856.0914.7212.70 MCUPPF1002202001.529.6313.05
(2)由表4可知,每一个电池容量中PF、UpPF和MCUPPF三种算法RUL预测结果的相对误差以及RMSE依次下降,其中相对误差分别维持在15%、10%和5%以内,而运行时间依次上升但相差不明显。同时每一种算法RUL预测结果RMSE和运行时间随不同跟踪集S、预测集N规模的增大基本上呈上升趋势,电池容量规模依次为M8-74/150、M5-93/195和M12-100/220。
(3)由表4和图13可知,每一电池容量中PF、UpPF和MCUPPF三种算法RUL预测结果RMSE 随仿真次数的增加均趋于稳定,其三种算法在M5、M8和M12电池数据集中达到稳定时的仿真次数依次为20、15和25次,即跟踪集S、预测集N规模越小,RMSE数值趋于稳定的速度越快。

图13 基于PF、UPPF和MCUPPF算法的不同电池容量方案下RUL预测结果的方均根误差对比(50次)
Fig.13 RMSE comparison of RUL prediction results based on PF, UPPF and MCUPPF algorithms under different schemes of battery capacity (50 times)
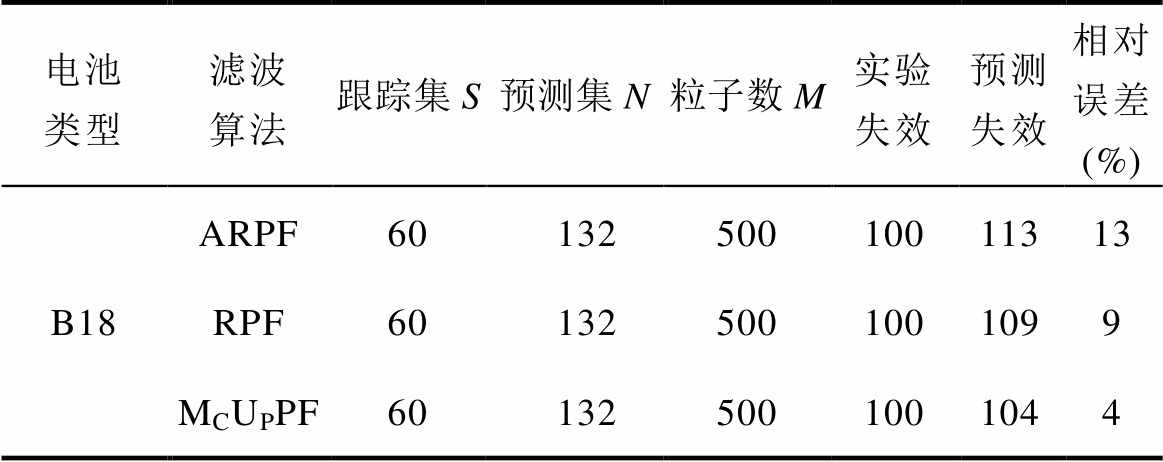
基于彭喜元构造的正则化PF(Regular PF, RPF)[21]、张凝创建的自回归时间序列PF(Auto Regression PF, ARPF)[24]和MCUPPF三种不同算法对锂离子电池RUL预测性能量化指标进行横向比较,基于ARPF、RPF和MCUPPF算法的锂离子电池RUL预测性能量化指标结果对比见表5,验证本文算法的有效性。仿真实验选择同一电池数据集NASA PCoE(B18),相同的参数设定(跟踪集S、预测集N、粒子数目M、失效阈值等)。由表5可知,三种不同算法RUL预测失效值分别为113、109和104次,且MCUPPF算法在实验对象和参数设定均相同的前提下,预测精度(相对误差)较其余两种改进算法最高(最小),精度(相对误差)分别提高(降低)69.2%和55.6%。
综合以上分析,MCUPPF算法在三种电池容量中相较于PF和UpPF算法RUL预测结果精度最高,相对误差均在5%以内,且PDF分布带宽区间最小,峰值最高,这表征预测结果状态的不确定性表达程度最低,且每个电池容量中MCUPPF算法预测结果RMSE最小,随仿真次数的增加趋于稳定且速度最快,而三种算法运行时间却相差不大;同时较ARPF和RPF两种算法在相同电池容量和参数设定的前提下,RUL预测精度最高。由此,相比其他方法,MCUPPF算法的优势是将状态跟踪训练的最新量测信息更新序贯重要性采样过程,舍弃先验估计假定以指导产生新的提议分布,引入M-H接受-拒绝准则,在改善粒子退化和枯竭现象的同时,并未明显地增加模型复杂度,因此该算法在保证预测高精度和计算高效率的前提下,还具有较强的适应性、稳定性和有效性等高可靠性优点。
表5 基于ARPF、RPF和MCUPPF算法的锂离子电池RUL预测性能量化指标结果对比
Tab.5 Comparison of quantitative indicators of lithium ion battery RUL prediction performance based on ARPF, RPF and MCUPPF algorithms
电池类型滤波算法跟踪集S预测集N粒子数M实验失效预测失效相对误差(%) B18ARPF6013250010011313 RPF601325001001099 MCUPPF601325001001044
本文以锂离子电池为研究对象,利用历史容量样本进行贝叶斯状态跟踪训练,优化辨识经验物理模型参数及过程噪声分布信息,提出运用状态跟踪训练量测信息更新提议分布方法改善粒子退化现象,采用以马尔科夫链-蒙特卡洛(MCMC)理论中的M-H抽样算法改良重采样策略的方法来解决粒子枯竭问题,进而构建基于MCMC的更新改进PF融合算法(MCUPPF)的锂离子电池状态跟踪与容量预测研究模型。
本文基于MCUPPF算法建立四种重采样策略预测模型,通过精度、计算时间及样本多样性多方面对比验证,MCUPPF算法选择残差重采样策略性能最优。同时本文通过不同规模的跟踪集S和粒子数M实验方案,揭示其对预测性能指标的影响规律,预测结果精度(相对误差和方均根误差RMSE)随参数规模的增大而增大(呈下降趋势),预测PDF分布区域(粒子状态离散、不确定性表达程度)随之减小(降低),而运算时间随之增加。
本文还设计采用马里兰CALCE和NASA PCoE两种不同类型电池容量数据,运用不同算法组合多种实验方案来验证MCUPPF算法RUL预测模型的适应性、稳定性和有效性。仿真表明,在三种不同电池容量(马里兰CALCE)下,MCUPPF算法相较于PF和UpPF算法预测结果精度最高,相对误差最小且均维持在5%以内,预测PDF分布带宽最窄,峰值最高,不确定性表达程度最低,RMSE最小且随仿真次数增加趋于稳定的速度最快,同时三种算法在同一电池容量下运行时间均相差不大;且MCUPPF算法在同一实验对象(NASA PCoE)、相同参数设定的条件下,较ARPF和RPF两种改进算法RUL预测精度最高,适应性和稳定性更强。
综上所述,本文所提出的基于MCUPPF算法的锂离子电池状态跟踪与RUL预测估计模型,具有状态跟踪拟合度好、RUL预测精度高、计算效率性能优良以及较强的稳定鲁棒性、泛化适应性、通用有效性等优点,为今后的锂离子电池状态跟踪与RUL预测研究工作提供了一定的参考和借鉴意义。
在本文现有的研究成果工作基础上,未来还可以在以下两个方面做进一步的研究:
1)增加补充包括温度在内的其他外部环境因素的电池充放电实验,以获取更为贴合真实运行工况下的容量数据,实现完善外部环境多因素影响下的锂离子电池状态跟踪与RUL预测研究工作。
2)针对容量“跳水”特性和状态空间模型噪声分布复杂未知问题优化本文提出的融合算法,实现完善各种类型电池、不同训练阶段方案下“完整”生命周期的锂离子电池RUL预测与状态评估工作。
参考文献
[1] 张振宇, 汪光森, 聂世雄, 等. 脉冲大倍率放电条件下磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2019, 34(8): 1769-1779.
Zhang Zhenyu, Wang Guangsen, Nie Shixiong, et al. State of charge estimation of LiFePO4 battery under the condition of high rate pulsed discharge[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1769-1779.
[2] 郑志坤, 赵光金, 金阳, 等. 基于库仑效率的退役锂离子动力电池储能梯次利用筛选[J]. 电工技术学报, 2019, 34(增刊1): 388-395.
Zheng Zhikun, Zhao Guangjin, Jin Yang, et al. The reutilization screening of retired electric vehicle Lithium-ion battery based on coulombic efficiency[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 388-395.
[3] 郭永芳, 黄凯, 李志刚. 基于短时搁置端电压压降的快速锂离子电池健康状态预测[J]. 电工技术学报, 2019, 34(19): 3968-3978.
Guo Yongfang, Huang Kai, Li Zhigang. Fast state of health prediction of Lithium-ion battery based on terminal voltage drop during rest for short time[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3968-3978.
[4] 黄凯, 郭永芳, 李志刚. 基于信息反馈粒子群的高精度锂离子电池模型参数辨识[J]. 电工技术学报, 2019, 34(增刊1): 378-387.
Huang Kai, Guo Yongfang, Li Zhigang. High preci- sion parameter identification of Lithium-ion battery model based on feedback particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 378-387.
[5] Darcovich K, MacNeil D, Recoskie S, et al. Coupled numerical approach for automotive battery pack lifetime estimates with thermal management[J]. Journal of Electrochemical Energy Conversion and Storage, 2018, 15(2): 021004-1-021004-12.
[6] Ning G, White R E, Popov B N. A generalized cycle life model of rechargeable li-ion batteries[J]. Electro- chimica Acta, 2006, 51(10): 2012-2022.
[7] Zhang Qi, White R E. Capacity fade analysis of a lithium ion cell[J]. Journal of Power Sources, 2008, 179(2): 793-798.
[8] An D, Choi J H, Kim N H. Prognostics 101: a tutorial for particle filter-based prognostics algorithm using Matlab[J]. Reliability Engineering & System Safety, 2013, 115: 161-169.
[9] Saha B, Goebel K, Christophersen J. Comparison of prognostic algorithms for estimating remaining useful life of batteries[J]. Transactions of the Institute of Measurement and Control, 2009, 31(3-4): 293-308.
[10] Kotecha J H, Djuric P M. Gaussian particle filtering[J]. IEEE Transactions on Signal Processing, 2003, 51(10): 2592-2601.
[11] 谢长君, 费亚龙, 曾春年, 等. 基于无迹粒子滤波的车载锂离子电池状态估计[J]. 电工技术学报, 2018, 33(17): 3958-3964.
Xie Changjun, Fei Yalong, Zeng Chunnian, et al. State-of-charge estimation of lithium-ion battery using unscented particle filter in vehicle[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(17): 3958-3964.
[12] 毕晓君, 胡菘益. 基于混合引导策略的高精度萤火虫优化粒子滤波算法[J]. 上海交通大学学报: 自然版, 2019, 53(2): 232-238.
Bi Xiaojun, Hu Songyi. Firefly algorithm with high precision mixed strategy optimized particle filter[J]. Journal of Shanghai Jiaotong University: Science, 2019, 53(2): 232-238.
[13] 何耀, 曹成荣, 刘新天, 等. 基于可变温度模型的锂电池SOC估计方法[J]. 电机与控制学报, 2018, 22(1): 43-52.
He Yao, Cao Chengrong, Liu Xintian, et al. SOC estimation method for lithium battery based on variable temperature model[J]. Electric Machines and Control, 2018, 22(1): 43-52.
[14] 刘月峰, 赵光权, 彭喜元. 锂离子电池循环寿命的融合预测方法[J]. 仪器仪表学报, 2015, 36(7): 1462-1469.
Liu Yuefeng, Zhao Guangquan, Peng Xiyuan. A fusion prediction method of lithium-ion battery cycle life[J]. Chinese Journal of Scientific Instrument, 2015, 36(7): 1462-1469.
[15] 杜蜀薇, 彭楚宁, 徐石明, 等. 基于贝叶斯层次模型的电能表检定装置在线核查方法[J]. 电力系统自动化, 2018, 42(18): 177-181.
Du Shuwei, Peng Chuning, Xu Shiming, et al. Online verification method of meter calibration equipment based on hierarchical Bayes model[J]. Automation of Electric Power Systems, 2018, 42(18): 177-181.
[16] 陈志敏, 吴盘龙, 薄煜明, 等. 基于自控蝙蝠算法智能优化粒子滤波的机动目标跟踪方法[J]. 电子学报, 2018, 46(4): 886-894.
Chen Zhimin, Wu Panlong, Bo Yuming, et al. Adaptive control bat algorithm intelligent optimization particle filter for maneuvering target tracking[J]. Acta Electronica Sinica, 2018, 46(4): 886-894.
[17] 张琪, 张志利, 李天梅, 等. 一种摄动粒子滤波故障检测方法[J]. 电机与控制学报, 2017, 21(11): 103-109.
Zhang Qi, Zhang Zhili, Li Tianmei, et al. A particle filter with perturbation for fault detection[J]. Electric Machines and Control, 2017, 21(11): 103-109.
[18] Zhang Min, Jia Haitao, Shen Zhen. Improved resampling procedure based on genetic algorithm in particle filter[J]. Journal of University of Electronic Science and Technology of China, 2015, 44(3): 344- 349.
[19] 朱晓荣, 王羽凝, 金绘民, 等. 基于马尔科夫链蒙特卡洛方法的光伏电站可靠性评估[J]. 高电压技术, 2017, 43(3): 1034-1042.
Zhu Xiaorong, Wang Yuning, Jin Huimin, et al. Reliability evaluation of photovoltaic power plant based on Markov Chain Monte Carlo method[J]. High Voltage Engineering, 2017, 43(3): 1034-1042.
[20] 中华人民共和国科学技术部. 2008年度EV用锂离子动力蓄电池性能测试规范[Z]. 4版. 北京: 科技部863现代交通技术领域办公室, 2008.
[21] 彭喜元, 彭宇, 刘大同. 数据驱动的故障预测[M].哈尔滨: 哈尔滨工业大学出版社, 2016.
[22] Wright R B, Motloch C G, Belt J R, et al. Calendar- and cycle-life studies of advanced technology deve- lopment program generation 1 lithium-ion batteries[J]. Journal of Power Sources, 2002, 110(2): 445-470.
[23] He Wei, Williard N, Osterman M, et al. Prognostics of lithium-ion batteries based on dempster–shafer theory and the bayesian Monte Carlo method[J]. Journal of Power Sources, 2011, 196(23): 10314-10321.
[24] 张凝, 徐皑冬, 王锴, 等. 基于粒子滤波算法的锂离子电池剩余寿命预测方法研究[J]. 高技术通讯, 2017, 27(8): 699-707.
Zhang Ning, Xu Aidong, Wang Kai, et al. Research on prediction of the remaining useful life of lithium- ion batteries based on particle filtering[J]. Chinese High Technology Letters, 2017, 27(8): 699-707.
State Tracking and Remaining Useful Life Predictive Method of Li-ion Battery Based on Improved Particle Filter Algorithm
Abstract A standard particle filter (PF) algorithm has the problems of low estimation accuracy, unstable algorithm and low computational efficiency in predicting the remaining useful life (RUL) of li-ion batteries. This paper presents a state tracking and RUL prediction estimation method based on an improved particle filter algorithm. Using the empirical physical model of battery capacity degradation, Bayesian theory is used to model the state tracking of historical samples and optimize training algorithm to determine physical model parameters and resampling strategy. The latest measurement information optimized by the state tracking training is used to replace the measurement information without considering the observation noise in the sequential importance sampling, which guides the generation of new proposed distributions and updates particle importance weights to improve particle degradation. Meanwhile, Metropolis-Hastings sampling algorithm based on Markov Chain Monte Carlo (MCMC) method enriches the diversity of sampling particles, and improves Sampling Importance Resampling (SIR) to solve the problem of particle depletion. The simulation reveals the influence law of model parameters on the prediction results, such as different tracking sets S and particle numbers M. Then the optimal fusion model of state tracking and RUL prediction based on real-time update proposal distribution is constructed combined with MCMC method and PF algorithm. It is an updated and improved particle filter fusion model based on MCMC. The simulation results show that the improved algorithm has good state tracking fitting, high prediction accuracy and good computational efficiency. The simulations of different types of battery capacity and algorithm models under various combined schemes are designed. It is proved that the improved algorithm has strong stability robustness, generalization adaptability and general availability.
keywords:Improved particle filter algorithm, Markov Chain Monte Carlo method, li-ion battery, state tracking, remaining useful life prediction
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.190750
国家自然科学基金(61741126)和广西研究生教育创新计划(YCBZ2019050)资助项目。
收稿日期 2019-06-21
改稿日期 2019-12-23
焦自权 男,1986年生,博士研究生,研究方向为智能化电器。E-mail: jiaomaomao202@163.com
范兴明 男,1978年生,教授,博士生导师,研究方向为智能化电器和高电压新技术。E-mail: fanxm_627@163.com(通信作者)
(编辑 陈 诚)