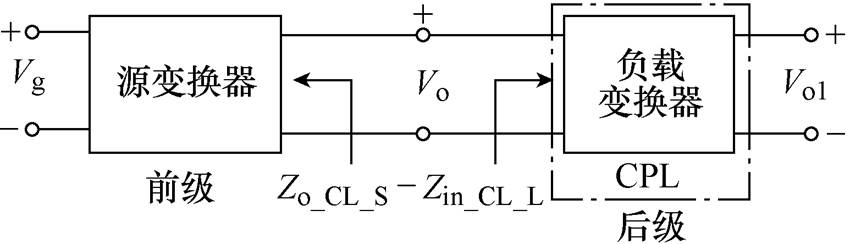
图1 级联系统
Fig.1 Cascaded system
摘要 级联DC-DC变换器结构是直流分布式电源系统的常用形式，级联系统中单独设计的单个变换器能够独立稳定运行，但级联后因源和负载变换器间相互作用可能引起整个系统的不稳定。该文以Buck变换器级联为例，通过状态空间平均法建立大信号模型分析级联系统的开环稳定性，并据此确定能在全负载范围内稳定的并联电阻范围；然后分析并联电阻对级联系统中源变换器输出阻抗影响，在此基础上提出一种基于并联虚拟电阻的有源阻尼控制策略，以改善级联系统的稳定性。该方法可在不影响源变换器的闭环动态性能下，满足与负载变换器输入阻抗相匹配的稳定要求。然后利用Lyapunov间接法得到该控制策略的稳定性判据，通过合理选择并联虚拟电阻可满足整个系统稳定。最后通过仿真和实验证了所提控制策略的有效性。
关键词：级联DC-DC 稳定性分析 虚拟电阻 Lyapunov间接法
直流分布式电源系统（DC distributed Power Systems, DPS）因其效率高、功率传输能力强、系统设计灵活等优点，被广泛应用于通信设备、混合动力汽车、飞机、舰船和服务器等供电系统中[1-3]。在DPS中，源变换器（前级）和负载变换器（后级）间一般采用级联式结构[1, 3]。该结构下，即使两变换器能独立稳定运行，但级联后因前、后级系统间阻抗不匹配，也可能导致整个级联系统失稳[1-4]。因此，调节前后级系统的输入输出阻抗，实现级联系统的稳定至关重要。
为保证级联系统的稳定性，通常需满足Middle- brook提出的阻抗匹配判据[5-6]，即要求源变换器的闭环输出阻抗Zo_CL_S与负载变换器的闭环输入阻抗Zin_CL_L之比满足奈奎斯特判据[6]。现有文献一般通过改变变换器的闭环阻抗以满足阻抗判据，这些方法可分为两类：①改变输出阻抗Zo_CL_S；②改变输入阻抗Zin_CL_L。
文献[1]分析了DC-DC变换器闭环输出阻抗特性及其影响因素，并提出了减小输出阻抗优化设计方法。文献[7]给出了三种不同的无源阻尼回路及其优化设计方法，以削减源变换器输出阻抗的谐振尖峰，使Zo_CL_S在全频率范围内小于Zin_CL_L。但是该方法会增加额外损耗，降低变换器的效率。对此，许多文献提出有源阻尼控制以实现在不降低系统效率的前提下增强系统的稳定性。文献[8]提出在源变换器和负载变换器之间并联同步Buck电路，并通过控制使其呈现电容特性，进而改变源变换器的输出阻抗特性。但该方法控制方式复杂且仍需增加额外电路和电源。文献[2, 9]通过在控制系统中引入电感电流反馈，实现等效增大源变换器的电感阻尼电阻，最终减小源变换器输出阻抗尖峰谐振。但是，通过有源阻尼控制改变源变换器的输出阻抗可能会使源变换器的动态性能变差[10]。文献[11]在控制系统中添加额外的前馈和反馈环节，实现在不影响源变换器的动态性能的前提下减小输出阻抗，使源变换器呈理想电压源特性，以提高级联系统的稳定性，此方法由于反馈环节中含有高阶微分项，实现起来较为复杂。
为了保证级联系统的稳定性和良好的前后级动态性能，一些学者提出通过改变负载变换器输入阻抗实现级联系统的稳定。其中文献[3]通过并联或串联虚拟阻抗，增大负载变换器的输入阻抗在源变换器谐振频率处的幅值，以满足Middlebrook判据。在此基础上，文献[12]进一步比较了串联和并联虚拟阻抗改变负载变换器输入阻抗幅值的不同。其结果表明，仅串联虚拟阻抗可保证级联系统在全负载和全输入电压范围内的稳定性，在此基础上提出一种自适应的控制策略，使后级在不同的前级变换器下均能稳定。改变后级变换器的输入阻抗可在不改变变换器动态性能的条件下使级联系统稳定，但是该文献方法实现复杂，系统可靠性降低。
针对级联DC-DC变换器系统，本文提出了一种基于并联虚拟电阻的有源阻尼控制方法。以后级输入阻抗作为参考，通过虚拟电阻与前级变换器的输出阻抗并联，改变变换器的输出阻抗，在不影响前级变换器的闭环动态性能下，满足与后级输入阻抗相匹配实现稳定。为了保证在全负载范围内级联系统都能稳定，本文给出了虚拟电阻的取值范围，并分析了在不同虚拟电阻取值下系统的阻抗比特性。在该范围内选择使等效负载电阻与源变换器闭环设计下的负载电阻相等的虚拟电阻，不影响前级的闭环动态性能。最后给出了仿真及实验结果，证明了有源阻尼控制的正确性与可行性。
直流分布式电源系统中的级联结构由源变换器和负载变换器组成。为使级联系统中的负载变换器输出稳定且有较好的响应速度，一般采用闭环控制。由于闭环控制后负载变换器的输入功率不变，因此其对前级表现为恒功率负载（Constant Power Load, CPL）[10-12]。级联系统如图1所示，图1中，Vg为源变换器的输入电压，Vo为源变换器输出电压，Vo1为负载变换器输出电压。
图1 级联系统
Fig.1 Cascaded system
DC-DC变换器典型电压闭环控制框图如图2所示[3]。图2中，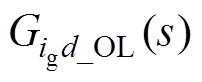
为占空比d对于输入电流ig的开环传递函数，Gvd_OL(s)为占空比d对于输出电压v的开环传递函数，
为输入电压vg对于输出电压v的开环传递函数，
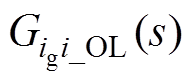为输出电流i对于输入电流ig的传递函数，Zin_OL(s)为开环输入阻抗，Zo_OL(s)为开环输出阻抗，其中Gcv(s)为控制器的传递函数，Gpwm(s)为PWM的传递函数，H(s)为采样的传递函数。由输入、输出阻抗的定义Zin_CL= vg/ig，Zo_CL=v/i，可得它们的传递函数为
图2 电压闭环控制框图
Fig.2 Voltage closed loop control block diagram
（1）式中，Tv为闭环环路增益，Tv=GcvGpwmHGvd_OL；Zin_CL为闭环输入阻抗；Zo_CL为闭环输出阻抗。根据式（1）得到电压闭环控制下Buck变换器输入输出阻抗传递函数为
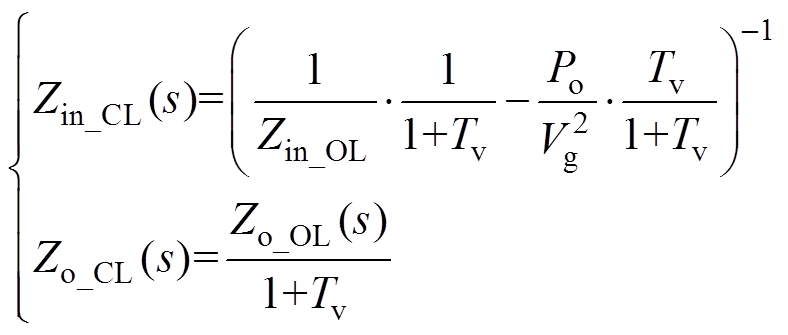（2）
式中，Po为Buck变换器的输出功率，由式（2）可得电压闭环控制下Zin_CL、Zo_CL的Bode图如图3所示。图中，wc为截止角频率。由式（2）和图3可知，当角频率小于wc，即|Tv|
1时，闭环输入阻抗为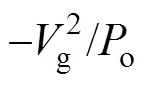
，呈负阻抗特性；当角频率大于wc，即|Tv|
1时，由式（2）可知Zin_CL近似等于Zin_OL；Zin_CL在Bode 图中随频率增大而增大，因而呈感性。
图3 电压闭环控制下输入输出阻抗Bode图
Fig.3 Input and output impedance Bode diagram under voltage closed loop control
本文以两级Buck变换器作为级联系统，带恒功率负载的Buck变换器如图4所示。后级Buck变换器为恒功率负载，输出功率为PCPL的恒功率负载小信号模型可等效为电阻RCPL与恒流源ICPL并联[2, 9, 13]。图4中，RCPL=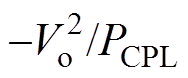
，ICPL=2PCPL/Vo，L、C为源变换器的滤波电感和电容，RL为电感电阻，S为开关管，VD为二极管，为保证级联系统在开环下能够稳定，在源变换器输出并联电阻Rv。
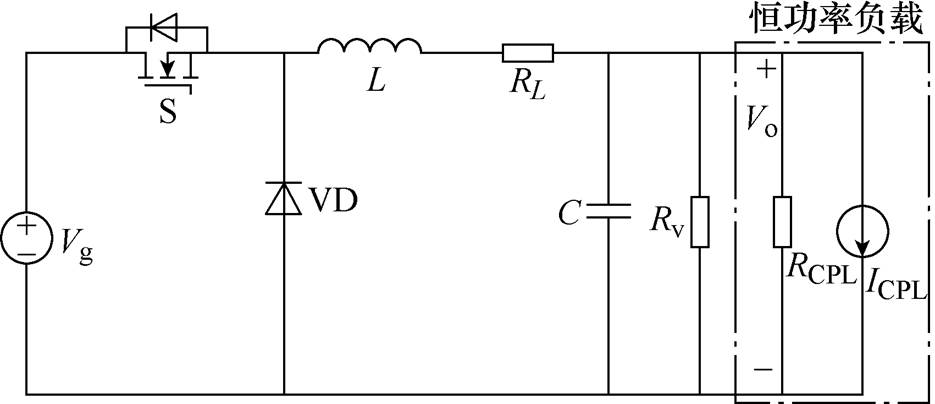
图4 带恒功率负载的Buck变换器
Fig.4 Buck converter with constant power load
采用状态空间平均法建立图4的大信号平均模型为
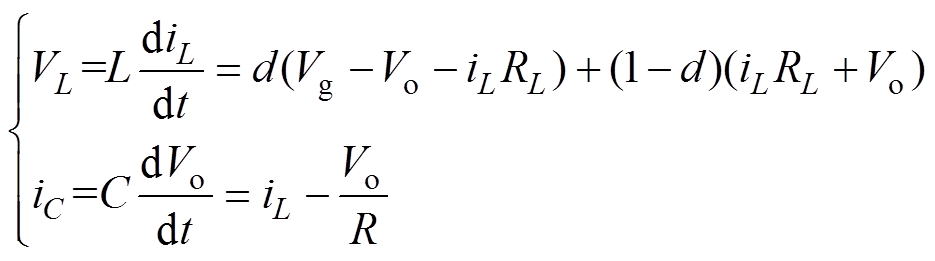（3）式中，d为开关管S控制信号的占空比；iL、iC分别为流过电感、电容的电流；VL为电感电压。由式（3）可得，控制对输出电压的传递函数[2]为
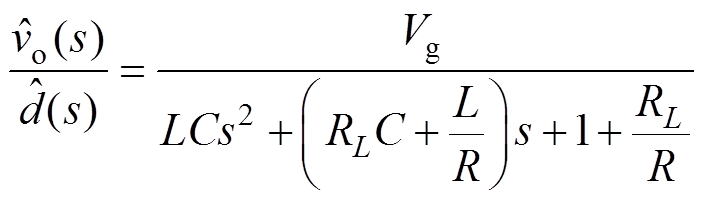（4）
式中，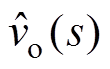
为输出电压的扰动量；
为占空比的扰动量；R为等效负载电阻，且R=Rv//RCPL。由式（4）可知，控制对于输出电压为二阶系统。为保证系统稳定性，其特征方程的各项系数须大于零。因此，系统稳定的条件为
（5）其中
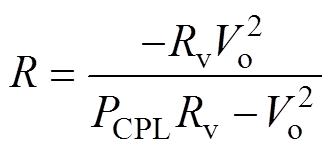（6）
由式（6）得当Rv变化时，等效负载电阻R随虚拟电阻Rv的变化如图5所示。设恒功率负载的调节范围为[0, Pmax]，Pmax为恒功率负载最大功率。由图5可知，R的取值分为两种情况。
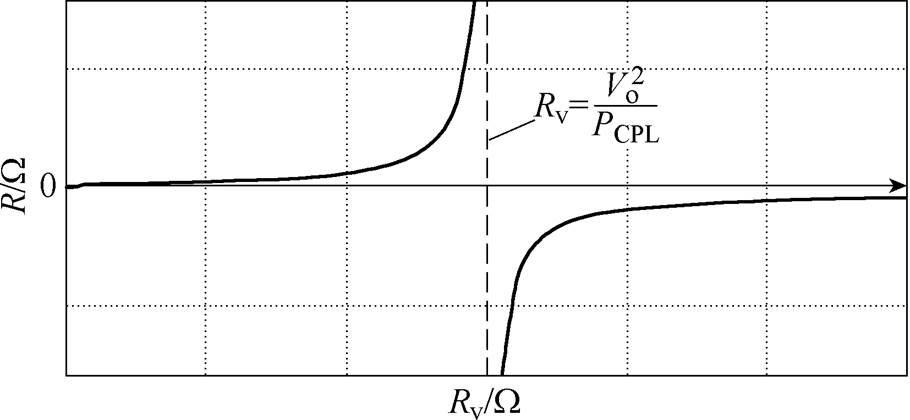
图5 等效负载电阻R随虚拟电阻Rv的变化
Fig.5 The variation of the equivalent load resistance R with the virtual resistance Rv
（1）当0＜Rv＜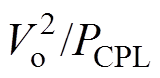
时，始终满足R＞0。因此，系统稳定条件式（5）可满足。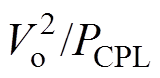随功率增大而减小，若系统需满足所有负载条件下保证 R＞0，即满足全负载范围内稳定条件，需使Rv＜
。
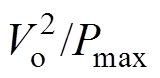（2）当Rv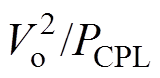＞时，R＜0。将R＜0代入式（5）得|R|＞Rmax，其中Rmax=max(RL, L/(RLC))。由式（6）和|R|＞Rmax得满足系统稳定Rv的范围为
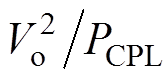＜Rv＜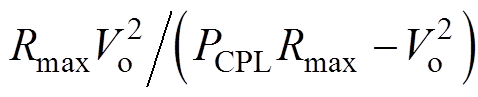
。可知Rv的范围随功率不断变化，则不能保证Rv＞
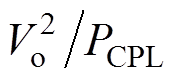，因此在该情况下不能在全功率范围内稳定。
由上述分析可知，Buck变换器带恒功率负载在全负载范围内稳定运行的条件为
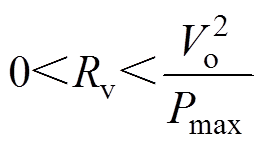（7）根据Middlebrook阻抗判据，为保证级联变换器稳定，应满足源变换器阻抗Zo_CL_S和负载变换器阻抗Zin_CL_L的阻抗比Tm=Zo_CL_S(s)/Zin_CL_L(s)的奈奎斯特曲线不包含点(-1, 0)且|Tm|1。由式（2）可知，Zin_CL_L(s)随输出功率不断变化，当通过控制改变Zin_CL_L(s)使|Tm|1时，易受负载功率的影响。而Zo_CL_S(s)由前级电路参数决定，不受负载变化的影响，因此通过改变Zo_CL_S(s)使|Tm|满足系统稳定的控制方式鲁棒性更高。由式（2）可知，当前级变换器采用电压闭环控制时，Zo_CL_S表达式为
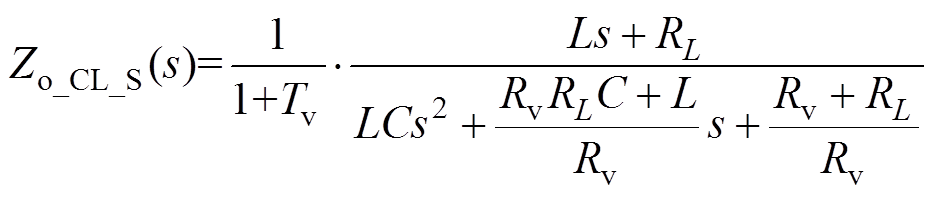（8）
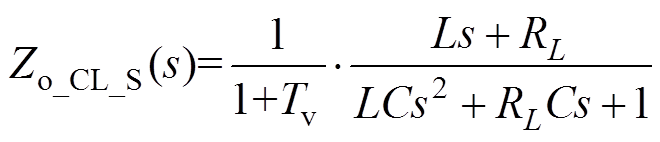（9）
式（8）为含Rv的Zo_CL_S；式（9）为无Rv的Zo_CL_S。由式（8）和式（9）得无电阻Rv时Zo_CL_S、Zin_CL_L的Bode图及阻抗比Tm的Nyquist图如图6所示，不同电阻Rv时Zo_CL_S、Zin_CL_L的Bode图及阻抗比Tm的Nyquist图如图7所示。图6a为无电阻Rv下源变换器Zo_CL_S(s)和负载变换器Zin_CL_L(s)的Bode图，由图6a可知Zo_CL_S(s)在谐振频率出现尖峰，导致Zin_CL_L(s)曲线与Zo_CL_S(s)曲线相交；该交点使得图6b中Tm的Nyquist曲线包含点(-1, 0)，且|Tm|＞1，因此无电阻Rv时级联系统不稳定。图7a为前级变换器输出处并联不同电阻Rv时输出阻抗变化，输出阻抗谐振尖峰随着Rv减小而减小，最后使两曲线不再相交；图7b为阻抗比Tm的Nyquist图，随着Rv减小，曲线逐渐缩小至单位圆内。因此，在源变换器和负载变换器之间并联Rv可改变Zo_CL_S(s)，同时可改善级联系统的稳定性。
图6 无电阻Rv时Zo_CL_S、Zin_CL_L的Bode图及阻抗比Tm的Nyquist图
Fig.6 Bode plot of Zo_CL_S, Zin_CL_L and Nyquist plot of Tm without resistance Rv
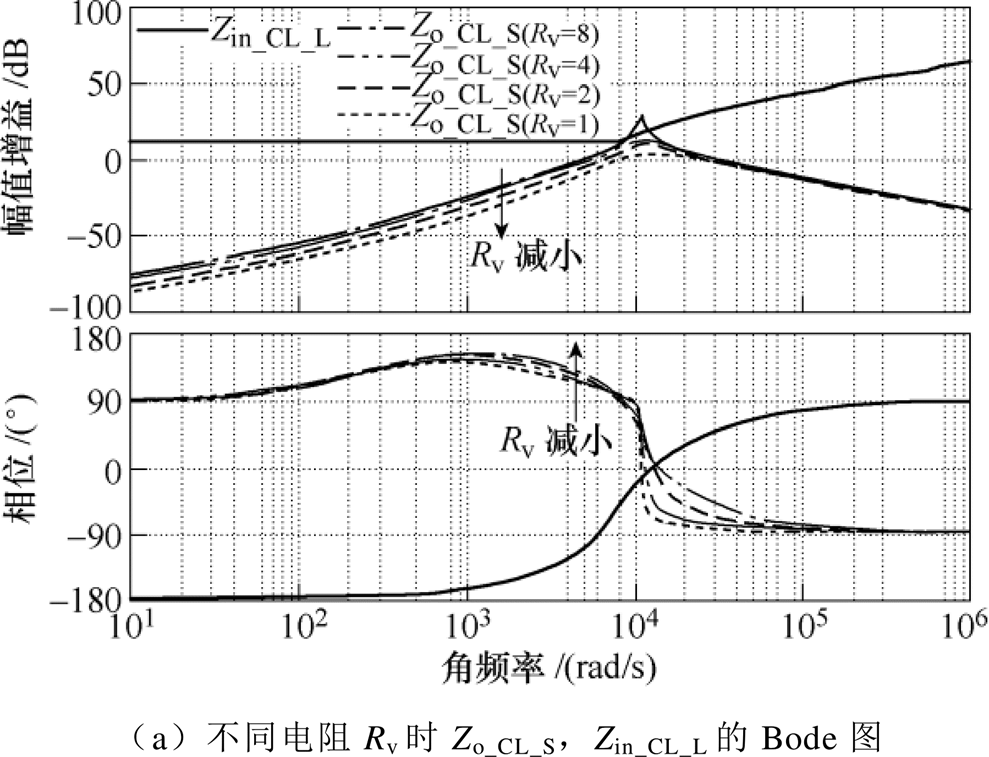
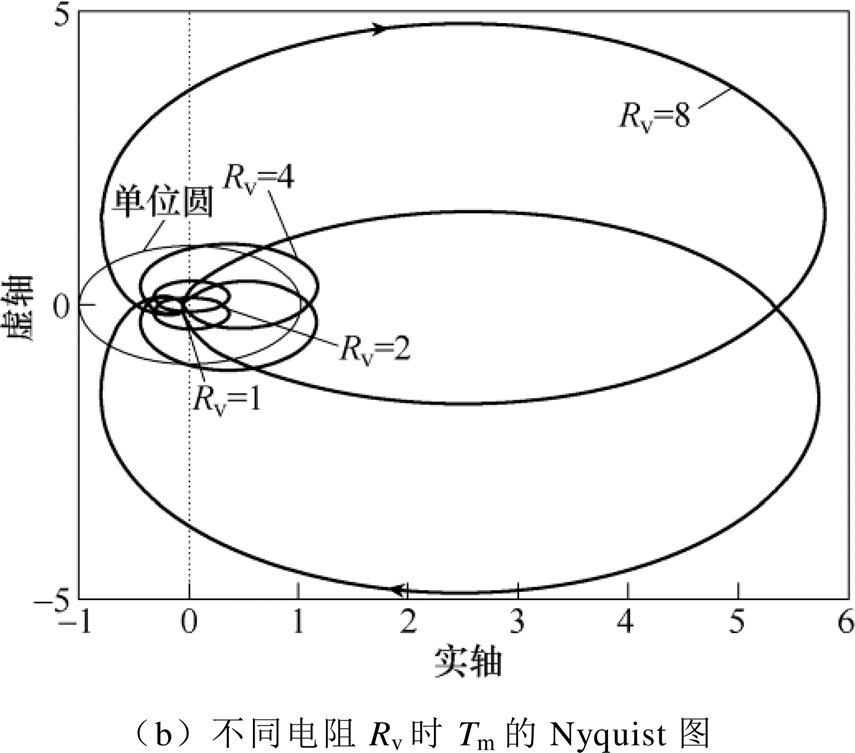
图7 不同电阻Rv时Zo_CL_S、Zin_CL_L的Bode图及阻抗比Tm的Nyquist图
Fig.7 Bode plot of Zo_CL_S, Zin_CL_L and Nyquist plot of Tm with different resistance Rv
前级变换器闭环补偿器一般在额定负载下设计；假设前级变换器环路设计额定负载电阻为Rd；考虑一定的裕度，Rd应不大于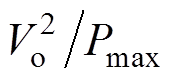
，为保证功率Pmax后级恒功率负载的接入不影响前级源变换器的环路和动态性能，使等效负载电阻R=Rd，即使Gvd_OL保持不变。由式（6）可知，则电阻Rv的取值为
（10）由式（10）可知，Rv=Rd//(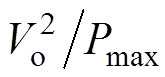
)，而Rd≤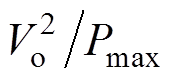，因此满足式（7）。带恒功率负载Buck变换器闭环控制框图如图8所示，图8中，Gc(s)为PI控制器传递函数，H(s)为采样回路传递函数；VTr为PWM载波的峰值，Voref为参考电压，Vg为变换器的输入电压，d为占空比，iL、iC分别为电感电流和电容电流。
图8 带恒功率负载Buck变换器闭环控制
Fig.8 Closed loop control of Buck converter with constant power load
图8中，Rv为实际电阻。通过对图8进行框图变换得到有源阻尼控制实现框图如图9所示。由图9可知，可将Rv由实际电阻转为虚拟电阻，即通过有源阻尼控制实现。图9中，反馈系数k=(sL+RL)VTr/ (VgCRvs)。由于RL较小，可知其对反馈系数k仅在低频处有影响，而输出电压Vo中仅含直流分量和与开关频率相等的高频分量，闭环控制时iC=C(dVo/dt)，低频分量不存在；因此忽略RL得到新的反馈系数k= LVTr/(VgCRv)。
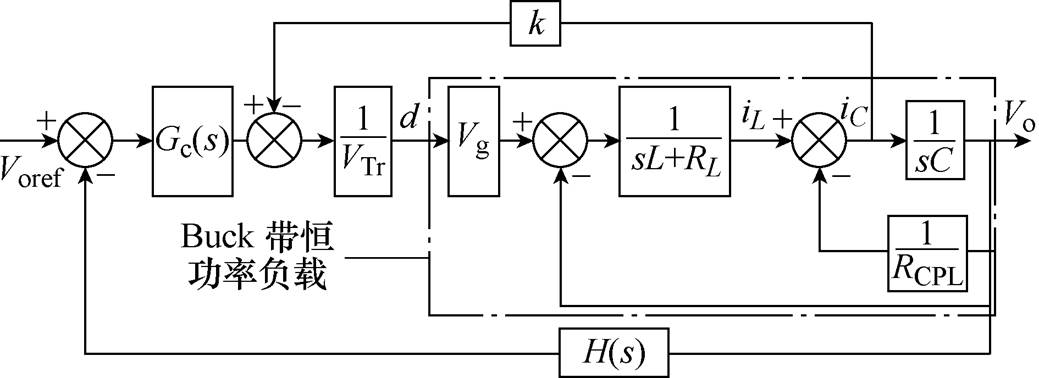
图9 有源阻尼控制实现框图
Fig.9 Active damping control implementation diagram
为了验证忽略RL后简化的有源阻尼控制能否稳定，由图9可建立系统的状态方程为
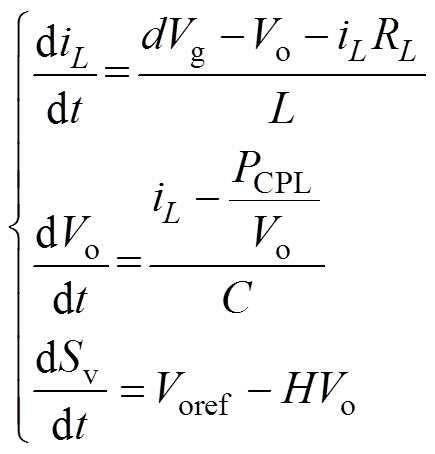（11）
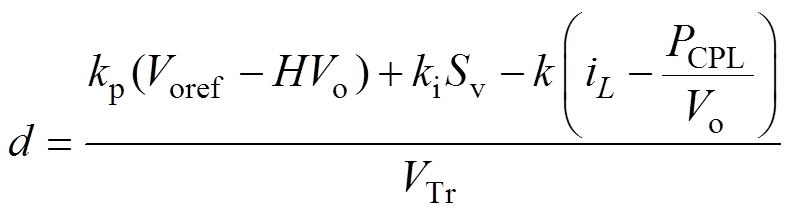（12）
式中，kp、ki为控制器的PI参数。恒功率负载不再用小信号模型1/RCPL，而使用大信号模型PCPL/Vo。
状态iL、Vo、Sv分别为系统的状态变量，Sv为电压误差的积分变量，反馈系数k=LVTr/(VgCRv)，Voref为参考输出电压。令式（11）等号左边为零，得到系统的平衡工作点Xe为
（13）由式（11）状态方程可知其为非线性系统，首先需要将非线性系统在平衡点处进行线性化，得到线性模型为
（14）
式中，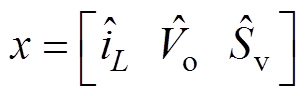
；B为输入矩阵；u为输入变量矩阵。
在平衡点处的雅克比矩阵A(Xe)[14-15]为
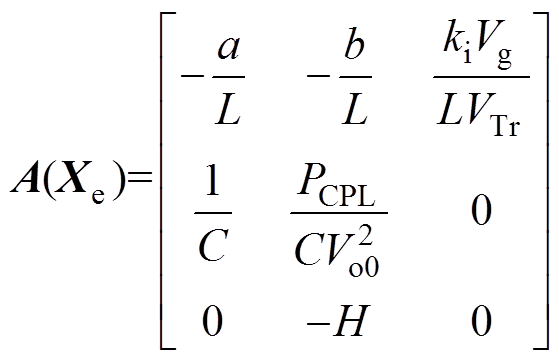（15）其中
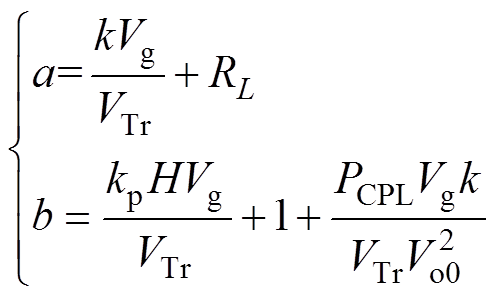（16）
由Lyapunov间接法可知，系统稳定的条件为系统的雅克比矩阵的特征值均在复平面的左半平面内，即Re(li)＜0。求解矩阵A(Xe)-lE的行列式为
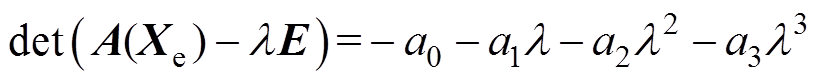（17）其中
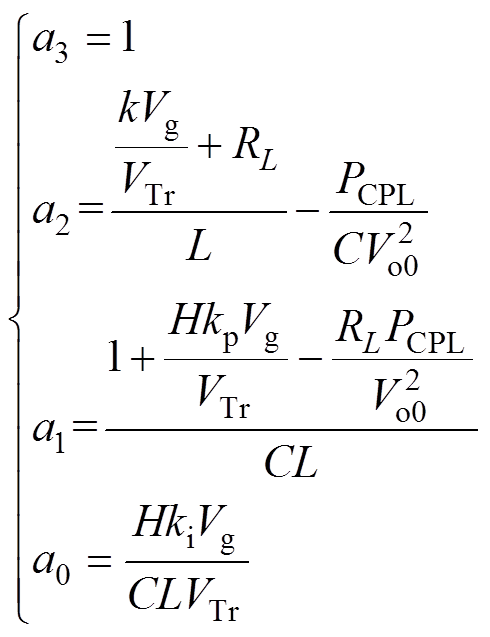（18）
式（17）是三阶多项式，根据劳斯判据若要求det( )=0的根位于复平面左半平面，需保证三阶多项式中的所有系数大于零且二次项系数与一次项系数的乘积大于三次项系数与常数项的乘积[16]，即 a2a1＞a3a0。可得下列不等式为
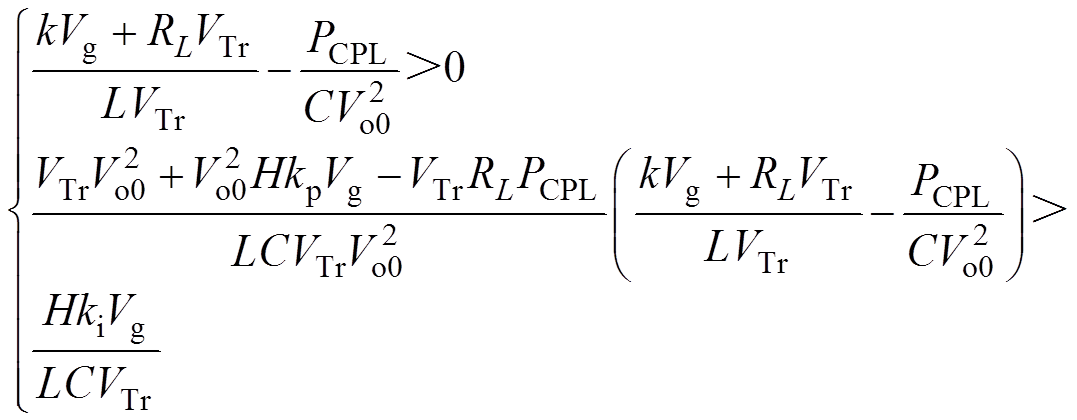（19）由式（19）得反馈系数k的范围为
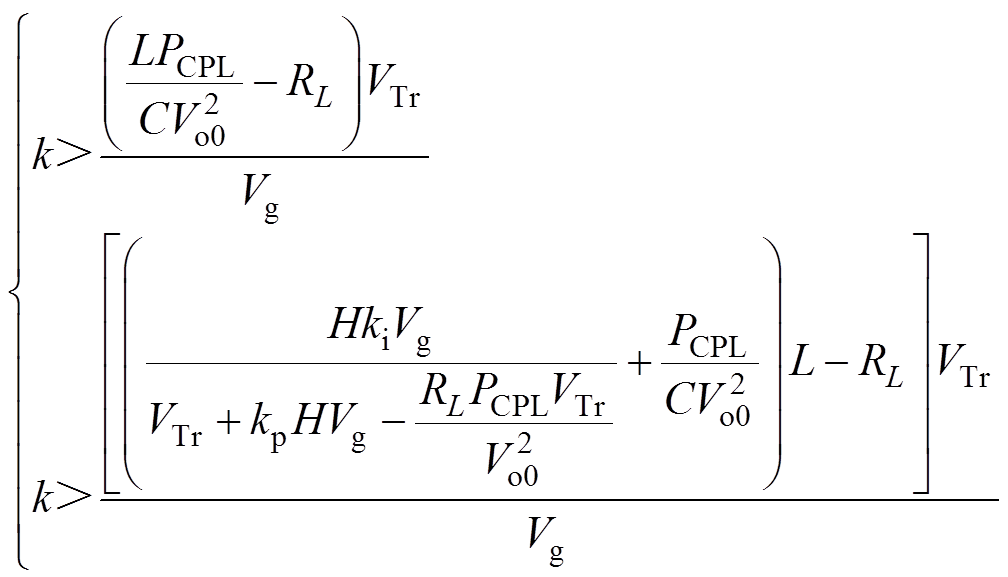（20）
将k=LVTr/(VgCRv)代入式（20），得满足系统稳定的Rv的取值范围为
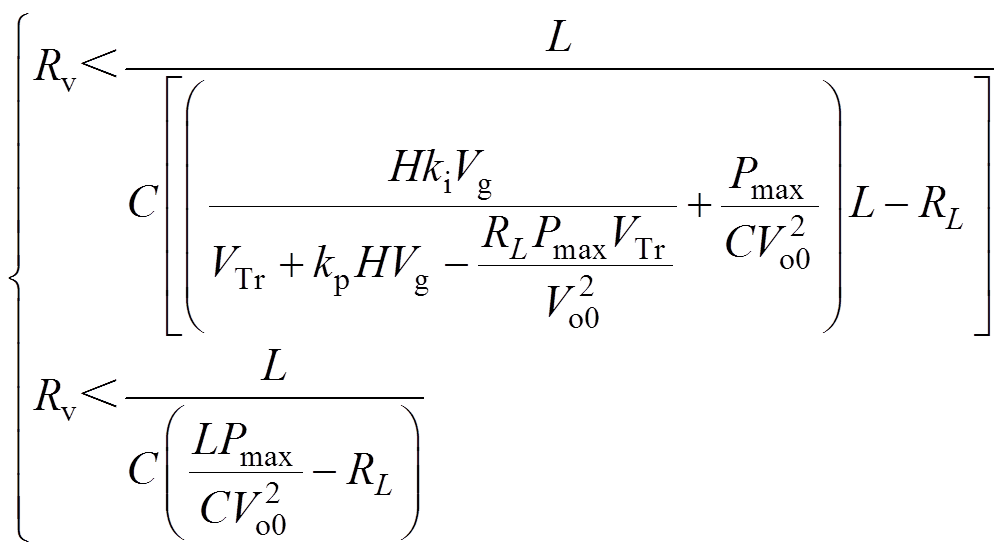（21）根据式（21）可判断整个级联系统闭环后的稳定性，而系统的动态性能由式（10）决定。由式（10）可知Rv随Rd减小而减小，因此可以通过适当减小Rd以满足系统稳定性要求。若要使虚拟电阻的参数既满足系统稳定性要求，同时不影响前级动态性能，Rv需同时满足式（10）和式（21）。依据此原则，Rv的选取流程如图10所示。
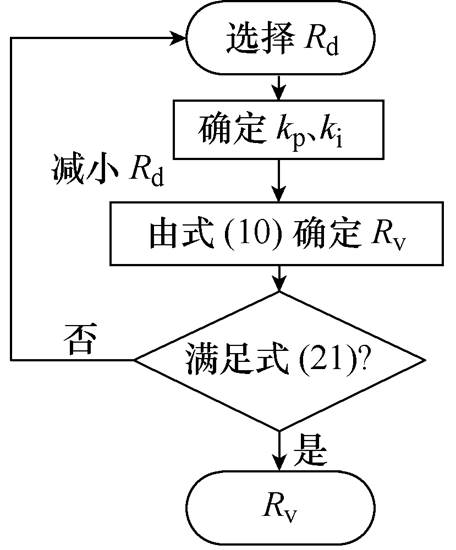
图10 虚拟电阻Rv的确定
Fig.10 The selection of virtual resistance Rv
首先选择电阻Rd，根据期望的动态性能确定前级PI参数kp、ki，然后由式（10）计算虚拟电阻Rv，再判断Rv是否满足式（21），若不满足则减小Rd，重新计算Rv；反之，直接得到既满足稳定性又不影响前级动态性能的Rv。
为验证所提出的有源阻尼控制策略的正确性，在Matlab/Simulink搭建了仿真平台，图11为两Buck变换器构成级联系统。有源阻尼控制通过采样电容电流乘以系数k（k=VTrL/(VgRvC)）后反馈至PI控制器的输出进行比较产生占空比d；后级Buck变换器电压闭环控制作为恒功率负载，额定功率为25W；图11中，S1、VD1分别为后级变换器的开关管和二极管，Vo1ref为负载变换器输出的参考电压，Io1为输出电流；IL1为流过电感L1的电流。仿真参数见表1和表2。
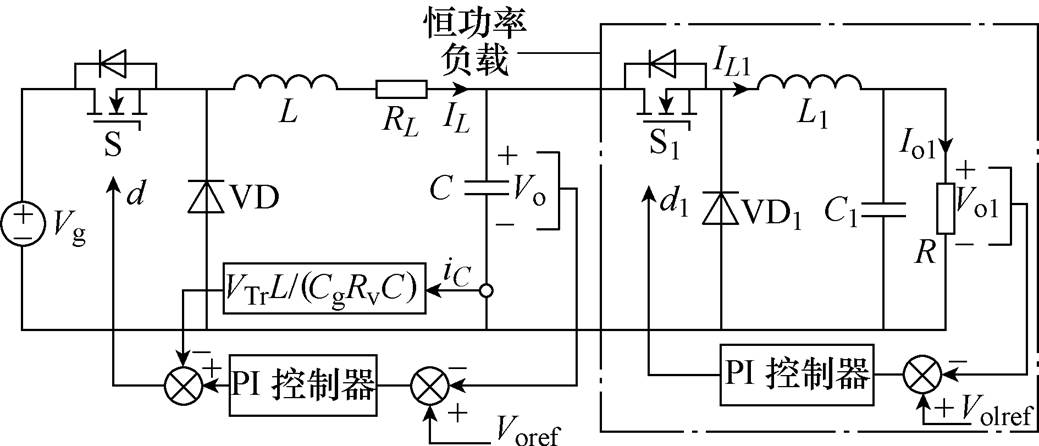
图11 双Buck变换器级联系统
Fig.11 Dual Buck converter cascaded system
表1 源Buck变换器参数
Tab.1 The parameter of source Buck converter
参 数数 值 输入电压Vg/V20 输出电压Vo/V10 开关频率fs/kHz50 电感L/mH200 电感电阻RL/W0.1 电容C/mF47 截止频率fc/Hz2 000 相位裕度Pm/(°)50
前级Buck变换器在设计闭环参数时选取Rd= 
=2W，此时由式（10）得Rv=4/3W，将Rv代入式（21）满足稳定条件。两级Buck变换器的输出均采用比例积分控制进行闭环调节。在此基础上得到源变换器和负载变换器的环路增益Bode图如图12所示。开环、闭环输入输出阻抗Bode图和阻抗比Tm的Nyquist图如图13所示。源变换器的截止频率大于负载变换器，在源变换器截止频率处，后级闭环输入阻抗已呈感性（见图13a中Zin_CL_L），这使级联系统有足够的幅值稳定裕度，图13a中Zin_OL_L、Zo_OL_S分别为负载变换器的开环输入阻抗和源变换器的开环输出阻抗。图13b为阻抗比，|Tm|
1且不包含点(-1, 0)；因而整个级联系统稳定，并有足够稳定裕度。
表2 负载Buck变换器参数
Tab.2 The parameter of load Buck converter
参 数数 值 输出电压Vo1/V5 开关频率fs/kHz20 电感L1/mH400 电容C1/mF100 截止频率fc/Hz1 000 相位裕度Pm/(°)50
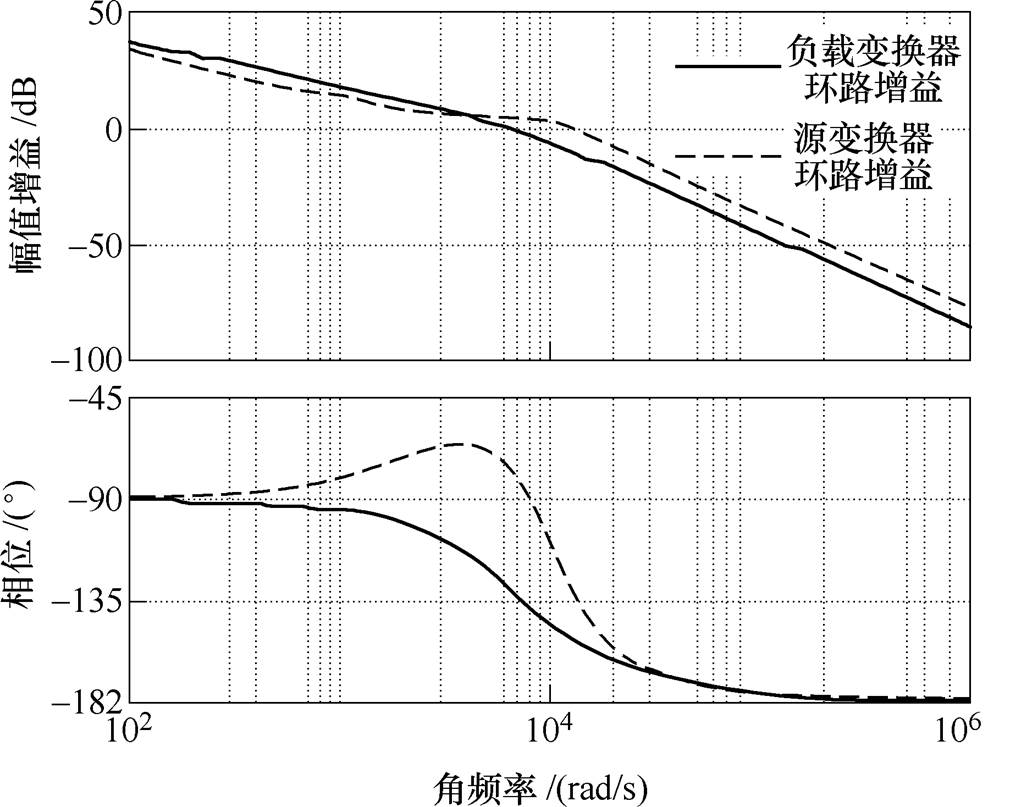
图12 源、负载变换器环路增益Bode图
Fig.12 Source and load converter loop gain Bode plot
图13 开环、闭环输入输出阻抗Bode图和阻抗比Tm的Nyquist图
Fig.13 Bode plot of open loop, closed loop input and output impendence and Nyquist plot of Tm
图14为两级变换器输出电压的仿真波形，在前0.025s两级变换器仅PI控制，输出电压波形振荡，系统不稳定；0.025s时加入有源阻尼控制，输出电压不再振荡。加入有源阻尼控制对已设计好的前级变换器闭环动态性能的影响如图15所示，由图15可知，加入有源阻尼控制对前级动态性能的影响主要在启动阶段，在0.025s输入电压由20V跳变至25V，有源阻尼控制和设计的性能基本一致。
图14 有、无有源阻尼控制对比
Fig.14 Comparison with or without active damping control
图16～图18为Rv=4/3W 时级联系统分别工作在满载、半载、10%负载下，输入电压从20V跳变至25V的仿真波形。由图16～图18可知，输入电压跳变后两级输出仍能跟随给定电压，由此可知，选择合适的Rv能够满足全功率范围内级联系统的稳定。图19和图20为在有源阻尼控制下t =0.01s时负载跳变的仿真波形，由此可得，系统突增负载和突减负载后，两级输出电压保持不变，满载时源变换器输出电压纹波大于半载时输出电压纹波。
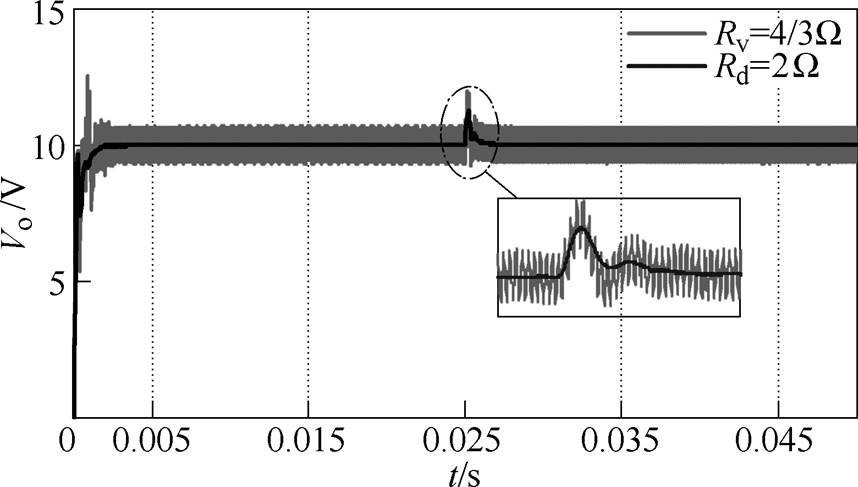
图15 有源阻尼控制对动态性能的影响
Fig 15 Influence of active damping control on dynamic performance
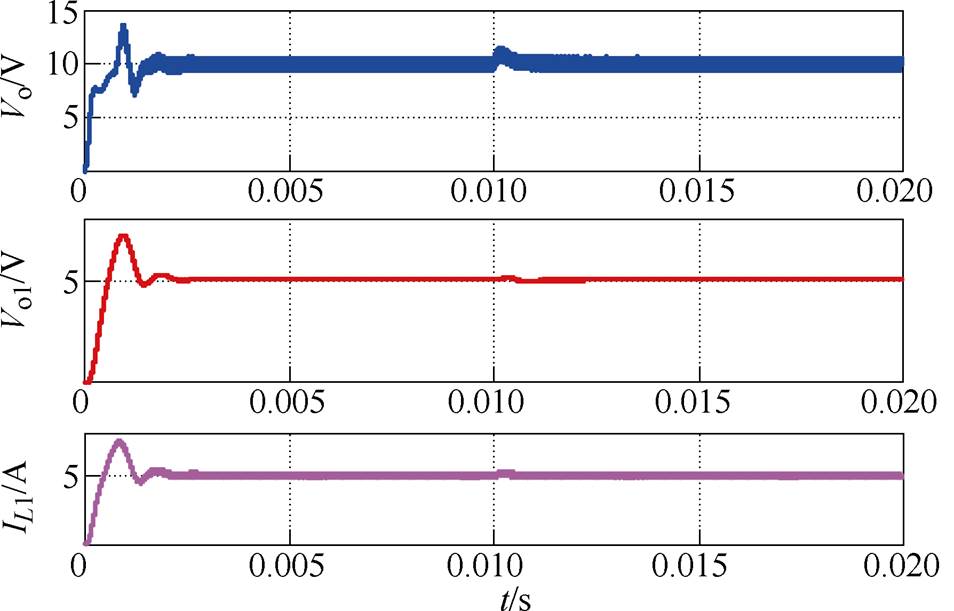
图16 0.01s满载下输入电压跳变仿真波形
Fig.16 Simulation waveforms under full load when input voltage jump at 0.01s
图17 0.01s时半载下输入电压跳变仿真波形
Fig.17 Simulation waveforms under 50% load when input voltage jump at 0.01s
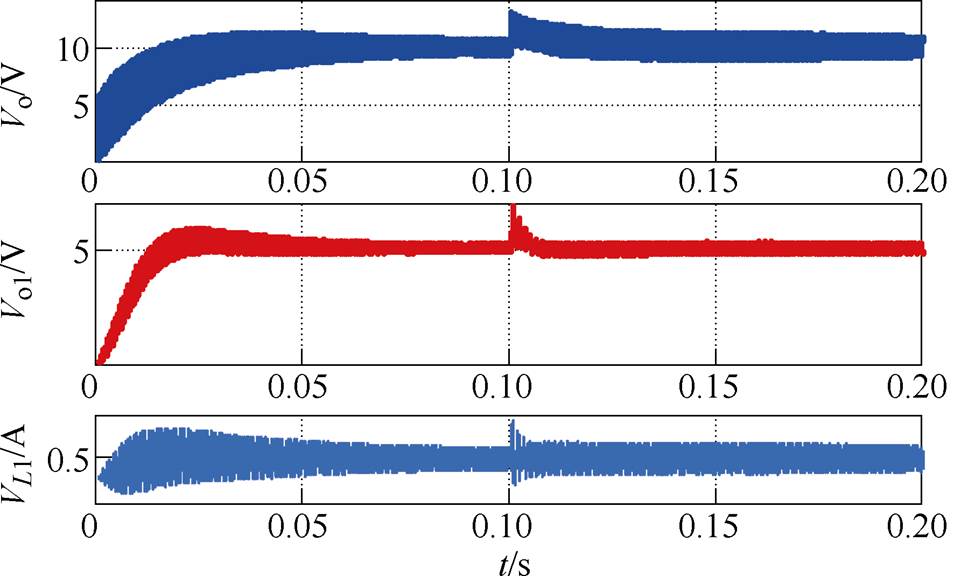
图18 0.1s时10%负载下输入电压跳变仿真波形
Fig.18 Simulation waveforms under 10% load when input voltage jump at 0.1s
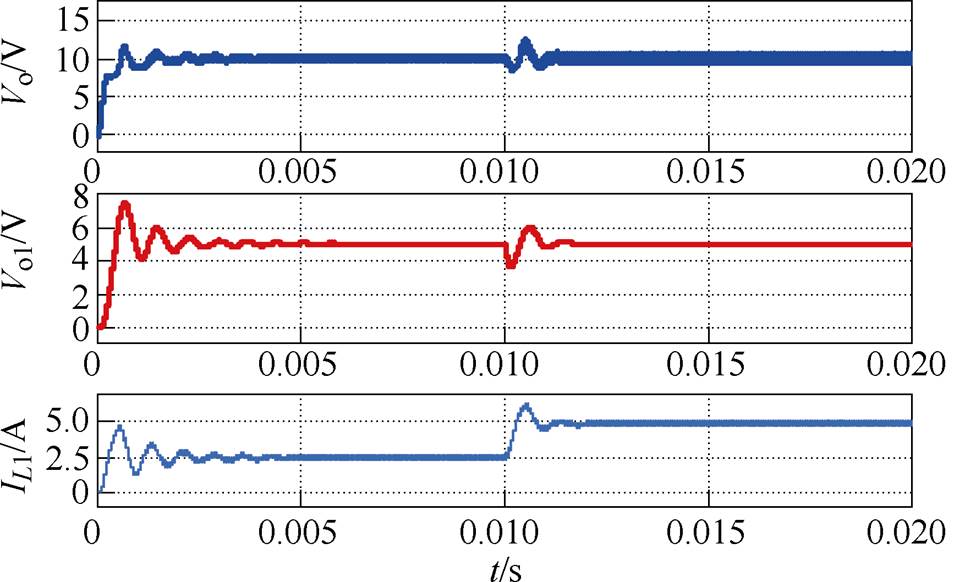
图19 0.01s时突然增加负载仿真波形
Fig.19 Simulation waveforms when load increase at 0.01s suddenly
图20 0.01s时突然减少负载仿真波形
Fig.20 Simulation waveforms when load decrease at 0.01s suddenly
为了验证本文所提出的控制策略的有效性，搭建了级联Buck变换器的实验平台，实验平台参数与仿真参数一致，两级变换器都采用TI公司的TMS320F28069作为系统的控制器。实验平台如图21所示。
图21 实验平台
Fig.21 Experimental platform
图22为在前级变换器加入有源阻尼控制前后的实验波形，在加入有源阻尼控制之前，前级输出电压处于振荡状态，加入控制后不再振荡，后级输出电压也趋于稳定。
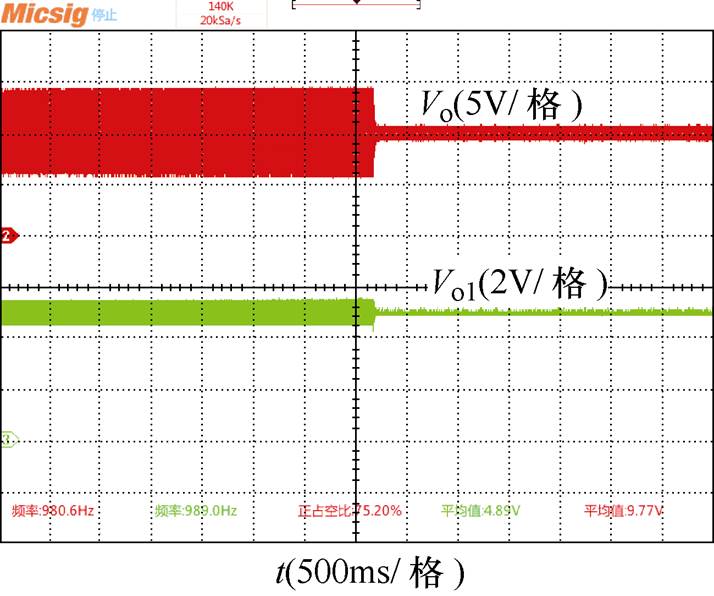
图22 加入阻尼控制前后的实验波形
Fig.22 Experimental waveforms before and after adding active damping control
级联系统前级和单独运行不加Rv前级变换器的动态性能比较如图23所示。由图23可知，两者在相同的输入电压跳变情况下动态性能基本一致，级联下前级变换器的纹波相对较大，其主要原因是前后级变换器直接级联，前级变换器的负载电流不连续导致纹波相对较大。
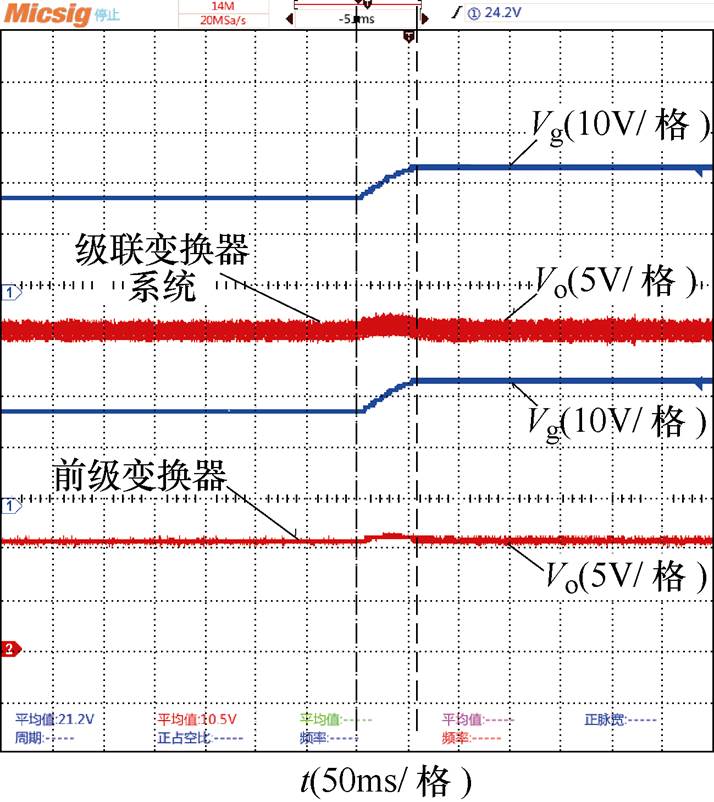
图23 级联系统和单独运行前级变换器的动态性能比较
Fig.23 Comparison of dynamic performance between cascaded system and stand-alone converter
有源阻尼控制加入到前级变换器的控制系统后，图24和图25分别为在100%负载（25W）和50%负载（12.5W）下突然改变级联系统的输入电压时前后级输出电压和输出电流的实验波形，由实验波形可知，在输入电压的扰动下级联系统仍能保持稳定，从而验证了级联系统在不同负载下都能稳定。
图26和图27分别为突增、突减负载扰动下，系统输入电压、前后级输出电压及输出电流的实验波形。由图可知，在突增和突减负载下前后级输出电压都能稳定，和仿真一样，满载时源变换器输出电压纹波大于半载时输出电压纹波。
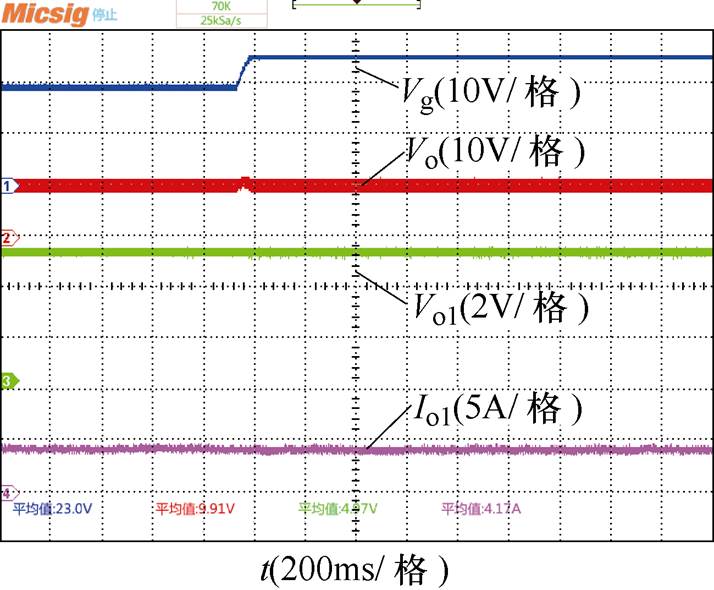
图24 100%负载下输入电压跳变的实验波形
Fig.24 Experimental waveforms at 100% load of input voltage jump
图25 50%负载下输入电压跳变的实验波形
Fig.25 Experimental waveforms at 50% load of input voltage jump
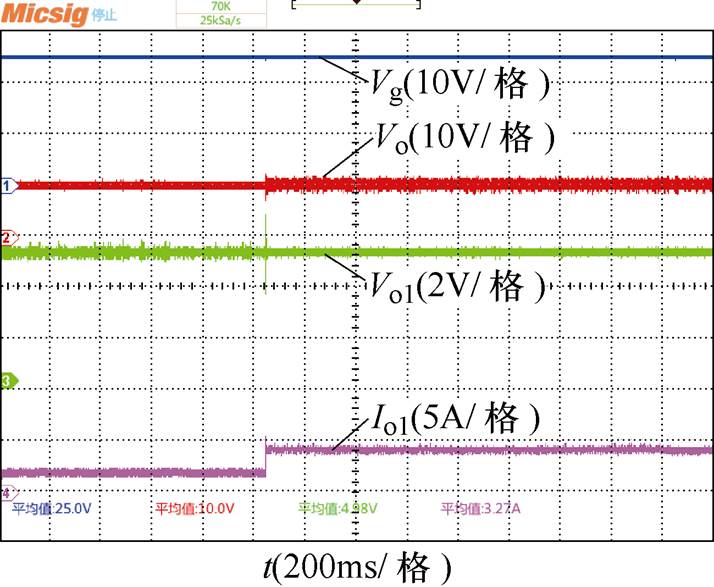
图26 突增负载的实验波形
Fig.26 Experimental waveforms when load increase
图27 突减负载的实验波形
Fig.27 Experimental waveforms when load decrease
本文提出了一种基于并联虚拟电阻的有源阻尼控制策略，在保证源变换器的动态性能下，改善了级联DC-DC变换器稳定性，得到以下结论：
1）通过源变换器的输出阻抗并联虚拟电阻，可改善由级联DC-DC系统中负载变换器的负阻抗特性造成的不稳定性问题。
2）本文给出了在源变换器开环运行下，保证全功率范围内稳定运行的并联电阻范围，并证明了并联电阻对源变换器输出阻抗的影响。
3）通过Lyapunov间接法得到并联虚拟电阻控制策略下级联DC-DC变换器闭环稳定的判据。
参考文献
[1] 姚雨迎, 张东来, 徐殿国. 级联式DC/DC变换器输出阻抗的优化设计与稳定性[J]. 电工技术学报, 2009, 24(3): 147-152.
Yao Yuying, Zhang Donglai, Xu Dianguo. Output impedance optimization and stability for cascade DC/DC converter[J]. Transactions of China Electro- technical Society, 2009, 24(3): 147-152.
[2] Rahimi A M, Emadi A. Active damping in DC/DC power electronic converters: a novel method to over- come the problems of constant power loads[J]. IEEE Transactions on Industrial Electronics, 2009, 56(5): 1428-1439.
[3] Zhang Xin, Ruan Xinbo, Zhong Qingchang. Improving the stability of cascaded DC/DC converter systems via shaping the input impedance of the load converter with a parallel or series virtual impedance[J]. IEEE Transactions on Industrial Electronics, 2015, 62(12): 7499-7512.
[4] 贾鹏宇, 李艳, 郑琼林. 电压型级联系统中减小源变换器输出阻抗的有源阻尼控制方法[J]. 电工技术学报, 2015, 30(8): 71-82.
Jia Pengyu, Li Yan, Zheng Qionglin. An active damping method to reduce output impedance of converters in voltage source cascaded system[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 71-82.
[5] 刘欣博, 高卓. 考虑恒功率负载与储能单元动态特性的直流微电网系统大信号稳定性分析[J]. 电工技术学报, 2019, 34(增刊1): 292-299.
Liu Xinbo, Gao Zhuo. Large signal stability analysis of DC microgrid system considering dynamic characteristics of constant power load and energy storage system[J]. Transactions of China Electro- technical Society, 2019, 34(S1): 292-299.
[6] Middlebrook R D. Input filter considerations in design and application of switching regulators[C]// IEEE IAS Annual Meeting, Chicago, 1976: 366-382.
[7] Cespedes M, Xing Lei, Sun Jian. Constant-power load system stabilization by passive damping[J]. IEEE Transactions on Power Electronics, 2011, 26(7): 1832-1836.
[8] Zhang Xin, Ruan Xinbo, Hyok Kim. Adaptive active capacitor converter for improving stability of cascaded DC power supply system[J]. IEEE Transa- ctions on Power Electronics, 2013, 28(3): 1807-1816.
[9] Cai Wen, Yi Fan, Eva Cosoroaba, et al. Stability optimization method based on virtual resistor and nonunity voltage feedback loop for cascaded DC/DC converters[J]. IEEE Transactions on Industry Appli- cations, 2015, 51(6): 4575-4583.
[10] Wu Mingfei, Dylan Dah-Chuan Lu. A novel stabili- zation method of LC input filter with constant power loads without load performance compromise in DC microgrids[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4552-4562.
[11] Ahmed Aldhaheri, Amirh Etemadi. Stabilization and performance preservation of DC/DC cascaded systems by diminishing output impedance magnitude[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 1481-1489.
[12] Xin Zhang, Zhong Qingchang, Ming Wenlong. Stabilization of cascaded DC/DC converters via adaptive series-virtual-impedance control of the load converter[J]. IEEE Transactions on Power Electro- nics, 2016, 31(9): 6057-6063.
[13] 滕昌鹏, 王玉斌, 周博恺, 等. 含恒功率负载的直流微网大信号稳定性分析[J]. 电工技术学报, 2019, 34(5): 973-982.
Teng Changpeng, Wang Yubin, Zhou Bokai, et al. Large-signal stability analysis of DC microgrid with constant power loads[J]. Transactions of China Elec- trotechnical Society, 2019, 34(5): 973-982.
[14] 庞圣钊, 皇甫宜耿, 郭亮, 等. 基于Lyapunov间接法分析的恒功率负载电源变换器宽稳定控制策略[J]. 电工技术学报, 2017, 32(14): 146-154.
Pang Shengzhao, Huangfu Yigeng, Guo Liang, et al. A novel wide stability control strategy of constant power load power converter based on the analysis of Lyapunvo indirect method[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 146-154.
[15] Huangfu Yigeng, Pang Shengzhao, Guo Liang, et al. Stability analysis and active stabilization of on-board DC power converter system with input filter[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 790-799.
[16] 吴蒙, 贺之渊, 阎发友, 等. 下垂控制对直流电网动态电压稳定性的影响分析[J]. 电力系统保护与控制, 2019, 47(10): 8-15.
Wu Meng, He Zhiyuan, Yan Fayou, et al. Influence of droop control on the dynamic voltage stability of DC grid analysis[J]. Power System Protection and Control, 2019, 47(10): 8-15.
Cascaded DC-DC Converter Stability Control Method Based on Paralleling Virtual Resistor
Abstract Cascaded DC-DC converter structure is a common form of DC distributed power systems. A converter designed individually can operate independently and stably. However, it may cause the instability of the whole system due to the interaction between the source and load converter after cascading. In this paper, a cascaded buck converter is taken as an example. The large-signal model is established by state space average method to analyze the open-loop stability of the cascaded system, and the parallel resistance range that can be stable in the full load range is derived. Then the influence of the resistance on the close-loop output impedance of the source converter is analyzed. Accordingly, an active damping control strategy based on paralleling virtual resistor is proposed to improve the stability of the cascaded system. This strategy can meet the stability requirement of matching the input impedance of the load converter without affecting the closed-loop dynamic of the source converter. The Lyapunov indirect method is used to analyze the stability conditions of the control strategy. The reasonable selection of the paralleling virtual resistor can satisfy the stability of the whole system. Finally, the effectiveness of the proposed control strategy is verified by simulation and experiment.
keywords：Cascaded DC-DC converters, stability analysis, virtual resistor, Lyapunov indirect method
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.190969
国家自然科学基金面上资助项目（51877017）。
收稿日期 2019-07-31
改稿日期 2019-12-09
黄远胜 男，1995年生，硕士研究生，研究方向为DC-DC变换器控制及其稳定性。E-mail: huangys@cqu.edu.cn（通信作者）
刘和平 男，1957年生，教授，博士生导师，研究方向为电力传动及其控制技术。E-mail: engineer@cqu.edu.cn
（编辑 陈 诚）