{A, B, C}，定义见表1。摘要 高铁及城市轨道交通三电平牵引变流器由于受变流器开关损耗的限制，开关频率通常较低（≤1kHz）。当变流器运行于中、高频区域时，载波比的下降会导致变流器输出电压中含有大量的低次谐波，所以需要采用同步调制策略加以抑制，而传统同步空间矢量调制策略仅能保证变流器输出波形的同步性与对称性，并未对输出波形质量进行进一步的优化，导致变流器输出波形依然含有幅值较高的低次谐波。针对这一问题，该文以变流器输出波形同步性、三相对称性、半波对称性为条件，推导得到同步空间矢量调制开关序列设计规则。在此基础上，形成备选开关序列集，并以输出线电压加权总谐波畸变率（WTHD）为评价指标，得到了不同脉冲数下的最优开关序列并形成改进多模式同步空间矢量调制策略。通过仿真与实验分析，验证了所提策略可以有效提升牵引变流器中、高频区输出波形质量。
关键词：三电平变流器 同步调制 空间矢量调制 谐波畸变
相比于两电平变流器，三电平变流器凭借其输出电压谐波含量少、开关器件承受电压应力低等诸多优点，被广泛应用于机车牵引、舰船推进等中高压大功率电机驱动领域[1-3]。然而，由于开关损耗与散热条件的限制，变流器开关频率通常较低（≤1kHz）。而牵引电机输出频率范围为0～200Hz，在整个调速范围内，载波比变化范围大；当牵引电机运行于中、高频区（载波比≤15）时，通常需要采用同步调制策略以保证变流器输出电压的同步性与对称性，抑制谐波畸变，保证牵引传动系统的控制性能[4]。
目前应用较为广泛的同步调制策略主要包括离线谐波优化调制策略[5-10]与同步空间矢量调制策 略[11-15]。离线谐波优化调制策略包括特定谐波消除调制策略[5-8]、电流谐波最小调制策略[9-10]。此类调制策略的基本特征是通过对调制波进行傅里叶分解，获得各次谐波的数学表达式。以此为基础，根据不同的优化目标，采用优化算法离线求解关于开关角的非线性方程。目前，以特定谐波消除调制为代表的离线谐波优化调制策略在轨道交通领域已得到较为广泛的应用，并且已有一些文献[7-8]提出可将特定谐波消除调制或电流谐波最小调制方法在线实现。但由于受微处理器计算能力的制约，可求解开关角个数有限。在大部分实际应用中，仍然需要离线求解，并将开关角以二维查找表（调制度-开关角）形式进行存储。当调制度变化时，需要在不同组开关角间进行切换。由于采用查表法这种离散方式存储，会导致切换时的开关角不连续，进而造成电机磁链与定子电流轨迹不连续[16]。若要实现高性能闭环控制，则需要采用定子磁链轨迹跟踪等较为复杂的控制算法[17-18]。
同步空间矢量调制策略是在传统异步调制的基础上提出的，具有脉冲对称的特点。此类策略通过合理设置参考矢量位置与合成各参考矢量的开关序列，保证变流器输出波形满足同步性、三相对称性、半波对称性等约束条件，从而达到优化谐波、提高变流器输出波形质量的目的[11]。文献[11]首次提出针对两电平变流器的四种同步空间矢量调制策略，即传统空间矢量调制、母线钳位调制、边界采样调制与不对称零矢量调制。文献[12]将上述四种调制策略进行对比分析，选出了不同脉冲数下的最优策略。文献[13]提出两种新型母线钳位调制策略，提升了变流器在高调制度工况下的输出性能。文献[14]将同步调制引入三电平变流器，提出了三电平同步调制开关序列设计规则。文献[15]进一步完善了序列设计规则，实现了同步调制脉冲数连续变化。
文献[19]将同步调制策略与特性谐波消除调制策略进行对比分析，验证了脉冲数较低时，空间矢量调制策略具有更优的输出性能。文献[20]利用DSP+FPGA双核控制器构架实现了多模式同步空间矢量调制策略，提高了算法的实时性与可靠性。
虽然文献[15]中提出的设计规则可以保证脉冲数连续变化，但每一脉冲数仅对应一种开关序列，而实际上，由于三电平变流器空间矢量调制中零矢量与小矢量均对应不止一种开关状态，所以针对某一特定脉冲数，可以设计出多种开关序列；针对三电平变流器的上述特性，本文以同步性与对称性条件为约束，完善三电平变流器同步空间矢量调制开关序列设计规则，构建不同脉冲数下的备选开关序列集，并以输出电压加权总谐波畸变率（Total Harmonic Distortion, THD）为评价指标，得到不同脉冲数下的最优开关序列及改进多模式调制策略，改善了三电平牵引变流器输出波形质量。
三电平变流器同步空间矢量调制的实现包括三个部分：参考矢量分布、基本矢量作用时间计算与开关序列设计。
中点钳位型（Neutral-Point-Clamped, NPC）三电平变流器拓扑结构如图1所示。变流器三相桥臂Sk，k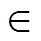{A, B, C}，定义见表1。
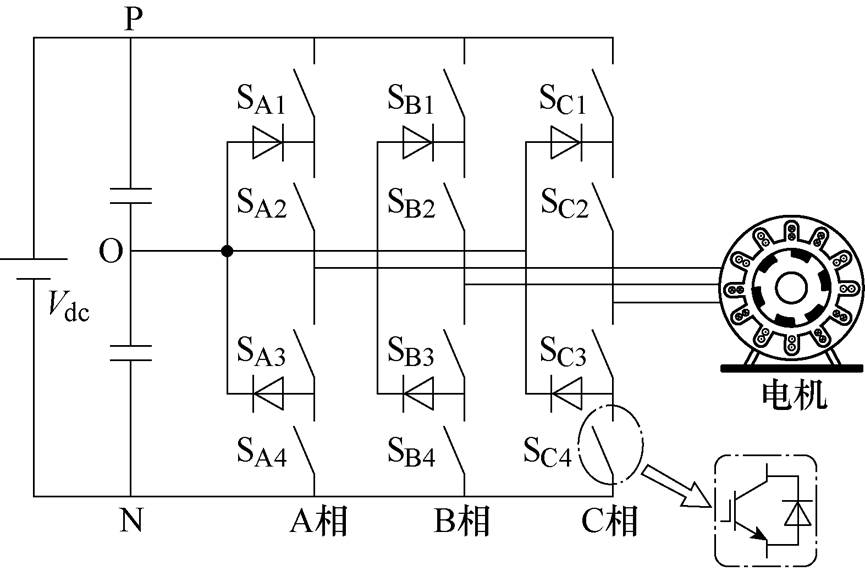
图1 中点钳位型三电平变流器拓扑结构
Fig.1 The topology of neutral-point-clamped three-level inverter
由表1可知，三电平变流器每相具有P、O、N三种开关状态，所以三相共有33=27种开关状态组合，对应的基本电压矢量如图2所示，按照矢量幅值不同可将基本矢量分为零矢量V0、小矢量V1～V6和对应的冗余小矢量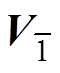
～
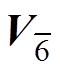（矢量幅值与角度相同，开关状态组合不同）、中矢量V7～V12、大矢量V13～V18。以中矢量为边界，可将空间矢量平面分为
～
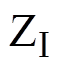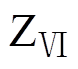6个扇区，每个扇区可进一步分为①～⑥ 6个小三角形。
表1 三相桥臂开关状态定义
Tab.1 The definition of switching state for three phases
开关状态SkSk1Sk2Sk3Sk4相电压vkO P导通导通关断关断Vdc/2 O关断导通导通关断0 N关断关断导通导通-Vdc/2
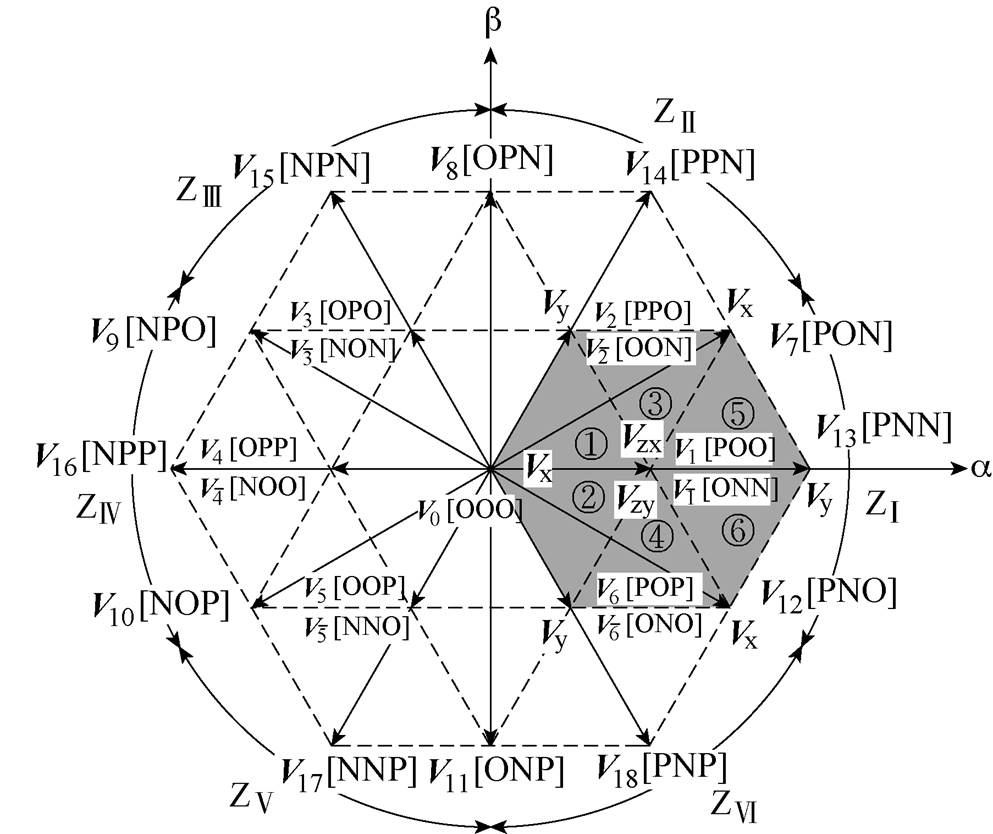
图2 三电平变流器空间矢量
Fig.2 The space vector diagram of three-level inverter
在传统同步空间矢量调制策略中，为保证变流器输出波形满足同步性与对称性条件，参考矢量需要在空间矢量平面内均匀分布，以参考矢量数N=5为例，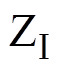
扇区内参考矢量Vr1～Vr5分布方式如图3所示，Vr1位于扇区边界，Vr2～Vr5依次以p/(3N)间隔均匀分布在扇区内。
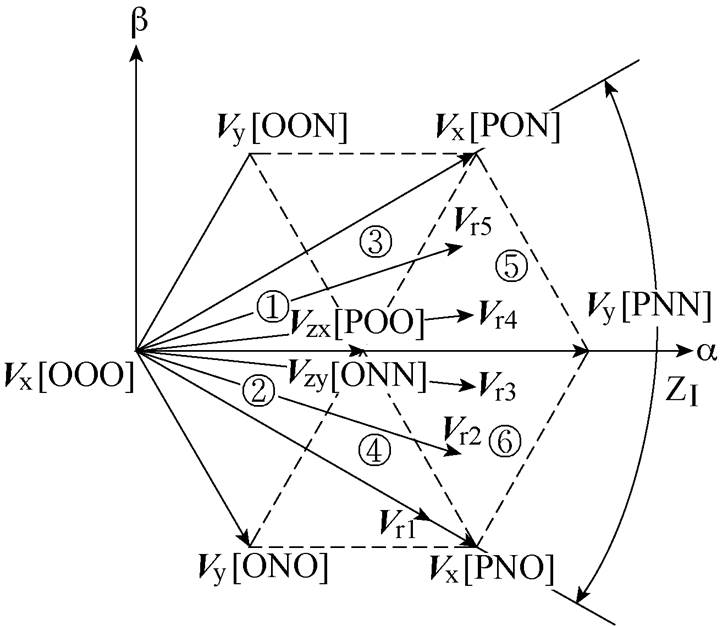
图3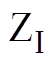 
扇区参考矢量Vr1～Vr5分布方式
Fig.3 The space vector diagram of three-level inverter
为方便开关序列设计，将各扇区内基本矢量进行重新定义。以第一扇区为例，位于扇区中心的小矢量V1[POO]与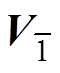[ONN]定义为Vzx与Vzy，将各小区域内与Vzx对应开关状态仅有一相发生变化的基本矢量定义为Vx，与Vzy对应开关状态仅有一相发生变化的基本矢量定义为Vy，如图2所示。三电平变流器空间矢量调制中，参考矢量通常由与其距离最近的三个基本矢量Vx、Vy与Vz合成。根据伏秒平衡原理，可得基本矢量作用时间为
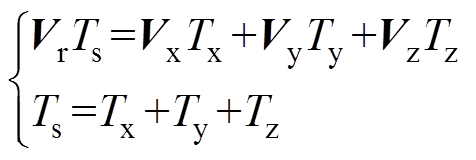（1）式中，Vr为参考矢量；Ts为采样周期；Tx与Ty分别为基本矢量Vx与Vy的作用时间；Tz为基本矢量Vzx与Vzy作用时间之和，通常Vzx与Vzy作用时间均为Tz/2。
同步空间矢量调制要求开关序列必须满足同步性条件
（2）三相对称性（Three Phase Symmetry，TPS）条件
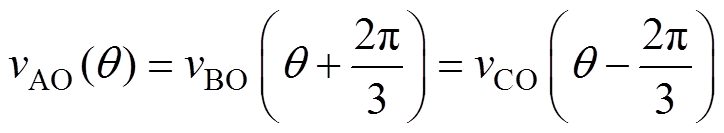（3）
及半波对称性（Half Wave Symmetry, HWS）条件
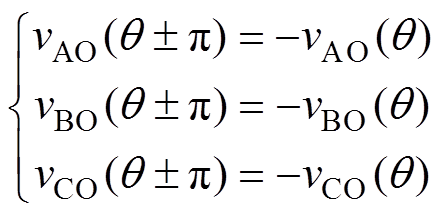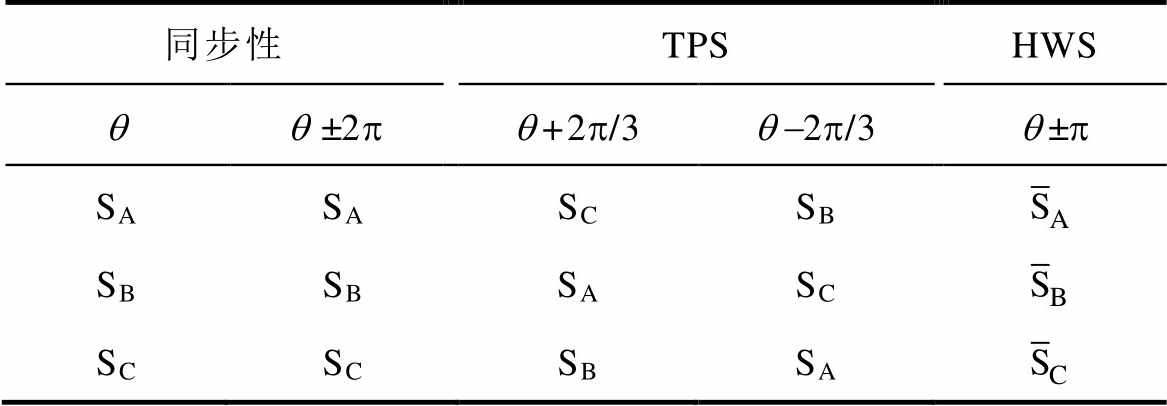
（4）式中，vAO、vBO与vCO为变流器三相输出相电压；q 为任意参考矢量角度。由上述约束条件可得同步调制开关序列作用下变流器三相开关状态需满足表2，其中，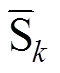
表示Sk的互补状态（P与N为互补状态，O的互补状态仍为O）。
表2 同步性与对称性条件约束下变流器开关状态
Tab.2 Conditions of synchronization and symmetry in terms of inverters states
同步性TPSHWS qq ±2pq+2p/3q-2p/3q±p SASASCSB SBSBSASC SCSCSBSA
以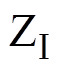扇区为例，满足表2的传统三电平同步空间矢量调制策略对应开关序列有三类。
类型1：每一扇区的第一个参考矢量对应开关状态为Vy→Vx→Vzx，其余参考矢量对应开关序列为Vzx↔Vx↔Vy↔Vzy，前一扇区第N个采样周期的最后一个开关状态Vzy为后一扇区第一个采样周期的第一个开关状态Vy，所以扇区切换时没有开关动作。一个基波周期内的脉冲数P=(3N-1)/2。
类型2：所有参考矢量对应开关序列均为Vzx↔ Vx↔Vy↔Vzy，前一扇区第N个采样周期的终止开关状态为Vzy，下一扇区第一个采样周期的起始开关状态为Vzx，所以扇区切换时会有额外一次开关动作。一个基波周期内的脉冲数为P=(3N+1)/2。
类型3：每一扇区的第一个参考矢量对应开关状态对Vx→Vy→Vx→Vzx，最后一个参考矢量对应开关状态为Vzx→Vx→Vy→Vx，其余参考矢量对应开关序列为Vzx↔Vx↔Vy↔Vzy，在扇区切换时，有一相开关状态变换两次，其余两相没有开关动作。一个基波周期内的脉冲数P=3N/2。
分析传统同步空间矢量调制三类开关序列可知，对应于特定脉冲数，传统同步空间矢量调制有且仅有一种开关序列。虽然变流器输出电压波形满足同步性与对称性要求，但低次谐波含量依然较高。
由图2可知，三电平变流器空间矢量图中零矢量与小矢量对应的开关状态并不唯一，通过合理制定设计规则，可以得到不同脉冲数条件下，满足同步性与对称性约束的若干开关序列。
根据表2所示同步性、三相对称性与半波对称性条件，可得如下设计规则：
规则1：关于a 轴对称分布的两参考矢量，其开关序列互为反向排列关系。
规则2：在合成参考矢量的开关序列中，基本矢量切换原则需遵循表3。
表3 基本矢量切换原则
Tab.3 Transition principle of basic space vectors
当前基本矢量下一基本矢量 VxVy或Vzx VyVx或Vzy VzxVx VzyVy
规则3：合成当前参考矢量的终止开关状态与合成下一参考矢量的起始开关状态一致。
规则4：用于相邻两个三角形间切换的开关状态，应在两个三角形公共开关状态中选取。
以N=5为例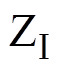，扇区内，参考矢量Vr1～Vr5依次分布于三角形④→⑥→⑥→⑤→⑤，如图3所示。将各扇区中第一个参考矢量定义为首矢量，最后一个参考矢量定义为尾矢量。N=5时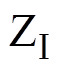扇区开关序列设计步骤如图4所示。
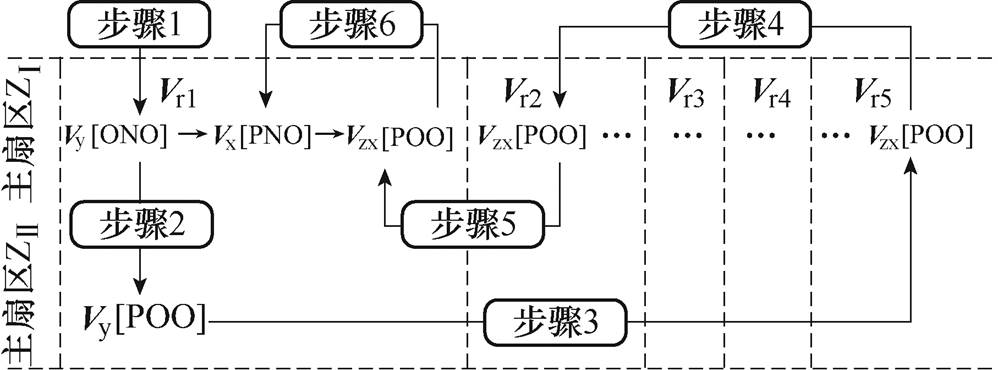
图4 N=5时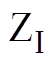扇区开关序列设计步骤
Fig.4 The procedure of designing switching sequences
按照上述设计规则1～4确定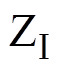扇区内各参考矢量对应的开关序列：
步骤1：确定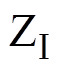扇区中合成首矢量的起始开关状态与合成尾矢量的终止开关状态。
根据规则4可知，合成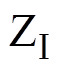扇区中首矢量的起始开关状态为Vy[ONO]，如图4中步骤1所示，合成
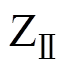扇区中首矢量的起始开关状态为Vy[POO]，如图4中步骤2所示。
根据规则3可知，合成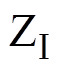扇区内尾矢量的终止开关状态为Vzx[POO]，如图4中步骤3所示。
步骤2：确定合成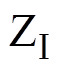中首矢量Vr1的作用序列。
根据规则1可知，Vr2的起始开关状态与Vr5的终止开关状态相同，为Vzx[POO]，如图4中步骤4所示。
根据规则3可知，首矢量Vr1的终止状态为Vzx[POO]，如图4中步骤5所示。
根据规则2可知，合成首矢量Vr1的序列为Vy[ONO]→Vx[PNO]→Vzx[POO]，如图4中步骤6所示。
步骤3：确定合成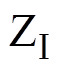扇区中参考矢量Vr2～Vr5的开关序列。
根据规则1～4，确定Vr2～Vr5对应的合成方式，进而得到N=5时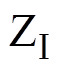，扇区中所有满足同步性、TPS与HWS的开关序列，见表4。
以N=5为例，各脉冲数下最优开关序列按照脉冲数P不同，可以分为三类，其中序列1对应脉冲数P=5；序列2与序列3对应脉冲数P=6；序列4～8对应脉冲数P=7。
表4 N=5，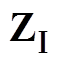
扇区内备选开关序列集
Tab.4 Switching sequences for sector 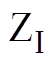with N=5
序列号开关序列脉冲数P 1VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx5 2VyVxVzx→VzxVxVy→VyVxVyVzy→VzyVyVxVy→VyVxVzx6 3VyVxVzx→VzxVxVyVx→VxVyVzy→VzyVyVx→VxVyVxVzx6 4VyVxVzx→VzxVxVyVx→VxVyVzyVy→VyVzyVyVx→VxVyVxVzx7 5VyVxVzx→VzxVxVyVx→VxVyVxVzx→VzxVxVyVx→VxVyVxVzx7 6VyVxVzx→VzxVxVyVx→VxVzxVxVy→VyVxVzxVx→VxVyVxVzx7 7VyVxVzx→VzxVxVyVzy→VzyVyVxVzx→VzxVxVyVzy→VzyVyVxVzx7 8VyVxVzx→VzxVxVyVzy→VzyVyVxVy→VyVxVyVzy→VzyVyVxVzx7
一般通常以输出电压总谐波畸变率VTHD与输出电压加权总谐波畸变率（Weighted Total Harmonic Distortion, WTHD）VWTHD作为变流器输出波形质量的评价指标，定义为
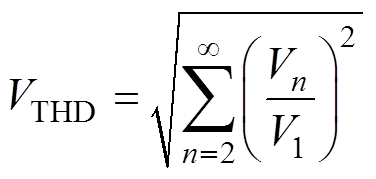（5）
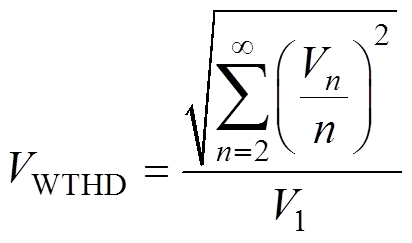（6）
式中，V1与Vn分别为线电压基波与n次谐波幅值。Vn表达式为
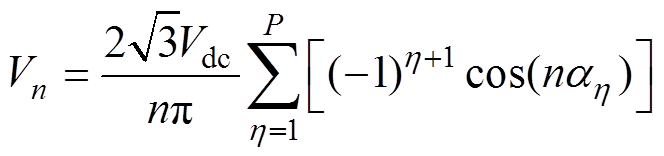（7）式中，ah（h =1, 2, …, P）为开关角。将式（7）代入式（6）可得序列1～8作用下变流器输出电压总谐波畸变率VTHD与输出电压加权总谐波畸变率VWTHD随调制度变化曲线，如图5所示。
从VTHD随调制度变化曲线可得，序列1～8作用下，变流器输出电压总谐波畸变率十分相近。分析VWTHD随调制度变化曲线，可以认为不同序列在总谐波畸变率不变的前提下改变了各次谐波含量的分布。某些序列可以有效抑制低次谐波，降低加权总谐波畸变率。从图5可以看出，当脉冲数P=5时，仅有序列1；脉冲数P=6时，序列2作用下VWTHD最小；脉冲数P=7时，序列5作用下VWTHD最小。由此可得，N=5时，各脉冲数下的最优开关序列见表5。
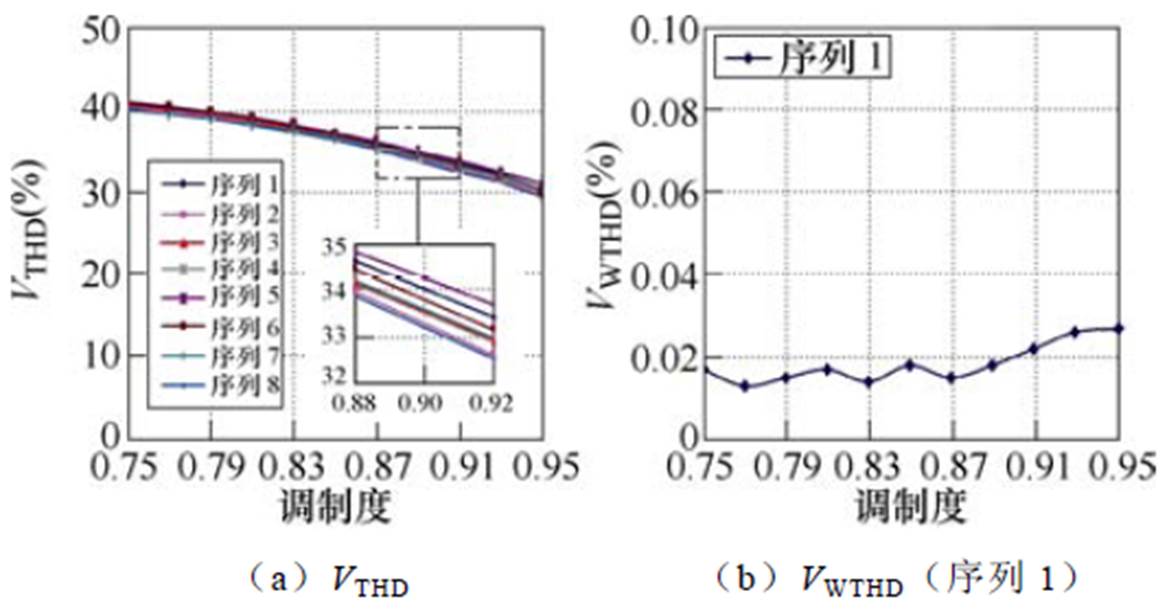
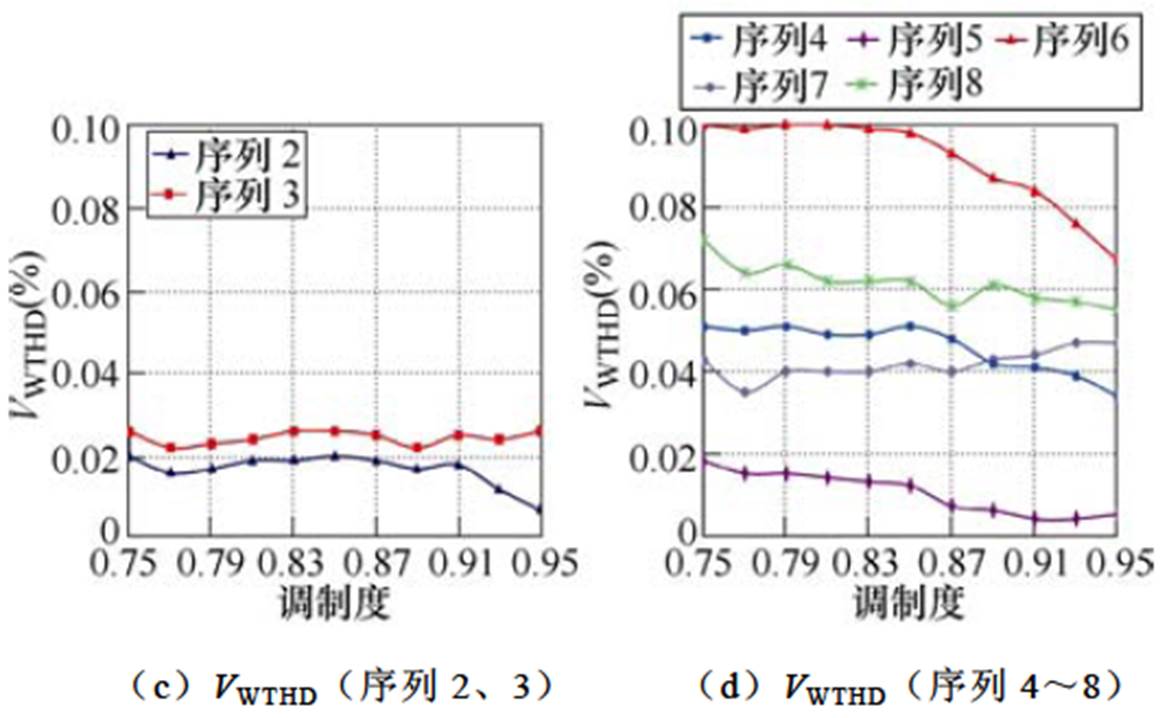
图5 序列1～8作用下变流器输出电压VTHD与VWTHD随调制度变化曲线
Fig.5 Variations of VWTHD and VTHD versus m for sequence 1～8
表5 N=5，各脉冲数下最优开关序列
Tab.5 The optimal switching sequence for N=5 with different P
序列号开关序列脉冲数P 1VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx5 2VyVxVzx→VzxVxVy→VyVxVyVzy→VzyVyVxVy→VyVxVzx6 3VyVxVzx→VzxVxVyVx→VxVyVxVzx→VzxVxVyVx→VxVyVxVzx7
图6所示为脉冲数P=7工况下，传统序列与最优序列作用时，变流器输出电流轨迹（两相静止坐标系下）。可以看出，与传统序列相比，最优序列作用下，变流器输出电流轨迹更接近于圆。说明最优序列作用下，变流器输出电流波动幅值小于传统序列。
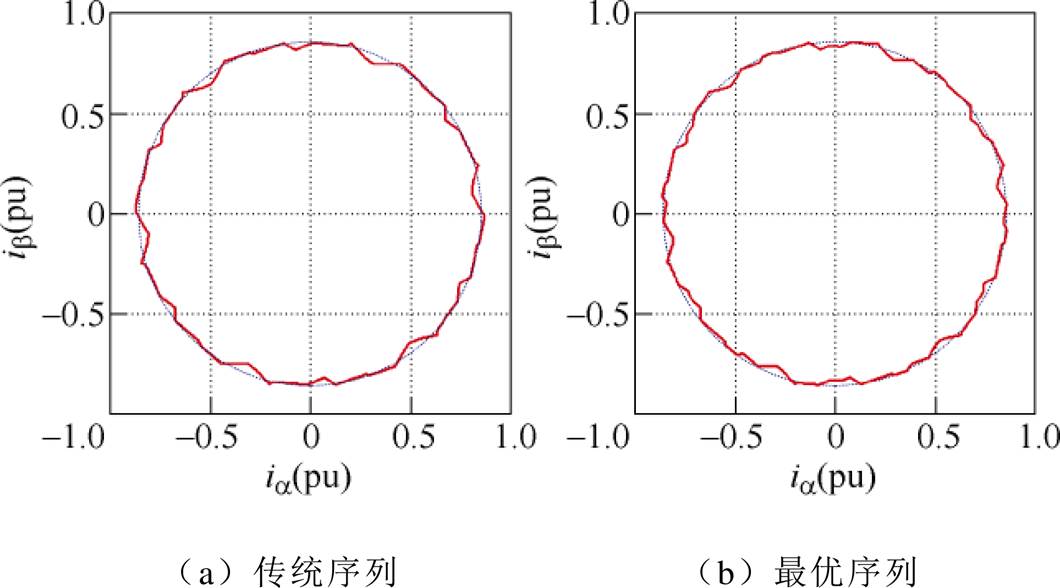
图6 脉冲数P=7工况下变流器输出电流轨迹（ab 坐标系）
Fig.6 Trajectory of current waveforms of the inverter under the condition of P=7 (in ab coordinate system)
图7所示为轨道交通牵引传动系统典型多模式分段同步调制作用下变流器开关频率随基波频率与调制度变化曲线。按照第2节中序列设计原则，可得不同脉冲数（P=15, 13, 11, 9, 7, 5）对应的备选开关序列集，并通过比较不同开关序列作用下输出电压VWTHD选出不同脉冲数下的最优开关序列，见表6。需要说明的是，同一脉冲数工况下，不同调制度区间内对应的最优序列可能会发生变化。因此，当系统参数发生变化时，表6所示的最优开关序列可能会发生变化。此时，需根据变流器输出基波频率与调制度的对应关系重新进行最优开关序列的选择。
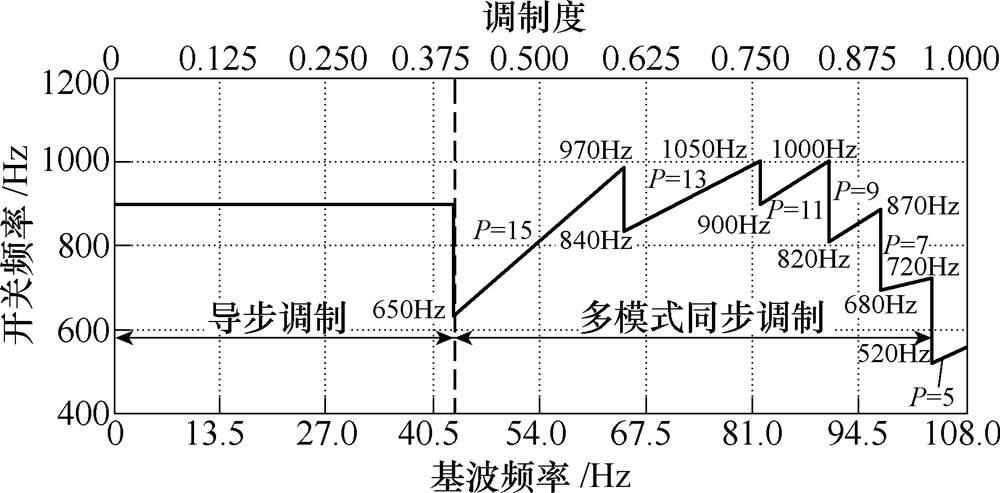
图7 变流器开关频率随基波频率与调制度变化曲线
Fig.7 Variations of switching frequency versus fundamental frequency for traction inverter
表6 不同脉冲数下最优开关序列
Tab.6 The optimal switching sequence with different P
脉冲数P最优序列 5VzxVxVy→VyVxVzxVx→VxVzxVx→VxVzxVxVy 7VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx 9VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzxVx→VxVzxVx →VxVzxVxVy 11VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx 13VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzxVx→VxVzxVx→VxVzxVxVy 15VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx→VzxVxVy→VyVxVzx
采用表6所示的最优序列可形成改进多模式同步调制策略，由第3节中分析可知，改进调制策略作用下变流器输出波形质量优于传统调制策略。
为验证本文所提改进多模式同步调制策略的有效性与可行性，采用德国dSPACE®公司快速原型开发系统DS1007作为控制电路，德国Infineon®公司IGBT模块F3L75R07W2E3_B11作为功率电路，构成三电平变流器实验系统样机，如图8所示。
图8 dSAPCE® DS1007驱动三电平变流器实验样机
Fig.8 The prototype of dSPACE® DS1007 driven three-level inverter
采用上述实验系统，在不同脉冲数工况下，对传统同步空间矢量调制开关序列与本文提出的最优开关序列进行实验对比，实验系统参数见表7。
表7 实验系统参数
Tab.7 Experimental parameters of the prototype
参 数数 值 直流电容C1, C2/mF2 000 直流电压Vdc/V100 死区时间td/ns600 负载电阻R/W10 负载电感L/mH40 额定频率f/Hz108
图9～图11所示分别为不同脉冲数（P=15, 11, 5）工况下，同步空间矢量调制传统序列与最优序列作用下变流器输出线电压vAB与电流iA波形。
由于变流器输出电流直接与系统损耗和转矩波动有关，所以在实验数据处理过程中采用电流总谐波畸变率ITHD作为变流器输出波形质量评价指标，定义为
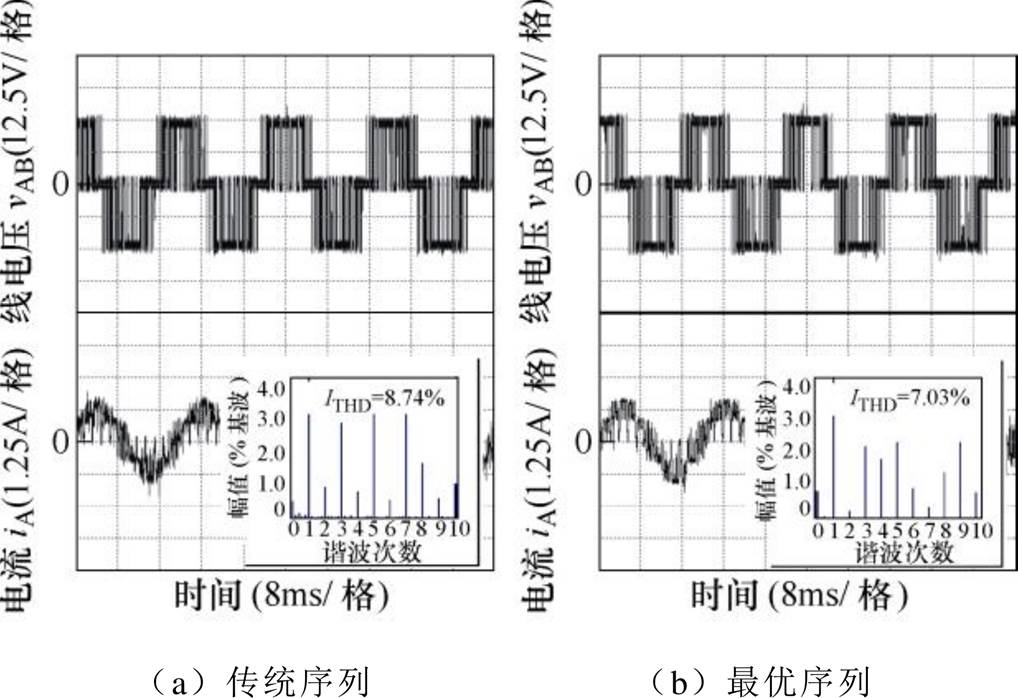
图9 脉冲数P=15工况下变流器输出电压与电流波形
Fig.9 Line-voltage and current waveforms of the inverter under the condition of P=15
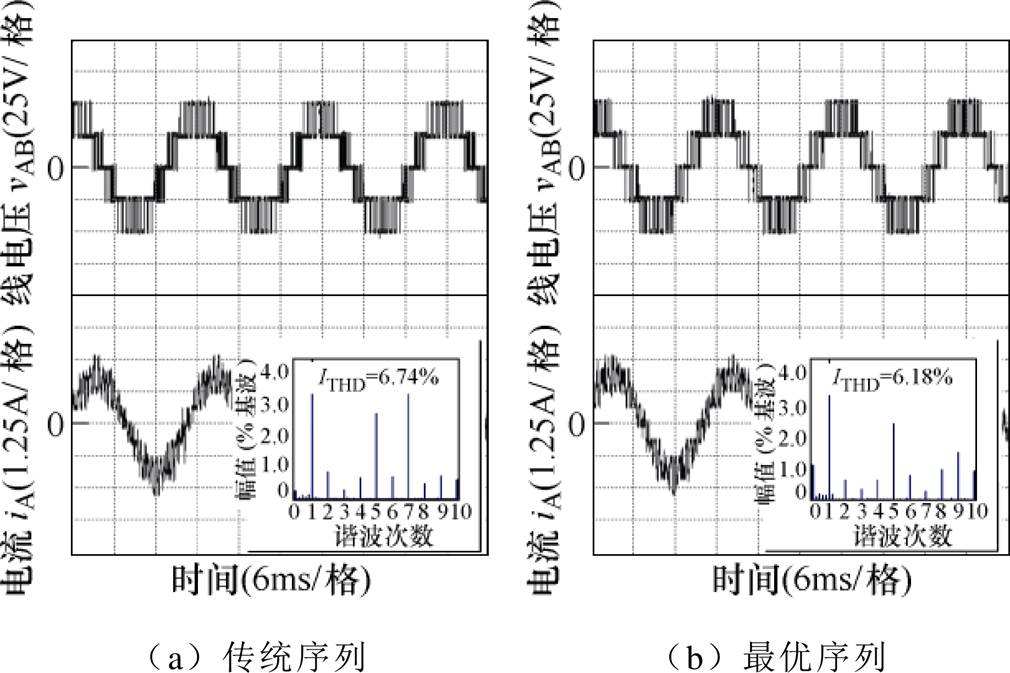
图10 脉冲数P=11工况下变流器输出电压与电流波形
Fig.10 Line-voltage and current waveforms of the inverter under the condition of P=11
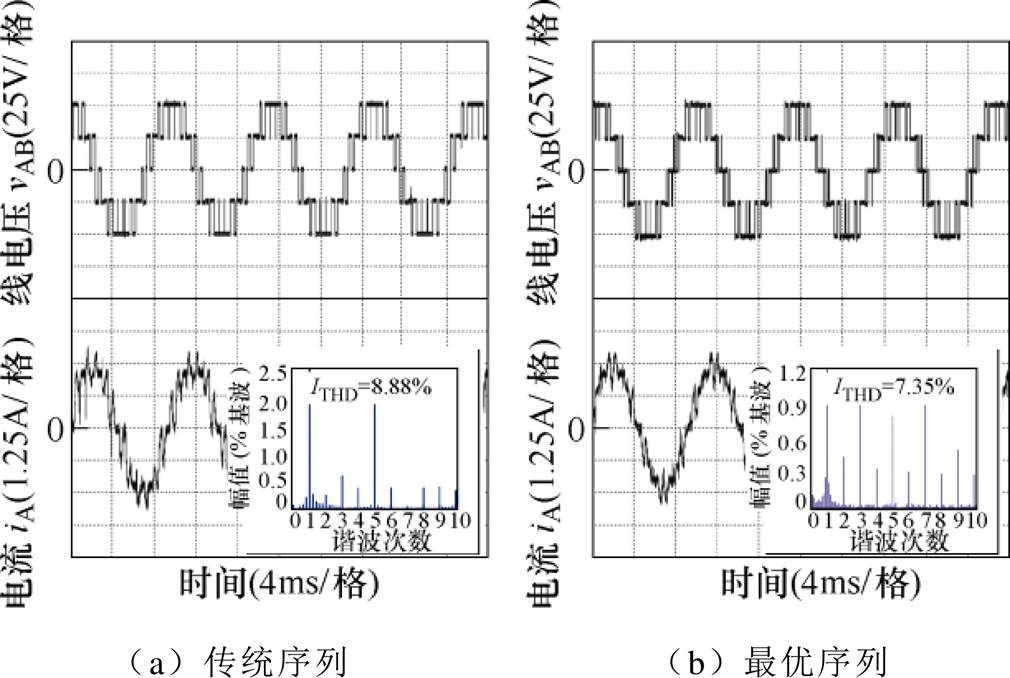
图11 脉冲数P=5工况下变流器输出电压与电流波形
Fig.11 Line-voltage and current waveforms of the inverter under the condition of P=5
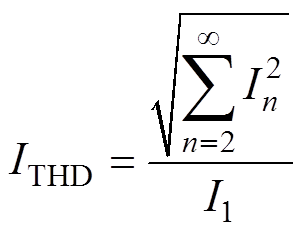（8）式中，I1和In分别为输出电流的基波分量和n次谐波分量的有效值。
由图9～图11可以看出，最优序列作用下变流器输出电流总谐波畸变率ITHD低于传统序列，说明最优序列作用下变流器输出波形质量更优。
图12所示为不同脉冲数下的传统序列与最优序列形成的传统多模式同步调制策略与改进多模式同步调制策略作用下变流器输出电流ITHD随调制度变化曲线。可以看出，在任意脉冲数工况下，改进策略作用下变流器输出波形质量均优于传统策略，验证了本文提出的改进策略的有效性。
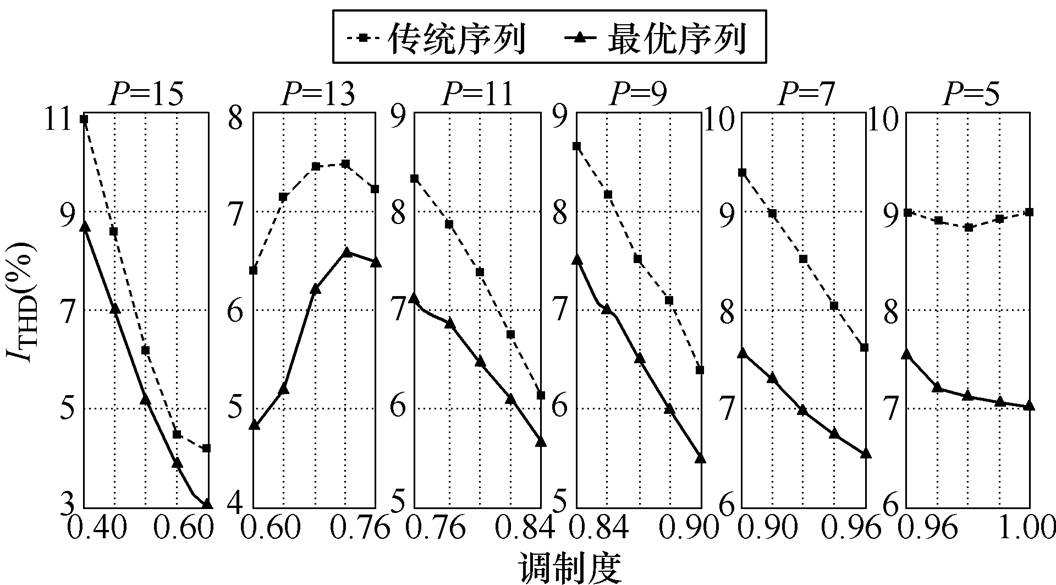
图12 改进多模式同步调制策略作用下变流器输出电流ITHD随调制度变化曲线
Fig.12 Variations of ITHD versus modulation index for improved multi-mode synchronized modulation strategy
此外，需要指出的是，为实现平滑切换，需保证不同脉冲数下开关序列切换前后的三相开关状态无开关动作且基波相位无突变。因此，本文以切换前后A相开关序列开关状态保持不变为原则，确定A相切换点。B相滞后A相2p/3进行切换，C相滞后B相2p/3进行切换，因此B、C两相切换时也不存在开关状态跳变，并保证在一个基波周期内完成脉冲数切换[21]。图13所示为本文提出的多模式同步空间矢量调制策略作用下变流器输出电压与电流波动，可以看出，脉冲数发生切换时不存在电流突变。
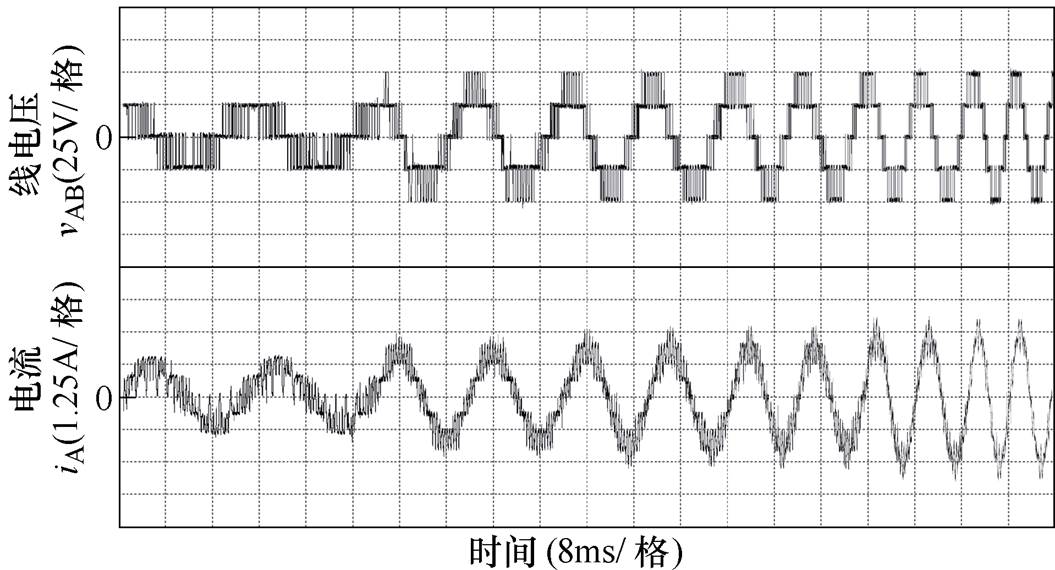
图13 脉冲数切换工况下变流器输出电压与电流波形
Fig.13 Line-voltage and current waveforms of the multi-mode modulation strategy
本文针对传统三电平同步空间矢量调制策略作用下变流器输出谐波含量较高的问题，以同步性与对称性为约束条件，得到同步开关序列设计规则；以此为基础，构成不同脉冲数下的备选开关序列集；以变流器输出电压VWTHD为评价指标选出最优序列并形成改进多模式同步空间矢量调制策略。实验结果验证了本文所提改进策略作用下变流器输出波形质量优于传统策略。
参考文献
[1] 史婷娜, 刘潮, 张国政, 等. 三电平逆变器综合性能优化不连续空间矢量调制策略[J]. 电工技术学报, 2018, 33(24): 5874-5883.
Shi Tingna, Liu Chao, Zhang Guozheng, et al. Discontinuous space vector PWM for three-level inverter with comprehensive performance optimi- zation[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5874-5883.
[2] 谷鑫, 刘潮, 张国政, 等. 三电平逆变器同步不连续空间矢量调制输出电流优化策略[J]. 电工技术学报, 2019, 34(5): 924-933.
Gu Xin, Liu Chao, Zhang Guozheng, et al. Space- vector based synchronous discontinuous PWM for three-level inverter with output current optimi- zation[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 924-933.
[3] 夏长亮, 张天一, 周湛清, 等. 结合开关表的三电平逆变器永磁同步电机模型预测转矩控制[J]. 电工技术学报, 2016, 31(20): 83-92.
Xia Changliang, Zhang Tianyi, Zhou Zhanqing, et al. Model predictive torque control with switching table for neutral point clamped three-level inverter-fed permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(20): 83-92.
[4] 陈炜, 陈玉健, 耿强. 基于改进混合粒子群优化的特定谐波消除脉宽调制策略[J]. 天津大学学报: 自然科学与工程技术版, 2016, 49(5): 498-505.
Chen Wei, Chen Yujian, Geng Qiang. Selective harmonic elimination pulse width modulation based on improved hybrid particle swarm optimization[J]. Journal of Tianjin University: Science and Techno- logy, 2016, 49(5): 498-505.
[5] 谷鑫, 姜勃, 耿强, 等. 基于3次谐波控制及脉冲波动分析的三电平SHE-PWM调制优化策略[J]. 电工技术学报, 2015, 30(7): 88-96.
Gu Xin, Jiang Bo, Geng Qiang, et al. An optimal SHE-PWM modulation strategy for three-level NPC converter based on third harmonic control and pulse fluctuation analysis[J]. Transactions of China Elec- trotechnical Society, 2015, 30(7): 88-96.
[6] 张志刚, 黄守道, 胡存刚, 等. 三电平SHEPWM与SVPWM混合控制策略及其矢量平滑切换方法的研究[J]. 电工技术学报, 2015, 30(14): 342-349.
Zhang Zhigang, Huang Shoudao, Hu Cungang, et al. Hybrid method of three-level SHEPWM and SVPWM and its vector smooth-switching[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 342-349.
[7] Balasubramonian M, Rajamani V. Design and real- time implementation of SHEPWM in single-phase inverter using generalized hopfield neural network[J]. IEEE Transactions on Industrial Electronic, 2014, 61(11): 6327-6336.
[8] Memona M A, Mekhilefa S, Mubina M, et al. Selective harmonic elimination in inverters using bio-inspired intelligent algorithms for renewable energy conversion applications: a review[J]. Rene- wable and Sustainable Energy Reviews, 2018, 82(3): 2235-2253.
[9] 张钢, 董侃, 刁利军, 等. 大功率牵引逆变器的中频区调制算法对比研究[J]. 电工技术学报, 2016, 31(增刊2): 1-9.
Zhang Gang, Dong Kan, Diao Lijun, et al. A comparative study of the modulation algorithm in middle frquency region for high power traction inverter[J]. Transactions of China Electrotechnical Society, 2016, 31(S2): 1-9.
[10] 董侃. 基于电流谐波优化的混合脉宽调制策略[J]. 电工技术学报, 2017, 32(20): 179-188.
Dong Kan. Hybrid pulse width modulation strategy based on current harmonic minimum technique[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 179-188.
[11] Narayanan G, Ranganathan V T. Synchronised PWM strategies based on space vector approach. part 1: principles of waveform generation[J]. IET Electrical Power Applications, 1999, 146(3): 267-275.
[12] Narayanan G, Ranganathan V T. Synchronised PWM strategies based on space vector approach. part 2: performance assessment and application to V/f drives[J]. IET Electrical Power Applications, 1999, 146(3): 276-281.
[13] Narayanan G, Ranganathan V T. Two novel synchro- nized bus-clamping PWM strategies based on space vector approach for high power drives[J]. IEEE Transactions on Power Electronics, 2002, 17(1): 84-93.
[14] Beig A R, Narayanan G, Ranganathan V T. Modified SVPWM algorithm for three level VSI with synchro- nized waveforms[J]. IEEE Transactions on Industrial Electronics, 2007, 54(1): 486-494.
[15] Beig A R. Synchronized SVPWM algorithm for the overmodulation region of a low switching frequency medium-voltage three-level VSI[J]. IEEE Transa- ctions on Industrial Electronics, 2012, 59(12): 4545- 4554.
[16] Yang Haitao, Zhang Yongchang, Yuan Guofeng, et al. Hybrid synchronized PWM schemes for closed- loop current control of high-power motor drives[J]. IEEE Transactions on Industrial Electronic, 2017, 64(9): 6920-6929.
[17] Akshay K R, Holtz J, Boller T. Synchronous optimal pulsewidth modulation for low-switching-frequency control of medium-voltage multilevel inverters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(7): 2374-2381.
[18] Holtz J, Xin Qi. Optimal control of medium-voltage drives-an overview[J]. IEEE Transactions on Indu- strial Electronics, 2013, 60(12): 5472-5481.
[19] 王堃, 游小杰, 王琛琛, 等. 低开关频率下SHEPWM和SVPWM同步调制策略比较研究[J]. 电工技术学报, 2015, 30(14): 333-341.
Wang Kun, You Xiaojie, Wang Chenchen, et al. Research on the comparison of synchronized modu- lation of SHEPWM and SVPWM under low switching frequency[J]. Transactions of China Elec- trotechnical Society, 2015, 30(14): 333-341.
[20] 吴瑕杰, 宋文胜, 冯晓云. 一种在线计算多模式空间矢量调制算法及其FPGA实现[J]. 电工技术学报, 2016, 31(18): 124-133.
Wu Xiajie, Song Wensheng, Feng Xiaoyun. An on-line calculation multi-mode SVPWM algorithm and implementation based on FPGA[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 124-133.
[21] 孙大南. 地铁车辆牵引电传动系统控制关键技术研究[D]. 北京: 北京交通大学, 2012.
An Improve Synchronized Space Vector Modulation Strategy for Three-Level Inverter
Abstract Due to the limitation of switching loss, the switching frequency of three-level traction inverter for high-speed railway and urban railway is usually low than 1kHz. If the inverter is operated in the medium and high frequency regions, the decrease of carrier ratio will lead to the increase of low-order harmonics in the output voltage, so synchronous modulation strategy should be adopted. The conventional strategy can only guarantee the synchronization and symmetry of the output waveform, and fails to further optimize the quality of the output waveform. As a result, the amplitudes of low-order harmonics in the output waveform are still high. The design rules of switching sequence for the synchronous space vector modulation (SVM) were deduced according to the restriction of synchronization, three-phase symmetry, half-wave symmetry and quarter-cycle symmetry. Then an alternative switching sequence set was established, and the optimal switching sequence was obtained by evaluating the weighted total harmonic distortion. Simulation and experimental results show that the proposed strategy can effectively improve the output waveform quality of traction inverter.
keywords：Three-level inverter, synchronous modulation, space vector modulation (SVM), harmonic distortion
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.190966
国家自然科学基金（51807140，51907142）和天津市自然科学基金（19JCYBJC21800）资助项目。
收稿日期2019-07-28
改稿日期 2019-12-14
张国政 男，1985年生，博士，讲师，研究方向为大功率变流系统及其控制。E-mail: zhanggz@tju.edu.cn
周湛清 男，1989年生，博士，讲师，研究方向为永磁电机系统及其控制。E-mail: zhzhq@tju.edu.cn（通信作者）
（编辑 崔文静）