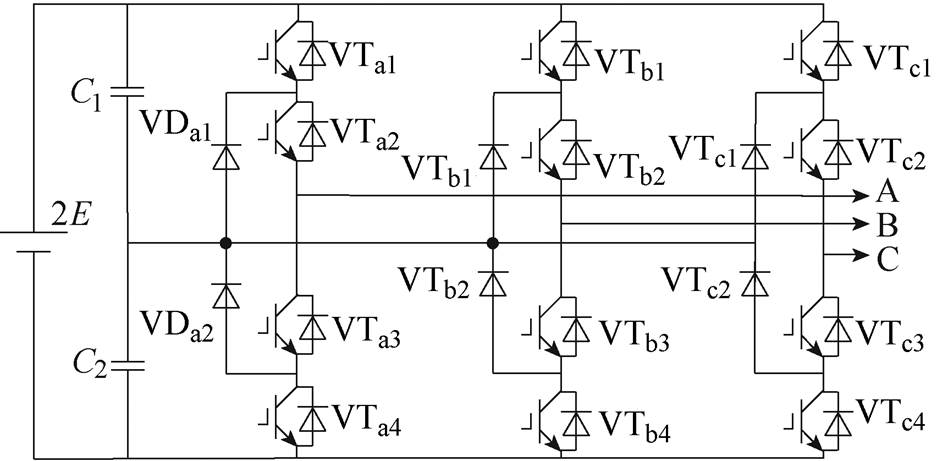
图1 三电平NPC变流器主电路拓扑
Fig.1 Topology of three-level NPC converter
摘要 当三电平变流器应用于大功率电机的牵引传动系统时，为优化谐波性能，通常在低载波比段使用同步调制。传统同步载波脉宽调制（SCBPWM）计算简单，但其只能在3的奇数倍载波比下使得输出电压波形满足三相对称和半波对称，且其无法进入方波。针对SCBPWM存在的缺陷，该文首先研究两类SVPWM开关序列在不同载波比下的相电压波形，并根据不同的波形特性基于调制波等效提出改进型SCBPWM（ISCBPWM），其可分别在3的奇数倍和偶数倍载波比下实现同步调制。通过在线计算功率器件动作的开关角，使得ISCBPWM可进入方波。在此基础上分析ISCBPWM的性能并设计基于ISCBPWM的全速度范围调制策略。最后仿真和实验结果表明，ISCBPWM相比传统SCBPWM，适用的载波比段更多、直流电压利用率更高。其可以在3的任意整数倍载波比下实现同步调制并可进入方波，其计算简单、实现方便。
关键词：三电平 同步调制 载波脉宽调制 方波 低载波比
高压大功率电机牵引传动系统在整个调速范围内具有载波比变化范围较大的特点[1-2]。针对变化范围较大的载波比，通常在高载波比下采用异步调制，此时由波形不对称性产生的不良影响较小；而在低载波比下（半个基波周期内的脉冲数小于15时），为充分利用开关频率并降低输出电流的谐波含量，需根据载波比的变化采用分段同步调制并最终过渡至方波运行[3-4]。高压大功率电机牵引传动系统大部分速度区域为低载波比工况，因此选择高性能的同步调制策略对牵引传动系统至关重要。
在高压大功率电机牵引传动系统中，三电平中点钳位（Neutral Point Clamped, NPC）变流器因其拓扑结构简单、可靠性较高，且易采用背靠背结构实现能量回馈的优点而得到了广泛应用，并在3kV及以下电压的高压大功率电机驱动领域占有优势地位[5-6]。
目前三电平NPC变流器常用同步调制策略有三种：特定谐波消除脉宽调制（Selected Harmonic Elimination PWM, SHEPWM）、同步空间矢量脉宽调制（Synchronized Space Vector PWM, SSVPWM）和同步载波脉宽调制（Synchronized Carrier Based PWM, SCBPWM）[7-20]。
针对SHEPWM，按照特定开关角动作，不仅能实现对基波电压的精确控制，还能实现对特定低次谐波的消除[7-9]。但SHEPWM需通过求解超越方程来得到开关角，较难实现实时计算，且不同调制比对应的开关角不同，当调制比变化时，SHEPWM的动态性能较差[6,10]。
针对SSVPWM，以满足输出电压波形的对称性为原则进行开关序列设计[11-16]。文献[12]分析了两电平下对称SVPWM脉冲生成规律，并总结了五种SSVPWM算法。文献[13-14]总结了三电平任意整数载波比下输出电压满足同步、三相对称（Three Phase Symmetry, TPS）、半波对称（Half Waveform Symmetry, HWS）和四分之一周期对称的脉冲发生规律，从而实现任意整数载波比下的SSVPWM。文献[15]指出在某些区段不满足四分之一周期对称约束的SSVPWM具有更低的线电压加权总谐波畸变值。以上SSVPWM的实现均需在固定采样点处计算各空间矢量的作用角度，运算量较大。
针对SCBPWM，利用调制波与载波比较得到各器件的PWM信号。相比SHEPWM，SCBPWM不根据离线计算的开关角动作，动态性能更好；相比SSVPWM，SCBPWM无需计算空间矢量的作用角度，工程实现更为简单[17-18]。但传统SCBPWM只能在载波比为3的奇数倍时才能使得输出电压波形同时满足TPS和HWS[14,19]，其无法进入方波运行且其直流电压利用率仅为86%[8]。以上缺陷限制了SCBPWM在大功率电机牵引传动系统中的应用。因此研究可在更多载波比段满足同步调制并可进入方波运行的SCBPWM，具有实际的工程应用价值。
本文首先分析了传统SCBPWM的原理及缺陷，然后根据两类SVPWM开关序列在不同载波比下的波形特性提出改进型SCBPWM（Improved SCBPWM, ISCBPWM），其可以在3的任意整数倍载波比下实现同步调制。通过在线计算功率器件动作的角度，使得ISCBPWM可进入方波。在此基础上分析了ISCBPWM的性能并设计了基于ISCBPWM的全速度范围调制策略。最后仿真和实验结果表明，相比传统SCBPWM，ISCBPWM适用的载波比段更多、直流电压利用率更高，并可在3的任意整数倍载波比下实现满足TPS和HWS的同步调制，可进入方波，计算简单、实现方便。
三电平NPC变流器的主电路拓扑如图1所示。通过控制各功率器件的通断，三电平NPC变流器每相可输出P、O、N三种不同的电平状态。以A相为例，P电平对应VTa1和VTa2导通、VTa3和VTa4关断；N电平对应VTa3和VTa4导通、VTa1和VTa2关断；O电平对应VTa2和VTa3导通、VTa1和VTa4关断。
图1 三电平NPC变流器主电路拓扑
Fig.1 Topology of three-level NPC converter
三电平NPC变流器脉宽调制策略的关键在于正确得到各功率器件的开关信号。传统SCBPWM利用三相正弦波与同相层叠的三角载波进行比较，并根据比较结果直接得到各功率器件的开关信号，SCBPWM的原理波形如图2所示。
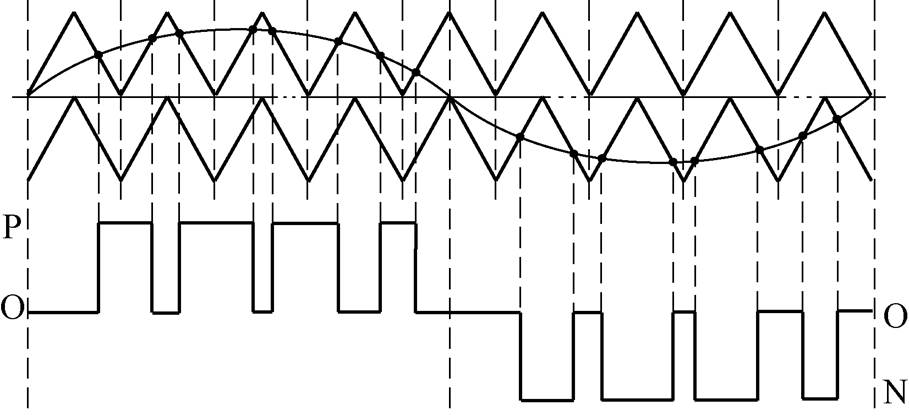
图2 SCBPWM的原理波形
Fig.2 Principle waveforms of SCBPWM
SCBPWM作用下的相电压波形为周期性开关波形，故可利用双重傅里叶级数对SCBPWM作用下的相电压谐波特性进行分析[17]，结果为
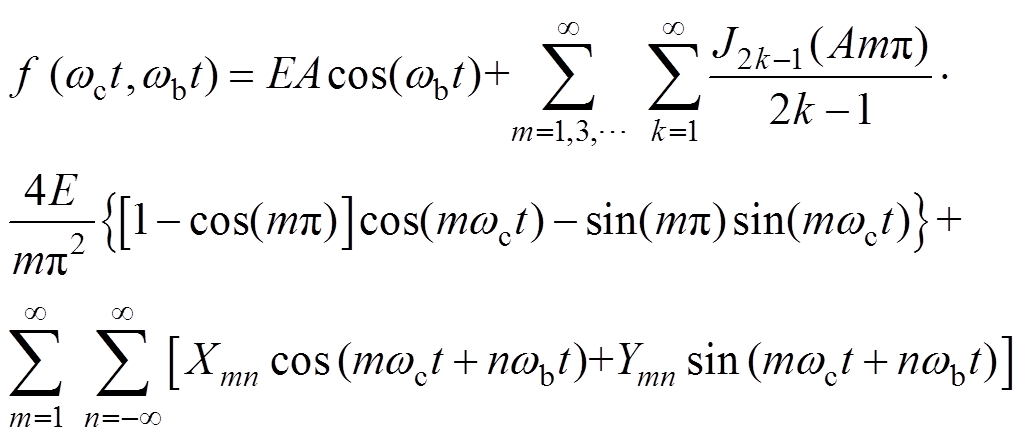（1）式中，m和n分别为载波和基波倍频次数；wc和wb分别为各自载波和基波角频率；E为直流电压值的二分之一；A为正弦波标幺后幅值；Xmn和Ymn为谐波分量的幅值系数，其具体展开为
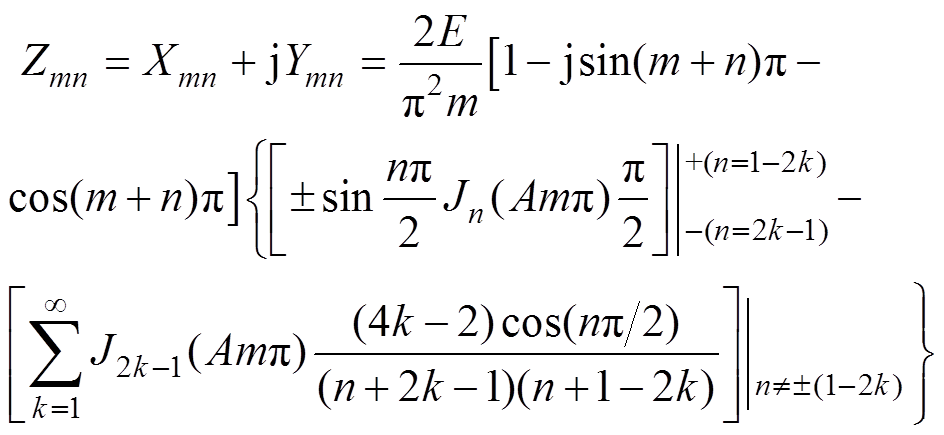（2）
由式（1）、式（2）分析SCBPWM作用下相电压的谐波分布，可得：①相电压基波幅值为EA；②载波谐波只在m为奇数时存在；③边带谐波只在m+n为奇数时存在。
为优化谐波性能，同步调制要求输出电压必须同时满足TPS和HWS[15]。定义载波比为载波频率与基波频率的比值，分析SCBPWM谐波分布可知，当载波比为3的奇数倍时，SCBPWM作用下的线电压不含3的倍数次谐波和偶数次谐波，对应电压波形同时满足TPS和HWS，符合同步调制对输出电压的要求。故三电平SCBPWM应在3的奇数倍载波比下实现。
定义V为输出相电压基波幅值，M为调制比。从直流电压利用率角度，M的计算方式为
（3）SCBPWM的相电压基波幅值为EA，A值最大为1。由式（3）可知，其对应最大调制比为0.866。故SCBPWM作用下直流电压利用率仅为86.6%。
通过分析SCBPWM相电压谐波特性可知，SCBPWM只能在3的奇数倍载波比下实现输出电压同时满足TPS和HWS的同步调制。而在3的偶数倍载波比下，SCBPWM无法使得输出电压满足HWS。此外，SCBPWM无法正常进入方波。
SCBPWM的直流电压利用率较低且其所适用的载波比段较少，无法进入方波，以上缺陷限制了SCBPWM在大功率电机牵引传动系统中的应用。
叠加特定零序分量的CBPWM与SVPWM具有等效性[20]，为拓宽传统SCBPWM适用的载波比段并提高直流电压利用率，首先分析三电平SVPWM的两类开关序列及其载波实现方式。
三电平变流器的空间矢量分布如图3所示，其中各空间矢量的具体分类总结见表1。
图4列出了三电平SVPWM常用的两类开关序列，其中，全P型开关序列在各60°扇区的第一个采样点处均采用P型小矢量首发的开关序列；NP型开关序列则在相邻扇区第一个采样点处分别采用P型和N型小矢量首发的开关序列。
使用非对称规则采样作为采样方式[21]，分别令载波比为6和9，分析全P型和NP型开关序列在一个基波周期内的三相输出相电压波形，两类开关序列作用下的三相电压如图5所示。
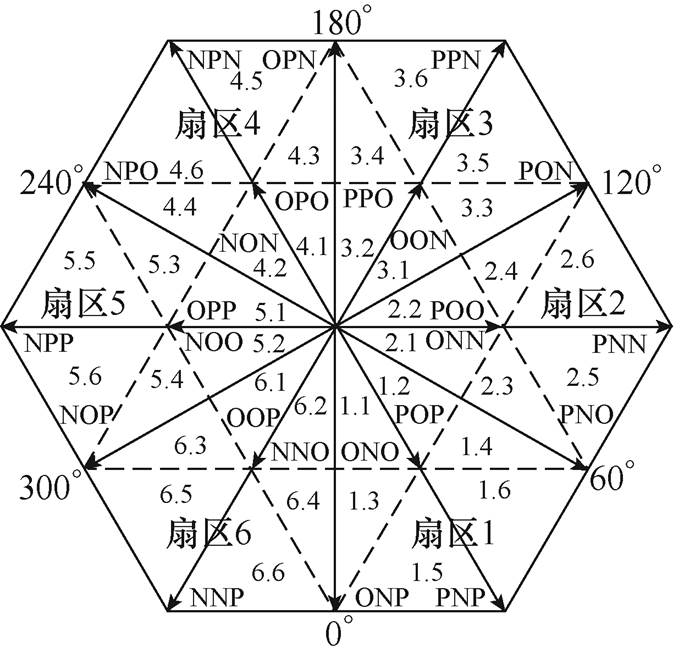
图3 三电平变流器对应的空间矢量
Fig.3 Space vector corresponding to three-level converter
表1 三电平NPC变流器各空间矢量分类
Tab.1 Classification of space vectors for NPC converter
空间矢量调制比矢量类别 OOO/PPP/NNN0零矢量 POO/PPO/OPO/OPP/OOP/POPP型小矢量 ONN/OON/NON/NOO/NNO/ONON型小矢量 PON/OPN/NPO/NOP/ONP/PNO中矢量 PNN/PPN/NPN/NPP/NNP/PNP大矢量
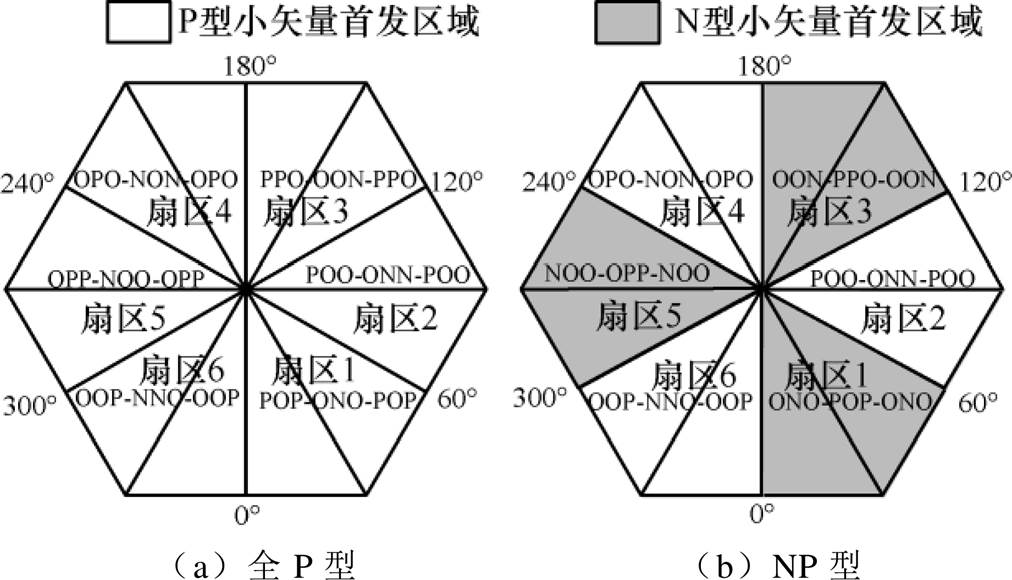
图4 三电平SVPWM的两类开关序列
Fig.4 Two switching sequences of three-level SVPWM
由图5对比全P型和NP型开关序列在不同载波比下的三相电压波形，可得出以下结论。
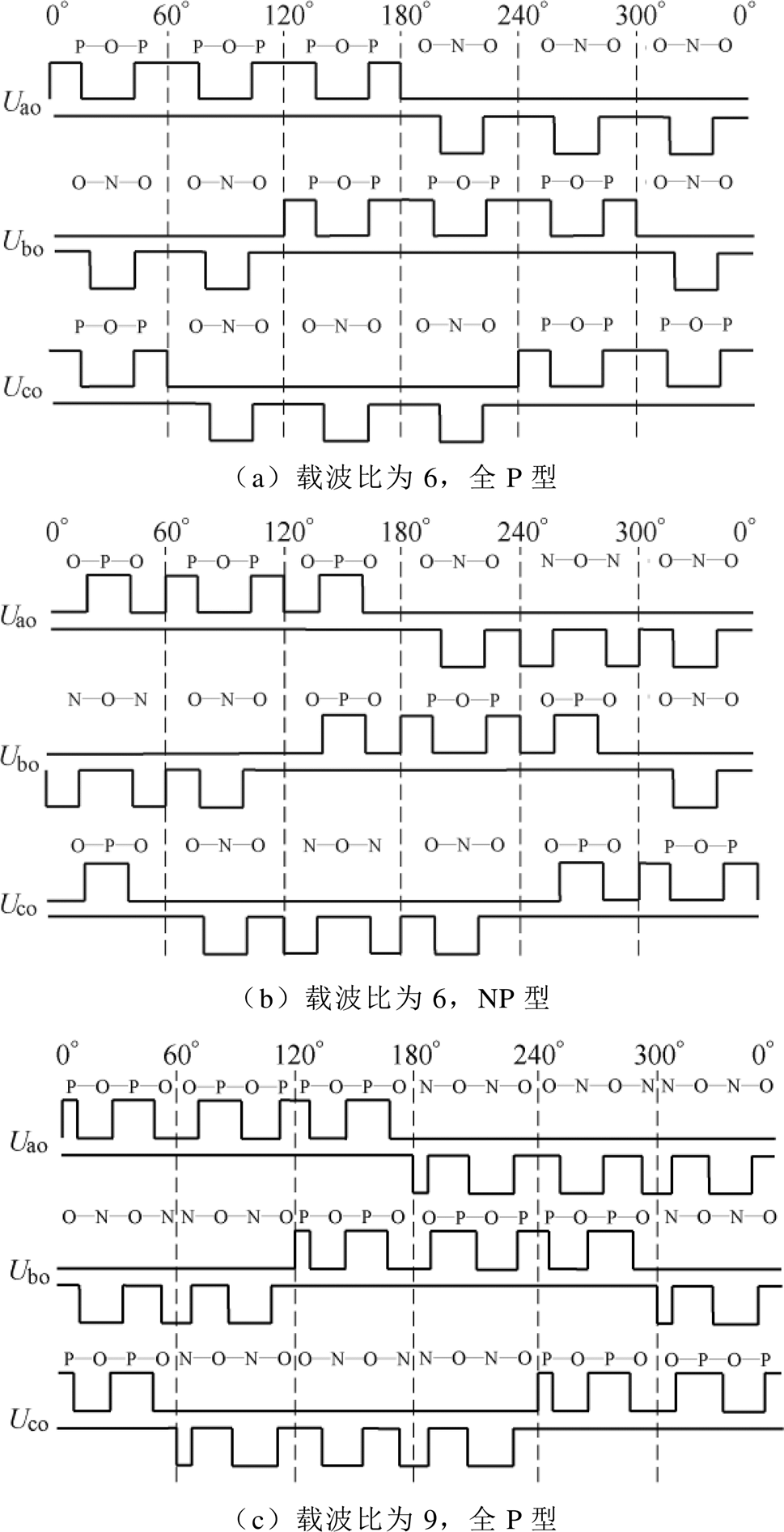
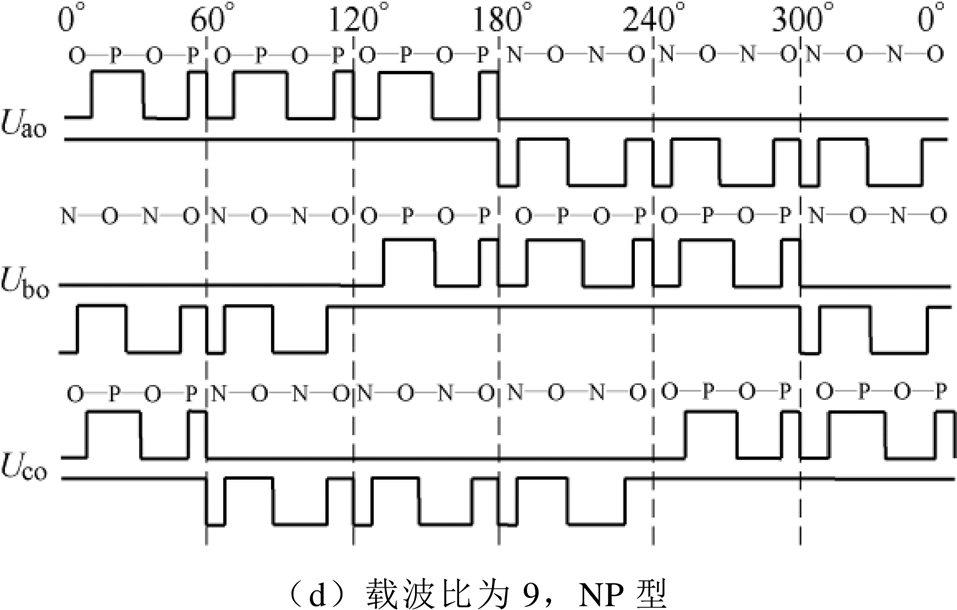
图5 两类开关序列作用下的三相电压
Fig.5 Three-phase voltage under two switching sequences
（1）载波比为6，对应3的偶数倍载波比。此时NP型作用下的相电压波形同时满足TPS和HWS，而全P型只满足TPS。故NP型开关序列可在3的偶数倍载波比下实现满足TPS和HWS的同步调制。
（2）载波比为9，对应3的奇数倍载波比。此时全P型作用下的相电压波形同时满足TPS和HWS，而NP型只满足TPS。故全P型开关序列可在3的奇数倍载波比下实现满足TPS和HWS的同步调制。
通过分析三相电压波形的特点可得到全P型和NP型各自满足TPS和HWS的载波比段，在此基础上进一步推导两类开关序列的载波实现方式。
首先推导两类开关序列对应的调制波表达式。两类开关序列本质为三电平SVPWM各空间矢量不同的排列组合，故其对应的调制波一致，均由三相正弦波叠加零序分量得到，即
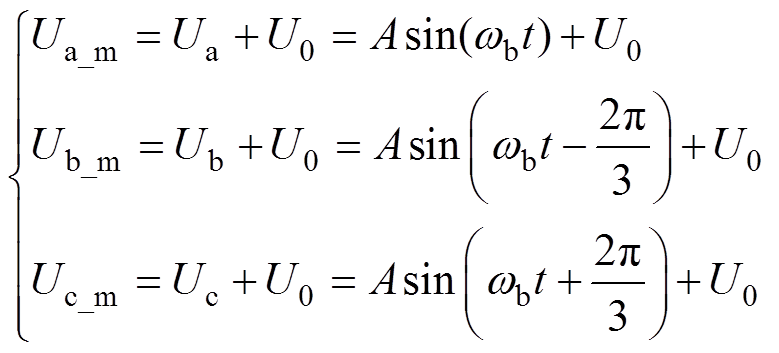（4）式中，Ua、Ub和Uc为三相正弦波；Ua_m、Ub_m和Uc_m对应的三相调制波；U0为零序分量。
针对三电平下CBPWM和SVPWM的调制波等效，文献[20]以图3的区域2.6为例，利用调制波等效原则推导出该区域下的零序分量表达式为
（5）式中，k为冗余小矢量作用时间因子。令k=0.5，推导图3各区域对应的U0分别为
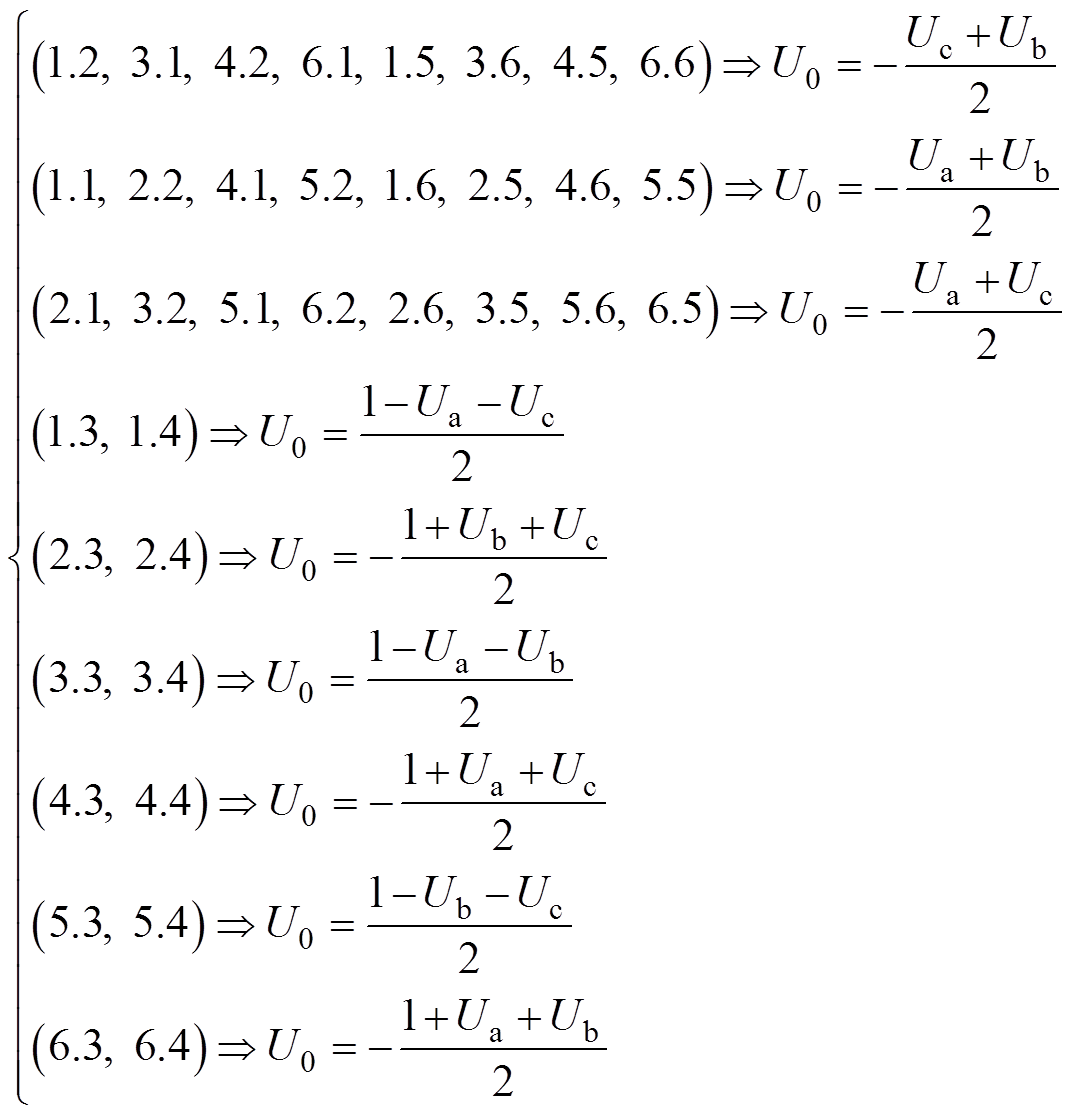（6）
定义Umax、Umin分别为Ua、Ub和Uc为正时值不变、为负时值加1后的最大值和最小值，则可将式（6）统一化简为
（7）将式（7）代入式（4）即可得全P型和NP型开关序列对应的调制波表达式。
在得到调制波表达式的基础上进一步分析全P型和NP型各自对应的三角载波。当参考电压位于图3区域2.6时，在一个采样周期内，调制波与上升、下降方向三角载波的比较示意图如图6所示。
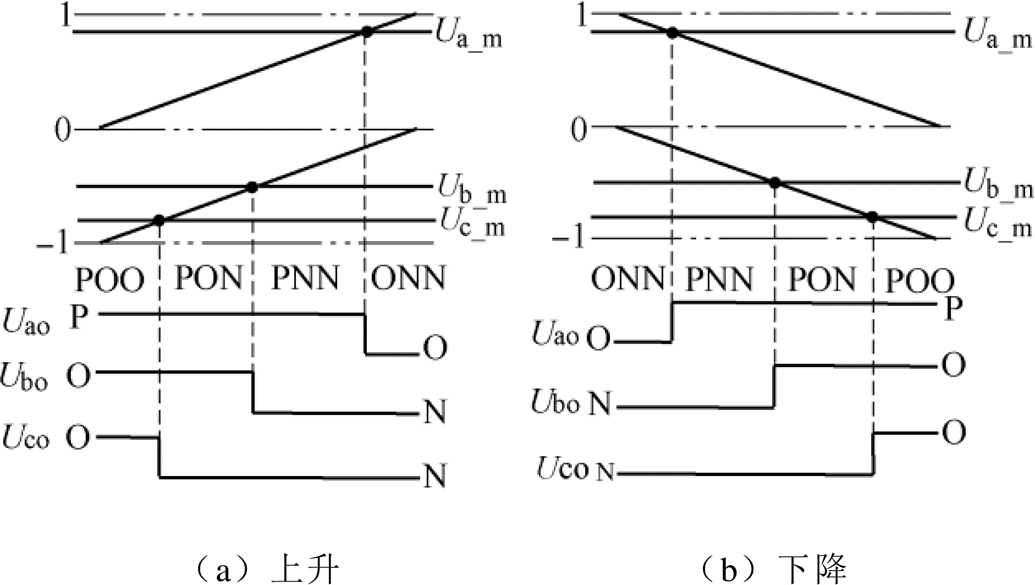
图6 调制波与上升/下降方向三角载波比较示意图
Fig.6 Comparison of modulation wave and triangular carrier in rising/falling direction
由图6可知，调制波与上升方向的三角载波比较可得到P型小矢量首发的开关序列；与下降方向的三角载波比较可得到N型小矢量首发的开关序列。全P型在各扇区的第一个采样点处均采用P型小矢量首发的开关序列，NP型则在相邻扇区分别采用P型和N型小矢量首发的开关序列。通过在各扇区第一个采样点处选择使用相应方向的三角载波与调制波进行比较，可基于载波分别实现全P型和NP型开关序列，其具体实现方式见表2。
表2 两类开关序列的载波实现方式
Tab.2 Carrier implementation of two switching sequences
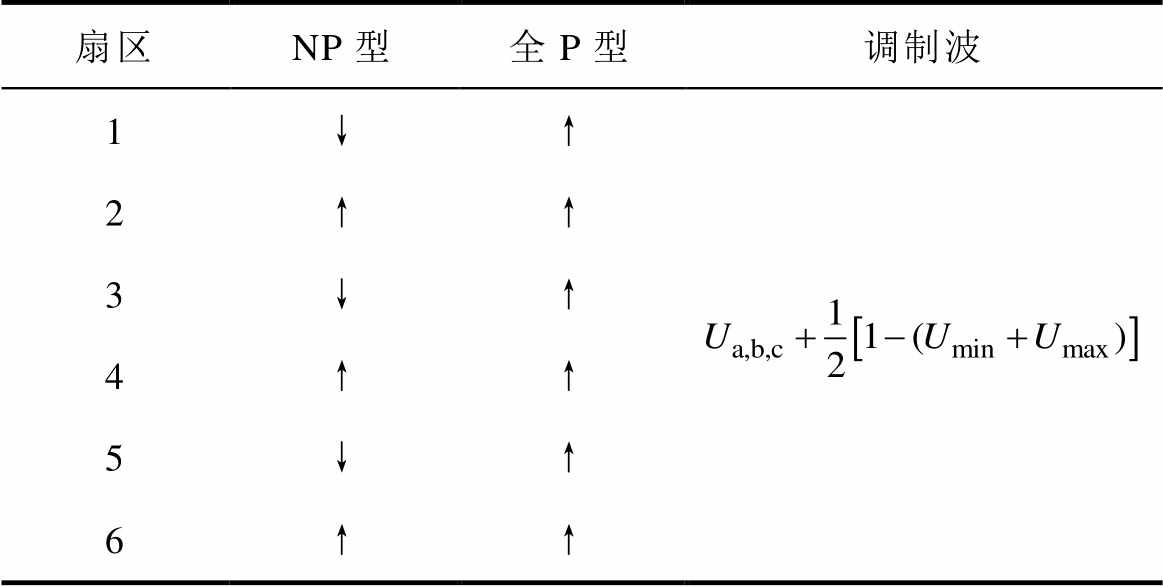
扇区NP型全P型调制波 1↓↑ 2↑↑ 3↓↑ 4↑↑ 5↓↑ 6↑↑
表2中，↑代表在各扇区的第一个采样点处，使用调制波与上升方向起始的三角载波比较；↓则代表使用调制波与下降方向起始的三角载波比较。
基于载波实现的全P型和NP型开关序列可分别在3的奇数倍和偶数倍载波比下使得输出电压同时满足TPS和HWS。作为对比，传统SCBPWM作用下的输出电压只能在3的奇数倍载波比下同时满足TPS和HWS。为拓宽传统SCBPWM所适用的载波比段，提出了ISCBPWM策略，其原理如下：
在3的奇数倍载波比下使用基于载波实现的全P型开关序列，在3的偶数倍载波比下使用基于载波实现的NP型开关序列，从而使得输出电压波形在任意3的整数倍载波比下均满足TPS和HWS。
为确定ISCBPWM适用的同步调制段，以载波比为9和6为例，分析ISCBPWM在3的奇数倍和偶数倍载波比下对应的开关波形，ISCBPWM作用下的相电压如图7所示。
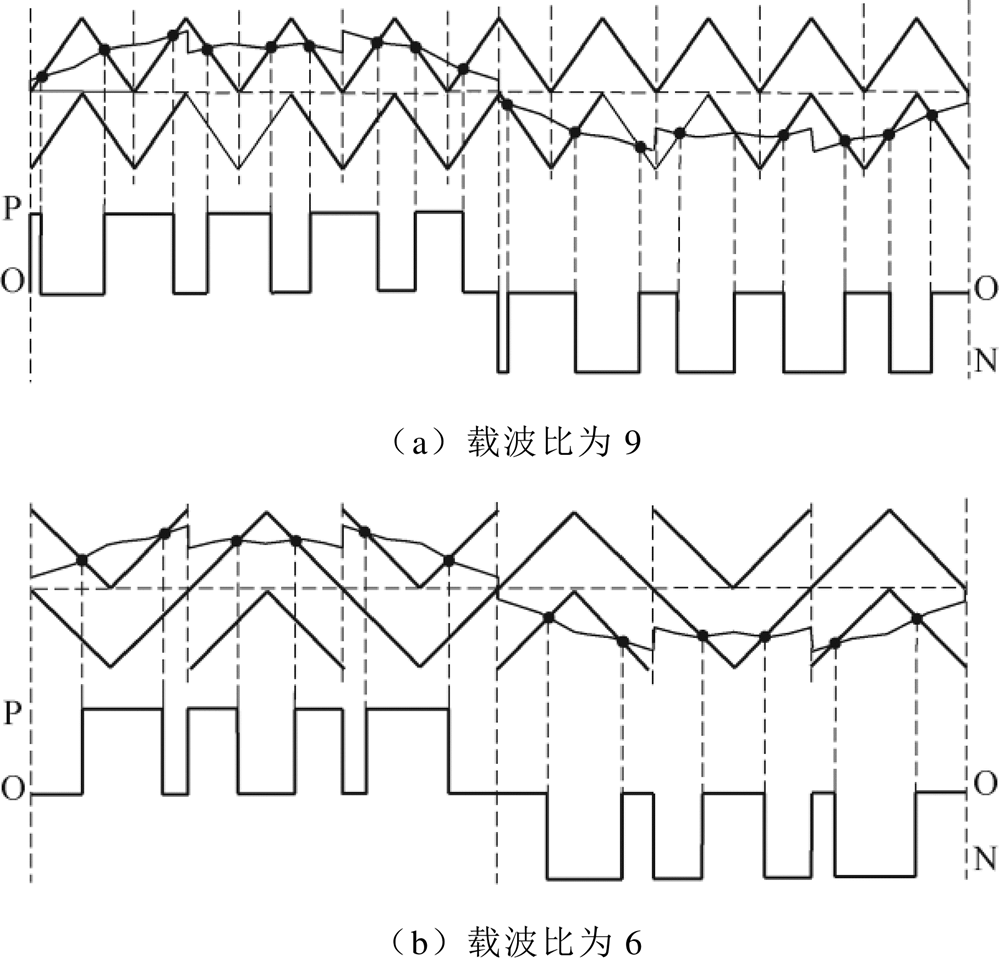
图7 ISCBPWM作用下的相电压
Fig.7 Phase voltage under ISCBPWM
定义基波频率为fb，载波频率为fc，分析图7可得到以下结论：
（1）由图7a可知，载波比为9，半个基波周期内相电压脉冲数为5，对应同步5次调制。推论可知，载波比为3的奇数倍时，ISCBPWM作用下开关频率固定为(fc+fb)/2，对应(载波比+1)/2次调制。则在载波比为27、21、15、9、3时，在ISCBPWM作用下可实现同步14、11、8、5、2次调制。
（2）由图7b可知，载波比为6，半个基波周期内相电压脉冲数为4，对应同步4次调制。推论可知，载波比为3的偶数倍时，ISCBPWM作用下开关频率固定为fc/2+fb，对应载波比/2+1次调制。则在载波比为24、18、12、6时，在ISCBPWM作用下可实现同步13、10、7、4次调制。
综合以上分析，当载波比分别为27、24、21、18、15、12、9、6、3时，在ISCBPWM作用下可实现输出电压波形同时满足TPS和HWS的同步14、13、11、10、8、7、5、4、2次调制。
方波下的三相电压如图8所示。ISCBPWM可实现同步14、13、11、10、8、7、5、4、2次调制，但其无法直接进入如图8所示的方波。
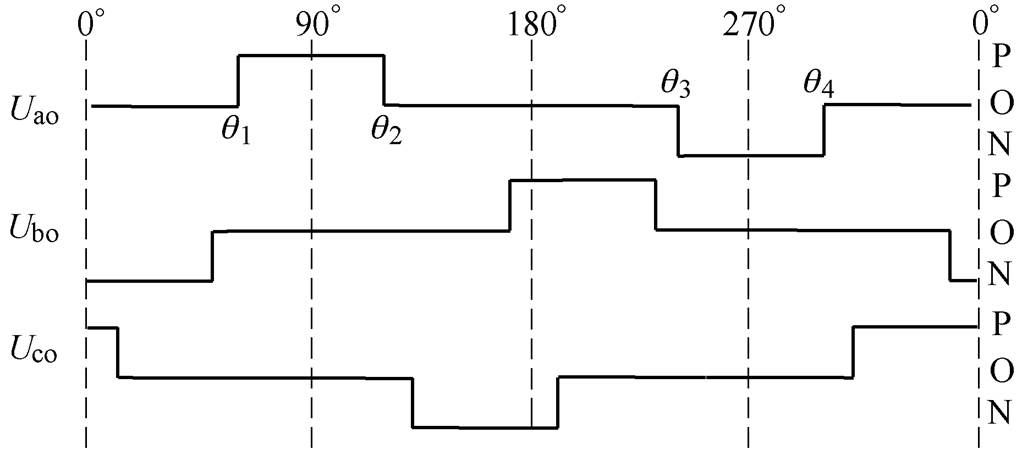
图8 方波下的三相电压
Fig.8 Three-phase voltage under square wave modulation
图8中，q1、q2、q3、q4为方波运行时A相功率器件动作的四个角度。为控制ISCBPWM进入方波，首先根据相电压的基波幅值在线计算q1、q2、q3、q4的值。由傅里叶级数可推导出
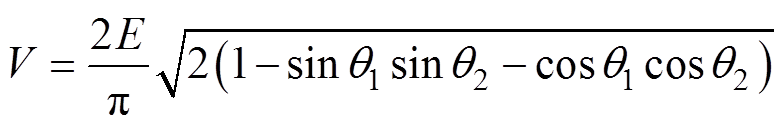（8）令q =p/2-q1，在相电压波形满足四分之一周期对称的情况下，可将式（8）化简为
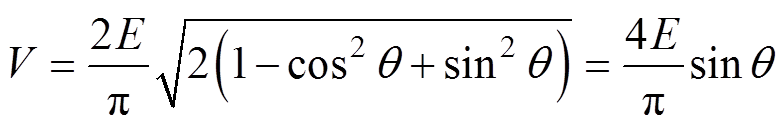（9）
ISCBPWM的相电压基波幅值为EA，由ISCBPWM进入方波应保证相电压基波幅值不变，即
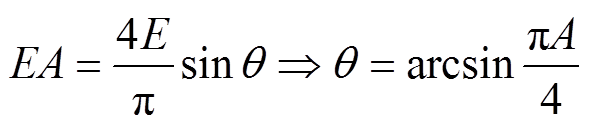（10）根据式（10）可计算得到A相功率器件动作的四个角度q1、q2、q3、q4的值分别为
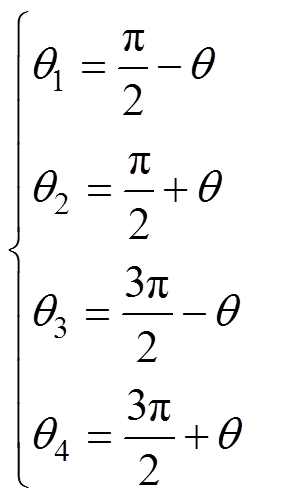（11）
则可得出ISCBPWM进入方波的方法如下：
（1）由式（10）和式（11）在线计算A相功率器件动作的四个角度q1、q2、q3、q4的值。
（2）检测A相调制波相位，控制A相在相位位于q1～q2之间时输出P电平；位于q3～q4之间时输出N电平；位于其余相位区间时输出O电平。
（3）将A相功率器件的开关状态分别右移、左移120°可得到B相和C相功率器件的开关状态。
本文提出的ISCBPWM及其进入方波方法的实现流程如图9所示。
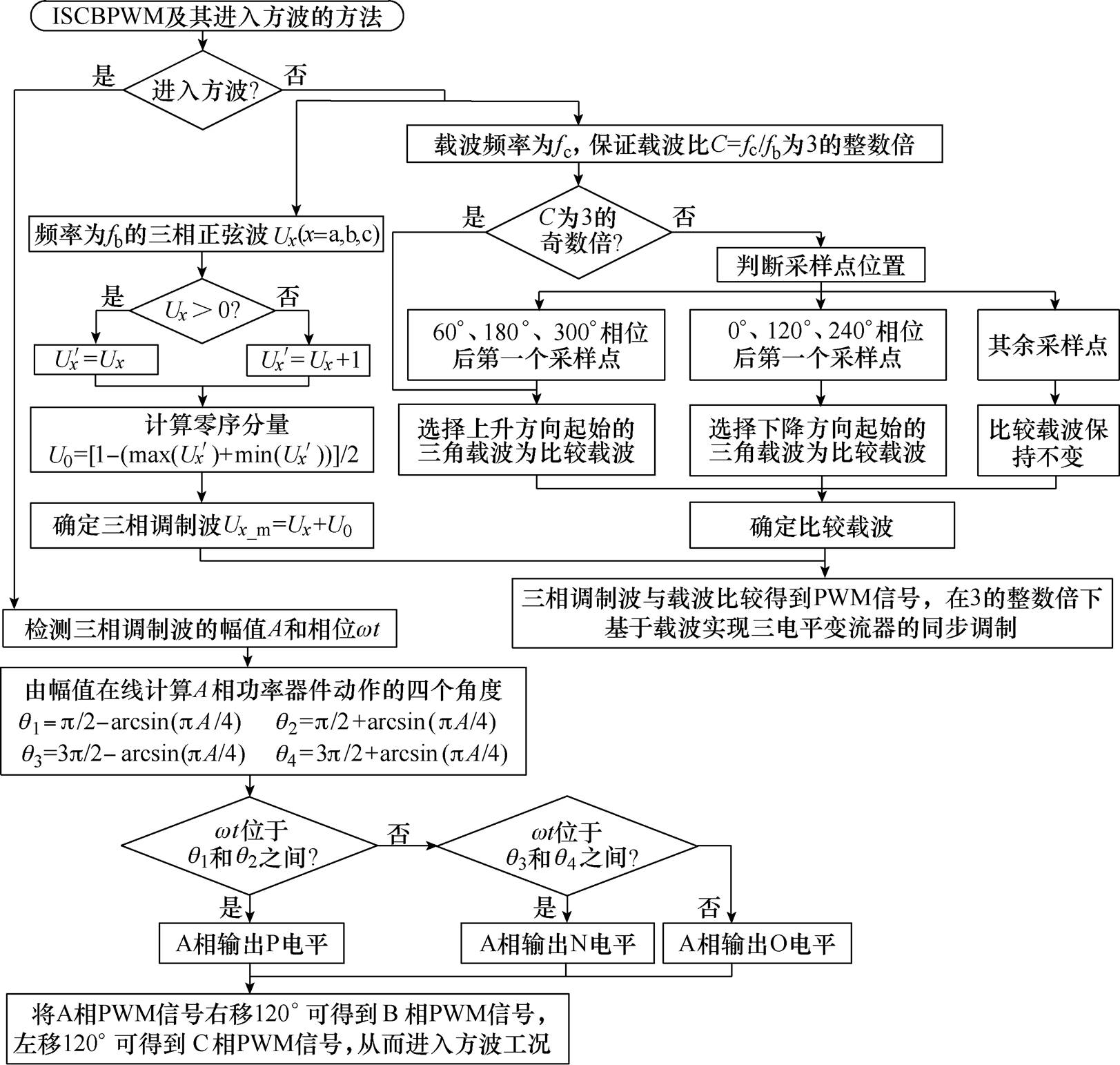
图9 ISCBPWM及其进入方波方法的实现流程
Fig.9 Flow chart of ISCBPWM and its method of entering square wave modulation
基于可进入方波的ISCBPWM策略，设计三电平变流器在全速度范围内的调制策略。具体如下：
在基波频率低于20Hz时，此时由波形不对称产生的不良影响较小。令载波频率保持不变，使用基于载波实现的全P型作为异步调制方式。
在基波频率超过20Hz时，为降低非特征次谐波产生的不良影响并优化谐波性能，令载波比分段变化，使用ISCBPWM作为同步调制方式。其中，在载波比为27、21、15、9、3时，使用基于载波实现的全P型，对应同步14、11、8、5、2次调制；在载波比为24、18、12、6时，使用基于载波实现的NP型，对应同步13、10、7、4次调制。
在基波频率超过140Hz时，令ISCBPWM过渡至方波运行。
在开关频率不超过430Hz的前提下，三电平变流器在全速度范围内的调制策略设计如图10所示。
针对本文所提可进入方波的ISCBPWM策略，分别从直流电压利用率、频谱特性和中点电位平衡能力三方面来分析其性能。
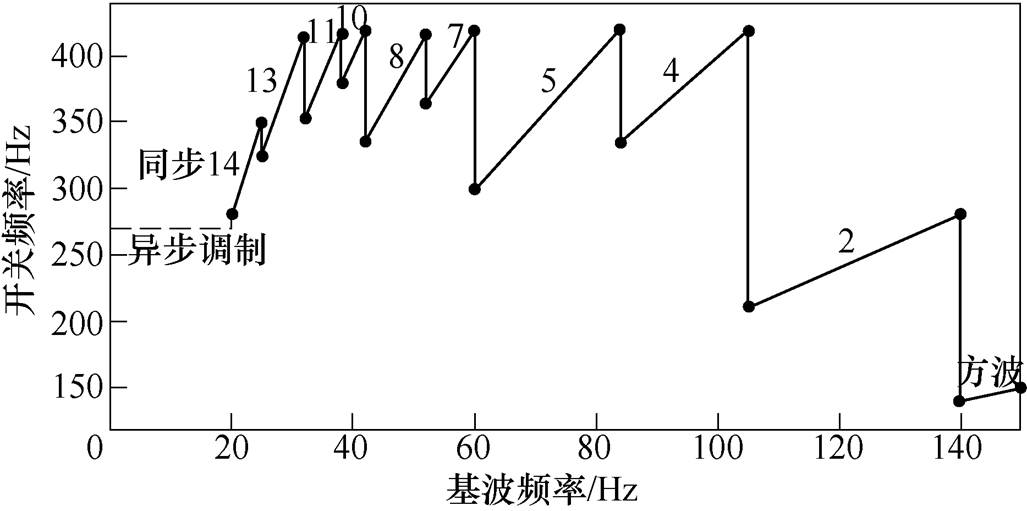
图10 全速度范围调制策略设计
Fig.10 Design of modulation strategy in full speed range
为分析ISCBPWM的直流电压利用率，首先分析ISCBPWM的调制波幅值。对于ISCBPWM，其三相调制波表达式为
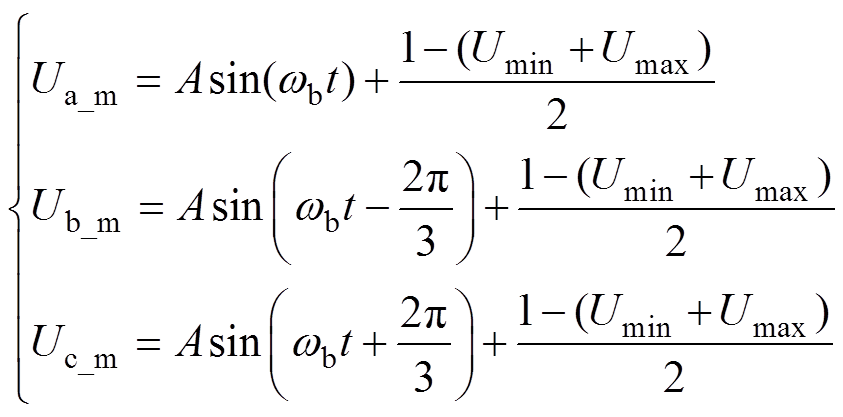（12）式中，Ua_m可在60°相位处取得最大值。在不过调制下，Ua_m能达到的最大值为1，此时有
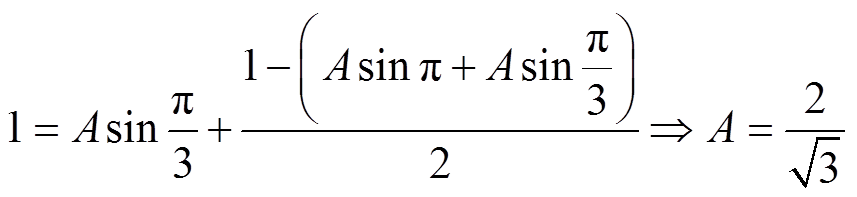（13）
ISCBPWM对应相电压基波幅值为EA，由式（13）可知，A值最大为1.154 7，对应最大调制比为1，故ISCBPWM作用下直流电压利用率为100%。
ISCBPWM进入方波后，在q1为0°时相电压基波幅值可取得最大值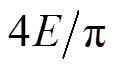
，对应最大调制比为1.103，故进入方波后，直流电压利用率可达110.3%。
作为对比，传统SCBPWM作用下的直流电压利用率仅为86.6%，故可进入方波的ISCBPWM有效地提升了直流电压利用率。
ISCBPWM分别在3的奇数倍和偶数倍载波比下使用基于载波实现的全P型和NP型开关序列作为调制方式。利用双重傅里叶级数分析基于载波实现的全P型和NP型开关序列各自对应的相电压谐波分量表达式，从而得到ISCBPWM的频谱特性。
对于基于载波实现的全P型开关序列，双重傅里叶级数展开为
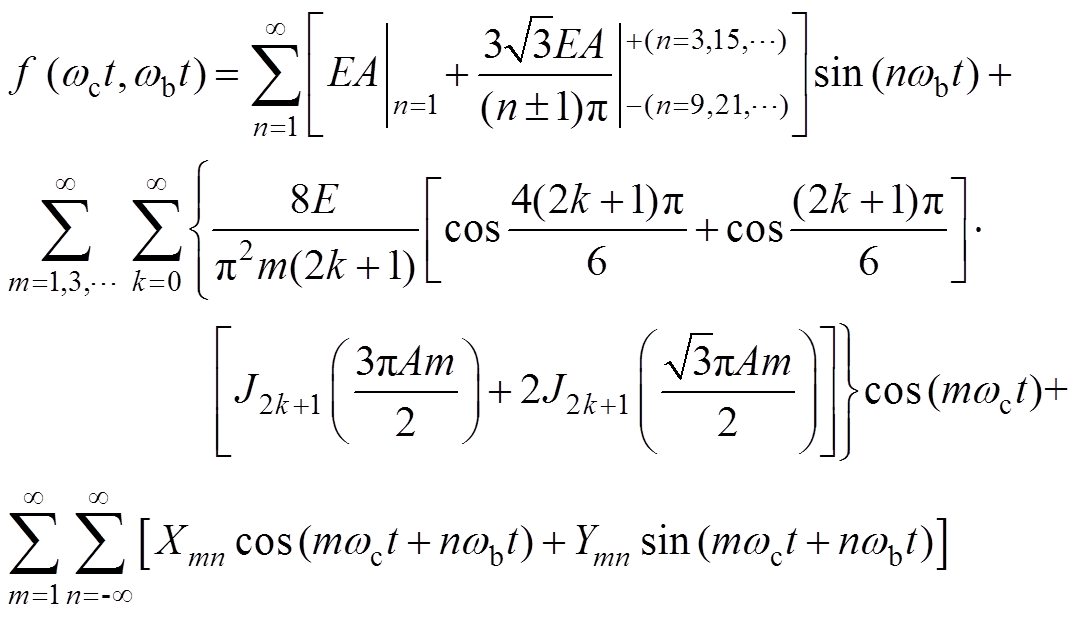（14）式中，Xmn和Ymn的具体展开式见附录。从中分析全P型开关序列作用下的输出相电压频谱特性，结论如下：
（1）直流偏置为0，故输出相电压不含直流偏置。
（2）基波分量X01=jEA，故输出相电压的基波幅值为EA。
（3）基带谐波只在n为3的奇数倍时存在，故相电压只在基波3的奇数倍频处存在基带谐波。
（4）载波谐波只在m为奇数时存在，故输出相电压只含奇数次载波倍频的载波谐波。
（5）边带谐波只在m+n为奇数时存在，故输出相电压只在n为偶数、m为奇数或n为奇数、m为偶数时在载波倍频附件存在边带谐波。
由输出相电压的载波谐波和边带谐波分布可知，当载波比为奇数时，基于载波实现的全P型开关序列作用下的相电压不含偶数次谐波。
对基于载波实现的NP型开关序列，对应谐波分量表达式为
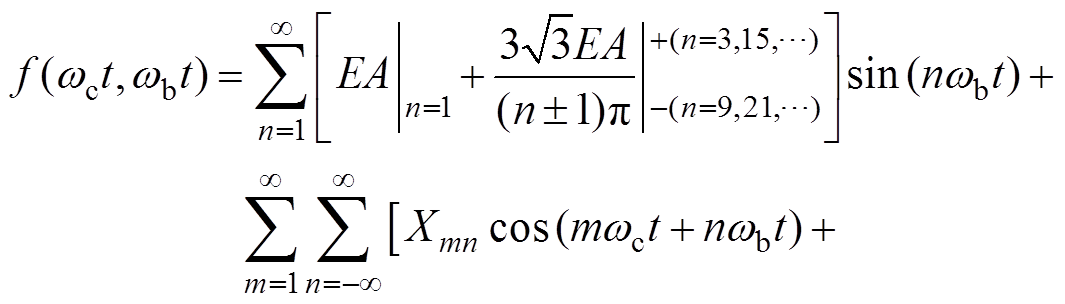
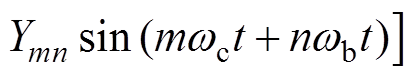（15）
利用NP型开关序列的谐波分量表达式（15）和式（A4）分析其作用下的输出相电压频谱特性，结论如下：
（1）直流偏置为0，故输出相电压不含直流偏置。
（2）基波分量X01=jEA，故输出相电压的基波幅值为EA。
（3）基带谐波只在n为3的奇数倍时存在，故相电压只在基波3的奇数倍频处存在基带谐波。
（4）载波谐波为零，故输出相电压不含载波谐波。
（5）边带谐波只在n为奇数时存在，故输出相电压只在n为奇数时在载波倍频附件存在边带谐波。
由输出相电压的频谱分布可知，当载波比为偶数时，基于载波实现的NP型开关序列作用下的相电压不含偶数次谐波。
ISCBPWM分别在3的奇数倍和偶数倍载波比下使用基于载波实现的全P型和NP型，则由以上频谱分析结果可知，ISCBPWM可在3的整数倍载波比下使得输出电压不含3的倍数次谐波和偶次谐波，从而使得输出电压波形同时满足TPS和HWS。
中点电位平衡控制是三电平变流器的关键问题，而ISCBPWM具备以基波周期作为时间单位调节中点电位平衡的能力。具体证明如下：
定义uo为ISCBPWM对应的中点电位偏差，有
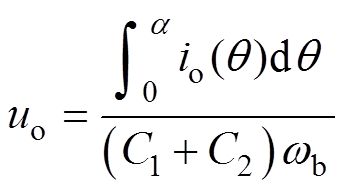（16）式中，io(q )为流经中点的电流；C1和C2分别为直流侧上端和下端电容。对于io(q )，有
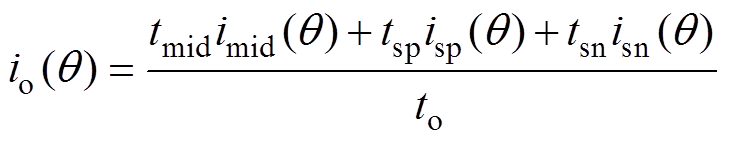（17）
式中，imid(q )、isp(q )、isn(q )和tmid、tsp、tsn分别为ISCBPWM等效的中矢量、P型小矢量、N型小矢量对应的中点电流及其作用时间；to为中点电流作用的总时间。
由式（16）、式（17）推导任意相位区域和其180°对称区域的中点电位偏差之和，即
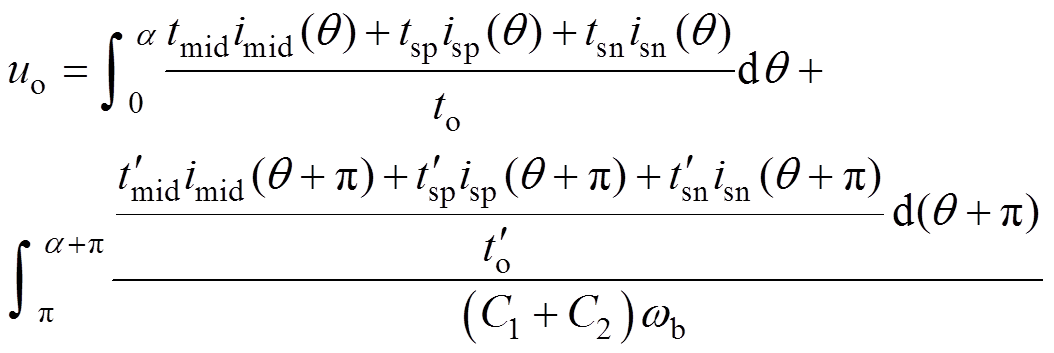（18）式中，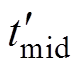
、
、
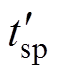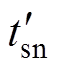分别为ISCBPWM在180°对称区域的等效中矢量、P型小矢量、N型小矢量对
应的中点电流作用时间。由于ISCBPWM的输出相电压波形满足HWS，故相差180°相位的等效中矢量、P型小矢量、N型小矢量作用时间相同，对应中点电流方向相反，即
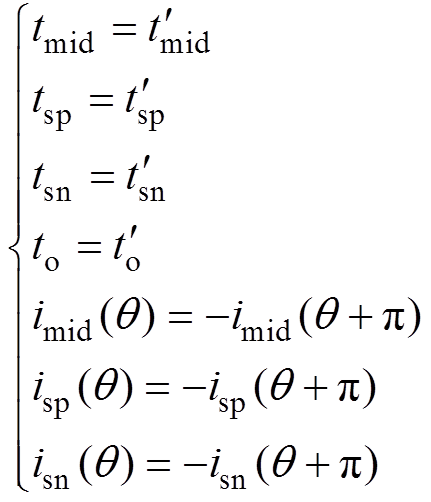（19）将式（19）代入式（18），有uo=0。故ISCBPWM基波周期可以作为时间单位调节中点电位的平衡。
利用PSIM软件搭建三电平NPC逆变器模型，对本文所提ISCBPWM的有效性进行仿真分析。仿真步长10ms，直流侧电压100V，仿真结果如图11所示。
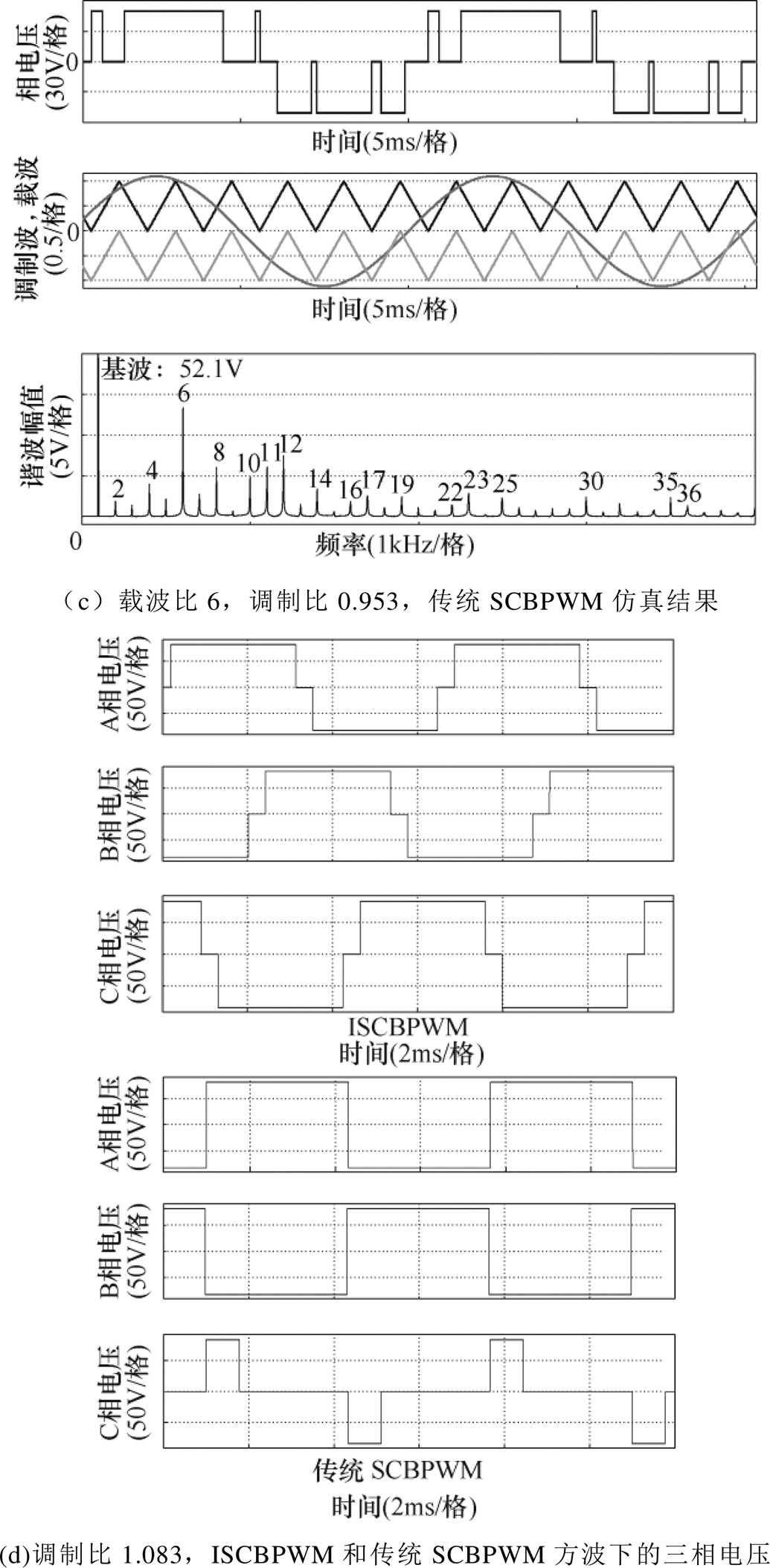
图11 ISCBPWM仿真结果
Fig.11 Simulation results of the ISCBPWM
由图11a可知，在3的奇数倍载波比下，ISCBPWM在各60°相位区域均使用相同方向的三角载波作为比较载波。在其作用下的相电压不含偶数次谐波，主要谐波为3次、9次谐波，分别对应基带谐波和载波谐波。其余谐波有11次、17次、25次、35次谐波，对应边带谐波。以上谐波分布符合ISCBPWM在3的奇数倍载波比下的频谱理论分析结果。
由图11b可知，在3的偶数倍载波比下，ISCBPWM在相邻60°相位区域使用不同方向的三角载波作为比较载波。在其作用下的相电压不含偶数次谐波，主要谐波为3次谐波，对应基带谐波。其余谐波有9次、11次、21次、23次谐波，对应边带谐波。以上谐波分布符合ISCBPWM在3的偶数倍载波比下的频谱理论分析结果。
由图11c可知，传统SCBPWM在3的偶数倍载波比下输出相电压不满足HWS，且其在调制比0.953下，调制波幅值大于1，处于过调制状态。
由图11d可知，ISCBPWM在进入方波后三相电压波形满足TPS和HWS，而传统SCBPWM无法正常进入方波调制。
对比图11，相比于传统SCBPWM，本文所提ISCBPWM可在任意3的整数倍载波比下使得输出电压波形满足HWS，且其可进入方波运行，最大直流电压利用率也有所提升。以上仿真结果证明了本文所提方法的有效性。
为验证仿真结果的正确性和所设计基于ISCBPWM的全速度范围调制策略的有效性，搭建了如图12所示的基于IGBT的三电平NPC变流器实验平台。该实验平台通过VME机箱进行控制，机箱内包含AD板、CPU、PWM板等。实验平台的功率器件选用英飞凌公司的FZ300R12KE3G。
实验条件如下：逆变输出负载为4mH电感串联6.6W 电阻，基波频率在1～150Hz间循环变化，使用如图10所示的全速度范围调制策略方案。实验结果如图13和图14所示。
图12 三电平NPC变流器样机
Fig.12 Three-level NPC converter prototype
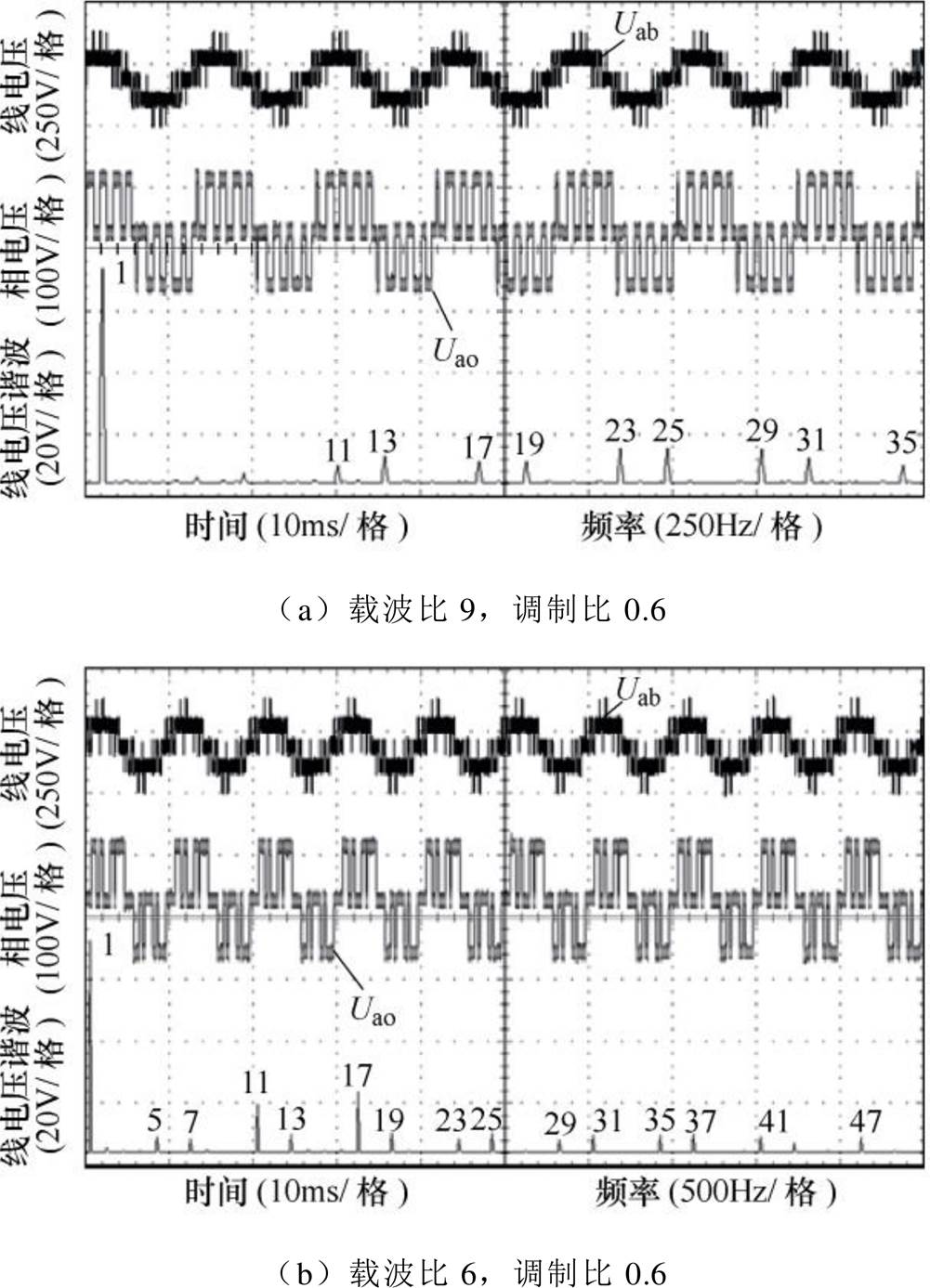
图13 ISCBPWM和SCBPWM实验结果
Fig.13 Experimental results of ISCBPWM and SCBPWM
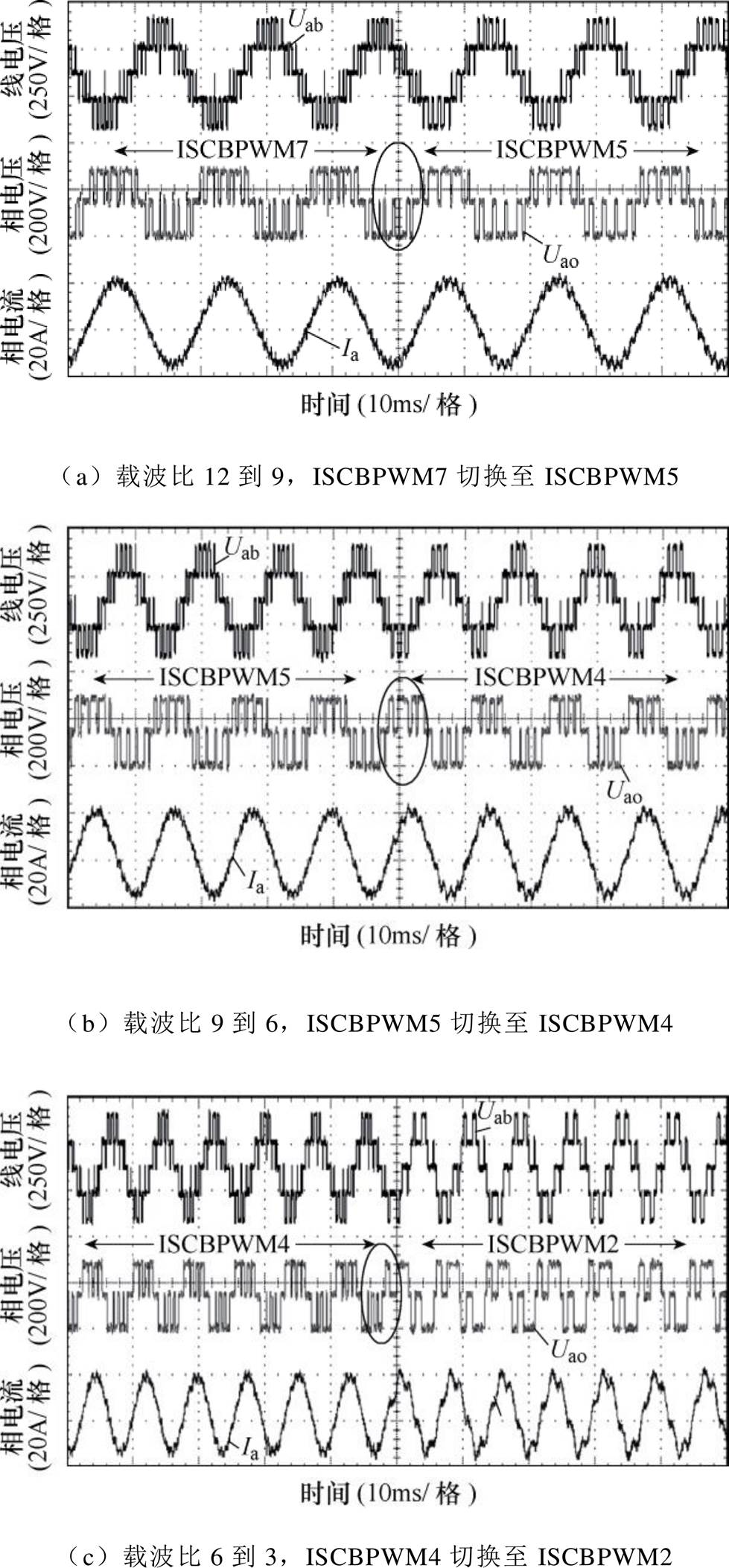
图14 全速度范围ISCBPWM实验结果
Fig.14 Experimental results of ISCBPWM in full speed range
图13a和图13b分别为ISCBPWM在载波比9和6下的实验结果，对比可知：
（1）ISCBPWM可分别在3的奇数倍和偶数倍载波比下消除线电压中的偶数次谐波和3的倍数次谐波分量，对应输出相电压波形满足HWS和TPS。
（2）在载波比为9时，ISCBPWM线电压主要谐波为13次、17次、23次、29次谐波，对应只在m+n为奇数时在载波倍频附近存在边带谐波，其中m为载波倍频次数，n为基波倍频次数。
（3）在载波比为6时，ISCBPWM线电压主要谐波为5次、11次、13次、17次谐波，对应只在n为奇数时在载波倍频附近存在边带谐波。
以上ISCBPWM的边带谐波实验分布结果与ISCBPWM的频谱特性理论分析结果一致。
图13c为传统SCBPWM在载波比6下的三相电压波形，其并不满足HWS，而本文所提ISCBPWM则可在3的偶数倍载波比下使得输出相电压满足HWS，克服了传统SCBPWM存在的缺陷。
图14显示了基波频率由低频到高频的各同步段切换过程。受限于文章篇幅，只列出同步7次后的实验结果。从中可得到以下结论：
（1）当载波比为21、15、9、3时，分别对应ISCBPWM 11、8、5、2次调制；当载波比为18、12、6时，分别对应ISCBPWM 10、7、4次调制。故ISCBPWM可分别在3的奇数倍和偶数倍载波 比下满足输出电压波形TPS和HWS的同步调制。
（2）ISCBPWM可过渡到方波运行，且方波下的输出电压波形满足HWS和四分之一周期对称。
（3）ISCBPWM各同步段间切换不会出现相电压两电平跳变且切换电流冲击较小，其动态性能 较好。
以上实验结果证明了本文所提ISCBPWM可在3的任意整数倍载波比下消除线电压中的偶数次谐波分量和3的倍数次谐波分量，从而实现输出电压同时满足HWS和TPS的同步调制并可进入方波。本文所提ISCBPWM计算简单、实现方便，其克服了传统SCBPWM适用同步调制段较少、直流电压利用率较低的缺陷，从而更适合在大功率电机牵引传动系统中应用。
传统SCBPWM只能在3的奇数倍载波比下使得输出电压满足TPS和HWS，且其无法进入方波，直流电压利用率较低。
针对传统SCBPWM存在的缺陷，本文首先分析了两类SVPWM开关序列在不同载波比下的相电压波形，发现全P型和NP型开关序列可分别在3的奇数倍和偶数倍载波比下使得输出电压满足TPS和HWS。在此基础上，基于调制波等效原则，通过在各扇区第一个采样点处选择使用相应方向的载波与调制波进行比较，提出了可在3的任意整数倍载波比下实现同步调制的ISCBPWM方法。通过在线计算每相功率器件动作的四个开关角，使得所提出的ISCBPWM可进入方波。
基于本文所提可进入方波的ISCBPWM，设计了全速度范围内的调制策略，并推导了ISCBPWM作用下的直流电压利用率、相电压频谱特性和中点电位平衡能力。
最后利用仿真和实验对ISCBPWM的有效性进行了验证，结果表明ISCBPWM可以在3的任意整数倍载波比下实现输出电压满足TPS和HWS的同步调制并可进入方波。其克服了传统SCBPWM适用载波比段较少、直流电压利用率较低的缺陷，且计算简单、实现方便。
针对周期性开关波形，均可利用双重傅里叶级数谐波分量表达式为
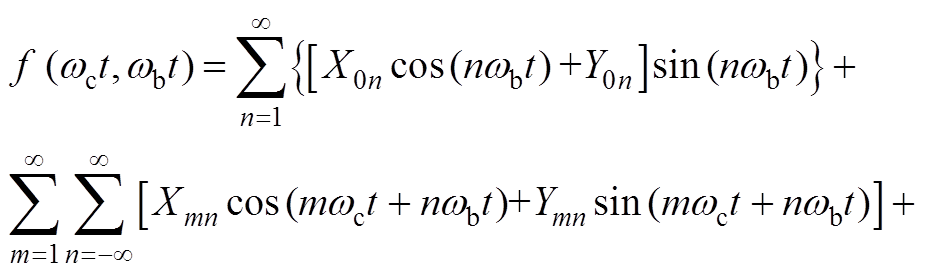
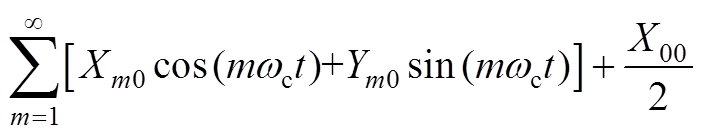（A1）
式中，谐波分量幅值系数Xmn和Ymn的具体展开为
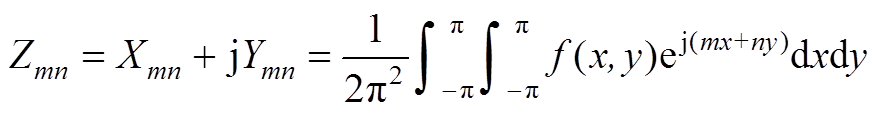（A2）式（14）对应基于载波实现的全P型开关序列谐波分量表达式（A1），其对应式（A2）的具体展开如式（A3）所示。
式（15）对应基于载波实现的NP型开关序列谐波分量表达式（A1），其对应式（A2）的具体展开如式（A4）所示。
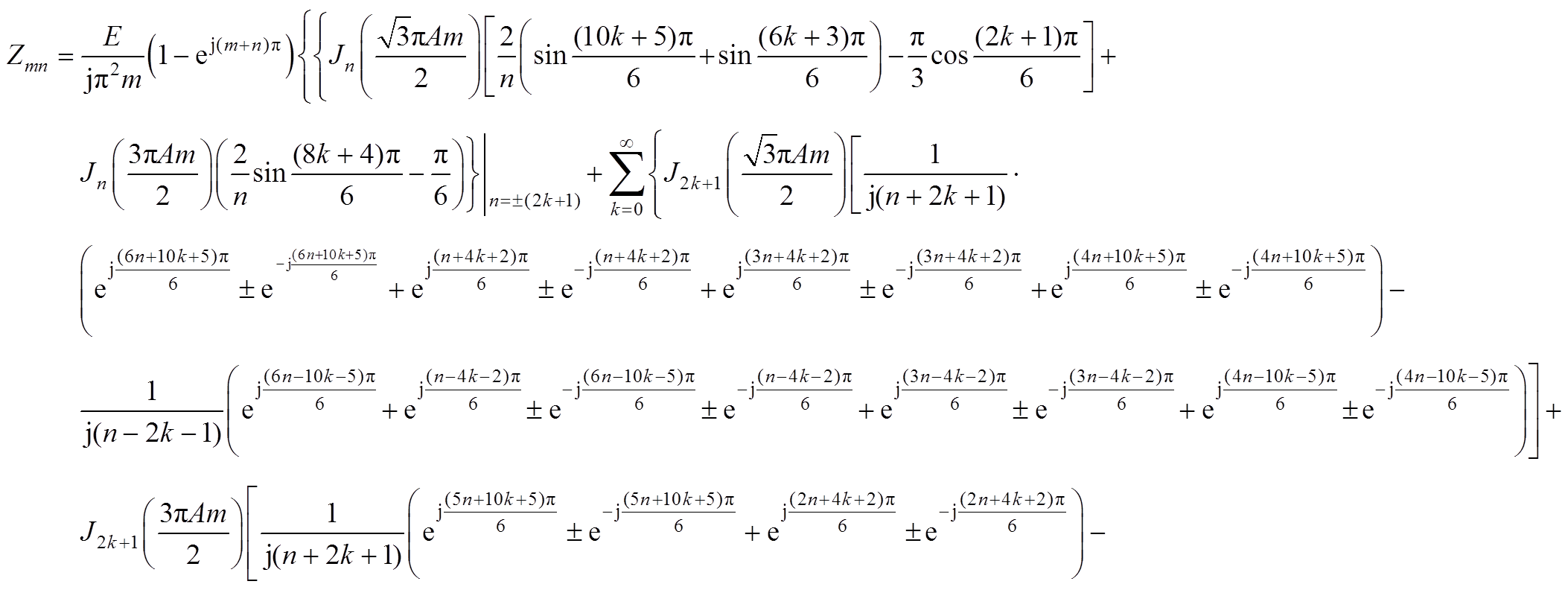
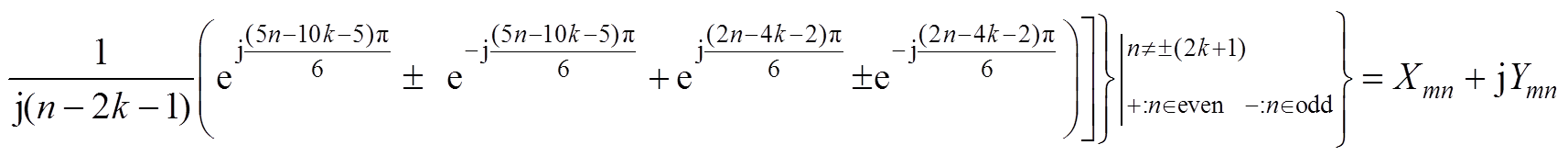（A3）
（A4）
参考文献
[1] Abu-Rub H, Holtz J, Rodriguez J, et al. Medium- voltage multilevel converters-state of the art, challenges, and requirements in industrial applications[J]. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2581-2596.
[2] 张钢, 董侃, 刁利军, 等. 大功率牵引逆变器的中频区调制算法对比研究[J]. 电工技术学报, 2016, 31(2): 1-9.
Zhang Gang, Dong Kan, Diao Lijun, et al. A comparative study of the modulation algorithm in middle frquency region for high power traction inverter[J]. Transactions of China Electrotechnical Society, 2016, 31(2): 1-9.
[3] 王琛琛, 周明磊, 游小杰. 大功率交流电力机车脉宽调制方法[J]. 电工技术学报, 2012, 27(2): 173- 178.
Wang Chenchen, Zhou Minglei, You Xiaojie. Research on the PWM method of high power AC electrical locomotive[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 173-178.
[4] 周明磊. 电力机车牵引电机在全速度范围的控制策略研究[D]. 北京: 北京交通大学, 2013.
[5] Wu Bin. High-power converters and AC drives[M]. Hoboken: Wiley-IEEE Press, 2006.
[6] 殷正刚. 大功率三电平逆变器脉宽调制及磁场定向控制的研究[D]. 北京: 中国科学院大学, 2012.
[7] 张志刚, 黄守道, 胡存刚, 等. 三电平SHEPWM与SVPWM混合控制策略及其矢量平滑切换方法的研究[J]. 电工技术学报, 2015, 30(14): 342-348.
Zhang Zhigang, Huang Shoudao, Hu Cungang, et al. Hybrid method of three-level SHEPWM and SVPWM and its vector smooth-switching[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 342- 348.
[8] 李贵彬, 李永东, 郑泽东, 等. 基于SHEPWM调制的电力机车全速度运行策略及切换方法研究[J]. 电机与控制学报, 2017, 21(4): 17-24.
Li Guibin, Li Yongdong, Zheng Zedong, et al. Research on the electric locomotive running and cutover methods using SHEPWM in whole speed range[J]. Electric Machines and Control, 2017, 21(4): 17-24.
[9] 张永昌, 赵争鸣, 张颖超. 三电平逆变器SHEPWM多组解特性比较及实验[J]. 电工技术学报, 2007, 22(3): 60-65.
Zhang Yongchang, Zhao Zhengming, Zhang Yingchao. Comparison and experiment of multiple solutions for SHEPWM applied to three-level inverter[J]. Transa- ctions of China Electrotechnical Society, 2007, 22(3): 60-65.
[10] Holtz J, Oikonomou N. Fast dynamic control of medium voltage drives operating at very low switching frequency-an overview[J]. IEEE Transactions on Industry Electronics, 2008, 55(3): 1005-1013.
[11] 王堃, 游小杰, 王琛琛, 等. 低开关频率下SHEPWM和SVPWM同步调制策略比较研究[J]. 电工技术学报, 2015, 30(14): 333-341.
Wang Kun, You Xiaojie, Wang Chenchen, et al. Research on the comparison of synchronized modu- lation of SHEPWM and SVPWM under low switching frequency[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 333-341.
[12] 王堃, 游小杰, 王琛琛, 等. 低开关频率下SVPWM同步调制策略比较研究[J]. 中国电机工程学报, 2015, 35(16): 4175-4183.
Wang Kun, You Xiaojie, Wang Chenchen, et al. Researchon synchronized SVPWM strategies under low switching frequency[J]. Proceedings of the CSEE, 2015, 35(16): 4175-4183.
[13] Beig A R, Narayanan G, Ranganathan V T. Modified SVPWM algorithm for three level VSI with synch- ronized and symmetrical waveforms[J]. IEEE Transa- ctions on Industrial Electronics, 2007, 54(1): 486- 494.
[14] Beig A R. Synchronized SVPWM algorithm for the overmodulation region of a low switching frequency medium-voltage three-level VSI[J]. IEEE Transac- tions on Industry Electronics, 2012, 59(12): 4545- 4554.
[15] 葛兴来, 张晓华, 岳岩. 低载波比下三电平NPC逆变器同步SVPWM算法[J]. 电机与控制学报, 2018, 22(9): 24-32.
Ge Xinglai, Zhang Xiaohua, Yue Yan. Comparative study on synchronized space vector PWM for three level neutral point clamped VSI under low carrier ratio[J]. Electric Machines and Control, 2018, 22(9): 24-32.
[16] 谷鑫, 刘潮, 张国政, 等. 三电平逆变器同步不连续空间矢量调制输出电流优化策略[J]. 电工技术学报, 2019, 34(5): 38-47.
Gu Xin, Liu Chao, Zhang Guozheng, et al. Space- vector based synchronous discontinuous PWM for three-level inverter with output current optimization[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 38-47.
[17] Holmes D G, Lipo T A. Pulse width modulation for power converters: principles and practice[M]. New York: IEEE Press, 2003.
[18] Wang Fei. Sine-triangle versus space-vector modu- lation for three-level PWM voltage-source inver- ters[J]. IEEE Transactions on Industry Applications, 2002, 38(2): 500-506.
[19] Kanchan R S, Gopakumar K, Kennel R. Synchronised carrier-based SVPWM signal generation scheme for the entire modulation range extending up to six-step mode using the sampled amplitudes of reference phase voltages[J]. IET Electric Power Applications, 2007, 1(3): 407-415.
[20] 吴洪洋, 何湘宁. 多电平载波PWM法与SVPWM 法之间的本质联系及其应用[J]. 中国电机工程学报, 2002, 22(5): 10-15.
Wu Hongyang, He Xiangning. Relationship between multilevel carrier-based PWM and SVPWM and its applications[J]. Proceedings of the CSEE, 2002, 22(5): 10-15.
[21] 许胜, 赵剑锋. 基于不对称规则采样法的级联H桥型变流器CPS-SPWM输出电压谐波特性分析[J]. 电工技术学报, 2011, 26(6): 121-128.
Xu Sheng, Zhao Jianfeng. Analysis of the harmonic characteristics of the CPS-SPWM output voltage of cascaded H-bridge converters based on irregular sampling[J]. Transactions of China Electrotechnical Society, 2011, 26(6): 121-128.
Research on Improved Synchronized Carrier Based PWM for Three-Level Neutral Point Clamped Converter under Low Carrier Ratio
Abstract When the three-level converter is applied to traction drive system of high power motor, synchronized modulation is usually used under low carrier ratio to optimize harmonic performance. Synchronized carrier based PWM (SCBPWM) is simple to calculate, but the carrier ratio must be an odd integer multiple of 3 to ensure synchronization, three-phase symmetry and half-wave symmetry, and it cannot enter the square wave modulation. In order to overcome the shortcomings of SCBPWM, this paper firstly studies the phase voltage waveforms of two SVPWM switching sequences under different carrier ratios, and then proposes an improved SCBPWM (ISCBPWM) based on modulation wave equivalence, which can realize synchronized modulation when the carrier ratio is an odd and an even integer multiples of 3, respectively. By calculating the switching angle online, the ISCBPWM can enter the square wave modulation. On this basis, the performance of ISCBPWM is analyzed and the modulation strategy based on ISCBPWM in full speed range is designed. Finally, the simulation and experimental results show that compared with the traditional SCBPWM, ISCBPWM has more suitable synchronous segments and higher DC voltage utilization. It can realize synchronous modulation at any integer multiple carrier ratio of 3 and enter the square wave modulation, and its implementation is very convenient.
keywords：Three-level, synchronized modulation, carrier based PWM, square wave, low carrier ratio
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.191027
国家重点研发计划高速磁浮交通系统关键技术研究课题（2016YFB1200602-20），国家重点研发计划电力电子变压器及其控制策略研究与应用课题（2017YFB1200901-14）和国家自然科学基金（51907188）资助项目。
收稿日期 2019-08-14
改稿日期 2019-10-21
高 瞻 男，1993年生，博士研究生, 研究方向为大功率电力电子变流器控制技术。E-mail: gz1993@mail.iee.ac.cn
赵 鲁 男，1984年生，副研究员, 硕士生导师, 研究方向为大功率变流器及高性能电机牵引控制技术。E-mail: zhaolu@mail.iee.ac.cn（通信作者）
（编辑 陈 诚）