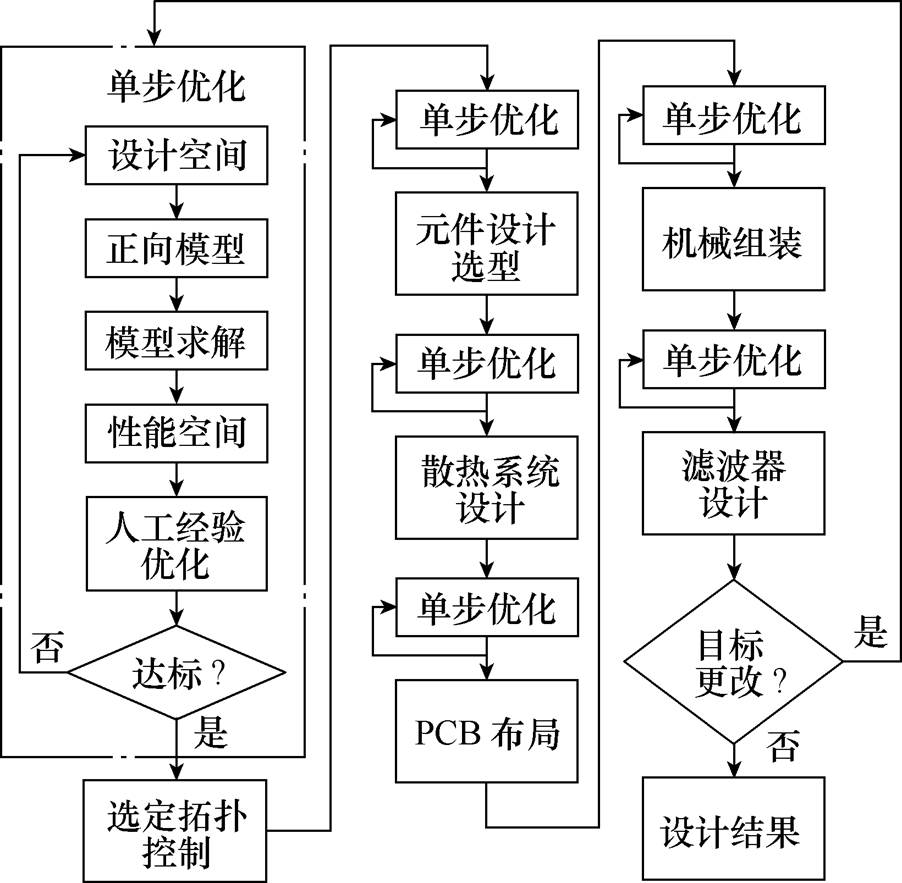
图1 传统人工设计流程
Fig.1 Traditional manual design procedure
摘要 电能路由器在未来能源互联网、泛在电力物联网等领域具有广泛的应用前景，具有多级联、多端口、多流向和多形态的特征，这些特征给传统人工设计带来诸多难题。电力电子设计自动化有望克服设计目标权衡困难、裕量设计浪费成本、硬件迭代耗时耗力、设计自动化程度低等挑战。在宽禁带器件蓬勃发展、计算机性能快速迭代、变换器应用场景延伸细化的三重推进下，电力电子设计自动化有望实现设计集成化、精细化和快速化。电能路由器设计问题可以抽象为多学科优化问题，该问题数学性质差、问题规模大，传统优化算法难以胜任，而遗传算法在解决此类优化问题上性能优异。该文在系统总结当前主流的电力电子系统的设计流程和设计软件架构的基础上，分析了遗传算法解决电力电子设计自动化问题的适用性，总结了电能路由器设计自动化潜在的问题和挑战，并给出相应的建议。
关键词：电力电子设计自动化 电能路由器 设计流程 设计软件 优化 遗传算法
伴随着新能源渗透率逐年提高[1-2]，能源互联网和泛在电力物联网[3-5]发展方兴未艾，电气化交 通[6-7]、数据中心[8]等新型负荷层出不穷，储能技术在能源优化配置中的重要性与日俱增[9-10]，当前电力系统亟需综合发展“源—网—荷—储”协同优化，对电能转换与能量互联设备提出了更高要求。电力电子变压器[11]以及由此发展出的电能路由器[12]具有多端口、多级联、多流向和多形态等全新特征，在未来开放、互联、对等、分享的电网格局下具有精确、连续、快速、灵活的调控手段[12]，但同时电力电子变压器和电能路由器的功能和运行规律更为复杂，面对更加严格和精细化的性能要求[13]。传统人工设计在解决设计问题时遇到颇多困难。
首先明确本文将讨论的电力电子设计的研究范围，在流程上介于电力电子变换器功能指标确定之后，硬件试制组配调试之前的原理分析、多物理场仿真以及性能分析阶段。在电力电子拓扑、参数、控制层面处于覆盖参数设计和控制参数设计两个层面，可以理解为在确定了拓扑方案和控制方案以后的元件参数与控制参数寻优设计，当然电力电子设计自动化也在发展，未来可能在智能拓扑选择和控制方案选择上取得突破，目前也可以处理简单的方案对比问题，只是需要利用多套优化模型进行多次优化比较结果。在传统人工的电力电子变换器设计流程中，每个步骤都需要工程师进行局部的优化设计和迭代寻优，并通过仿真或实验的方法进行分析验证，最终保证设计出的电力电子变换器满足要求，如图1所示。这样做的缺点在于：
（1）由于分步进行局部优化，散热、磁路、机械和滤波器设计位于辅助角色，无法与电路参数和控制参数实现综合分析，即使有局部的联立耦合设计，得到的结果并非全局最优[14]。
（2）设计要求之间存在矛盾，难以实现定量的权衡取舍。
（3）电、热、磁、机械等多物理场相互耦合，电力电子开关瞬态过程非理想，各时间尺度特性相互影响[15-16]，依赖人工难以同时满足所有限制条件。
图1 传统人工设计流程
Fig.1 Traditional manual design procedure
（4）依赖硬件实验的评估和迭代方法严重耗费时间、人力和物力，设计过程效率低下，投资较大。
（5）变换器设计目标更改或增减时，需要重复整个过程，自动化程度低。
电力电子设计自动化有望解决上述问题。虽然该项技术仍处于起步阶段，学术界和工业界尚未对设计方法和设计工具形成广泛的共识。但在宽禁带器件高速发展和变换器应用场景延伸细化的双重推进下，在设计需求愈加复杂化、精细化、系统化的趋势下，电力电子设计自动化正在得到越来越多研究者和专家的关注。2018年，第一届电力电子设计自动化研讨会（Design Automation for Power Electronics workshop, DAPE）在美国波特兰召开，会议上全球各学术机构、设备制造商和计算机辅助设计软件提供商进行了热烈的介绍和交流，第二届DAPE将在意大利热那亚召开，电力电子设计自动化的重要性和研究热度不言自明。
一般地，提升变换器设计效果、提高设计效率可以从四个方面入手：改进设计流程架构、改进正向模型与特性分析过程、改进寻优算法和高效设计工具的软件实现。在设计流程架构上，电力电子设计自动化将传统单步顺序优化改进为多学科设计优化[17]。多学科设计优化提供了一种解决复杂耦合问题的数学描述框架和求解范式，可以处理电力电子设计过程中电、热、磁、机械等多学科的特性耦合问题。在正向模型与特性分析上，增加建模的复杂度和准确度，同时用计算机代替人工以减少求解过程的耗时，在精确和快速之间谋求平衡。在寻优算法上，同样用计算机取代人工，或寻找在收敛能力和搜索能力上达到性能较高的算法，提高全局寻优能力和自动化水平。最后，软件实现提供了实用的设计软件工具，对外实现用户交互，对内完成设计流程自动化调度。在这四方面中，多学科设计优化架构研究成熟，研究成果可以互相借鉴，电力电子学科在正向模型和特性分析方面的研究也汗牛充栋，设计者可以借助设计软件自定义正向问题，但对优化算法的重视程度却不够，这严重局限了设计自动化的发展。
早前，经典的寻优算法被应用在电力电子变换器优化设计领域，例如，顺序无约束最小化算法[18]、增广拉格朗日算法[19]。上述算法的缺点是它们对问题的数学性质有较高的要求，如必须已知梯度或Hessian矩阵等信息。遗憾的是，电力电子变换器的设计问题本质上非常复杂，且不具有好的数学性质，以电能路由器为例来讲：
（1）电能路由器的控制特性、高频高速开关特性、母排布局、磁路特性和散热特性存在极强的耦合关系，这代表问题具有极强的非线性，甚至由于复杂的耦合关系造成目标函数和约束条件非凸。
（2）多级多模块意味着使用元器件众多，每种元器件都有不同的特性，其中电容、开关器件选型和磁心材料选型等设计参数一般是离散取值，电感、变压器尺寸、控制参数等设计参数可以连续取值，设计参数存在离散和连续的混杂。
（3）不同拓扑和方案作为设计参数的一部分，如串联级数的选择、三电平与两电平的选择，涉及整数优化和组合优化问题，导致整个问题变为混合优化问题。
（4）不同优化目标之间此消彼长，需要权衡取舍，如内部工作频率的增加会使效率降低，但可以提高功率密度，使得性能空间中呈现多目标寻优的特点。
为了克服经典算法的局限性，研究者开发了元启发式算法[20]。遗传算法为元启发式算法的一类分支，其优势在多年的探索和使用中日趋明显，具有良好的并行运算能力、搜索能力和收敛能力，因此多用于求解空间复杂、因维度灾难无法穷举可行解或因问题性质不佳无法使用分析方法的问题。如涉及组合优化问题在离散空间寻优的旅行商问题[21]和涉及多维组合和多目标优化的工程问题[22]等。电能路由器设计问题性质与之相似，使用遗传算法作为寻优算法效果可期。
本文介绍了当前电力电子设计自动化研究现状，总结了设计自动化研究的基本内容。进一步针对遗传算法进行了详细介绍，包括其技术起源、发展和应用，特别地，提出遗传算法应用于电能路由器设计的处理方法及改进方向。最后展望了电能路由器设计自动化中的研究难点和挑战。
电力电子设计自动化的主流发展方向包括设计流程架构、建模与特性分析、优化算法和软件实现四个方面。设计流程架构、建模与特性分析和软件实现将在本节进行介绍，优化算法将在第2节单独介绍。
承袭多学科优化的研究范式和框架搭建，电力电子变换器设计得以实现认识上的提升，研究者提出了应用于电力电子设计自动化的设计流程架构[23]，进一步扩展归纳如图2所示。
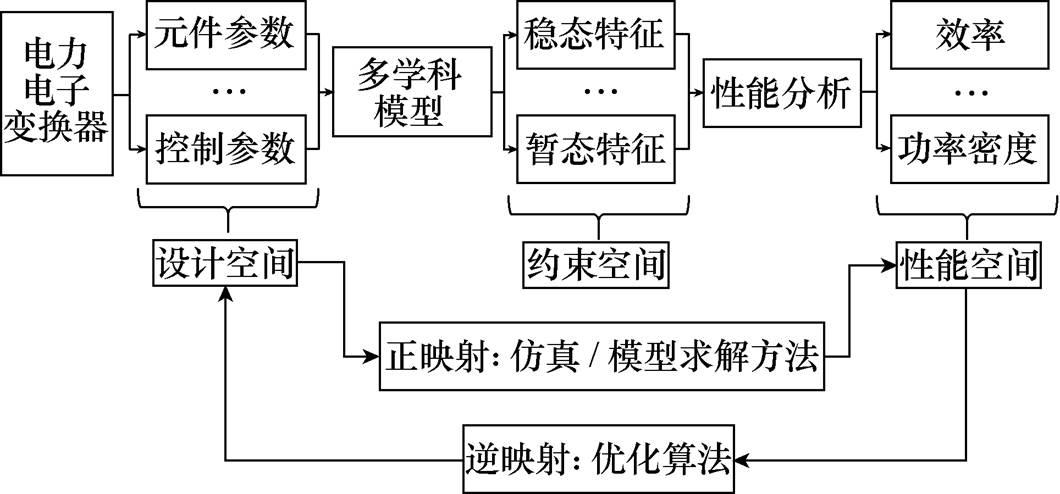
图2 电力电子设计自动化的设计流程架构
Fig.2 Design framework of design automation for power electronics
图中对电力电子变换器的分析，是寻找“设计空间”到“性能空间”的正映射[24]；而优化设计，则是寻找上述映射的逆映射[25]。对于多输入多输出的电力电子系统，设计优化问题的本质就是多目标优化问题[26]，目标函数为“性能空间”的指标，决策变量为“设计空间”的参数，约束为“运行空间”。
“设计空间”指的是材料、电路元件和系统参数的选择等，具体解释见第2.2节；“运行空间”多指变换器正常工作需要满足的基本条件，包括稳态暂态和电磁能量瞬态等不同时间尺度的要求，对于工业产品，要求也更加严格，波形畸变率、绝缘性能、温升、安全性和可靠性满足国际或国内标准，具体信息在2.3节进行了详细阐述；“性能空间”指的是成本、体积、质量、效率或它们之间的排列组合，具体信息在2.4节进行了罗列。
进一步总结，电力电子设计自动化的基础架构可以表述为“三空间两映射”。设计问题可以纳入运筹学的范畴，并借助数学模型表述成标准的优化 问题。
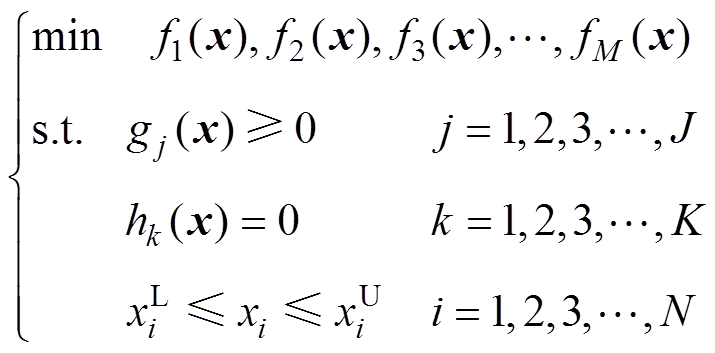（1）式中，优化问题中的决策变量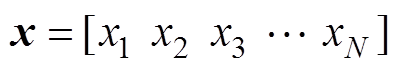
对应于电能路由器的设计参数；目标函数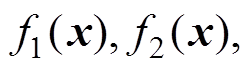
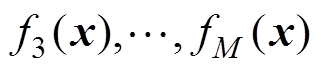对应于性能参数和设计目标，约束条件
和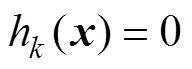
对应于系统安全性、可靠性或者性能参数的约束。从决策变量到目标函数的映射，即已知设计参数从而得到性能参数的正映 射[24]，本质上就是电力电子变换器的性能分析或实验测试过程；而从目标函数求解决策变量的逆映射，即预先给定要求的性能参数，寻求设计参数最优解，本质上就是设计过程，是分析过程的逆过程，通常需要优化算法进行求解。
在建模方面，主要有基于电力电子模块组件（Power Electronics Building Blocks, PEBB）的模块化设计和分层建模设计两种主流方法。模块化设计由美国弗吉尼亚理工大学电力电子系统研究中心提出，该方法首先将集成电力电子模块（Integrated Power Electronics Module, IPEM）作为基本变换单元，在杂散参数、散热、机械方面进行精细化设计[27]，降低整体设计的难度；然后借助PEBB思想将基本变换单元搭建起复杂的电力电子变换器[28]，控制和布局上更规范协调，设计结果具有可扩展性[29]，西班牙IKERLAN-IK4技术研究中心也应用这一思想设计了MW级模块化牵引变换器[30]。分层建模作为目前主流的电力电子系统建模方法，在多电飞机[31]，单相功率因数校正（Power Factor Correction, PFC）整流器[32]、隔离DC-DC、DC-AC[33]等变换器设计中已经有成熟的分析框架。典型的分层建模包括两部分：①将系统性能按照一定的层次分拆，进行局部和整体建模，如拓扑选择、变换器模型、元件模型[31]，调制控制模型、波形模型、元件模型[32]； ②按层次进行局部设计和整体设计，如元件模型在内部优化环内进行设计，设计结果供外部优化环进行设计时调用[33]，其中典型的研究范式为苏黎世联邦理工学院提出的“虚拟原型设计”。
在正向问题求解方面，则有数值仿真、简单行为模型、代理模型、复杂行为模型、降阶场域模型等解算方法。数值仿真方法一般用于解算精确模型，适用于多物理场特性混杂的应用场景，缺点在于解算时间长、调用复杂、数据传输耗时，故研究机械设计、有限元分析、电路仿真和热仿真等工具软件间的协同机制显得尤为重要[34-35]。为了加快模型解算速度，简单行为模型、代理模型等简化模型被大量应用[23, 32-33]，但同时牺牲了模型的精确性。英国诺丁汉大学电力电子与电机控制研究团队在设计电力电子装置自动化布局问题[36]时，放弃等效电路而直接采用了场域模型[37]，涉及杂散参数、热、机械和器件开关瞬态等非理想因素，为了提高求解速度，采用了模型降阶（Model Order Reduction, MOR）方法对杂散参数、温度分布的解算进行简化和加速[38]。在这些求解过程中，解算速度和精度一直是核心矛盾，新的建模技术和仿真解算底层技术将为该矛盾解决提供支撑。
许多学术界和工业界的变换器设计软件工具经过多年的发展都已初具实用性。商业化的多学科设计优化软件具备调用第三方仿真工具的能力，已经形成成熟的问题框架定义，内置了多样的优化算法，经典的电力电子设计自动化软件架构如图3所示。
目前典型的软件都具有类似架构，如Simulia iSight®，ModeFrontier®和ModelCenter®以及开源的openMDAO®。专业的电力电子设计自动化软件如powerforge®内置了DC-DC、DC-AC、多电平变换器等模型，为用户提供包括器件、材料等数据库，以及参数扫描、方案对比、仿真文件导出等功能，具有一定的实用性和易用性。G2E Lab发布的Vesta- Cades®软件声称可以对复杂电力电子变换器进行综合设计，但在公开发表的论文中尚未查阅到相关 记录。
然而，上述软件的优化算法往往内置并进行封装，只将正向问题的建模和求解开放给用户，寻优解算的复杂度和数值稳定性不清晰。事实上，优化算法的特性设计与正向问题的特性具有统一性，正映射更多侧重物理特性的分析，而逆映射则更多侧重数学特性的描述。好的优化算法应当与正向问题紧密配合，以期达到更好效果。对优化算法的选择和改进正是本文的出发点和落脚点。在这之前，回顾电力电子变换器尤其是电能路由器的优化设计的特点为：
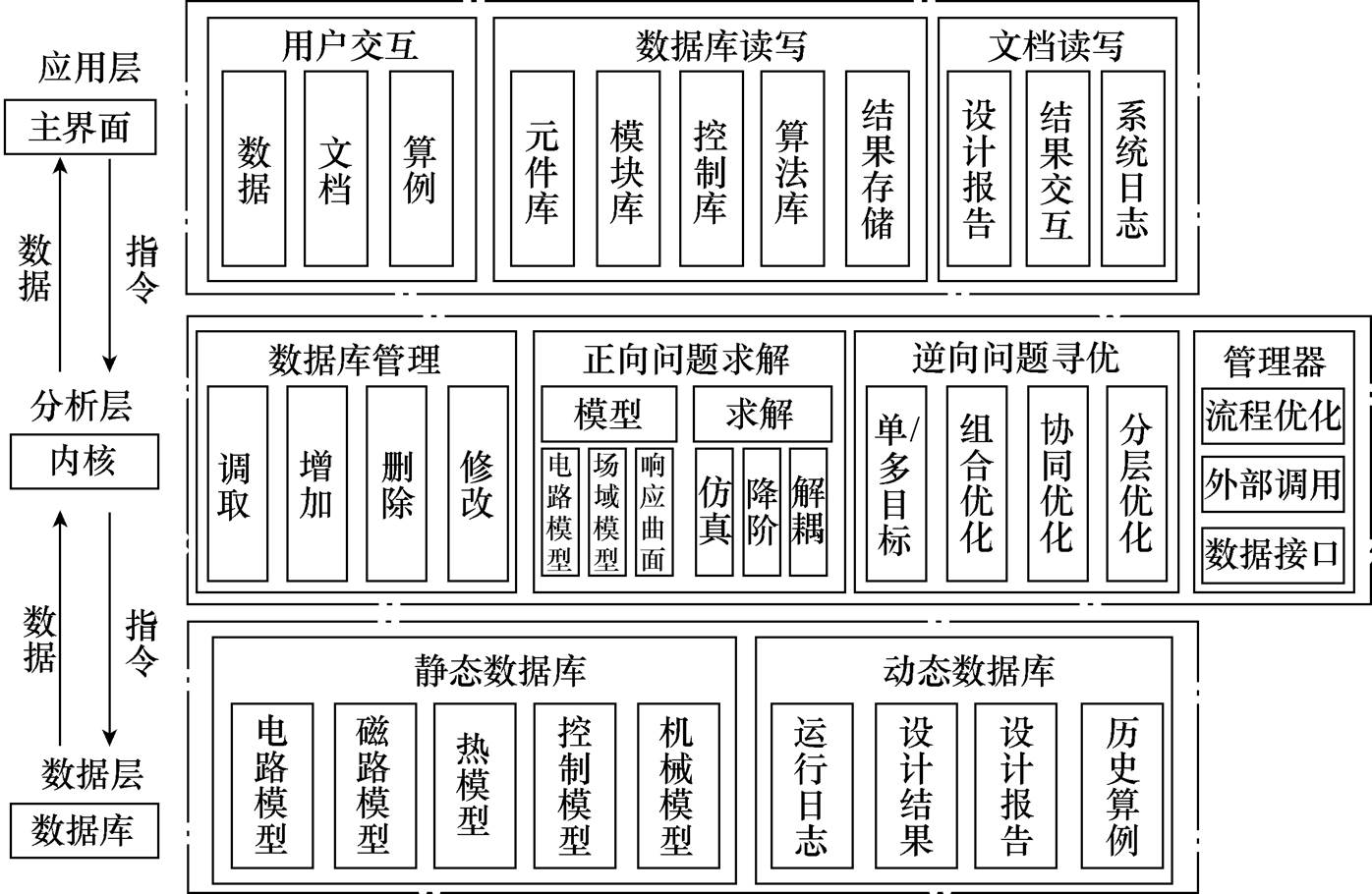
图3 电力电子设计自动化软件架构
Fig.3 Software framework of design automation for power electronics
（1）涉及多物理场耦合问题，正向映射复杂，求解正向映射过程耗时。
（2）目标函数非线性非凸，甚至可能包含参数优化和组合优化的混合优化问题。
（3）约束条件非线性非凸，种类多、数目多，电力电子系统不同环节时间尺度差别大、具有强刚性问题。
（4）决策变量存在离散和连续的混杂，且数目多。
传统优化算法应用于电力电子领域已有典型案例，其对于电力电子的平均模型和小信号模型已有成熟研究，但面对质量、损耗、成本等非线性目标函数或约束条件，研究者对两个经典传统非线性优化算法进行了研究：其一为顺序无约束最小化方法[39]（Sequential Unconstrained Minimization Tech- nique, SUMT）；其二为增广拉格朗日罚函数法[40-41]（Augmented Lagrangian, ALAG），两个算法的收敛性和计算资源消耗在一个设计案例中进行了对比，该设计案例为Buck变换器，决策变量有25个，约束16个，设计目标为单目标质量优化[19]。
元启发式算法各式各样[42]，有许多属性可以对它们进行分类[43]，其技术分类如图4所示，其中的演化算法（Evolutionary Algorithm, EA）为元启发式算法的一类分支。
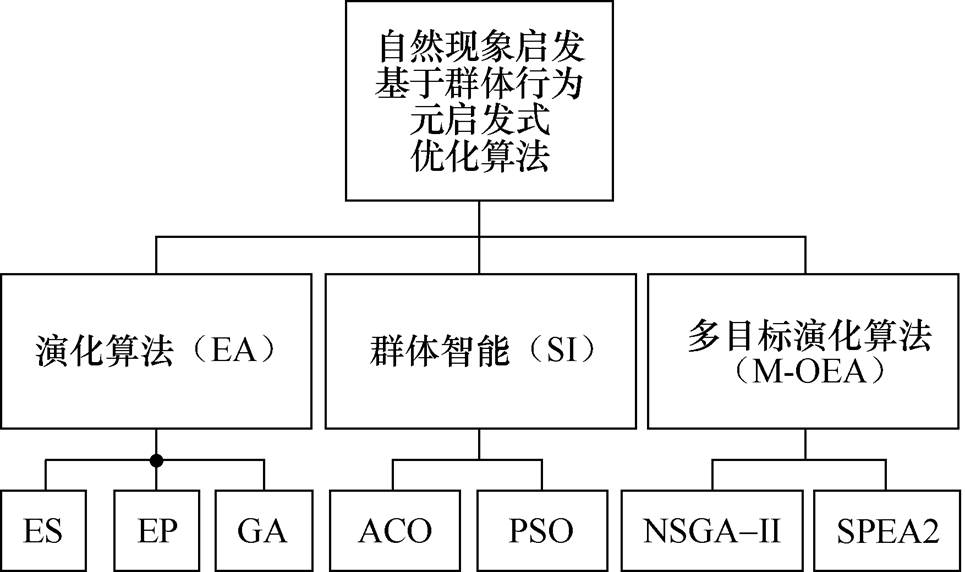
图4 元启发式算法分类
Fig.4 Classification of metaheuristic algorithms
值得说明的是，本文将讨论的遗传算法（Genetic Algorithm, GA）和演化算法（Evolutionary Algorithm, EA）在大多数情况下可以相互替换，它们都表示一大类算法的统称；另外，遗传算法也可以特指J. H. Holland在1975年提出的特定算法[44]。在英文文献中也存在遗传算法和演化算法相互混用的情况，这与算法诞生、扩展、细化、总结和归类的历史有关。在本文大部分情况下，遗传算法理解为一类算法，仅当遗传算法字样后存在文献引用时理解为一个具体算法。此外，由遗传算法发展出的算法可以用XXGA格式，如NSGA-II，也可以用XXEA格式，如RVEA。
演化算法包括遗传算法[44]、演化策略（Evolu- tion Strategy, ES）[45-46]、演化规划（Evolutionary Programming, EP）[47]和遗传程序设计（Genetic Programming, GP）[48]，也包括差分演化（Differential Evolution, DE）[49]，它们之间独立提出且稍有差别，许多文献对演化计算进行过总结[50-53]或分类[54]。
遗传算法的灵感来自于生物对大自然的适应以及它们的繁衍进化过程。遗传算法可以视作计算模型对进化过程的模拟，其流程如图5所示。遗传算法的主要流程包括编码、初始化、遗传算子、终止条件四个部分。其中，编码使得决策变量易于被遗传算子作用发生改变，与算法的搜索能力密切相关。初始化随机产生了多个决策变量，从而形成种群，算法因此具有并行计算能力；将不同遗传算子应用于当前群体的个体以生成下一代群体的个体，称为一次迭代。经过多次迭代之后，适应值更高的个体存活的概率更大；最终在满足一定条件后算法终止，给出最优解及相应的目标函数。
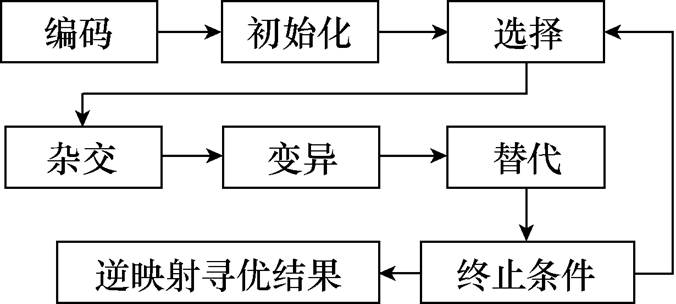
图5 遗传算法流程
Fig.5 Porcedure of genetic algorithms
当演化算法应用于多目标优化领域时，多目标演化算法（Multi Objective Evolutionary Algorithm, MOEA）成为演化算法的新分支，包括NSGA-II[55]、MOEA/D[56]、SPEA2[57]、MOPSO[58]和PESA2[59]。有研究给出了多目标演化算法的综述[60]。
在多目标优化问题中，利用遗传算法基于种群的特点，通过精巧地设置不同算子，可以使得种群个体收敛到帕累托前沿并均匀分布，同时得到多个可行解，这进一步拓宽了遗传算法的应用领域。图6展示了多目标演化算法NSGA-II流程。
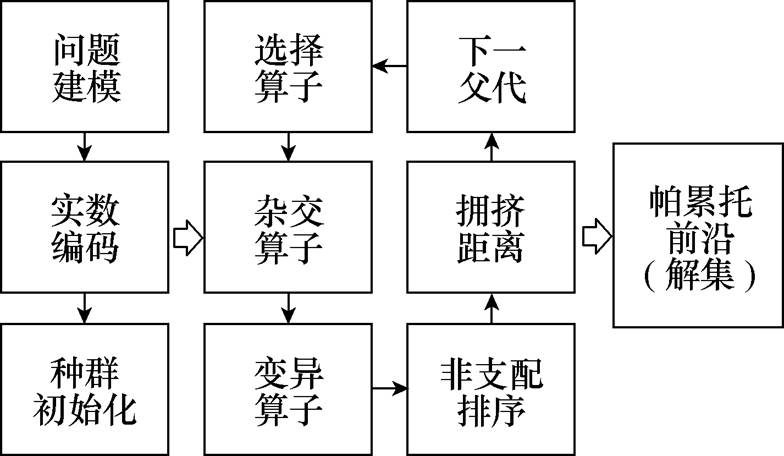
图6 NSGA-II流程
Fig.6 Procedure of NSGA-II
当前遗传算法仍在不断发展，其中一个重要发展方向就是多目标优化算法，这里的多目标指代的是Many Objective，一般要求目标函数大于10。而前述的多目标指代的是Multi Objective，一般针对目标函数介于2～3个的优化问题。前者可以看作后者的加强，在本文中用英文标注进行区别，但不做过多区分。在多目标演化算法中，两个最为经典的算法分别是NSGA-III[61-62]和RVEA[63]，他们率先使用了参考点和参考向量的方法，克服了传统多目标演化算法在高维目标空间中的非支配解比例大导致的传统遗传算子作用后进化慢、个体之间性能比较时计算复杂度大等缺点。
目前还没有研究者将演化计算应用于电能路由器自动化设计中，但一个显著的趋势是设计对象的复杂度随时间发展逐渐增大，从简单的Buck电路[64]，到复杂的隔离DC-DC变换器[65]、DC-AC逆变器[66]、AC-DC变换器[67]等电能路由器基本变换单元。设计对象的另一发展趋势是磁性元件。随着电力电子变换器开关频率的提高，磁性元件如电感[68]、高频变压器[69]、滤波器[70]获得了极大的关注。主要的关注点在于磁性元件的损耗，以及由此产生的发热问题影响变换器正常工作；此外，设计对象不仅仅局限在变换器和元件层面，系统级的布局[71]作为装置机械层面优化也有典型成果。
总的来看，电力电子变换器自身的发展迅速丰富了设计对象的选择种类，演化计算经过丰富而深刻的研究，解决复杂问题的能力得到了长足提升，被越来越广泛地应用于工程实践。算法发展和应用的时间线对比如图7所示。可以看到，两者时间上的差距越来越小，早期的研究者并未关注到遗传算法，遗传算法从被提出到应用经过了30余年的时间，但群体智能算法的时间间隔已经缩短到10余年，而多目标算法的时间间隔甚至降至低于10年，且算法针对电力电子的适应性改进越来越多，成为电力电子设计自动化的有力工具。
图7 算法诞生与算法应用于电力电子自动化设计时间线对比
Fig.7 Comparison of timelines between birth of algorithms and their application in DAPE
设计参数在变换器设计优化中定义了问题的决策变量，根据系统层次的不同，常见的设计参数 包括：
（1）材料级别的选择（如半导体材料、导电材料、导磁材料、电介质材料、导热材料和机械材料等）。
（2）电路元器件的选型和参数设计（如半导体器件、连接件、电感电容、变压器和散热器等）。
（3）系统级别的选择（如电路拓扑、控制方法、散热系统和机械系统等）。
根据数学性质的不同，可以分为：
（1）一般离散变量（如电容取值）。
（2）整数离散变量（如级联数、匝数、铁心并联数等，特别是开关频率，为了控制准确度取整数倍kHz或整数倍百Hz）。
（3）连续变量（如电容参数、比例积分微分控制参数、导线直径、铁心尺寸和散热器尺寸等）。
（4）其他变量（用于表示材料选择、开关选型、拓扑选择、控制模式和散热模式等）。
一项关于双向有源桥式（Dual Active Bridge, DAB）DC-DC变换器设计案例中包含了25个设计参数[72]，毫无疑问，在设计电能路由器时，决策变量的数量将会更多。
一个问题是，演化计算如何处理复杂多类的决策变量。事实上，通过编码可以解决绝大多数混杂变量问题[65]。首先演化计算可以对每一个决策变量都设置上下界，保证变量在杂交变异算子作用后仍然在合理的取值范围内。其次编码的方法随变量的不同而变化，对于连续变量，可以通过实数编码进行简单表示，对于离散变量，可以通过实数编码并进行取整操作实现变量的离散化，同时也可以使用整数编码。对于其他变量，可以使用二进制编码将不同方案表示成“0-1”字符串。最后对应地使用与编码方式配合的杂交变异等演化计算算子实现对决策变量的改变或重组，从而实现算法对不同决策变量的扰动和搜索。
值得注意的是，编码主要为了增加算法处理实际问题中混杂变量的能力，要转变成正向模型能够处理的输入变量，需要在遗传算子处理之后正向模型处理之前进行解码处理。
约束条件在变换器优化设计中占据十分重要的地位，从正向看它约束了变换器的“运行空间”，刻画了优化问题的“可行域”；从反向来看，也间接地定义了优化设计中的决策变量自由度。
根据设计对象的不同，常见的约束条件主要 包括：
（1）设计要求（如电流连续模式、电磁干扰、温升极限、共模电容、开关频率、电流电压纹波、总谐波失真和效率等）[66, 73]。
（2）决策变量取值范围（如电阻取值、电感取值、电容取值和半导体器件型号等）[67]。
（3）系统安全工作区（如半导体器件结温极限、导线通流能力、绝缘耐压能力、铁心温升极限、电压电流应力峰值和电压电流交流有效值等）[74]。
（4）对于特殊的磁性元件设计，还包括尺寸（窗口大小、导线直径）[69]和磁元件特性（磁通饱和磁元件损耗、磁元件最高温升）[75]。
（5）专门的设计目标（软开关约束、传输功率约束、开关频率约束、电流断续或连续模式等）[76-77]。
在处理约束条件时，遗传算法倾向于从两个方向进行解决。第一个方法是将对约束的违背定义为罚函数，并乘以系数使得超出约束的部分成为数量级较高的正数，由于遗传算法的标准问题为极小化问题，故违背约束条件的解适应值将偏低，在种群中处于劣势，在约束条件范围内的解适应值高，则将被选择、保存进入精英池并替代适应值偏低的解；第二个方法则通过比较和排序选择出“约束支配值”较高的个体，“约束支配值较高”的定义将适应值和约束条件违背置于同一框架下考虑，当以下任一条件满足时“A解优于B解”成立[62]：①A解和B解都满足约束，但A支配B（A的所有目标函数小于等于B的对应值，且A不等于B）；②A解满足约束，B解不满足约束；③A解和B解都不满足约束，但A解违反约束的程度较小。
前文对变换器设计目标列举和分析并不充分，分析和梳理现有研究中设计目标，笔者认为变换器设计目标常常是基础目的和特殊目的的排列组合，其中基础目的保证了电力电子变换器能够达到基本的设计功能，如基本的能量变换能力。设计目标包括电力电子变换器需要达到的稳态、暂态甚至是电磁瞬态特性，如电压电流应力、电压电流纹波、输出电压纹波、输出电压稳态误差、过冲和稳定时间、输出电压纹波、动态响应特性快速无超调等。这些特性可以按照时间尺度进行分类，长的时间尺度可以达到电网、电机等外接电源或负载的秒级波动，中等的时间尺度包括开关频率导致的的百微秒级电磁能量脉冲，短的时间尺度可以小到控制脉冲所受到的纳秒级电磁干扰[78]。
在满足了以上特性后，电力电子变换器还可以在实现高级的设计目标，如体积小、质量轻、成本低、效率高、电压电流比范围大等。对于一些特殊的部件一般有特殊的优化目标，如对极小化散热器热阻、质量和体积，磁元件参数精确性。现有研究绝大多数并不会考虑所有设计目标，而是选择最为关心的若干指标作为设计目标。
这意味着演化计算将要处理的目标函数更多，传统的方法将不同目标函数进行加权平均，但这样做的问题是，不同目标函数值域相差极大，人为定义权重因子可能无形中忽略数值范围较小的目标函数，造成结果的偏移。故多目标算法成为重要的算法，该算法能够通过帕累托前沿展示的寻优结果为设计目标的权衡取舍提供直观帮助。
另外，在目标函数数量较高的情况下，绝大多数解都不存在支配关系；其次在多维空间中，不同解的距离很远，维持解的均匀分布成为问题，如果按传统的方法计算“拥挤距离”，将极大耗费计算资源，增加算法复杂度。基于此，有研究提出了基于参考点的NSGA-III算法[61-62]，经过几代的发展，又相继对该方法进行了改进，使得参考点的选取更加合理[79]，之后，基于参考向量的RVEA算法也被提出[63]。演化算法自身也随着应用问题在演变进步。
电能路由器的设计目标与传统电力电子变换器的设计目标一脉相承，更高的变换效率、更高的功率密度、更低的成本是不变的发展方向[80]。通过设计，还可以满足更为细致的指标，如系统安全性、可靠性，各类稳态、暂态甚至电磁瞬态的性能要求。针对电能路由器“四多”的特征，设计目标需要具备新的特点：①为了适应未来端口电压和功率等级的扩容或缩容的情况，设计时必须考虑设计结果的灵活性和可扩展性；②为了使得电能路由器在不同端口状态和不同电能流向时都具有良好的电能转换性能，保障设计结果的通用性和普适性，设计时必须充分考虑电力电子器件、模块、变换单元的组合以及配合问题。但现有的设计方法仅仅找到可行解，无法保证解的最优性[14]。设计集成化、精细化、快速化有助于解决上述问题。
电能路由器的发展经历了多个阶段，其主要的发展脉络为工频变压器-高频变压器-电子变压器-固态变压器-电力电子变压器-高频高压化发展-多端口发展[12]。电能路由器的拓扑在演变的过程中不断分化，呈现几点显著差异：其一，在实现AC-AC变换功能上，多种拓扑被提出，有基于矩阵变换器的拓扑[81]，也有经典的AC-DC-AC拓扑；其二，在电力电子变压器运用于交流系统中或者是电力牵引的单向系统中，电力电子变压器的某一端口都会连接电压等级较高的配电网，此时多电平技术[82]和级联式H桥技术[83]都被用以解决这项问题；其三，电力电子变压器中需要有能量汇集和缓冲的部件，根据能量汇集点的不同，分为共交流母线[84]和共直流母线[85]两种不同的技术方案；其四，隔离高频变压器相对于AC-DC-AC三级变换器的级联位置，分为后端隔离和前端隔离两类拓扑[86]等。总之，电能路由器不同于以往的常规电力电子变换器，拓扑组合上不拘一格。
不同的拓扑各有特点，世界上主要的电力电子实验室也都制作了原理样机证明其可行性。但对于特定的端口电压等级和不同运行场景，拓扑之间的优劣无法定量区分。具体来讲，电能路由器不管应用于电力拖动还是电网，一般存在一个kV电压等级的电压源端口，但由于半导体器件的绝缘限制，势必要通过多模块或多电平的方法达到额定电压，常见的拓扑有多电平拓扑[82]，也有级联式拓扑[87]，随着宽禁带器件的飞速发展，甚至出现了两电平拓 扑[88]。但这些方案孰优孰劣仅有损耗层面的定量比较[89]，缺少全面定量精细的性能对比。
此外，在不同的应用场景电能路由器有不同的功能需求和能量流向。当用于电力牵引时，需要间歇高功率运行；用于配电网时，需要长时间额定工况运行；用于微电网时，功率流动方向复杂、传输功率变化范围大。值得注意的是，由于电能路由器多流向的特点，存在功率双向流动的工况，甚至是多个端口向一个端口传输功率的工况，复杂的工况给设计带来了极大挑战。电能路由器的设计不再仅仅依赖于单个变换单元实现效率最优，而是在多工况、多流向条件下实现多级变换单元效率配合最优，在特定的运行场景下实现性能最优。这代表在单次优化过程中设计者希望优化的部件更多，更接近真实运行场景，如设计一个同时考虑前后端滤波器、逆变器、电机、控制、电磁兼容多个组件的高度集成的电机驱动系统[90]。
要实现集成优化的目标，必须将控制模型和电路模型进行综合考虑，在算法上体现为多目标优化和协同优化。在Buck变换器设计自动化时，有研究提出将变换器分为主电路部分和反馈网络部分，使用和改进了多种启发式算法完成控制参数和电路参数的协同优化。典型的如伪随机协同进化算法[64]、正交局部搜索算法[91]、蚁群及其改进算法[92]、粒子群及其改进算法[93-94]。但相比于Buck电路，电能路由器的电路模型和控制模型更为复杂，给设计者提出了极大挑战。
复杂精细的模型有利有弊，优点在于涵盖了多层次的性能要求，提高了设计的集成度和精度；缺点在于解算速度较慢，甚至可能出现数值稳定性收敛性等问题。为了更好更快地进行电能路由器设计，需要在正向问题和逆向问题上同时推进，在正向问题上，在模型复杂度和时间复杂度上在进行取舍，或通过建模和仿真底层理论创新突破限制性因素。在逆向算法上，需要降低算法时间复杂度和空间复杂度，避免算法陷入维度灾，增加算法的搜索能力和收敛能力。
近年来，半导体技术发展势头不减，在器件层面推进并支撑电力电子装置快速迭代，推陈出新。碳化硅、氮化镓等宽禁带器件以高耐热水平、高开关速度被广泛关注。但与其特性相随的驱动串扰、开关尖峰和振荡以及电磁兼容等问题愈加明显。笔者所在团队在三个关键技术问题上实现了突破，这些问题包括功率半导体器件失效机理及其模型的建立；基于分布杂散参数的瞬态变换拓扑模型及其能量平衡；电磁能量脉冲序列分析及控制。同时提出了适用于系统级仿真分析的IGBT-Diode换流单元和SiC MOSFET-SiC Schottky Barrier Diode换流单元的简化行为模型。相关模型有效地解决了传统机理模型、行为模型仿真不易收敛的问题，且全部参数可不依赖实验，而是通过器件手册获取[78, 95-96]。基于这些研究，还进一步发展了计算SiC MOSFET开关损耗的解析模型[97]，这些工作使研究者通过高效的数值仿真就能对器件的开关尖峰和损耗加以评估，对实现电力电子装置的精准化设计有着重要意义。同时，包含开关瞬态的电力电子变换器系统级仿真方法[98-102]，以及基于级间解耦和模型降阶方法的电能路由器仿真模型[103]，都有助于极大地提高仿真效率，减小求解正映射问题的“昂贵性”，从而缩短设计时间。
电能路由器自动设计层面改进方法见表1。对于前述提到的三个设计改进方向，都可以从模型、求解和算法三个方面进行针对性的改进。总体看来，未来的挑战仍然巨大，从模型层面看，集成系统精细的模型仍然面临速度和精度的矛盾；从求解层面看，除加快速度，对于设计框架和设计流程的改进也是提高求解速度的一个方向；从算法层面看，也存在算法寻优能力和算法复杂度的矛盾。
表1 电能路由器自动设计层面改进方法
Tab.1 Improvement of design automation for electrical energy routers
设计改进方向模型层面求解层面算法层面 设计系统化控制—拓扑集成模型设计框架流程改进多目标优化与协同优化 设计精细化考虑瞬态非理想因素精确仿真多目标优化与协同优化 设计快速化模型降阶或简化快速仿真与设计框架流程改进控制算法复杂度
此外，在本文的构想中，未来电能路由器设计自动化流程如图8所示。相比于图1所示的传统人工设计流程，电能路由器设计自动化流程具有三个显著特点：①不再单步寻优而是借助优化算法整体寻优，从而使得设计结果最优得到保障；②自动化程度增加，正向求解过程和优化算法都由计算机辅助软件或程序实现，从而将设计人员从繁琐的重复工作中解放出来，使得设计人员能够将精力投入重要的模型搭建和结果权衡中；③考虑了多物理场的耦合，模型足够系统和精细，并且还具有可拓展性，根据设计者的需要，横向可以增加变压器设计、印制电路板（Printed Circuit Board, PCB）布局设计等，纵向可以进一步考虑热模型和机械模型的耦合和最终对于损耗模型的影响和修正。
设计自动化极度依赖计算机的计算资源，但电力电子设计自动化这一优化问题仍然需要人工的参与。需要指出的是，在任何领域的工程设计实践中，处于主导地位的一定是人。研究电力电子装置的自动化、系统化设计方法，其目的也绝非取代人，而是为了更高效地解决低效且重复性的“试—错”问题，使电力电子研究人员和工程师能够更加专注于技术统筹、架构优化等更为依赖设计者的直觉和创新的基础性问题。如多目标优化可以得到帕累托前沿，但对结果的偏好或取舍仍需设计人员决定。又如设计优化可以将已存在的拓扑和控制达到全局最优，但人工能够提出新的拓扑和新的控制方法，因此本文调研的文献中将不涉及新拓扑和新控制方法的内容，只是借助了计算机辅助工具将传统人工设计方法的效果增强，时间减小。
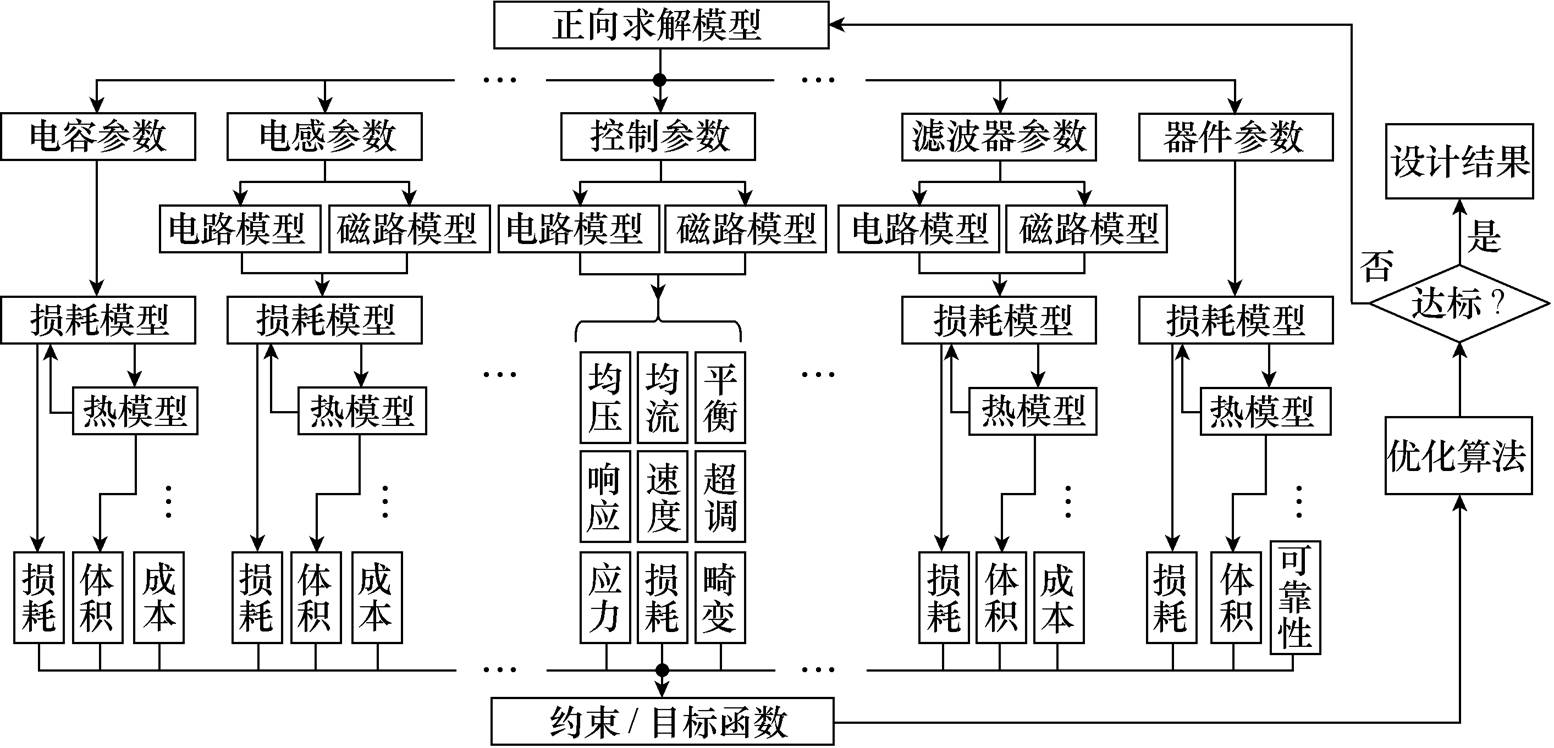
图8 电能路由器设计自动化流程
Fig.8 Procedure of design automation of electrical energy router
除此之外，对结果的处理和验证是计算机不能够替代的。设计自动化是向下兼容的，传统的设计经验也将以一定的形式反映到设计结果中，需要人工分析设计结果和设计要求的关系，发掘数学结果和物理本质的统一规律。此外，设计自动化对传统设计的拓展，利用设计框架内的组件，可以容易地分析设计结果的鲁棒性、参数敏感度、关键限制性因素等，在意大利热那亚举办的第二届电力电子设计自动化研讨会中，ETHZ大学的J. W. Kolar教授团队展示了他们对于设计空间多样性（Design Space Diversity, DSD）的研究成果[104]，他们的研究从遍历搜索开始，得到了6 600万个解，其中，1 600万为可行解，30万个准最优解。其中，准最优解包括位于帕累托边界上的解以及边界上的解所支配的非最优解，非最优解对应的设计目标——损耗，不超过最优解对应损耗的15%。进一步地，他们研究了开关频率这一设计参数的影响，发现变压器的最优频率并非变换器的最优频率，并定量给出了介于两者之间的频率参数对于损耗的影响。这一工作可以视作对电力电子设计参数准确度和鲁棒性的早期尝试，目前尚未在文献中发现电力电子设计自动化领域中对于电感、电容、变压器等参数鲁棒性的研究。
最后，设计的结果一定需要硬件试制、组配、调试一系列工作进行实验验证，从而证明设计结果的可行性或针对设计与实验的差异改进模型、修正框架、完善算法。
本文从电力电子设计自动化的角度出发，梳理电力电子设计自动化的体系，该体系包括设计流程架构、建模与特性分析、优化算法、软件实现等四个方面。讨论了遗传算法应用于电能路由器设计自动化的技术起源、发展和应用，针对电能路由器特殊的性质，提出遗传算法对电力电子设计自动化这一优化问题的处理方法及改进方向。最后展望了电能路由器这一特殊电力电子装置在设计中的研究难点和前瞻性问题，包括拓扑选择、运行工况和控制方法三位一体的集成优化问题，也指出精细化、系统化、快速化将是设计发展的方向和挑战。随着电力电子设计自动化这一课题被越来越多研究者关注，应用于复杂电力电子系统如电能路由器设计的优化算法将得到长足的进步和发展。
参考文献
[1] Blaabjerg F, Yang Yongheng, Ma Ke, et al. Power electronics-the key technology for renewable energy system integration[C]//IEEE 2015 International Con- ference on Renewable Energy Research and Applications, Glasgow, 2015: 1618-1626.
[2] Carrasco J M, García Franquelo L, Bialasiewicz J T, et al. Power-electronic systems for the grid integr- ation of renewable energy sources: a survey[J]. IEEE Transactions on Industrial Electronics, 2006, 53(4): 1002-1016.
[3] 国家电网《泛在电力物联网建设大纲》正式发布[EB/OL]. (2019-03-11). http://www.chinasmartgrid. com.cn/news/20190311/632172.shtml.
[4] 关于推进“互联网+”智慧能源发展的指导意见[EB/OL]. (2016-02-29). http://www.nea.gov.cn/2016- 02/29/c_135141026.htm.
[5] 孙宏斌, 郭庆来, 潘昭光. 能源互联网: 理念、架构与前沿展望[J]. 电力系统自动化, 2015, 39(19): 1-8.
Sun Hongbin, Guo Qinglai, Pan Zhaoguang. Energy internet: concept, architecture, and frontier outlook[J]. Automation of Electric Power Systems, 2015, 39(19): 1-8.
[6] Sarlioglu B, Morris C T. More electric aircraft: review, challenges, and opportunities for commercial transport aircraft[J]. IEEE Transactions on Transport- ation Electrification, 2015, 1(1): 54-64.
[7] Dujic D, Zhao Chuanhong, Mester A, et al. Power electronic traction transformer-low voltage proto- type[J]. IEEE Transactions on Power Electronics, 2013, 28(12): 5522-5534.
[8] Krein P T. Data center challenges and their power electronics[J]. CPSS Transactions on Power Electro- nics and Applications, 2017, 2(1): 39-46.
[9] Chen Haisheng, Cong Thang Ngoc, Yang Wei, et al. Progress in electrical energy storage system: a critical review[J]. Progress in Natural Science, 2009, 19(3): 291-312.
[10] Bragard M, Soltau N, Thomas S, et al. The balance of renewable sources and user demands in grids: power electronics for modular battery energy storage systems[J]. IEEE Transactions on Power Electronics, 2010, 25(12): 3049-3056.
[11] She Xu, Huang Alex Q, Burgos R. Review of solid- state transformer technologies and their application in power distribution systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2013, 1(3): 186-198.
[12] 赵争鸣, 冯高辉, 袁立强, 等. 电能路由器的发展及其关键技术[J]. 中国电机工程学报, 2017, 37(13): 3823-3834.
Zhao Zhengming, Feng Gaohui, Yuan Liqiang, et al. The development and key technologies of electric energy router[J]. Proceedings of the CSEE, 2017, 37(13): 3823-3834.
[13] 冯高辉, 赵争鸣, 袁立强. 基于能量平衡的电能路由器综合控制技术[J]. 电工技术学报, 2017, 32(14): 34-44.
Feng Gaohui, Zhao Zhengming, Yuan Liqiang. Synthetical control technology of electric energy router based on energy balance relationship[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 34-44.
[14] 曹阳, 袁立强, 朱少敏, 等. 面向能源互联网的配网能量路由器关键参数设计[J]. 电网技术, 2015, 39(11): 3094-3101.
Cao Yang, Yuan Liqiang, Zhu Shaomin, et al. Parameter design of energy router orienting energy internet[J]. Power System Technology, 2015, 39(11): 3094-3101.
[15] 赵争鸣, 施博辰, 朱义诚. 对电力电子学的再认识——历史, 现状及发展[J]. 电工技术学报, 2017, 32(12): 5-15.
Zhao Zhengming, Shi Bochen, Zhu Yicheng. Recon- sideration on power electronics: the past, present and future[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 5-15.
[16] 赵争鸣, 袁立强, 鲁挺. 电力电子系统电磁瞬态过程[M]. 北京: 清华大学出版社, 2017.
[17] Martins J R R A, Lambe A B. Multidisciplinary design optimization: a survey of architectures[J]. AIAA Journal, 2013, 51(9): 2049-2075.
[18] Wu C J, Lee F C, Balachandran S, et al. Design optimization for a half-bridge DC-DC converter[C]// 1980 IEEE Power Electronics Specialists Conference, Atlanta, 1980: 57-67.
[19] Balachandran S, Lee F C. Algorithms for power converter design optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 1981(3): 422- 432.
[20] De León-Aldaco S E, Calleja H, Alquicira J A. Metaheuristic optimization methods applied to power converters: a review[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 6791-6803.
[21] Reinelt G. TSPLIB-a traveling salesman problem library[J]. ORSA Journal on Computing, 1991, 3(4): 376-384.
[22] Tomoiagă B, Chindriş M, Sumper A, et al. Pareto optimal reconfiguration of power distribution systems using a genetic algorithm based on NSGA-II[J]. Energies, 2013, 6(3): 1439-1455.
[23] Li Qian, Burgos R, Boroyevich D. Hierarchical weight optimization design of aircraft power electronics systems using metaheuristic optimization methods[C]//2018 AIAA/IEEE Electric Aircraft Tech- nologies Symposium (EATS), New Orleans, 2018: 1-10.
[24] Biela J, Kolar J W, Stupar A, et al. Towards virtual prototyping and comprehensive multi-objective optimisation in power electronics[C]//Proceedings of the International Power Conversion and Intelligent Motion Conference, Nuremberg, 2010: 515-538.
[25] Kolar J W. Multi-objective optimization in power elec- tronics[Z]. Sun-Yat-Sen-National University (NSYSU), ETH Zurich, 2017.
[26] Waffler S, Preindl M, Kolar J W. Multi-objective optimization and comparative evaluation of Si soft- switched and SiC hard-switched automotive DC-DC converters[C]//2009 35th Annual Conference of IEEE Industrial Electronics, Porto, 2009: 3814-3821.
[27] Lee F C, Van Wyk J D, Boroyevich D, et al. An integrated approach to power electronics systems[C]// IEEE Proceedings of the Power Conversion Con- ference, Osaka, 2002, 1: 7-12.
[28] Ghizoni D, Burgos R, Francis G, et al. Design and evaluation of a 33kW PEBB module for distributed power electronics conversion systems[C]//2005 IEEE 36th Power Electronics Specialists Conference, Piscataway, 2005: 530-536.
[29] Celanovic I, Celanovic N, Milosavljevic I, et al. A new control architecture for future distributed power electronics systems[C]//2000 IEEE 31st Annual Power Electronics Specialists Conference. Conference Pro- ceedings, Vancouver, 2000, 1: 113-118.
[30] Viscarret U, Etxeberria-Otadui I, Azurmendi J M, et al. Design of power electronic building blocks (PEBB) for multiMW modular traction converters[C]//2010 IEEE Energy Conversion Congress and Exposition, Atlanta, 2010: 4217-4222.
[31] Tardy A, Roboam X, Zanchetta P, et al. Towards more optimization for aircraft energy conversion systems[C]//More Electric Aircraft (MEA 2015), Toulouse, 2015, 1-17.
[32] Kolar, Biela, Minibock. Exploring the Pareto front of multi-objective single-phase PFC rectifier design optimization-99.2% efficiency vs. 7kW/dm3 power density[C]//IEEE International Power Electronics & Motion Control Conference, Wuhan, 2009: 9-29.
[33] Burkart R M. Advanced modeling and multi- objective optimization of power electronic converter systems[D]. ETH Zurich, 2016.
[34] Chen Zhou. Integrated electrical and thermal modeling, analysis and design for IPEM[D]. Virginia Tech, 2004.
[35] Wu Yingxiang. Describing integrated power elec- tronics modules using STEP AP210[D]. Virginia Tech, 2004.
[36] Evans P L, Castellazzi A, Johnson C M. Design tools for rapid multidomain virtual prototyping of power electronic systems[J]. IEEE Transactions on Power Electronics, 2015, 31(3): 2443-2455.
[37] Li Ke, Evans P, Johnson M. Developing power semiconductor device model for virtual prototyping of power electronics systems[C]//2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, 2016: 1-6.
[38] Chinesta F, Ladeveze P, Cueto E. A short review on model order reduction based on proper generalized decomposition[J]. Archives of Computational Methods in Engineering, 2011, 18(4): 395-404.
[39] Fiacco A V, McCormick G P. The sequential unconstrained minimization technique for nonlinear programing, a primal-dual method[J]. Management Science, 1964, 10(2): 360-366.
[40] Powell M J D. A method for nonlinear constraints in minimization problems[J]. Optimization, 1969: 283- 298.
[41] Hestenes M R. Multiplier and gradient methods[J]. Journal of Optimization Theory and Applications, 1969, 4(5): 303-320.
[42] Bianchi L, Dorigo M, Gambardella L M, et al. A survey on metaheuristics for stochastic combinatorial optimization[J]. Natural Computing, 2009, 8(2): 239- 287.
[43] Blum C, Roli A. Metaheuristics in combinatorial optimization: overview and conceptual comparison[J]. ACM Computing Surveys (CSUR), 2003, 35(3): 268- 308.
[44] Holland J H. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence[M]. Cambridge, MIT Press, 1992.
[45] Vent W. Rechenberg, ingo, evolutionsstrategie— optimierung technischer systeme nach prinzipien der biologischen evolution. 170 S. mit 36 Abb. frommann- holzboog-verlag. stuttgart 1973. broschiert[J]. Feddes Repertorium, 1975, 86(5): 337.
[46] Shwefel H P. Numerische optimierung von computer- modellen[D]. PhD Thesis, Decision Support Methods for Global Optimization, 1974.
[47] Fogel L J, Owens A J, Walsh M J. Application of evolutionary programming[C]//Record of the IEEE Systems Science and Cybernetics Conference, Washington D C, 1966: 945-956.
[48] Koza J R, Koza J R. Genetic programming: on the programming of computers by means of natural selection[M]. MIT Press, 1992.
[49] Storn R, Price K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359.
[50] Back T. Evolutionary algorithms in theory and practice: evolution strategies, evolutionary programming, genetic algorithms[M]. Oxford: Oxford University Press, 1996.
[51] Fogel D B. Introduction to evolutionary com- putation[M]. Evolutionary Computation, 2000.
[52] Spears W M. Evolutionary algorithms: the role of mutation and recombination[M]. Springer Science & Business Media, 2013.
[53] Michalewicz Z, Fogel D B. How to solve it: modern heuristics[M]. Springer Science & Business Media, 2013.
[54] Calégari P, Coray G, Hertz A, et al. A taxonomy of evolutionary algorithms in combinatorial optimi- zation[J]. Journal of Heuristics, 1999, 5(2): 145-158.
[55] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
[56] Zhang Qingfu, Li Hui. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731.
[57] Zitzler E, Laumanns M, Thiele L. SPEA2: improving the strength Pareto evolutionary algorithm[Z]. TIK- report 103, 2001.
[58] Coello C A C, Lechuga M S. MOPSO: a proposal for multiple objective particle swarm optimization[C]// IEEE Proceedings of the 2002 Congress on Evolu- tionary Computation, Honolulu, 2002, 2: 1051-1056.
[59] Corne D W, Jerram N R, Knowles J D, et al. PESA-II: region-based selection in evolutionary multio- bjective optimization[C]//Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation, San Francisco, 2001: 283-290.
[60] Deb K. Multi-objective optimization using evolu- tionary algorithms[M]. John Wiley & Sons, 2001.
[61] Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2013, 18(4): 577-601.
[62] Jain H, Deb K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: handling constraints and extending to an adaptive approach[J]. IEEE Transactions on Evolutionary Computation, 2013, 18(4): 602-622.
[63] Cheng Ran, Jin Yaochu, Olhofer M, et al. A reference vector guided evolutionary algorithm for many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 773-791.
[64] Zhang Jun, Chung H S H, Lo W L. Pseudocoevo- lutionary genetic algorithms for power electronic circuits optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2006, 36(4): 590-598.
[65] Versele C, Deblecker O, Lobry J. A computer-aided design tool dedicated to isolated DC-DC converters based on multiobjective optimization using genetic algorithms[J]. COMPEL-The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2012, 31(2): 583-603.
[66] Mirjafari M, Balog R S. Multi-objective design optimization of renewable energy system inverters using a descriptive language for the components[C]// 2011 Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, 2011: 1838-1845.
[67] Escobar G, Stankovic A M, Carrasco J M, et al. Analysis and design of direct power control (DPC) for a three phase synchronous rectifier via output regulation subspaces[J]. IEEE Transactions on Power Electronics, 2003, 18(3): 823-830.
[68] Schumacher D, Bilgin B, Emadi A. Inductor design for multiphase bidirectional DC-DC boost converter for an EV/HEV application[C]//2017 IEEE Trans- portation Electrification Conference and Expo (ITEC), Chicago, 2017: 221-228.
[69] Versèle C, Deblecker O, Lobry J. Multiobjective optimal design of transformers for isolated switch mode power supplies[C]//IEEE SPEEDAM, Pisa, 2010: 1687-1692.
[70] Mühlethaler J. Modeling and multi-objective optimi- zation of inductive power components[D]. ETH Zurich, 2012.
[71] Ning Puqi, Wang Fei, Ngo K D T. Automatic layout design for power module[J]. IEEE Transactions on Power Electronics, 2011, 28(1): 481-487.
[72] Burkart R M, Kolar J W. Comparative h-r-s Pareto optimization of Si and SiC multilevel dual-active- bridge topologies with wide input voltage range[J]. IEEE Transactions on Power Electronics, 2016, 32(7): 5258-5270.
[73] Tran D, Chakraborty S, Lan Yuanfeng, et al. Optimized multiport DC/DC converter for vehicle drivetrains: topology and design optimization[J]. Applied Sciences, 2018, 8(8): 1351-1368.
[74] Busquets-Monge S, Crebier J C, Ragon S, et al. Design of a boost power factor correction converter using optimization techniques[J]. IEEE Transactions on Power Electronics, 2004, 19(6): 1388-1396.
[75] Lefranc P, Jannot X, Dessante P. Virtual prototyping and pre-sizing methodology for Buck DC-DC converters using genetic algorithms[J]. IET Power Electronics, 2012, 5(1): 41-52.
[76] Rosskopf A, Volmering S, Ditze S, et al. Autonomous circuit design of a resonant converter (LLC) for on-board chargers using genetic algorithms[C]//2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, 2018: 96-101.
[77] Neugebauer T C, Perreault D J. Computer-aided optimization of DC/DC converters for automotive applications[J]. IEEE Transactions on Power Elec- tronics, 2003, 18(3): 775-783.
[78] 施博辰, 赵争鸣, 蒋烨, 等. 功率开关器件多时间尺度瞬态模型(Ⅰ)——开关特性与瞬态建模[J]. 电工技术学报, 2017, 32(12): 16-24.
Shi Bochen, Zhao Zhengming, Jiang Ye, et al. Multi-time scale transient models for power semi- conductor devices (part I: switching characteristics and transient modeling)[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 16-24.
[79] Jain H, Deb K. An improved adaptive approach for elitist nondominated sorting genetic algorithm for many-objective optimization[C]//International Con- ference on Evolutionary Multi-Criterion Optimization, Springer, Berlin, Heidelberg, 2013: 307-321.
[80] Schanen J L. Design of power electronics converter: beyond topology[R/OL]. (2017-03-16)[2019-07-09]. http://seeds.cnrs.fr/IMG/pdf/b04-jls_optimisation_des_ convertisseurs.pdf.
[81] Gupta R K, Castelino G F, Mohapatra K K, et al. A novel integrated three-phase, switched multi-winding power electronic transformer converter for wind power generation system[C]//IECON'09. 35th Annual Conference of IEEE Industrial Electronics, Porto, 2009: 4481-4486.
[82] Tripathi A K, Hatua K, Mirzaee H, et al. A three- phase three winding topology for dual active bridge and its DQ mode control[C]//2012 Applied Power Electronics Conference and Exposition (APEC), 2012: 1368-1372.
[83] Wang Gangyao, Baek S, Elliott J, et al. Design and hardware implementation of Gen-1 silicon based solid state transformer[C]//2011 Applied Power Electronics Conference and Exposition (APEC), Fort Worth, 2011: 1344-1349.
[84] Li Kai, Zhao Zhengming, Yuan Liqiang, et al. Synergetic control of high-frequency-link based multi-port solid state transformer[C]//2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, 2018: 5630-5635.
[85] Shi Jianjiang, Gou Wei, Yuan Hao, et al. Research on voltage and power balance control for cascaded modular solid-state transformer[J]. IEEE Transa- ctions on Power Electronics, 2011, 26(4): 1154-1166.
[86] Huber J E, Rothmund D, Kolar J W. Comparative evaluation of isolated front end and isolated back end multi-cell SSTs[C]//2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 2016: 3536- 3545.
[87] Nabae A, Takahashi I, Akagi H. A new neutral- point-clamped PWM inverter[J]. IEEE Transactions on Industry Applications, 1981, IA-17(5): 518-523.
[88] She Xu, Yu Xunwei, Wang Fei, et al. Design and demonstration of a 3.6kV-120V/10kVA solid-state transformer for smart grid application[J]. IEEE Transactions on Power Electronics, 2013, 29(8): 3982-3996.
[89] Falcones S, Mao Xiaolin, Ayyanar R. Topology com- parison for solid state transformer implementation[C]// 2010 IEEE Power and Energy Society General Meeting, Calgary, 2010: 1-8.
[90] Wang Fei, Shen Wei, Boroyevich D, et al. Design optimization of industrial motor drive power stage using genetic algorithms[C]//Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, USA, 2006, 5: 2581-2586.
[91] Huang Tao, Huang Jian, Zhang Jun. An orthogonal local search genetic algorithm for the design and optimization of power electronic circuits[C]//2008 IEEE Congress on Evolutionary Computation, Hong Kong, 2008: 2452-2459.
[92] Zhang Jun, Chung H S H, Lo A W L, et al. Extended ant colony optimization algorithm for power electronic circuit design[J]. IEEE Transactions on Power Electronics, 2008, 24(1): 147-162.
[93] Zhang Jun, Shi Yuan, Zhan Zhihui. Power electronic circuits design: a particle swarm optimization approach[C]//Asia-Pacific Conference on Simulated Evolution and Learning, Springer, Berlin, Heidelberg, 2008: 605- 614.
[94] Zhan Zhihui, Zhang Jun. Orthogonal learning particle swarm optimization for power electronic circuit optimization with free search range[C]//2011 IEEE Congress of Evolutionary Computation (CEC), New Orleans, 2011: 2563-2570.
[95] 蒋烨, 赵争鸣, 施博辰, 等. 功率开关器件多时间尺度瞬态模型(Ⅱ)——应用分析与模型互联[J]. 电工技术学报, 2017, 32(12): 25-32.
Jiang Ye, Zhao Zhengming, Shi Bochen, et al. Multi-time scale transient models for power semicon- ductor devices (part II: applications analysis and model connection)[J]. Transactions of China Electro- technical Society, 2017, 32(12): 25-32.
[96] 朱义诚, 赵争鸣, 王旭东, 等. SiC MOSFET与SiC SBD换流单元瞬态模型[J]. 电工技术学报, 2017, 32(12): 58-69.
Zhu Yicheng, Zhao Zhengming, Wang Xudong, et al. Analytical transient model of commutation units with SiC MOSFET and SiC SBD pair[J]. Transactions of China Electrotechnical Society 2017, 32(12): 58-69.
[97] Wang Xudong, Zhao Zhengming, Li Kai, et al. Analytical methodology for loss calculation of SiC MOSFETs[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 7(1): 71-83.
[98] Shi Bingqing, Zhao Zhengming, Zhu Yicheng. Piecewise analytical transient model for power switching device commutation unit[J]. IEEE Transa- ctions on Power Electronics, 2018, 34(6): 5720- 5736.
[99] Li Boyang, Zhao Zhengming, Yang Yi, et al. A novel simulation method for power electronics: discrete state event driven method[J]. CES Transactions on Electrical Machines and Systems, 2017, 1(3): 273- 282.
[100] 杨祎, 赵争鸣, 檀添, 等. 离散状态事件驱动仿真方法及自适应预估校正算法[J]. 电工技术学报, 2017, 32(12): 33-41.
Yang Yi, Zhao Zhengming, Tan Tian, et al. Discrete state event driven method and self-adapted predictor- corrector algorithm[J]. Transactions of China Elec- trotechnical Society, 2017, 32(12): 33-41.
[101] 李帛洋, 赵争鸣, 檀添, 等. 后向离散状态事件驱动电力电子仿真方法[J]. 电工技术学报, 2017, 32(12): 42-49.
Li Boyang, Zhao Zhengming, Tan Tian, et al. A backword discrete state event driven simulation method for power electronics based on finite state machine[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 42-49.
[102] 施博辰, 赵争鸣, 朱义诚, 等. 离散状态事件驱动仿真方法在高压大容量电力电子变换系统中的应用[J]. 高电压技术, 2019, 45(7): 2053-2061.
Shi Bochen, Zhao Zhengming, Zhu Yicheng, et al. Application of discrete state event-driven simulation framework in high-voltage power electronic hybrid systems[J]. High Voltage Technology, 2019, 45(7): 2053-2061.
[103] 易姝娴, 袁立强, 李凯, 等. 面向区域电能路由器的高效仿真建模方法[J]. 清华大学学报: 自然科学版, 2019, 59(10): 796-806.
Yi Shuxian, Yuan Liqiang, Li Kai, et al. High efficiency modeling method for regional energy routers[J]. Journal of Tsinghua University: Science and Technology, 2019, 59(10): 796-806.
[104] Guillod T, Kolar J W. Handling design space diversity of power electronics multi-objective opti- mization[R/OL]. IEEE Design Automation for Power Electronics Workshop (DAPE), Genoa, Italy, September 6, 2019. [2019-12-11]. https://www.pes-publications. ee.ethz.ch/uploads/tx_ethpublications/workshop_pub- lications/8_DAPE_guillod_2019.pdf.
Design Automation for Electrical Energy Router-Design Workflow Framework and Genetic Algorithm: a Review
Abstract Electrical energy routers are promising in energy Internet, ubiquitous electric Internet of Things and other scenarios, and have the features of multi-cascade, multi-port, multi-flow, and multi-modal. These features bring many difficulties to traditional manual design. Design automation for power electronics is expected to overcome the challenges such as difficulty in weighing design objectives, wasting costs on marginal design, time-consuming and labor in hardware iterations, and low degree of design automation. With the rapid development of wide bandgap devices, rapid iteration of computer performance, and extension and refinement of converter application scenarios, design automation for power electronics is expected to achieve design integration, refinement and rapidity. The electrical energy router design problem can be abstracted as a multidisciplinary optimization problem with poor mathematical nature and large scale. Regarding such optimization problems, genetic algorithms have better performance than the traditional optimization algorithms. Based on a systematic summary of the current mainstream design workflow and design software architecture, this paper analyzes the applicability of genetic algorithms to solve design automation problems of power electronics, summarizes the potential problems and challenges in design automation for electrical energy routers, and gives corresponding suggestions.
keywords：Design automation for power electronics, electrical energy router, design workflow, design software, optimization, genetic algorithm
中图分类号：TM46; TP301
DOI: 10.19595/j.cnki.1000-6753.tces.191022
国家自然科学基金资助项目（51577100，51490683）。
收稿日期 2019-08-11
改稿日期 2019-12-17
袁立强 男，1976年生，博士，副研究员，博士生导师，研究方向为大容量电力电子变换器、电能路由器。E-mail: ylq@mail.tsinghua.edu.cn
赵争鸣 男，1959年生，博士，教授，博士生导师，研究方向为电力电子系统动力学表征、能源互联网。E-mail: zhaozm@tsinghua.edu.cn（通信作者）
（编辑 崔文静）