图1 高速载流摩擦磨损实验机
Fig.1 High-speed tester of friction and wear with electric current
摘要 在电气化铁路弓网系统中，受电弓滑板与接触线之间的摩擦振动加速度反映了弓网载流摩擦的接触状况，影响弓网的离线概率以及磨损状态。该文通过对弓网接触状态的分析，建立弓网摩擦副的弹簧-阻尼-质量模块摩擦振动模型。通过实验研究，在考虑法向压力、运行速度及电流强度三要素对摩擦振动的影响下，分析摩擦振动模型中特性参数和受力与三要素的函数关系；在此基础上，利用实验数据求解函数关系中的常数参数。最后通过实验验证摩擦振动模型的精确性，为进一步研究弓网系统的载流摩擦磨损机理以及离线概率提供理论依据。
关键词：弓网系统 载流摩擦振动加速度 振动模型
受电弓与接触网是电气化轨道交通牵引供电系统的重要组成部分，电力机车通过受电弓滑板与接触线的滑动接触，从接触网获得电能保证电力机车的正常运行。在机车运行的过程中，受电弓滑板与接触线摩擦副由于相互接触滑动运动，必然会产生非线性摩擦振动，而受电弓滑板与接触线在竖直方向上的振动，会造成弓网离线，产生电弧，是机车的受流质量、稳定运行以及滑板使用寿命的主要影响因素[1-3]。所以研究弓网竖直方向的非线性振动具有重要的理论意义和实际价值。
目前，有关弓网系统载流状态下接触表面形貌变化，受电弓滑板与接触线线性与非线性受力分析以及纯机械的摩擦振动研究已经取得了一定的成果。文献[4-6]分析了弓网载流摩擦接触过程中，法向压力、运行速度和电流强度对接触表面的影响，利用智能算法建立弓网的最优载荷以及接触面摩擦力的数学模型，利用载流实验数据验证了模型的准确性，但文献未涉及弓网摩擦副的受力分析以及摩擦振动计算。文献[7-9]研究了高速列车的各种磨损以及动力学影响规律，提出了线性和非线性的受电弓与接触网垂向耦合动力学模型，利用仿真验证了模型的准确性，并指出了非线性模型与线性模型的应用条件，但文献未涉及弓网运行速度、电流强度对接触面表面的影响。文献[10-11]中以纯机械的单自由度弹簧-阻尼-质量模块模型为基础，建立了双自由度以及多自由度的摩擦振动模型，分析了速度、压力、刚度以及摩擦环境等对摩擦振动的影响，并以实际的城市轨道交通第三轨受流器为例，建立了摩擦振动动力学模型，完善了波动载荷下的动力学模型，并通过ADAMS软件验证了模型的有效性，但文献中摩擦振动模型为纯机械的弹簧-阻 尼-质量模块模型，考虑了运行中运行条件对摩擦振动的影响，但不涉及强电流下模型参数以及摩擦振动的变化规律。
本文在分析了弓网摩擦副接触结构的基础上，建立了受电弓滑板与接触线的摩擦振动模型，研究了弓网的摩擦振动运动状态以及弓网运行条件下摩擦振动加速度的变化规律，利用实验数据求解了摩擦振动模型的常数参数并验证了模型的准确性，为以后弓网系统摩擦振动对弓网磨损以及离线概率的进一步研究提供一定的理论基础。
实验采用自行研制的高速载流摩擦磨损实验机如图1所示。接触线固定在实验机转盘边沿，与接触线相接触的受电弓滑板固定于滑台上，并通过滑台进行往复移动，模拟实际弓网运行条件下的Z字形运动轨迹。电流通过电源—滑板—接触线—滑板—电源形成回路。实验中，通过微机调节电动机转速进而控制接触线与滑板之间的相对速度，利用调压器调节接触电流强度，通过音圈电机等设备控制浸金属碳滑板与接触线的接触压力。整体实验机能够有效地模拟出弓网实际工况下受电弓滑板与接触线的摩擦接触振动。而测量摩擦振动的加速度传感器固定在滑板的滑台侧，能够准确地测量摩擦振动加速度。实验机的主要性能参数见表1。
图1 高速载流摩擦磨损实验机
Fig.1 High-speed tester of friction and wear with electric current
表1 实验机性能参数
Tab.1 Performance parameters of the experimental machine
参 数数 值 功率P/kW22 速度v/(kW/h)0～300 压力F/N0～200 电流I/A0～800
实验中采用的铜导线性能参数见表2。
表2 铜导线性能参数
Tab.2 Performance parameters of copper conductor
参 数数 值 硬度(HBR)96.2 密度D/(103kg/m3)8.9 电阻率r/(mW·m)0.018 51 热导率l/[W/(m·K)]380 比热容cp/[J/(kg·K)]387
浸金属碳滑板的化学成分百分比见表3。
表3 滑板材料化学成分百分比
Tab.3 Chemical compositions of slide material
化学元素数值(%) C92.95 Pb0.98 Cu3.91 Sb0.55 其他1.61
弓网系统在接触受流时，会受到多个力的作用：①受电弓通过支架可以调整受电弓滑板对导线的法向压力，同时导线会对受电弓滑板有一个大小相等、方向相反的反作用力；②受电弓滑板与铜导线表面存在铜基体与氧化膜层，这两部分在弓网运行当中，会受到外力的作用。在进行动力学分析时，将两部分等效成弹性系数很大的弹性元件，而弹性元件的硬度和阻尼会在弓网运行过程中产生力的作用参与弓网的力学分析；③弓网系统中存在大电流，会在周围形成磁场，在磁场与电流作用下，会对弓网系统产生电磁力。
根据以上对弓网接触系统的结构以及运动机理分析，建立描述弓网系统运行状态的动力学模型，对弓网的摩擦接触状态进行分析。利用集总参数法，把滑板及其连接部分简化成质量为m的集中模块，把铜基体和氧化膜层等效的弹性元件串联成一个弹性元件，进而在动力学模型建立时把弹性元件对质量模块的作用简化为等效硬度k和系统等效阻尼c的作用。质量集中模块m受到法向压力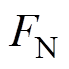
的反作用力
作用，v是对等效弹性元件阻尼产生作用的速度，近似等于机车的运行速度。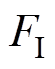
是电磁力，忽略外界环境中影响较小的外力作用，将受电弓碳滑板与接触线的摩擦振动模型简化为如图2所示的弹簧-阻尼-质量模块的形式，图中，接触线与受电弓滑板之间有电流流过。
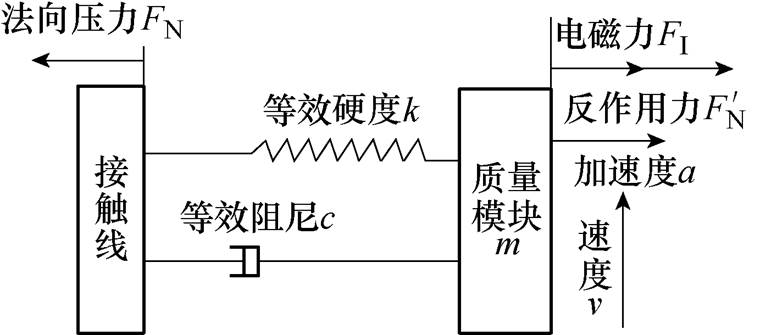
图2 单自由度弓网摩擦振动系统等效模型
Fig.2 Equivalent model of single freedom friction vibration system
根据以上的分析以及图2，建立摩擦振动系统的动力学方程为
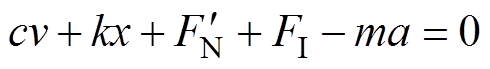（1）式中，a为弓网间竖直方向的摩擦振动加速度。
2.2.1 理想稳定接触状态
当受电弓滑板与接触线处于理想稳定的接触状态时，摩擦振动加速为零，运行速度、接触压力、电磁力均为稳定状态的稳定值，即
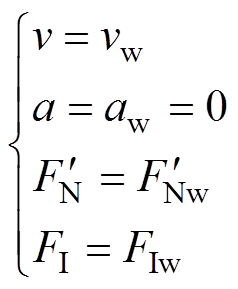（2）式中，
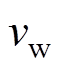和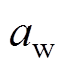
分别为稳定接触状态下的稳定运行速度和加速度；
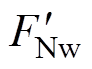为稳定状态下的法向压力的反作用力；
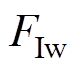为稳定状态下的电磁力。将式（2）代入式（1），有
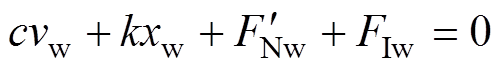（3）
式中，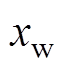
为该状态下的弹性元件形变量。
理想稳定的接触状态下，集中模块m所受的多种力的合力为零，所以模块的加速度为零，此时的受电弓与接触网处于良好的接触状态，有利于电力机车的运行。但是实际弓网接触表面不可能绝对光滑，接触表面存在凹凸点，所以振动是必然存在的，加速度为零的状态只存在加速度方向变换的临界点或离线状态下的受电弓的某些点。
2.2.2 非理想稳定状态
当系统处于非理想稳定状态时，受电弓滑板与接触网的接触状态分为未接触与接触两种状态。
1）未接触状态
当接触面处于未接触状态时，接触线与受电弓滑板分离，但由于受电弓滑板与接触线分离距离小，两分离的接触表面间电场强度大，会产生气体放电现象，形成离线电弧，受电弓滑板仍有电流通过。
对接触线进行受力分析：①导线在电流和磁场下受到电磁力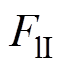
作用；②离线状态下，导线失去受电弓滑板提供的法向压力，自身重力和支持装置提供的拉力不平衡，两者合力产生一个向下的作用力
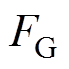。接触线的受力方程为
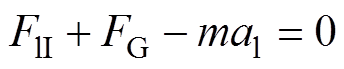（4）得到加速度表达式为
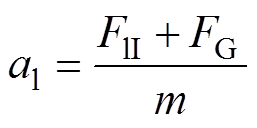（5）
对受电弓滑板进行受力分析：由于弓网处于离线状态：①受电弓滑板与接触线未接触，法向接触压力为零，导致法向压力的反作用力为零；②弹性元件的阻尼c和硬度k对接触面的作用力为零；③由于离线电弧存在，受电弓滑板有电流流过，滑板受到电磁力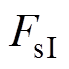
作用，即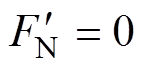
，
，
。
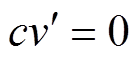受电弓滑板的受力方程为
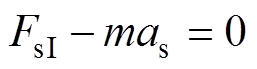（6）得到加速度表达式为
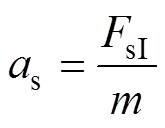（7）
弓网离线时，接触线在合力作用下产生一个向受电弓滑板位移的加速度，加速度的大小和合力大小呈正相关。在加速度的作用下，接触线和受电弓滑板之间的距离逐渐减小，直到重新接触。
对于弓网系统，弓网离线率是反映弓网稳定接触的重要指标，计算方法为离线时间与运行时间的比值。电力机车实际运行过程中，为保证电力机车的良好受流，实际的离线率很低。运行速度为240km/h以上时，离线率大约4%[12]。
2）接触状态
当受电弓滑板与接触线处于非稳定状态，且接触面接触时，以理想稳定接触点为参考原点，偏移稳定状态的偏移量与稳定状态量之和表示此时的运行过程中的状态量，有
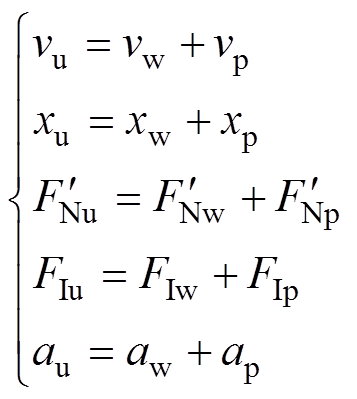（8）式中，
为弓网运行速度；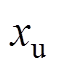
为弹性元件的位移；
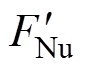为质量模块m受到的法向压力的反作用力；
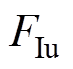为电磁力；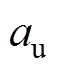
为摩擦振动加速度；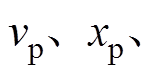
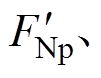
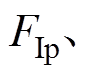
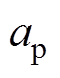为对应的状态量在非理想稳定的接触状态下与理想稳定接触状态下的差值。
将式（8）的关系式代入动力学方程式（1），有
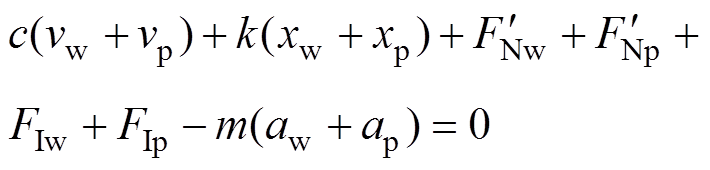（9）将该方程与理想稳定接触状态的方程做差，有
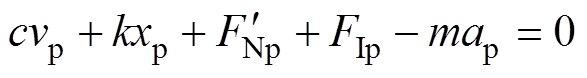（10）
得到摩擦振动加速度表达式有
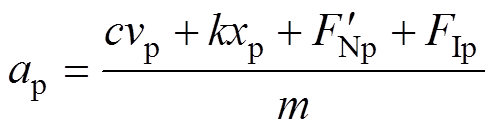（11）通过式（11）可以看出，非理想稳定的接触状态下摩擦振动加速度的大小与弹性元件阻尼、运行速度、弹性元件的硬度和偏移量、法向接触压力及电磁力呈正相关，与模块质量呈负相关。
理想稳定接触状态、非理想稳定的未接触和接触状态是受电弓滑板与接触线在电力机车运行过程中的三种接触状态。在实际运行中，为保证电力机车的良好受流，非理想稳定的接触状态是弓网接触的主要接触状态，占弓网运行的绝大多数时间。因此，以非理想稳定的接触状态的受力情况作为实验中摩擦副的摩擦振动受力进行模型受力计算。
利用实验室自制的载流摩擦磨损实验机，进行弓网滑动摩擦振动实验。采用控制变量法，分别改变法向压力、运行速度和电流强度，研究不同影响因素对摩擦振动加速度的影响。
实际弓网运行过程中，法向压力均值一般大于80N[13-14]，为保证实验条件下滑板与接触线正常接触，法向压力变量分别取80N、90N、100N、110N；而普通客运、货运列车电流强度一般不大于300A[15]，考虑到变量的梯度变化，取电流强度分别为100A、150A、200A、250A。目前普通客运、货运列车运行速度一般低于160km/h[15]，普遍处于100km/h，所以实验中运行速度分别取60km/h、80km/h、100km/h、120km/h。
3.1.1 实验结果
在电流强度为150A，运行速度分别为60km/h、80km/h、100km/h、120km/h，法向压力分别为80N、90N、100N、110N的实验条件下，记录实验数据并计算实验中加速度有效值，绘制加速度与法向压力的特性如图3所示。
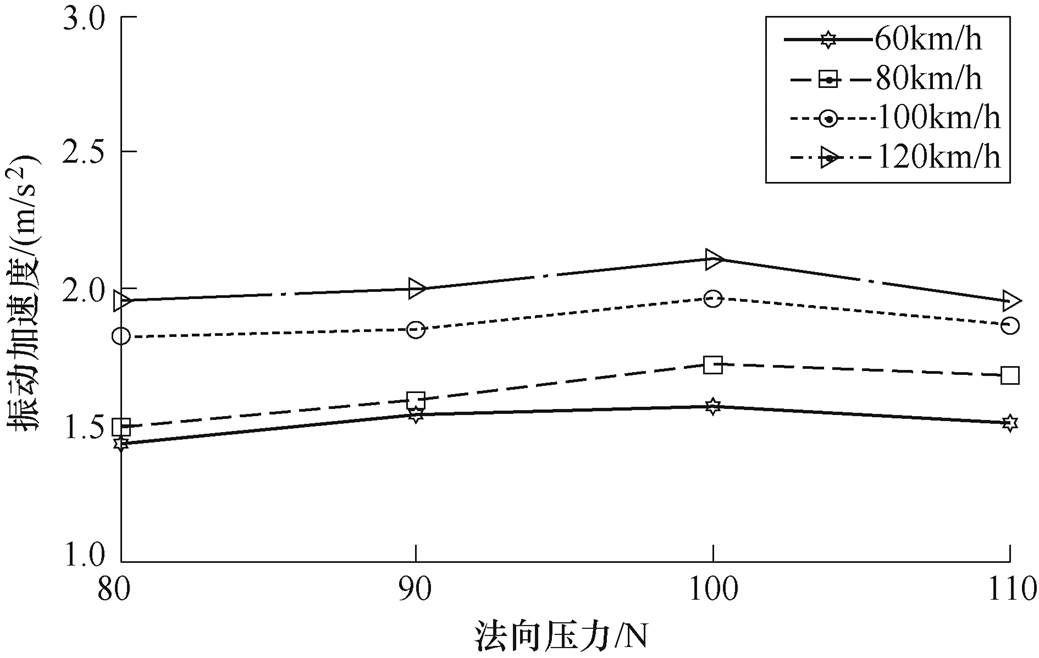
图3 加速度与法向压力的特性
Fig.3 Characteristic diagram of acceleration with normal pressure
在法向压力为80N，电流强度分别为100A、150A、200A、250A，运行速度分别为60km/h、80km/h、100km/h、120km/h的实验条件下，记录实验数据并计算实验中加速度有效值，绘制摩擦振动加速度与运行速度的特性如图4所示。
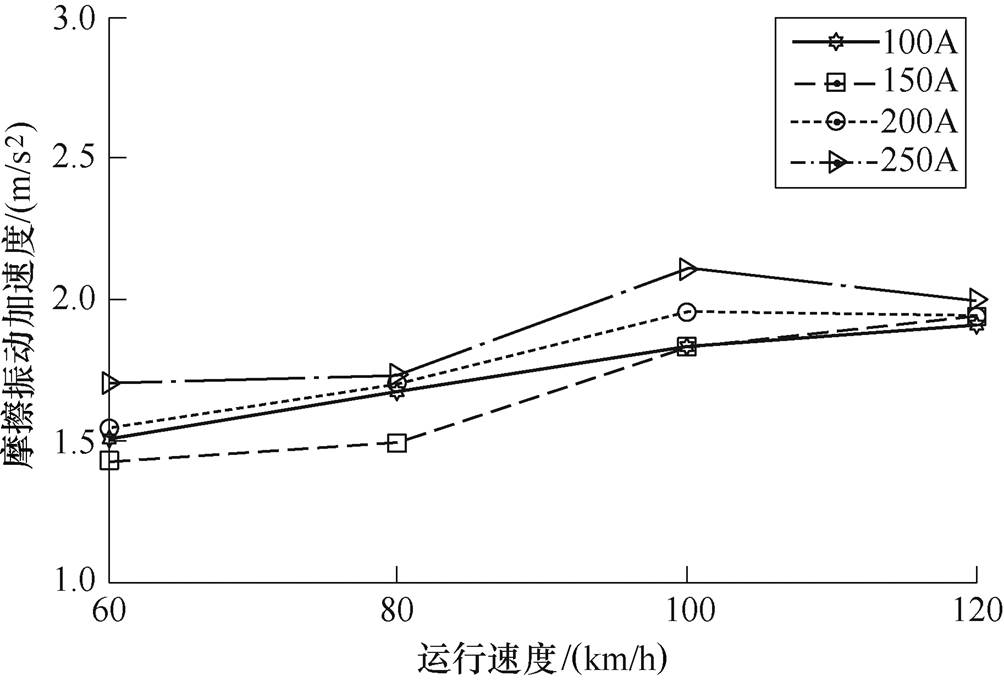
图4 加速度与运行速度的特性
Fig.4 Characteristic diagram of acceleration with running speed
在法向压力为90N，运行速度分别为60km/h、80km/h、100km/h、120km/h，电流强度分别为100A、150A、200A、250A的实验条件下，记录实验数据并计算实验中加速度有效值，绘制加速度与电流强度的特性如图5所示。
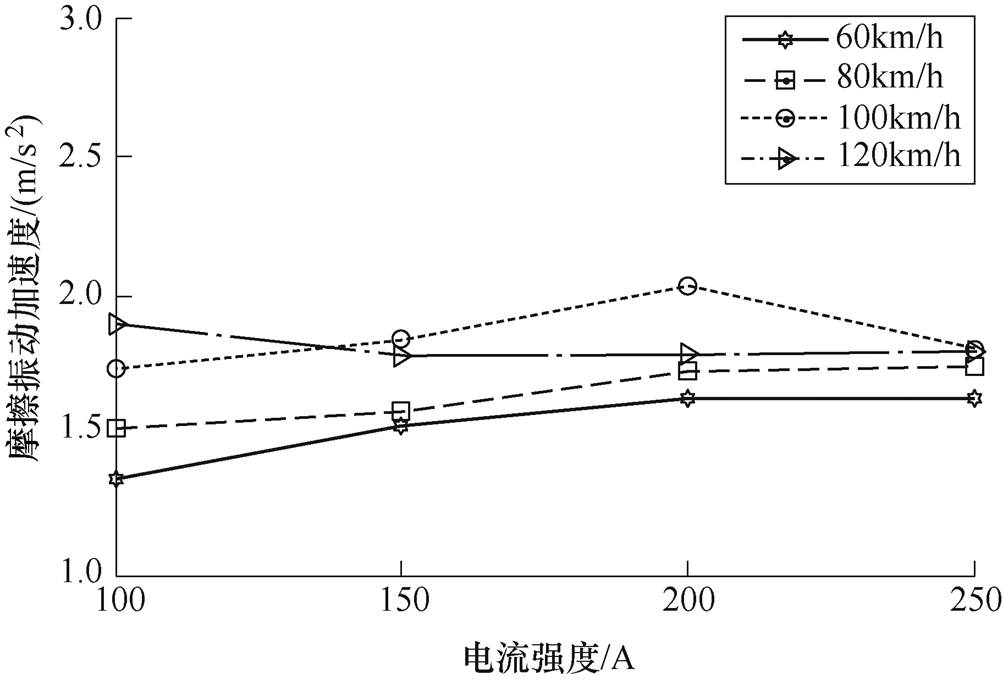
图5 加速度与电流强度的特性
Fig.5 Characteristic diagram of acceleration with current intensity
结合实验特性可知，随着法向压力、运行速度和电流强度的不断增加，摩擦振动加速度逐渐增大，增长的幅度逐渐减小。
3.1.2 实验结果分析
从实验结果的特性曲线来看，摩擦振动加速度随着法向压力、运行速度以及电流强度的增加而增加，这是因为：①根据非理想稳定接触状态下的摩擦振动加速度表达式（11）可知，摩擦振动加速度与法向压力、运行速度呈正相关，运行速度、法向压力的增加会导致摩擦振动加速度增加；②增加电流强度会使电磁力增加，根据摩擦振动加速度表达式（11），电磁力增加、摩擦振动加速度增加；③法向压力、运行速度和电流强度增加会使摩擦热和焦耳热增加，使得接触表面的温度升高，温升会造成材料内部成分析出，在接触表面形成高粘性、低流动性的金属氧化膜层，增加系统的阻尼[16-17]，根据摩擦振动加速度表达式（11），弹性元件阻尼增加，加速度增加。
摩擦振动加速度的增长幅值逐渐降低，这是因为：
（1）法向压力、运行速度和电流强度增加使得接触表面温度升高，造成表面材料的软化和塑性变形，使形状圆润的微凸体比率增加[18-19]，弱化受电弓滑板的受力作用，且法向压力、运行速度以及电流强度越大，接触面软化越明显，弱化效果越明显[20-22]。
（2）法向压力、运行速度和电流强度造成的温升会改变弹性元件的阻尼系数，但随着温度升高，阻尼变化幅值逐渐减小[23]，根据摩擦振动加速度表达式（11）可知，加速度变化幅值减小。
结合实验特性和理论分析可知，摩擦振动模型的弹性阻尼系数、弹性元件硬度产生的弹性力、电磁力等受到法向压力、运行速度以及电流强度的影响。以非理想稳定接触状态的受力分析为基础，对摩擦振动模型参数进行求解。
3.2.1 弹性元件参数计算
弹性元件受力计算主要分为阻尼力和弹性力的计算。而阻尼力主要与弹性元件的阻尼系数相关。
1）弹性元件的阻尼系数计算
通过法向压力、运行速度和电流强度与摩擦振动加速度的特性分析，结合实验特性的变化趋势，考虑到阻尼逐渐增加并趋于稳定的特点，对比多个函数的拟合结果，选取最合适的拟合曲线如下：
法向压力对于弹性元件阻尼的作用记做cF，即
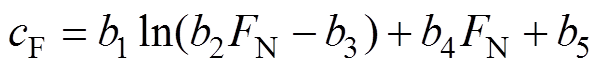（12）运行速度对弹性元件阻尼的作用记做cs，即
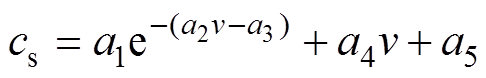（13）
电流强度作用造成的弹性元件阻尼的作用记做cI，即
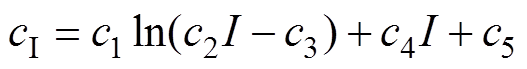（14）式中，ai、bi、ci分别为对应公式内常数项参数，i= 1,…, 5。
受电弓滑板与接触线在滑动运行过程中，弹性元件阻尼系数受到法向压力、运行速度和电流强度的共同作用，记弹性元件的阻尼系数c为
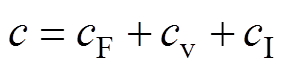（15）2）弹性元件的弹性力计算
等效弹性元件中，除了阻尼力之外，还存在弹簧弹性位移产生的弹性力kx。根据弹簧弹性力主要与接触压力有关的特性以及摩擦振动过程中接触面弹性位移量变化小的特点，记弹簧弹性力表达式为
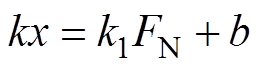（16）式中，k1为弹簧弹性力与法向压力的比例系数。
3.2.2 电磁力计算
弓网系统中，受电弓滑板在磁场存在和带电的条件下，会使电磁力对滑板产生作用[24-25]。按照电磁力的计算公式，有
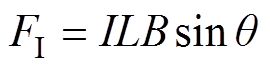（17）式中，I为电流强度，取电流的有效值；L为导线的长度；B为磁感应强度；q 为滑板与磁场的夹角。
由于磁感应强度是由接触线当中的电流产生的，对于电流强度为I的圆形导线在其轴线上的磁感应强度，有
（18）式中，R为圆形导线的圆周半径；x为其圆心到轴线上场点的距离；m0为真空磁导率，为常数。
将磁感应强度代入电磁力的计算公式（17）有
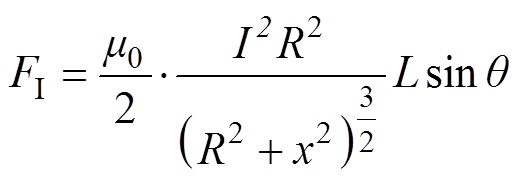（19）在实际的运行中，R、x、q、L为常数，定义电磁力系数c6，有
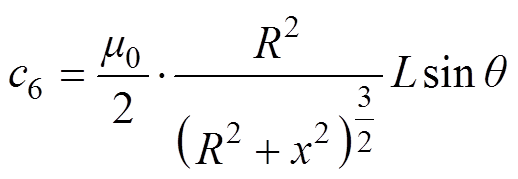（20）
考虑到实际运行中，接触线与受电弓滑板的电流均会产生磁场影响电磁力，因而对电磁力进行部分补偿，根据电磁力最大值与电流的二次方相关，综合电磁力计算公式（20）与补偿项，有
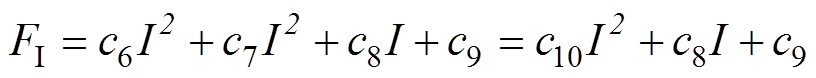（21）3.2.3 摩擦振动模型能量补偿
对摩擦振动加速度的计算，主要是受电弓滑板质量模块的受力计算，其加速度的大小与其所受合外力相关。但由于实际弓网摩擦副表面不光滑，摩擦振动过程，接触表面的微凸体高速碰撞造成的能量交互同样对加速度存在一定的影响。对于物体的能量，有
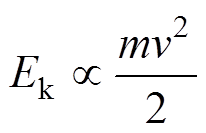
由于接触表面的微凸体碰撞属于非弹性碰撞，两个微凸体碰撞之后，对于两个微凸体构成的系统不满足能量守恒定律，但由于能量最大值与速度的二次方相关，所以运行速度对摩擦振动加速度的补偿项利用二次函数可以表示为
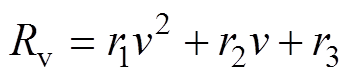（22）
式中，r1、r2、r3为能量补偿方程的常数项参数。
3.2.4 摩擦振动模型常数参数计算
将弹性元件阻尼系数表达式（15），弹簧弹性力表达式（16），电磁力表达式（21）代入摩擦振动动力学方程式（1）中，有
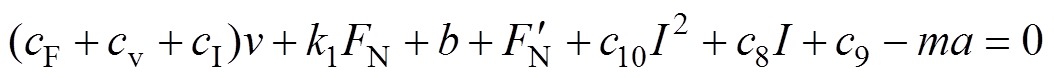（23）将弹性元件阻尼系数函数关系式（12）～式（14）代入方程式（23）中，有
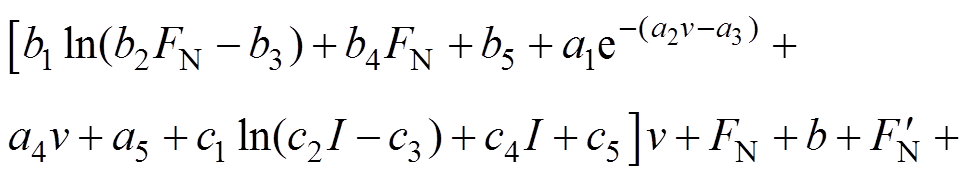
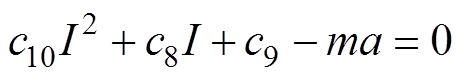（24）利用式（24）求解摩擦振动加速度，加入速度补偿项，得摩擦振动加速度为
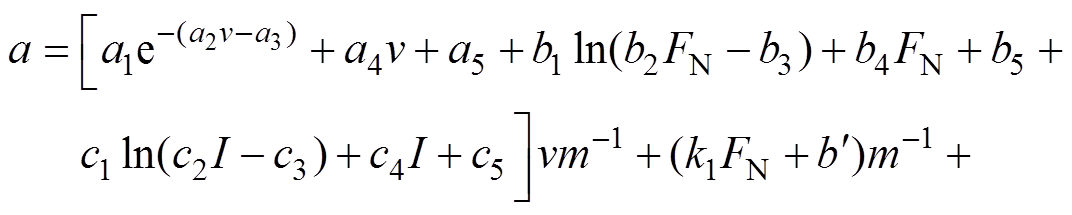
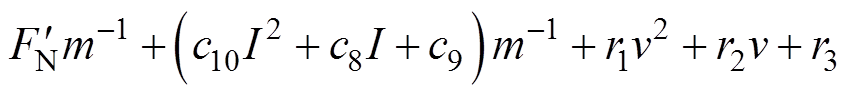（25）对同类项和常数项系数合并，有
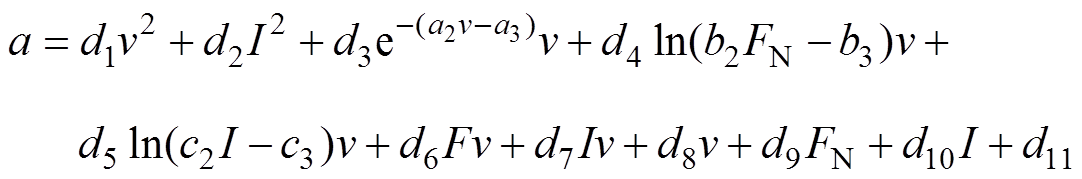（26）
式中，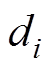
（i=1,…, 11）项均为化简后的常数项，有
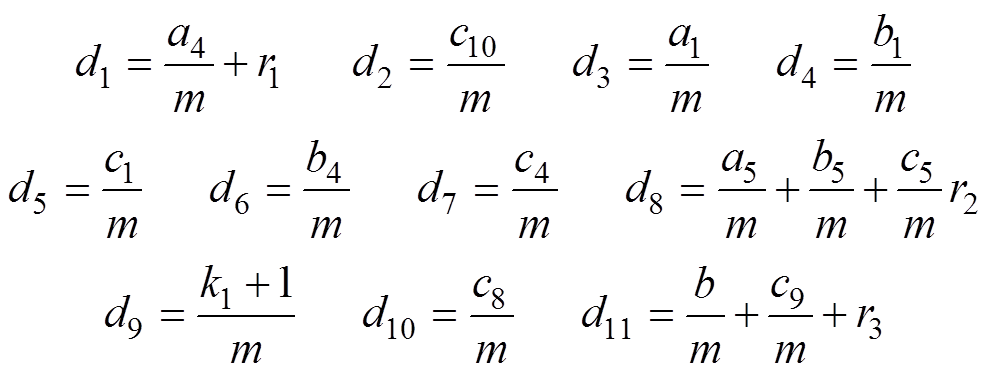
结合实验数据对方程当中的常数项系数求解，摩擦振动方程参数拟合值见表4。
表4 摩擦振动方程参数拟合值
Tab.4 Parameter fitting values of friction vibration equation
参 数输出值 d1-0.000 224 878 512 545 279 d22.644 123 651 084 03×10-5 d30.849 529 888 296 793 d41.140 594 234 987 79 d50.002 906 479 908 892 44 d6-0.001 568 483 411 157 79 d7-4.417 780 196 250 42×10-5 d8-2.595 852 208 852 08 d90.002 864 904 900 295 02 d10-0.007 951 431 296 728 44 d11-1.101 579 156 272 67 a20.093 474 867 646 531 1 a30.935339247687522 b2-0.015 660 917 709 678 8 b310.218 524 926 825 5 c20.016 459 389 381 578 c31.222 040 562 841 33
根据本文的分析，在考虑法向压力、运行速度和电流强度三要素的影响条件下，建立了弓网摩擦振动模型，求解了摩擦振动加速度的表达式（25）。为了验证模型的准确度，额外进行了一组对比验证实验。实验条件取法向压力F=90N，电流强度I分别为100A、150A、200A、250A，运行速度v分别为70km/h、90km/h、110km/h、130km/h，通过实验获得实际的摩擦振动加速度。同时，将实验条件代入摩擦振动加速度方程式（25），求得预期的摩擦振动加速度大小，将摩擦振动加速度实际值与不同的预期值进行比较如图6所示。
图6中，M1曲线是利用弓网摩擦振动模型计算的加速度值曲线，FACT曲线是给定条件下实验测得的实际加速度曲线。实验共四个单位组，每组内编号分别为（1, 2, 3, 4），（6, 7, 8, 9），（11, 12, 13, 14），（16, 17, 18, 19）。单位组内运行速度变化；不同单位组之间，组内排序位置相同点，电流强度不同。
实验的实际值与模型计算值的相对误差以及相对误差平均值见表5。
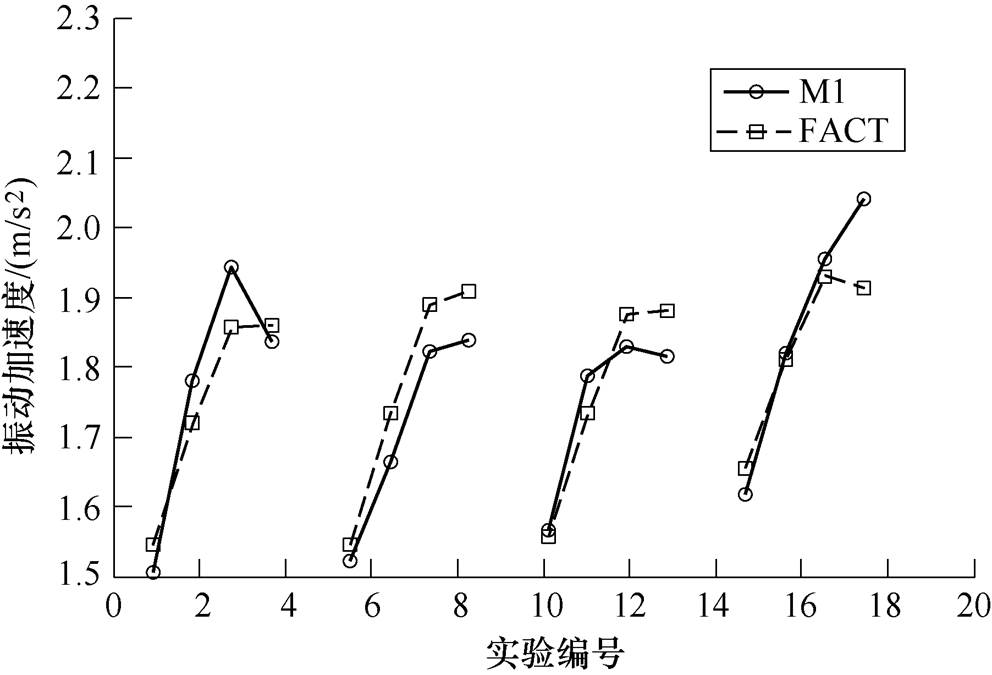
图6 加速度真实值与预测值对比
Fig.6 Comparison diagram of real and predicted acceleration values
表5 数据误差值
Tab.5 Experimental data table
实验编号相对误差相对误差平均值 10.0302 00.030 801 446 20.0372 9 30.0477 3 40.0146 9 60.0159 2 70.0472 8 80.0395 0 90.0415 6 110.0063 1 120.0324 4 130.0270 4 140.0397 3 160.0263 7 170.0058 6 180.0136 8 190.0671 5
通过图6可以看出，弓网摩擦振动模型计算得到的加速度曲线M1能够较好地贴近实际加速度。
由图6可知，加速度真实值与预测值仍存在一定的误差。这是因为：①实际测得的摩擦振动加速度主要是碳滑板与接触线的摩擦振动加速度，但还包含微量的滑台横向移动以及转盘的高速转动产生的振动加速度（低于测得摩擦振动加速度值的3%）；②在摩擦振动系统受力分析中，忽略了风动力、接触应力等对接触表面力的作用，因其值远小于法向压力；③对于电磁力以及摩擦振动能量的补偿函数采用的高次方的拟合函数，也会带来一定的误差。
从误差数据分布来看，真实值与预测值的相对误差集中于4.5%以下，占验证实验数据的81.25%，高于4.5%的仅为18.75%。实验数据的最小相对误差为0.586%，最大相对误差为6.715%，相对误差均值仅为3.080%。
通过实验的相对误差数据可以看出，误差分析中忽略的因素对摩擦振动加速度影响较小，在此基础上建立的摩擦振动系统的动力学方程是合理的。
综合图像和数据的分析，证明了在考虑运行速度、法向压力和电流强度三要素的情况下所建立的振动模型确实能够准确地反映弓网振动加速度的变化情况。
1）弓网接触面摩擦振动加速度随着法向压力、运行速度以及电流强度的增大而增大，且随着三者的增加，增长幅度逐渐变缓。
2）根据传统的摩擦振动模型，建立了弓网弹 簧-阻尼-质量模块的摩擦振动加速度模型，分析了不同状态下的接触面受力状况，说明了弹性元件阻尼、弹性力、法向压力、运行速度、电磁力是影响摩擦振动加速度主要因素。
3）深入分析机车运行时，法向压力和运行速度以及电流强度对于阻尼参数及受力的影响，建立了三者与摩擦振动加速度模型的函数关系式（25），通过实验数据求解函数关系式（25）中常数项，通过实验验证了模型的准确性，为进一步研究摩擦振动加速度与弓网磨损以及离线概率的关系奠定了基础。
参考文献
[1] 郭凤仪, 王贺, 王智勇, 等. 弓网系统动态接触压力特性[J]. 辽宁工程技术大学学报: 自然科学版, 2017, 36(6): 640-644.
Guo Fengyi, Wang He, Wang Zhiyong, et al. Dynamic contact pressure characteristics of the pantograph- catenary system[J]. Journal of Liaoning Technical University: Natural Science Edition, 2017, 36(6): 640-644.
[2] Adrian Plesca. Thermal analysis of sliding electrical contacts with mechanical friction in steady state conditions[J]. International Journal of Thermal Sciences, 2014, 84: 125-133.
[3] 郭凤仪, 陈明阳, 陈忠华, 等. 弓网滑动电接触摩擦力特性与建模研究[J]. 电工技术学报, 2018, 33(13): 2982-2990.
Guo Fengyi, Chen Mingyang, Chen Zhonghua, et al. Characteristics and modeling of the frictional contact friction of the pantograph-catenary system[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(13): 2982-2990.
[4] 陈忠华, 平宇, 陈明阳, 等. 波动接触力下弓网载流摩擦力建模研究[J]. 电工技术学报, 2019, 34(7): 1434-1440.
Chen Zhonghua, Ping Yu, Chen Mingyang, et al. Modeling of the current-carrying friction force of the pantograph-catenary under wave contact force[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1434-1440.
[5] 赵春雨. 弓网最优接触压力载荷决策与受电弓主动控制研究[D]. 辽宁: 辽宁工程技术大学, 2017.
[6] 梅桂明, 张卫华. 受电弓/接触网系统动力学模型及特性[J]. 交通运输工程学报, 2002(1): 20-25.
Mei Guiming, Zhang Weihua. Dynamics model and characteristics of pantograph-catenary system[J]. Journal of Traffic and Transportation Engineering, 2002(1): 20-25.
[7] 宋冬利, 江亚男, 张卫华, 等. 基于受电弓框架模型的部件危险点动应力计算方法[J]. 中国铁道科学, 2016, 37(6): 75-81.
Song Dongli, Jiang Yanan, Zhang Weihua, et al. Calculation method of dangerous point dynamic stress of components based on pantograph frame model[J]. China Railway Science, 2016, 37(6): 75-81.
[8] 杨艺, 周宁, 李瑞平, 等. 基于有限元法的弓网过渡段处动态性能仿真分析[J]. 振动与冲击, 2016, 35(18): 71-75, 116.
Yang Yi, Zhou Ning, Li Ruiping, et al. Simulation analysis of dynamic performance of transition section of pantograph-catenary based on finite element method[J]. Journal of Vibration and Shock, 2016, 35(18): 71-75, 116.
[9] 刘江涛. 含动摩擦两自由度碰撞振动系统动力学特性研究[D]. 兰州: 兰州交通大学, 2018.
[10] 姚亚航, 王国权, 王书文, 等. 盘式制动器摩擦振动的非线性动力学研究[J]. 北京信息科技大学学报: 自然科学版, 2018, 33(4): 33-39.
Yao Yahang, Wang Guoquan, Wang Shuwen, et al. Nonlinear dynamics of friction vibration of disc brakes[J]. Journal of Beijing Information Science and Technology University: Natural Science, 2018, 33(4): 33-39.
[11] 唐人寰. 受流器/第三轨摩擦振动特性研究[D]. 北京: 北京交通大学, 2017.
[12] 封力民, 刘浩, 王黎, 等. 电力机车弓网离线监测系统[J]. 机车电传动, 2005(2): 57-58, 60.
Feng Limin, Liu Hao, Wang Li, et al. Off-line monitoring system for electric locomotive pantograph- catenary system[J]. Locomotive Electric Drive, 2005(2): 57-58, 60.
[13] 金柏泉, 吴积钦, 李岚. 我国高速铁路弓网相互作用特点[J]. 中国铁路, 2011(1): 49-52.
Jin Baiquan, Wu Jiqin, Li Lan. Characteristics of the interaction of high-speed railway bow and net in China[J]. China Railways, 2011(1): 49-52.
[14] 时光, 陈忠华, 郭凤仪, 等. 基于最优载荷的受电弓自适应终端滑模控制[J]. 电工技术学报, 2017, 32(4): 140-146, 153.
Shi Guang, Chen Zhonghua, Guo Fengyi, et al. Adaptive terminal sliding mode control of pantograph based on optimal load[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 140-146, 153.
[15] 项杨. 浅谈运输组织变化对列车能耗及列车电流的影响[J]. 电气化铁道, 2018, 29(5): 25-28.
Xiang Yang. Discussion on the influence of trans- portation organization change on train energy consumption and train current[J]. Electric Railway, 2018, 29(5): 25-28.
[16] 布美娜. 新型结构磁流变阻尼器的研究[D]. 石家庄: 石家庄铁道大学, 2016.
[17] 宫厚增, 欧阳青, 曹迎春, 等. 高冲击下电流变阻尼器多物理场建模与仿真[J]. 机床与液压, 2016, 44(9): 119-122, 136.
Gong Houzeng, Ouyang Qing, Cao Yingchun, et al. Multiphysics modeling and simulation of electro- rheological damper under high impact[J]. Machine Tool & Hydraulics, 2016, 44(9): 119-122, 136.
[18] 李白, 鲁军勇, 谭赛, 等. 滑动电接触界面粗糙度对电枢熔化特性的影响[J]. 电工技术学报, 2018, 33(7): 1607-1615.
Li Bai, Lu Junyong, Tan Sai, et al. Effect of sliding electrical contact interface roughness on armature melting characteristics[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1607-1615.
[19] 林雪燕, 吴青艳, 单栋梁. 连接器贵金属镀层材料的微动接触性能[J]. 电工技术学报, 2018, 33(1): 64-70.
Lin Xueyan, Wu Qingyan, Shan Dongliang. Fric- tional contact performance of bonded precious metal coatings[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 64-70.
[20] 章赛丹, 陈光雄, 杨红娟. 接触压力对碳滑板/铜接触线载流摩擦磨损性能的影响[J]. 润滑与密封, 2012, 37(9): 41-45.
Zhang Saidan, Chen Guangxiong, Yang Hongjuan. Effect of contact pressure on the wear resistance of carbon slide/copper contact line current-carrying friction[J]. Lubrication and Sealing, 2012, 37(9): 41-45.
[21] 胡艳, 董丙杰, 黄海, 等. 碳滑板/接触线摩擦磨损性能[J]. 交通运输工程学报, 2016, 16(2): 56-63.
Hu Yan, Dong Bingjie, Huang Hai, et al. Friction and wear properties of carbon slider/contact wire[J]. Journal of Traffic and Transportation Engineering, 2016, 16(2): 56-63.
[22] 李卓. 轴表面粗糙度引起的船体板架振动特性研究[C]//第21届全国结构工程学术会议, 北京, 2012: 362-368.
[23] Li Jing, Yao Huan, Lei Yan, et al. Numerical simulation of magnetic fluid hyperthermia based on multiphysics coupling and recommendation on preferable treatment conditions[J]. Current Applied Physics, 2019,19(9): 1031-1039.
[24] 赵云云, 吴广宁, 高国强, 等. 弓网系统电磁作用力的研究[J]. 铁道学报, 2014, 36(10): 28-32.
Zhao Yunyun, Wu Guangning, Gao Guoqiang, et al. Study on electromagnetic force of pantograph- catenary system[J]. Journal of the China Railway Society, 2014, 36(10): 28-32.
[25] 赵云云. 高速铁路弓网系统电磁力的计算与仿真分析[D]. 四川: 西南交通大学, 2014.
Analysis and Modeling of High Current Sliding Electrical Contact Friction Dynamics in Pantograph-Catenary System
Abstract In the pantograph-catenary system of electrified railway, the frictional vibration acceleration between the pantograph slider and the catenary wire reflects the contact condition of the current-carrying friction, and affects the off-line probability and wear state of pantograph-catenary system. In this paper, by analyzing the contact state between the pantograph slider and catenary wire, the spring-damping-quality module friction vibration model of the pantograph-catenary friction pair was established. According to the experiments, the relationship of characteristic parameters and force with three factors in frictional vibration model was analyzed by considering the influence of normal pressure, running speed and high current on frictional vibration. Then, the experimental data was used to solve the constant parameters in the functional relationship. Finally, the accuracy of the frictional vibration model was verified by experiments, which provides a theoretical basis for further study on the current-carrying frictional wear mechanism and off-line probability of the pantograph-catenary system.
keywords：Pantograph-catenary system, current-carrying friction vibration acceleration, vibration model
中图分类号：U225
DOI: 10.19595/j.cnki.1000-6753.tces.190932
国家自然科学基金（51477071）和辽宁省‘兴辽英才计划’（XLYC1802110）资助项目。
收稿日期 2019-07-25
改稿日期 2019-09-24
陈忠华 男，1965年生，教授，博士生导师，研究方向为电机与电器、电接触理论及其应用。E-mail: zhchen0915@126.com
唐 俊 男，1994年生，硕士研究生，研究方向为电接触理论及其应用。E-mail: 1400549890@qq.com（通信作者）
（编辑 陈 诚）