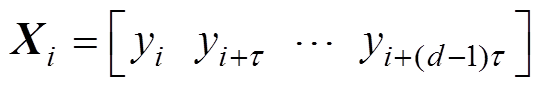（1）摘要 针对采用振动信号识别高压断路器（HVCBs）机械缺陷困难及难于实现工程应用问题，提出一种基于定量递归分析（RQA）的振动信号分析方法，并将其应用于变电站在运高压断路器机械缺陷辨识中。为便于缺陷部位的准确定位，将高压断路器振动信号分割为各功能子区，将各功能子区信号映射至高维相空间，以充分展示高压断路器动力学变化特征，并在相空间进行递归图重构。最后，引入递归率（RR）、确定率（DET）、最大对角线长度（Lmax）、信息熵（ENT）、层状度（LAM）和捕获时间（TT）对各功能子区递归图进行定量分析，以实现高压断路器机械缺陷的有效辨识。试验结果表明，所提方法能够准确地辨识高压断路器的机械缺陷，在实际工程应用中也表现出较高的准确率。
关键词：高压断路器 机械缺陷检测 振动信号 信号分割 定量递归分析
高压断路器（High-Voltage Circuit Breaker, HVCB）是电力系统中重要的保护和控制设备，其性能直接或间接影响着电力系统的可靠性和稳定性[1-3]。近年来，基于状态检/监测的高压断路器检修技术成为人们关注的重点，即通过对高压断路器某些信号的检测/监测，实现故障预知，并采取相应的措施预防故障的发生。
许多研究表明，机械异常是导致高压断路器故障的主要原因[4-8]。另外，根据某省电力公司在2006～2015年对该省的电网开关设备故障的调查，高压断路器的故障中有32.6%是由于机构异常引起的；中国电力科学研究院调查结果表明，2015年国家电网公司由高压断路器（72.5～1 100kV）故障引起的故障跳闸为22次，其中，14次为机械故障引起的，占比63.6%。因此，有效预防机械故障对于保证高压断路器的安全稳定运行至关重要。
采用高压断路器分、合闸动作过程中产生的振动信号对其机械状态做出判断已被证明是一种可行的方法[9-13]。该方法类似中医诊脉（根据手指感受到的振动响应的显现部位（深、浅）、速率（快、慢）、强度（有力、无力）、节律（整齐与否、有无歇止）和形态等方面的表现，以了解疾病内在变化的诊断方法），其内在机理是高压断路器在分、合闸动作时机械零部件相互作用（摩擦、碰撞等）产生相应的冲击波，而这些冲击波蕴含着丰富、重要的高压断路器机械状态信息。
到目前为止，已有许多研究者对采用振动信号判断高压断路器的机械状态进行了深入的研究，并取得了一些成果。例如，文献[14]利用高压断路器的分闸振动信号实现分闸缓冲器的状态评估；文献[15]探究了采用振动信号识别高压断路器触头超程状态的可能性；文献[16]结合振动信号特征提取与智能分类器对高压断路器的机械状态与故障类型进行分类；文献[17]提出一种利用振动信号提取高压断路器合闸过程中运动时间参数的方法。然而，目前的研究局限于实验室，很少应用于实际工程，这是由于存在以下主要难点制约了该技术的工程应用：①传感器类型及安装位置影响有效信号的采集；②高压断路器型号众多且现场情况复杂多变；③现场提取的振动信号和实验室模拟的信号存在差异，影响算法的实际使用效果；④比对样本严重不足；⑤通用性的高辨识度故障信息难于提取。
本文在大量试验研究的基础上提出了高压断路器振动信号分区分割、定量递归分析等方法，并进行了工程实践应用初探，主要内容如下：①提出将振动信号按高压断路器动作特性进行分区分割的思想，以实现异常信号的准确定位；②将子区信号映射至高维相空间，并进行递归图重构及定量递归分析，以提取区分性和重复性较好的缺陷特征；③结合实验室试验与现场实测案例，验证所提方法的有效性和优势。
由Eckmann等提出的递归图（Recurrence Plot, RP）分析方法是将动力系统产生的非线性时间序列转化为二维平面图来描绘动力系统的内在变化规 律[18]。时域信号向递归图转化过程举例如图1所示。设由动力系统产生的一维信号为yt（见图1a所示的信号），采样时刻t =1, 2,…, N。根据Taken时滞嵌入理论[19]，该信号可以被重构到d维相空间中Xi（见重构到图1b的三维相空间中），记为
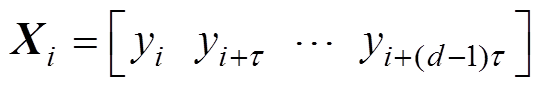（1）式中，d为嵌入维数；t 为时间延迟，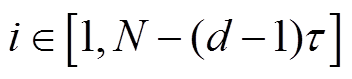
。
递归图可分为无阈值递归图和有阈值递归图两种。相空间重构后，两向量Xi和Xj之间的距离为Dist(i, j)，则无阈值递归图可定义为
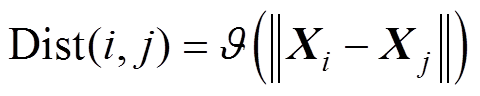（2）式中，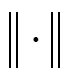
表示范数，本文采用Euclidean范数；
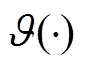为“色码函数”，它将距离映射为颜色，即以颜色的深浅（称为色标）表示距离的大小。
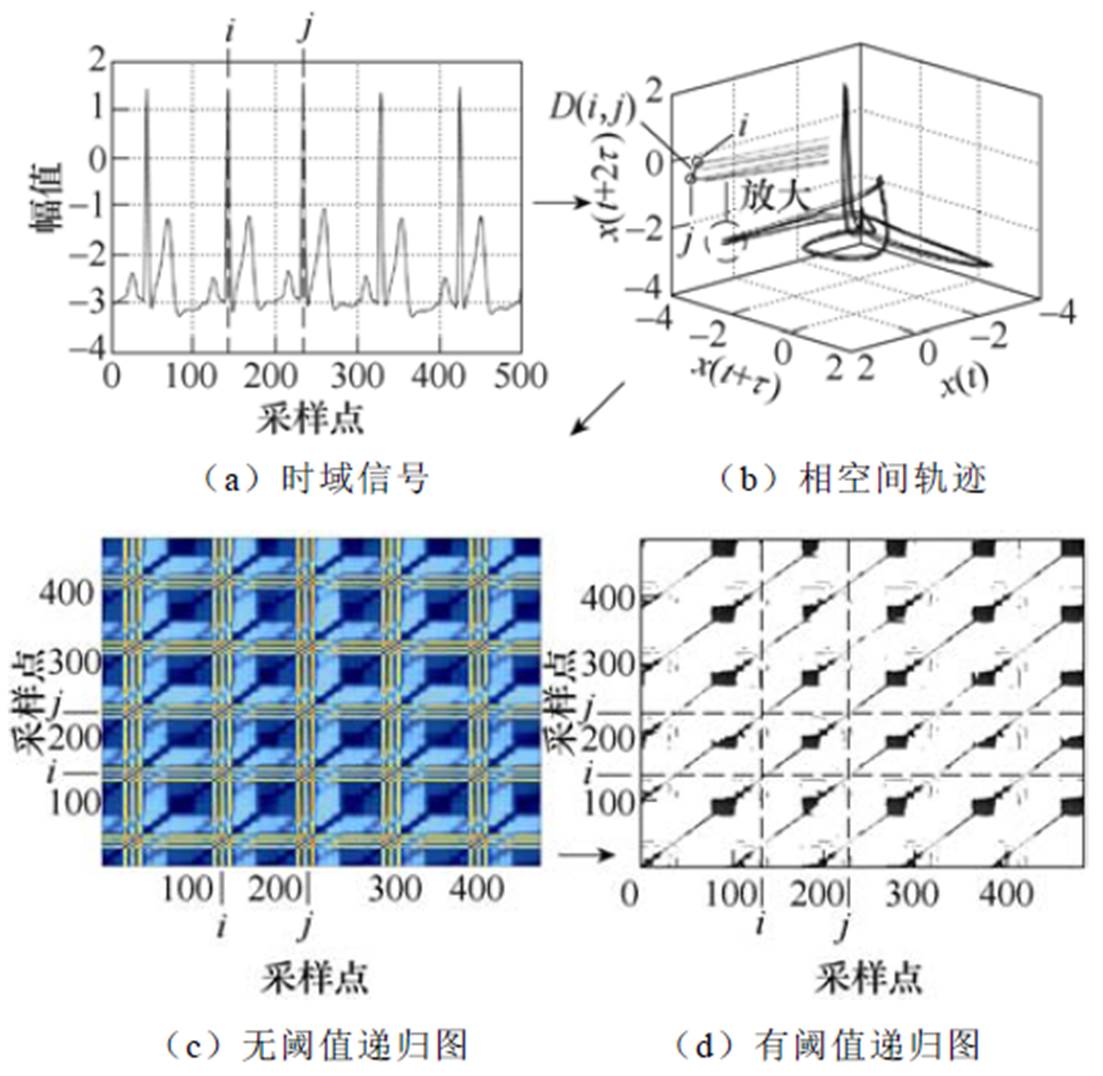
图1 时域信号向递归图转化过程举例
Fig.1 An example for the transformation of a time domain signal to recurrence plot
而有阈值递归图（见图1d）通过以下方式构造。
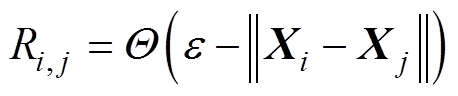（3）式中，
为Heaviside函数，即当x≥0时，
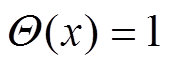；当x＜0时，
；
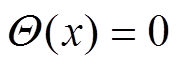为Euclidean阈值；Ri, j为矩阵R（递归图矩阵）中的第i行第j列元素，若Xi与Xj之间的距离小于等于阈值，则Ri, j=1（递归点）；否则，Ri, j=0。
递归图以二维图像的形式将隐含在信号中的动力系统信息展示出来，递归图的拓扑结构和纹理模式随着动力系统状态的改变而变化。然而，递归图只能定性地分析动力系统，而定量递归分析（Recurrence Quantification Analysis, RQA）[20]可以量化描述递归图的结构特征。本文采用的RQA主要包括：
1）递归率
递归图中递归点所占的比例称为递归率（Recur- rence Rate, RR）[21]，可计算为
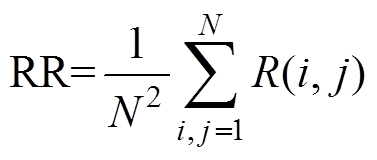（4）式中，N为时间序列点数。
2）确定率
确定率（Determinism, DET）[22]描述的是构成对角结构的递归点与所有递归点的比值，即
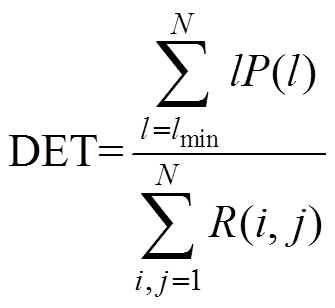（5）式中，P(l)为递归图中长度为l的对角线个数；lmin为最小对角线长度，一般取lmin=2。
3）最大对角线长度
最大对角线长度（Lmax）[22]测量递归图中对角线的最大长度，这与振动信号冲击波的持续时间有关，其定义如下
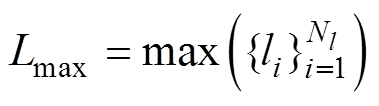（6）式中，
为对角线的总数；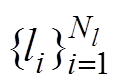
为递归图中各对角线的长度。
4）信息熵
信息熵（Entropy, ENT）表示系统变化的不确定程度，定义为对角线分布的Shannon熵[23]，即
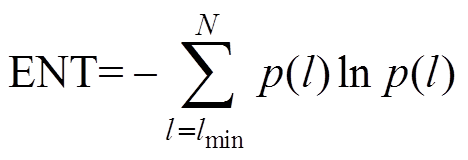（7）式中，p(l)为对角线为l的概率（l∈[阈值l，主对角线长（即N）]）。
5）层状度
类似于决定论的定义，层状度（Laminarity, LAM）[24]量化构成垂直结构的递归点与所有递归点的比值，这与振动信号冲击波的强度有关，其定义为
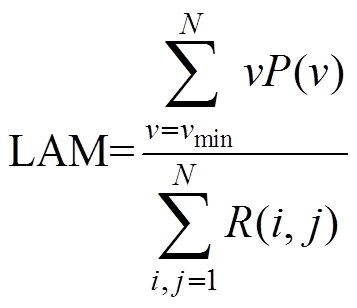（8）式中，P(v)为递归图中长度为v的垂线数；vmin为最小垂线长度，一般取vmin=2。
6）捕获时间
捕获时间（Trapping Time, TT）描述的是递归图中的垂直结构，它计算递归图中的垂线大于设定阈值的平均长度[25]为
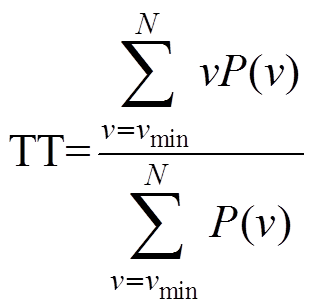（9）断路器在分、合闸动作过程中产生的机械振动信号是其内部零部件相互作用的结果，其产生和传播是一个非常复杂的过程。由于断路器内部振源数量多、各零部件相互制约等原因，导致振动波在传播过程中发生分散、衰减、混叠，使得有效的特征提取十分困难。
图2所示是某一220kV变电站一台在运的山东泰开252kV SF6高压断路器C相操动机构的实测合闸振动信号（测试时间：2019年6月17日），可以看出，该合闸振动信号包含多个幅值不一、持续时间不一的冲击子波。考虑到这些冲击子波是按照断路器零部件动作的时间先后顺序出现的，断路器的结构和动作信息，如弹簧释放、机构解列、机构传动及制动等信息包含在相应的冲击子波中。因此，如将振动信号分割成各个子波序列再进行分析，则能大大提高振动信号特征提取的可靠性与缺陷辨识的准确性。考虑到弹簧操动类断路器的结构特点（均由储能弹簧、锁扣装置、传动构件、缓冲制动装置等组成）及动作特性（均经历触发脱扣、机构解列、机构传动、制动限位等动作阶段）的相似性，本文将断路器振动信号分割成4个部分后再分别对每部分进行定量递归分析。
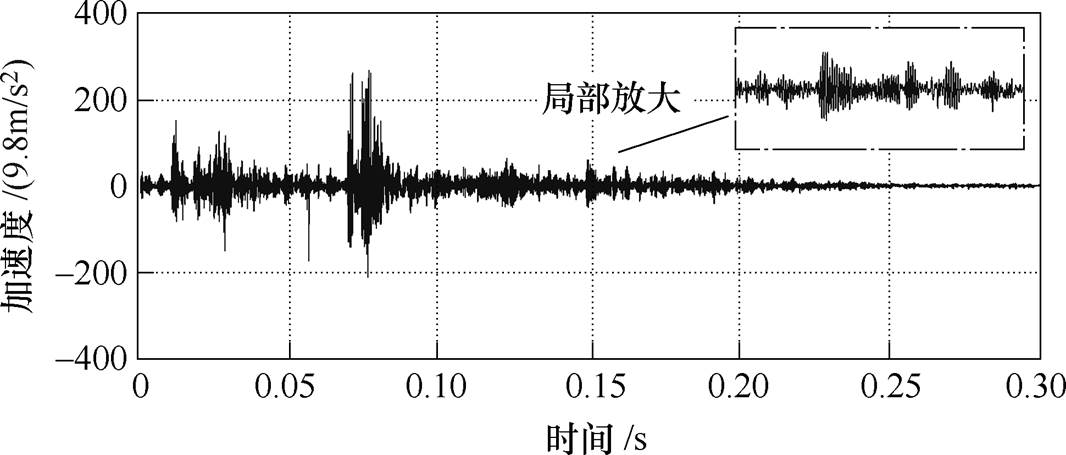
图2 实测在运252kV SF6高压断路器（山东泰开）C相操动机构合闸振动信号
Fig.2 A measured closing vibration signal of C-phase operating mechanism of an in service 252kV SF6 HVCB made by Shandong Taikai
在断路器振动信号采集过程中往往会受到噪声的干扰，进一步分析之前应先对振动信号降噪处理。考虑到断路器振动信号的特殊性（非平稳非线性的时变冲击信号），本文采用小波分析的方法进行降噪处理。以图2所示的振动信号为例，采用coif5小波函数，进行5层分解，采用无偏估计阈值的原则对各层进行软阈值降噪，降噪后的波形如图3所示。对比降噪前后的振动信号波形（见图2和图3中的局部放大区域），可以看出，降噪后的信号中冲击子波的清晰度有了明显的提高，证明了小波降噪的有效性。
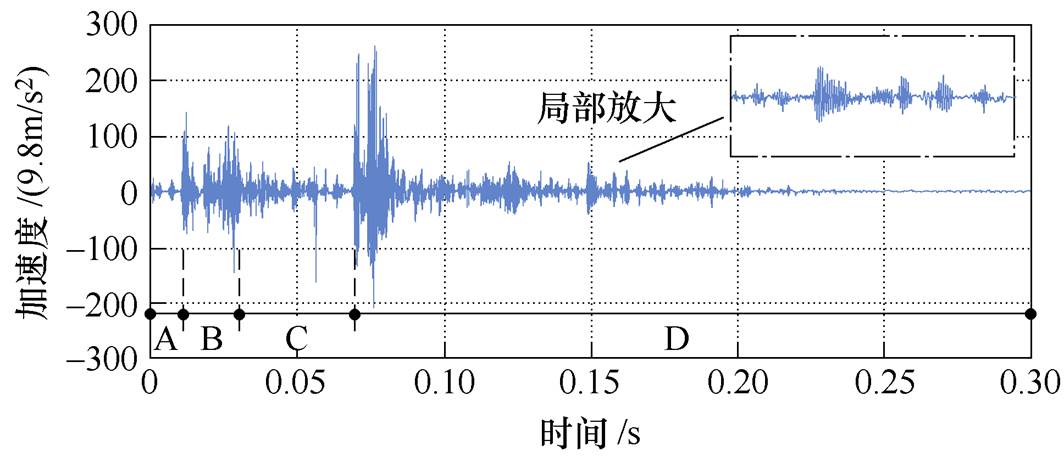
图3 小波降噪后的振动信号
Fig.3 Results of wavelet denoising for the vibration signal shown in Fig.2
将上述降噪后的振动信号分割成4个区域（见图3中的区域A、B、C和D），分别对应断路器动作过程中的脱扣阶段、机构解列阶段、传动阶段和制动阶段。将分割后的各子区信号单独抽取出来，如图4所示。这种对振动信号按照断路器的动作特性进行分区分割的好处是可以实现异常信号的快速定位，进而实现缺陷的准确识别。
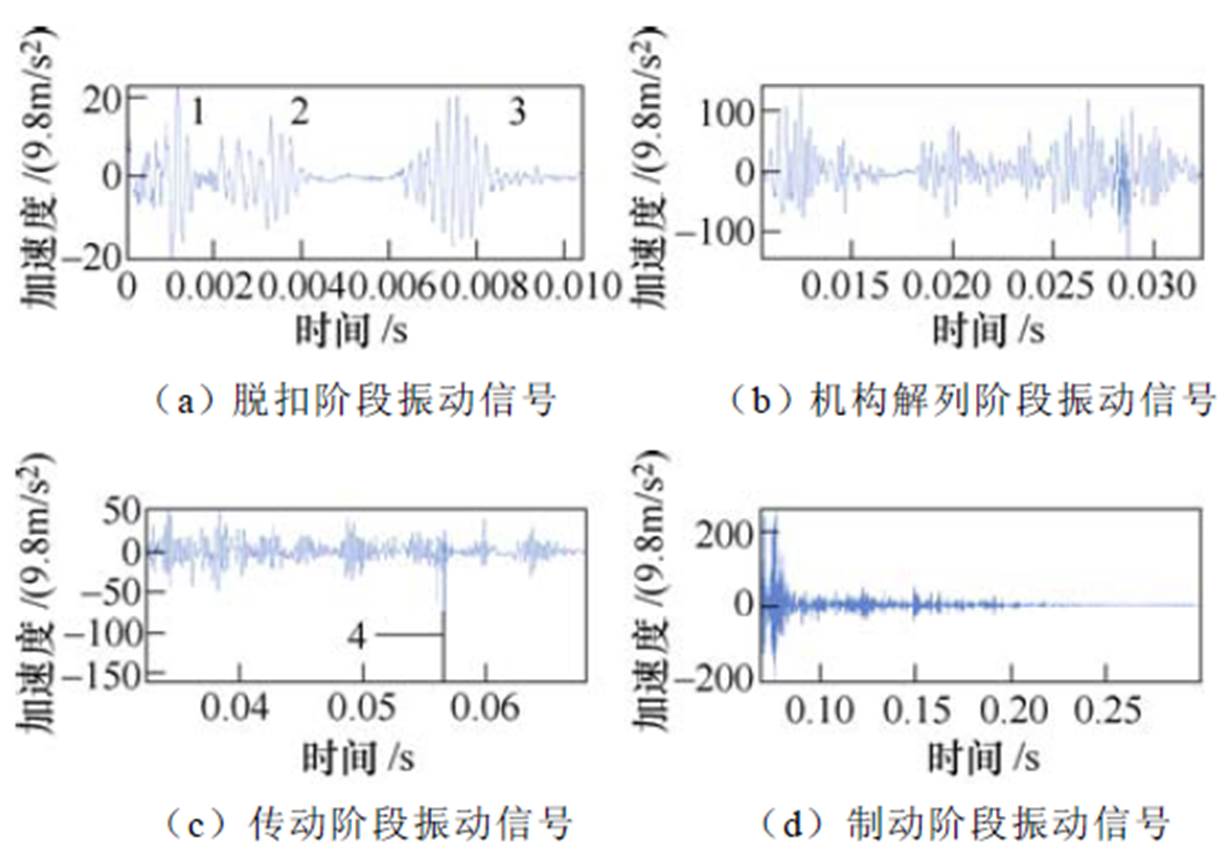
图4 振动信号分区分割结果
Fig.4 Division results of the vibration signal
在对高压断路器振动信号分区分割后，为了能够充分提取各子区信号中包含的断路器动力学特征，将其映射到高维相空间并进行递归图重构。图5所示为图4中各阶段振动信号的相空间轨迹及相应的递归图，可以看出各阶段振动信号的相空间轨迹及递归图差异明显、各有特点。
对比图4各阶段的振动信号与图5中的相应递归图，可以明显看出：
（1）振动信号中的每一个冲击波在递归图中都有一条白带与之对应（见图4a中的冲击波1、2、3 分别对应图5a中的白带1、2、3）。
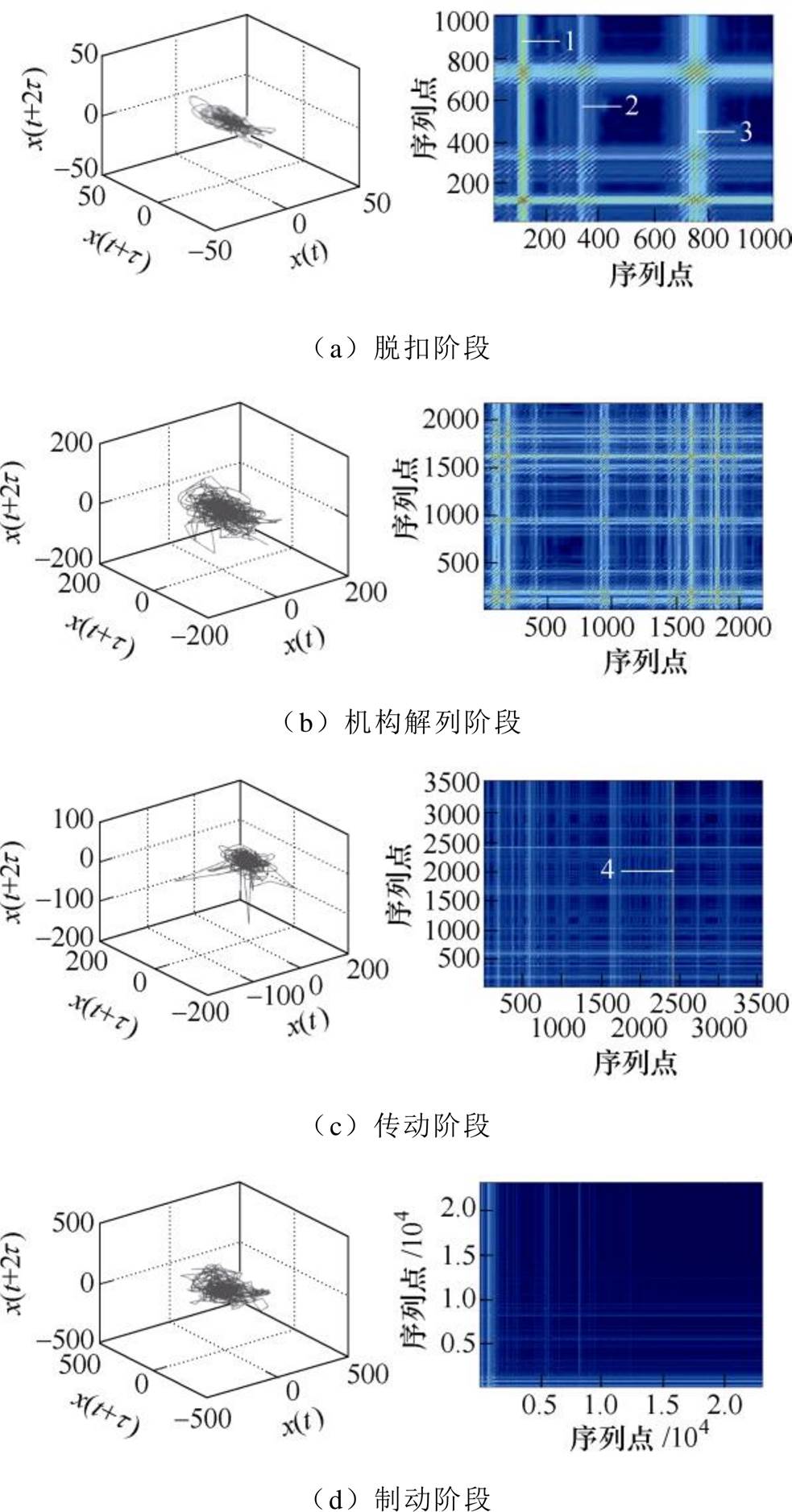
图5 子区信号相空间轨迹（左）及重构递归图（右）
Fig.5 Phase space trajectories (left) and reconstructed recurrence plots (right) for the sub-region vibrational signals
（2）冲击波出现的时刻与白带的位置一致、冲击波的持续时间与白带的宽度相同。
（3）冲击波越强（振幅越强），白带越明显。
（4）信号中的一小突变奇异点也能被准确地检测出来（见图4c中的突变点4对应图5c中的线4）等。
不仅如此，递归图的纹理结构描绘了断路器内在动力学机理，而时域振动信号却只能描述振动时间历程的表面现象。基于此，本文探究了利用振动信号递归图特征对断路器机械缺陷进行辨识的可能性，通过试验与现场实测进行了有效性和实用性 验证。
试验装置如图6所示，试验断路器采用弹簧操动机构，额定电压、额定电流和额定短路开断电流分别为12kV、1 250A和25kA。振动信号是在电动操作该断路器分、合闸动作时采集的，不包括电机储能信号。振动信号采集系统包括加速度传感器、数据采集卡、显示器及电源等，采样率设为100kHz，采样时间为0.04s。
图6 试验装置
Fig.6 Experimental setup
振动信号经过去趋势项、小波降噪预处理后，被分割成4个子区间（分别对应断路器脱扣阶段、机构解列阶段、传动阶段和制动阶段的振动信号），再对各子区信号进行定量递归分析以实现断路器机械缺陷的有效识别，具体流程如图7所示。
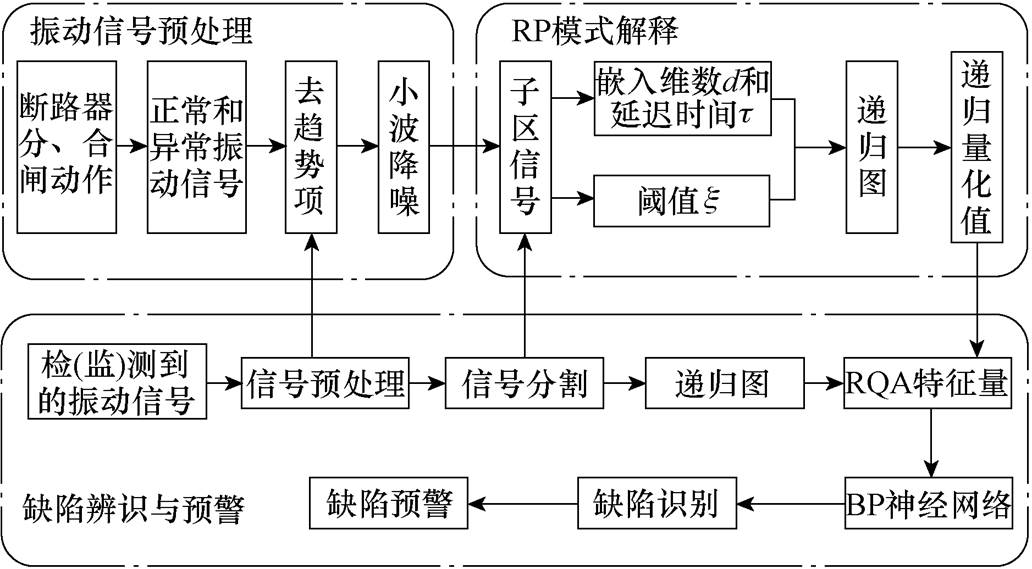
图7 断路器机械缺陷识别流程
Fig.7 Process of mechanical defect identification for CB
通常情况下，设置与实际在运断路器完全相同的机械缺陷难度较大。本文模拟设置了试验断路器四种常见的机械缺陷：
（1）通过增大铁心运动阻力模拟合闸脱扣器异常（Close Coil Anomaly, CCA）。
（2）通过加大主轴连板与传动杆连接的夹紧力模拟机构卡涩（Operating Mechanism Jam, OMJ）。
（3）通过替用较小直径的连接轴销模拟绝缘拉杆轴销磨损（Insulating Linkage Anomaly, ILA）。
（4）通过调节有效缓冲行程模拟分闸缓冲器异常（Opening Damper Anomaly, ODA）。
考虑到断路器振动信号具有一定的分散性（即便断路器状态、采集条件完全相同，采集到的振动信号也不可能完全一致），因此，在每种缺陷下，各采集了至少10组有效的分、合闸振动信号用于评估所提方法的有效性和鲁棒性。
将振动信号进行分区分割便于异常信号定位，在此基础上将各子区信号重构至高维相空间并进行定量递归分析，能够将断路器动力学变化特征充分显现出来，从而便于缺陷辨识。断路器振动信号定量递归分析流程如图8所示。图8a中①所示为断路器正常状态下的某一分闸振动信号，与图8b中①所示的分闸缓冲器完全失效时的分闸振动信号区别不是很明显，很难从整个时域波形上判断该断路器的机械状态。按3.1节所述的分割方法对振动信号进行分割（分割为4段：脱扣阶段、机构解列阶段、传动阶段和制动阶段，如图8中步骤②、③所示），并绘制分割信号的高维相空间轨迹及递归图，如图8中步骤④～⑥所示。由图8可以明显看出：
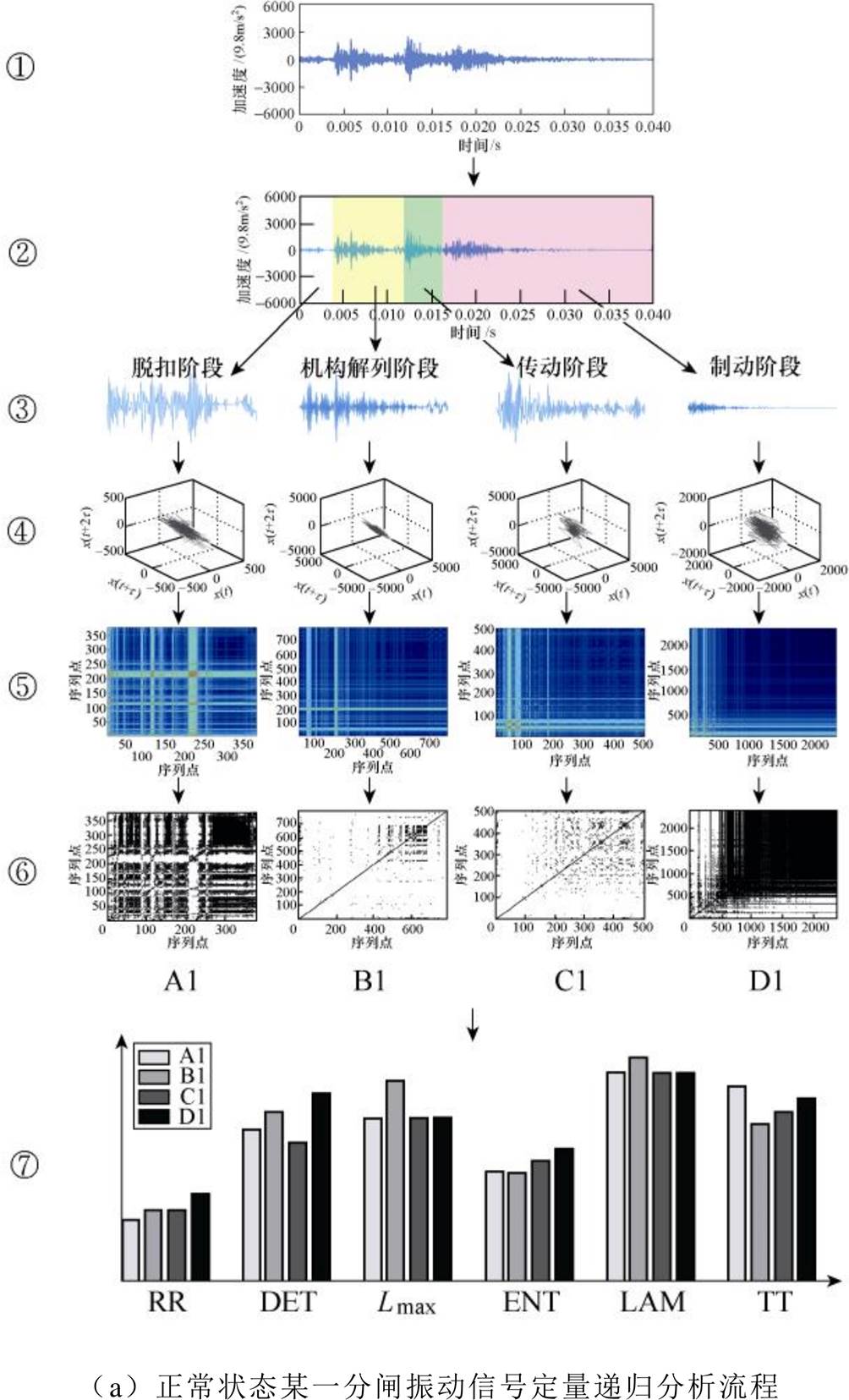
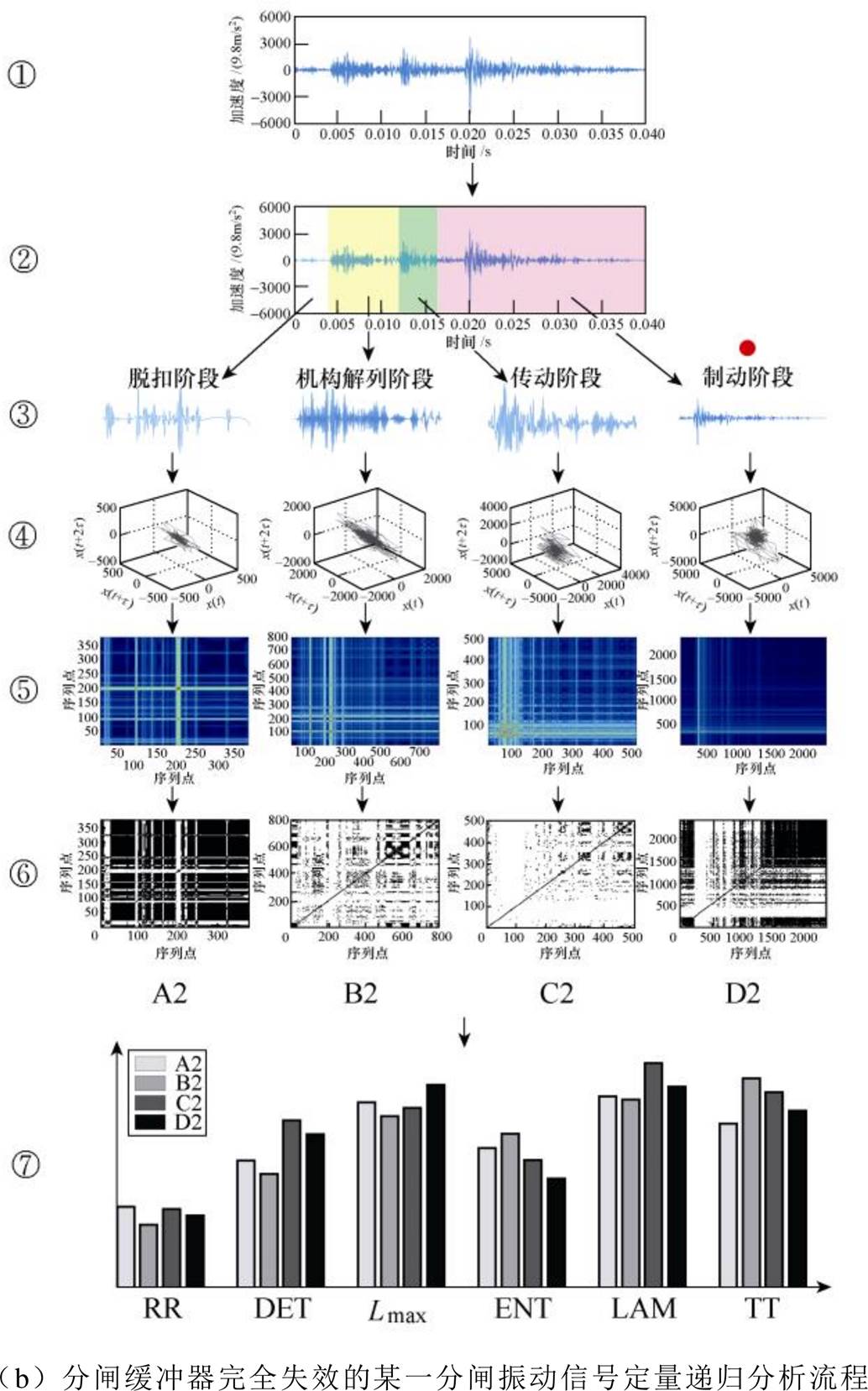
图8 断路器振动信号定量递归分析流程
Fig.8 Process of recurrence quantification analysis for CB’s vibration signal
（1）子区信号（见步骤③）每出现一个冲击波，对应递归图（见步骤⑤或⑥）相应位置出现一白色条状结构，白色条状结构越明显，表明信号突变越强烈。
（2）同一振动信号各阶段的递归图差异较大（如A1、B1、C1、D1），不同振动信号同一阶段的递归图既有相似（如C1与C2）亦有差异（如D1与D2）。由此可知，递归图的结构特征与断路器的状态息息相关，断路器状态发生变化将导致递归图结构发生相应的改变，即递归图能够很好地表征断路器的状态。
为能较全面地描述递归图的特征，本文从递归图中提取6个典型的RQA特征量（即RR、DET、Lmax、ENT、LAM和TT）对其进行定量分析，并探究这些特征量表征断路器不同机械缺陷的能力（区分度与稳定性）及模式识别的效果。以分闸缓冲器异常为例，分闸缓冲器只在断路器分闸动作的末期起作用，其状态信息仅体现在断路器分闸制动阶段的振动信号中（见图8中的D区）。图9给出了分闸缓冲器失效与正常状态下该区的其中3个RQA特征（ENT、DET和TT）的一维、二维和三维分布情况。图9a为ENT的分布情况，可以看到，分闸缓冲器异常（ODA）和正常（NO）的ENT分布存在一定的差异，但区分性不是很明显；图9b是ENT和DET的二维散点图，叉点表示分闸缓冲器异常、圆点表示正常，可以看出，二维特征已经能够较好地将分闸缓冲器异常与正常状态区分开来，但也存在交叉区域；更进一步地，图9c为采用3个RQA特征的三维分布，可以明显看出，这3个特征能够很好地区分分闸缓冲器异常与正常状态。同时注意到，分闸缓冲器异常的特征分布比较散，不像正常状态时相对较集中，说明分闸缓冲器异常导致断路器制动阶段动力学特性不稳定。
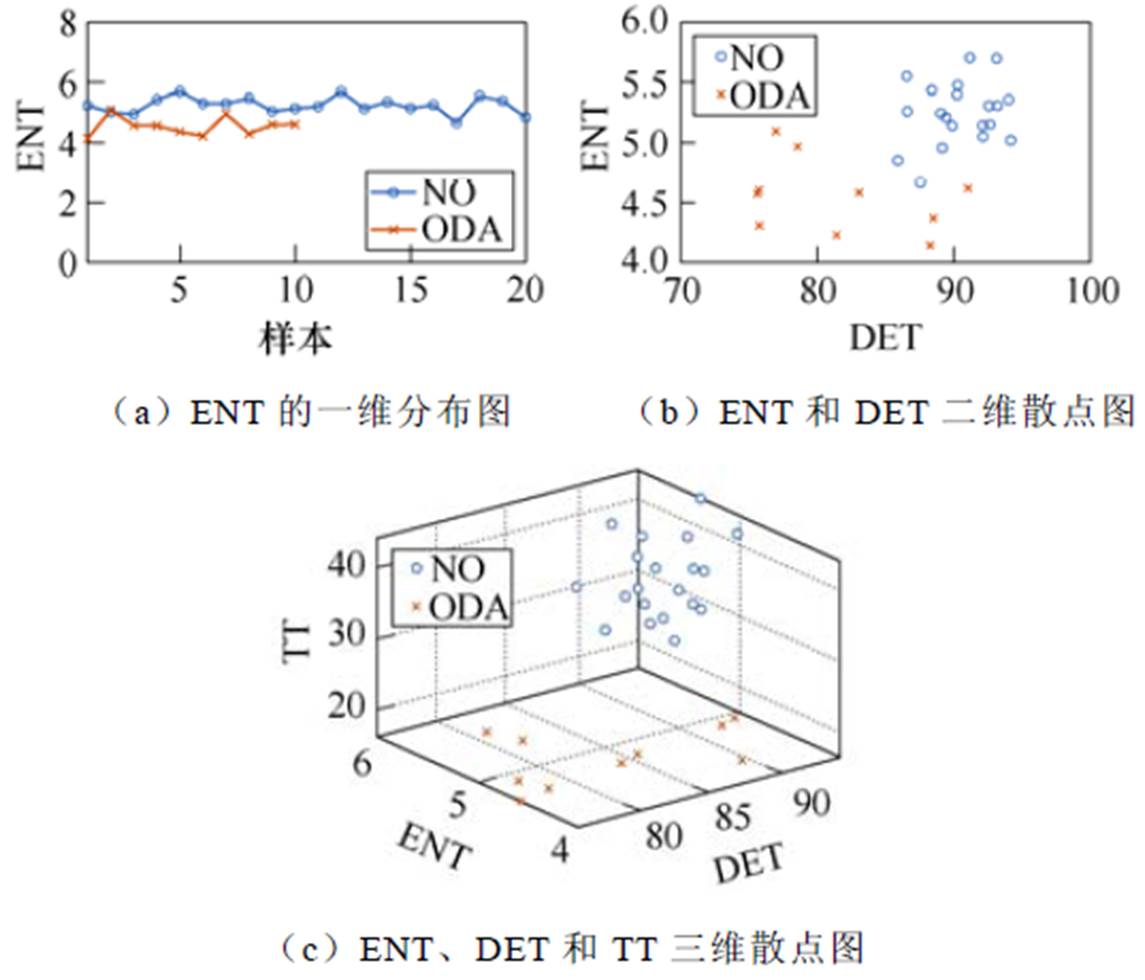
图9 分闸缓冲器失效与正常状态递归特征分布
Fig.9 Distribution of recurrence features under opening damper failure and normal conditions
对于其他三种机械缺陷，考虑到：①合闸脱扣器异常（CCA）主要影响断路器脱扣阶段（A区）动力学特性，机构解列阶段（B区）受机构卡涩（OMJ）的影响较大，绝缘拉杆轴销磨损（ILA）将导致断路器分、合闸末期绝缘拉杆“窜动”即对制动阶段（D区）影响较大；②有些缺陷只会影响合闸过程（如合闸脱扣器异常只影响合闸过程），有些缺陷只影响分闸过程（如分闸缓冲器异常只影响分闸过程）。因此，综合断路器这些特点，图10给出了这三种机械缺陷相应阶段的RQA特征分布情况（为方便与图9对比，仍以ENT、DET和TT特征为例）。
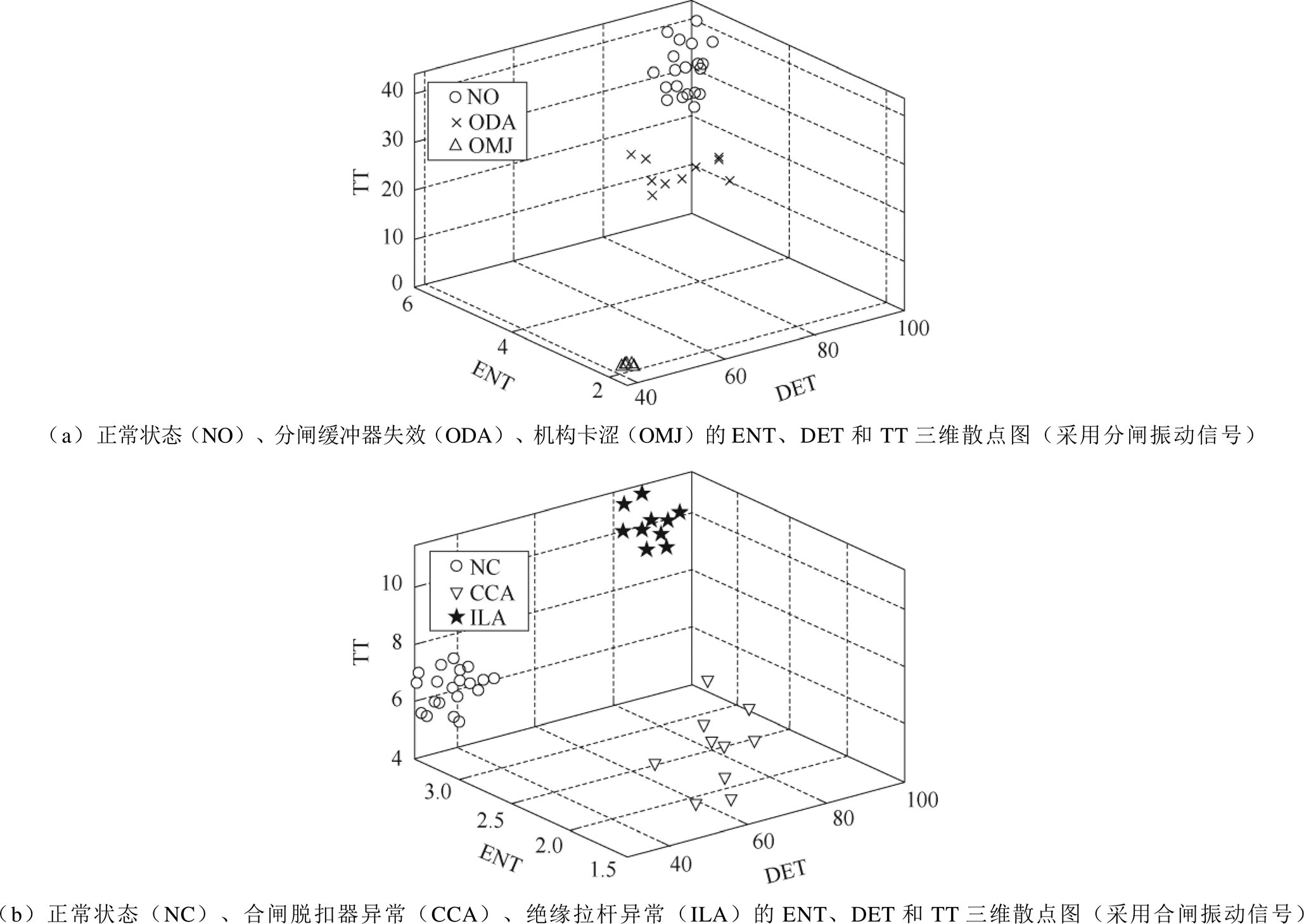
图10 断路器不同状态的递归特征分布
Fig.10 Distribution of recurrence features under CB’s different conditions
由图10可知，断路器不同缺陷下的振动信号经预处理、分区分割、递归图重构和定量递归分析处理后，按照缺陷类型聚集在一起，并且不同缺陷类型之间界限明显，说明RQA特征具有较好的区分度和稳定性，这将非常有利于后续采用智能算法对断路器机械缺陷进行模式识别。
本文采用BP神经网络对断路器机械缺陷进行识别。将总共80个样本（正常分、合闸振动信号各20个样本，4类缺陷振动信号各10个样本）随机抽取65%用于训练，剩余35%用于测试。BP神经网络的输入层为6个节点（与RQA特征维数相同），隐含层调节为20个神经元，输出层6个节点（与断路器状态类别标签对应，标签1～6分别对应：断路器正常分闸（NO）、断路器正常合闸（NC）、分闸缓冲器失效（ODA）、操动机构卡涩（OMJ）、合闸脱扣器异常（CCA）、绝缘拉杆轴销磨损（ILA））。隐含层和输出层的传递函数均选择双曲正切S型函数，训练算法采用动量梯度下降法，学习率设为0.1，最大训练次数1 000次，训练目标为0.01。神经网络识别结果如图11所示（因训练与测试样本是随机选取的，多次试验的结果会有一定的差别，该结果为10次试验内的最佳性能）。可以看出，采用本文所提的振动信号多区域递归特征识别断路器状态的准确率可达92.9%，说明RQA特征能够有效地表征断路器的状态。
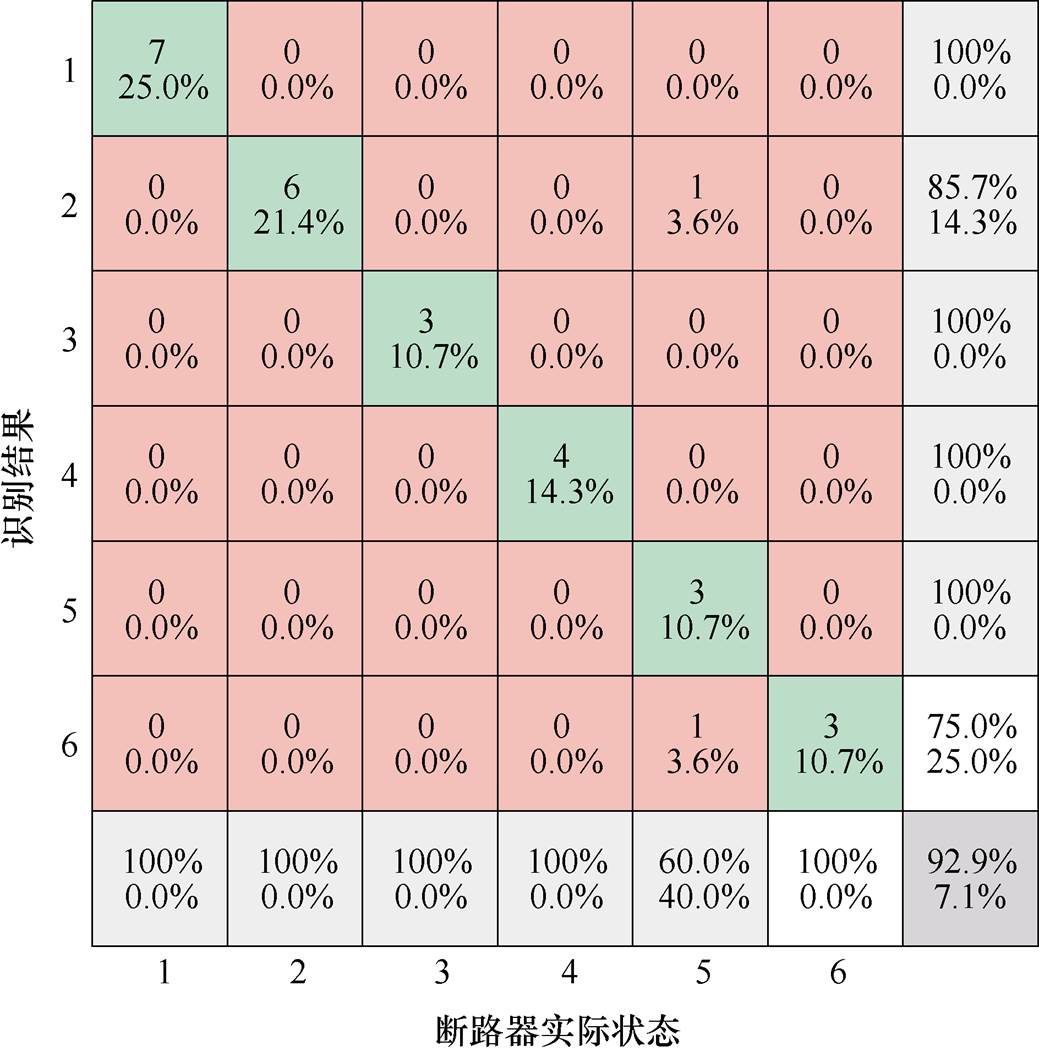
图11 神经网络缺陷识别结果
Fig.11 Diagnosis result of CB defects using BP neural network
为进一步探究所提方法的工程实际应用效果，开展了现场实测分析工作。以某220kV变电站的某一在运252kV SF6高压断路器为例，现场实测图如图12所示。该断路器三相各有一液压操动机构，如图12a所示，测试时，将加速度传感器分别固定在A、B、C三相操动机构顶部，具体如图12b所示。
图13给出了某次测试的原始合闸振动信号，可以看出，观察这些振动信号很难对该断路器的状态做出判断。采用本文所提方法，对图13所示的振动信号进行小波去噪、分区分割（按上述方法分成4个功能区域后，对每个区域再细分为二，即总共分成8个区域）、对各个分割区域进行相空间递归图重构，最后，进行定量递归分析。
以RQA特征的LAM特征为例，现场测试分析结果如图14所示，可以看出，区域5和区域6的LAM值明显异常，两个区域的C相LAM值突变均较明显。该断路器的合闸时间厂家规定为(105±5)ms，即触头接触阶段为100～110ms，对应于区域5；而区域6则为机构制动阶段。结合该对应关系，图14表明：
图12 某220kV变电站在运252kV SF6高压断路器振动信号现场实测图
Fig.12 Field vibration testing for a 252kV SF6 HVCB in a 220kV substation
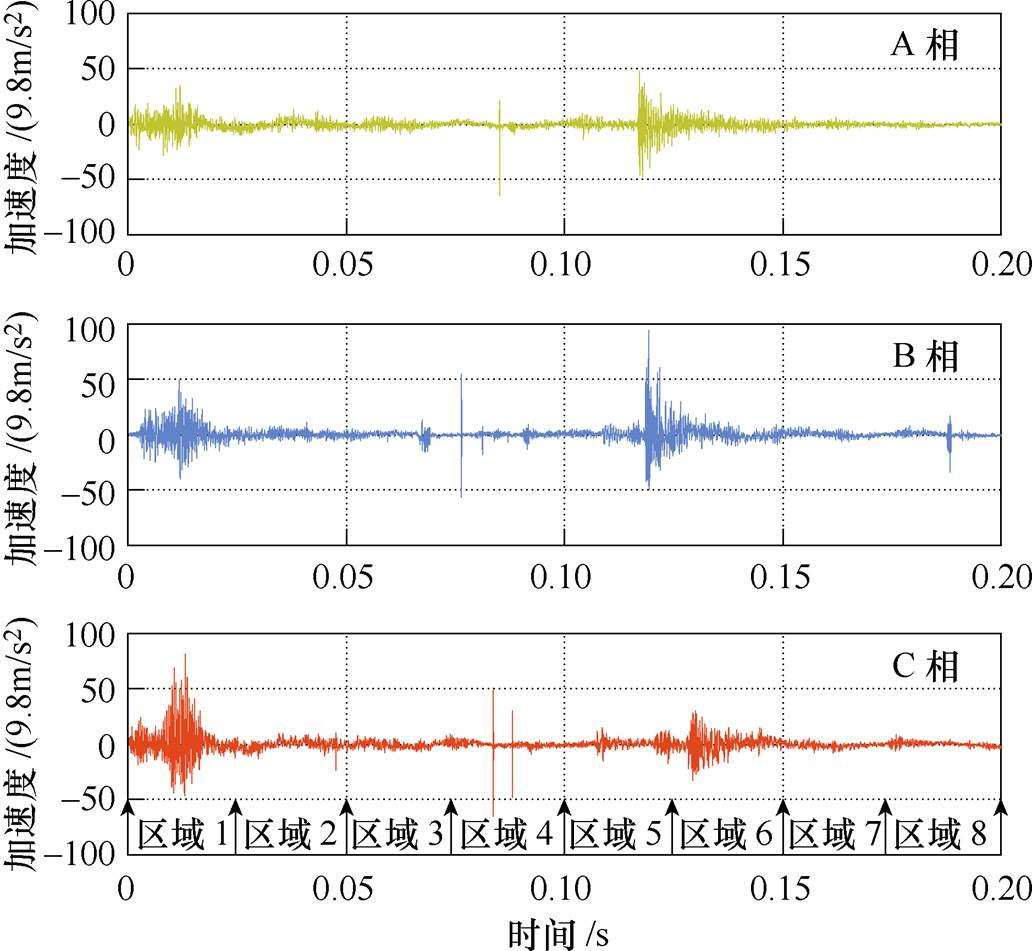
图13 现场采集的某一组合闸振动信号
Fig.13 Closing vibration signals obtained from field testing
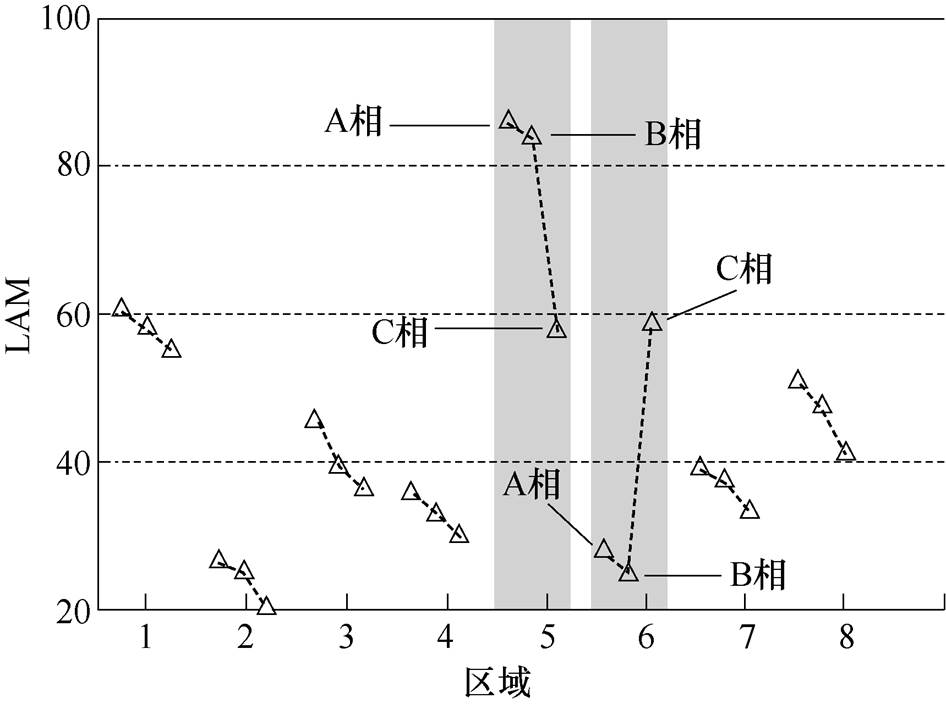
图14 现场测试分析结果
Fig.14 Analysis results for the field testing
（1）由于区域5（触头接触阶段）中的C相LAM值发生较大的偏离，说明该相在触头接触阶段可能存在异常，如合闸时间可能不合格。
（2）区域6（机构制动阶段），C相LAM值亦明显异于A、B相，表明C相在机构制动阶段也可能存在异常，如液压阀（启闭）异常、液压油流通道堵塞等导致的制动异常等。
现场检修人员对该断路器进行机械特性测试，结果表明该断路器的C相合闸时间确实偏长（测试结果为128.1ms，而厂家标准为(105±5)ms，这与上述诊断结果（1）一致；在换油时，发现C相油缸过滤器积污较严重，清理过后，C相区域6的LAM值明显降至与A、B相同一水平，C相消缺后的测试分析结果如图15所示，表明诊断结果（2）的有效性。
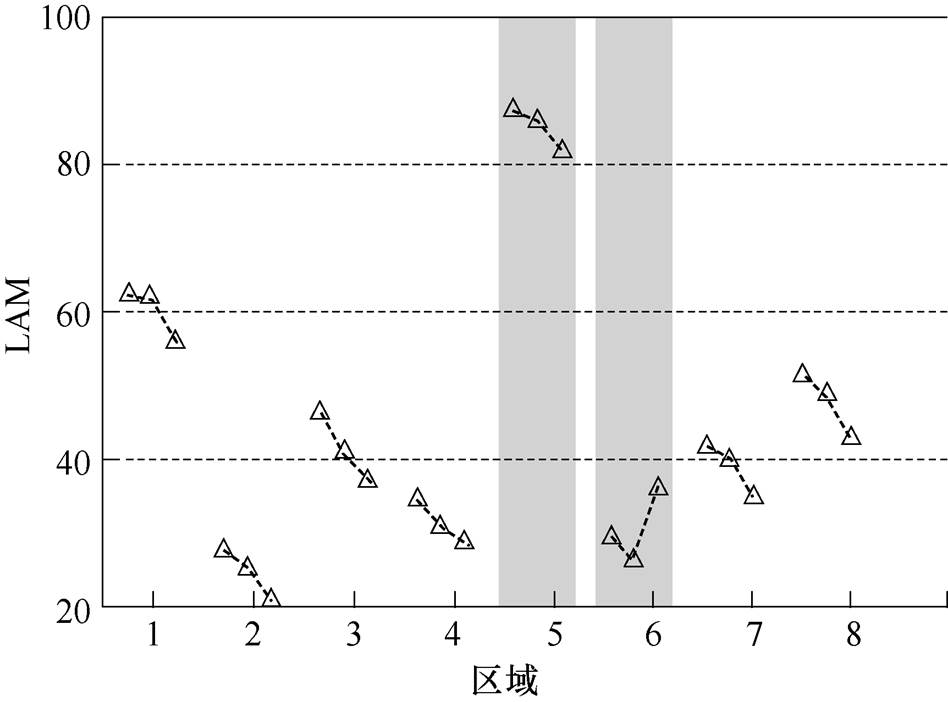
图15 C相消缺后的测试分析结果
Fig.15 Analysis results after eliminating C-phase defect
本文主要通过对断路器振动信号进行处理与分析以实现机械缺陷辨识。实际上，目前监测断路器机械状态的信号还包括线圈电流信号、触头行程信号等，这些信号同样蕴含着断路器机械状态信息。线圈电流信号包含着二次回路状态（包括辅助开关等）、线圈本身状态、操动机构机械锁扣装置状态等信息，与线圈动作相关联的断路器元器件若发生异常，线圈电流会发生相应的改变。例如，图16所示的是某变电站一台在运的高压断路器正常操作和操作电压异常（电压降至90%，即断路器动作电压为DC 198V）时的分、合闸线圈电流信号。可以看到，当断路器操作电压异常时，其线圈电流波形发生了明显的变化。因此，可以通过提取线圈电流波形的特征参数对断路器相应元器件的状态进行诊断。
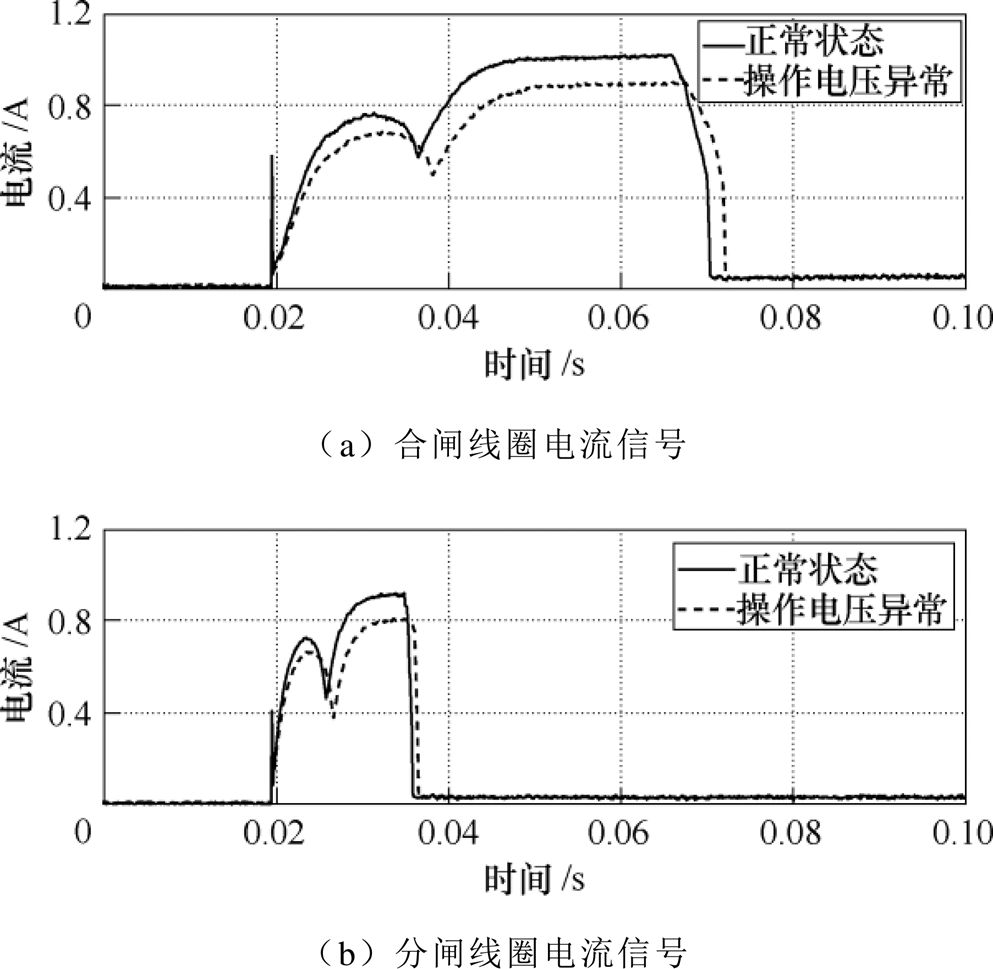
图16 某一在运高压断路器线圈电流信号
Fig.16 Coil current signals of an in service HVCB
然而，当操动机构锁扣装置被线圈触发解列后，线圈就不再参与后续的机构本体运动过程，即操动机构本体的机械状态，无法反映到线圈电流信号中。而机械振动信号却蕴含着丰富的操动机构本体状态信息。因此，后续工作可将振动信号与线圈电流信号相结合，以更全面地评估断路器的状态。
另外，近年来永磁机构发展较快，对永磁机构的故障辨识也受到人们越来越多的关注。永磁机构与弹簧机构虽然功能一样但结构大不相同，弹簧机构的分、合闸过程可分为四个阶段：脱扣阶段、机构解列阶段、传动阶段和制动阶段。而永磁机构由于省去了合闸弹簧、脱扣装置（当铁心力大于反力时脱扣）、保持装置（靠永磁体磁力保持）等，其结构更简单，对应的振动信号相较于弹簧机构的简洁。如图17所示为一ZW45-12型永磁机构的合闸振动波形[26]，根据永磁机构的结构特点及运动特性（见图17的触头行程曲线），可将该类型永磁机构的振动信号分割为：A驱动阶段、B压缩触头弹簧阶段、C触头碰撞及制动阶段。在对永磁机构的振动信号分区分割后，亦可采用本文所提方法进行RQA特征提取，以实现永磁机构的机械故障辨识。
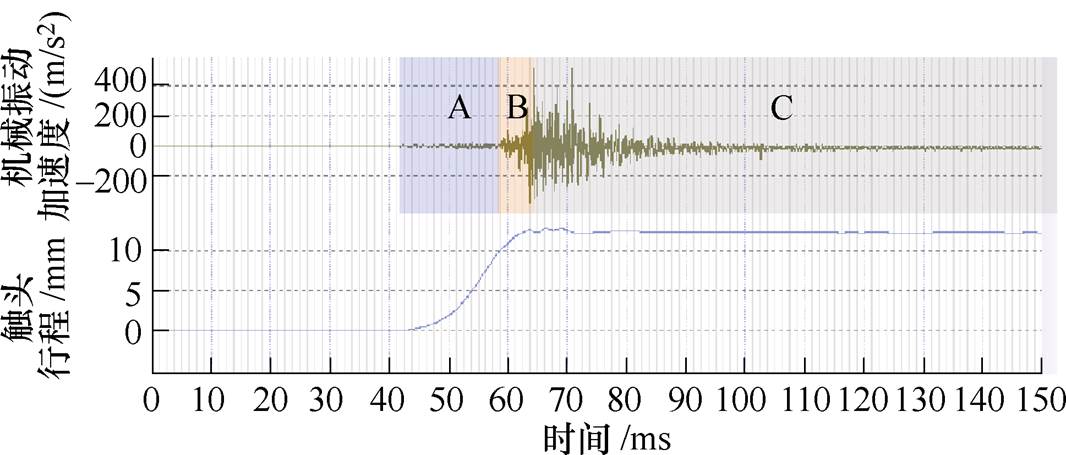
图17 ZW45-12型永磁机构合闸振动波形（上）及其触头行程曲线（下）
Fig.17 Closing vibration waveform (upper) and contact travel (curve) lower for a ZW45-12 permanent magnet operating mechanism
1）提出根据高压断路器的结构特点和分、合闸动作特性对振动信号进行分区分割的思想。根据该思想，可总体上将振动信号分割成4个功能区域（即断路器脱扣阶段、机构解列阶段、传动阶段和制动阶段对应的振动信号），但详细应根据具体类型的断路器振动信号特点进行划分。这种振动信号分区分割的思想有助于确定断路器机械缺陷的部位。
2）递归图能够较清晰地描述振动信号中的冲击波特点，其纹理结构特征蕴含着断路器丰富的动力学特性；而定量递归分析能够实现递归图的模式识别，进而实现断路器机械缺陷的辨识。
3）通过实验室的模拟试验（采用12kV真空断路器）探索并验证了本文所提方法的有效性。随着RQA特征维数的增多（见图9中的一维、二维和三维RQA特征分布），断路器不同缺陷之间的区分性越来越显著，在此基础上，采用BP神经网络识别断路器机械缺陷的准确率可达92.9%。
4）通过对变电站在运高压断路器开展现场实测工作，验证了所提方法的实用性和优势。所提方法能够有效定位高压断路器的异常部位，诊断结果与实际情况基本一致。
参考文献
[1] 郑一鸣, 徐华, 金佳敏, 等. 断路器特性对切除35kV空母线并联电抗器操作过电压的抑制效果[J]. 电工技术学报, 2018, 33(22): 5282-5291.
Zheng Yiming, Xu Hua, Jin Jiamin, et al. Suppression effects of circuit breaker characteristics on switching overvoltage of cutting shunt reactor on 35kV no-load busbar[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5282-5291.
[2] Rovelli E, Scarpaci S, Lidozzi A, et al. An HVCB electronic drive for modern electrical substations in distribution power systems[J]. IEEE Transactions on Power Delivery, 2016, 31(2): 665-673.
[3] Razi-Kazemi A, Vakilian M, Niayesh K, et al. Priority assessment of online monitoring investment for power system circuit breakers—Part I: qualitative- quantitative approach[J]. IEEE Transactions on Power Delivery, 2013, 28(2): 928-938.
[4] 孟晓承, 韩学山, 许易经, 等. SF6高压断路器机械故障概率的非精确条件估计[J]. 电工技术学报, 2019, 34(4): 693-702.
Meng Xiaocheng, Han Xueshan, Xu Yijing, et al. Imprecise estimation for conditional mechanical outage probabilities of SF6 high voltage circuit breakers[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 693-702.
[5] 关永刚, 杨元威, 钟建英, 等. 高压断路器机械故障诊断方法综述[J]. 高压电器, 2018, 54(7): 10-19.
Guan Yonggang, Yang Yuanwei, Zhong Jianying, et al. Review on mechanical fault diagnosis methods for high-voltage circuit breakers[J]. High Voltage Apparatus, 2018, 54(7): 10-19.
[6] 杨元威, 关永刚, 陈士刚, 等. 基于声音信号的高压断路器机械故障诊断方法[J]. 中国电机工程学报, 2018, 38(22): 6730-6736.
Yang Yuanwei, Guan Yonggang, Chen Shigang, et al. Mechanical fault diagnosis method of high voltage circuit breaker based on sound signal[J]. Proceedings of the CSEE, 2018, 38(22): 6730-6736.
[7] 程序, 关永刚, 张文鹏, 等. 基于因子分析和支持向量机算法的高压断路器机械故障诊断方法[J]. 电工技术学报, 2014, 29(7): 209-215.
Cheng Xu, Guan Yonggang, Zhang Wenpeng, et al. Diagnosis method on the mechanical failure of high voltage circuit breakers based on factor analysis and SVM[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 209-215.
[8] 常广, 王毅, 王玮. 采用振动信号零相位滤波时频熵的高压断路器机械故障诊断[J]. 中国电机工程学报, 2013, 33(3): 155-162.
Chang Guang, Wang Yi, Wang Wei. Mechanical fault diagnosis of high voltage circuit breakers utilizing zero-phase filter time-frequency entropy of vibration signal[J]. Proceedings of the CSEE, 2013, 33(3): 155-162.
[9] Yang Qiuyu, Ruan Jiangjun, Zhuang Zhijian, et al. A new vibration analysis approach for detecting mechanical anomalies on power circuit breakers[J]. IEEE Access, 2019(7): 14070-14080.
[10] 黄新波, 胡潇文, 朱永灿, 等. 基于卷积神经网络算法的高压断路器故障诊断[J]. 电力自动化设备, 2018, 38(5): 136-140.
Huang Xinbo, Hu Xiaowen, Zhu Yongcan, et al. Fault diagnosis of high-voltage circuit breaker based on convolution neural network[J]. Electric Power Auto- mation Equipment, 2018, 38(5): 136-140.
[11] 万书亭, 豆龙江, 李聪, 等. 基于VMD和样本熵的高压断路器故障特征提取及分类[J]. 振动与冲击, 2018, 37(20): 32-38.
Wan Shuting, Dou Longjiang, Li Cong, et al. Fault feature extraction and classification of high voltage circuit breakers based on VMD and sample entropy[J]. Journal of Vibration and Shock, 2018, 37(20): 32-38.
[12] 赵书涛, 王亚潇, 孙会伟, 等. 基于自适应权重证据理论的断路器故障诊断方法研究[J]. 中国电机工程学报, 2017, 37(23): 7040-7046.
Zhao Shutao, Wang Yaxiao, Sun Huiwei, et al. Research of circuit breaker fault recognition method based on adaptive weighted of evidence theory[J]. Proceedings of the CSEE, 2017, 37(23): 7040-7046.
[13] 孙曙光, 张强, 杜太行, 等. 基于振动信号的低压万能式断路器分合闸故障程度评估方法的研究[J]. 中国电机工程学报, 2017, 37(18): 5473-5482.
Sun Shuguang, Zhang Qiang, Du Taihang, et al. Study of evaluation method for low voltage con- ventional circuit breaker switching fault degree based on vibration signal[J]. Proceedings of the CSEE, 2017, 37(18): 5473-5482.
[14] 杨秋玉, 阮江军, 黄道春, 等. 基于振动信号时频图像识别的高压断路器分闸缓冲器状态评估[J]. 电工技术学报, 2019, 34(19): 4048-4057.
Yang Qiuyu, Ruan Jiangjun, Huang Daochun, et al. Opening damper condition evaluation based on vibration time-frequency images for high-voltage circuit breakers[J]. Transactions of China Electro- technical Society, 2019, 34(19): 4048-4057.
[15] 杨秋玉, 阮江军, 黄道春, 等. 基于振动信号的高压断路器触头超程状态识别[J]. 电机与控制学报, 2019, 23(6): 27-34.
Yang Qiuyu, Ruan Jiangjun, Huang Daochun, et al. Over-travel state identification for electrical contact of high-voltage circuit breaker using vibration signature[J]. Electric Machines and Control, 2019, 23(6): 27-34.
[16] 黄南天, 王斌, 蔡国伟, 等. 基于Tsallis熵与层次化混合分类器的含未知故障断路器机械故障诊断[J]. 高电压技术, 2019, 45(5): 1518-1525.
Huang Nantian, Wang Bin, Cai Guowei, et al. Mechanical fault diagnosis containing unknown fault of high voltage circuit breaker based on Tsallis entropy and hybrid classifier[J]. High Voltage Engin- eering, 2019, 45(5): 1518-1525.
[17] 万书亭, 豆龙江, 李聪, 等. 基于振动信号的高压断路器合闸特性参数在线检测方法研究[J]. 振动工程学报, 2019, 32(2): 359-367.
Wan Shuting, Dou Longjiang, Li Cong, et al. Study on on-line detection of high voltage circuit breaker closing characteristic parameters based on vibration signal[J]. Journal of Vibration Engineering, 2019, 32(2): 359-367.
[18] Eckmann J P, Kamphorst S O, Ruelle D. Recurrence plots of dynamical systems[J]. Europhysics Letters, 1987, 4(9): 973-977.
[19] Takens F, Rand D A, Young L S. Detecting strange attractors in turbulence[J]. Dynamical Systems and Turbulence, Lecture Notes in Mathematics, 1981, 898: 666-681.
[20] Webber C L, Zbilut J P. Dynamical assessment of physiological systems and states using recurrence plot strategies[J]. Journal of Applied Physiology, 1994, 76: 965-973.
[21] Terrill P I, Wilson S J, Suresh S, et al. Attractor structure discriminates sleep states: recurrence plot analysis applied to infant breathing patterns[J]. IEEE Transactions on Biomedical Engineering, 2010, 57(5): 1108-1116.
[22] Nguyen C D, Wilson S J, Crozier S, et al. Automated quantification of the synchrogram by recurrence plot analysis[J]. IEEE Transactions on Biomedical Engin- eering, 2012, 59(4): 946-955.
[23] Censi F, Calcagnini G, Cerutti S. Proposed corre- ctions for the quantification of coupling patterns by recurrence plots[J]. IEEE Transactions on Biomedical Engineering, 2004, 51(5): 856-859.
[24] Marwan N, Romano M C, Thiel M, et al. Recurrence plots for the analysis of complex systems[J]. Physics Reports, 2007, 438(5-6): 237-329.
[25] 刘小峰, 杨康俊, 柏林. 基于Lamb波递归量化分析的复合材料裂纹损伤定征研究[J]. 振动与冲击, 2019, 38(10): 250-255.
Liu Xiaofeng, Yang Kangjun, Bo Lin. Crack damage investigation of composite materials based on the Lamb wave and recursive quantitative analysis[J]. Journal of Vibration and Shock, 2019, 38(10): 250- 255.
[26] 李斌. 永磁机构真空断路器运动特性状态评估方法研究[D]. 沈阳: 沈阳工业大学, 2013.
Study and Application of Mechanical Defect Identification for High-Voltage Circuit Breakers Using Recurrence Quantification Analysis
Abstract Diagnosing potential mechanical defects in an in service high-voltage circuit breakers (HVCB) using vibration signals is a challenging research task, which has broad rospective applications. This paper proposes a novel vibration signal analysis method based on recurrence quantification analysis (RQA) and applies it to a real substation. In order to locate the defect accurately, the vibration signal is divided into several functional sub-regions of HVCB. The signals of each sub-region are mapped to a lagged phase space to fully display the dynamic characteristics, and the recurrence plot is reconstructed in the phase space. Finally, recurrence rate (RR), determinism (DET), maximum diagonal line length (Lmax), entropy (ENT), laminarity (LAM) and trapping time (TT) are introduced to quantitatively analyze the recurrence plot of each sub-signal. The experimental results show that the proposed approach can effectively identify the mechanical defects in HVCBs, and shows high accuracy in practical engineering applications.
keywords：High-voltage circuit breaker (HVCB), mechanical defect detection, vibration signals, signal division, recurrence quantification analysis (RQA)
中图分类号：TM561
DOI: 10.19595/j.cnki.1000-6753.tces.190944
国家重点研发计划资助项目（2017YFB0902400）。
收稿日期 2019-07-31
改稿日期 2019-09-11
杨秋玉 男，1986年生，博士研究生，研究方向为高压开关设备结构设计、断路器机-电耦合计算分析、电气设备状态检测与评估。E-mail: qiuyu.yang@whu.edu.cn（通信作者）
阮江军 男，1968年生，教授，博士生导师，研究方向为电工装备电磁-温度-流体-力学多物理场分析、电气设备状态检测与评估、气体绝缘预测理论、防雷与接地等。E-mail: ruan308@126.com
（编辑 陈 诚）