图1 气体绝缘母线结构简图
Fig.1 Schematic diagram of GIB
摘要 为实现对气体绝缘母线（GIB）过热性故障的及时诊断，该文提出一种GIB设备触指和外壳温度快速精确计算方法。该方法基于热电类比和传热学原理，建立包含触头结构的GIB热网络模型。利用圆盘接触的单热流通道（CMY）模型计算了触指与导电杆、基座之间的接触热阻，通过有限元数值模拟试验获取GIB各部件表面的非线性对流换热热阻及辐射换热热阻。利用GIB温升原型物理试验对基于热网络模型的GIB触指和外壳平均温度计算结果进行了验证。结果表明：在不同测试电流作用下，热网络法的计算速度约为有限元法的34倍，GIB外壳及触指温度热网络模型计算值与实测值之间误差最大为9.5%，最小为0.2%，验证了所建立的气体绝缘母线热网络模型的有效性。该模型可用于快速评估GIB设备外壳及触指温度，为GIB设备的热设计和温升状态监测提供了一种有效的分析方法。
关键词：气体绝缘母线 热网络模型 热电类比 温升计算 接触热阻
气体绝缘母线（Gas Insulated Bus bars, GIB）作为高电压、大电流电能传输设备被广泛应用于电力系统输、配、变电环节[1-2]。插接式触头是GIB电气回路的主要连接装置，稳定且较低的接触电阻和温升是GIB设备的重要指标[3-4]，近年来国内外对气体绝缘设备故障的调查统计结果表明，触头接触温升过高占整体故障比例的29%[5-6]，因此GIB设备特别是触头部位的温升计算对于气体绝缘设备的设计安装和状态监测具有重要意义。
目前，电力设备的温升计算方法主要包括基于求解传热和流动偏微分方程的“场”计算[7-12]和基于热电类比原理的“路”计算，基于物理场计算的方法可以准确地反映GIB设备的温度场分布情况，但也存在计算资源大、计算时间长、难以收敛等缺点，因此不适用于需要快速获取GIB设备关键部位温升计算的场合。基于热电类比原理的热网络法可以将少量的节点温升作为求解对象，而与数百万量级计算规模的“场”计算相比，具有物理概念简单明确、计算开销低、求解快速等突出优点，尤其适合于只针对特定部位热点温升的设备热分析场合[13-18]。目前针对GIB热网络法的研究通常只包含导电杆、SF6和外壳[19-20]，对于触指这一热点温升尚缺乏相关研究，且GIB各部件非线性对流换热热阻的计算过度依赖于与表面尺寸、特征温度相关的经验公式，计算结果偏差较大。文献[21]基于流体-热耦合计算得到对流换热系数在GIB各表面上的分布，再次提出了传统方法在处理对流换热问题上的不足。
本文基于热电类比原理，构建了包含触头结构的GIB热网络模型，利用M. G. Cooper等提出的圆盘接触单热流通道模型[22]（以下简称CMY模型）求解触指与导电杆、基座之间的接触热阻；基于有限元数值实验，计算分析在环境温度一定、无风无太阳辐射条件下各表面对流换热系数随负荷电流动态变化关系，并获取了不同负荷电流下各表面的非线性对流换热热阻参数，提高了GIB热网络模型精度。利用Matlab/Simulink ode45求解器实现了GIB热网络模型各节点温度的求解，开展了不同电流下GIB温升原型物理试验，GIB外壳、触指温度的计算值与实测值的对比结果验证了所建立的GIB热网络模型的有效性。研究结果可用于快速估算GIB设备外壳及触指温度，为GIB设备的热设计和温升监测提供一种有效的分析方法。
本文以单相GIB为研究对象，其结构如图1所示。主要包括外壳、导电杆、触头、法兰和基座。其中外壳、导电杆和基座材料为铝合金6063-T6，触指材料为纯铜板T2-Y，导电杆和触指表面镀银以提高导电性。基座与导电杆之间通过并联的16片触指联通。导电杆与基座通过螺栓栓接在与绝缘连接的法兰盘上。腔体内部充有0.4MPa的SF6气体以保证绝缘性能。
图1 气体绝缘母线结构简图
Fig.1 Schematic diagram of GIB
基于有限元数值试验计算GIB各部件表面对流换热热阻，并根据试验结果得出各表面对流换热系数与所加测试电流之间关系，给出随测试电流变化的对流换热热阻表达式。在有限元数值试验及热网络模型计算过程中，做出如下假设：
（1）在有限元数值试验中，基于Hertz接触假设，忽略视在接触区域内的微观表面形貌，假定导体与触指的接触发生在单一等效导电斑点上。导电斑点用体积微小的导电桥代替，模型简化及热量传递网络如图2所示。
（2）在热量传递过程中，只考虑触指与导电杆及基座之间的接触热阻，忽略导电桥自身的热容及其辐射换热、对流换热热阻。
（3）忽略各触指与导电杆间的接触差异，认为各触指与导电杆之间均匀接触。
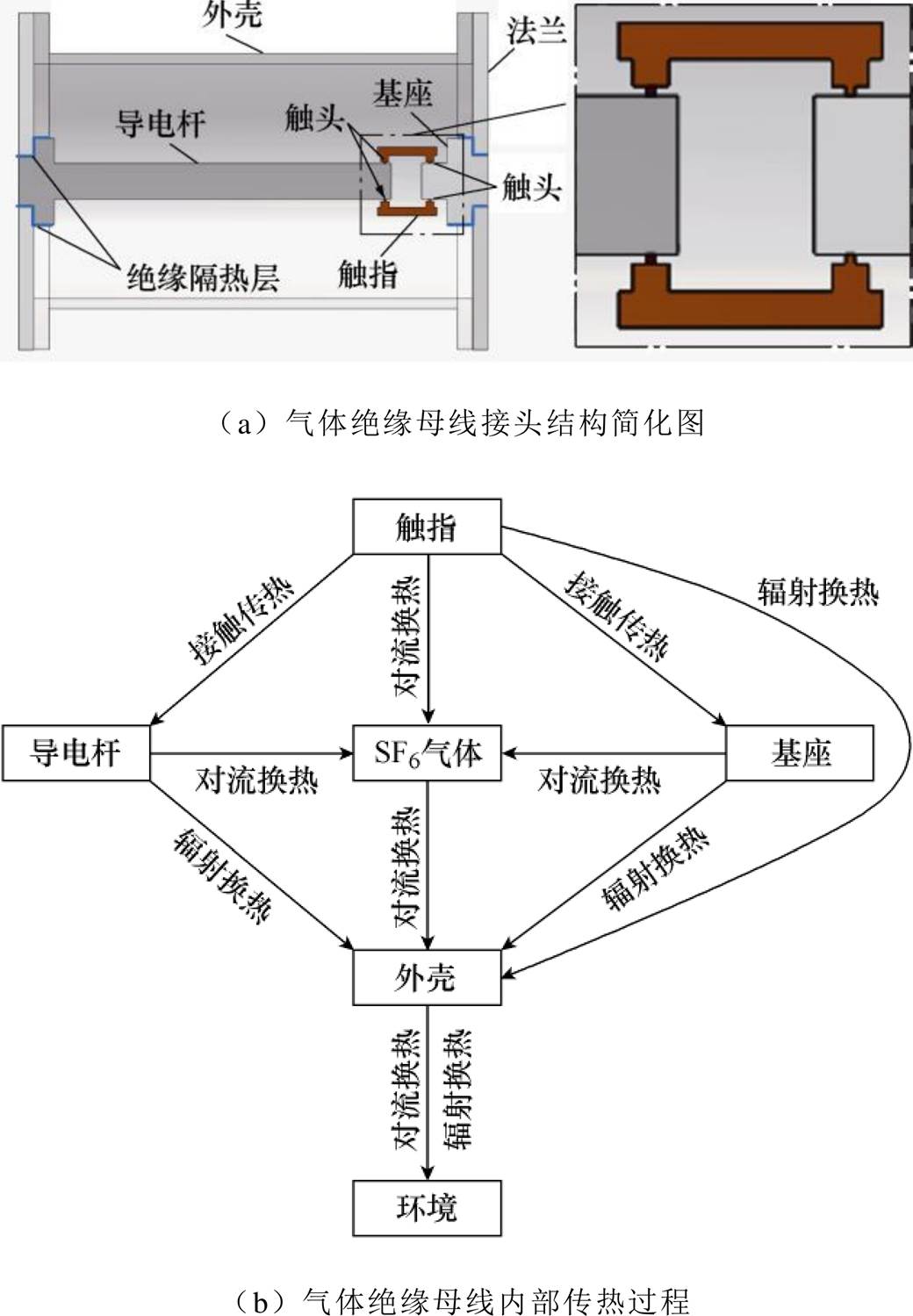
图2 模型简化及热量传递网络
Fig.2 Model simplification and heat transfer network
（4）整个模型在计算过程中温度不超过200℃，在该温度范围内，认为气体比热容为一常数，忽略气体比热容在整个计算过程中随温度变化（小于2%）所引起的计算结果差异。
在GIB热网络模型的搭建过程中，为计算方便，对模型进行简化处理，忽略对计算结果影响较小的细微几何特征。简化后结果如图2a所示（为直观显示，图中只画出了部分触指，仿真计算时考虑了所有触指）。
GIB内部传热过程可由图2b表示，测试电流通过基座、触指、导电杆体电阻以及触指与基座、导电杆之间接触电阻产生焦耳热损耗，内部导体产生的焦耳热通过与SF6气体之间的对流换热以及与外壳之间辐射换热传递至外壳内壁；同时，触指与基座、导电杆之间通过接触热阻传递热量；测试电流在外壳内产生涡流损耗，外壳外壁通过与空气的对流换热以及与周围环境的辐射换热耗散热量。当各部件的产热量等于散热时，整个模型温升达到稳态。在达到稳态时，整个模型内存在两层热平衡关系：①外壳与空气的对流换热量及外壳辐射换热量之和等于整个模型的焦耳损耗；②内部导体与腔内SF6气体的对流换热量及与导体的辐射换热量之和等于导体的焦耳损耗。
根据GIB内部传热过程建立了如图3所示的GIB热网络模型，图中，Tc1、Tj1、Tc2、Ts、Tt、T0分别表示GIB热网络模型六个节点（导电杆、触指、基座、SF6气体、外壳、环境）的温度；测试电流通过导电杆、基座体电阻所产生的焦耳热损耗分别为
和
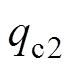；由于测试电流在接触电阻与触指体电阻产生的热损耗位置很近，将这两部分热量合并为触指上的热损耗
；
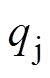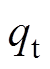为测试电流在外壳中感应产生的涡流损耗；C1～C5分别为导电杆、触指、基座、SF6气体以及外壳的热容；R1～R5分别为导电杆与SF6气体之间、基座与SF6气体之间、外壳内壁与SF6气体之间、触指与SF6气体之间、外壳外壁与外部空气之间的对流换热热阻；Rr1、Rr2分别为导电杆、基座与外壳之间辐射换热热阻，Rrc为触指与外壳之间辐射换热热阻，Rr5为外壳与外部环境之间辐射换热热阻；Rj1为触指与导电杆、基座之间的接触热阻。
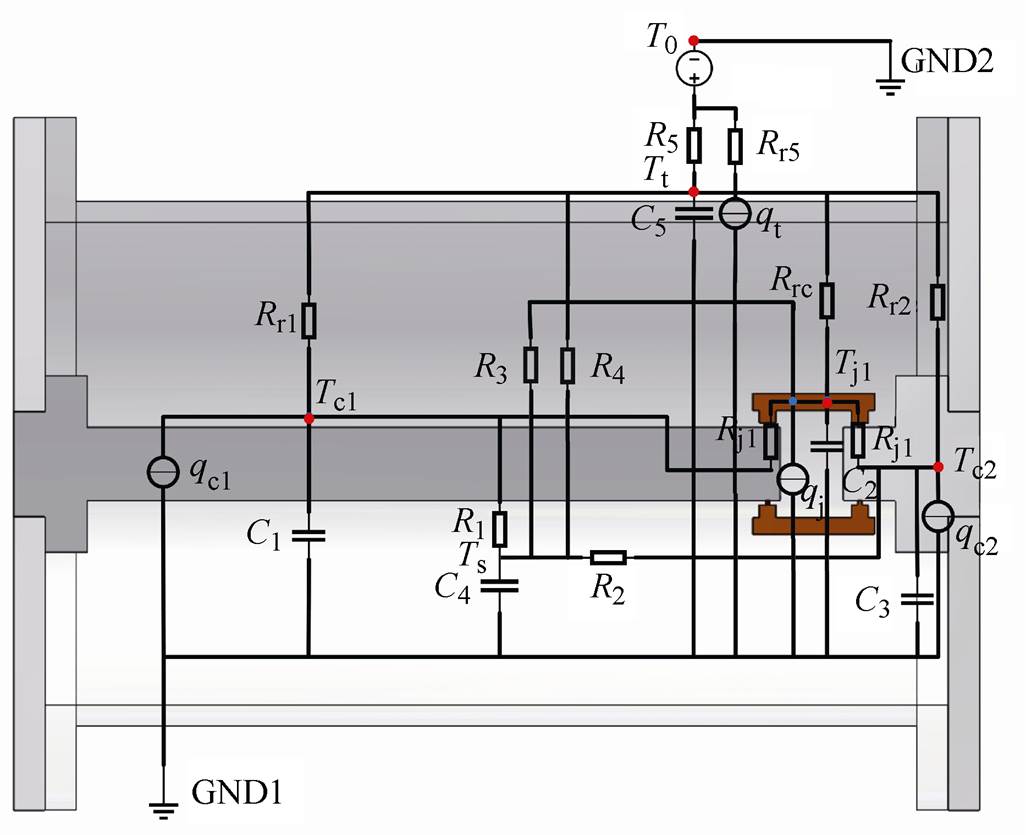
图3 GIB热网络模型
Fig.3 Thermal network of GIB
包含16片触指的GIB内部热量传递网络如图4所示，在图3的基础上添加了2～16片触指的节点温度、热源、热容及对应热阻元件。模型中，Tc1、Tc2分别为导电杆及基座的平均温度，Tj1～Tj16为16片触指的温度。为显示简洁，图中虚线部分省略了从3片触点至15片触点在整个模型中的电路连接。根据GIB模型的几何对称性及上文提出的模型假设，可知各触指相连接的热路元件数目及数值均相等。即
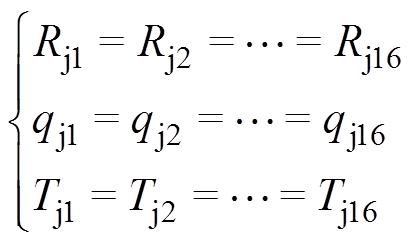（1）式中，Rj1～Rj16分别为各片触指与导电杆及基座之间的接触热阻；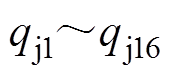
分别为各片触指的焦耳热损耗。
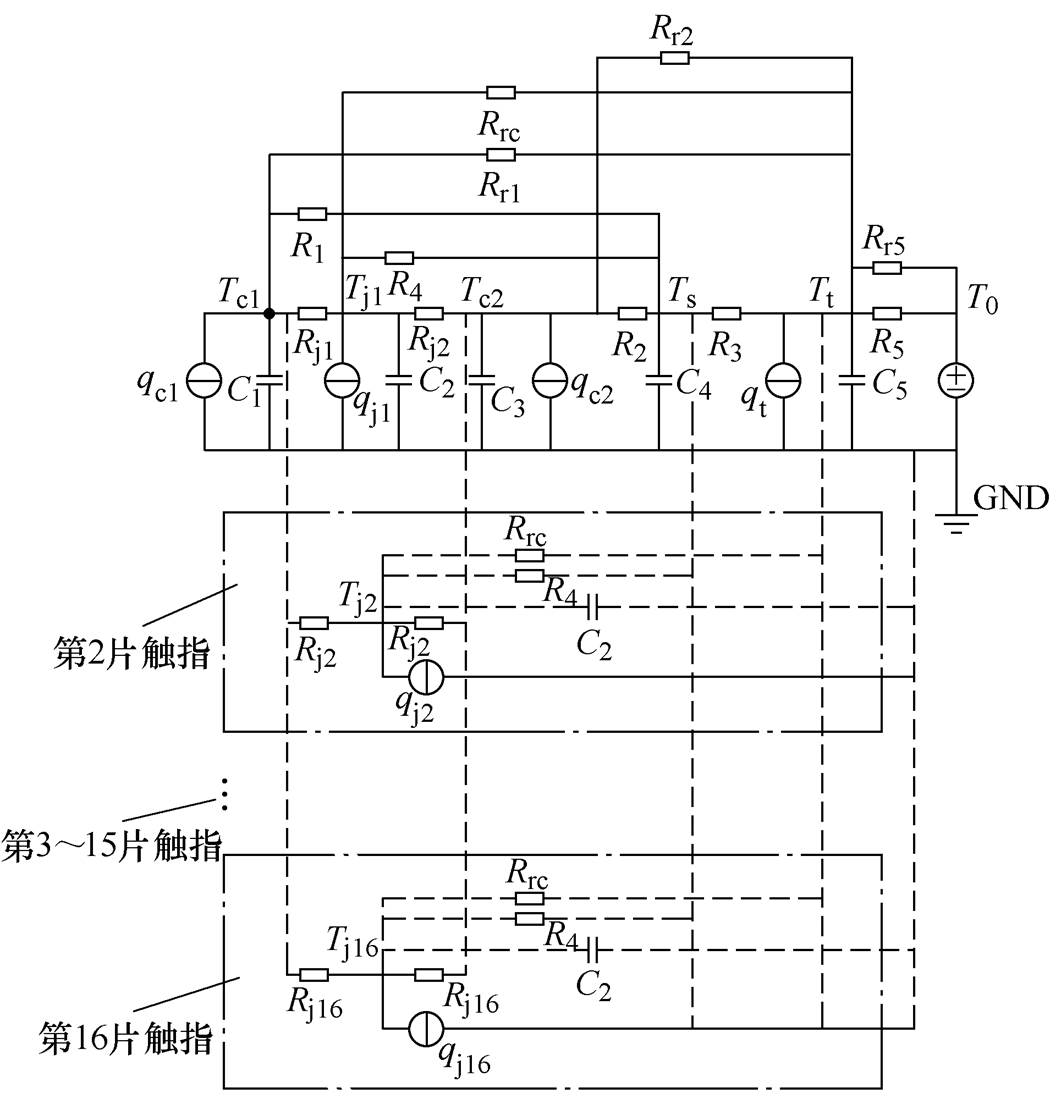
图4 包含全部触指的GIB热网络模型
Fig.4 GIB thermal network model containing all fingers
在热路模型中，对温度相同的节点进行合并。合并节点Tj1～Tj16。节点合并后触指与导电杆、基座之间的接触热阻Rj、触指与SF6气体之间的对流换热热阻R4、触指与外壳之间辐射换热热阻Rrc均减小为原来的1/16。Tj节点的注入电流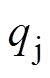增大为原来的16倍。依据电路理论对图4简化，简化后得到的GIB热网络模型如图5所示。图中，Rj、
、
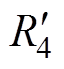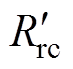分别为Rj1、R4、Rrc的1/16，、
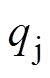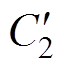分别为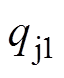
、C2的16倍。
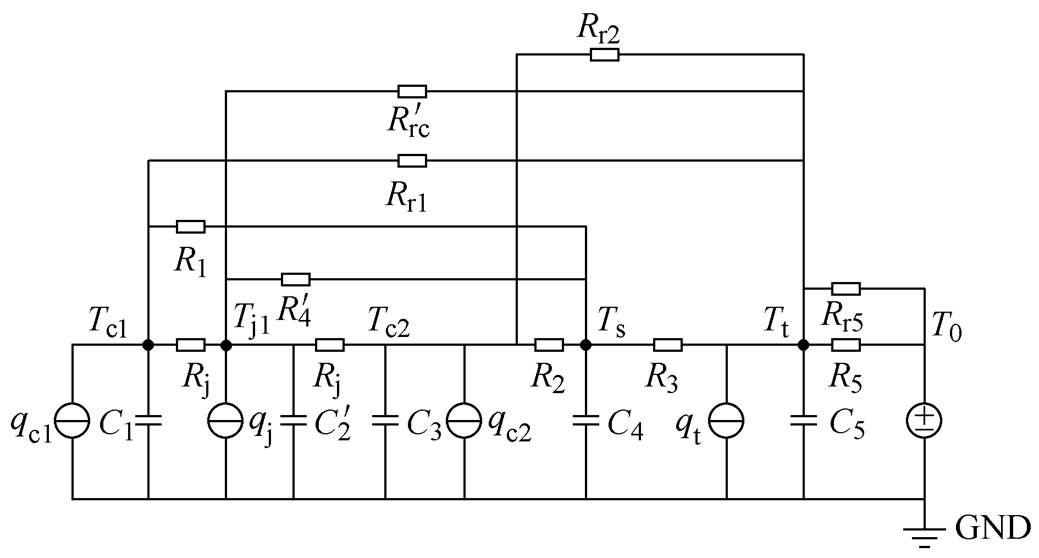
图5 GIB热网络模型简化
Fig.5 Simplified diagram of GIB thermal network model
GIB热网络模型主要包含反映触头整体热量损耗的热源元件、反映各部件热容大小的热容元件以及反映各部件之间换热效率的热阻元件。根据不同元件所反映的不同物理量，通过以下方法分别确定其参数值。
2.2.1 热源
GIB模型中，热量来源主要包括测试电流通过导电杆、基座及接触电阻产生的焦耳损耗及外壳中感应电流产生的涡流损耗。考虑交流电流在导体中传导的趋肤效应，内部焦耳损耗可表示为
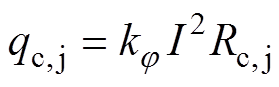（2）式中，下标c、j分别代表导体及触点；kj 为交流趋肤效应系数；I为电流有效值；Rc,j为导体体电阻或触指与导电杆间接触电阻。
考虑导体电阻随温度动态变化特性，导体电阻随温度变化规律[23-24]为
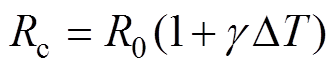（3）式中，R0为20℃下导体电阻；g 为温度系数，对于铝合金和铜触头，取g=0.004 2/℃；DT为温度变化量。
感应电流在外壳中产生的涡流损耗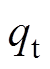为
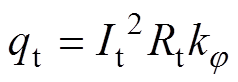（4）式中，It为外壳涡流有效值；Rt为外壳电阻。
2.2.2 热容
GIB各部分组件的热容Cx可表示为
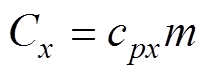（5）式中，下标x代表不同材料；cpx为对应材料的比热容；m为对应部件的质量。
为方便计算GIB热网络模型中各元件的参数值，在表1中给出了GIB各部件的材料属性。
表1 GIB各部件材料属性
Tab.1 Material properties of each component of GIB
部件质量/kg比热容/[J/(kg·℃)]密度/(kg/m3)备注 基座0.53868 960铝 触指0.0188802 700铜(单片触指) SF60.39665.1826.080.4MPa 导电杆1.253862 700铝 外壳12.33862 700铝
2.2.3 热阻
在GIB热网络模型中，热阻主要包括不同温度固体之间相互接触而产生的接触热阻、气体与固体交界面的对流换热热阻以及非接触固体之间的辐射换热热阻。
1）接触热阻
Cooper提出的CMY模型接触热阻计算模型揭示了接触热阻与接触表面粗糙度之间数值关系，接触热阻计算公式为
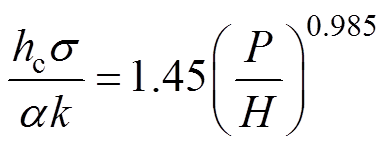（6）式中，hc为接触热导；s为接触面粗糙度的方均值，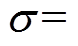
；a 为平均绝对轮廓斜率，a=2a1a2/(a1+a2)；k为调谐平均导热系数，k=2k1k2/(k1+k2)；P为接触面载荷；H为维氏硬度。
为计算触指与基座、导电杆之间的接触热阻Rj，在试验前利用光学轮廓仪测量了触指、基座。导电杆各接触表面的粗糙度如图6所示（图6中，横坐标表示与端面之间的距离S，纵坐标表示测试线上不平整峰（谷）高度L）。根据GIB触头制造规范，接触件表面粗糙度不得大于6.3mm，由图6可知，各表面的粗糙度最大为1.01mm，满足规范要求。接触面载荷可以由弹簧的形变量及刚度系数获取，再结合所测得的接触面粗糙度即可通过式（6）计算接触热阻。
2）对流换热热阻
GIB内部流-固之间换热遵从牛顿冷却公式，即
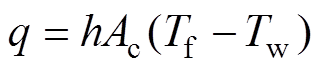（7）
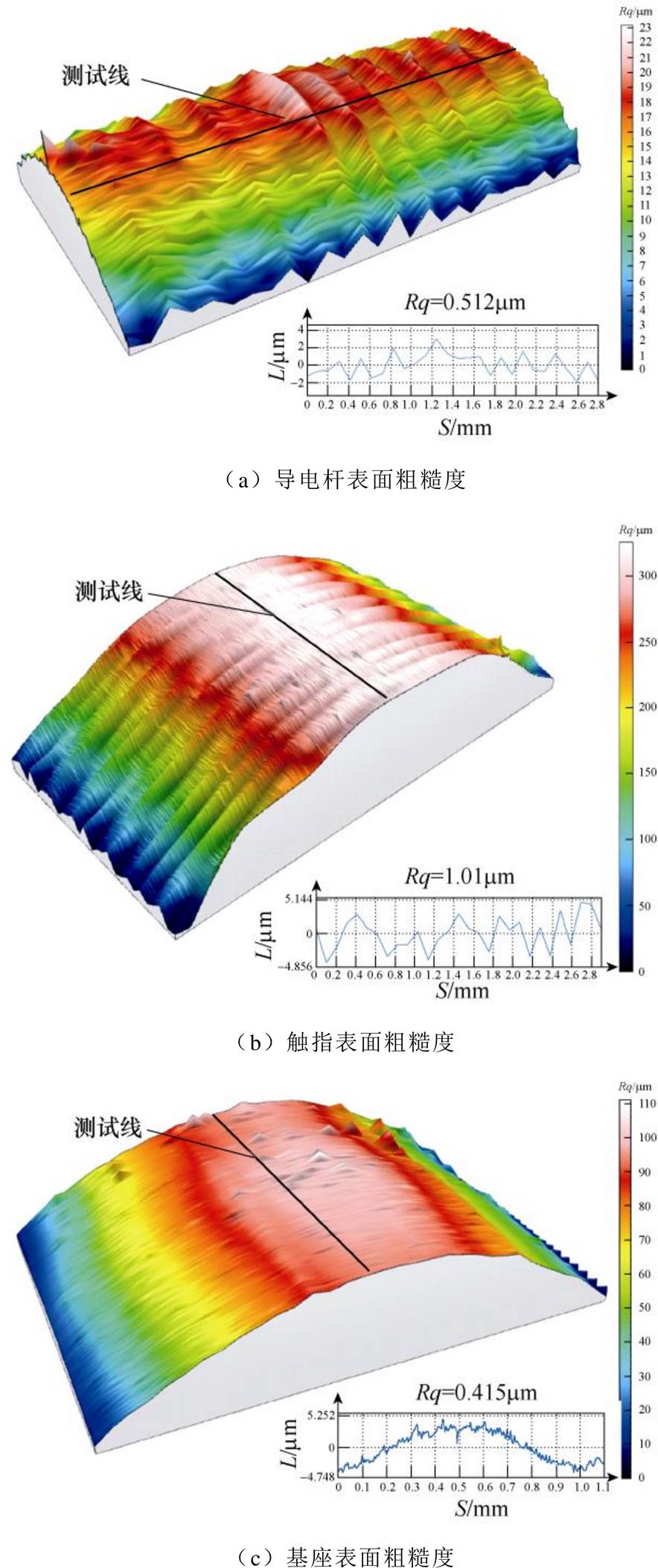
图6 各接触面粗糙度
Fig.6 Roughness of each contact surface
式中，q为对流换热量；h为固体表面对流换热系数；Ac为对流换热面积；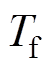
与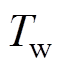
分别为固体及流体温度。
因此对流换热热阻R可表示为
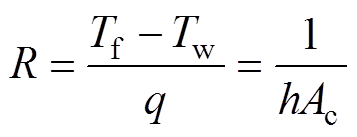（8）传统方法基于换热面的特征长度并通过传热学经验公式来计算对流换热系数，未考虑对流换热在各表面上的分布，导致计算结果偏差较大。因为影响GIB各表面对流换热特性的因素众多，如固体与气体之间的温差、气体流动速度、气体压强及密度等，为减小对流换热参数的计算误差，本文基于有限元数值进行试验，通过各表面的对流换热系数对面积积分并求倒数来获取其非线性对流换热热阻，即
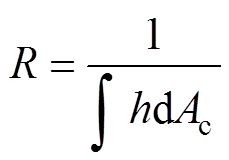（9）
有限元数值试验计算对流换热系数的流程如图7所示。首先根据抱紧弹簧的物理参数以及气体间绝缘母线接头各部件的尺寸计算触指与导电杆之间的接触压力，根据接触压力计算导电桥接触电阻。将计算结果作为输入参数代入有限元数值模型，计算各部件在测试电流作用下的焦耳损耗及涡流损耗。将各损耗作为热负荷导入流场有限元计算模型，计算模型各部件的温度分布。判断温度场计算结果是否收敛（以前后两步计算结果差值是否小于0.5%为判据），若不收敛则更新参数重新计算电磁场功率损耗；若收敛则提取并输出对流换热系数计算结果。
为直观表示各对流换热热阻参数的具体含义，图8给出了工频450A电流下各表面对流换热系数的分布以及对流换热热阻R1～R5所对应的对流换热表面，对流换热热阻值直接由式（9）求取。由图8可知，外壳与空气之间的对流换热分布较为均匀，导电杆表面的对流换热在轴向呈现较大梯度。但是由于导电杆的表面积远远小于外壳，因此其对流换热总量（对流换热系数在表面的面积分）仍小于外壳。
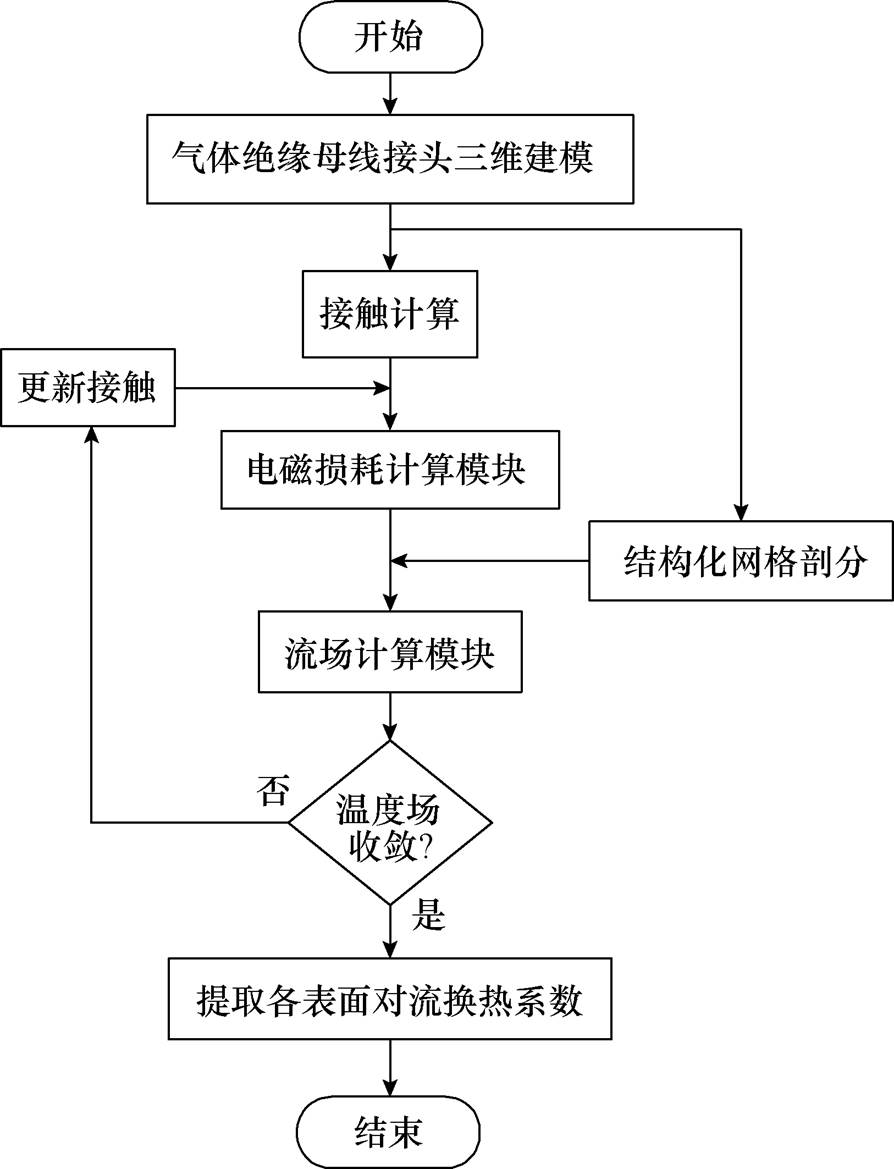
图7 对流换热系数计算流程
Fig.7 Calculation process of convection heat transfer coefficient
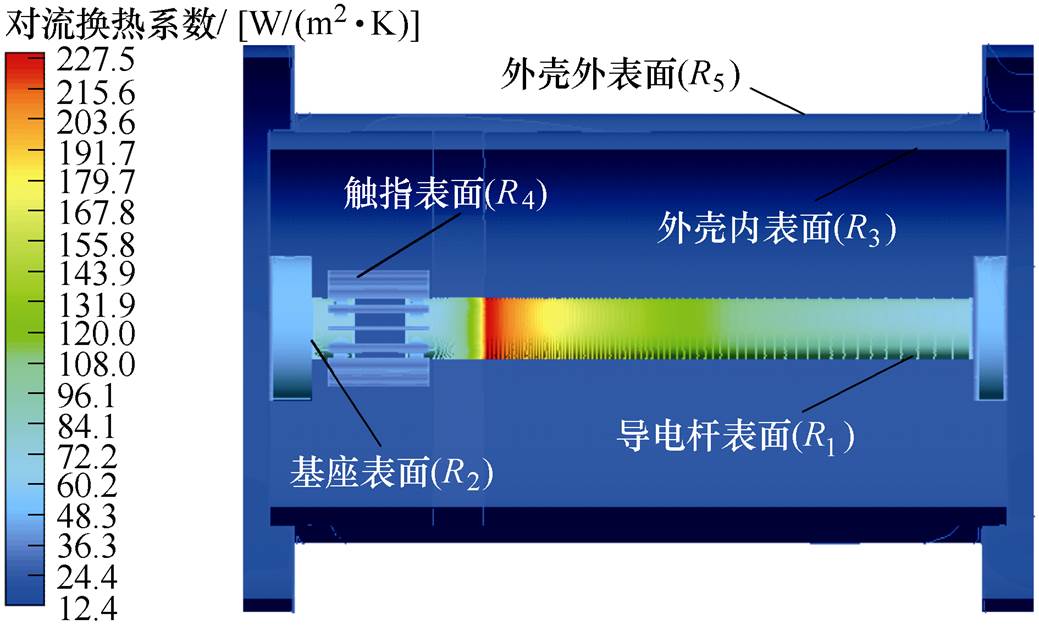
图8 对流换热系数分布图
Fig.8 Diagram of convective heat transfer coefficient distribution
3）辐射换热热阻
GIB各部件之间的辐射换热均可近似等效为灰体辐射[25]，在本文所建立的GIB热网络模型中，辐射换热包含基座与外壳、导电杆与外壳、触指与外壳以及外壳与外部环境之间的辐射换热。辐射换热热阻Rr（由辐射换热公式推得）计算式为
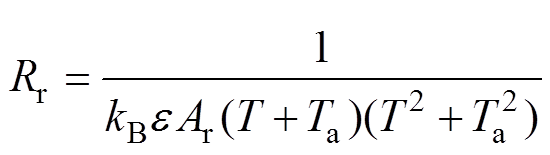（10）式中，kB为玻耳兹曼常数；e 为参与换热的固体表面发射率；Ar为辐射换热面面积；T为辐射换热过程中高温物体的温度；Ta为辐射换热过程中低温物体的温度。
由于辐射换热参数只跟参与辐射换热的两个部件温度相关，各部件的温度值即为本文GIB热网络模型的求解自由度，因此对于已知拓扑的热网络而言并未增加其他变量，可直接作为未知参量代入模型求解。
通过有限元数值试验验证GIB热网络模型中对流换热热阻数学模型的有效性，在此基础之上，通过热网络模型计算环境温度27℃，不同测试电流下GIB外壳及触指的稳态温升，进而开展相同环境条件下外壳及触指的稳态温升物理试验。并与热网络模型计算值对比以验证GIB热网络模型的有效性。
在环境温度27℃恒定、无风无太阳辐射条件下，各固体表面的对流换热热阻与所加测试电流之间存在一定数量关系。基于有限元数值试验分别计算不同测试电流下各固体表面的对流换热系数，以测试电流作为单一变量，给出了各固体表面对流换热热阻随测试电流变化关系式。不同测试电流下，各表面的对流换热热阻有限元数值试验结果见表2。
表2 不同测试电流下各表面对流换热热阻
Tab.2 Convective heat transfer resistance of each surfaces under different test currents
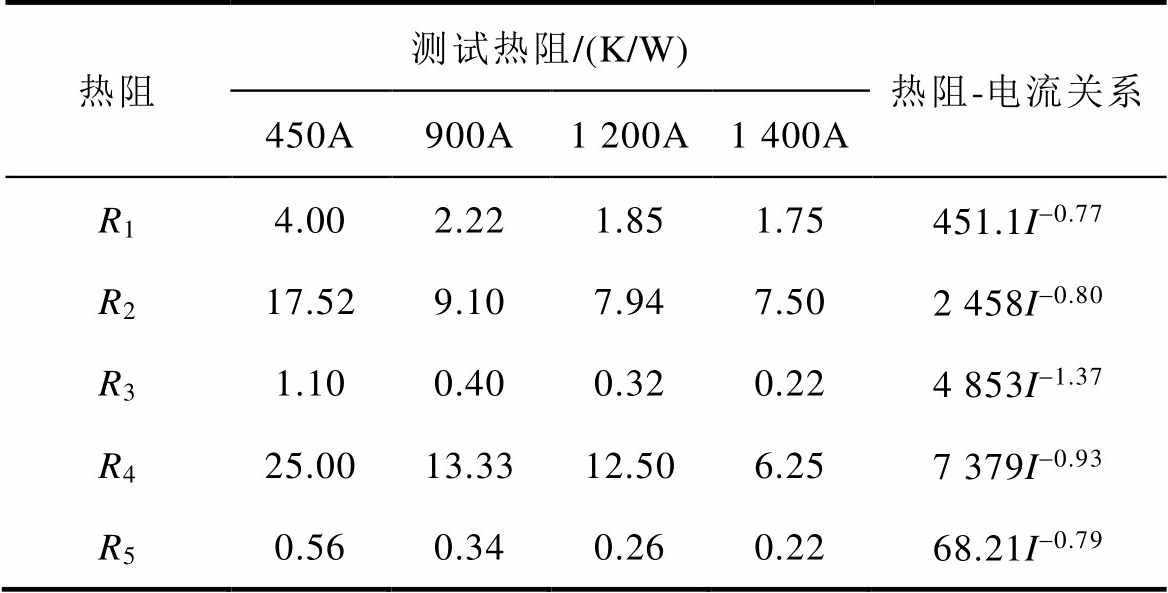
热阻测试热阻/(K/W)热阻-电流关系 450A900A1 200A1 400A R14.002.221.851.75451.1I-0.77 R217.529.107.947.502 458I-0.80 R31.100.400.320.224 853I-1.37 R425.0013.3312.506.257 379I-0.93 R50.560.340.260.2268.21I-0.79
为验证表2中热阻-电流关系的准确性，通过有限元数值实验计算测试电流为1 600A时，各表面对流换热热阻的阻值，将试验结果与利用热阻-电流关系求得的值进行比较。在1 600A电流下，R1～R5有限元数值试验值分别为1.61K/W、7.05K/W、0.22K/W、7.11K/W、0.23K/W，利用表2中热阻-电流关系式计算其数值分别为1.54K/W、6.72K/W、0.21K/W、7.72K/W、0.20K/W。通过对比可知，对流换热热阻参数的计算误差在工程允许范围以内，进而验证了对流换热参数的准确性。
在已验证了对流换热热阻数学模型有效性的基础上，搭建了如图9所示的GIB触头稳态温升物理试验平台。试验前先对接线铜排打磨处理除去其表面的氧化膜，通过调节大电流发生器（2 000A/5V）端口的输出电压控制流经的测试电流；分别在触指接触区域、导电杆、外壳及环境空气固定NiCr-Ni（K型）热电偶，腔体内的热电偶通过法兰上的航插接头将线引出，并与多路温度采集器连接。多路温度采集器将四个热电偶的温度数据上传至工控机进行后处理。试验过程中温度采集间隔为1min，当各热电偶的温度在30min内变化均少于1℃时，认为试验温度值达到稳态。
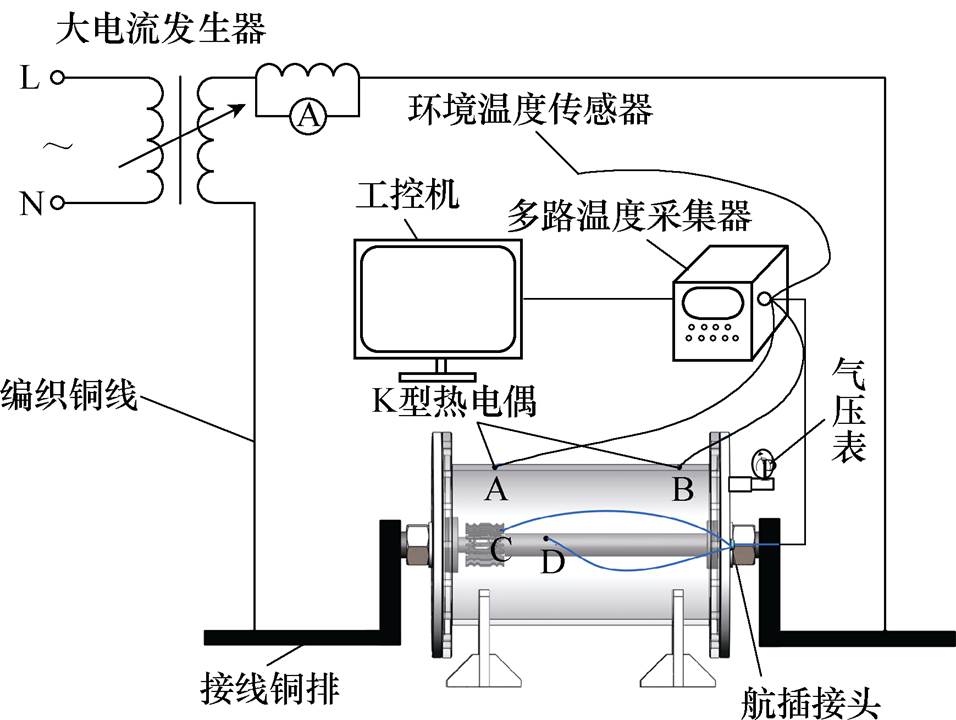
图9 GIB触头稳态温升试验平台
Fig.9 GIB steady-state temperature rise test platform
热网络模型以各部件的平均温度作为部件的温度，忽略各部件温度场的分布。考虑到外壳几何尺寸较长，靠近热源（触头）的位置A温度偏高，远离热源处B温度较低，为减小试验的系统误差，试验过程中以A、B两个位置热电偶的温度平均值作为外壳的温度，采用C、D热电偶分别测量触指温度以及导电杆温度，图10为试验时外壳及触指传感器布置的实物图。当在环境温度27℃时，不同测试电流下GIB外壳及触指温度的热网络模型计算结果如图11所示，由图11可知，触指的温度上升速度明显地快于外壳温度上升速度，整个模型温升在通流3.5h左右达到平衡。
表3给出了不同测试电流下GIB外壳及触指达到稳态温度时的热路仿真值和实测值对比。
图10 K型热电偶布置实物图
Fig.10 K type thermocouple arrangement diagram
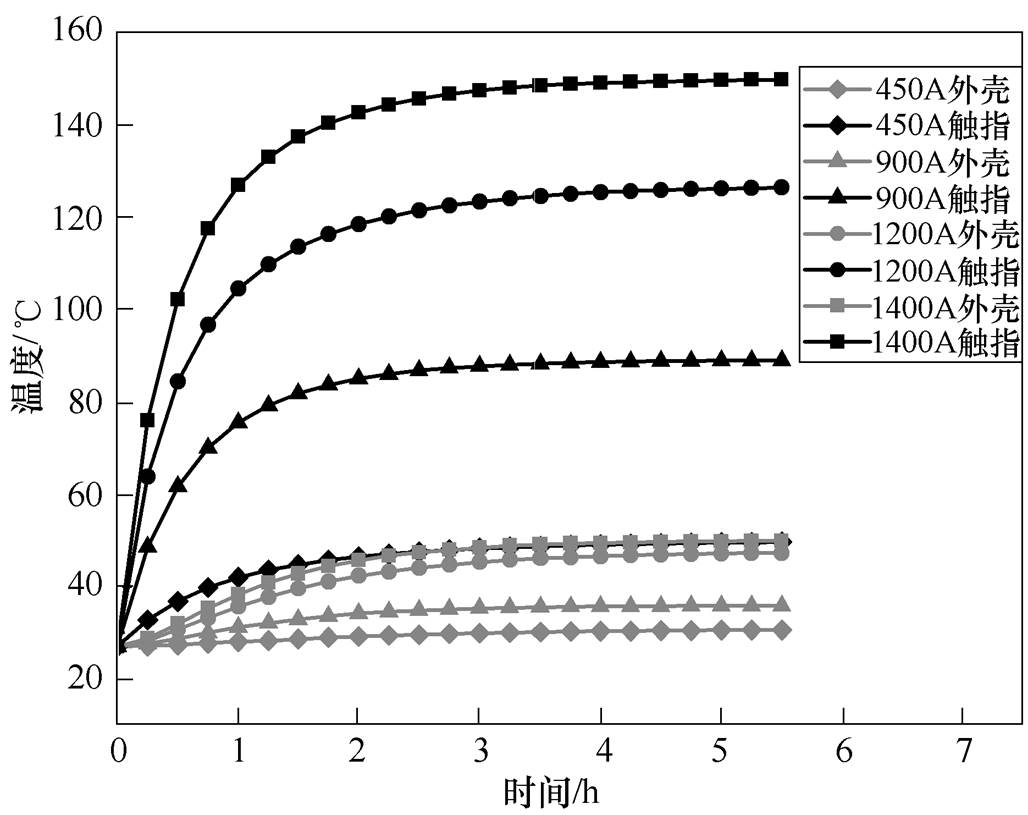
图11 不同测试电流下GIB外壳及触指温升曲线
Fig.11 Temperature rise curve of GIB shell and finger under different test currents
表3 不同测试电流下GIB温升计算值与实测值对比
Tab.3 Comparison of calculated and measured values of GIB temperature rise under different test current
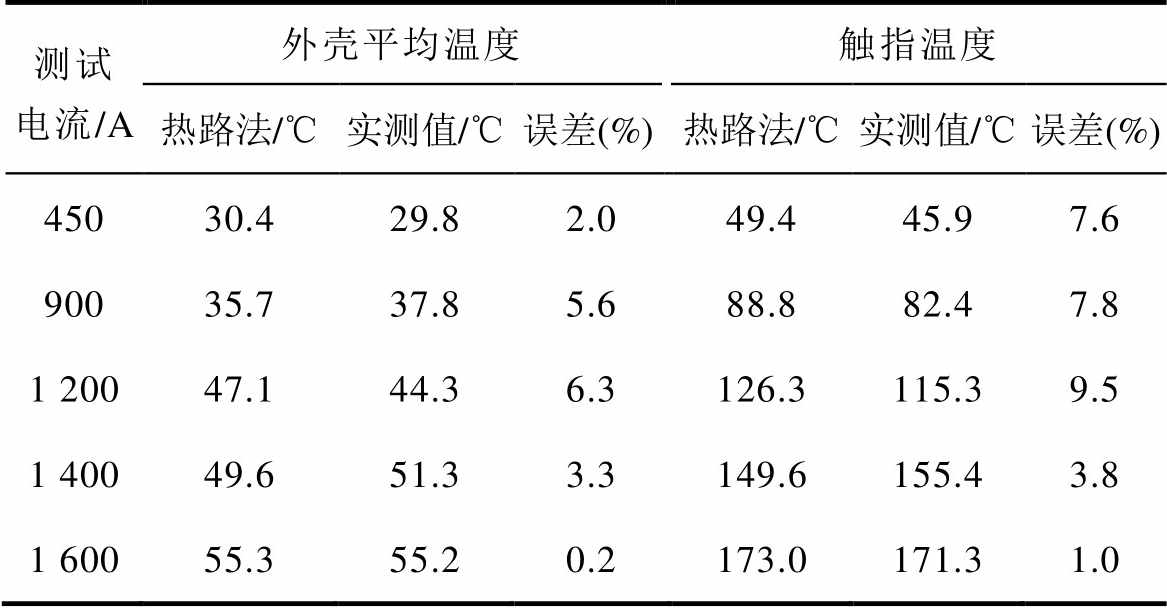
测试电流/A外壳平均温度触指温度 热路法/℃实测值/℃误差(%)热路法/℃实测值/℃误差(%) 45030.429.82.049.445.97.6 90035.737.85.688.882.47.8 1 20047.144.36.3126.3115.39.5 1 40049.651.33.3149.6155.43.8 1 60055.355.20.2173.0171.31.0
对比表3结果发现：在不同测试电流作用下，GIB外壳及触指稳态温度的热网络模型计算值与实测值之间最大误差为9.5%，最小误差仅为0.2%，外壳及触指稳态温升计算结果误差在工程允许范围内，验证了本文所建立的GIB稳态温升热网络模型的准确性。
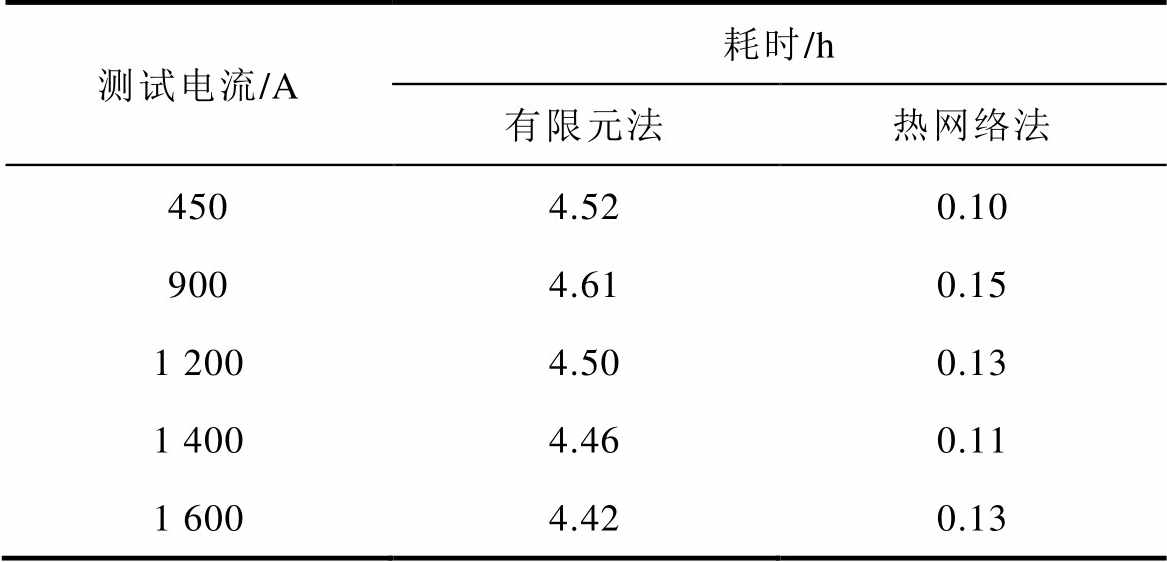
分别采用热网络平衡法以及有限元数值求解法计算不同电流下的GIB稳态温升并记录求解总耗时（GIB从环境温度上升至稳态温度所需的时间）。图12给出了两种方法计算结果与实测值之间的对比。表4对比了两种方法计算GIB稳态温升的总耗时，其中有限元法网格数量为300万，热网络法计算采用Simulink ode45求解器。
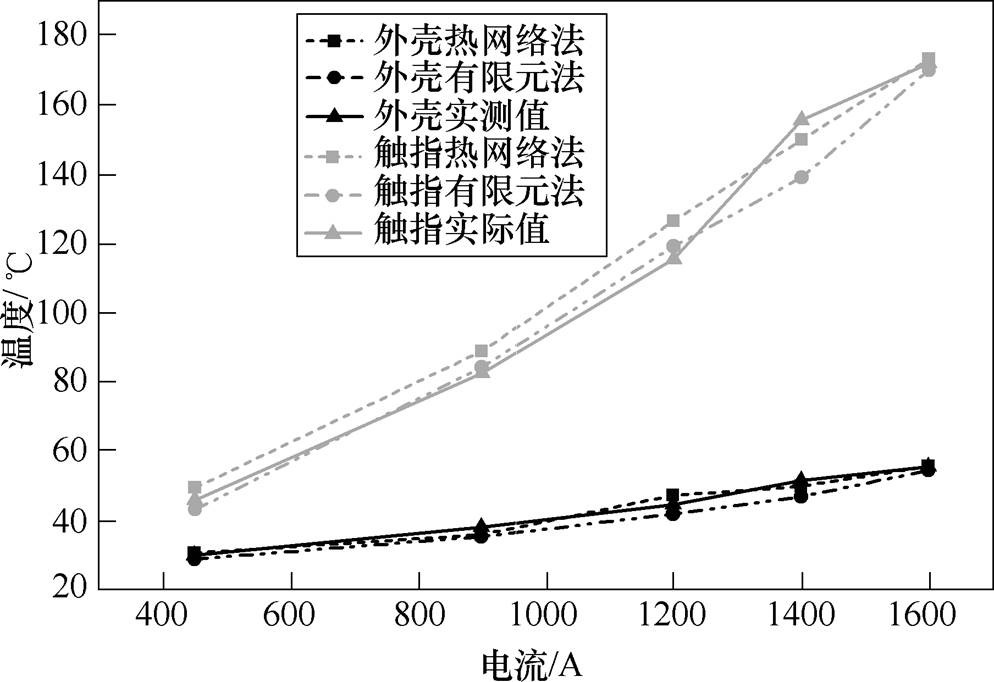
图12 有限元法及热网络法计算结果对比
Fig.12 Calculation results comparison of FEM and thermal network method
表4 计算耗时对比
Tab.4 Calculating time-consuming comparison
测试电流/A耗时/h 有限元法热网络法 4504.520.10 9004.610.15 1 2004.500.13 1 4004.460.11 1 6004.420.13
由图12以及表4可知，在不同电流作用下，虽然热网络法在触指温升计算结果的准确度上略低于有限元数值计算，但是在整个计算过程的耗时上，有限元法远高于（约34倍）热网络法。因此热网络法在快速估算GIB稳态温升上具有较大优势。
本文基于传热学及热电类比原理，构建了包含触头结构的GIB热网络模型，基于该模型计算分析了不同负荷电流下的GIB外壳及导电杆的温升，得出以下结论：
1）传统方法将导电杆和触头看作一个等温体，忽视了因触头接触电阻及接触热阻而造成的接触区域温升局部偏高的问题，本文建立的GIB热网络模型考虑到触头结构，并基于CMY模型计算触头接触位置的接触热阻。
2）对流换热系数的三维分布表明了传统方法在计算对流换热热阻时，采用传热学经验公式估算出各表面的对流换热系数方法的不准确性，本文基于有限元数值模拟试验，建立了无风、无太阳辐射时对流换热热阻与所加负荷电流之间的关系，通过对流换热系数在各表面的积分来求解对流换热热阻，以提高计算模型参数的准确性。
3）不同测试电流下，GIB外壳及触指温度热网络模型计算值与实测值之间误差最大为9.5%，最小仅为0.2%，验证了所建立的GIB热网络模型的有效性。
4）在相同运行条件下，GIB温升计算的有限元数值法耗时约为热网络平衡法的34倍。研究结果可用于快速估算GIB设备外壳及触指温度，为GIB设备的热设计和温升监测提供了一种有效的分析方法。
参考文献
[1] Istad M, Runde M. Thirty-six years of service experience with a national population of gas- insulated substations[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2448-2454.
[2] 周安春, 高理迎, 冀肖彤, 等. SF6/N2混合气体用于GIS母线的研究与应用[J]. 电网技术, 2018, 42(10): 3429-3435.
Zhou Anchun, Gao Liying, Ji Xiaotong, et al. Research and application of SF6/N2 mixed gas used in GIS bus[J]. Power System Technology, 2018, 42(10): 3429-3435.
[3] IEC 62271-1-2011 High-voltage switchgear and control gear—part 1: common specifications for alternating current switchgear and control gear[S]. 2011.
[4] IEC 60865-1-2011 Short-circuit currents—calculation of effects—part 1: definitions and calculation methods[S]. 2011.
[5] 王俊波, 苗银银, 罗容波, 等. GIS触头接触状况检测现状分析[J]. 高压电器, 2013, 49(12): 137-140.
Wang Junbo, Miao Yinyin, Luo Rongbo, et al. Analysis of present situation of GIS contact detection[J]. High Voltage Apparatus, 2013, 49(12): 137-140.
[6] Runde M. Failure frequencies for high-voltage circuit breakers, disconnectors, earthling switches, instrument transformers and gas-insulated switchgear[J]. IEEE Transactions on Power Delivery, 2013, 28(1): 529- 530.
[7] 金向朝, 黄松波, 谢志杨, 等. 考虑粗糙表面接触的气体绝缘开关设备接头接触电阻数值计算与影响因素分析[J]. 电网技术, 2015, 39(6): 1725-1730.
Jin Xiangchao, Huang Songbo, Xie Zhiyang, et al. Numerical calculation and influence factors analysis of gas insulated switchgear connector contact resistance considering rough surface contact[J]. Power System Technology, 2015, 39(6): 1725- 1730.
[8] 孙国霞, 舒乃秋, 吴晓文, 等. 基于多物理场耦合的气体绝缘母线触头接触温升有限元计算[J]. 电工技术学报, 2013, 28(增刊2): 408-413.
Sun Guoxia, Shu Naiqiu, Wu Xiaowen, et al. Finite element analysis of contact temperature rise in gas insulated bus bars based on coupled multi-physics[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 408-413.
[9] Guan Xiangyu, Shu Naiqiu, Kang Bing, et al. Multi- physics analysis of plug-in connector under steady and short circuit conditions[J]. IEEE Transactions on Components, Packaging and Manufacturing Tech- nology, 2015, 5(3): 320-327.
[10] Wu Xiaowen, Shu Naiqiu, Li Hongtao, et al. Contact temperature prediction in three-phase gas-insulated bus bars with the finite-element method[J]. IEEE Transactions on Magnetics, 2014, 50(2): 277-280.
[11] 李冰, 肖登明, 赵谡, 等. 第二代气体绝缘输电线路的温升数值计算[J]. 电工技术学报, 2017, 32(13): 271-276.
Li Bing, Xiao Dengming, Zhao Su, et al. Temperature rise numerical calculation of the second generation gas insulated transmission line[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 271- 276.
[12] 冯海文, 刘晓明, 李龙女, 等. 电器电场有限元精细求解器研究[J]. 电工技术学报, 2018, 33(24): 5789-5796.
Feng Haiwen, Liu Xiaoming, Li Longnü, et al. Finite element method algorithm with precise solver for electric apparatus electric field[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5789- 5796.
[13] Kim J K, Lee J Y, Wee S B, et al. A novel coupled magneto thermal-flow analysis for temperature rise prediction of power apparatus[C]//International Con- ference on Electrical Machines & Systems, Wuhan, China, 2008: 585-588.
[14] Shenkman A L, Chertkov M. Experimental method for synthesis of generalized thermal circuit of polyphase induction motors[J]. IEEE Transactions on Energy Conversion, 2000, 15(3): 264-268.
[15] Zoran R, Kurt F. A new method for the calculation of the hot-spot temperature in power transformers with ONAN cooling[J]. IEEE Transactions on Power Delivery, 2003, 18(4): 1284-1292.
[16] 应展烽, 杜志佳, 冯凯, 等. 高压架空导线径向热路模型及其参数计算方法[J]. 电工技术学报, 2016, 31(4): 13-21.
Ying Zhanfeng, Du Zhijia, Feng Kai, et al. Radial thermal circuit model and parameter calculation method for high voltage overhead transmission line[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 13-21.
[17] 李剑, 刘兴鹏, 王有元, 等. 以箱壁温度为判据的油浸式变压器绕组热点温度计算模型及试验分析[J]. 高电压技术, 2011, 37(10): 2344-2349.
Li Jian, Liu Xingpeng, Wang Youyuan, et al. Model of hot spot temperature in oil-immersed transformers using temperature estimation of tank wall[J]. High Voltage Engineering, 2011, 37(10): 2344-2349.
[18] 吕安强, 寇欣, 尹成群, 等. 三芯海底电缆中复合光纤与导体温度关系建模[J]. 电工技术学报, 2016, 31(18): 59-65.
Lü Anqiang, Kou Xin, Yin Chengqun, et al. Modeling of temperature relation between optical fiber and conductor in 3-core submarine power cable[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 59-65.
[19] 李彦彰, 陈梦, 刘亚男, 等. 气体绝缘母线动态热网络模型的研究[J]. 科学技术与工程, 2017, 17(12): 184-189.
Li Yanzhang, Chen Meng, Liu Yanan, et al. Study on dynamic thermal-circuit model of gas insulated bus[J]. Science Technology Engineering, 2017, 17(12): 184- 189.
[20] 汪军衡, 张改杰, 夏雨潇, 等. 基于等效热路的气体绝缘母线动态热模型研究[J]. 陕西电力, 2013, 41(12): 35-39.
Wang Junheng, Zhang Gaijie, Xia Yuxiao, et al. Equivalent heat circuit based dynamic thermal model for GIS bus bars[J]. Shaanxi Electric Power, 2013, 41(12): 35-39.
[21] Dawidowski P, Szewczyk M, Sowa K, et al. Thermal behavior analyses of gas-insulated switchgear compartment using thermal network method[J]. IET Generation, Transmission & Distribution, 2016, 10(12): 2833-2841.
[22] Cooper M G, Mikic B B, Yovanovich M M. Thermal contact conductance[J]. International Journal of Heat and Mass Transfer, 1969, 12(3): 279-300.
[23] 纽春萍, 陈德桂, 刘颖异, 等. 交流接触器温度场仿真及影响因素的分析[J]. 电工技术学报, 2007, 22(5): 71-77.
Niu Chunping, Chen Degui, Liu Yingyi, et al. Temperature field simulation of AC contactor and analysis of its influence factors[J]. Transactions of China Electrotechnical Society, 2007, 22(5): 71-77.
[24] 程礼椿. 电接触理论及应用[M]. 北京: 机械工业出版社, 1985.
[25] 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 2006.
Gas Insulated Bus Thermal Network Model Considering Contact Structure
Abstract In order to achieve timely diagnosis of overheating faults of gas insulated bus bars (GIB), this paper established a GIB temperature rise thermal network model including contact structure based on thermoelectric analogy and heat transfer theory. The contact thermal resistances between the finger, the conductive rod and the substrate were calculated by the disk- contact single heat flow channel model (CMY model), and the nonlinear convective heat transfer resistance and the radiant heat transfer resistance of GIB were obtained by finite element numerical simulation. The physical tests of steady-state temperature rise of GIB under different test currents were carried out. The results show that: under different test currents, the calculation speed of thermal network method is about 34 times that of finite element method, the maximum temperature error between the calculated and measured values is 9.5%, and the minimum is 0.2%, which verifies the thermal network model of GIB. This model can be used to quickly estimate the finger and shell temperature of GIB, providing an effective analysis method for GIB thermal design and temperature rise monitoring.
keywords：Gas insulated bus bars (GIB), thermal network model, thermoelectric analogy, temperature rise calculation, thermal contact resistance
中图分类号：TM595
DOI: 10.19595/j.cnki.1000-6753.tces.190885
国家自然科学基金资助项目（51607124）。
收稿日期 2019-07-17
改稿日期 2019-09-18
吴 亮 男，1994年生，硕士研究生，研究方向为电力设备在线监测与故障诊断。E-mail: wdwuliang@whu.edu.cn（通信作者）
彭 辉 男，1975年生，副教授，硕士生导师，研究方向为电力设备在线监测与故障诊断。E-mail: huipeng@whu.edu.cn
（编辑 陈 诚）