 (1)
(1)摘要 高频信号注入法是广泛应用于内置式永磁同步电机(IPMSM)无位置传感器控制领域的经典方法,在电机低速段具有良好的动态特性和稳态特性。但是,伴随着高频谐波的注入,高频响应电流产生的高频噪声成为一个主要的噪声来源。为降低这种噪声,该文提出一种基于变频电流信号注入的内置式永磁同步电机无位置传感器控制策略,通过连续改变谐波电流的频率,分散谐波在频谱上的能量,消除尖峰,从而降低高频电流噪声。为实现变频谐波电流注入,重新设计电机的电流环,采用线性自抗扰控制器与谐振控制器实现高频电流信号注入。实验结果表明,该方法能够有效地改善谐波电流的频谱分布,从而降低高频电流噪声。
关键词:永磁同步电机 无传感器控制 自抗扰控制器 噪声抑制
内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM)具有高功率密度、高效率等优点,已广泛用于工业、家电及电动汽车等领域,具有良好的应用前景。为降低系统成本,提高系统可靠性,IPMSM无位置传感器算法一直是学术界研究的热点[1-4]。经过多年发展,IPMSM无位置传感器算法已接近成熟,分别发展出适用于中高速段的基于电机反电动势估计的算法[5-6]和适用于低速段的基于谐波注入的算法[7-9]。
适用于低速段的无传感器算法需要向电机注入高频的谐波电流,而高频电流会引起电机线圈振动,存在一定的高频噪声问题[10-11]。因此,在一些强调安静性和舒适性的应用场合,这种无传感器控制方法受到一定的限制。为解决这一问题,国内外学者展开了相关研究,基本的技术路径有降低谐波幅值、降低谐波频率、提高谐波频率以及扩展谐波频率等。
降低谐波幅值是减小高频噪声最直接有效的方法,但此方法会导致转子位置信息的信噪比下降,有效信息易被噪声淹没,从而导致系统失去稳定性。为解决这一问题,有文献提出利用过采样方法或信号处理算法提高转子位置信息的获取能力,但这类方法需要额外的硬件系统支持[12-13]。
降低或提高谐波频率也是一种有效的降噪方法。高频注入信号引起的谐波噪声处于人耳较为敏感的频段,通过降低谐波频率,使噪声频率离开人耳的敏感区域,从而能够达到降噪的目的。但是,降低谐波频率同样会导致信噪比下降[14]。提高谐波频率可将噪声频率移出人类的听觉范围,理论上能彻底消除谐波噪声。但是,提高谐波频率受到元器件开关频率与开关损耗的限制,需要更高频的开关器件支持[15-16]。
有研究结果表明,高频噪声与高频电流的频谱分布相关,当谐波电流在频谱上存在明显的尖峰时,说明能量向该频率聚集,同时,这种频谱分布容易产生噪声;相反,当谐波电流频谱向一个较宽范围的频段分散时,消除明显的尖峰,就能改善高频噪声特性。基于这一原理,提出通过扩展谐波频率实现噪声抑制。常用的频率扩展方法是频率随机切换法,这种方法主要来源于随机脉宽调制(Random Pulse Width Modulation, RPWM)技术,其基本原理是使谐波频率在选定的多个频率之间随机切换,利用多个谐波频率分散谐波在频谱上的能量,从而降低高频噪声[17-19]。这种方法的优势是不降低系统稳定性,同时没有额外的硬件需求。
本文提出一种新的频率扩展方式,采用频率扫描的方式,连续地改变注入谐波的频率,将谐波从几个频率扩展成一个频段。相比随机频率注入,这种方法能够进一步地分散谐波能量,降低电流谐波在频谱上的尖峰,从而达到降低噪声的目的。为实现谐波频率改变,本文采用谐波电流注入的方式,利用线性自抗扰控制器(Linear Active Disturbance Rejection Control, LADRC)与谐振控制器实现电流闭环。实验表明,本文提出的谐波注入方法能够有效地降低谐波频谱的尖峰,改善电流谐波的频谱分布,从而有效降低噪声。
在dq坐标系下,IPMSM的数学模型为
 (1)
(1)式中,ud、uq和id、iq分别为dq坐标系下的定子电压和电流;Ld和Lq分别为电机直轴电感和交轴电感;R为定子绕组电阻;w 为转子电角速度;yr为电机永磁体磁链;p为微分算子。
在IPMSM无速度传感器控制系统中,由于转子位置角q 无法通过测量直接得到,坐标变换无法完成,因此不能直接获取实际的ud、uq、id和iq。为完成坐标变换,在本文中,驱动系统采用一个以估计速度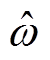 旋转的虚拟坐标系gd,作为矢量控制的变换坐标系。dq坐标系与gd 坐标系之间的关系如图1所示。
旋转的虚拟坐标系gd,作为矢量控制的变换坐标系。dq坐标系与gd 坐标系之间的关系如图1所示。
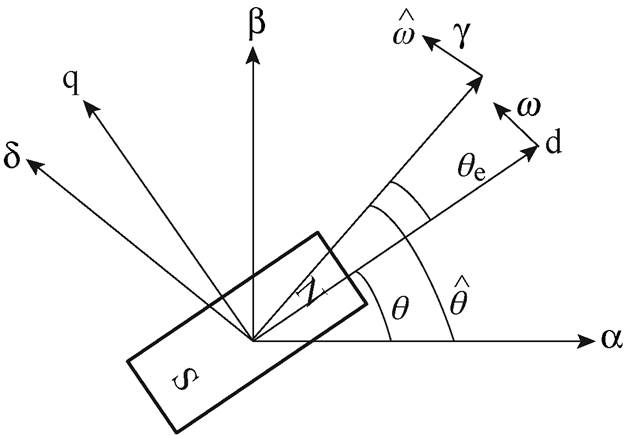
图1 虚拟坐标系gd 和实际dq坐标系
Fig.1 Estimated gd frame and actual dq frame
为实现转子位置估计,需要向电机绕组中注入高频电流信号,在gd 坐标系中,考虑高频信号的电机电压方程表示为
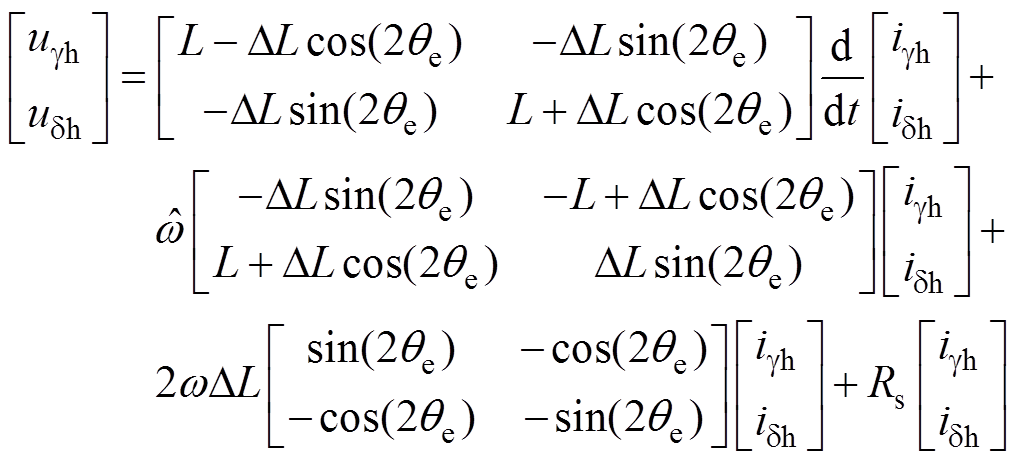 (2)
(2)式中,ugh、udh为gd 坐标系下驱动系统注入的高频电压;igh、idh为gd 坐标系下高频响应电流;L、DL为电感参数,其表达式分别为
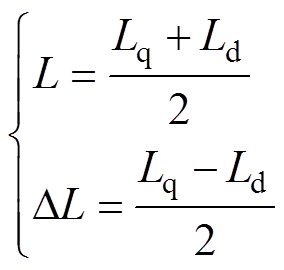 (3)
(3)
角度误差信号qe的表达式为
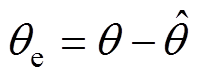 (4)
(4)式中,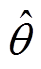 为gd 坐标系下估计的转子位置角。
为gd 坐标系下估计的转子位置角。
由式(2)可知,注入电机的高频分量中含有转子位置信息。在电压注入方法中,输入电压固定,位置信息存在于高频电流分量中;而在电流注入方法中,高频电流确定,位置信息存在于高频电压分量中。
本文采用电流注入方法,为简化设计并减少转矩波动,令idh=0,则式(2)可简化为
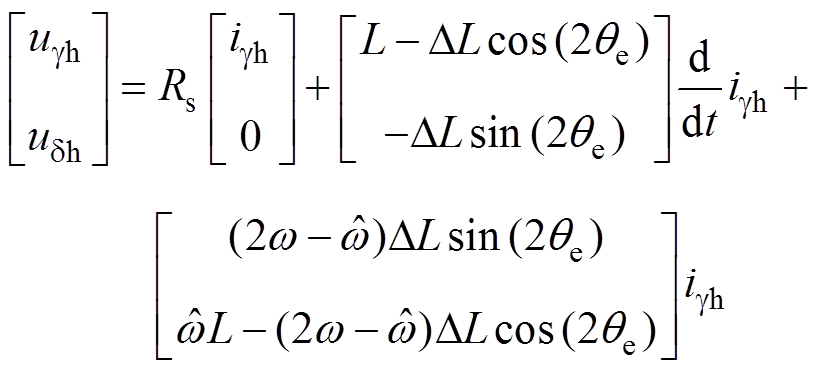 (5)
(5)电机绕组呈感性,因此注入的高频电流信号必须是一个连续函数;同时,为便于控制系统设计,本文选择正弦信号作为高频注入信号。
与电压注入法相比,电流注入法在原理上没有忽略定子电阻Rs,因此可允许更低的谐波注入频率,实现降频。电压注入法中,注入的高频电压信号容易实现,难点在于高频电流信号的提取,需要高通滤波器实现高频信号的分离。理论上,随着注入频率的降低,滤波器动态响应与带宽变得难以平衡,进而增加了高通滤波器的设计难度。在电流注入法中,整个系统无需滤波器,但是对电流环的设计提出了较高要求;为实现电流谐波注入,必须重新设计电流环,满足系统要求。
为实现电流谐波注入,控制系统需要在g 轴的电流给定信号中加入高频谐波分量,而电机电流环一方面需要实现对高频给定信号的无误差跟踪;另一方面需要实现电流信号快速响应,提高控制系统动态性能。
传统的PI控制器无法实现对谐波给定信号的无误差跟踪,为改善电流环的控制特性,本文提出采用谐振控制器与自抗扰控制器相结合的电流控制方法,实现谐波电流注入。
当高频注入信号为正弦波时,注入信号为
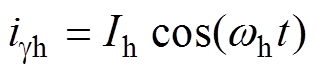 (6)
(6)式中,Ih为谐波幅值;wh为谐波频率。
将式(6)代入到式(5)中,可得
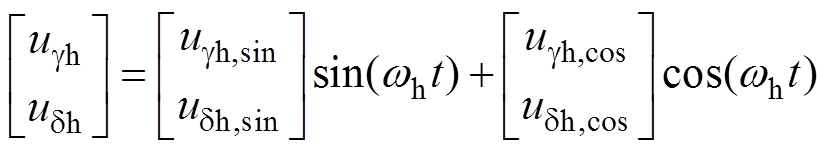 (7)
(7)其中
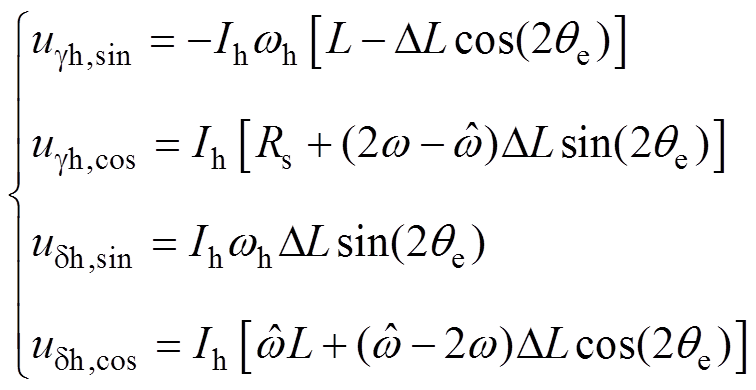 (8)
(8)
为了减小高频噪声,可通过调整注入高频信号的频率分散电流频谱的能量。假定系统采用两个频率,两者可以自由切换,则有
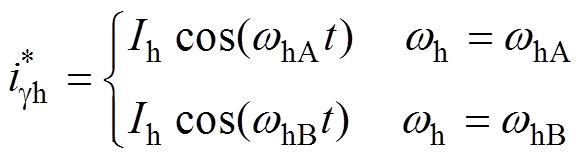 (9)
(9)将式(9)代入到式(8),在系统稳定时,有
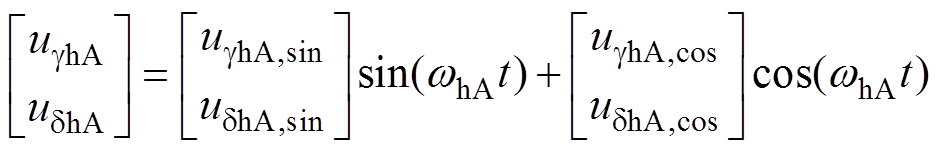 (10)
(10)
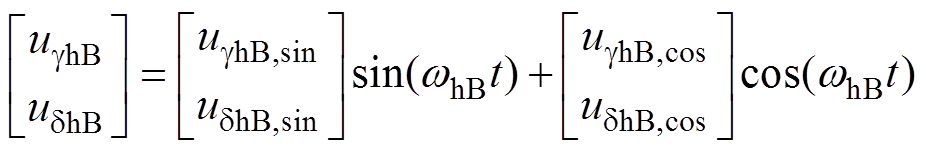 (11)
(11)其中
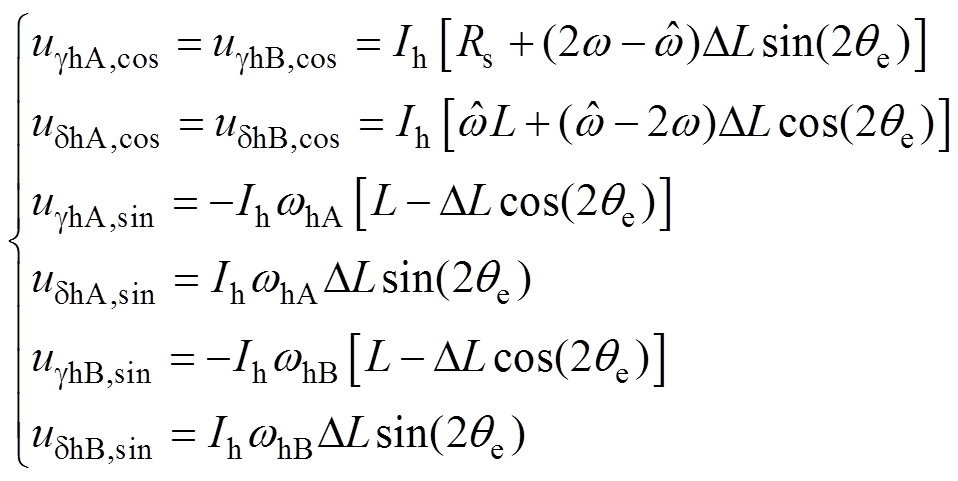 (12)
(12)
从式(12)可以看出,当频率切换时,高频电压的余弦分量的幅值ugh,cos和udh,cos没有发生变化,正弦分量的幅值ugh,sin和udh,sin有变动。
在本文中,IPMSM控制方法采用基于查表法的最大转矩电流比(Maximum Torque Per Ampere, MTPA)控制,在g 轴,电流控制器需要使电流追踪高频给定信号;在d 轴,电流控制器则需要抑制高频扰动。为实现上述目的,本文利用线性自抗扰控制器实现电流控制,并采用谐振控制器对LADRC进行改进,实现高频电流的无误差注入。
LADRC的核心是状态扩张观测器(Linear Extended State Observer, LESO),g 轴与d 轴采用相同结构的LESO,以d 轴为例,以id 为观测对象,其LESO的数学表达式为
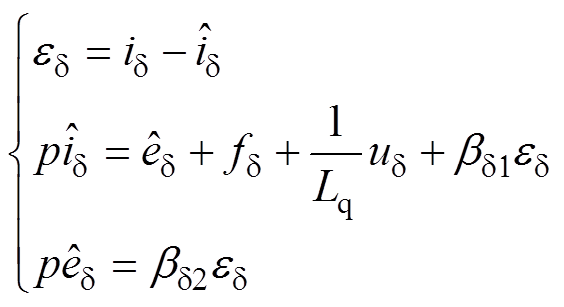 (13)
(13)式中,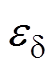 为估计误差;
为估计误差;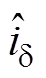 为电流估计值;
为电流估计值;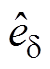 为估计扰动;
为估计扰动;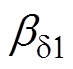 和
和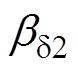 为LESO的增益;
为LESO的增益;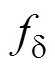 为谐振控制器的输出。
为谐振控制器的输出。
经典的谐振控制器的传递函数为
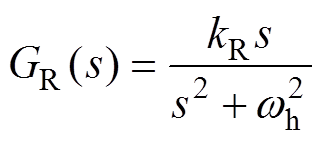 (14)
(14)式(14)为定频谐振设计的,为实现谐振频率的变化,需要对谐振控制器进行改进,改进后的谐振控制器为
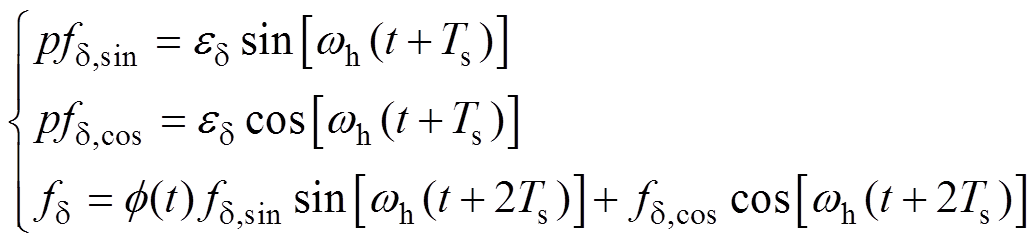 (15)
(15)
式中,Ts为IGBT开关周期;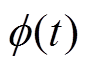 为阶跃函数,用于补偿式(12)中正弦分量的幅值变动,降低频率切换对系统造成的影响,使切换过程更为平滑,其表达式为
为阶跃函数,用于补偿式(12)中正弦分量的幅值变动,降低频率切换对系统造成的影响,使切换过程更为平滑,其表达式为
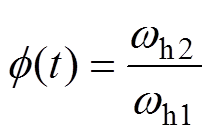 (16)
(16)式中,wh1为系统正在注入的频率;wh2为即将切换的频率。
除LESO,LADRC还包括控制律与一阶线性微分跟踪器(Linear Tracking Differentiator, LTD)。LTD的作用是将指令的阶跃信号变为平滑过渡的连续信号,其表达式为
 (17)
(17)式中,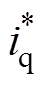 为q轴电流给定值;
为q轴电流给定值;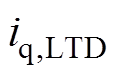 为LTD的输出量;kLTD为LTD的调节系数。
为LTD的输出量;kLTD为LTD的调节系数。
当系统稳定时,存在
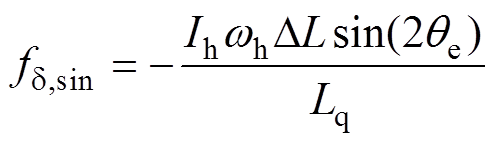 (18)
(18)因此,当qe较小时,角度误差可近似表示为
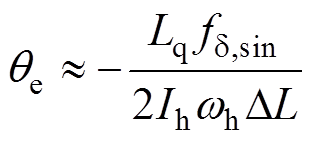 (19)
(19)
估计出qe后,可利用锁相环(Phase Locked Loop, PLL)实现转子位置估计,电流环整体结构如图2所示。
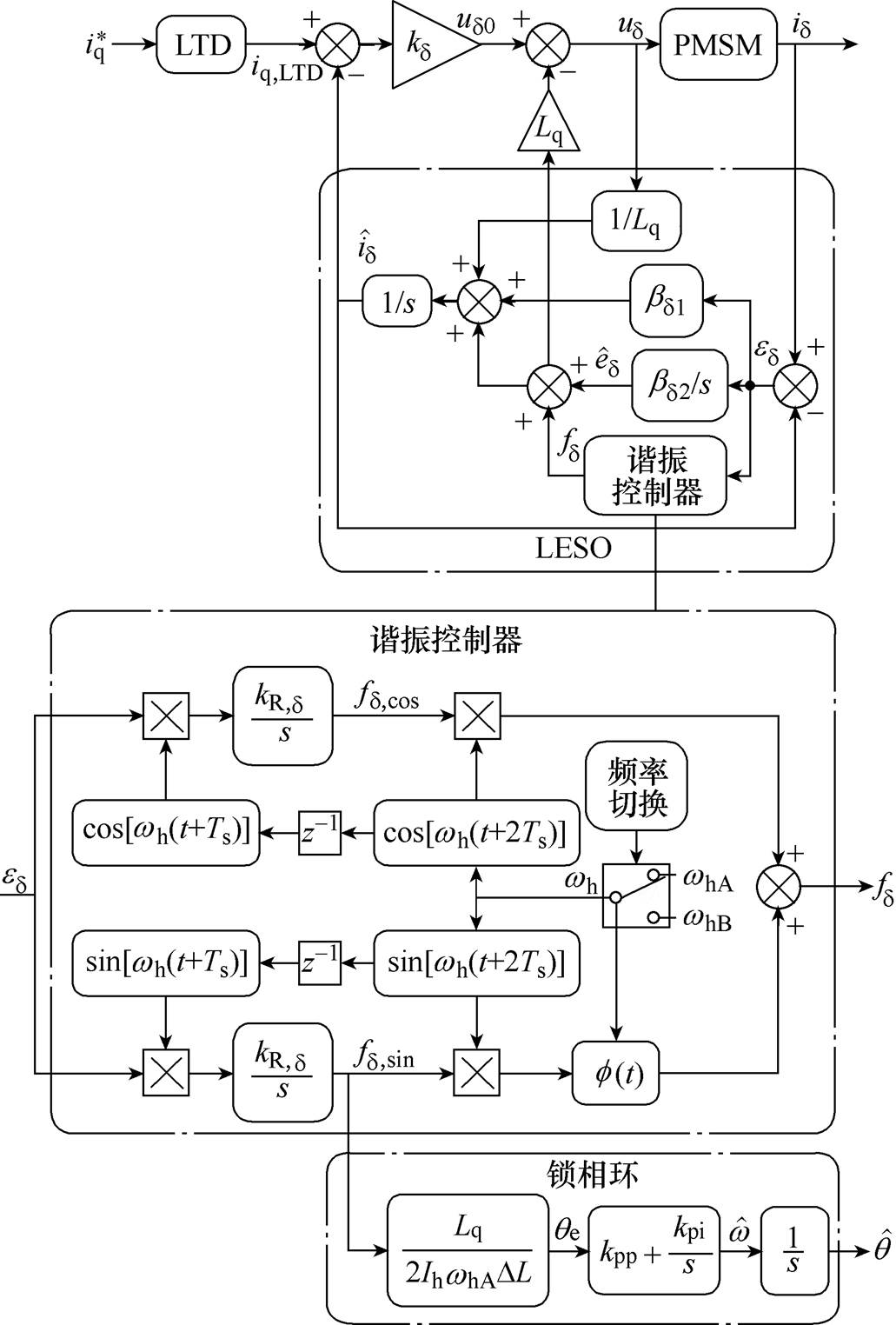
图2 d 轴电流环的线性自抗扰控制器
Fig.2 LADRC of d axis current loop
在控制律方面,g 轴与d 轴则有所区别,由于d轴无需谐波注入,只需要通过LESO中的谐振控制器进行扰动补偿即可,因此,d 轴仍采用比例调节。而g 轴需要注入谐波,因此采用比例谐振调节,g 轴电流环的线性自抗扰控制器如图3所示,谐振控制器的结构形式与LESO中的谐振控制器完全相同。
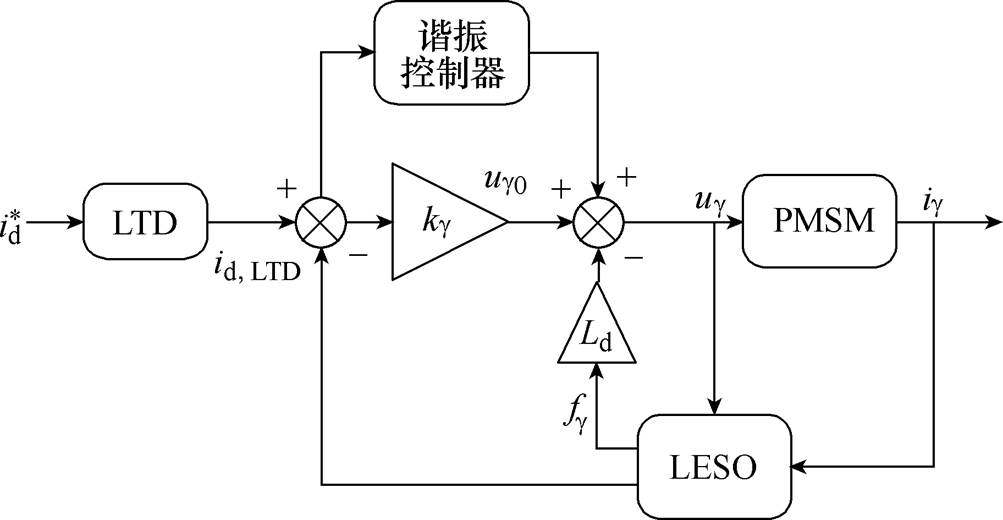
图3 g 轴电流环的线性自抗扰控制器
Fig.3 LADRC of g axis current loop
目前常用的频率切换策略有零点切换和极值点切换,即在谐波电流过零点时或到达极值点时切换。这两种切换策略需要控制程序执行半个或一个谐波周期,注入谐波的周期只能选择开关周期的整数倍,因此谐波频率的选择受到一定限制。
理论上,本文提出的控制方法可在任意时刻进行频率切换,因此对谐波周期的选择没有要求。为便于实现,本文采用定时切换模式,即每次频率切换的间隔固定时间为Th,每次谐波频率改变Dwh,频率变化规则为从最低谐波频率whL开始运行,逐渐增加频率,当谐波频率到达最高值whH后,开始减小频率,循环往复,谐波电流注入策略如图4所示。
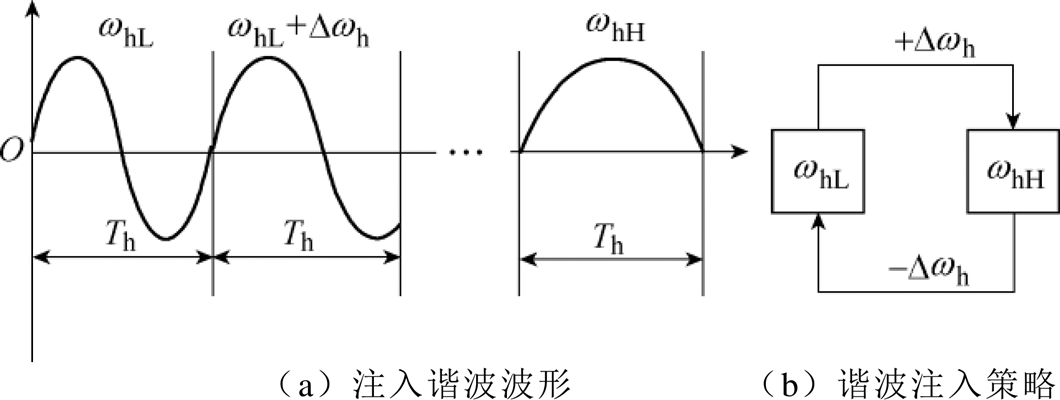
图4 谐波电流注入策略
Fig.4 Strategy of injected current
为验证算法的可行性,在实验平台上进行了相关的实验,电驱动系统实验平台如图5所示。实验中采用了一台8kW的永磁同步电机作为样机,电机参数见表1。驱动系统的主控芯片采用TI公司的DSP,型号为TMS320F28335,IGBT开关频率为10kHz。

图5 电驱动系统实验平台
Fig.5 Platform of electric drive system
表1 实验电机参数
Tab.1 Parameters of test motor
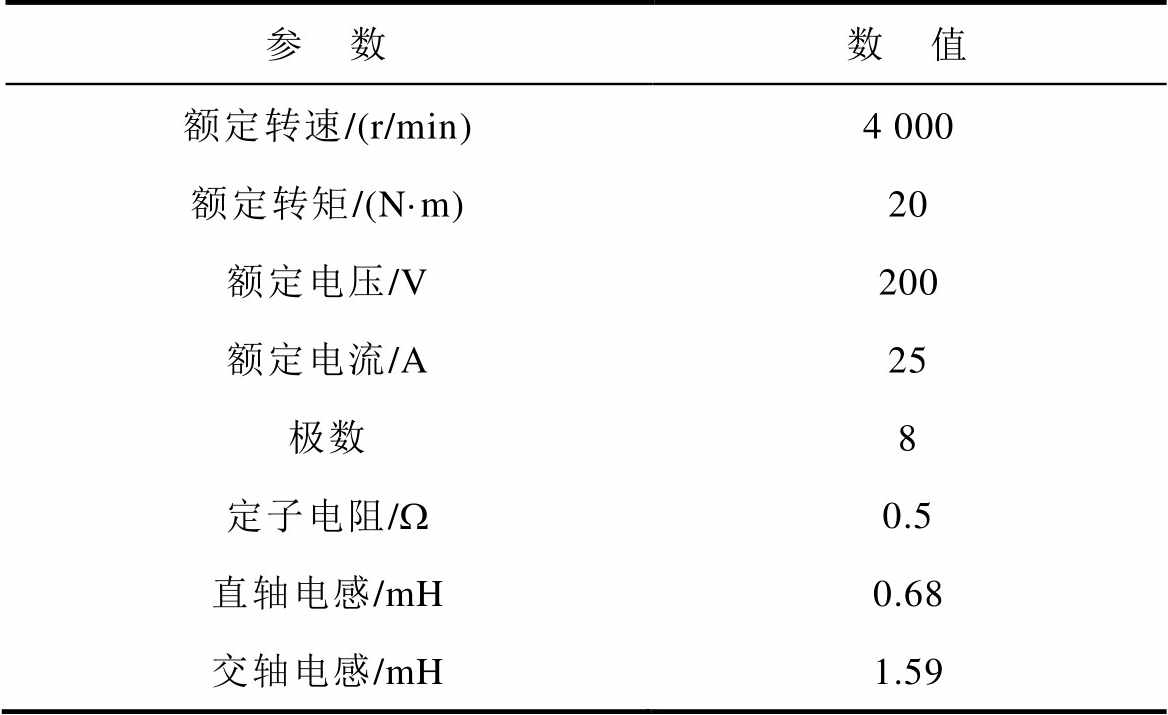
参 数数 值 额定转速/(r/min)4 000 额定转矩/(N·m)20 额定电压/V200 额定电流/A25 极数8 定子电阻/W0.5 直轴电感/mH0.68 交轴电感/mH1.59
实验中,利用查表法,采用最大转矩电流比控制策略驱动测试电机。分别对固定频率方法、双频率随机切换方法与频率扫描方法三种谐波注入方法进行了实验对比验证,实验中,上述三种方法均采用本文提出的电流控制方法,LADRC、谐振控制器与锁相环的参数完全相同,区别仅在于高频谐波信号的选择。
实验中注入谐波的幅值统一为Ih=1.5A,固定频率方法选择的频率为200Hz与400Hz,双频率随机切换方法同样选择200Hz与400Hz,频率扫描方法为whL=200Hz,whH=400Hz,Dwh=0.5Hz。
图6~图8分别给出了采用固定频率方法、双频率随机切换方法与频率扫描方法在电机静止状态下的电流波形。从图中实验波形可以看出,无论采用何种方法,本文所提出的电机电流控制方法都能够实现响应电流对指令信号的稳定跟踪,且误差较小。同时,当谐波频率进行切换时,切换造成的电流波动较小。从上述实验结果可以得出,本文提出的方法能够实现高频注入谐波的频率变化。
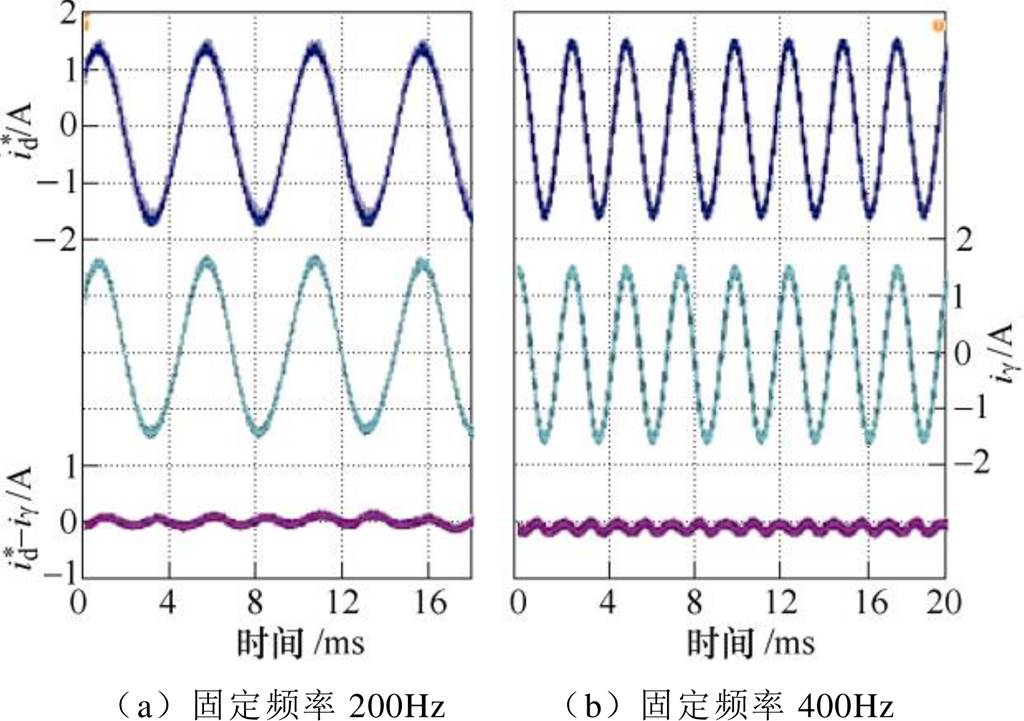
图6 静止状态下固定频率方法的电流波形
Fig.6 Current waveforms of fixed frequency switching method in stationary state

图7 静止状态下双频率随机切换方法的电流波形
Fig.7 Current waveforms of random frequency switching method in stationary state
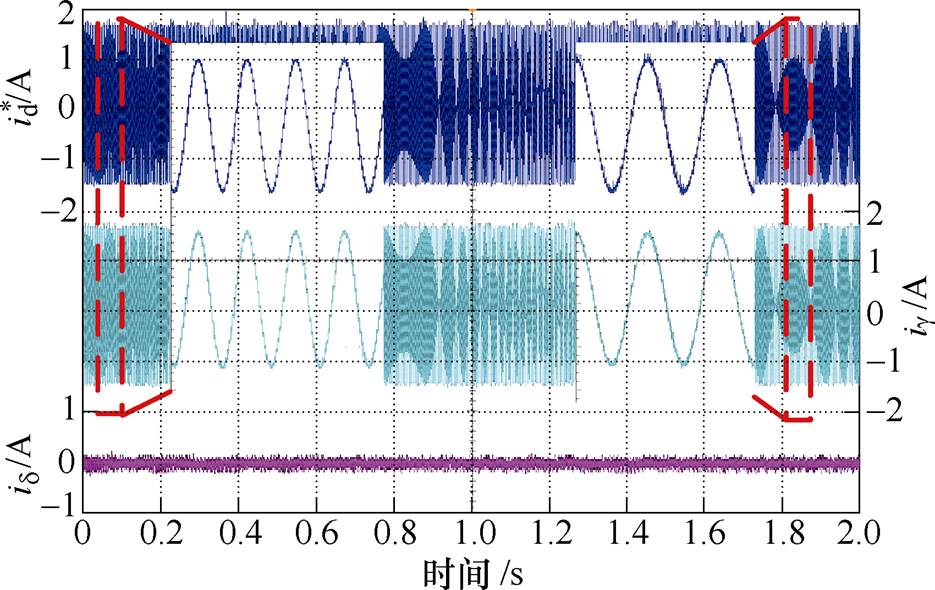
图8 静止状态下频率扫描方法的电流波形
Fig.8 Current waveforms of sweep-frequency switching method in stationary state
图9为采用固定频率方法、双频率随机切换方法与频率扫描方法在电机稳态工况下的波形对比,主要对比估计电角度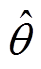 与实际电角度q 的波形,工况为转速100r/min,转矩20N·m。从实验波形看出,这三种方法均能够准确地实现转子位置的稳定跟踪;从稳态波形可以得出,当电流环参数一致时,谐波频率注入方法对电机的稳态性能影响较小。
与实际电角度q 的波形,工况为转速100r/min,转矩20N·m。从实验波形看出,这三种方法均能够准确地实现转子位置的稳定跟踪;从稳态波形可以得出,当电流环参数一致时,谐波频率注入方法对电机的稳态性能影响较小。
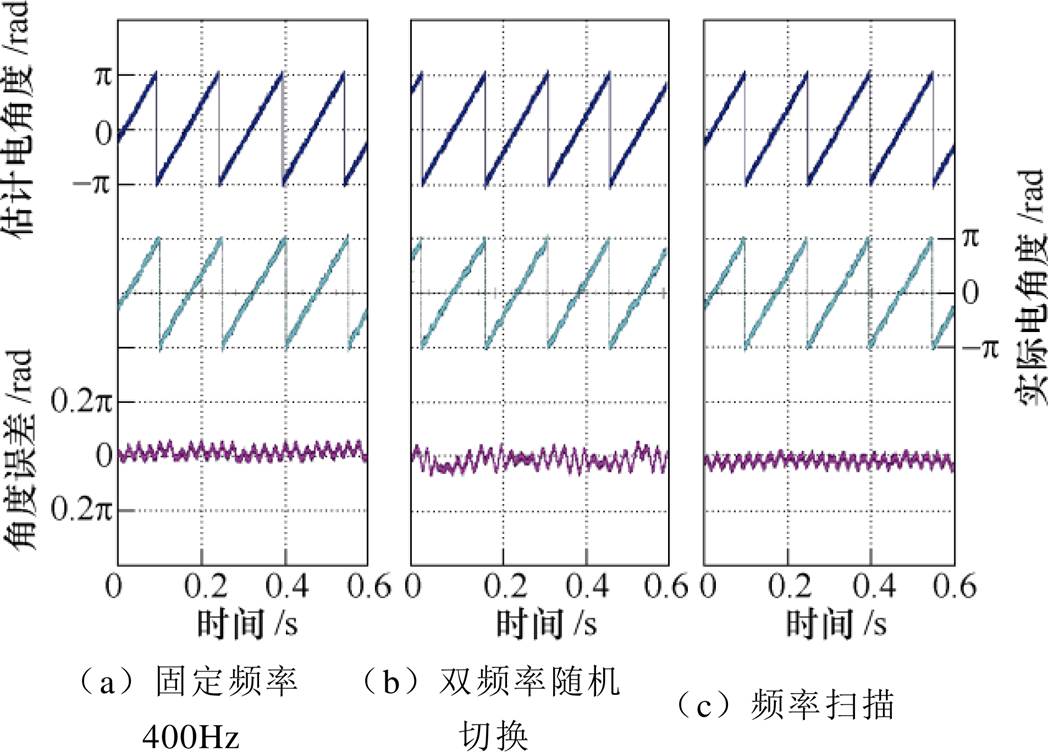
图9 采用谐波频率扫描方法时电机稳态工况下估计电角度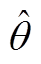 与实际电角度q
与实际电角度q
Fig.9 Actual and estimated rotor position of sweep-frequency switching method in steady state
图10和图11分别为动态条件下基于谐波频率扫描方法电机动态工况下和转矩突变条件下相关实验波形。图10为电机20N·m负载下的加减速实验波形。图11为400r/min时转矩波动实验波形,转矩从0上升到20N·m,再减小到0。从实验结果来看,该方法具有良好的动态响应能力,在动态响应条件下,转子位置误差较小。
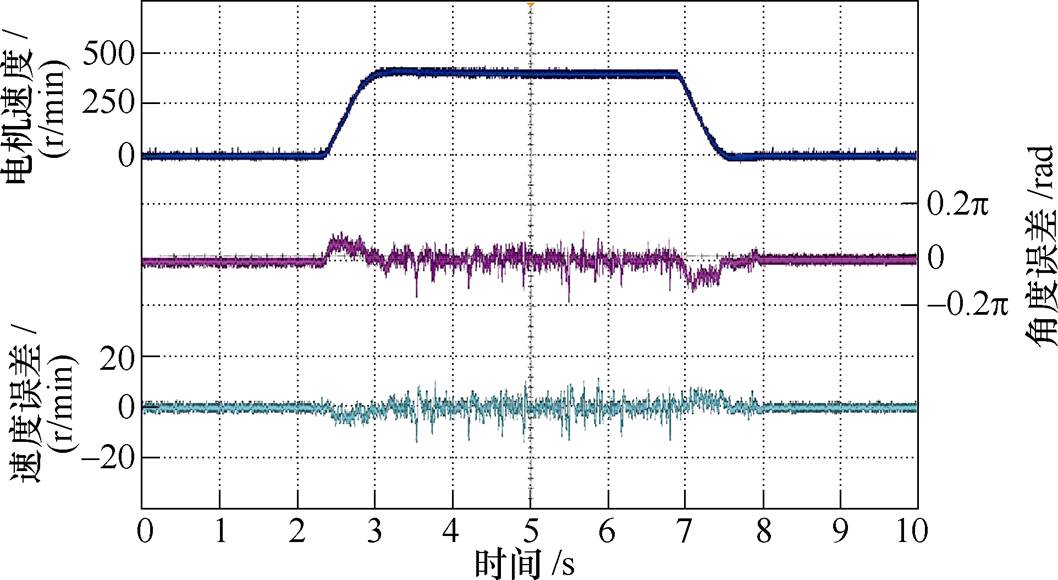
图10 采用谐波频率扫描方法时电机动态工况下角度估计误差与速度估计误差
Fig.10 Position and speed estimation error for sweep- frequency switching method during the dynamic process
为对比三种方法的谐波频谱分布,需要对电机相电流做快速傅里叶变换(Fast Fourier Transform, FFT)。实验中,将电机工况固定为转速100r/min,负载转矩10N·m。在该工况下,分别对三种方法下的电机A相电流进行分析。图12为固定谐波频率为200Hz和400Hz时电机A相电流波形FFT结果,谐波电流峰值在0.6A左右。图13与图14分别为采用随机频率切换方法和频率扫描方法时,电机A相电流波形。与采用固定频率方法的谐波频率相比,采用随机频率切换方法后,谐波电流峰值有所下降,但仍有明显的电流尖峰。而采用频率扫描方法后,谐波电流幅值大幅度下降,且没有明显的电流尖峰,因此这种频谱分布有利于进一步降低噪声。

图11 采用谐波频率扫描方法时转矩突变条件下的相关实验波形
Fig.11 Experimental waveforms for sweep-frequency switching method with step load disturbance
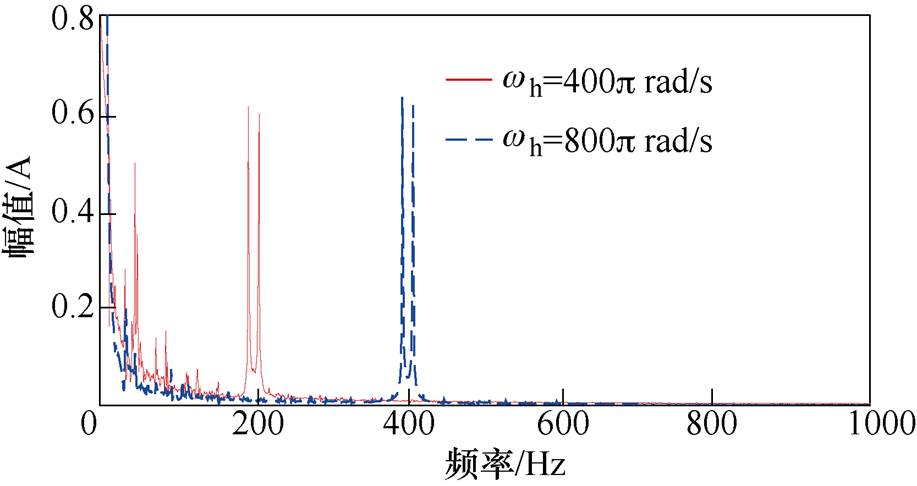
图12 固定谐波频率下电机相电流傅里叶变换
Fig.12 FFT results of fixed-frequency injection methods
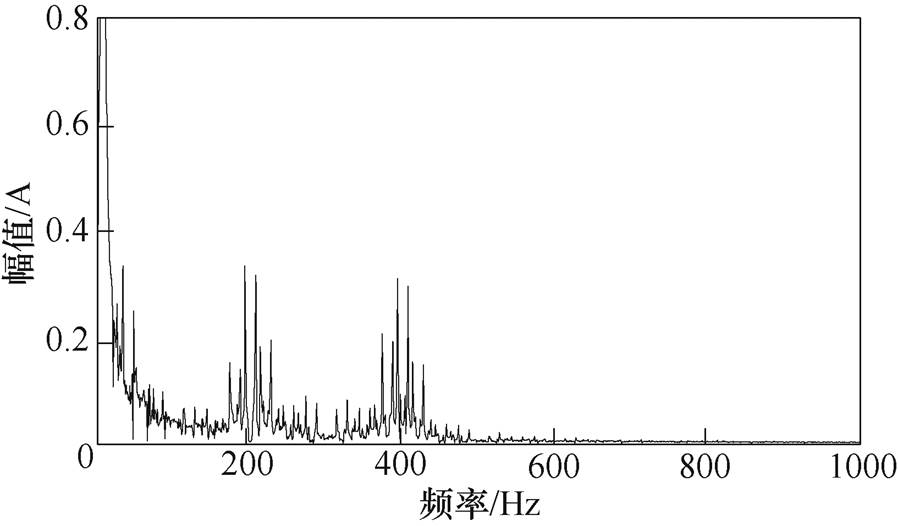
图13 采用随机频率切换方法时电机相电流傅里叶变换
Fig.13 FFT results of random frequency switching methods
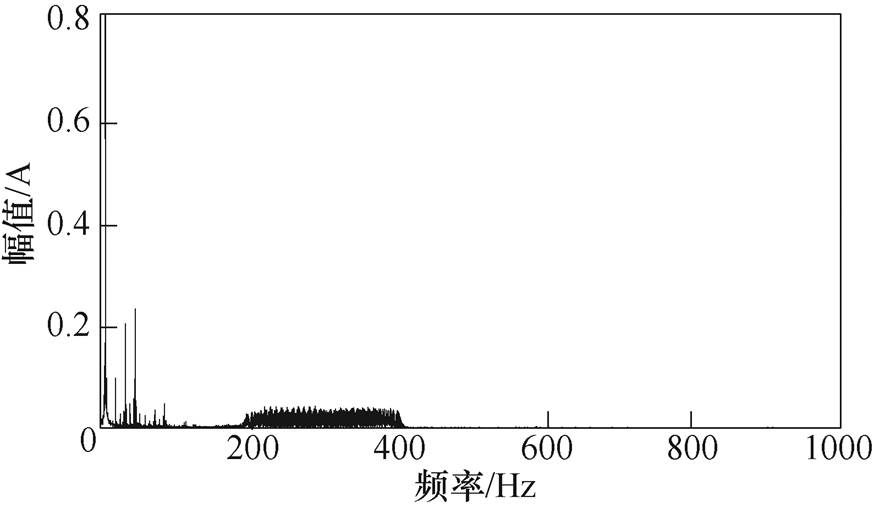
图14 采用频率扫描方法时电机相电流傅里叶变换
Fig.14 FFT results of sweep-frequency switching methods
本文提出了一种基于谐波注入的IPMSM无传感器控制方法,这种方法能够改变注入谐波的频率,分散谐波能量,从而抑制谐波造成的高频噪声。为实现注入谐波频率的实时变化,提出了一种基于LADRC和谐振控制器的电机电流控制方法,该方法在改变谐波频率的同时,仍能实现转子位置估计。为实现噪声抑制,提出了基于频率扫描的谐波注入方法,与传统的双频率随机切换方法相比,该方法能进一步改善谐波频谱分布,消除谐波在频谱上的尖峰,从而减少谐波引起的噪声。最后,通过样机进行了实验验证,实验表明,本文所提方法具有良好的动态和稳态特性,同时,注入谐波的频谱也得到了大幅度改善。
参考文献
[1] 张立伟, 李行, 宋佩佩, 等. 基于新型滑模观测器的永磁同步电机无传感器矢量控制系统[J]. 电工技术学报, 2019, 34(增刊1): 70-78.
Zhang Liwei, Li Hang, Song Peipei, et al. Sensorless vector control using a new sliding mode observer for permanent magnet synchronous motor speed control system[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 70-78.
[2] 倪启南, 杨明, 徐殿国, 等. 低分辨率位置传感器永磁同步电机精确位置估计方法综述[J]. 电工技术学报, 2017, 32(22): 70-81.
Ni Qinan, Yang Ming, Xu Dianguo, et al. Review of precise position estimation method of PMSM with low-resolution position sensor[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 70-81.
[3] 刘计龙, 肖飞, 沈洋, 等. 永磁同步电机无位置传感器控制技术研究综述[J]. 电工技术学报, 2017, 32(16): 76-88.
Liu Jilong, Xiao Fei, Shen Yang, et al. Position- sensorless control technology of permanent-magnet synchronous motor-a review[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 76-88.
[4] Zhang Guoqiang, Wang Gaolin, Xu Dianguo, et al. ADALINE-network-based PLL for position sensorless interior permanent magnet synchronous motor drives[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1450-1460.
[5] Du Bochao, Wu Shaopeng, Han Shouliang, et al. Application of linear active disturbance rejection controller for sensorless control of internal permanent- magnet synchronous motor[J]. IEEE Transactions on Industrial Electronic, 2016, 63(5): 3019-3027.
[6] 魏海峰, 韦汉培, 张懿, 等. 基于转子磁链模型的永磁同步电机转子位置估计策略[J]. 电工技术学报, 2018, 33(13): 106-113.
Wei Haifeng, Wei Hanpei, Zhang Yi, et al. New rotor position estimation strategy for permanent magnet synchronous motor based on rotor flux model[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 106-113.
[7] Xu Peilin, Zhu Ziqiang. Novel carrier signal injection method using zero sequence voltage for sensorless control of PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2053-2061.
[8] Yoon Y D, Sul S K, Morimoto S, et al. High- bandwidth sensorless algorithm for AC machines based on square-wave-type voltage injection[J]. IEEE Transactions on Industrial Application, 2011, 47(3): 1361-1370.
[9] 李浩源, 张兴, 杨淑英, 等. 基于高频信号注入的永磁同步电机无传感器控制技术综述[J]. 电工技术学报, 2018, 33(12): 2653-2664.
Li Haoyuan, Zhang Xing, Yang Shuying, et al. Review on sensorless control of permanent magnet synchronous motor based on high-frequency signal injection[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2653-2664.
[10] Shibano Y, Kubota K. Pole position estimation method of IPMSM at low speed without high frequency components injection[C]//Applied Power Electronics Conference and Exposition, Washington, DC, USA, 2009: 233-239.
[11] Kimu S, Kwon Y C, Sul S K, et al. Position sensor- less operation of IPMSM with near PWM switching frequency signal injection[C]//Power Electronics and ECCE Asia, Jeju, South Korea, 2011: 1660-1665.
[12] Tauchi Y, Kubota H. Audible noise reduction method in IPMSM position sensorless control based on high frequency current injection[C]//International Power Electronics Conference, Hiroshima, Japan, 2014: 3119-3123.
[13] Medjmadj S, Diallo D, Mostefai M, et al. PMSM drive position estimation: contribution to the high- frequency injection voltage selection issue[J]. IEEE Transactions on Energy Conversion, 2015, 30(1): 349-358.
[14] Yongsoon P, Seung-Ki S. A novel method utilizing trapezoidal voltage to compensate for inverter non- linearity[J]. IEEE Transactions on Power Electronics, 2012, 27(12): 4837-4846.
[15] Yoon Y D, Sul S K. Sensorless control for induction machines based on square-wave voltage injection[J]. IEEE Transactions on Power Electronics, 2014, 29(7): 3637-3645.
[16] Park N C, Kim S H. Simple sensorless algorithm for interior permanent-magnet synchronous motors based on high-frequency voltage injection method[J]. IET Electric Power Application, 2014, 8(2): 68-75.
[17] Wang Gaolin, Yang Lei, Yuan Bihe, et al. Pseudo- random high-frequency square-wave voltage injection based sensorless control of IPMSM drives for audible noise reduction[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7423-7433.
[18] Wang Gaolin, Yang Lei, Zhang Guoqiang, et al. Comparative investigation of pseudorandom high- frequency signal injection schemes for sensorless IPMSM drives[J]. IEEE Transactions on Power Elec- tronics, 2017, 32(3): 2123-2132.
[19] Shun T, Yasui K, Yuki K. Noise reduction method by injected frequency control for position sensorless control of permanent magnet synchronous motor[J]. International Power Electronics Conference, Hiroshima, Japan, 2014: 2465-2469.
A Variable Frequency Current Injection Sensorless Control Strategy of IPMSM for Audible Noise Reduction
Abstract High frequency (HF) signal injection is a classical method widely used in sensorless control of interior permanent magnet synchronous motors (IPMSM), acquiring good dynamic and steady characteristics. However, the audible noise created by the injected HF signal becomes one of the main sources of noise. In this paper, a variable frequency current injection method is proposed to reduce this noise. By continuously changing the frequency of harmonic current, the energy of the harmonics in the spectrum is dispersed, and the peak is eliminated. In this way, the high frequency current noise can be reduced. In order to realize the variable frequency harmonic current injection, the current loop of the motor is redesigned, and the high frequency current signal injection is realized by the linear active disturbance rejection controller and the resonance controller. The experimental results show that this method can effectively improve the spectral distribution of harmonic current and reduce the high frequency current noise.
keywords:Permanent magnet synchronous motors, sensorless control, active disturbance rejection control, noise suppression
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.191057
国家重点研发计划(2017YFB0102400)和国家自然科学基金青年科学基金(51807034)资助项目。
收稿日期 2019-08-14
改稿日期 2019-10-08
杜博超 男,1986年生,博士,讲师,研究方向为电机系统及其控制,电驱动系统故障诊断技术。E-mail: dubc3124@126.com(通信作者)
崔淑梅 女,1964年生,教授,博士生导师,研究方向为电动汽车电机系统。E-mail: cuism@hit.edu.cn
(编辑 陈 诚)