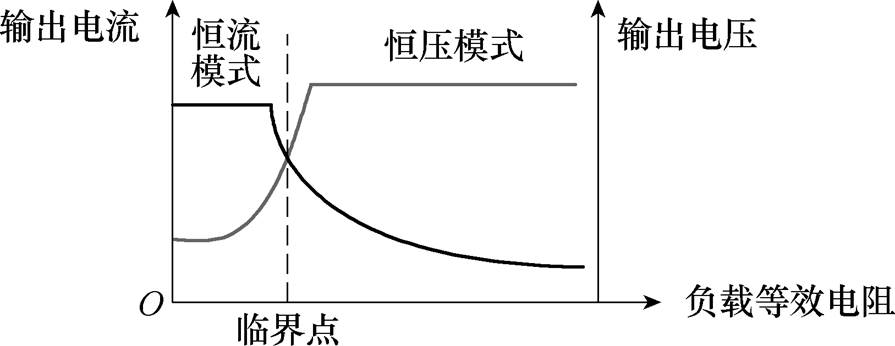
图1 电动汽车锂电池的典型充电特性
Fig.1 Typical charging characteristics of lithium batteries used in electric vehicles
摘要 电动汽车的无线电能传输系统具有安全可靠、便捷等优点。该文根据电动汽车车载锂电池的充电特性,通过对松散耦合变压器及补偿电路特性的研究,提出一种由一次侧串联二次侧串联(PS-SS)补偿拓扑和一次侧串联二次侧LCL(PS-SLCL)补偿拓扑所组成的无线电能传输电路拓扑。该拓扑随着锂电池负载的变化,其充电模式从恒流模式自动切换到恒压模式,同时在整个充电过程中可以实现逆变器的软开关。该文基于此新型补偿拓扑的输出特性及工作模式,在理论分析的基础上对拓扑参数和变压器模型进行设计。通过构建仿真模型,验证了电路拓扑的恒流与恒压输出特性。最后搭建了一套功率为1kW的样机,通过实验验证了该拓扑的可行性。
关键词:电动汽车 无线充电 恒流恒压输出 自切换
电动汽车已成为我国政府鼓励发展的新能源交通工具。电动汽车车载电池的充电方式有无线式和接触式两种,无线电能传输系统相比于传统的有线接触式电能传输系统,具有非接触性、无磨损、高效安全可靠等诸多优点[1-2]。因此,该技术常被应用到恶劣的工作环境中:如器官移植的后续供电[3],这利于提高移植者的生活质量;如水下供电[4],解决了无人水下航行器更换电池的问题;尤其是针对电动汽车电池的充电需求[5-6],无线电能传输技术有效地实现了电气和机械的隔离,在充电过程中电能发射端和接收端不需要直接接触,可以确保锂电池充电的方便和安全。
电动汽车广泛使用锂离子电池进行能量存储。电动汽车锂电池的典型充电特性[7]如图1所示,电池开始充电时以恒流(Contant Current, CC)的模式工作,随着负载等效电阻的增加,当电阻大到临界点时,充电模式切换到恒压(Contant Voltage, CV)模式进行充电,此后电池处于恒压状态。为了延长电池的使用寿命,需要准确控制充电电流和电压,防止恒流时过充和恒压时欠电压的工况。

图1 电动汽车锂电池的典型充电特性
Fig.1 Typical charging characteristics of lithium batteries used in electric vehicles
锂电池在充电过程中内阻会发生变化[8],所提供的恒流或恒压输出需应对大范围的负载变化。文献[9-11]在松散耦合变压器一次侧引入闭环回路,输出信号可通过调节占空比来实现,但该系统需外加动力装置,导致成本、体积等增加。文献[12-13]中指出,采用变频控制法会增加无功功率,可能导致频率分叉而系统不稳定。对高频逆变器,文献[14]在固定频率下的相移控制法可调整信号输出,但逆变器不能在零电压启动状态下进行大负荷变动,这会导致系统效率的下降,增加电磁干扰。文献[15]将恒流输出和恒压输出的拓扑结合起来,但需要通过控制附加的交流开关来实现,切换时会出现电池充电电压发生跳变的现象,影响电池寿命。因此,如何保证电动汽车锂电池在充电过程中能有效、平滑地在恒流与恒压之间自动切换,对于保护充电电池、延长电池寿命和促进电动汽车发展有着重要意义。
多参数谐振方案在传统的隔离型开关电源中被广泛应用。文献[16]在第四类LLC谐振型变流器的基础上,总结归纳了相应的拓扑特征以及有效的拓扑结构。文献[17]基于双变压器结构提出了一种新型的多谐振软开关双向直流变换器,可以在较宽的电压增益范围内具有较高的工作效率。对于无线充电技术,由于其松散耦合变压器存在较大的漏感,通常采用谐振的方式进行参数补偿。文献[18]基于双LCL补偿拓扑探讨分析了在偏移下系统的工作特性。文献[19]对于双向无线充电系统中所采用的串联、LCL以及LCC补偿拓扑进行传输功率、系统效率等方面的分析研究。
本文提出了一种适用于电动汽车充电的恒流恒压输出自适应的无线电能传输系统,与上述分析所采用的谐振补偿方案不同的是,该系统由一次侧串联二次侧串联(Primary side Series Secondary side Series, PS-SS)补偿网络和一次侧串联二次侧LCL(Primary side Series Secondary side LCL, PS- SLCL)补偿网络的两种拓扑结构组合而成,通过对两种拓扑结构工作特性的分析,寻找输出电流、输出电压与负载之间的关系及电路所具有的特点,同时对提出的新型结构进行工作模式分析,实现该系统在负载变化的情况下,电池充电在恒流和恒压两种模式间自动切换,然后在理论分析的基础上对电路参数和松散耦合变压器进行设计,最后通过搭建仿真模型和试验平台,对理论分析进行验证。
松散耦合变压器作为电动汽车无线充电电能传输系统的核心元件,其存在较大的漏磁通,一次侧和二次侧的漏感会导致电路的传输能力降低。为了提高系统整体的传输效率,通常利用变压器自感和补偿电容进行谐振,来减少系统的无功功率。
针对电动汽车锂电池先恒流后恒压的充电特性,本文提出一种恒流恒压输出的自切换无线电能传输系统,如图2所示。系统一次侧采用全桥逆变电路,产生高频方波信号up,经松散耦合变压器和一次侧补偿网络将能量传递到二次侧,二次侧的两个补偿电路经过各自全桥整流后并联输出。Ui为系统的直流输入电压,开关管S1~S4组成全桥逆变器,一次侧的变压器绕组Lpp和电容Cpp串联为谐振网络作为发射电路,接收电路有两个接收绕组及各自补偿电路组成,其中一个绕组采用串联拓扑补偿电路,包括接收绕组Lsi、谐振电容Csi,另一个绕组采用LCL结构的补偿电路,包括接收绕组Lsv、谐振电容Csv、谐振补偿电感Lss,这两种拓扑结构的补偿电路与各自的整流电路连接后进行并联,为电池负载充电,充电电压为Uo,C为滤波电容,M12为一次绕组Lpp与二次绕组Lsi之间的互感,M13为一次绕组Lpp与二次绕组Lsv之间的互感,M23为二次绕组Lsi和Lsv之间的互感。
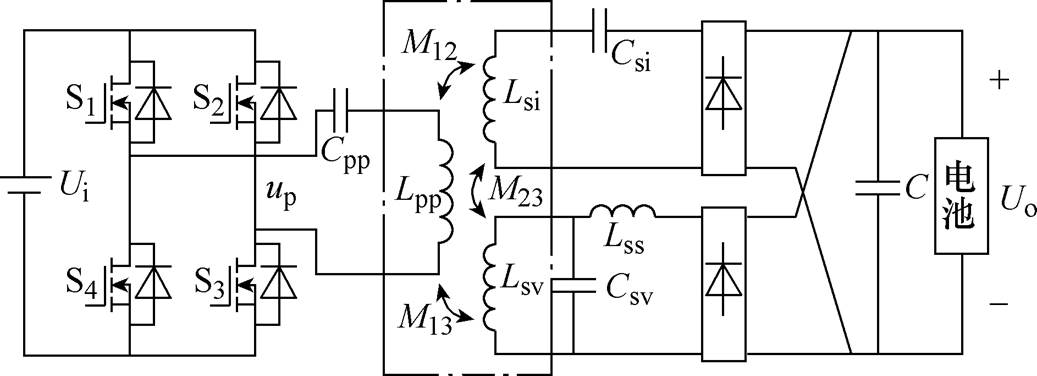
图2 恒流恒压输出的自切换无线电能传输系统
Fig.2 Wireless power transfer system with Automatic witching characteristic of constant current and constant voltage output
图3为PS-SS谐振拓扑等效电路,其中,Lpp和Lsi分别为松散耦合变压器一次侧和二次侧的自感,M12为变压器的互感,Cpp和Csi为一次侧补偿电容和二次侧补偿电容,up是由直流电源经过全桥逆变器逆变后桥臂两端输出的电压,经过傅里叶分解后得到,Re1为负载R整流桥前的交流等效电阻。
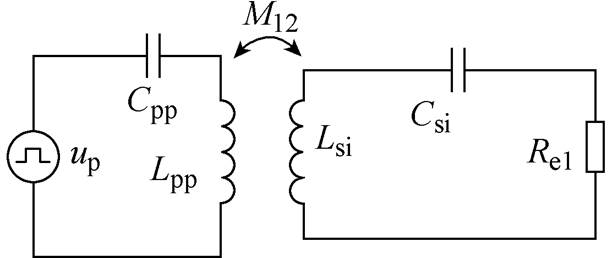
图3 PS-SS谐振拓扑等效电路
Fig.3 PS-SS resonant topology equivalent circuit
因电路处于完全谐振状态,电感Lpp和Lsi分别与串联谐振电容Cpp和Csi在开关频率下进行谐振,故其谐振频率fs1为
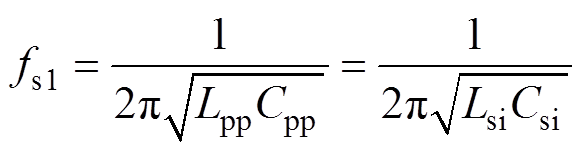 (1)
(1)采用基波分析法,可得
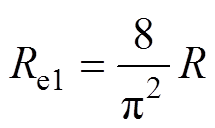 (2)
(2)
从互感角度分析,将PS-SS电路等效成互感模型,如图4所示,ipp为一次电流,isi为二次电流,urs为二次侧反射到一次侧的电压,urp为二次侧互感电压。
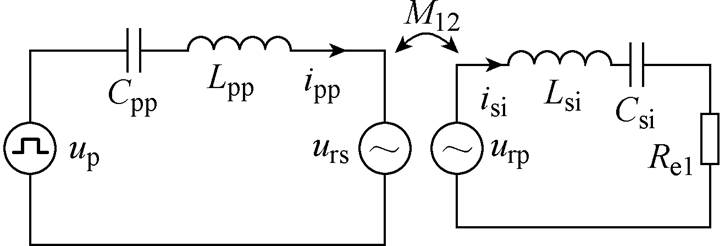
图4 等效互感模型
Fig.4 Equivalent mutual inductance model
利用互感模型,二次侧的互感电压urp的相量表示为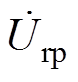 ,有
,有
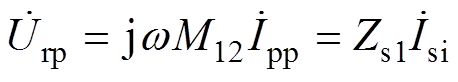 (3)
(3)式中, 为ipp的相量;
为ipp的相量;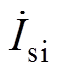 为isi的相量。由于二次侧的影响,反射到一次电压urs的相量表示为
为isi的相量。由于二次侧的影响,反射到一次电压urs的相量表示为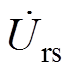 ,有
,有
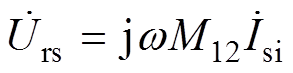 (4)
(4)
一次侧等效阻抗Zp1和二次侧等阻抗Zs1分别为
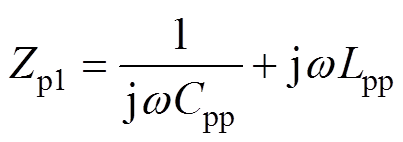 (5)
(5)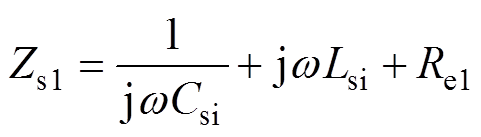 (6)
(6)
因电路工作于谐振状态,故输入阻抗Zin1为
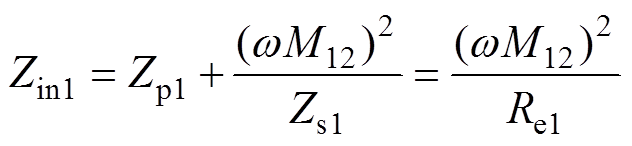 (7)
(7)逆变器输出的电压up的相量表示为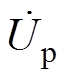 ,有
,有
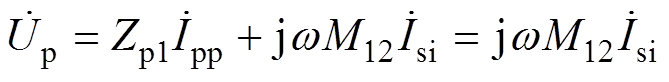 (8)
(8)
令Up为电压up的幅值。因PS-SS电路处于完全谐振状态,输出的电流幅值Isi和电压增益Av分别为
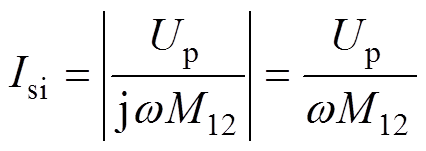 (9)
(9)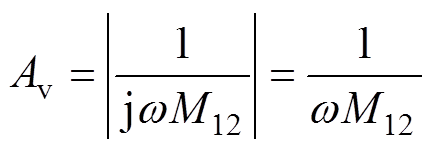 (10)
(10)
由式(7)、式(9)和式(10)可知,PS-SS补偿拓扑电路在完全谐振状态下,可实现输入阻抗Zin1的相位为零,系统输出的电流与负载无关,电流增益在不同的负载条件下保持恒定。
图5为PS-SLCL谐振拓扑等效电路,一次侧采用串联补偿,二次侧采用LCL型补偿,其中,Csv为二次侧补偿电容,Lss为二次侧附加谐振补偿电感,其设计与接收绕组Lsv的自感系数相等,Re2为负载整流桥前的交流等效电阻。
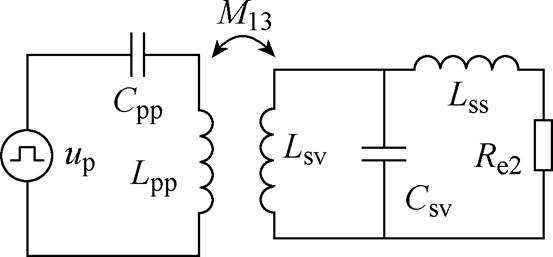
图5 PS-SLCL谐振拓扑等效电路
Fig.5 PS-SLCL resonant topology equivalent circuit
因电路处于完全谐振状态,故谐振频率fs2为
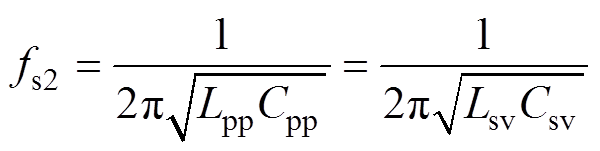 (11)
(11)因谐振,一次侧等效阻抗Zp2=0,则二次侧等效阻抗Zs2和输入阻抗Zin2分别为
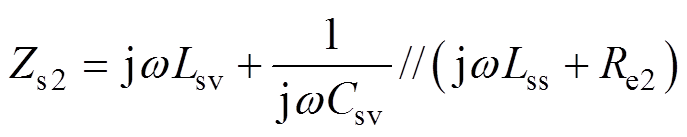 (12)
(12)
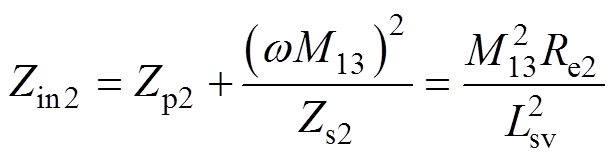 (13)
(13)输出的电压幅值Uout和电压增益Gv分别为
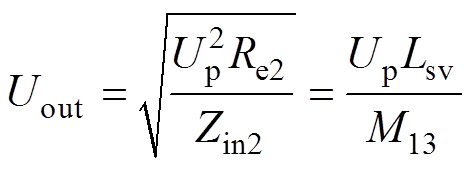 (14)
(14)
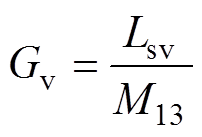 (15)
(15)由式(13)~式(15)可知,PS-SLCL 拓扑电路在完全谐振状态下,可实现输入阻抗Zin2的相位为零,输出电压与负载无关,电压增益在不同的负载条件下保持恒定。但通常情况,为了实现一次侧逆变器开关管的软开关特性,调整输入阻抗为弱感性,因而将一次侧补偿电路中的电感Lpp取值略大于理论值,将电路调整为弱感性输入阻抗。
经上述分析可知,在电路处于完全谐振时,两种补偿拓扑电路都可实现零输入阻抗角,PS-SS电路工作时,可实现恒流输出,且输出电流与负载无关,而PS-SLCL电路工作时,可实现恒压输出,且输出电压与负载无关,因此这两种拓扑电路结合可实现恒流恒压输出特性。另外,由于二次侧的两个接收绕组互不影响,因此在分析拓扑的工作模式时,可以将其视为两个独立的电源,两路拓扑电路整流后并联供电给负载,如图6所示。
从图6中可知,二次侧串联补偿支路的输出电压为uo1,二次侧LCL补偿支路的输出电压为uo2,uo1和uo2两路电压被整流桥互相隔离。当输出电压uo1>uo2时,一路整流桥输入侧的电压uo2被Uo钳位,这时电压Uo的大小由uo1决定;当输出电压uo1<uo2时,整流桥输出的电压Uo由uo2决定;当uo1=uo2时,电压Uo的大小由uo1和uo2共同决定。为便于分析,将串联补偿支路的负载等效为交流电阻Re3,LCL补偿支路的负载等效为交流电阻Re4。两条补偿支路的等效电路如图7所示。
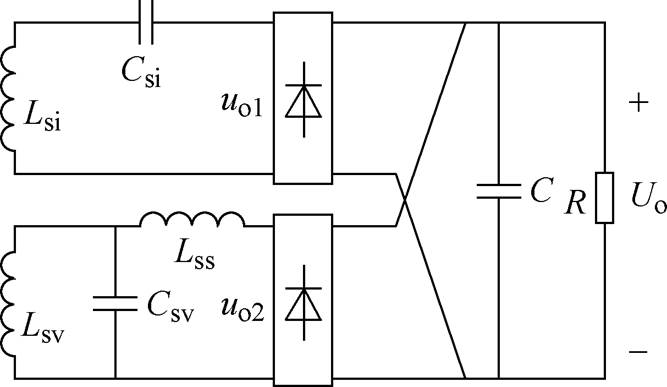
图6 两路拓扑电路整流后并联供电给负载
Fig.6 Two topological circuits are rectified and then connected in parallel to the load
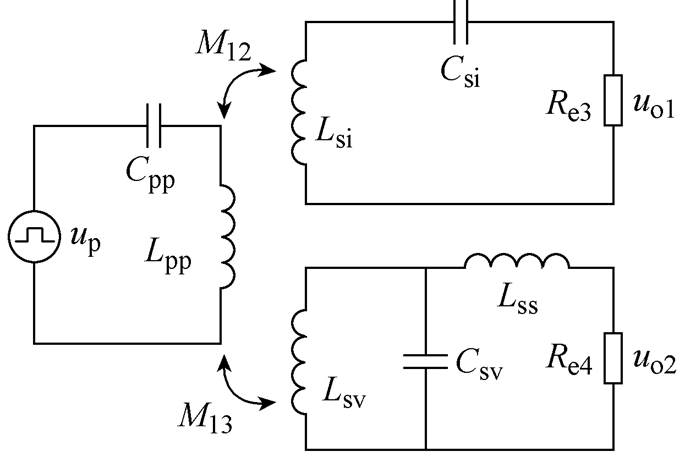
图7 两个补偿支路的等效电路
Fig.7 Equivalent circuits of two compensation branches
因对每个支路进行完全补偿,则输出电压uo1的相量表示为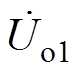 ,有
,有
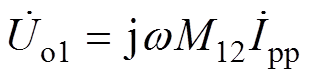 (16)
(16)根据式(12)中LCL补偿支路的阻抗计算,其输出电压uo2的相量表示为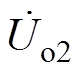 ,有
,有
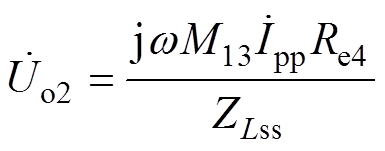 (17)
(17)
式中,ZLss为电感Lss的感抗,由式(16)和式(17)得出Uo1与Uo2的比值为
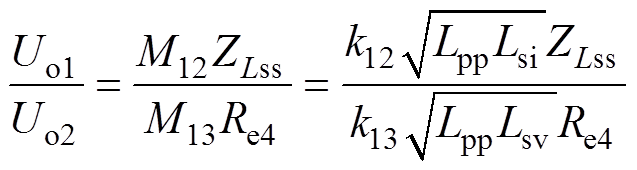 (18)
(18)式中,Uo1和Uo2分别为交流电压uo1和uo2的有效值;k12为发射绕组与接收绕组1的耦合系数;k13为发射绕组与接收绕组2的耦合系数。为方便电路的工作状态分析,在设计一次绕组作为发射端,二次绕组作为接收端时,将绕组一次侧与二次侧上下位置相同,无错位现象。使得发射绕组与接收绕组的耦合系数k相等,又因Lss=Lsv,可得出
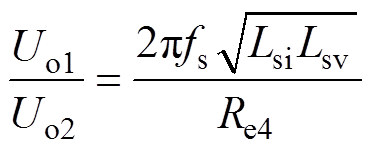 (19)
(19)
式中,fs为电路的谐振频率,因开关频率固定,且二次侧的两个接收绕组已固定,因而Uo1与Uo2的比值只与负载有关,当Uo1与Uo2的比值为1时,存在临界电阻点Rt,有
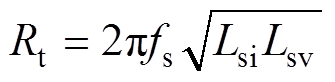 (20)
(20)当Re4>Rt时,则有Uo1<Uo2;当Re4<Rt时,则有Uo1>Uo2。
分析上述两种工作模式如图8所示,当Uo1<Uo2时,系统输出依赖Uo2,串联补偿电路被阻塞,其输出开路,Re3电阻趋向于无穷大,因此,电流isi为零,则反射到一次侧的阻抗近似为零,因而一次侧输入电压基本都分配在LCL补偿支路等效到一次侧的阻抗上,分配在串联补偿支路等效到一次侧阻抗上的电压基本为零,串联补偿支路基本不工作。因此系统工作于LCL补偿支路,Re4电阻取决于负载电阻的大小,如图8a所示,得到与第一部分分析的输入阻抗角为零。输出电压与负载无关的输出特性。
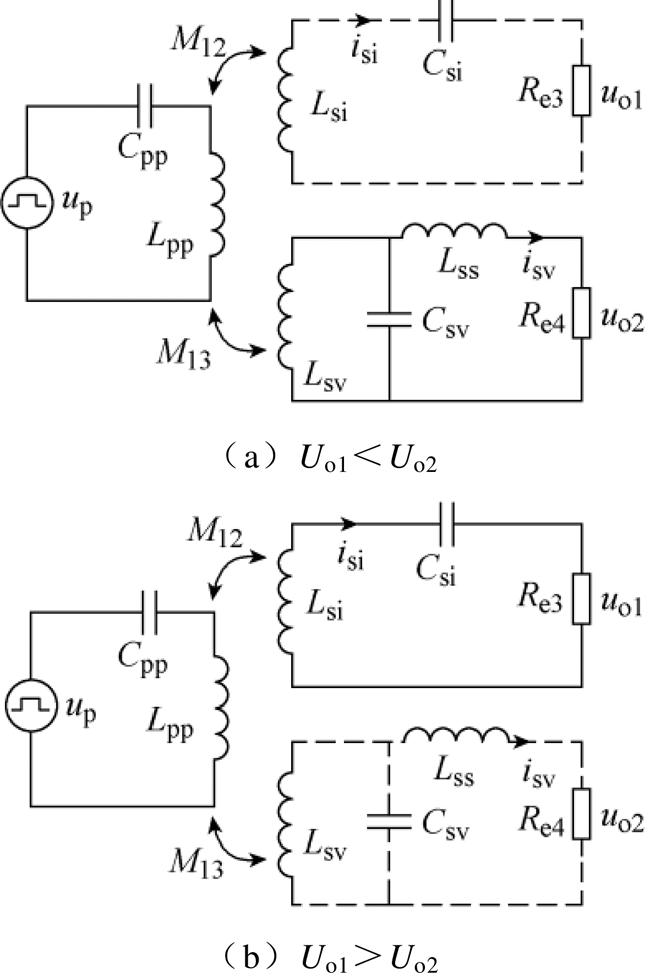
图8 系统工作模式
Fig.8 The operating modes of system
当Uo1>Uo2时,系统输出依赖Uo1,电流isv=0,Re4电阻趋向于无穷大,如图8b所示,PS-SLCL补偿支路退出,系统工作于PS-SS补偿支路,Re3电阻取决于负载电阻的大小,而PS-SLCL补偿支路的二次侧等效阻抗Zs2为
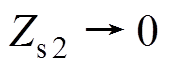 (21)
(21)则反射到一次侧的阻抗Zsr2为
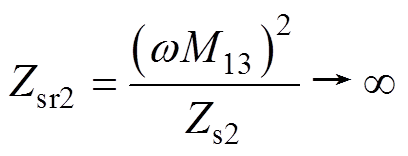 (22)
(22)
由式(21)和式(22)可知,Zsr2导致一次电流ipp下降,输出电压Uo1下降,使得Uo1下降到Uo2时,电流isv不再为零,PS-SLCL补偿支路开始有功率输出,因此在Uo1>Uo2时,PS-SS补偿支路工作到Uo1=Uo2时两个补偿支路同时工作。
因双面单绕组的结构具有高磁通[20]及双解耦绕组结构耦合特性[21],构建接收绕组互解耦的松散耦合变压器,一次侧采用双面单绕组的螺线管型线圈结构,二次侧采用两个单面双解耦绕组结构,接收从一次侧传输的磁场能量。若二次侧两个单面绕组存在耦合,则相互之间传递能量,存在高频环流特性,为此需要将二次侧的两个绕组之间进行解耦设计。设计时,在保证总尺寸600mm×600mm不变的情况下,调整两个二次侧的线圈宽度,通过MAXWELL仿真,得到此时的互感值。若互感值较大,调整线圈宽度,再进行仿真,直到仿真的互感值接近为0,此时二次侧线圈互相解耦,因此可视为互相独立。在偏移情况下,互感值会略有上升,在水平方向上偏移时,二次侧线圈之间的互感值上升较慢,当偏移小于200mm时,基本可以保证解耦效果,而在垂直方向上偏移时,互感变化较大,因此只能在较小的偏移范围内保持解耦。
图9为松散耦合变压器一次侧螺线管型结构和二次侧双解耦结构,绕组采用400mm×0.1mm尺寸的利兹线,一次侧双面单绕组有6条480mm×40mm× 10mm的磁心均匀放置,利兹线以螺线管型的绕法绕制于磁心上,并放置于600mm×600mm的铝背板上,防止其他磁场干扰和泄漏,磁心与铝板之间用环氧树脂板起到支撑与绝缘的作用。二次侧双解耦绕组结构最下层放置大小与一次侧相同的铝背板,上面放置与一次侧一样大小和结构的磁心,将两个解耦的线圈以430mm×600mm的环形形状绕制,并用环氧树脂板将其固定,两解耦线圈交叠部分为260mm,用于二次侧串联补偿的线圈采用紧密型环形绕制,而LCL型补偿网络的线圈采用疏散型环形绕制,两个线圈的环形大小相同。因此该变压器二次侧拓扑结构的两个接收绕组被相互解耦,故在分析拓扑的工作模式时,可以将其视为两个独立的绕组,松散耦合变压器一次侧与二次侧的间距为20cm。
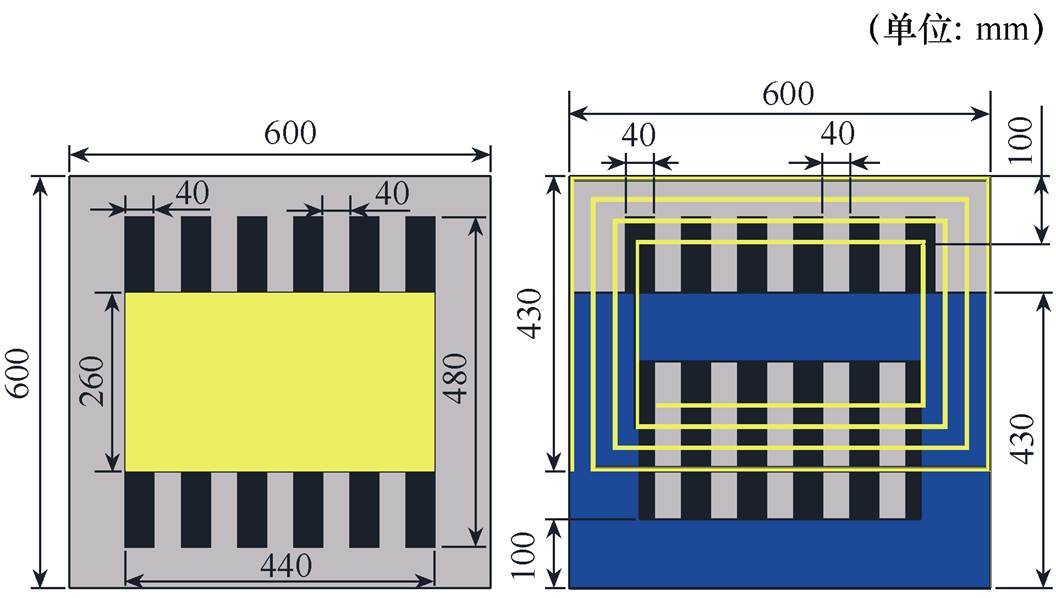
图9 耦合变压器的结构
Fig.9 Structure diagram of the coupling transformer
根据第1.3节的分析,系统的运行状态随着负荷的大小而发生改变,因此临界电阻点Rt是决定系统运行状态的首要因素,Rt是整流桥前的负载等效电阻,故可得出负载转折电阻Rl为
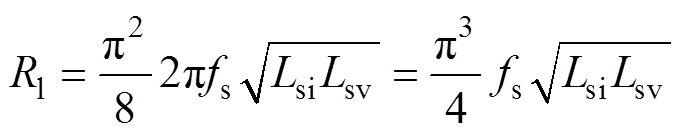 (23)
(23)当负载电阻R>Rl时,系统工作于PS-SLCL补偿支路,其输出直流电压Uo为
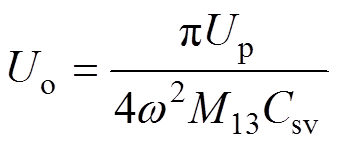 (24)
(24)
负载电阻R<Rl时,PS-SS补偿支路和PS-SLCL补偿支路同时给系统供电,在此条件下,总满足
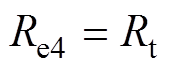 (25)
(25)当两个补偿支路各自整流后,并联输出,可以得出电阻Re为
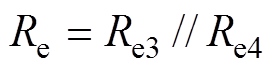 (26)
(26)
由式(26)可得
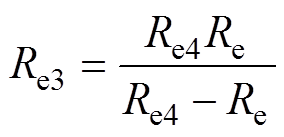 (27)
(27)根据式(7)和式(13)可得出输入阻抗Zin为
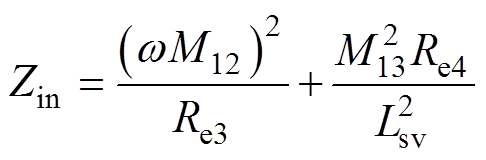 (28)
(28)
理想情况下,根据能量守恒定律,输入功率与输出功率相等,即可得出
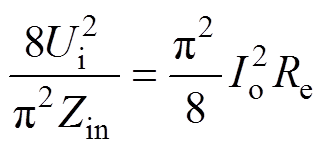 (29)
(29)式中,Ui为系统的直流电源;Io 为直流输出电流,可得Io为
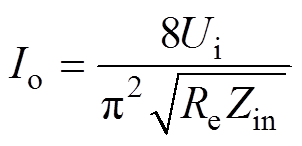 (30)
(30)
选择谐振电路参数见表1,可以根据式(23)、式(24)和式(30)计算出负载转折电阻、输出电压和输出电流。
表1 谐振电路参数
Tab.1 Resonant circuit parameters
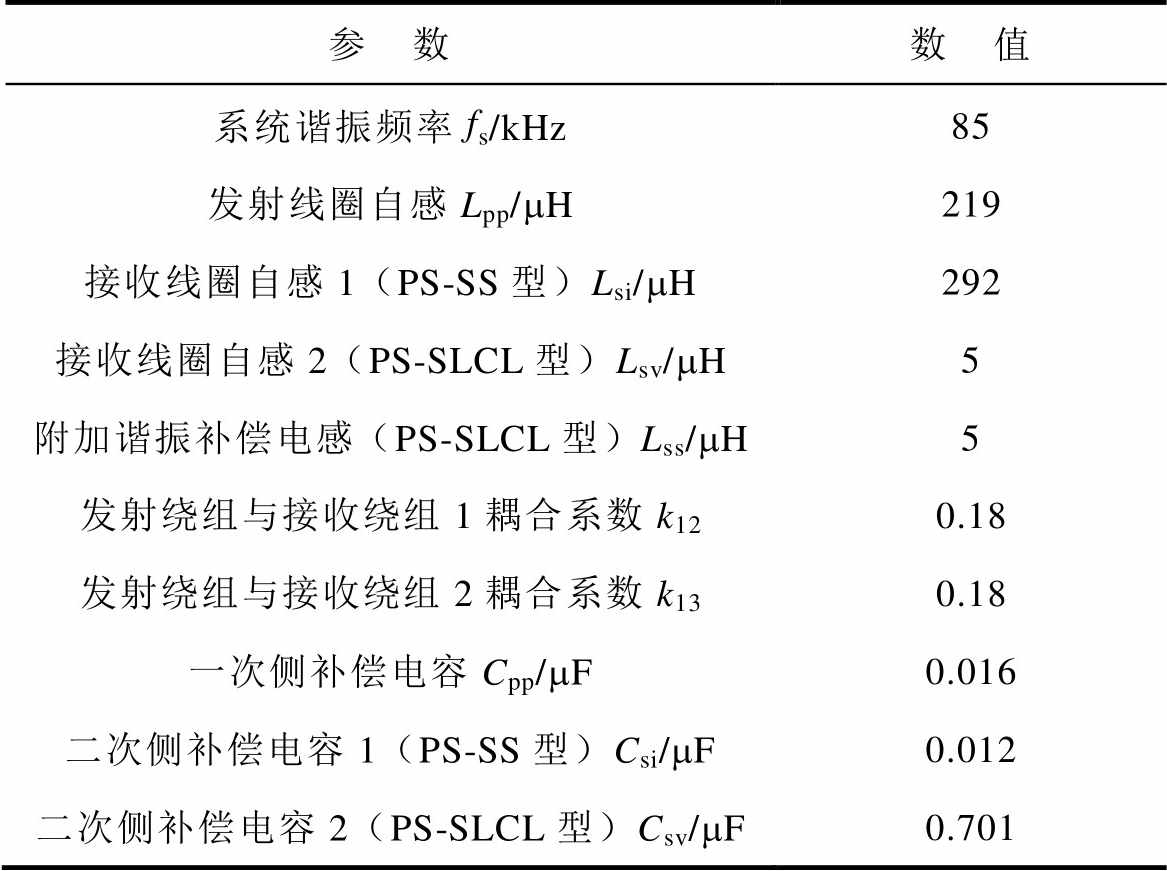
参 数数 值 系统谐振频率fs/kHz85 发射线圈自感Lpp/mH219 接收线圈自感1(PS-SS型)Lsi/mH292 接收线圈自感2(PS-SLCL型)Lsv/mH5 附加谐振补偿电感(PS-SLCL型)Lss/mH5 发射绕组与接收绕组1耦合系数k120.18 发射绕组与接收绕组2耦合系数k130.18 一次侧补偿电容Cpp/mF0.016 二次侧补偿电容1(PS-SS型)Csi/mF0.012 二次侧补偿电容2(PS-SLCL型)Csv/mF0.701
利用Matlab中的Simulink组件,研究系统在不同负载等效电阻R及耦合系数k时,两种拓扑结构的电流增益Av、电压增益Gv、输入阻抗Zin及电压电流波形以及本文所提拓扑结构工作时,恒流恒压自切换输出波形和恒流或恒压输出波形。仿真电路参数见表1,波形如图10~图12所示,图10为PS-SS补偿拓扑电路在不同负载等效电阻R及耦合系数k下系统的输出电流增益Av和输入阻抗Zin的变化。图11为PS-SLCL补偿拓扑电路在不同负载等效电阻R及耦合系数k下系统的电压增益Gv和输入阻抗Zin的变化。在耦合系数k相同,图10中负载变化时输出电流增益Av基本不变,图11中则是电压增益Gv在不同负载等效电阻R下保持恒定,而在不同耦合系数k下,图10中电流增益Av和图11中电压增益Gv与耦合系数k均成反比,在同一耦合系数k下,图10中输入阻抗Zin与负载等效电阻R大小成反比例函数,而图11中输入阻抗Zin与负载等效电阻R大小成正比例函数。
图12所示为本文所提拓扑结构在恒流-恒压模式下的输出特性,同时在图中也列出了该结构在恒流工作状态下对应的二次侧串联补偿支路的输出电流波形以及在恒压工作状态下对应的二次侧LCL补偿支路的输出电压波形。其中,电流输出特性对应的是左纵轴,电压输出特性对应的是右纵轴。对于双路并联的输出电流与电压曲线,即为系统对于锂电池的充电电流与充电电压特性,其可以与图1中的锂电池充电特性相对应。从图12中可知,二次侧串联补偿支路的输出电流基本不随负载变化,二次侧LCL补偿支路的输出电压与负载基本无关,具有近似恒流与恒压输出的特点,这非常有利于系统在闭环下的控制策略优化。该拓扑结构负载转折电阻Rl=26W,当负载等效电阻R小于转折电阻Rl时,电路处于恒流工作状态,相应的充电电压逐渐上升;当R大于转折电阻Rl时,电路处于恒压状态,相应的充电电流逐渐下降,电路能自然地实现恒流模式到恒压模式的切换。从图12仿真结果可知,在恒流和恒压阶段,输出的电流和电压略有变化,其主要原因有:①电路一次侧逆变器开关管因需要实现软开关特性,电路的输入阻抗为弱感性,则输入阻抗不为零,导致系统在恒流或恒压模式工作时,输出电压和电流会发生一定变化;②在电路工作过程中,二次侧LCL支路在某些情况下会处于断续状态,因此输出电压会随负载电阻的变化略有增大。
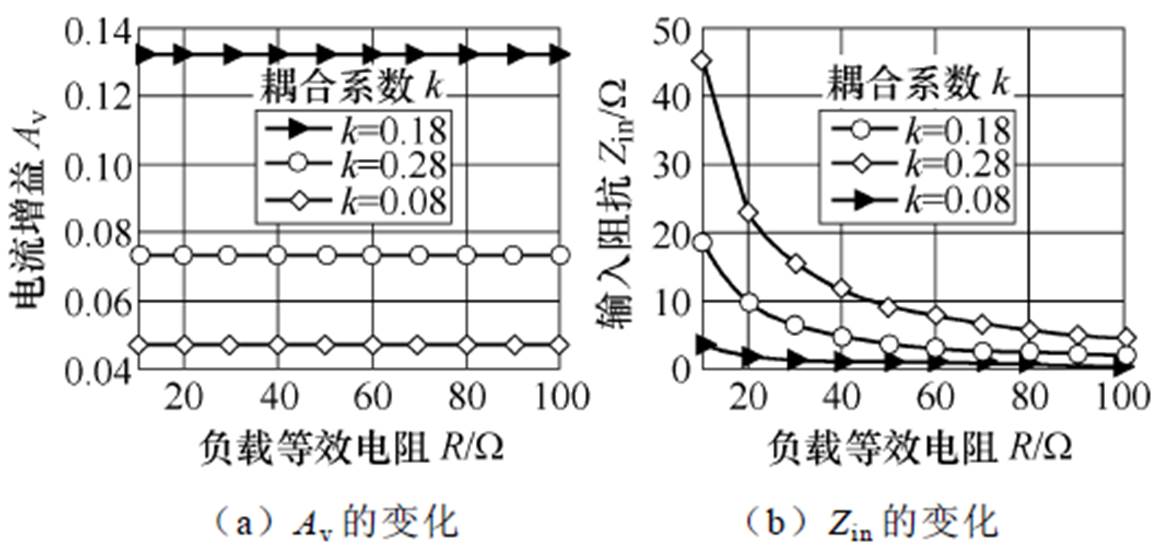
图10 PS-SS补偿电路在不同负载等效电阻R及耦合系数k下系统的输出电流增益Av和输入阻抗Zin的变化
Fig.10 Variation of the output current gain Av and input impedance Zin of the PS-SS compensation circuit under different loads R and coupling coefficient k
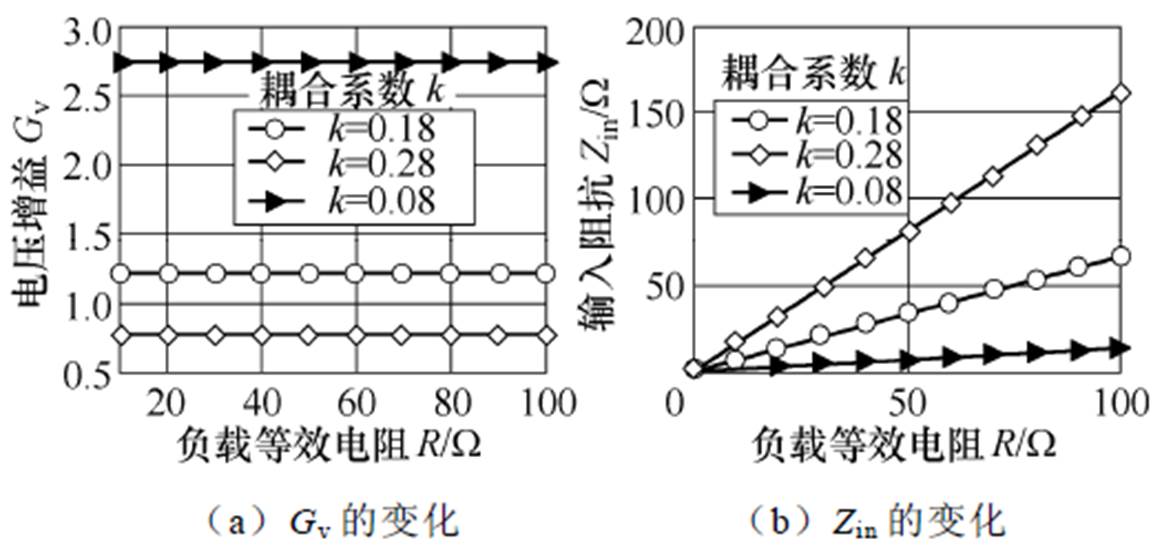
图11 PS-SLCL补偿拓扑电路在不同负载等效电阻R及耦合系数k下系统的输出电压增益Gv和输入阻抗Zin的变化
Fig.11 Variation of the output voltage gain Gv and input impedance Zin of the PS-SLCL compensation circuit under different loads R and coupling coefficient k
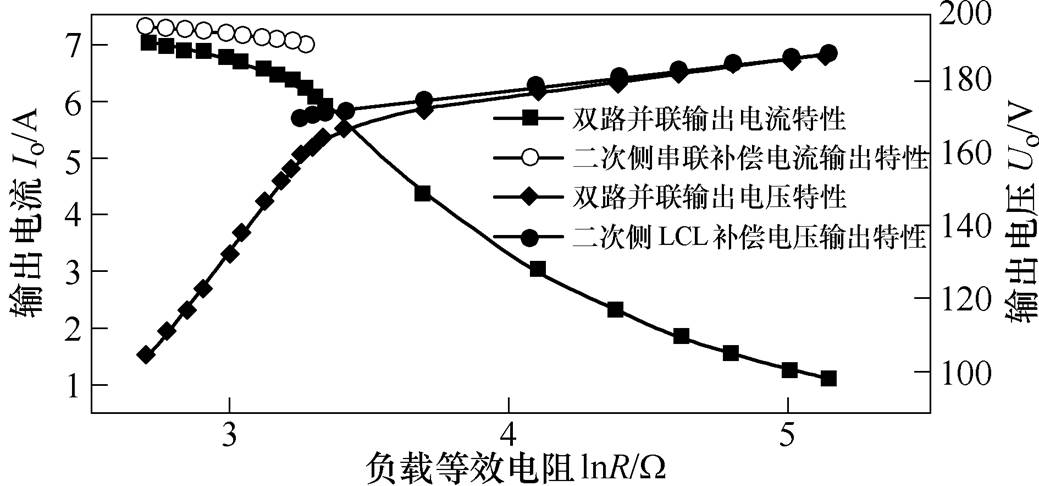
图12 系统输出特性及各支路输出特性
Fig.12 Output characteristics of system and each branch
为验证上述分析的正确性,搭建了一套功率为1kW的实验样机如图13a所示,谐振电路参数见表1,整个主电路由直流电源、高频逆变器、一次侧串联补偿电路、松散耦合变压器、二次侧串联谐振网络及整流电路、二次侧LCL型谐振网络及整流电路和负载组成。松散耦合变压器结构如图13b所示,发射线圈作为一次绕组为螺线管型结构,接收线圈作为二次绕组为双解耦结构。

图13 实验样机和变压器结构
Fig.13 Experimental prototype and structure of transformers
恒流恒压工作模式自切换过程实验结果如图14所示。从图中可见,输出电流恒定切换到输出电压恒定的负载转折电阻Rl=27W 时,当负载等效电阻R<Rl时,系统工作于恒流模式;当负载等效电阻R>Rl时,系统工作于恒压模式。因此,系统的运行模式随负载变化而自动进行切换。在此基础上,若系统通过调节工作频率,来实现闭环控制,可以实现更精确的恒流或恒压输出特性。通过对图12和图14系统在仿真和实验条件下的输出特性对比,可知仿真和实验结果相吻合。
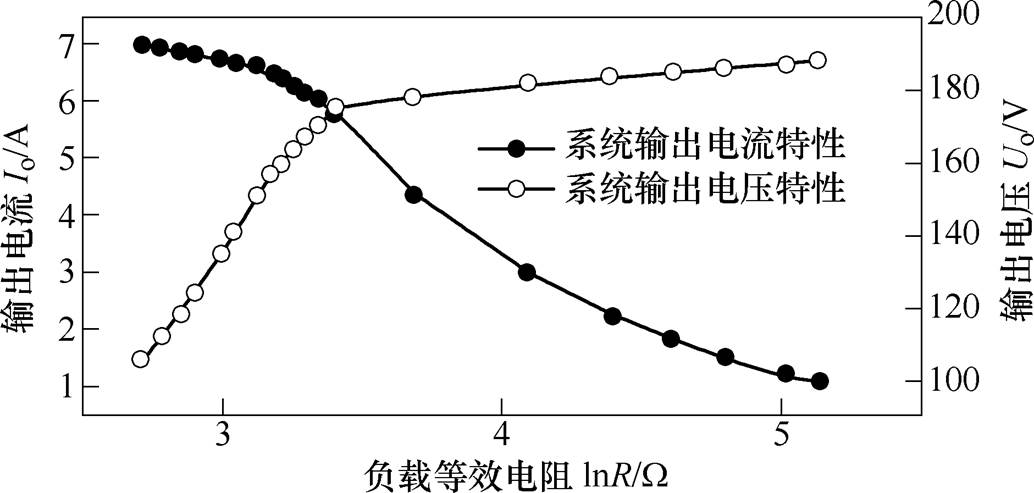
图14 开环状态下系统的输出特性
Fig.14 Output characteristics of the system in open loop state
图15和图16分别为两种充电模式下二次电流isi和isv的分布波形,图15为系统工作于恒流模式时,两路补偿支路都参与工作,以C1为参考地的实线波形为PS-SS输出电流isi的电流分布,以C2为参考地的虚线波形为PS-SLCL输出电流isv的分布波形,图16中可见串联补偿支路无电流,系统在恒压模式下工作于LCL补偿支路,经分析系统的输出模式与对应的运行状态与1.3节分析的一致。
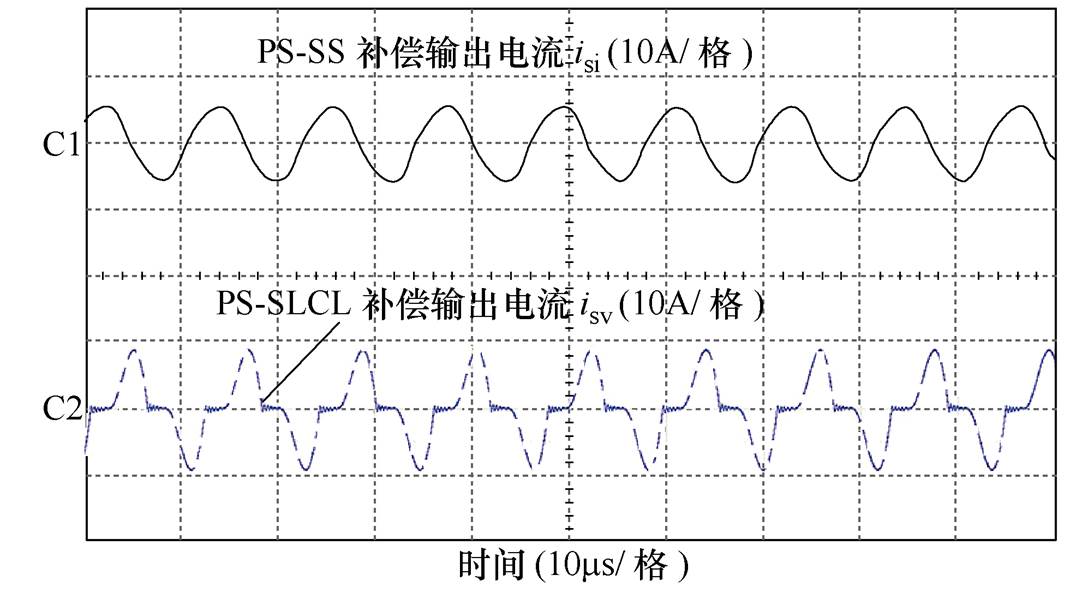
图15 在恒流模式下,负载为15W 时的两路电流波形
Fig.15 Two current waveforms with 15W load in CC mode
图17和图18分别为锂电池等效内阻在15W 和40W 下的高频逆变器一次电压输出的方波波形up和一次电流输出的正弦波波形ipp,以及系统的直流输出电流Io和直流输出电压Uo。由图中可见,在系统运行时,逆变器输出的电压相位总时略超前于电流,系统处于弱感性输入阻抗,因而系统在软开关状态下工作。
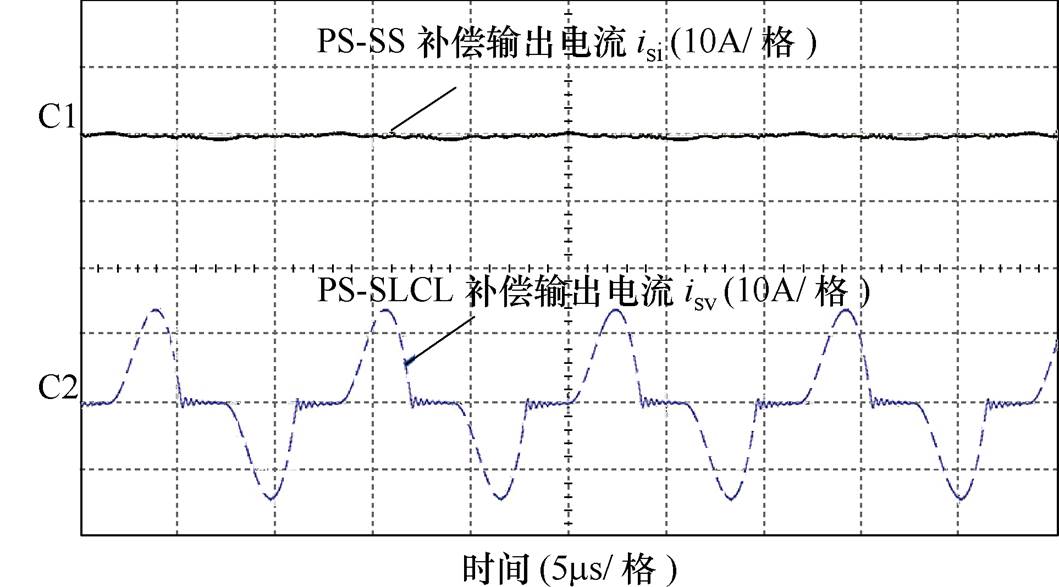
图16 在恒压模式下,负载为40W 时的两路电流波形
Fig.16 Two current waveforms with 40W load in CV mode
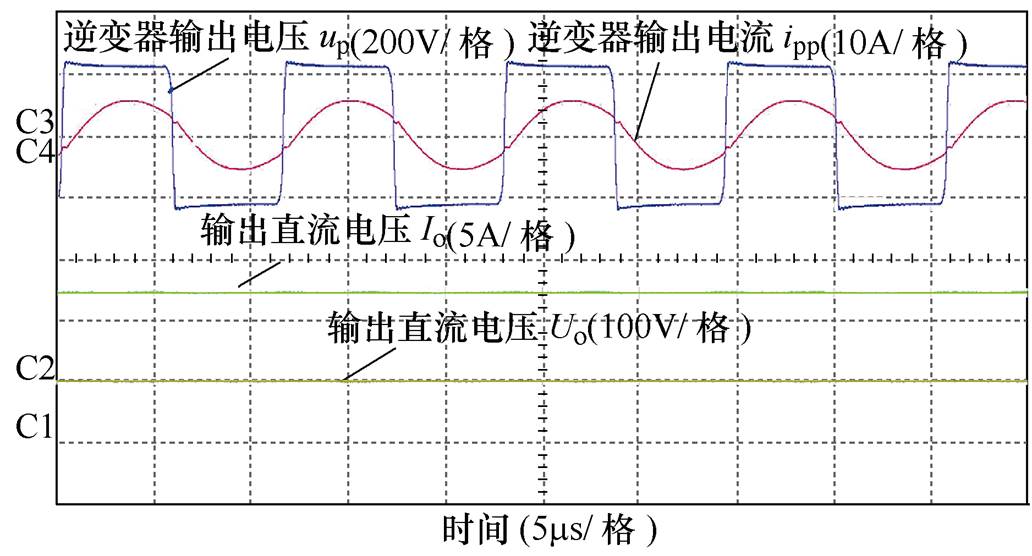
图17 负载为15W 时,逆变器输出的电流(ipp)电压(up)波形和系统输出的电流(Io)电压(Uo)波形
Fig.17 When the load is 15W,the current and voltage waveforms of the inverter output and the current and voltage waveforms of the system output
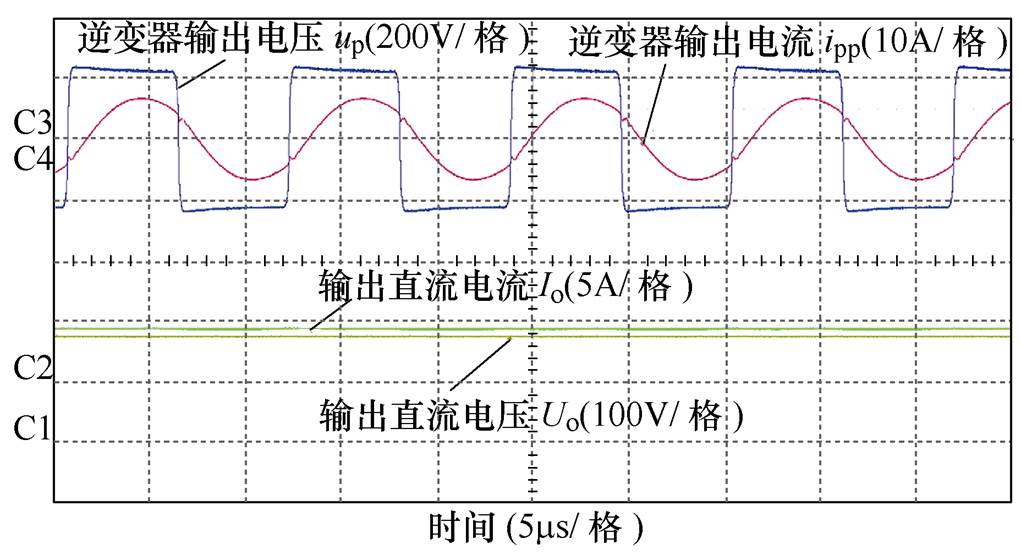
图18 负载为40W 时,逆变器输出的电流(ipp)电压(up)波形和系统输出的电流(Io)电压(Uo)波形
Fig.18 When the load is 40W, the current and voltage waveforms of the inverter output and the current and voltage waveforms of the system output
本文针对电动汽车充电电池的充电特性,提出了一种适用于电动汽车无线充电的电能传输系统,通过对该拓扑结构的工作模式和电路特性进行分析,设计了相关电路参数和松散耦合变压器的参数,使得该系统在负载条件变化的情况下,输出信号在恒流和恒压两种模式间自然切换,其符合电动汽车车载电池的充电特性。借助仿真对电路进行了分析,通过实验样机对系统进行了验证。
参考文献
[1] 赵争鸣, 刘方, 陈凯楠. 电动汽车无线充电技术研究综述[J]. 电工技术学报, 2016, 31(20): 30-40.
Zhao Zhengming, Liu Fang, Chen Kainan. New progress of wireless charging technology for electric vehicles[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 30-40.
[2] Mi C C, Buja G, Choi S Y, et al. Modern advances in wireless power transfer systems for roadway powered electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6533-6545.
[3] Fernandez C, Avrcia O, Prieto R, et al. Overview of different alternatives for the contactless transmission of energy[C]//Proceedings of IEEE Industrial Electronics Society Conference (IECON), Spain, 2002: 1318-1323.
[4] 王宏健, 于乐, 陈江, 等. 无人水下航行器无线能量传输系统补偿网络研究[J]. 电工技术学报, 2015, 30(19): 39-46.
Wang Hongjian, Yu Le, Chen Jiang, et al. Study on compensation network for wireless power trans- mission system of unmanned underwater vehicle[J]. Transactions of China Electrotechnical Society, 2015, 30(19): 39-46.
[5] 徐桂芝, 李晨曦, 赵军, 等. 电动汽车无线充电电磁环境安全性研究[J]. 电工技术学报, 2017, 32(22): 152-157.
Xu Guizhi, Li Chenxi, Zhao Jun, et al. Electro- magnetic environment safety study of wireless electric vehicle charging[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 152-157.
[6] Lu Fei, Zhang Hua, Hofmann H, et al. A dynamic charging system with reduced output power pulsation for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6580-6590.
[7] Potanina E E, Potanina V Y. Li-ion battery charger with three-parameter regulation loop[C]//Proceedings of IEEE 36th Conference on Power Electronics Specialists, Germany, 2005: 836-2840.
[8] 张昊. 基于IC曲线特征参数的锂离子电池SOH估计及DSP实现[D]. 北京: 北京交通大学, 2018.
[9] Li Zhenjie, Zhu Chunbo, Jiang Jinhai, et al. A 3kW wireless power transfer system for sightseeing car supercapacitor charge[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3301-3316.
[10] Kim M, Joo D, Lee B K. Design and control of inductive power transfer system for electric vehicles considering wide variation of output voltage and coupling coefficient[C]//Proceedings of IEEE Applied Power Electronics Conference and Exposition (APEC), USA, 2017: 3648-3653.
[11] Yuan Xiaofang, Zhang Yunling, Wang Yan, et al. Output voltage control of inductive power transfer system based on extremum seeking control[J]. IET Power Electronics, 2015, 8(11): 2290-2298.
[12] Wang C S, Stielau O H, Covic G A. Design considerations for a contactless electric vehicle battery charger[J]. IEEE Transactions on Industrial Electronics, 2005, 52(5): 1308-1314.
[13] Budhia M, Covic G A, Boys J T. Design and optimization of circular magnetic structures for lumped inductive power electronics[J]. IEEE Transa- ctions on Power Electronics, 2011, 26(11): 3096- 3018.
[14] Berger A, Agostinelli M, Vesti S, et al. A wireless charging systems applying phase-shift and amplitude control to maximize efficiency and extractable power[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6338-6348.
[15] Qu Xiaohui, Han Hongdou, Wong S C, et al. Hybrid IPT topologies with constant current or constant voltage output for battery charging applications[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6329-6337.
[16] 陈威, 吕征宇. 第四类LLC谐振变流器模块功能准同构拓扑探求及变形研究[J]. 中国电机工程学报, 2009, 29(9): 35-42.
Chen Wei, Lü Zhengyu. Investigation on set of quasi-isomorphic topologies and structural variations of type-4 LLC resonant DC-DC converter based on module function identification[J]. Proceedings of the CSEE, 2009, 29(9): 35-42.
[17] 王萍, 陈博, 王议锋, 等. 一种多谐振隔离双向DC-DC变换器[J]. 电工技术学报, 2019, 34(8): 1667-1676.
Wang Ping, Chen Bo, Wang Yifeng, et al. An isolated three-port bidirectional LCLC multi-resonant DC-DC converter[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1667-1676.
[18] 刘闯, 郭赢, 葛树坤, 等. 基于LCL谐振补偿的电动汽车无线主电系统特性分析与实验验证[J]. 电工技术学报, 2015, 30(15): 127-135.
Liu Chuang, Guo Ying, Ge Shukun, et al. Characteri- stics analysis and experimental verification of the double LCL resonant compensation network for electric vehicles wireless power transfer[J]. Transa- ctions of China Electrotechnical Society, 2015, 30(15): 127-135.
[19] 陈凯楠, 赵争鸣, 刘方, 等. 电动汽车双向无线充电系统谐振拓扑分析[J]. 电力系统自动化, 2017, 41(2): 66-72.
Chen Kainan, Zhao Zhengming, Liu Fang, et al. Resonant topology analysis of bi-directional wireless charging system for electric vehicles[J]. Transactions of Power System Automation, 2017, 41(2): 66-72.
[20] Budhia M, Covic G, Boys J. A new IPT magnetic coupler for electric vehicle charging systems[C]// Proceedings of IEEE Industrial Electronics Society Conference (IECON), USA, 2010: 2487-2492.
[21] Zaheer A, Covic G A, Kacprzak D. A bipolar pad in a 10kHz 300W distributed IPT system for AGV appli- cations[J]. IEEE Transactions on Industrial Electro- nics, 2014, 61(7): 3288-3301.
A Wireless Power Transfer System Topology with Automatic Switching Characteristics of Constant Current and Constant Voltage Output for Electric Vehicle Charging
Abstract Wireless power transfer system has the advantages of safety, reliability and convenience for electric vehicle charging. According to charging characteristics of lithium batteries used in electric vehicles and previous research on the loosely coupled transformer and compensation topologies, a wireless power transfer system design consisting of PS-SS and PS-SLCL compensation topologies is proposed in this paper. The charging mode of the system automatically changes from the CC mode to the CV mode with the change of the load impedance. Soft switching characteristics of the primary inverter can be obtained in the whole charging process. Topology parameters and transformer model dimensions are designed in terms of theoretical analysis on the system characteristics. Simulation results verify the constant current and constant voltage outputs of the system, and a 1kW experimental platform is built to verify the effectiveness of the proposed design.
keywords:Electric vehicle, wireless power transfer, constant current and constant voltage output, automatic switching
中图分类号:TM910.6; U469.72
DOI: 10.19595/j.cnki.1000-6753.tces.191051
浙江省基础公益研究计划(LGG18E070003)、国家自然科学基金(51577171)和浙江省教育厅(Y201534452)项目资助。
收稿日期2019-08-16
改稿日期 2019-11-13
吴丽君 女,1976年生,硕士,副教授,研究方向为电动汽车无线电能传输及应用。E-mail: 492522964@qq.com(通信作者)
李冠西 男,1994年生,博士研究生,研究方向为电动汽车无线电能传输。E-mail: maestrolgx@163.com
(编辑 崔文静)