0 引言
气体绝缘输电管道(Gas Insulated Transmission Line, GIL)具有传输容量大、占地面积小、可靠性高和环境友好等特点,在电力系统中得到了广泛应用[1-3]。随着电压等级的提升,气体绝缘输电管道及绝缘子的尺寸不断增大,但这种通过增加尺寸来提升系统绝缘性能的方法存在“饱和效应”。虽然在设计时留有一定的绝缘裕度,但国内气体绝缘设备在运行过程中依旧事故频发,严重危害电力系统的安全稳定运行[4-5]。
一般认为,电场不均匀分布是绝缘子沿面放电甚至击穿的重要原因。为了缓解局部电场集中现象,目前应用于气体绝缘输电管道的措施包括优化绝缘子几何结构、安装屏蔽电极和内嵌电极等[6]。这些措施效果有限,同时造成绝缘结构复杂,设备制造和维护成本增加。近些年,国内外学者围绕“功能梯度材料(Functional Gradient Materials, FGM)”的概念展开了大量的研究工作。在电气绝缘领域,功能梯度材料是指材料的介电特性(介电常数、电导率等)在内部空间位置上呈现梯度变化,从而提高材料整体电气绝缘性能。功能梯度材料的出现为绝缘子电场优化提供了新途径,通过调控材料的介电参数分布,就可以达到均匀电场分布的目的[7-13]。在交流输电管道中,盆式绝缘子的沿面电场分布主要取决于介电常数分布。通过设计绝缘子介电常数的梯度分布,可以有效提高绝缘子沿面闪络电压[7-8]。文献[14]采用逐点迭代优化的策略对盆式绝缘子内部每个有限元网格的介电常数进行调整,直至介电常数分布达到最优,文献中定义最优介电常数分布为“可以最大效率地缓解绝缘子表面和周围电场集中的分布”。文献[15]对上述方法进行了继承与发展,采用逐层迭代的策略对绝缘子沿面电场分布进行优化,同时对比了缩减系数、叠层数和介电常数约束范围对优化效果的影响。文献[16]引入拓扑优化的概念,对圆台绝缘子的空间介电常数分布进行优化,优化策略较为复杂,建模难度大。文献[17]将圆台绝缘子分割成若干个三角形区域,采用粒子群算法对各个区域中介电常数的取值进行优化,缺点是网格剖分较细时粒子群规模较大,计算量繁重。文献[18]以∆ɛ 为步长,每次仅对盆式绝缘子最大电场强度所在层的介电常数进行调整,导致迭代次数过多(40~400 次),收敛速度较慢。本文提出一种同样基于迭代算法的功能梯度绝缘子介电常数分布优化方法,优点是策略简单,经过较少的迭代次数(小于10 次)就可以获得最优解。
1 介电常数分布优化
1.1 功能梯度绝缘子模型
为了方便与已有文献的研究结果进行对比,本文以两种典型的绝缘子模型(圆台和盆式)进行介电常数分布优化的计算。圆台绝缘子高度为10 mm,电压为交流10 kV。盆式绝缘子外径为100 mm,高压导体内径为40 mm,电压为交流100 kV。两种功能梯度绝缘子的介电常数分别在高度和半径方向上呈现连续梯度变化,如图1 所示。

图1 介电功能梯度绝缘子仿真模型
Fig.1 Simulation model of ε-FGM insulator
利用有限元方法对绝缘子的电场分布进行计算。在仿真计算中,将SF6 气体的相对介电常数设置为1。绝缘子为环氧树脂的复合绝缘材料,考虑实际的填充效果,约束相对介电常数最小值 εmin 为3,最大值 εmax 为60。
气固绝缘系统的绝缘薄弱环节在气固界面,绝缘子内部电场畸变相对于环氧树脂的绝缘强度非常微小,因此本文只关注绝缘子的沿面电场畸变。图2 为两种匀质绝缘子的切向沿面电场分布。圆台绝缘子的沿面电场强度从高压电极向地电极递减,只有一个路径(Path)上的电场分布需要优化。盆式绝缘子则需要兼顾凹凸两个表面(Path 1 和Path 2)的电场分布,其沿面电场强度在Path 1 上递减,在Path 2 上则相对均匀。
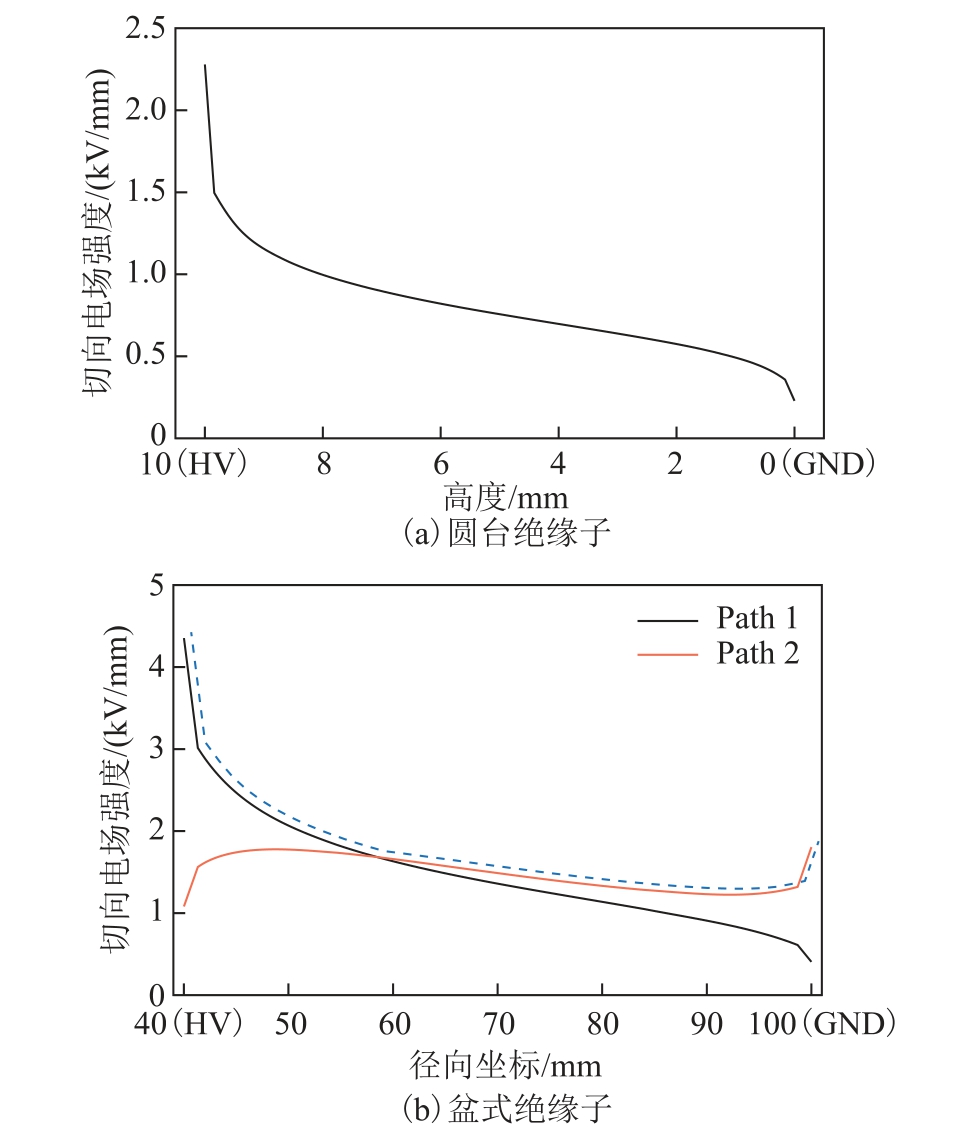
图2 匀质绝缘子沿面电场分布
Fig.2 Surface E-field distribution of homogeneous insulator
1.2 迭代优化算法
本文提出一种同样基于迭代算法的功能梯度绝缘子介电常数分布优化方法,特点是策略简单、收敛速度快。算法流程如图3 所示,初始条件下的匀质绝缘子的相对介电常数设置为3,整个优化过程中约束相对介电常数在3~60 之间。每个迭代过程需要进行如下操作:
(1)利用有限元方法,以当前的介电常数分布εi 为输入参数计算绝缘子沿面电场分布Ei。
(2)判断终止条件是否满足(本文设置终止条件为迭代5 次),如果满足该条件,则迭代终止;否则,继续迭代。根据高斯定律可知,最优的介电常数分布和电场分布具有相似性[14],因此可以依据式(1)或式(2)修改介电常数分布。盆式绝缘子需要兼顾凹凸两个表面(Path 1 和Path 2)的电场分布,因此用于调整介电常数的参照电场强度取两个表面电场强度的最大值,如图2 中虚线所示。
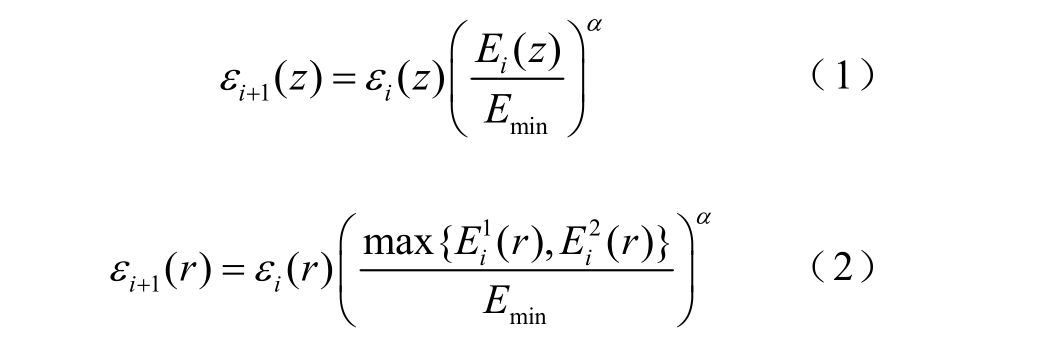
其中,式(1)适用于圆台绝缘子,其介电常数沿着z 方向(高度方向)梯度分布;式(2)适用于盆式绝缘子,其介电常数沿着r 方向(半径方向)梯度分布。εi 为当前迭代使用的介电常数分布;εi+1为下一次迭代使用的介电常数分布;Ei 为圆台绝缘子沿面电场强度; Ei1 和 Ei 2分别为盆式绝缘子上、下表面的沿面电场强度;Emin 为参考电场强度分布的最小值;系数α 用于调整收敛速率,数值越大代表每次迭代对介电常数分布的调整幅度越大,收敛速度越快,但数值过大可能引起超调。为了保证较快的收敛速度,同时避免超调,本文将系数α 设置为1[14-15]。
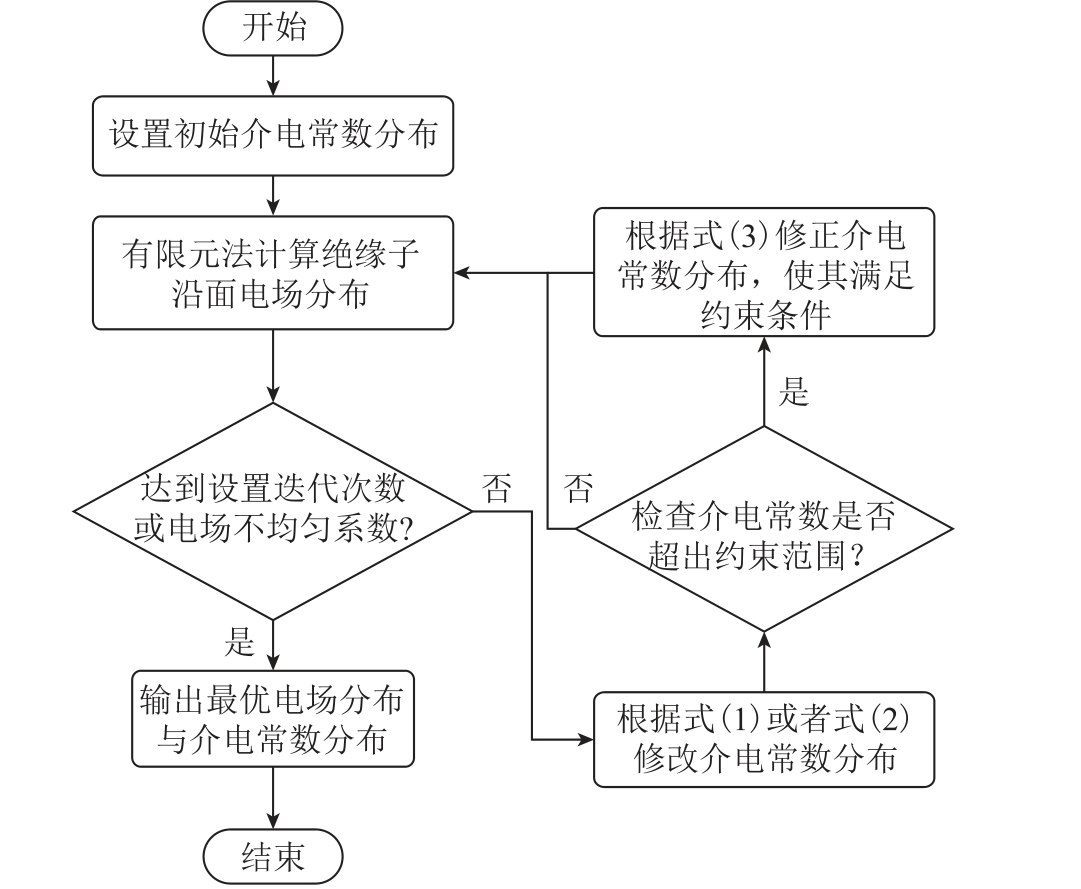
图3 介电常数分布优化流程
Fig.3 Flow chart of optimizing permittivity distribution
(3)判断当前介电常数分布是否在约束范围内。若超出约束范围,利用式(3)对其进行线性缩放,并重新计算绝缘子电场分布。线性缩放与其他的非线性缩放策略相比,可以尽可能地减小缩放前后电场分布的差异。

式中,ε 和ε′分别为缩放前和缩放后介电常数分布;εmax 和εmin 分别为缩放前介电常数分布的最大值与最小值;60 和3 分别为介电常数约束范围的上、下限。
2 结果及分析
2.1 圆台绝缘子
图4 为优化过程中圆台绝缘子的介电常数与沿面电场分布随迭代次数的变化。可以看出,经过4 次迭代,绝缘子的介电常数与沿面电场分布已经收敛至最优解。最优的绝缘子介电常数分布与沿面电场分布具有相似性,均呈现出由高压电极向地电极递减的趋势。绝缘子的介电常数最大值达到了约束范围的上限(εmax=60),最小值不随迭代次数变化。圆台绝缘子的沿面电场强度最大值由2.3kV/mm 降至1.1kV/mm,电场不均匀系数由2.3 降至1.1,降低幅度超过50%。与文献[15]相比,本文优化后的电场分布与之相似,但迭代次数却远远小于文献(大于12次),这证明了本文所提优化方法的有效性与高效性。
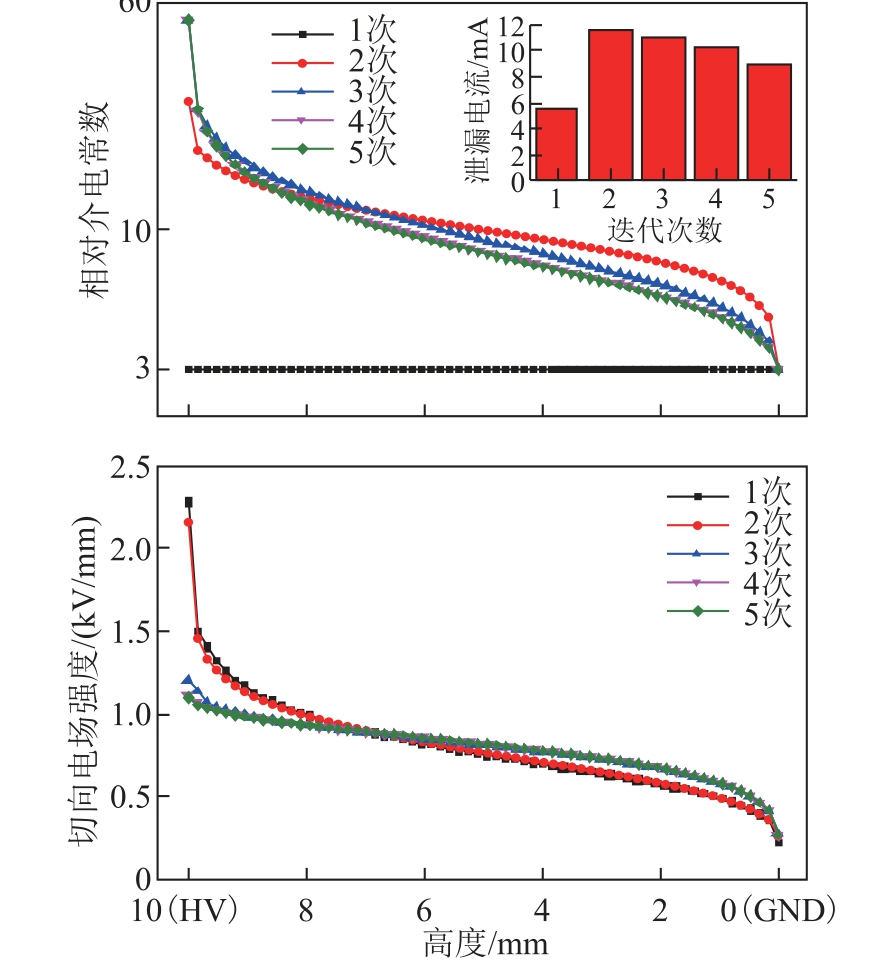
图4 优化过程中圆台绝缘子介电常数与沿面电场分布
Fig.4 Permittivity and surface E-field distributions during optimization process
图5 为匀质圆台绝缘子与介电功能梯度绝缘子的空间电场强度分布。对于匀质绝缘子来说,局部电场集中出现在高压电极、绝缘子与SF6 气体的三结合点区域。由于SF6 气体的绝缘强度远低于环氧树脂绝缘子,该气固绝缘系统的主要故障形式为气体放电导致的沿面闪络,而不是绝缘子体击穿。对于优化后的介电功能梯度绝缘子来说,该气固绝缘系统气体侧的电场集中得到了极大的缓解,电场集中的现象由气体侧转移到固体侧的地电极附近。虽然固体侧承受的电场强度增加了,但是远远小于绝缘子的击穿强度;此时气体侧承受的电场强度降低,气固绝缘系统的整体绝缘性能仍是增强的。
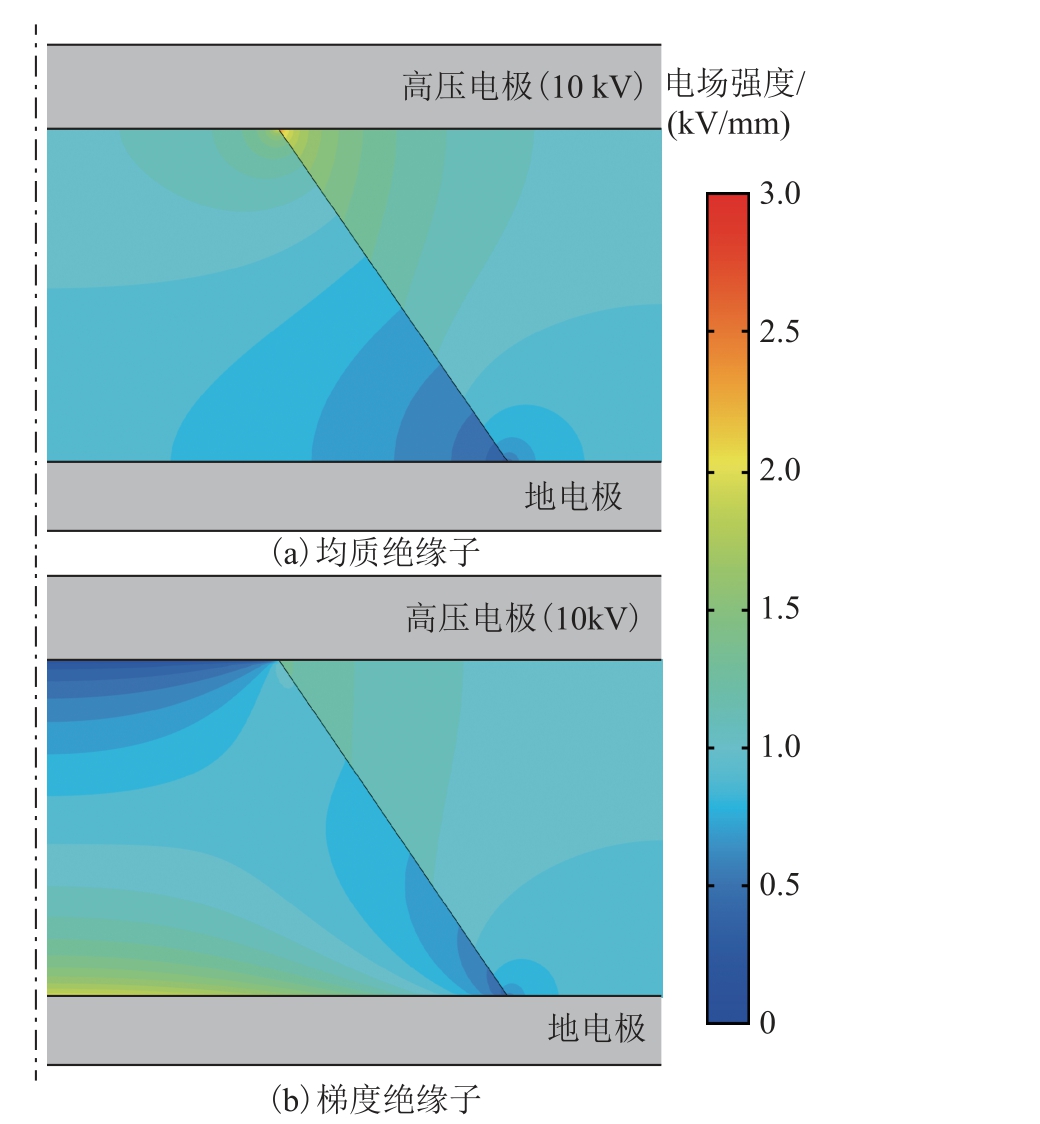
图5 匀质圆台绝缘子与优化后的梯度绝缘子电场强度分布
Fig.5 E-field contour of conventional and optimized cone-type insulator
2.2 盆式绝缘子
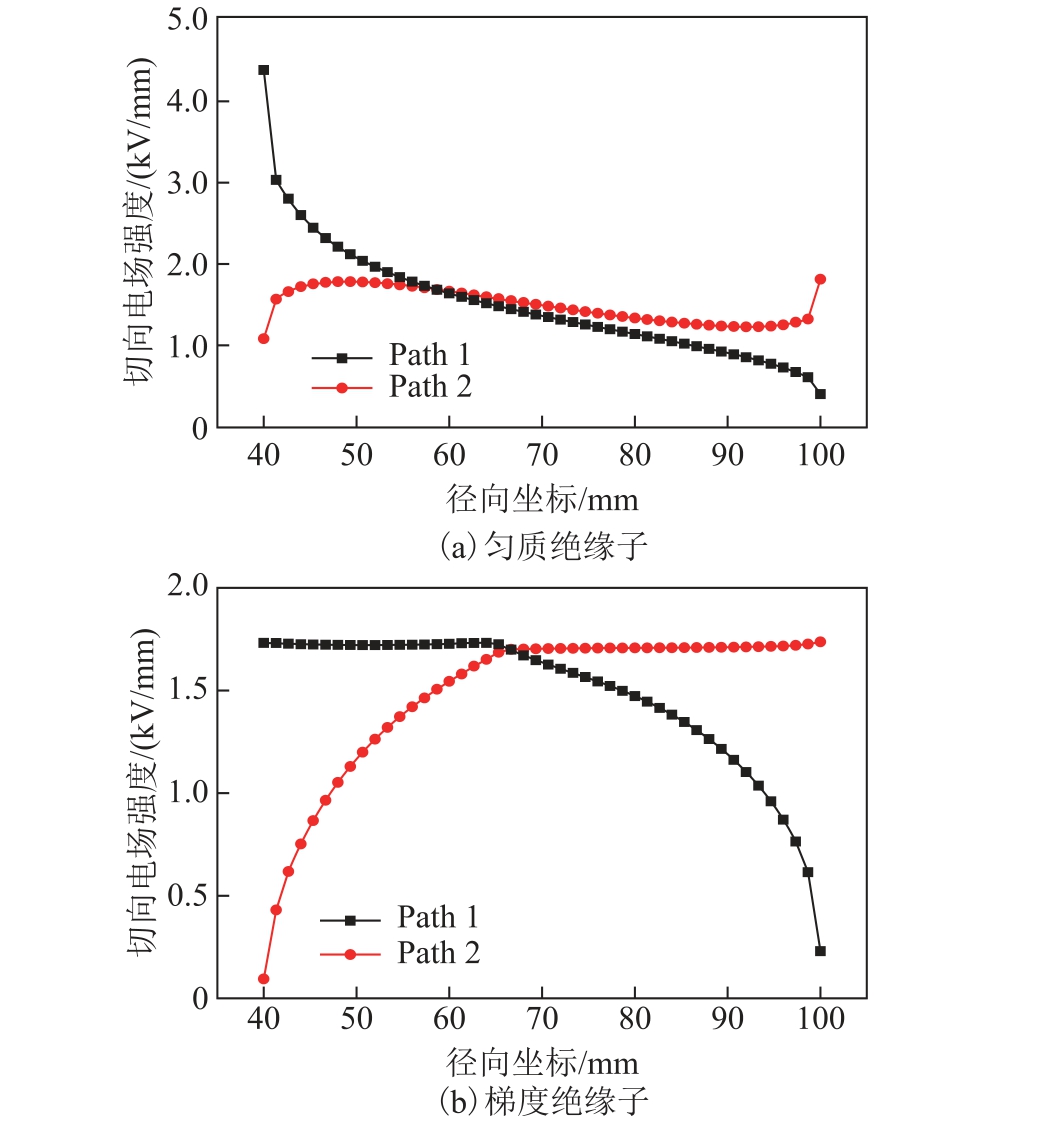
图6 匀质盆式绝缘子与优化梯度绝缘子的沿面电场强度分布
Fig.6 Surface E-field distribution of the conventional and optimized basin-type insulators
图 6 为匀质盆式绝缘子与优化后梯度绝缘子的沿面电场强度分布。对于匀质绝缘子而言,凹面(Path 1)的电场强度分布是极不均匀的,最大电场强度高达4.5 kV/mm。凸面(Path 2)的电场强度最大值出现在外壳(地电极)附近,约为2 kV/mm。经过优化后,梯度绝缘子的两个表面的沿面电场强度最大值均被钳制在1.75 kV/mm 附近,凹面(Path 1)的沿面电场强度最大值下降幅度超过60%。
图7 为盆式绝缘子的相对介电常数分布在优化过程中随迭代次数的变化。经过5 次迭代后,盆式绝缘子的相对介电常数分布已经收敛至最优解。优化后的盆式绝缘子的相对介电常数分布呈现出“中间低,两头高”的趋势。凹面(Path 1)的电场强度最大值出现在导杆附近,导致导杆附近的介电常数增大;凸面(Path 2)的电场强度最大值出现在外壳附近,导致外壳附近的介电常数增大。与文献[14,16-17]相比,本文所用的迭代策略不仅迭代次数少,而且沿面电场分布更加均匀。与文献[15, 18]相比,本文所用的迭代策略除了迭代次数较少外,介电常数分布的上限也较小,本文的最优介电常数分布上限约为27,文献中约为50~80。绝缘子的介电常数越大,意味着运行过程中的泄漏电流越大,这对电力设备的正常运行是不利的。
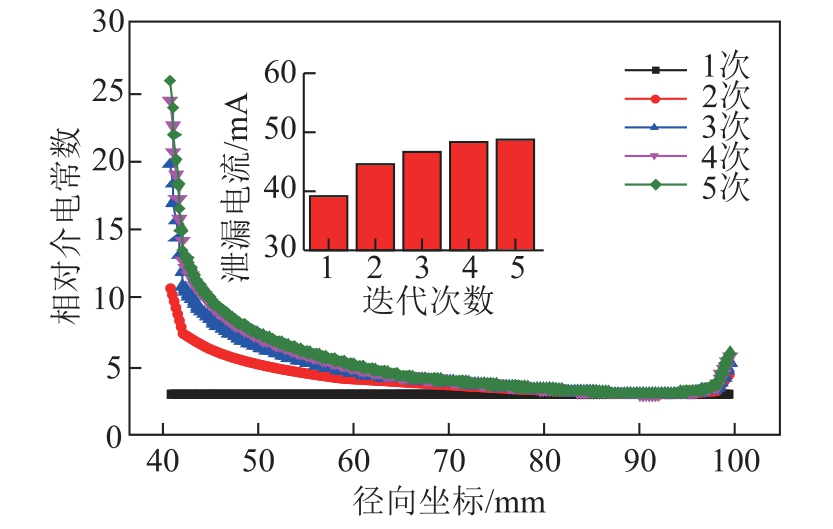
图7 优化过程中盆式绝缘子相对介电常数分布
Fig.7 Permittivity distributions during optimization
图8 为匀质盆式绝缘子与介电功能梯度绝缘子的空间电场强度分布。对于匀质盆式绝缘子来说,局部电场集中出现在盆式绝缘子凹面的高压三结合点区域。高压三结合点区域的电场集中容易诱发局部放电,严重时发展成为沿面闪络故障。经过优化后,梯度绝缘子靠近导体区域的相对介电常数升高,等效容抗变小,分压减小,有效地缓解了局部电场集中现象。可以看出,梯度绝缘子表面区域的电场强度分布相对于均质绝缘子得到了明显的改善。梯度绝缘子的“均压”作用,导致甚至在高压导体的表面也形成了一个低场区,有助于抑制气体绝缘输电管道中导体表面的局部放电现象。

图8 匀质盆式绝缘子与优化后的梯度盆式绝缘子电场分布
Fig.8 E-field contour of conventional and optimized basin-type insulator
2.3 梯度离散化方案
考虑到实际应用中构造连续梯度分布非常困难,因此需要对优化后的连续介电常数分布进行离散化处理,然后再利用叠层法或3D 打印等技术构造离散梯度绝缘子。基于最优的连续介电常数分布,本文提出两种策略对其进行离散化处理,离散层数为5 层,既有明显的离散性,又尽可能贴合连续分布曲线,如图9 所示。
(1)等厚梯度:将绝缘子划分为等厚度(∆h)的5 层,每层的介电常数取对应区间的最大值。
(2)等差梯度:将最优的介电常数分布划分为等差值(∆ε)的5 个区间,依据区间所处的坐标范围确定每层的厚度,每层的介电常数取区间最大值。

图9 介电常数分布离散化方案
Fig.9 Discretization methods of permittivity distribution
图10 为不同离散方案下,梯度盆式绝缘子的沿面电场分布。离散后的梯度绝缘子在界面处存在参数突变,导致沿面电场分布的跳跃畸变。在绝缘子的凹面和凸面,等差梯度的电场分布都优于等厚梯度。此外,等差梯度绝缘子的高介电常数区小于等厚梯度,泄漏电流较小。本文的离散梯度绝缘子只有5 层,此时等差梯度是一种明显优于等厚梯度的离散化方案。但随着分层数目的增加,等差梯度与等厚梯度的区别开始减小,逐渐向连续梯度逼近。

图10 不同离散方案的沿面电场分布
Fig.10 Surface E-field distributions of different discretization methods
3 结论
本文以圆台和盆式绝缘子为模型,提出一种基于迭代算法的功能梯度绝缘子介电常数分布优化方法。与文献相比,本文所提优化方法简单、迭代次数少、效率高。主要结论如下:
1)圆台绝缘子的沿面电场分布从高压电极三结合点向地电极递减,优化后的介电常数分布与沿面电场分布相似。在约束范围内,圆台绝缘子的沿面电场强度最大值由2.3kV/mm 降至1.1kV/mm,电场不均匀系数由2.3 降至1.1,下降幅度超过50%。
2)优化盆式绝缘子的介电常数分布需要兼顾凹面和凸面的电场分布。优化后,盆式绝缘子的相对介电常数分布呈现出“中间低,两头高”的趋势,凹面电场强度最大值下降幅度超过60%。
3)本文提出两种介电常数梯度离散化方案,即等厚梯度与等差梯度。在梯度数目只有5 层时,等差梯度的电场分布畸变较小,泄漏电流也较小,明显优于等厚梯度。但随着分层数目的增加,等差梯度与等厚梯度的区别开始减小,逐渐向连续梯度逼近。
[1] 韩智云, 邹亮, 辛喆, 等. 直流GIL 绝缘子环氧树脂/碳纳米管复合涂层关键物理性能的分子动力学模拟[J]. 电工技术学报, 2018, 33(20): 4692-4703.Han Zhiyun, Zou Liang, Xin Zhe, et al. Molecular dynamics simulation of vital physical properties of epoxy/carbon nanotube composite coatings on DC GIL insulators[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4692-4703.
[2] 张博雅, 张贵新. 直流GIL 中固-气界面电荷特性研究综述Ⅰ: 测量技术及积聚机理[J]. 电工技术学报, 2018, 33(20): 7-20.Zhang Boya, Zhang Guixin. Review of charge accumulation characteristics at gas-solid interface in DC GIL, part I: measurement and mechanisms[J].Transactions of China Electrotechnical Society, 2018,33(20): 7-20.
[3] 张连根, 路士杰, 李成榕, 等. GIS 中线形和球形金属微粒的运动行为和危害性[J]. 电工技术学报,2019, 34(20): 4217-4225.Zhang Liangen, Lu Shijie, Li Chengrong, et al. Motor behavior and hazard of spherical and linear particle in gas insulated switchgear[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4217-4225.
[4] 程显, 徐晖, 王瑞雪, 等. 等离子体复合薄膜沉积抑制金属微粒启举[J]. 电工技术学报, 2018, 33(20):30-39.Cheng Xian, Xu Hui, Wang Ruixue, et al. Composite thin film deposited by plasma to inhibit the lifting of metal particles[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 30-39.
[5] 乔胜亚, 周文俊, 王勇, 等. 典型吸附剂对GIS 固体绝缘介质放电特征气体变化规律影响[J]. 电工技术学报, 2018, 33(19): 213-221.Qiao Shengya, Zhou Wenjun, Wang Yong, et al.Effect of typical adsorbents on gas change characteristics of gas insulated switchgear solid insulation dielectric[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 213-221.
[6] 杜进桥, 张施令, 李乃一, 等. 特高压交流盆式绝缘子电场分布计算及屏蔽罩结构优化[J]. 高电压技术, 2013, 39(12): 3037-3043.Du Jinqiao, Zhang Shiling, Li Naiyi, et al. Electric field distribution calculation and shielding electrode structure optimization of UHVAC basin-type insulator[J]. High Voltage Engineering, 2013, 39(12): 3037-3043.
[7] Kurimoto M, Kato K, Hanai M, et al. Application of functionally graded material for reducing electric field on electrode and spacer interface[J]. IEEE Transactions on Dielectrics & Electrical Insulation,2010, 17(1): 256-263.
[8] Kato K, Kurimoto M, Shumiya H, et al. Application of functionally graded material for solid insulator in gaseous insulation system[J]. IEEE Transactions on Dielectrics & Electrical Insulation, 2006, 13(2): 362-372.
[9] 张冠军, 李文栋, 刘哲, 等. 介电功能梯度材料在电气绝缘领域的研究进展[J]. 中国电机工程学报,2017, 37(14): 4232-4245.Zhang Guanjun, Li Wendong, Liu Zhe, et al. Research progress on dielectric functionally graded materials for electrical insulation[J]. Proceedings of the CSEE,2017, 37(14): 4232-4245.
[10] 李信, 刘海昌, 滕元成, 等. 功能梯度材料的研究现状及展望[J]. 材料导报, 2012, 26(增刊1): 370-373.Li Xin, Liu Haichang, Teng Yuancheng, et al. Research status and future directions on functionally gradient materials[J]. Materials Review, 2012, 26(S1): 370-373.
[11] Li Chuanyang, Lin Chuanjie, Hu Jun, et al. Novel HVDC spacers by adaptively controlling surface charges-part I: charge transport and control strategy[J].IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(4): 1238-1247.
[12] 李进, 张程, 杜伯学, 等. 直流GIL 用非线性电导环氧绝缘子电场仿真[J]. 高电压技术, 2019, 45(4):1056-1063.Li Jin, Zhang Cheng, Du Boxue, et al. Electrical field simulation of epoxy spacer with nonlinear conductivity for DC GIL[J]. High Voltage Engineering, 2019, 45(4): 1056-1063.
[13] Tu Youping, Chen Geng, Li Chuanyang, et al. ±100kV HVDC SF6/N2 gas-insulated transmission line[J].IEEE Transactions on Power Delivery, 2020, 35(2):735-744.
[14] Okubo H, Shumiya H, Ito M, et al. Optimization techniques on permittivity distribution in permittivity graded solid insulators[C]//Conference Record of the 2006 IEEE International Symposium on Electrical Insulation, Toronto, 2006: 519-522.
[15] 李文栋, 刘哲, 有晓宇, 等. 叠层式介电功能梯度绝缘子的介电常数分布优化[J]. 西安交通大学学报, 2016, 50(10): 19-26.Li Wendong, Liu Zhe, You Xiaoyu, et al. Permittivity distribution optimization for multi-layer dielectric FGM insulator[J]. Journal of Xi’an Jiaotong University, 2016, 50(10): 19-26.
[16] Liu Zhe, Li Wendong, Wang Yibo, et al. Topology optimization and 3D-printing fabrication feasibility of high voltage FGM insulator[C]//2016 IEEE International Conference on High-Voltage Engineering and Applications (ICHVE), Chengdu,2016: 1-4.
[17] Qasim S A, Gupta N. Use of particle swarm optimization in the computation of an optimal permittivity distribution in functionally graded material insulators[C]//2015 International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Bangalore, India, 2015: 184-188.
[18] 孙秋芹, 郭晓和, 张永涛, 等. 基于介电功能梯度材料的盆式绝缘子电场分布优化[J]. 湖南大学学报, 2018, 45(8): 99-106.Sun Qiuqin, Guo Xiaohe, Zhang Yongtao, et al.Optimization of electric field distribution for spacer based on dielectric functionally graded material[J].Journal of Hunan University, 2018, 45(8): 99-106.