0 引言
绝缘子污秽闪络严重威胁着输电线路的安全运行，其闪络过程复杂且随机性强[1]。现有的绝缘缺陷非接触式检测方法由于缺乏放电机理与检测信号关联的研究而准确率不高[2-4]。流注放电[5]是污秽绝缘子表面放电的初始阶段[6]，随着流注过程的发展，放电通道能量增加，导致流注温度不断升高，转换为高温热电离通道，从而形成表面电弧[7]。通过计算绝缘子表面流注放电过程的体系能量变化，有利于深入研究污秽绝缘子表面流注至电弧放电[8]的转换过程，为绝缘子表面放电理论研究与状态检测方法提供参考和依据。
流注放电过程中，电子是能量传递的最主要载体，气体放电形成低温等离子体时，大部分能量用来加热电子并产生高能电子（＞5eV）[9]，这些具有较高能量的电子通过碰撞离解、激发和电离把能量传递给气体分子或离子。现有的关于流注理论能量变化的研究多集中于流注放电过程中的电子平均能量分布规律，以此揭示流注放电的微观粒子随时间的演化规律， 如典型的电子能量分布函数Maxwellian 分布、Druyvesteyn 分布[10]和通过求解Boltzmann 方程得到分布函数[11]等。但这些研究多集中于微观粒子运动层面，未深入到能量交换的本质——量子跃迁和电离进行分析，也未对整个体系的能量变化进行研究。
在产生流注放电的污秽绝缘子表面空间内，由水、空气、污秽中物质原子微粒组成的微观体系与外界环境的能量交换，形式虽然多样，如碰撞换能、热交换、光吸收与辐射、声波振动传导等，但究其微观根源，能量的输入与输出可归结为两个方面，即体系中粒子的能级跃迁和电离。能量的向外输出来自粒子的辐射和消电离，向内输入来自粒子的激发和电离，粒子体系与外界能量交换情况如图1 所示。因此，本文提出基于量子跃迁概率的污秽绝缘子表面流注放电能量计算方法，从微观层面能量变化的本质出发进行分析，不受能量交换形式的限制。
图1 中，外加电场给粒子体系1 所提供的能量记为W；粒子体系1 从外电场2 得到的能量一部分用于各种形式的电离（包含碰撞、热、光电离），产生离子和电子，这部分体系吸收的能量为E1，发生电离比例为Pe（计算出的最外层跃迁概率）；粒子体系1 从外电场2 得到的另一部分能量，先用于电离，后又发生消电离，产生中性粒子和光子，部分光子被粒子体系吸收，粒子受激而跃迁到高能级，吸收的能量为E2，比例为fμ；吸收光子后粒子的体系1 能量升高，处于不稳定状态，高能级不稳定辐射出光子，跃迁到低能级，粒子体系1 向外界体系2 释放的能量为E3，比例为Pr。
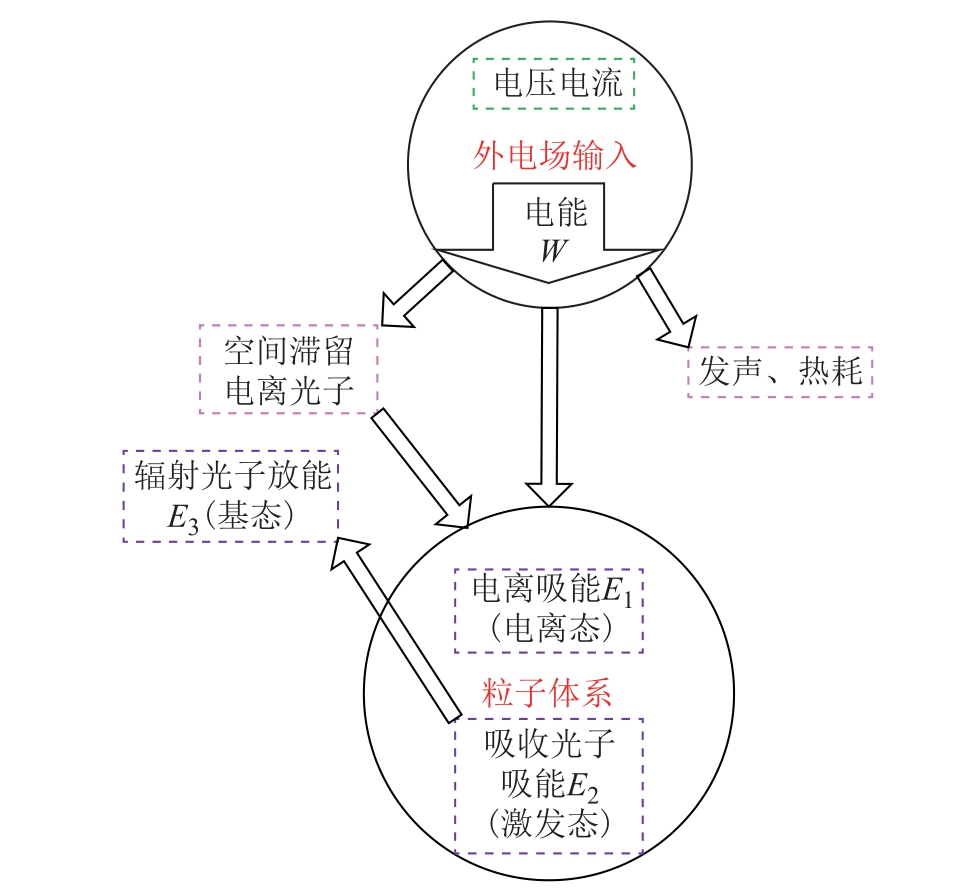
图1 粒子体系与外界能量交换
Fig.1 Energy exchange between particle system and external environment
1 污秽绝缘子表面放电粒子能级跃迁
1.1 污秽层微粒化学成分分析
在绝缘子表面相同体积下，存在质量比为空气:污秽=1:1 000（空气密度1.29kg/m3，假设饱和湿润污秽密度按照稍微大于水，即1.29×103 kg/m3）。其中，空气的成分为：N2 为78%，O2 为21%，稀有气体为0.94%, CO2 为0.03%。人工污秽的成分质量比按GB/T 4585-2004 中硅藻土配比[12]，如图2 所示。除了极为稳定的稀有气体和SiO2 外，各成分物质的量在粒子体系中的占比见表1。
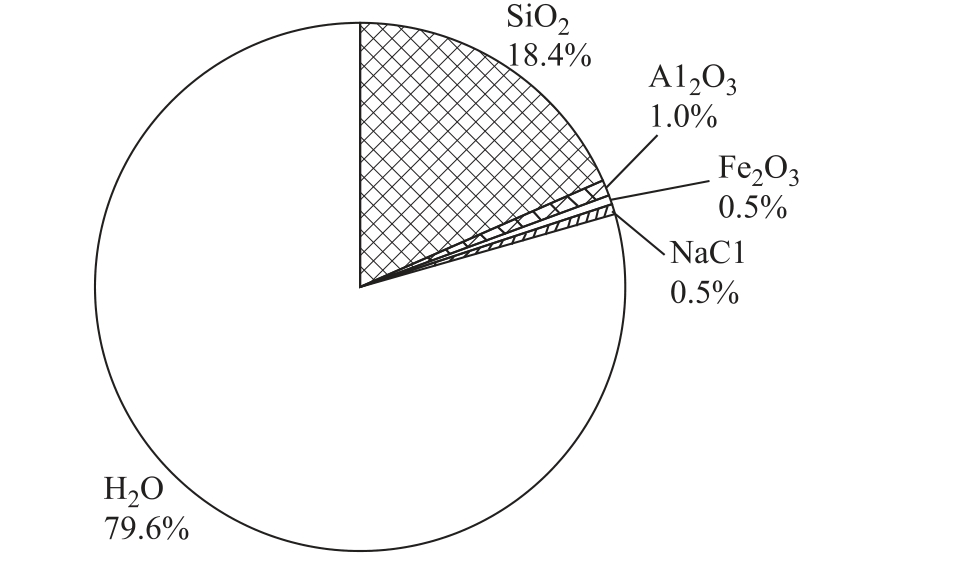
图2 人工污秽成分
Fig.2 Components of artificial pollution
表1 饱和湿润污秽绝缘子表面粒子成分
Tab.1 Particle composition of saturated wet polluted insulator surface
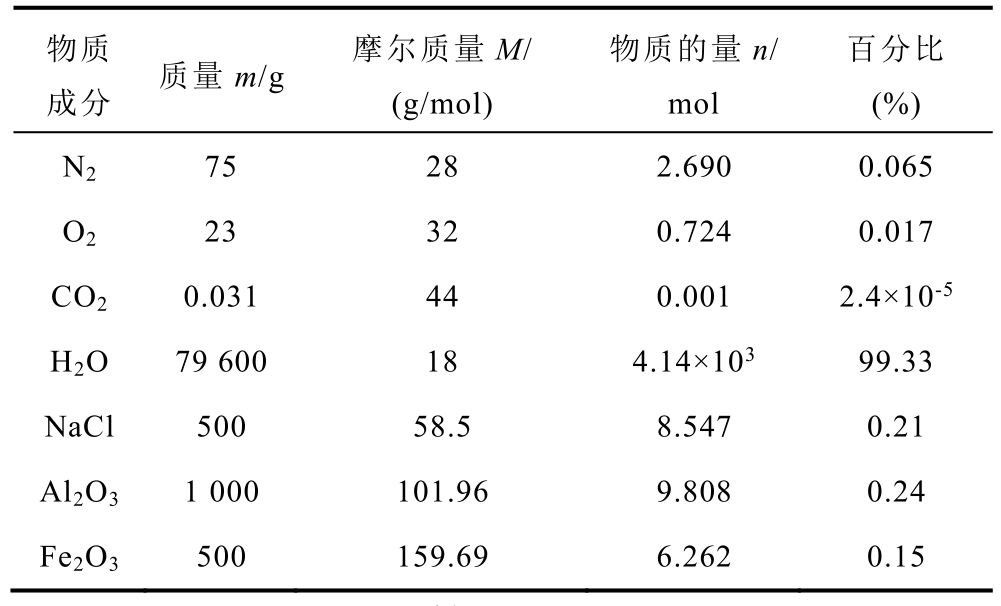
物质成分 质量m/g 摩尔质量M/(g/mol)物质的量n/mol百分比(%)N2 75 28 2.690 0.065 O2 23 32 0.724 0.017 CO2 0.031 44 0.001 2.4×10-5 H2O 79 600 18 4.14×103 99.33 NaCl 500 58.5 8.547 0.21 Al2O3 1 000 101.96 9.808 0.24 Fe2O3 500 159.69 6.262 0.15
1.2 能级跃迁概率计算
上述能级跃迁概率模型可结合粒子数目求取能级跃迁电子数期望值，作为介质表面击穿过程中光电离和辐射产生的光子数目计算的基本依据。粒子在电场作用下运动，电势能远大于其他种类的势能，因此势能随时间的变化关系为
式中，e 为电子电荷数；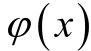
为电势分布。其中电压分布的表达式可通过对绝缘子进行有限元仿真得到。
将式（4）代入式（3）即可求取粒子能级间的跃迁概率为
表2 各粒子的化学参数
Tab.2 Chemical parameters of particles
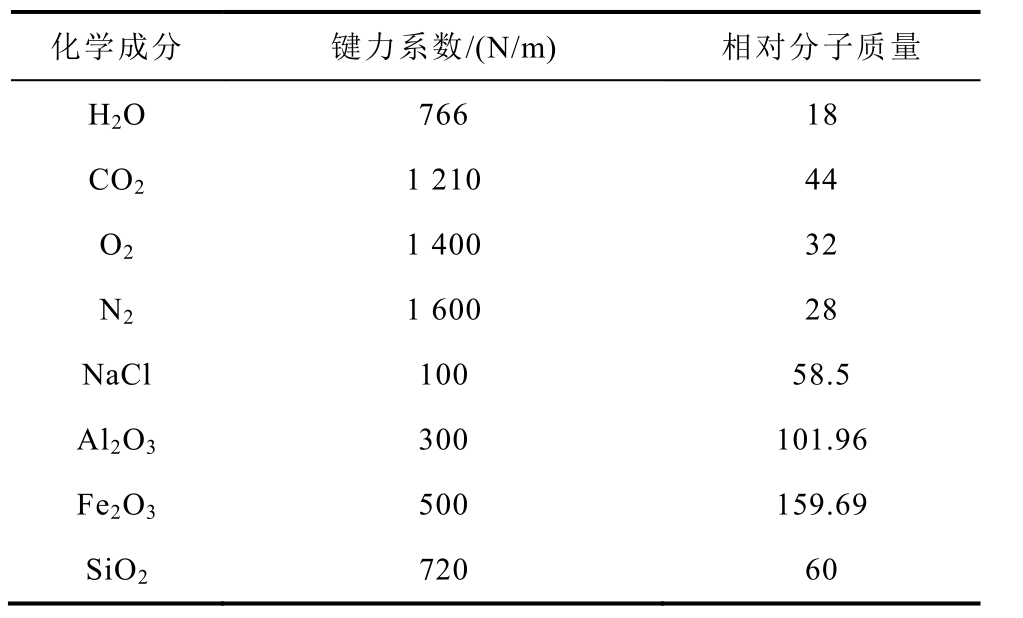
化学成分 键力系数/(N/m) 相对分子质量H2O 766 18 CO2 1 210 44 O2 1 400 32 N2 1 600 28 NaCl 100 58.5 Al2O3 300 101.96 Fe2O3 500 159.69 SiO2 720 60
按照跃迁选择定则和坐标x 表征下的矩阵元计算公式，分别求出相邻两能级间粒子的跃迁概率，可以证明同一组相邻高、低能级间跃迁概率相等。图3 为不同粒子从低能级到相邻高能级的跃迁概率情况。
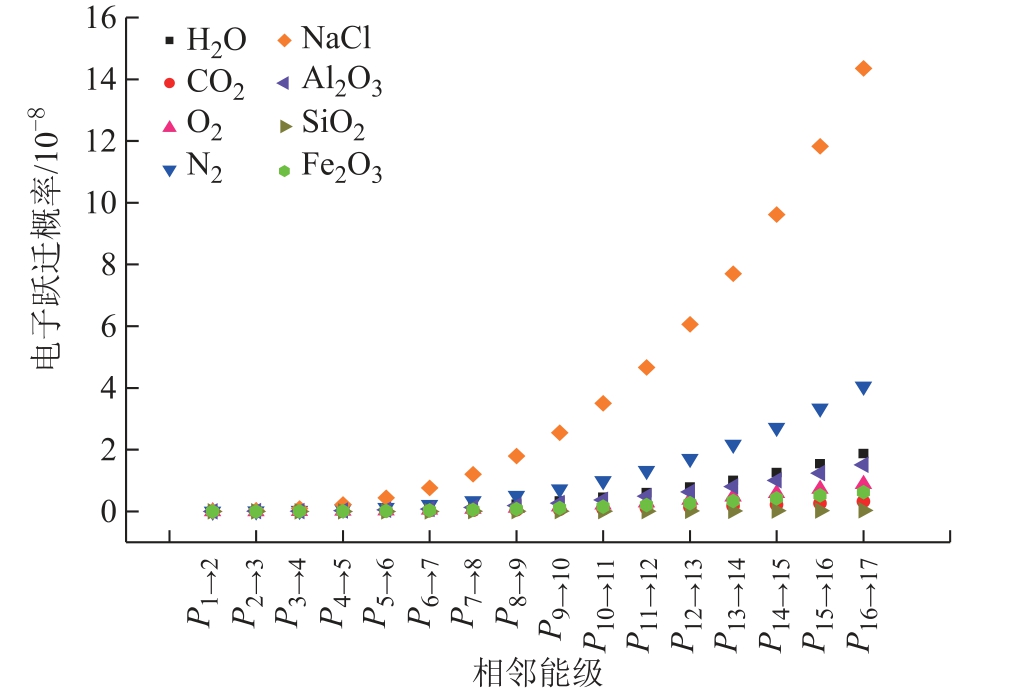
图3 各粒子从低能级到相邻高能级的跃迁概率
Fig.3 Transition probabilities of particles from low energy level to adjacent high energy level
2 流注放电的粒子体系能量计算
（1）确定粒子体系中物质种类及化学成分，包括容易跃迁的气体和污层中离子化合物。由于SiO2不易分解，电子跃迁概率极低，本文计算过程中未考虑SiO2 的影响。
（2）对于电离导致的能量交换：可由已有的实验统计得到微观粒子数目范围，结合电离系数的半经验公式或已计算出的电离比例，计算得到电离粒子数目，通过查表得到不同粒子的电离能，从而计算出总的电离能。
（3）对于能级跃迁导致的能量交换：根据已有实验统计到的原子数目范围，结合量子跃迁概率公式（概率本质上反映了一种统计规律），求得电子在不同能级间跃迁吸收或辐射能量的概率，从而得到发生跃迁的原子数目，再按照Redburg 方程[10]求取不同原子各能级的能量，将对应不同能级的原子数和能量值进行运算，从而计算出总的能级跃迁能量增量。
（4）最终将跃迁和电离导致的能量变化相加即可得到体系短时内总能量变化。
为简化计算，计算电离能量时，只考虑粒子中元素最常见的一种价态；本文在计算跃迁能量时，只考虑最外层的一个电子发生跃迁。根据第1 节的污秽成分分析结果，可知干燥情况下，各种物质的分子数所占比例见表3。
表3 干燥情况下各分子所占比例
Tab.3 Proportion of particles in drying conditions
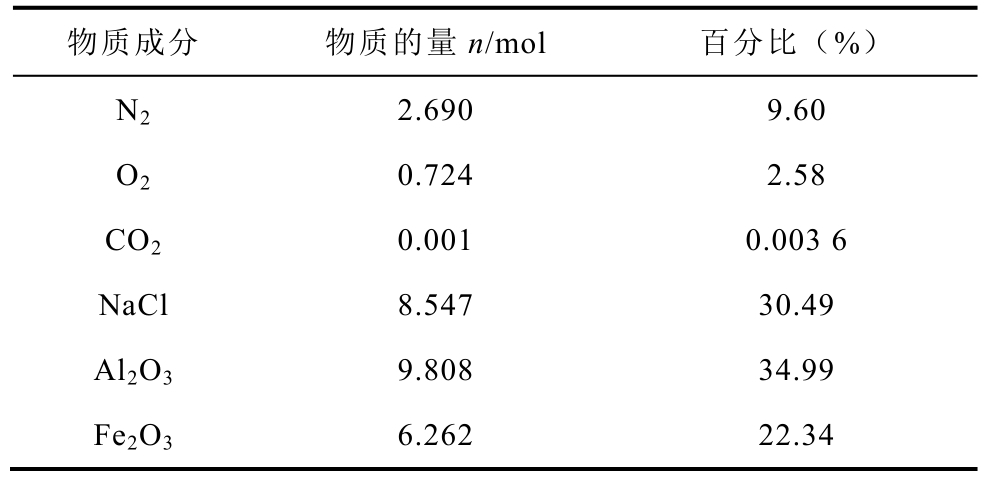
物质成分 物质的量n/mol 百分比（%）N2 2.690 9.60 O2 0.724 2.58 CO2 0.001 0.003 6 NaCl 8.547 30.49 Al2O3 9.808 34.99 Fe2O3 6.262 22.34
标准状态下，大气中含有约1019 个/cm3 数量级的气体分子。由表3 可知，气体分子约占12.2%，因此在初始状态下，物质中总粒子数目近似为N=1019/12.2%×(π×102×30-π×52×20) =6.43×1023（空间体积要减去绝缘子实体体积）。所以粒子的总物质的量约为n=N/NA=1.07 mol，NA 为阿伏伽德罗常数，N=6.02 × 1 02 3 mol −1，因此空间粒子数的总物质的量
A约为1 mol。
2.1 跃迁能量计算
同一原子的不同能级间的能量差（单位为J）可由Redburg 公式[11]计算得到，即。
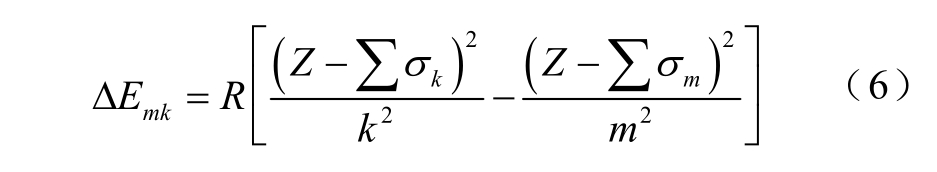
式中，系数 R =2.179 × 1 0−18；Z 为原子序数（核电荷数）；σ 为屏蔽常数。
2.1.1 屏蔽常数的计算
屏蔽常数的计算方法如下：对于单电子的原子轨道，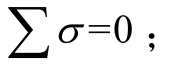
对于多电子的原子轨道，可以根据Slater 规则[15]进行估算，将各同组电子及所有内层电子对当前电子的屏蔽常数求和，得到
。
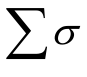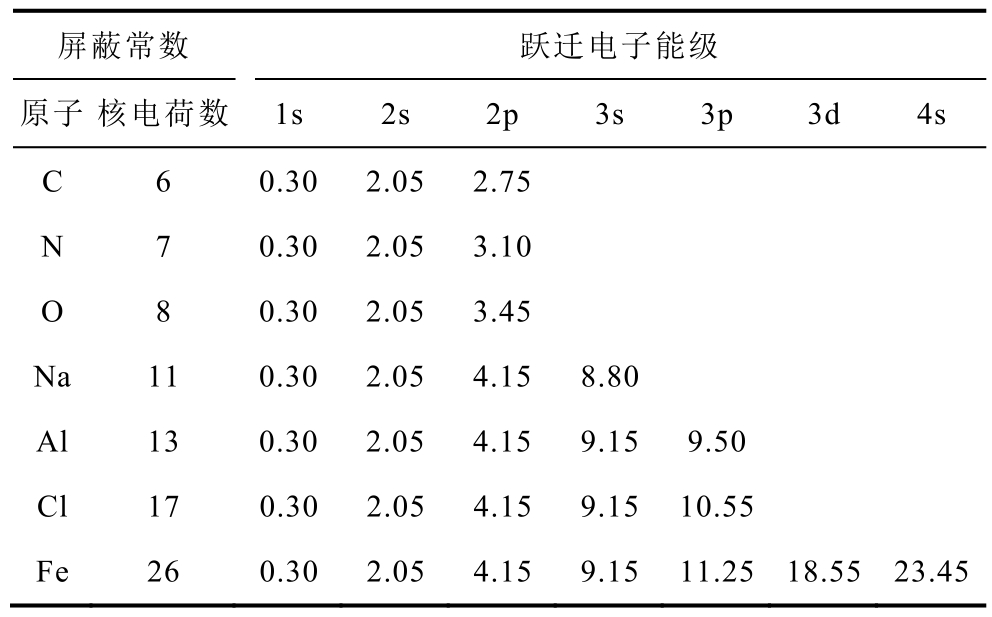
人工污秽中各粒子组分元素的能级排布为：C：1s22s22p2；N：1s22s22p3；O：1s22s22p4；Na：1s22s22p63s1，Al：1s22s22p63s23p1；Cl：1s22s22p63s23p4；Fe：1s22s22p63s23p63d64s2，且考虑同一能级上最外面一个电子发生跃迁。按照上述方法，计算得到所需的屏蔽常数见表4。
表4 能级轨道的屏蔽常数
Tab.4 Screening constant of energy level
屏蔽常数 跃迁电子能级原子核电荷数 1s 2s 2p 3s 3p 3d 4s C 6 0.30 2.05 2.75 N 7 0.30 2.05 3.10 O 8 0.30 2.05 3.45 Na 11 0.30 2.05 4.15 8.80 Al 13 0.30 2.05 4.15 9.15 9.50 Cl 17 0.30 2.05 4.15 9.15 10.55 Fe 26 0.30 2.05 4.15 9.15 11.25 18.55 23.45
2.1.2 吸收和辐射光子能量
根据求得的屏蔽常数计算各原子轨道的能量，如图4 所示。
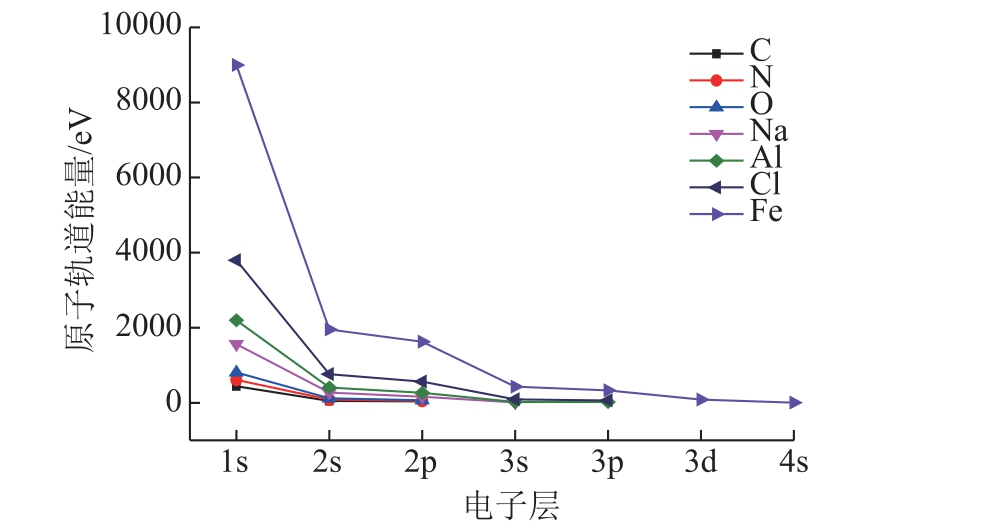
图4 原子轨道能量计算值
Fig.4 Calculated values of atomic orbital energy
结合式（6），并令跃迁之前的能级为最外层电子所在能级，跃迁之后的能级为无穷大，即可求出单个电子能级跃迁的能量差。以N2 为例（1s22s22p3），占空气比例为78%，根据跃迁概率分布可知，基态粒子碰撞导致激发比例为 Pe=P2→3=5.81×10-11。根据气体固有性质，选取吸收系数μ=5×105 cm-1，因此吸收比例为 fμ=1.25×10-2；吸收光子后再辐射的比例为Pr=Pe/fμ=4.65×10-9。
粒子的跃迁（激发）吸收能量为
表5 体系各粒子吸收光子后跃迁激发的能量
Tab.5 Energy excited by transition of photons absorbed by particles in the system
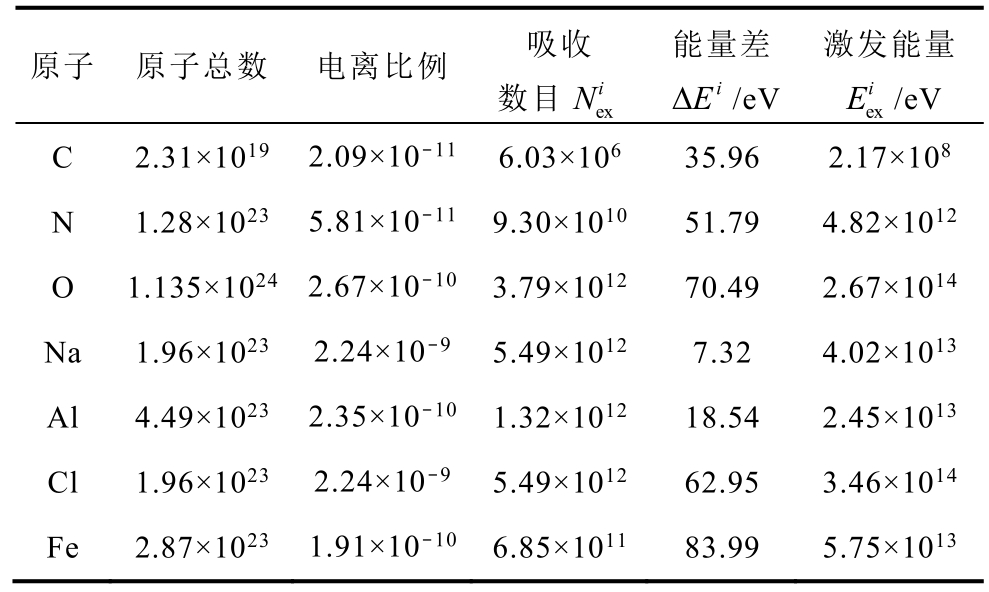
原子 原子总数 电离比例 吸收数目 ex i N能量差i E Δ /eV激发能量ex i E /eV C 2.31×1019 2.09×10-11 6.03×106 35.96 2.17×108 N 1.28×1023 5.81×10-11 9.30×1010 51.79 4.82×1012 O 1.135×1024 2.67×10-10 3.79×1012 70.49 2.67×1014 Na 1.96×1023 2.24×10-9 5.49×1012 7.32 4.02×1013 Al 4.49×1023 2.35×10-10 1.32×1012 18.54 2.45×1013 Cl 1.96×1023 2.24×10-9 5.49×1012 62.95 3.46×1014 Fe 2.87×1023 1.91×10-10 6.85×1011 83.99 5.75×1013
表6 体系各粒子放出光子后跃迁辐射的能量
Tab.6 Energy of transition radiation after photon emission from particles in the system
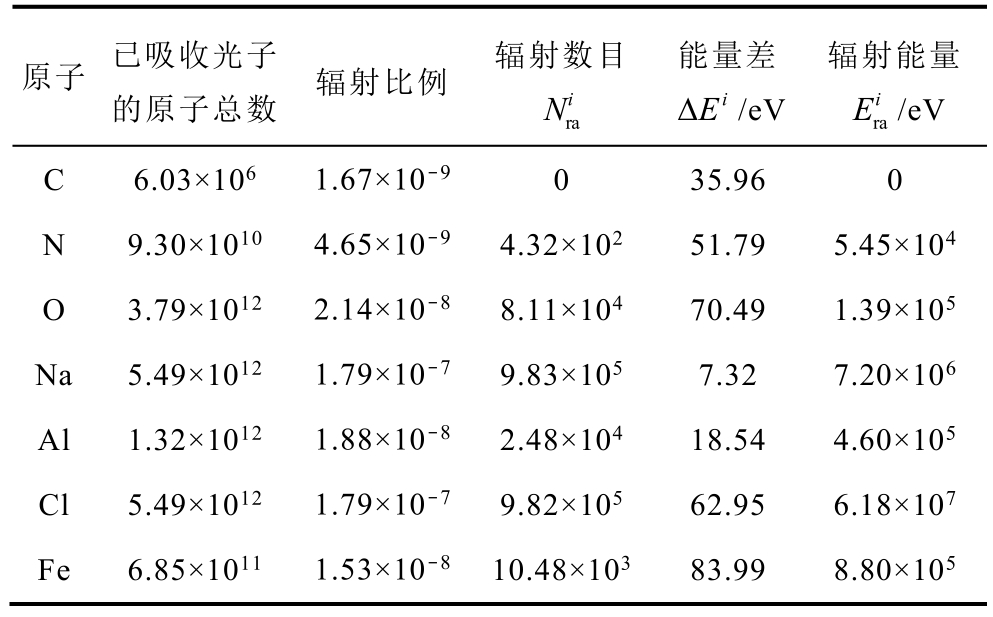
原子 已吸收光子的原子总数 辐射比例 辐射数目ra i N能量差i E Δ /eV辐射能量ra i E /eV C 6.03×106 1.67×10-9 0 35.96 0 N 9.30×1010 4.65×10-9 4.32×102 51.79 5.45×104 O 3.79×1012 2.14×10-8 8.11×104 70.49 1.39×105 Na 5.49×1012 1.79×10-7 9.83×105 7.32 7.20×106 Al 1.32×1012 1.88×10-8 2.48×104 18.54 4.60×105 Cl 5.49×1012 1.79×10-7 9.82×105 62.95 6.18×107 Fe 6.85×1011 1.53×10-8 10.48×103 83.99 8.80×105
根据表5，可以求出粒子体系吸收光子的能量为根据表6，可以求出体系中激发态粒子辐射光子的能量为
2.2 电离能量计算
2.2.1 电离能等级的选择
电离能是指基态原子从最外层先后电离出1、2、3 个电子所需的能量（累计值）。理论上，某元素存在多少个电子就有多少级电离能。通过相关研究统计资料，查表可知各种元素的电离能。
针对人工污秽中的几种元素，电离能列表仅考虑前6 级，整理出的各级电离能见表6。对于正离子，按照失去电子数选择电离能等级，如H+、C4+、Na+、Al3+、Fe3+；对于负离子，按照得到电子数选择电离能等级，如N3-、O2-、Cl-。
2.2.2 体系电离能总增量
粒子电离吸收的能量为
表7 体系各粒子电离吸收的能量
Tab.7 Absorbing energy of ionization from particles in the system
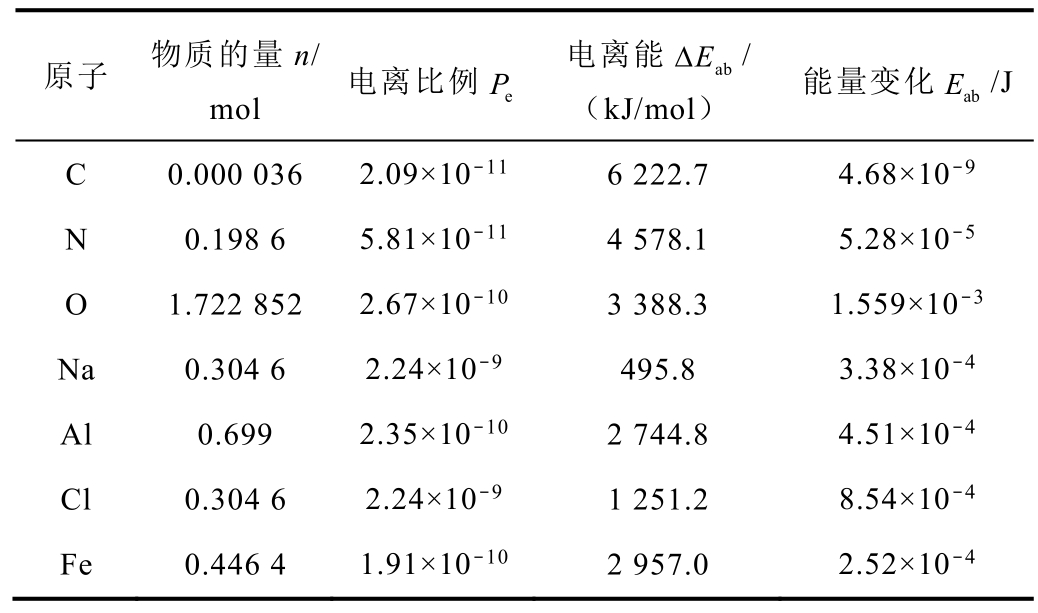
原子 物质的量n/mol 电离比例 eP 电离能 abEΔ /（kJ/mol） 能量变化 abE /J C 0.000 036 2.09×10-11 6 222.7 4.68×10-9 N 0.198 6 5.81×10-11 4 578.1 5.28×10-5 O 1.722 852 2.67×10-10 3 388.3 1.559×10-3 Na 0.304 6 2.24×10-9 495.8 3.38×10-4 Al 0.699 2.35×10-10 2 744.8 4.51×10-4 Cl 0.304 6 2.24×10-9 1 251.2 8.54×10-4 Fe 0.446 4 1.91×10-10 2 957.0 2.52×10-4
将所有的电离能相加，即可得到体系吸收的电离能量为
3 体系能量变化实验验证与分析
3.1 实验方案
3.1.1 实验装置和原理
图5 为实验器材和设备的接线及布局方式，可见光相机选用 SONY a550 数码相机，紫外成像仪型号为DayCor Superb，测量装置为JFD-3 局部放电检测仪和TDS 2014 型示波器。耦合电容约为1 000pF，阻抗值约为3.2MΩ，限流电阻为5kΩ，采样电阻为1kΩ。
在探究绝缘子表面放电之前，采用针板模型验证本文计算方法，有利于排除不确定性因素。实验所用的针板放电模型如图6 所示，钨铜针尖尖角为15°，直径为10mm；钨铜板外径为80mm，厚度为10mm，侧边倒圆角半径为5mm；支架材质选用绝缘性能优异的有机玻璃。
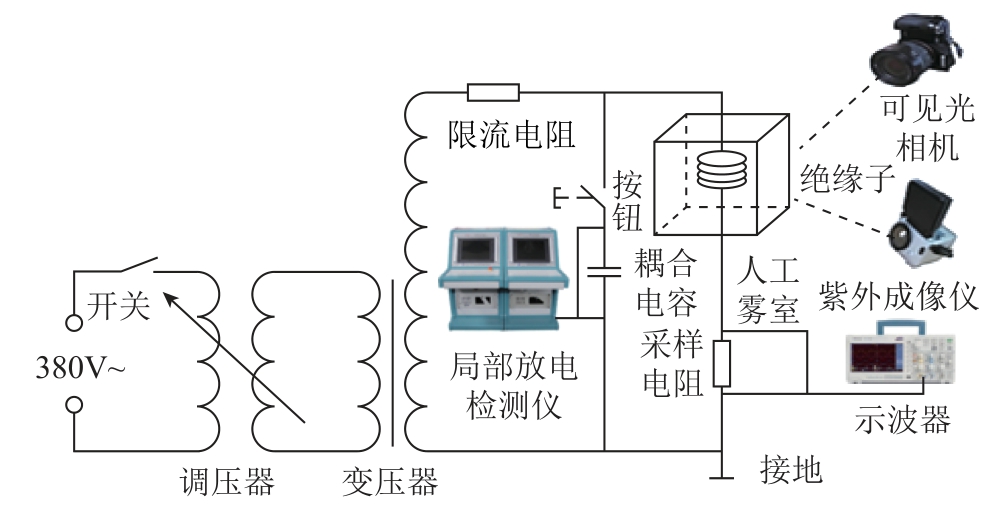
图5 实验原理
Fig.5 Experimental circuit diagram
图6 实验模型
Fig.6 Experimental model
绝缘子表面污秽放电实验选用支柱式陶瓷绝缘子，其型号为ZSW-10/4。根据GB/T 26218.1—2010[16]，将污秽等级III 对应的盐密取为0.2 mg/cm2，将盐密与灰密之比取为1:7，并按照GB/T 4585—2004[12]配置人工污液，将洗净的绝缘子涂成污秽等级III，并自然阴干24h，得到污秽绝缘子。在1m×0.8m× 0.8m的人工雾室里进行高压实验，风速为0，环境温度约为10℃。
3.1.2 实验方法
针板实验过程中，在环境相对湿度为50%条件下，将针板模型接入工频耐压测试系统中，针尖与平板距离为5mm，实验过程中逐渐加压到6kV。
将绝缘子置于人工雾室内，湿度计选用希玛AR807，用加湿器将人工雾室内的气体加湿到所需湿度（相对湿度RH=90%）后，加10kV 交流电压维持1min，使得受潮后的绝缘子能出现完整的放电现象。紫外成像仪拍摄时距离绝缘子约为3m，仪器的增益设置为110%，同时需要打开光子计数功能。4 个测量装置采用“准同步”记录，记录形式为视频或屏幕录制，在启动加压的同时，由人工控制的方法近似同时启动仪器的测量和记录，允许同步偏差在1s 以内。局部放电检测仪测量放电量，示波器测量采样电阻两端电压，进而转换为绝缘子表面泄漏电流，可见光相机用于记录整个放电过程中绝缘子表面的各种放电现象，紫外成像仪用于记录绝缘子紫外图像和紫外光子数。
3.2 放电能量计算
当粒子体系首次发生流注放电时，体系的能量增量为
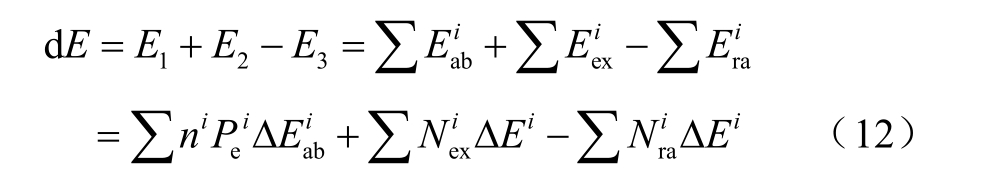
对于针板放电，式（12）计算过程中只考虑空气中粒子的能量变化，对于绝缘子表面放电，则同时考虑空气和污秽层中的粒子。
外界电源对流注放电体系输入的能量值为流注放电发生后的电源对绝缘子的能量输入增量。即
式中，U(t)为绝缘子两端电压，其有效值在实验过程中保持不变；I(t)为流注放电发生后的泄漏电流；I0(t)为流注放电前的泄漏电流，针板放电的I0(t)基本为0。流注放电由泄漏电流波形的畸变和紫外成像仪记录的光子数同步判定，放电时刻泄漏电流及其图像如图7 所示。
图7 放电时刻泄漏电流及其图像
Fig.7 Leakage current and image at discharge time
体系输入和输出的能量差记为dW=W-dE，这部分多出的能量可能用于热耗散与振动发声现象，在理论计算时未考虑。由于热、光、声过程互相耦合，各过程无法割裂，微观上按照本文方法暂时无法求取各形式能量比例，只能做宏观上的实验测量和统计。
3.3 实验结果及误差分析
按照上述能量计算过程与实验方法，通过调节绝缘子两端的电压进行了10 组实验，得到粒子体系能量变化的理论计算值和实际值，如图8 所示。
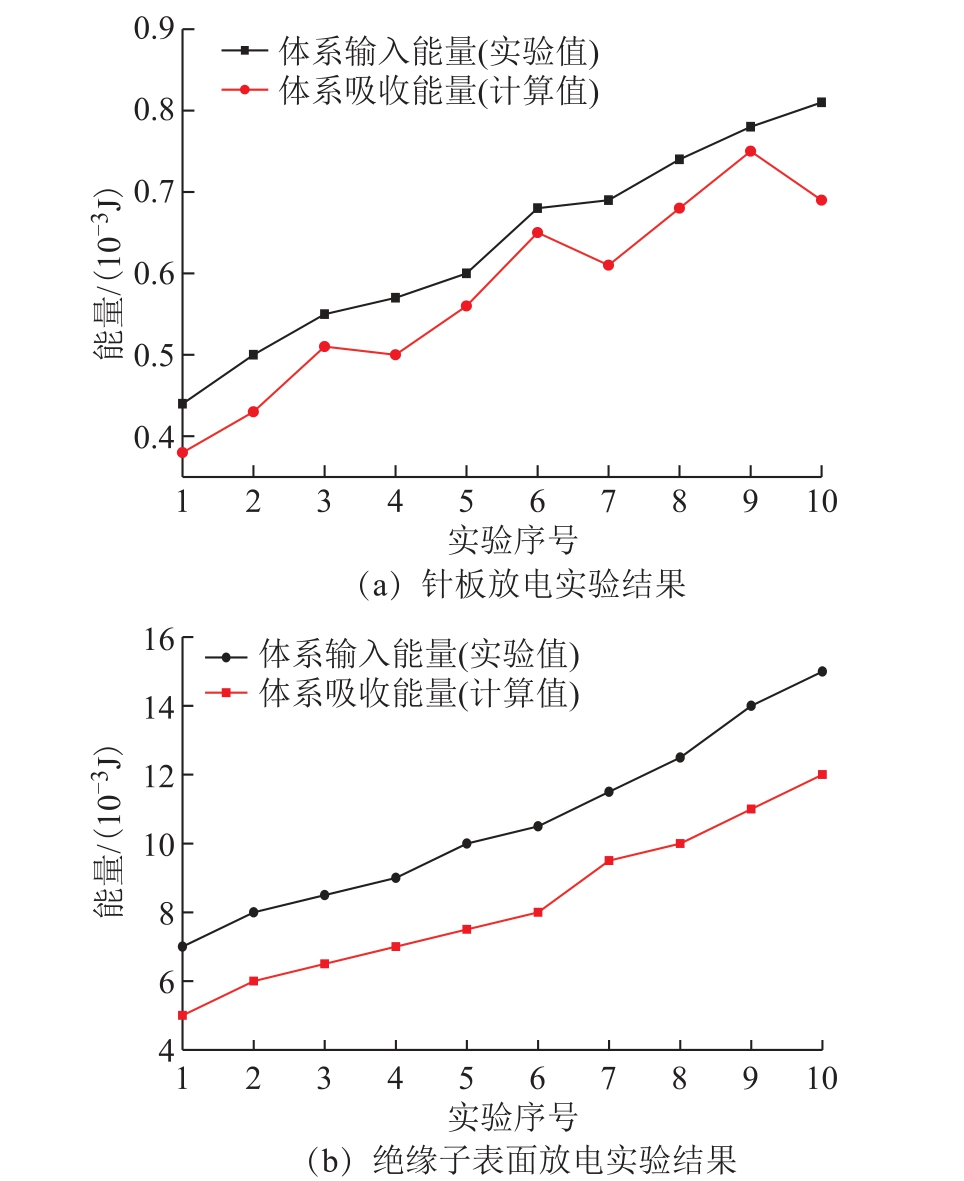
图8 流注击穿时体系能量变化实际值与理论值
Fig.8 The actual and theoretical values of the energy change in the system during the stream breakdown
从图8 中可以看出，计算值普遍比实验值偏小，计算值约在实验值的70%～85%之间，两者的偏差具有一定规律性；且针板放电模型的计算偏差要小于绝缘子表面放电偏差，这是因为绝缘表面粒子种类更多，且其电场影响因素更为复杂，带来的偏差更大。除实验测量误差外，计算值与实验值误差还可能来源于两方面：一方面是计算时未考虑到的热耗散、声波及电磁波等形式释放的能量。另一方面是计算简化过程导致计算误差：①在模型求解过程中，为简化计算，本文仅考虑了最为可能发生的低能级向相邻高能级跃迁的概率，在计算时也仅运用了基态粒子向相邻高能级的跃迁概率，未考虑激发态粒子的跃迁，同时也忽略了跨越多个能级跃迁的概率；②在计算粒子综合跃迁概率时，本文将各粒子独立作用时的能级跃迁概率按比例加权，未考虑粒子间的相互作用。
4 结论
本文介绍了绝缘子表面放电过程中流注放电时的体系能量变化计算方法，从微观粒子能级的角度分析了能量的输入与输出形式，得到如下结论：
1）分析了绝缘子表面污秽粒子成分，计算了放电空间内各类粒子数量。
2）计算了绝缘子在额定电压下表面不同粒子的电子跃迁和电离比例，结合不同粒子数目及其电子能级能量计算方法，分别计算出粒子体系的跃迁、电离等过程中吸收和释放的能量。
3）通过粒子体系的能量变化与外界输入能量的实验对比分析对本文计算结果进行验证，发现按照本文计算方法算出的能量变化值与实际的差值具有一定的规律性。
[1] 孟志高, 蒋兴良, 董冰冰, 等. 自然雾条件下严重染污玻璃、复合绝缘子交流污闪特性[J]. 电工技术学报, 2016, 31(12): 65-71.Meng Zhigao, Jiang Xingliang, Dong Bingbing, et al.AC pollution flashover characteristics of surged polluted glass and composite insulators under natural fog conditions[J]. Transactions of China Electrotechnical Society, 2016, 31(12): 65-71.
[2] 艾建勇, 金立军. 基于紫外图像的接触网棒瓷绝缘子污秽状态检测[J]. 电工技术学报, 2016, 31(10):112-118.Ai Jianyong, Jin Lijun. Rod porcelain insulator filth state detection of catenary based on ultraviolet image[J].Transactions of China Electrotechnical Society, 2016,31(10): 112-118.
[3] 邓红雷, 陈力, 鲁强, 等. 超声导波检测绝缘子用玻璃钢芯棒缺陷[J]. 电工技术学报, 2017, 32(12):268-276.Deng Honglei, Chen Li, Lu Qiang, et al. Defect detection for fiber reinforced plastics rod of composite insulator with ultrasonic guided wave[J].Transactions of China Electrotechnical Society, 2017,32(12): 268-276.
[4] 熊兰, 刘钰, 姚树友, 等. 污秽绝缘子紫外在线监测系统[J]. 电工技术学报, 2010, 25(7): 186-191.Xiong Lan, Liu Yu, Yao Shuyou, et al. Ultraviolet on-line monitoring system for contaminated insulators[J].Transactions of China Electrotechnical Society, 2010,25(7): 186-191.
[5] Meek J M, Craggs J D. Electrical breakdown of gases[D]. Oxford: Clarendon Press, 1953.
[6] 杨津基. 气体放电[M]. 北京: 科学出版社, 1983.
[7] 孟晓波, 梅红伟, 陈昌龙, 等. 绝缘介质表面流注发展特性的机理研究[J]. 中国电机工程学报, 2013,33(22): 155-165, 24.Meng Xiaobo, Mei Hongwei, Chen Changlong, et al.Research on characteristics of streamer propagation along insulation surfaces[J]. Proceedings of the CSEE, 2013, 33(22): 155-165, 24.
[8] 杨庆, 汪锐, 司马文霞, 等. 基于电路网络的绝缘子交流污闪动态模型研究[J]. 中国电机工程学报,2013, 33(25)：204-212, 29.Yang Qing, Wang Rui, Sima Wenxia, et al. Study on the dynamic model of polluted insulators under AC voltage based on the circuit network[J]. Proceedings of the CSEE, 2013, 33(25): 204-212, 29.
[9] 张文静. 大气压介质阻挡放电物理过程的数值模拟[D]. 上海: 东华大学, 2007.
[10] 陈宗旺. 电离气体发光动力学[M]. 北京: 科学出版社, 1996.
[11] Hagelaar G J M, Pitchford L C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models[J].Plasma Sources Science and Technology, 2005, 14:722-733.
[12] 中国国家标准化管理委员会. GB/T 4585—2004 交流系统用高压绝缘子的人工污秽试验方法[S]. 北京: 中国标准出版社, 2004.
[13] 陈洪, 袁宏宽. 量子力学[M]. 北京: 科学出版社, 2014.
[14] 杨金文. 普朗克常数和里德堡常数的测定实验[J].太原师范学院学报：自然科学版, 2010, 9(4): 93-95.Yang Jinwen. Planck constant and Rydberg constant determination experiment[J]. Journal of Taiyuan Normal University Natural Science Edition, 2010,9(4): 93-95.
[15] 李凤东. 屏蔽效应与斯莱特规则的应用[J]. 电大理工, 2010(4)：42-43.Li Fengdong. Application of shielding effect and slater rule[J]. Radio and Television University,2010(4): 42-43.
[16] 中国国家标准化管理委员会. GB/T 26218.1—2010污秽条件下使用的高压绝缘子的选择和尺寸确定第1 部分: 定义、信息和一般原则[S]. 北京: 中国标准出版社, 2010.