0 引言
伴随着我国电气化铁路飞速发展,其电能质量问题由早期的无功影响、负序、谐波等问题转换为负序为主的电能质量问题[1-4]。为降低牵引负荷对电力系统公共连接点(Point of Common Coupling,PCC)处不平衡的影响,通常在分相分区处设置电分相,采用轮换相序、分相分区供电的方案[5]。电分相的存在会带来机车掉速、过电压、施工选址受限等问题,对于机车的正常运行存在一定的安全隐患[3-6]。此外,以青藏线和川藏线为代表的电气化铁路建设存在外部电源薄弱,长大坡道多,不宜过多设定电分相等问题,对既有牵引供电方式提出了新的挑战。
针对负序和电分相等问题,国内外学者和工程人员进行了大量研究及工程实践[4-13]。俄罗斯等国采用双边供电省去变电所之间分区所处的电分相,但会产生均衡电流,同时负序问题亦存在[4]。德国通过自建电厂或利用公用电网向机车供电,能够有效解决负序及电分相等问题,由于成本较高,只在少数国家采用[7]。日本学者提出的功率融通装置能够较好地实现负序等电能质量问题的治理,但电分相问题仍存在[8-12]。为解决电分相问题,德国、法国、日本等国研究了过分相技术,仍有一定不足,装置寿命受影响,投资较大,对施工选址亦有要求[13]。西南交通大学科研团队在同相供电领域进行了大量研究,在解决负序等电能质量问题的同时,可取消牵引变电所出口处的电分相[2-4]。
为了进一步解决长大坡道的电气化铁路供电问题,有必要研究长距离无分相贯通供电技术,最大限度减少电分相的数量,同时不会带来新的电能质量问题。文献[14]提出了一种牵引电缆贯通供电系统;文献[15]提出了一种牵引变电所群贯通供电系统,针对其负序问题,可采用集中补偿进行负序治理。集中补偿时需异地实时采集待补偿的牵引负荷数据,若以有功型方式进行负序集中补偿,需调度有功潮流进行负序补偿,增加了难度,负荷较大时可能出现功率反送的现象。因此,需研究新的补偿方式,而采用无功型补偿方式可作为负序集中补偿的有效手段之一。
鉴于静止无功发生器(Static Var Generator, SVG)的优点[16-17],可利用SVG 进行负序集中补偿。针对较为复杂的负序集中补偿,本文提出一种基于YNd 变压器与SVG 的电气化铁路同相供电综合补偿方案及策略,构建适用于二端口和三端口补偿模式的综合补偿数学模型,并给出了确定补偿方案的方法;研究了对应的综合补偿方案的控制策略;通过仿真验证了同相供电综合补偿方案和控制策略的有效性。
1 同相供电综合补偿方案
基于YNd 变压器与SVG 的同相供电系统由单相接线牵引变压器、负序综合补偿装置(Negative Sequence Comprehensive Compensation Device, NCD)和牵引网等构成,其中,NCD 由YNd 变压器与SVG构成。该系统可分为单所同相供电和长距离无分相贯通供电,其中两种典型的长距离无分相贯通供电方案示意图分别如图1 和图2 所示。

图1 牵引变电所群贯通供电方案示意图
Fig.1 Schematic diagram of interconnected power supply scheme of traction substation group
图1 中,将电网同一变电站三相中相同两相(每相同一母线的不同分段)以树形(辐射式)结构给n(n≥2)个牵引变电所SS1, SS2, ···, SSn 供电,这n个牵引变电所为1 个牵引变电所群,单相接线变压器一次侧获得相同相位,二次侧牵引网贯通连接,构成牵引变电所群贯通供电方案。当PCC 处负序超标时,选择群中一个牵引变电所设置NCD 进行集中补偿,补偿后PCC 处负序达到国标要求[18],称该所为中心牵引变电所(Central Traction Substation,CTS),如图1 中的牵引变电所SS1 作为CTS。其余n-1 个牵引变电所为普通牵引变电所(Ordinary Traction Substation, OTS)。
图2 中主牵引变电所馈出110kV(线电压)至单相电缆,输送至各个牵引变电所SS,通过各个SS中的单相接线变压器向牵引网供电,单相接线变压器一次侧获得相同相位,二次侧牵引网贯通连接,构成牵引电缆贯通供电方案。当PCC 处负序超标时,在主牵引变电所设置NCD 进行集中补偿,补偿后负序满足相关标准要求。图1 和图2 中牵引网为直供方式,显然也适用于自耦变压器(Autotransformer,AT)供电等供电方式。
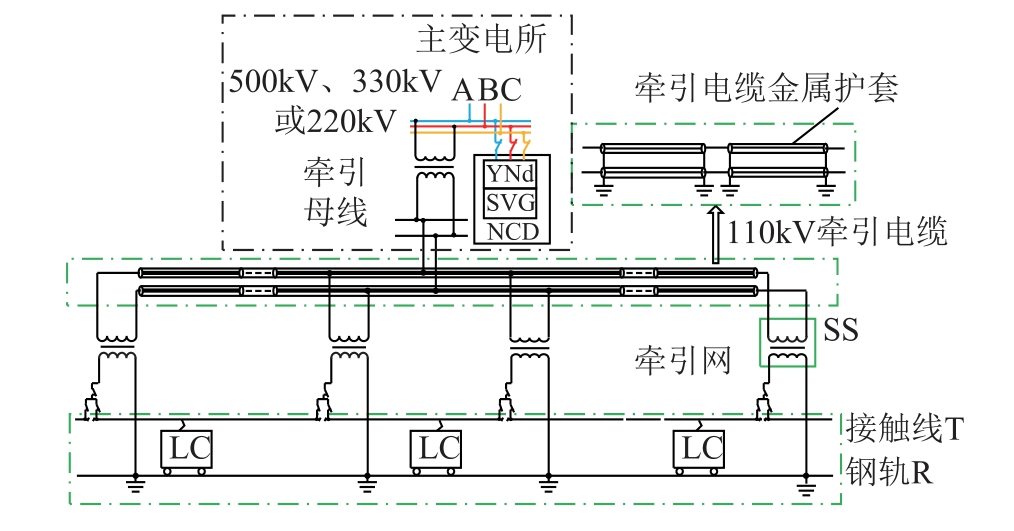
图2 牵引电缆贯通供电方案示意图
Fig.2 Schematic diagram of interconnected power supply scheme of traction cable
基于YNd 变压器与SVG 的同相供电综合补偿方案的区别在于牵引负荷数据的采集:一类是设置NCD 的牵引变电所需要异地实时采集待补偿的牵引负荷数据,如图1 中的牵引变电所群贯通供电方式的负序集中补偿;另一类则是在设置NCD 的牵引变电所即可采集到需要补偿的牵引负荷数据,如图 2 中的牵引电缆贯通供电方案及单所同相供电方案。
显然,以牵引变电所群贯通供电方式的负序集中补偿方式更为复杂,故本文重点针对该方案的负序集中补偿进行分析。图1 中YNd 变压器以YNd11接线为例,牵引负荷接在电力系统AB 相。根据NCD的拓扑结构,将基于YNd 变压器与SVG 的综合补偿方案分为二端口补偿模式和三端口补偿模式,如图3 所示。图3a 中无功补偿单元SVG1 和SVG2 分别连接至YNd11 变压器二次侧对应的ac 和ba 端口,记为二端口补偿模式;图3b 中无功补偿单元SVG1、SVG2 和SVG3 分别连接至YNd11 接线变压器二次侧对应的ac、ba 和ca 端口,记为三端口补偿模式。
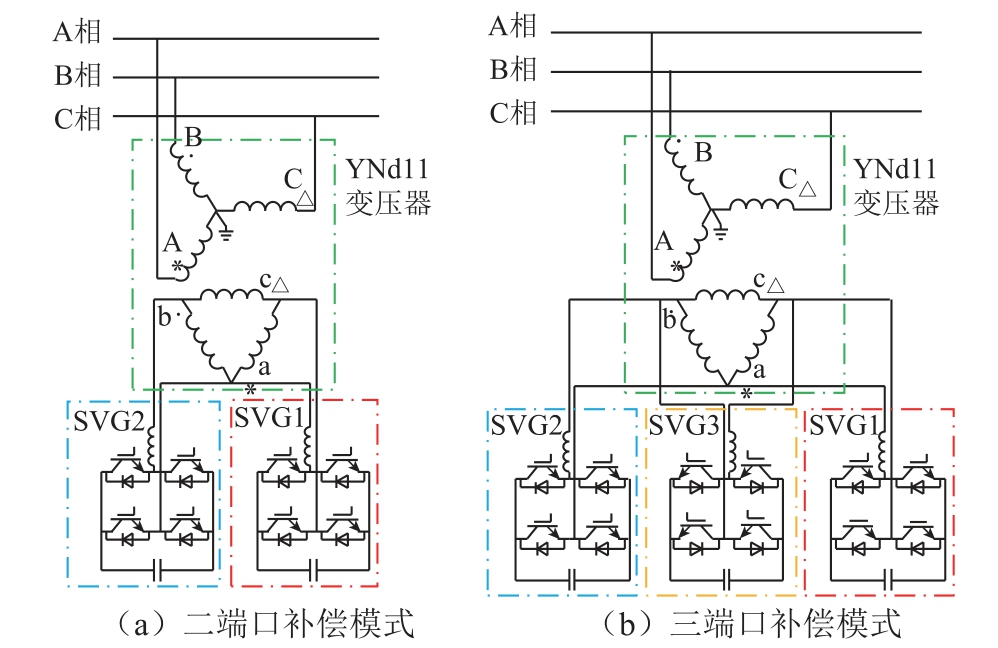
图3 不同补偿模式对应的NCD 示意图
Fig.3 Schematic diagram of NCD corresponding to
different compensation modes
2 同相供电综合补偿原理及模型
2.1 基本原理
文献[18]中规定负序的考核点在PCC。在一定拓扑结构下,通过SVG 发出无功电流补偿PCC 处的负序电流,使PCC 处负序满足国标要求。设定PCC 处牵引负荷总电流和功率因数角分别为 LI˙和Lϕ ,以牵引工况下牵引负荷滞后为例进行分析。
1)二端口补偿模式原理

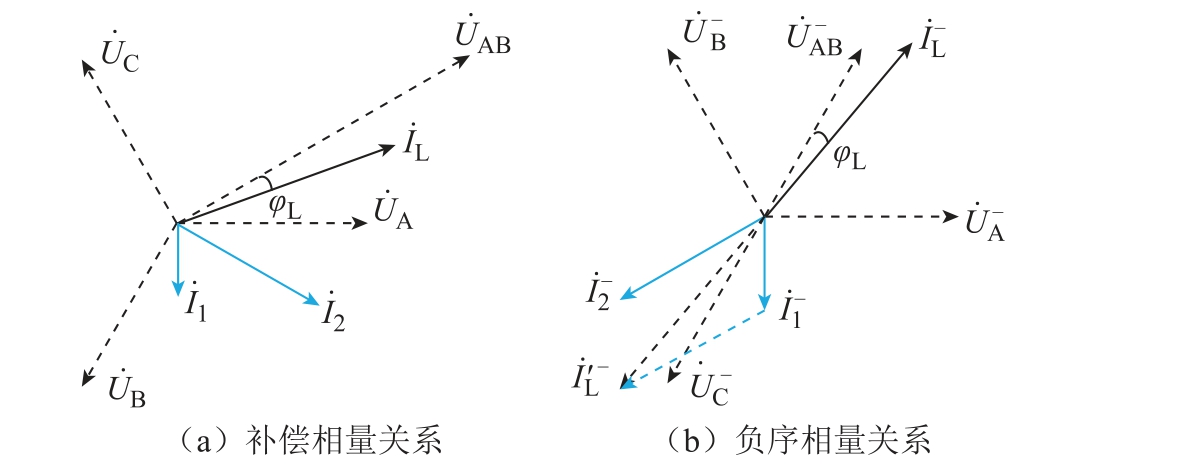
图4 二端口补偿模式原理相量图
Fig.4 Two-port compensation principle phasor diagram
2)三端口补偿模式原理

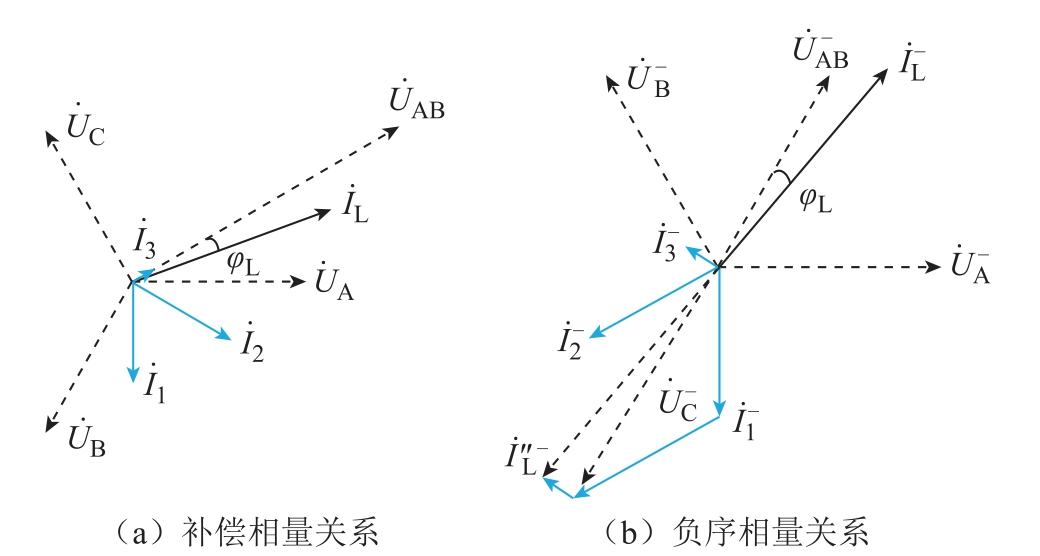
图5 三端口补偿原理相量图
Fig.5 Three-port compensation principle phasor diagram
2.2 综合补偿数学模型

式中,S1L、φ1L 分别为CTS 处牵引负荷的视在功率和功率因数角;Sk、φk 分别为补偿端口处SVG 的视在功率(无功功率)和功率因数角;m 为补偿端口的数量,若为二端口补偿模式,则m=2,若为三端口补偿模式,则m=3;KC 为无功补偿度。
由式(1)得到KC 为

采用NCD 进行补偿后,PCC 处总牵引负荷和SVG 形成的负序复功率S−˙ 为

由式(4)得到KN 为
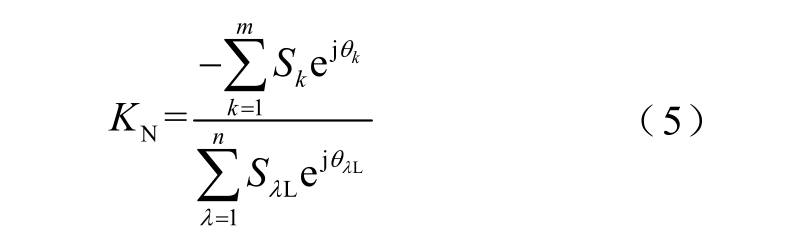
式中,KN 为补偿后PCC 处负序补偿量与原有负荷造成的PCC 处的负序功率的比值,通过KN 对PCC处负序进行约束,通常KN 取实数。式(3)中KC 表示CTS 处无功补偿量与CTS 处牵引负荷无功功率的比值,通过KC 对CTS 处功率因数进行约束。将(5)按照实部与虚部展开并与式(3)联立,得到综合补偿模型为

由式(7)求解得到S21 和S22 分别为
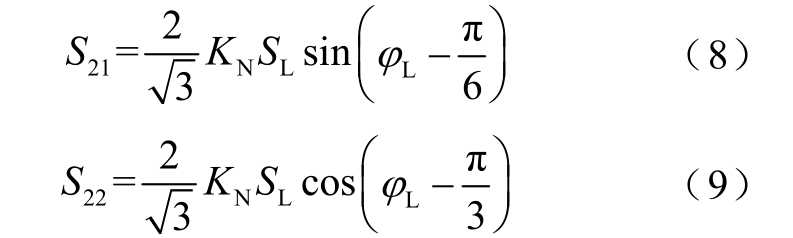
式(8)和式(9)中,若S2i>0(i=1, 2),则表示SVG 发出容性无功功率;S2i<0,则表示SVG 发出感性无功功率。将式(8)和式(9)两边同时除以 CTS 处端口电压的有效值 U1L 得到 SVG1 和SVG2 发出的电流I21 和I22 分别为

2)三端口补偿模式
相较于二端口补偿模式,三端口补偿模式由SVG1、SVG2 和SVG3 共同进行负序电流补偿,三者发出的无功功率分别为 S31、S32 和 S32。仍令φ1=φ2=φ3=-π/2,根据式(6)得到三端口补偿模式综合补偿模型为
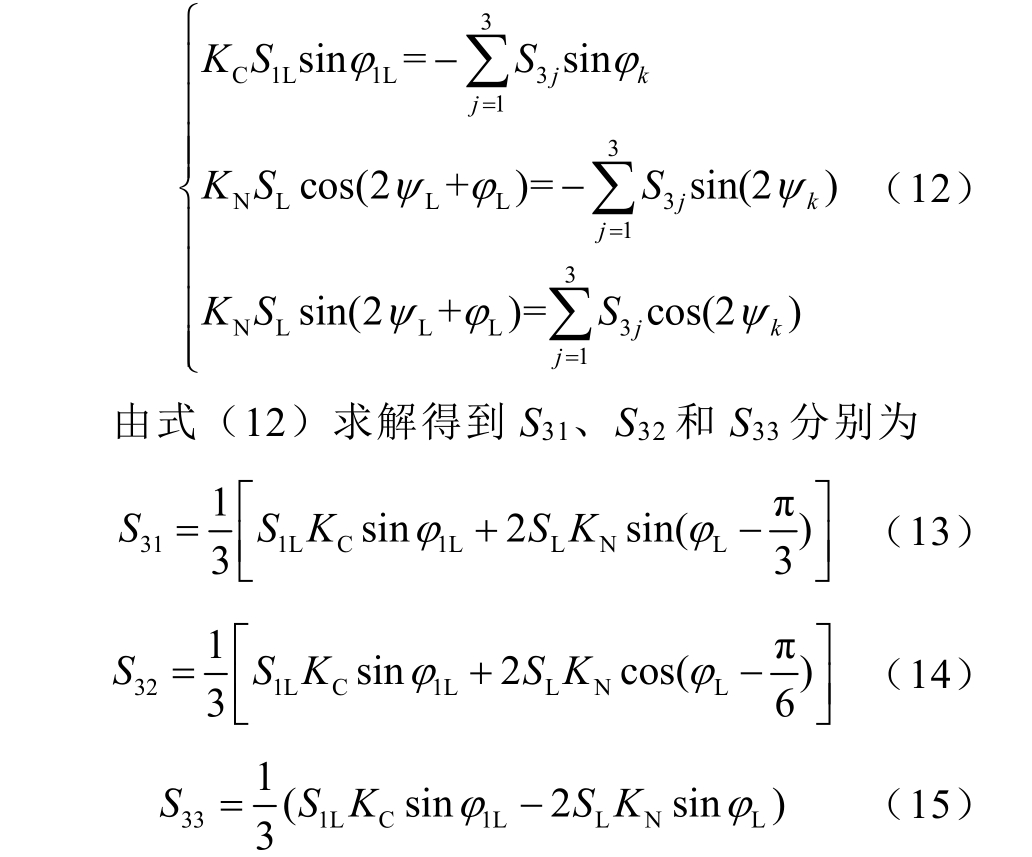
式(13)~式(15)中,若S3j>0(j=1,2,3),则表示SVG 发出容性无功功率;若S3j<0,则表示SVG 发出感性无功功率。式(13)~式(15)分别除以U1L 得到SVG1、SVG2 及SVG3 发出的无功电流I31、I32 和I33 分别为

式(16)~式(18)中,若I3j>0(j=1, 2, 3),则表示SVG 发出容性无功电流;若I3j<0,则表示SVG 发出感性无功电流。由式(16)~式(18)可知,当牵引负荷功率因数为 1 时,不需要在端口增加SVG3,仅依靠SVG1 和SVG2 就可以实现负序的完备补偿,同时CTS 处的功率因数不受影响。
谐波的考核点在PCC 处[19],因此在补偿负序电流的同时还兼顾PCC 处谐波电流补偿。仍以牵引负荷接于AB 相为例,二端口补偿模式下,SVG1 和SVG2 需补偿的电流分别为 1HI˙ 和 2HI˙ ,牵引负荷谐波电流为 LHI˙ ,则PCC 处C 相谐波电流 CH=0I˙ ,A 相和B 相谐波电流 AHI˙ 和 BHI˙ 分别为

2.3 补偿方案的比选
无论是二端口补偿模式还是三端口补偿模式,补偿后负序和无功均应达到国标要求。对于二端口补偿模式,CTS 处的功率因数无法通过KC 直接设定,若补偿后CTS 处功率因数满足相关标准要求,则二端口补偿模式可行,否则只有三端口补偿模式满足要求。对于三端口补偿模式,通过设定KN 和KC可以实现负序与无功的完备补偿。
当二端口补偿模式和三端口补偿模式均可实现负序补偿时,可通过如下步骤确定合适的补偿方案。

3)定义最大无功补偿量QΣ,二端口补偿模式和三端口补偿模式的最大无用补偿量分别为Q2Σ 和Q3Σ,如式(22)和式(23)所示,最大无功补偿量越大,需要的SVG 装置容量也越大,投资也越大。
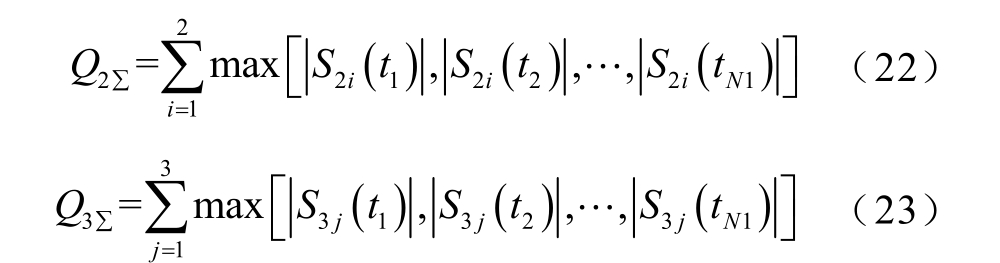
4)由式(22)和式(23)计算出最大无功补偿量后,选择其中取值较小的情形,作为合适的补偿方案,无功补偿容量越小,投资越少。
3 综合补偿控制策略
设定t 时刻牵引负荷端口电压瞬时值uL(t)和电流瞬时值iL(t)分别为

基波电流的有功分量和无功分量分别为 ILp=ILcosφL 和ILq=ILsinφL。式(25)两边乘以sin(ωt+π/6)得到瞬时功率 Lp( )p t 为
3.1 2 端口补偿模式下控制策略
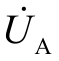 和
和  经锁相环PLL 产生同步信号cos(ωt)和cos(ωt-2π/3),牵引工况下SVG1、SVG2 分别为感性、容性端口,对应的同步信号分别为-cos(ωt)和cos(ωt-2π/3),补偿后的SVG1 和SVG2 的期望补偿电流理论值 i1′ 和 i2′ 分别为
经锁相环PLL 产生同步信号cos(ωt)和cos(ωt-2π/3),牵引工况下SVG1、SVG2 分别为感性、容性端口,对应的同步信号分别为-cos(ωt)和cos(ωt-2π/3),补偿后的SVG1 和SVG2 的期望补偿电流理论值 i1′ 和 i2′ 分别为
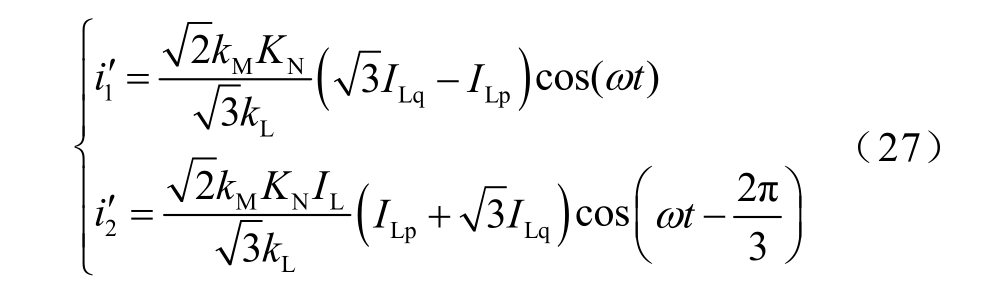
将期望补偿电流理论值 1i′和 2i′与实际电流值i1和i2 比较,经PI 环节,利用三角波调制产生控制SVG 的驱动信号[20-22]。由式(27)得到补偿电流检测框图,如图6a 所示,图中LPF 为低通滤波器,以SVG1 控制为例,其控制原理框图如图6b 所示,对于SVG2 的控制相同。
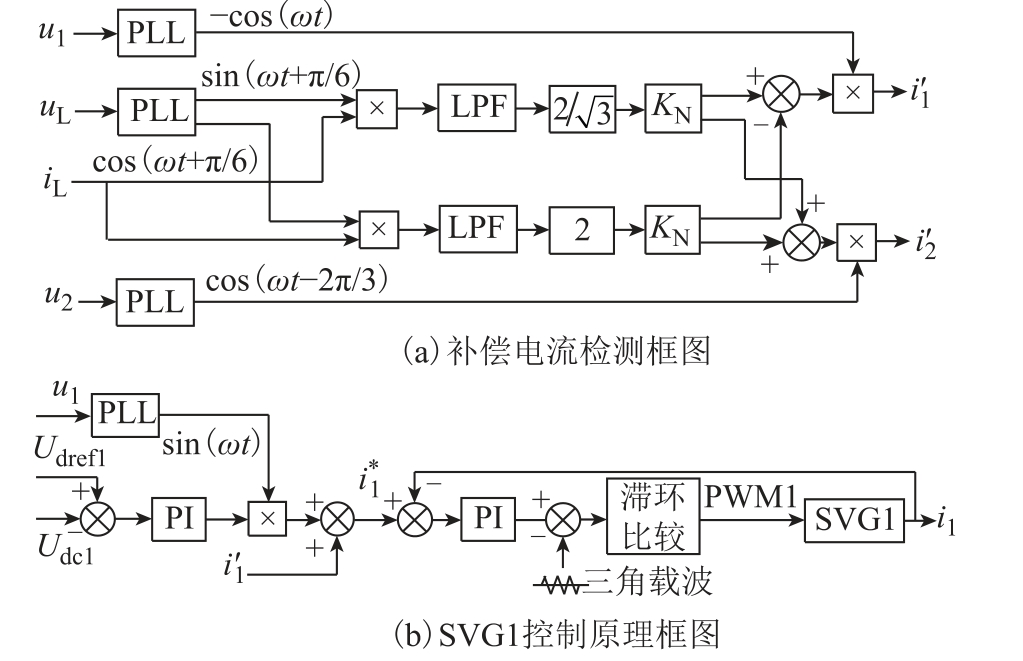
图6 二端口补偿模式下控制原理框图
Fig.6 Control principle block diagram for 2-port compensation mode
3.2 三端口补偿模式下控制策略模式
采用三端口补偿后, AU˙ 、 BU˙ 、 CU˙ 经PLL 产生的同步信号为cos(ωt)、cos(ωt-2π/3)和cos(ωt+2π/3),牵引工况下SVG1、SVG2 和SVG3 分别为感性,容性和感性端口,则同步信号分别为-cos(ωt)、cos(ωt-2π/3)和-cos(ωt+2π/3),SVG1、SVG2 和SVG3 的期望补偿电流理论值 1i′、 2i′和 3i′分别为式中,IL1q = IL1sinφL1。
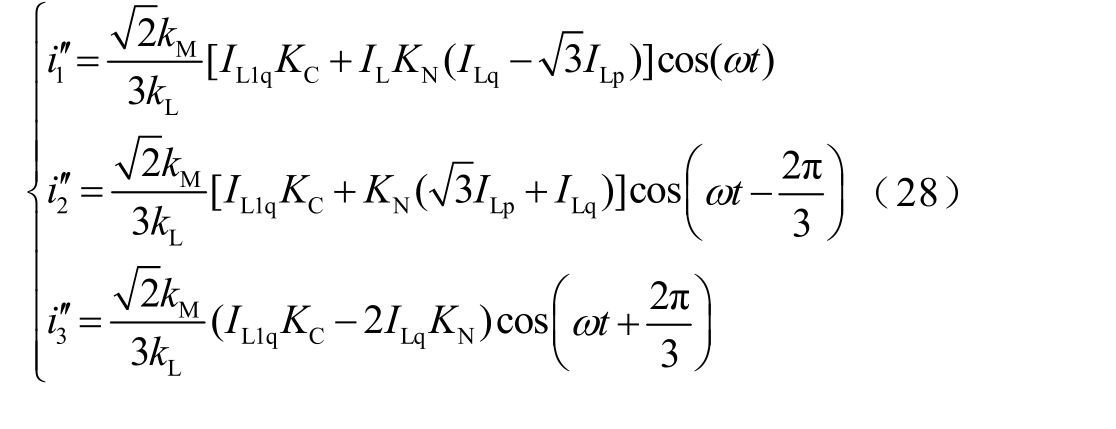
同理,根据式(28)得到三端口补偿模式下补偿电流检测框图如图7 所示,SVG1、SVG2 和SVG3的控制与图6b 相同。

图7 三端口补偿模式下补偿电流检测框图
Fig.7 Compensation current detection block diagram for 3-port compensation mode
3.3 KC 和KN 取 值 的 确 定
将式(1)与式(2)联立,得到 CK 的另一种表达形式为
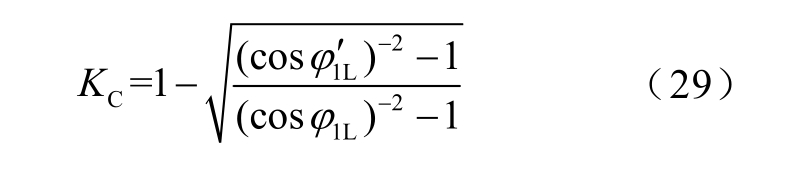
设偿后PCC 处三相电压不平衡度期望值为εU1,根据文献[18]得到PCC 处负序功率允许值Sε 为

获取t 时刻各个牵引负荷端口的牵引负荷实时数据,确定t 时刻的 cosϕ 1′L ( t)和 εU1(t),由式(29)和式(31)可确定t 时刻的KC(t)和KN(t),进而根据图6 和图7 可分别实现二端口补偿模式和三端口补偿模式下的负序实时补偿和控制。
以某牵引变电所24h 数据为例,三端口补偿模式下补偿后功率因数不变,即KC(t)=0。当三相电压不平衡度小于等于期望限值时,KN(t)=0,补偿装置不投入工作;当三相电压不平衡度超出期望限值时,KN(t)=1-εU1(t)Sd/SL(t),补偿装置投入工作。不同时刻下的KN 取值如图8 所示。

图8 不同时刻下的KN 取值
Fig.8 Value of KN at different times
4 仿真分析
4.1 二端口补偿模式仿真分析
以单所同相供电为例分析二端口补偿模式。仿真条件:设定PCC 处短路容量为1 500MV·A,牵引变压器为单相接线,一次侧线电压为110kV,电压比为 110kV/27.5kV;牵引负荷端口负荷功率为30MV·A,功率因数为0.98;NCD 处于待机状态,在0.3s 时刻投入。
忽略牵引负荷的谐波,二端口补偿模式下的完全补偿和部分补偿后PCC 处三相电流如图9a 和图9b 所示。其中,采用二端口补偿模式全补偿时,补偿后三相电压不平衡度期望值 εU1=0%,即KN=1;采用二端口补偿模式部分补偿时,εU1=1.3%,即KN=0.35。

图9 忽略牵引负荷谐波的补偿后PCC 处三相电流
Fig.9 Three-phase current with compensation at PCC ignoring traction load harmonics
对PCC 处对应波形数据进行傅里叶分析及相关计算,得到忽略牵引负荷谐波的负序及功率因数相关统计值见表1。补偿后的三相电压不平衡度达到了预期的期望值,由于NCD 发出的容性无功功率较感性偏多,故功率因数较补偿前有一定提高。
表1 忽略牵引负荷谐波的相关数据统计值
Tab.1 Statistical value of relevant data of traction load ignoring traction load harmonics

策略A 相电压/kV 三相电压不平衡度(%)功率因数正序分量 负序分量补偿前 62.96 1.26 2.00 0.98完全补偿 63.47 0.073 0.12 0.99部分补偿 63.14 0.83 1.31 0.99
SVG 补偿的无功功率计算值与实际值见表2。实际值与计算值基本接近,说明了数学模型的准确性,采用部分补偿后一定程度上能够降低补偿装置的容量,进而降低投资。
表2 SVG 补偿的无功功率计算值与实际值
Tab.2 Calculation value and actual value of reactive power compensated with SVG

策略SVG1 容量/(V·A) SVG2 容量/(V·A)实际值 计算值 实际值 计算值完全补偿 10.76 11.00 23.15 22.95部分补偿 3.80 3.85 7.52 8.04
考虑牵引负荷谐波,在牵引负荷处增加谐波源,其他参数设置第3 节。采用二端口补偿模式完全补偿(εU1=0%,即KN=1)和部分补偿(εU1=1.3%,即KN=0.35)后PCC 处三相电流如图10 所示。考虑牵引负荷谐波的负序及功率因数相关统计结果见表3。由表1 和表3 结果可知,两表中统计结果基本一致,说明负序与谐波的补偿是独立的。PCC 处总谐波畸变率情况见表4,补偿后三相电压和电流总谐波畸变率均明显下降,说明在补偿负序的同时可以兼顾PCC 处牵引负荷引起的谐波电流的补偿。
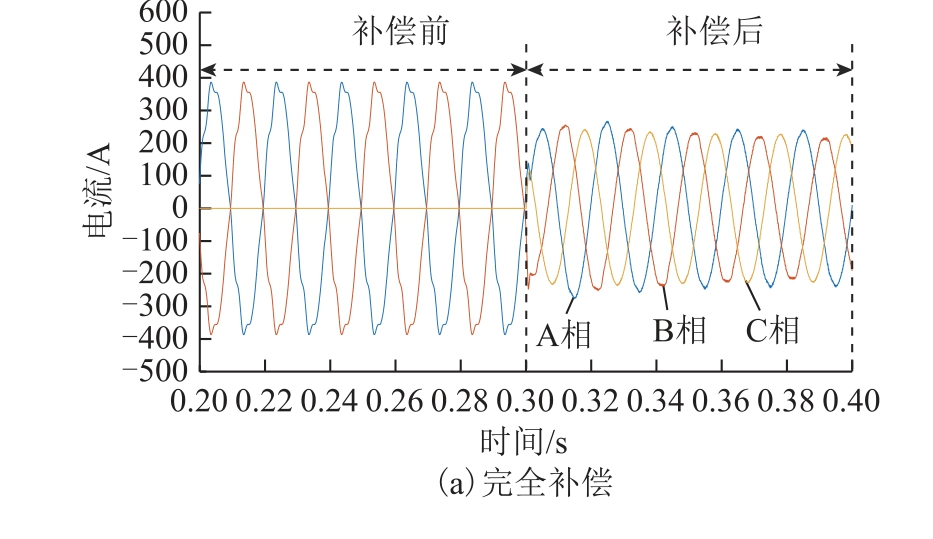

图10 考虑牵引负荷谐波的补偿后PCC 处三相电流
Fig.10 Three-phase current with compensation at PCC with traction load harmonics
表3 考虑牵引负荷谐波的相关数据统计值
Tab.3 Statistical value of relevant data of traction load with traction load harmonics
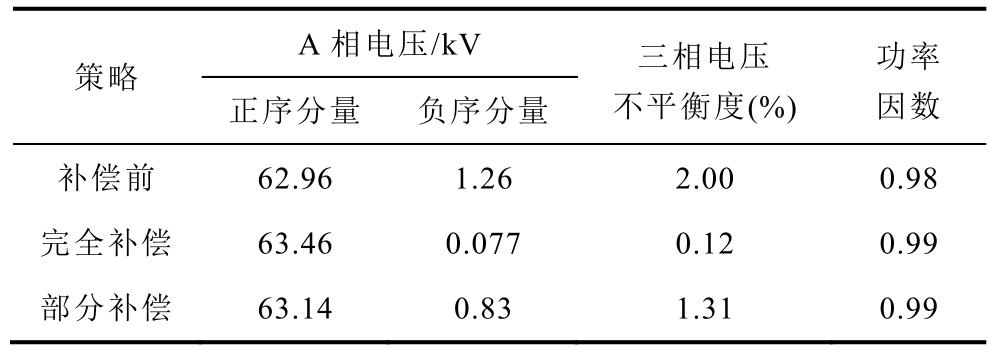
策略A 相电压/kV 三相电压不平衡度(%)功率因数正序分量 负序分量补偿前 62.96 1.26 2.00 0.98完全补偿 63.46 0.077 0.12 0.99部分补偿 63.14 0.83 1.31 0.99
表4 PCC 处总谐波畸变率情况
Tab.4 Total harmonic distortion at PCC
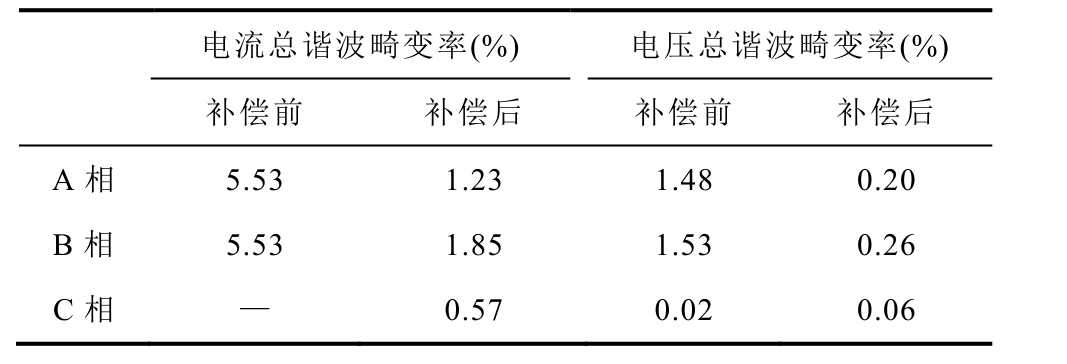
电流总谐波畸变率(%) 电压总谐波畸变率(%)补偿前 补偿后 补偿前 补偿后A 相 5.53 1.23 1.48 0.20 B 相 5.53 1.85 1.53 0.26 C 相 — 0.57 0.02 0.06
若采用三端口补偿模式,补偿后功率因数为0.99,即KC=0.30,根据式(23)计算得到KN=1 和KN=0.73下的SVG总无功量分别为35.312MV·A和12.22MV·A。对应的二端口补偿模式分别为33.95MV·A 和11.89MV·A。相较三端口补偿模式,二端口补偿模式下的SVG 容量较小。因此,选择二端口补偿模式进行补偿。进一步分析,若补偿后三相不平衡度满足 εU1∈[0,1.3%],即KN∈[0.35,1],最大无功补偿量和功率因数取值情况如图11 所示。由图11 可知,二端口补偿模式在一定程度上可以提高CTS 处的功率因数,但可能会带来过补偿的情形,导致功率因数较低。
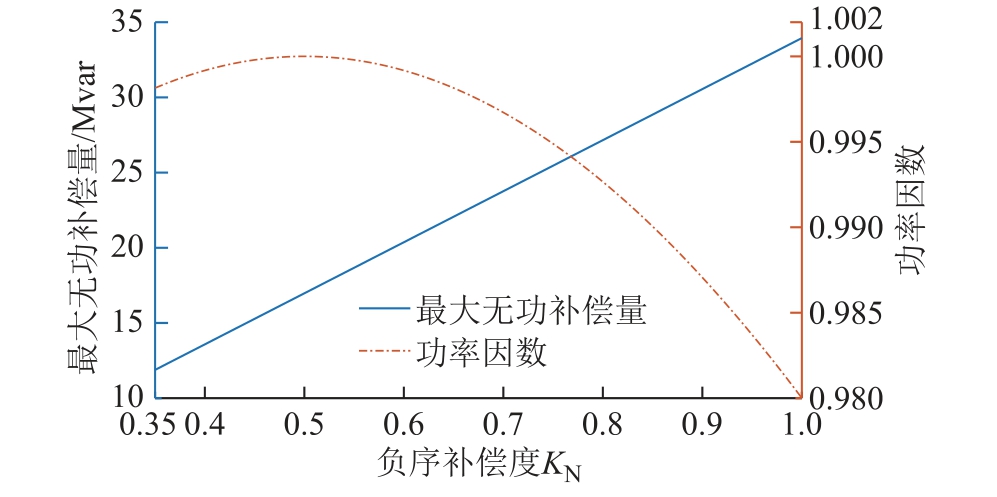
图11 最大无功补偿量和功率因数取值情况
Fig.11 The second simulating results of single cophase power supply
4.2 3 端口补偿模式仿真分析
以牵引变电所所群数量为3 为例分析,依次为牵引变电所1(CTS)、牵引变电所2、牵引变电所3。系统短路容量仍为1 500MV·A,某段时间内,3 个牵引所的视在功率分别为 20MV·A、25MV·A 和27MV·A,功率因数均为 0.98,PCC 处线电压为110kV,单相接线变压器电压比为110/27.5。
(1)采用三端口补偿模式完全补偿(εU1=0%,即KN=1;补偿后功率因数不变,即KC=0)和部分补偿(εU1=1.3%,即KN=0.73;补偿后期望功率因数不变仍为0.98,即KC=0)后PCC 处三相电流如图12a 和图12b 所示。补偿后三相电压不平衡度分别为0.16%和1.31%;补偿对应的功率因数均为0.97,基本达到设定要求。

图12 牵引变电所群贯通供电系统PCC 处补偿结果
Fig.12 Simulating results of interconnected traction power supply system for traction substation group at PCC
(2)采用二端口补偿模式部分补偿(εU1=1.3%,即KN=0.73)后PCC 处三相电流如图12c 所示。补偿后三相电压不平衡度分别为1.34%;补偿对应的功率因数为0.79,功率因数不符合相关标准要求[23]。
综上,二端口补偿模式虽然可以实现对于负序的补偿,但是由于造成功率因数较低,不满足相关国标的要求。因此,只有三端口补偿模式满足要求。
进一步分析,若补偿后三相不平衡度满足εU1∈[0,1.3%],即KN∈[0.73,1],如图13a 所示;功率因数不低于当前功率因数0.98,即KC∈[0,1],如图13b所示;此时根据式(23)确定该时间段内最大无功补偿量情况如图13c 所示。由图13 可知,补偿后的εU1 和功率因数取值变化时,KN 和KC 的取值不同,对应的SVG 容量也不同,统计最大无功补偿量的最小值为65.62MV·A,该最小值对应的 εU1 和功率因数分别为1.3%和1,即KN=0.73,KC=1,此时投资较少。因此,确定最大无功补偿量最小值对应的εU1和功率因数后,根据式(29)和式(31)可分别确定不同时刻KC 和KN 的取值。

图13 三端口补偿模式下相关值计算结果
Fig.13 Calculation results of relevant values for 3-port compensation mode
5 结论
本文提出一种基于YNd 变压器与SVG 的电气化铁路同相供电综合补偿方案及策略,得到如下结论:
1)基于YNd 变压器与SVG 的电气化铁路同相供电综合补偿方案分为二端口补偿模式和三端口补偿模式,对于任意功率因数牵引负荷三端口补偿模式是完备的;而二端口补偿模式在功率因数不为1的情形是不完备的,在一定范围内可实现负序的治理,同时提高了设置补偿装置处牵引所的功率因数,但是当出现过补偿的时候,会导致功率因数降低。
2)所提综合补偿方案及控制策略具有普适性,既适用于单所同相供电,同时也适用于长距离无分相贯通同相供电。相较全补偿,采用部分补偿模式后,在一定程度上能够降低各端口SVG 的容量,考虑到经济性及设备的容量,在国标允许的范围内采用部分补偿即可。
3)本文所提方案在实现PCC 点处负序治理的同时,可兼顾PCC 处因牵引负荷引起的谐波的治理。
[1] 李群湛. 牵引变电所供电分析及综合补偿技术[M].北京: 中国铁道出版社, 2006.
[2] 李群湛, 张进思, 贺威俊. 适于重载电力牵引的新型供电系统的研究[J]. 铁道学报, 1988(4): 23-31.Li Qunzhan, Zhang Jinsi, He Weijun. Study of a new power supply system for heavy haul electric traction[J]. Journal of the China Railway Society,1988(4):23-31.
[3] 李群湛. 我国高速铁路牵引供电发展的若干关键技术问题[J]. 铁道学报, 2010, 32(4): 119-124.Li Qunzhan. On some technical key problems in the development of traction power supply system for high-speed railway in China[J]. Journal of the China Railway Society, 2010, 32(4): 119-124.
[4] 李群湛. 论新一代牵引供电系统及其关键技术[J].西南交通大学学报, 2014, 49(4): 559-568.Li Qunzhan. On new generation traction power supply system and its key technologies for electrification railway[J]. Journal of Southwest Jiaotong University,2014, 49(4): 559-568.
[5] 李群湛. 论干线铁路与城市轨道统一牵引供电方式[J]. 中国科学: 技术科学, 2018, 48(11): 1179-1189.Li Qunzhan. Unified traction power supply mode for trunk railway and urban rail transit [J]. Scientia Sinica Technologica, 2018, 48(11): 1179-1189.
[6] 宫衍圣. 电力机车过关节式电分相过电压研究[J].铁道学报, 2008(4): 103-107.Gong Yansheng. Research of over-voltages of electric locomotive passing the articulated phase insulator [J].Journal of the China Railway Society, 2008(4): 103-107.
[7] [德]哈特穆特·比泽内克, 等. 电气化铁路牵引供电系统[M]. 戚广枫, 译. 北京: 中国铁道科学出版社,2019.
[8] 马茜, 郭昕, 罗培, 等. 一种基于超级电容储能系统的新型铁路功率调节器[J]. 电工技术学报, 2018,33(6): 1208-1218.Ma Qian, Guo Xin, Luo Pei, et al. A novel railway power conditioner based on super capacitor energy storage system[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1208-1218.
[9] 罗培, 杨维民, 周冠东, 等. 考虑供电臂电压波动的铁路功率调节器多目标优化设计[J]. 电工技术学报, 2018, 33(22): 5346-5356.Luo Pei, Yang Weimin, Zhou Guandong, et al. Multiobjective optimization design of railway static power conditioner considering voltage fluctuation of power supply arm[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5346-5356.
[10] 马茜, 郭昕, 罗培, 等. 基于超级电容储能的新型铁路功率调节器协调控制策略设计[J]. 电工技术学报, 2019, 34(4): 765-776.Ma Qian, Guo Xin, Luo Pei, et al. Coordinated control strategy design of new type railway power regulator based on super capacitor energy storage[J].Transactions of China Electrotechnical Society, 2019,34(4): 765-776.
[11] 王鹏程, 李勇, 安柏楠, 等. 基于不对称接线平衡变压器的电气化铁路电能质量混合调节系统[J].电工技术学报, 2019, 34(21): 4590-4600.Wang Pengcheng, Li Yong, An Bonan, et al.Asymmetrical connection balance transformer based hybrid power quality control system for electrical railway[J]. Transactions of China Electrotechnical Society, 2019, 34(21): 4590-4600.
[12] Uzuka T, Ikedo S, Ueda K. A static voltage fluctuation compensator for AC electric railway[C]//IEEE 35th Annual Power Electronics Specialists Conference,Aachen, German, 2004, 3: 1869-1873.
[13] 温建民, 王帮田, 方志国. 高速铁路地面自动过分相系统的研究与运用[J]. 铁道标准设计, 2011(4):104-108.Wen Jianmin, Wang Bangtian, Fang Zhiguo. Studies and applications of ground auto-passing neutral section separation system for high speed railway[J].Railway Standard Design, 2011(4): 104-108.
[14] 李群湛.城市轨道交通交流牵引供电系统及其关键技术[J].西南交通大学学报, 2015, 50(2): 199-207.Li Qunzhan.Industrial frequency single-phase AC traction power supply system and its key technologies for urban rail transit[J]. Journal of Southwest Jiaotong University, 2015, 50(2): 199-207.
[15] 李群湛, 郭锴, 解绍锋, 等. 一种电气化铁路外部电网供电构造: 中国, CN207045163U[P]. 2018-02-27.
[16] 邓惠华, 李国良, 周晓明, 等. 基于协调控制SVG的低压配网三相负荷不平衡治理技术[J]. 电工技术学报, 2017, 32(增刊1): 75-83.Deng Huihua, Li Guoliang, Zhou Xiaoming, et al. The control technology of three-phase unbalance load in low voltage distribution networks based on coordinated controlled SVGs[J]. Transactions of China Electrotechnical Society, 2017, 32(S1): 75-83.
[17] 翟灏, 卓放, 易皓, 等. 基于SVG 的电网多节点电压不平衡综合抑制方法[J]. 电力系统自动化, 2017,41(12): 40-47.Zhai Hao, Zhuo Fang, Yi Hao, et al. SVG based comprehensive unbalance suppression method for multi-node voltage[J]. Automation of Electric Power System, 2017, 41(12): 40-47.
[18] 中国国家标准化管理委员会. GB/T15543-2008 电能质量: 三相电压不平衡度[S]. 北京: 中国标准出版社, 2008.
[19] 中国国家标准化管理委员会. GB/T 14549—1993电能质量: 公用电网谐波[S]. 北京: 中国标准出版社, 1993.
[20] 王兆安, 杨君, 刘进军, 等. 谐波抑制和无功功率补偿[M]. 2 版. 北京: 机械工业出版社, 2005.
[21] 高本锋, 王飞跃, 于弘洋, 等. 应用静止同步串联补偿器抑制风电次同步振荡的方法[J]. 电工技术学报, 2020, 35(6): 1346-1356.Gao Benfeng, Wang Feiyue, Yu Hongyang, et al. The suppression method of wind power sub-synchronous oscillation using static synchronous series comnensator[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1346-1356.
[22] 王辉, 李群湛, 解绍锋, 等. 采用YNd-SVG 的电气化铁路负序补偿模型及控制策略[J/OL]. 高电压技术, 1-12[2020-05-12], https://doi.org/10.13336/j.1003-6520. hve.20200507027.Wang Hui, Li Qunzhan, Xie Shaofeng, et al. Negative sequence compensation model and control strategy of electrified railway with YNd tansformer and SVG[J/OL]. High Voltage Engineering, 1-12[2020-05-12], https://doi. org/ 10.13336/ j.1003-6520.hve.20200507027.
[23] 张丽艳, 李群湛, 易东, 等. 同相供电系统潮流控制器容量的优化配置[J]. 电力系统自动化, 2013,37(8): 59-64.Zhang Liyan, Li Qunzhan, Yi Dong, et al. Capacity optimization of power flow controller used in a cophase traction power supply system[J]. Automation of Electric Power System, 2013, 37(8): 59-64.