0 引言
随着智能配电网的快速发展，以及大量的精密仪器和敏感设备被广泛应用，越来越多的电能质量问题逐渐突显出来，而其中的电压跌落问题便是影响电力负荷稳定运行的最主要问题之一[1-6]。动态电压恢复器（Dynamic Voltage Restorer, DVR）凭借其运行效率高、可靠性高和快速性好等优势，成为目前解决电力系统中电压跌落问题最为经济、有效的动态补偿装置[7-10]。
DVR 的电压补偿策略主要有同相电压补偿、完全电压补偿以及最小能量补偿三种[11]。同相电压补偿需要输出的补偿电压幅值较小，但输出有功较大，对直流侧储能容量要求较高。最小能量补偿可以实现DVR 有功注入的最小化，充分有效地利用直流侧储能设备，但需要输出的补偿电压幅值较大，对逆变器容量要求较高[12]。目前，基于此方法对DVR的研究主要体现在优化控制策略、改进拓扑结构等方面[13-17]。优化控制策略方面：文献[14]以DVR 最大持续补偿时间作为控制目标，对最小能量补偿策略进行改进，并提出一种新的时间优化补偿策略，减少了直流侧能量损耗，延长了补偿时间；文献[15]提出了一种优化综合补偿策略，将同相补偿与最小能量补偿结合使用，在避免相角跳变的基础上，减小了有功输出并优化能量利用。但文献[14-15]并没有解决采用最小能量补偿策略时输出电压幅值增大的问题。改进拓扑结构方面：文献[16]提出在负载侧并联一个晶闸管控制电抗器（TCR）/晶闸管投切电容器（TSC）补偿器的改进型DVR 拓扑结构，减小了DVR 直流侧能量的消耗，达到减小储能设备容量和延长补偿时间的效果；文献[17]对DVR 接入系统的拓扑结构进行改进，在负载侧并联一个可调电抗器，提出了暂时降低负载功率因数的最小能量补偿策略，可扩大纯无功补偿的范围，减小有功消耗。但文献[16-17]同时也增加了设备的体积和成本。
总体来说，DVR 采用最小能量补偿策略时，虽然可在一定程度上降低有功需求，延长补偿时间，增大补偿能力，但不可避免地带来DVR 输出电压幅值增大的问题。如何在降低补偿过程中有功需求的同时，降低输出电压等级以有效降低装置整体容量，值得深入研究与探讨。针对以上问题和需求，本文借鉴LC 耦合并联型电能质量补偿装置的研发思想[18-20]，提出了一种串联电容耦合型DVR。相比于传统的DVR 结构，该系统在LC 滤波器的基础上增加了一个串联电容，基于最小能量补偿方法的同时通过合理设计，使串联电容上承受一个比较大的、滞后负载电流90°的电压，从而在不改变滤波效果的基础上，能够显著地降低逆变器的输出电压，进而有效地降低逆变器容量和直流侧电压等级。
本文首先介绍了串联电容耦合型DVR 的基本电路结构及工作原理，并与传统结构DVR 进行对比，分析了其优越性。然后，对逆变器的运行边界进行分析，给出了适用于串联电容耦合型DVR 的运行状态调整策略，在负载波动的情况下保证装置的正常稳定运行。接着，结合电压电流双闭环控制策略，分析了串联电容对控制系统稳定性及动态性能的影响，并完成了串联电容耦合型DVR 结构的选取。最后，通过仿真和实验验证了所提串联电容耦合型DVR 的有效性与可行性。
1 串联电容耦合型DVR 的基本电路结构及工作原理分析
1.1 拓扑结构
串联电容耦合型DVR 的基本电路结构如图1所示，该DVR 主要由六个部分构成[21-22]：由全控器件构成的PWM 逆变器、直流侧储能电容Cdc、LC输出滤波器、串联变压器T、旁路开关S 以及串联电容C。相比于传统DVR，该结构中增加了一个串联电容C，根据串联电容C 安装位置的不同，可分为两种不同的结构，即安装在滤波电容Cf 的右边（方案a）或者左边（方案b），如图1 所示。串联电容C 最优位置的确定将在第3 节进行详细阐述。
图1 串联电容耦合型DVR 的基本电路结构及控制框图
Fig.1 Circuit structure and control block diagram of series capacitance coupled DVR
串联电容耦合型DVR 在a、b 两种方案下的系统等效电路如图2 所示。为了简化分析，将串联变压器视为理想变压器，理论分析中忽略了变压器耦合的影响。图中Lf、Cf 分别为滤波电感、滤波电容；C1、C2 为串联电容；Uinv 为逆变器输出电压，UL 为滤波电感上的电压，UC 为串联电容上的电压；Us、Ul、Udvr 分别为网侧电压、负载侧电压及DVR 注入的补偿电压；Zl 为负载等效阻抗。
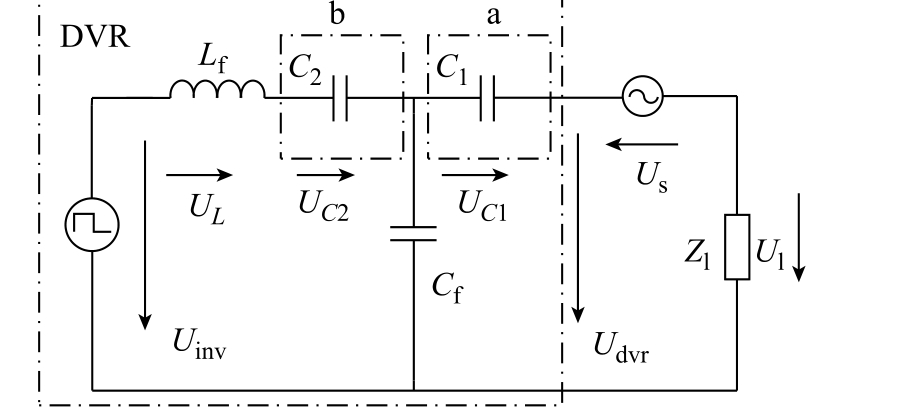
图2 系统等效电路
Fig.2 System equivalent circuit diagram
1.2 工作原理及参数设计
1.2.1 工作原理分析
相比于传统的DVR 结构，该系统在LC 滤波器的基础上增加了一个串联电容C，通过合理设计C的大小，在DVR 采用最小能量补偿策略时，串联电容C 上能够承受一个比较大的滞后负载电流90°的电压，从而在不改变滤波效果的基础上，能够显著降低逆变器的输出电压，进而有效地降低逆变器容量和直流侧电压等级。
当电网电压跌落时，实现DVR 有功注入的最小化可充分利用直流侧储能，提高DVR 的补偿能力。因此，最小能量补偿策略成为DVR 控制策略的最佳选择[23]。基于最小能量补偿策略，根据电网电压跌落深度的不同，DVR 存在三种不同的运行模式，包括纯无功补偿（ U s＞ U l cosϕ ）、临界补偿（ U s = U lcosϕ）和最小有功补偿（ U s＜ U l cosϕ ）[24]。传统DVR 和串联电容耦合型DVR 工作在这三种模式下时的相量图以及传统DVR 采用同相补偿策略时的相量图如图3 所示。
图3 DVR 工作相量图
Fig.3 Phasor diagram of DVR
则故障期间电网电压为
DVR 注入补偿电压的幅值和角度分别为
其中
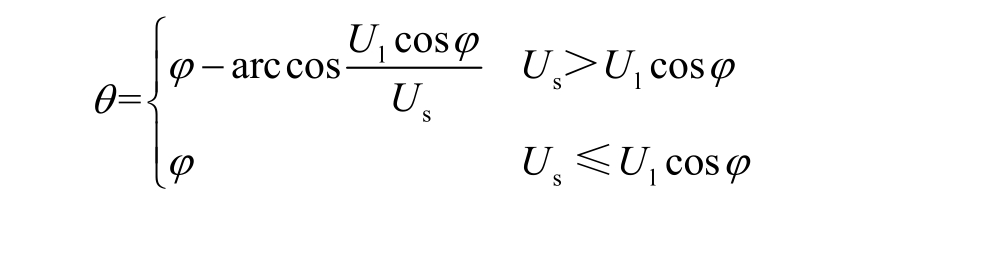
由此可得，传统DVR 和串联电容耦合型DVR的逆变器输出电压分别为
由式（6）可见，在同等系统参数环境下，通过合理设计 U˙ C的大小，可以有效减少逆变器输出电压U˙ inv，又由于逆变器输出电压的降低，从而可在串联电容后实现逆变器直流侧电压等级的降低。
1.2.2 串联电容的参数设计
本文所提结构中，滤波支路上承受电压的大小和串联电容 C 的大小密切相关，并且电网电压跌落幅度的不确定性以及负载的随机波动性也会对其产生影响。串联电容的参数设计需要综合考虑以上因素，既要满足系统的安全性、可靠性又要兼顾经济性。
该结构滤波支路上所承受的电压大小为
式中，Udvrn 为DVR 额定补偿电压；k 为承担系数，k 的取值需要综合考虑电网电压跌落幅度的不确定性及负载的随机波动性。当DVR 应用于电网电压跌落幅度较小的场合时，k 值可适当减小；反之，k值可适当增大。
对式（7）求解并化简，可得
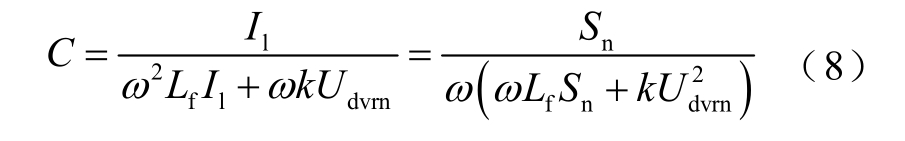
式中，Sn 为DVR 的额定容量。
同时，为使滤波支路的基波阻抗在工频下呈容性，而在特征谐波频率（主要是开关频率）下呈感性，需满足
式中， sω 为开关频率的角频率。
串联电容C 可由式（8）和式（9）确定。此外，对于滤波电感Lf 和滤波电容Cf 仍按照传统DVR 的选取原则进行确定。
1.3 串联电容耦合型DVR 的优势分析
1.3.1 逆变器的输出电压比较
根据式（5）和式（6）并结合仿真数据可以绘制出电网电压幅值跌落从10%至50%工况下，采用最小能量补偿策略时传统DVR、串联电容耦合型DVR以及采用同相补偿策略时传统DVR 的逆变器输出电压的基波有效值对比图，如图4 中实线折线所示。
图4 不同工况下的逆变器输出电压和有功功率对比
Fig.4 Comparison of inverter output voltage and active power under different operating conditions
以电网电压幅值跌落30%为例，采用最小能量补偿策略时串联电容耦合型DVR 和传统DVR 的逆变器输出电压的基波有效值分别为43V 和170V，采用同相补偿策略时传统DVR 的逆变器输出电压的基波有效值为88V。通过对比可以看出，除一些跌落幅度较小的场合，采用最小能量补偿策略时串联电容耦合型DVR 的逆变器输出电压不仅要比传统DVR 低得多，同时也比采用同相补偿策略时的传统DVR 低。如果仅用于治理跌落幅度较小的场合，可以通过适当增大C 的容值达到降低逆变器的输出电压的效果。
总的来说，串联电容耦合型DVR 与传统结构相比，由于耦合电容C 上承受了一个滞后负载电流90°的电压UC，在采用最小能量补偿策略后可以使得逆变器的输出电压得到有效降低。
1.3.2 逆变器的功率等级比较
DVR 的逆变器输出功率可表示为
式中， invP 和 invQ 分别为逆变器输出的有功功率和无功功率。
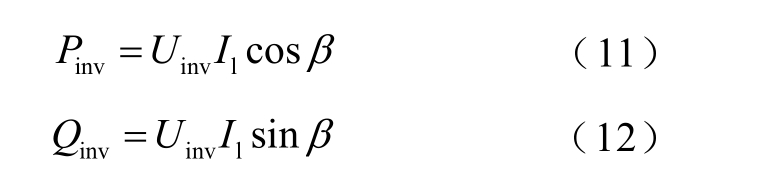
根据式（11）并结合图3 可以得到，在同一工况下，传统结构的DVR 与串联电容耦合型DVR 的逆变器输出有功功率相同，如式（13）所示。
同样地，可以得到两种结构DVR 的逆变器输出无功功率分别为
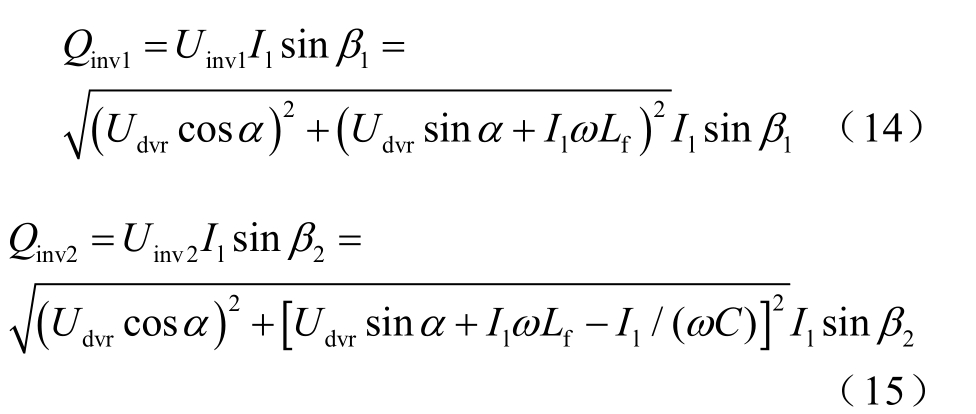
从式（14）和式（15）的分析对比可以看出，由于串联电容C 的存在，逆变器的输出无功可以得到一定的降低。如图4 中虚线折线所示，在DVR 整体控制模式不发生变化的情况下，其有功需求不变，但由于无功需求得到减小，那么逆变器整体的容量也就可以得到相应的减小。
2 负载波动下串联电容耦合型DVR 的运行状态调整策略
本文所提出的串联电容耦合型DVR，通过合理设计C 的大小，在采用最小能量补偿法补偿电网电压时，使得串联电容C 能够承受一个较大的滞后负载电流90°的电压UC，从而能够有效地降低逆变器的输出电压和容量。然而，UC 的值会受负载波动的影响而发生变化，逆变器所需输出的电压也将随之发生变化。考虑到逆变器的最大输出能力，在负载波动的情况下，为使逆变器输出电压不超过其极限值，必要时需做出相应的调整策略，以保证装置的正常稳定运行。
2.1 负载电流波动下的调整策略分析
滤波支路上承受电压ULCC 的大小直接受负载电流Il 的影响，当负载发生波动导致负载电流减小时，ULCC 也会随之减小。当负载电流减小而导致ULCC 过小时，可能会使逆变器输出电压超出其极限电压值，此时需要进行相应的运行状态调整，以保证逆变器输出电压在其极限范围之内，并且使得DVR 工作于输出能力范围内的最小能量补偿状态。
当负载电流减小时，表征DVR 运行状态的电压相量关系如图5a 所示。其中以O 为圆心的虚线圆弧表示逆变器输出电压的极限圆。从图5a 可以看出，由于负载电流Il 的减小，ULCC 也会随之减小，导致逆变器的输出电压Uinv 随之增大。当Il 减小到一定程度时，Uinv 便会超出其极限电压值Uinv-max，进一步会影响DVR 的正常工作。
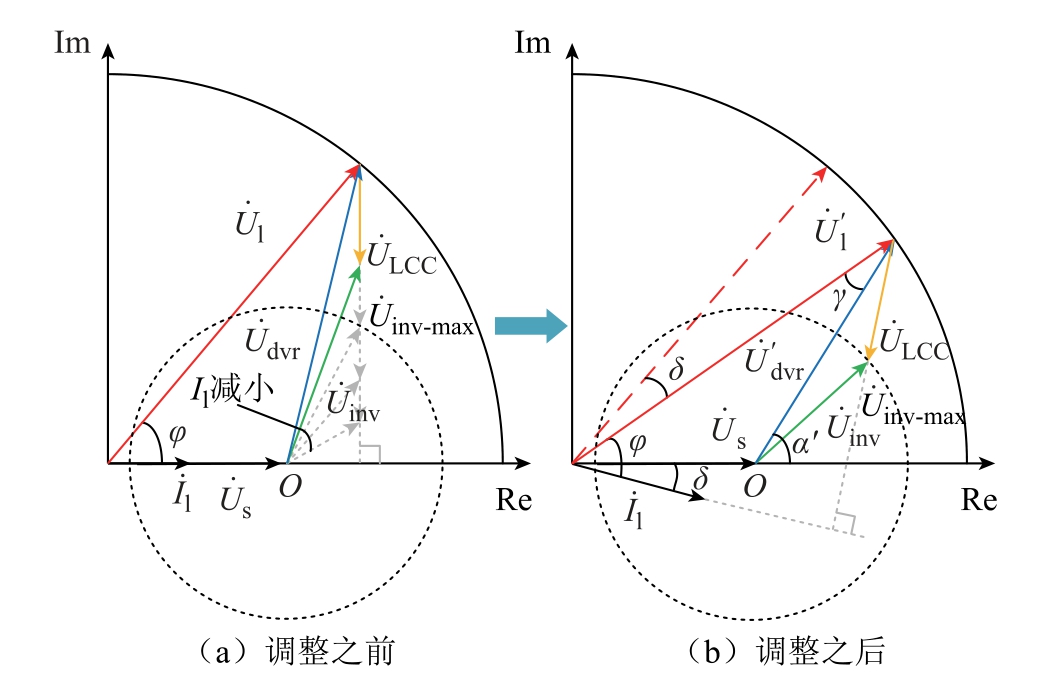
图5 负载电流变化时DVR 的工作相量图
Fig.5 Phasor diagram of DVR when load current changes
为避免负载电流减小带来的不利影响，需对DVR 的运行状态进行调整，具体如图5b 所示。为使得逆变器输出电压满足其极限输出要求，需要对负载电压Ul 进行一定角度的调整，这一调整角度可表示为δ 。
这里，逆变器输出电压Uinv 满足条件
式中，M 为调制比；Udc 为逆变器的直流侧电压。可以得到逆变器可输出的极限电压值为 U inv-max = MUdc 。
根据Us 和Ul 之间的关系，δ 可以由式（17）和式（18）推导出来。
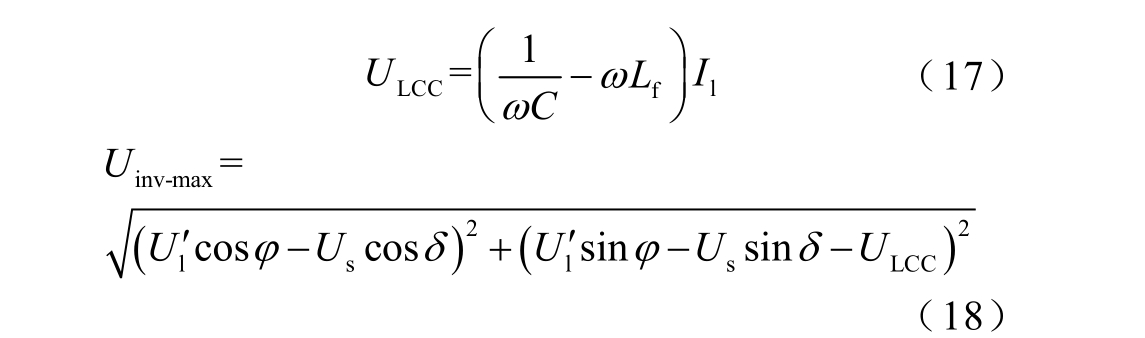
在确定了调整角度δ 之后，可以得到调整后的补偿电压幅值为
由式（19）、式（21）可知，通过调节角度δ 的大小，可以改变补偿电压的幅值和相位，从而最终使得逆变器输出电压满足其极限电压要求。
2.2 负载功率因数波动下的调整策略分析
当负载发生波动导致负载功率因数角ϕ 变化的情况下，由于ULCC 的大小不变，而DVR 所需输出的补偿电压幅值增大，也可能导致逆变器输出电压超出其极限电压范围，如图6a 所示。从图中可以看出，由于功率因数角ϕ 的不断增大，从而使得逆变器输出电压 Uinv 也随之增大，并最终超出了逆变器输出电压的极限圆。当然，功率因数角ϕ 减小的情况也可能会使逆变器输出电压超出其极限范围。
图6 功率因数变化时DVR 的工作相量图
Fig.6 Phasor diagram of DVR when power factor changes
因此，当负载功率因数角发生变化导致逆变器输出电压超出了其极限范围时，同样需要进行相应的运行状态调整，如图6b 所示。同理，调整角度δ 、调整后补偿电压幅值 dvrU' 和相位 'α 的计算过程与2.1 节类似。
3 串联电容耦合型DVR 最优结构的确定
为了探究串联电容对DVR 输出性能的影响，进而确定最优拓扑，下面将传统DVR 与串联电容耦合型DVR 在控制稳定性以及滤波效果等方面进行分析比较。两种不同方案下串联电容耦合型DVR的系统控制框图如图7 所示。
图7 串联电容耦合型DVR 的系统控制框图
Fig.7 System control block diagram of series capacitance coupled DVR
图7 中，Us 和Ul 分别为电网电压和负载电压，U*dvr、Uinv 和Udvr 分别为DVR 参考补偿电压给定值、逆变器电压指令值以及输出电压；Il、ILf 分别为负载电流和滤波电感电流；UC 为串联电容上所承受的电压；KPWM 为逆变器等效增益，为了简化分析这里取KPWM 为1。根据图7 中的控制框图，可以推导出不同方案下的系统传递函数。
根据式（22）、式（24），并通过改变串联电容C 的大小，可以得到输出电压实际值对参考补偿电压给定值的频率响应伯德图，如图8 所示；根据式（23）、式（25），并通过改变串联电容C 的大小，可以得到输出电压实际值对负载电流的频率响应伯德图，如图9 所示。
图8 输出电压对参考电压的伯德图
Fig.8 Bode plot of output voltage relative to reference voltage
图9 输出电压对负载电流的伯德图
Fig.9 Bode plot of output voltage relative to load current
从图8 可以看出：当采用方案b 时，其幅频特性和相频特性曲线在 100Hz 附近存在一个谐振尖峰，并且随着C 的逐渐增大，这一谐振尖峰会向左移动，由于这一谐振尖峰的存在可能会引起谐振，影响整个系统的稳定性；当采用方案a 时，则不会出现谐振尖峰，也就是说在滤波电容右侧增加了串联电容C 后，并不会影响系统的稳定性。同时可以看出，不论采用方案a 还是方案b，其幅频特性曲线和相频特性曲线都与传统DVR 基本重合，也就是说与传统DVR 相比，其在高低频段的频率响应特性基本不变，因此，增加串联电容C 后对滤波器的滤波效果影响很小。
从图9 可以看出：当采用方案b 时，其幅频特性曲线和相频特性曲线在100Hz 附近同样存在一个谐振尖峰。在低频段，对于串联电容耦合型DVR，当串联电容C 取值相同时，无论串联电容在滤波电容左侧还是右侧，其幅频特性曲线和相频特性曲线基本重合，表明这两种方案下系统对负载电流扰动在低频段的抑制作用基本相同。在高频段，采用方案b 时与传统DVR 的幅频特性曲线和相频特性曲线基本重合，即两者的高频衰减能力基本一样；但采用方案a 时，能够看出其在高频段具有更好的高频衰减能力，可以更好地抑制负载电流中的谐波分量对输出电压的影响，并且C 的增大可以使其在高频段具有更好的高频衰减能力，可以更好地抑制负载电流中的谐波分量对输出电压的影响。
综合上述分析，本文最终选取方案a 的结构。
4 仿真与实验验证
4.1 仿真分析
为了验证串联电容耦合型DVR 的可行性，在Matlab/Simulink 仿真平台中搭建了单相DVR 仿真模型进行仿真分析，仿真参数见表1。
表1 DVR 仿真参数
Tab.1 Simulation parameters of DVR
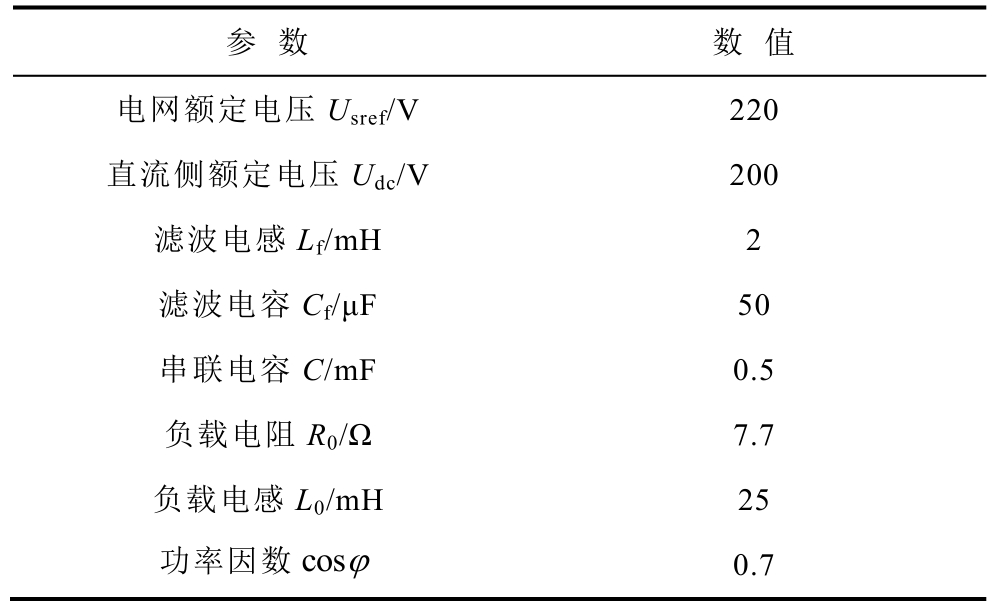
参 数 数 值电网额定电压Usref/V 220直流侧额定电压Udc/V 200滤波电感Lf/mH 2滤波电容Cf/μF 50串联电容C/mF 0.5负载电阻R0/Ω 7.7负载电感L0/mH 25功率因数cosϕ 0.7
4.1.1 补偿功能仿真
图10 为串联电容耦合型DVR 补偿电网电压的仿真波形。图中，0.10～0.20s 时电网电压跌落幅度为20%，0.30～0.40s 时电网电压跌落幅度为40%。按照式（3）可计算得到，0.10～0.20s 时DVR 的输出参考值为 
= 71.8V ；0.30～0.40s 时DVR 的输出参考值为 
= 159V 。从图10 可以看出，在直流侧电压仅为200V 的情况下，串联电容耦合型DVR仍然可以正常工作。在电网电压跌落时，串联电容耦合型DVR 能够输出足够大的电压来完成补偿，且逆变器的输出电压较小。随着电压跌落幅度的增大，串联电容耦合型DVR 在逆变器输出电压Uinv较低的情况下，Udvr 依然可以达到参考值 U d*vr，能够实现对跌落电网电压的补偿。即使在较低的直流侧电压等级下，串联电容耦合型DVR 也能拥有良好的补偿效果。
图10 串联电容耦合型DVR 补偿验证的仿真波形
Fig.10 Simulation waveforms of series capacitance coupled DVR compensation verification
图11 为DVR 与系统输出功率对比结果。在0.10～0.20s 期间，由于 U s＞ U l cosϕ ，DVR 工作在纯无功补偿状态，其输出的有功功率Pdvr 几乎为零，主要是通过输出无功功率Qdvr 来补偿电网电压。此外，在DVR 补偿期间，系统侧输出有功功率Ps 基本上可以维持不变。在 0.30～0.40s 期间，由于U s＜ U l cosϕ，DVR 工作在最小有功补偿状态，DVR需要输出一定有功功率Pdvr，但主要仍是输出无功功率Qdvr 进行电网电压补偿。
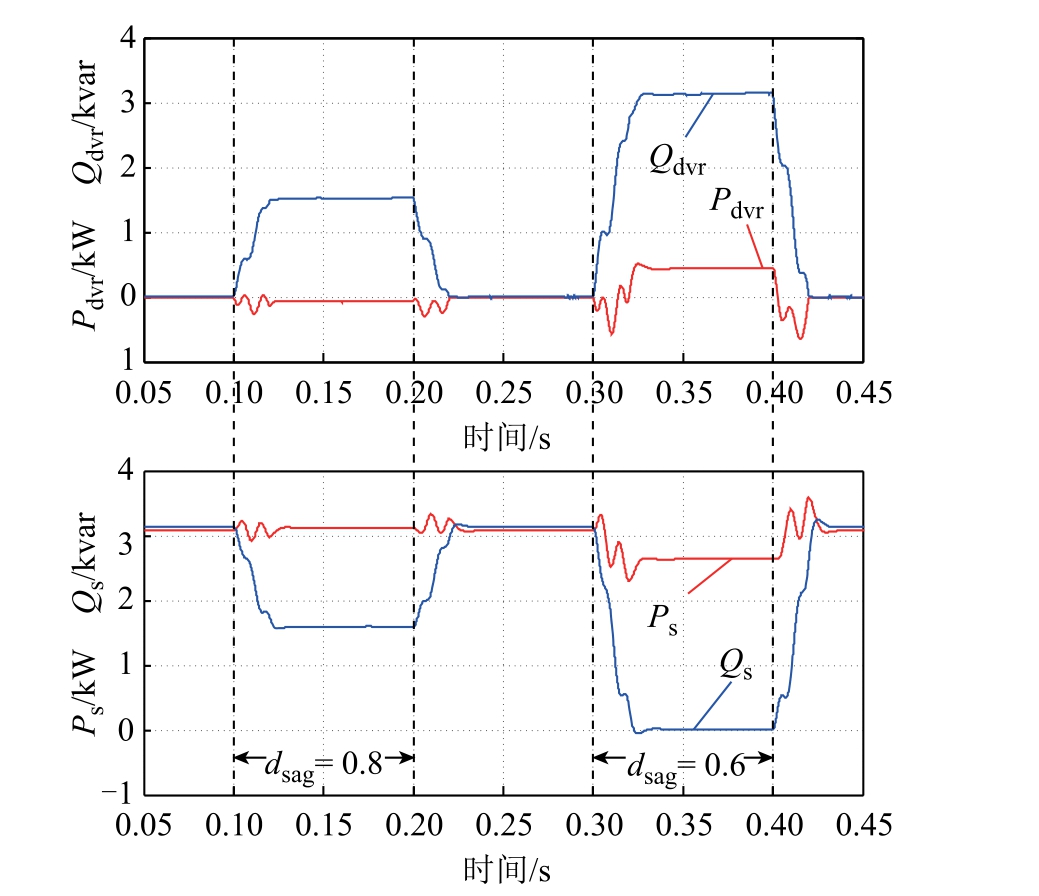
图11 DVR 与系统输出功率仿真波形
Fig.11 DVR and system output power simulation waveforms
4.1.2 运行状态调整策略仿真
图12 为串联电容耦合型DVR 在负载波动时进行状态调整的仿真波形。当负载电流减小到原来的1/4，DVR 滤波支路上的电压ULCC 也减小到原来的1/4，因此导致逆变器输出电压随之升高。根据仿真参数，设定逆变器输出电压的极限值为Uinv-max=0.4（pu）=88V。仿真中设置电网电压在0.30～0.50s 期间发生跌落，跌落幅度为30%，其中0.30～0.40s 未进行状态调整，0.40～0.50s 进行了相应的状态调整。
图12 串联电容耦合型DVR 进行状态调整仿真波形
Fig.12 Simulation waveform for state adjustment of series capacitance coupled DVR
负载电流减小后，根据式（17）可计算得到，滤波支路上所承受的电压也随之减小为ULCC=29V。在0.30～0.40s 未进行状态调整期间，逆变器的输出电压大大提高并超出了设定的极限范围Uinv-max=88V，进而导致DVR 输出的补偿电压未能达到对应的参考值，且谐波含量较大，影响最终的补偿效果。在0.40～0.50s 期间进行了状态调整，根据2.1 节计算公式可以得到，调节角度 δ= 15.24o、调整后补偿电压幅值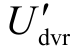
=116.8V 以及相位 
=72.2o。在进行调整后，所需输出的补偿电压得到降低，并且将逆变器输出电压限制到其极限范围内，保证了串联电容耦合型DVR 依然拥有良好的补偿效果。
对于因负载功率因数角变化而导致逆变器输出电压超出了其极限范围的情况，同样可以进行相应的运行状态调整，调整原理相似。
4.2 实验验证
为了进一步验证本文所提串联电容耦合型DVR 的正确性和有效性，对所提DVR 进行了实验验证，实验参数与仿真参数保持一致。
4.2.1 补偿功能实验
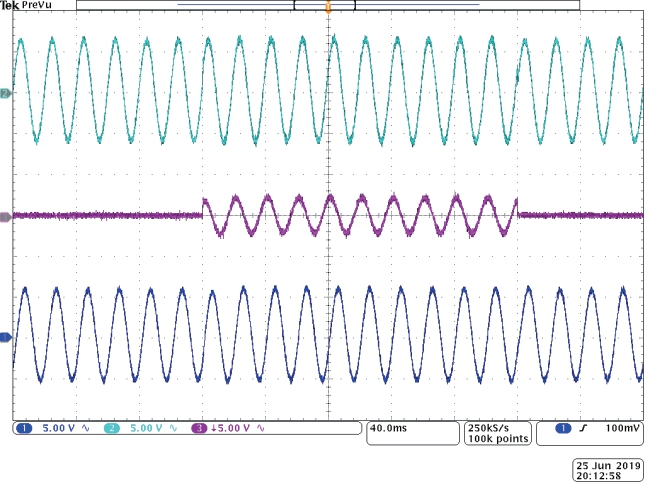
图13 dsag=0.8 时的实验波形
Fig.13 Experimental waveforms when dsag=0.8
电网电压跌落20%工况下的实验波形如图13所示。从图13a 可以看出，电网电压跌落期间，在直流侧电压只有200V 的情况下，串联电容耦合型DVR 可以快速并准确地补偿电网电压，具有很好的补偿效果；从图13b 可以看出，在逆变器输出电压Uinv=38V 时，串联电容耦合型DVR 的输出电压仍可达到71.8V，能有效地完成电压补偿。此外，从图13c 可知，在DVR 补偿期间，Udvr 与 lI 成90°的相位差，即DVR 工作在纯无功补偿状态，有效地减小了DVR 的有功消耗。
电网电压跌落40%工况下的实验波形如图14所示。从图14a 和图14b 可以看出，当电网电压跌落幅度为40%时，DVR 所需注入的补偿电压达到159V。在直流侧电压仍然采用200V 时，串联电容耦合型DVR 依然能够在逆变器输出电压较低的情况下，实现对跌落电网电压的补偿。由图14c 可知，在此工况下，Udvr 与 lI 成82°的相位差，电压补偿期间DVR 工作在最小有功补偿状态，主要仍是输出无功功率进行补偿。
图14 dsag=0.6 时的实验波形
Fig.14 Experimental waveforms when dsag=0.6
4.2.2 运行状态调整策略实验的实验波 电流减小 小到了29的输出电 由于受到 偿电压只 考值157V差。但在 小不变的 极限范围 到了调整期间的参考值117V，并且依然与负载电流成90°相位差，使得DVR 正常工作在临界补偿状态，具有良好的补偿效果。
图15 串联电容耦合型DVR 进行状态调整实验波形
Fig.15 Experimental waveforms for state adjustment of series capacitance coupled DVR
5 结论
本文提出了一种串联电容耦合型DVR，通过分析对比得到了串联电容耦合型DVR 最优拓扑结构，使其在保证稳定性的同时也具有很好的动态性能；考虑到负载波动的情况下，可能导致逆变器的输出电压超出其极限范围，给出了适用于串联电容耦合型DVR 的运行状态调整策略，以保证装置的正常稳定运行。最后，通过仿真和实验充分验证了本文所提串联电容耦合型DVR 的有效性与可行性，在采用最小能量补偿策略时，所提结构不仅可实现最小有功输出，还可以显著降低逆变器的输出电压，从而有效地降低逆变器的容量和直流侧电压等级。
对于串联电容耦合型DVR 的实际工程应用，仍有部分问题需要注意，比如考虑DVR 系统与电网侧耦合，串联电容可能会和线路寄生参数、变压器及电机等感性设备产生电气振荡等问题。后续将着重关注这一方面，继续深入研究其工程化应用提供更多的理论基础和技术指导。
[1] 涂春鸣, 孙勇, 郭祺, 等. 适用于动态电压恢复器的最小能量柔性切换控制策略研究[J]. 电工技术学报, 2019, 34(14): 3035-3045.Tu Chunming, Sun Yong, Guo Qi, et al. Study on the minimum energy soft-switching control strategy for dynamic voltage restorer[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3035-3045.
[2] 李哲, 吴正国, 夏立, 等. 任意负载条件下动态电压恢复器的复合谐振控制策略[J]. 中国电机工程学报, 2013, 33(25): 130-138, 20.Li Zhe, Wu Zhengguo, Xia Li, et al. Compound resonant control for dynamic voltage restorers under arbitrary load conditions[J]. Proceedings of the CSEE,2013, 33(25): 130-138, 20.
[3] 邓杰, 姜飞, 涂春鸣. 美国NIST 互操作性智能电网框架分析与启示[J].电力系统保护与控制, 2020,48(3): 9-21.Deng Jie, Jiang Fei, Tu Chunming. Study of NIST’s interoperable smart grid technology architecture[J].Power System Protection and Control, 2020, 48(3): 9-21.
[4] 陈汝斯, 林涛, 毕如玉, 等. 基于有限量测数据的主动配电网电压暂降源精确定位策略[J]. 电工技术学报, 2019, 34(增刊1): 312-320.Chen Rusi, Lin Tao, Bi Ruyu, et al. Strategy to precisely locate voltage sag source in active distribution grid with data measured by limited power quality observations[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 312-320.
[5] 杨用春, 肖湘宁, 郭世枭, 等. 基于模块化多电平变流器的统一电能质量调节器工程实验装置研究[J].电工技术学报, 2018, 33(16): 3743-3755.Yang Yongchun, Xiao Xiangning, Guo Shixiao, et al.Research of unified power quality conditioner engineering experiment device based on modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3743-3755.
[6] 马茜, 王文立, 许倩. 储能式统一电能质量控制器负载电压全补偿容量配置策略[J]. 电力系统自动化, 2019, 43(20): 90-99.Ma Qian, Wang Wenli, Xu Qian. Capacity allocation strategy for full compensation of load voltage in UPQC with energy storage[J]. Automation of Electric Power Systems, 2019, 43(20): 90-99.
[7] 施烨, 吴在军, 窦晓波, 等. 单相动态电压恢复器复合控制技术[J]. 电工技术学报, 2015, 30(17): 85-95.Shi Ye, Wu Zaijun, Dou Xiaobo, et al. Study on compound control technology of single-phase dynamic voltage restorer[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 85-95.
[8] 王艺博, 蔡国伟, 刘闯, 等. 基于双极性直接式AC/AC 变换的单相动态电压恢复器[J]. 电力系统自动化, 2020, 44(6): 171-180.Wang Yibo, Cai Guowei, Liu Chuang, et al. Singlephase dynamic voltage restorer based on bipolar direct AC/AC conversion[J]. Automation of Electric Power Systems, 2020, 44(6): 171-180.
[9] 陈国栋, 朱淼, 蔡旭. 功率因数与电压跌落深度双影响因子下中压 H 桥链式动态电压恢复器的滤波器优化设计[J]. 电工技术学报, 2016, 31(9): 75-84.Chen Guodong, Zhu Miao, Cai Xu. Optimization of filter based on power factor and voltage sag depth for medium-voltage cascaded H-bridge dynamic voltage restorer[J]. Transactions of China Electrotechnical Society, 2016, 31(9): 75-84.
[10] 涂春鸣, 孙勇, 李珺, 等. 双PWM 型动态电压恢复器的最大输出能力分析[J]. 电工技术学报, 2018,33(21): 5015-5025.Tu Chunming, Sun Yong, Li Jun, et al. Analysis of maximum output capability for dual-PWM dynamic voltage restorer[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 5015-5025.
[11] 刘颖英, 肖湘宁, 徐永海. 动态电压恢复器的能量稳定补偿特性分析[J]. 中国电机工程学报, 2010,30(13): 69-74.Liu Yingying, Xiao Xiangning, Xu Yonghai. Analysis of energy stability compensation characteristics of dynamic voltage restorer[J]. Proceedings of the CSEE,2010, 30(13): 69-74.
[12] 孙哲, 郭春林, 肖湘宁, 等. 基于负荷电压的 DVR补偿策略分析方法及最小能量控制[J]. 中国电机工程学报, 2010, 30(31): 43-49.Sun Zhe, Guo Chunlin, Xiao Xiangning, et al.Analysis method of DVR compensation strategy based on load voltage and minimum energy control[J].Proceedings of the CSEE, 2010, 30 (31): 43-49.
[13] 王世巍, 黄科, 许杏桃. 动态电压恢复器中的无电流内环控制策略[J]. 电力系统自动化, 2014, 38(18):93-98.Wang Shiwei, Huang Ke, Xu Xingtao. Control strategy for dynamic voltage restorer without inner current loops[J]. Automation of Electric Power Systems, 2014, 38(18): 93-98.
[14] 党存禄, 严鋆, 张晓英. 动态电压恢复器的时间优化补偿策略研究[J]. 电力系统保护与控制, 2011,39(5): 11-16.Dang Cunlu, Yanyun, Zhang Xiaoying. Analysis of time optimal compensation strategy for dynamic voltage restorer[J]. Power System Protection and Control, 2011, 39(5): 11-16.
[15] 李正明, 李文文, 张国松, 等. 一种补偿电网电压凹陷的 DVR 优化补偿策略[J]. 电力系统保护与控制, 2016, 44(17): 139-145.Li Zhengming, Li Wenwen, Zhang Guosong, et al. An optimized compensation strategy of DVR for gird voltage sag compensation[J]. Power System Protection and Control, 2016, 44(17): 139-145.
[16] 王晶, 徐玲玲, 王志琦. 改进型动态电压恢复器的最小能量法[J]. 电力系统保护与控制, 2013, 41(4):73-78.Wang Jing, Xu Lingling, Wang Zhiqi. Minimum energy method for improved dynamic voltage restorer[J]. Power System Protection and Control,2013, 41(4): 73-78.
[17] 唐治德, 余小闯, 金幸, 等. 动态电压恢复器的补偿策略研究与仿真分析[J]. 电气自动化, 2010,32(4): 63-65.Tang Zhide, Yu Xiaochuang, Jin Xing, et al.Compensation strategy and simulation for dynamic voltage restorer[J]. Electric Automation, 2010, 32(4):63-65.
[18] Karanki S B, Geddada N, Mishra M K, et al. A DSTATCOM topology with reduced DC-link voltage rating for load compensation with nonstiff source[J].IEEE Transactions on Power Electronics, 2012, 27(3):1201-1211.
[19] 成佳富, 何志兴, 周钦贤, 等. LC 耦合式级联STATCOM 及其控制策略[J]. 电力自动化设备,2018, 38(10): 127-132, 139.Cheng Jiafu, He Zhixing, Zhou Qinxian, et al. LC coupled cascade STATCOM and its control strategy[J].Power Automation Equipment, 2018, 38(10): 127-132,139.
[20] 罗培, 黄强, 陈跃辉, 等. 一种中性线串接电容的LC 耦合型配电网静止同步补偿器拓扑结构[J]. 电网技术, 2018, 42(10): 3385-3392.Luo Pei, Huang Qiang, Chen Yuehui, et al. A neutralline series capacitor LC-coupled distribution network static synchronous compensator topology[J]. Power System Technology, 2018, 42 (10): 3385-3392.
[21] 黄本润, 夏立, 吴正国, 等. 线电压补偿型动态电压恢复器的双前馈加反馈控制策略[J]. 电力自动化设备, 2011, 31(10): 61-64, 69.Huang Benrun, Xia Li, Wu Zhengguo, et al. Double feedforward plus feedback control strategy for line voltage compensated DVR[J]. Power Automation Equipment, 2011, 31 (10): 61-64, 69.
[22] 张新闻, 同向前. 电容耦合型动态电压恢复器参数建模与控制[J]. 电工技术学报, 2016, 31(6): 212-218.Zhang Xinwen, Tong Xiangqian. Parameter modeling and control of capacitor-coupled dynamic voltage restorer[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 212-218.
[23] 侯世英, 刘早晨, 嵇丽明, 等. 基于最小有功注入策略的新型级联 H 桥逆变器动态电压恢复器[J].电网技术, 2009, 33(17): 96-101.Hou Shiying, Liu Zaochen, Ji Liming, et al. A novel cascaded H-bridge inverter for dynamic voltage restorer based on minimum active power injection strategy[J]. Power System Technology, 2009, 33(17):96-101.
[24] 黄永红, 徐俊俊, 孙玉坤. 基于最小能量补偿控制的微网动态电压恢复器[J]. 电工技术学报, 2014,29(12): 128-136.Huang Yonghong, Xu Junjun, Sun Yukun. Dynamic voltage restorer in micro-grid based on a minimum energy compensation control scheme[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 128-136.