0 引言
以风电为代表的新能源大规模接入电网成为现代电力系统的主要特征[1-2]。为了提高大规模风电场运行性能,需要配置各类无功补偿设备,静止无功发生器(Static Var Generator, SVG)由于控制灵活被广泛应用[3-4]。风电机组采用电力电子变流器接入电网,电力系统电力电子化特征明显,容易引发次同步振荡(Subsynchronous Oscillation, SSO)问题[5-6]。2015 年7 月,新疆哈密地区风电汇集区域发生了次同步频率下的大范围功率振荡[7],证实了弱交流电网和直驱风电机组(Direct Drive Permanent Magnet Synchronous Generator, D-PMSG)的相互作用可能引发相当严重的SSO。SVG 等电力电子设备的并网,加剧了大规模风电并网分析SSO 问题的困难。
分析直驱风电场并网引发的SSO 问题有多种方法,阻抗分析法是主流研究方法之一[8-9]。国内外已有文献采用阻抗分析法研究了直驱风电机组接入弱交流电网引发SSO 的机理与特性。文献[10]采用阻抗分析法研究了直驱风电场并网SSO 特性,并提出了锁相环参数优化设计方法。文献[11]通过将直驱风电机组和电网看成两个独立的子系统,通过阻抗建模及阻抗稳定判据分析风电机组与电网交互作用而引发的SSO 问题,随着电网连接电感值的增大,系统振荡频率降低,阻尼减小,系统发生不稳定SSO 的风险升高。
针对SVG 对风电机组并网SSO 的影响问题,文献[12]采用基于状态空间模型的特征根分析法研究了SVG 对风电场并网SSO 的影响。文献[13]研究了双馈风机与SVG 之间的交互作用及振荡特性,通过时域仿真分析了SVG 控制方式及控制参数对系统SSO 的影响。文献[14-15]从开环模式谐振的角度分析静止同步补偿器与多台直驱永磁风机之间的SSO 问题。文献[16-18]通过线性化状态空间方法研究直驱风机与SVG 的SSO 特性及交互作用,指出SVG 部分控制参数对系统SSO 特性的影响。
SVG 呈现怎样的序阻抗特性、如何从阻抗的角度揭示SVG 接入后系统产生SSO 的机理、SVG 控制方式及参数的变化对系统SSO 稳定性的影响规律,还需进一步分析。
鉴于此,本文针对含SVG 的直驱风电场并网系统,采用谐波线性化的建模方法,建立了SVG 的正负序阻抗模型。将传统的基于阻抗的稳定判据推广应用至多子系统,从阻抗的角度揭示了SVG 接入对风电场并网SSO 稳定性的影响机理,并从机理方面解释了SVG 在不同控制方式下系统SSO 稳定性不同这一实际问题。基于灵敏度给出了影响次同步振荡的静止无功发生器主导控制参数,分析了控制参数变化对振荡稳定性影响的规律。
1 静止无功发生器序阻抗模型
1.1 风电场并网系统结构
直驱风电场、SVG 并网系统如图1 所示。假定各直驱风电机组型号和运行控制参数相同,风电机组经升压后汇集接入35kV 母线。风电场汇集母线处安装无功补偿装置SVG。为后续研究方便,本文将风电机组和与其直接相连的箱式变压器看成一个整体,定义为风电场子系统;将SVG 定义为SVG子系统;将系统其余部分定义为电网子系统。
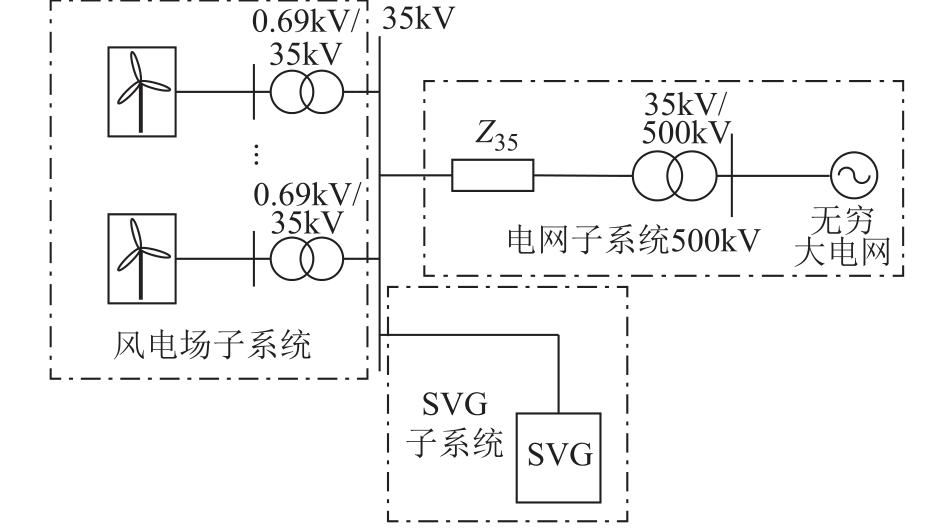
图1 直驱风电场并网系统结构示意图
Fig.1 Structure diagram of D-PMSGs integrated in an AC grid
1.2 SVG 序阻抗建模
1.2.1 系统概述
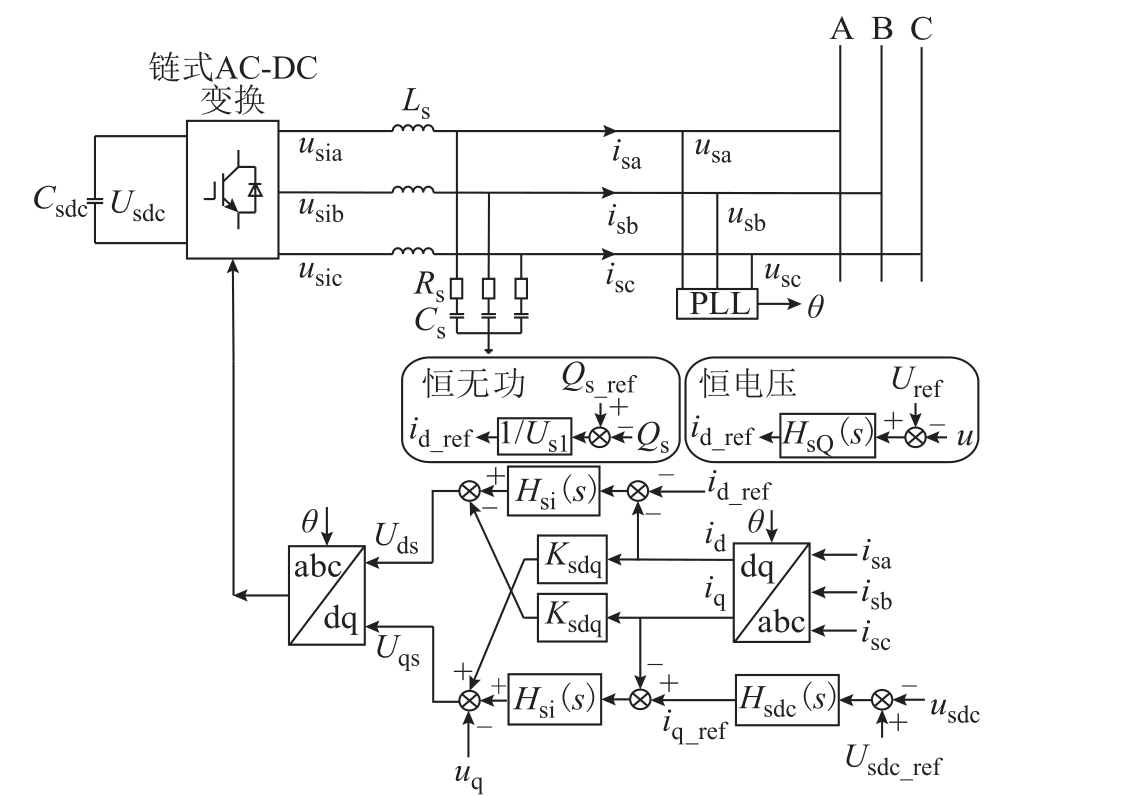
图2 SVG 电路及控制结构示意图
Fig.2 Schematic diagram of SVG
典型SVG 采用链式H 桥变流器电路,其控制结构示意图如图2 所示。其中usia、usib、usic 是变流器输出三相电压;isa、isb、isc 和usa、usb、usc 分别是SVG 并网点三相电流、电压;Csdc 是SVG 直流侧电容;Usdc 是直流侧电容电压。Ls、Cs 构成SVG 机端滤波电路;Hsi(s)是电流内环dq 控制环节的传递函数;Hsdc(s)是直流电压外环控制传递函数,Ksdq 是d轴与q 轴的交叉解耦系数,Ksdq=ω1Ls。SVG 具有恒无功、恒电压两种控制方式,HsQ(s)是采用恒电压控制方式时的外环传递函数。
为了获得SVG 在三相静止坐标系下的序阻抗模型,在并网点处注入谐波电压,该扰动经过控制回路及主电路后,在SVG 的输出电流中产生谐波电流响应。通过分析谐波电压、电流的幅值和相位,即可获得SVG 在三相静止坐标系下的输出正负序阻抗模型。
由于SVG 控制结构与直驱风电机组相类似,已有文献给出直驱风电机组的详细建模过程[11,16],这里SVG 与直驱风机相类似的部分模型不再赘述,仅对SVG 不同的重要环节进行建模。
考虑锁相环(Phase Locked Loop, PLL)的动态特性,并网点三相电流经过abc→dq 变换后,其频域解析式如式(1)所示。其推导过程与直驱风电机组类似[11],区别只在于直驱风机发有功,电压电流同相位,而SVG 发无功,电压电流互差90°,从而可得到dq 轴电流频域表达式为
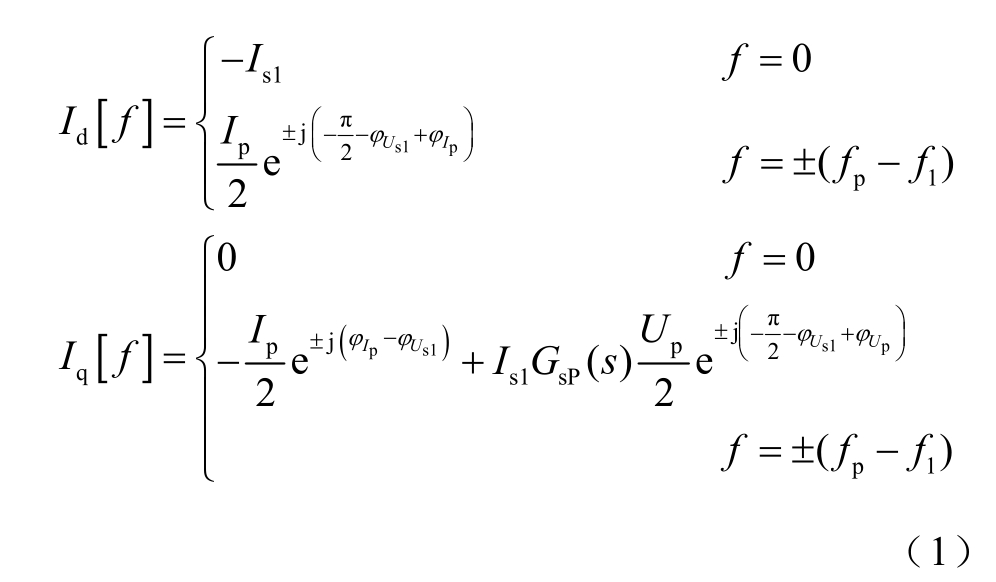
式中,Is1 为并网点基波电流幅值;Ip 为正序扰动电流幅值;φIp 为正序扰动电流初相位;φUs1 为并网点基波电压初相位;GsP(s)为PLL 传递函数;Up 为正序扰动电压幅值;φUp 为正序扰动电压初相位;fp 为正序扰动频率;f1 为基频。
1.2.2 无功功率外环建模
1)SVG 恒电压控制方式
SVG 恒电压模式下,为了保证并网点电压的稳定,SVG 无功功率外环以并网点电压u 和其参考值Uref 的差值为输入信号,经过比例积分PI 控制后得到d 轴电流参考值信号。根据并网点三相电压信号usa、usb、usc 可以获得无功功率外环输入电压信号u,即并网点电压有效值,计算公式为
依据三相半波可控整流原理,稳态时max(usa,usb, usc)输出相当于触发延迟角α=0°时的波形,此时输出电压平均值为
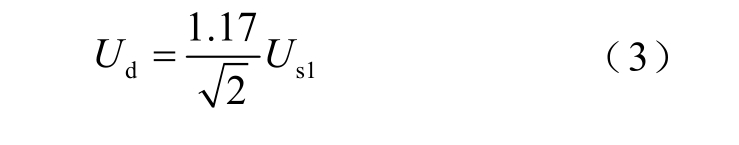

式中,Gi(s)为一阶惯性环节传递函数,其频域解析式为
式中,Gs 为一阶惯性环节的增益;Ts 为时间常数。
由式(4)可以进一步获得d 轴电流参考值扰动量的频域解析式为
式中,HsQ(s)为无功功率外环电压调节器传递函数。
2)SVG 恒无功控制方式
SVG 处于恒无功控制方式时,采用直接计算并输出电流参考值的控制方式,d 轴电流参考值为
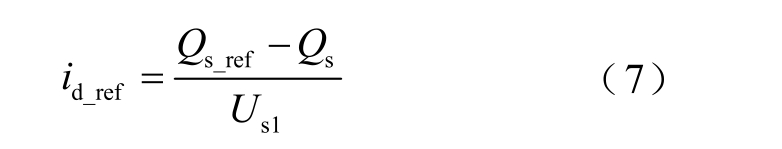
式中,Qs_ref 为无功功率参考值;Qs 为SVG 实际输出无功功率。
dq 坐标系下,SVG 输出无功功率与并网点电压、电流的关系为
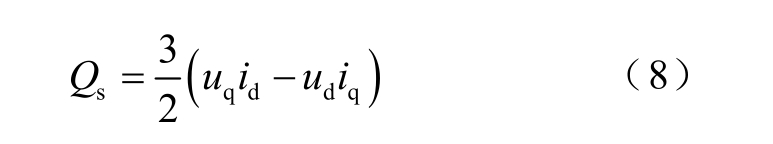
式中,ud、uq 和id、iq 分别为并网点电压和电流的d、q 轴分量。
由于稳态时SVG 输出有功功率接近于0,因此,并网点电流q 轴稳态分量iq0≈0,三相电压矢量定于-q 轴,因此,并网点电压d 轴分量ud0=0,所以,无功功率扰动量为
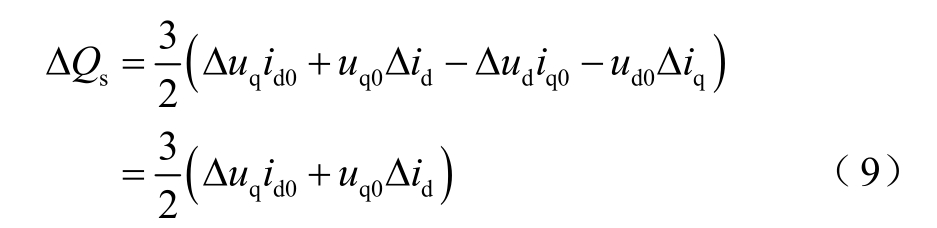
式中,Δid、id0 分别为并网点电流d 轴扰动值和并网点电流d 轴稳态值;Δuq、uq0 分别为并网点电压q轴扰动值和并网点电压q 轴稳态值。
将Δuq、Δid 代入式(9)可以获得SVG 输出无功功率扰动量频域解析表达式为
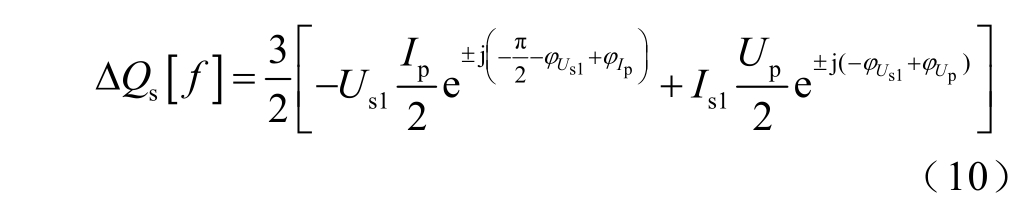
由式(10)可以进一步获得d 轴电流参考值扰动量的频域解析式为
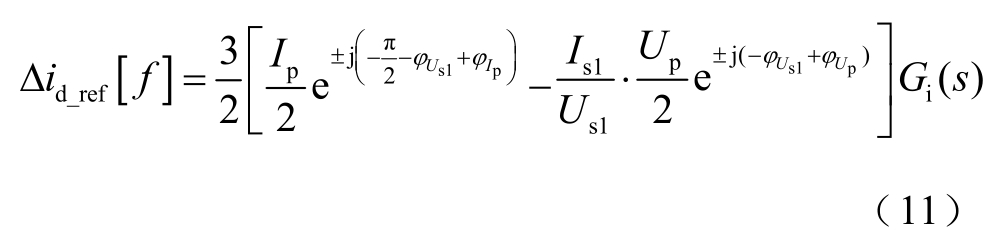
1.2.3 直流电压动态建模
与直驱风电机组直流电压动态建模过程相类似,根据直流侧与交流侧之间的功率平衡来推导直流电压扰动量的解析表达式。
SVG 直流侧电压扰动量为

式中,Uid0、Uiq0 和Iid0、Iiq0 分别为稳态时变流器输出电压Ui 和电流Ii 的d、q 轴分量;ΔUid、ΔUiq 分别为变流器输出电压d、q 轴扰动量;ΔIid、ΔIiq 分别为变流器输出电流d、q 轴扰动量;Usdc0 为稳态时SVG 直流母线电压;Csdc 为SVG 直流侧电容。
变流器出口电压Uid、Uiq 与并网点电压Ud、Uq和电流Id、Iq 之间的联系为
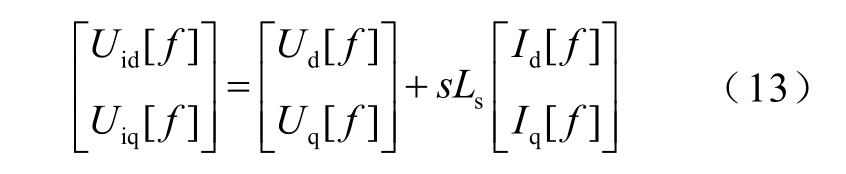
联立式(12)、式(13),将Ud[f]、Id[f]、Uq[f]、Iq[f]代入,便可进行SVG 直流侧电压扰动量的计算,如式(14)所示。
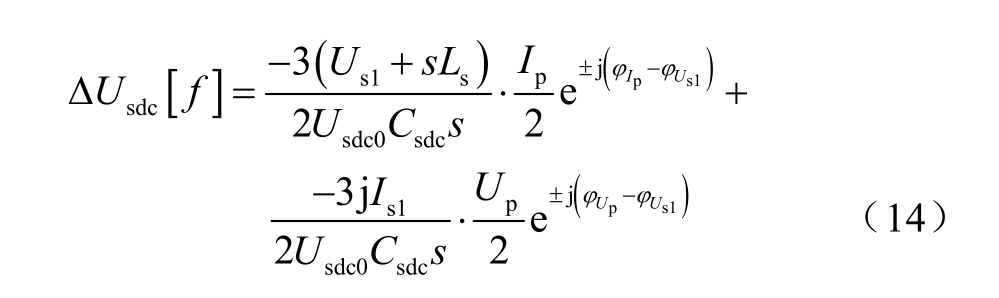
1.2.4 SVG 正负序阻抗解析表达式
dq 轴电流解耦控制环节输出信号Uds、Uqs 扰动量为
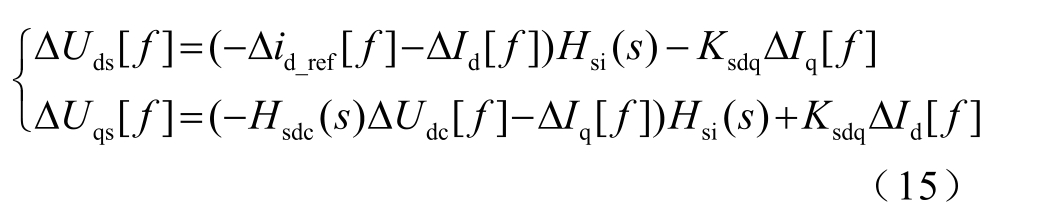
最后,通过解析推导,在恒电压控制模式和恒无功控制模式下的SVG 所输出的正序阻抗的数学解析表达式分别如式(16)和式(17)所示。依据相同的方法,可以获得SVG 在恒电压和恒无功两种模式下的输出负序阻抗数学解析表达式。
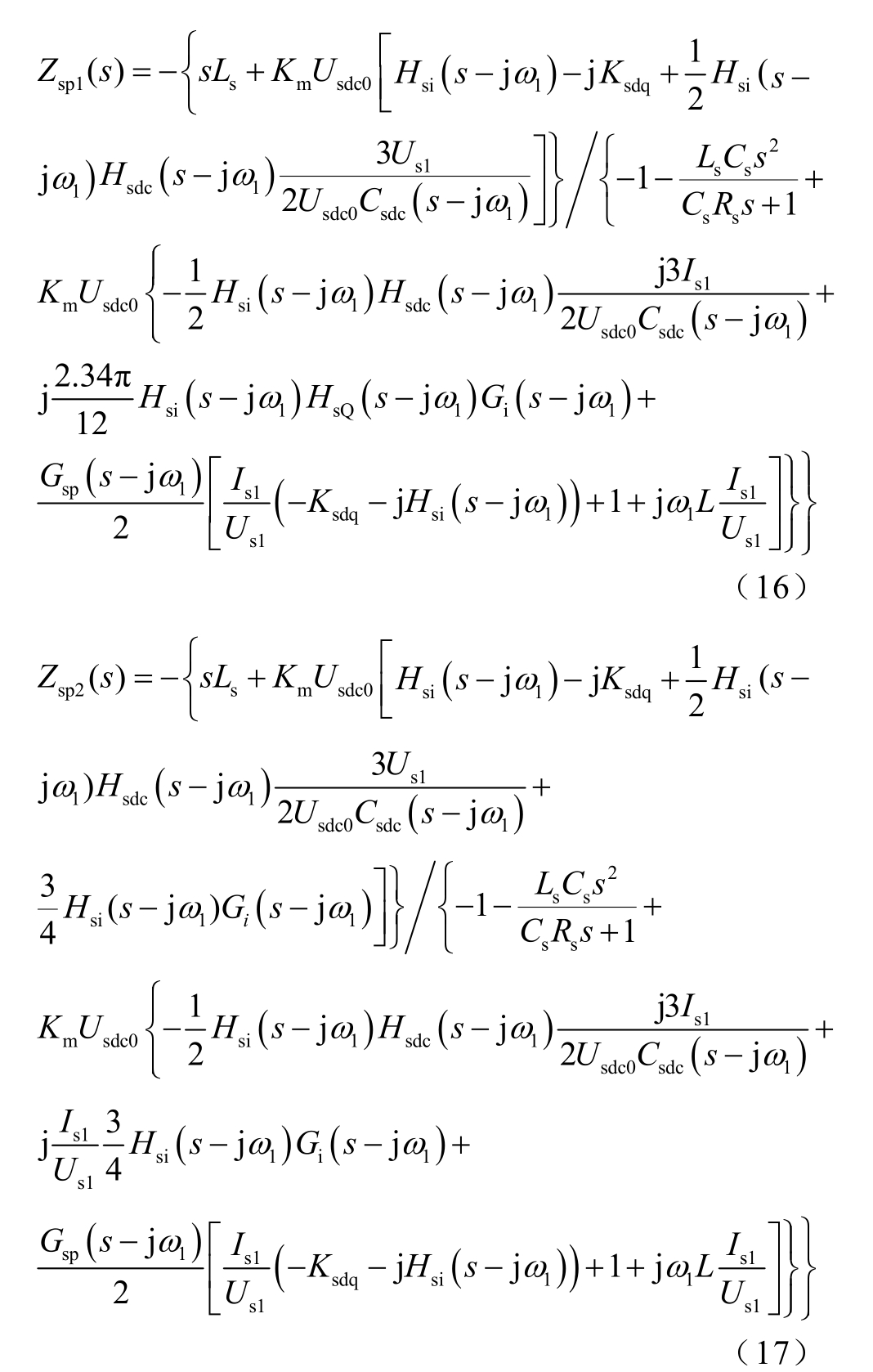
1.3 直驱风电机组序阻抗建模
本文采用谐波线性化的方法,考虑锁相环、电流内环、直流电压等环节,建立直驱风电机组输出正负序阻抗模型。直驱风电机组阻抗建模及参数已有文献论述[8,11]。
1.4 电网序阻抗建模
一般采用电阻和电感串联等值电网阻抗,并且常用连接的电抗值表征接入电网的强弱,所以本文采用电网侧阻抗模型为
1.5 SVG 输出正负序阻抗模型的验证
在PSCAD/EMTDC 仿真软件上依据图2 所示的SVG 电路结构及控制策略搭建SVG 时域仿真模型。SVG 并网系统参数见表1。
表1 SVG 并网系统参数
Tab.1 SVG grid-connected system parameters

参 数 数 值直流电压外环比例增益Ksdcp 15直流电压外环积分增益Ksdci 100无功功率外环比例增益KsQp 10无功功率外环积分增益KsQi 1 000电流内环比例增益Ksip 1电流内环积分增益Ksii 100锁相环比例增益Kspp 50锁相环积分增益Kspi 900额定直流电压Usdc0/kV 11.5滤波电感Ls/mH 0.075一阶惯性环节增益Gs 1一阶惯性环节时间常数Ts/s 0.02 dq 轴交叉解耦系数Ksdq 0.047 1直流侧电容Csdc/μF 90 000
在时域仿真模型中,通过频率“扫描”可以获得SVG 的输出正负序阻抗[11,19]。图3、图4 所示是5~1 000Hz 范围内,通过解析推导获得的SVG 输出正、负序阻抗解析曲线与时域仿真模型“扫描”获得的正、负序阻抗的对比。
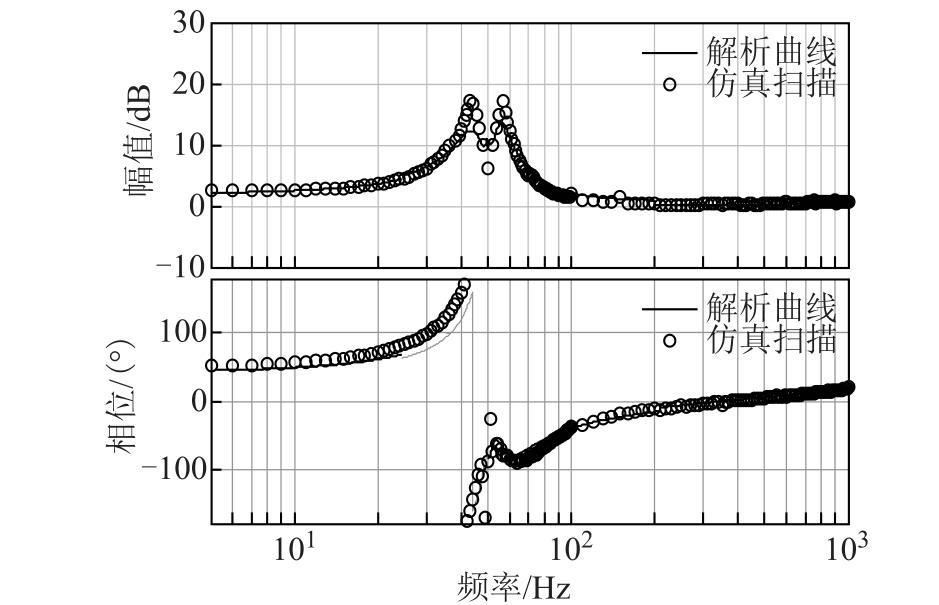
图3 SVG 正序阻抗曲线对比
Fig.3 SVG positive-sequence impedance comparison
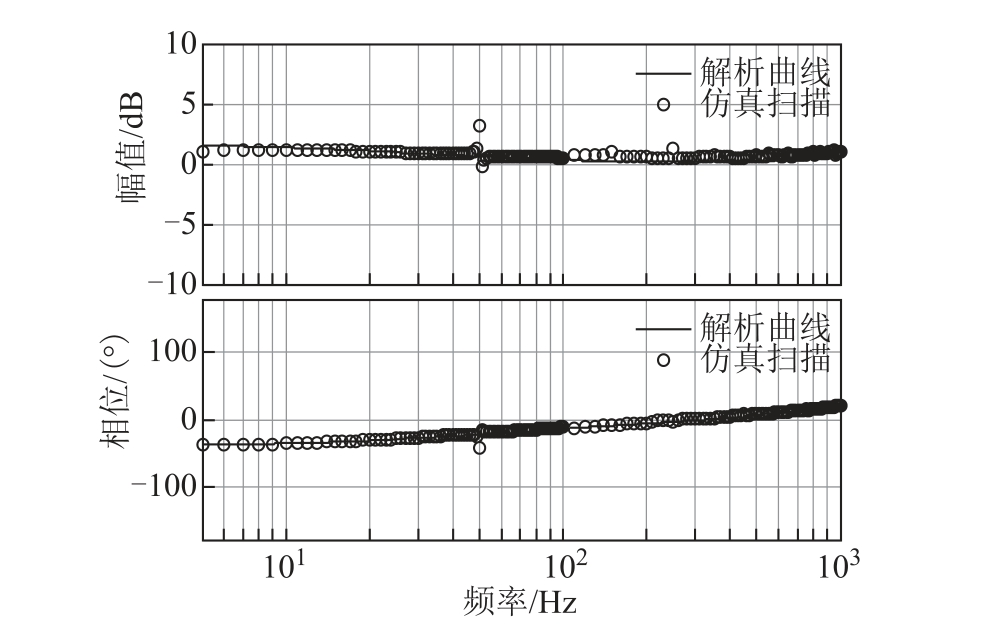
图4 SVG 负序阻抗曲线对比
Fig.4 SVG negative-sequence impedance comparison
结果表明,仿真“扫描”所得曲线和通过解析推导所得的SVG 输出正序阻抗曲线、负序阻抗曲线基本吻合,验证了阻抗解析表达式的正确性。谐波线性化是一种分析非线性系统的近似分析方法,通过准确推导可以获得较小的误差,得到较好的吻合效果。
2 基于序阻抗模型稳定判据的推广
2.1 基于阻抗的稳定判据原理
传统的基于序阻抗模型的稳定判据大多应用于两个子系统互联的稳定性分析,基于序阻抗模型的稳定判据如何应用至三个甚至多个子系统互联的稳定分析,目前还应用较少。所以,有必要说明基于序阻抗模型的稳定判据应用于三个子系统互联稳定分析的依据。
由于SVG 阻抗特性与直驱风电机组和电网均不相同,将SVG、直驱风电机组和电网看成三个独立的子系统,利用诺顿等效原则,可以将直驱风电场并网系统等效成由理想电流源、风电场输出阻抗、SVG 输出阻抗和电网输入阻抗组成的小信号电路等效模型[20],如图5 所示。根据电路叠加原理,图5 中电流I(s)的表达式可写为
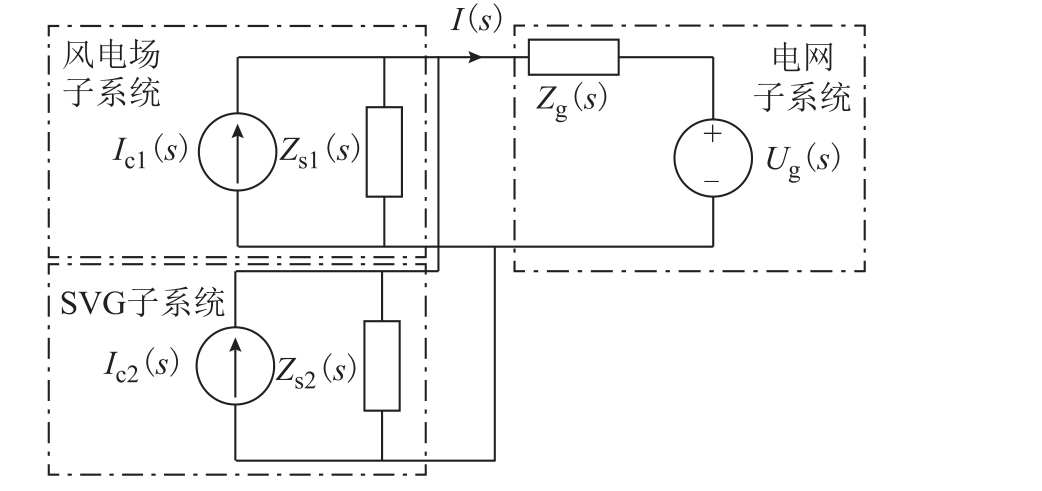
图5 基于阻抗稳定分析的小信号电路模型
Fig.5 Small-signal equivalent circuit based on impedance system stability criterion
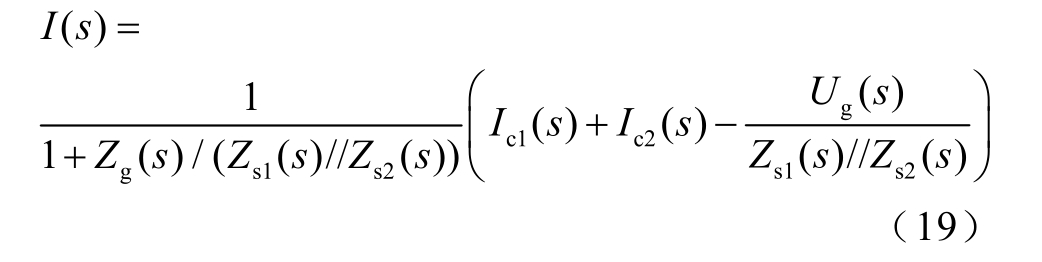
式中,Zs1(s)、Zs2(s)分别为风电场子系统、SVG 子系统输出阻抗;Zg(s)为电网输入阻抗。
若忽略直驱风电场和SVG 各自内部的振荡模式,仅考虑直驱风电场、SVG 与电网交互产生的SSO 问题。式(19)中,Ic1(s)、Ic2(s)是稳定的;Ug(s)/(Zs1(s)//Zs2(s))也是稳定的,因此I(s)的稳定性取决于式(20)是否稳定。
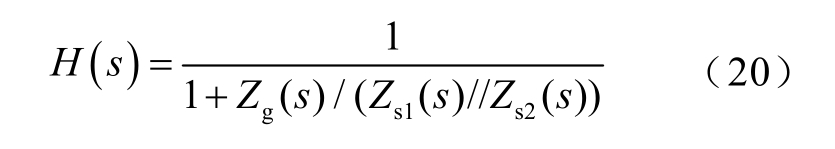
H(s)稳定的前提是Zg(s)/(Zs1(s)//Zs2(s))满足奈奎斯特稳定判据。
2.2 基于等效“RLC”电路的稳定判据
基于等效“RLC”电路模型的SSO 稳定性判别方法,省去了绘制奈奎斯特曲线的麻烦,并且可以从物理意义上解释直驱风电场并网产生SSO 的原因,因而在当前新能源发电并网稳定分析领域获得了应用。此等效电路模型认为,在振荡频率附近可以将直驱风电场并网系统总阻抗等效成为一个“RLC”二阶振荡电路[21]。根据三个子系统下的基于序阻抗模型的稳定判据,系统总阻抗Ztotal(s)为
等效“RLC”电路模型认为,Ztotal(s)虚部-频率特性曲线反映了系统呈现的电感/电容特性;Ztotal(s)实部-频率特性曲线反映了系统呈现的电阻特性。当某一频率下系统呈现的等效感抗与等效容抗相等,即系统总电抗为零时,系统发生谐振,此时,该频率对应的系统等效电阻的正、负决定了系统在SSO模式下的稳定性。
若等效电阻为正,系统在SSO 模式下的阻尼为正,系统SSO 稳定;反之,系统SSO 不稳定。
3 SVG 接入对风电场并网SSO 稳定性影响机理分析
3.1 稳定分析
第2 节在解析推导风电机组和SVG 输出正负序阻抗模型时所采用的基准电压不同,风电机组正负序阻抗模型是在0.69kV 为基准电压下获得的。为了后续分析的方便,本文将各子系统阻抗归算至35kV 侧。
设与风电机组相连的箱式变压器T1 的电压比为K1,等值阻抗为Z1(归算至35kV 侧)。由此,将式(21)进一步细化得到风电场并网系统总正序阻抗的计算公式为
式中,n 为并网风机数量;Zp(s)为单台直驱风机的正序输出阻抗;Zsp(s)为SVG 的正序输出阻抗。
SVG 的投入运行会改变系统总阻抗特性,从而使风电场并网SSO 特性发生改变。直驱风电场中并网风机数量为 500 台,每台风电机组出力水平为6.7%,2015 年新疆哈密振荡事故风机出力水平较低,所以选择低出力。电网等值阻抗Rg=0、Lg=0.013 4H,变压器T1 等值电抗为12.25Ω(高压侧);SVG 工作在恒电压模式。图6 所示为通过式(22)计算得到的风电场并网系统总阻抗Ztotal(s)的阻抗-频率曲线。

图6 SVG 接入前后系统阻抗特性
Fig.6 Impedance-frequency curve before and after SVG connected
基于阻抗模型的理论分析结果表明,SVG 并网后,系统等效电阻由1.152Ω 减小至-0.168 6Ω,呈现负电阻特性,系统发生不稳定SSO 的风险增加。
3.2 机理分析
在本文所研究的模型中,直驱风电机组并网SSO 振荡频率主要在60~80Hz 范围内的超同步频率段内。风电场和SVG 在60~100Hz 范围内的等效电抗曲线如图7 所示。
不难看出,对于风电场并网系统而言,由于风电场等效电抗在60~100Hz 范围内为负值,呈现电容特性,所以其容易与呈现电感特性的电网相互作用引发SSO。
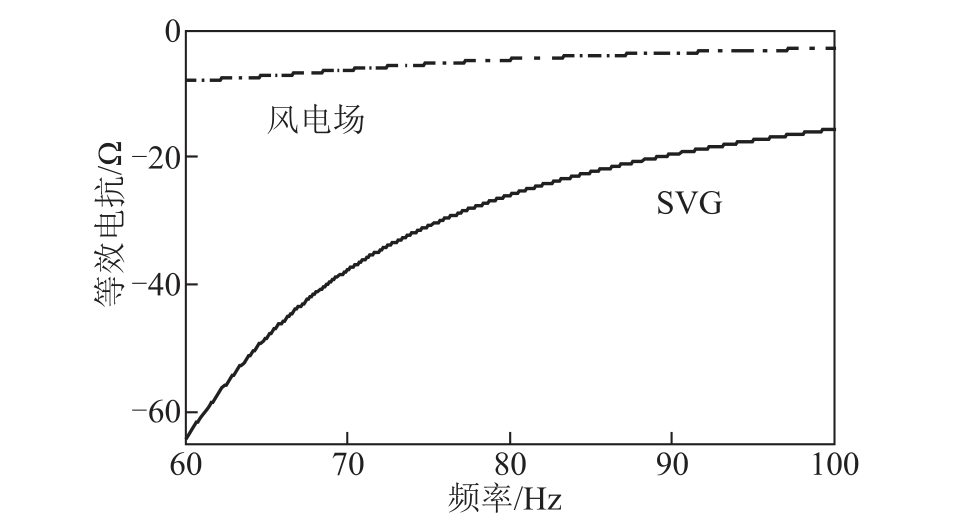
图7 风电场和SVG 的等效电抗曲线
Fig.7 Equivalent reactance curves of wind farm and SVG
由于SVG 在这一频率范围内也呈现电容特性,因此,SVG 的接入使得风电场与SVG 阻抗并联后电容特性更加明显,由于系统等效电容的增加,使得电容-电感谐振频率f 降低。同时,SVG 接入使系统等效电阻减小,最终呈现负电阻特性,在谐振频率处相当于负电阻与L、C 发生了振荡,导致不稳定SSO 风险。
4 SVG 控制方式及参数的影响
4.1 SVG 控制方式的影响及其机理分析
SVG 控制方式的不同会影响其输出阻抗特性,进而影响系统SSO 稳定性。直驱风电场中并网风机台数n=500,每台风电机组出力水平为6.7%;SVG采用典型运行控制参数,正常运行时SVG 补偿无功功率14Mvar,变压器T1 等值电抗为12.25Ω(高压侧),电网等值阻抗采用电阻与电感串联等效代替,等值电阻Rg=0;等值电感Lg=0.013 4H。图8 所示为SVG 分别处于恒电压和恒无功两种控制方式下系统阻抗Ztotal(s)的阻抗-频率曲线。

图8 SVG 不同控制方式下系统阻抗-频率曲线
Fig.8 System impedance-frequency curves in different SVG control method
基于阻抗模型的理论分析结果表明,SVG 处于恒电压控制方式时,系统等效电阻R=-0.120 9Ω,等效电阻为负,该工况下系统SSO 不稳定。SVG 处于恒无功控制方式时,系统等效电阻R=0.151 1Ω,等效电阻为正,该工况下系统SSO 稳定。
采用频率传递函数极点稳定性分析方法,恒电压模式下 tatalZ 一对极点为0.42±j2π×65.43;恒无功模式下Z(s)一对极点为-1.43±j2π×65.58。结果表明,SVG 处于恒电压控制方式下系统振荡频率为65.43Hz,阻尼为-0.42s-1,阻尼为负,系统SSO 不稳定;SVG 处于恒无功控制方式下系统振荡频率为65.58Hz,阻尼为1.43s-1,阻尼为正,系统SSO 稳定,与以上等效RLC 分析结论一致。
基于阻抗模型和阻抗稳定判据的分析结果说明,随着SVG 控制方式由恒电压转变为恒无功,系统振荡频率略微上升,阻尼增强,系统发生不稳定SSO 的风险降低。
60~100Hz 范围内,SVG 恒电压和恒无功两种控制方式下等效电抗曲线如图9 所示。
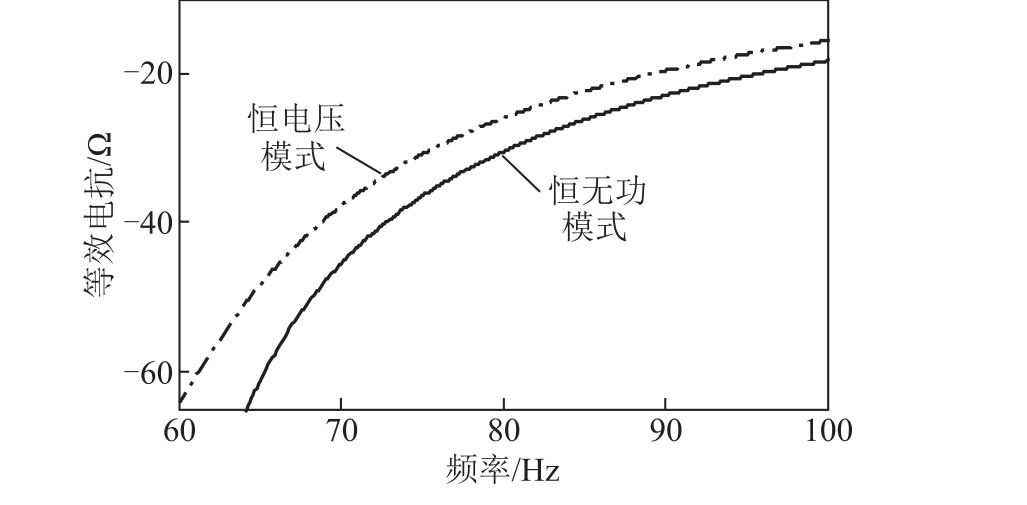
图9 SVG 恒电压和恒无功控制方式下等效电抗曲线
Fig.9 Equivalent reactance curves of SVG constant voltage and constant reactive power
结果表明,SVG 在恒电压和恒无功两种方式下均呈现电容特性;相比恒无功模式,SVG 在恒电压模式下等效容抗更小,呈现的电容特性更加明显。因此,当SVG 转变为恒无功模式后,由于系统等效电容的减小,使得电容-电感谐振频率f 升高,系统等效电阻增加,最终呈现正电阻特性,降低了系统发生不稳定SSO 的风险。
4.2 SVG 控制参数的影响
文献[11]提出通过计算系统阻抗对风机控制参数的阻抗灵敏度,直观地反映参数变化对系统阻抗的影响,从而确定影响风电并网SSO 稳定性的主导因素。同样,通过计算风电场并网系统阻抗Ztotal(s)对SVG 控制参数的阻抗灵敏度,可以确定SVG 控制参数中影响系统SSO 稳定性的主导因素,为高效制定基于SVG 控制参数优化调整SSO 抑制方案奠定基础。阻抗灵敏度表征了调节SVG 控制参数带来的系统阻抗频率特性变化大小,而系统SSO 稳定性和Ztotal(s)的频率特性存在直接的联系。
风电场运行及控制参数与4.1 节一致,SVG 处于恒无功控制方式,正常运行时SVG 补偿无功功率14Mvar,电网等值电阻Rg=0、等值电感Lg=0.014 7H。本文以60~80Hz 区间为例进行阻抗灵敏度分析,恒无功模式下SVG 各参数对应的阻抗灵敏度-频率曲线,如图10 所示。参数Ksip对应的阻抗实部灵敏度、阻抗虚部灵敏度数值均为最大,SVG 其他控制参数影响都较小。SVG 控制参数中,电流内环比例增益Ksip 是影响风电并网SSO 稳定性的主导因素。从图中看出,参数Ksip 的阻抗虚部灵敏度为负值,说明随着参数值的增大,等效电抗会减小,曲线下移,谐振频率增大;而阻抗实部灵敏度为正值,说明随着参数值的增大,等效电阻会增大,曲线上移,因此等效阻抗逐渐由负值变为正值,阻尼增强,SSO稳定性增强。
表2 Ksip 变化对系统SSO 稳定性的影响
Tab.2 Influence of Ksip change on system SSO stability
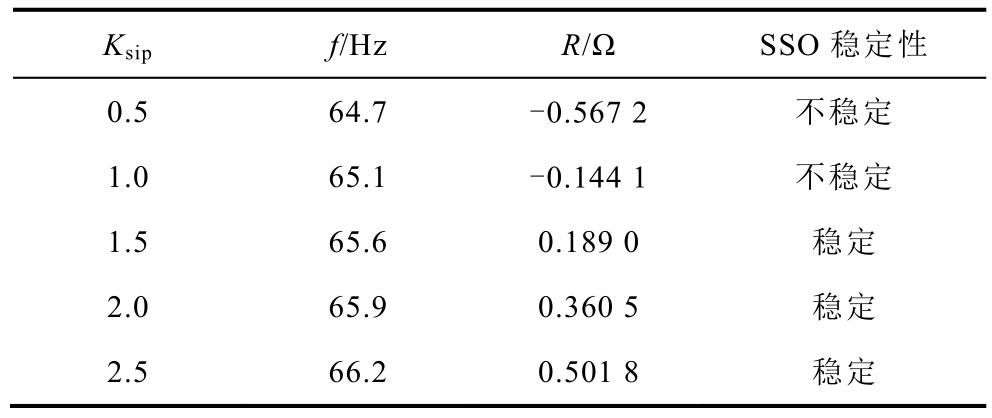
Ksip f/Hz R/Ω SSO 稳定性0.5 64.7 -0.567 2 不稳定1.0 65.1 -0.144 1 不稳定1.5 65.6 0.189 0 稳定2.0 65.9 0.360 5 稳定2.5 66.2 0.501 8 稳定
表2 中结果说明,随着电流内环比例增益的增大,等效电容-电感谐振频率升高,系统等效电阻增加,SSO 稳定性增强。这与灵敏度分析结果一致。
5 时域仿真
在PSCAD/EMTDC 仿真软件上依照图1 搭建直驱风电场并网系统时域仿真模型,电网采用电阻与电感串联进行等值。
并网风机台数n=500,采用500 台直驱风机机组等效,进行等值处理,每台风电机组出力水平为6.7%,并且将连接在风电汇集母线上的SVG 等值为一台,设置电网等值电阻Rg=0、等值电感Lg=0.013 4H,1s 时向系统加入一个扰动,激发出风电机组的暂态特性,2s 时SVG 以恒电压控制方式投入并网运行。风电场输出有功功率波形如图11 所示。
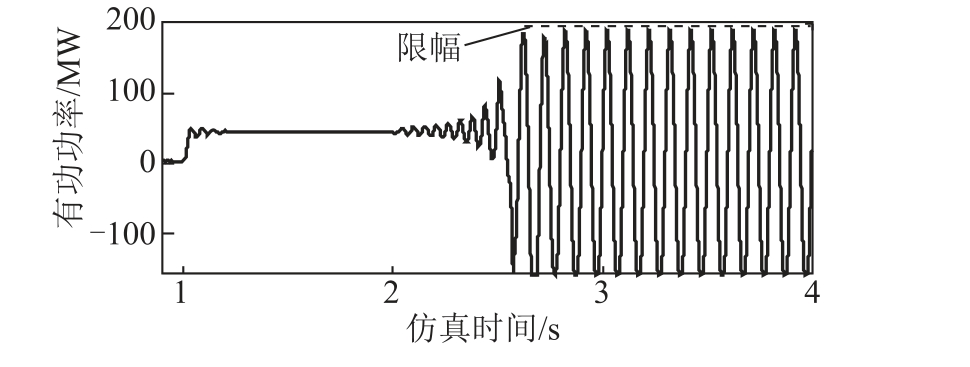
图11 SVG 并网前后风电场输出有功功率波形
Fig.11 Wind farm output active power before and after SVG connected

图10 SVG 控制参数阻抗灵敏度曲线
Fig.10 Impedance sensitivity curve of control parameters
单独改变电流内环比例增益Ksip 时,系统等效电阻R 及等效电容-电感谐振频率f 的变化情况见表2。
仿真结果表明,SVG 并网前,系统加入扰动后,系统保持SSO 稳定;随着SVG 的并网运行,风电场有功功率波形逐渐发散至限幅,系统SSO 不稳定。这说明,随着SVG 的并网运行,系统发生不稳定SSO 的风险增加,这一结论与基于阻抗模型的理论分析结果一致。
并网风机台数n=500,每台风电机组出力水平为6.7%,Rg=0、Lg=0.013 4H,2s 时SVG 以恒电压模式投入运行,2.4s 时将SVG 控制方式由恒电压转变为恒无功,补偿无功功率14Mvar。风电场输出有功功率波形如图12 所示。
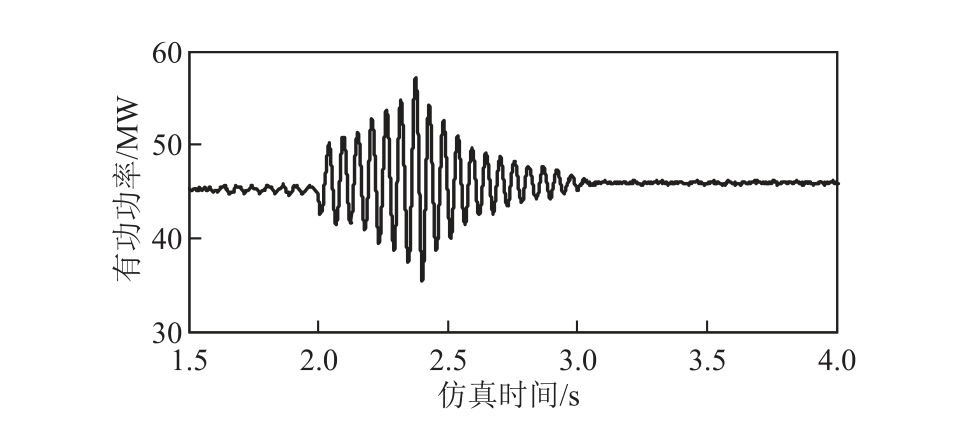
图12 SVG 不同控制方式下风电场输出有功功率波形
Fig.12 Wind farm output active power waveform in different SVG control method
仿真结果表明,随着SVG 控制方式由恒电压转变为恒无功,风电场输出有功功率波形由发散到收敛,系统稳定性提高,系统发生不稳定SSO 的风险降低。这一结论与基于阻抗模型的理论分析结果一致。
6 结论
本文针对含SVG 的直驱风电场并网SSO 问题,基于阻抗分析法,从阻抗特性的角度揭示了SVG 接入对系统SSO 稳定性的影响机理,并分析了其影响因素。
1)采用谐波线性化的建模方法,建立了SVG在恒电压、恒无功两种控制方式下的正负序阻抗模型,并验证了阻抗模型的正确性。
2)分析了SVG 接入对风电场并网SSO 稳定性的影响,并从阻抗的角度揭示了其影响机理。分析表明,SVG 接入后增加了系统发生不稳定SSO 的风险,其原因在于SVG 呈现的电容特性使得其与风电场阻抗并联后呈现更强的电容性质,更易于与电网交互作用产生SSO,同时系统等效电阻的减小使得SSO 更易失稳。
3)分析了 SVG 不同控制方式对风电场并网SSO 稳定性的影响。相比于恒无功模式,SVG 在恒电压模式下呈现更强的电容特性,系统等效电容-电感谐振频率的降低使得系统等效电阻减小,系统SSO 更易失稳。
4)分析了SVG 控制参数对系统SSO 稳定性影响的规律,并通过阻抗灵敏度分析辨识出SVG 控制参数中影响系统 SSO 稳定性的主导因素,在PSCAD/EMTDC 时域仿真模型上进行了验证。
SVG 不同控制方式的接入会影响并网点电压及电网运行方式,进而影响次同步振荡特性,未来还需对这一问题作进一步的研究分析。
[1] 盛逸标, 林涛, 陈宝平, 等. 面向新能源外送系统次/超同步振荡的控制器参数协调优化[J]. 电工技术学报, 2019, 34(5): 983-993.Sheng Yibiao, Lin Tao, Chen Baoping, et al.Coordination and optimization of controller parameters for subsynchronous/super-synchronous oscillation in new energy delivery systems[J].Transactions of China Electrotechnical Society, 2019,34(5): 983-993.
[2] 肖湘宁, 廖坤玉, 唐松浩, 等. 配电网电力电子化的发展和超高次谐波新问题[J]. 电工技术学报,2018, 33(4): 707-720.Xiao Xiangning, Liao Kunyu, Tang Songhao, et al.Development of power-electronized distribution grids and the new supraharmonics issues[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 707-720.
[3] 崔正湃, 王皓靖, 马锁明, 等. 大规模风电汇集系统动态无功补偿装置运行现状及提升措施[J]. 电网技术, 2015, 39(7): 1873-1878.Cui Zhengpai, Wang Haojing, Ma Suoming, et al.Operation situation analysis and improvement measure study for dynamic reactive compensation equipment applied in large-scale wind power systems[J]. Power System Technology, 2015, 39(7):1873-1878.
[4] 张智, 刘丽楠. STATCOM 在抑制次同步谐振及提高串补度的应用研究[J]. 电气技术, 2018, 19(11):46-54.Zhang Zhi, Liu Linan. Research on the suppression of subsynchronous oscillation and the improvement of series compensation by STATCOM[J]. Electrical Engineering, 2018, 19(11): 46-54.
[5] 谢小荣, 刘华坤, 贺静波, 等. 直驱风机风电场与交流电网相互作用引发次同步振荡的机理与特性分析[J]. 中国电机工程学报, 2016, 36(9): 2366-2372.Xie Xiaorong, Liu Huakun, He Jingbo, et al.Mechanism and characteristics of subsynchronous oscillation caused by the interaction between fullconverter wind turbines and AC systems[J].Proceedings of the CSEE, 2016, 36(9): 2366-2372.
[6] 苏田宇, 杜文娟, 王海风. 多直驱永磁同步发电机并联风电场次同步阻尼控制器降阶设计方法[J].电工技术学报, 2019, 34(1): 116-127.Su Tianyu, Du Wenjuan, Wang Haifeng. A reduced order design method for subsynchronous damping controller of multi-PMSGs parallel wind farm[J].Transactions of China Electrotechnical Society, 2019,34(1): 116-127.
[7] 李景一, 毕天姝, 于钊, 等. 直驱风机变流控制系统对次同步频率分量的响应机理研究[J]. 电网技术, 2017, 41(6): 1734-1740.Li Jingyi, Bi Tianshu, Yu Zhao, et al. Study on response characteristics of grid converter control system of permanent magnet synchronous generators(PMSG) to subsynchronous frequency component[J].Power System Technology, 2017, 41(6): 1734-1740.
[8] Cespedes M, Sun Jian. Impedance modeling and analysis of grid-connected voltage-source converters[J].IEEE Transactions on Power Electronics, 2013, 9(3):1254-1261.
[9] Bo Wen, Boroyevich D, Burgos R, et al. Small-signal stability analysis of three-phase AC systems in the presence of constant power loads based on measured d-q frame impedances[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5952-5963.
[10] 张冲, 王伟胜, 何国庆, 等. 基于序阻抗的直驱风电场次同步振荡分析与锁相环参数优化设计[J].中国电机工程学报, 2017, 37(23): 6757-6767.Zhang Chong, Wang Weisheng, He Guoqing, et al.Analysis of sub-synchronous oscillation of fullconverter wind farm based on sequence impedance and an optimized design method for PLL parameters[J]. Proceedings of the CSEE, 2017, 37(23):6757-6767.
[11] 张明远, 肖仕武, 田恬, 等. 基于阻抗灵敏度的直驱风电场并网次同步振荡影响因素及参数调整分析[J]. 电网技术, 2018, 42(9): 2768-2777.Zhang Mingyuan, Xiao Shiwu, Tian tian, et al.Analysis of SSO influencing factors and parameter adjustment for grid-connected full-converter wind farm based on impedance sensitivity[J]. Power System Technology, 2018, 42(9): 2768-2777.
[12] 王雪薇, 谢欢, 刘青, 等. SVG 对风电次同步振荡影响的研究[J]. 华北电力技术, 2017, 46(6): 37-41.Wang Xuewei, Xie Huan, Liu Qing, et al. Research on the effects of SVG to wind subsynchronous oscillation[J]. North China Electric Power, 2017,46(6): 37-41.
[13] 迟永宁, 田新首, 汤海雁, 等. 双馈风电机组与静止无功发生器交互作用原理及系统振荡特性研究[J]. 电网技术, 2017, 41(2): 486-492.Chi Yongning, Tian Xinshou, Tang Haiyan, et al.Interactions between DFIGs and SVG and oscillation characteristic of power grid connected wind turbines[J]. Power System Technology, 2017, 41(2):486-492.
[14] 任必兴, 杜文娟, 王海风. 静止同步补偿器与直驱永磁风机的次同步控制交互研究[J]. 电工技术学报, 2018, 33(24): 5884-5896.Ren Bixing, Du Wenjuan, Wang Haifeng. Analysis on sub-synchronous control interaction between static synchronous compensator and permanent magnet synchronous generator[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5884-5896.
[15] 王洋, 杜文娟, 王海风. 基于开环子系统模式信息的次同步谐振机理研究[J]. 电工技术学报, 2019,34(24): 5209-5220.Wang Yang, Du Wenjuan, Wang Haifeng. Mechanism study of subsynchronous resonance based on openloop modal information[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5209-5220.
[16] 周佩朋, 李光范, 宋瑞华, 等. 直驱风机与静止无功发生器的次同步振荡特性及交互作用分析[J].中国电机工程学报, 2018, 38(15): 4369-4378.Zhou Peipeng, Li Guangfan, Song Ruihua, et al.Subsynchronous oscillation characteristic and interactions of direct drive permanent magent synchronous generator and static var generator[J].Proceedings of the CSEE, 2018, 38(15): 4369-4378.
[17] 周佩朋, 宋瑞华, 李光范, 等. 直驱风电机组次同步振荡阻尼控制方法及其适应性[J] . 电力系统自动化, 2019, 43(13): 177-184.Zhou Peipeng, Song Ruihua, Li Guangfan, et al.Damping control method of subsynchronous oscillation for direct drive wind turbine generator and its adaptability[J]. Automation of Electric Power Systems, 2019, 43(13): 177-184.
[18] 刘宇明, 黄碧月, 孙海顺, 等. SVG 与直驱风机间的次同步相互作用特性分析[J]. 电网技术, 2019,43(6): 2072-2080.Liu Yuming, Huang Biyue, Sun Haishun, et al. Study on subsynchronous interaction between D-PMSG-based wind turbines and SVG[J]. Power System Technology, 2019, 43(6): 2072-2080.
[19] 陈斐泓, 杨健维, 廖凯, 等. 基于频率扫描的双馈风电机组次同步控制相互作用分析[J]. 电力系统保护与控制, 2017, 45(24): 84-91.Chen Feihong, Yang Jianwei, Liao Kai, et al. Subsynchronous control interaction analysis in doubly-fed induction generator based on frequency scanning[J].Power System Protection and Control, 2017, 45(24):84-91.
[20] Sun Jian. Impedance-based stability criterion for gridconnected inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3075-3078.
[21] Liu Huakun, Xie Xiaorong, Zhang Chuanyu, et al.Quantitative SSR analysis of series-compensated DFIG-based wind farms using aggregated RLC circuit model[J]. IEEE Transactions on Power Systems, 2016,32(1): 474-483.