0 引言
随着能源紧缺和环境污染等问题的日益严峻，可再生能源利用规模不断扩大。可再生能源固有的分散性、小规模、远离负荷中心等特点，使得采用交流输电技术或传统的直流输电技术联网经济性较差。另外，城市用电负荷的快速增加，需要不断扩充电网容量，这就要求利用有限的输电走廊输送更多的电能。采用基于可关断型器件的模块化多电平换流器（Modular Multilevel Converter, MMC）和柔性直流输电技术可以很好地解决以上问题[1-3]。由于模块化多电平换流器拓扑采用了子模块级联的方式，再加上最近电平逼近调制策略的引入，使得柔性直流输电具有运行灵活、易于拓展等特点，研究意义广泛。
同时，伴随直流电网的迅速发展[4]，包含高压直流断路器以及直流潮流控制器（DC Power Flow Controller, DCPFC）在内的关键设备的研制也受到了研究人员的大量关注[5-6]。当换流站不能实现所有线路都可控时，配置潮流控制器可针对直流电网潮流控制自由度不足的问题，优化网络内部潮流分布，防止线路过载。
逐步将交直流混合系统中直流部分替换为柔性直流电网，并探讨其相关运行、调度与控制技术已经成为当下的研究热点[7-10]。由于大规模直流电网接入交流网络会对系统的安全稳定造成一定影响，研究如何有效调整控制柔性直流电网的有功及无功功率，保证交直流系统运行在最优状态是目前亟待解决的重要问题。
文献[11]针对含有电压源换流器型高压直流输电（Voltage Source Converter High-Voltage Direct Current, VSC-HVDC）的交直流混合系统建立了原对偶内点法和预测-校正内点法两种最优潮流模型；文献[12]将系统经济性和环保因素作为优化目标，采用改进非劣排序多目标遗传算法（Non-dominated Sorting Genetic Algorithm-2，NSGA-2）对潮流模型进行求解；文献[13]提出了一种基于模糊理论的有功潮流优化方法，通过给定各目标函数的隶属度函数，求解得到VSC 换流站有功功率的最优分配方案；文献[11-13]只分析了双端系统点对点拓扑结构但没有考虑换流器损耗带来的影响；文献[14]提出基于差分进化算法的统一混合算法，算法寻优能力强，收敛速度快，但是没有考虑下垂控制对系统运行的影响；文献[15]推导了电压下垂运行方式下的控制方程式，并对目标函数进行归一化处理，但直流电网中没有考虑加装DCPFC。目前，已有大量文献研究介绍了含VSC-HVDC 的交直流系统最优潮流问题，但是鲜有文献考虑换流器为MMC，同时直流网络中配置DCPFC 的混合系统最优潮流问题。
文献[11]中采用的内点法相比于基于分解的多目标进化算法（Multi-Objective Evolutionary Algorithm Based on Decomposition, MOEA/D）对模型的要求较高，模型中雅可比矩阵和Hessian 矩阵不易求取，且修正方程的可逆性在不同模型中是无法保证的；文献[12]中采用的NSGA-2 在解的均匀程度和计算复杂程度等方面均没有MOEA/D 有优势。鉴于目前少有论文提出使用MOEA/D 求解含MMC-HVDC 的最优潮流问题，同时MOEA/D 具有计算效率高、解的分布比较均匀、对模型的要求低和收敛性能好等优点，本文采用MOEA/D 求解此问题得到帕累托最优解集并与NSGA-2 比较，借助熵权法（Entropy Weight Method, EWM）对优化结果进行分析决策，得到可供研究人员选择的最佳折中解。
1 MMC-HVDC 稳态数学模型
1.1 换流站的稳态功率特性
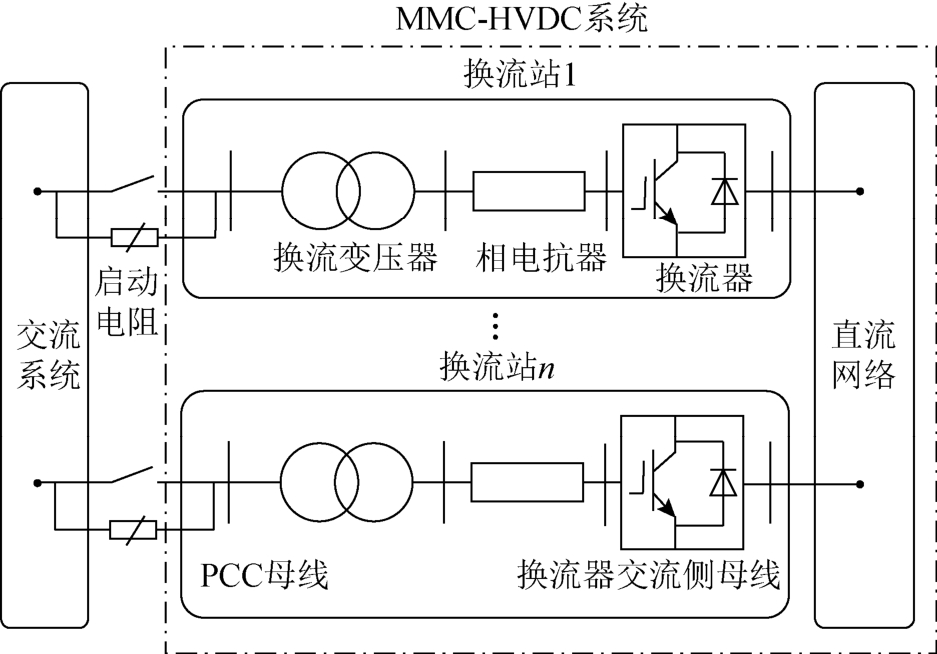
图1 含MMC-HVDC 的交直流系统
Fig.1 AC/DC system with MMC-HVDC
图1 为含MMC-HVDC 的交直流混合系统的一般结构。该结构包括三个部分：交流系统、柔性直流输电系统换流站（简称MMC 换流站）和直流网络。由于MMC 换流站的谐波水平低，不需装设滤波器，因此MMC 换流站的主要设备包括启动电阻、换流变压器、相电抗器、换流器；直流网络中主要包括直流电源、直流线路、直流负载、DCPFC和直流断路器等。为了防止冲击电流过大损坏设备，在MMC 启动过程中接入启动电阻，充电完成后自动合上旁路刀开关将启动电阻旁路。
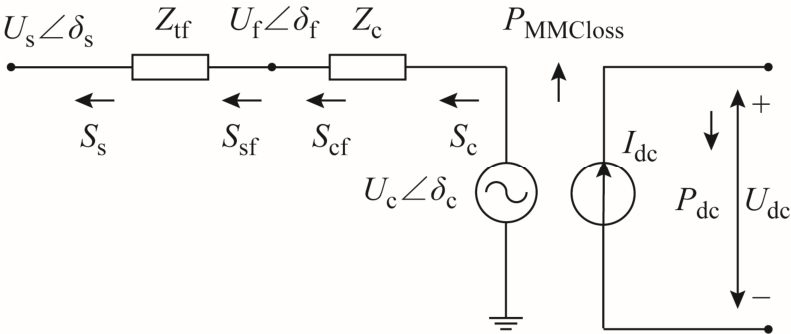
图2 MMC 换流站的等效单相潮流模型
Fig.2 Equivalent single-phase power flow model of MMC converter stations
式中，a 为恒定损耗系数；b 为线性损耗系数；c为二次损耗系数； cI 为流经换流器的电流。
MMC 输出电压和直流侧电压关系为
式中，M 为电压调制度。
1.2 含DCPFC 的直流电网潮流模型
类似于传统的交流潮流方程，可以得到直流网络的潮流表达式。直流节点i 的注入功率为
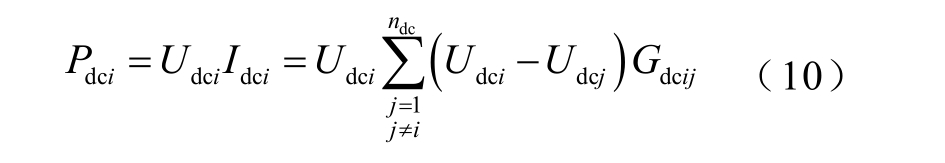
式中， dciP 为节点i 的注入功率； dciI 为节点i 的注入电流； dciU 、 dcjU 分别为节点i、j 的电压； dcijG 为支路-i j 的电导； dcn 为直流网络的节点数。
根据文献[16]给出的改变电压型DCPFC 等效外特性模型可知（本文不再赘述），DCPFC 对直流电网的影响可等效为将DCPFC 所在线路首端节点对该线路的电压值变为原来的m 倍，加入DCPFC 之后，节点i 的注入功率应为
式中，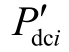
为加入DCPFC 后节点i 的注入功率。合并 dcn 个节点的所有注入电流，可得
1.3 MMC 换流站的控制方式
柔性直流输电系统可同时独立调节有功功率和无功功率，无需无功功率补偿，运行方式灵活。其MMC 换流站包含三种有功功率控制目标和两种无功功率控制目标，不同的控制目标对直流电网潮流模型的影响不同。
（1）定有功功率：换流器将恒定的有功功率 siP注入交流电网，潮流计算时 siP 已知。
（2）定直流电压：无论有功功率如何变化，换流器都将其端子处的直流节点电压 dciU 保持为恒定值，潮流计算时 dciU 已知。
（3）下垂控制：注入直流网络的有功功率 dciP 取决于直流节点电压 dciU 的实际值，分别给定电压和功率的设定值 dc0U 、 dc0P 以及下垂控制系数 dck ，曲线表达式为
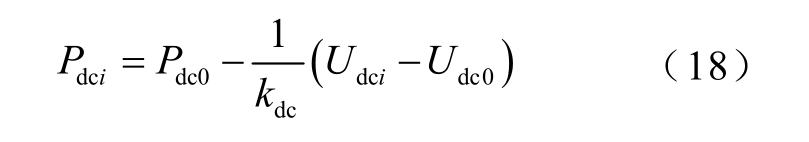
采用下垂控制时，对修正方程式（15）进行修改可得加入DCPFC 后的雅可比矩阵为
（4）定无功功率：换流器将恒定的无功功率 siQ注入交流电网，潮流计算时 siQ 已知。
（5）定交流电压：换流器根据无功功率的大小进行相应调整以获得恒定的交流电压 siU 。
在进行潮流计算时，每个MMC 换流站都需要选择两个控制目标，一般分别从有功目标和无功目标中确定以满足计算要求。
2 接入DCPFC 的含MMC-HVDC 的交直流混合系统多目标最优潮流模型
多目标最优潮流模型的求解属于复杂非线性规划问题[17]，可将其划分为目标函数、决策变量、交流系统以及柔性直流系统的约束条件。
2.1 目标函数
为了保证交直流系统具有良好的经济性[18]和电压质量，本文以网络损耗最小及电压偏差最小作为最优潮流模型的目标函数。
混合系统网损最小方程包含线路损耗、换流器损耗及DCPFC 的损耗。即
式中， N B为线路总集； N MMC为换流站节点总集；N q为接入DCPFC 节点总集；P l oss,k为线路k 的损耗；Gk 为线路k 的导纳，两端节点的电压大小为 U i、U j且相位差为 θ ij；P M MCloss,o为换流器o 的损耗；P DCPFCloss,p为第p 个 DCPFC 的损耗； U p、 I p分别为加装DCPFC 节点电压和电流。
电压偏差最小方程为
式中， ACN 和 DCN 分别为交流节点总集和直流节点
2.2 决策变量
对于接入DCPFC 的含MMC-HVDC 交直流混合系统，决策变量X 包括系统控制变量、状态变量以及寻优变量。
2.3 约束条件
约束条件包括等式约束条件以及不等式约束条件。其中，等式约束条件由交流系统等式约束和直流系统等式约束组成，如式（23）和式（15）所示。
交流系统等式约束为
式中， Δ Pi和 ΔQ i为交流节点i 的功率偏差量； Pg i和Qg i为发电机注入节点i 的功率； Ps i和 Qs i为换流器注入节点i 的功率； Gi j和 Bi j分别为节点i、 j 的电导和电纳； Pd i和 Qd i为节点i 负载功率。
交流系统不等式约束条件主要包括节点电压幅值约束、节点注入功率约束、线路传输容量约束和变压器电压比约束等，本文不再详细介绍。
直流网络不等式约束和MMC 换流站约束组成了直流系统不等式约束条件[19]。
直流节点的电压约束和直流线路的电流约束可表示为
因为MMC 可忽略其交流端口电压下限，所以换流器交流端口电压可表示为
式中， c maxiU 为换流器交流端口电压幅值上限，可由式（9）代入数值求得，因此还需考虑换流器的电压调制度约束，如式（26）所示。
式中， c maxiI 为换流器内部元件可承载电流上限。
3 交直流混合系统最优潮流模型求解与决策
最优潮流问题不仅是模型求解问题，对优化结果进行评估及决策也是最优潮流问题的一部分，故求解过程可分两步进行。首先，采用MOEA/D 对多目标潮流模型进行处理得到帕累托最优解集；其次，借助熵权法对最优解集进行决策支持，并通过分析给出最佳折中解。图3 为分步求解框图。
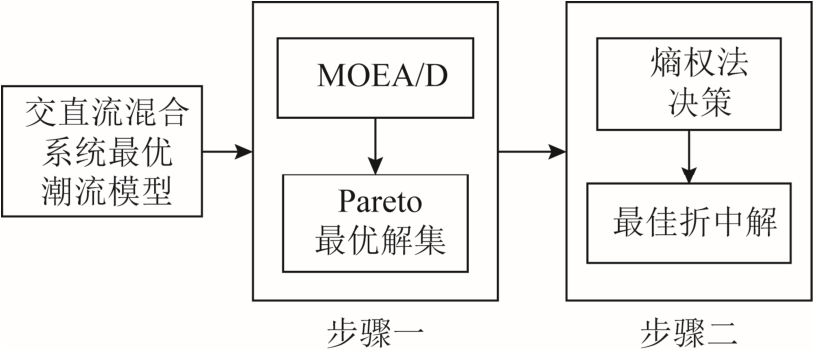
图3 基于最优潮流模型的分步求解框图
Fig.3 Step-by-step solution framework based on optimal power flow model
3.1 基于分解的多目标最优潮流优化方法
MOEA/D 是一种基于分解的多目标优化算法。它将一个多目标优化问题分解成若干个标量优化子问题，采用Tchebycheff 聚合方法将原多目标问题转换为如下标量问题[20-21]。
同时，对式（28）进行优化。每一个子问题都是通过使用来自它的几个相邻子问题的信息优化的，可以避免陷入局部最优。图4 为基于MOEA/D的多目标最优潮流求解流程。
图4 MOEA/D 流程
Fig.4 Flow chart of MOEA/D
该算法的求解步骤如下：
1）设置初始参数并读入。
（1）交流系统参数、换流器、DCPFC 参数及直流网络参数。其中，交流系统参数由母线参数（包括负荷参数）、发电机节点参数、支路参数及系统容量基准值构成；换流器由MMC 数量及其运行方式组成；直流网络由直流母线参数、直流线路参数及直流网络接线方式和容量基准值构成。
（2）MOEA/D 参数。给定种群大小N（子问题的数量）、进化代数、目标函数、均匀分布的N 个权重向量、邻居种群规模T（每个权向量领域内权向量的个数）、决策变量数量以及决策变量的上下限。
2）初始化种群。
（1）计算任意两个权重向量间的欧式距离，查找每个权向量最近的 T 个权重向量的索引。令
是 iλ 最近的T个权重变量。
（2）在可行空间根据决策变量的性质（2.2 节已进行介绍）采用混合编码方式并均匀随机产生初始种群 1, , N x x… 。
（3）根据每次产生的新种群，采用交替求解算法对含DCPFC 的混合系统进行潮流计算，并更新目标函数值。
（4）初始化z，
（5）创建一个外部种群（EP）用于存储过程优秀个体，初始为空。
3）种群迭代更新。
（1）从邻集 B ( i )中随机选取两个序号u 和l，运用基因重组遗传算子让 x u 和 x l产生新解y。
（2）对y 运用一个启发式方法进行改进得到y′。
（3）进行模拟二进制交叉操作（SBX）和多项式变异。
4）条件终止。根据停止条件终止，并输出EP。否则迭代次数加1，更新交直流系统数据后重复步骤3）。
3.2 结果处理与决策
本文利用熵权法对多目标优化结果进行分析与决策[22-23]。熵权法是一种客观赋权法，根据多个目标函数观测值所提供信息的大小确定多个目标权重。一般若某一目标的信息熵越小，说明该目标的变异程度越大，其可利用的信息量越多，不确定性越小，在综合评估中所能起到的作用也越大，相应的权重也越大。相反，某个目标的信息熵越大，说明该目标的变异程度越小，可利用的信息量也越少，在综合评估中所起到的作用也越小，权重也越小。
数据的归一化和标准化：
（1）假设给定n 个样本m 个目标函数值，则 ijx为第i 个样本的第 j 个目标函数的数值
对目标函数进行同趋势性转换，在进行评估时不同目标函数之间应该具有相同的趋势。由于本文中的两个目标函数分别为网络损耗及电压偏差方程，为了保证系统的经济稳定运行都取最小，无需进行转换。
（2）归一化处理，由于正向目标函数和负向目标函数代表的含义不同（正向目标函数越大越好，负向目标越小越好），所以，用不同的算法对数据进行处理， ijx′为第i 个样本的第j 个目标函数的数值，归一化后仍用 ijx 表示。
正向目标函数为
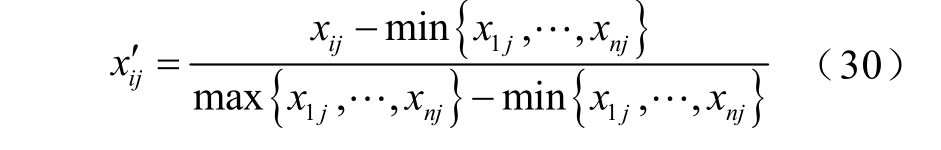
负向目标函数为
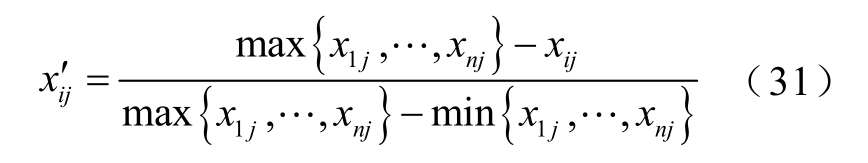
（3）标准化处理，计算第j 个目标函数下第i 个样本所占的比重 ijp 为
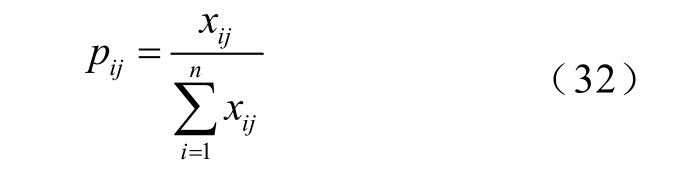
各个目标函数的信息熵为
各个目标函数的权重为
各样本的综合评分为
权重 jw 体现了目标函数的信息量，熵权值越大表示该目标函数对综合决策的作用越大，直观有效地反映了目标函数之间的差异程度。
4 算例分析
为了验证本文算法处理多目标最优潮流问题的能力，分别对两端及三端MMC 混合系统进行讨论，以修改后的IEEE 多节点系统为例进行仿真计算，验证MOEA/D 对于不同系统的适应性。需要注意的是，直流系统可控支路数遵循N-1 原则，若直流系统有d 个换流站，t 条线路，则加装DCPFC 的数量为 +1t d− 。因此，针对本文的算例系统，两端直流系统不需配置DCPFC。
4.1 IEEE 5 节点测试系统
4.1.1 二端及三端MMC 交直流混合输电系统
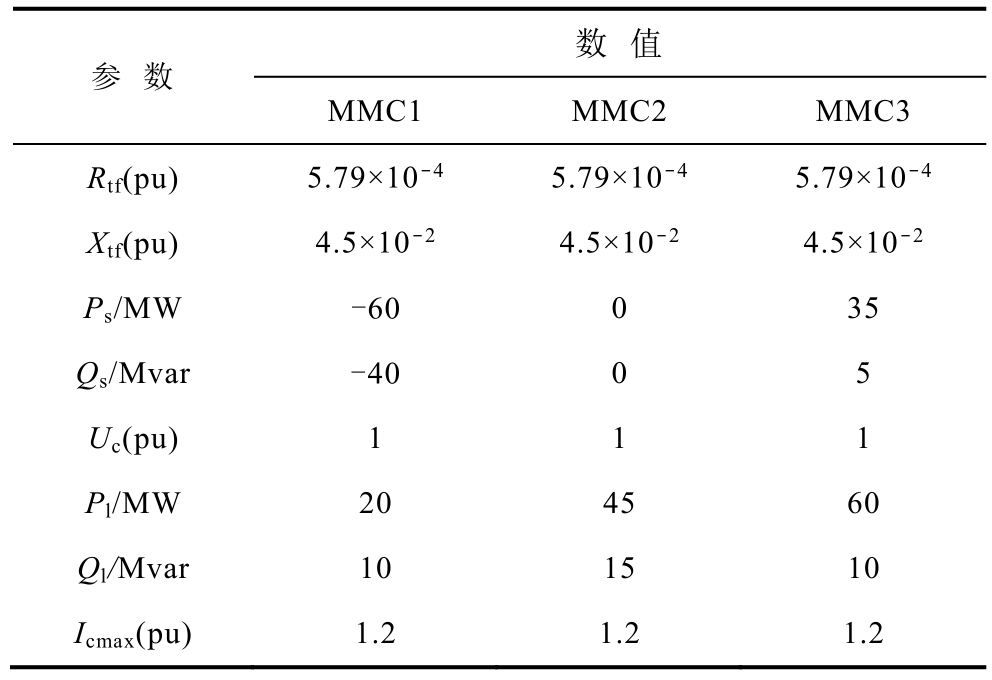
图5 为含三端MMC 的交直流系统，IEEE 5 节点交流系统中节点1 和节点2 为发电机节点。在节点2 和3 处增加两个MMC 换流站和一条直流线路与原交流系统组成含两端MMC 的交直流混合系统。在此混合系统的基础上，在节点5 新增一个MMC 换流站，并经由两条直流线路连接其余两个换流站，共同组成含三端MMC 的交直流混合系统。MMC 换流站参数设定值见表1。表中， lP 为负荷有功功率， Ql 为负荷无功功率， I cmax为换流器最大允许电流。
图5 含三端直流网络的交直流系统
Fig.5 AC/DC system of the three-terminal DC network
表1 MMC 换流站参数
Tab.1 Parameters of MMC converter stations
参 数数 值MMC1 MMC2 MMC3 Rtf(pu) 5.79×10-4 5.79×10-4 5.79×10-4 Xtf(pu) 4.5×10-2 4.5×10-2 4.5×10-2 Ps/MW -60 0 35 Qs/Mvar -40 0 5 Uc(pu) 1 1 1 Pl/MW 20 45 60 Ql/Mvar 10 15 10 Icmax(pu) 1.2 1.2 1.2
两端MMC 混合系统中，MMC1 的控制方式设定为定 Ps i和 Qs i，MMC2 的控制方式设定为定 U dci和U si。三端MMC 混合系统中，MMC1、MMC2 和MMC3 的控制方式分别为定 Ps i和 Qs i、定 U dci和 Usi以及定 Ps i和 Qs i。两系统在常规潮流（PF）计算和最优潮流（OPF）计算后的结果见表2。
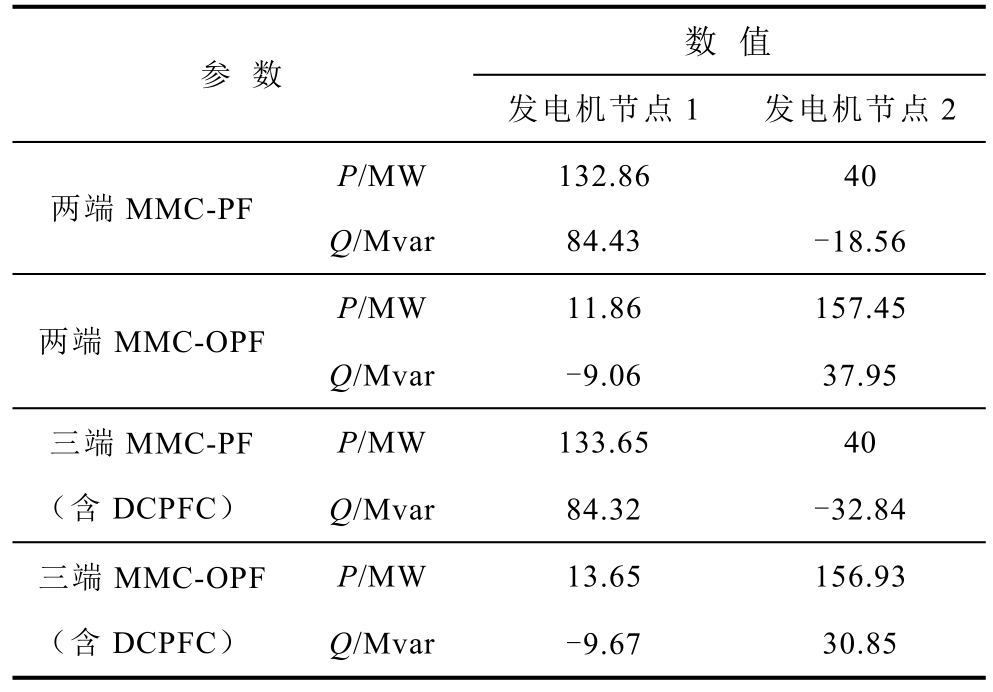
表2 不同直流系统优化前后发电机出力比较
Tab.2 Comparison of generators output from different DC systems before and after optimization
参 数数 值发电机节点1 发电机节点2两端MMC-PF P/MW 132.86 40 Q/Mvar 84.43 -18.56两端MMC-OPF P/MW 11.86 157.45 Q/Mvar -9.06 37.95三端MMC-PF（含DCPFC）P/MW 133.65 40 Q/Mvar 84.32 -32.84三端MMC-OPF（含DCPFC）P/MW 13.65 156.93 Q/Mvar -9.67 30.85
通过表2 可知：两端MMC 混合系统中发电机总出力由172.86MW 降至169.31MW，潮流优化前后总网损由7.342MW 降至4.238MW；三端MMC混合系统（含DCPFC）发电机总出力由173.65MW降至170.58MW，潮流优化前后总网损由7.863MW降至4.309MW。由此，为了满足系统发电经济性的要求，两端及三端MMC 混合系统中的发电机均合理安排了各自的出力，同时，潮流优化之后混合系统运行的经济性得到提升。
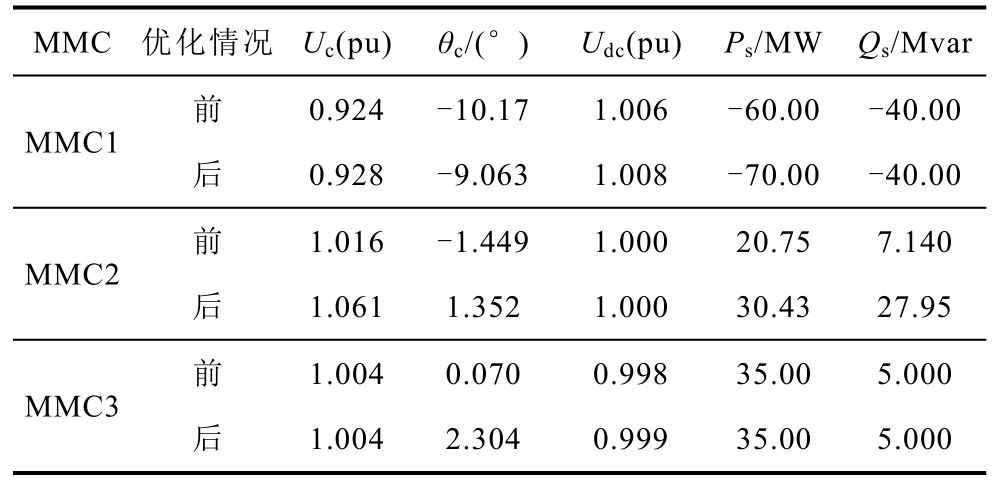
表3 为直流线路加装DCPFC 前后系统潮流分布。将DCPFC 的控制系数设定为1.001 1，对比三端MMC 混合系统中有无DCPFC 常规潮流结果可知：配置DCPFC 可以改变线路潮流分布，对潮流控制起到了补充作用，原系统直流线路损耗由0.55MW 降为配置DCPFC 后的0.36MW；对比三端MMC 混合系统中有无DCPFC 最优潮流结果可知：交流线路损耗降低，同时，直流线损由0.73MW降为0.49MW。综上所述，体现了DCPFC 具有优化直流电网内部功率从而降低线路损耗，保证所有线路均可控的特点。相应地，可以通过改变DCPFC 控制系数实现不同的潮流控制。表4 为优化前后含DCPFC 三端MMC 换流站状态变量和控制变量数据。
表3 DCPFC 对直流电网潮流分布的影响
Tab.3 Effect of DCPFC on DC grid power flow distribution
线 路 PF/OPF 起始节点功率/MW终止节点功率/MW线路损耗/MW线路无DCPFC L12 PF 31.02 -30.77 0.25 OPF 38.04 -37.67 0.37 L23 PF 8.16 -8.14 0.02 OPF 5.27 -5.26 0.01 L13 PF 27.95 -27.67 0.28 OPF 30.89 -30.54 0.35线路含DCPFC L12 PF 24.57 -24.41 0.16 OPF 31.56 -31.3 0.26 L23 PF 7.22 -7.21 0.01 OPF 4.33 -4.33 0 L13 PF 22.68 -22.49 0.19 OPF 25.59 -25.36 0.23
表4 优化前后MMC 换流站参数
Tab.4 Parameters of MMC converter stations before and after optimization
MMC 优化情况 Uc(pu) θc/(°) Udc(pu) Ps/MW Qs/Mvar MMC1前 0.924 -10.17 1.006 -60.00 -40.00后 0.928 -9.063 1.008 -70.00 -40.00 MMC2前 1.016 -1.449 1.000 20.75 7.140后 1.061 1.352 1.000 30.43 27.95 MMC3前 1.004 0.070 0.998 35.00 5.000后 1.004 2.304 0.999 35.00 5.000
4.1.2 算法比较
本文通过对比MOEA/D 和NSGA-2 在优化效果以及优化时间两方面的不同，验证MOEA/D 的优越性（在后续的仿真中将默认三端直流系统中已配置DCPFC）。将两种算法的种群大小和进化代数都设置为200。图6 为两种算法在三端MMC 情况下的帕累托最优前沿。采用不同算法时换流站注入交流电网的有功和无功功率见表5。表6 为交直流混合系统的节点电压幅值。
图6 两种算法的帕累托最优解
Fig.6 Pareto optimal solution for two algorithms
表5 换流站注入交流电网的有功及无功功率
Tab.5 Active and reactive power injected into the AC grid by the converter stations
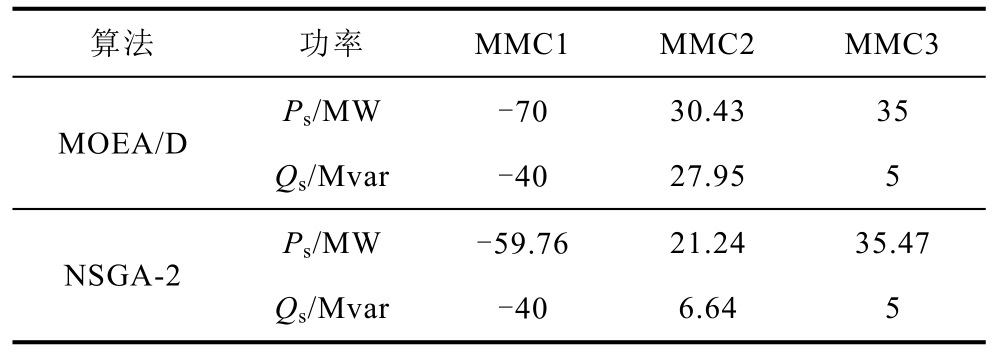
算法 功率 MMC1 MMC2 MMC3 MOEA/D Ps/MW -70 30.43 35 Qs/Mvar -40 27.95 5 NSGA-2 Ps/MW -59.76 21.24 35.47 Qs/Mvar -40 6.64 5
表6 交直流混合系统节点电压幅值
Tab.6 Voltage amplitude of the AC/DC hybrid system nodes
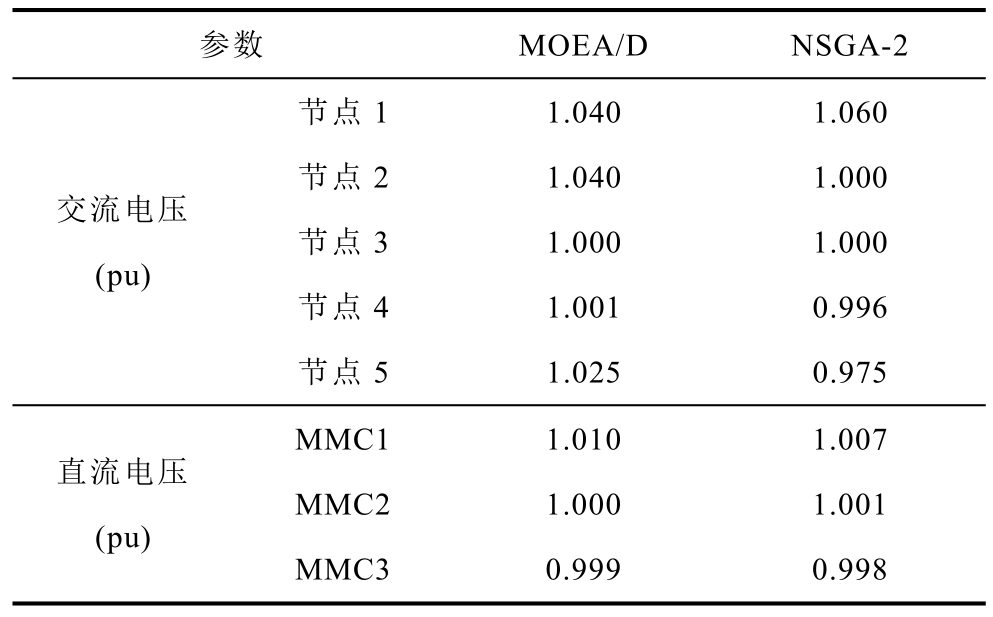
参数 MOEA/D NSGA-2交流电压(pu)节点1 1.040 1.060节点2 1.040 1.000节点3 1.000 1.000节点4 1.001 0.996节点5 1.025 0.975直流电压(pu)MMC1 1.010 1.007 MMC2 1.000 1.001 MMC3 0.999 0.998
针对两目标问题，MOEA/D 相较于NSGA-2 更易于获取均匀分布的权重向量，而权重向量的均匀分布则直接导致了对应解的均匀分布。由图6 可以看出，在Pareto 解分布的均匀性上，MOEA/D 优于NSGA-2。其次，在计算复杂度上，MOEA/D 为O ( m × N × T)，NSGA-2 为 O ( m × N2)，显然，T＜N，所以，MOEA/D 也是优于NSGA-2 的。最后，NSGA-2 和MOEA/D 同属遗传算法的范畴，其Pareto 解的优劣取决于迭代搜索过程中种群多样性的保持，NSGA-2 是通过拥挤距离估计来保证种群多样性，而MOEA/D 是通过生成不同的子问题来对应不同的种群，自然保证了种群的多样性，由于权重向量可以被正确选择，求得更优的Pareto 解是必然的。综上所述，MOEA/D 求得的帕累托最优解要优于NSGA-2，在图6 中则表现为MOEA/D 的帕累托最优解更靠近坐标轴。
表7 为优化前后两种算法目标函数的对比。由表7 可以看出，对于两目标优化问题，NSGA-2 对于网络损耗和电压偏差的优化没有MOEA/D 效果明显，后者大幅降低了两个目标函数值，尤其是电压偏差，相比于优化前分别降低了84%和98%。其次，MOEA/D 比NSGA-2 平均优化时间快4 倍以上，这主要是因为MOEA/D 具有较低的计算复杂度，并且收敛速度比NSGA-2 法快。
表7 两种算法优化前后参数对比
Tab.7 Comparison of parameters before and after optimization of two algorithms
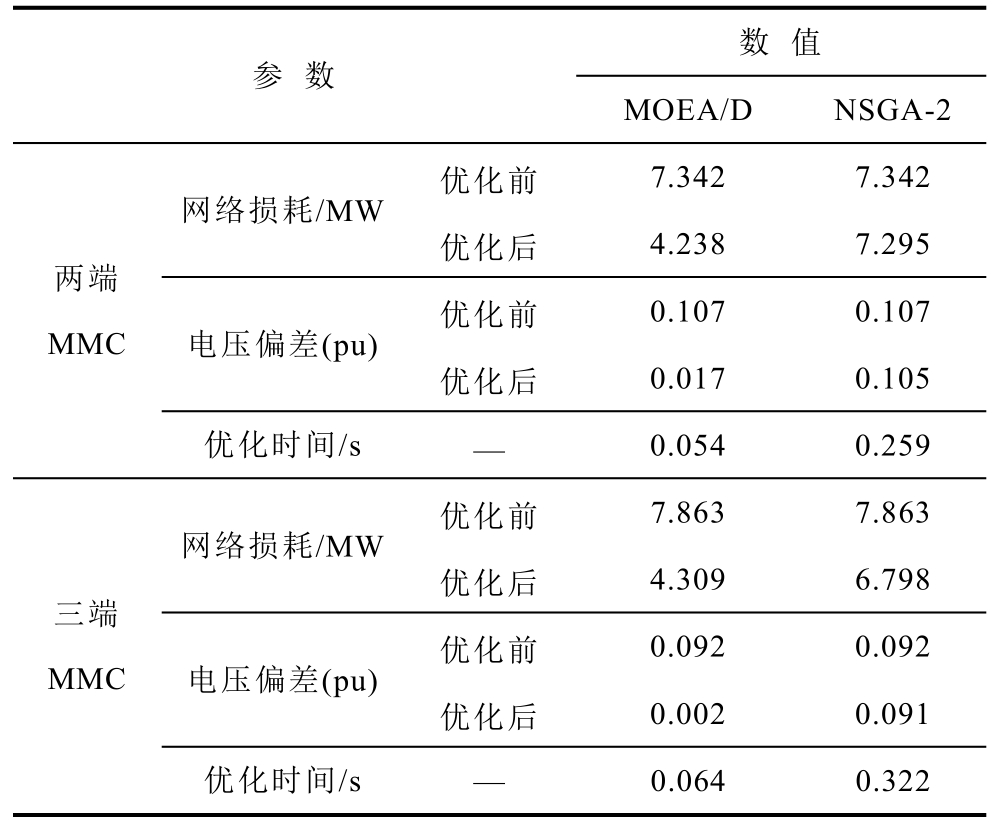
参 数数 值MOEA/D NSGA-2两端MMC网络损耗/MW 优化前 7.342 7.342优化后 4.238 7.295电压偏差(pu) 优化前 0.107 0.107优化后 0.017 0.105优化时间/s — 0.054 0.259三端MMC网络损耗/MW 优化前 7.863 7.863优化后 4.309 6.798电压偏差(pu) 优化前 0.092 0.092优化后 0.002 0.091优化时间/s — 0.064 0.322
4.1.3 优化结果决策
根据帕累托最优解集，可知两个目标函数是互相冲突的，需要对两目标的重要程度进行评价，分析其对优化结果的贡献性。采用EMW 法对结果综合评分并提取3 个折中解，计算各目标的权重。表8 针对含DCPFC 三端MMC 混合系统给出两种算法各目标数据。
表8 两种算法各目标数据及权重
Tab.8 Target datas and weights of two algorithms
?
根据表8 中数据可知：采用NSGA-2 时，两目标函数的权重数值相近，所提供的信息量差异较小，对综合决策的影响较小，再加上两目标函数之间的矛盾特征，会提高对有效数据选择的难度；而采用MOEA/D 时，网络损耗的权重远远大于电压偏差且近似等于1，在进行综合决策时可以重点考虑网络损耗的影响，进而划分目标函数的优先等级。通过MOEA/D 与EWM 算法的相互结合，有利于得到Pareto 最优解和综合决策方案。
4.2 不同控制方式对优化结果的影响
在电力系统实际运行中，不可能只使用一种控制策略进行潮流调控，为了满足系统多方面的需求，本文将不同系统在不同控制方式下两种算法的优化结果加以对比。根据1.3 节的介绍，将定 U dci、定 Qsi设置为方式①；定 U dci、定 U si为方式②；定 Ps i、定Qs i为方式③；定 Ps i、定 U si为方式④；下垂、定 Qsi为方式⑤；下垂、定 U si为方式⑥。表9 为不同算例系统在不同控制方式下的潮流优化结果对比。
表9 不同控制方式下两算法优化结果对比
Tab.9 Comparison of the results of the two algorithms optimization under different control methods
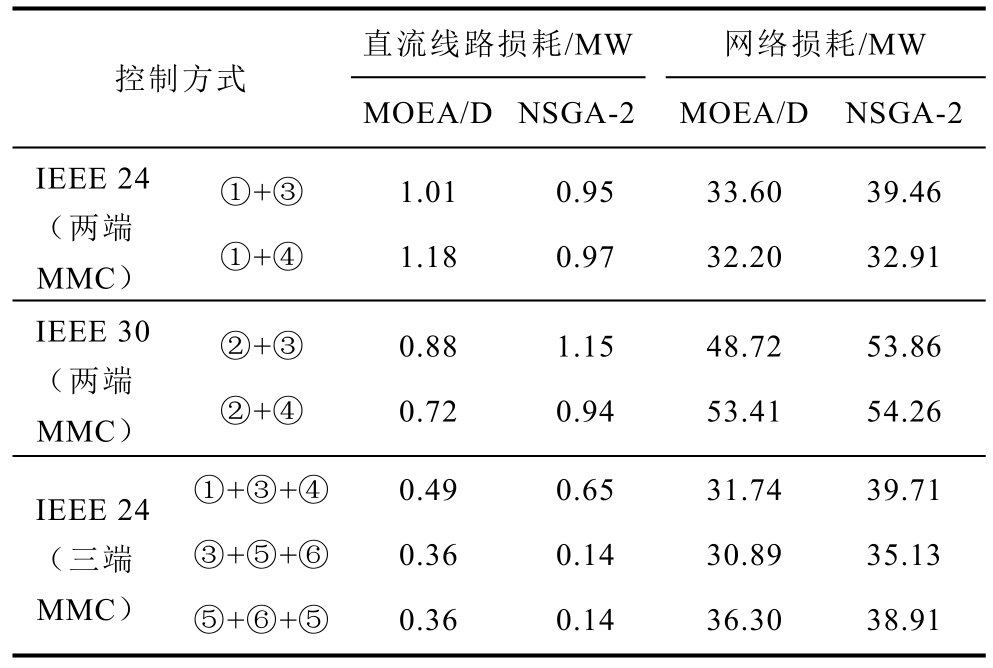
控制方式直流线路损耗/MW 网络损耗/MW MOEA/D NSGA-2 MOEA/D NSGA-2 IEEE 24（两端MMC）①+③①+④1.01 1.18 0.95 0.97 33.60 32.20 39.46 32.91 IEEE 30（两端MMC）②+③②+④0.88 0.72 1.15 0.94 48.72 53.41 53.86 54.26 IEEE 24（三端MMC）①+③+④ 0.49 0.65 31.74 39.71③+⑤+⑥⑤+⑥+⑤0.36 0.36 0.14 0.14 30.89 36.30 35.13 38.91
由表9 可知，当算例系统被设置为不同的控制方式时，潮流优化的结果并不是相同的，这主要是因为采用不同的控制方式，对决策变量的选取是有差异的，相当于间接提高了系统的运行约束；由于采用下垂控制时求解最优潮流需要满足式（18）功率特性曲线，还需要对雅可比矩阵做出修正，故优化结果也与采用松弛控制有较大不同。由于篇幅限制，图7 只给出IEEE 24 节点采用两种不同控制方式时交流系统注入的功率。根据MOEA/D 和NSGA-2在网络损耗上的差异，可知前者的网络损耗较小，对于不同算例的适用性较好，验证了该算法的适用性和有效性。
图7 两种算法采用不同控制时交流系统注入功率
Fig.7 Active and reactive power injected by AC grid of two algorithms with different controls
5 结论
1）本文针对考虑换流器损耗的 MMC-HVDC一般稳态模型，以网络损耗和电压偏差为目标，建立了加装DCPFC 的含MMC-HVDC 的交直流混合系统最优潮流数学模型，协调系统的经济性和电压质量。
2）建立配置DCPFC 后直流电网的潮流模型，分析其影响，推导了下垂控制方式的雅可比矩阵计算公式。仿真表明DCPFC 可以优化直流电网内部潮流分布，具有控制线路潮流的作用。
3）利用MOEA/D 多目标优化算法对模型加以求解，将所得Pareto 最优解与NSGA-2 对比，在优化效果与时间上，MOEA/D 均优于NSGA-2。通过将MOEA/D 和EWM 进行有机结合，有利于研究人员做出正确决策。
4）利用MOEA/D 对不同控制方式下的两端及三端MMC 混合系统进行仿真，不同算例验证了该算法的有效性和适用性。
[1] 韦延方, 卫志农, 孙国强, 等. 一种新型的高压直流输电技术——MMC-HVDC[J]. 电力自动化设备,2012, 32(7): 1-9.Wei Yanfang, Wei Zhinong, Sun Guoqiang, et al. New HVDC power transmission technology: MMCHVDC[J]. Electric Power Automation Equipment,2012, 32(7): 1-9.
[2] 吴杰, 王志新. 多端柔性直流输电系统的改进下垂控制策略[J]. 电工技术学报, 2017, 32(20): 241-250.Wu Jie, Wang Zhixin. Improved droop control strategy for multi-terminal voltage source converter-HVDC[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 241-250.
[3] 陈鹏远, 黎灿兵, 周斌, 等. 异步互联电网柔性直流输电紧急功率支援与动态区域控制偏差协调控制策略[J]. 电工技术学报, 2019, 34(14): 3025-3034.Chen Pengyuan, Li Canbing, Zhou Bin, et al. VSCHVDC emergency power support and dynamic area control error coordinated control strategy for improving the stability of asynchronous interconnected power grids[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3025-3034.
[4] 姚良忠, 吴婧, 王志冰, 等. 未来高压直流电网发展形态分析[J]. 中国电机工程学报, 2014, 34(24):6007-6020.Yao Liangzhong, Wu Jing, Wang Zhibing, et al.Pattern analysis of future HVDC grid development[J].Proceedings of the CSEE, 2014, 34(24): 6007-6020.
[5] Chen Wu, Zhu Xu, Yao Liangzhong, et al. A novel interline DC power flow controller (IDCPFC) for meshed HVDC grids[J]. IEEE Transactions on Power Delivery, 2016, 31(4): 1719-1727.
[6] 武文, 吴学智, 荆龙, 等. 适用于多端直流输电系统的模块化多端口直流潮流控制器[J]. 电工技术学报, 2019, 34(3): 539-551.Wu Wen, Wu Xuezhi, Jing Long, et al. A modular multi-port DC power flow controller for multiterminal DC transmission system[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 539-551.
[7] 张释中, 裴玮, 杨艳红, 等. 基于柔性直流互联的多微网集成聚合运行优化及分析[J]. 电工技术学报, 2019, 34(5): 1025-1037.Zhang Shizhong, Pei Wei, Yang Yanhong, et al.Optimization and analysis of multi-microgrids integration and aggregation operation based on flexible DC interconnection[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1025-1037.
[8] 王家融, 艾欣, 王坤宇, 等. 基于增广雅可比矩阵的交直流解耦潮流新算法[J]. 电工技术学报, 2018,33(6): 1382-1389.Wang Jiarong, Ai Xin, Wang Kunyu, et al. A novel AC-DC decoupled power flow calculation method based on the augmented Jacobian matrix[J].Transactions of China Electrotechnical Society, 2018,33(6): 1382-1389.
[9] Baradar M, Hesamzadeh M R, Ghandhari M.Second-order cone programming for optimal power flow in VSC-type AC-DC grids[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4282-4291.
[10] Feng Wang, Tuan L A, Tjernberg L B, et al. A new approach for benefit evaluation of multiterminal VSCHVDC using a proposed mixed AC/DC optimal power flow[J]. IEEE Transactions on Power Systems, 2014,29(1): 432-443.
[11] 卫志农, 季聪, 孙国强, 等. 含VSC-HVDC 的交直流系统内点法最优潮流计算[J]. 中国电机工程学报, 2012, 32(19): 89-95.Wei Zhinong, Ji Cong, Sun Guoqiang, et al. Interiorpoint optimal power flow of AC-DC system with VSC-HVDC[J]. Proceedings of the CSEE, 2012,32(19): 89-95.
[12] 李扬, 李亚辉, 李国庆, 等. 考虑经济性和环境因素的含VSC-HVDC 交直流系统多目标最优潮流[J].电网技术, 2016, 40(9): 2661-2667.Li Yang, Li Yahui, Li Guoqing, et al. A multiobjective optimal power flow approach considering economy and environmental factors for hybrid AC/DC grids incorporating VSC-HVDC[J]. Power System Technology, 2016, 40(9): 2661-2667.
[13] 邓健俊, 文安, 魏承志, 等. 含柔性直流输电的交直流并列系统有功潮流优化方法[J]. 电力系统保护与控制, 2014, 42(11): 118-123.Deng Jianjun, Wen An, Wei Chengzhi, et al. An optimization method for active power flow in AC/VSC-HVDC parallel transmission systems[J].Power System Protection and Control, 2014, 42(11):118-123.
[14] 卫志农, 季聪, 郑玉平, 等. 计及VSC-HVDC 的交直流系统最优潮流统一混合算法[J]. 中国电机工程学报, 2014, 34(4): 635-643.Wei Zhinong, Ji Cong, Zheng Yuping, et al. Optimal power flow of AC-DC systems with VSC-HVDC based on a novel unified hybrid algorithm[J].Proceedings of the CSEE, 2014, 34(4): 635-643.
[15] 苗丹, 刘天琪, 王顺亮, 等. 含柔性直流电网的交直流混联系统潮流优化控制[J]. 电力系统自动化,2017, 41(12): 70-76.Miao Dan, Liu Tianqi, Wang Shunliang, et al. Optimal control for power flow of AC/DC hybrid system with flexible DC grid[J]. Automation of Electric Power Systems, 2017, 41(12): 70-76.
[16] 姜舒婷, 齐磊, 崔翔, 等. 含潮流控制器的直流电网潮流计算方法[J]. 电网技术, 2015, 39(7): 1793-1799.Jiang Shuting, Qi Lei, Cui Xiang, et al. Power flow algorithm method for DC grid with power controller[J]. Power System Technology, 2015, 39(7):1793-1799.
[17] Cao Jun, Du W, Wang H F. An improved corrective security constrained OPF for meshed AC/DC grids with multi-terminal VSC-HVDC[J]. IEEE Transactions on Power Systems, 2016, 31(1): 485-495.
[18] Cao Jun, Du Wenjuan, Wang Haifeng, et al.Minimization of transmission loss in meshed AC/DC grids with VSC-MTDC networks[J]. IEEE Transactions on Power Systems, 2013, 28(3): 3047-3055.
[19] Beerten J, Cole S, Belmans R. Generalized steadystate VSC MTDC model for sequential AC/DC power flow algorithms[J]. IEEE Transactions on Power Systems, 2012, 27(2): 821-829.
[20] Das S, Suganthan P N. Differential evolution: A survey of the state-of-the-art[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 4-31.
[21] Yao Weifeng, Zhao Junhua, Wen Fushuan, et al. A hierarchical decomposition approach for coordinated dispatch of plug in electric vehicles[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2768-2778.
[22] 张涛, 朱彤, 高乃平, 等. 分布式冷热电能源系统优化设计及多指标综合评价方法的研究[J]. 中国电机工程学报, 2015, 35(14): 3706-3713.Zhang Tao, Zhu Tong, Gao Naiping, et al. Optimization design of distributed cold and heat energy system and multi-index comprehensive evaluation method[J].Proceedings of the CSEE, 2015, 35(14): 3706-3713.
[23] 杜琳, 孙亮, 陈厚合. 计及电转气规划的综合能源系统运行多指标评价[J]. 电力自动化设备, 2017,37(6): 110-116.Du Lin, Sun Liang, Chen Houhe. Multi-indicator evaluation of integrated energy system operation considering electro-gas conversion planning[J]. Electric Power Automation Equipment, 2017, 37(6): 110-116.