0 引言
在可再生能源和分布式发电领域中,存在大量输出电压较低的发电单元[1]。例如,单个光伏(Photovoltaic, PV)模块的输出电压一般在20~50V之间[2],燃料电池(Fuel Cell, FC)单元的输出电压通常也较低[3]。这些较低的电压需要通过具有高电压增益的DC-DC 变换器抬升到380~400V,甚至更高的电压,以供给后级并网逆变器,或与直流微电网母线连接[2-4]。因此,具有高效率、高功率密度及低成本的高电压增益DC-DC 变换器是近年来电力电子功率变换器领域的研究热点[5-6]。
Boost 变换器的最大电压增益受到电感寄生参数的限制,而且极端占空比条件运行会导致器件电压和电流应力高、二极管反向恢复问题严重、开关管开关损耗大等问题。所以传统Boost 变换器不适合需要高电压增益的应用场合。
磁耦合(变压器或耦合电感)技术是实现高电压增益的常用方法。通过增加磁性元件的匝比可以提升电压增益,并且允许在电路低压侧使用低额定电压的半导体器件。但过高的匝比会增加磁性元件的设计和制造难度,并且导致其铜损较大,降低变换器效率[7]。具有变压器隔离的输入电压型DC-DC升压变换器的输入电流纹波较大,会增加输入电容的电流应力,并对电源的利用率和寿命产生不利的影响[8]。过高的匝比还会增加变压器或耦合电感的漏感,而漏感引起的振荡会增加器件的电压应力和开关损耗,通常需要使用有源或无源钳位电路来吸收漏感能量[7,9-10] 。 文献[11-15] 提出了一类Boost-Flyback 型变换器,其Boost 部分与Flyback部分共用耦合电感和主开关管,两部分的输出电容串联以拓展变换器电压增益,Boost 部分的整流二极管和输出电容同时可作为无源钳位电路吸收耦合电感漏感能量。但是此类变换器需要考虑两部分输出电容的电压平衡问题[5]。文献[16-19]将耦合电感倍压单元与传统单相或交错并联Boost 电路相结合,以拓展电压增益,降低主开关管电压应力和导通损耗,并利用耦合电感的漏感降低二极管反向恢复损耗,通过增加有源和无源钳位电路吸收耦合电感漏感的能量。然而,文献[16,18]的主开关管只能实现零电流开关(Zero-Current Switching, ZCS)开通。另外,文献[16-19]提出的变换器中,耦合电感二次侧二极管的电压应力仍然较高,影响变换器效率。
开关电容(Switched-Capacitor, SC)变换器采用电容作为储能元件,具有功率密度高、易于集成等优点。而且SC 电路结构灵活,可以通过多单元级联实现很高的电压转换比,同时保持半导体器件的低电压应力[20-22]。然而传统SC 变换器的电压转换比由电路结构决定,电压调节能力差。另外,由于SC 电路没有磁性元件,在开关切换时不同电压的电容相互充放电会产生很高的电流尖峰。提高由开关电容和电路等效电阻决定的充放电时间常数 τ可以降低电流尖峰[23],但是这会导致变换器体积过大。另外,传统SC 变换器的输入电流为脉冲形式,电流纹波较大。上述问题限制了SC 变换器的应用场合和功率等级。
如何实现SC 电路的软换流并拓展其电压调节能力,是近年来的一项研究热点[24-31]。文献[24-25]利用线路杂散电感或外加小电感与电容谐振来实现开关管的ZCS 开关,消除电流尖峰,但此类谐振SC 变换器的电压转换比仍是固定的[26]。文献[27-29]提出混合型 SC 变换器,将输入或输出电感引入SC 电路,具有PWM 电压调节能力,并保持了半导体器件的低电压应力等优点,同时限制了输入电流纹波。但此类变换器并不能完全消除开关切换时的电流尖峰问题[30]。文献[31]在混合型SC 变换器中加入谐振电感,实现所有开关管的零电压开关(Zero-Voltage Switching, ZVS)开通以及对所有二极管反向恢复过程的有效抑制。但该拓扑仅依靠SC 网络来提升电压增益,二极管数量较多,二极管导通损耗限制了变换器效率,并增加了硬件成本。
本文提出一种将SC 网络与三绕组耦合电感相结合的高电压增益DC-DC 变换器。该变换器具有PWM 电压调节能力,能够在非极端占空比条件下实现高电压增益,且所有开关管和二极管具有低电压应力。与文献[31]相比,耦合电感的引入可以增加变换器电压增益,从而减少SC 网络的器件数量。耦合电感的漏感能量被SC 网络吸收,不会产生增加器件电压应力的振荡。耦合电感的漏感帮助变换器获得良好的软开关特性,消除了传统SC 变换器的电流尖峰问题,所有开关管可实现ZVS 开通,所有二极管的反向恢复过程受到有效抑制。本文首先分析变换器基本工作原理,然后对关键的稳态特性进行理论推导,最后通过一台600W 原理样机对理论分析进行实验验证。
1 工作原理
本文提出的高电压增益DC-DC 变换器拓扑结构如图1 所示。图1 中,Vin 和VO 分别为变换器的输入电压和输出电压;RO 为等效负载电阻;开关管S2、二极管VD1~VD4、开关电容C1~C4 以及输出电容CO 组成SC 升压网络,其中C1~C4 的容值均为Cr;绕组Ⅰ为耦合电感一次绕组,绕组Ⅱ和绕组Ⅲ为耦合电感的两个二次绕组,三个绕组的匝数分别为n1、n2 和n3;绕组Ⅰ与开关管S1 和S2 组成Boost结构,绕组Ⅱ和绕组Ⅲ分别与C2 和C4 串联。开关管S1 和S2 互补导通,二者驱动信号之间有适当的死区时间。耦合电感三个绕组的匝数n1、n2 和n3 存在关系

式中,n 为耦合电感的匝比。
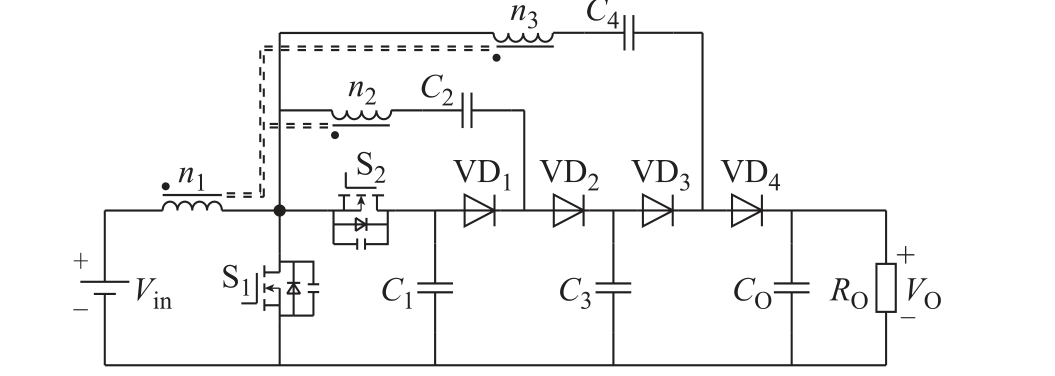
图1 本文提出的高电压增益DC-DC 变换器拓扑结构
Fig.1 The topology of the proposed high voltage gain DC-DC converter
采用励磁电感与理想变压器并联的模型替代耦合电感,得到变换器的等效电路如图2 所示。图2中,Lm 为耦合电感一次侧励磁电感,Lk1 和Lk2 分别为耦合电感折算到二次绕组Ⅱ和二次绕组Ⅲ的等效漏感,且二者感值均为Lk。图2 标出了主要物理量的正方向。耦合电感一次电流ip 由励磁电感电流和二次侧折算到一次侧的电流决定,满足表达式
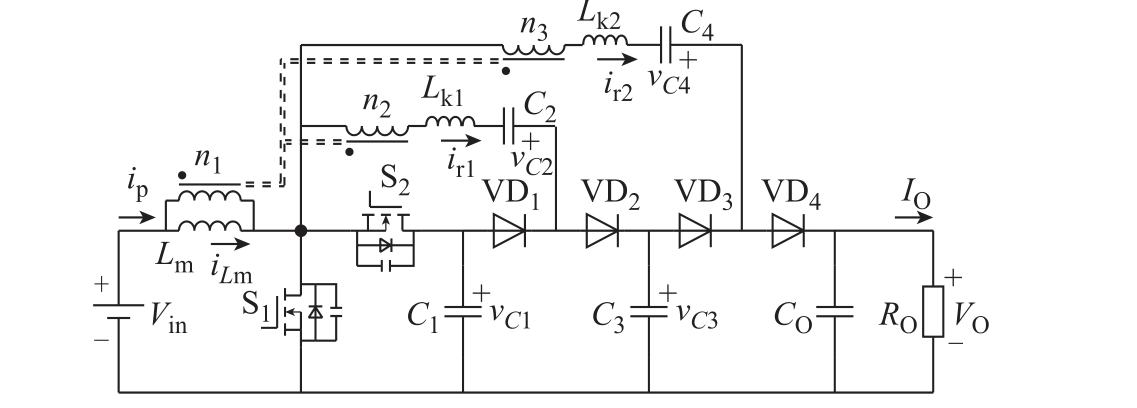
图2 等效电路
Fig.2 Equivalent circuit
为简化工作原理分析,做出如下假设:①除了考虑MOSFETs(S1 和S2)的寄生并联结电容和反并联二极管之外,其他各元器件均视为理想元器件;②输入电压Vin 保持恒定;③CO 足够大,输出电压纹波可以忽略;④变换器工作于稳态。
电路主要稳态工作波形如图3 所示。图3 中,Ts为开关周期,D 为主开关管S1 对应的占空比。耦合电感两个二次电流之间的差异很小,可以忽略,即

图3 稳态工作波形
Fig.3 Steady-state waveforms
变换器在一个开关周期内的工作过程可分为7 个阶段,各阶段的等效电路如图4 所示。各阶段的具体工作情况如下。


图4 各阶段等效电路
Fig.4 Equivalent circuit for each stage
阶段1 [t0, t1]:t0 时刻之前,耦合电感二次电流ir1 和ir2 为零,一次电流ip 与励磁电流im 相等,并流过开关管S1。t0 时刻,S1 关断,im 开始为S1 的并联结电容CS1 充电,为S2 的并联结电容CS2 放电。充放电完成后,S2 的反并联二极管开始导通,S2 漏源间电压vS2 被钳位为零。t1 时刻,S2 驱动信号上升沿到来,死区时间结束,S2 实现ZVS 开通。
阶段2 [t1, t2]:随着开关管S1 关断后漏源极电压vS1 上升,ir1 和ir2 开始上升,二极管VD2 和VD4开始导通,VD1 和VD3 仍处于关断状态。电容C2和C4 处于放电状态,C3 处于充电状态,能量通过VD4 由输入侧传递到负载侧。此阶段内,由于2ir < ip,开关管S2 流过负向电流,电容C1 处于充电状态。励磁电流im 在Vin 和C1 电压共同作用下近似线性下降。如果忽略C1~C4 的电压纹波,在t0~t2 时间段内,ir1、ir2 和im 的表达式分别为
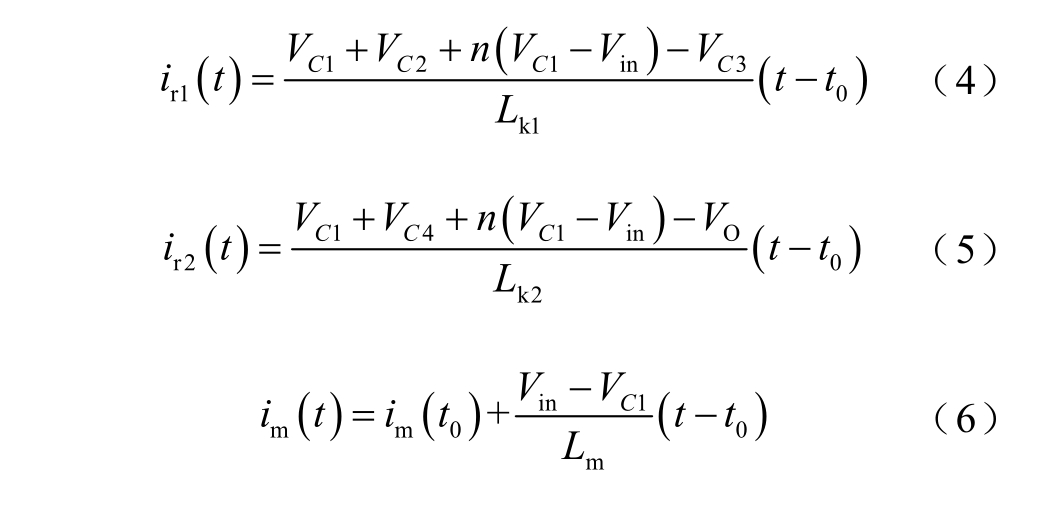
式中,VCm(m = 1, 2, 3, 4)表示电容Cm 的平均电压。
阶段3 [t2, t3]:t2 时刻,ir1 和ir2 之和上升到与ip 相等,即2ir = ip,如图3 所示。流过开关管S2 的电流由负向变为正向,电容C1 由充电状态变为放电状态。电路其他部分工作情况与阶段2类似。
阶段4 [t3, t4]:t3 时刻,由于2ir>ip,开关管S2 在流过正向电流的状态下被关断。S1 的并联结电容CS1 开始放电,S2 的并联结电容CS2 被充电。充放电过程完成后,S1 的反并联二极管开始导通,S1 漏源间电压vS1 被钳位为零。t4 时刻,S1 驱动信号上升沿到来,死区时间结束,S1 实现 ZVS开通。
阶段5 [t4, t6]:随着开关管S1 漏源极电压vS1下降,ir1 和ir2 开始下降。t5 时刻,ir1 和ir2 之和下降到与ip 相等,即2ir = ip,流过S1 的电流由负向变为正向。此阶段内,电容C1 既不充电也不放电,电容C2~C4 的充放电状态与阶段2 和阶段3 相同。励磁电流im 在S2 关断时达到最小值,之后在输入电压Vin 的作用下线性上升。在t3~t6 时间段内,ir1、ir2和im 的表达式分别为
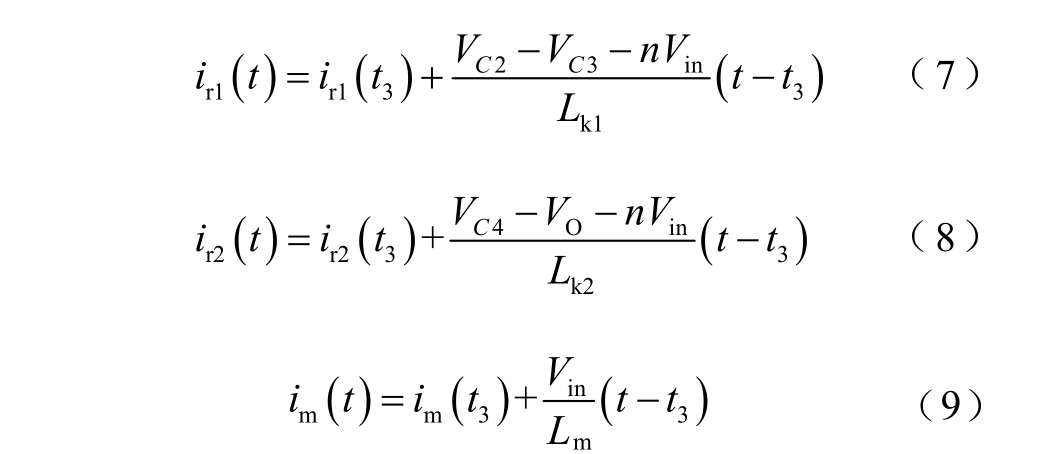
阶段6 [t6, t7]:t6 时刻,ir1 和ir2 下降到零,由正向变为负向,并进入谐振状态。二极管 VD2 和VD4 关断,VD1 和VD3 开始导通。由于ir1 和ir2 下降的速率di/dt 受到二次侧等效漏感的限制,所以VD2 和VD4 关断时的反向恢复问题得到有效抑制。此阶段内,励磁电流im 继续线性上升,电容C2 和C4 处于充电状态,C1 和C3 处于放电状态,输出电容CO 单独为负载供电。C1、VD1、C2、Lk1、绕组Ⅱ和S1 组成一个谐振回路;C3、VD3、C4、Lk2、绕组Ⅲ 和S1 组成另一个谐振回路。其中,绕组Ⅱ和绕组Ⅲ 可视为稳定电压源,各谐振回路等效谐振电容为Cr/2,那么,ir1 和ir2 对应的谐振频率fr1 和fr2以及特征阻抗Zr1 和Zr2 分别为
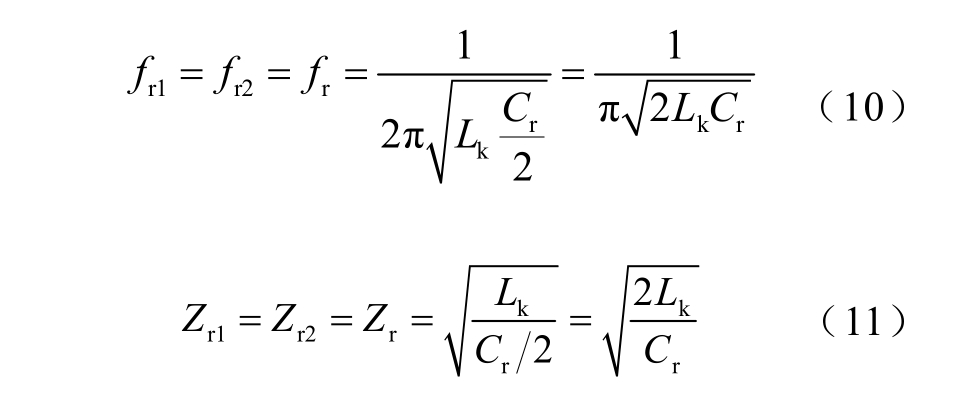
则ir1 和ir2 在此阶段内的表达式为
式中, ω r = 2πfr;Ir-,p 为ir1 和ir2 在此阶段的峰值。
阶段7 [t7, t0]:t7 时刻,ir1 和ir2 经过半个谐振周期之后重新变为零,二极管VD1 和VD3 实现ZCS自然关断,之后谐振过程被二极管VD1和VD3阻断。此阶段内,VD1~VD4 均为关断状态,电容C1~C4既不充电也不放电,输出电容CO 单独为负载供电。励磁电流im 继续线性上升。t0 时刻,开关管S1 关断,电路进入下一个开关周期。
2 稳态工作特性
2.1 电压增益
在电路稳态运行的情况下,根据励磁电感 Lm的伏秒平衡原则可知,电容C1 的平均电压VC1 与输入电压Vin 存在关系

耦合电感二次侧漏感Lk1 和Lk2 在t0~t6 时间段内符合伏秒平衡原则,结合式(4)、式(5)、式(7)和式(8)可得
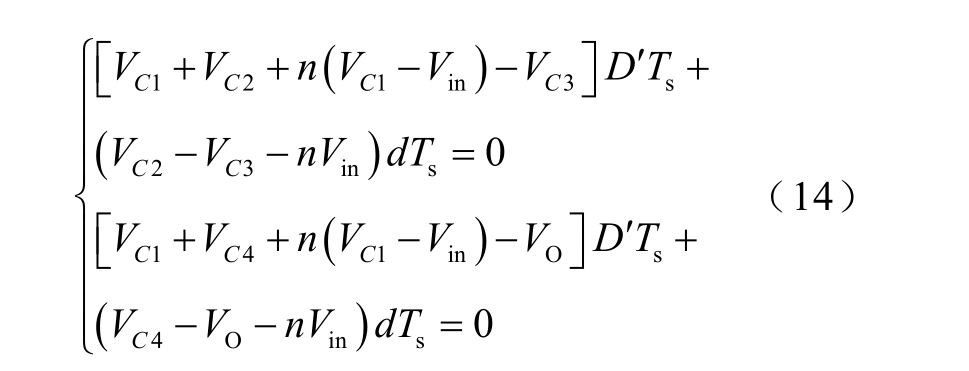
式中,d 为ir1 和ir2 由正向峰值下降到零所需要的时间与开关周期之比。
由Lk1 和Lk2 在t6~t7 时间段内的伏秒平衡原则可得
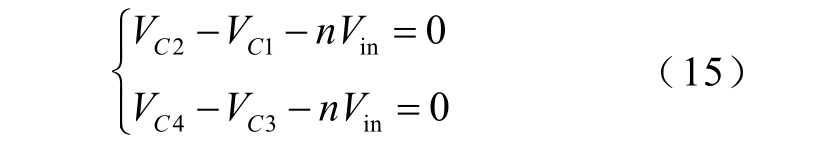
联立式(13)~式(15)可得
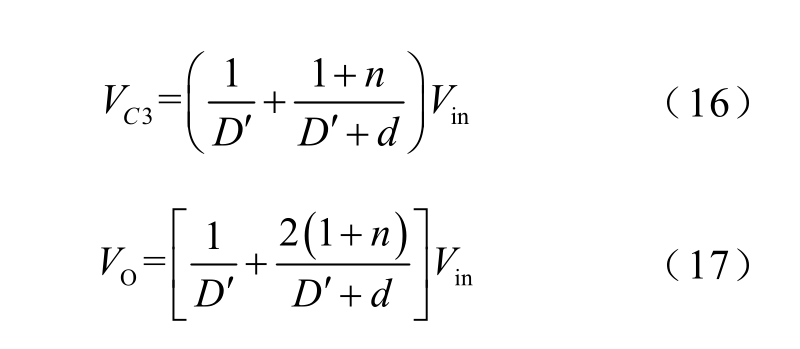
电容C1~C4 和CO 在一个开关周期内的平均电流等于零,所以二极管VD1~VD4 的平均电流均等于负载电流IO。其中,二极管VD2 仅在t0~t6 时间段内流过电流,且等于二次绕组II 的电流ir1,则有
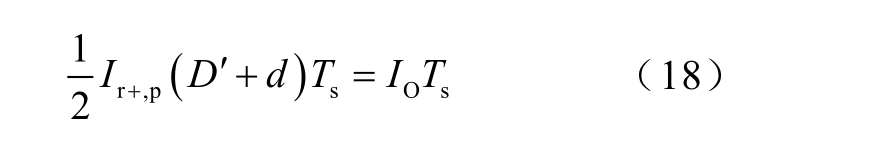
式中,Ir+,p 为ir1 在t3 时刻取得的正向峰值。结合式(4)和式(13)~式(17)可得Ir+,p 的表达式为
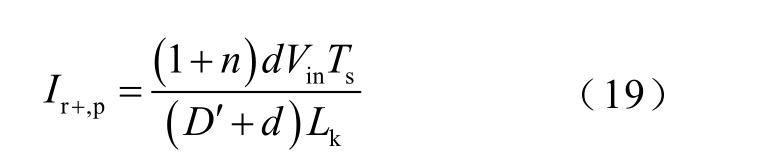
联立式(18)和式(19)可得
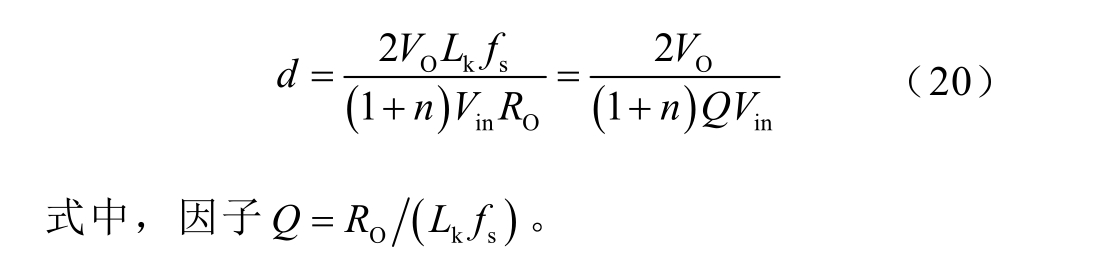
结合式(17)和式(20)可解得变换器的直流增益M 的表达式为

由式(21)可知,变换器的电压增益不仅与占空比D 和耦合电感的匝比n 有关,而且受到漏感Lk、开关频率fs 及负载功率的影响。电压增益M 与占空比D 关系曲线如图5 所示,其中使用的相关参数有Lk=4.5μH,fs=100kHz。图5a 为在PO=600W 条件下不同耦合电感匝比n 对应的增益曲线,图5b为n=4/7 条件下不同负载功率PO 对应的增益曲线。由图5a 可知,变换器可以在非极端的占空比条件下实现高电压增益,而且耦合电感匝比n 的增加可以大幅度增加电压增益,从而减少二极管和电容的数量。相比于文献[31]提出的混合SC 变换器,本文提出的变换器的耦合电感匝比n 是一个新的设计自由度。由图5b 可知,负载功率PO 的变化对增益曲线的影响不大,在负载功率较大时电压增益略有降低。总之,本文提出的变换器可在非极端占空比条件和较宽功率范围内取得高电压增益。

图5 电压增益曲线
Fig.5 Voltage gain plots
2.2 器件电压应力
根据变换器基本工作原理分析可知,开关管和二极管的电压应力由相关的电容电压钳位,它们存在如下关系
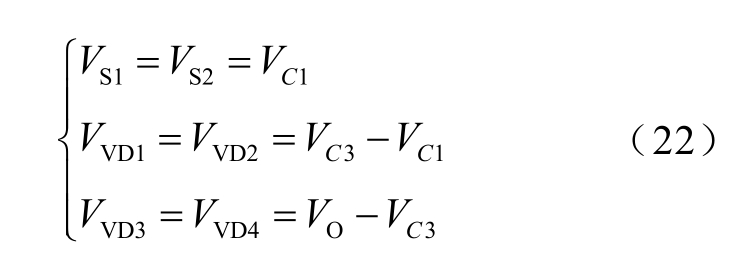
各电容的平均电压可由2.1 节分析得到。结合式(13)~式(17)和式(22),可得各电容和半导体元器件的电压应力,见表1。
表1 元器件电压应力
Tab.1 Voltage stresses of the components

元器件 电压应力C1 in 1 V D′C2 in 1 n V D■ ■+■ ■′■ ■C3 in 1 1 n V D D d+■■+■■′ ′+■■C4 in 1 1 n n V D D d+■■+ +■■′ ′+■■CO ( )in 2 1+1 n V D D d■■+■■′ ′+■■ S1, S2 in 1 V D′VD1~VD4 in 1 n V D d+′+
由表1 可知,电容C1~C4 的电压逐级上升,但均低于输出电压VO。开关管S1 和S2 的电压应力只与输入电压和占空比有关,二极管VD1~VD4 的电压应力还与耦合电感匝比n 有关。开关管与二极管的电压应力均远低于输出电压VO。软开关特性避免了MOSFETs 的硬开通,并使二极管反向恢复问题得到有效的抑制。SC 电路可以吸收耦合电感的漏感能量,起到良好的电压钳位作用。这些因素有效防止了电路杂散参数产生电压尖峰并抬高器件电压应力的问题。低电压应力允许变换器选择额定电压较低的半导体器件。低额定电压的MOSFETs 具有更低的通态电阻和更好的开关特性,低额定电压的二极管具有更低的导通压降和更好的关断特性,它们能够有效降低半导体器件导通损耗,提高变换器的效率。这对于低输入电压、高输入电流的高电压增益变换器来说具有重要意义。
2.3 输入电流纹波
耦合电感二次侧在一个开关周期内的电流平均值为零,结合式(2)可知,输入电流(一次电流)ip 与励磁电流im 的平均值相等,此平均值表达式为
由式(6)和式(9)可得耦合电感一次侧励磁电流纹波峰峰值ΔIm,p-p 的表达式为

则im 的最大值和最小值为
ip 的最大值与im 的最大值相等。ip 在t3 时刻取得最小值,由式(2)可得
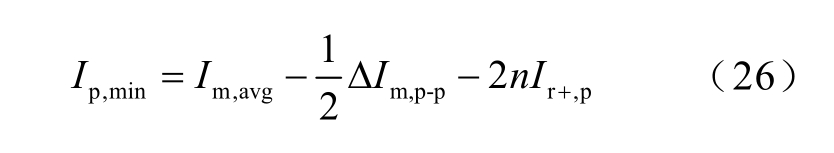
联立式(25)、式(26)和式(18)可得输入电流ip 的纹波峰峰值ΔIp,p-p 表达式为

式中,Ir+,p、ΔIm,p-p 分别如式(19)和式(24)所示。
2.4 电容电压纹波
由2.1 节分析可知,二极管VD1~VD4 的平均电流等于负载电流IO,则电容C2~C4 在一个开关周期内的充电或放电电荷均为QO = IOTs,可得C2~C4 的电压纹波峰峰值为
如第1 节基本工作原理分析,电容C1 在t0~t2时间段内充电,充电电荷为QC1,其表达式为

式中,Im,max 的表达式如式(25)所示。由式(4)、式(5)及表1 可得
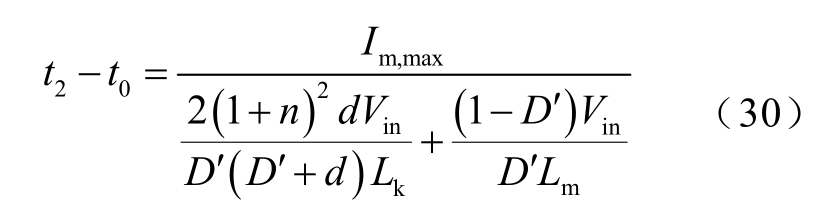
则C1 的电压纹波峰峰值表达式为
在t6~t7时间段内,C1与二极管VD1电流相等,放电电荷为 QO 。C1 在t2~t3 时间段也处于放电状态,所以C1 在一个开关周期内总的放电电荷 QC 1> Q O ,故C1 的电压纹波峰峰值要大于C2~C4 的电压纹波峰峰值。
2.5 软开关条件
如图3 所示,t0 时刻,开关管S1 关断,励磁电流im 达到其最大值,励磁电流为S1 和S2 的寄生并联电容CS1 和CS2 充放电。由于励磁电感中存储的能量足够完成CS1 和CS2 的充放电过程,所以同步整流管S2 容易实现ZVS 开通。
t3 时刻,开关管S2 关断,耦合电感二次电流之和2ir 与一次电流ip 之间的差值开始为CS1 和CS2 充放电。开关管的并联电容与耦合电感的漏感处于谐振状态,谐振期间S1 漏源间电压的表达式为
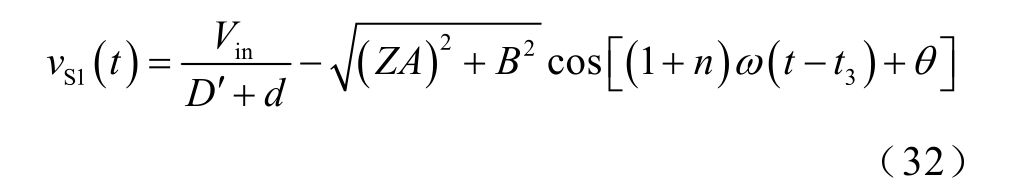
其中


由式(35)可知,当耦合电感漏感值Lk 不够大时,会导致S1 不能完全实现ZVS 开通。而减小一次侧励磁电感Lm可以降低励磁电流的最小值Im,min,有利于S1 实现ZVS 开通。
3 实验
为验证本文提出的高电压增益DC-DC 变换器的特性及理论分析结果,搭建了一台额定功率为600W 的实验样机。样机的主要参数和器件型号见表2。样机实物照片如图6 所示,印制电路板(Printed Circuit Board, PCB)上虚线框内的器件是属于本文实验样机,PCB 其他部分属于未来研究内容。
在PO=600W、输入电压Vin 分别为25V 和40V的条件下,Vin、输出电压VO、耦合电感一次电流ip和开关管S1驱动电压vgs,S1的实验波形如图7 所示。一次电流ip 的波形符合原理分析。在两种不同输入电压情况下,输出电压均能稳定在400V,表明变换器能够实现高电压增益和PWM 调压。
表2 实验样机参数和器件型号
Tab.2 Parameters and components of the prototype
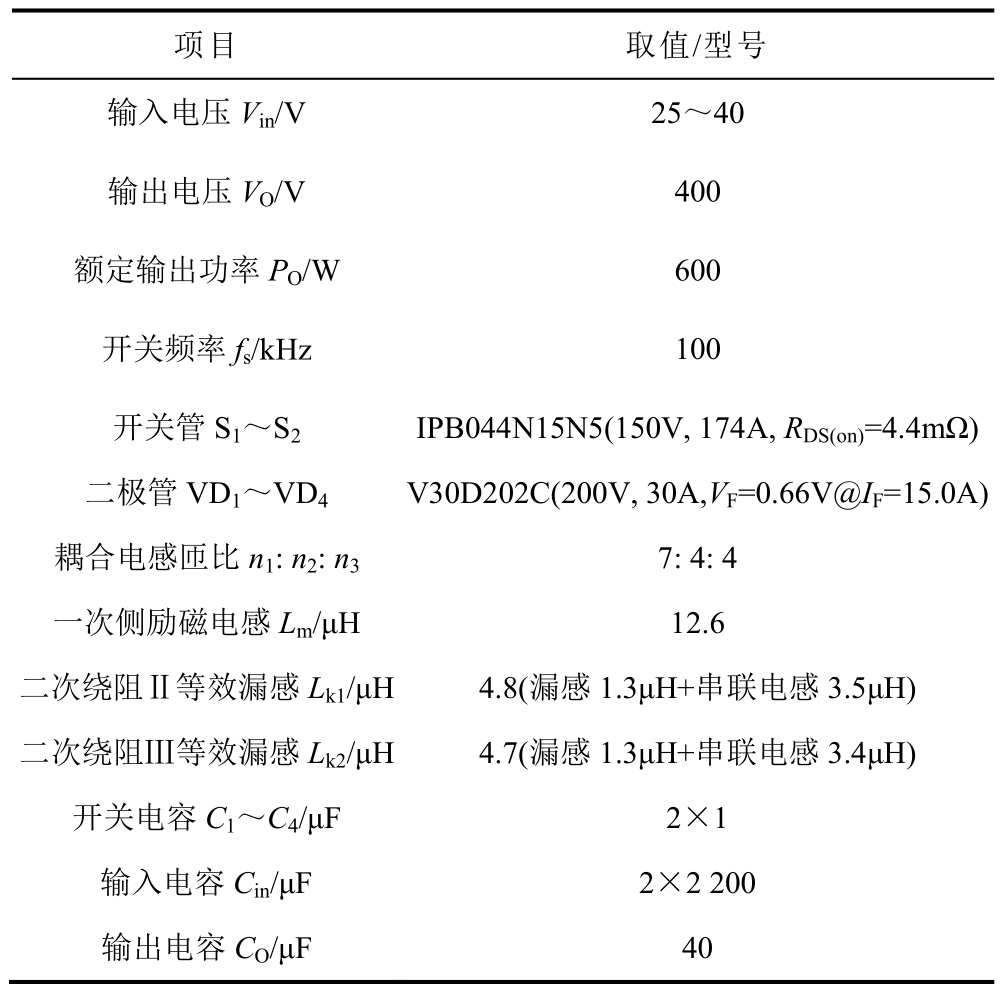
项目 取值/型号输入电压Vin/V 25~40输出电压VO/V 400额定输出功率PO/W 600开关频率fs/kHz 100开关管S1~S2 IPB044N15N5(150V, 174A, RDS(on)=4.4mΩ)二极管VD1~VD4 V30D202C(200V, 30A,VF=0.66V@IF=15.0A)耦合电感匝比n1: n2: n3 7: 4: 4一次侧励磁电感Lm/μH 12.6二次绕阻Ⅱ等效漏感Lk1/μH 4.8(漏感1.3μH+串联电感3.5μH)二次绕阻Ⅲ等效漏感Lk2/μH 4.7(漏感1.3μH+串联电感3.4μH)开关电容C1~C4/μF 2×1输入电容Cin/μF 2×2 200输出电容CO/μF 40

图6 实验样机
Fig.6 Experimental prototype
在PO=600W、Vin=25V 条件下,开关管S1 和S2 的开通过程如图8 所示。由图8a 可知,S1 开通时,ip 处于最小值;由图8b 可知,S2 开通时,有ip=im,且im 处于最大值。S1 和S2 的漏源极电压在对应的驱动电压上升之前已经下降到零,均实现了ZVS 开通。S1 和S2 的电压应力较低,均为100V 左右,符合2.2 节分析。

图7输入电压Vin、输出电压VO、耦合电感一次电流ip和S1 驱动电压vgs,S1 实验波形
Fig.7 Experimental waveforms of Vin, VO, ip and vgs,S1
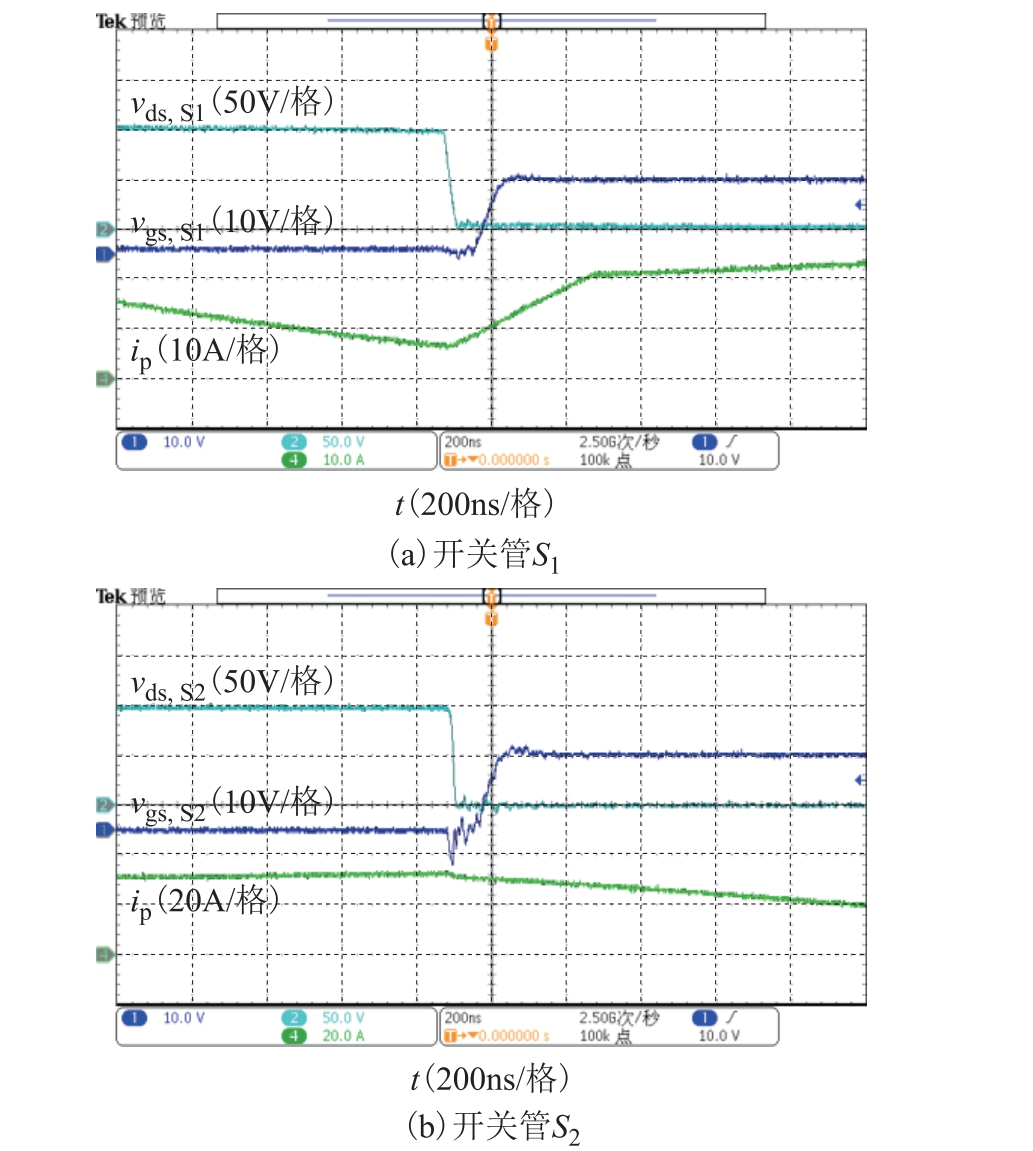
图8 开关管软开关波形
Fig.8 ZVS waveforms of the active switches
在PO=600W、Vin=25V 条件下,开关电容C1~C4电压波形如图9 所示。电容电压平均值符合2.2 节分析。电容C1 的电压纹波峰峰值约为11V,而电容C2~C4 的电压纹波峰峰值约为8V,均符合2.4 节分析。
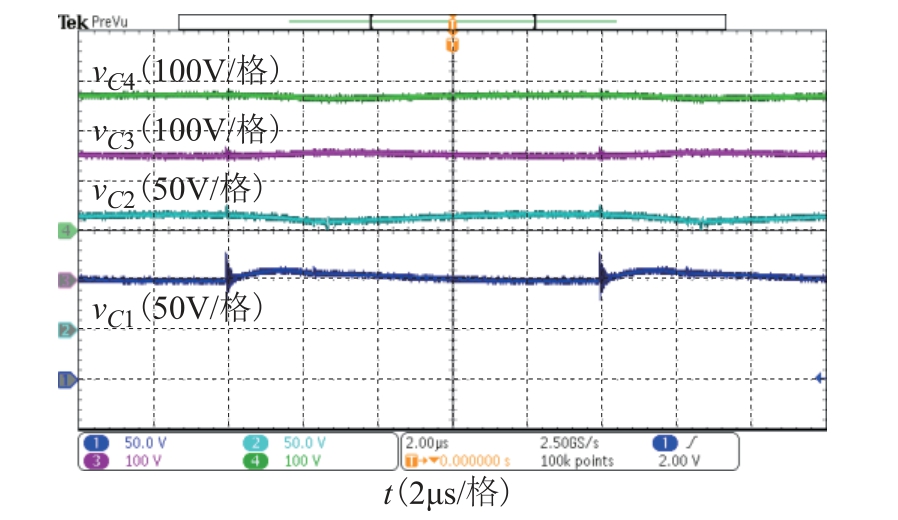
图9 开关电容电压波形
Fig.9 Experiment waveforms of vC1~vC4
在二次电流和 示。电流ir1 合电感漏感 恢复问题得 振电流,实 升过程均没 漏感对二极 到的电压钳 应力,均为1

图10 耦合电感二次电流和二极管电压波形
Fig.10 Experiment waveforms of ir1, ir2 and VD1~VD4
本文与文献[31]样机测试效率对比如图11 所示。对于本文提出的变换器,Vin=25V 条件下,输出功率为300W 和400W 时取得97.2%的最高效率,满载时效率为97.0%;Vin=40V 条件下,输出功率为500W 和满载时取得97.7%的最高效率。本文实验样机在输出功率 300~600W 范围内效率均不低于97.0%,而25V 输入电压对应的效率曲线低于40V输入电压对应的效率曲线,因为更低的输入电压意味着更高的输入电流和导通损耗。
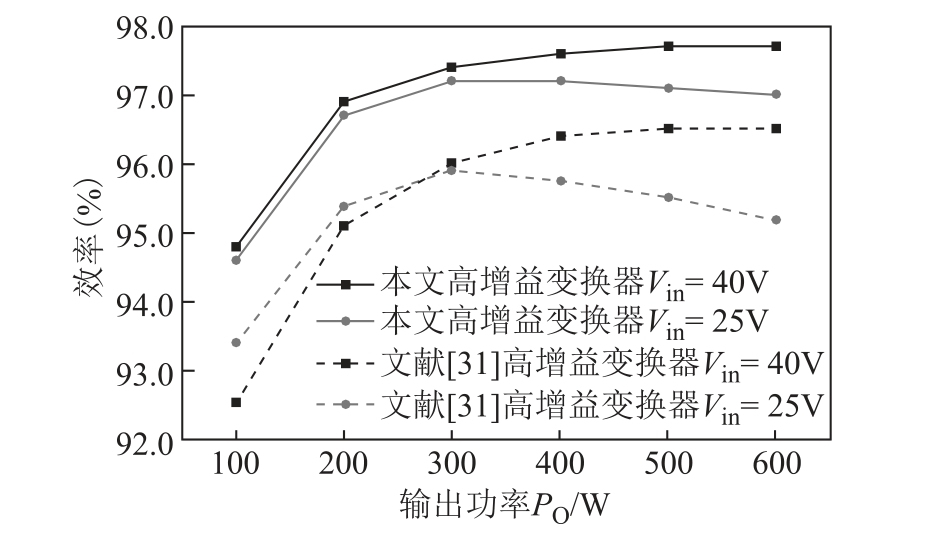
图11 本文与文献[31]实验样机测试效率对比
Fig.11 Measured efficiency comparison between this work and Ref. [31]
相比于文献[31],在相同工况下,本文样机测试效率提高超过1%。由于引入耦合电感,本文提出的变换器的开关管电压应力更低,故可选用具有更小通态电阻的MOSFETs,这对于电流应力较大的主开关管S1 来说非常重要。同时,二极管和谐振电感数量的减少也有利于降低损耗。另外,本文选用的二极管与文献[31]的二极管相比,额定电压相同而导通压降更低,有利于降低二极管导通损耗。
本文提出的变换器与近年来已发表的文献中其他高增益DC-DC 变换器的对比见表3。表3 中列出的变换器具有相近的输入输出电压等级和功率等级,所对比的关键特性包括电压增益、器件数量、软开关情况、样机效率及半导体器件电压应力等。文献[13]将Boost-Flyback 型变换器[11-12]与SC 升压单元结合,但开关管不能实现软开关,且耦合电感二次侧二极管关断时,漏感与二极管寄生电容之间存在明显振荡,导致损耗增加。文献[17-19]将传统Boost变换器与耦合电感倍压单元结合。其中,文献[17]为单相结构,器件数量较少,但在耦合电感匝比相同的情况下其电压增益较小;文献[18]采用交错并联结构,半导体和磁性器件数量较多,包括2 个输入端滤波电感和1 个三绕组耦合电感。文献[17,19]需要耦合电感一次侧产生负向电流来实现主开关管的ZVS 开通。文献[29,31]依靠SC 结构实现高电压增益,半导体器件数量较多。文献[29]在SC 电路中引入输入电感实现PWM 电压调节和连续输入电流,但这种混合型SC 变换器的开关管和二极管不能实现软开关,变换器效率受到限制。文献[31]在混合SC 电路的基础上,利用谐振软开关技术实现所有开关管的ZVS 开通和二极管的软关断,其磁性元件包括1 个输入滤波电感和3 个感值较小的谐振电感。
表3 本文提出的变换器与其他高增益DC-DC 变换器的对比
Tab.3 Comparison of the proposed converter with other high step-up DC-DC converters
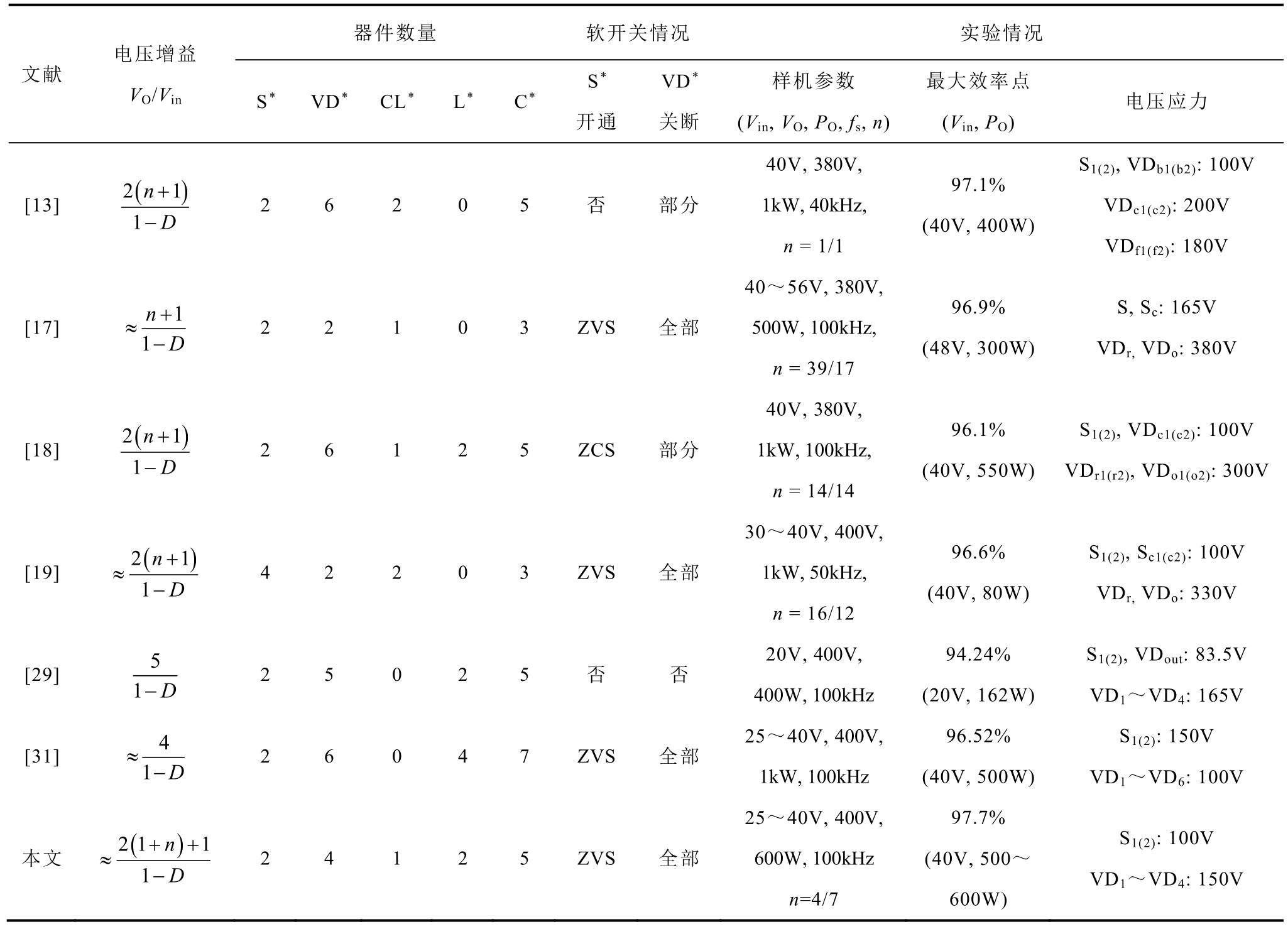
注:S*为开关管;VD*为二极管;CL*为耦合电感;L*为单电感;C*为电容。
文献电压增益VO/Vin器件数量 软开关情况 实验情况S* VD* CL* L* C* S*开通VD*关断样机参数(Vin, VO, PO, fs, n)最大效率点(Vin, PO)电压应力[13] ( )2 1 1 n+D− 2 6 2 0 5 否 部分40V, 380V,1kW, 40kHz,n = 1/1 97.1%(40V, 400W)S1(2), VDb1(b2): 100V VDc1(c2): 200V VDf1(f2): 180V[17] 1 n+1 D≈ − 2 2 1 0 3 ZVS 全部40~56V, 380V,500W, 100kHz,n = 39/17 96.9%(48V, 300W)S, Sc: 165V VDr, VDo: 380V[18] ( )2 1 1 n+D− 2 6 1 2 5 ZCS 部分40V, 380V,1kW, 100kHz,n = 14/14 96.1%(40V, 550W)S1(2), VDc1(c2): 100V VDr1(r2), VDo1(o2): 300V[19] ( )2 1 1 n+D≈ − 4 2 2 0 3 ZVS 全部30~40V, 400V,1kW, 50kHz,n = 16/12 96.6%(40V, 80W)S1(2), Sc1(c2): 100V VDr, VDo: 330V[29] 5 1 D− 2 5 0 2 5 否 否20V, 400V,400W, 100kHz 94.24%(20V, 162W)S1(2), VDout: 83.5V VD1~VD4: 165V[31] 4 1 D≈ − 2 6 0 4 7 ZVS 全部25~40V, 400V,1kW, 100kHz 96.52%(40V, 500W)S1(2): 150V VD1~VD6: 100V本文 ( )2 1 1 1 nD+ +≈ − 2 4 1 2 5 ZVS 全部25~40V, 400V,600W, 100kHz n=4/7 97.7%(40V, 500~600W)S1(2): 100V VD1~VD4: 150V
本文提出的变换器在混合型SC 变换器的基础上引入了多绕组耦合电感,增强了变换器的电压增益能力。由表3 可知,本文提出的变换器的半导体数量少于文献[13, 18, 29, 31],与文献[19]数量相同。相比于文献[31]减少了磁性元件和电容的数量,其中2 个单电感和4 个开关电容的感值或容值都很小。这些特点都有利于降低变换器成本。本文提出的变换器继承了SC 变换器半导体器件电压应力低的优点,其中开关管电压应力相比于文献[31]进一步降低,而所有二极管电压应力均为150V,略高于文献[31],但远远低于文献[17-19]中的二极管电压应力。另外,本文与文献[31]同样具有良好的软开关特性,且所有二极管在关断时都不存在电压振荡尖峰,保证了变换器能够在较宽范围内实现较高的转换效率。综合表3 所列的高增益DC-DC 变换器,本文提出的变换器具有明显的效率优势。
4 结论
本文提出一种非隔离型软开关高电压增益DC-DC 变换器拓扑。通过对DC-DC 变换器基本工作原理、稳态特性以及实验结果的分析,可得出以下结论:
1)变换器将 SC 结构与多绕组耦合电感相结合,可以实现在非极端占空比条件下的高电压增益,并具有PWM 电压调节能力。
2)耦合电感的引入可减少二极管和开关电容的数量,有效降低变换器导通损耗和硬件成本。
3)所有开关管和二极管的电压应力均远低于输出电压,允许变换器选用具有低导通损耗和更好开关性能的低额定电压半导体器件。
4)变换器具有良好的软开关特性,所有开关管均可实现ZVS 开通,一部分二极管可实现ZCS 关断,其他二极管的反向恢复过程也得到有效抑制,有效降低变换器开关损耗。
原理样机的实验结果显示,变换器可在较宽的功率范围内获得不低于97.0%的效率,最高效率为97.7%。综上所述,本文提出的变换器适用于将低压新能源电源进行高电压增益变换的应用场合。
在后续研究中,将结合交错并联技术降低输入电流纹波,减轻输入电容的压力,提高变换器功率容量。另外,为进一步提高磁性元件利用率和变换器功率密度,将考虑应用磁集成技术优化磁性元件。
[1] Blaabjerg F, Chen Zhe, Kjaer S B. Power electronics as efficient interface in dispersed power generation systems[J]. IEEE Transactions on Power Electronics,2004, 19(5): 1184-1194.
[2] Meneses D, Blaabjerg F, García Ó, et al. Review and comparison of step-up transformerless topologies for photovoltaic AC-module application[J]. IEEE Transactions on Power Electronics, 2013, 28(6):2649-2663.
[3] Lai J S, Ellis M W. Fuel cell power systems and applications[J]. Proceedings of the IEEE, 2017,105(11): 2166-2190.
[4] Dong Dong, Cvetkovic I, Boroyevich D, et al.Grid-interface bidirectional converter for residential DC distribution systems-part one: high-density two-stage topology[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1655-1666.
[5] Li Wuhua, He Xiangning. Review of nonisolated high-step-up DC/DC converters in photovoltaic grid-connected applications[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1239-1250.
[6] Forouzesh M, Siwakoti Y P, Gorji S A, et al. Step-up DC-DC converters: a comprehensive review of voltage-boosting techniques, topologies, and applications[J]. IEEE Transactions on Power Electronics, 2017, 32(12): 9143-9178.
[7] Gu Bin, Dominic J, Chen Baifeng, et al. Hybrid transformer ZVS/ZCS DC-DC converter with optimized magnetics and improved power devices utilization for photovoltaic module applications[J].IEEE Transactions on Power Electronics, 2015, 30(4):2127-2136.
[8] Esram T, Chapman P L. Comparison of photovoltaic array maximum power point tracking techniques[J].IEEE Transactions on Energy Conversion, 2007,22(2): 439-449.
[9] Watson R, Lee F C, Hua G C. Utilization of an active-clamp circuit to achieve soft switching in flyback converters[J]. IEEE Transactions on Power Electronics, 1996, 11(1): 162-169.
[10] Wu T F, Lai Y S, Hung J C, et al. Boost converter with coupled inductors and Buck-Boost type of active clamp[J]. IEEE Transactions on Industrial Electronics, 2008, 55(1): 154-162.
[11] Zhao Qun, Lee F C. High performance coupledinductor DC-DC converters[C]//Eighteenth Annual IEEE Applied Power Electronics Conference and Exposition, Miami Beach, FL, USA, 2003: 109-113.
[12] Tseng K C, Liang T J. Novel high-efficiency step-up converter[J]. IEE Proceedings-Electric Power Applications, 2004, 151(2): 182-190.
[13] Tseng K C, Huang C C. High step-up high-efficiency interleaved converter with voltage multiplier module for renewable energy system[J]. IEEE Transactions on Industrial Electronics, 2014, 61(3): 1311-1319.
[14] 吴琨, 钱挺. 一种带三绕组耦合电感的级联型高增益功率变换器[J]. 电工技术学报, 2017, 32(20):124-132.Wu Kun, Qian Ting. A cascaded high step-up DC-DC converter with three-winding coupled inductor[J].Transactions of China Electrotechnical Society, 2017,32(20): 124-132.
[15] 林雪凤, 许建平, 周翔. 谐振软开关耦合电感高增益DC-DC 变换器[J]. 电工技术学报, 2019, 34(4):747-755.Lin Xuefeng, Xu Jianping, Zhou Xiang. Softswitched high step-up DC-DC converter with coupled inductor of resonance[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 747-755.
[16] Li Wuhua, Zhao Yi, Wu Jiande, et al. Interleaved high step-up converter with winding-cross-coupled inductors and voltage multiplier cells[J]. IEEE Transactions on Power Electronics, 2012, 27(1):133-143.
[17] Zhao Yi, Li Wuhua, He Xiangning. Single-phase improved active clamp coupled-inductor-based converter with extended voltage doubler cell[J]. IEEE Transactions on Power Electronics, 2012, 27(6):2869-2878.
[18] Li Wuhua, Li Weichen, Xiang Xin, et al. High step-up interleaved converter with built-in transformer voltage multiplier cells for sustainable energy applications[J]. IEEE Transactions on Power Electronics, 2014, 29(6): 2829-2836.
[19] Forouzesh M, Shen Yanfeng, Yari K, et al. Highefficiency high step-up DC-DC converter with dual coupled inductors for grid-connected photovoltaic systems[J]. IEEE Transactions on Power Electronics,2018, 33(7): 5967-5982.
[20] Sanders S R, Alon E, Le H P, et al. The road to fully integrated DC-DC conversion via the switchedcapacitor approach[J]. IEEE Transactions on Power Electronics, 2013, 28(9): 4146-4155.
[21] Schaef C, Rentmeister J, Stauth J T. Multimode operation of resonant and hybrid switched-capacitor topologies[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10512-10523.
[22] 薛利坤, 王萍, 王议锋, 等. 基于开关电容和耦合电感的交错并联型高电压增益双向DC-DC 变换器[J]. 电工技术学报, 2016, 31(24): 181-187,194.Xue Likun, Wang Ping, Wang Yifeng, et al.Interleaved high gain bidirectional DC-DC converter with switched capacitor and coupled inductor[J].Transactions of China Electrotechnical Society, 2016,31(24): 181-187,194.
[23] Ben-Yaakov S. Behavioral average modeling and equivalent circuit simulation of switched capacitors converters[J]. IEEE Transactions on Power Electronics, 2012, 27(2): 632-636.
[24] Law K K, Cheng K W E, Yeung Y P B. Design and analysis of switched-capacitor-based step-up resonant converters[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers, 2005, 52(5): 943-948.
[25] Vasić M, Serrano D, Toral V, et al. Ultraefficient voltage doubler based on a GaN resonant switched-capacitor converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics,2019, 7(2): 622-635.
[26] Ioinovici A, Tse C K, Chung H S H. Comments on“Design and analysis of switched-capacitor-based step-up resonant converters”[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers, 2006,53(6): 1403.
[27] Abutbul O, Gherlitz A, Berkovich Y, et al. Step-up switching-mode converter with high voltage gain using a switched-capacitor circuit[J]. IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, 2003, 50(8): 1098-1102.
[28] Rosas-Caro J C, Ramirez J M, Peng F Z, et al. A DC-DC multilevel Boost converter[J]. IET Power Electronics, 2010, 3(1): 129-137.
[29] Prabhala V A K, Fajri P, Gouribhatla V S P, et al. A DC-DC converter with high voltage gain and two input boost stages[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4206-4215.
[30] Lei Yutian, May R, Pilawa-Podgurski R. Split-phase control: achieving complete soft-charging operation of a Dickson switched-capacitor converter[J]. IEEE Transactions on Power Electronics, 2016, 31(1):770-782.
[31] 雷浩东, 郝瑞祥, 游小杰, 等. 基于开关电容的软开关高电压增益DC-DC 变换器[J]. 电工技术学报,2018, 33(12): 2821-2830.Lei Haodong, Hao Ruixiang, You Xiaojie, et al.Soft-switching high voltage gain DC-DC converter based on switched-capacitor[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 2821-2830.