0 引言
与同等容量的硅（Si）器件相比，碳化硅（SiC）金属氧化物半导体场效应晶体管（MOSFET）具有更高的开关速度和更低的通态电阻[1-5]，使得SiC 器件的开关过程更易受杂散参数的影响，表现出更强的开关瞬态过电流、过电压、寄生振荡，影响系统运行效率、波形质量和电磁干扰，严重时对器件的安全构成威胁。因此，为正确、充分发挥SiC MOSFET器件的应用潜力，有必要研究SiC MOSFET 器件在电路中的开关瞬态过程，掌握影响器件开关瞬态过电流、过电压的因素及影响规律，从而为 SiC MOSFET 电力电子电路的优化设计和高效运用提供指导。
目前国内外已对SiC MOSFET 的开关瞬态过程和开关性能进行了研究。但是，在分析SiC 器件的开关瞬态过程及建模时，大多基于器件理想的开关过程，假设漏源电压变化和漏极电流变化非同时进行[6]，在分析器件的开关性能时，多聚焦于器件的某单一性能（如开通速度[7]、栅源电压振荡[8-9]、漏源过压[10]、温度效应[11-14]、开关损耗[10]、电磁干扰（EMI[15]等），或单一因素对开关瞬态行为的影响[15-21]，而且多通过仿真进行定性分析[10,15,18]，鲜有文献综合电路中的多影响因素，定量研究器件在电路中的非理想开关行为与电路元素间的互动关系。
文献[6,19-20]基于SiC MOSFET 的理想开关过程（假设漏源电压变化与漏极电流变化非同时进行，而实测波形并非如此），分栅源电压变化（低于阈值电压阶段）、漏电流变化、漏源电压变化和振荡等阶段建立了SiC MOSFET 器件的开关瞬态过程模型，并基于所建模型，仿真研究了SiC MOSFET 器件的开关瞬态行为。文献[19]分段建立了SiC MOSFET和SiC SBD 换流单元瞬态模型，但对栅源电压进行了较大的近似，且未考虑驱动回路杂散电感的影响。文献[21]推导出了SiC MOSFET-二极管换流电路中SiC MOSFET 开通过电流峰值的解析表达式，但推导过程基于器件的理想开关过程，且假设电流变化率恒定，分析结果的准确性难免受影响。文献[7]研究了SiC MOSFET 的极限开通速度及寄生电容和门极驱动电阻对开通速度的影响，但未谈及其他开关性能。文献[21]研究了SiC MOSFET 非线性结电容Cds 的建模，分析了Cds 建模准确性对器件开关过程瞬态行为仿真结果的影响。文献[15]分别研究了DC-DC 半桥电路中漏极、源极和栅极寄生电感单独对器件开关瞬态过程的影响，未考虑三者的综合影响，且仅根据仿真和实验波形对寄生电感的影响规律进行了定性分析，未做定量分析。文献[10]通过仿真，定性分析了半桥电路模块中上管和下管之间线路寄生电感对开关损耗、电压尖峰的影响。文献[8]在SiC MOSFET 半桥电路中，研究了栅漏极结电容和共源寄生电感对器件栅源电压的影响，但未论及能量脉冲的瞬态行为。
截至目前，尚未有文献综合考虑电路中的多影响因素，且计及器件寄生电容的非线性，对器件在电路中的开关瞬态过电流、过电压进行定量计算和敏感性分析。不同于已有文献基于SiC MOSFET 器件的理想开关过程，本文将结合实测的开关瞬态过程，计及电路中的寄生参数和器件寄生电容的非线性，通过解析的方法，定量研究系统多因素对SiC MOSFET 器件在电路中的开关瞬态行为的综合影响，梳理出其敏感因素。首先给出SiC MOSFET 在电路中的开关瞬态过程实例；然后结合实测波形，探究电磁能量脉冲畸变严重的开通瞬态过程及其换流回路；推导开通瞬态过程中电压、电流的时域解析计算式，在此基础上，通过极大值计算，定量分析影响SiC MOSFET 半桥电路开关瞬态过电流、过电压的敏感因素及影响规律。最后通过大量仿真和实验验证了理论分析的正确性。
1 SiC MOSFET 在系统中的开关瞬态过程
1.1 SiC MOSFET 半桥双脉冲测试电路开关瞬态过程实例
半桥电路是构成逆变电路、PWM 整流电路、多电平变流器等众多电力电子电路的基本单元，故本文以SiC MOSFET 半桥电路为研究对象，研究SiC MOSFET 器件在电路中的开关瞬态行为。
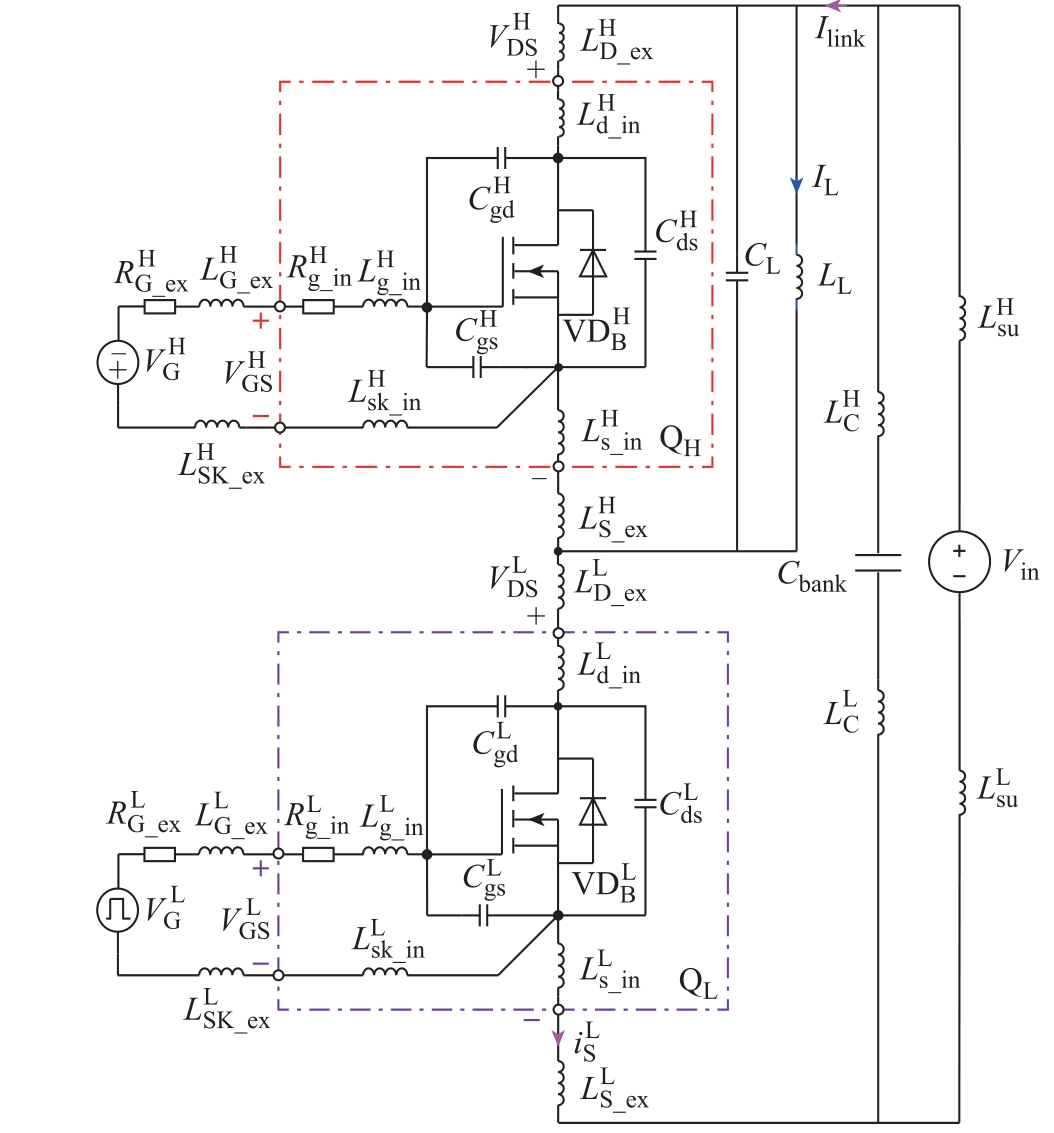
图1 考虑杂散参数的SiC MOSFET 半桥双脉冲测试
电路原理
Fig.1 Half-?bridge double pulse test circuit with parasitic parameters
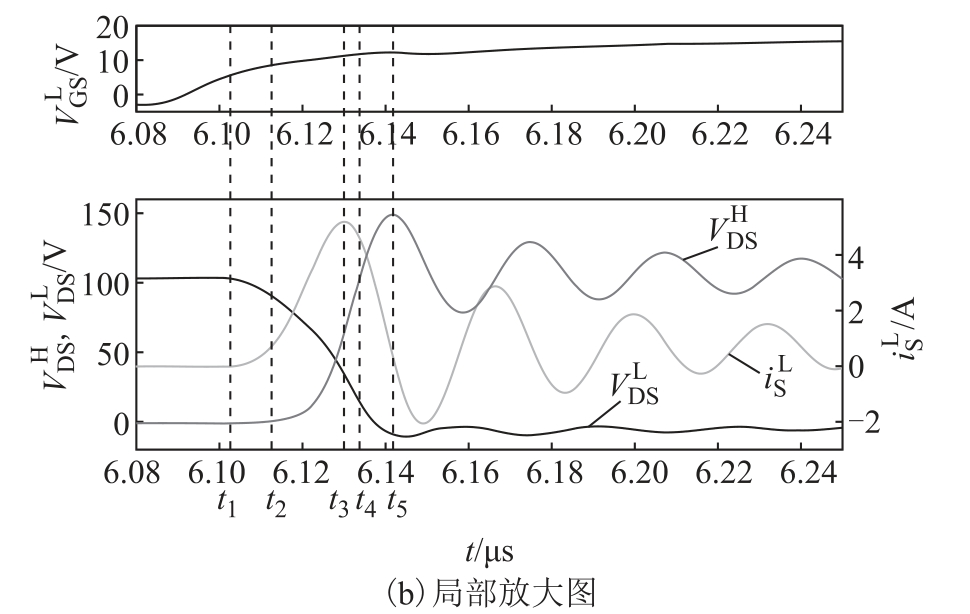
图 2 双脉冲测试波形
Fig.2 The typical waveforms of double pulse tests
由图2 可知，测试电路在QL 开通瞬态过程中展现出较强的非理想行为，在上述测试条件下
过冲最高达402.72%，
过冲最高达48.8%，且伴随有电压、电流振荡，电压、电流振荡频率基本相等。而器件在关断瞬态过程中的非理想行为并不十分严重。因此，下面着重分析半桥电路在QL 开通时的瞬态过程。在许多应用中，QL 和QH 为一对互补开关，具有对偶性，QH 与QL 的开通瞬态过程类似，因此，以QL 为例，分析半桥电路的开关瞬态行为不失一般性。
1.2 SiC MOSFET 半桥电路下管开通时的瞬态过程分析
SiC MOSFET 器件可等效为一个理想开关SW与寄生元件的组合电路，如图3 所示。图中D、S、G 表示SiC MOSFET 器件外部端口，d、s、g 表示SiC MOSFET 器件内部芯片结电极，实测波形均为外部端口电压和电流。虽然由于寄生参数的原因，器件外部电压与内部芯片电压不相等，但器件外部电压变化规律能反映内部芯片电压变化规律。图3 中，Rds 为SiC MOSFET 电阻，Rds 的大小受栅源电压Vgs 控制。当SW 闭合或体二极管VDB 正向导通时，漏源结电容Cds 被旁路；在SW 或VDB 开关瞬态过程中，应考虑Cds 和Cgd 的非线性变化及其充放电行为。于图5 状态。图5 中，Lstray1 指除电源支路和缓冲电容支路外Ilink 回路中总的寄生电感，即
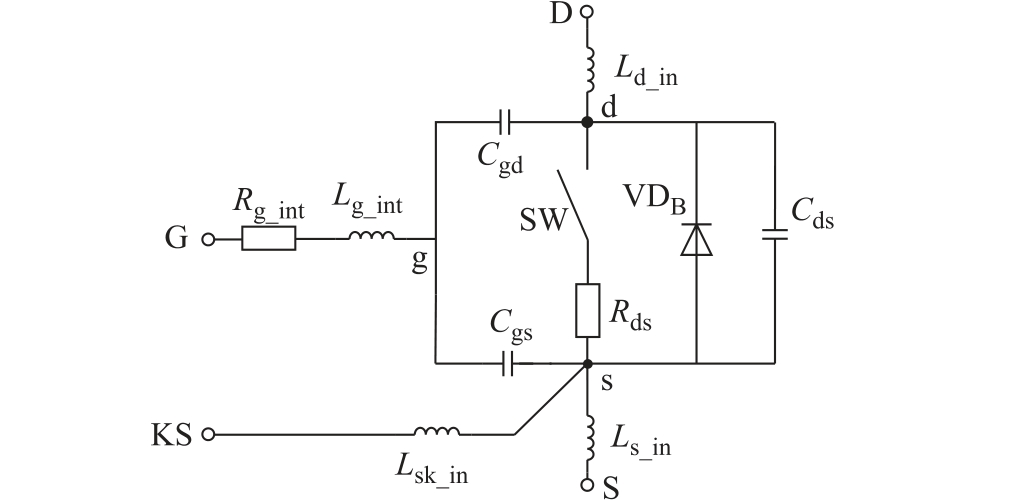
图3 SiC MOSFET 简化等效电路
Fig.3 The simplified equivalent circuit of SiC MOSFET
图4 负载电流经QH 体二极管续流时的稳态等效电路
Fig.4 The steady state equivalent circuit during the load current freewheeling through the body diode of QH
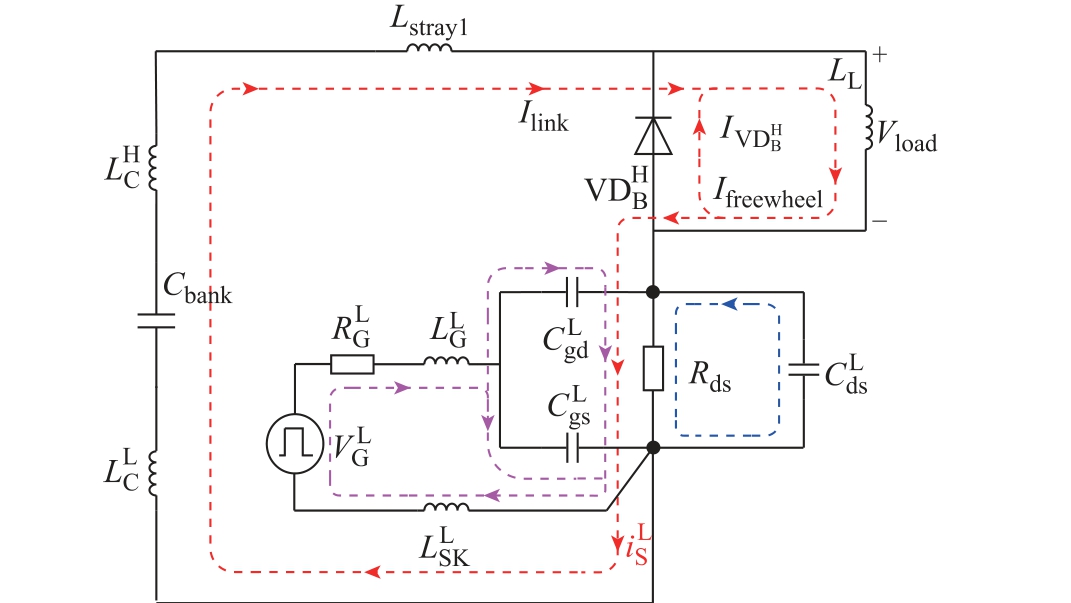
图5 Q 初始开通、 
尚在续流时的半桥瞬态
L等效电路
Fig.5 The transient circuit of half bridge duringQ Linitial turn-on and
freewheeling
从t4 时刻开始，半桥电路进入QL 开通后的开关寄生振荡，在这之前达到的电流尖峰（电流最大值）与振荡环路参数一起共同决定后续电压、电流振荡的幅值。在双脉冲测试中，负载电感通常设计为远大于功率环路杂散电感，在开关瞬态过程中，负载电感电流近似不变，负载电感可等效为恒流源。因此，在研究开关瞬态过程中的振荡行为时，可忽略负载电感的影响。此时SiC MOSFET 半桥的高频振荡信号等效电路如图7 所示。由于功率直流电源（Vin）和栅极驱动电源均为直流电压源性质，因此，在研究开关瞬态过程中的高频谐振信号时，两者均可处理为短路。
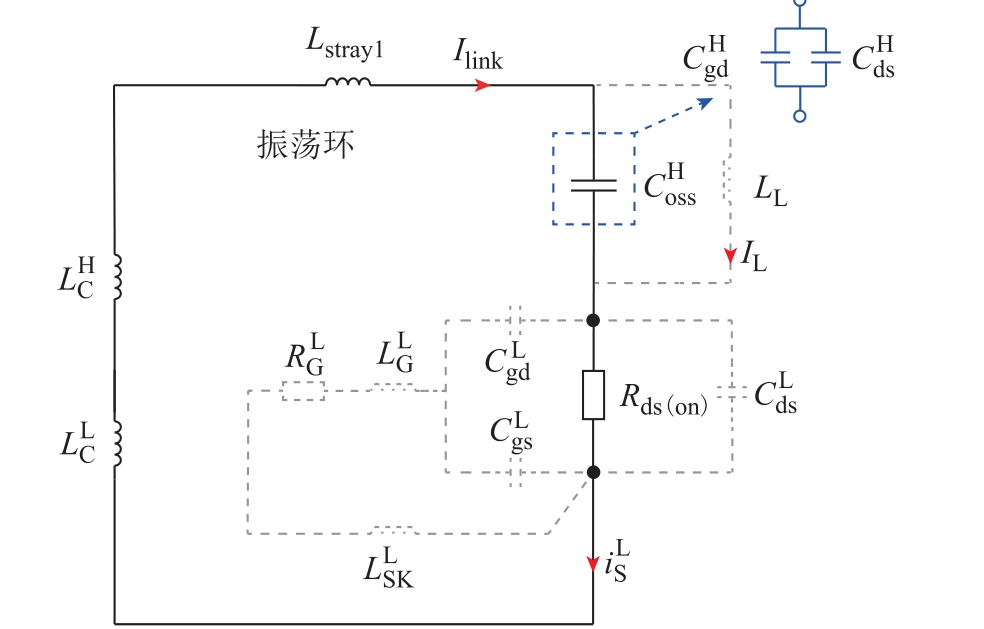
图7 LQ 开通后振荡时的半桥瞬态等效电路
Fig.7 The transient equivalent circuit of the half bridge during the transition ofLQ turn-on and oscillation
2 SiC MOSFET 开关瞬态过电流、过电压建模与影响因素分析
第1 节分析了SiC MOSFET 的开通瞬态过程。本节将分析开通瞬态过电流、过电压建模与敏感因素分析。
2.1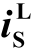 
最大冲击量
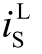最大冲击量出现在第一个电流尖峰处，位于图2 中的t1～t4 时段内。t4 时刻QL 进入完全导通，则可认为QL 在t1～t4 时段内工作于饱和区。由Cree官网提供的器件LTspice 模型可知，饱和区沟道电流可表示为
表1 式（3）中变量的值
Tab.1 Values of the variables in Equ.(3)
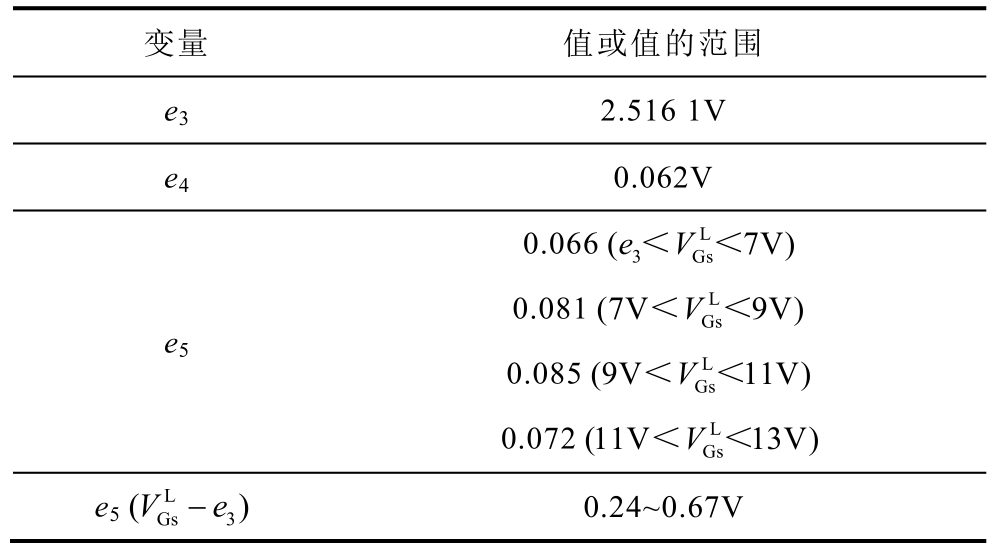
变量 值或值的范围e3 2.516 1V e4 0.062V e5 0.066 L 3 Gs( 7V)e V＜ ＜0.081 L Gs(7V 9V)V＜ ＜0.085 L Gs(9V 11V)V＜ ＜0.072 L Gs(11V 13V)V＜ ＜e5 L Gs 3( )V e− 0.24～0.67V
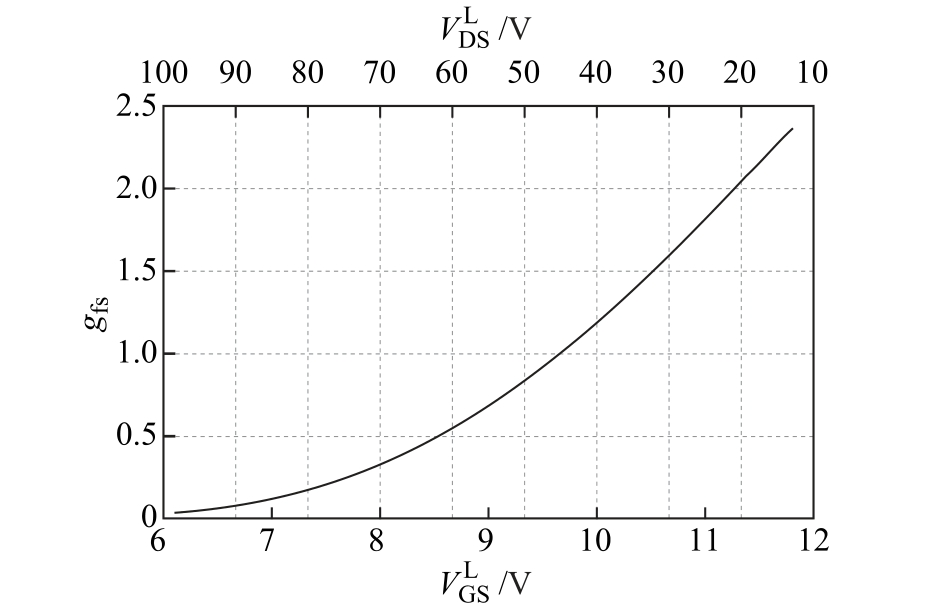
图8 跨导系数 fsg 变化曲线
Fig.8 The varying curve of transconductance fsg
在t2～t4 时间段内，SiC MOSFET 半桥瞬态电路可通过式（9）～式（17）描述。
式中，τa 和 τb 为式（19）的两个实特征根，α±βi为式（19）的一对共轭复根。τa、τb 和 α±βi 以及C1、C2、C3 和C4 的求解过程详见附录。理论上，式（19）的特征根可能有三种情况，分别为两个实根、一对共轭复根；两对共轭复根；四个实根。根据表2 所示的半桥电路实验平台参数值，本文式（19）的特征根只有一种可能，即为两个实根和一对共轭复根。故式（20）的推导过程以及下面的分析中均只考虑了该种情况。
通过式（20）即可精确计算出t2～t4 时段内
随时间的变化，以及
能达到的最大冲击量，还可分析影响
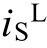最大冲击量的因素。本文将采用数值方法研究各参数对最大冲击电流的影响，具体做法是：留一个参数可调，根据所选器件和半桥电路实验平台实际情况、实验条件设定其余参数（见表2），然后根据式（20）计算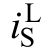
最大冲击电流。此外，式（20）中的
、
、 
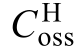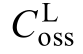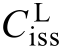、 LgdC 的电容值均随电压非线性变化。
表2 SiC MOSFET 测试电路参数值
Tab.2 The value of parameters of SiC MOSFET test circuit
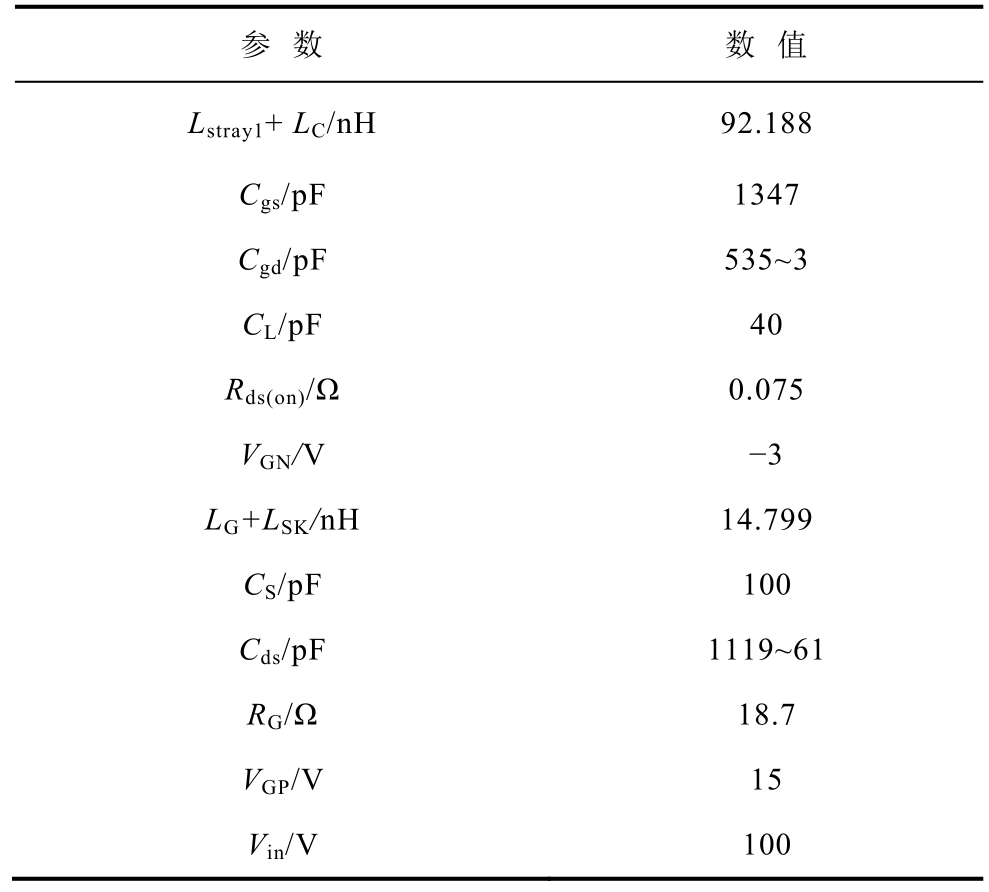
参 数 数 值Lstray1+ LC/nH 92.188 Cgs/pF 1347 Cgd/pF 535～3 CL/pF 40 Rds(on)/Ω 0.075 VGN/V −3 LG+LSK/nH 14.799 CS/pF 100 Cds/pF 1119～61 RG/Ω 18.7 VGP/V 15 Vin/V 100
根据Cree 官网提供的所用器件LTspice 模型，Cds 和Cgd 与电压Vds 的非线性关系如式（21）和式（22）所示。图9 显示了Coss、Ciss 和Crss 随电压变化的曲线，以及器件datasheet 提供的C-V 变化曲线。图9 表明式（21）和（22）拟合的电容值与实测结果十分接近。
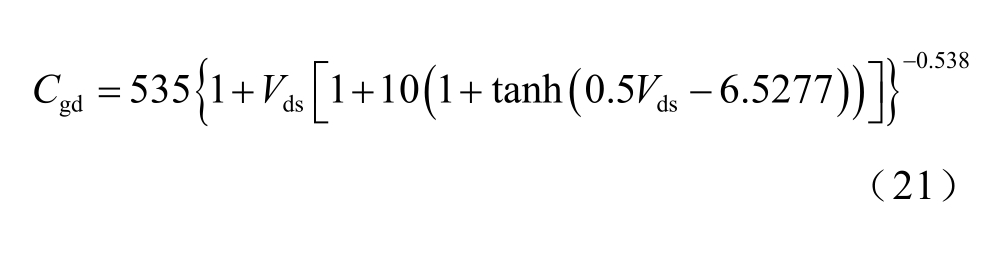
图9 SiC MOSFET 的寄生电容
Fig.9 The parasitic capacitances of SiC MOSFET
图10 电路参数对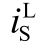
过冲的影响
Fig.10 Impact of the parameters on 
overshoot
2.2 VDSH 最大冲击量
2.3 QL 开通瞬态过程过电流、过电压敏感影响因素分析
3 仿真与实验验证
在确定了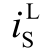
和 
最大冲击量的主要影响因素后，本节将通过仿真与实验，分析和验证上述SiC MOSFET 半桥电路开关瞬态过电流、过电压解析模型的正确性。
3.1 实验平台介绍
本文采用Cree 公司的SiC MOSFET 评估电路板KIT8020-CRD-5FF0917P-2，其电路原理如图12a所示，由两只TO-247-4 封装的Cree 第三代SiC MOSFET C3M0075120K 及其驱动电路和相关连接插件组成。图 12b 为运用该评估板搭建的 SiC MOSFET 半桥双脉冲测试平台。实验中使用的示波器和测试探头见表3。
图12 搭建的SiC MOSFET 半桥双脉冲测试平台
Fig.12 SiC MOSFET half-bridge circuit for double pulse test
表3 实验中使用的示波器和电压/电流探头
Tab.3 The measurement setup used in the experiment
测试组件 产品型号 带宽/MHz 测量信号数字示波器 DPO4104B 1 000 —电压差分探头 TA043 100 VGSL电压差分探头 TA043 100 VDSH电压差分探头 TA043 100 VDSL电流探头 TCPA300+TCP312A 100 iSL
3.2 仿真模型介绍
的非线性由一个可变电容器并联一个理想二极管来模拟[24]，可变电容器模型采用Cree 官网提供的所测器件（C3M0075120K）LTspice 模型中Cds 和Cgd模型并联，其电容值由二极管电压控制，其电容值与电压之间的关系如式（21）和式（22）所示。由图9 可知，所建模型基本可准确反映Coss 的非线性特性。此外，以恒流源iL 代替QL 开通瞬态过程中的负载电流。
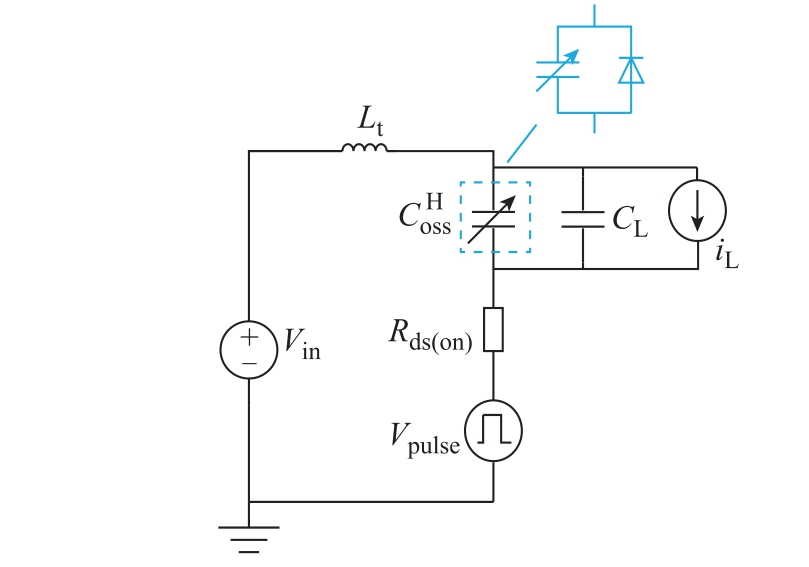
图13 双脉冲测试仿真原理
Fig.13 The simulation schematic of double pulse test
3.3 所建仿真模型的正确性验证
根据表2 参数值，可得Lt=92.188nH。Vpulse 下降时间设置为20ns（与图2 下降时间基本一致），在输入电压为100V 的条件下，在Simulink 中对所建仿真模型进行仿真。之所以选择100V 测试电压，是因为 Cds 和 Cgd 的强非线性变化主要集中在0～100V 的VDS 电压，如图9 所示。
通过仿真波形与实验波形在同一时间尺度的比较可知，仿真结果与实验结果基本一致，如图14所示。图14 中，6.115µs 时刻，Vpulse 开始按预设的斜率下降。仿真波形和实验波形的振荡频率近似相等，仿真波形和实验波形的幅值偏差可能由功率回路总电阻和总电容建模欠精确及测量误差等原因引起的。所建仿真模型中，功率回路电阻只考虑了QL 的通态电阻Rds(on)，并设定为恒值0.082 5Ω（器件手册中给出的典型值0.075Ω 与最大值0.09Ω 的平均值）。而实际电路中，功率回路电阻还包括导线和接插件寄生电阻，且QL 的沟道电阻在饱和工作区随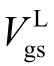 
的上升而减小，并非保持Rds(on)不变。所建仿真模型中功率回路电阻应小于实际值，因此，仿真电流波形振荡幅值（第一个波谷之后）比实验波形偏大。而仿真电流尖峰值偏小，可能因功率回路总电容建模欠精确引起，实际电路中，在QH 和QL 两端均并有100pF 瓷片电容和10Ω 电阻串联组成的吸收电路，图13 仿真电路中未考虑该吸收电容的影响。但总的来说，仿真结果能反映QL 开通瞬态过程中的 
和
的变化规律，表明所建简化模型用于仿真QL 开通瞬态过程的变化规律是可行、有效的。因此，下面将从仿真的角度，验证第2 节中的理论分析。
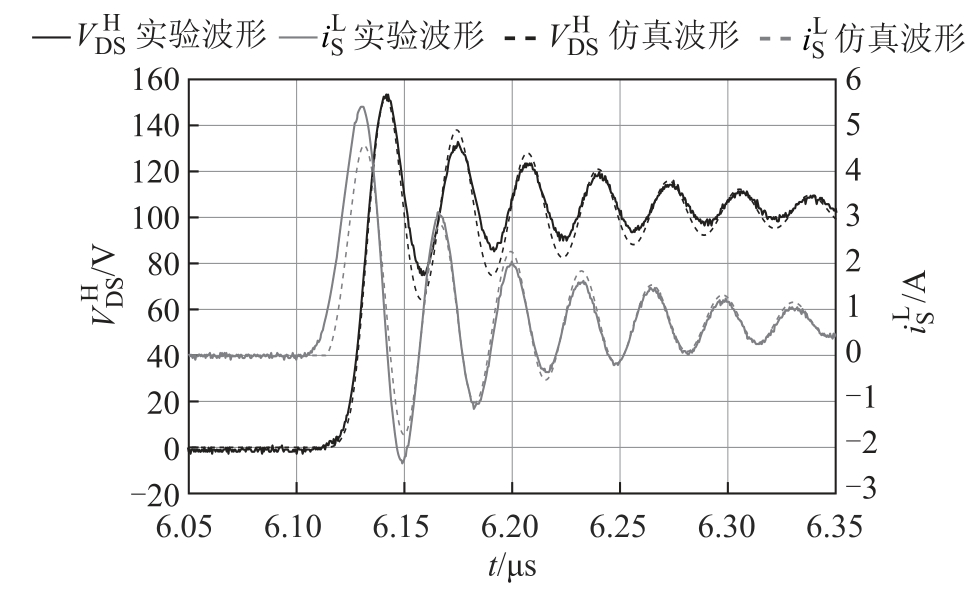
图14 仿真与实验波形比较
Fig.14 The simulation and experiment waveform comparison
3.4 仿真验证
本文的重点在于研究SiC MOSFET 半桥电路的开关瞬态行为，因此，本节仿真均未考虑负载引入的CL。
3.4.1 杂散电感Lt 的影响
调整Lt值，观察Lt对QL开通瞬态过程中
和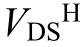
过冲的影响。不同Lt 下开关瞬态波形如图15 所示。
图15 不同Lt 下的波形对比
Fig.15 The waveform comparison under various Lt
由图15 可知：当Lt 从100nH 增至400nH 时，QL开通瞬态过程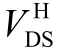 
电压过冲从156.9V 增至217.5V，分别为56.9%、94.1%、109.2%、117.5%；
电流过冲从 4.521A 降至 3.763A，分别为 338.93%、312.71%、29.0%和265.33%，与第2 节理论分析一致。可见，Lt 变化对电压过冲和电流过冲的影响趋势相反。在设计电路时，通常将Lt 限制到最小，然后通过其他方式优化电流过冲。
3.4.2 输出电容 
的影响
在图13 中，将不同容值的电容器并联在 
两端，其他参数保持不变，通过调整并联电容器的值，模拟 
变化对开关瞬态行为的影响。不同 
下开关瞬态波形如图16 所示。
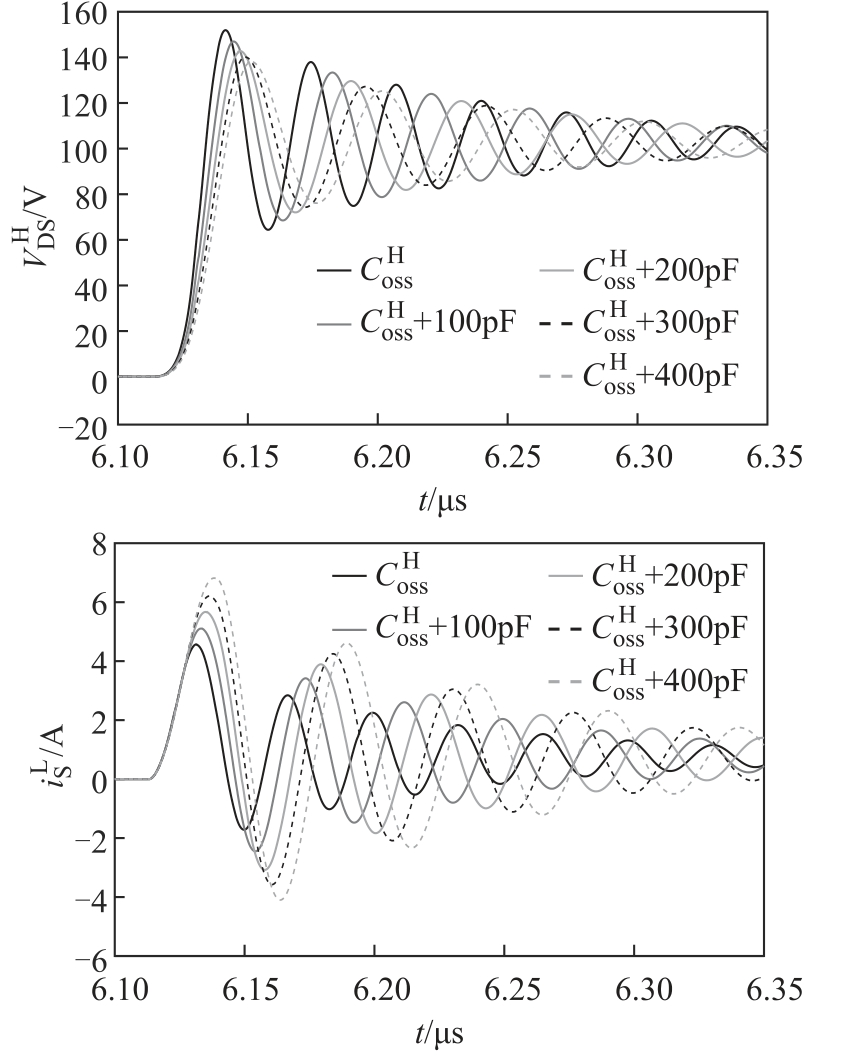
图 16 不同 
下的波形对比
Fig.16 The waveform comparison of various 
由图 16 可知：当并联电容值从 100pF 增至400pF 时，QL 开通瞬态过程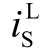
电流过冲从4.565A增至6.815A，分别为343.2%、395.33%、449.51%、502.62%、561.26%； 
电压过冲从 151.9V 降至138.1V，分别为51.9%、47.0%、42.7%、40.1%、38.1%。可见，
是影响SiC MOSFET 半桥电路QL 开通瞬态行为的重要因素，与第3 节理论分析一致。 
变化对电压过冲和电流过冲的影响趋势相反，在实际应用时应根据需求进行合理折中，可通过外并缓冲电路来增加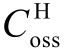 
，而 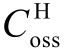的最小值受限于器件本身。电感负载的寄生电容会叠加在 
上，因此，为了优化半桥电路开关瞬态过程的非理想特性，除应优化器件的输出结电容Coss 外，还应考虑电感负载寄生电容的影响。
3.4.3 QL 驱动回路参数的影响
驱动回路参数主要影响器件开关速度，即di/dt和dv/dt，在建立的仿真模型（如图13 所示）中，通过调整Vpulse 的下降时间（即dv/dt）来体现驱动回路参数的影响。调整Vpulse 的下降时间，其他参数保持不变，不同Vpulse 下降时间下的开关瞬态波形如图17 所示。
图17 不同RG 下的波形对比
Fig.17 Waveforms comparison of various RG
图17 表明，当Vpulse 下降时间从10ns 增至40ns时，QL 开通瞬态过程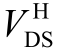 
电压过冲从161.1V 降至135V，分别为61.1%、51.9%、43.6%、35.0%；
电流过冲从4.83A 降至3.699A，分别为368.93%、343.2%、292.52%、260.29%。表明随着Vpulse 下降时间增加，开关速度降低，SiC MOSFET 开关过程中
电流尖峰和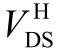 
电压尖峰均呈下降趋势。根据本节分析，
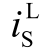过冲和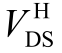 
过冲主要受驱动回路参数
、
影响，这些参数增大均会使开关速度降低，相当于Vpulse 下降时间增加。因此，与本节理论分析一致。
4 结论
本文以SiC MOSFET 半桥电路为研究对象，结合实测开关瞬态过程，考虑电路中的寄生参数，研究了SiC MOSFET 器件在电路中的开关瞬态行为；以下管开通瞬态过程为例，以电流冲击峰值和电压冲击峰值为开关非理想瞬态行为的关键特征，推导出综合考虑电路主要寄生参数和器件寄生结电容非线性特性的SiC MOSFET 半桥电路开关瞬态电流、电压的解析计算式，通过该解析式，可分析影响SiC MOSFET 半桥电路开关瞬态行为的关键因素，也可定量分析各影响因素对SiC MOSFET 开关瞬态过程中的电压和电流最大冲击量的影响。理论分析、仿真和实验结果表明：
1）驱动回路参数RG 和Cgs、器件输出电容Coss及功率回路寄生电感Lt是影响器件开通瞬态过程中电流最大冲击量的关键因素。
2）器件开通过程中，器件电压过冲主要由储存在功率回路寄生电感Lt 中的能量向器件输出电容Coss 转移引起，减小电流冲击和功率回路寄生电感Lt 均可有效降低电压过冲，可见减小电流过冲是优化半桥电路开关瞬态过程的首要任务。
附 录
式中，ω=−0.5+0.866i(i 为虚数单位)；k=1,2,3。代入k 值，选取使得|m|最大的一组（m, S, T），则式（19）的四个特征根为[25]
根据m、S 可以判定式（19）的特征根的情况。当m、S 为实数时，式（19）有4 个实根，则
当m、S 为纯虚数时，式（19）有两对共轭复根，则
当m、S 为复数时，式（19）有一对共轭复根和两个实根，则
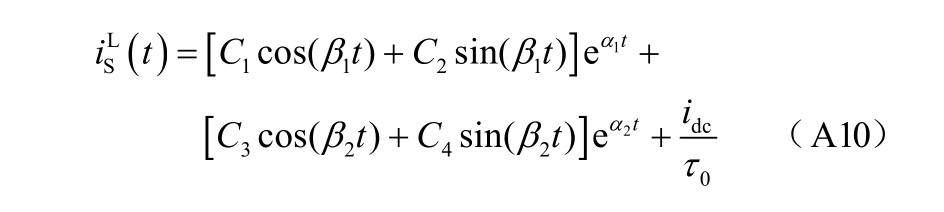
式中，τa、τb、τc 和 τd 表示实根；α1±β1i 和 α2±β2i 表示共轭复根。
式（A8）～式（A10）中，系数C1、C2、C3 和C4的求解过程如下。
首先，求解
的初值（在本文例子中，为t2 时刻的值）
将
及其一阶至三阶导数的初值及 t=0 代入式（A8）～式（A10）中，可得关于系数C1、C2、C3 和C4的四元一次方程组。以式（A9）为例，表达式为
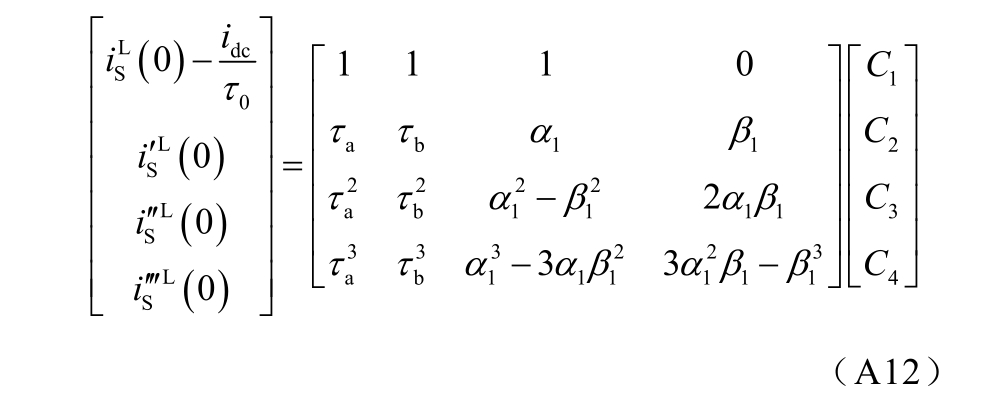
式（A12）可表示为IS(0)=XC，因此系数C1、C2、C3 和C4 即可通过C=X−1IS(0)计算得到。
下面简述 ( )HDSV t 的推导过程。式（23）的特征方程的特征根为
[1] 盛况, 郭清, 张军明, 等. 碳化硅电力电子器件在电力系统的应用展望[J]. 中国电机工程学报, 2012,32(30): 1-7.Sheng Kuang, Guo Qing, Zhang Junming, et al.Development and prospect of SiC power devices in power grid[J]. Proceedings of the CSEE, 2012,32(30): 1-7.
[2] Yin Shan, Tseng K J, Simanjorang R, et al. A 50-kW high-frequency and high-efficiency SiC voltage source inverter for more electric aircraft[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11):9124-9134.
[3] Hazra S, De A, Cheng Lin, et al. High switching performance of 1700V, 50A SiC power MOSFET over Si IGBT/BiMOSFET for advanced power conversion applications[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4742-4754.
[4] Zhang Lei, Yuan Xibo, Wu Xiaojie, et al.Performance evaluation of high-power SiC MOSFET modules in comparison to Si IGBT modules[J]. IEEE Transactions on Power Electronics, 2019, 34(2):1181-1196.
[5] 王莉娜, 邓洁, 杨军一, 等. Si 和SiC 功率器件结温提取技术现状及展望[J]. 电工技术学报, 2019,34(4): 71-84.Wang Lina, Deng Jie, Yang Junyi, et al. Junction temperature extraction methods for Si and SiC power devices—a review and possible alternatives[J].Transactions of China Electrotechnical Society, 2019,34(7): 71-84.
[6] Ahmed M R, Todd R, Forsyth A J. Predicting SiC MOSFET behavior under hard-switching,soft-switching, and false turn-on conditions[J]. IEEE Transactions on Industrial Electronics, 2017, 64(11):9001-9011.
[7] Cittanti D, Iannuzzo F, Hoene E, et al. Role of parasitic capacitances in power MOSFET turn-on switching speed limits: a SiC case study[C]//IEEE Energy Conversion Congress and Exposition (ECCE),Cincinnati, OH, 2017: 1387-1394.
[8] 梁美, 李艳, 郑琼林, 等. 桥式电路中不同封装SiC MOSFET 串扰问题分析及低栅极关断阻抗的驱动电路[J]. 电工技术学报, 2017, 32(18): 162-174.Liang Mei, Li Yan, Zheng Qionglin, et al. Analysis for crosstalk of SiC MOSFET with different packages in a phase-leg configuration and a low gate turn-off impedance driver[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 162-174
[9] 李辉, 黄樟坚, 廖兴林, 等. 一种抑制 SiC MOSFET 桥臂串扰的改进门极驱动设计[J]. 电工技术学报, 2019, 34(2): 77-87.Li Hui, Huang Zhangjian, Liao Xinglin, et al. An improved SiC MOSFET gate driver design for crosstalk suppression in a phase-leg configuration[J].Transactions of China Electrotechnical Society, 2019,34(8): 77-87.
[10] Yang Fei, Wang Zhiqiang, Zhang Zheyu, et al.Analysis and experimental evaluation of middle-point inductance's effect on switching transients for multiple-chip power module package[J]. IEEE Transactions on Power Electronics, 2019, 34(7):6613-6627.
[11] Jiang Dong, Burgos R, Wang Fei, et al.Temperature-dependent characteristics of sic devices:performance evaluation and loss calculation[J]. IEEE Transactions on Power Electronics, 2012, 27(2):1013-1024.
[12] 孙凯, 陆珏晶, 吴红飞, 等. 碳化硅MOSFET 的变温度参数建模[J]. 中国电机工程学报, 2013, 33(3):37-43.Sun Kai, Lu Juejing, Wu Hongfei, et al. Modeling of SiC MOSFET with temperature dependent parameters[J]. Proceedings of the CSEE, 2013, 33(3):37-43.
[13] Gonzalez J O, Alatise O, Hu Ji, et al. An investigation of temperature sensitive electrical parameters for SiC power MOSFETs[J]. IEEE Transactions on Power Electronics, 2017, 32(10):7954-7966.
[14] Ji Shiqi, Zheng Sheng, Wang Fei, et al.Temperature-dependent characterization, modeling, and switching speed-limitation analysis of third-generation 10-kV SiC MOSFET[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4317-4327.
[15] Han Di, Sarlioglu B. Comprehensive study of the performance of SiC MOSFET-based automotive DC-DC converter under the influence of parasitic inductance[J]. IEEE Transactions on Industry Applications, 2016, 52(6): 5100-5111.
[16] 曾正, 邵伟华, 陈昊, 等. 基于栅极驱动回路的SiC MOSFET 开关行为调控[J]. 中国电机工程学报,2018, 38(4): 1165-1176.Zeng Zheng, Shao Weihua, Chen Hao, et al. On-off behavior control of SiC MOSFET by gate drive loops[J]. Proceedings of the CSEE, 2018, 38(4):1165-1176.
[17] 王旭东, 朱义诚, 赵争鸣, 等. 驱动回路参数对碳化硅MOSFET 开关瞬态过程的影响[J]. 电工技术学报, 2017, 32(13): 23-30.Wang Xudong, Zhu Yicheng, Zhao Zhengming, et al.Impact of gate-loop parameters on the switching behavior of SiC MOSFETs[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 23-30.
[18] Zhang Zheyu, Wang F, Tolbert L M, et al. Evaluation of switching performance of SiC devices in PWM inverter-fed induction motor drives[J]. IEEE Transactions on Power Electronics, 2015, 30(10):5701-5711.
[19] 朱义诚, 赵争鸣, 王旭东, 等. SiC MOSFET 与SiC SBD 换流单元瞬态模型[J] . 电工技术学报, 2017,32(12): 58-69.Zhu Yicheng, Zhao Zhengming, Wang Xudong, et al.Analytical transient model of commutation units with SiC MOSFET and SiC SBD pair[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 58-69.
[20] Wang Jianjing, Chung H S, Li R T. Characterization and experimental assessment of the effects of parasitic elements on the MOSFET switching performance[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 573-590.
[21] Chen Kainan, Zhao Zhengming, Yuan Liqiang, et al.The impact of nonlinear junction capacitance on switching transient and its modeling for SiC MOSFET[J]. IEEE Transactions on Electron Devices,2015, 62(2): 333-338.
[22] Cree. C3M0075120K silicon carbide power MOSFET C3M MOSFET technology[R]. 2017.
[23] McNutt T R, Hefner A R, Mantooth H A, et al.Silicon carbide power MOSFET model and parameter extraction sequence[J]. IEEE Transactions on Power Electronics, 2007, 22(2): 353-363.
[24] Cree. Design considerations for designing with Cree SiC modules part.1 understanding the effects of parasitic inductance[R]. 2013.
[25] Zwillinger D. CRC standard mathematical tables and formulas[M]. 3rd ed. Boca Raton, FL, USA: CRC Press, 2017.