0 引言
电力变压器在空载合闸或者故障恢复重新投入电网时,由于变压器铁心磁通的饱和及铁心材料的非线性特性,会产生幅值相当大的励磁涌流流过变压器差动保护,导致差动保护误动作[1-3]。励磁涌流含有多个谐波成分及直流分量,会降低电力系统供电质量,同时涌流中的高次谐波对连接到电力系统中的敏感电力电子器件有极强的破坏作用。因此如何削弱励磁涌流受到国内外学者的高度重视[4-6]。
励磁涌流是铁心磁通饱和所引起的冲击电流,其大小与变压器等值阻抗、合闸初相角、剩磁大小、绕组联结方式、铁心结构及材质等因素有关[7-8]。对于三相变压器来说,还要考虑三相绕组的联结方式。为了减小励磁涌流对电力系统的影响,有效地削弱变压器励磁涌流,现在主要有三种方法:串联电阻法、选相合闸技术和投切涌流抑制器。
串联电阻法通过改变一次电阻值来降低流过铁心的磁通幅值[9-10]。在一次侧或者变压器中性点串联电阻就是基于这个原理。但是串联电阻法单独使用时抑制涌流的效果并不理想,往往需要配合其他方法共同使用,而且最优串联电阻值的选取仍是难点。
选相合闸技术是选择在合适的电压初始相位处合闸,通过削弱暂态磁通达到降低流过铁心磁通的目的[11-14]。传统的选相合闸技术主要有快速合闸、延迟合闸和同时合闸三种。其中同时合闸技术只适用于特定的变压器三相剩磁模式,即一相剩磁为零,其他两相剩磁大小相等、方向相反且剩磁水平较高的模式。该模式需结合三相剩磁,过程复杂。延迟合闸技术和快速合闸技术均采用先合其中一相,再同时合剩余两相的合闸顺序,但是两者都仅适用于中性点接地的三相变压器。因为对于中性点不接地的三相变压器,当只合其中一相时,电源和变压器各绕组均不能形成通路,所以对于中性点不接地变压器首次合闸至少要合两相。文献[15-16]针对中性点不接地变压器考虑剩磁的影响提出了先合闸两相,再合剩余一相的策略,并给出了最佳合闸时刻的计算方法,但是文献[15]未给出合闸过程动态磁通的变化规律,文献[16]虽给出了磁通的变化规律,但选择首合闸的两相仍然依赖剩磁的准确测量。文献[17]提出通过控制三相断路器的分闸时刻和顺序来确定合闸时刻和顺序,这依赖于分闸可控且准确度高,另外分合闸时刻不宜相差过久,工程实际应用难度较高。选相合闸技术选取的合闸时刻与铁心中的剩磁量密切相关,由于剩磁测量一直是技术难题,因此选相合闸技术的实现还有待研究[18]。
投切涌流抑制器是通过控制变压器一次电压平滑启动来消除变压器暂态磁通的产生,实现励磁涌流的主动抑制。文献[19]提出了由二阶欠阻尼电路和分压器共同作用产生缓慢上升的电压,达到抑制励磁涌流的目的,但是要实现涌流抑制的效果需增加第三绕组,工程实现难度较大。文献[20]提出了一种电压斜坡软启动器,是通过控制晶闸管的触发延迟角来实现变压器电压按一定斜率缓慢上升到稳态值,该方法与变压器联结方式、剩磁大小和合闸初相角等因素无关,但单独采用反并联晶闸管会产生大量谐波,更适用于对谐波要求不高的电弧炉变压器。
在此基础上,本文首先分析了变压器励磁涌流产生的机理,针对反并联晶闸管单独作用时会产生大量谐波的问题,提出了一种基于软启动的涌流抑制原理。该原理是利用由反并联晶闸管和滤波电路组成的涌流抑制器来保证变压器一次电压平滑上升到稳态值,避免暂态磁通产生,以实现抑制涌流的效果。其次根据反并联晶闸管导通过程中仅产生奇次谐波的特征,选择滤波电路结构并进行参数优化。最后通过Matlab/Simulink 软件仿真三相变压器组和三相三柱式变压器的三种不同联结方式下涌流抑制器的抑制效果,验证了所提涌流抑制器的有效性。
1 基于软启动的变压器涌流抑制原理
一个空载的单相变压器,因二次侧无电流,一次电流就是励磁电流,当t=0 时,将正弦电压U1 加在变压器一次侧,则一次侧回路方程为
式中,U1 为一次电压;Um 为电压幅值;α 为变压器合闸时刻电压初相位;i0 为励磁涌流瞬时值;φ为磁通瞬时值;R1 为一次电阻;N1 为一次绕组匝数。
饱和时磁通φ与电流i0 呈非线性关系,若取正常运行时一次绕组的平均电感L1=N1φ/i0 为暂态过程电感,则式(1)可改为
假定初始时刻t=0 时φ= rφ ,则解式(2)可得
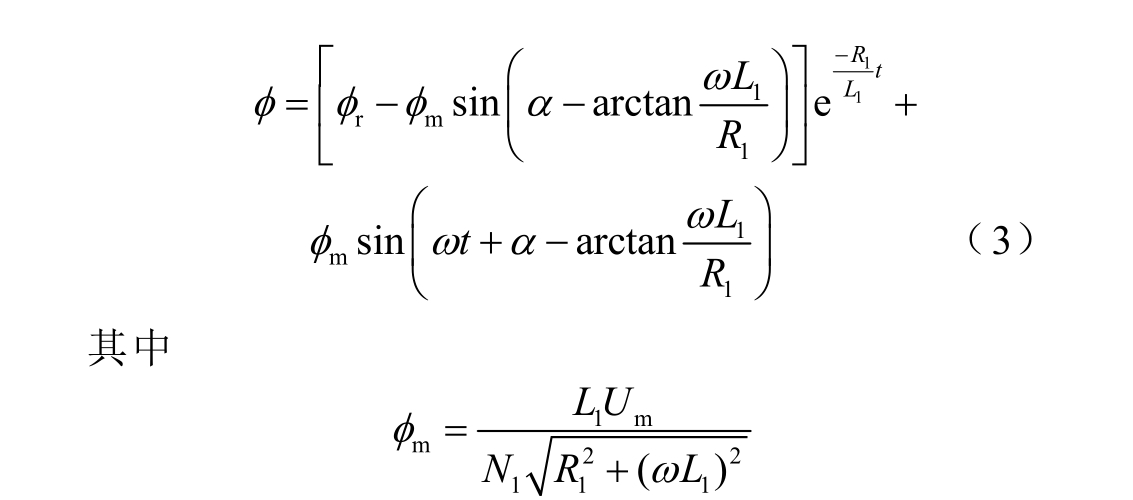
考虑到变压器参数 R1 ≪ωL1,则 arctan(ωL1/R1)≈90°,磁通瞬时值可以简化为

由式(5)可以看出,若想有效地抑制变压器励磁涌流的影响,一是通过改变电阻R1 的值,降低流过铁心的磁通幅值;二是选择在合适电压初始相位合闸,通过削弱暂态磁通达到降低流过铁心的磁通的目的,也就是选相合闸技术。从式(4)可以看出,如果 α=0°(变压器合闸时刻t0= 0),则磁通![]()
![]() 磁 通 达 到 最 大 值φmax≈2φm+φr。此时空载变压器严重饱和,励磁电流成百倍地增长,可能达到额定电流的5~10 倍。如果α=ωt0=arccos(-φr/φm),则磁通φ=-φmcos(ωt+α),变压器铁心中将不会产生暂态磁通,变压器直接进入稳态运行,这个就是选相合闸技术应用的基本原理。这两种方法都是从涌流的公式组成出发去找削弱涌流的方法,但是改变电阻值对涌流削弱的效果比较弱,需要与其他方法配合;选相合闸技术依赖于对铁心剩磁的准确测量,而剩磁的测量是变压器技术难点之一,而且这两种方法只能尽可能削弱涌流,并不能完全消除涌流。
磁 通 达 到 最 大 值φmax≈2φm+φr。此时空载变压器严重饱和,励磁电流成百倍地增长,可能达到额定电流的5~10 倍。如果α=ωt0=arccos(-φr/φm),则磁通φ=-φmcos(ωt+α),变压器铁心中将不会产生暂态磁通,变压器直接进入稳态运行,这个就是选相合闸技术应用的基本原理。这两种方法都是从涌流的公式组成出发去找削弱涌流的方法,但是改变电阻值对涌流削弱的效果比较弱,需要与其他方法配合;选相合闸技术依赖于对铁心剩磁的准确测量,而剩磁的测量是变压器技术难点之一,而且这两种方法只能尽可能削弱涌流,并不能完全消除涌流。
涌流产生是由于变压器电压突然增大,产生暂态磁通使磁通进入到饱和区,从这个机理出发,出现了另外一种涌流抑制方法。这类方法通过涌流抑制回路确保变压器一次电压按照既定曲线平滑上升到稳态值,以达到抑制励磁涌流的效果。本文提出的涌流抑制器就是基于这个原理,该方法既不需要串联电阻,也不需要计算铁心剩磁和变压器合闸角,主要依赖于反并联晶闸管和滤波电路共同构成的涌流抑制器来主动抑制变压器励磁涌流,其简化模型如图1 所示。
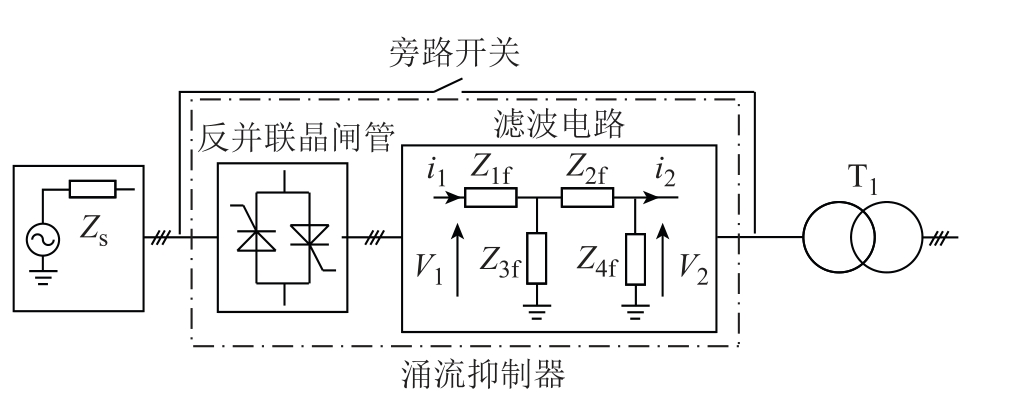
图1 三相变压器涌流抑制器的简化模型
Fig.1 Simplified model of three-phase transformer’s inrush current suppression circuit
通过控制晶闸管的触发延迟角,使变压器输入电压从零以预设函数关系逐渐上升到额定电压。但是单独采用反并联晶闸管会带来大量的谐波注入,对变压器甚至系统造成严重影响(图2b)。图2 中给出了励磁涌流、仅含反并联晶闸管的涌流抑制器以及含反并联晶闸管和滤波电路的涌流抑制器三种情况下的变压器铁心相空间轨迹和二维相平面图。相空间轨迹是变压器电压和磁链随时间的运动演化过程,相平面图就是相空间轨迹在电压和磁链构成二维相平面的投影。如果相平面轨迹中磁链超过1(pu),则变压器铁心磁链进入饱和区;若相平面轨迹非圆闭合有畸变,则变压器磁链出现谐波畸变,畸变程度与谐波含量密切相关。由图2 可知,发生励磁涌流时铁心磁链发生严重饱和且有畸变;在含反并联晶闸管的涌流抑制器作用下,启动开始时磁链发生严重谐波畸变,直到启动过程结束系统逐渐恢复稳定后,磁链才恢复正常,但是此时铁心未饱和,系统不会产生较大的涌流。当反并联晶闸管和滤波电路结合作为涌流抑制器时,磁链随时间变化逐渐上升到稳定值,未发生谐波畸变且不存在饱和现象,不会产生涌流。这些特性也可从附图1 磁链波形图中观察得到。因此本文考虑将反并联晶闸管与滤波电路配合实现软启动,达到涌流抑制的目的。软启动过程结束后投入旁路开关,同时退出涌流抑制器。
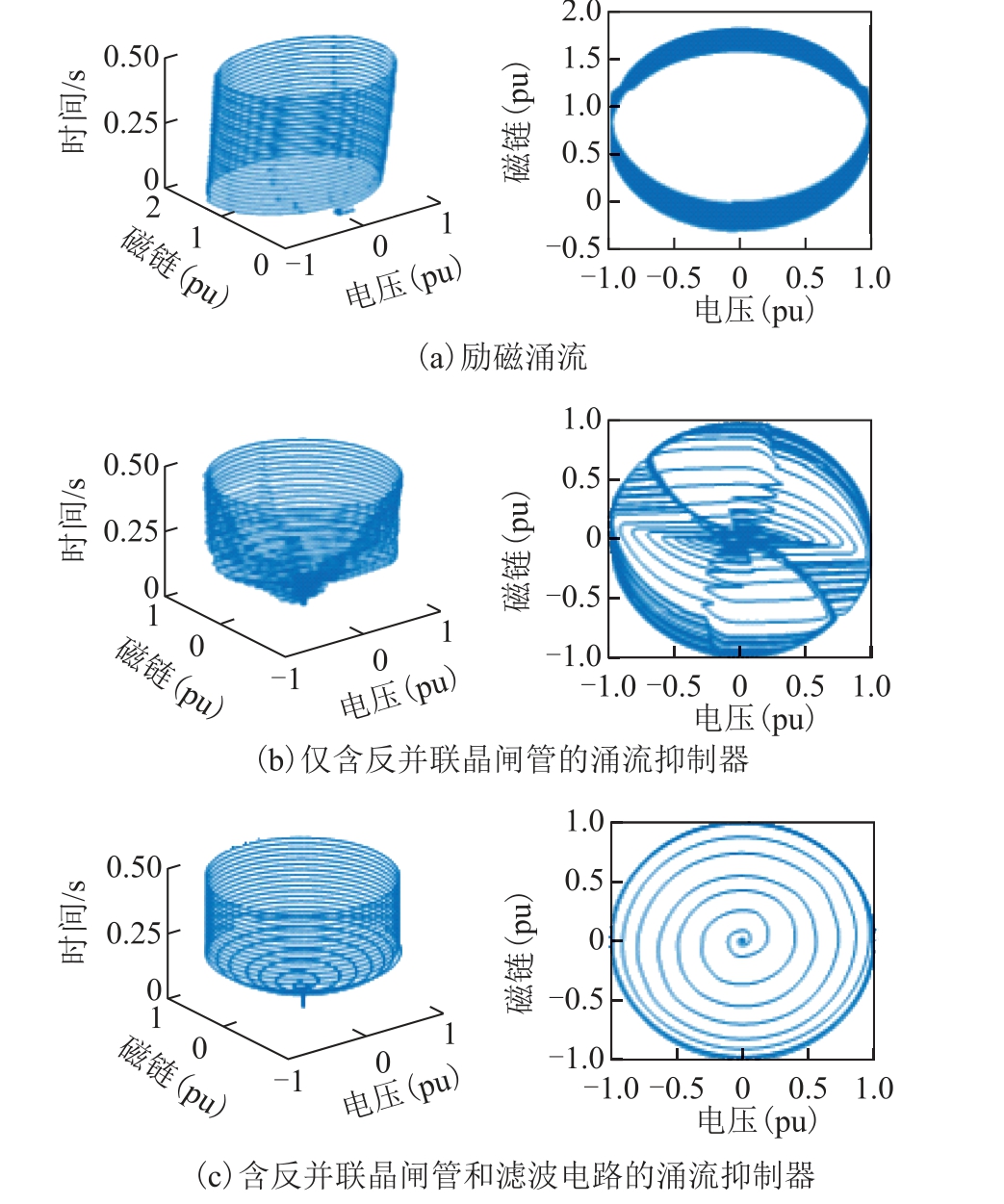
图2 不同情况下的相空间轨迹和相平面图
Fig.2 Phase space trajectory and phase plant diagram of the transformer under different conditions
2 基于软启动的涌流抑制器结构及参数设计
2.1 基于反并联晶闸管的涌流抑制器及控制方式
根据三相联结形式的不同,三相软启动开关具有多种形式,如图3 所示,分别是星形联结、支路控制三角形联结和中点控制三角形联结。由中性点的不同联结方式,星形联结又可分为三相三线和三相四线两种。根据应用的变压器结构,本文软启动开关采用星形联结的三相四线结构。
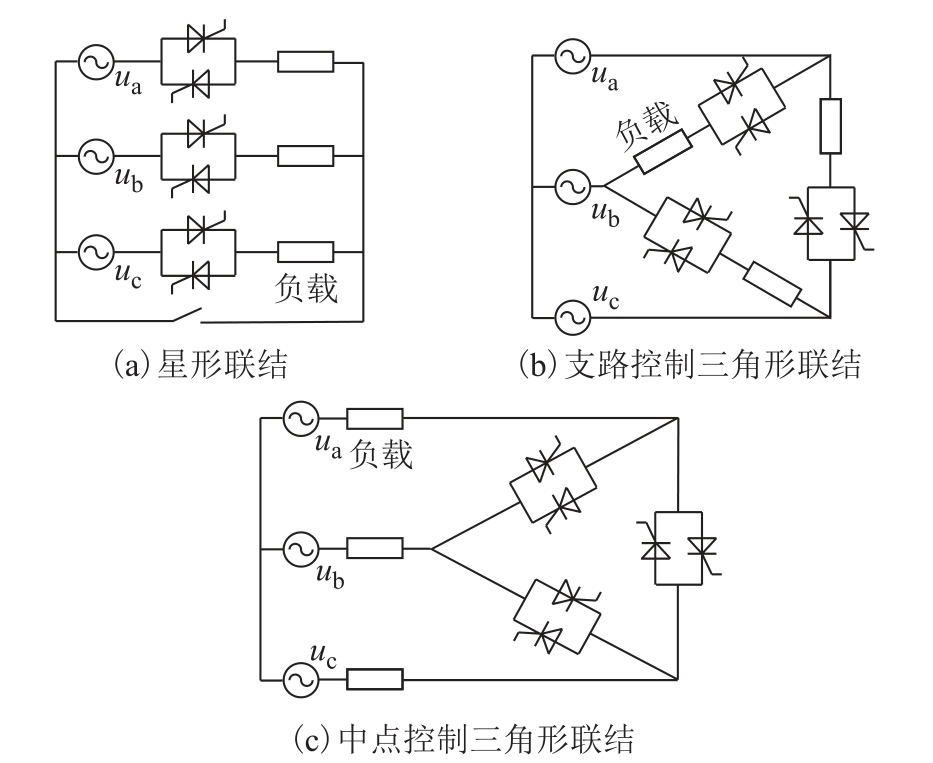
图3 基于晶闸管的软启动开关不同拓扑结构
Fig.3 Alternative connection for a soft starter based on thyrister
当采用三相四线时,相当于三个单相交流调压电压的组合,三相工作互相错开120°,单相软启动开关电路的工作原理与分析方法均适用于此电路。以A 相为例,假设A 电压源电压为
当正向晶闸管在ωt=β 时刻开通,则前半周负载电流为

式中,Z、φ 分别为负载阻抗和阻抗角;θ 为晶闸管导通角。后半周反向晶闸管导通时,ia 与式(7)随时间变化相似,但是极性相反。由此可知,负载电流正负半波对称,因此不含直流分量和偶次谐波,而以3、5、7 等奇次谐波为主,同时随着谐波次数的增加,谐波含量减少[21-22]。
现有的软启动开关既可以通过开环控制,也可以通过闭环控制实现电压缓慢上升到稳态值。开环控制通过计算目标参数,将目标指令一次性输入受控对象。文献[20]给出了控制目标为角度斜坡函数,通过直接比较电压角度与给定斜坡控制晶闸管触发延迟角 β 从180°到0°逐渐变化,实现电压平稳上升,达到消除电弧炉变压器合闸产生的励磁涌流。但这种直接控制方式易受电网电压波动和环境变化等扰动的影响。因此本文提出采用闭环对触发延迟角进行控制。具体的控制系统如图4 所示。

图4 软启动开关控制
Fig.4 Control loop of soft-start switch
从图4 可知,将启动过程中得到的变压器一次电压与参考电压进行比较,再经PI 和PWM 控制器得到晶闸管触发脉冲来控制软启动开关电路中6 个晶闸管的导通,实现变压器电压平滑上升的目的,具体触发脉冲的产生如图5 所示。PWM 控制器将三角波与预先得到的参考曲线进行比较得到晶闸管的触发脉冲,控制晶闸管的导通,图5 中只给出了正向晶闸管的导通脉冲。

图5 晶闸管触发脉冲的产生
Fig.5 Thyristor trigger pulse generation
2.2 涌流抑制器的滤波电路结构
几种无源高阶滤波电路结构如图6 所示。

图6 典型高阶滤波电路结构
Fig.6 Typical structure diagrams of the high order filter
在滤波电路中串联电阻的无源阻尼方案是抑制谐振频率、实现系统稳定运行的常用解决方案。含等效串联电阻的LCLC 高阶滤波电路(图6a)的电压转移比为

得到相应伯德图如图7 所示。
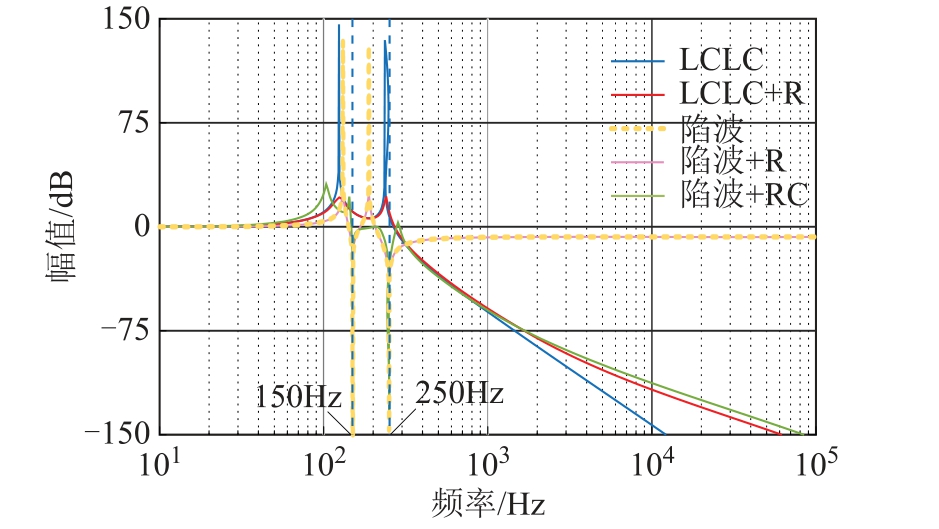
图7 典型高阶滤波电路电压传输特性
Fig.7 Voltage transmission characteristic of the high order filter
从图7 中看出,LCLC 滤波电路具有两个谐振频率,这会降低两个振荡频率之间的低次谐波衰减水平,不利于滤除低次谐波。从图中可以看出3 次谐波和5 次谐波基本没有衰减,说明这两个谐波无法通过LCLC 高阶滤波电路滤除。而串联电阻R 只是降低了谐振频率的幅值,并不能提高谐波滤除效果。因此考虑用LC 陷波支路代替单纯的电容支路,文中两个LC 陷波支路主要滤除晶闸管开关产生的占比较高的3 次谐波和5 次谐波分量。含等效串联电阻的高阶陷波滤波电路(图6b)的电压转移比为

从图7 可知,高阶陷波滤波电路串联电阻后可抑制谐振尖锋,简单方便但会降低滤波电路高次谐波滤波效果,增加系统损耗[23]。考虑用并联RC 阻尼阻容电路代替纯电阻实现阻尼效应,从图中可知,不仅可以抑制谐波幅值,而且可以增大高次谐波衰减水平[24],达到需要的滤波效果,因此文中采用含RC 阻尼阻容的高阶陷波滤波电路(图6d),其电压转移比为

传递函数系数见附录式(A1)~式(A3)。并联了RC 阻尼阻容电路的陷波支路L3C1 的阻抗特性为

对于高阶陷波滤波电路,一般选择支路两个电容的和等于LCLC 高阶滤波电路该支路的电容值[25],即图6中 Ct1+Cd=C1 , Ct2+Cm=C2 。 这 里 定 义 Ct1=α1C1(0.1≤α1≤0.9),而Cd=(1-α1)C1,则式(11)可以化简为

式中,ωa、ωb 分别为二阶无阻尼系统谐振频率和一阶微分环节转折频率;ωc、ζ 分别为振荡环节无阻尼自然振荡频率和阻尼比,具体取值见式(A4)。由此得到并联了RC 阻尼阻容电路的陷波支路阻抗幅值特性,并与常规串联阻抗谐振频率抑制方法进行比较,结果如图8 所示。由图可知,相较传统串联阻抗方法,并联RC 电路方法更优,一方面是因为该方法能保持高频斜率衰减特性,另一方面是电流将在两个支路中进行分流,降低了电阻器的功率损耗。但是,并联RC 电路会产生一个新的谐振频率,这是参数设计时需要考虑的问题,将在下一节进行详细介绍。

图8 不同并联阻抗支路的幅值
Fig.8 Magnitude of different parallel impedance
2.3 涌流抑制器的滤波电路参数优化
LCLC 滤波电路的设计已经在文献[26-28]中进行了详细的介绍,而陷波滤波电路在文献[29-30]进行了讨论,因此本文主要对并联RC 阻尼阻容电路的参数进行优化设计。
增加并联RC 阻尼阻容电路后可能会在陷波频率后产生新的谐振频率frc(见图8),这会导致陷波频率与谐振频率之间的幅值衰减突然减小,减弱该频段谐波分量的滤除效果。因为LC 陷波电路会滤除3 次和5 次谐波分量,所以文中主要考虑7 次和9次谐波分量的衰减情况。图9 给出了7 次和9 次谐波分量的幅值随α1、α2 的变化情况,其中 α1 和α2 分别为两个陷波支路电容与其RC 阻尼阻容支路的电容比。


图9 不同 α1 和 α2 时7 次和9 次谐波的幅值
Fig.9 The amplitude of the 7th and 9th harmonics at different α1 and α2
不同 α1 和 α2 时5 次谐波之后的谐振点最大峰值如图10 所示。
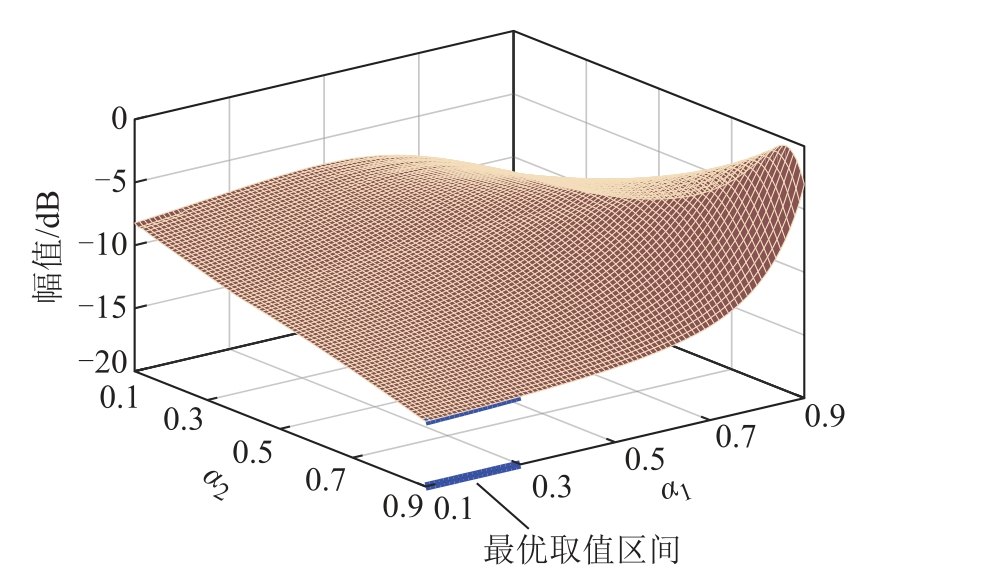
图10 不同α1 和 α2 时5 次谐波之后的谐振点最大峰值
Fig.10 Maximum amplitude of resonance point after 5th harmonic at different α1 and α2
由图10 可知,α1 在较小值范围内变化时对5 次谐波之后的谐振点峰值影响较小;而α2 直接影响5次谐波之后的谐振点最大峰值,α2 越大,峰值越小。综上所述,同时满足谐振点幅值最小,且7 次和9次谐波衰减大于-20dB 的 α1 和 α2 取值为
文中取 α1=0.2,α2=0.9。当Rd、Rm 变化时,7 次和9 次谐波分量峰值以及5 次谐波之后的谐振点最大峰值如图11 所示。由图11 可知,当Rd=0.1、Rm=0.5时,5 次谐波之后的谐振点幅值达到最小,同时7 次和9 次谐波峰值衰减最大,这就是所需的最优点。

图11 不同Rd 和Rm 时7 次和9 次谐波峰值以及5 次谐波之后的谐振点最大峰值
Fig.11 The amplitude of the 7th and 9th harmonics and maximum amplitude of resonance point after 5th harmonic at different α1 and α2
3 仿真验证

图12 仿真系统
Fig.12 Simulated system
为了验证本文给出的涌流抑制方法抑制励磁涌流幅值的有效性,通过Matlab/Simulink 平台搭建模型进行仿真,仿真结构如图12 所示。变压器空载或轻载投入时将涌流抑制器投入运行,启动过程结束后投入旁路开关同时退出涌流抑制器。模型具体参数如下:电源电压110kV,变压器电压比为110kV/10kV,容量为60MV·A,短路电压百分比为10.5%,短路损耗为370kW。工程中变压器常用的联结方式分别为YNd11、Yd11 和Yyn 三种,因此文中分别分析三相变压器组和三相三柱式变压器两种常用变压器的三种联结方式。高阶滤波电路采用的参数见表1。
表1 高阶滤波电路参数
Tab.1 The parameters of high-order filter circuit

参 数 数 值 参 数 数 值L1/mH 2.26 Ct1/mF 1.02 L2/mH 2.1 Ct2/mF 4.32 L3/mH 1.1 Cm/mF 0.48 L4/μH 93.8 Cd/mF 4.08 Rm/Ω 0.5 Rd/Ω 0.1
3.1 三相变压器组
3.1.1 YNd11 联结方式
变压器空载投入时采用涌流抑制器后变压器一次电压电流波形如图13 所示。因变压器三相对称,图中仅给出了A 相电压、电流波形,下同。其中涌流抑制器由反并联晶闸管和含RC 阻尼阻容的高阶陷波滤波电路组成。由图13 可知,涌流抑制器实现了变压器电压平稳上升到稳态值,并且因为变压器电压未发生骤变,不会产生暂态磁链,所以变压器磁链不会进入饱和区,不会产生励磁涌流。

图13 变压器一次电压和电流波形
Fig.13 The voltage and current waveforms on primary side of transformer
为了比较不同滤波电路的效果,图14 分别给出了涌流抑制器采用不同滤波电路时变压器一次电压有效值变化情况,以及电压达到稳态值的一半时对应的电压谐波分析情况。几种不同滤波电路分别为含等效串联电阻的LCLC 高阶滤波电路、含等效串联电阻的高阶陷波滤波电路以及含RC 阻尼阻容的高阶陷波滤波电路。

图14 不同情况下变压器电压有效值及其谐波分析
Fig.14 Transformer voltage RMS and its harmonic analysis on different conditions
图14 中变压器电压都在接近t=0.3s 时达到稳定值,含等效串联电阻的LCLC 高阶滤波电路可以滤除11 次及以上谐波分量,却含有较高的3 次、5 次和7 次谐波,这是因为LCLC 滤波电路会产生两个谐振频率,两个谐振频率之间或者附近的频率分量无法被有效滤除,此时电压总谐波畸变率达到24.68%,无法满足系统运行要求,而且大量的谐波分量导致变压器电压达到稳定仍然有较大幅度的波动。
对于含等效电阻的高阶陷波滤波电路,虽然可以较好地滤除3 次谐波和5 次谐波,但是却含有一定的11 次及以上谐波分量,这是因为含等效电阻的高阶陷波滤波电路增加了陷波电路后,相应地会牺牲较高次谐波分量的滤除效果。此时电压的总谐波畸变率为7.34%,虽然相较含等效串联电阻的LCLC高阶滤波电路,谐波畸变率有了明显减少,但是仍然不能达到稳定要求。由图15 给出的变压器电压和磁链的相空间轨迹图可以看出,此时磁链仍存在饱和的可能性,可能产生一定的励磁涌流。另外,此时谐波分量的存在导致变压器电压达到稳定后仍然有一定幅度的波动。而含RC 阻尼阻容的高阶陷波滤波电路不仅可以有效滤除全部谐波分量,而且电压达到稳态后基本没有波动。此时电压总谐波畸变率为4.75%,满足系统运行要求。
3.1.2 Yd11 联结方式
对于Yd11 联结的变压器,空载投入时采用由反并联晶闸管和含RC 阻尼阻容的高阶陷波滤波电路组成涌流抑制器后,变压器相空间轨迹分别如图16a所示。从图中观察可知变压器磁链能平稳上升到稳态值,未发生饱和现象,涌流抑制器可以有效地抑制变压器涌流的产生。

图15 不同滤波电路时变压器电压和磁链的相空间轨迹
Fig.15 Phase space trajectory of voltage and flux of transformer in different filter circuits

图16 不同接线时变压器电压和磁链的相空间轨迹
Fig.16 Voltage and current waveforms on primary side of transformer in different wring methods
3.1.3 Yyn 联结方式
对于Yyn 联结方式的变压器,空载投入时采用由反并联晶闸管和含RC 阻尼阻容的高阶陷波滤波电路组成涌流抑制器,变压器电压和磁链相空间轨迹如图16b 所示。由图可知,变压器一次侧联结方式与Yd11 联结方式一致,都不含接地回路,因此两种情况下变压器一次电压和磁链相空间轨迹变化趋势基本一致,变压器磁链平稳上升到稳态值,未发生饱和,涌流抑制器可以有效地抑制变压器涌流的产生。
3.2 三相三柱式变压器
针对三相三柱式变压器,当其空载投入时,比较本文方法的涌流抑制器与文献[19]方法的涌流抑制器不同的作用效果。文献[19]主要是在三绕组变压器的第三绕组增加一个涌流抑制器,该涌流抑制器是由一个二阶欠阻尼模块和一个分压器模块构成,其中二阶欠阻尼模块主要用以实现变压器电压的缓慢上升,是涌流抑制器的核心模块,文献中也给出了二阶欠阻尼模块的具体电路结构。本文采用的是两绕组变压器,不需要考虑分压器模块,只需保留文献中的二阶欠阻尼模块即可。同时为了将该涌流抑制器应用于两绕组变压器,需在变压器一次侧增加旁路开关,当空载变压器合闸时将涌流抑制器投入运行,变压器平稳启动后退出涌流抑制器,投入旁路开关,涌流抑制器单相电路如图17 所示。

图17 文献[19]涌流抑制器单相电路
Fig.17 Single-phase structure diagram of a inrush current suppression equipment in Ref.[19]
比较两种涌流抑制器作用下励磁涌流的峰值和到达稳态的时间变化情况见表2,表中T 为电压变化时间常数。从表中观察可知,时间常数T 与涌流到达稳态的时间(即启动时间)密切相关,理论上应是T 越小启动时间越短,但是当T=0.05s 时,涌流达到稳态值的时间反而增加至3s,同时涌流峰值增加。这是因为当涌流抑制器的电感L、电容C参数不变的情况下,时间常数T 与R 的取值密切相关,T 取值越小,R 值越大,当R 值大到一定程度时,将使变压器支路出现较大分流,变压器铁心将逐渐进入饱合区,产生较大的励磁涌流。而且饱和现象会导致变压器一次电压出现超调现象,变压器一次电压有效变化情况如图18 所示。因此涌流达到稳态值的时间反而增加,这说明时间常数T不能取值过小,至少取T=0.5s,此时到达稳态所需时间为2.5s。相较而言,本文方法不仅涌流峰值较小,而且涌流达到稳定状态的时间只需要0.3s。
表2 励磁涌流峰值和到达稳态的时间对比情况
Tab.2 Comparison of the peak value of the inrush current and the time to reach the steady state

联结方式 时间常数T/s 涌流峰值(pu)到达稳态的时间/s YNd11 1 0.037 6 0.5 0.037 2.5 0.1 0.043 1.5 0.05 0.057 3本文方法 0.041 0.3 Yd11 1 0.037 6 0.5 0.037 2.5 0.1 0.043 1.5 0.05 0.057 3本文方法 0.035 0.3 Yyn 1 0.037 6 0.5 0.037 2.5 0.1 0.043 1.5 0.05 0.057 3本文方法 0.035 0.3

图18 变压器一次电压有效变化情况
Fig.18 Transformer voltage RMS on the primary side of the transformer
4 结论
本文分析了变压器涌流产生的机理,提出了一种基于软启动的涌流抑制原理。该原理是利用由反并联晶闸管和滤波电路组成的涌流抑制器实现变压器一次电压平稳上升到稳态值,以消除涌流的产生。基于Matlab/Simulink 建立了涌流抑制器模型,仿真三相变压器组和三相三柱式变压器不同联结方式下的电压、电流和磁链特性,仿真结果表明:
1)提出了含RC 阻尼阻容的高阶陷波滤波电路来滤除反并联晶闸管导通过程中产生的大量谐波。克服了LCLC 高阶滤波电路无法滤除3 次、5 次谐波分量,以及含等效串联电阻的高阶陷波滤波电路虽可滤除3 次、5 次谐波分量,但牺牲了11 次及以上的高次谐波分量滤除效果的问题。
2)本文涌流抑制方法不需要考虑剩磁和变压器中性点接地方式的影响,适用于不同的变压器结构和不同联结方式,具有更广泛的适用性。
3)本文所用涌流抑制方法具有更短的启动时间。
附 录
1. 铁心磁链波形

附图1 不同情况下的铁心磁链波形
App.Fig.1 Waveforms of iron core magnetic flux under different conditions
附图1 比较了励磁涌流、仅含反并联晶闸管的涌流抑制器以及含反并联晶闸管和滤波电路的涌流抑制器三种情况下的变压器磁链的变化情况。从图中可知,发生励磁涌流时铁心磁链严重饱和;在含反并联晶闸管的涌流抑制器作用下,启动过程中受谐波影响铁心磁链波形发生畸变,直到启动过程结束系统恢复稳定后,磁链才恢复正常。而当反并联晶闸管和滤波电路结合作为涌流抑制器时,磁链逐渐上升到稳定值,未发生谐波畸变且不存在饱和现象。2. 含RC 阻尼阻容的高阶陷波滤波电路传递函数的系数

3. 陷波支路阻抗特性相关参数

[1] 刘涛, 刘鑫, 梁仕斌, 等. 基于极性变化直流电压源的铁磁元件铁心剩磁通测量方法[J]. 电工技术学报, 2017, 32(13): 137-144.Liu Tao, Liu Xin, Liang Shibin, et al. Residual flux measuring method on the core of ferromagnetic components based on alternating polarity DC voltage source[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 137-144.
[2] 周念成, 李春艳, 王强钢. 基于多变量多尺度熵的变压器励磁涌流识别方法[J]. 电工技术学报, 2018,33(15): 3426-3436.Zhou Niancheng, Li Chunyan, Wang Qianggang. An algorithm to identify transformer inrush currents based on multivarite multiscale sample entropy[J].Transactions of China Electrotechnical Society, 2018,33(15): 3426-3436.
[3] 郭倩雯, 莫文雄, 郑方晴. 一种基于部分Hausdorff距离的励磁涌流识别新方法[J]. 电力系统保护与控制, 2019, 47(1): 41-48.Guo Qianwen, Mo Wenxiong, Zheng Fangqing. A new method of inrush current identification based on partial Hausdorff distance[J]. Power System Protection and Control, 2019, 47(1): 41-48.
[4] 丛伟, 王伟旭, 肖静, 等. 控制合闸电压幅值的变压器励磁涌流抑制方案[J]. 电力系统自动化, 2017,41(8): 159-165.Cong Wei, Wang Weixu, Xiao Jing, et al. Transformer inrush current restraining scheme based on switching voltage amplitude controlling method[J]. Automation of Electric Power System, 2017, 41(8): 159-165.
[5] 刘涛, 颜廷武, 卜新良, 等. 基于合闸电阻的变压器励磁涌流相控技术研究[J]. 高压电器, 2018,54(3): 109-114.Liu Tao, Yan Tingwu, Bu Xinliang, et al. Research on phase⁃controlled technology of inrush current based on closing resistance[J]. High Voltage Apparatus,2018, 54(3): 109-114.
[6] 莫峻, 蔡义明. 计及瞬时通信故障的变压器保护可靠性评估[J]. 电工技术学报, 2019, 34(4): 807-816.Mo Jun, Liang Yiming. Reliability evaluation of transformer protection considering transient communication fault[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 807-816.
[7] 姚东晓, 张凯, 贺要锋, 等. 变压器多特征励磁涌流识别方案研究[J]. 电力系统保护与控制, 2017,45(13): 149-154.Yao Dongxiao, Zhang Kai, He Yaofeng, et al.Research on multi feature recognition scheme of transformer inrush current[J]. Power System Protection and Control, 2017, 45(13): 149-154.
[8] 刘鹏辉, 黄纯, 石雁祥, 等. 配电线路励磁涌流自适应闭锁方案[J]. 电工技术学报, 2019, 34(11):2395-2404.Liu Penghui, Huang Chun, Shi Yanxiang, et al. An adaptive blocking scheme for magnetizing inrush current in distribution lines[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2395-2404.
[9] Xu W, Abdulsalam S G, Cui Yu, et al. A sequential phase energization technique for transformer inrush current reduction—part Ⅱ: theoretical analysis and design guide[J]. IEEE Transactions on Power Delivery,2005, 20(2): 950-957.
[10] Cui Yu, Abdulsalam S G, Chen Shiuming, et al. A sequential phase energization technique for transformer inrush current reduction—partⅠ: simulation and experimental results[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 943-949.
[11] 李伟, 黄金, 方春恩, 等. 基于相控开关技术的空载变压器励磁涌流抑制研究[J]. 高压电器, 2010,46(5): 9-13.Li Wei, Huang Jin, Fang Chunen, et al. Research on elimination of no-load power transformers inrush currents based on controlled switching[J]. High Voltage Apparatus, 2010, 46(5): 9-13.
[12] Chiesa N, Hoidalen H K. Novel approach for reducing transformer inrush currents: laboratory measurements,analytical interpretation and simulation studies[J].IEEE Transactions on Power Delivery, 2010, 25(4):2609-2616.
[13] Brunke J H, Frohlich K J. Elimination of transformer inrush currents by controlled switching-part Ⅱ:application and performance considerations[J]. IEEE Transactions on Power Delivery, 2001, 16(2): 281-285.
[14] Brunke J H, Frohlich K J. Elimination of transformer inrush currents by controlled switching-part Ⅰ: theoretical considerations[J]. IEEE Transactions on Power Delivery, 2001, 16(2): 276-280.
[15] Cano-González R, Bachiller-Soler A, Rosendo-Macías J A, et al. Inrush current mitigation in threephase transformers with isolated neutral[J]. Electric Power Systems Research, 2015, 121: 14-19.
[16] 陈川江, 方春恩, 李伟, 等. 计及剩磁的中性点不接地变压器选相合闸仿真与实验[J]. 高电压技术,2019, 45(11): 3521-3528.Chen Chuanjiang, Fang Chunen, Li Wei, et al.Simulation and experiment of controlled switching for isolated neutral transformer considering residual flux[J]. High Voltage Engineering, 2019, 45(11):3521-3528.
[17] Fang Shuhua, Ni Haimiao, Lin Heyun, et al. A novel strategy for reducing inrush current of three-phase transformer considering residual flux[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7):4442-4451.
[18] 许家源, 华争祥, 朱苛娄, 等. 选相关合技术抑制空载变压器励磁涌流的实验研究[J]. 电力系统保护与控制, 2018, 46(8): 135-141.Xu Jiayuan, Hua Zhengxiang, Zhu Kelou, et al.Experimental research on inrush current suppression of unloaded transformers based on the controlled switching[J]. Power System Protection and Control,2018, 46(8): 135-141.
[19] 何越, 林湘宁, 黄景光. 一种直接消除变压器合闸励磁涌流的方法[J]. 电工技术学报, 2011, 26(11):141-149.He Yue, Lin Xiangning, Huang Jingguang. A method to eliminate the magnetizing inrush current of energized transformers[J]. Transactions of China Electrotechnical Society, 2011, 26(11): 141-149.
[20] Pires I A, Machado A A P, de Jesus Cardoso Filho B.Mitigation of electric arc furnace transformer inrush current using soft-starter-based controlled energization[J].IEEE Transactions on Industry Applications, 2018,54(4): 3909-3918.
[21] 谢仕宏, 孟彦京, 陈君, 等. 感应电机离散变频转矩脉动原因及改进方法[J]. 电机与控制学报, 2018,22(10): 103-111.Xie Shihong, Meng Yanjing, Chen Jun, et al. Cause and improvement of the discrete variable frequency torque ripple of induction motor[J]. Electric Machines and Control, 2018, 22(10): 103-111.
[22] 谢仕宏, 孟彦京, 李宏涛, 等. 感应电机离散变频磁链控制策略[J]. 电工技术学报, 2019, 34(11):2354-2363.Xie Shihong, Meng Yanjing, Li Hongtao, et al. Flux control strategy of induction motor discrete variable frequency[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2354-2363.
[23] Peña-Alzola R, Liserre M, Blaabjerg F, et al. Analysis of the passive damping losses in LCL-filter-based grid converters[J]. IEEE Transactions on Power Electronics,2013, 28(6): 2642-2646.
[24] Wu Weimin, He Yuanbin, Tang Tianhao, et al. A new design method for the passive damped LCL and LLCL filter-based single-phase grid-tied inverter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(10):4339-4350.
[25] Beres R N, Wang X, Blaabjerg F, et al. Optimal design of high-order passive-damped filters for gridconnected applications[J]. IEEE Transactions on Power Electronics, 2016, 31(3): 2083-2098.
[26] Thompson I V, Brennan P V. Fourth-order PLL loop filter design technique with invariant natural frequency and phase margin[J]. IEE Proceedings-Circuits, Devices and Systems, 2005, 152(2): 103-108.
[27] Tang N, Nguyen B, Molavi R, et al. Fully integrated Buck converter with fourth-order low-pass filter[J].IEEE Transactions on Power Electronics, 2017, 32(5):3700-3707.
[28] Arthur Williams F J T. Electronic filter design handbook[M]. New York: McGraw-Hill Companies,2006.
[29] Wu Weimin, He Yuanbin, Blaabjerg F. An LLCL power filter for single-phase grid-tied inverter[J].IEEE Transactions on Power Electronics, 2012, 27(2):782-789.
[30] Fang Jingyang, Li Xiaoqiang, Yang Xu, et al. An integrated trap-LCL filter with reduced current harmonics for grid-connected converters under weak grid conditions[J]. IEEE Transactions on Power Electronics, 2017, 32(11): 8446-8457.