0 引言
封闭母线短路电流下的稳定性分析对电力系统的正常运行起到了重要的作用。在短路工况下,母线导体会产生较高的温升,导体之间会产生较大的电动力,对电力系统及母线造成了较大的危害。因此,保证母线的动-热稳定性是母线设计的重要的前提条件。许多学者将其研究成果加入到设计指南中[1],精确地计算母线在短路电流下的电动力与温升有助于提升母线的动-热稳定性,减少系统可能出现的故障[2],对于强制风冷封闭母线尤为重要。
对于封闭母线的动稳定性而言,封闭母线的电动力大小主要由短路故障的类型和短路电流的振幅决定。为研究封闭母线的动稳定性,通常分析电流密度达到最大值、母线导体相间距离达到最小值时封闭母线受到的电动力[3-6]。目前主要的分析方法有解析法和有限元法(Finite Element Method, FEM)。在测试现场,为快速得到母线的电动力,辅助设计与改进,常在解析法的基础上,利用经验公式的方法进行计算。严兆君等利用解析法对离相封闭母线(Enclosed Isolated Phase Bus, EIPB)的电动力进行分析,并提出了轴向焊接的要求建议[7]。白志胜等利用解析法分析铜铝复合母线短时耐受能力,并对计算结果进行了实验验证[8]。D. P. Labridis 等利用解析法对三相长方形母线的电动力进行了分析,得出了电动力的计算公式,并比较了有限元法的结果和解析法的结果[9]。I. C. Popa 等利用数值方法,考虑了温升的影响,对三相长方形母线的电动力结果进行了修正,并研究了尺寸参数对电动力的影响[10]。近年来,更多的学者使用有限元法对母线的动稳定性进行分析。
国内外许多学者对封闭母线短路电流下的热稳定性问题进行了研究[11-13]。李江涛等利用有限元仿真方法分析了母线温度分布特性的影响因素[14-16]。李彦彰等提出了气体绝缘母线动态等效热路模型[17]。C.H. Leung 提出了利用热网络分析母线导体温升的方法[18]。Guo Bin 等分析了ITER 中不同的冷却方式对母线导体温升的影响[19]。G. Kadkhodaei 等均考虑了电动力、母线温升、机械强度等其他因素的相互作用,分析了短路工况对母线导体的影响[20-22]。这些方法大多针对小尺寸的母线或试验段的母线进行研究,研究对象尺寸较小、结构较简单。而由于电力系统网络的复杂性,实际使用的母线往往尺寸较大、结构复杂、计算规模庞大,难以通过直接进行解析的方法或有限元分析的方法得到母线的温升状况。
对于母线的动-热稳定性问题,许多学者对强制风冷条件下的耦合仿真方法进行了研究[24-25],取得了较好的效果,所研究对象为系统中的典型传输段,温度与流体耦合仿真过程有一定的复杂性,同时需要一定的仿真时长,对复杂部件的等效方式及大系统下的整体仿真探讨较少[25]。
本文提出了一种基于统一节点连接矩阵的封闭母线分段联合仿真分析方法,通过理论计算与试验段母线实测比对的方式确定各分段传导对流系数等关键参数,结合各子段的仿真结果得到整体模型的温度分布。将该方法应用于某型号大型封闭母线的仿真分析中,建立其分段联合有限元仿真模型,在计算资源有限的条件下,进行一定精度的模型计算,得到了母线整体在自然冷却条件与一定风冷条件下的温升分布,并建立了短路状态下母线的动稳定性计算模型,计算得到短路电流下的电动力。
1 离相封闭母线热稳定性分析
1.1 母线热稳定性的计算模型
热分析均以热力学第一定律为基础,表达式为
式中,Q 为系统中的热量(在本模型中为焦耳热);W 为系
统内部所做的功; UΔ 为系统的内能; KEΔ为系统的动能; PEΔ 为系统的势能。在本模型中,![]()
在本模型中,主要考虑传导和对流两种传热方式,表达式为
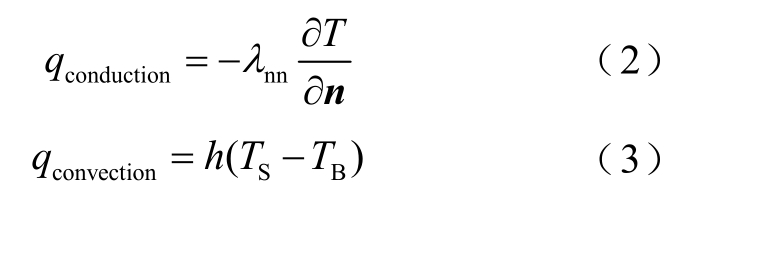
式中, qc onduction为热流密度,W/m2; λ nn为热导率,W/(m⋅K);∂ T /∂n 为温度梯度;h 为表面传热系数,W/(m2⋅K); TS 为固体的表面温度; TB 为固体周围的流体温度。
根据热力学第一定律及本模型中传热方式,建立母线三维热场的数学模型为

式中, vq 为生热率,W/m3;S1、S2 为边界面; Sq 为边界上的热流密度,W/m3。
依据以上有限元法及热场计算基本公式,考虑将有限元模型进行分段计算,研究其求解及计算过程,如图1 所示。

图1 分段计算方法仿真流程
Fig.1 Sub-segments calculation flow chart of the FEM model of EIPB
使用经过验证的热对流散热系数等参数,计算从首段开始建立统一节点热传导矩阵,将温度及温度梯度信息传递至下一段进行计算,直至末段。每段可单独使用PC 进行计算,传导矩阵通过网络数据传输实时实现,这样可在普通PC 上就能实现仅能在工作站进行大型母线的计算。
1.2 母线热稳定性分段联合仿真方法的模型建立
本模型中母线导体材料为铜,外壳材料为铝。为得到准确的母线温升分布状况,建立封闭母线系统的整体CAD 模型,如图2 所示。采用强制风冷方式,三相母线通入同向空气,空气流动方向如图2中箭头所示。将整体模型进行分网,得到的有限元模型节点和单元数见表1。
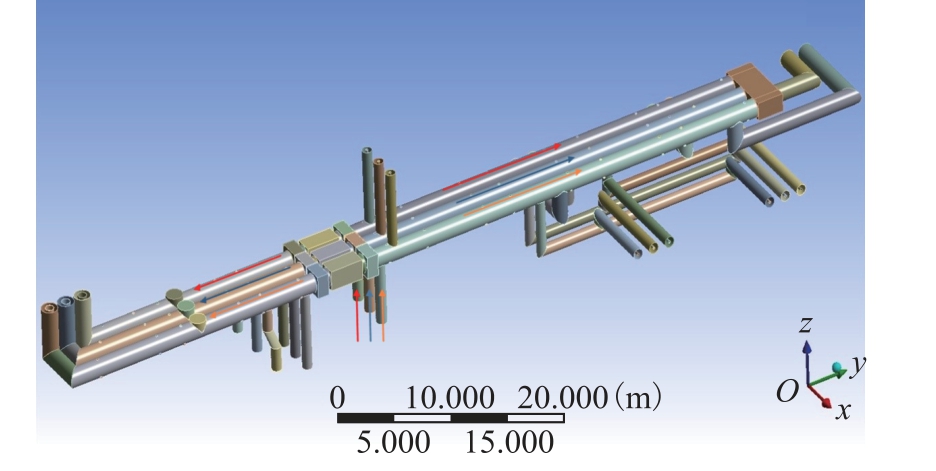
图2 封闭母线热稳定性整体CAD 模型
Fig.2 The CAD model of thermal stability of EIPB
表1 母线整体模型规模
Tab.1 The scale of whole FEM model

节点数 单元数母线导体 1 500 000 400 000整体模型 5 000 000 2 000 000
由于母线整体模型较大,难以直接对其进行仿真分析,因此将整体模型进行子段划分。分段思想在电力领域应用较多[26],但对于离相封闭母线的有限元模型,需要依据结构进行合理划分,从左向右依次为第一、二、三、四段,分别进行仿真分析。对分段后的模型进行分网,分网后得到的有限元模型如图3 所示,分段后的模型规模见表2。


图3 分段后的封闭母线有限元分析模型Fig.3 The FEM model of sub-segments of EIPB
表2 各母线分段模型规模
Tab.2 The scale of the FEM model of sub-segments

节点数 单元数第一段 294 765 141 722第二段 1 372 327 279 775第三段 1 806 232 627 790第四段 1 284 557 269 935
在母线热稳定性的计算模型中,着重考虑位于第二段的中间衔接部分,由于中间由发电机断路器(Generator Circuit Breaker, GCB)连接,其温升对母线整体的热稳定性影响较大。因此对中间的衔接部分采取精细的规则分网,如图4 所示。

图4 母线连接段分网细节
Fig.4 The details of the joint part in FEM model
在分段联合仿真中,对流散热系数等热仿真参数是重要的参数条件。为了能够更好地模拟实际封闭母线发热以及风冷效果,建立试验段母线,依据其实验数据,进行模型评价,并确定更为合理的参数设置,从而为后续整体模型的仿真提供参数数据基础。
试验段母线结构为单组三相母线,其中一相具有强制通风装置,冷却风仅在本相中流动,并不与其他两路联通,母线与外壳间采用四组绝缘支撑作为连接与支撑件,同时端部采用连接接地。试验段整体结构及测温点位置与编号如图5 所示。
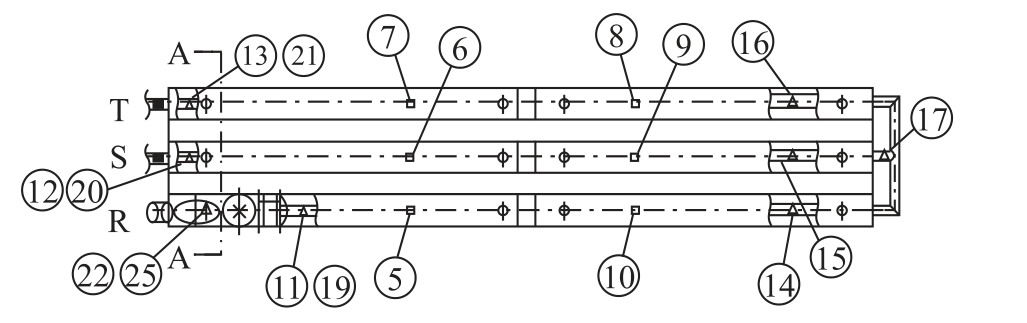
图5 试验段整体结构
Fig.5 The structural model of test section
依据实际尺寸建立CAD 三维模型,在建模过程中,对于圆柱连接部分采用过渡连接的方式,使得连接更为合理,为后续有限元仿真在连接面上的合理分网提供了较好的基础。另外,两端堵头并未在CAD 模型中建立实体,而是在后续有限元仿真过程中通过端部条件的设置来实现的。
利用CAD 软件建立母线导体各零件的CAD 模型并组装,试验段整体CAD 模型如图6 所示。

图6 试验段整体CAD 模型
Fig.6 The CAD model of test section
通过计算散热系数,同加载母线电流载荷、传热条件与边界条件设置等,对已经建立的有限元模型进行求解。提取有限元仿真计算结果,对比实验测试中的测温点(测温点位置如图5 所示),验证有限元仿真结果。测温点中部分关键点的实验与仿真对比结果见表3。
表3 部分关键点的实验与仿真对比结果
Tab.3 Comparison of some key point experiments and simulation results

测温点 实验结果/℃ 仿真结果/℃ 相对误差(%)12 107.0 106.2 0.748 15 111.0 106.2 4.324 13 87.1 90.5 3.843 16 95.9 98.3 2.525 14 73.0 74.7 2.327 6 57.1 52.9 7.292 9 57.5 52.9 8.042 5 38.7 38.8 0.359 7 51.2 46.4 9.352
由表3 可知,实验结果与仿真结果的最大相对误差约为9.35%,平均相对误差约为5.10%,因此比较实验结果与仿真结果,可以认为该仿真计算模型的结果较好地模拟了母线的发热情况。
依据该建模方法及试验对比,经计算得到离相封闭母线模型在短路电流36 000A、环境温度40℃风冷条件下的散热系数见表4。
表4 封闭母线各部分散热系数
Tab.4 The heat transfer coefficient of different parts of EIPB(单位:W/mm2)
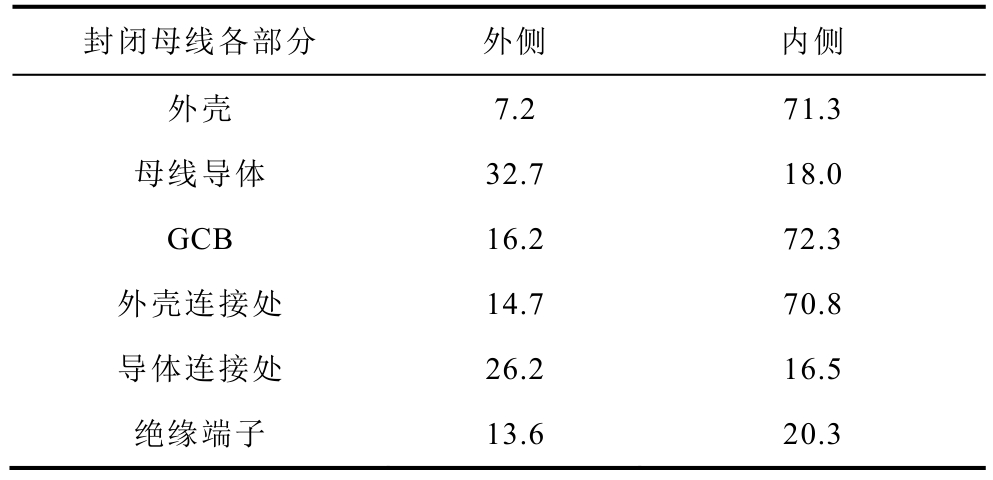
封闭母线各部分 外侧 内侧外壳 7.2 71.3母线导体 32.7 18.0 GCB 16.2 72.3外壳连接处 14.7 70.8导体连接处 26.2 16.5绝缘端子 13.6 20.3
确认关键参数后,对热稳定性模型施加载荷。研究母线的热稳定性时,考虑最严重状况下封闭母线的温升,即向封闭母线通入三相短路电流。具体步骤如下:①将电流密度载荷加载至封闭母线;②将温度载荷加载至封闭母
线。
一方面,对于不同散热方式在母线导体与外壳表面加载相应大小的对流散热系数,模拟母线的散热情况;另一方面,对不同子段的母线模型,通过在子段连接处加载温度载荷的方式传递边界条件。
1.3 母线热稳定性仿真结果
母线三相通入短路电流36 000 A,将环境温度设为40 ℃。通过改变各表面的对流散热系数模拟母线内部通风状况。最终得到的封闭母线温度分布如图7 和图8 所示。

图7 封闭母线分段仿真温度
Fig.7 Simulation temperature of sub-segments of EIPB

图8 封闭母线温度分布图
Fig.8 Temperature distribution of EIPB
由图7 和图8 可知,外壳达到的最高温度为83℃,位于第二子段连接部分;而母线导体达到的最高温度为109℃,同样位于第二子段。这验证了本文的假设,即第二子段为母线温升较高的部分,对母线热稳定性影响较大。另外,相比主干部分的温升幅度,分支部分的温升较小,这主要是由于分支部分流过的电流幅度较主干部分小,发热相对较少。
由于实际产品热稳定性指标为外壳可承受最大温升45℃,母线导体可承受温升70℃,考虑在不同工况下为达到该可承受温升范围需要的最低通风量,分别对环境温度为-10℃、0℃、10℃、20℃、30℃、40℃,短路电流有效值为34 000A、36 000A 工况进行分段联合仿真分析,计算结果见表5。
表5 不同温度下空气流量计算值
Tab.5 The calculation result of ventilation rate

电流/A 空气流量/(kg/h)-10℃ 0℃ 10℃ 20℃ 30℃ 40℃34 000 82 000 82 500 83 000 84 000 86 000 88 000 36 000 90 000 93 000 96 000 100 000 130 000 150 000
由表5 可知:
(1)短路电流相同时,随着环境温度的提高,所需的空气流量逐渐增加,并且短路电流越大,所需空气流量增加的幅度越大。
(2)环境温度相同时,随着短路电流的增加,所需的空气流量逐渐增加。
2 离相封闭母线动稳定性分析
2.1 母线动稳定性的计算模型
根据Maxwell 电磁理论,载流导体在磁场中会受到力的作用,且该电动力可以分解为两个分量:垂直于磁感应强度的方向和平行于磁感应强度的方向。母线周围的磁场强度满足
母线导体在磁场中受到的Lorenz 力为
式中,D、J、H、B 分别为电位移矢量、全电流密度、磁场强度和磁感应强度; LF 为Lorenz 力;Ise 为短路电流。
2.2 母线动稳定性有限元模型的建立
在母线热稳定性分析的基础上,建立母线动稳定性有限元模型。将热稳定性分析的温升结果加载到动稳定性仿真中。同时为研究封闭母线的动稳定性,向封闭母线施加最严重状况下的电动力,即仿真分析电流密度达到最大值、母线导体相间距离达到最小值时封闭母线受到的电动力。利用有限元软件Ansys 建立母线导体的动稳定性2D 模型。三相封闭母线的母线导体和外壳的材料均为铝,三相母线并排平行放置。将封闭母线的三相分别标记为X相、Y 相、Z 相,如图9 所示。封闭母线相间距离最小时,相邻两相母线轴线间的距离为1 600mm,母线导体直径为180mm,外壳直径为200mm。
通过控制分网精细程度的方式对母线的动稳定性模型进行分网,得到母线动稳定性有限元模型,如图10 所示。

图9 封闭母线标记示意图
Fig.9 The label of the 2-D model
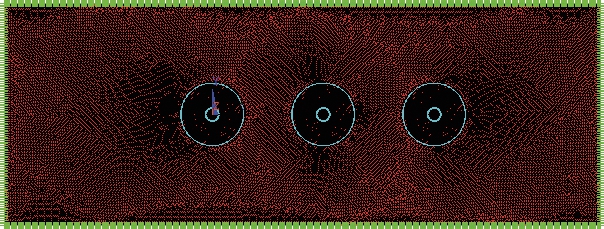
图10 封闭母线动稳定性有限元模型
Fig.10 The FEM model of the brunch EIPB cross-section
有限元分析的主要目的是检验母线在特定工况下受到的电动力。因此,有两种加载方式:实体模型加载和有限元模型加载。实体模型加载是指将载荷加至实体模型上,而有限元模型加载是指将载荷加至节点上。相对而言,实体模型加载更为方便,因此使用实体模型加载。具体加载步骤是:
(1)将电流密度载荷加载至封闭母线。向三相母线导体施加三相短路电流,并向三相母线外壳施加反方向的三相短路电流。
(2)向周围的空气施加磁场平行载荷。
2.3 母线动稳定性仿真结果
2.3.1 理想状况下封闭母线的电动力计算结果
在理想状况下,向三相母线导体通入1 200kA 短路电流,向三相母线外壳通入反向1 200kA 短路电流。仿真可知,对母线外壳产生的三相电动力峰值分别为4.1N/m、4.7N/m 和4.0N/m。当Y 相达到最大值时,三相母线受到的电动力均接近最大值。此时,X 相受到的电动力与Y 相受到的电动力方向相反,因此X相与Y 相外壳有相互吸引的趋势。反之,当Y 相达到反向最大值时,Z 相与Y 相外壳有相互吸引的趋势。但由于该电动力较小,其对母线外壳影响较小。
由于每相的母线导体与外壳实际上是通过绝缘子相互连接固定的,每相的母线导体与外壳成为了机械的整体。当考虑母线受到的电动力时,需要将母线导体与外壳整体考虑。在理想状态下,各项母线导体受到的最大合力分别为-0.1N/m、0.1N/m 和0.1 N/m。当Y 相的电动力达到最大值时,母线受到的合力约为0。因此在理想状况下封闭母线不会受到电动力作用。
2.3.2 非理想状况下封闭母线的电动力计算结果
在非理想状况下,向三相母线导体通入1 200kA短路电流,而流过外壳的电流较母线导体电流稍小。根据实验结果,流过外壳的电流约为流过母线导体的短路电流的95%。因此对封闭母线外壳产生的电动力随时间变化曲线如图11 所示。
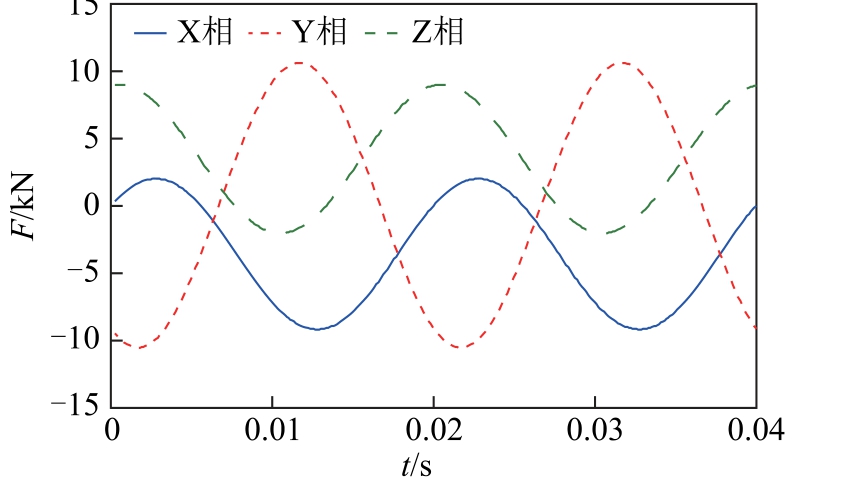
图11 封闭母线外壳电动力随时间变化曲线
Fig.11 The electrodynamic force of branch shell vs. time
三相母线的电动力峰值分别为-9 200.00 N/m、10 586.80N/m 和8 970.40N/m。当某相的电动力达到最大值时,三相各自的电动力最大值见表6。
表6 封闭母线外壳电动力最大值
Tab.6 The maximum force of the branch shell(单位:N/m)

电磁力 X 相 Y 相 Z 相X 相最大值 -9 200.00 9 953.00 -693.40 Y 相最大值 -8 867.60 10 586.80 -1 684.60 Z 相最大值 560.00 -9 789.60 8 970.40
由表6 可见,最大电磁力出现在Y 相,达到了10 586.80N/m。当Y 相接近最大值时,三相母线受到的电动力均达到了最大值。此时,X 相受到的电动力与Y 相受到的电动力方向相反,因此X 相与Y相外壳有相互吸引的趋势。反之,当Y 相达到反向最大值时,Z 相与Y 相外壳有相互吸引的趋势。
在非理想状况下,向三相母线导体通入1 200kA短路电流,流过外壳的电流约为流过母线导体的短路电流的95%。因此对封闭母线导体产生的电动力随时间变化曲线如图12 所示。

图12 封闭母线导体电动力随时间变化曲线
Fig.12 The electrodynamic force of the branch bus conductor vs. time
三相母线的电动力峰值分别为8 740.20N/m、-10 057.70N/m 和-8 522.10N/m。当某相的电动力达到最大值时,三相各自的电动力值见表7。
表7 封闭母线导体电动力最大值
Tab.7 The maximum force of the branch bus conductor(单位:N/m)

电磁力 X 相 Y 相 Z 相X 相最大值 8 740.20 -9 455.50 658.70 Y 相最大值 8 424.40 -10 057.70 1 600.40 Z 相最大值 -532.00 9 300.30 -8 522.10
由表7 可见,最大电磁力出现在Y 相,达到了-10 057.70N/m。当Y 相接近最大值时,三相母线导体受到的电动力均达到了最大值。此时,X 相受到的电动力与Y 相受到的电动力方向相反,因此X 相与Y 相导体有相互吸引的趋势。反之,当Y 相达到反向最大值时,Z 相与Y 相导体有相互吸引的趋势。
由于每相的母线导体与外壳实际上是通过绝缘子相互连接固定的,每相的母线导体与外壳成为了机械的整体。此时,封闭母线受到的电动合力如图13 所示。由图13 可知,在非理想状态下,各相母线导体受到的最大合力分别为-459.0 N/m、529.1N/m和448.3 N/m。当Y 相的电动力达到最大值时,母线受到的合力约为529.1 N/m。
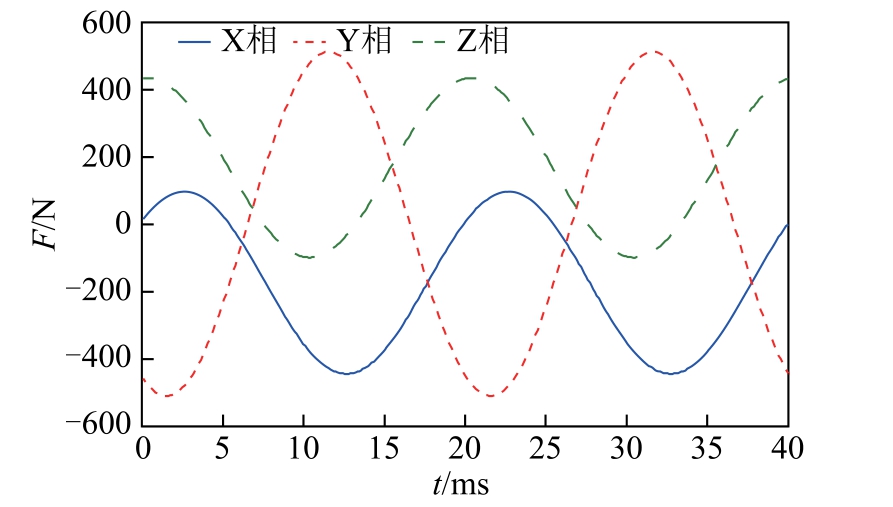
图13 封闭母线整体电动力随时间变化曲线
Fig.13 The resultant force of the branch bus and the shell vs.time
3 结论
1)针对电力系统中的离相封闭母线,基于统一交接面温度矩阵传递函数,研究了一种可用于封闭母线热稳定性分析的分段有限元模型建模与分析方法。
2)对于模型中的关键参数,理论计算了对流散热系数,依据试验段实测数据修正不同条件下的对流散热系数,并应用于该分段模型的仿真分析中。仿真结果表明不同环境温度、短路电流下维持稳定温升所需的空气流量也不同。随着环境温度的提高和短路电流的增加,所需空气流量增加。
3)计算了某电力系统中典型封闭母线在短路状态下的电动力。在理想状况下,封闭母线导体和外壳在短路状态下所承受的电流峰值几乎相同,此时母线相间电动力较小,甚至可以忽略;而在非理想状况下,封闭母线导体承受的电流峰值高于外壳承受的电流峰值,母线相间电动力较大。当中间相电动力达到最大值时,两侧两相的电动力接近最大值,此时母线相间的电动力最大。
该分段建模分析方法,在计算资源有限的情况下,实现了一定精度的大型封闭母线的强制风冷状态下动-热稳定性仿真分析,在实施过程中由于GCB等部分采用等效处理的方式,因此在其附近区域的精算有待提升,这也是后续精度提升的关注点之一。
[1] IEEE 605—1998 IEEE Guide for the Design of Substation Rigid-Bus Structures[S]. 1998.
[2] 郭雨豪, 薛永端, 徐攀, 等. 含同母线环路的配电网单相接地故障特征及选线[J]. 电力系统自动化,2019, 43(1): 234-242.Guo Yuhao, Xue Yongrui, Xu Pan, et al.Characteristic and feeder selection of single-phase grounding fault in distribution network with the same bus loop[J]. Automation of Electric Power Systems,2019, 43(1): 234-242.
[3] Labridis D P, Dokopoulos P S. Electromagnetic forces in three-phase rigid busbars with rectangular crosssections[J]. IEEE Transactions on Power Delivery,1996, 11(2): 793-800.
[4] Triantafyllidis D G, Dokopoulos P S, Labridis D P.Parametric short-circuit force analysis of three-phase busbars-a fully automated finite element approach[J].IEEE Transactions on Power Delivery, 2003, 18(2):531-537.
[5] Yang J, Liu Yuan, Hu Degui, et al. Transient electromagnetic force analysis of GIS bus based on FEM[C]// 2016 International Conference on Condition Monitoring and Diagnosis (CMD), Xi'an, 2016: 554-557.
[6] Guan Xiangyu, Shu Naiqiu. Electromagnetic field and force analysis of three-phase enclosure type GIS bus capsule[C]// 2014 IEEE PES T&D Conference and Exposition, Chicago, 2014: 1-4.
[7] 严兆君, 吴军. 大容量离相封闭母线轴向焊接与电动力分析[J]. 高压电器, 2015, 51(7): 78-86.Yan Zhaojun, Wu Jun. Analyses on axial welding and electromagnetic force of large capacity enclosure type isolated-phase bus[J]. High Voltage Apparatus, 2015,51(7): 78-86.
[8] 白志胜, 陈建兵, 忻尚芝. 铜铝复合母线短时耐受能力研究[J]. 电子科技, 2016, 29(2): 109-111.Bai Zhisheng, Chen Jianbing, Xin Shangzhi. Shorttime withstand capability of copper aluminum composite bus bar[J]. Electronic Science and Technology, 2016, 29(2): 109-111.
[9] Labridis D P, Dokopoulos P S. Electromagnetic forces in three-phase rigid busbars with rectangular crosssections[J]. IEEE Transactions on Power Delivery,1996, 11(2): 793-800.
[10] Popa I C, Dolan A I. Numerical modeling of threephase busbar systems: Calculation of the thermal field and electrodynamic forces[C]// 2016 International Conference on Applied and Theoretical Electricity(ICATE), Craiova, 2016: 1-9.
[11] 李江涛, 孙义, 李擎宇, 等. 大电流开关柜温度分布特性的影响因素分析[J]. 电气技术, 2018, 19(9):13-18.Li Jiangtao, Sun Yi, Li Qingyu, et al. Analysis of influencing factors on temperature distribution characteristics of high current switchgear[J].Electrical Engineering, 2018, 19 (9): 13-18.
[12] 陈彪, 罗东豪, 王嗣翔, 等. 新型节能铜包铝管母线的温升分析与实验[J]. 电气技术, 2018, 19(3): 85-89.Chen Biao, Luo Donghao, Wang Sixiang, et al. The temperature analysis and experiment of the new-type energy-saving copper-clad aluminum busbar[J].Electrical Engineering, 2018, 19(3): 85-89.
[13] 宁宇, 孙洪宇, 张伟, 等. GIS 高压母线段间连接缝隙造成的过热分析[J]. 电工技术学报, 2017,32(1): 217-224.Ning Yu, Sun Hongyu, Zhang Wei, et al. Overheat analysis on the connection gap in GIS with the sections connected by bolts[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 217-224.
[14] 陈强, 李庆民, 丛浩熹, 等. 引入多重边界条件的GIS 母线温度分布多场耦合计算及影响因素分析[J].电工技术学报, 2016, 31(17): 187-195.Chen Qiang, Li Qingmin, Cong Haoxi, et al.Numerical calculation and correlative factors analysis on temperature distribution of GIS bus bar based on coupled multi-physics methodology combined with multiple boundary conditions[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 187-195.
[15] 杨国清, 魏帅, 王得意, 等. 纳米改性环氧树脂绝缘型封闭母线的温升特性研究[J]. 大电机技术,2016(5): 56-60.Yang Guoqing, Wei Shuai, Wang Deyi, et al. Research on temperature rise of nano-modified epoxy resin insulated enclosed bus[J]. Large Electric Machine and Hydraulic Turbine, 2016(5): 56-60.
[16] 孙国霞, 舒乃秋, 吴晓文, 等. 基于多物理场耦合的气体绝缘母线触头接触温升有限元计算[J]. 电工技术学报, 2013, 28(2): 408-413.Sun Guoxia, Shu Naiqiu, Wu Xiaowen, et al. Finite element analysis of contact temperature rise in gas insulated busbars based on coupled multi-physics[J].Transactions of China Electrotechnical Society, 2013,28(2): 408-413.
[17] 李彦彰, 舒乃秋, 刘亚男, 等. 基于外壳热分布的气体绝缘母线温度计算模型[J]. 电测与仪表, 2017,54(18): 111-117.Li Yanzhang, Shu Naiqiu, Liu Ya'nan, et al. Thermalcircuit calculation model of gas insulated bus temperature based on heat distribution of tank[J].Electrical Measurement and Instrumentation, 2017,54(18): 111-117.
[18] Leung C H, Lee A, Wang Bor-Jenq. Thermal modeling of electrical contacts in switches and relays[J]. IEEE Transactions on Components, Packaging, and Manufacturing Technology: Part A, 1996, 19(3): 346-352.
[19] Guo Bin, Song Zhiquan, Fu Peng, et al. Thermal dissipation modelling and design of ITER PF converter alternating current busbar[J]. Plasma Science and Technology, 2016, 18(10): 1049-1054.
[20] Kadkhodaei G, Sheshyekani K, Hamzeh M, et al.Multiphysics analysis of busbars with various arrangements under short-circuit condition[J]. IET Electrical Systems in Transportation, 2016, 6(4): 237-245.
[21] Kadkhodaei G, Sheshyekani K, Hamzeh M. Coupled electric-magnetic-thermal-mechanical modelling of busbars under short-circuit conditions[J]. IET Generation, Transmission & Distribution, 2016, 10(4):955-963.
[22] Jin Lei, Zhong Jianying, Wu Shijin, et al. A 3-D steady-state analysis of thermal behavior in EHV GIS busbar[J]. Journal of Electrical Engineering and Technology, 2016, 11(3): 781-789.
[23] 纽春萍, 赵鹏, 吴翊, 等. 基于 Ansys 的强迫风冷封闭母线热分析[J]. 高电压技术, 2018, 44(7): 1-6.Niu Chunping, Zhao Peng, Wu Yi, et al. Thermal analysis of forced air-cooled enclosed bus based on Ansys[J]. High Voltage Engineering, 2018, 44(7): 1-6.
[24] 金向朝, 谢志杨, 刘秀甫, 等. 基于有限元法的三相同壳结构 GIS 母线热分析[J]. 武汉大学学报(工学版), 2013, 46(5): 654-658.Jin Xiangchao, Xie Zhiyang, Liu Xiufu, et al. Thermal analysis of three-phase enclosed GIS bus bar based on finite-element method[J]. Engineering Journal of Wuhan University, 2013, 46(5): 654-658.
[25] 吴晓文. 气体绝缘母线温升计算及监测方法的研究[D]. 武汉:武汉大学, 2013.
[26] 陈亦平, 李崇涛, 杨若朴, 等. 云南异步电网中频率振荡的分段线性模型分析方法[J]. 电力系统自动化, 2020, 44(6): 186-197.Chen Yiping, Li Chongtao, Yang Ruopu, et al.Analysis method of piecewise linear model for frequency oscillation in asynchronous power grid of Yunnan in China[J]. Automation of Electric Power Systems, 2020, 44(6): 186-197.