0 引言
直流牵引供电系统采用的轨道回流方式不可避免地造成轨道电位以及杂散电流问题。由于轨道自身存在电阻率,轨道回流电流会在轨道上产生几十伏甚至上百伏的轨道电位;且轨道对地之间并非完全绝缘,地铁列车牵引电流一部分会通过轨道对地过渡电阻流入地下,并沿着埋地金属返回到轨道,最终流入牵引变电所负极,这部分电流被称为杂散电流[1]。杂散电流会引起地下金属管线、隧道结构钢筋发生电化学腐蚀,进而导致自来水、天然气、石油的泄露并对结构钢筋造成破坏,产生严重安全隐患。直流牵引供电系统牵引所负极接地方式通常为悬浮接地或直接接地两种,广泛采用的悬浮接地直流牵引供电系统虽然能降低杂散电流,但在牵引所位置产生与列车位置电压大小相同的轨道电位,一旦超过安全阈值对牵引所设备接地与人员安全造成威胁[2],过电压保护装置启动牵引所负极直接接地;直接接地虽然能将牵引所电位减小为零,但会造成更多的杂散电流和列车位置更高的轨道电位[3],因此实际系统运行存在不同接地方式的频繁切换。
国内外学者关于轨道电位与杂散电流的主要研究包括:①考虑对地的多层结构轨道电位与杂散电流模型和理论分布,难以测量各层金属间过渡参数,且没有考虑牵引所不同接地方式切换,参数来源不准确[4-10];②用于模拟轨道电位与杂散电流定值电阻系统无法反映在列车运动情况下的轨道电位和杂散电流分布[11-12];③用于解决城市轨道交通中的迷流和轨道电位等问题,提出了基于RSCC 的直流自耦变压器牵引供电系统[13];④直接接地单列车工况的轨道电位与杂散电流模拟的动态模拟系统,由于列车不同运行工况电流方向不同,难以实现双向电流的模拟[14-15],实际中牵引变电所一般在直接接地和悬浮接地中切换[16],简单的动态模拟系统难以模拟直流牵引供电系统采用的多接地方式切换[17]。
本文首先对比研究了牵引所悬浮接地和直接接地两种方式、沿轨道分布的轨道电位与杂散电流三维数学模型,然后提出了双向电流轨道电阻和双向电流轨道对地过渡电阻模型以及基于上述模型的硬件模拟系统方案,进而实现不同接地方式下的轨道电位和杂散电流动态分布规律模拟。最后通过仿真和硬件实验模型,对本文所提出理论分析和控制的有效性及可行性进行了仿真和实验验证。
1 数学解析与电路模型
城市轨道交通直流牵引供电系统目前广泛采用双边集中式供电,其中牵引变电所接地方式主要有直接接地、悬浮接地、二极管接地、过电压保护装置(Over Voltage Protection Device, OVPD)接地四种,如图1 所示,典型轨道-排流网的电阻分布网络如图2 所示[18-19]。
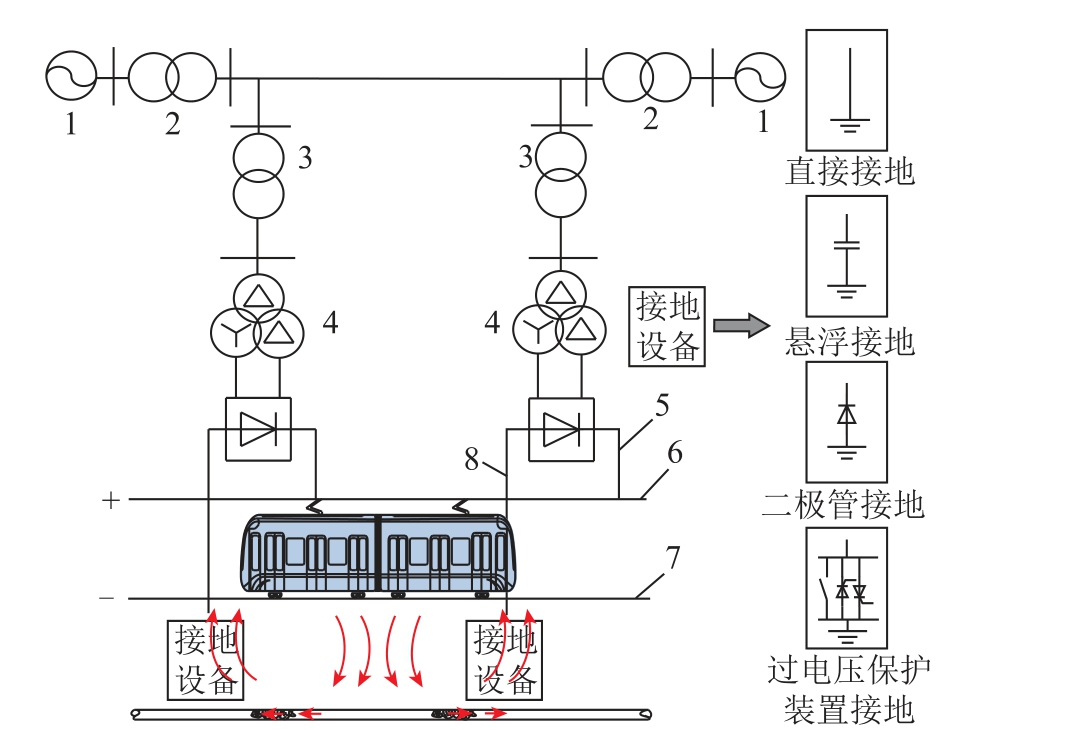
图1 双边供电系统与接地方式示意图1—发电厂 2—升压变压器 3—主降压变压器 4—牵引变电所5—馈电线 6—接触网 7—轨道 8—负回流线
Fig.1 Schematic diagram of bilateral power supply system and grounding mode

图2 双边供电系统轨道-排流网电阻模型
Fig.2 Rail-drainage net resistance model of bilateral power supply system
从图2 可以看出,轨道电位Urm、轨道电流Ir、杂散电流Im 与列车牵引电流I、牵引变电所距离L、列车距离左侧牵引所L1、轨道纵向电阻Rr、轨道对排流网的过渡电阻Rrm、排流网纵向电阻Rm 等参数有关。为此,下文对杂散电流和轨道电位的推导围绕这些参数进行,推导过程中各参数物理意义与单位见附表1。
表1 不同接地方式下列车任意位置沿轨道电位和杂散电流分布规律
Tab.1 Distribution of rail potential, stray current and rail current at any position under different grounding mode

接地方式 列车左侧(x<y)列车右侧(x>y)悬浮接地 直接接地 悬浮接地 直接接地边界条件 ( ) ( )I I I L I r 0=t p r 1 t p−,= ( ) ( )−U I L I −0 0,rm r 1 t p= = ( ) ( )I L I I I=r 1 t r r t r−, L= ( ) ( )−I L U L=r 1 t r rm, 0=I −轨道电位Urm/V ( )( )R I L y x y L yα r /2 1 /8− −+2( )( )R Ix L y L yα r r−■■ ■■2(1 /2)+ ( )( )R Iy y L x L L yα+ −■/2 1+ −■2/8■■( )( )R yI L x L L yα■ ■+ −■■r -1 2/2杂散电流Im/A ( ) ( )− + ( )( )( )( )R I L y x x y R L yα r − −r 2 2 1 /8 2 rm ( )−+−− +α R I L y x y x y R y L 2 1 /2 rm( )( )( )− −− ■ ■+ −■■R Iy x L x y R L L yα r 2 2 1 /8 rm− − +− ■ ■+ −■■R y x y x L y R L L yα r 2 2 2 1 /2 rm ( )( )( )
为简化分析,本文以图2 中的轨道-排流网两层结构数学模型为例进行分析,并作如下假设:①轨道纵向电阻与轨道对地过渡电阻沿轨道方向均匀分布;②牵引供电系统采用双边供电方式;③列车牵引电流用电流源表示;④排流网电阻率远小于土壤电阻率,杂散电流以排流网为流通路径,通过轨道对排流网过渡电阻返回。
1.1 悬浮接地与直接接地系统的三维模型
以列车左侧的轨道电阻、轨道对地电阻和排流网构成的微元电阻网络如图3 所示。

图3 轨道对地电阻与排流网电阻网络微元段
Fig.3 Infinitesimal section of resistance network of rail and drainage net
当牵引供电系统采用不同接地方式时,根据基尔霍夫定律,可以得到

式中,α=(Rm+Rr)/Rrm,根据支路约束条件和基尔霍夫定律可得轨道电流与排流网电流关系式(4),列车左右两侧电流满足式(5)。
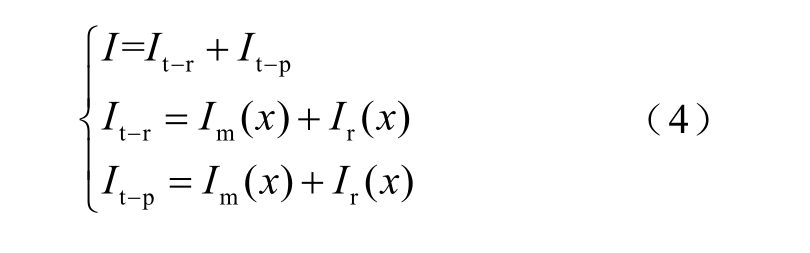

悬浮接地与直接接地方式下轨道电位、轨道电流和杂散电流表达式中 C1、C2 与边界条件有关。表1 给出了不同接地方式下轨道电位和杂散电流三维分布表达式,其中列车位置为y,沿轨道位置为x。图4 给出了不同接地方式下,牵引电流恒定时的轨道电位和杂散电流的三维分布。其中牵引供电系统参数为:牵引所1 位置为0 km,牵引所2 位置为2 km,牵引电流恒定1 000 A,轨道纵向电阻Rr 为0.03 Ω/km,轨道对排流网过渡电阻Rrm 为30 Ω·km,排流网纵向电阻Rm 为0.15 Ω/km。
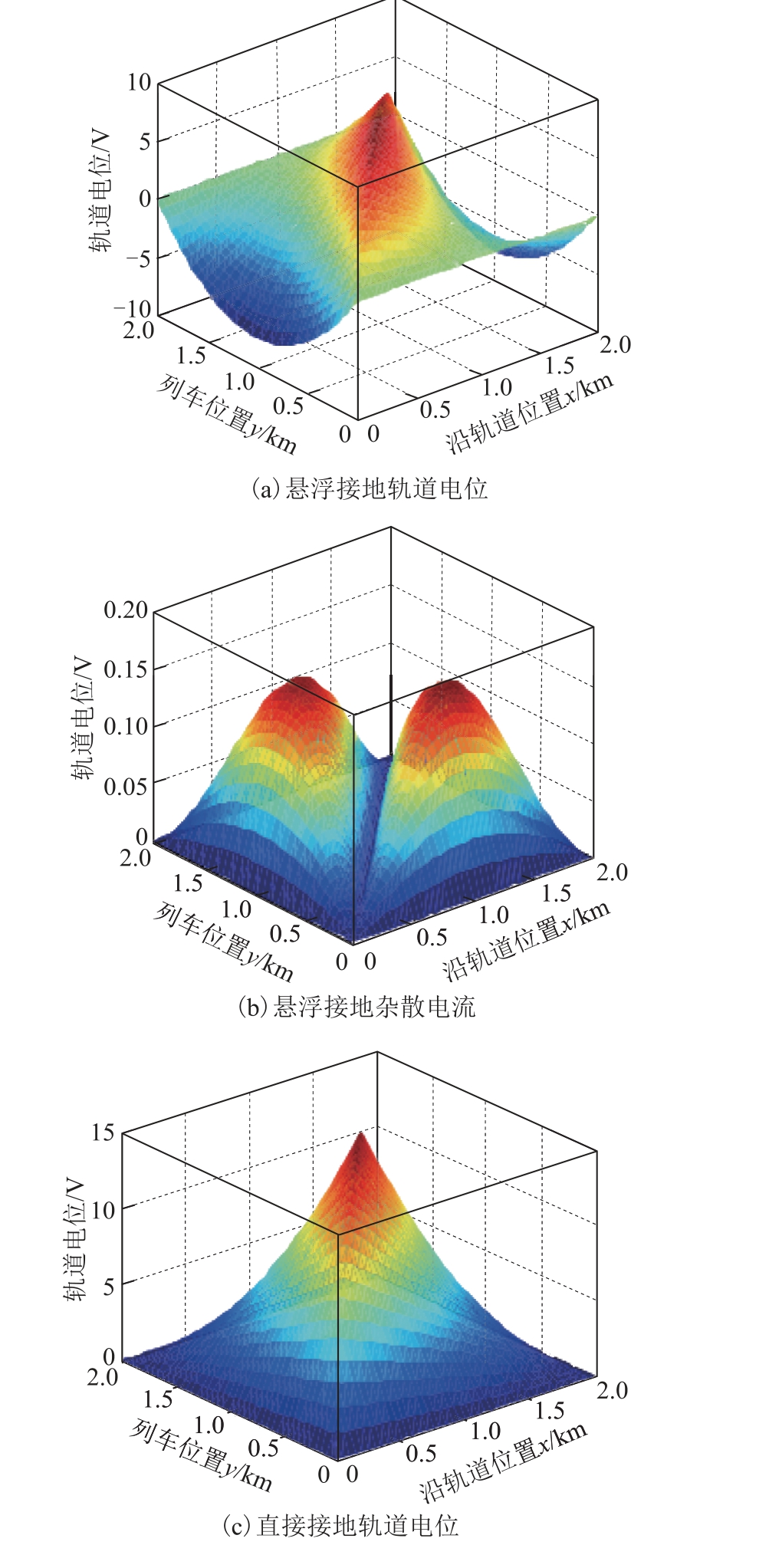
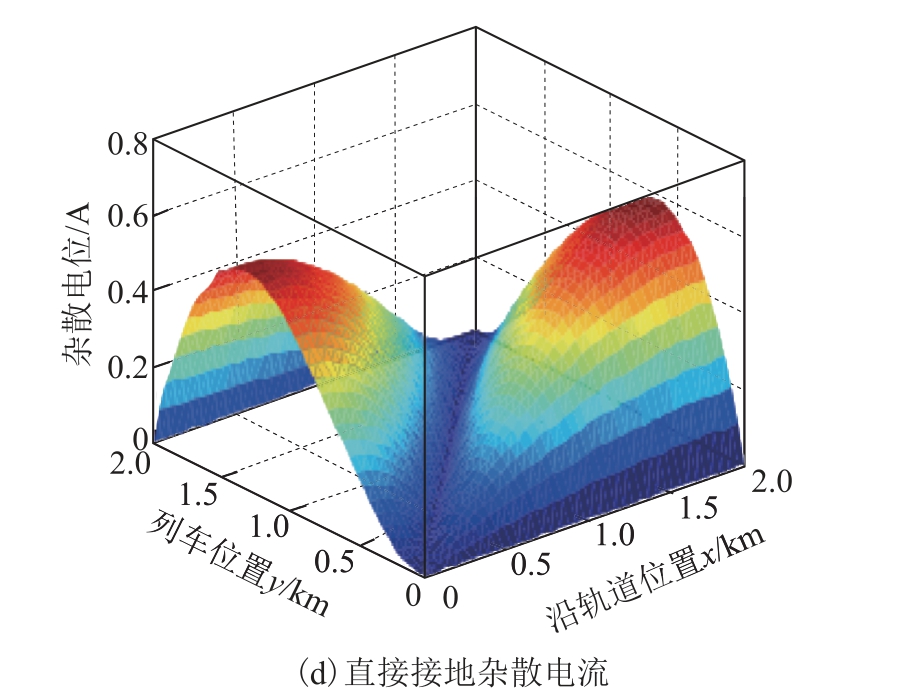
图4 沿轨道分布的轨道电位和杂散电流的三维曲面图
Fig.4 3D curved graph of rail potential and stray current distributed along the rail
图4a 与图4c 对比可知,由于牵引所直接接地,使牵引所处的电位钳位为0,会造成整个轨道电位抬升,沿线路上轨道电位的最大值是悬浮接地时最大值的2 倍,两种接地方式轨道电位最大点均在列车位置平面处。
图4b 与图4d 对比可知,直接接地情况下最大杂散电流出现在牵引所位置,悬浮接地情况下最大杂散电流出现在牵引所与列车位置中点处。由于轨道电位抬升,直接接地最大杂散电流变为悬浮接地最大杂散电流的4 倍。从理论上解释了牵引所长期直接接地不仅会造成列车位置的更高电位,同时牵引所附近金属管线、结构钢筋电化学腐蚀更为严重。
1.2 两种接地方式分析
沿列车位置对图4 中的轨道电位三维分布图做的截面如图5 所示,截面表示列车在固定点处沿轨道分布的轨道电位。其中列车位置为H,牵引所1 位置为0,牵引所2 位置为L。由图5 可知,系统悬浮接地时,轨道电位零点出现在列车与牵引所中点位置G2、G3,轨道电位最大点在列车位置处为URT1,且列车与牵引所处电位幅值相等,方向相反;系统直接接地时,轨道电位零点出现在牵引所位置G1、G4,轨道电位最大点在列车位置处为URT2。不同接地方式下沿轨道分布杂散电流等于各点轨道电位与轨道过渡电阻比值的积分。沿轨道总杂散电流表达式为
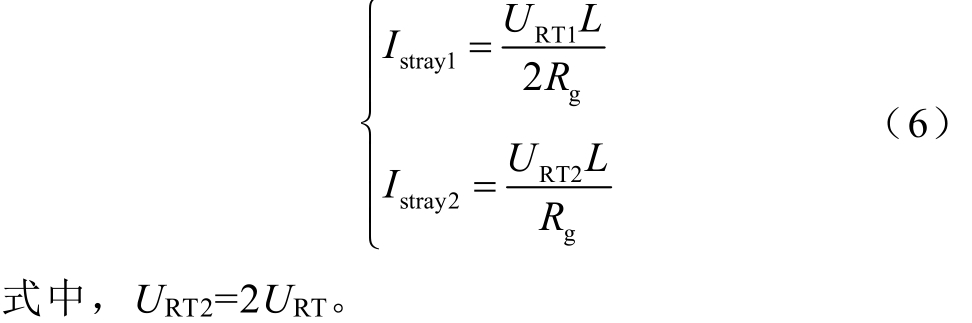

图5 列车位置固定沿轨道分布轨道电位
Fig.5 Rail potential distribution along the rail
2 多接地轨道电位与杂散电流动模实验
多接地轨道电位与杂散电流动模实验平台(Muti-Grounded Rail Potential And Stray Current Dynamic Emulator, MGDE)如图6 和图7 所示。在双边供电直流牵引供电系统结构基础上,结合两种电力电子电路模拟了列车运动过程中轨道纵向电阻和轨道对地过渡电阻变化。图中,Utps1 和Utps2 表示两个牵引变电所,Rr1、Rr2 表示随列车运动过程轨道纵向电阻,Rg1、Rg2 表示变化的轨道对地过渡电阻,电流源I 表示列车牵引电流。根据1.2 节中两种接地方式的分析可知,悬浮接地列车与牵引所中点电位为零,通过改变系统接地点G1、G2、G3、G4 接入对地电阻的方式,可以实现满足系统的不同接地情况的模拟。
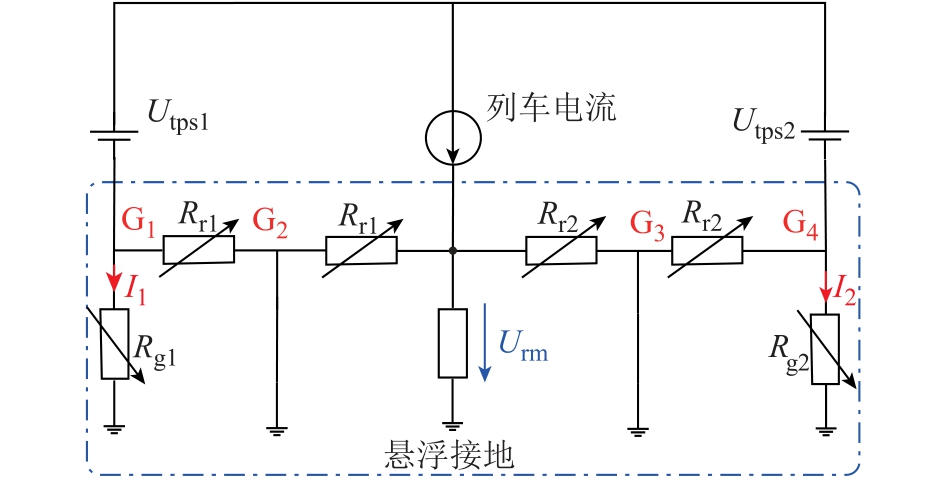
图6 悬浮接地轨道电位与杂散电流动模实验电路
Fig.6 Floating grounded rail voltage and stray current dynamic emulator

图7 直接接地轨道电位与杂散电流动模实验电路
Fig.7 Solidly grounded rail potential and stray current dynamic emulator
列车运行在牵引工况、惰行工况和制动状态下牵引电流方向相反。轨道纵向电阻和轨道对地过渡电阻随列车位置改变,因此两种可变电阻模块均需具有电流双向流动且等效输入阻值随列车位置变化而变化的特点。轨道电阻与过渡电阻由于其阻值变化范围相差很多,分别采用两种双向电流可变电阻模块进行模拟。其中,双向电流轨道电阻模块(Bidirectional Current Railway Longitudinal Resistance Module, BCRLRM)和双向电流轨道对地过渡电阻模块(Bidirectional Current Railway to Ground Resistance Module, BCRGRM)是实现轨道电位动态模拟的关键。
2.1 双向电流轨道电阻模块
图8 为双向电流轨道纵向电阻BCRLRM 拓扑,其中BCRLRM 由一个电源Udc、一个开关管S、一个滤波电感L、一个滤波电容C、两个电阻R1 和R2以及5 个二极管VD1~VD5 组成。采用整流桥的形式实现外部电流双向功能,通过控制开关管S 占空比d 改变子模块等效电阻。
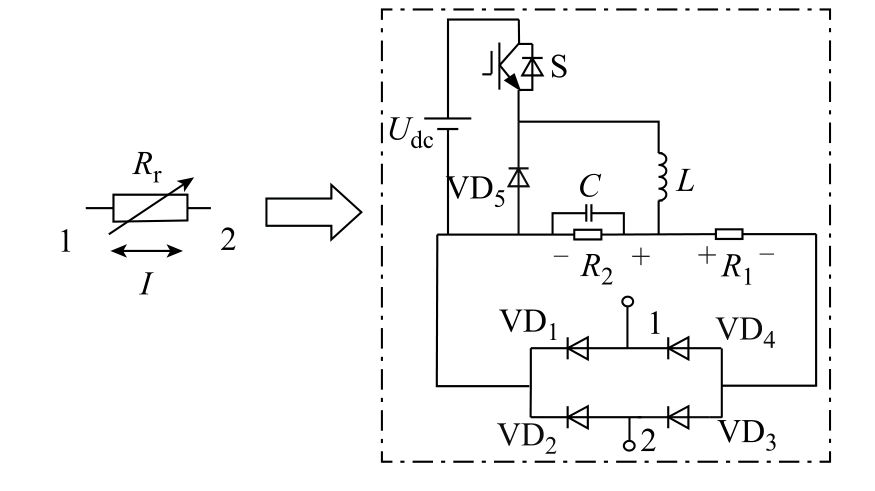
图8 双向电流可变轨道电阻模块
Fig.8 Bidirectional current variable rail resistance module
图9 为BCRLRM 电流方向不同电路开关模态。
1)当列车电流从1 流入2 流出,S 导通时,二极管VD1、VD3 导通,VD2、VD4、VD5 截止,电感开始储能,电流增加;S 关断时,二极管VD1、VD3、VD5 导通,VD2、VD4 截止,电感释放能量,电流减小。
2)当列车电流反向时,通过整流桥实现内部电流方向不变,工作原理同上。

图9 BCRLRM 开关模态
Fig.9 Swich modes of BCRLRM
R2 两端电压为dUdc,R1 两端电压为IR1,子模块等效电阻RBCRLRM 为
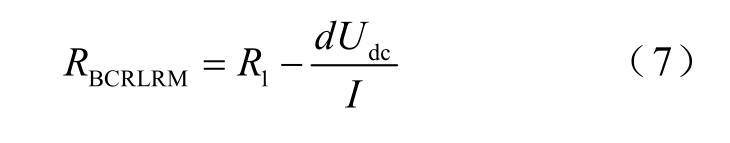
通过控制BCRLRM 占空比可以实现目标电阻值的正确跟踪,图10 给出了等效电阻与占空比曲线。当R1 和Udc 取不同值时BCRLRM 可实现不同范围的等效电阻。
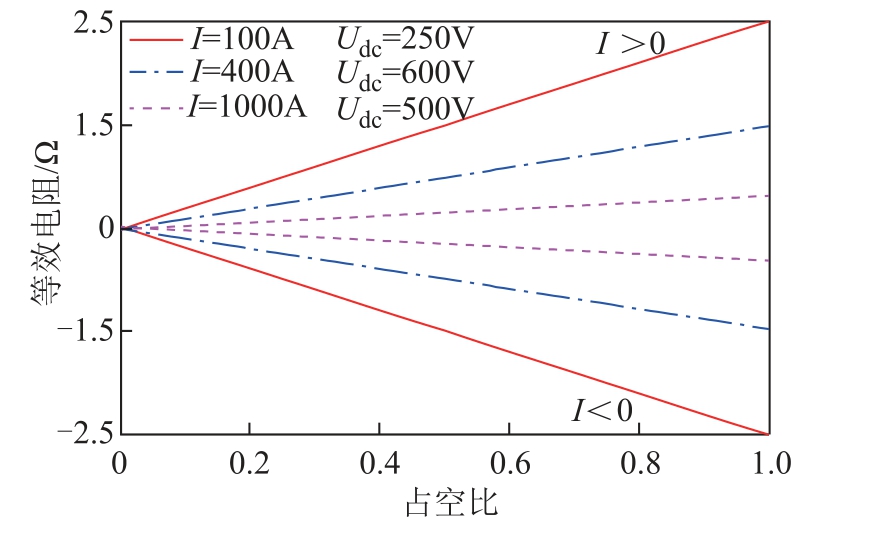
图10 等效轨道电阻与占空比
Fig.10 Equivalent rail resistance varies with duty cycle
2.2 双向电流轨道对地电阻模块
图11 为双向电流轨道纵向电阻BCRGRM 拓扑,其中BCRGRM 由两个开关管S1 和S2、一个滤波电感L、一个滤波电容C、两个大小相等的电阻Rmax1 和Rmax2 以及1 个二极管VD 组成。通过控制开关管S1、S2 占空比改变BCRGRM 的等效电阻。
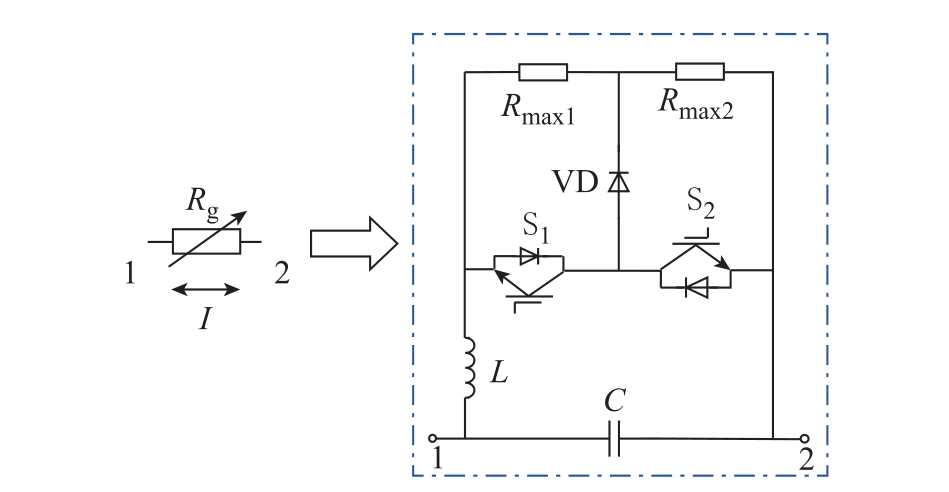
图11 双向电流轨道对地过渡电阻模块
Fig.11 Bidirectional current variable rail to ground resistance module
图12 为电流方向不同时BCRGRM 开关模态。
(1)当杂散电流从1 流入2 流出,S1 导通,S2导通时,电感开始储能电流增加;S1 导通,S2 关断时,电感释放能量电流减小。
(2)当杂散电流反向时,通过反串联开关管实现电流的双向流通,工作原理同上。
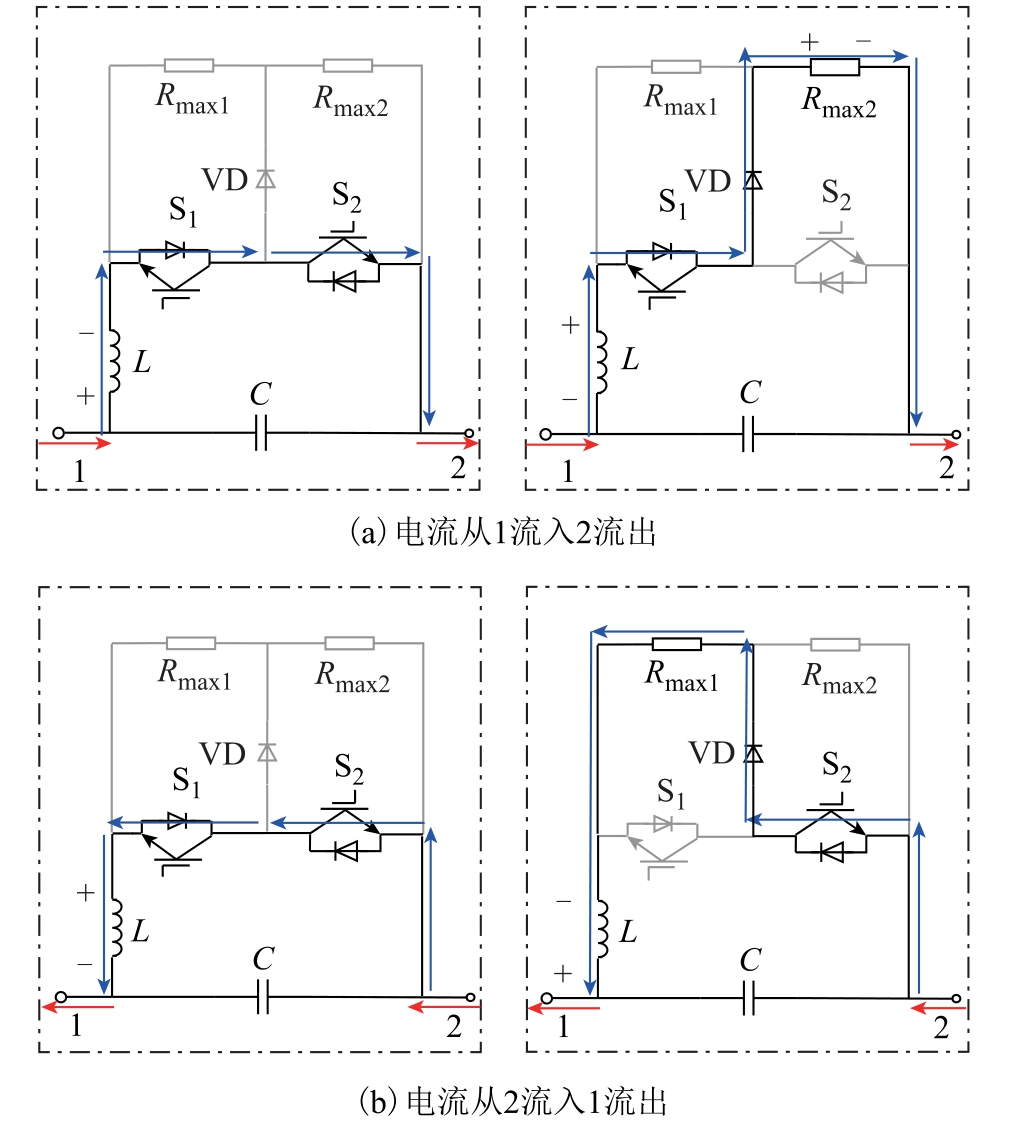
图12 BCRGRM 开关模态
Fig.12 Swich modes of BCRGRM
子模块等效电阻RBCRGRM 为
通过控制BCRGRM 占空比可以实现目标电阻的跟踪,图13 给出了等效过渡电阻与占空比曲线。当Rmax 取不同值时BCRGRM 可实现不同范围的等效电阻。
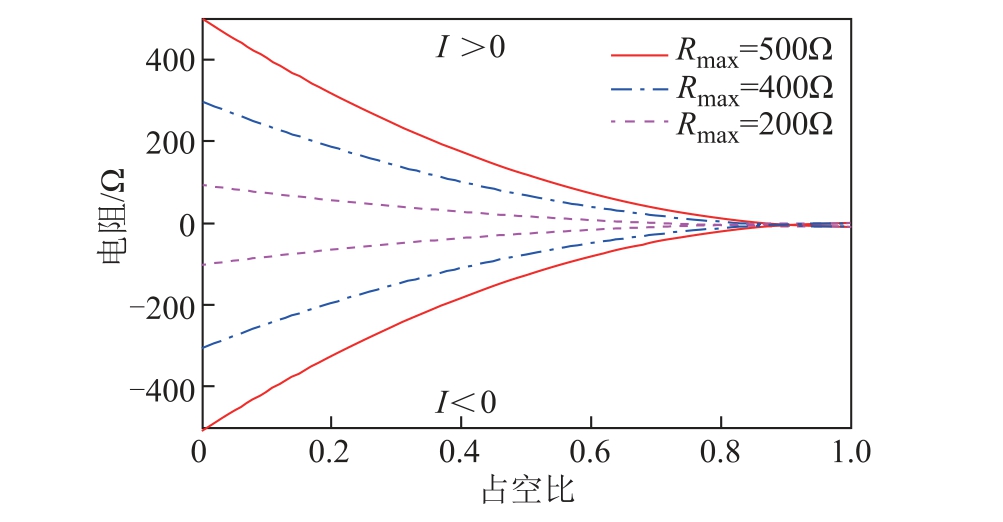
图13 等效过渡电阻与占空比曲线
Fig.13 Equivalent rail to earth resistance varies with duty cycle
2.3 轨道电位与杂散电流动模实验系统控制策略
如图14 所示,MGDE 控制由两部分组成:①根据系统接地方式、列车电流曲线和列车运行位置曲线计算区间内轨道纵向电阻参考电压和轨道对地过渡电阻参考电流;②根据①计算出各个可变电阻模块的参考电压或参考电流,与反馈信号经过闭环比例积分器(Proportional Integrator, PI)产生控制子模块占空比调制波信号,经过正弦脉宽调制(Sinusoidal Pulse Width Modulation, SPWM)得到4 路可变轨道电阻模块驱动信号 PWMBCRLRMk(其中k=1,2,3,4)和2 路可变轨道对地电阻模块驱动信号PWMBCRGRMj(其中j=1,2)。
3 仿真与实验
基于Matlab/Simulink 搭建了多接地实验平台MGDE 仿真模型,对双向电流轨道电阻和双向电流轨道对地电阻的工作原理与控制策略进行了仿真验证。牵引供电系统参数选择根据CJJ 49—1992《地铁杂散电流腐蚀防护技术规程》中地铁回流系统参数要求,地铁轨道对地过渡电阻新建线路不能小于15Ω·km,轨道采用60kg/m 钢材,单位距离轨道电阻0.026Ω/km,供电区间一般在1~3km,列车牵引电流1 000~3 000A。下面给出仿真中直流牵引供电系统电气参数:L=3km,Rr=0.04Ω/km,Rm=0.02Ω/km,Rrm=100Ω·km,I=2 000A。
3.1 悬浮接地系统仿真
采用悬浮接地的MGDE 系统结构如图6 所示,系统悬浮接地列车匀速工况下从牵引所1 到牵引所2,列车位置处的轨道电位与杂散电流曲线仿真和数学推导结果如图15 所示。
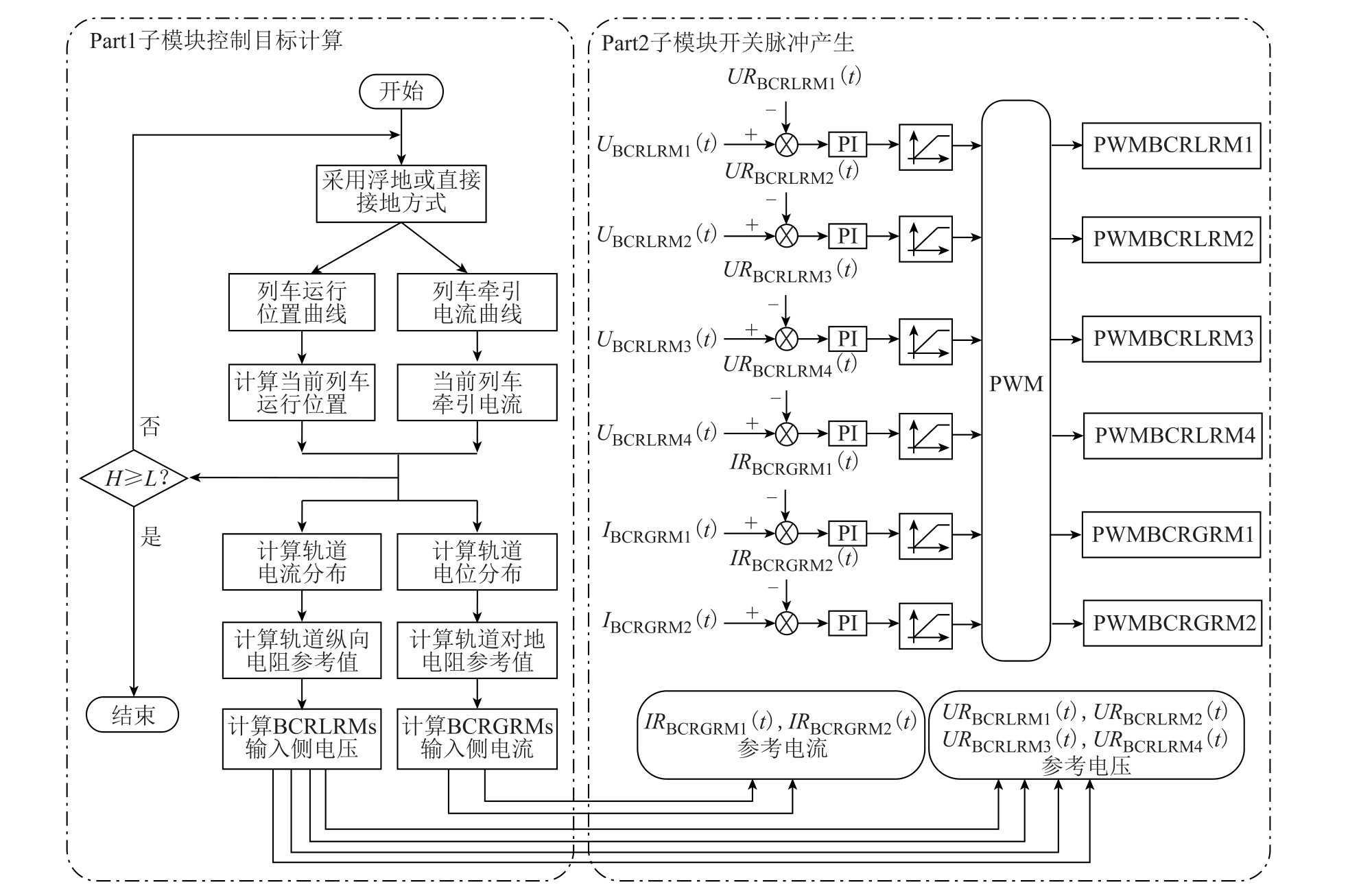
图14 多接地系统可变电阻控制框图
Fig.14 Multi-grounded system variable resistance dynamic control diagram

图15 悬浮接地轨道电位与杂散电流
Fig.15 Floating grounded rail potential and stray current
3.2 直接接地系统仿真
采用直接接地方式的MGDE 系统结构如图7 所示,列车单一匀速工况下从牵引所1 到牵引所2 列车位置处的轨道电位与杂散电流曲线仿真和数学模型对比如图16 所示。

图16 直接接地轨道电位与杂散电流
Fig.16 Solidly grounded rail potential and stray current
图15a、图15b 与图16a、图16b 分别为系统悬浮接地、直接接地时,列车从牵引所1 匀速运动至牵引所2 列车位置轨道电位与总杂散电流。通过列车位置轨道电位最大值、总杂散电流对比可知,系统轨道电位最大值在直接接地时是悬浮接地时的2 倍,是最大杂散电流的4 倍,这与1.2 节的理论分析一致。
图15c、图15d 与图16c、图16d 分别为系统悬浮接地、直接接地时,列车运动时沿线路轨道电位分布。对比分析可知,由于牵引所直接接地将线路轨道电位最低点钳位为0,此时牵引所之间轨道电位均大于零,且在两侧牵引所位置杂散电流最大。对比分析可知,目前广泛采用的悬浮接地能够有效降低最大轨道电位与牵引所位置杂散电流。
3.3 双向电流轨道电阻模块实验
通过双向电流可变轨道电阻模块、固定轨道对地过渡电阻与列车电流源搭建了小容量的实验平台,模拟了列车从牵引所1 匀速运动至牵引所2 的列车位置轨道电位曲线,验证了轨道电位与杂散电流动模实验平台的可行性,表2 为实验参数。
表2 实验参数与线路参数
Fig.2 The parameter of experiment and metro line

参 数 数 值双向可变电阻模块电阻R1,R2/Ω 6电容C/μF 10电感L/mH 1电压源Udc/V 60线路对地过渡电阻Rrm/(Ω·km) 5000线路长度L/km 3轨道纵向电阻Rr/(Ω/km) 2牵引所电压Utps/V 50
图17 为双向电流可变轨道电阻模块在外部电流I 分别为2A、4A 时的实验结果。从实验结果可以看出通过电压的闭环控制实现了等效电阻0~6Ω的可调。
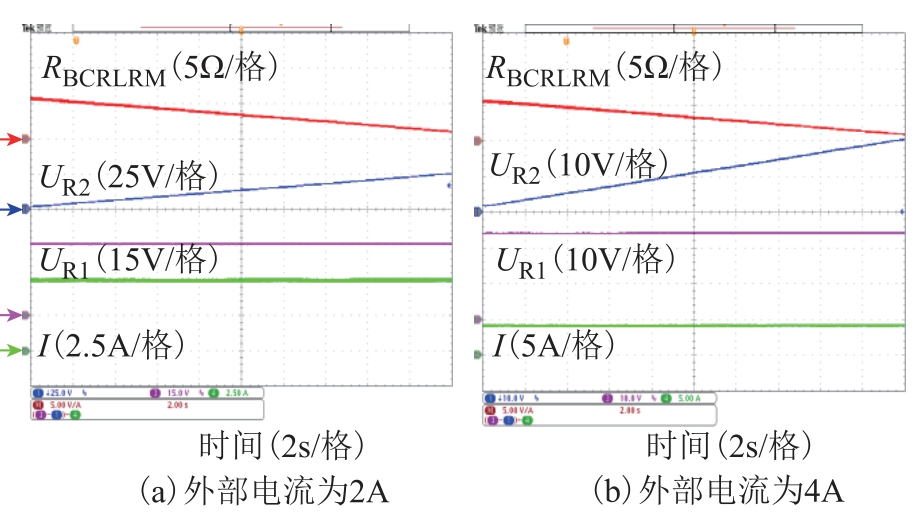
图17 双向电流可变轨道电阻模块实验结果
Fig.17 Bidirectional current variable rail resistance module experiment result
图18 为双边供电系统在两种不同接地方式下的列车位置轨道电位实验曲线。从列车位置轨道电位曲线可以看出,系统直接接地列车最大轨道电位为6V,系统悬浮接地时列车最大轨道电位为3V,这与前面的理论以及实验结果相符合。

图18 系统不同接地方式下列车位置轨道电位实验结果
Fig.18 The rail potential of the moving train Under different grounding schematic experiment result
4 结论
本文研究了双边供电系统在悬浮接地与直接接地两种方式下,轨道电位与杂散电流的分布规律与列车位置的关系。并在理论研究的基础上,提出了一种多接地方式切换的轨道电位与杂散电流的动模实验平台。通过理论分析、仿真结果与实验验证,得到以下结论:
1)根据多接地系统的轨道电位与杂散电流的三维模型,对列车位置做截面,得到列车运动任意位置处,两牵引所之间的轨道电位与杂散电流分布;对两牵引所之间任意一点做截面,能得到这一点随着列车位置变化的轨道电位与杂散电流分布。因此上述三维模型能够用于轨道电位和杂散电流的预测与分析。
2)两种双向电流可变电阻模块 BCRLRM 和BCRGRM 根据列车位置控制占空比分别模拟列车运动过程左右两侧轨道电阻以及轨道对地电阻的变化,并能适应列车不同工况下的轨道电位与杂散电流模拟。
3)多接地轨道电位与杂散电流动模实验平台MGDE 根据列车运行过程中轨道以及轨道对地过渡电阻分布式参数模型,提出了两种双向电流可变电阻模块模拟变化的电阻,并结合系统不同接地方式特点,实现了列车运动过程中对列车和牵引所处的轨道电位与杂散电流的动态模拟。采用集中式的可变电阻代替了分布式的轨道和过渡电阻,使系统具有结构简单、准确性高、可操作性强的优点。
附 录
附表1 推导所用符号单位及物理意义
App.Tab.1 Derive symbolic units and physical meanings

符号 单位 物理意义Rr Ω/km 轨道纵向电阻Rm Ω/km 排流网纵向电阻Rrm Ω·km 轨道对排流网的过渡电阻Rg Ω·km 轨道对大地的过渡电阻x km 轨道上任意点到变电所1 的距离y km 地铁列车到变电所1 的距离Urm(x) V 轨道与排流网之间在x 处的轨道电位Ir(x) A x 处轨道电流L km 两牵引变电所的最大距离L1 km 列车到牵引变电所1 的距离L2 km 列车到牵引变电所2 的距离I A 地铁列车电流Im A 流过排流网的杂散电流Ir A 流过轨道的电流It-p A 列车位置从左侧回流轨道电流It-r A 列车位置从右侧回流轨道电流URT1 V 悬浮接地轨道电位最大幅值URT2 V 直接接地轨道电位最大幅值
[1] Jamali S, Alamuti M M, Savaghebi M. Effects of different earthing schemes on the stray current in rail transit systems[C]//2008 43rd International Universities Power Engineering Conference, Padova, Italy, 2008: 1-5.
[2] 杜贵府, 张栋梁, 王崇林, 等. 直流牵引供电系统电流跨区间传输对钢轨电位影响[J]. 电工技术学报, 2016, 31(11): 129-139.Du Guifu, Zhang Dongliang, Wang Chonglin, et al.Effect of traction current transmission among power sections on rail potential in DC mass transit system[J].Transactions of China Electrotechnical Society, 2016,31(11): 129-139.
[3] Cotton I, Charalambous C, Aylott P, et al. Stray current control in DC mass transit systems[J]. IEEE Transactions on Vehicular Technology, 2005, 54(2):722-730.
[4] Rodríguez J V, Feito J S. Calculation of remote effects of stray currents on rail voltages in DC railways systems[J]. IET Electrical Systems in Transportation,2013, 3(2): 31-40.
[5] Alamuti M M, Nouri H, Jamali S. Effects of earthing systems on stray current for corrosion and safety behaviour in practical metro systems[J]. IET Electrical Systems in Transportation, 2011, 1(2): 69-79.
[6] Charalambous C A, Aylott P. Dynamic stray current evaluations on cut-and-cover sections of DC metro systems[J]. IEEE Transactions on Vehicular Technology, 2014, 63(8): 3530-3538.
[7] Du Guifu, Wang Chonglin, Liu Jianhua, et al. Effect of over zone feeding on rail potential and stray current in DC mass transit system[J]. Mathematical Problems in Engineering, 2016(2016): 15.
[8] Du Guifu, Zhang Dongliang, Li Guoxin, et al.Maximum safety regenerative power tracking for DC traction power systems[J]. Energies, 2017, 10(2): 244.
[9] Gu Jingda, Yang Xiaofeng, Zheng Trillion Q.Influence factors analysis of rail potential in urban rail transit[J]. Microelectronics Reliability, 2018, 88-90:1300-1304.
[10] 李星, 杨帆, 余晓, 等. 基于内源式电阻抗成像的接地网缺陷诊断逆问题研究[J]. 电工技术学报,2019, 34(5): 902-909.Li Xing, Yang Fan, Yu Xiao, et al. Research on the inverse problem of grounding grid fault diagnosis based on inner source EIT[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 902-909.
[11] Charalambous C A. Comprehensive modeling to allow informed calculation of DC traction systems’stray current levels[J]. IEEE Transactions on Vehicular Technology, 2017, 66(11): 9667-9677.
[12] Charalambous C A, Cotton I, Aylott P. A simulation tool to predict the impact of soil topologies on coupling between a light rail system and buried thirdparty infrastructure[J]. IEEE Transactions on Vehicular Technology, 2008, 57(3): 1404-1416.
[13] 王淼, 杨晓峰, 郑琼林. 谐振开关电容变换器中硬开通问题[J]. 电工技术学报, 2019, 34(增刊1): 154-162.Wang Miao, Yang Xiaofeng, Zheng Trillion Q. The hard turning-on problems of resonant switched capacitor converter[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 154-162.
[14] Ibrahem A, Elrayyah A, Sozer Y, et al. DC railway system emulator for stray current and touch voltage prediction[J]. IEEE Transactions on Industry Applications, 2017, 53(1): 439-446.
[15] Yang Xiaofeng, Xue Hao, Wang Huikang, et al. Stray current and rail potential simulation system for urban rail transit[C]//2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 2018: 1-6.
[16] Xu Shaoyi, Li Wei, Wang Yuqiao. Effects of vehicle running mode on rail potential and stray current in DC mass transit systems[J]. IEEE Transactions on Vehicular Technology, 2013, 62(8): 3569-3580.
[17] 杨晓峰, 薛皓, 郑琼林. 基于双向可变电阻模块的杂散电流与轨道电位动态模拟系统[J]. 电工技术学报, 2019, 34(13): 2793-2805.Yang Xiaofeng, Xue Hao, Zheng Trillion Q. Stray current and rail potential dynamic simulation system based on bidirectional variable resistance module[J].Transactions of China Electrotechnical Society, 2019,34(13): 2793-2805.
[18] Ogunsola A, Sandrolini L, Mariscotti A. Evaluation of stray current from a DC-electrified railway with integrated electric-electromechanical modeling and traffic simulation[J]. IEEE Transactions on Industry Applications, 2015, 51(6): 5431-5441.
[19] Charalambous C A, Aylott P, Buxton D. Stray current calculation and monitoring in DC mass-transit systems:interpreting calculations for real-life conditions and determining appropriate safety margins[J]. IEEE Vehicular Technology Magazine, 2016, 11(2): 24-31.