0 引言
轨道加速器中,两根轨道中变化的电流将引起电流密度分布不均匀。如果只考虑电流波形对导体内部电流分布的影响,在瞬态电流上升段,轨道中电流将趋向于表面流动;在平顶段,轨道中电流将从表面向内扩散;在瞬态电流下降段,轨道中电流将趋向于内部中心流动。可见,整个加速过程中轨道内的电流密度分布是不均匀的,较大的电流密度将引起较大的欧姆损耗,进而使加速器轨道局部温度过高[1-6]。
加速器轨道局部温升过高是产生烧蚀的主要原因之一。温度过高会导致铜材轨道发生结构强度减小、热变形等变化,其与高速相对运动枢轨之间的摩擦和振动,共同构成了烧蚀现象的主要原因。在连续多次加速时,热累积效应会更明显,这时需要考虑对轨道进行冷却,以带走不能及时散去的热量,保证加速器连续工作的稳定性[7]。
J. F. Kerrisk 在二维模型下应用有限差分的数值方法计算了枢轨热量及温度分布,他是最早研究轨道加速器热量及温度的学者之一[8]。D. E. Johnson 等利用简化的一维Kerrisk 模型对轨道炮的电流分布和温度进行了数值计算[9]。J. C. Nearing 和M. A. Huerta运用绝热法,提出了计算电流产生的电枢表面热效应的方法[10]。K. T. Hsieh 应用EMAP3D 对耦合场下电枢表面的温度进行了有限元计算,发现铝电枢表面的最高温度小于铝材料的熔点[11]。金龙文等提出了热源及温升的计算方法,利用Ansys 施加热密度仿真后,发现电枢表面温度最大值为1 400℃[12]。李强等应用简化的枢轨模型计算并分析了单次加速焦尔热对枢轨表面温升的影响[13]。李小将等利用Ansys Workbench 仿真软件对三种典型截面轨道的温度场与热应力进行了数值仿真[14]。李鹤等对焦耳热和摩擦热瞬态温度场进行了有限元仿真建模和求解,发现摩擦热对电枢热性能的影响较小[15]。
上述文献只对轨道和电枢的热或应力进行了分析计算,未对连续工作的轨道加速器进行冷却分析。本文结合轨道加速器动态加速的特点,采用电磁-流场耦合编程的方法,实现了轨道加速器连续工作时流体冷却的仿真计算,该研究对轨道加速器的热管理具有一定的指导意义。
1 电磁-流体耦合场分析方法和问题
1.1 多物理场耦合介绍
在有限元分析中,多物理场的耦合方式分为两种。一种是耦合分析自始至终使用同一种单元,此单元包括仿真计算的所有自由度,称为直接耦合。实际应用时,尤其是在特殊领域,一种单元的自由度难以包括所有相关量,造成了此方法应用的局限性;另一种方式称为间接耦合,即将一个单元的计算结果作为另一个单元的载荷进行加载计算,此方式有时会造成程序运行的不稳定,例如单元损坏等[16]。
对于电磁场-流场的耦合仿真,目前尚无可以进行直接耦合的单元类型。因此,采用间接耦合的方法,将电磁场有限元仿真结果加载到流场中进行温升的计算,并采取映射网格划分方法,减少流体计算时单元的损坏数量。仿真时,忽略了以下因素:①温升对导体电阻率的影响;②电枢运动对电磁场的影响;③流体的相变;④小数量单元的损坏[17-18]。
1.2 电磁-流体耦合场分析流程
本耦合场仿真程序分为三个子程序,所涉及有限元计算单元有:电磁场仿真子程序PLANE13 和SOLID97;流场、温度场仿真子程序FLUID142。耦合场分析总体流程如图1 所示。
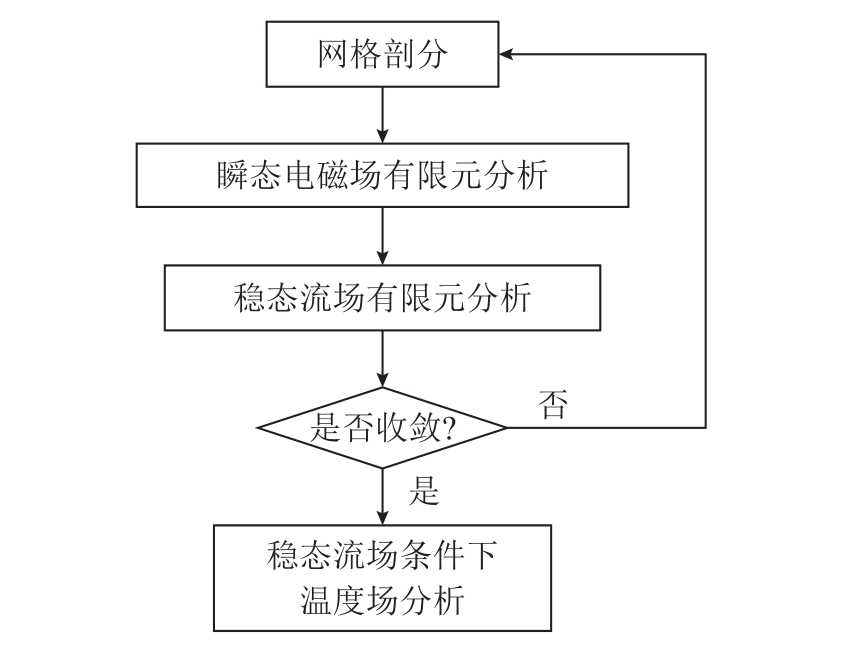
图1 耦合场分析总体流程
Fig.1 Overall flow chart of coupled field analysis
为了得到精确的结果,本程序使用了映射网格划分,实现了由平面单元 PLANE13 向立体单元SOLID97 的转换,在实体棱边上,映射网格剖分能更好地保持网格特性的稳定[19-20]。
流场分析时,输入初始参数和迭代步数后,进行稳态求解。当变量(主要包括水流速和水压)的监测值都小于收敛值并停止增加,说明求解结果是收敛的,否则可多次运行求解程序或者重新剖分网格,直至收敛结束。流场仿真迭代收敛过程如图2所示,一般认为,当各变量的变化率降到1%以下,视为收敛。
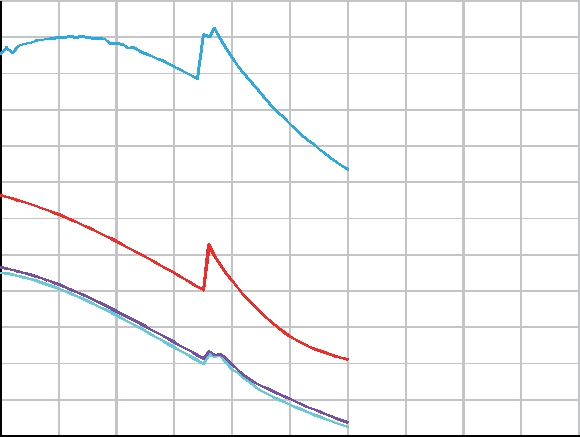
图2 流场仿真迭代收敛过程
Fig.2 Iterative convergence process of flow field simulation
1.3 存在的问题及解决方法
电磁-流场耦合分析中,需要对两个问题进行处理。
1.3.1 电枢运动效果的处理
实际上,每次加速后电枢是不留在管道内的,然而仿真时电枢是静止的,多次加速后电枢温度会严重影响轨道的温度。因此,在将电磁计算结果加载到流场时,应适时舍弃电枢焦耳热的加载,电枢运动效果处理方法如图3 所示,流场第二次循环求解时将舍弃电枢焦耳热。此外,根据电磁场计算结果得到电枢的运动轨迹,热加载时,只针对电枢走过的单元加载焦耳热,对没有走过的单元施加零热源。
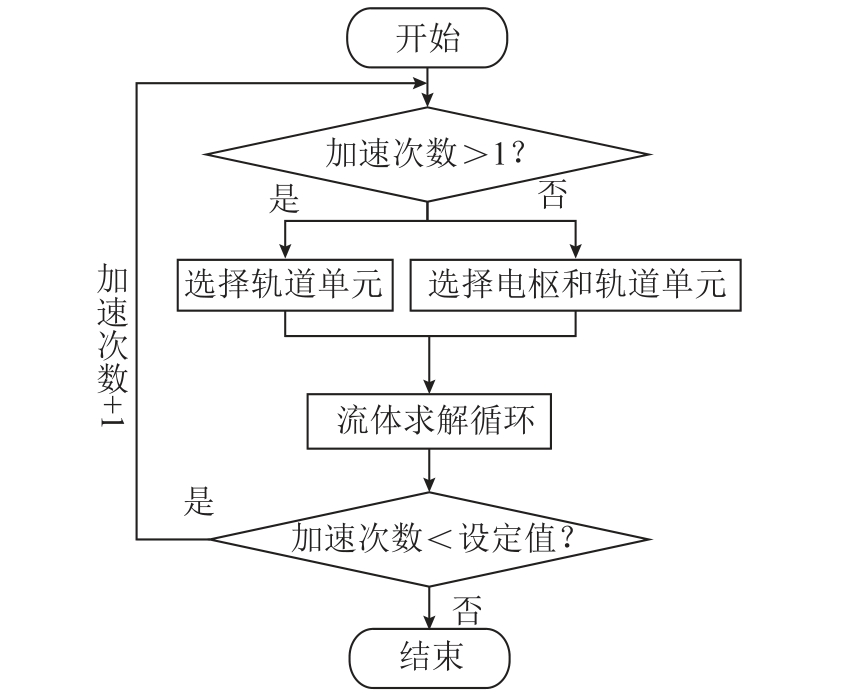
图3 电枢运动效果处理方法
Fig.3 Treatment method of armature movement effect
1.3.2 时间步的选择
轨道加速器的单次加速时间为数毫秒,加速频次以6 次/min 计算,间歇时间约为10s。应为不同的计算阶段设置不同的计算步长,加速阶段时间步长较短,冷却(间歇)阶段时间步长较大,热源加载时间步长小于电磁仿真时间步长N 时,流场仿真结果更精确。流体求解流程如图4 所示。
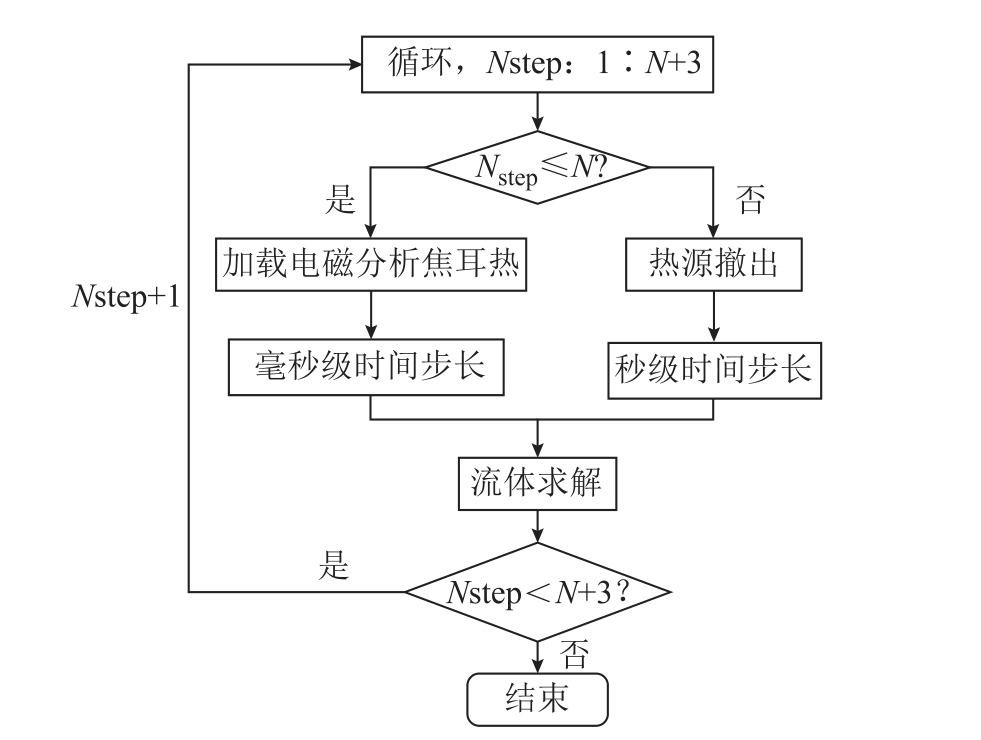
图4 流体求解流程
Fig.4 Flow chart of fluid solution
2 自然冷却工况仿真及分析
2.1 加速工况
以公开文献中轨道加速器的设计为参考,为仿真程序设计了一种加速工况。加速器口径为方形40mm×30mm,加速长度5m,电枢质量0.35kg。加载的激励电流波形如图5 所示,电流幅值1 160kA,电流持续时间3.5ms。冷却介质为恒温源,环境温度为25℃。加速频次为6 次/min[21]。

图5 激励电流波形
Fig.5 Waveform of exciting current
2.2 电流密度分布
由于轨道间需要绝缘支撑体来固定间距,故在轨道内侧边缘留有绝缘支撑台阶。电流在两根轨道内呈相反方向流动时,实际上可以将轨道、电枢和馈电回路看作是一个闭合回路,瞬态电流在此闭合回路中表现出临近效应和趋肤效应[22]。
电流上升沿,电流趋于轨道内侧,表现为临近效应,同时单个轨道内,电流趋于边缘流动,表现为趋肤效应,二者共同作用的结果如图6a 所示。电流下降沿,电流应趋于轨道外侧边沿流动,然而瞬态电流密度分布是渐变的,由于时间较短,呈现出如图6b 所示逐渐扩散的态势。

图6 电流密度分布
Fig.6 Current density distribution
较高的电流密度通过轨道电阻发热引起较高的温升,而较高的温升又会引起本部位电阻率有较快的增长,从而导致电流密度较快地下降。因此,电流密度与温度之间是互相影响的,是一种加强型的耦合。
最终,电流密度分布不均匀会导致轨道局部温度过高,尤其是连续工作时,会影响轨道的力学性能甚至导致试验失败。
2.3 自然冷却条件下温升状况
在自然冷却条件下,通道为空气,流动速度为0。仿真得到单次和连续18 次加速的轨道温升结果,如图7 所示。加速1 次,轨道最高温度为194.3℃,位于轨道尾部内侧边缘,此处承载电流时间最长。加速18 次后,轨道最高温度为1 226.0℃,此温度已超过金属铜的熔点1 080℃。

图7 自然冷却条件下轨道温升分布
Fig.7 Distribution of temperature rise of the rails under natural cooling condition
图8 给出了连续加速18 次轨道最高温度的变化。在自然冷却条件下,轨道最高温度不断攀升。单次加速,经过周期10s 的自然散热后,温度降到92.6℃;5 次连续工作后,轨道最高温度已超过铜的软化温度400℃;每个加速冷却周期中,前5s 时间内,最高温度下降最快,后5s 内,温度下降不明显,这可以为加速频次的设定提供依据。
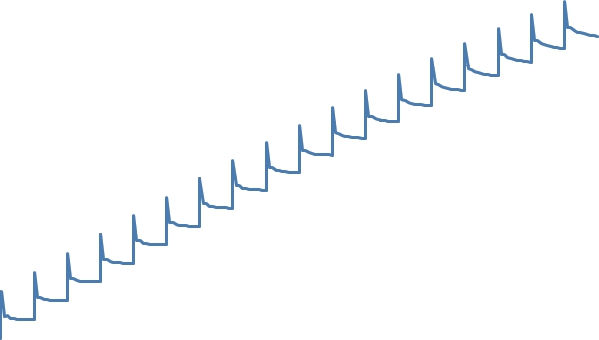
图8 连续加速18 次轨道最高温度变化曲线
Fig.8 Maximum temperature curve of the rails in 18 consecutive accelerations
3 单次加速水冷仿真及分析
3.1 单次水冷仿真及分析
单次加速仿真时,对水流参数进行了如下设置:孔径为5mm,数量为3,密度为1 000kg/m3,导热系数为0.63W/m/℃,比热容为4 200J/kg/℃,流速为1m/s,水初温为25℃,环境温度为25℃。
单次加速水冷效果如图9 所示,经过单次加速和10s 水流冷却后,轨道最高温度降到80.6℃,水流的最高温度为80.4℃。冷却水的温升特点是,温度最高值沿轨道方向呈梯次分布并逐渐减小,轨道尾部出现最低温度区域。可见,水流逐渐将热量从轨道尾部向电枢运动方向驱散。

图9 单次加速水冷效果图
Fig.9 Water cooling effect after single acceleration
由于水流温度变化会直接影响冷却方式是否可行,故需要分析各个时间点的水流温度,单次加速过程水流最高温度变化如图10 所示。在单次加速过程中,水流的最高温度为134.8℃,超过沸点100℃的时间大于1s。对比单次加速自然冷却与水冷的效果,轨道最高温度从92.6℃降到了80.6℃,效果并不明显。

图10 单次加速过程水流最高温度变化
Fig.10 Variation of maximum flow temperature during acceleration
因此,有必要改变冷却介质参数,分析各参数对轨道冷却效果的敏感度,为冷却介质的选择提供方向。
3.2 冷却水参数的敏感度分析
以轨道的最高温度降幅为目标量,以冷却水的导热系数、比热容、流速和水初温为变量,变化幅度为±20%,进行敏感度分析,仿真计算结果见表1和表2。
表1 流体参数敏感度计算(+20%)
Tab.1 Sensitivity calculation of fluid parameters(+20%)
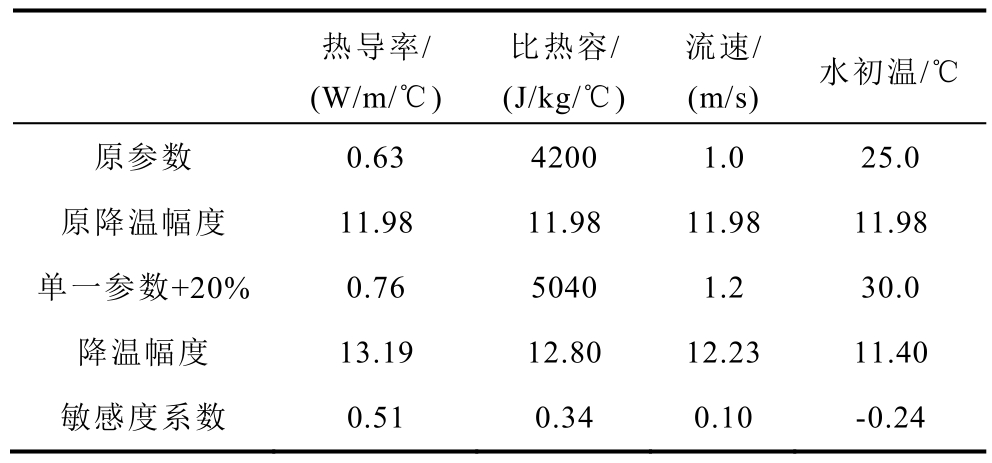
热导率/(W/m/℃)比热容/(J/kg/℃)流速/(m/s) 水初温/℃原参数 0.63 4200 1.0 25.0原降温幅度 11.98 11.98 11.98 11.98单一参数+20% 0.76 5040 1.2 30.0降温幅度 13.19 12.80 12.23 11.40敏感度系数 0.51 0.34 0.10 -0.24
表2 流体参数敏感度计算(-20%)
Tab.2 Sensitivity calculation of fluid parameters(-20%)
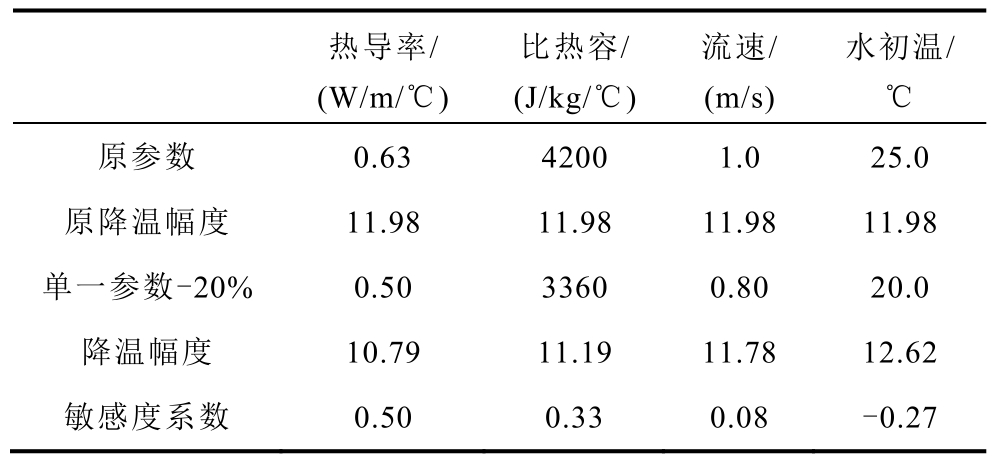
热导率/(W/m/℃)比热容/(J/kg/℃)流速/(m/s)水初温/℃原参数 0.63 4200 1.0 25.0原降温幅度 11.98 11.98 11.98 11.98单一参数-20% 0.50 3360 0.80 20.0降温幅度 10.79 11.19 11.78 12.62敏感度系数 0.50 0.33 0.08 -0.27
由表1、表2 敏感度数据可以看出,对轨道温度降幅作用的敏感程度顺序为:热导率系数>比热容>水初温>流速,其中水初温为负敏感。
水具有较高的热导率和比热容,是比较理想的冷却母液。向水中添加乙二醇等有机溶剂可以降低水溶液的冰点、提高沸点,且对水的热导率和比热容影响较小,最终可以较好地增强冷却效果。当水溶液中乙二醇的体积百分数为50%时,介质冰点为-37℃,沸点为140℃,热导率为0.42W/m/℃,定压比热容为3 650J/kg/℃。
4 多次加速冷却仿真及分析
4.1 多次加速冷却效果分析
采用上述乙二醇水溶液作为冷却介质,经多组仿真对比,当介质流速达到1.5m/s、介质初温为-15℃时,可达到预期冷却效果。在18 次加速过程中,轨道温度最高时的分布情况如图11 所示,冷却液将轨道尾部较集中的热量向前方“推送”,整个轨道的最高温度为308.7℃,分布在小于铜材料的软化温度400℃。

图11 18 次加速过程中轨道温度最高时的温度分布
Fig.11 Temperature distribution of rails after multiple accelerations
通过提取每次加速过程中轨道的最高温度值,来观察乙二醇水溶液的冷却效果,18 次加速过程中轨道和冷却液的最高温度变化趋势如图12 和图13所示。

图12 18 次加速过程中轨道最高温度变化趋势
Fig.12 Variation trend of maximum temperature of rails in multiple accelerations

图13 18 次加速过程中冷却液最高温度变化趋势
Fig.13 Variation trend of maximum temperature of flow in multiple accelerations
由图12 和图13 可以看出,在7 次加速之后,轨道和冷却液的最高温度基本不再上升。轨道最高温度在 230.8~308.7℃之间振荡,最高温度为308.7℃;冷却液的最高温度在230.1~291.0℃之间振荡,最高温度为291.0℃。可以认为,7 次加速之后冷却液吸热与轨道发热达到一个平衡状态。
4.2 冷却液仿真存在的问题
轨道长度方向上冷却液温度分布如图14 所示,距离轨道尾部将近1m 范围内的冷却液,其温度在其沸点140℃以下;距离尾部1m 之外,冷却液的最高温度已达291℃。

图14 多次加速后冷却液温度分布
Fig.14 Temperature distribution of flow after multiple accelerations
图15 给出了距离轨道尾部1.9m 处的冷却液温度分布截面图。可以看出,冷却液的最高温度仅出现在与轨道的接触面上,其中心温度较低,即使接触面上的液体发生汽化,遇见低温冷却液,也会重新液化。
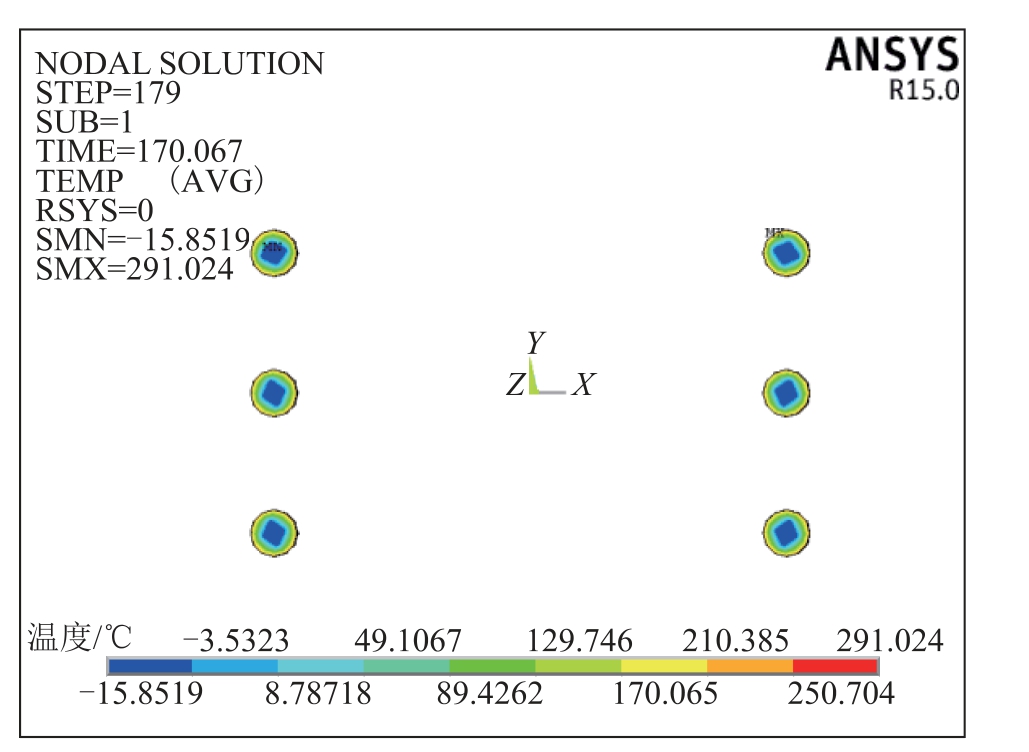
图15 距离轨道尾部1.9m 处冷却液温度分布截面图
Fig.15 Cross-section diagram of flow temperature distribution 1.9m distance from the tail of rails
5 结论
1)研究了电磁-流场耦合仿真分析方法,解决了电枢运动情况下轨道热源的加载、时间步长的差异等关键问题,给出了针对轨道加速器的电磁-流场耦合仿真流程,编制了仿真程序。
2)利用仿真程序加载幅值1 160kA、持续时间为3.5ms 的瞬态电流,进行频次为6 次/min 的加速仿真。由于瞬态电流的趋肤效应和邻近效应的共同作用,轨道的电流密度呈现不均匀分布,整体上表现为轨道尾部内侧边缘温升比较高。
3)在无水冷的情况下,加速1 次,轨道最高温度为194.0℃,5 次连续加速后,轨道最高温度已超过铜的软化温度400℃,15 次连续加速后,轨道最高温度已超过金属铜的熔点1 080℃。
4)在单次加速水冷工况下,对冷却水各个参数的敏感度进行了对比分析。结果表明,水各参数对轨道温度降低的作用敏感度顺序为:热导率>比热容>初始温度>流速,其中水流初始温度为反向敏感。
5)选取50%体积浓度的乙二醇水溶液作为冷却液,在7 次加速之后,冷却液与轨道最高温度基本不再上升,轨道最高温度为308.7℃,未超过铜材料的软化温度。仿真程序对于冷却液发生的相变尚不能进行仿真,后续工作中将进一步对该问题进行研究。
[1] 杨玉东, 王建新, 薛文. 轨道炮速度趋肤效应的分析与仿真[J]. 强激光与粒子束, 2011, 23(7): 1965-1967.Yang Yudong, Wang Jianxin, Xue Wen. Simulation and analysis of velocity skin effect of railgun[J]. High Power Laser and Particle Beams, 2011, 23(7): 1965-1967.
[2] 袁建生, 李军, 左鹏, 等. 不同截面形状轨道的电磁炮电流分布特性研究[C]//2011 中国电工技术学会学术年会论文集, 贵阳, 2011: 65-71.Yuan Jiansheng, Li Jun, Zuo Peng, et al. Study on the current distribution characteristics of electromagnetic gun with different cross-section of rails[C]//2011 Proceedings of the China Electrotechnical Society:Guiyang, 2011: 65-71.
[3] 刘旭堃, 于歆杰, 刘秀成, 等. 电磁轨道炮运行阶段系统发射效率和电枢出膛动能研究[J]. 电工技术学报, 2017, 32(3): 210-217.Liu Xukun, Yu Xinjie, Liu Xiucheng, et al. Researches on the system launch efficiency and the armature muzzle kinetic energy of a constructed electromagnetic railgun[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 210-217.
[4] Bayati M S, Keshtkar A. Novel study of the rail’s geometry in the electromagnetic launcher[J]. IEEE Transactions on Plasma Science, 2015, 43(5): 1652 -1656.
[5] Tan Sai, Lu Junyong, Li Bai, et al. A new finiteelement method to deal with motion problem of electromagnetic rail launcher[J]. IEEE Transactions on Plasma Science, 2017, 45(7): 1374-1379.
[6] 李军, 严萍, 袁伟群. 电磁轨道炮发射技术的发展与现状[J]. 高电压技术, 2014, 40(4): 1052-1064.Li Jun, Yan Ping, Yuan Weiqun. Electromagnetic gun technology and its development[J]. High Voltage Engineering, 2014, 40(4): 1052-1064.
[7] Trevor W, Francis S. The effect of current and speed on perimeter erosion in recovered armatures[J]. IEEE Transactions on Magnetics, 2005, 41(1): 448-452.
[8] Kerrisk J F. Electrical and thermal modeling of railguns[J]. IEEE Transactions on Magnetics, 1984,20(2): 399-402.
[9] Johnson D E, Bauer D P. The effect of rail resistance on railgun efficiency[J]. IEEE Transactions on Magnetics, 1989, 25(1): 271-276.
[10] Nearing J C, Huerta M A. Skin and heating effets of railgun current[J]. IEEE Transactions on Magnetics,1989, 22(6): 1561-1566.
[11] Hsieh K T. A Lagrangian formlation for mechanically,thermally coupled electromagnetic diffusive processes with moving conductors[J]. IEEE Transactions on Magnetics, 1995, 31(1): 605-609.
[12] 金文龙, 雷彬, 张倩, 等. 电磁轨道炮热生成机理及温度场数值仿真[J]. 火炮发射与控制学报, 2012,24 (4): 9-12.Jin Longwen, Lei Bin, Zhang Qian, et al. Thermal generation mechanism and numerical simulation of temperature field in electromagnetic railgun[J]. Journal of Artillery Launching and Control, 2012, 24(4): 9-12.
[13] 李强, 范长增, 贾元智, 等. 电磁轨道炮导轨和电枢中的焦耳热分析[J]. 弹道学报, 2006, 18(4): 38-40.Li Qiang, Fan Changzeng, Jia Yuanzhi, et al. Analysis of joule heating in rail and armature of electromagnetic railgun[J]. Journal of Ballistics, 2006, 18(4): 38-40.
[14] 李小将, 万敏, 王志恒, 等. 电磁轨道炮温度场与热应力数值仿真[J]. 火力与指挥控制, 2017, 42(2):336-340.Li Xiaojiang, Wan Min, Wang Zhiheng, et al.Numerical simulation of temperature field and thermal stress of electromagnetic railgun[J]. Fire and Command Control, 2017, 42(2): 336-340.
[15] 李鹤, 雷彬, 吕庆敖, 等. 电磁轨道炮电枢接触界面温度场仿真研究[J]. 润滑与密封, 2012, 37(11): 22-26.Li He, Lei Bin, Lü Qingao, et al. Simulation of temperature distribution on contact surface of armature for electromagnetic railgun[J]. Lubrication Engineering, 2012, 37(11): 22-26.
[16] 林庆华, 栗保明. 电磁轨道炮瞬态温度场的数值模拟[J]. 工程热物理学报, 2017, 38(1): 149-154.Lin Qinghua, Li Baoming. Numerical simulation of transient temperature field in the electromagnetic railgun[J]. Journal of Engineering Thermophysics,2017, 38(1): 149-154.
[17] 蒋晓东, 张凤阁, 周党生, 等. 双定子笼障转子无刷双馈发电机冷却空气流变特性数值分析[J].电工技术学报, 2019, 34(3): 466-473.Jiang Xiaodong, Zhang Fengge, Zhou Dangsheng, et al. Numerical analysis of cooling air flow characteristic for double stator cage-barrier rotor brushless doubly-fed generator[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 466-473.
[18] 田振国, 安雪云. 复合型电磁轨道的多物理场耦合分析[J]. 火炮发射与控制学报, 2017, 38(3): 1-5.Tian Zhenguo, An Xueyun. Multi-physical field coupling analysis of composite electromagnetic rails[J]. Journal of Artillery Launching and Control,2017, 38(3): 1-5.
[19] 王小飞, 代颖, 罗建. 基于流固耦合的车用永磁同步电机水道设计与温度场分析[J].电工技术学报,2019, 34(增刊1): 22-29.Wang Xiaofei, Dai Ying, Luo Jian. Waterway design and temperature field analysis of vehicle permanent magnet synchronous motor based on fluid-solid coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 22-29.
[20] 吴柏禧, 万珍平, 张昆, 等. 考虑温度场和流场的永磁同步电机折返型冷却水道设计[J]. 电工技术学报, 2019, 34(11): 2306-2313.Wu Boxi, Wan Zhenping, Zhang Kun, et al. Design of reentrant cooling channel in permanent magnet synchronous motor considering temperature field and flow field[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2306-2313.
[21] 常馨月, 于歆杰, 刘旭堃. 一种实现电枢出膛速度控制的电磁轨道炮脉冲电源触发策略[J]. 电工技术学报, 2018, 33(10): 2261-2266.Chang Xinyue, Yu Xinjie, Liu Xukun. A velocitycontrolling triggering strategy of capacitive pulsed power supply electromagnetic railgun system[J].Transactions of China Electrotechnical Society, 2018,33(10): 2261-2266.
[22] 邢彦昌, 吕庆敖, 陈建伟, 等. 轨道炮不同激励电流下的发射特性对比分析[J]. 火力与指挥控制,2019, 44(11): 58-60.Xing Yanchang, Lü Qingao, Chen Jianwei, et al.Comparative analysis of launching characteristic for railgun with different excitation current[J]. Fire Control & Command Control, 2019, 44(11): 58-60.