0 引言
传输线广泛应用于各类电气系统及电子设备中,随着电磁环境复杂性的提升,电气系统及电子设备的电磁兼容问题也越来越严重。传输线辐射敏感度作为电磁兼容中的一类重要问题也越来越受到研究人员的重视。在确定性条件下,文献[1]得出了双导体传输线在入射场影响下的传输线方程的解;随后文献[2-3]将双导体传输线扩展到多导体传输线,并得到多导体传输线在入射场激励下的频域响应。
然而在实际情况中,由于电气设备自身位置的改变或辐射源位置的改变,使入射场的相关参数(如仰角θ、方位角ψ 、偏振角η 以及电平幅值E0)表现出不确定性,因此对于入射场激励所产生的多导体传输线辐射敏感度的不确定性问题展开研究是十分必要的。文献[4]采用统计方法对不同几何参数以及不同负载的多导体传输线在随机平面波激励情况下的统计特性进行了分析研究。文献[5]在横电磁波室中对均匀及非均匀传输线的辐射敏感度进行了测试,并对其结果进行了对比分析。文献[6]采用三阈值概率分布法对多导体传输线的寄生参数进行预测分析。文献[7]利用有源传输线理论建立了地-线缆耦合模型,并对高频下参数的适用范围进行了分析,为多导体传输线电磁耦合问题的预测和抑制提供了有力支撑。文献[8]采用Taylor 与Agrawal 传输线模型,利用节点导纳分析法对外场激励下的传输线响应电压进行了研究。文献[9]将传输线理论与蒙特卡洛法相结合,得到了线束串扰的概率分布。文献[10]通过传输线模型对非均匀缠绕的双绞线传输线模型的辐射敏感度进行了预测。相似地,文献[11]建立了一种受到非均匀电磁场辐射的双绞线模型,并利用该模型对以地面为参考导体的双绞线的辐射敏感度频域响应进行了分析。而文献[12]基于一致性的原则对传输线辐射敏感度进行了等效测试。文献[13]针对多导体传输线电磁耦合的不确定性问题,结合全因子数值积分法、稀疏网格数值积分法与最大熵法,建立了多导体传输线电磁耦合的概率分布模型。
对于不确定性问题的研究主要是对模型各不确定性输入对于模型输出造成的不确定性进行量化。同样,全局灵敏度分析量化了模型各个输入变量对模型输出结果的影响程度。由于全局灵敏度分析对模型是否是线性系统不做要求,因此全局灵敏度分析同时还可以量化模型输入变量之间相互作用对于模型输出的影响。全局灵敏度分析方法主要包括基于方差分解的Sobol 法等[14]。文献[15]将响应面法与Sobol 法相结合,对电力变压器绕组的电气参数对绕组的全局灵敏度进行了分析。文献[16]将基于拉普拉斯变换数值反演的线性灵敏度分析方法与分段分解技术相结合,对带有非线性负载的有耗传输线进行了灵敏度分析。文献[17]结合一阶可靠度与二阶可靠度方法对场线耦合情况下的可靠度和全局灵敏度进行了分析。文献[18]利用灵敏度分析对并网型微电网容量进行了优化配置,类似的文献[19]基于灵敏度分析对直流输电接地极的选址进行了优化。
本文提出采用广义混沌多项式(Generalized Polynomial Chaos, gPC)法对多导体传输线辐射敏感度感应电流(电压)的不确定性问题进行量化分析,并将gPC 与基于方差分解的Sobol 全局灵敏度分析法结合,对多导体传输线辐射敏感度模型中的随机输入变量进行全局灵敏度分析,计算相应的灵敏度指标,并分析各个输入变量对模型输出响应的影响程度,最后将计算结果与蒙特卡洛法(Monte Carlo method, MC)进行对比,对本文方法的正确性和高效性进行验证。
1 广义混沌多项式与全局灵敏度分析
1.1 广义混沌多项式法
混沌多项式起源于Wiener 理论中的齐次函数,最早被用来分析湍流问题[20]。Wiener 最初采用基于高斯随机变量的埃尔米特正交多项式构建了混沌多项式,但是对于服从非高斯分布的变量来说,Wiener混沌多项式的收敛速度慢,计算效果不理想。随后Xiu Dongbin 和G. E. Karniadakis 推出的Askey 方案将其推广至更多传统的随机变量分布类型[21-22],比如均匀分布、指数分布等,使得推广后的混沌多项式收敛速度快,计算精度高,得到了更适用于一般参数分布形式的gPC,并得到了广泛的研究与应用。接下来对gPC 法进行介绍。
令原始模型为 Y = ,对其进行广义混沌多项式展开,展开结果为
,对其进行广义混沌多项式展开,展开结果为

表1 传统分布类型对应的正交多项式
Tab.1 Orthogonal polynomials corresponding to traditional distribution types

分布类型 概率密度函数 正交多项式基 权函数 变量范围正态 − Hermite ( )1 e 2π x2/2 H x 2/2 n − [ ]e x -∞ ∞,+均匀 1/2 Legendre ( )nP x 1 [ ]1,1-β ( ) ( )( )α−x β α β ( ) ( ),1 1x x 1 1 e 2 1, 1 α β+ +1− ++ + Jacobi ( )( )x x Bα β nP x α β− + [ ]1,1-指数 e x− Laguerre ( )n L x e x− [ ]0,+∞
理论上混沌多项式展开式的项数是无穷的,为了在满足计算精度的前提下提高计算效率,通常对其在某一阶数p 处截断,对应的p 阶混沌多项式展开模型表示为

式中,P 为p 阶截断后,除了 0 0c Φ 以外的混沌多项式展开项的数量。
相应的,p 阶截断混沌多项式展开项的数量Q随着阶数p 以及随机变量ξ 的维数d 的增大而增大,Q 的值可以由式(3)得到。

构建好混沌多项式展开模型后,对混沌多项式展开项系数进行求取,一般采用回归法或Galerkin投影法对其进行计算。在本文中采用Galerkin 投影法对展开项的系数进行计算,将式(4)两边同时投影到各正交多项式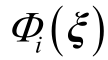 上,得到
上,得到

混沌多项式展开项的系数可以通过计算式(6)得到,式(6)中的分母是对已知的各维随机变量所对应的正交多项式求取期望值,因此很容易计算,关键在于对分子的计算。本文利用全因子数值积分法对分子进行计算,由此可以计算出式(6)中的分母与分子,即可计算得出gPC 的各项系数并得到模型响应的均值与方差。
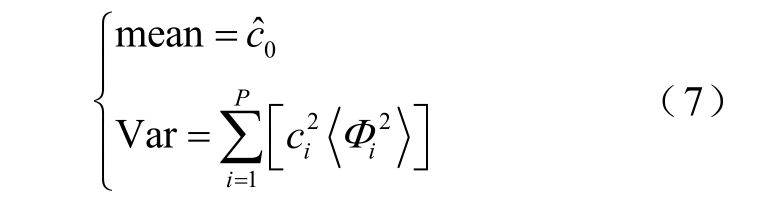
1.2 基于gPC 的全局灵敏度分析
在全局灵敏度分析方法中,Sobol 法是最经典的方法。该方法基于方差分解(ANOVA)的思想,通过量化单个输入变量或多个输入变量之间的相互作用对输出方差的贡献量来评价该变量或变量间的相互作用对输出模型的影响程度。利用Sobol 法,输出模型可以分解为2n 个递增项之和的形式。

式中, 为n 维输入变量(ξ1 ξ2 … ξn); 0y 为常数且为Y(ξ)的均值。各分解项之间满足正交关系。通过积分对展开项之和进行递归计算,即可得到式(8)中各分解项的系数,为了得到方差分解式,对式(8)两边同时取方差得
为n 维输入变量(ξ1 ξ2 … ξn); 0y 为常数且为Y(ξ)的均值。各分解项之间满足正交关系。通过积分对展开项之和进行递归计算,即可得到式(8)中各分解项的系数,为了得到方差分解式,对式(8)两边同时取方差得

式(9)中不同的分解项表示了不同的输入变量以及变量之间相互作用对输出响应方差的影响,将Sobol 灵敏度指标定义为

式中,Si 为一阶灵敏度指标,表示单个输入对输出响应方差的贡献。将各个输入变量的一阶灵敏度指标以及各变量间相互作用的灵敏度指标之和定义为总灵敏度指标。
在Sobol 法提出的早期,总灵敏度指标和各阶灵敏度指标是利用MC 进行计算,但是MC 的计算成本较高,计算效率低下。因此本文结合前文介绍的gPC 对全局灵敏度指标进行计算。将截断后的p阶混沌多项式展开式(2)改写成递增求和的形式为


根据混沌多项式基函数的正交性,可以推导得出
结合式(10),即可得到基于gPC 的Sobol 全局灵敏度指标,包括一阶灵敏度指标和总灵敏度指标。
2 多导体传输线辐射敏感度混沌多项式模型
在本文中,主要的研究对象是以无限大地面为参考导体的均匀无耗多导体传输线,在实际应用中,主要的不确定性输入参数集中在入射场的相关参数中,如仰角θ、方位角ψ 、偏振角η 以及入射平面波的电平幅值E0,入射平面波的入射角度与极化方向如图1 所示。接下来将结合前文介绍的广义混沌多项式法建立相应的代理模型,通过代理模型对多导体传输线辐射敏感度的不确定性进行分析。
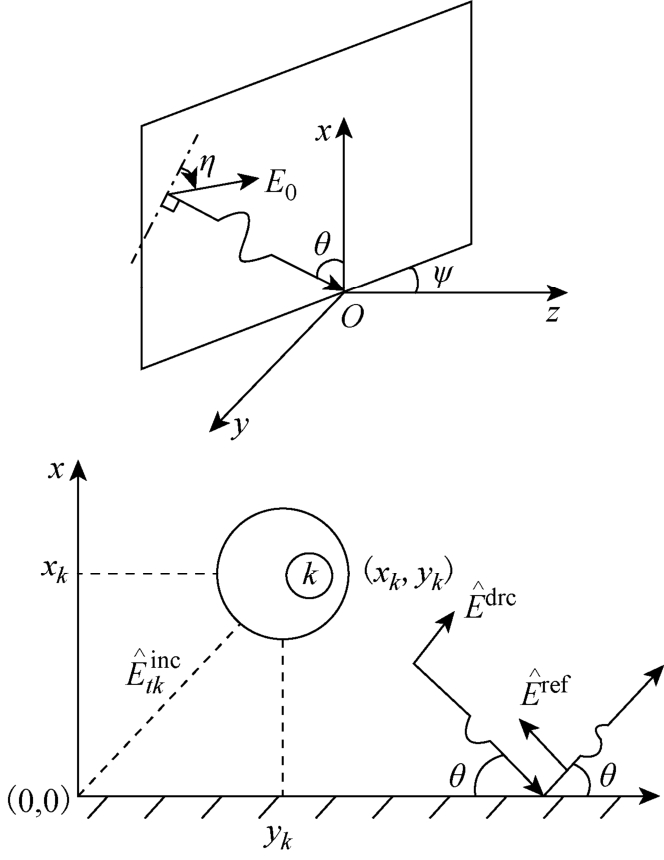
图1 平面入射波与传输线位置关系
Fig.1 Relation between plane incident wave and transmission lines position
假设图1 中入射场的相关随机输入变量都服从相应的分布类型,例如仰角θ 在区间[0,π/2]上服从均匀分布,那么可以将θ 表示为
式(16)中 ξ i服从区间[-1,1]上的标准均匀分布。多导体传输线辐射敏感度的输出响应会不可避免地与类似于仰角θ 这样的随机输入变量![]() 相关,因此导致有入射场存在的传输线方程中的感应电压与感应电流会包含强制分量。
相关,因此导致有入射场存在的传输线方程中的感应电压与感应电流会包含强制分量。

式中,z 为传播方向。设传输线的数量为N,那么上式中的矩阵维度为2N。结合第1 节中介绍的广义混沌多项式法,对式(17)、式(18)进行正交多项式展开并于p 阶截断为

式中,Φk(ξ)为各个随机变量所对应的正交多项式。为了保证正交性,将多元多项式建立成一元正交多项式的乘积形式。应用正交多项式的正交性,可以将式(19)、式(20)写为

式(21)、式(22)中的每个方程都是确定的,并且强制函数的第k 个分量对传输线的激励是一致的,因此随机问题的解可以变为每一个单独分量的叠加。在传播方向z 上,设传输线的长度为L,基于链参数矩阵解微分方程得

式中 为2N×2N 的链参数矩阵;VFT,k 和IFT,k 为强制函数与链参数矩阵的卷积。更进一步地结合终端条件,可以计算得到响应电压与响应电流的值为
为2N×2N 的链参数矩阵;VFT,k 和IFT,k 为强制函数与链参数矩阵的卷积。更进一步地结合终端条件,可以计算得到响应电压与响应电流的值为

在均匀入射平面波的辐射下,VFT 和IFT 的解析解为

式中,ETj 为横向场在第j 根传输线上的分量;M±和N±为入射场的函数;其余项仅与纵向场相关。由此得到包含正交多项式基底的多导体传输线辐射敏感度方程。
3 算例应用
在本节中,将结合gPC 法与全局灵敏度分析法对以地面为参考导体的多导体传输线辐射敏感度的不确定性以及各个输入变量的全局灵敏度进行计算分析。设受到入射均匀平面波辐射的传输线是均匀无耗的,长度为L,令传输线沿z 轴方向,传输线的总数为N,位于y-x 平面上的第i 根传输线的坐标用 (yi, xi)表示,第i 根传输线左右两端的负载分别为RiL 和RiR。传输线处于均匀介质中,电导率与磁导率均为自由空间中的ε0 与μ0。多导体传输线辐射敏感度系统中的随机输入变量为入射平面波的仰角θ、方位角ψ 、偏振角η 以及电平幅值E0,当其分布类型确定时,多导体传输线辐射敏感度的输出响应可以由传输线方程式(23)~式(27)求出。
令传输线的数量N=14,传输线的长度L=2m,每一根传输线的半径r=1mm,传输线的负载均为50Ω,以上为多导体传输线模型中的确定参数,传输线在y-x 平面上的横截面如图2 所示。

图2 y-x 平面上多导体传输线横截面示意图
Fig.2 Cross section diagram of multiconductor
transmission lines on y-x plane
在算例中存在四维随机输入变量,分别是入射平面波的仰角θ、方位角ψ 、偏振角η 以及电平幅值E0,令四个变量分别服从不同的分布,设仰角θ 服从区间[0, 0.5π]上的均匀分布,方位角ψ 服从区间[-π,π]上的均匀分布,偏振角η 服从区间[0, 2π]上的均匀分布,电平幅值 E0 服从均值为 1V/m、标准差为0.2V/m 的正态分布。利用式(23)~式(27),建立多导体传输线辐射敏感度的gPC 模型。对于利用gPC 法计算多导体传输线辐射敏感度的不确定性问题来说,不同的截断阶数计算得到的结果精度不同,截断阶数越高计算精度也越高。需要指出的是,针对截断阶数的选择问题,学者们已开展了一定研究,并取得了一些成果,例如以留一法(Leave One Out,LOO)误差分析为代表的自适应方法[23],是以1 阶为步长,从低阶到高阶逐一计算设定范围内(如[10,30]阶)不同阶数下的模型误差,选取达到预期误差标准的阶数作为截断阶数。虽然该方法能够较为有效地选取符合要求的截断阶数,但是由于针对不同截断阶数都需要对模型重新计算,在计算效率方面仍然存在不足,有待进一步研究。在此对相关方法不做详细讨论,仅通过选取代表性的部分阶数与MC 法计算结果进行对比,说明gPC 法的计算精度和计算效率。接下来将混沌多项式的截断阶数p 设置为5、10、15、20 以及25,对传输线辐射敏感度的均值和标准差进行计算,将分析的频率范围设置为[10MHz, 1GHz],分别将采用gPC 法计算得到的均值以及标准差与20 000 次MC 法的计算结果进行对比,以图2 中3 号传输线右端的感应电流值IR3 为例,对比结果如图3 所示。


图3 20 000 次MC 均值与标准差计算结果与不同截断阶数的gPC 计算结果对比
Fig.3 Comparisons between the results of 20 000 MC mean and standard deviation and the results of gPC with different truncation orders
从图3 中的对比结果看到,对于感应电流IR3 的均值来说,5 阶、10 阶、15 阶、20 阶及25 阶截断的gPC 计算结果与MC 的计算结果基本一致。但是对比标准差的结果可以明显的看到,低阶截断的gPC 标准差计算结果并不理想,与MC 的计算结果相差较大,但是随着截断阶数的增加,标准差的计算结果也越接近MC 的计算结果。这证明了gPC 的截断阶数对于计算均值的影响并不大,但是对于高阶统计矩的计算具有较大的影响。同时也证明了gPC 截断阶数越高,gPC 的计算精度也越高。接下来在频段中挑选一些频点,分别采用20 阶截断以及25 阶截断的gPC 法计算不同频点处IR3 的概率密度函数,并与20 000 次MC 法的计算结果进行对比。
对比图4 中20 阶截断与25 阶截断的计算结果并综合均值与标准差的对比结果,可以看到20 阶截断gPC 法的计算精度与25 阶截断基本一致,都可以得到有效的多导体传输线辐射敏感度的概率分布,证明20 阶截断已经保证了足够的计算精度。采用gPC 法的程序运算时间与20 000 次MC 法的程序运算时间对比见表2。

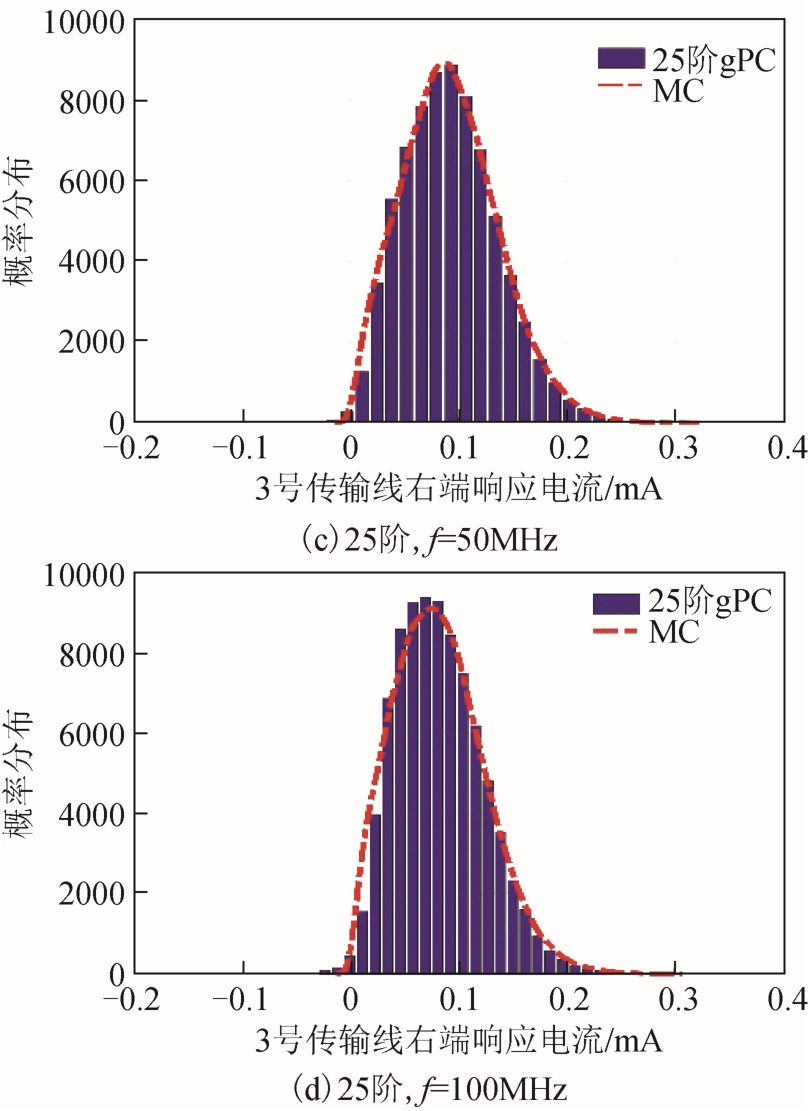
图4 不同频点处20 阶截断与25 阶截断gPC 计算3 号传输线右端响应电流概率分布函数对比
Fig.4 Comparisons of probability distribution functions of response current at right end of #3 transmission line calculated by 20-order truncation and 25-order truncation gPC at different frequency points
表2 gPC 法与MC 法程序运行时间对比
Tab.2 Comparisons of running time between gPC method and MC method

计算方法 程序运行时间/s gPC p=5 4.272 8 p=10 5.543 9 p=15 16.022 9 p=20 25.074 4 p=25 56.893 6 MC (20 000 次) 3 295.747 7
结合表2 可知,相比于25 阶截断,20 阶截断在保证计算精度的前提下程序运行时间节省了55.93%,计算效率更高,因此在接下来的计算中均采用20 阶截断。本文使用的计算机CPU 主频为2.3GHz,运行内存为8GB。同时可以从表2 中看到,相比于20 000 次MC 的程序运行时间,20 阶截断的gPC 法在保证精度的前提下,计算速度提升了131 倍,证明本文所采用的方法可以有效地提高计算效率,节省计算时间。
综合上述的计算结果,本文采用的gPC 法可以得到有效的均值与标准差。在实际情况中,感应电流IR3 是有界的,区间[μ-3σ,μ+3σ]可以作为感应电流IR3 近似的上限与下限,在此基础上,可以利用高分位数的置信度(例如0.95,0.99,0.995 等)来证明IR3 可以有效地作为上限,但是这超出了本文的范围,本文采用20 000 次MC 计算结果进行验证,如图5 所示。

图5 gPC 法计算得到响应电流上限曲线与20 000 次MC 仿真曲线对比
Fig.5 Comparing the response current upper limit curves calculated by gPC method with the 20 000 MC simulation curve
由图5 可知,基于gPC 法计算得到的虚线上限曲线较好地覆盖了绝大部分的仿真曲线,证明了 μ+3σ 可以有效地作为感应电流IR3 变化范围的上限。图5 中没有显示下限曲线,这是由于对于多导体传输线的辐射敏感度问题来说,上限更具有研究意义,而基于 3μ σ- 得到的下限曲线在某些频点处可能会得到负的感应电流值,因此在图中仅显示上限曲线。
通过上述的计算与分析,说明本文所采用的gPC 法能够高效准确地计算多导体传输线辐射敏感度不确定性问题中相关统计特征参数(如感应电流(电压)的均值、标准差、概率分布等)。接下来,可以结合gPC 展开项的系数对多导体传输线辐射敏感度中的各随机输入变量进行全局灵敏度分析,明确相关的随机输入变量对传输线辐射敏感度的影响程度。
利用式(10)、式(11),并结合前文中计算得到的gPC 的各项展开项系数计算Sobol 的全局灵敏度指标,以3 号传输线在150MHz 处的响应电流为指标,计算得到各输入变量的总灵敏度指标以及一阶灵敏度指标如图6 所示。

图6 基于gPC 法计算得到的总灵敏度指标以及一阶灵敏度指标与基于MC 法计算结果对比
Fig.6 Comparisons of total sensitivity indices and firstorder sensitivity indices calculated by gPC method with those calculated by MC method
观察图6 可以看到,在计算总灵敏度指标以及一阶灵敏度指标时,基于gPC 法计算得到的结果与基于MC 法计算得到的结果基本一致,各个输入变量对于模型总体的影响程度也是一致的,仰角θ 与方位角ψ 的总灵敏度指标与一阶灵敏度指标更高一些,是影响多导体传输线辐射敏感度的主要因素,同时gPC 法的计算速度更快,效率更高。证明本文采用的方法在计算多导体传输线辐射敏感度的总灵敏度指标与一阶灵敏度指标时是有效的。
为了更精确地量化分析不同频点处随机输入变量对于模型的影响,针对频段[10MHz,1GHz]上各参数对传输线辐射敏感度的影响程度的总灵敏度指标进行计算,如图7 所示。
通过分析图7,在[10MHz, 1GHz]的频段上,电平幅值 E0 对于模型整体的影响程度较低,但是在较高的频率范围内,如[600MHz, 1GHz],电平幅值E0 的影响程度有所提高;仰角θ 对于模型的影响程度仅在[10MHz, 200MHz]的低频率范围上较弱,当频率大于200MHz 时,仰角θ 成为了模型的重要影响因素;方位角ψ 对模型的影响程度与仰角θ 的变化趋势相反,随着频率的增加,其对模型的影响程度基本上呈下降趋势,它在[10MHz, 200MHz]的频率范围对模型有着重要影响程度;而偏振角η 在[10MHz, 1GHz]频率范围内均对于模型有着较强的影响程度。由式(27)可知,相对于入射平面波的仰角θ、方位角ψ 以及偏振角η,电平幅值E0 的横向分量 TjE 仅对多导体传输线辐射敏感度的感应电压产生有限的影响,因此电平幅值对于模型整体的影响程度比入射平面波的仰角θ、方位角ψ 以及偏振角η 的影响程度要弱一些。在高频段中,仰角θ与偏振角η 的影响较为明显,所以在工程应用中,如果已知辐射源位置以及频率范围,那么在电气系统的设计过程中应当依此对受扰的传输线位置进行合理的选择或调整,尽量避免系统电磁兼容问题的发生。

图7 [10MHz, 1GHz]频率范围内各参数对传输线辐射敏感度的影响程度
Fig.7 The influence of parameters on radiation sensitivity of transmission lines in the [10MHz, 1GHz]frequency range
4 结论
本文采用以无限大地面为参考导体的多导体传输线模型,令相关随机输入变量仰角θ、方位角ψ 、偏振角η 以及电平幅值E0 服从不同的分布类型,利用广义混沌多项式法对其不确定性问题进行分析,得到传输线上感应电流(电压)的均值、标准差、概率分布等相关统计信息,并将其与20 000 次MC法仿真结果进行对比验证,从而证明了gPC 法通过简化模型能够在保证计算精度的同时,极大地提高计算效率,实现多导体传输线辐射敏感度不确定性问题的快速有效分析。同时,又结合gPC 法与Sobol全局灵敏度分析方法,对多导体传输线辐射敏感度模型中的相关随机输入变量的总灵敏度指标与一阶灵敏度指标进行了计算,得到相关参数对传输线辐射敏感度的影响程度,同样通过MC 法对其可行性进行了验证。因此,本文所提出的多导体传输线辐射敏感度不确定性问题以及全局灵敏度分析方法能够为系统线缆电磁兼容设计和整改提供有效的理论依据。
[1] Taylor C , Satterwhite R , Harrison C. The response of a terminated two-wire transmission line excited by a nonuniform electromagnetic field[J]. IEEE Transactions on Antennas and Propagation, 1965, 13(6): 987-989.
[2] Paul C R. Frequency response of multiconductor transmission lines illuminated by an electromagnetic field[J]. IEEE Transactions on Electromagnetic Compatibility, 1976, EMC-18(4): 183-190.
[3] Paul C R. Analysis of multiconductor transmission lines[M]. 2nd ed. New York: Wiley, 2008.
[4] Pignari S, Bellan D. Statistical characterization of multiconductor transmission lines illuminated by a random plane-wave field[C]//IEEE International Symposium on Electromagnetic Compatibility,Washington DC, 2000: 606-609.
[5] Vogtardatjew R, Leferink F. Experimental plane wave and random field coupling to uniform and nonuniform transmission lines[C]//IEEE International Symposium on Electromagnetic Compatibility,Dresden, Germany, 2015: 767-772.
[6] 赵亮, 王世山, 娄千层, 等. 基于三阈值概率分布的多导体传输线电磁参数特性[J]. 电工技术学报,2018, 33(8): 1663-1673.Zhao Liang, Wang Shishan, Lou Qianceng, et al.Equivalent theory and its realization of the radiated immunity test with incident field excitation coupling to multi-conductor transmission lines based on the consistency[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1663-1673.
[7] 朱峰, 邱日强, 牛大鹏, 等. 基于有源传输线模型的地架空屏蔽线缆耦合特性分析与参数计算[J].电工技术学报, 2016, 31(4): 22-27.Zhu Feng, Qiu Riqiang, Niu Dapeng, et al. Coupling characteristic analysis and parameter calculation of ground and above-ground shielded cables based on transmission line with a distributed source model[J].Transactions of China Electrotechnical Society, 2016,31(4): 22-27.
[8] 卢斌先, 王泽忠. 外场激励下多导体传输线响应的节点导纳分析法[J]. 电工技术学报, 2007, 22(10):145-149.Lu Binxian, Wang Zezhong. Nodal admittance method for response of multiconductor transmission line excited by electromagnetic field[J]. Transactions of China Electrotechnical Society, 2007, 22(10): 145-149.
[9] 张昭,王世山,赵亮. 多导体线束内串扰概率分布的预测[J]. 电工技术学报, 2017, 32(7): 204-214.Zhang Zhao, Wang Shishan, Zhao Liang. Prediction of crosstalk probability distribution in cable bundles[J].Transactions of China Electrotechnical Society, 2017,32(7): 204-214.
[10] Spadacini G, Pignari S A. Numerical assessment of radiated susceptibility of twisted-wire pairs with random nonuniform twisting[J]. IEEE Transactions on Electromagnetic Compatibility, 2013, 55(5): 956-964.
[11] SpadaciniG, Grassi F, Marliani F, et al. Transmissionline model for field-to-wire coupling in bundles of twisted-wire pairs above ground[J]. IEEE Transactions on Electromagnetic Compatibility, 2014,56(6): 1682-1690.
[12] 高欣欣, 王世山, 娄千层, 等. 基于“一致性”原则的“场-多导体”传输线辐射敏感度测试的等效理论及实现[J]. 电工技术学报, 2018, 31(7): 1588-1598.Gao Xinxin, Wang Shishan, Lou Qianceng, et al.Equivalent theory and its realization of the radiated immunity test with incident field excitation coupling to multi-conductor transmission lines based on the consistency[J]. Transactions of China Electrotechnical Society, 2018, 31(7): 1588-1598.
[13] Gao Le, Yu Quanyi, Wu Dingchao, et al. Probabilistic distribution modeling of crosstalk in multi-conductor transmission lines via maximum entropy method[J].IEEE Access, 2019, 7(1): 103650-103661.
[14] Sobol I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics & Computers in Simulation,2001, 55(1-3): 271-280.
[15] 李妍, 周洪伟, 沈小伟, 等. 电力变压器绕组电气参数对绕组变形的全局灵敏度分析[J]. 电力系统保护与控制, 2018, 46(7): 31-37.Li Yan, Zhou Hongwei, Shen Xiaowei, et al. Global sensitivity analysis of winding electrical parameters on power transformer winding deformation [J]. Power System Protection and Control, 2018, 46(7): 31-37.
[16] Lum S, Nakhla M, Zhang Q J. Sensitivity analysis of lossy coupled transmission lines with nonlinear terminations[J]. IEEE Transactions on Microwave Theory and Techniques, 1994, 42(4): 607-615.
[17] Kouassi A, Bourinet J M, Lallechere S, et al.Reliability and sensitivity analysis of transmission lines in a probabilistic EMC context[J]. IEEE Transactions on Electromagnetic Compatibility, 2016,58(2): 561-572.
[18] 李咸善, 方婧, 郭诗书, 等. 基于灵敏度分析的并网型微电网容量优化配置[J]. 电力系统保护与控制, 2018, 46(23): 14-23.Li Xianshan, Fang Jing, Guo Shishu, et al. Capacity sizing optimal for grid-connected micro-grid based on sensitivity analysis[J]. Power System Protection and Control, 2018, 46(23): 14-23.
[19] 陈庆涛, 田宇, 丁国成, 等. 基于灵敏度分析的直流输电接地极优化选址方法研究[J]. 电力系统保护与控制, 2018, 46(21): 131-136.Chen Qingtao, Tian Yu, Ding Guocheng, et al.Optimization method of grounding pole location for HVDC transmission system based on sensitivity analysis[J]. Power System Protection and Control,2018, 46(21): 131-136.
[20] Xiu D, Karniadakis G E. Modeling uncertainty in flow simulations via generalized polynomial chaos[J].Journal of Computational Physics, 2003, 187(1): 137-167.
[21] Xiu Dongbin, Karniadakis G E. The Wiener-Askey polynomial chaos for stochastic differential equations[J]. SIAM Journal on Scientific Computing,2002, 24(2): 619-644.
[22] Wiener N. The homogeneous chaos[J]. American Journal of Mathematics, 1938, 60(4): 897-899.
[23] 刘学艺, 李平, 郜传厚. 极限学习机的快速留一交叉验证算法[J]. 上海交通大学学报, 2011, 45(8):1140-1145.Liu Xueyi, Li Ping, Gao Chuanhou. Fast leave-one-out cross-validation algorithm for extreme learning machine[J]. Journal of Shanghai Jiaotong University,2011, 45(8): 1140-1145.