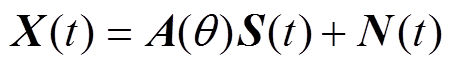 (1)
(1)摘要 基于特高频天线阵列的敞开式变电站局部放电测向系统已获得应用,但该系统的阵列尺寸过大,给巡检带来不便。为缩小阵列尺寸,空间谱估计被应用于局部放电测向系统。鉴于空间谱估计算法种类众多,且不同算法的测向性能受信号的信噪比、入射方向等因素的影响程度有所不同,故需研究适用于变电站站域局部放电空间谱估计算法的选择问题。该文建立局部放电仿真系统,通过改变阵元数目、信噪比和入射方位角等参数,比较双边相关变换(TCT)、旋转信号子空间和信号子空间变换等宽带聚焦算法的性能,以及多重信号分类、求根-多重信号分类、旋转不变子空间、加权子空间拟合等窄带测向算法的测向精度。仿真结果表明,双边相关变换算法运算速度最快,有效测向范围最宽,在信噪比较高时拥有最高的测向精度;求根-多重信号分类(Root- MUSIC)算法在小阵元数目条件下测向误差最小,抑制噪声的能力较强,运算时间较短。实验结果表明,采用双边相关变换算法和求根-多重信号分类算法的局部放电测向系统,方位角测向偏差和标准差分别小于3.2°和2.9°,具有较好的测向性能。
关键词:变电站 局部放电 特高频 测向 空间谱估计
敞开式变电站内电力设备众多,确保系统安全稳定运行意义重大。局部放电是设备绝缘劣化的征兆,若未被早期发现,将逐渐发展为设备的击穿放电,给变电站带来不可估量的经济损失[1-3]。如今常用的局部放电检测技术是把传感器固定安装在变压器、气体绝缘组合电器设备等单一设备上,但对断路器、隔离开关等设备的状态检测缺乏有效的手 段[4-5]。为此,英国学者提出建立一个可移动式的巡检平台,利用特高频天线阵列对变电站所有电力设备进行全方位的局部放电检测与定位[6-8]。然而,为保证系统定位精度,天线阵列的阵元间距超过了1.1m[6],给巡检带来不便。
为缩小阵列尺寸,提高巡检效率,空间谱估计算法被应用于变电站局部放电特高频测向系统 中[9-10]。空间谱估计算法是来自电子对抗领域的一种无源测向算法,它利用信号在空间各个方向的能量分布,计算放电信号的波达方向,具有干扰抑制能力强、波束控制灵活和空间分辨能力高等优点。
田野等布置了四天线矩形阵列,利用多重信号分类(Multiple Signal Classification, MUSIC)算法对放电信号进行波达方向估计,发现了架空线路上的放电源[11]。为避免求解时间差算法中的非线性方程组,上海交通大学江秀臣等提出了基于L形天线阵列与旋转不变子空间(Estimation of Signal Parameters via Rotational Invariance Techniques, ESPRIT)算法的局部放电特高频测向方法,阵列的天线间距超过了1m[12]。然而,多数学者将研究工作集中在新算法的引入和实验测试等方面,没有系统地对比不同算法应用于局部放电检测系统中的优 缺点。
笔者在文献[9]中搭建了基于空间谱估计的局部放电测向算法架构:①采用不同中心频率的数字带通滤波器将阵列接收信号分散到不同频率点上;②通过宽带聚焦算法把不同频率上的信号聚焦到某一参考频率上;③利用窄带测向算法绘制信号空间谱图,得到信号波达方向角。宽带聚焦和窄带测向是空间谱估计中的重要步骤,对站域局部放电检测系统的测向精度影响很大。然而,这两类算法的种类众多,且不同算法的测向性能受信号的信噪比、入射方向等因素的影响程度有所不同,故需探索适用于变电站站域局部放电测向算法的选择问题。
本文通过仿真与实验研究了不同算法应用于变电站站域局部放电检测系统时各自的优缺点,可为局部放电测向系统中选择合理的算法提供理论 基础。
本文的空间谱估计理论模型基于文献[9, 13-14]。设局部放电检测系统的采样频率为fs、采样点数为L;均匀直线阵列的天线数目为N、间距为d,阵元1号为参考阵元;放电信号共M个,入射方位角为qi、波长为li(i=1, 2,…, M),则阵列数据接收矩阵X(t)为
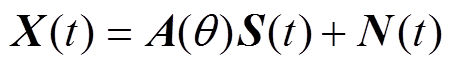 (1)
(1)式中,S(t) 为M´L的信号矩阵;N(t)为N´L的噪声矩阵;A(q )为N´M的阵列流型矩阵,与信号特征参量(l 和q )、阵列布置方式(d)相关,是求解信号波达方向的重要矩阵,表达式为
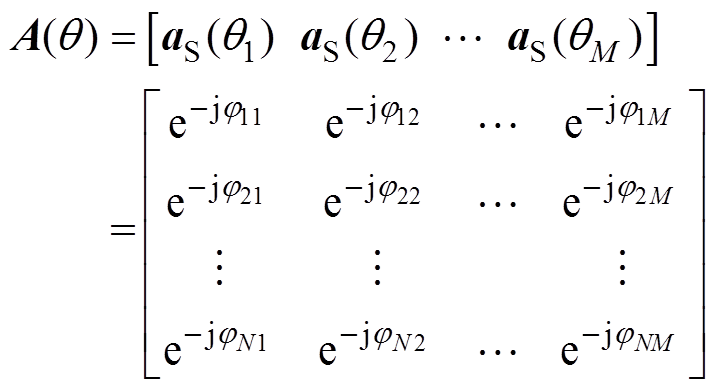 (2)
(2)
式中,j为虚数单位;aS(q )为信号导向矢量;jki为第i个信号到达第k个阵元(k=1, 2,…, N)相对于1号阵元的相位差,有
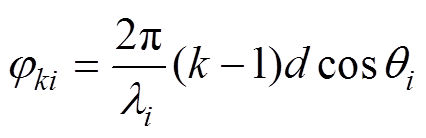 (3)
(3)聚焦算法的功能是把J个不同中心频率点的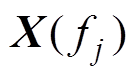 通过聚焦矩阵
通过聚焦矩阵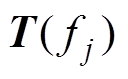 聚集到参考频率f0上,从而得到窄带信号
聚集到参考频率f0上,从而得到窄带信号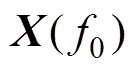 ,有
,有
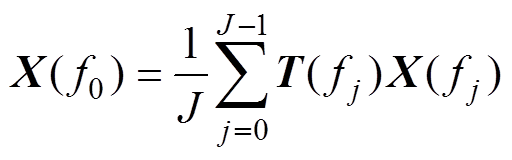 (4)
(4)常见的聚焦算法有双边相关变换(Two-side Correlation Transformation, TCT)、旋转信号子空间(Rotating Signal Subspace, RSS)和信号子空间变换(Signal Subspace Transformation, SST)算法。不同聚焦算法求解参考频率的方法是相同的,区别在于构造聚焦矩阵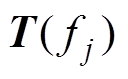 的方法,有
的方法,有
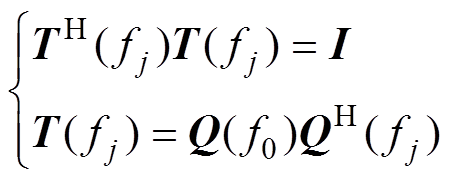 (5)
(5)
式中,“H”表示共轭转置;I为单位矢量矩阵。
TCT算法: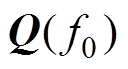 和
和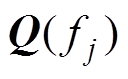 分别是
分别是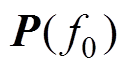 和
和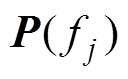 的特征矢量矩阵;RSS算法:
的特征矢量矩阵;RSS算法: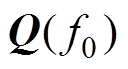 和
和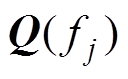 分别是
分别是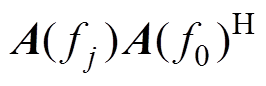 的右奇异值和左奇异值矩阵;SST算法:
的右奇异值和左奇异值矩阵;SST算法: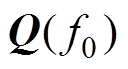 和
和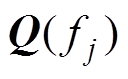 分别是
分别是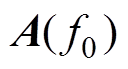 和
和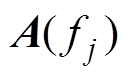 的左奇异值矩阵。
的左奇异值矩阵。
对于RSS算法和SST算法,要计算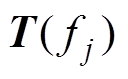 需先计算
需先计算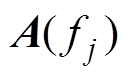 ,而
,而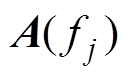 与信号来波方向q 相关,故需预估信号入射方向q0。为了提高测向精度,可将计算结果作为预估入射角进行多次迭代。
与信号来波方向q 相关,故需预估信号入射方向q0。为了提高测向精度,可将计算结果作为预估入射角进行多次迭代。
目前常用的窄带测向算法有MUSIC、求根MUSIC(Root-MUSIC)、ESPRIT算法和加权子空间拟合(Weighted Subspace Fitting, WSF)算法。其中,MUSIC、Root-MUSIC和ESPRIT算法为子空间分解类算法,该类算法利用两个子空间的正交特性构造出针状谱峰,大大地提高了算法分辨力;WSF算法为子空间拟合算法,该算法可归结为多维参数的优化问题。
1.3.1 MUSIC算法
MUSIC算法的主要步骤如下:
(1)对聚焦后的窄带信号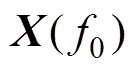 求协方差矩阵的最大似然估计Rxx。
求协方差矩阵的最大似然估计Rxx。
(2)对Rxx进行特征分解,得到相互正交的信号子空间US和噪声子空间UN。
(3)利用子空间的近似正交性,进行谱峰搜索,得到放电源波达方向角 ,有
,有
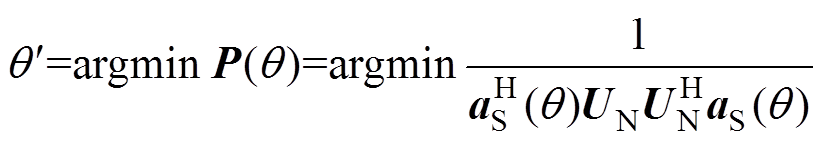 (6)
(6)1.3.2 Root-MUSIC算法
利用式(7)所示的z(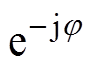 ),代替MUSIC算法中导向矢量aS(q ),再对式(8)的多项式
),代替MUSIC算法中导向矢量aS(q ),再对式(8)的多项式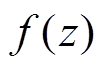 求根即可得到信号波达方向。
求根即可得到信号波达方向。
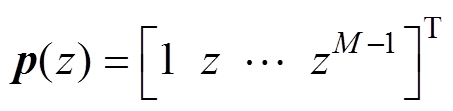 (7)
(7) (8)
(8)
在理想无噪声条件下,多项式的根正好位于单位圆上;而在实际应用中,由于噪声的存在,多项式的根不可能刚好在单位圆上,故选择离单位圆最近的根作为真实信号波达方向的解。
1.3.3 ESPRIT算法
ESPRIT算法利用各子阵信号子空间的旋转不变特性求解波达方向。设子阵A1包括阵元1~N-1号,数据矩阵为X1;子阵A2包括阵元2~N号,数据矩阵为X2,由1.1节可知,有
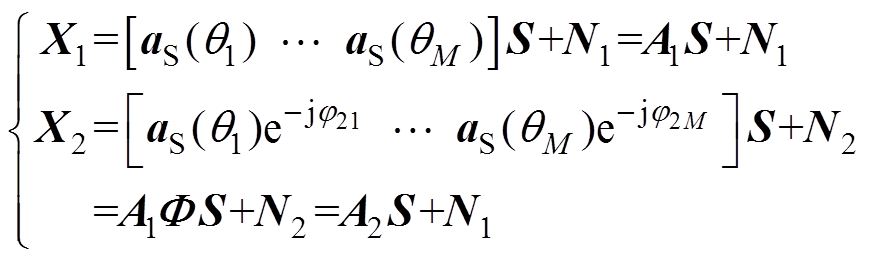 (9)
(9)式中,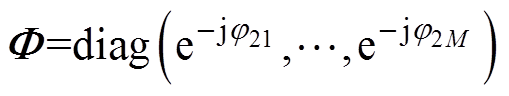 ,即子阵A1和A2间的固定间距。由数学知识可知,在理想无噪声条件下,子阵A1和A2的信号特征矩阵US与阵列流型矩阵A张成的信号子空间相同,即存在一个唯一的非奇异矩阵T,使
,即子阵A1和A2间的固定间距。由数学知识可知,在理想无噪声条件下,子阵A1和A2的信号特征矩阵US与阵列流型矩阵A张成的信号子空间相同,即存在一个唯一的非奇异矩阵T,使
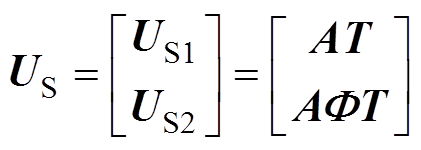 (10)
(10)
对式(10)进行变换,可得
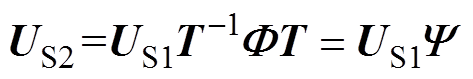 (11)
(11)式中,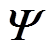 反映子阵A1和A2信号特征矩阵间的旋转不变关系。
反映子阵A1和A2信号特征矩阵间的旋转不变关系。
下面给出ESPRIT算法求波达方向的具体步骤:
(1)求X1和X2的协方差矩阵Rxx1和Rxx2。
(2)对Rxx1和Rxx2进行特征分解,分别得到信号子空间US1和US2。
(3)矩阵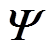 为
为
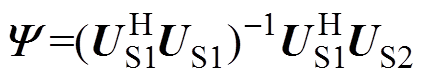 (12)
(12)对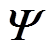 作特征分解,得到
作特征分解,得到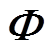 ,再由式(3)和式(9)求得信号波达方向。
,再由式(3)和式(9)求得信号波达方向。
1.3.4 WSF算法
当有噪声存在时,信号特征矩阵与阵列流型矩阵张成的空间不相等,即式(10)不一定成立。WSF算法就是构造一个拟合关系,找出使式(10)成立的一个非奇异矩阵T,使US和AT在最小二乘的意义条件下拟合得最好。该算法在式(10)的基础上,对信号特征矩阵US增加权重W,即
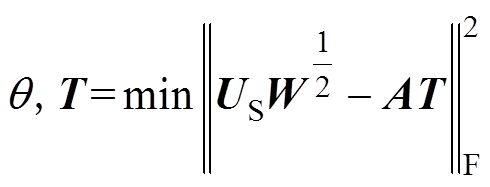 (13)
(13)式中,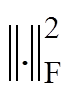 表示求矩阵2-范数;权重矩阵
表示求矩阵2-范数;权重矩阵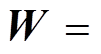
 ,其中,s2为噪声功率。由于算法关注波达方向估计参量q,而T仅为辅助参量,因此,对式(13)固定A即可得到T的最小二乘解,有
,其中,s2为噪声功率。由于算法关注波达方向估计参量q,而T仅为辅助参量,因此,对式(13)固定A即可得到T的最小二乘解,有
 (14)
(14)由式(13)和式(14),可得关于波达方位角q的解为
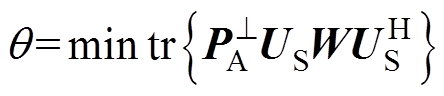 (15)
(15)
式中,tr{·}为求矩阵的迹;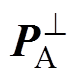 为流型矩阵A的正交投影矩阵,定义为
为流型矩阵A的正交投影矩阵,定义为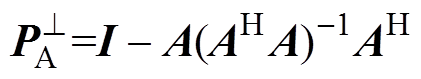 。
。
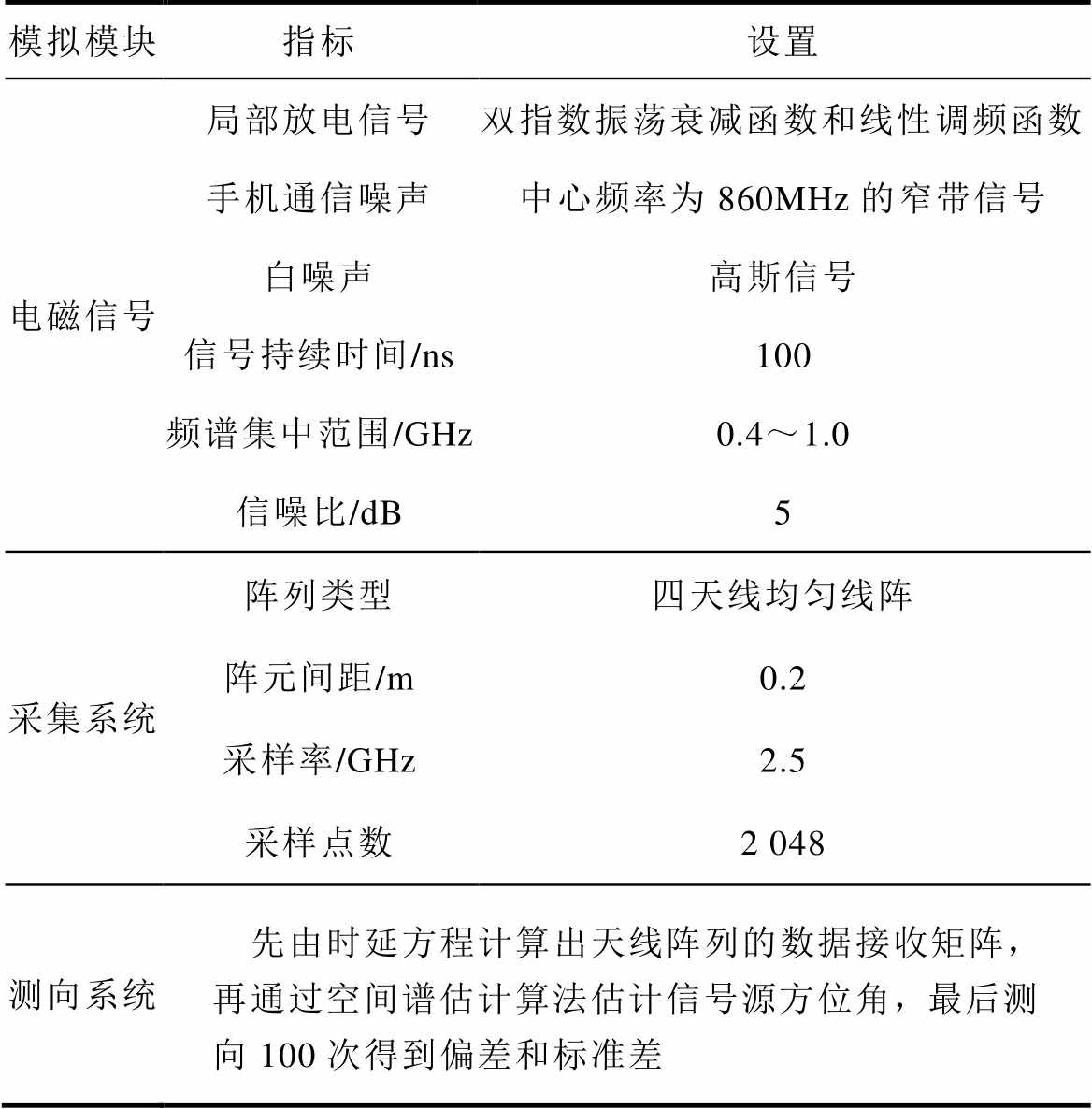
局部放电测向的仿真系统分为电磁信号模拟、采集系统模拟和定位系统模拟三个模块,其参数设置见表1。定位性能由测向偏差和测向标准差衡量。其中,偏差作为定位算法的有偏估计衡量其精度;标准差衡量定位的稳定性和离散程度。
表1 局部放电测向的仿真系统模块
Tab.1 Simulation system module of partial discharge direction finding
模拟模块指标设置 电磁信号局部放电信号双指数振荡衰减函数和线性调频函数 手机通信噪声中心频率为860MHz的窄带信号 白噪声高斯信号 信号持续时间/ns100 频谱集中范围/GHz0.4~1.0 信噪比/dB5 采集系统阵列类型四天线均匀线阵 阵元间距/m0.2 采样率/GHz2.5 采样点数2 048 测向系统先由时延方程计算出天线阵列的数据接收矩阵,再通过空间谱估计算法估计信号源方位角,最后测向100次得到偏差和标准差
窄带测向采用Root-MUSIC算法,分别改变算法迭代次数q、阵元数目N、信噪比(Signal to Noise Ratio, SNR)和入射方位角q,比较TCT算法、RSS算法和SST算法的测向性能。
2.2.1 迭代次数q
方位角测向误差与迭代次数的关系如图1所示。当迭代次数超过3时,两种算法测向误差均较小;SST算法比RSS算法的测向结果向准确值收敛得更快,且测向精度更高。

图1 迭代次数对方位角测向性能的影响
Fig.1 Effect of iteration number on direction finding performance of azimuth angle
2.2.2 阵元数目N
方位角测向精度随阵元数目的变化情况如图2所示。显然,阵元数目N越大,方位角测向精度越高;当N>8时,方位角测向误差基本不变。TCT算法和SST算法在小阵元数目(N<8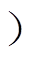 条件下具有更高的测向精度,其中SST算法在阵元数目仅为2时,测向偏差eq 和测向标准差dq 均小于1°;当N>8时,三种算法测向精度近似相同。
条件下具有更高的测向精度,其中SST算法在阵元数目仅为2时,测向偏差eq 和测向标准差dq 均小于1°;当N>8时,三种算法测向精度近似相同。
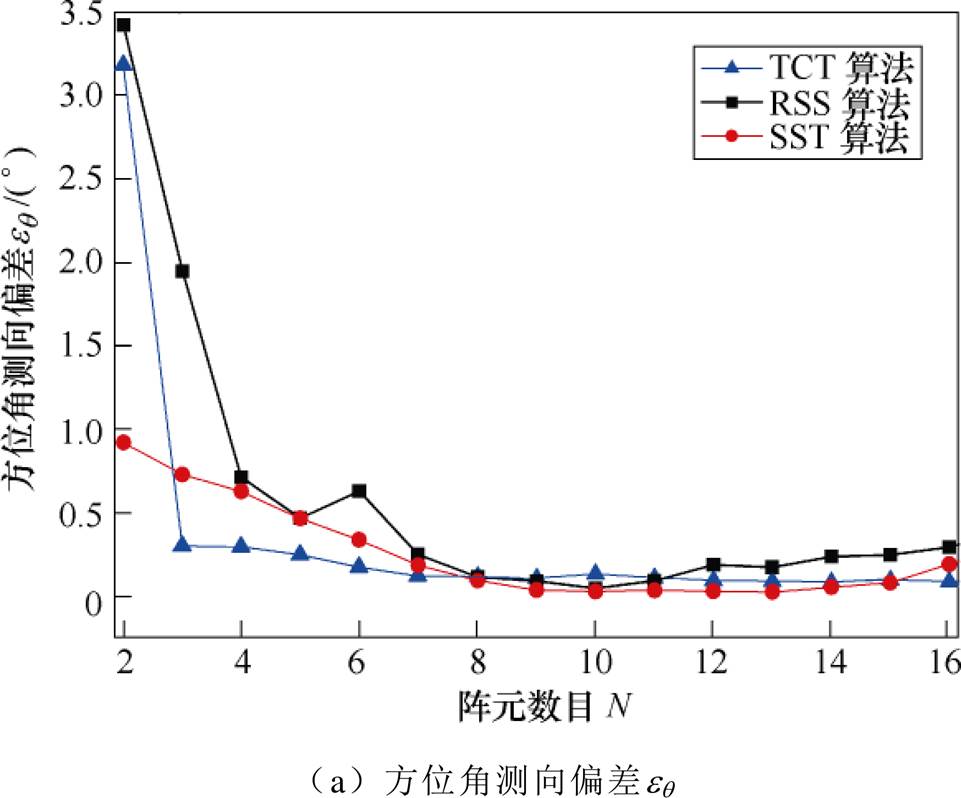
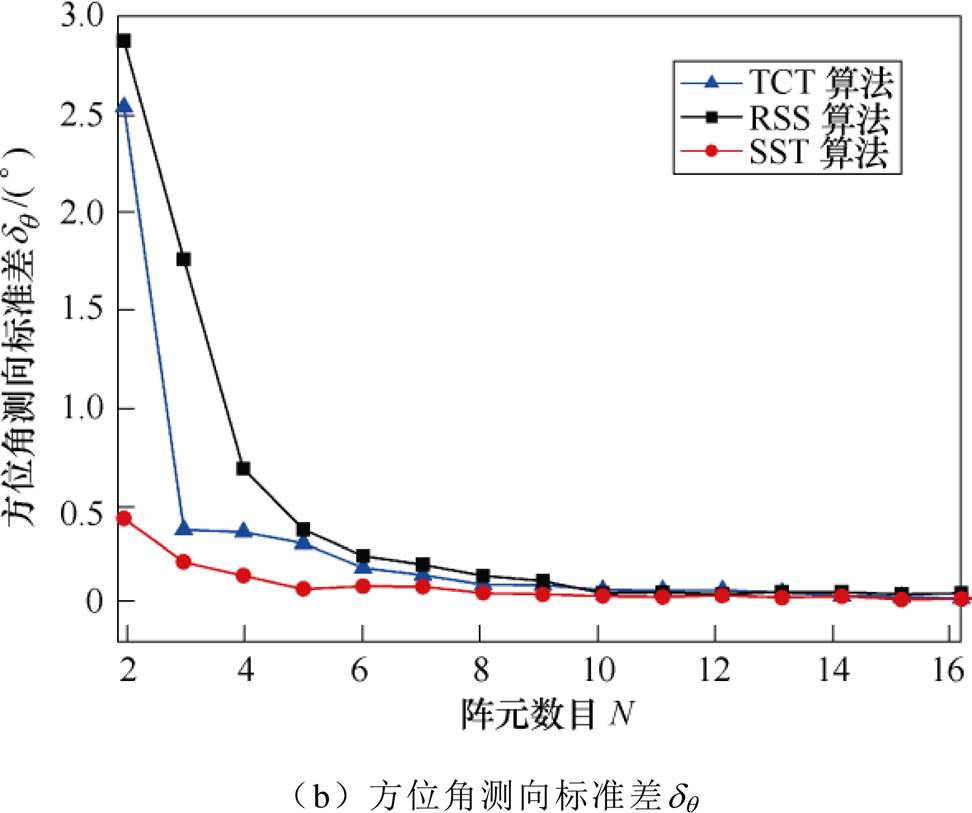
图2 阵元数目N对方位角测向性能的影响
Fig.2 Effect of number of array elements N on direction finding performance of azimuth angle
2.2.3 信噪比
方位角测向精度随信噪比的变化情况如图3所示。显然,测向精度与信号源信噪比呈正相关。当信噪比小于5dB时,TCT算法的测向精度最低,而RSS和SST算法由于进行了多次迭代,具有更强的抑制噪声干扰的能力,其中SST算法测向精度最高;当信噪比大于5dB时,TCT算法的测向偏差eq 最小,而SST算法的测向标准差dq 最小,RSS算法的eq 和dq 均最大。

图3 SNR对方位角测向性能的影响
Fig.3 Effect of SNR on direction finding performance of azimuth angle
2.2.4 入射方位角q
方位角测向精度随入射方位角的变化情况如图4所示,可见,当入射方位角越接近0°或180°,即信号入射方向越接近阵列所在轴线方向时,阵列测向误差过大,无法完成测向。以eq 和dq 小于2°时对应的入射方位角范围作为系统的有效测向范围,有效测向范围最大的是TCT算法,达到20°~165°;RSS算法次之,为25°~165°;测向范围最小的是SST算法,仅为45°~140°。当方位角为45°~140°时,TCT算法的测向偏差eq 最小,SST算法的测向标准差dq 最小,RSS算法的eq 和dq 均较大。
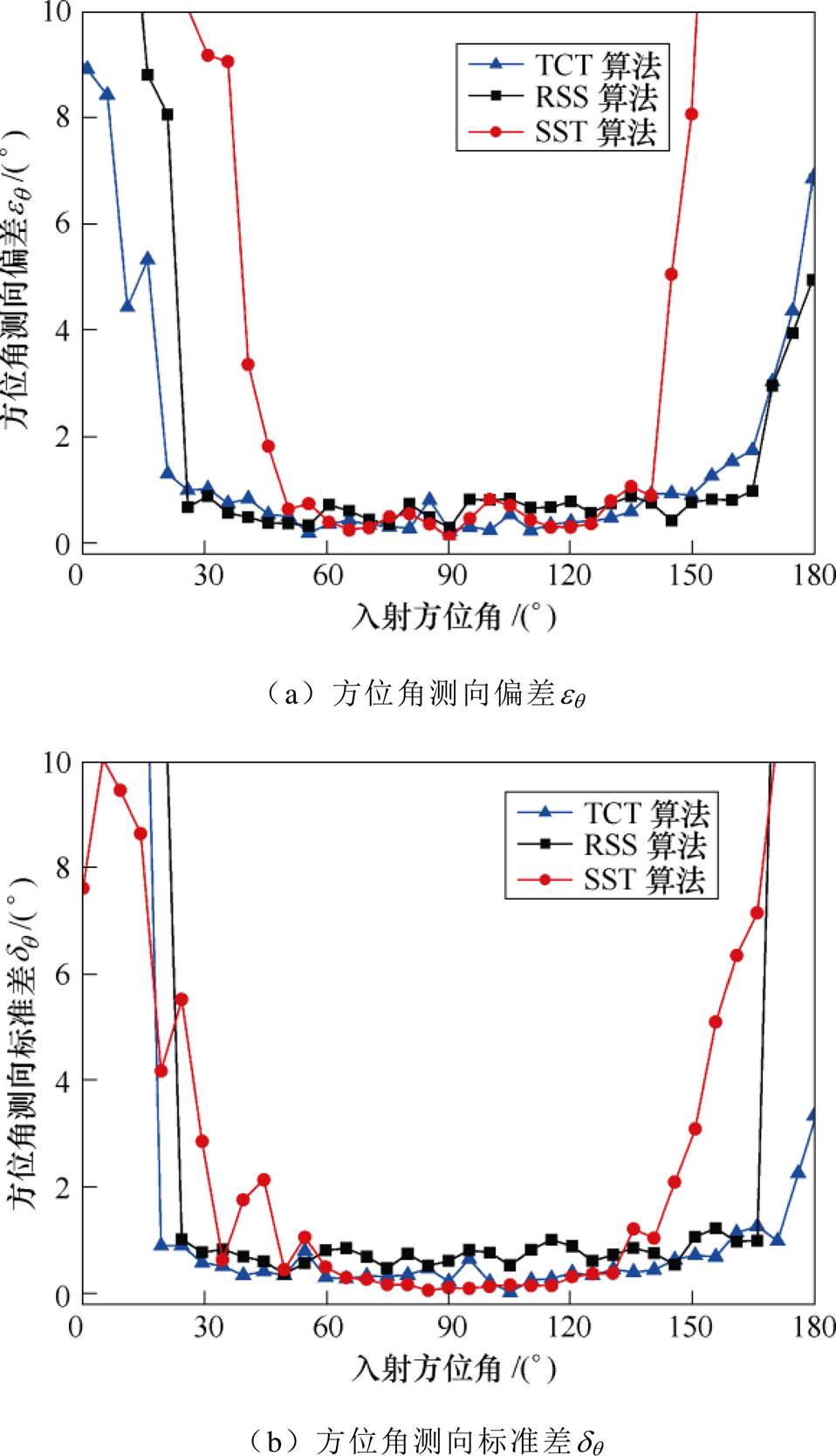
图4 入射方位角q对方位角测向性能的影响
Fig.4 Effect of incident azimuth q on direction finding performance of azimuth angle
2.2.5 小结
三种宽带聚焦算法性能对比见表2。相较而言,TCT算法运算速度最快,有效测向范围最宽,且在信噪比较高时拥有最高的测向精度,是最适合用于变电站局部放电检测的宽带聚焦算法。
分别改变阵元数目N、SNR和入射方位角q,其他参数保持不变,比较MUSIC、Root-MUSIC、ESPRIT和WSF算法的测向性能。
表2 宽带聚焦算法性能对比
Tab.2 Performance comparison of broadband focusing algorithms
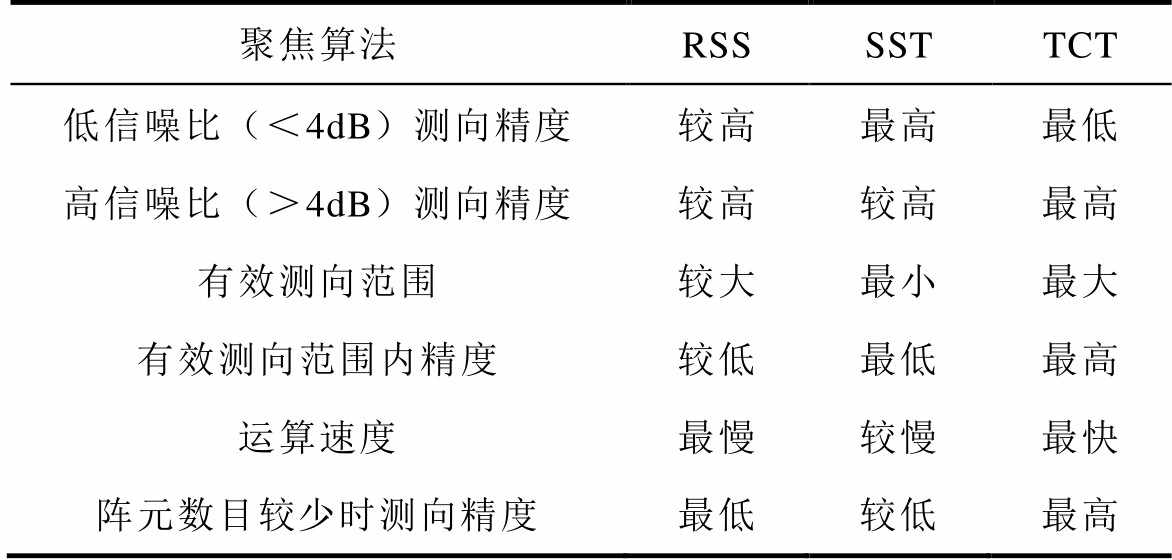
聚焦算法RSSSSTTCT 低信噪比(<4dB)测向精度较高最高最低 高信噪比(>4dB)测向精度较高较高最高 有效测向范围较大最小最大 有效测向范围内精度较低最低最高 运算速度最慢较慢最快 阵元数目较少时测向精度最低较低最高
2.3.1 阵元数目N
四种算法的方位角测向误差随阵元数目N的变化关系如图5所示。当阵元数目N<4时,方位角测向误差最小的是Root-MUSIC算法,然后依次是ESPRIT、WSF和MUSIC算法;当阵元数为3时,仅Root-MUSIC算法的eq 和dq 小于0.5°,其他算法的eq 和dq 分别在1°和2°以上;当阵元数目N从4 增长至8的过程中,测向精度有一定的提高,其中WSF算法的测向误差相对更大;当阵元数目N从9增长至16的过程中,测向精度变化不大,各算法的测向误差基本相同。
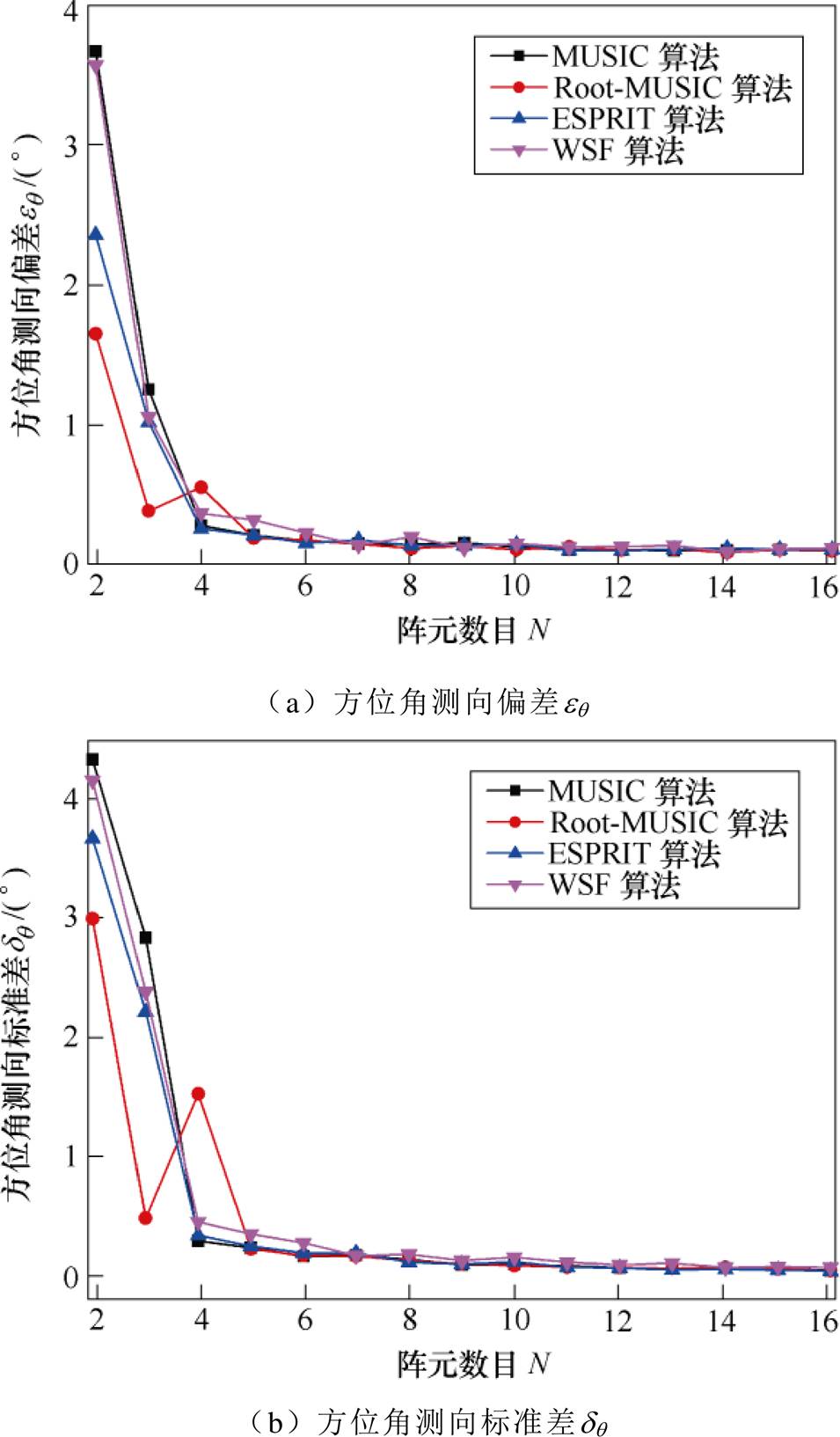
图5 阵元数目N对方位角测向性能的影响
Fig.5 Effect of number of array elements N on direction finding performance of azimuth angle
2.3.2 信噪比
四种算法的方位角测向误差随SNR的变化情况如图6所示。可见,测向误差受信噪比的影响比较大,且四种算法的变化趋势大体相同,说明系统抑制白噪声干扰的能力主要由前文选择的TCT聚焦算法决定。当信噪比大于6dB时,四种算法的eq 和dq 基本相同,小于0.42°;当信噪比在-8~6dB范围内时,MUSIC和WSF算法的测向误差相对较小,ESPRIT算法的测向误差相对较大;当信噪比小于-8dB时,各种算法的eq 和dq 分别在3°和4°以上,测向性能较差。
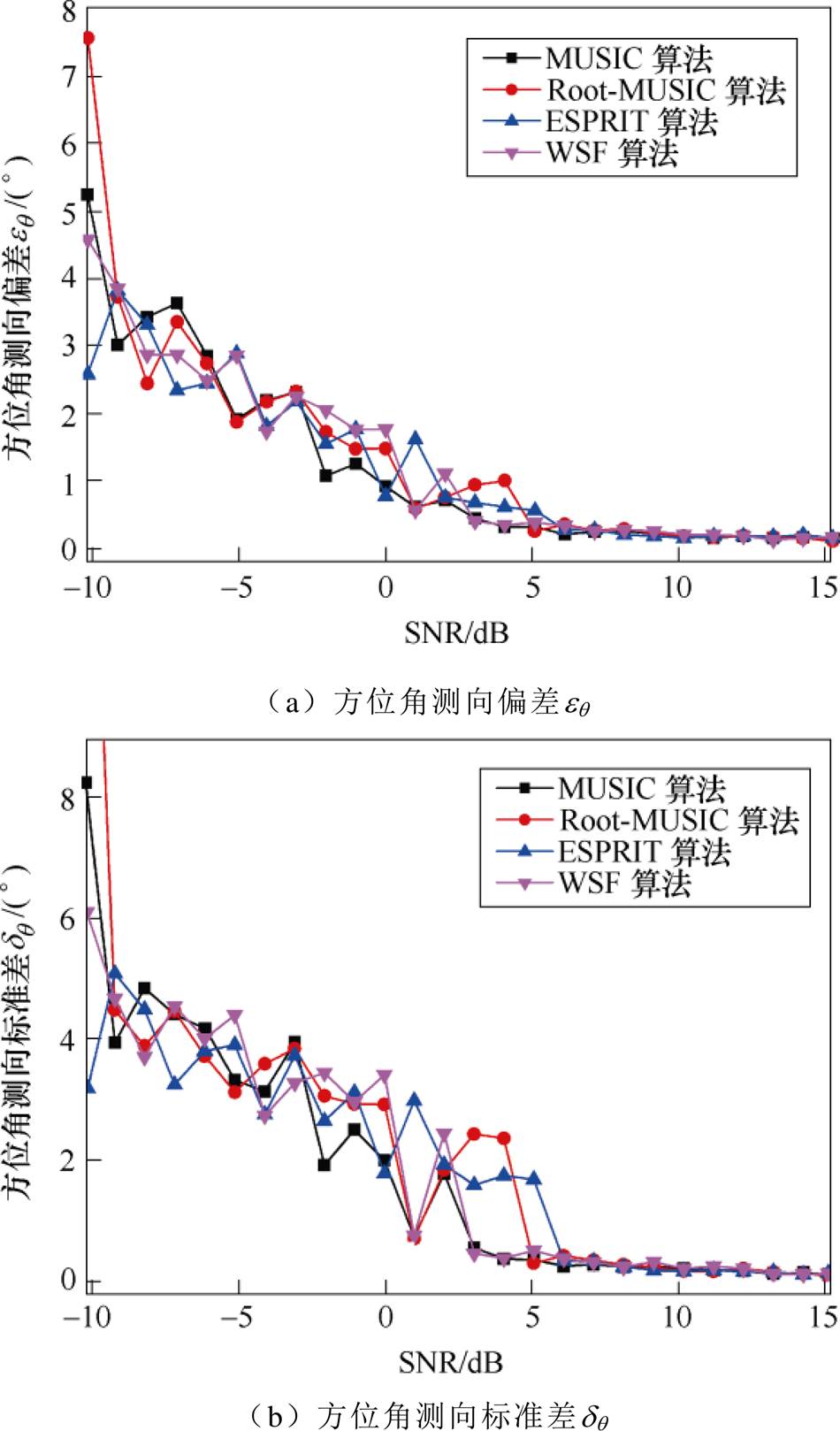
图6 SNR对方位角测向性能的影响
Fig.6 Effect of SNR on direction finding performance of azimuth angle
2.3.3 入射方位角q
四种算法的方位角测向误差随入射方位角q的变化情况如图7所示,其中入射方位角q 以5°为步长从0°增加到180°。把eq 和dq 均小于2°时对应的入射方位角范围作为系统有效测向范围,则测向范围最大的是MUSIC和WSF算法,达15°~165°;Root-MUSIC和ESPRIT算法的测向范围相对较小,分别是20°~165°和15°~160°。当入射方位角在20°~160°范围内,四种算法的测向误差基本相同。
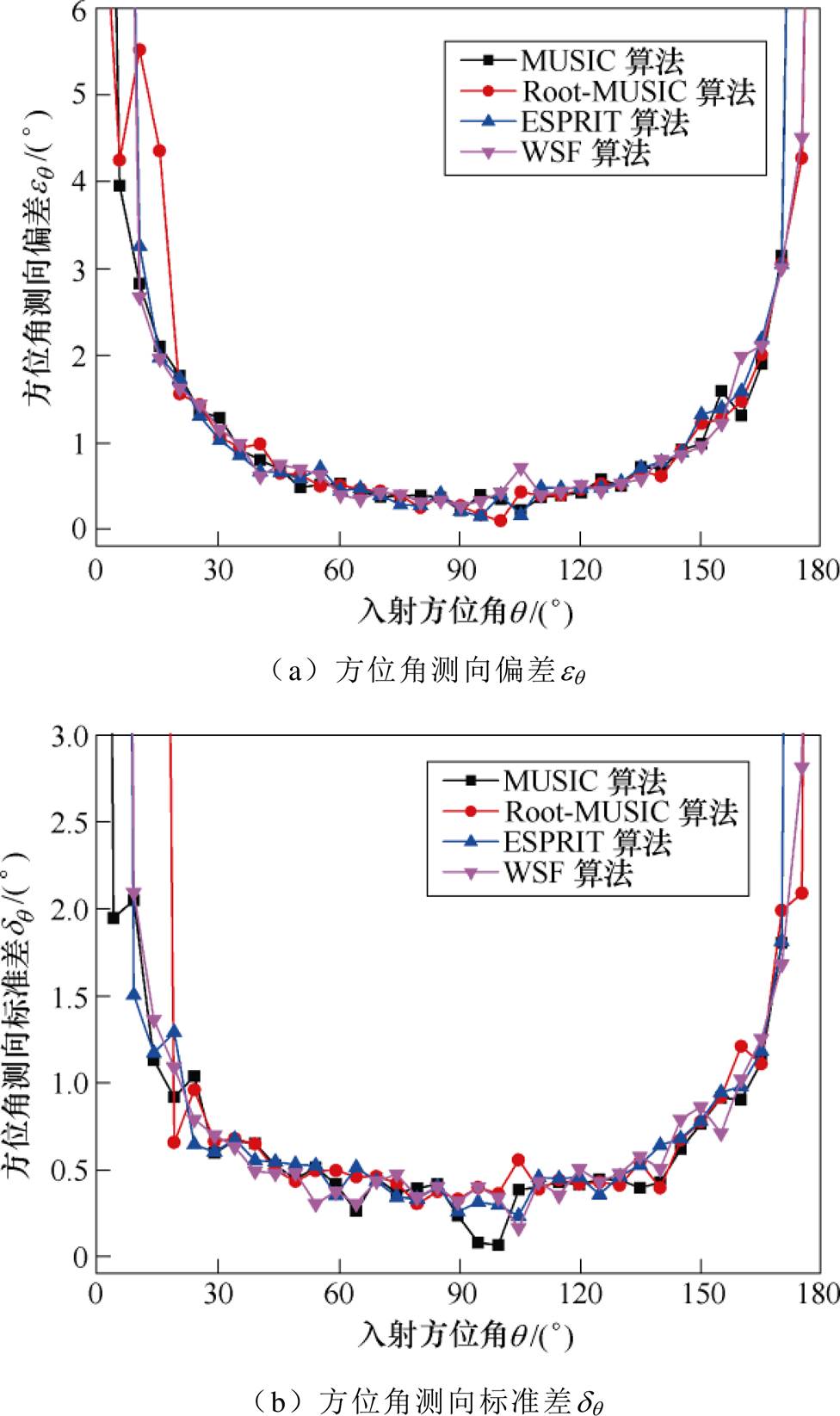
图7 入射方位角q 对方位角测向性能的影响
Fig.7 Effect of incident azimuth q on direction finding performance of azimuth angle
2.3.4 小结
由仿真可知,四种窄带测向算法性能对比见表3。相比聚焦算法,四种窄带测向算法对测向性能的影响较小。考虑到天线数量、计算速度、抑制噪声干扰能力等因素,选择Root-MUSIC算法对放电源进行窄带测向。
表3 窄带测向算法性能对比
Tab.3 Performance comparison of narrowband direction finding algorithm
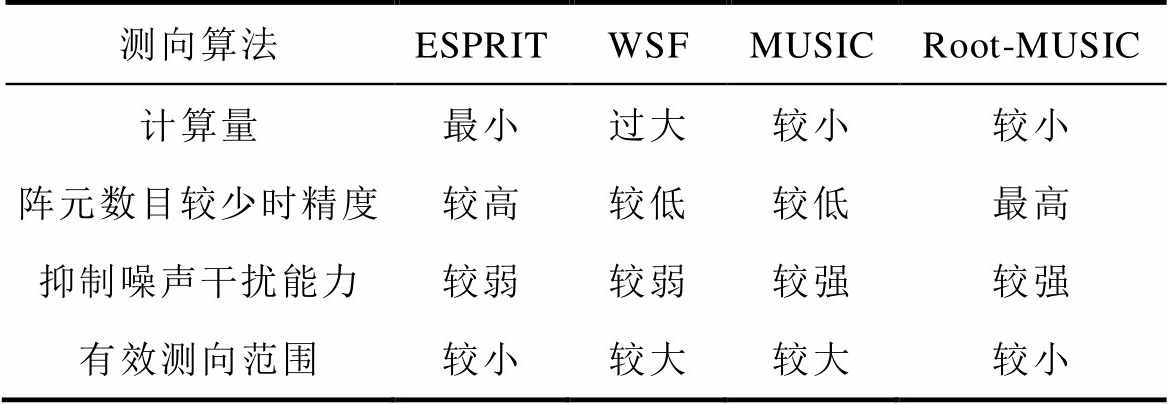
测向算法ESPRITWSFMUSICRoot-MUSIC 计算量最小过大较小较小 阵元数目较少时精度较高较低较低最高 抑制噪声干扰能力较弱较弱较强较强 有效测向范围较小较大较大较小
局部放电测向的实验模块设置见表4。为检测系统在各个方向的测向精度,局部放电源被放置于天线阵列附近的若干个位置上,其方位角分别是 0°、10°、18.5°、30.8°、48.9°、55.2°、68.5°、72.6°、81.4°。对于不同位置的放电源,采集系统将被触发100次,并由处理系统对每次采集到的信号进行波达方向估计。通过仿真可知,聚焦算法的选择对测向精度的影响较大,故在实验中对TCT、RSS和SST算法的性能作进一步对比;窄带测向算法的选择对测向误差的影响相对较小,测向性能比较接近,采用抑制噪声能力强、测向精度高的Root- MUSIC算法。
表4 局部放电测向的实验模块
Tab.4 Experimental module of partial discharge direction finding

模块指标参数 电磁信号局部放电源便携式气体放电装置 放电量/pC500 UHF信号持续时间/ns60 频谱范围/GHz0.2~0.8 采集系统天线选择全向双锥天线 天线检测频带/GHz0.3~2 阵元选择四天线均匀线阵 阵元间距/m0.2 采集卡采样率/GHz2.5 采样点数2 048
图8为三种聚焦算法方位角测向偏差和标准差随实际方位角的变化关系。显然,局部放电信号入射方位角越大,即入射方向远离天线所在轴线方向时,线阵的测向精度越高。若以eq 和dq 均在5°以内时所对应的入射方位角作为算法有效测向范围,则TCT、RSS、SST算法有效测向范围分别大于18.5°、30.8°、48.9°,可见TCT算法更具有优势。在各算法有效测向范围内,TCT、RSS、SST算法的测向偏差eq 分别小于3.2°、4.3°、3.4°,标准差dq 分别小于2.9°、4.4°、3.5°,可见TCT算法具有较宽的测向范围和较高的测向精度。

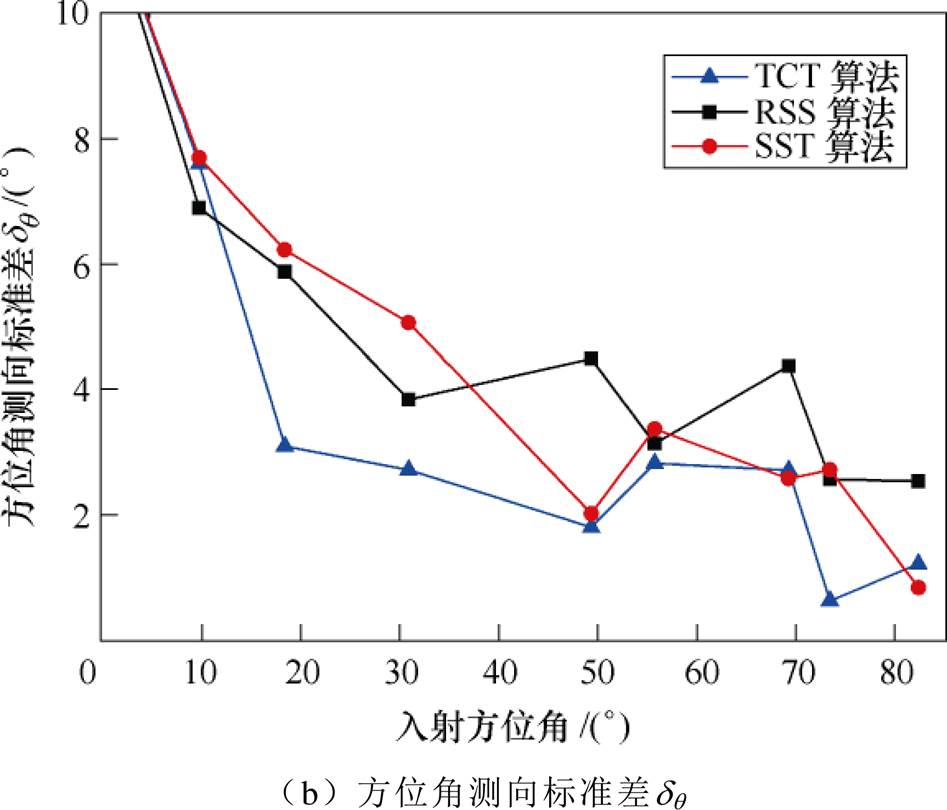
图8 实验中不同宽带聚焦算法性能对比
Fig.8 Performance comparison of different wideband focusing algorithms in the experiment
当入射方位角在算法有效测向范围以外,空间谱图上无法形成单一高瘦的谱峰,此时测向误差过大,无法完成测向。为此,在采用均匀线阵对变电站站域局部放电信号进行测向时,若发现测向标准差dq 过大,则表明真实方位角在有效测向范围之外,需移动天线阵列使其保持在高精度测向范围内。
将本文与参考文献中提到的系统的尺寸和定位精度进行对比,见表5,可以看出,本文采用的阵列间距虽然只有0.6m,但仍然具有较高的测向精度,证明了空间谱算法应用于变电站局部放电测向系统中的先进性。
表5 本文与参考文献中提到系统的尺寸和定位精度对比
Tab.5 Comparison of size and positioning accuracy with similar systems

文献天线阵列形状定位精度 [7]矩形2×4可定位到设备 [12]矩形1.16×1.58误差实测小于36cm [15]矩形50×501.58m [16]矩形/菱形2×4误差约几十cm 本文线阵0.6测向范围内误差小于3.2°
本文在数值仿真中改变信号和阵列结构参数,对比了不同宽带聚焦和窄带测向算法的测向误差,总结出各算法的优缺点;在实验室开展模拟放电源测向实验,验证算法应用于局部放电检测的可行性。得到如下结论:
1)聚焦算法对变电站站域局部放电测向性能的影响大于窄带测向算法。
2)TCT算法运算速度最快,有效测向范围最宽,在信噪比较高时拥有最高的测向精度,是最适合用于变电站局部放电检测的宽带聚焦算法。
3)Root-MUSIC算法在小阵元数目条件下测向误差最小,且抑制噪声的能力较强,运算时间较短,是最适合用于变电站局部放电检测的窄带测向 算法。
4)在实验中采用TCT和Root-MUSIC算法的测向系统,方位角测向偏差和标准差分别小于3.2°和2.9°,测向性能较好。
5)阵元数目越多、信噪比越高、入射方位角越远离线阵轴线方向、迭代次数越多,系统测向精度越高。
参考文献
[1] 李臻, 罗林根, 盛戈皞, 等. 基于压缩感知的特高频局部放电定位法[J]. 电工技术学报, 2018, 33(1): 202-208.
Li Zhen, Luo Lingen, Sheng Gehao, et al. Ultrahigh frequency partial discharge localization methodology based on compressed sensing[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 202-208.
[2] 周南, 罗林根, 宋辉, 等. 基于最大似然估计的变电站特高频局部放电定向方法[J]. 电工技术学报, 2019, 34(15): 3285-3292.
Zhou Nan, Luo Lingen, Song Hui, et al. A substation UHF partial discharge directional of arrival estimation method based on maximum likelihood estimation[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3285-3292.
[3] 张崇兴, 任明, 周洁睿, 等. 振荡操作冲击电压下绝缘子气隙缺陷局部放电特性研究[J]. 电工技术学报, 2019, 34(14): 3074-3083.
Zhang Chongxing, Ren Ming, Zhou Jierui, et al. Analysis for partial discharges behavior in SF6 gas filled void in gas insulated switchgear under oscillating switching impulses[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3074- 3083.
[4] 周波, 胡与非, 杨新春, 等. 特高频及超声波法在GIS设备带电检测中的应用[J]. 高压电器, 2019, 55(1): 54-58.
Zhou Bo, Hu Yufei, Yang Xinchun, et al. Application of ultrahigh frequency and ultrasonic method in the live detection of GIS equipment[J]. High Voltage Apparatus, 2019, 55(1): 54-58.
[5] 崔鲁, 陈伟根, 杜劲超, 等. 植物油-纸绝缘气隙放电形态及发展特征[J]. 电工技术学报, 2018, 33(3): 618-626.
Cui Lu, Chen Weigen, Du Jingchao, et al. Investi- gation on air-gap discharge patterns and development characteristics of vegetable oil-paper insulation[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 618-626.
[6] Moore P J, Portugues I E, Glover I A. Partial discharge investigation of a power transformer using wireless wideband radio-frequency measurements[J]. IEEE Transactions on Power Delivery, 2006, 21(1): 528-530.
[7] Portugues I E, Moore P J, Glover I A, et al. RF-based partial discharge early warning system for air- insulated substations[J]. IEEE Transactions on Power Delivery, 2009, 24(1): 20-29.
[8] Moore P J, Portugues I E, Glover I A. Remote diagnosis of overhead line insulation defects[C]// IEEE Power Engineering Society General Meeting, Denver, 2004: 1831-1835.
[9] 刘青, 朱明晓, 王彦博, 等. 基于特高频相控阵原理的变电站站域局部放电测向方法[J]. 中国电机工程学报, 2017, 37(20): 6126-6135.
Liu Qing, Zhu Mingxiao, Wang Yanbo, et al. Partial discharge orientation method in substation based on ultra-high frequency phased array theory[J]. Pro- ceedings of the CSEE, 2017, 37(20): 6126-6135.
[10] Liu Qing, Zhu Mingxiao, Wang Yanbo, et al. UHF antenna array arrangement optimization for partial discharge direction finding in air-insulated substation based on phased array theory[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(6): 3657-3668.
[11] Tian Ye, Tatematsu A, Tanabe K, et al. Development of locating system of pulsed electromagnetic inter- ference source based on advanced TDOA estimation method[J]. IEEE Transactions on Electromagnetic Compatibility, 2014, 56(6): 1326-1334.
[12] Hou Huijuan, Sheng Gehao, Jiang Xiucheng. Localization algorithm for the PD source in sub- station based on L-shaped antenna array signal processing[J]. IEEE Transactions on Power Delivery, 2015, 30(1): 472-479.
[13] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004.
[14] 赵拥军, 李东海, 赵闯, 等. 宽带阵列信号波达方向估计理论与方法[M]. 北京: 国防工业出版社, 2013.
[15] 王署东, 尹柏强, 何怡刚, 等. 基于正则化的变电站局部放电定位方法[J]. 中国电机工程学报, 2019, 39(6): 1825-1833.
Wang Shudong, Yin Baiqiang, He Yigang, et al. A partial discharge location method in substations based on regularization[J]. Proceedings of the CSEE, 2019, 39(6): 1825-1833.
[16] Zhu Mingxiao, Wang Yanbo, Liu Qing, et al. Localization of multiple partial discharge sources in air-insulated substation using probability-based algo- rithm[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(1): 157-166.
Optimal Selection on Spatial Spectrum Estimation Algorithms for UHF Direction Finding of Partial Discharge in Substation
Abstract The partial discharge (PD) direction finding system based on ultra-high frequency array has been tried to apply in air-insulted substation nowadays. However, the size of antenna array is too large that is not convenient for onsite application. To reduce the array size, high-resolution direction finding and focusing algorithm are used in the direction finding system. In the spatial spectrum estimation method, the PD signal is focused into narrowband signal by broadband focusing algorithm, and then the direction of arrival is obtained by narrowband direction finding algorithm. There are many kinds of broadband focusing and narrowband direction finding algorithms, and the direction finding performance of different algorithms is affected by signal-to-noise ratio, incident direction and so on. Therefore, it is necessary to study the selection of algorithms suitable for PD direction finding in substation station domain. In this paper, a PD simulation system is established. By changing the number of array elements, signal-to-noise ratio and incident azimuth angle, the performance of broadband focusing algorithms such as two-side correlation transformation (TCT), rotating signal subspace and signal subspace transform is compared; in addition, the direction finding accuracy of narrowband direction finding algorithms is compared, such as multiple signal classification, root multiple signal classification (Root-MUSIC), and signal parameter estimation via rotational invariance techniques and weighted subspace fitting. The simulation results show that TCT algorithm has the fastest operation speed, the widest effective direction finding range and the highest direction finding accuracy when the signal-to-noise ratio is high. Root-MUSIC algorithm has the smallest direction finding error when the number of array elements is small, and has strong ability of noise suppression and short calculation time. In experiments, when TCT and root MUSIC algorithm are used in PD direction finding system, the deviation and standard deviation of azimuth direction finding are less than 3.2°and 2.9°respectively, which have better direction finding performance.
keywords:Substation, partial discharge, ultra-high-frequency, direction finding, spatial spectrum estimation
中图分类号:TM855
DOI: 10.19595/j.cnki.1000-6753.tces.190821
收稿日期2019-07-02
改稿日期 2019-12-15
刘 青 男,1994年生,硕士,研究方向为局部放电检测与定位。E-mail: lq7557@qq.com
邓军波 男,1976年生,副教授,博士生导师,研究方向为局部放电检测与定位。E-mail: dengjb@mail.xjtu.edu.cn(通信作者)
(编辑 崔文静)