图1 电子雷达PPL基本结构及划分
Fig.1 Structure and its partition for digital-radar PPL
摘要 以现代电子雷达为代表的脉冲功率负载包含了大量电力电子开关器件,工作周期通常为10-2~10-1s级,若接入独立微电网运行,将给系统的安全稳定带来极大挑战。为研究脉冲功率负载接入对独立微电网系统稳定性的影响,提出基于开关函数的脉冲功率负载大信号模型。该模型基于脉冲功率负载等效拓扑结构,以三相不可控整流器、Buck变换器和直流开关负载为核心,通过分析整流器、变换器和直流开关负载各开关器件的工作状态及相应开关函数,建立脉冲功率负载与外部电网接口的电压电流动态方程。分析结果表明,采用上述模型所得出的柴油发电机组——脉冲功率负载系统频率波动率df和直流电压波动率du_dc的分析结论与实验结果相一致,验证了所提出脉冲功率负载大信号模型的正确性。
关键词:脉冲功率负载 等效拓扑 大信号模型 独立微电网
随着电力电子技术的发展,以现代电子雷达[1-2]为代表的负载包含了大量电力电子开关器件。这类负载的工作周期通常为10-2~10-1s级,一个工作周期内消耗功率并不恒定,呈典型的连续脉冲特性,表现为峰值功率约为平均功率的3~8倍[3],因此称作脉冲功率负载(Pulsed Power Load, PPL)[4]。PPL的负荷特性与传统RLC负载迥异,也不同于单次冲击运行的电动机负载,可用工作周期Ts、峰值功率PL、占空比D参数来描述[5]。当PPL作用于系统时,由于反复、频繁地加卸载作用,系统不仅要满足瞬时的高功率需求,还要在控制上及时响应脉冲功率切换引起的连续冲击。尤其当PPL接入以柴油发电机组为分布式电源的独立微电网时,因系统惯性小、承受负荷扰动的能力较弱,不仅引起系统频率和电压的快速波动,且波动范围也很大,给微电网的安全稳定运行带来极大挑战。
微电网的稳定问题可分为小信号稳定和大信号稳定两个方面,其中前者常采用小信号模型[6-9],假设系统状态始终处于平衡点附近。当PPL作用于系统时,PPL的频繁负荷投切使系统状态在各切换点之间迁移,且很难保证始终位于平衡点附近,因此采用PPL小信号模型[10-12]分析系统稳定问题具有局限性,宜通过建立PPL大信号模型,分析系统的大信号稳定性。
由文献[5, 11]可知,不可控整流器和DC-DC变换器是PPL负载结构中的重要组成部分。在不可控整流器和DC-DC变换器大信号建模方面,已有文献[13-15]开展了相关研究。其中,马凡等针对船舶、飞机等独立电力系统中常见的电能变换单元,建立了电流断续模式(Discontinuous Current Mode, DCM)下不可控整流器的大信号模型[13];杜韦静等针对常见的电力电子级联系统,基于功率守恒原理建立了DC-DC变换器在不同工作模式下的统一大信号模型[14-15]。另一方面,开关函数在电力电子变流器建模中具有重要作用,例如,文献[16]利用开关函数建立了模块化多电平换流器模型,并用于直流电网;文献[17]通过变流器的开关函数建模,研究了空间矢量调制的最优控制策略;文献[18-19]基于开关函数模型研究了不对称故障下的系统特性。上述研究成果均为建立PPL大信号模型提供了思路。
为此,本文延续文献[5]的工作,在所提出PPL等效拓扑的基础上,通过分析PPL各开关器件的工作状态,进一步提出了基于开关函数的PPL大信号模型。分析表明,采用上述模型所得出的柴油发电机组——脉冲功率负载系统频率和直流电压波动分析结论与实验结果相一致,验证了所提出PPL大信号模型的正确性。
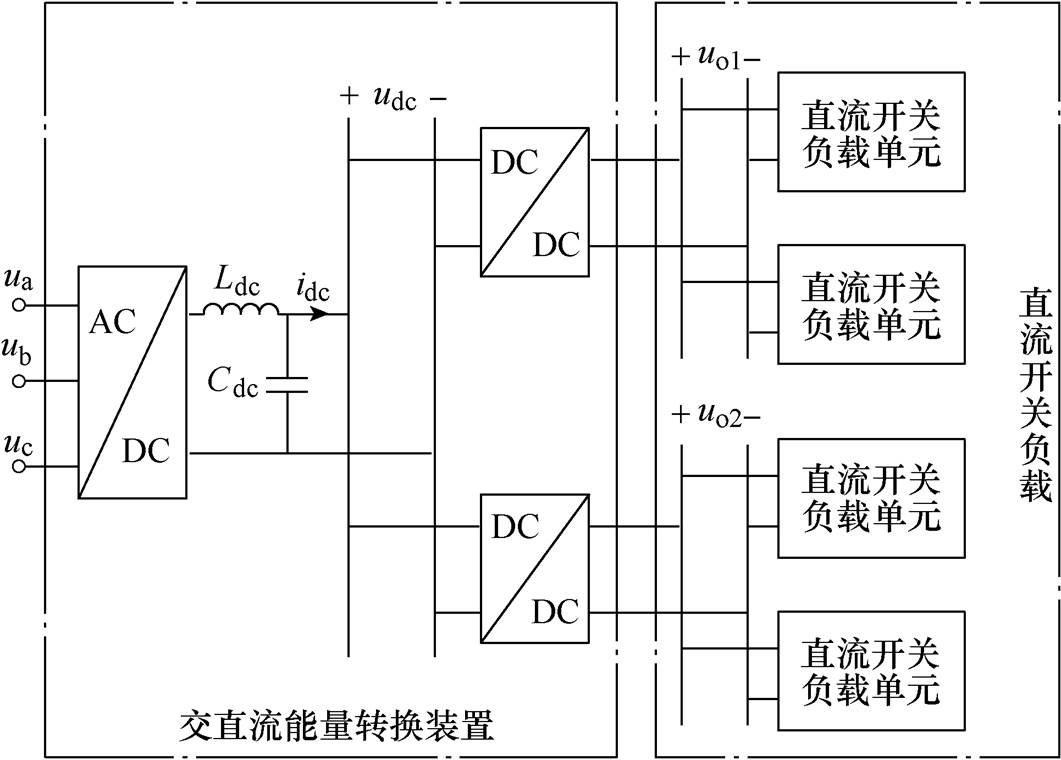
图1给出了现代电子雷达PPL的基本结构和划分,包括AC-DC变换器、DC-DC变换器、直流开关负载单元等,其末端供电方式为直流电压。图中,udc为直流母线电压,uo1、uo2为直流开关负载供电电压,ua、ub、uc为三相电压,Ldc为平波电抗,Cdc为波波电容;idc为直流母线电流,三相电源的输出经AC-DC变换器向直流母线供电,因直流母线电压等级较高,再经DC-DC变换后向开关负载供电。

图1 电子雷达PPL基本结构及划分
Fig.1 Structure and its partition for digital-radar PPL
由于具体设备的内部电路各不相同,为便于研究,将图1所示PPL结构划分为交直流能量转换装置和直流开关负载两个部分。通过对上述两个部分分别采取等效方法建立相应的拓扑,得出了如图2所示的脉冲功率负载等效拓扑结构。图2中,ia、ib、ic为三相输入电流,LC为换相电抗,VD1~VD6为整流桥臂上的二极管;Rcon为Buck电路等效内阻,Buck电路由开关VTB控制,VD7为续流二极管,Lf、Cf为滤波电感、电容,iLf、iCf分别为流经Lf、Cf的电流;io为Buck电路输出电流,io流入直流开关负载,该负载由开关VTL控制通断,RL为其等效电阻;Ton表示开关VTL的导通时间,占空比D表示为Ton与Ts的比值。
对比图1和图2可知,图2采用开关器件串联电阻的方式等效直流开关负载,且保留了DC-DC变换器在直流电压稳定控制中的作用,以不可控整流器级联DC-DC变换器的方式对交直流能量转换部分进行等效。该等效方式与传统的相控整流器级联LC滤波器的等效方式[12]相比,更接近PPL的基本结构,具体分析可详见文献[5]。
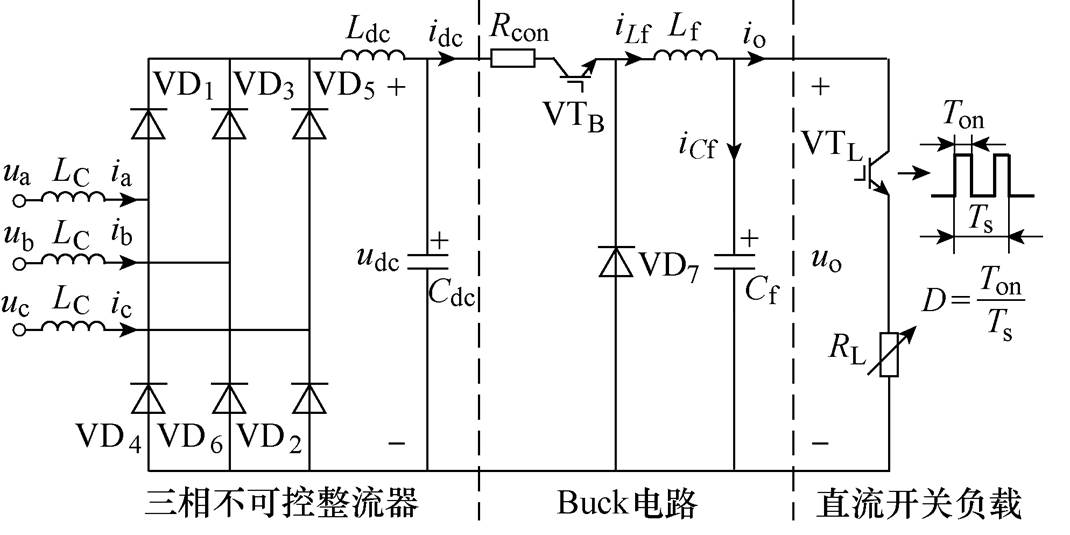
图2 脉冲功率负载等效拓扑结构
Fig.2 Novel equivalent topology of PPL
图2给出的PPL等效拓扑中,三相不可控整流器、Buck变换器、直流开关负载等各部分均含有电力电子器件,通常由开关函数控制,利用开关函数建立大信号分析模型已成为电力电子化的电力系统暂态分析的常用方法之一[20]。图3标识了脉冲功率负载各器件的开关函数,包括整流器开关函数Sa(t)、Sb(t)、Sc(t),Buck变换器开关函数ST(t),以及直流开关负载的开关函数SL(t)。通过开关函数的时域表达式即可给出图3所示电压、电流关系,从而建立脉冲功率负载开关函数模型。
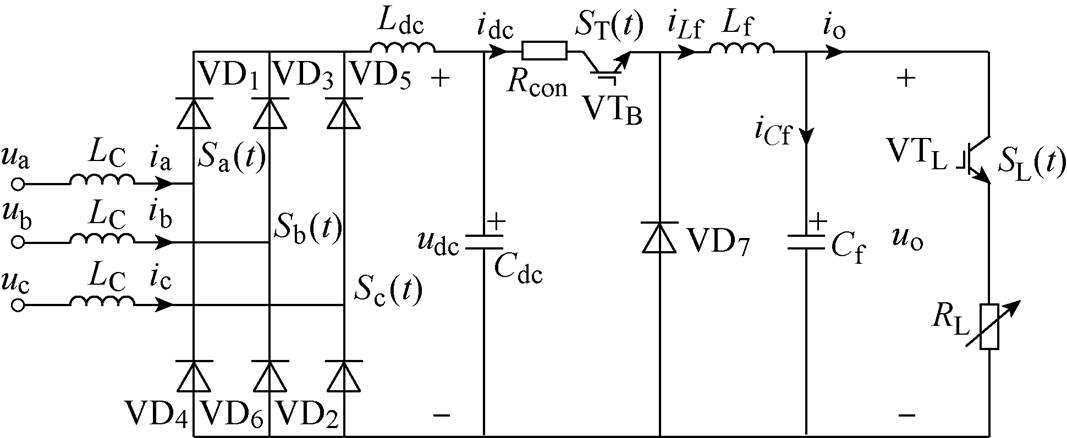
图3 脉冲功率负载中各器件的开关函数模型
Fig.3 Switching function model of devices in PPL
由图3可知,脉冲功率负载运行时不可控整流器交直流两侧电压、电流与开关函数Sa(t)、Sb(t)、Sc(t)有关,而Buck变换器的输出电压和电流分别与开关函数ST(t)和SL(t)有关。具体分析如下。
2.1.1 三相不可控整流器开关函数Sa(t)、Sb(t)、Sc(t)
不可控整流器的运行状态与触发延迟角a =0°的相控整流器相同,则根据三相桥式电路工作原理,得出各相桥臂的导通时序。以a相桥臂上的二极管VD1和VD4为例,设交流电压频率为w,当0≤wt<2p/3时,VD1导通;当p ≤wt<5p/3时,VD4导通。因此开关函数Sa(t)可表示为
 (1)
(1)将式(1)按Fourier级数展开,可得
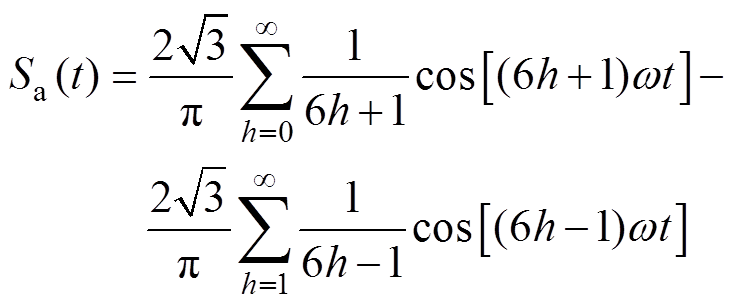 (2)
(2)
同理,可得三相不可控整流器开关函数Sb(t)和Sc(t)的表达式分别为
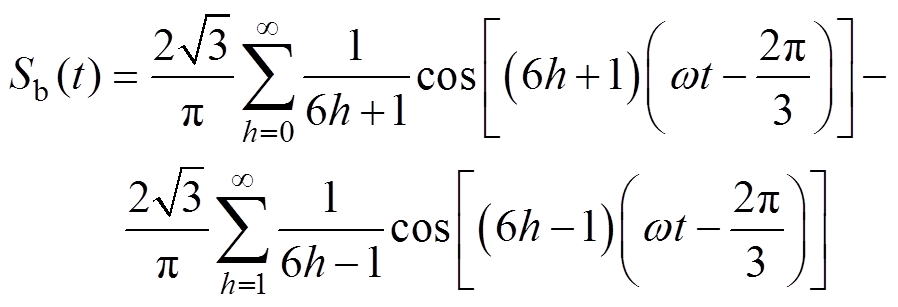 (3)
(3)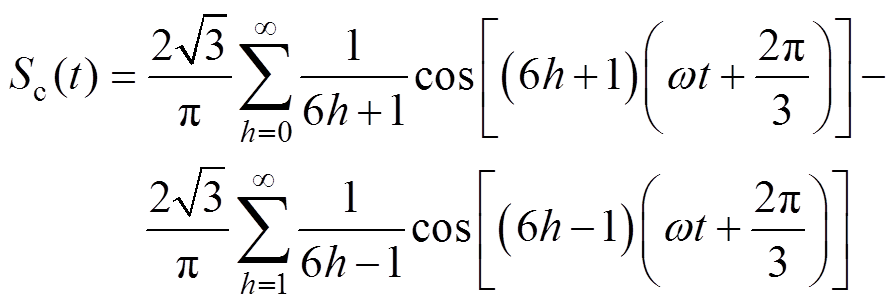 (4)
(4)
2.1.2 Buck变换器开关函数ST(t)
由Buck变换器工作原理可知,图3中开关器件VTB的导通受开关函数ST(t)的控制。开关函数ST(t)可表示为
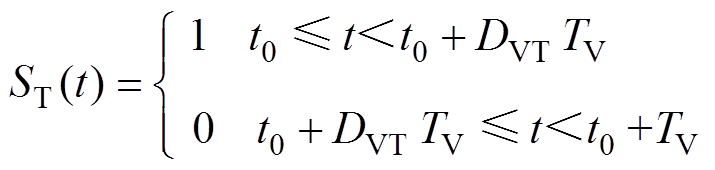 (5)
(5)式中,t0为初始时间,当ST(t)=1时,VTB导通;开关工作周期TV由器件VTB的PWM开关频率决定;占空比DVT由Buck变换器的电压控制策略决定。若已知Buck变换器的工作周期TV和占空比DVT,则可将式(5)按Fourier级数展开成时域表达式为
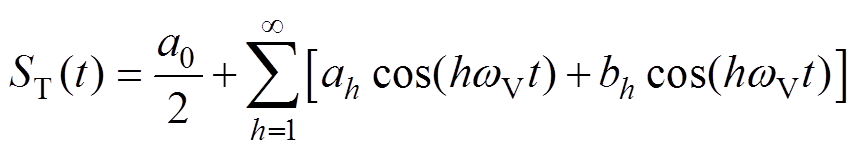 (6)
(6)
式中
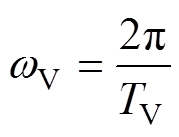 (7)
(7)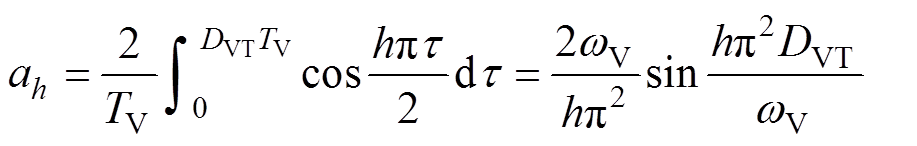 (8)
(8)
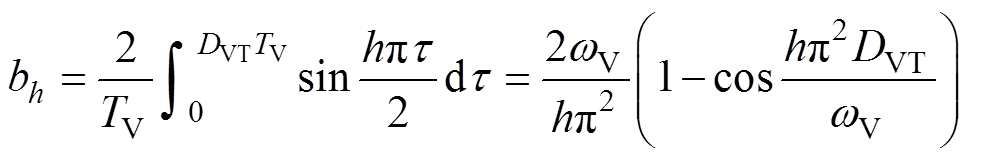 (9)
(9)
式中,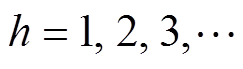 。
。
2.1.3 直流负载开关函数SL(t)
由脉冲功率特性可知,图3中开关器件VTL的导通与PPL的工作模式相关。VTL的开关函数SL(t)可表示为
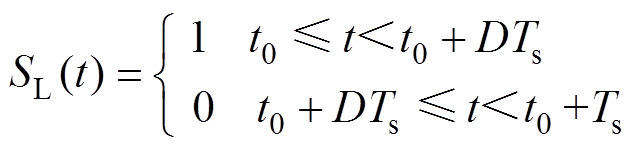 (10)
(10)式中,Ts、D分别为脉冲功率负载工作周期、占空比。当ST(t)=1时VTL导通,直流负载加载。
与式(6)的形式接近,开关函数ST(t)也可展开为Fourier级数,即
 (11)
(11)式中
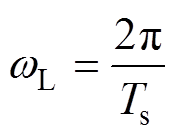 (12)
(12)
为建立PPL大信号模型,须得到PPL等效拓扑结构中交流侧接口的电压、电流的完整时域表达式。首先,由三相不可控整流器工作原理可知,直流电压udc和三相电流ia、ib、ic可分别表示为
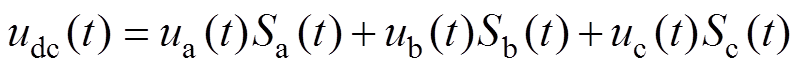 (13)
(13)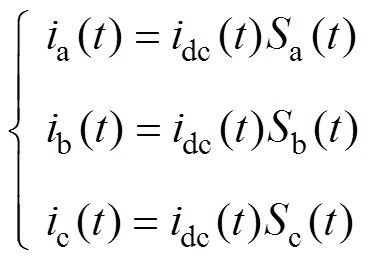 (14)
(14)
式中,直流电流idc与PPL的工作电流有关。
由于图3中VTL的工作周期通常为10-2~10-1s级(对应频率为10~100Hz),而VTB的开关频率大于等于1kHz,以至于当PPL工作时,易出现VTB导通、VTL截止、电容Cf充电的情况,此时Buck变换器输出电流io处于断续工作状态;又因图3中电容Cf取值较大(通常达103~104mF级),当io=0时电容Cf的充电时间很短,易形成充电饱和,此时电感电流iLf =0,Buck变换器工作在断续电流模式(Discon- tinuous Current Mode, DCM)下。因此,考虑图3中的开关VTL具有两种状态,Buck变换器工作在DCM下具有三种状态,则PPL直流部分具有2×3=6种状态,脉冲功率负载直流部分的运行状态如图4所示,图中用粗实线和箭头标识电流流过的路径。
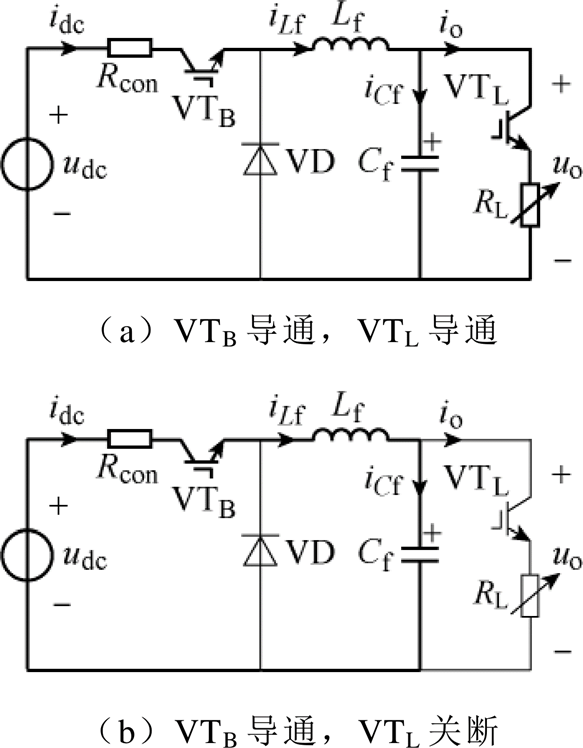
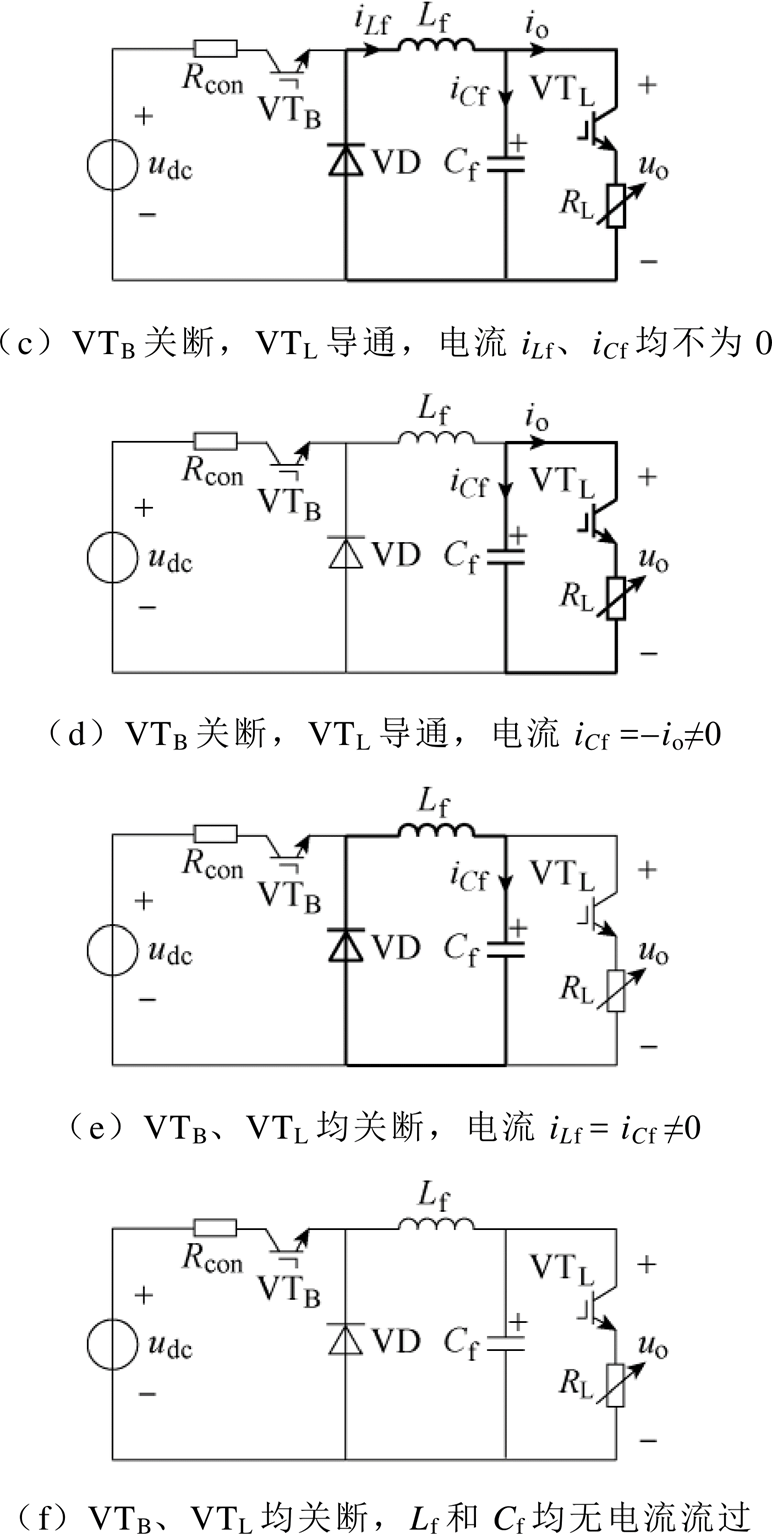
图4 脉冲功率负载直流部分的运行状态
Fig.4 Operating condition of DC circuit in PPL
已知开关VTB、VTL分别由ST(t)、SL(t)控制,则通过图4可得出PPL与外部电网交互时的直流电压、电流关系为
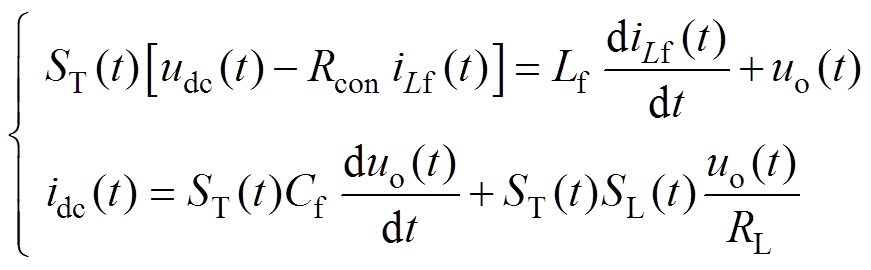 (15)
(15)由式(13)~式(15)可知,udc、idc既分别与ua、ub、uc和ia、ib、ic有关,也与uo及开关函数ST(t)、SL(t)有关,反映了PPL接入下的电压、电流动态。联立式(2)~式(4)、式(6)~式(9)和式(11)~式(15)即可得出PPL与外部电网接口的电压、电流完整时域表达式。据此,PPL大信号模型可写成微分-代数方程(DAE)的形式为
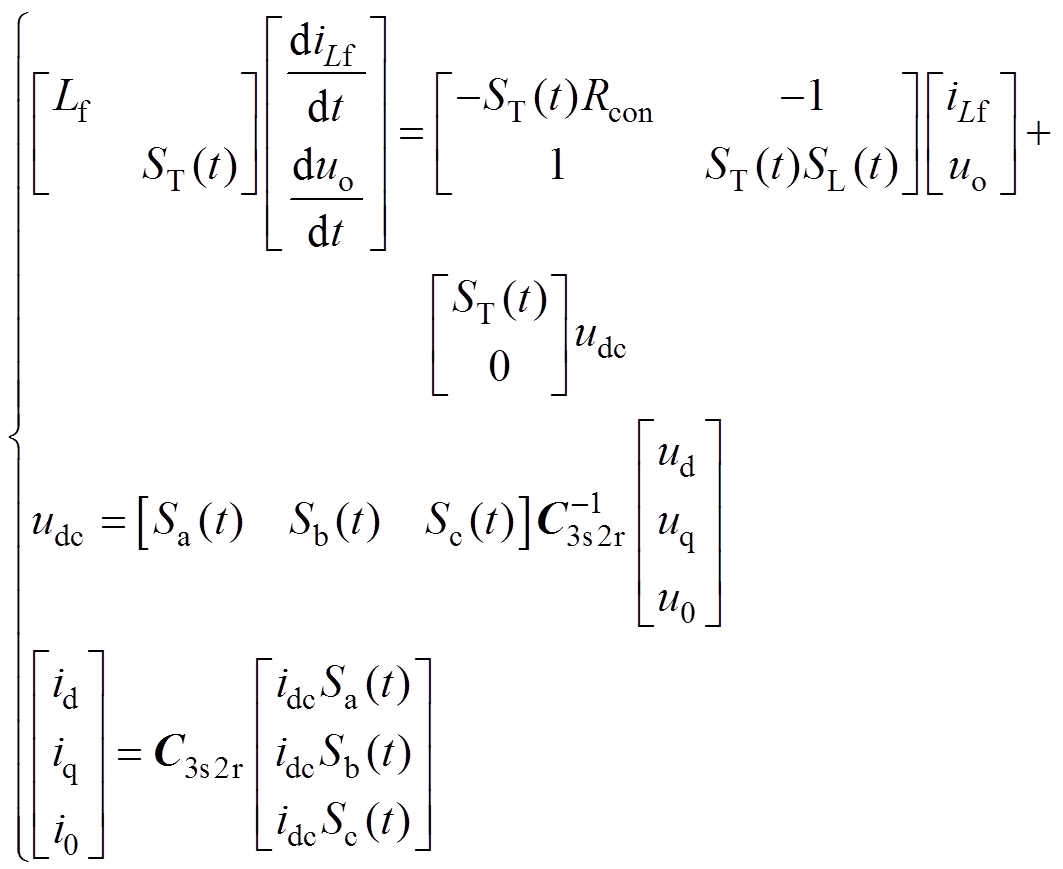 (16)
(16)
式中,C3s2r为Park变换矩阵;电压ud、uq、u0和电流id、iq、i0为PPL与外部电网的接口电压和电流,可与dq0坐标下的同步发电机模型[22]相对应。由式(16)可知,PPL模型中的非线性动态主要由开关函数表示,因而称为基于开关函数的PPL大信号模型。假设Buck变换器工作在DCM下,文中所讨论PPL模型主要适用于Buck变换器开关频率wV远大于直流负载开关频率wL的电子雷达脉冲功率负载。
图5给出了由柴油发电机组和PPL构成的算例系统,将2.2节给出的PPL开关函数模型与柴油发电机组模型联立,可得出相应的系统分析模型,其中柴油机控制模型和同步发电机模型详见文献[21-22]。在配置2.30GHz双核处理器、8G内存的计算机上,用软件Maple 18编程实现上述系统分析模型,通过刻画系统状态轨迹,分析PPL参数变化对系统频率和直流母线电压的影响。设PPL模型中DC-DC变换器电感Lf=0.19mH、电容Cf =2 800mF,开关器件VTB的开关频率为1kHz;受电压控制策略的影响,占空比DVT在0.60~0.76(pu)之间变化。其他算例参数见附表1和附表2。
图6给出了PPL工作周期Ts=60ms、峰值功率PL=0.6(pu)条件下,柴油发电机组——脉冲功率负载系统相轨迹极限环随占空比D的变化情况。
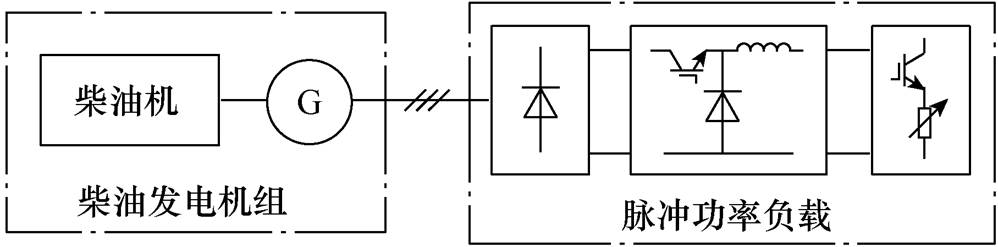
图5 算例系统结构
Fig.5 Brief topology of study case
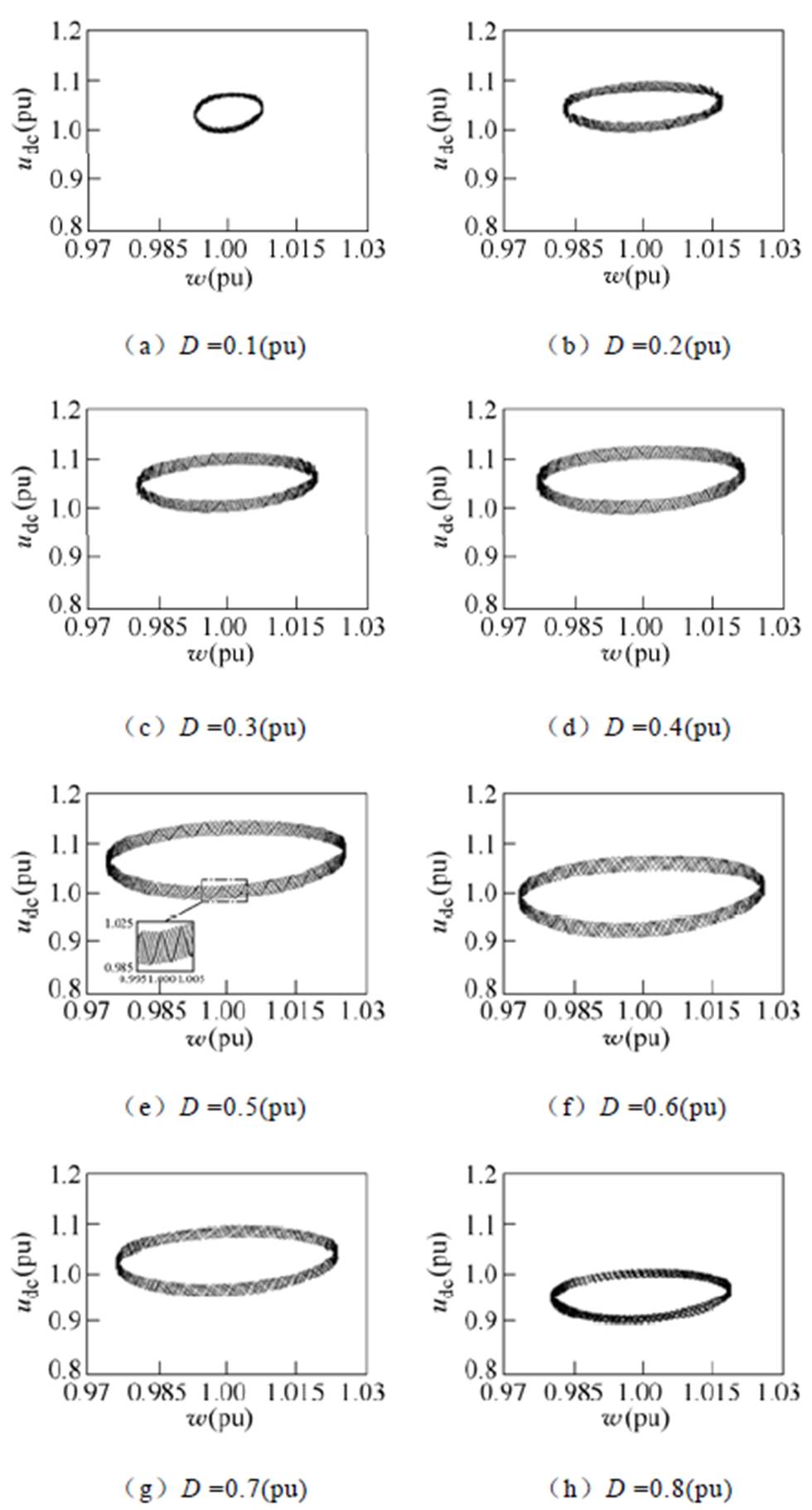
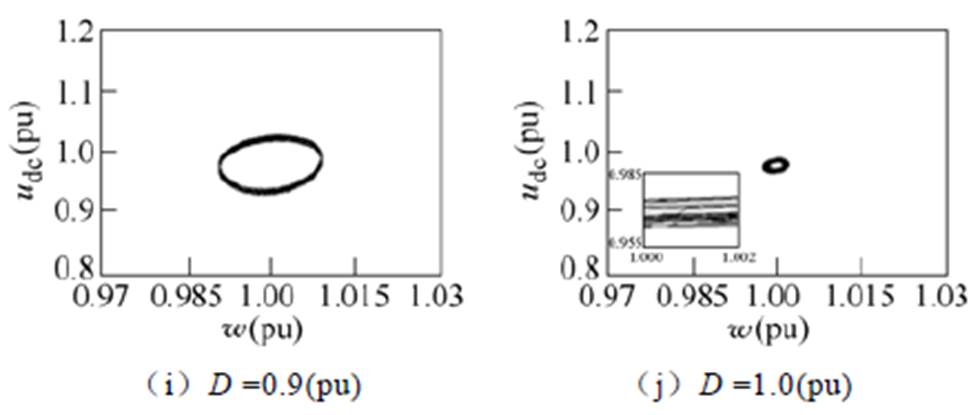
图6 改变占空比条件下的柴油发电机组——脉冲功率负载系统相轨迹极限环
Fig.6 Limit cycles of the diesel generator system with PPL at different duty ratio
对于如图5所示的系统,由于开关器件的切换作用,若系统稳定则相轨迹收敛于极限环[20]。从图6可以看出,因PPL作用下系统状态在连续加卸载过程中频繁切换,使得相轨迹显现出弯折现象,表现为极限环存在一定的宽度。当D =0.1~1.0(pu)时系统轨迹均收敛于极限环,表明在上述条件下系统可稳定运行。然而,当占空比由0.1(pu)升至0.3(pu)时,系统极限环所围成面积显著增大,同时极限环的宽度也相应增加,表明当D =0.1~0.3(pu)时,系统频率和电压波动幅度明显增大,不利于稳定;当D =0.3~0.7(pu)时,从相轨迹上可明显看出由脉冲功率冲击造成的轨迹弯折现象,此时的极限环所围成面积呈现出“先增大、后减小”趋势(最大值在D = 0.5~0.6(pu)区间),但变化幅度与D =0.1~0.3(pu)时相比较为缓和;当D =0.7~1.0(pu)时,极限环所围成面积迅速减小,表明脉冲功率冲击明显减弱。可见,随占空比D的变化,系统相轨迹极限环总体呈现“先增大、后减小”趋势,当D =0.3~0.7(pu)时,系统频率和电压波动幅度相对较大,不利于系统稳定。
根据图6中的相轨迹,可按式(17)和式(18)计算各PPL工况下的系统频率波动率df和直流电压波动率du_dc,并拟合相应的df和du_dc曲线。
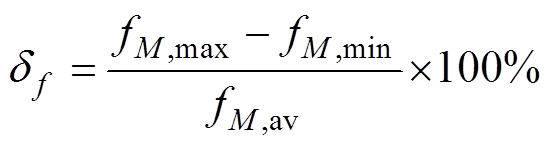 (17)
(17)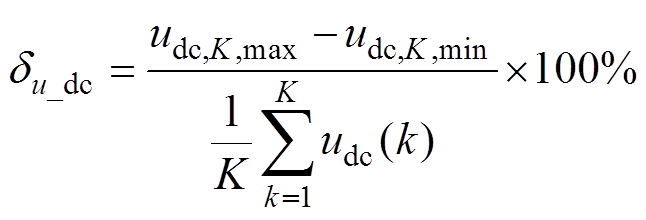 (18)
(18)
式中,fM,max、fM,min、fM,av分别为连续采样M个交流电压周波频率的最大值、最小值、平均值;udc,K,max、udc,K,min分别为连续K个采样点得到的直流母线电压最大值、最小值;udc(k)为第k个采样点得到的直流母线电压瞬时值。
依据图2给出的等效拓扑设计了如图7所示PPL模拟装置结构(已授权专利号:ZL201721588371.1),并构建由50kW柴油发电机组和最大峰值功率为50kW的PPL组成的实验系统。实验中,参照3.1节的算例参数,设置PPL工作周期Ts=60ms、峰值功率PL=0.6(pu),占空比D从0.1~1.0(pu)变化(间隔0.1(pu))。按式(17)和式(18)计算各PPL工况下系统频率波动率df和直流电压波动率du_dc,进一步得出如图8所示的df、du_dc拟合曲线,并与3.1节算例分析得出的df和du_dc拟合曲线相比较。
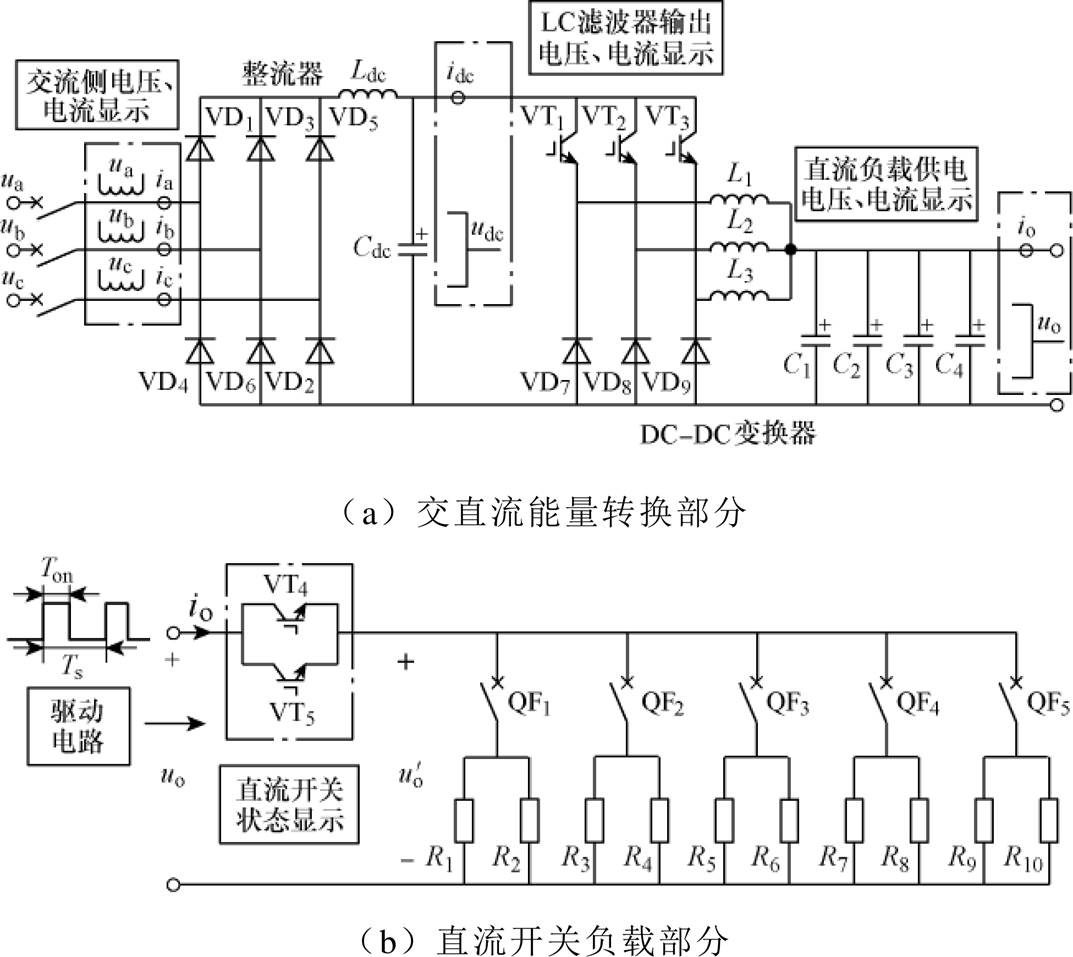
图7 PPL模拟装置结构
Fig.7 Diagram of topology for PPL simulator
由图8a可知,随占空比D增大,频率波动率δf呈现“先增大、后减小”趋势,峰值顶点位于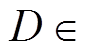
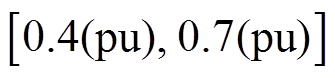 区间;图8b中,直流电压波动率du_dc在
区间;图8b中,直流电压波动率du_dc在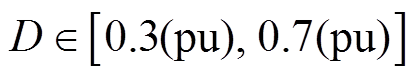 内数值较大,呈现“中间高、两侧低”的趋势。图8中算例和实验结果之间的相对误差见表1,由表1可知,上述最大相对误差小于5.9%,算例和实验结果趋势一致。
内数值较大,呈现“中间高、两侧低”的趋势。图8中算例和实验结果之间的相对误差见表1,由表1可知,上述最大相对误差小于5.9%,算例和实验结果趋势一致。
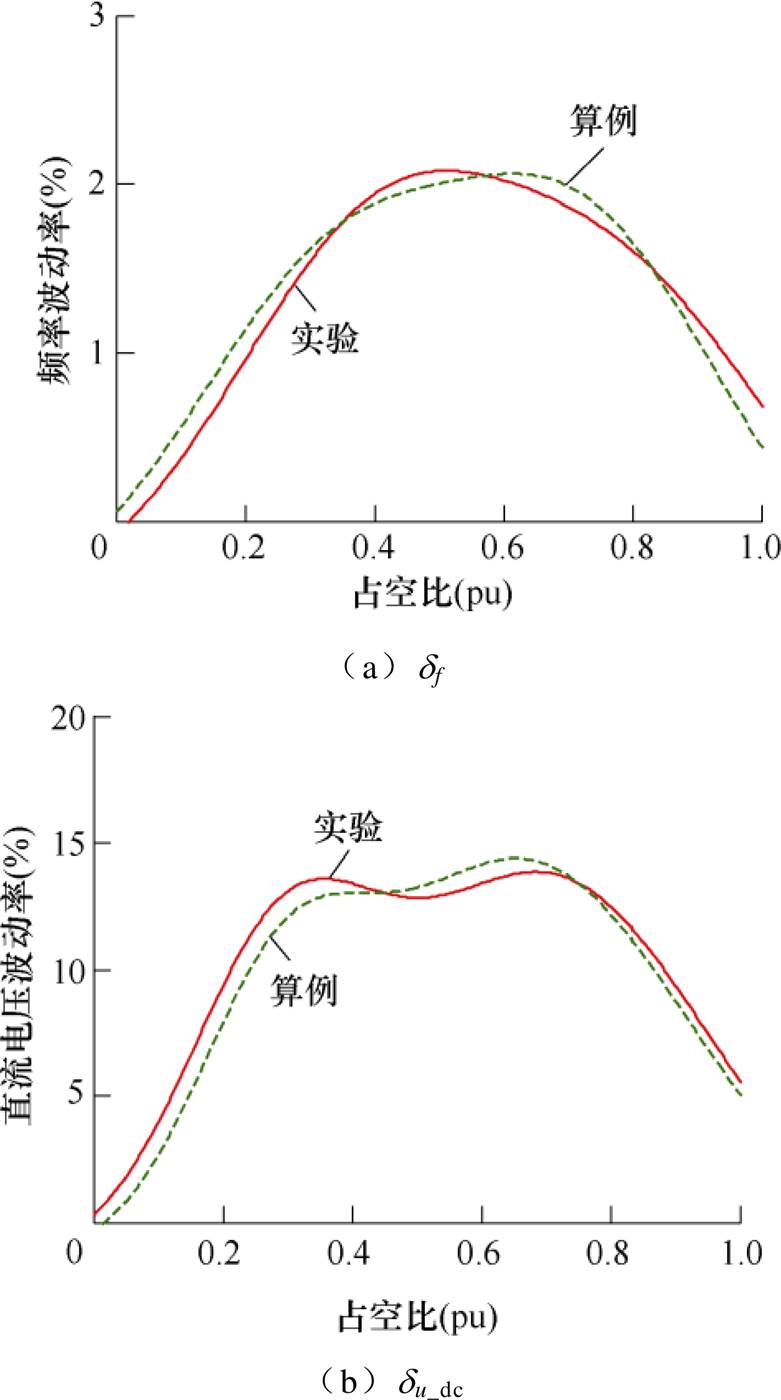
图8 频率和直流电压波动率拟合曲线
Fig.8 Fitting curves of fluctuation ratio for frequency and DC voltage
表1 算例和实验结果之间的相对误差
Tab.1 Relative error between the study case and test
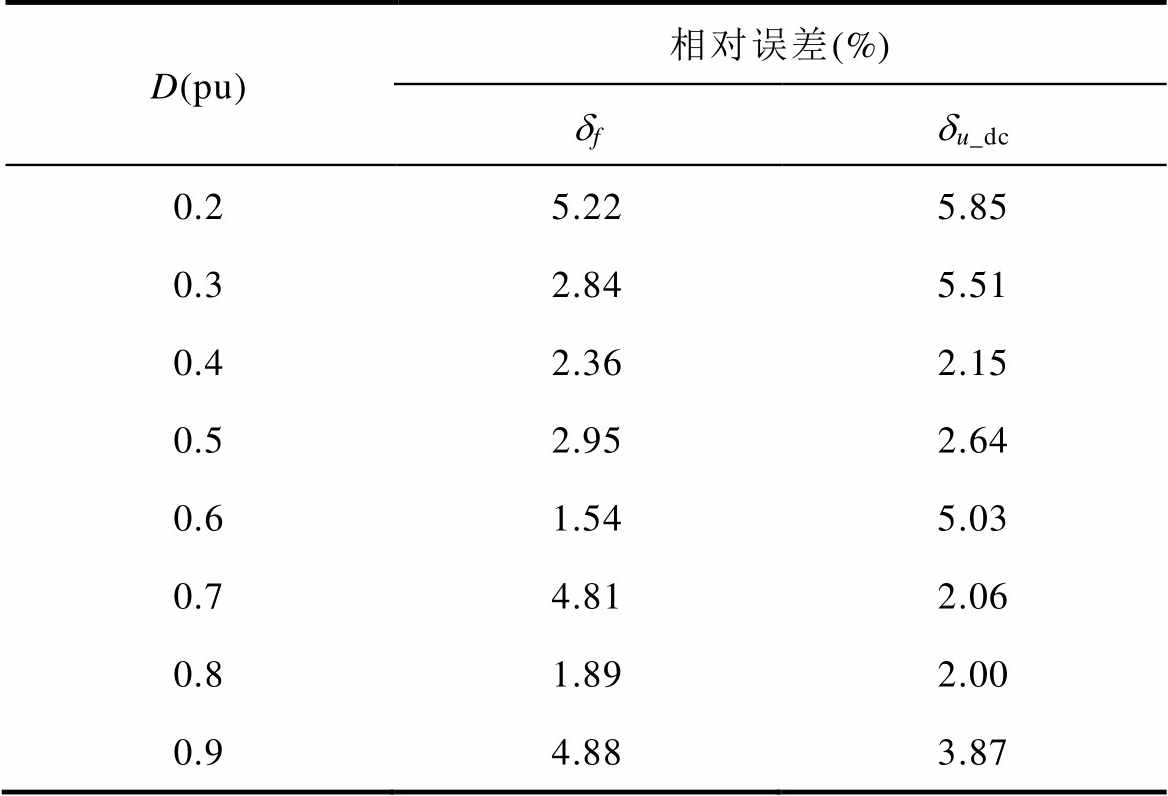
D(pu)相对误差(%) dfdu_dc 0.25.225.85 0.32.845.51 0.42.362.15 0.52.952.64 0.61.545.03 0.74.812.06 0.81.892.00 0.94.883.87
本文以现代电子雷达为例,通过分析PPL等效拓扑结构中各开关器件的工作状态,提出了基于开关函数的PPL大信号模型。分析表明,采用上述模型后得出的柴油发电机组——脉冲功率负载系统频率波动率df和直流电压波动率du_dc的分析结论与实验结果相一致,验证了该PPL大信号模型的正确性。
文中所建立的PPL大信号模型为研究独立微电网中微电源(如柴油发电机)与PPL相互作用关系,以及系统大信号稳定性分析提供了模型基础。下一步工作是基于PPL大信号模型,进一步分析PPL峰值功率、占空比、脉冲工作周期等参数对独立微电网系统稳定性的影响规律。
柴油发动机及调速系统可表示为如附图1所示的控制框图[21],附图中,w、wref为发动机转速及其参考值,uRG、uTH分别为转速调节器和油门执行器输出,Tm为机械转矩。3.1节算例分析涉及的柴油发动机及调速系统参数见附表1。

附图1 柴油发动机及调速系统控制框图
App.Fig.1 Block diagram of diesel engine and its speed control
附表1 柴油发动机及调速系统算例参数
App.Tab.1 Study-case parameters for diesel engine and its speed control

参数数值(pu) 调速器控制参数1 T10.2 调速器控制参数2 T20.01 调速器控制参数3 T30.000 2 执行器控制参数1 T40.25 执行器控制参数2 T50.009 执行器延迟时间常数T60.384 涡轮增压器增益KTU15.0 机组等效延迟时间常数TDEG0.024
进一步地,由文献[22]可知,与同步发电机有关的参数包括电机绕组参数和励磁系统参数,3.1节算例分析涉及的同步发电机及励磁系统参数见附表2。
附表2 同步发电机及励磁系统算例参数
App.Tab.2 Study-case parameters for synchronous generator and its field control
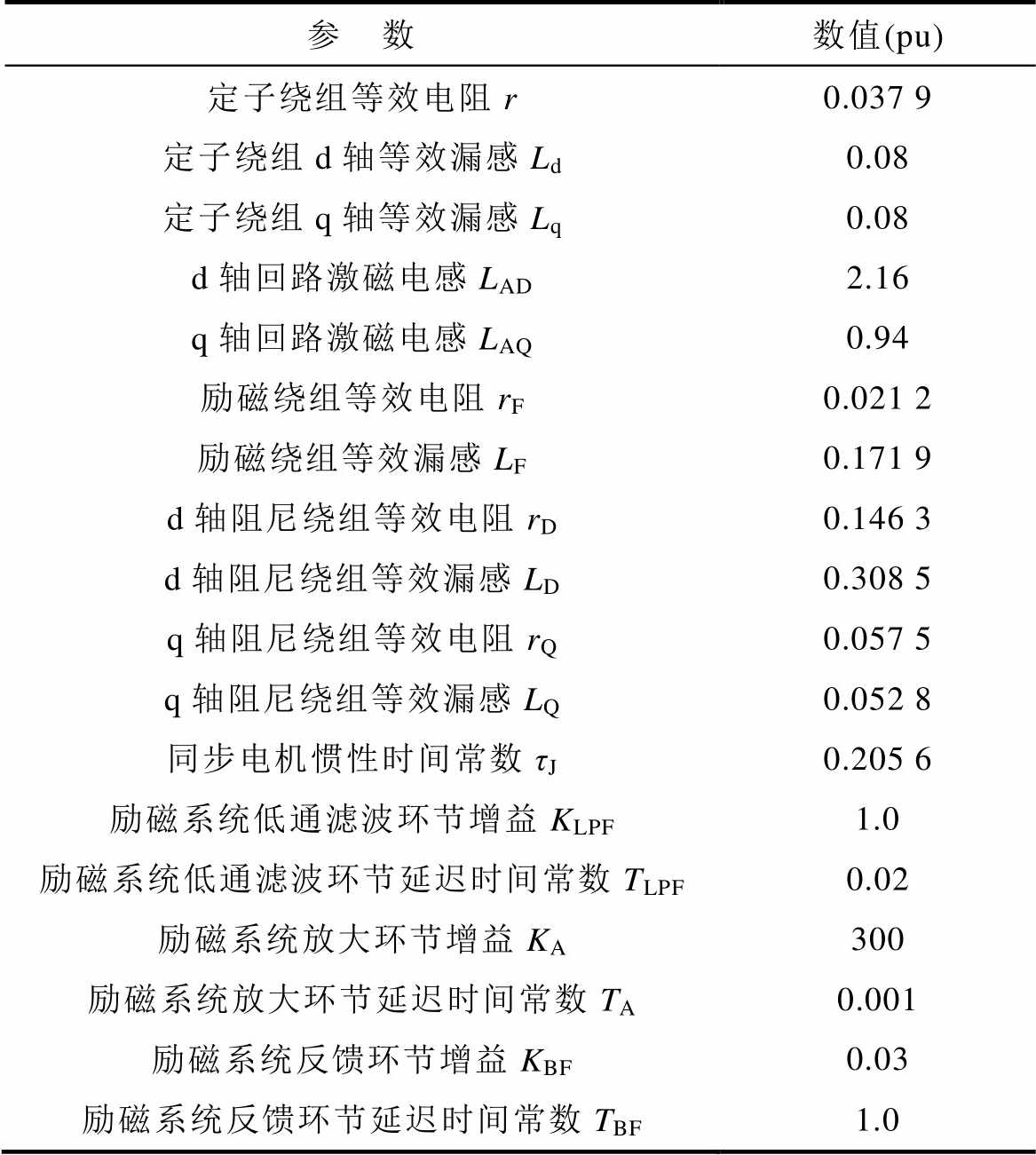
参数数值(pu) 定子绕组等效电阻r0.037 9 定子绕组d轴等效漏感Ld0.08 定子绕组q轴等效漏感Lq0.08 d轴回路激磁电感LAD2.16 q轴回路激磁电感LAQ0.94 励磁绕组等效电阻rF0.021 2 励磁绕组等效漏感LF0.171 9 d轴阻尼绕组等效电阻rD0.146 3 d轴阻尼绕组等效漏感LD0.308 5 q轴阻尼绕组等效电阻rQ0.057 5 q轴阻尼绕组等效漏感LQ0.052 8 同步电机惯性时间常数τJ0.205 6 励磁系统低通滤波环节增益KLPF1.0 励磁系统低通滤波环节延迟时间常数TLPF0.02 励磁系统放大环节增益KA300 励磁系统放大环节延迟时间常数TA0.001 励磁系统反馈环节增益KBF0.03 励磁系统反馈环节延迟时间常数TBF1.0
参考文献
[1] 郑玉军, 田康生, 刘俊凯, 等. 早期预警雷达和多功能相控阵雷达的目标指示交接方法[J]. 兵工学报, 2017, 38(1): 106-113.
Zheng Yujun, Tian Kangsheng, Liu Junkai, et al. The target designation and handover method of early- warning radar and multifunction phased array radar[J]. Acta Armamentarii, 2017, 38(1): 106-113.
[2] Fulton C, Salazar J L, Zhang Y, et al. Cylindrical polarimetric phased array radar: beamforming and calibration for weather applications[J]. IEEE Transa- ctions on Geoscience and Remote Sensing, 2017, 55(5): 2827-2841.
[3] Huang Xinze, Ruan Xinbo, Du Fangjun, et al. High power and low voltage power supply for low frequency pulsed load[C]//Proceedings of the 32nd Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA: 2859- 2865.
[4] Arnaud C, Basataud D, Nebus J, et al. An active pulsed RF and pulsed DC load-pull system for the characterization of HBT power amplifiers used in coherent radar and communication systems[J]. IEEE Transactions on Microwave Theory & Techniques, 2016, 48(12): 2625-2629.
[5] 严鋆, 王金全, 黄克峰, 等. 脉冲功率负载等效拓扑及潮流计算模型分析[J]. 电工技术学报, 2018, 33(23): 5523-5531.
Yan Jun, Wang Jinquan, Huang Kefeng, et al. Analysis of equivalent topology and power-flow calculation model for pulsed power load[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(23): 5523-5531.
[6] Li Z, Shahidehpour M. Small-signal modeling and stability analysis of hybrid AC/DC micro-grids[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 2080- 2095.
[7] 曾绍桓, 周国华, 周述晗, 等. 电流型控制三态Boost变换器的小信号建模与负载瞬态特性分析[J].电工技术学报, 2019, 34(7): 1468-1477.
Zeng Shaohuan, Zhou Guohua, Zhou Shuhan, et al. Small-signal modeling and load transient characteristic analysis of current mode controlled tristate Boost converter[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1468-1477.
[8] Leitner S, Yazdanian M, Mehrizi-Sani A, et al. Small-signal stability analysis of an inverter-based microgrid with internal model-based controllers[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5393- 5402.
[9] 季宇, 王东旭, 吴红斌, 等. 提高直流微电网稳定性的有源阻尼方法[J]. 电工技术学报, 2018, 33(2): 370-379.
Ji Yu, Wang Dongxu, Wu Hongbin, et al. The active damping method for improving the stability of DC microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 370-379.
[10] Hou Pengfei, Xu Ye, Li Jianke, et al. A pulsed load model and its impact on a synchronous-rectifier system[J]. International Journal of Electronics, 2017, 104(2): 343-354.
[11] Elsayed A T, Youssef T A, Mohammed O A. Modeling and control of a low-speed flywheel driving system for pulsed-load mitigation in DC distribution networks[J]. IEEE Transactions on Industry Applications, 2016, 52(4): 3378-3387.
[12] 李建科. 脉冲负载下微电网运行特性及储能系统虚拟惯量技术研究[D]. 南京: 解放军理工大学, 2015.
[13] 马凡, 马伟明, 付立军, 等. 直流侧电流断续时不控整流器的动态大信号数学模型建立与验证[J]. 中国电机工程学报, 2010, 30(12): 36-42.
Ma Fan, Ma Weiming, Fu Lijun, et al. Dynamic large signal modeling and validation of diode rectifiers operating in discontinuous current mode[J]. Proceedings of CSEE, 2010, 30(12): 36-42.
[14] 杜韦静, 张军明, 张阳, 等. 一种新型研究Boost电路大信号稳定性的模型[J]. 电工技术学报, 2013, 28(3): 188-194.
Du Weijing, Zhang Junming, Zhang Yang, et al. A novel model for the large-signal stability analysis of Boost converter[J]. Transactions of China Electro- technical Society, 2013, 28(3): 188-194.
[15] Du Weijing, Zhang Junming, Zhang Yang, et al. Stability criterion for cascaded system with constant power load[J]. IEEE Transactions on Power Electro- nics, 2013, 28(4): 1843-1851.
[16] 孙谦浩, 李亚楼, 宋强, 等. 基于桥臂基波平均开关函数的MMC模型在直流电网仿真中的应用[J].电力自动化设备, 2018, 38(8): 24-30.
Sun Qianhao, Li Yalou, Song Qiang, et al. Application of MMC model based on arm fundamental wave average switching function in DC grid simulation[J]. Electric Power Automation Equipment, 2018, 38(8): 24-30.
[17] 李遥, 许烈, 李永东. 模块化多电平矩阵变换器开关次数最优的拓扑连接策略[J]. 电工技术学报, 2018, 33(2): 342-352.
Li Yao, Xu Lie, Li Yongdong. Topology connecting strategy of the modular multilevel matrix converter for optimal switching times[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 342-352.
[18] 李子林, 汪娟娟, 李瑶佳, 等. 基于实际换相电压过零点的高压直流换流器开关函数建模[J]. 中国电机工程学报, 2017, 37(18): 5389-5398.
Li Zilin, Wang Juanjuan, Li Yaojia, et al. A switching function model of HVDC converters based on actual zero crossing points of commutating voltages[J]. Proceedings of CSEE, 2017, 37(18): 5389-5398.
[19] 范志华, 苗世洪, 刘子文, 等. 模块化多电平换流器子模块故障特性分析与解耦控制策略[J]. 电工技术学报, 2018, 33(16): 3707-3718.
Fan Zhihua, Miao Shihong, Liu Ziwen, et al. Modular multilevel converter sub-module fault characteristics analysis and decoupling control strategy[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(16): 3707-3718.
[20] 朱蜀, 刘开培, 秦亮, 等. 电力电子化电力系统暂态稳定性分析综述[J]. 中国电机工程学报, 2017, 37(14): 3948-3962.
Zhu Shu, Liu Kaipei, Qin Liang, et al. Analysis of transient stability of power electronics dominated power system: an overview[J]. Proceedings of the CSEE, 2017, 37(14): 3948-3962.
[21] 林岩, 张建成. 含虚拟同步发电机的光/柴/储独立微网控制策略[J]. 电网技术, 2017, 41(4): 1277- 1284.
Lin Yan, Zhang Jiancheng. Control strategy of islanded photovoltaic-diesel-storage microgrid with virtual synchronous generator[J]. Power System Technology, 2017, 41(4): 1277-1284.
[22] Anderson P M, Fouad A A. 电力系统控制与稳定[M]. 王奔, 译. 北京: 电子工业出版社, 2012.
Study on Large-Signal Model for Pulsed Power Load Based on Switching Functions
Abstract As the representative of pulsed power load (PPL), the modern electronic radar contains a large number of power-electronic devices, and the working cycle of the radar usually ranges from 10-2s to 10-1s. If it is connected to an isolated microgrid, its operation mode will bring great challenges to the safety and stability of the microgrid system. In order to analyze the influence of PPL on the stability of the isolated microgrid, this paper proposed a large-signal model for PPL based on the switching functions. This model adopted a novel equivalent topology of PPL, which consists of a three-phase diode rectifier, a Buck converter and a DC switching load. By analyzing the operation states and switching functions of power electronic components for the rectifier, converter and switching load, this model established the equations of dynamic voltages and currents for the interface between the PPL and the external grid. Based on the PPL modeling, a diesel generator system with PPL could be modeled, and the corresponding indicators such as the fluctuation ratios of frequency and DC voltage, df and du_dc respectively, could be analyzed. The analyzing results indicate that the tendencies of df and du_dc solved by the model consist with those from the test under the same conditions, which verifies the correctness of the proposed large-signal model for PPL.
keywords:Pulsed power load, equivalent topology, large-signal model, isolated microgrid
中图分类号:TM71
DOI: 10.19595/j.cnki.1000-6753.tces.190849
国家自然科学基金(51861135312)和江苏省自然科学基金(BK20190574)资助项目。
收稿日期 2019-07-17
改稿日期 2019-09-02
严 鋆 男,1985年生,博士,研究方向为独立微电网分析与保护。E-mail: yanjunnorton@126.com
沈 沉 男,1970年生,博士,教授,研究方向为电力系统的分析与控制。E-mail: shenchen@mail.tsinghua.edu.cn(通信作者)
(编辑 陈 诚)