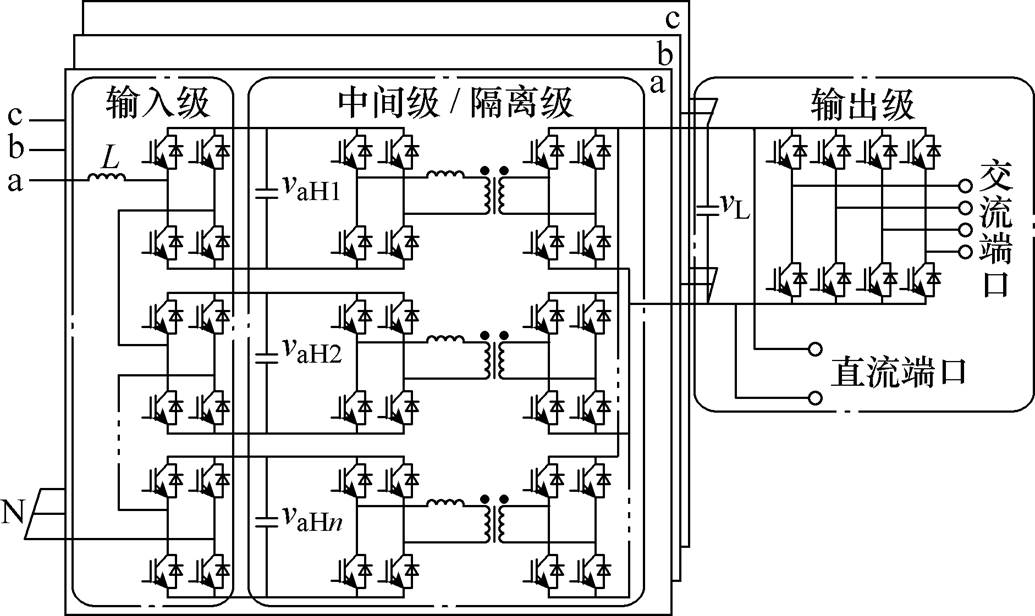
图1 SST拓扑结构
Fig.1 Topology of the SST
摘要 故障重合闸是配电网提高供电可靠性的有效手段，采用电力电子技术集成的多端口固态变压器（SST）受控制策略的影响显著，面对配电网重合闸时的运行机制不明晰。基于此，该文研究重合闸机制下SST的运行特点，通过分析指出，若不采用一定的控制策略，SST在面对重合闸时将可能出现过电流，进而提出结合光伏电源接入的冲击电流抑制策略来提升SST的运行能力。首先，该文简析SST的拓扑结构与控制策略，并分析重合闸过程中SST冲击电流产生机理；其次，根据不同的初始工况以及输入级最大允许电流求得光伏电源功率调整的范围进行功率补偿，并提出冲击电流抑制策略；最后，通过仿真与实验验证了该文理论分析与所提策略的正确性与有效性。
关键词：固态变压器 自动重合闸 冲击电流 光伏电源
随着智能电网、能源互联网等未来电网技术的快速发展，一种能够替代传统电力变压器的多端口固态变压器（Solid State Transformer, SST）得到了越来越广泛的应用和关注[1-3]。SST除了能够实现传统变压器电压等级变化、电气隔离外，还能够实现故障隔离、功率调校与控制等功能，因此成为未来智能电网、能量互联网中的重要电能变换设备，其主要应用于轨道交通系统、智能电网/能源互联网和分布式可再生能源发电并网系统[4-9]。
目前，针对固态变压器拓扑结构与基础控制策略的研究已较为全面。在拓扑结构方面，固态变压器以三级式结构居多，包括输入级、隔离级和输出级；在控制策略方面，可以分为采用输入级均压、隔离级均功率[10-12]和采用隔离级均压、输入级均功率两大类[13]。多端口固态变压器作为一种应用于电力系统中新型的电力变压器和大容量电力电子变流器，其稳定性与可靠性是评价其性能的重要指标。然而，由于SST输入级与电网相连，电网发生故障时，会直接影响到SST的稳定运行，因此，针对电网故障下，SST的故障穿越控制受到了国内外众多学者的关注和研究。
当电网发生不对称故障时，文献[14]通过对传统PI控制器加入复数积分和微分环节，实现消除稳态误差并且快速跟踪目的，在电网发生不对称故障时仍能保证稳定输出三相电压。文献[15]针对电网不平衡故障下固态变压器高压级的相间均压问题和对电网电压的支撑问题，分析比对了负序电流注入法，并提出了一种新的适用于电力电子变压器（Power Electronic Transformer, PET）相间均压的零序电压注入法，保证高压级三相电流对称，对电网负序电压无影响。当电网发生单相断路故障时，文献[16]分析了单相开路操作对电网和SST本身的影响，提出了SST中压级联H桥级的控制策略。通过控制正序电流来实现单相开路下电流控制，同时注入适当的负序电压以使群电压同步，保证固态变压器在单相开路下持续运行，从而提供比传统低频变压器更好的电源可持续性。文献[17-19]利用超级电容、锂离子电池等储能装置作为电力储能环节，并提出了相应的模型和控制策略，同时文献[19]指出，通过储能环节能维持电网电压中断时SST低压直流母线电压的稳定，但忽略了其并网瞬间冲击电流以及快速起动的问题。然而，在电网中，电力系统运行经验表明，架空线路绝大多数的故障都是“瞬时性”的，永久性的故障一般不到10%[20]。因此，在继电保护装置动作切除短路故障后，断路器将在较短时间内合闸一次，即自动重合闸，以保证供电的安全性和可靠性。目前，对SST的研究仅限于架空线路发生永久故障下的控制方法的研究，未涉及重合闸等暂态过程中对SST的研究。
本文首先简析了三相级联型SST的拓扑结构及其控制，并通过仿真发现在传统控制下，输入级馈线断路器重合闸将导致SST产生一个较大的冲击电流；然后，根据输入级的控制策略，分析冲击电流产生的原因及其影响因素，并通过不同初始工况以及输入级最大允许电流求得调整功率范围，提出一种基于光伏电源支撑的多端口固态变压器冲击电流抑制策略；最后，仿真与实验结果证明了本文理论研究的正确性与有效性。
SST主电路主要是由输入级、中间/隔离级和输出级构成的三级结构，SST拓扑结构如图1所示[21-22]。输入级采用三相星形联结，每相由级数为n的级联H桥变换器（Cascade H-Bridge converter, CHB）拓扑组成。中间/隔离级采用能控制能量双向流动的双主动桥变换器（Dual Active Bridge converter, DAB）拓扑，其一次侧H桥分别与输入级的高压直流电容相连，总数量为3n；二次侧H桥并联组成低压直流母线。输出级为低压直流母线形成的直流端口以及采用电压源型逆变器（Voltage Source Inverter, VSI）拓扑得到的交流输出端口。
图1 SST拓扑结构
Fig.1 Topology of the SST
基于多端口固态变压器的典型交直流混合微电网系统如图2所示，主网通过SST连接得到直流端口和交流端口。与直流端口相连的分布式能源（Distributed Energy Resources, DER），如光伏电源等，主要通过DC-DC变换器并网；与交流端口相连的DER，如燃汽轮机等，主要通过DC-AC、AC-DC-AC等变换器并网。分布式电源根据自身的合理需求，选择直流或交流端口接入。
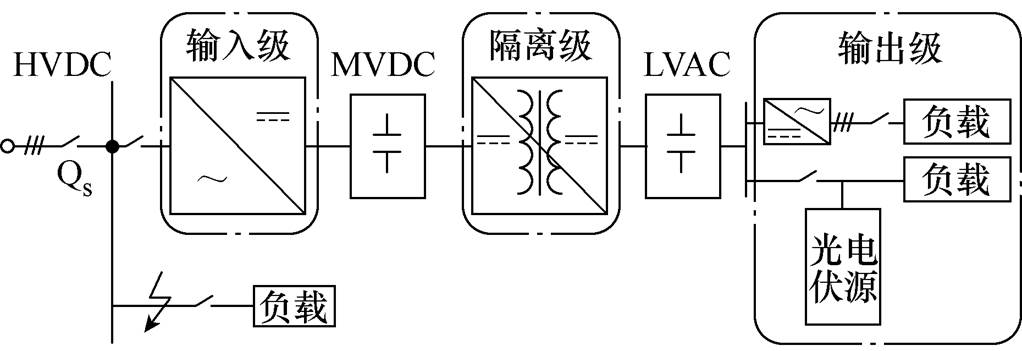
图2 交直流混合微电网系统
Fig.2 System structure of hybrid AC-DC microgrid
输入级采用电压电流双闭环控制，输入级级联H桥控制框图如图3所示。输入级三相电压经过锁相后得到控制所需的基准相位；整体直流电压控制根据给定高压直流侧电压参考值来控制直流电压之和的稳定；电流解耦通过dq解耦控制后，以快速跟踪参考电流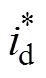
。
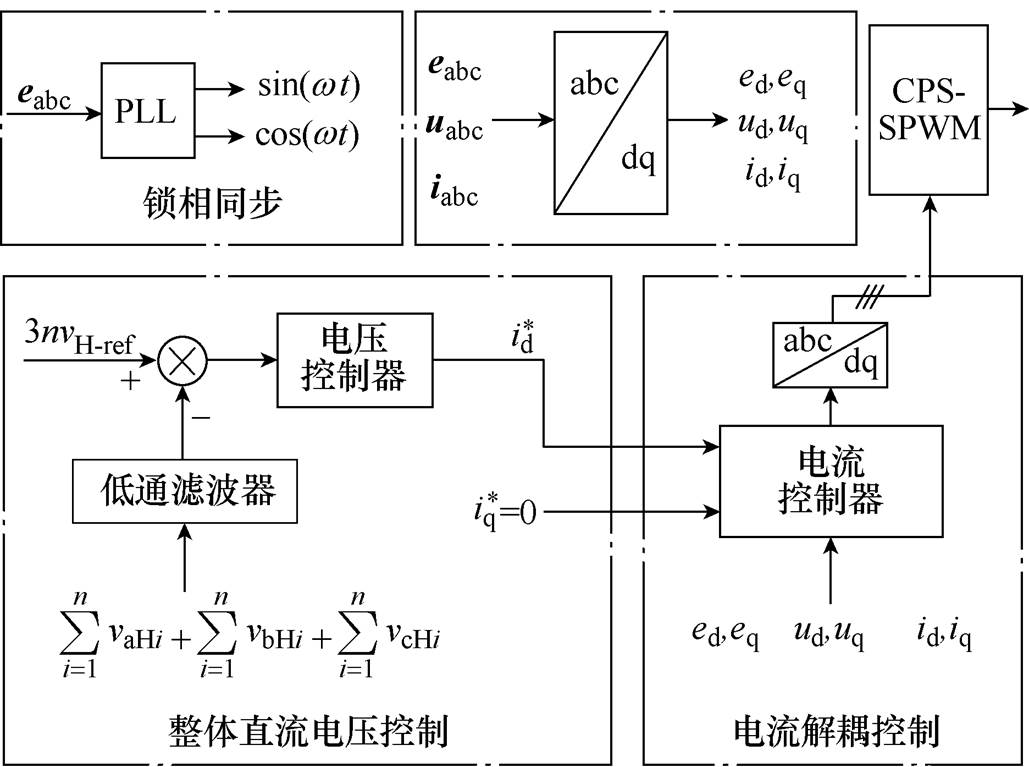
图3 输入级级联H桥控制框图
Fig.3 Control block diagram of cascaded H bridge in input stage
在隔离级DAB共同移相占空比的基础上，设计电压均衡控制环来调整三相各级DAB的移相占空比，实现对低压直流电压和各相各级高压直流电压的控制，隔离级DAB均压控制框图如图4所示。
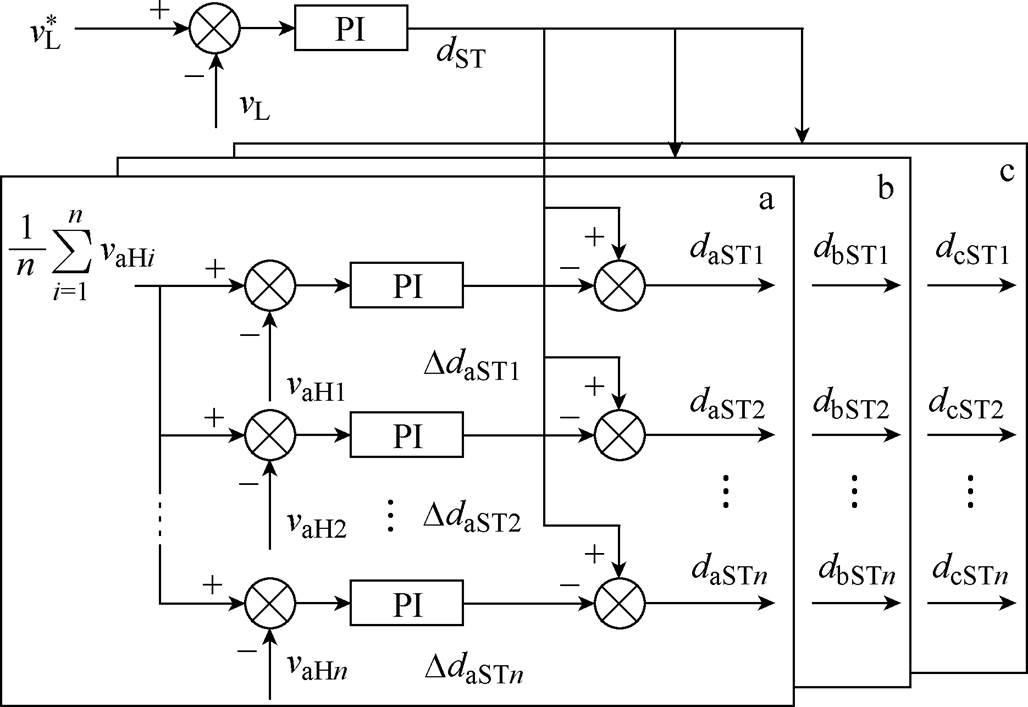
图4 隔离级DAB均压控制框图
Fig.4 Control block diagram of DAB in middle stage
在传统控制方式下，若与SST并联的架空线路发生故障，导致断路器Qs自动重合闸，时间为1s，SST依旧按正常工况运行，则高、低压侧电压波形及输入级电流波形如图5所示。
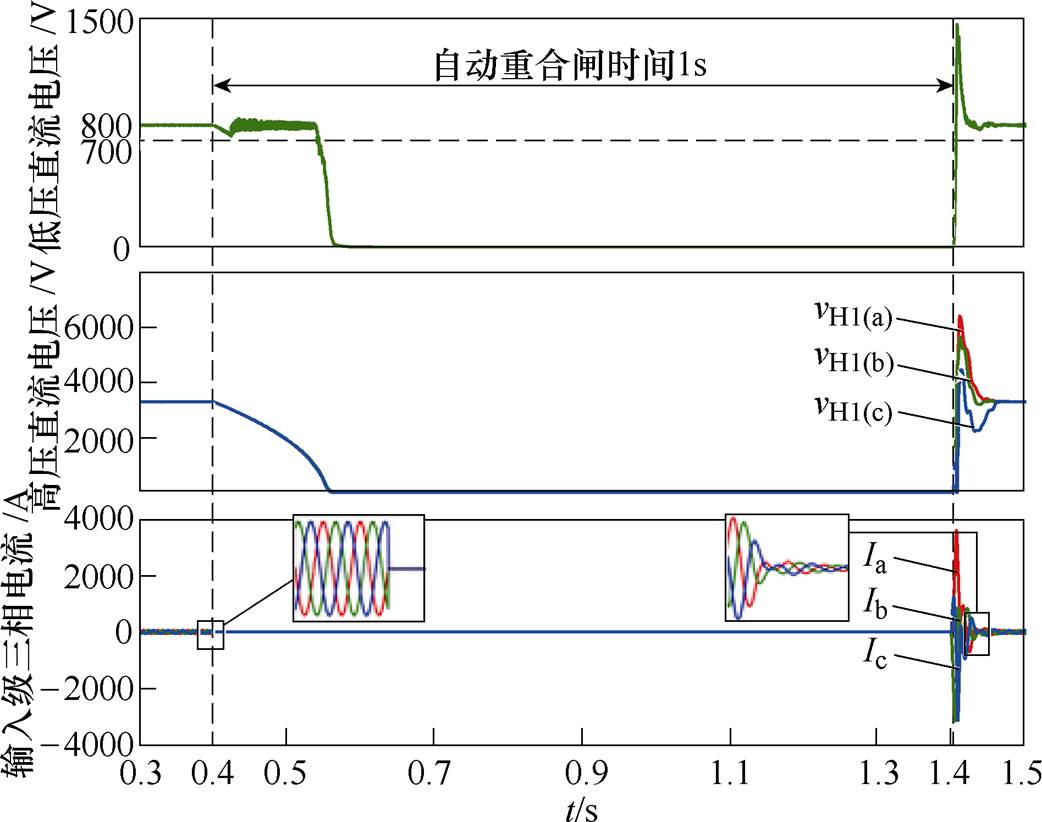
图5 传统控制下，自动重合闸发生时电压、电流波形
Fig.5 Voltage and current waveforms while automatic reclosing occurs under traditional control
从图5中可以明显看出，自动重合闸发生时，SST三相输入电流为0，高压直流电压开始跌落，跌落至一定值（趋近于0）时，低压直流电压开始跌落直至0；在1.4s合闸时，高低压直流电压立即抬升，同时输入电流出现一个很大的冲击。
输入级采用三相星形联结，每相级联H桥多电平拓扑结构由数量为n的H全桥模块级联组成，输入级级联H桥拓扑结构如图6所示。
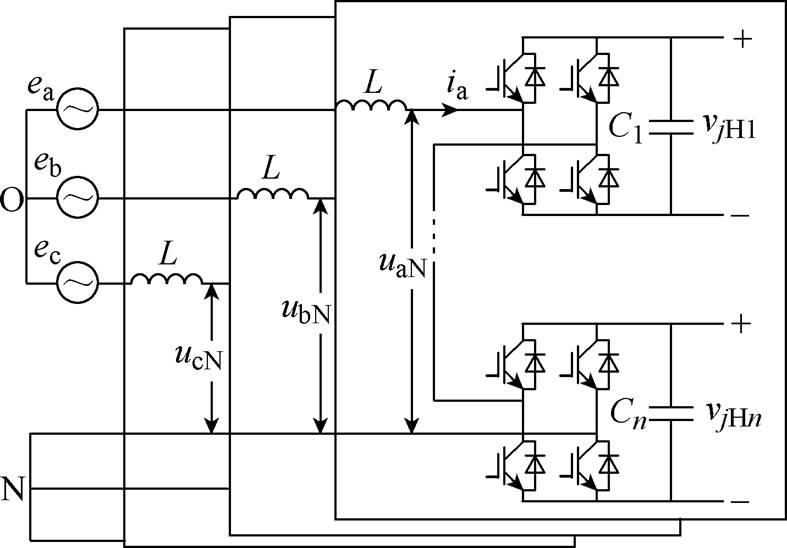
图6 输入级级联H桥拓扑结构
Fig.6 Topology of cascaded H bridge in input stage
由图6所示拓扑可行，其状态方程可以表示为
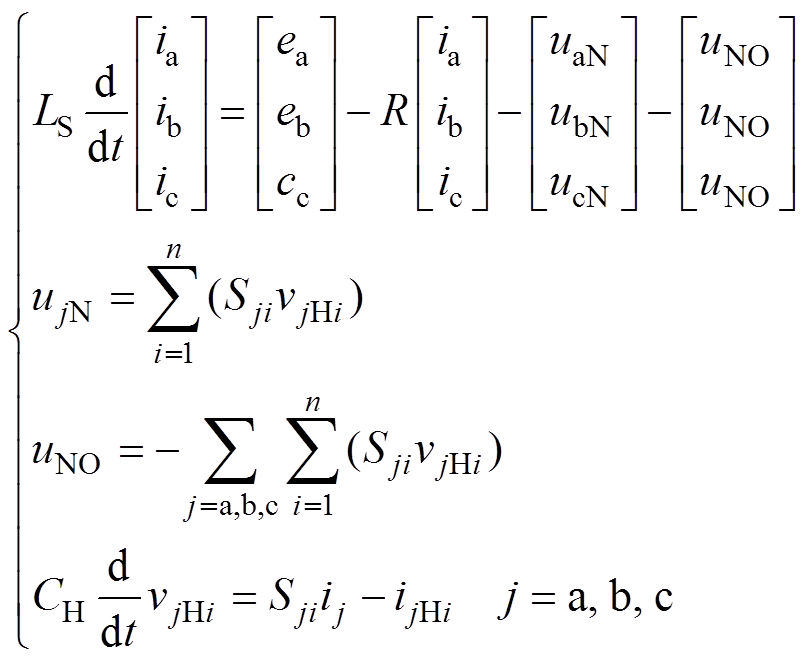（1）式中，e(a,b,c)为网侧相电压；i(a,b,c)为网侧相电流；u(a,b,c)N为级联H桥交流侧电压；uNO为中性点对地电压；S(a,b,c)i、v(a,b,c)Hi、i(a,b,c)Hi分别为a、b、c相第i级整流器的开关函数、高压侧直流电压和输出电流。
当电网电压平衡且三相SST系统稳定时，有uNO=0。为了实现dq解耦控制以及无差控制，将系统转化到dq旋转坐标系下进行分析，则输入级在dq坐标系下的状态方程可表示为
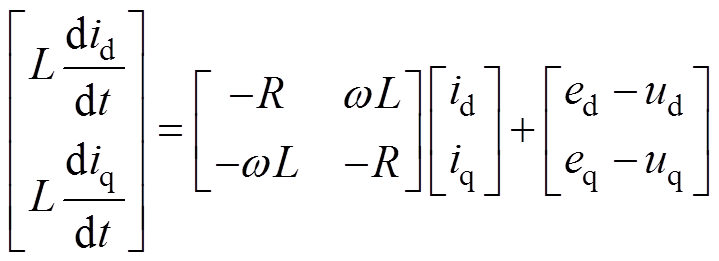（2）式中，ed、eq，id、iq，ud、uq分别为e(a,b,c), i(a,b,c), u(a,b,c)N在d、q轴的分量；w 为电网电压角频率。
输入级采用PI调节器作为外环整体直流电压控制和内环电流解耦控制的控制器，其解耦控制方程为
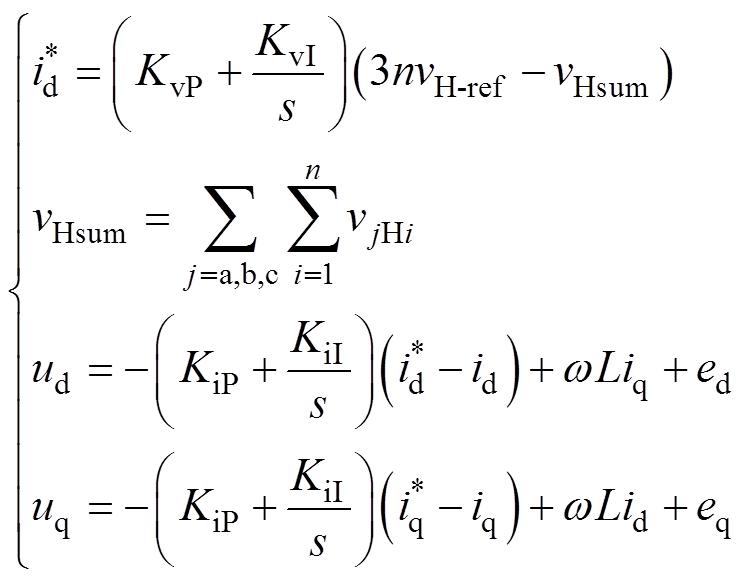（3）式中，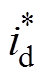
、
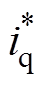分别为输入级三相电流的d、q轴的参考值；vH-ref为高压直流电压参考值；vHsum为三相各级高压直流电压之和；KvP、KvI分别为输入级电压外环比例、积分系数；KiP、KiI分别为输入级电流内环比例、积分系数。
将式（3）代入式（2）可得
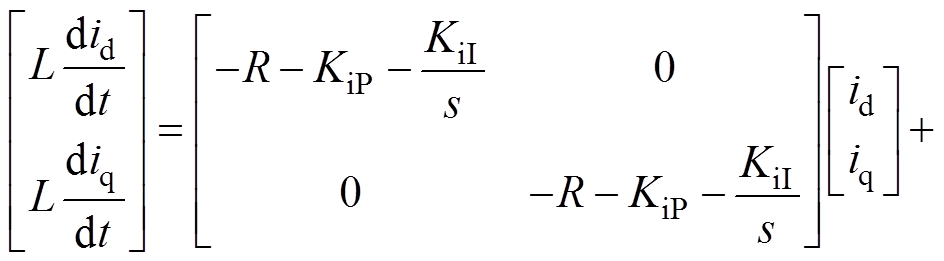
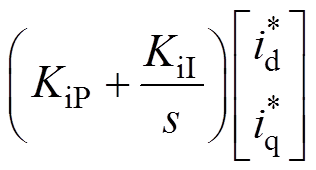（4）
由式（4）实现电流id和iq的解耦控制。同时id的变化率[23]为
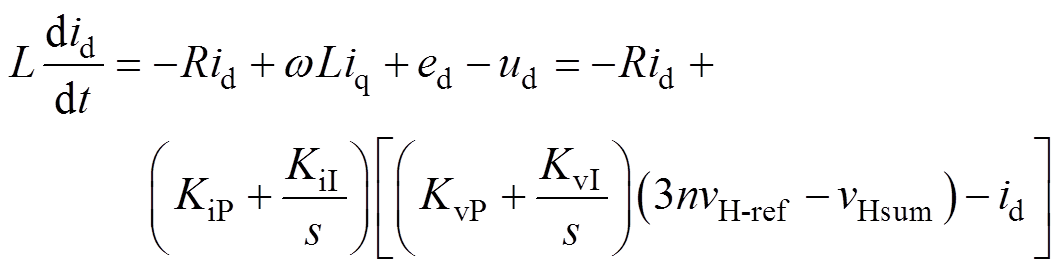（5）重合闸发生时，高压直流侧电容能量缺失或溢出将导致在合闸时，直流侧电压给定期望值3nvH-ref与其总电压实测值vHsum存在一个较大的偏差。作差之后经过式（3）中第一个公式，得到一个较大的d轴电流参考值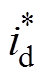，再经过式（5）可知，d轴上的电流变化率较大，导致冲击电流的出现。直至id超过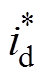，并使得式（5）=0时达到最大值。
由于冲击电流产生时间非常短，忽略积分过程产生的积分量，则当式（5）=0时，可求得冲击电流最大值为
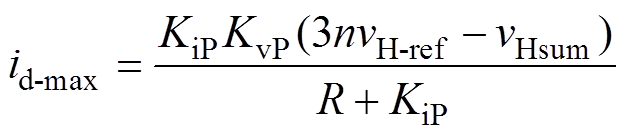（6）由式（6）可以看出，高压直流侧电压实际值越接近参考值，冲击电流越小。
2.1节中分析了在输入级采用电压、电流双闭环控制时，输入级馈线断路器合闸瞬间冲击电流产生的原因。本节将分析断路器合闸时电网电压初始相位对输入电流的影响。取a相进行分析，输入级a相的等效电路如图7所示[23]。
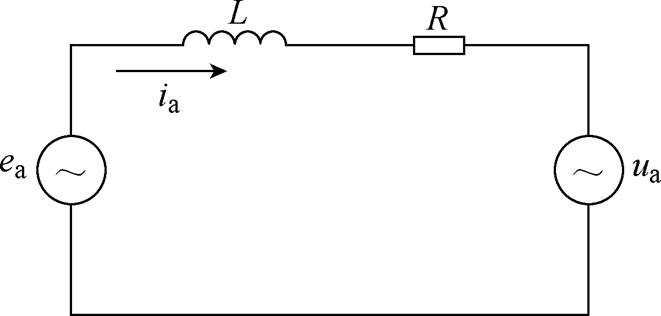
图7 a相级联H桥基波等效电路
Fig.7 Fundamental wave equivalent circuit of a-phase in cascaded H-bridge
由图7可得其回路方程为
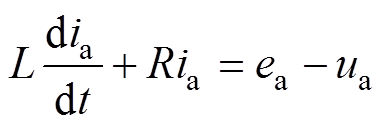（7）式中，a相交流侧电压ua的开关函数表达式为
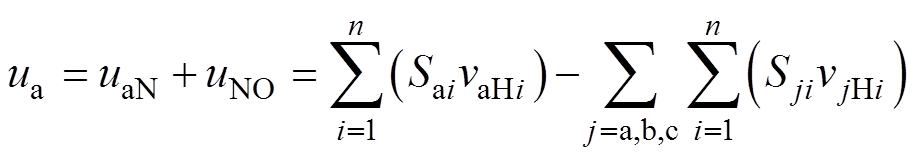（8）
由于输入级级联H桥通常采用载波移相控制，其各相交流侧电压波形均是以额定频率正弦波为基波的含有2n+1个电平的PWM波形。由于电网中滤波电感的作用，近似地取其基波分量进行分析。
设ea和ua的基波表达式分别为
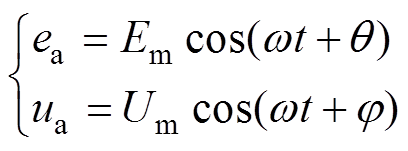（9）式中，q 为ea的初始相位；j 为ua的初始相位；Em、Um分别为ea、ua的幅值。
将式（9）代入式（7），可得
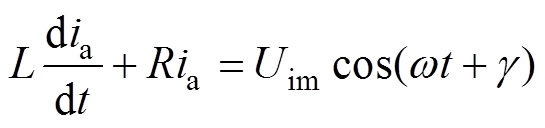（10）其中
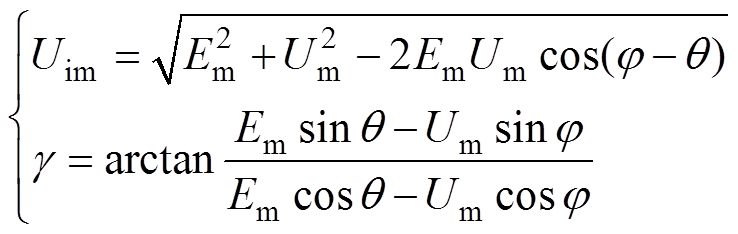（11）
断路器在合闸瞬间，ia(t0)=0，求解式（10）微分方程可得
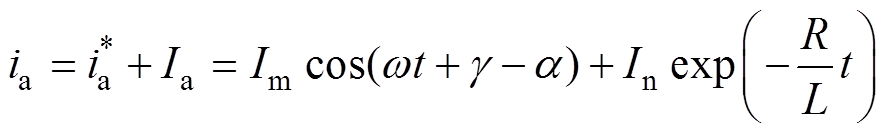（12）其中
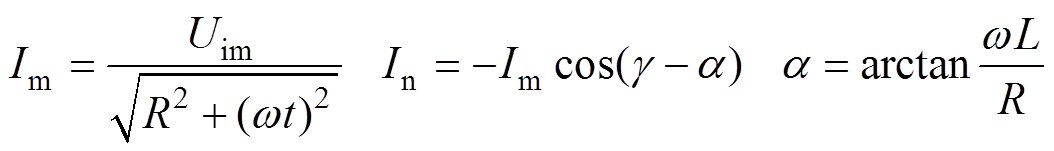
则有
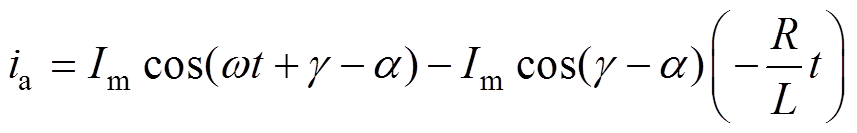（13）同理，可类推出b，c相起动电流表达式。
根据式（13）可知，合闸时a相电流与g -a 有关，即与输入级a相交流侧电压ua的初始相位j 和电网电压ea的初始相位q 有关，适当调整初始角度可以减小冲击电流。
设SST输出功率为PO，高压侧电容容值为CH，低压侧电容容值为CL，DAB传输效率为m，重合闸时间间隔为ts；记重合闸开始时刻为0，在t1时刻，光伏电源开始调整功率为PPV(t1)；在t2时刻，重新合闸。功率流动方向如图8所示。
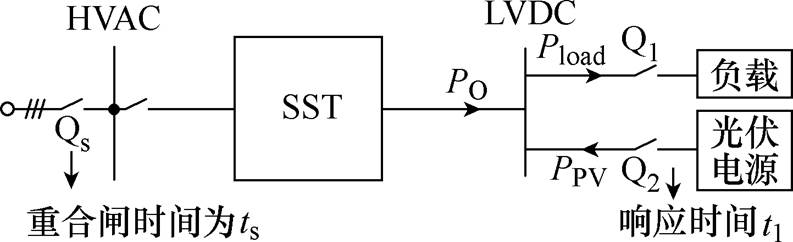
图8 功率流动方向
Fig.8 Diagram of power flow direction
为保证低压直流侧电压稳定，须在低压直流侧电压跌落之前，即高压直流侧电压跌落至0之前，进行功率补偿，这段时间记为t0，则有
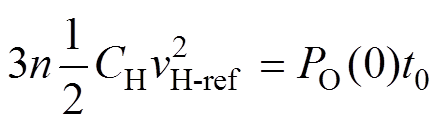（14）其中
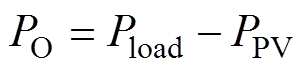
通常情况下，交直流微电网中的光伏电源处于最大出力状态，SST的功率输出PO(0)较小，且光伏电源通常由电力电子装置控制，其响应较快，因此，能在高压直流母线跌落至0之前进行控制。
1）当重合闸发生时，PPV(0)≥Pload(0)
由于SST与电网断开，在光伏电源响应时间t1内，溢出的能量将存储在高压直流侧电容上，导致高压直流侧电压上升，此时有
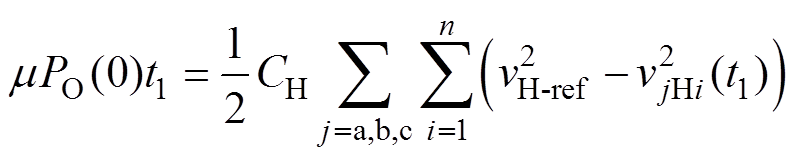（15）在t1时刻，光伏电源减小功率输出，使其小于负载功率，适当消耗高压直流侧电容上的能量，则
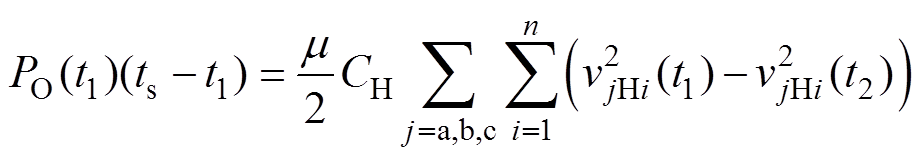（16）
其中
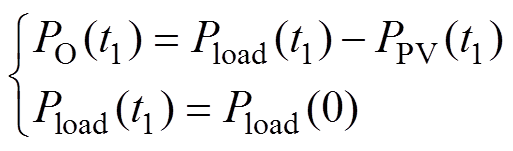
由式（15）、式（16）可得，在t1时刻，调整光伏电源功率输出为
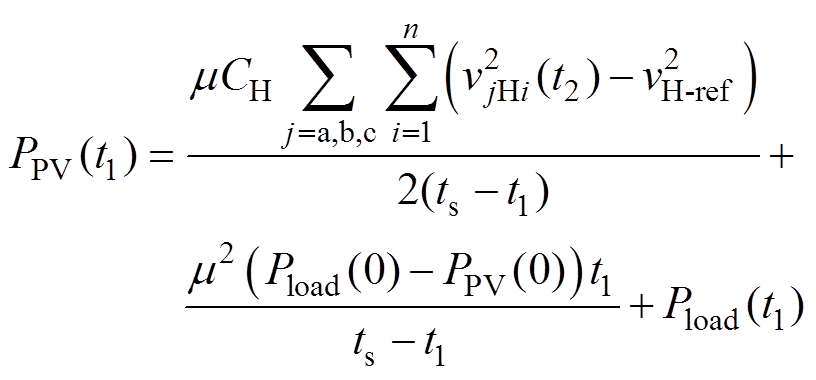（17）
2）当重合闸发生时，PPV(0)＜Pload(0)
在光伏电源响应时间t1内，缺失的能量将由高压直流侧电容提供，导致高压直流侧电压的跌落，此时有
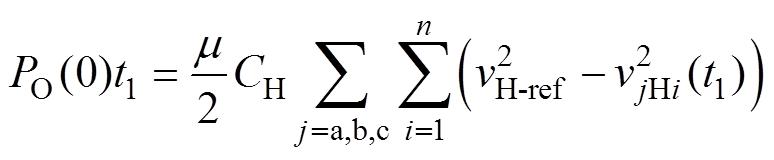（18）t1时刻，需切断负载。同时，由光伏电源补偿高压直流电容能量的缺额，则
（19）
其中
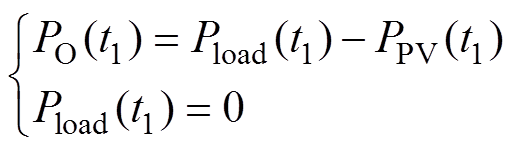
由式（15）、式（16）可得，在t1时刻，调整光伏电源功率输出为
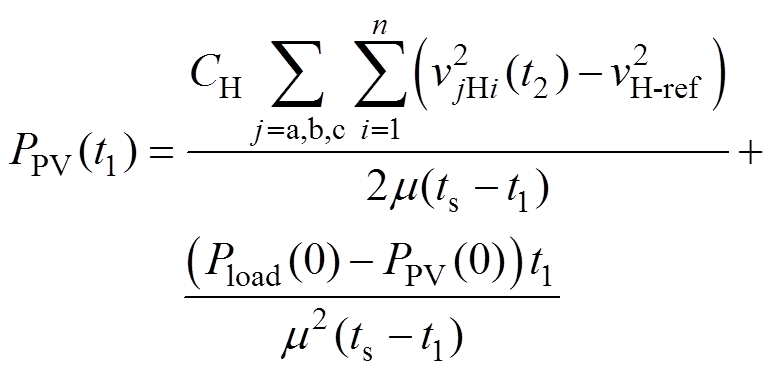（20）
在第2节中，冲击电流的大小与合闸时刻高压直流侧电压的大小vHsum相关，为保证架空线路在合闸时，SST产生的冲击电流不会导致断路器误动作，要保证冲击电流小于1.2～1.3倍的额定电流，即
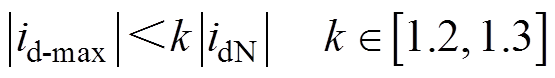（21）将式（21）代入式（6）可得
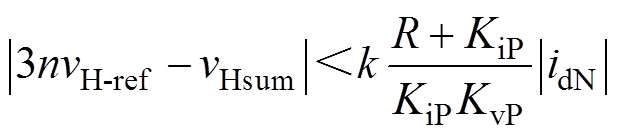（22）
根据式（17）、式（20）和式（22），且各级高压侧电压相等，在冲击电流达到要求时，即|id-max|≤ |kidN|，光伏电源补偿功率为
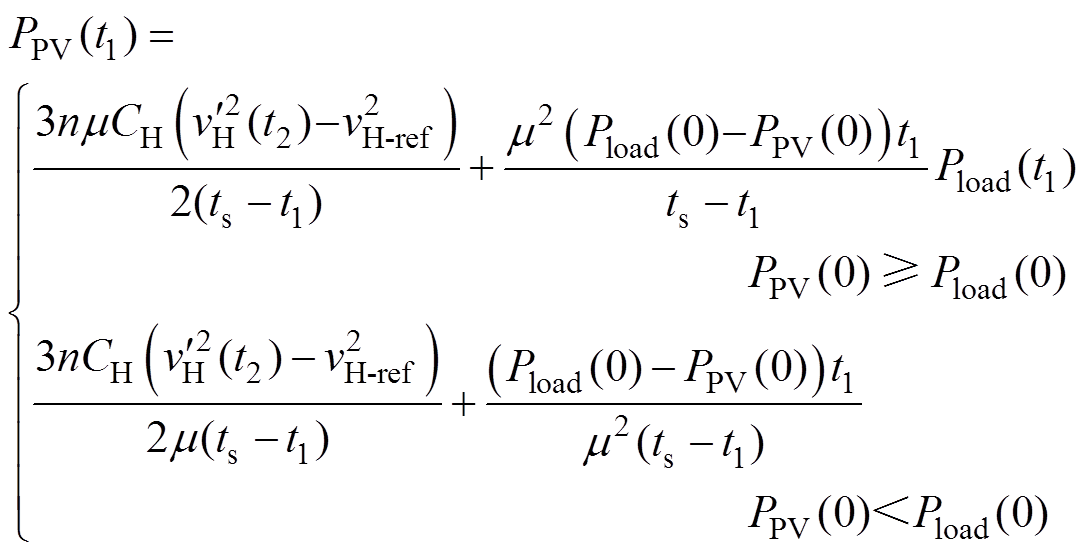（23）其中，合闸时，高压直流电压取值范围为
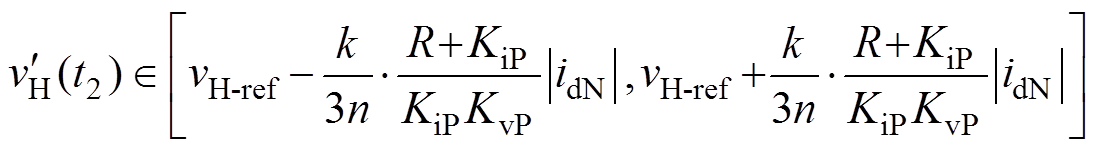（24）
当高压交流母线或与SST并联的线路发生瞬时故障时，母线与大电网之间的断路器Qs将发生自动重合闸现象，此时SST将暂时脱离电网运行一段时间，即Qs发生自动重合闸时间ts。断路器跳闸后，由于光伏电源调控存在一个响应时间t1，在t1时间内，系统中不论多余或缺失的能量都将由高压直流侧电容处理，导致与参考电压产生一个较大的差值，在合闸时将带来冲击电流。为减小冲击电流，在合闸前，需要通过处理高压直流侧电容上的能量，控制其电压值，冲击电流抑制控制策略如图9所示。
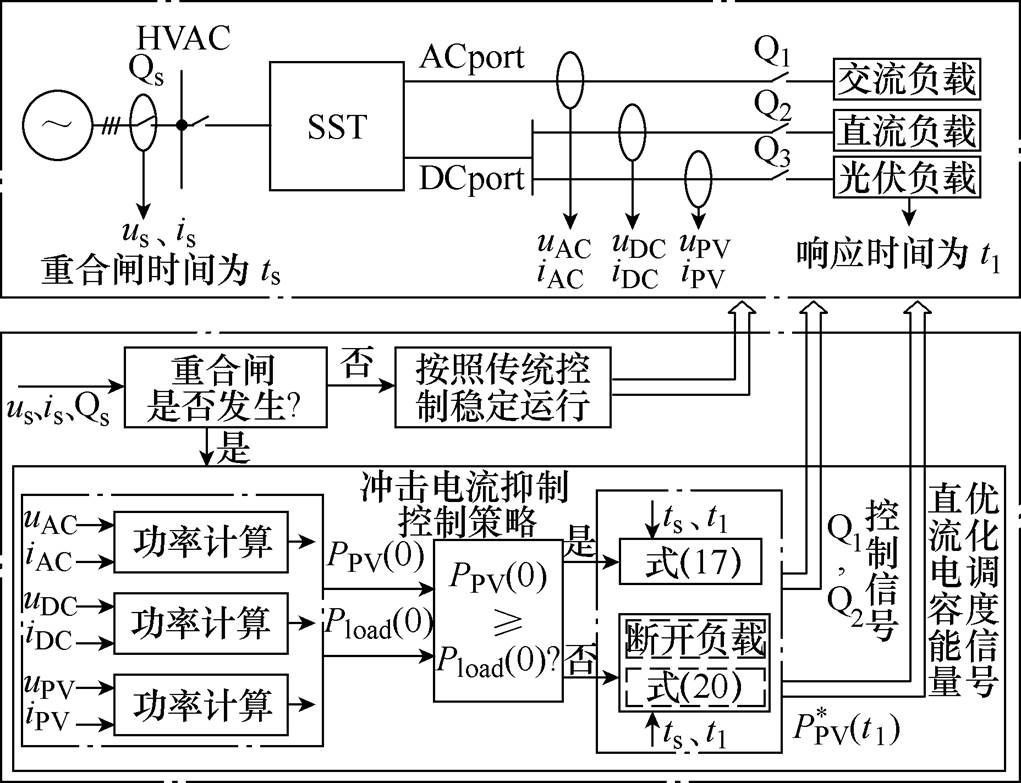
图9 冲击电流抑制控制策略
Fig.9 Control strategy of impulse current suppression
根据3.1节中高压直流侧电压取值范围以及不同控制策略的处理方式，可求得冲击电流抑制策略的可行域如图10所示。
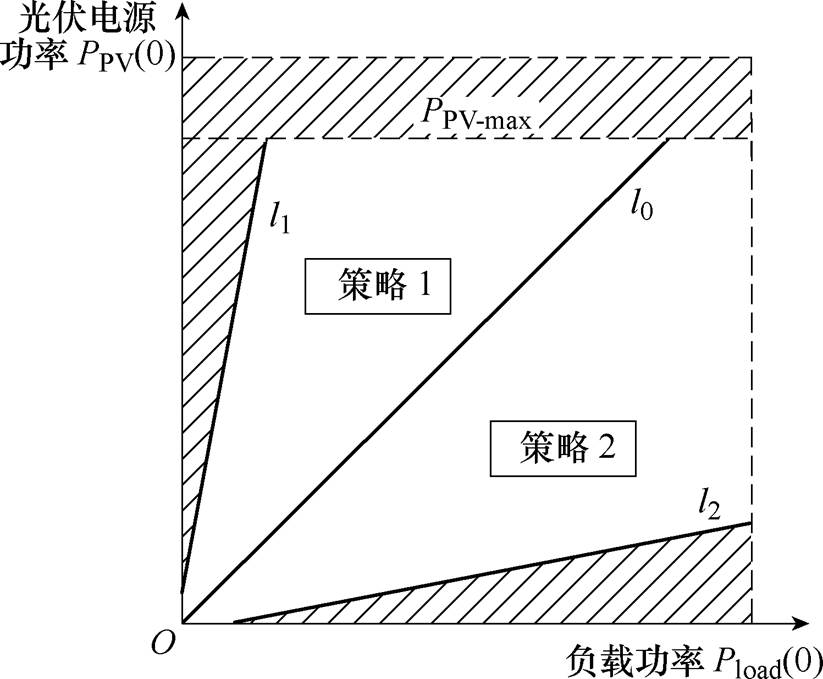
图10 冲击电流抑制策略可行域
Fig.10 Feasible domain of impulse current suppression strategy
其中
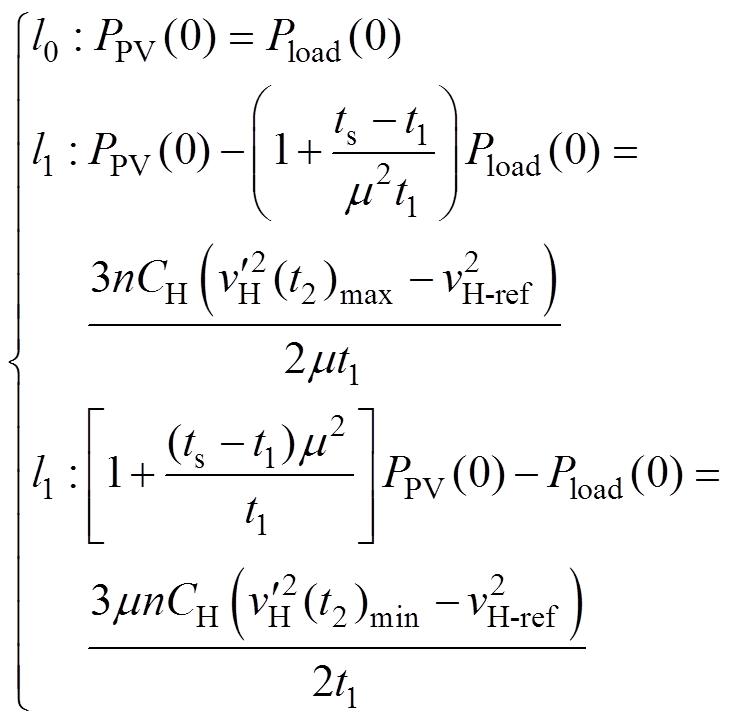（25）（1）策略1：Qs跳闸后，当PPV(0)≥Pload(0)时，高压侧电压将逐渐抬升，低压侧电压仍能维持稳定，Q1保持闭合状态。此时，光伏电源响应后，需要通过负载消耗高压侧电容多余的能量，在光伏电源响应后，光伏电源调整功率为
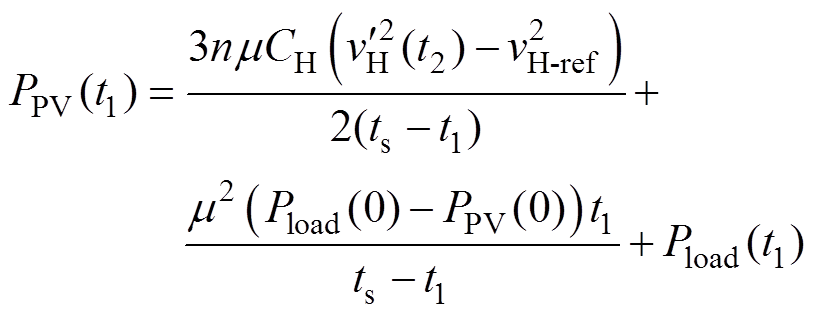（26）
（2）策略2：Qs跳闸后，当PPV(0)＜Pload(0)时，高压侧电压将逐渐降低，低压侧电压仍能维持稳定。由于光伏电源无法满足负载需求，需切断负载，即Q1断开，在光伏电源响应后，断路器合闸之前开始补偿高压直流侧电容所需能量，所需光伏电源功率为
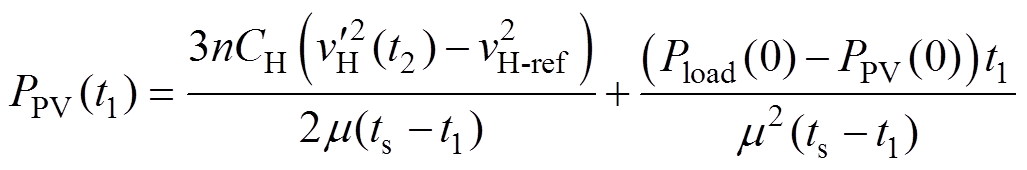（27）为验证重合闸后冲击抑制的有效性，建立了含光伏电源的三相三级联型SST的Matlab/Simulink仿真模型，三相级联型SST仿真参数见表1。
表1 三相级联型SST仿真参数
Tab.1 Simulation parameters of three-phase cascade SST
参 数数 值 输入级额定电压/kV10 滤波电感/mH10 每相模块级联数3 高压直流侧电容/mF2 000 低压直流侧电容/mF8 000 高压直流侧电压/V3 300 低压直流侧电压/V800 低压直流侧安全电压/V700 隔离级各级高频变压器电压比33:8 隔离级各级高频变压等效漏感/mH0.2 隔离级各级传输效率为m0.93 负载功率/(kV·A)0～640 光伏电源功率/(kV·A)0～600 光伏电源响应时间/s0.1 输入级电压外环比例系数KvP0.1 输入级电压外环积分系数KvI10 输入级电流内环比例系数KiP1 000 输入级电流内环积分系数KiI10
由式（14）、式（21）可知，重合闸开始后，高压直流侧电压跌落至0的最短时间为
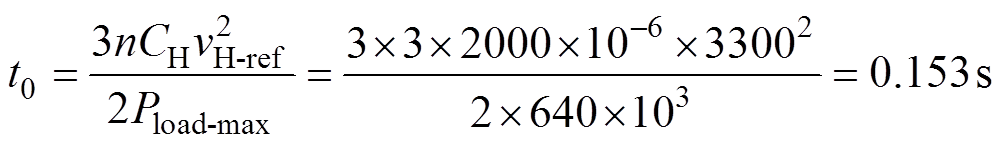
额定正序电流值为
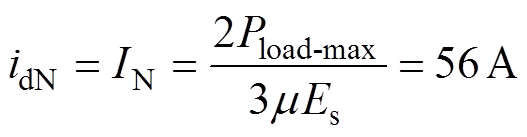
式中，Es、IN分别为电网电压幅值和额定电流幅值。
合闸时，根据式（21），可得1.3倍额定冲击电流内，高压直流侧电压运行范围为
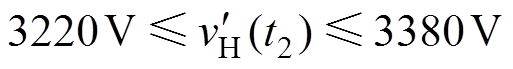
在0.4s时刻重合闸发生，重合闸时间间隔为1s。
1）初始状态：PPV(0)=500kV·A，Pload(0)=400kV·A，即PPV(0)≥Pload(0)
跳闸后，高压直流侧电容处于充电状态，电压值逐渐抬升，经过0.1s后，若光伏电源调整功率输出为PPV(t1)=400kV·A，传统控制下，高低压直流侧电压波形以及电流波形如图11所示。
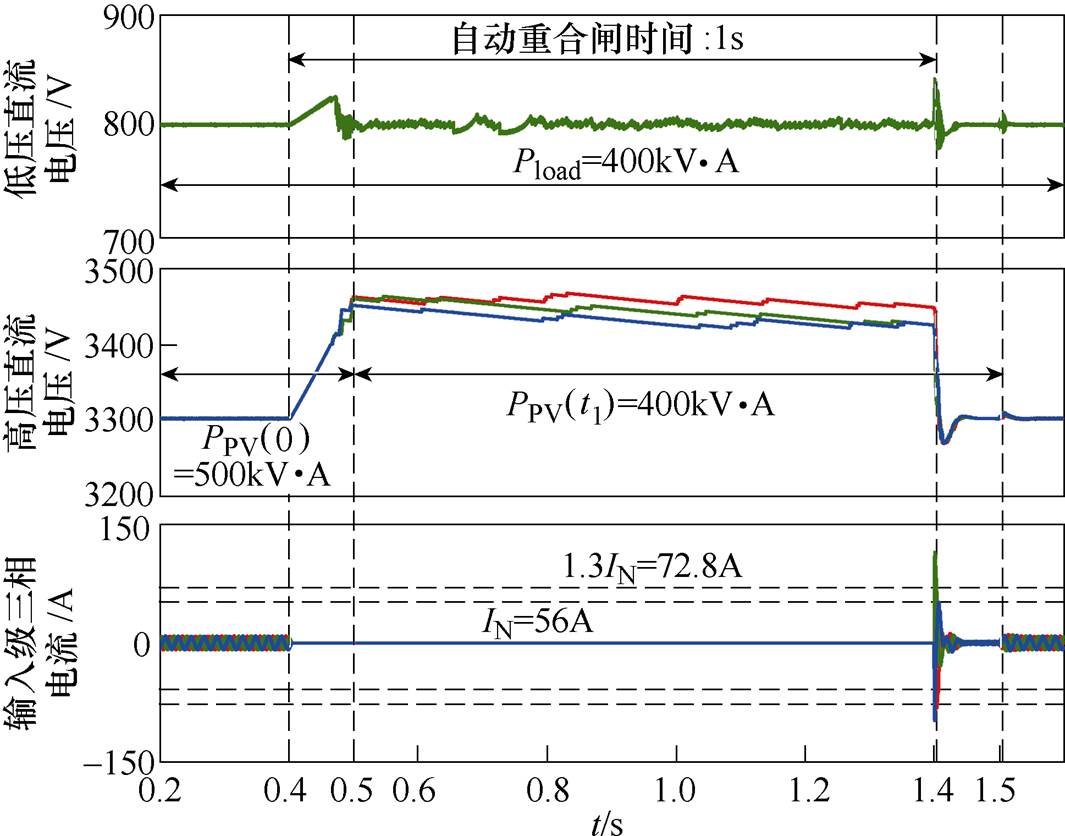
图11 PPV(0)≥Pload(0)时，传统控制下的仿真波形
Fig.11 Simulation waveforms while PPV(0)≥Pload(0) under traditional control
从图10可见，合闸时冲击电流超过了最大允许电流，因此根据式（23）可得，光伏电源调整功率范围为
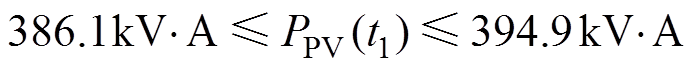
取PPV(t1)=386.1kV·A进行功率调整后，直流母线电压波形以及重合闸电流波形如图12所示。
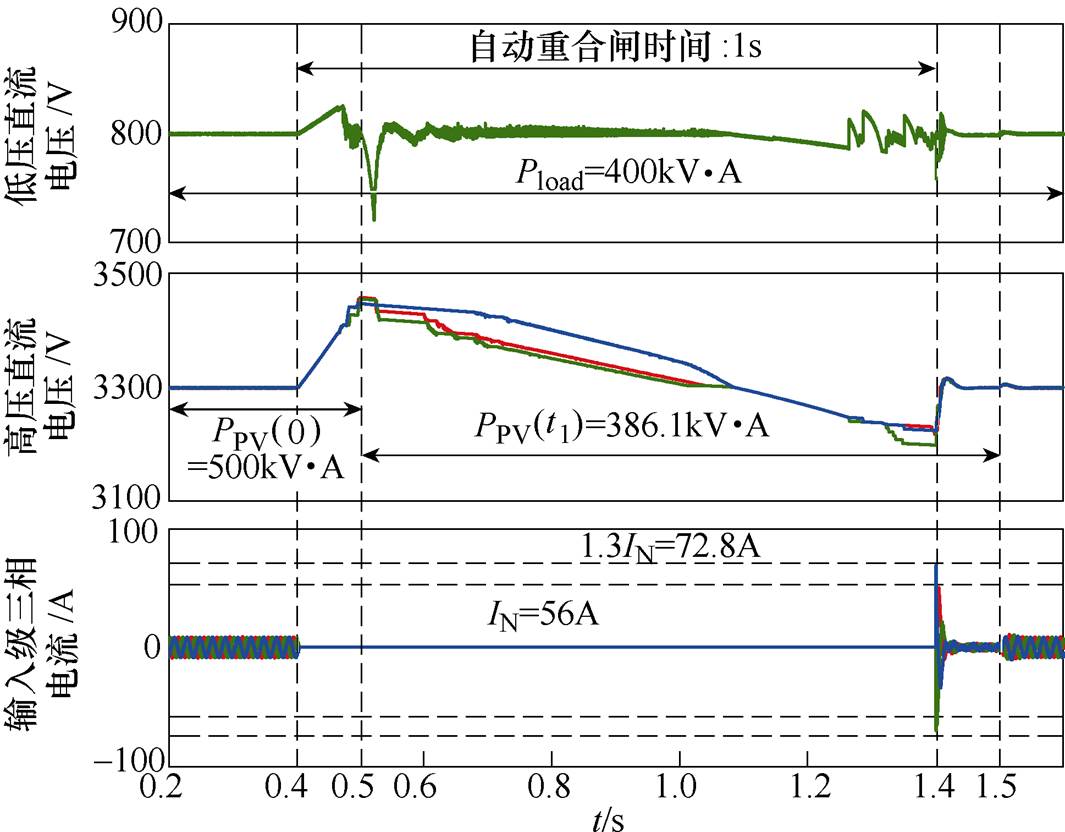
图12 PPV(0)≥Pload(0)时，采用抑制策略下的仿真波形
Fig.12 Simulation waveforms while PPV(0)≥Pload(0) under suppression strategy
2）初始状态：PPV(0)=300kV·A，Pload(0)=400kV·A，即PPV(0)＜Pload(0)
跳闸后，高压直流侧电容处于放电状态，电压值逐渐降低，经过0.1s后，由于光伏电源无法完全提供负载所需功率，因此需断开负载。此时若调整光伏电源输出功率PPV(t1)=0，则采用控制策略时，高低压直流侧电压波形以及电流波形如图13所示。
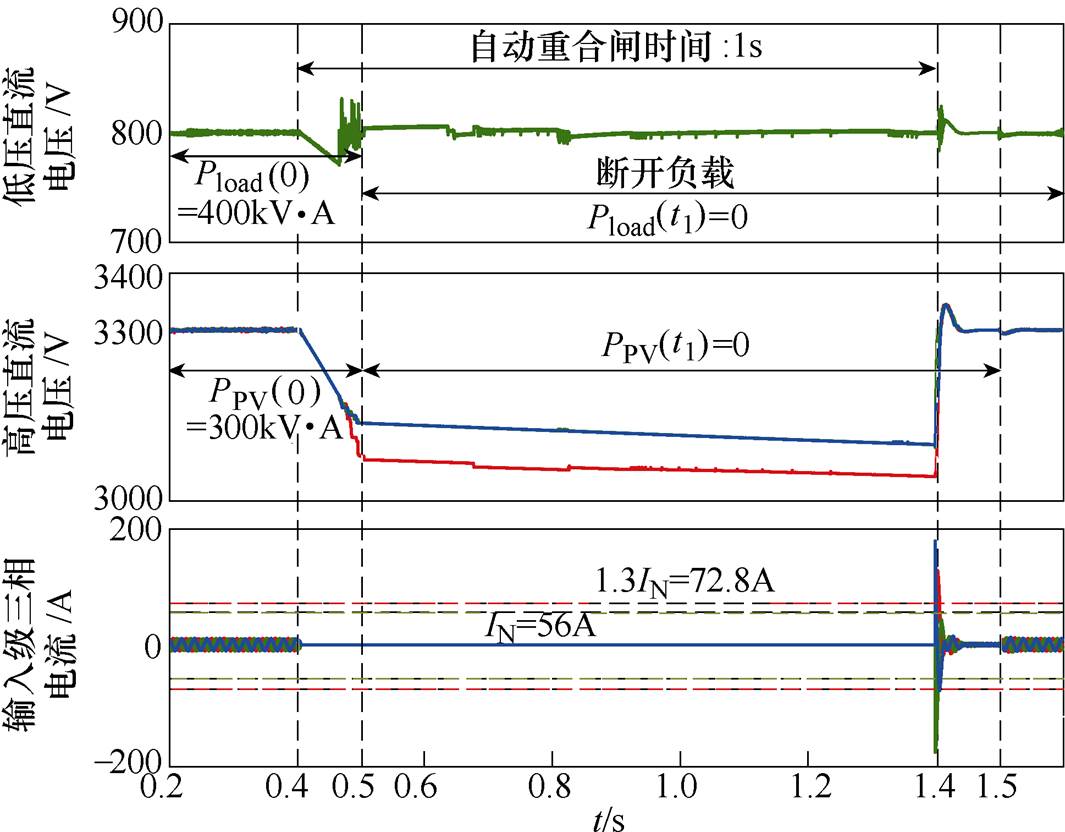
图13 PPV(0)＜Pload(0)时，传统控制下的仿真波形
Fig.13 Simulation waveforms while PPV(0)＜Pload(0) under traditional control
从图13可见，合闸时冲击电流超过了最大允许电流，因此根据式（23）可得，光伏电源调整功率范围为
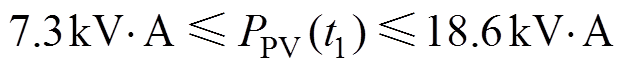
取PPV(t1)=18.6kV·A进行功率调整后，直流母线电压波形以及重合闸电流波形如图14所示。
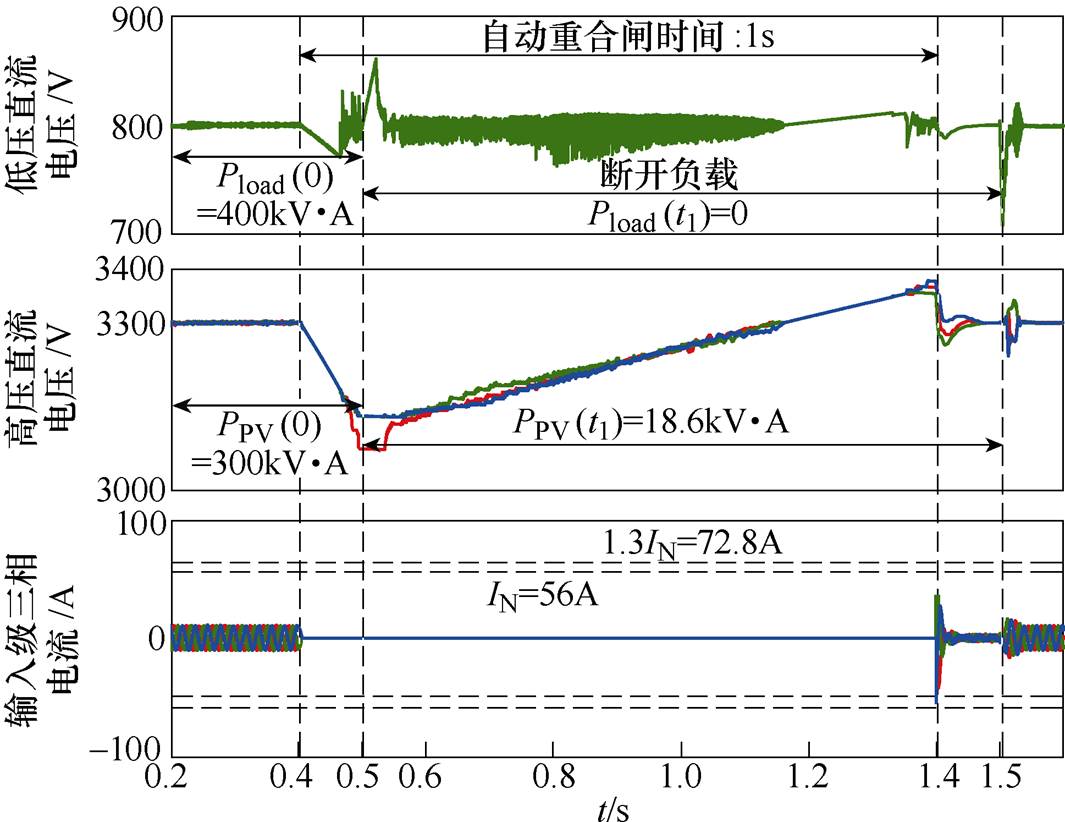
图14 PPV(0)＜Pload(0)时，采用抑制策略下的仿真波形
Fig.14 Simulation waveforms while PPV(0)＜Pload(0) under suppression strategy
对比图10和图11以及图12和图13，可以明显看出，经过光伏电源功率调整后，在1.4s合闸时刻，SST产生的冲击电流保持在1.3倍的额定电流以内，实现了冲击电流抑制。
为进一步验证本文所提抑制策略的正确性和有效性，对所提控制策略进行了低压实验验证。实验参数见表2。设计两种工况：工况1，PPV(0)=4kV·A，Pload(0)=3kV·A，即PPV(0)≥Pload(0)；工况2，PPV(0)= 2kV·A，Pload(0)=3kV·A，即PPV(0)＜Pload(0)。根据第3节中的控制策略进行光伏电源功率调整，利用所得光伏电源调制范围的边界值进行实验，所得实验结果如图15和图16所示，分别给出了高压直流电压波形和输入级a相电流波形。
表2 三相级联型SST实验参数
Tab.2 Experimental parameters of three-phase cascade SST
参 数数 值 输入级额定电压/V380 滤波电感/mH2 每相模块级联数3 高压直流侧电容/mF500 低压直流侧电容/mF4 000 高压直流侧电压/V150 隔离级各级高频变压器电压比1.6～1.7 隔离级各级高频变压等效漏感/mH40～60 低压直流侧电压/V90 低压直流侧安全电压/V700 隔离级各级传输效率为m0.92～0.94 负载功率/(kV·A)0～6 光伏电源功率/(kV·A)0～4 光伏电源响应时间/s0.1
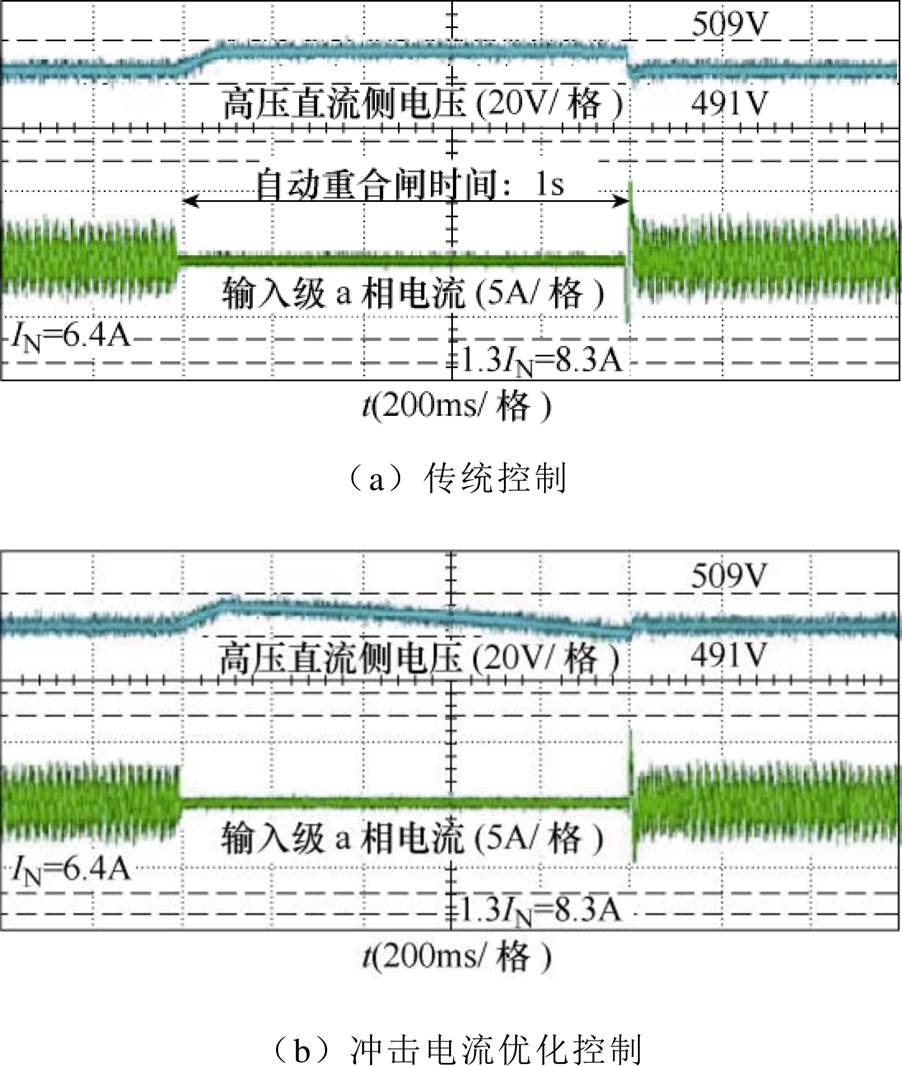
图15 工况1，直流母线电压波形和输入电流波形
Fig.15 DC voltage waveforms and input current waveforms in working Condition 1
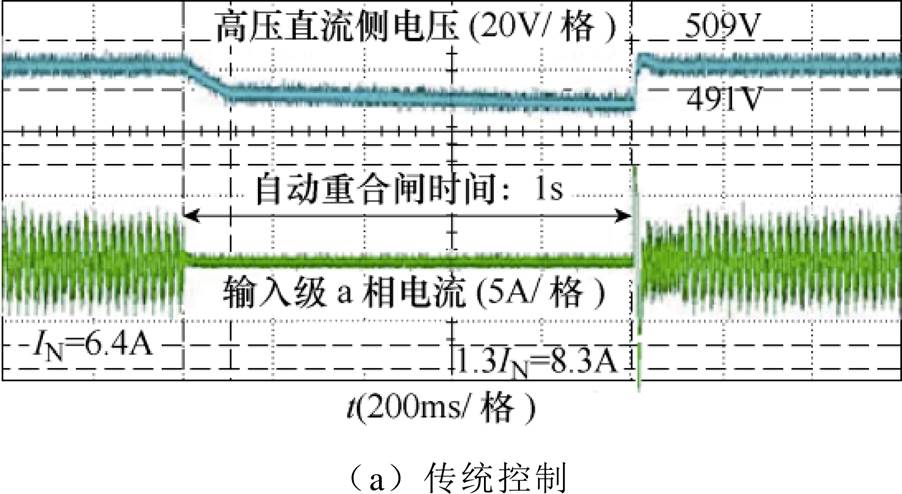
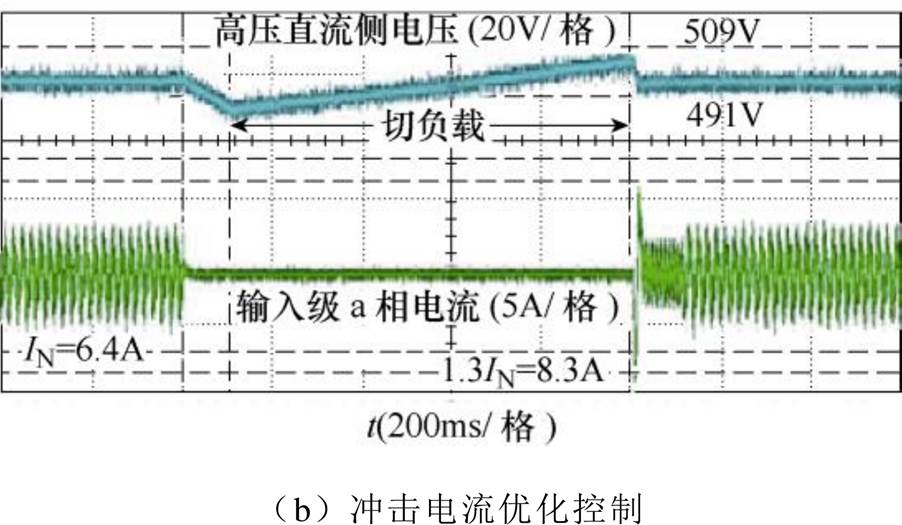
图16 工况2，直流母线电压波形和输入电流波形
Fig.16 DC voltage waveforms and input current waveform in working Condition 2
由图15、图16可以看出，重合闸发生后，经过光伏电源和负载的功率调整，高压直流侧电压在合闸时刻达到要求范围。因此合闸时，输入级产生的冲击电流在允许范围（1.3倍额定电流）内。根据第3节中式（23），求得冲击电流为0时，光伏电源调整功率，并进行实验，所得实验波形如图17所示。
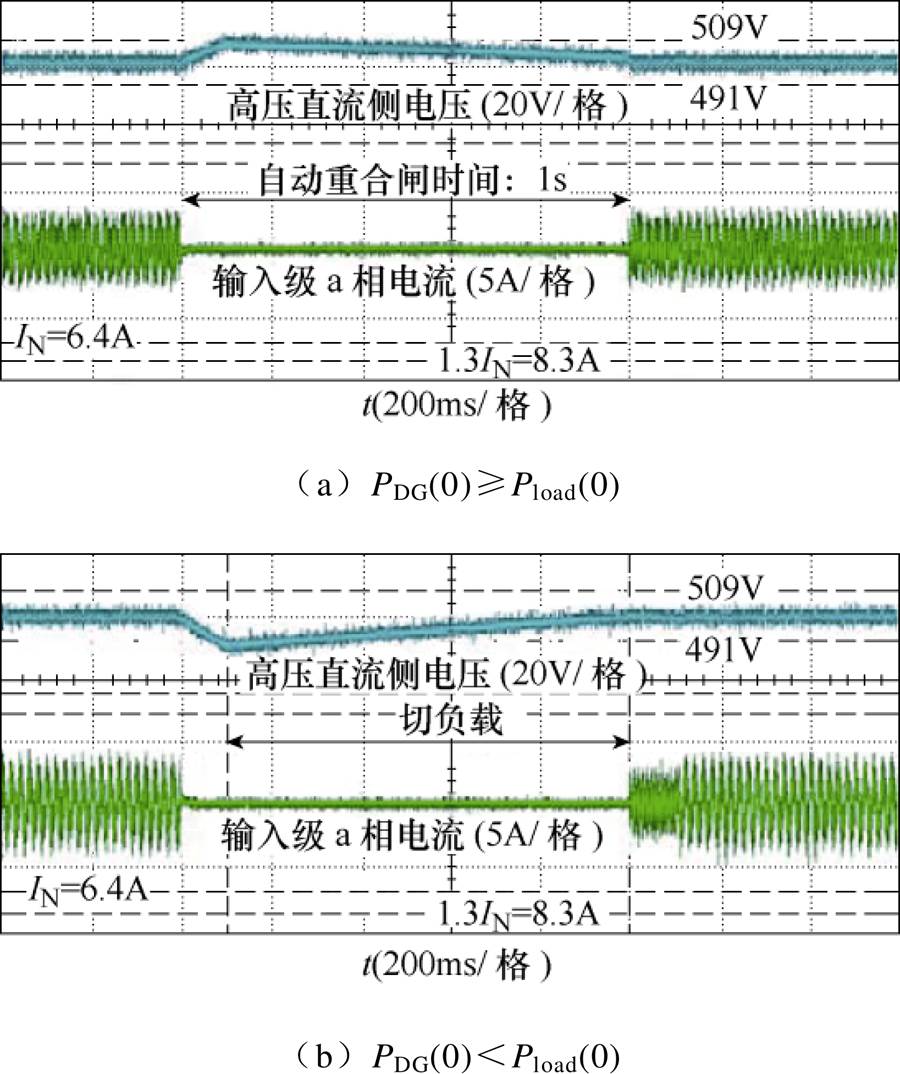
图17 冲击电流为0，直流母线电压波形和输入电流波形
Fig.17 DC voltage waveforms and input current waveforms while impulse current is zero
综上所示，本文所提冲击电流抑制策略能够在保证低压直流母线电压稳定的同时，解决重合闸过程SST产生的冲击电流，达到冲击电流抑制的目的。
本文针对多端口固态变压器在输入级馈线断路器因架空线路故障而重合闸时产生冲击电流的问题，从理论上分析了冲击电流的产生机理，得知影响因素主要为合闸瞬间直流侧电容电压实际值，并基于所分析的机理，提出了基于光伏电源支撑的多端口固态变压器冲击电流抑制策略。根据初始工况的不同，选择合适的控制策略，以调控高低压侧电容上的能量，合理减小重合闸时高压侧电压实际值与参考值的差值，从根本上达到抑制冲击电流的效果，仿真和实验均验证了该方法的合理性和有效性。
参考文献
[1] 赵争鸣, 冯高辉, 袁立强, 等. 电能路由器的发展及其关键技术[J]. 中国电机工程学报, 2017, 37(13): 3823-3834.
Zhao Zhengming, Feng Gaohui, Yuan Liqiang, et al. The development and key technologies of electric energy router[J]. Proceedings of the CSEE, 2017, 37(13): 3823-3834.
[2] 涂春鸣, 肖凡, 袁靖兵, 等. 级联型电力电子变压器直流电压二次纹波抑制策略[J]. 电工技术学报, 2019, 34(14): 2990-3003.
Tu Chunming, Xiao Fan, Yuan Jingbing, et al. DC ripple voltage suppression strategy for cascaded power electronic transformer[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2990-3003.
[3] 李子欣, 王平, 楚遵方, 等. 面向中高压智能配电网的电力电子变压器研究[J]. 电网技术, 2013, 37(9): 2592-2601.
Li Zixin, Wang Ping, Chu Zunfang, et al. Research on medium- and high-voltage smart distribution grid oriented power electronic transformer[J]. Power System Technology, 2013, 37(9): 2592-2601.
[4] 涂春鸣, 肖凡, 兰征, 等. 微电网中电力电子变压器的电压质量控制策略研究[J]. 电工电能新技术, 2018, 37(6): 1-9.
Tu Chunming, Xiao Fan, Lan Zheng, et al. The power control of power electronic transformer in hybrid AC-DC microgrid[J]. Transactions of China Electro- technical Society, 2018, 37(6): 1-9.
[5] 刘建强, 赵楠, 孙帮成, 等. 基于LLC谐振变换器的电力电子牵引变压器控制策略研究[J]. 电工技术学报, 2019, 34(16): 3333-3344.
Liu Jianqiang, Zhao Nan, Sun Bangcheng, et al. Research on control strategy of power electronic traction transformer based on LLC resonant converter[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3333-3344.
[6] 涂春鸣, 黄红, 兰征, 等. 微电网中电力电子变压器与储能的协调控制策略[J]. 电工技术学报, 2019, 34(12): 2627-2636.
Tu Chunming, Huang Hong, Lan Zheng, et al. Coordinated control strategy of power electronic transformers and energy storage in microgrids[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2627-2636.
[7] Feng Jianhua, Chu W Q, Zhang Zhixue, et al. Power electronic transformer-based railway traction systems: challenges and opportunities[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 1237-1253.
[8] 兰征, 涂春鸣, 肖凡, 等. 电力电子变压器对交直流混合微网功率控制的研究[J]. 电工技术学报, 2015, 30(23): 50-57.
Lan Zheng, Tu Chunming, Xiao Fan, et al. Study on power control of AC/DC hybrid microgrid by power electronic transformer[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 50-57.
[9] Kolar J W, Ortiz G I. Solid-state-transformers: key components of future traction and smart grid systems[C]//Proceedings of the International Power Electronics Conference, Hiroshima, Japan, 2014.
[10] Zhao Tiefu, Wang Gangyao, Bhattacharya S, et al. Voltage and power balance control for a cascaded H-bridge converter-based solid-state transformer[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1523-1532.
[11] 李响, 郝瑞祥, 游小杰, 等. 一种级联电力电子变压器直流电压平衡控制策略[J]. 电工技术学报, 2017, 32(2): 238-245.
Li Xiang, Hao Ruixiang, You Xiaojie, et al. A DC voltage balance control strategy for the cascaded power electronic transformer[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 238-245.
[12] 王杉杉, 王玉斌, 林意斐, 等. 级联型电力电子变压器电压与功率均衡控制方法[J]. 电工技术学报, 2016, 31(22): 92-99.
Wang Shanshan, Wang Yubin, Lin Yifei, et al. Voltage and power balance control for cascaded power electronic transformer[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 92-99.
[13] Liu Jianqiang, Yang Jingxi, Zhang Jiepin, et al. Voltage balance control based on dual active bridge DC/DC converters in a power electronic traction transformer[J]. IEEE Transactions on Power Electro- nics, 2018, 33(2): 1696-1714.
[14] 张晓东, 张大海. 电力电子变压器在电网故障中的控制策略[J]. 电力系统及其自动化学报, 2014, 26(1): 39-43.
Zhang Xiaodong, Zhang Dahai. Control strategy of power electronic transformer in power grid failure[J]. Automation of Electric Power Systems, 2014, 26(1): 39-43.
[15] 冯宇鹏, 吴金龙, 王先为, 等. 电网不平衡故障下电力电子变压器控制策略[J]. 电力建设, 2016, 37(7): 84-90.
Feng Yupeng, Wu Jinlong, Wang Xianwei, et al. Power electronic transformer control strategy under unbalanced network faults[J]. Electric Power Con- struction, 2016, 37(7): 84-90.
[16] Ouyang Shaodi, Liu Jinjun, Chen Xinqiang, et al. Control strategy for single-phase open-circuit oper- ation of a modular solid-state transformer[J]. IEEE Transactions on Power Electronics, 2019, 34(9): 8555-8573.
[17] 金一丁, 宋强, 刘文华. 基于公共直流母线的链式可拓展电池储能系统及控制[J]. 电力系统自动化, 2010, 34(15): 66-70.
Jin Yiding, Song Qiang, Liu Wenhua. Control and analysis of extensible cascaded battery energy storage system based on a common DC bus[J]. Auto- mation of Electric Power Systems, 2010, 34(15): 66-70.
[18] García P, Saeed S, Navarro-Rodríguez Á, et al. Switching frequency optimization for a solid state transformer with energy storage capabilities[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 6223-6233.
[19] 党存禄, 慈航乐, 党媛. 具有储能环节的电力电子电能质量研究[J]. 电子技术应用, 2019, 45(3): 118- 121, 126.
Dang Cunlu, Ci Hangle, Dang Yuan. Research on power quality of solid state transformer with energy storage[J]. Electronic Technology Application, 2019, 45(3): 118-121, 126.
[20] 袁宇春, 张保会. 对整定线路重合闸时间的讨论[J]. 继电器, 2000(1): 13-15.
Yuan Yuchun, Zhang Baohui. Discussion on setting the reclosing time of lines[J]. Relay, 2000(1): 13-15.
[21] 李子欣, 高范强, 赵聪, 等. 电力电子变压器技术研究综述[J]. 中国电机工程学报, 2018, 38(5): 1274-1289.
Li Zixin, Gao Fanqiang, Zhao Cong, et al. Review of power electronic transformer technology research[J]. Proceedings of the CSEE, 2018, 38(5): 1274-1289.
[22] She Xu, Huang A Q, Burgos R. Review of solid-state transformer technologies and their application in power distribution systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2013, 1(3): 186-198.
[23] 许敏, 张宏川, 王淑红, 等. 电网电动势初始相位角对三相PWM整流器启动电流的影响分析[J]. 工矿自动化, 2013, 39(10): 59-63.
Xu Min, Zhang Hongchuan, Wang Shuhong et al. Analysis of the influence of the initial phase angle of the grid's electromotive force on the starting current of the three-phase PWM rectifier[J]. Industry and Mine Automation, 2013, 39(10): 59-63.
Fault Ride-Through Control Strategy of Solid State Transformer with PV Power Generation
Abstract Reclosing is an effective measure to improve the reliability of distribution network. The multi-port solid-state transformer (SST) integrated with power electronics is significantly affected by the control strategy, and the operating mechanism of SST is unclear during the reclosing of the distribution network. Therefore, this paper studies the operating characteristics of SST under the reclosing mechanism. It is pointed out that if a certain control strategy is not adopted, SST may have impulse current in the face of reclosing. Accordingly, this paper proposes an impulse current suppression strategy for the SST with photovoltaic (PV) power generation to improve the operational capabilities. Firstly, this paper analyzes the topology and control strategy of SST as well as the mechanism of SST impulse current during reclosing. Secondly, according to different initial working conditions and the maximum allowable current of the input stage, the power compensation range of the PV power generation is obtained, and the impulse current suppression strategy is proposed. Finally, simulation and experiment verify the correctness and effectiveness of the theoretical analysis and proposed strategy.
keywords：Solid state transformer, automatic reclosing, impulse current, photovoltaic power generation
中图分类号：TM41; TM921.5
DOI: 10.19595/j.cnki.1000-6753.tces.190929
国家重点研发计划资助项目（2018YFB0904100）。
收稿日期 2019-07-25
改稿日期 2019-11-05
涂春鸣 男，1976年生，博士，教授，研究方向为电能质量与控制、电力电子技术在电力系统中的应用等。E-mail: chunming_tu@263.net
肖 凡 男，1988年生，博士，研究方向为电力电子技术在电力系统中的应用。E-mail: woliaokk123@126.com（通信作者）
（编辑 陈 诚）