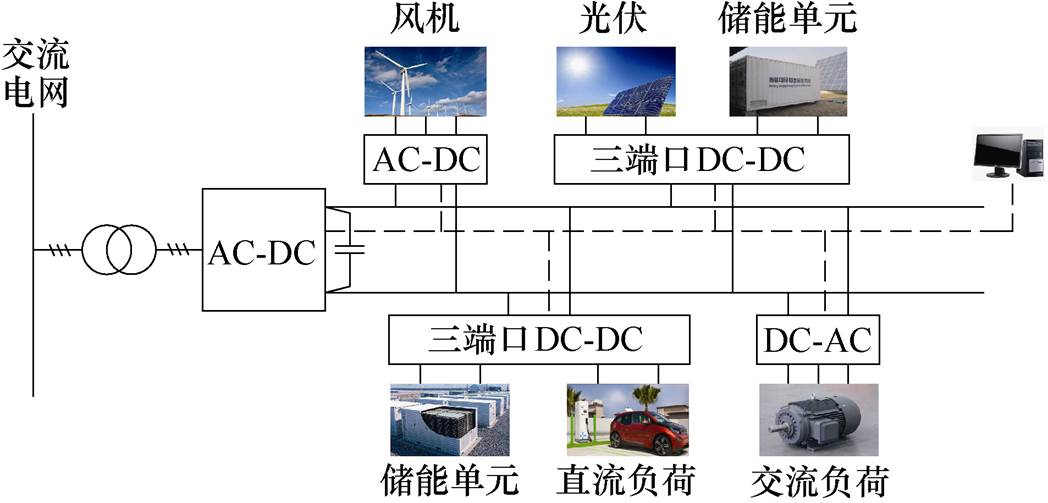
图1 采用三端口DC-DC变换器的直流微电网结构
Fig.1 DC micro-grid structure using three-port DC-DC converter
摘要 为提高直流微电网中三端口隔离双向DC-DC变换器的动态性能，针对三有源桥（TAB）DC-DC变换器，该文提出一种模型预测控制（MPC）策略。考虑TAB变换器各端口的控制目标，基于移相控制和平均值模型建立TAB变换器离散化预测模型，通过MPC问题最优求解设计预测控制器，以实现端口间的解耦控制效果。进一步分析系统参数偏差对MPC策略控制效果的影响，设计抑制稳态误差的TAB变换器MPC控制方案。基于TMS320F28335+FPGA_XC6SLX16的双处理器控制内核搭建TAB样机，实验结果验证了该文所提方法的有效性，且具有更快的动态特性及端口功率解耦运行能力。
关键词：直流微电网 三端口DC-DC变换器 移相控制 平均值模型 模型预测控制
随着分布式可再生能源发电、储能及电力电子技术的快速发展，微电网正成为国内、外研究热点。微电网是由分布式电源、储能设备、电力变换器、负荷等组成的一种智能配用电系统形式，既可以并网运行也可以孤岛运行，同时配备储能装置平抑可再生能源发电与负荷的功率波动，是实现分布式电源大规模接入配电网的有效方案[1-4]。相比交流微电网，直流微电网无需考虑系统内无功功率，无需对电压相位、频率进行跟踪，供电架构简单，并且能更加可靠地接纳分布式可再生能源、储能设备及各类直流负荷[5-8]。近年来，中国、欧盟、美国和日本等国家和地区均开展了直流微电网相关的研究及示范工程建设。
直流微电网中的风、光等分布式电源、储能装置以及电动汽车、LED照明等直流负荷往往具有不同的端口特性与电压等级，需要采用很多独立的DC-DC变换器和DC-AC变换器将其连接到直流母线上，电力变换设备的数量以及设备之间的通信增加了直流微电网的复杂性与建设成本。在这个背景下，多端口隔离双向DC-DC变换器因其能量管理灵活、端口相互隔离、成本低、功率密度和效率高等特点，引起了越来越多的研究和关注。图1为采用三端口DC-DC变换器的直流微电网结构，这种结构能实现不同设备的集中控制，便于微电网能量管理。
图1 采用三端口DC-DC变换器的直流微电网结构
Fig.1 DC micro-grid structure using three-port DC-DC converter
图2所示为基于三有源桥（Triple Active Bridge, TAB）的三端口隔离双向DC-DC变换器，由三个全桥和一个三绕组高频变压器组成。文献[9]最早提出该拓扑并将其应用于燃料电池/储能电池混合系统。自提出以来，TAB变换器主要应用于可再生能源发电与储能系统[10-14]、电动汽车[15]、不间断电源[16]等领域。文献[10]通过引入桥内移相控制，实现TAB全移相范围的零电压开通，同时基于瞬时值积分建立小信号模型，在控制环路中采用对角矩阵解耦法实现端口功率的解耦。文献[11]也采用类似的策略实现端口功率的解耦，区别在于其小信号模型是基于基波等效模型建立的。文献[12]在变压器绕组电路中加入陷波滤波器，通过设计滤波器的参数削弱TAB端口功率的耦合性。文献[13]通过在变压器绕组电路加入LC串联谐振网络，从硬件电路设计角度削弱端口功率的耦合性。国内外学者对于TAB变换器的研究主要集中于端口功率的解耦，以提高端口的动态性能。
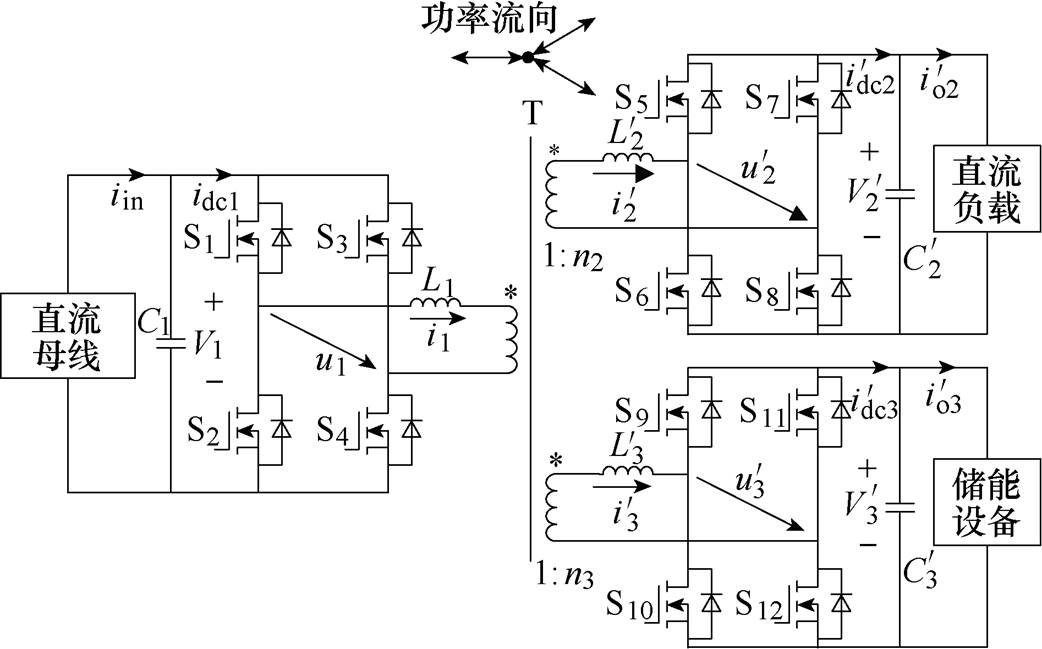
图2 TAB变换器拓扑
Fig.2 Topology of TAB converter
模型预测控制（Model Predictive Control, MPC）是一类基于控制对象数学模型的控制策略[17]。近年来，模型预测控制越来越多地应用于DC-DC变换器[18-25]。文献[20-21]建立双有源桥（Dual Active Bridge, DAB）DC-DC变换器平均值模型并采用无差拍预测控制，可提高变换器对于输入电压突变及负载突变时的响应速度。文献[22]针对DAB变换器设计模型预测加PI的控制策略，模型预测控制用于提高动态性能，PI控制用于消除静态误差。文献[23]对移相全桥DC-DC变换器建立离散时间非线性模型，实现预测控制目标的同时加入了峰值电流约束，并采用二分法获取MPC问题的在线数值解。文献[24]针对Boost电路提出带电感峰值电流约束的模型预测控制，采用两个龙伯格观测器分别观测扰动和负载，降低了控制的参数依赖性。文献[25]针对两相交错并联双向DC-DC变换器，建立Buck模式下离散数学模型，设计带约束的MPC问题，采用粒子群算法求解优化问题。
相比传统的PI控制，模型预测控制具有更快的动态响应速度，且适用于包括TAB变换器在内的非线性多输入多输出的控制对象[17]。目前尚未有文献研究TAB变换器的模型预测控制，且因为三个端口之间的耦合关系，应用于DAB变换器的模型预测控制无法直接用于TAB变换器。
本文面向TAB变换器在直流微电网中的应用，通过建立TAB变换器的离散化平均值模型，针对TAB变换器各端口的控制目标，推导TAB变换器预测模型，建立MPC问题并求数值最优解，实现预测控制器的优化设计。最后，搭建TAB样机，对研究内容进行实验验证。
在图2所示的TAB变换器拓扑中，直流端口1、2、3分别连接微电网直流母线、直流负载和直流储能单元，图中带上标“＇”的变量代表2、3端口对应的电气量实际值，电压、电流的正方向按照图2中所示定义，因此从直流微电网输入变换器的功率流向为正方向，从变换器输出至直流负载和储能设备的功率为正功率。直流端口和高频变压器绕组间通过三个H全桥连接，实现双向功率传输。三绕组变压器的主要功能是匹配三个直流端口电压并提供电气隔离。变压器的1端口绕组与2端口、3端口绕组的电压比分别为1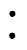
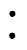n2、1n3，L1、
、
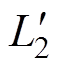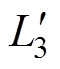为变压器各绕组的漏感。
隔离变压器等效电路及电压、电流波形如图3所示。图3a为高频变压器2、3端口折算至1端口的星形等效电路。各电气量与参数的折算过程为：ux=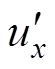
/nx, ix=
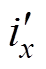nx, Lx=
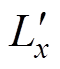/nx（x=2, 3）。为了统一分析，将直流端口各电气量与参数也进行相同折算：Vx=
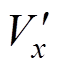/nx, Cx=
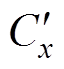nx, idcx=
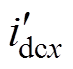nx, iox=
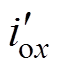nx。进一步简化分析，将星形电路转换为的三角形等效电路，如图3a所示。图中，L12、L23、L31为
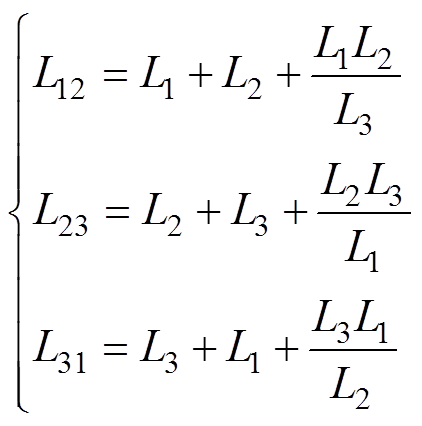（1）
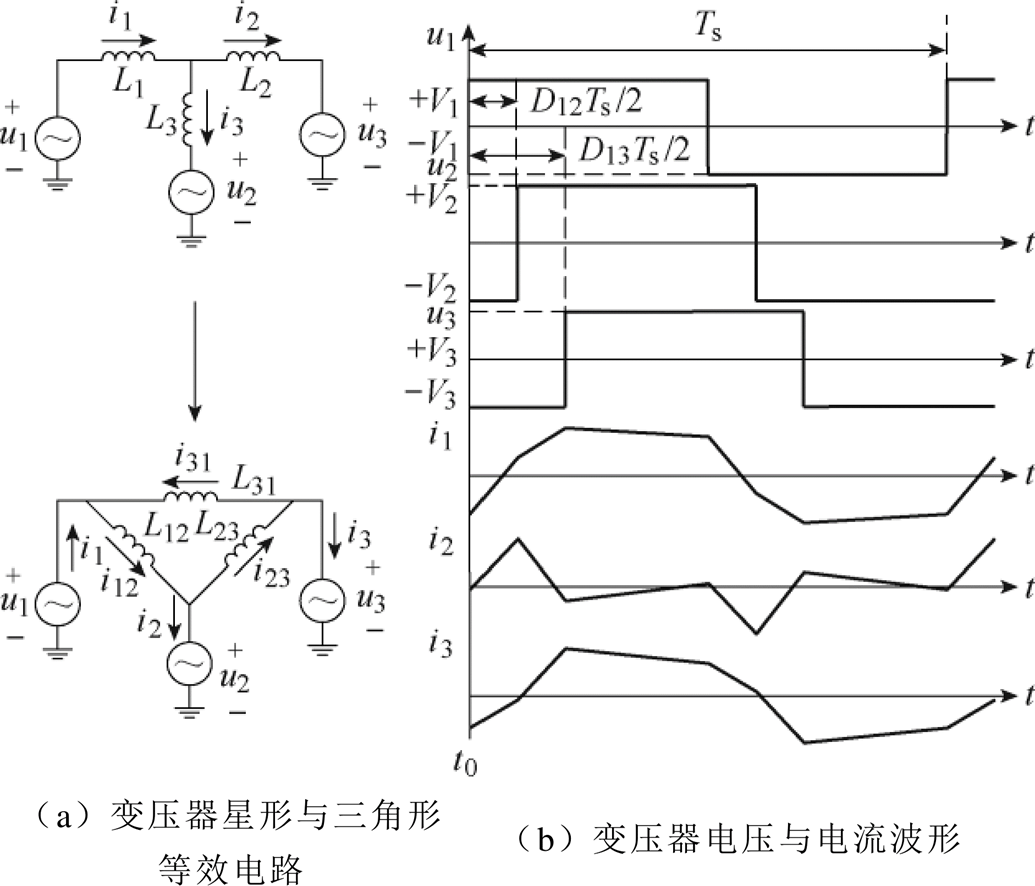
图3 隔离变压器等效电路及电压、电流波形
Fig.3 Equivalent circuit, voltage and current waveforms of isolation transformer
TAB变换器的高频变压器一般满足如下条件[11]：
（1）为使各端口具有相同的功率传输能力，以三角形等效电路各支路电感L12、L23、L31相等为目标设计变压器绕组漏感，定义L=L12=L23=L31。
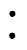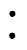（2）三绕组变压器电压比与三个直流端口额定电压比匹配，即1n2n3=V1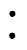
。
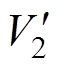
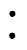
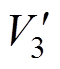TAB变换器通常采用移相调制，三个端口H桥开关频率相同，各开关器件均为180°导通。以图2中1端口H桥为例，驱动信号S1与S4极性相同，S2与S3极性相同但与S1、S4极性相反，这样变压器1端口绕组电压u1为占空比50%的方波。同理，2、3端口H桥对应各管子驱动信号分别滞后1端口H桥驱动信号D12Ts/2和D13Ts/2，变压器各绕组端口因此产生相位不同的方波电压u1、u2和u3如图3b所示。其中，Ts为开关周期，即Ts=1/fs，D12、D13分别为变压器2、3绕组端口电压滞后1绕组端口电压的移相占空比。通常，移相占空比满足-0.5≤D12, D13≤0.5。
定义变压器各绕组端口一个开关周期内的平均功率分别为P1、P2、P3，可以通过瞬时值积分获取平均功率表达式[10]，即
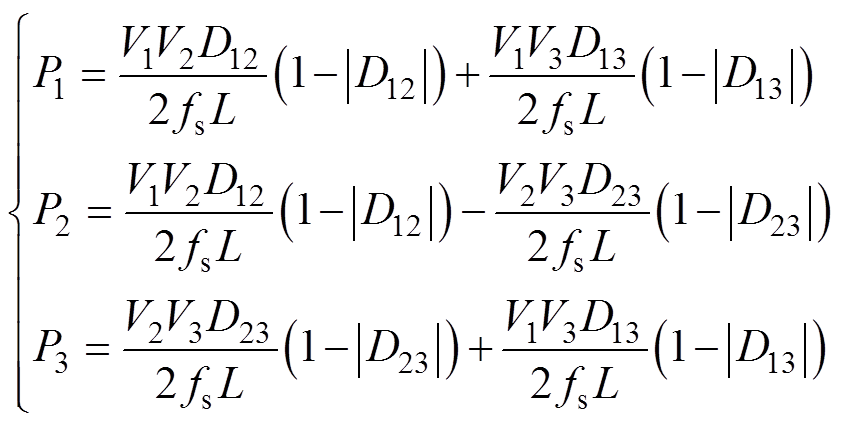（2）式中，D23=D13-D12。
从式（2）可以看出，P2、P3因移相占空比D23耦合，这也是TAB相比DAB的不同之处。忽略所有开关器件的功率损耗，可得直流稳压电容与H桥之间电流idc1、idc2、idc3的开关周期平均值，分别用Idc1、Idc2、Idc3表示为
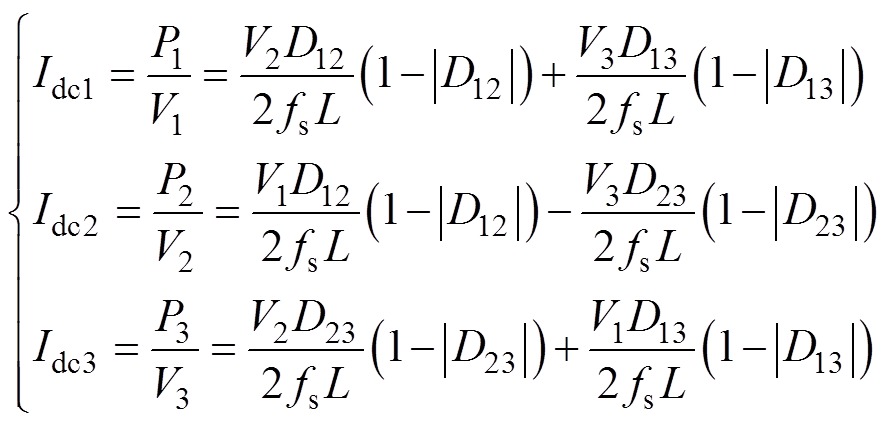（3）TAB变换器不同于传统的Buck、Boost等DC- DC变换器，TAB变换器中的电感电流为纯交流量，稳态下开关周期平均值为0，因此可以建立直流端口电压为状态变量的TAB变换器数学模型，建立如图4所示的平均值模型等效电路。其中，Iin、Io2、Io3分别为iin、io2、io3的开关周期平均值；忽略直流母线电压波动，即Iin=Idc1，因此可省略稳压电容C1；Idc1、Idc2、Idc3的具体表达式由式（3）给出。需要注意的是，该等效电路仍是折算至1端口的等效电路，2、3端口的各电气量均为折算量。
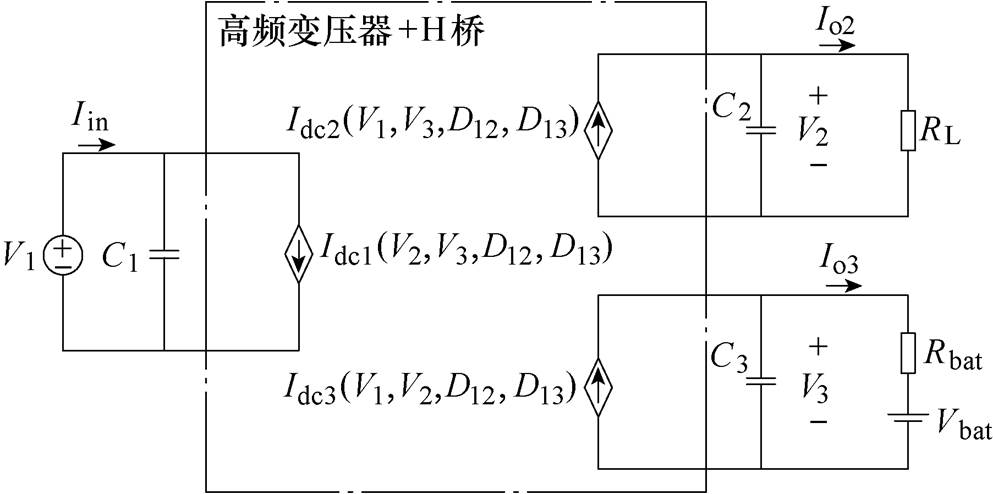
图4 TAB变换器的平均值模型等效电路
Fig.4 Average model equivalent circuit of TAB converter
由图4所示平均值等效电路，以V2、V3为状态变量，根据基尔霍夫电流定律可建立TAB变换器的状态空间方程为
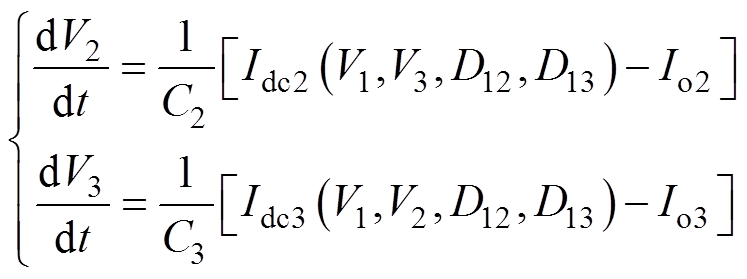（4）采用前向欧拉法对式（4）离散化处理，可得离散化TAB变换器的状态空间方程为
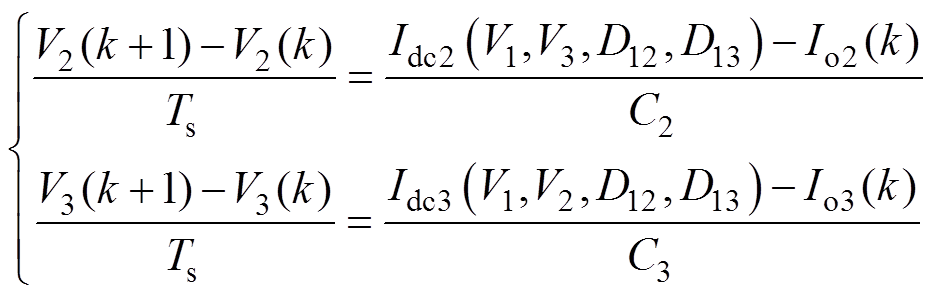（5）
式中，Vx(k)、Iox(k)（x=2, 3）分别为x端口在k周期内的平均电压和输出电流；Vx(k+1)为x端口在k+1周期内的平均电压。
式（4）和式（5）所示TAB变换器的状态空间方程表明，TAB变换器是多输入多输出非线性耦合系统，在设计控制器时需要额外的解耦环节，增加了控制的计算复杂性，且一定程度上影响了系统动态性能。为了改善这个问题，本文提出模型预测控制，在实现TAB变换器端口解耦控制的同时提高了端口的动态性能。
模型预测控制是一类基于控制对象数学模型的控制策略，预测控制器设计通常包括预测模型建立、MPC优化问题描述和滚动时域优化等几个步骤。
因三绕组变压器电压比与三个直流端口额定电压比匹配，可将Idc2、Idc3表达式中的V2、V3用V1替换。重写式（5）所示TAB变换器离散状态空间方程，得到预测模型为
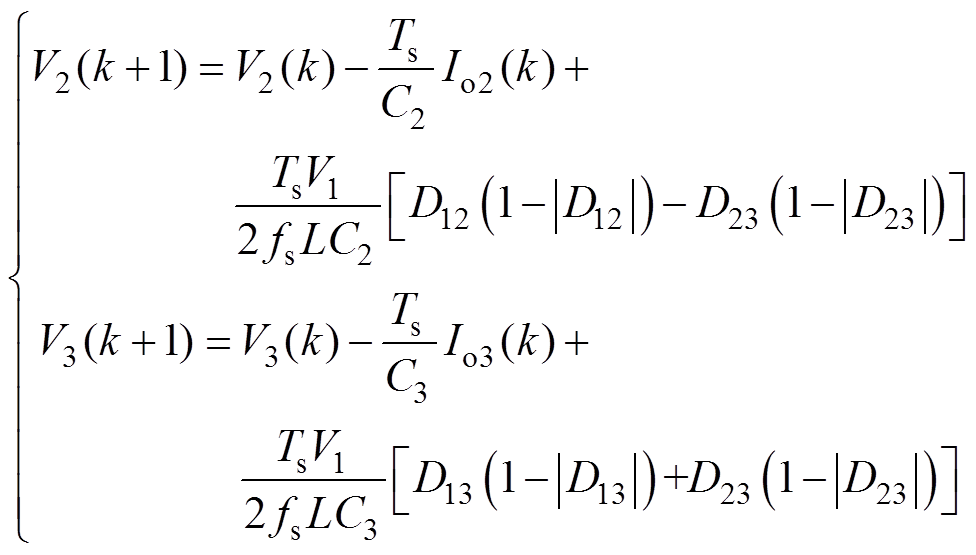（6）2端口连接负载，通常工作在电压控制模式。而考虑到储能电池的荷电状态（State of Charge, SOC）能量管理，3端口需要具备电流控制（功率控制）和电压控制两种控制模式。为实现电流控制目标，考虑3端口储能电池直流电压变化较为缓慢，3端口的输出电流预测模型可表示为
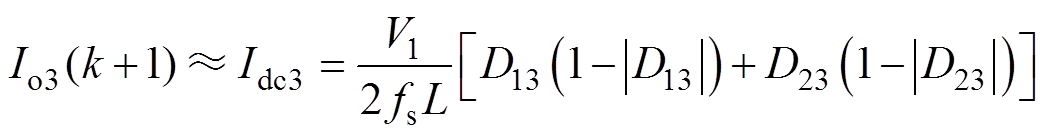（7）
模型预测控制中，在每个开关周期k内，控制器根据状态变量x(k)，计算出能使成本函数在长度N的有限范围内被最小化的控制量u(k)。本文选择预测优化时域长度N=1，以降低计算复杂性。考虑2端口控制目标为电压、三端口控制目标为电压或电流，因此成本函数可表示为
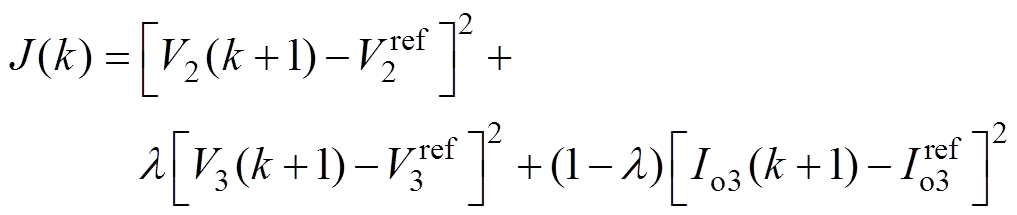（8）式中，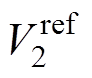
、
、
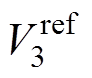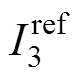分别为2端口电压参考、3端口电压参考和电流参考；l 为储能端口控制模式，l =1、0分别代表储能端口为电压或电流控制模式。成本函数的设计综合考虑了2、3端口控制目标，每个开关周期k内计算移相占空比D12、D13使2、3端口控制量的偏差都尽可能小，以实现动态过程的解耦控制效果。
加入移相占空比的范围约束，MPC问题可以描述为
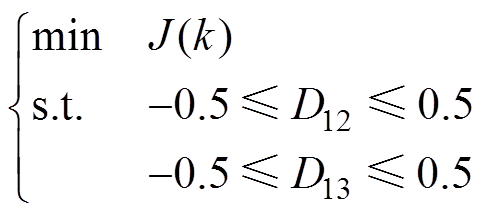（9）为求解上述MPC问题，构造式（9）的KKT（Karush-Kuhn-Tucker）条件[26]为
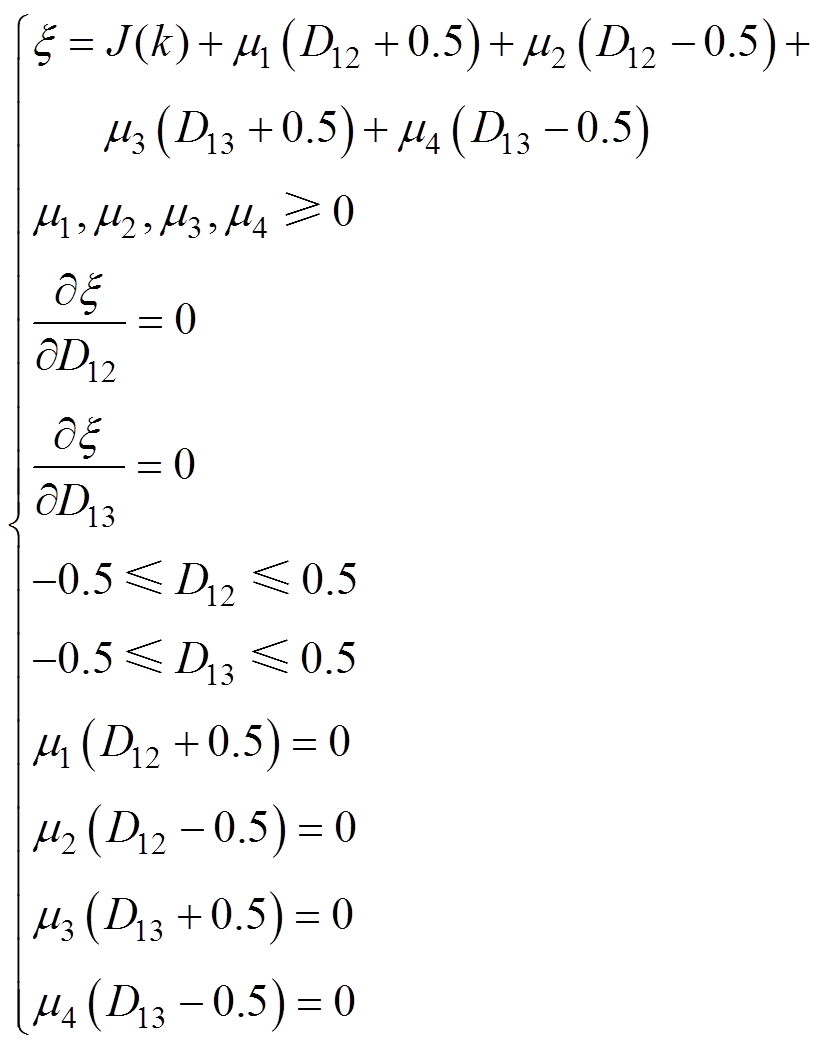（10）
式中，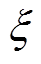
为拉格朗日函数；uj为KKT乘子，j=1, 2, 3, 4。
求解式（10），得出MPC下D12、D13满足的表达式为
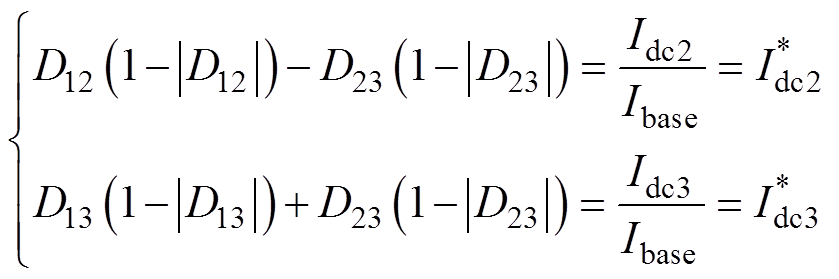（11）
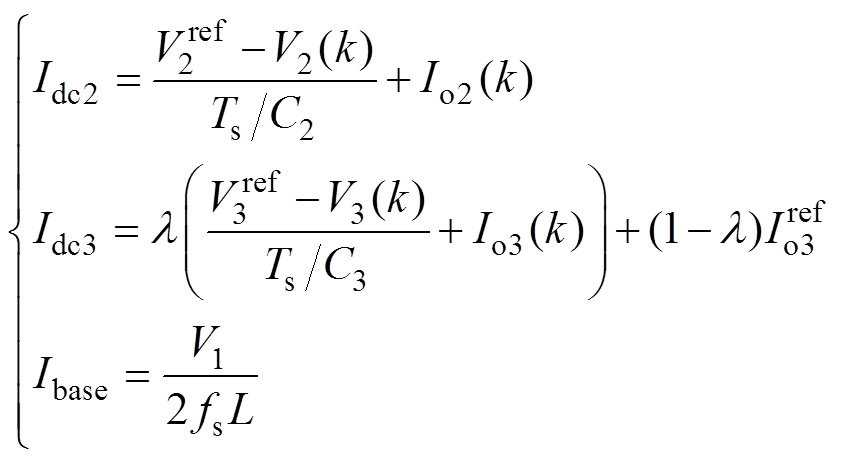（12）
式中，Ibase为电流基值；Idc2、Idc3反映要达到控制目标最优、k+1时刻的目标电流值，对其进行标幺化处理，得到标幺化电流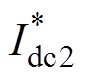
、
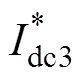。根据对偶关系，式（11）可以进一步简化为
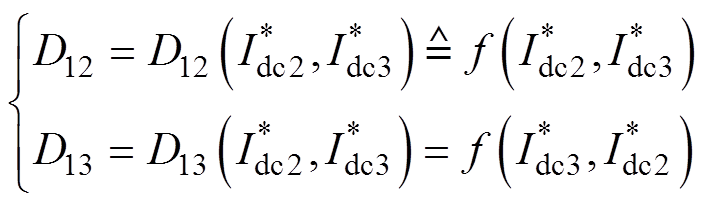（13）根据式（13）的数值解，可以得到MPC下移相占空比D12、D13与标幺化电流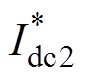、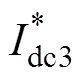的关系，如图5所示。从图5中可以看出，当标幺化电流在可调区域内，移相占空比可以在有效区间（-0.5, 0.5）内调节，使控制目标快速达到参考值；当标幺化电流超过可调区域，移相占空比将以最大能力输出（+0.5或-0.5），失去调节能力。
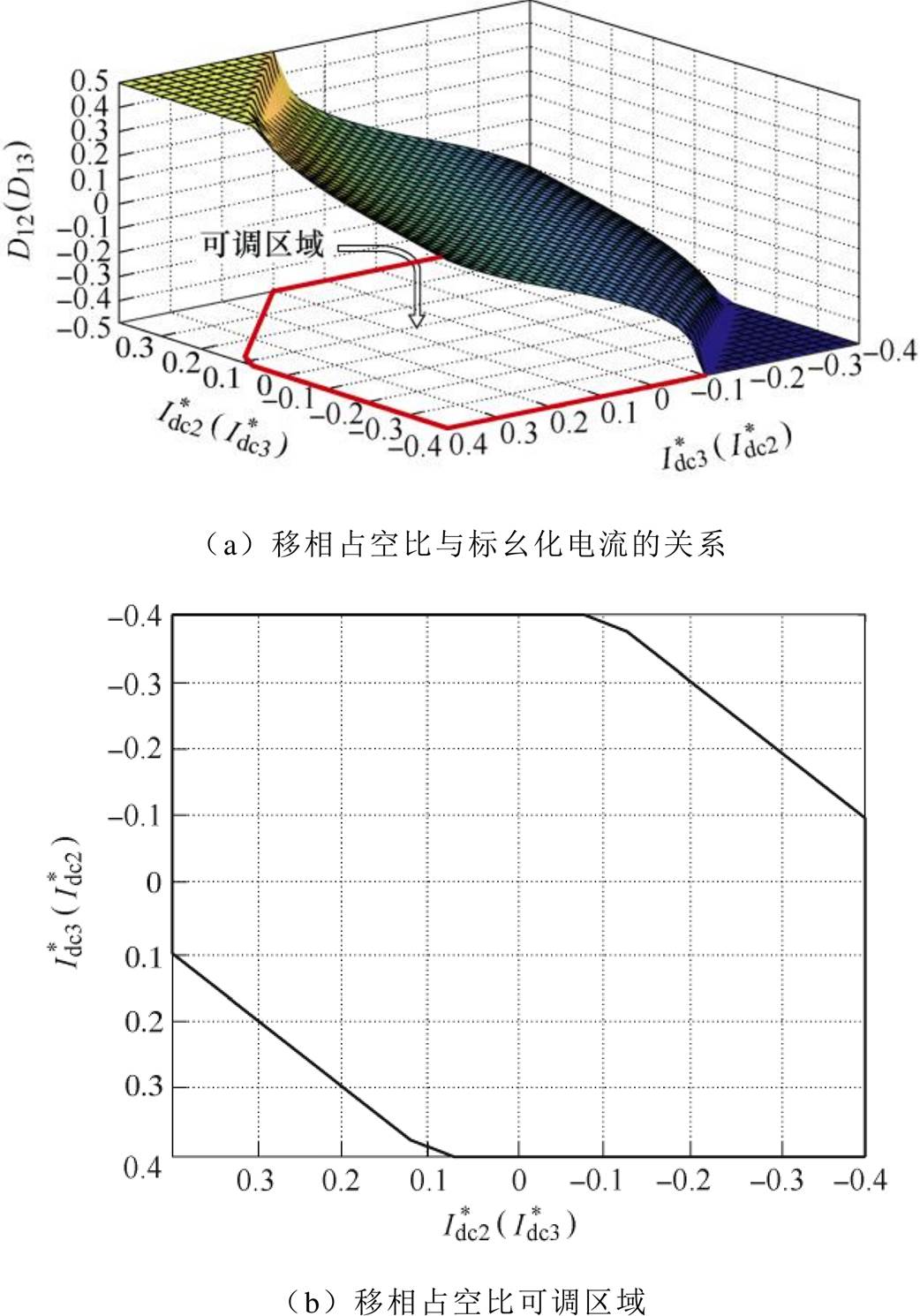
图5 移相占空比与标幺化电流的关系及移相占空比可调区域
Fig.5 Relationship between phase-shifting duty ratio and standard current, adjustable area of phase-shifting duty ratio
由上述MPC求解结果可知，控制中移相占空比的计算需要用到C2、C3、L三个模型参数，参数真实值与控制中所用值的偏差将导致稳态误差，需要进一步分析参数不匹配对MPC的影响。
为了简化分析，定义变压器电感参数不匹配度gL为控制中所用值Ln与真实值L的比值，可表示为
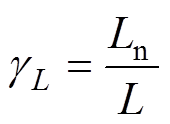（14）定义采用Ln计算得到的电流基值为Ibasen= V1/(2fsLn)=Ibase/gL。类似地，定义电容参数不匹配度gC2、gC3，可分别表示为
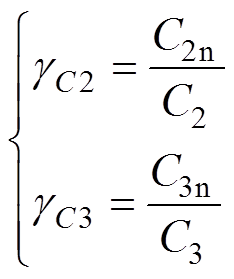（15）
式中，C2n、C3n分别为控制中采用的2、3端口稳压电容。
采用控制参数Ln、C2n和C3n计算得到的标幺化电流定义为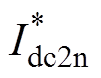
、
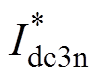，可分别表示为
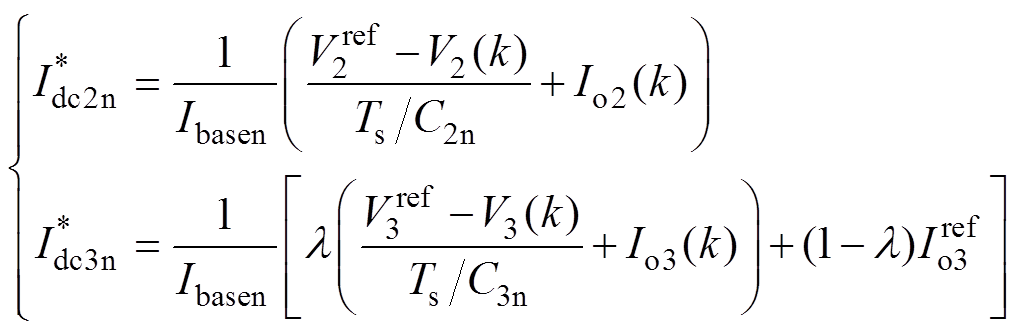（16）由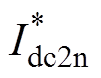、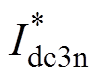计算得到移相占空比满足关系为
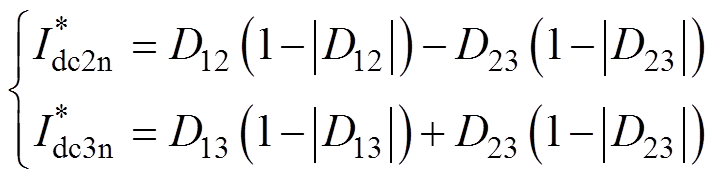（17）
电流真实值Idc2、Idc3分别满足关系为
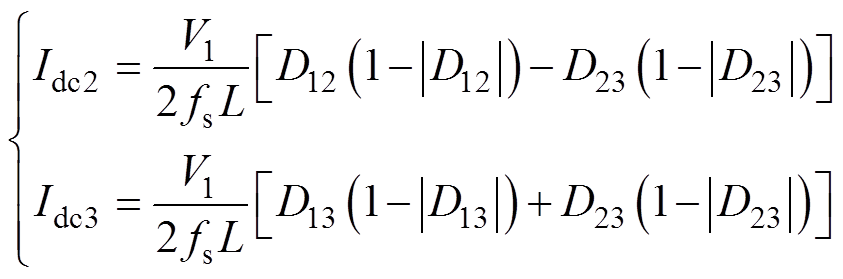（18）将式（17）代入式（18）可得
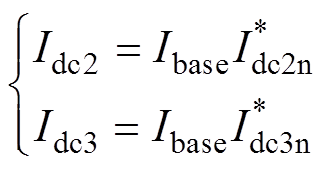（19）
进一步地，将式（16）代入式（19）可得
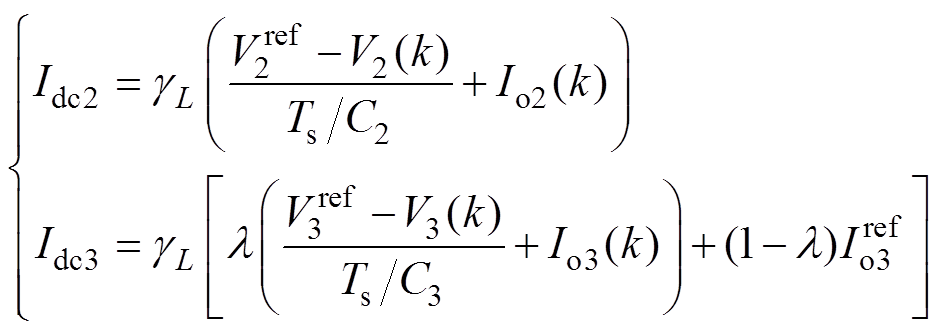（20）稳态下，Idc2=Io2, Idc3=Io3，因此式（20）又可表示为
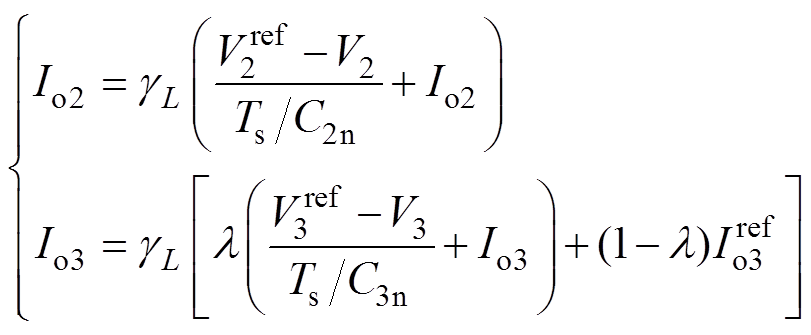（21）
考虑到储能电池的控制需求，3端口需要具备电流控制（功率控制）和电压控制两种控制模式，因此需要分别分析两种控制模式下产生的稳态误差。
1）电压控制模式稳态误差（l =1）
假设2、3端口传输功率均为额定功率Pn，则Io2=Pn/V2, Io3=Pn/V3，代入式（21）可得
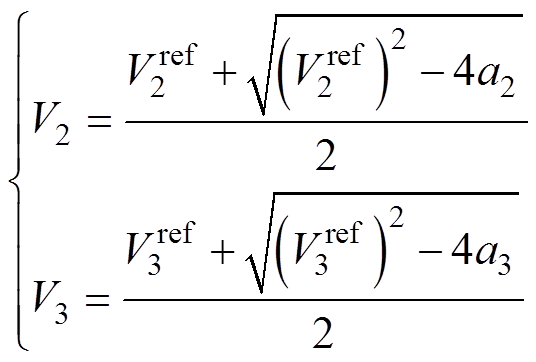（22）其中
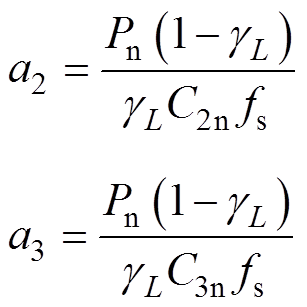
由式（22）可知，误差电压值仅与变压器电感不匹配度lL有关，而与电容不匹配度gC2、gC3无关。定义电压误差为
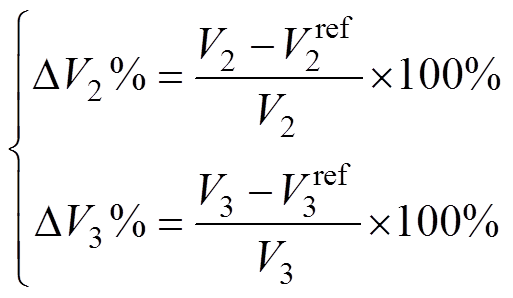（23）TAB实验样机参数见表1，由表1可得电压误差与变压器电感不匹配度gL的关系曲线，如图6所示。可以看出，电感不匹配度对于电压稳态误差的影响低于1%，可以忽略。这也说明在本文提出的TAB模型预测控制下端口电压具有很高的控制精度。
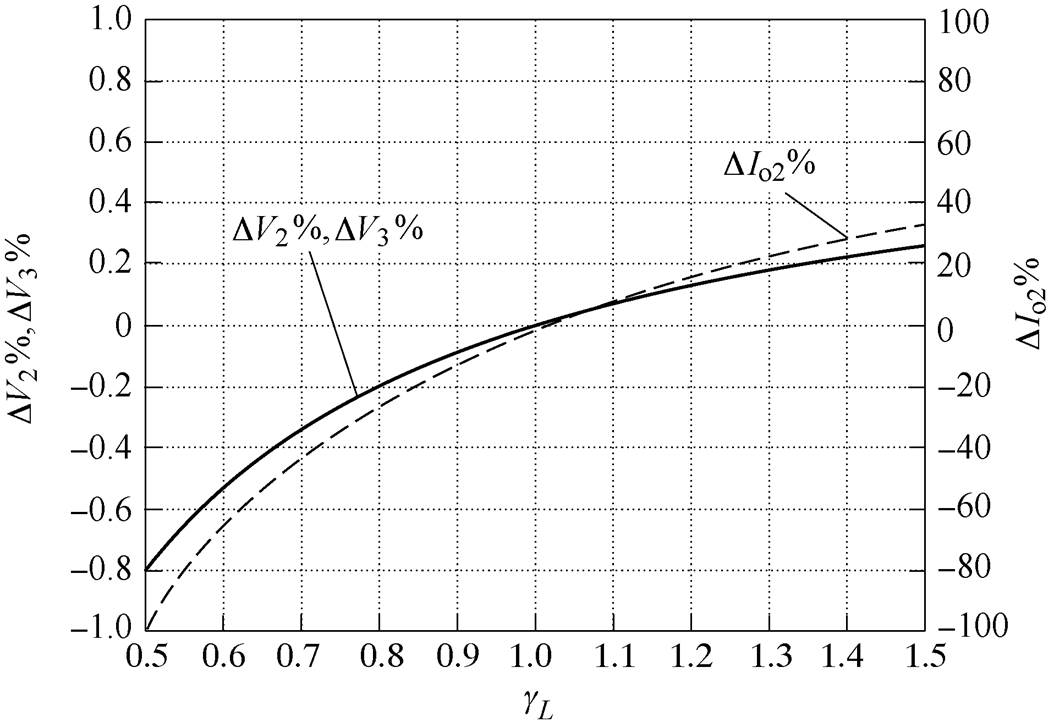
图6 电压、电流误差与变压器电感不匹配度gL的关系曲线
Fig.6 The relationship curves between voltage, current error and gL
2）电流控制模式问题误差（l =0）
由式（21）可得电流控制下3端口稳态输出电流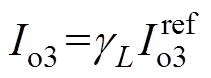
，电流误差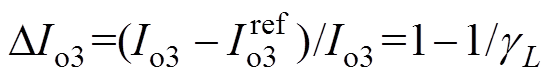
。从图6中可以看出，电流误差受电感不匹配度影响较大，当不匹配度为0.5时，误差甚至可以达到-100%。因此，应加入积分环节消除稳态误差。
综合上述MPC问题的优化求解与参数灵敏性分析，本文所提出的TAB变换器模型预测控制框图如图7所示。图7中，电压控制环路内负载电流以前馈的形式加入控制环路，能快速反映负载的变化信息，从而提高控制系统的动态响应速度。电流控制环路中增加额外的积分环节以补偿稳态误差。控制中通过式（13）获取移相占空比，以实现端口解耦。相比传统的对角矩阵解耦方法，该方法控制所用电感、电容等参数均可以通过实测得到，仅电流补偿环积分参数ki需要整定[27]，且控制中不需要多维矩阵运算，计算更为简单。
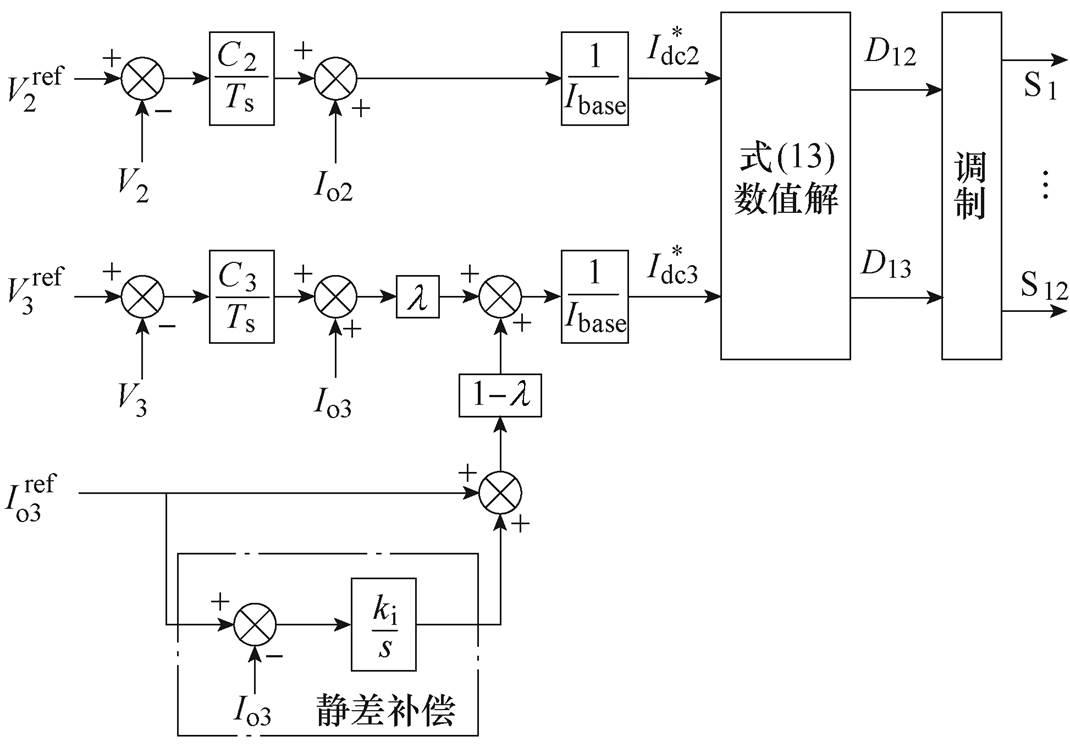
图7 TAB变换器的模型预测控制框图
Fig.7 Model prediction control block diagram of TAB converter
为验证所提出的TAB变换器模型预测控制策略的可行性与控制效果，本文基于TMS320F28335 + FPGA_XC6SLX16的双处理器控制内核，搭建TAB样机进行了实验验证和结果分析。实验样机如图8所示，样机参数见表1。
为验证和对比本文提出预测控制策略的运行效果，选择传统PI控制、对角矩阵解耦控制[10]进行动态性能对比实验。实验测试条件包括：①2端口负载突变；②3端口储能目标电流（功率）突变。
在负载突变实验中，1端口输入电压为300V，2、3端口电压控制目标分别为260V、150V。2端口负载从2 000W突减至1 000W动态过程波形如图9所示。图9中，PI控制中2、3端口电压环采用控制参数kp=0.000 3、ki=0.02；对角矩阵解耦控制中2、3端口电压环控制参数kp=0.24、ki=3；模型预测控制所采用的电感、电容参数见表1。
图8 TAB变换器实验样机
Fig.8 TAB converter prototype
表1 TAB实验样机参数
Tab.1 Parameters of TAB prototype
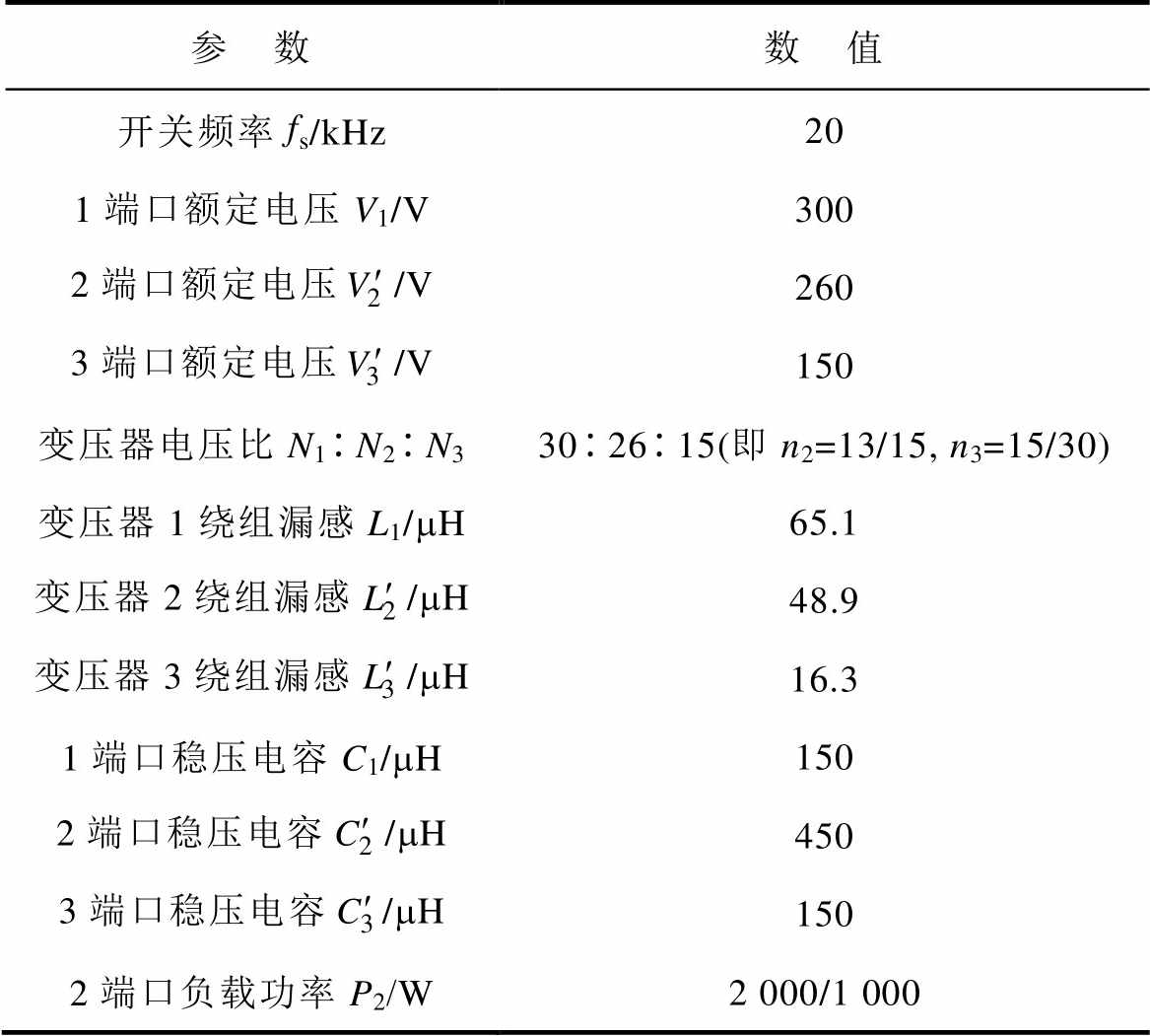
参 数数 值 开关频率fs/kHz20 1端口额定电压V1/V300 2端口额定电压/V260 3端口额定电压/V150 变压器电压比N1N2N3302615(即n2=13/15, n3=15/30) 变压器1绕组漏感L1/mH65.1 变压器2绕组漏感/mH48.9 变压器3绕组漏感/mH16.3 1端口稳压电容C1/mH150 2端口稳压电容/mH450 3端口稳压电容/mH150 2端口负载功率P2/W2 000/1 000
由图9可知，传统PI控制动态响应速度较慢（约为90ms），且2、3端口存在严重功率耦合，2端口负载突变下不仅2端口电压产生波动（幅值约为10V），3端口电流也产生幅值为1.1A的波动。对角矩阵解耦控制相比传统PI控制动态响应速度并没有提升（动态响应时间约为109ms），2端口电压波动幅值也与传统PI控制下相当，但对角矩阵解耦控制可以有效地减弱2、3端口之间的功率耦合，在2端口负载突变时维持3端口电流稳定（波动幅值约为0.1A）。模型预测控制下，变换器的动态响应时间约为5ms，2端口电压不产生波动，不仅如此，模型预测控制还同时实现了端口的解耦，3端口电流在2端口负载突变时不发生波动。
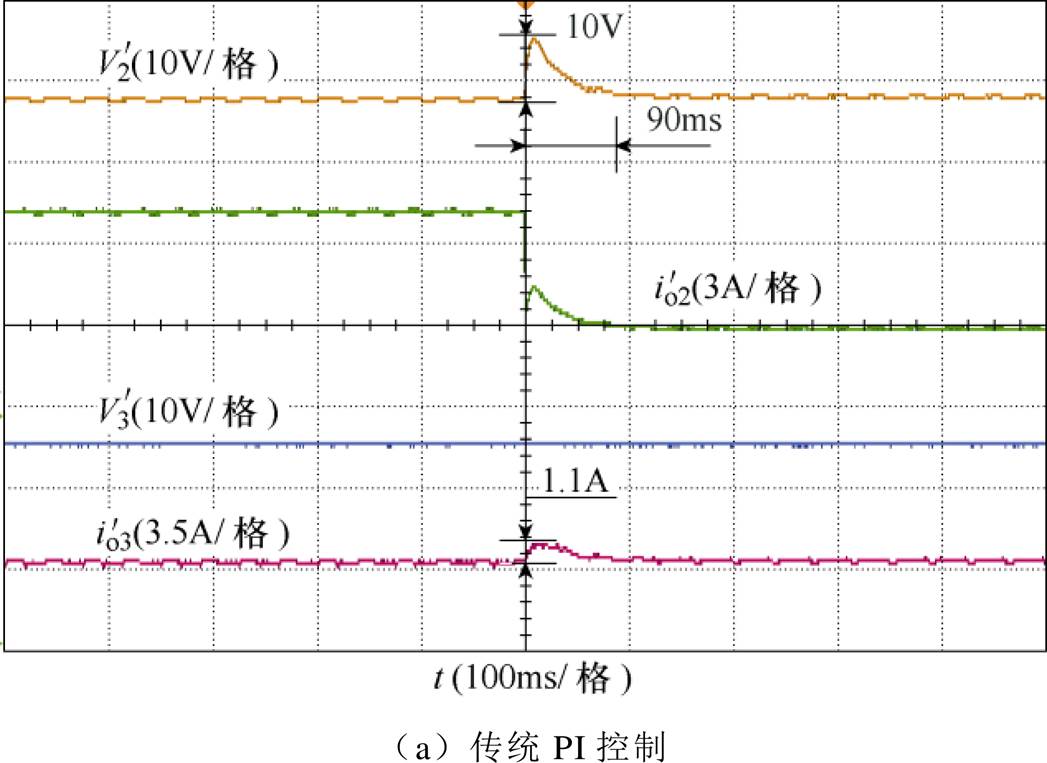
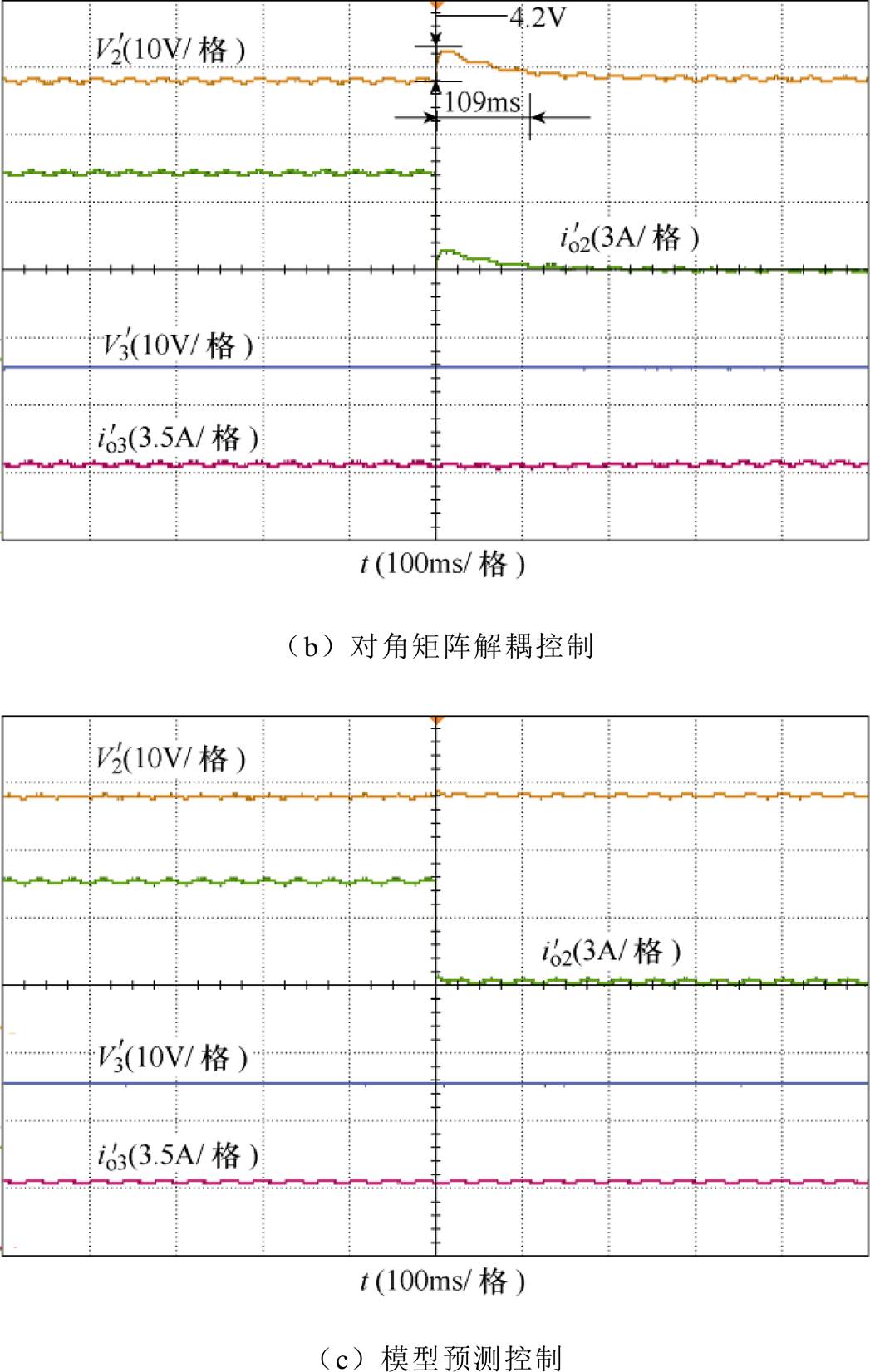
图9 2端口负载突减时不同控制策略下，2、3端口电压、电流实验波形
Fig.9 Voltage and current waveforms of port-2 and 3 under different control strategies when load of port-2 step down
图10为模型预测控制下，2端口负载功率突减暂态过程中高频变压器电流实验波形，从图10中可以看出，变压器暂态电流无明显过电流尖峰，也没有出现直流偏置电流，这表明模型预测控制下高频变压器偏磁及峰值电流过电流并不严重。
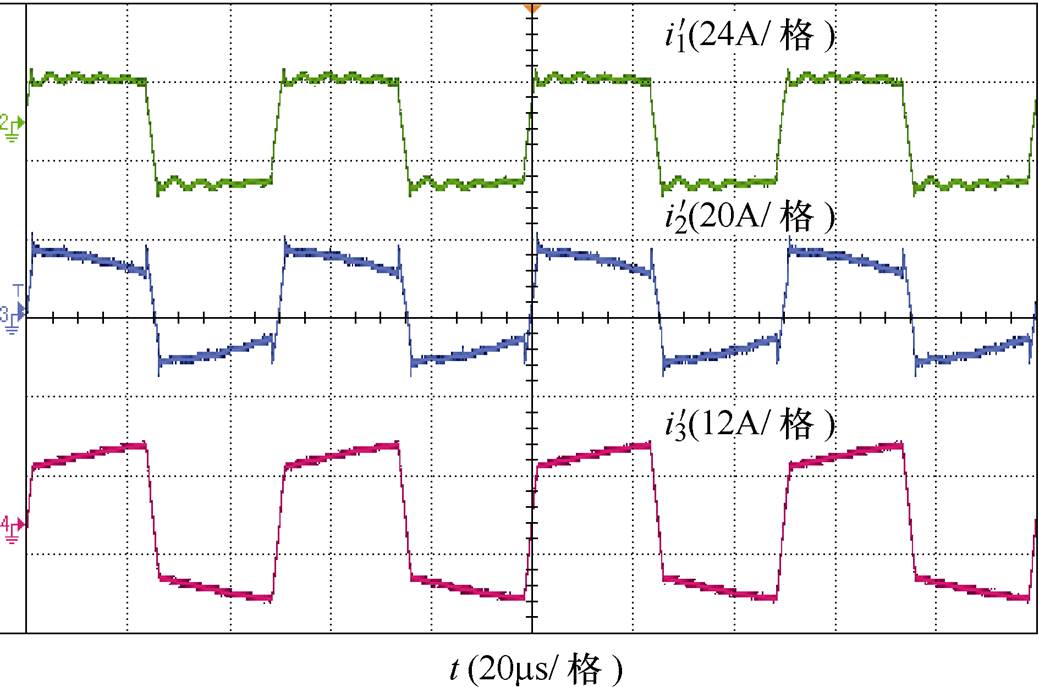
图10 模型预测控制下，2端口负载功率突减暂态过程中高频变压器电流实验波形
Fig.10 Transient current waveforms of high-frequency transformer under MPC when load of port-2 step down
在电流给定突变实验中，1端口电压为300V，2端口电压控制目标为260V，3端口电流控制目标从5A突增至10A。动态过程波形如图11所示。其中，2端口电压环参数与负载突变实验中参数相同；PI控制下3端口电流环参数kp=0.005、ki=0.5；对角矩阵解耦控制中3端口电流环参数kp=0.8、ki=6；模型预测控制3端口电流静差补偿环节ki=0.1。
由图11可以得出与图9类似的结论，传统PI控制与对角矩阵解耦控制动态响应速度均较慢，分别为85ms和86ms，传统PI控制下在3端口给定电流突增时，2端口产生幅值为3.5V的电压波动；而在对角矩阵解耦控制中，2端口电压能够维持稳定（波动幅值约为0.5V），表明对角矩阵解耦控制可有效地减弱2、3端口之间的功率耦合。模型预测控制下TAB变换器的动态响应时间为5ms，3端口电流给定阶跃下2端口电压也不产生波动，极大地提升了TAB变换器的端口动态控制性能。
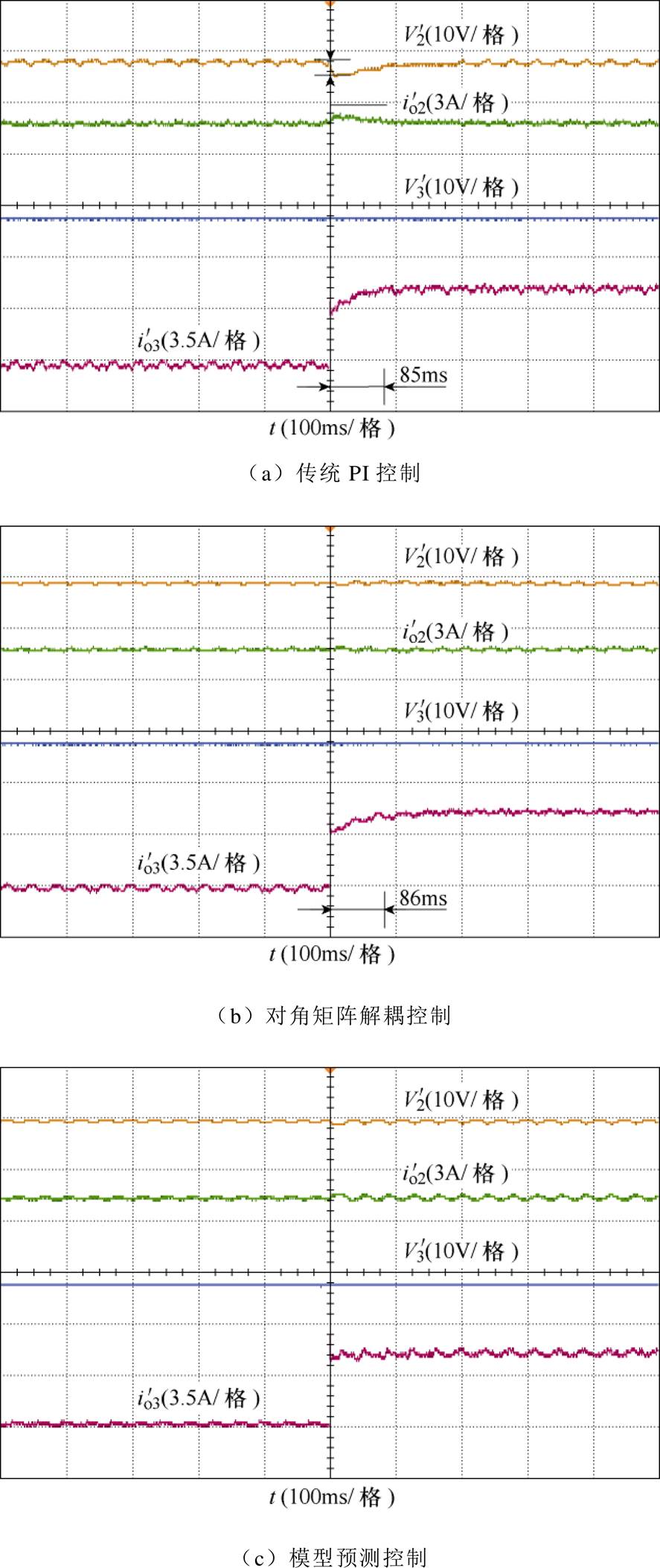
图11 3端口电流参考值突增时不同控制策略下，2、3端口电压、电流实验波形
Fig.11 Voltage and current waveforms of port-2,3 under different control strategies when current reference of port-3 step up
本文针对TAB变换器的端口功率耦合问题与端口动态特性，提出一种模型预测控制（MPC）策略。该策略中电压环路采用电流前馈控制，电流环路采用额外积分环节补偿静差，移相占空比离线计算得到，具有控制结构简单、计算复杂度低等优点。与传统PI、对角矩阵解耦控制策略实验结果对比表明，本文方法不仅可以避免TAB变换器端口功率耦合问题，还能实现端口的快速动态响应。
参考文献
[1] 刘文, 杨慧霞, 祝斌. 微电网关键技术研究综述[J]. 电力系统保护与控制, 2012, 40(14): 154-157.
Liu Wen, Yang Huixia, Zhu Bin. Survey on key technologies of microgrid[J]. Power System Pro- tection and Control, 2012, 40(14): 154-157.
[2] 涂春鸣, 黄红, 兰征, 等. 微电网中电力电子变压器与储能的协调控制策略[J]. 电工技术学报, 2019, 34(12): 2627-2636.
Tu Chunming, Huang Hong, Lan Zheng, et al. Coordinated control strategy of power electronic transformer and energy storage in microgrid[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2627-2636.
[3] 张继元, 舒杰, 宁佳, 等. 考虑SOC自均衡的光储独立微电网协调控制[J]. 电工技术学报, 2018, 33(增刊2): 527-537.
Zhang Jiyuan, Shu Jie, Ning Jia, et al. Coordinated control for PV/storage hybrid islanded microgrid considering SOC balancing[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 527-537.
[4] 许伟, 肖湘宁. 基于模式转换的独立微电网实时运行控制[J]. 电工技术学报, 2019, 34(增刊1): 282- 291.
Xu Wei, Xiao Xiangning. Real-time operational control of stand-alone microgrid based on mode switch[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 282-291.
[5] 李霞林, 郭力, 王成山, 等. 直流微电网关键技术研究综述[J]. 中国电机工程学报, 2016, 36(1): 2-17.
Li Xialin, Guo Li, Wang Chengshan, et al. Key technologies of DC microgrids: an overview[J]. Proceedings of the CSEE, 2016, 36(1): 2-17.
[6] 王闪闪, 赵晋斌, 毛玲, 等. 基于电动汽车移动储能特性的直流微网控制策略[J]. 电力系统保护与控制, 2018, 46(20): 31-38.
Wang Shanshan, Zhao Jinbin, Mao Ling, et al. A control strategy based on mobile energy storage characteristic of electric vehicles in DC micro-grid[J]. Power System Protection and Control, 2018, 46(20): 31-38.
[7] 王宝华, 蒋力. 基于精确反馈线性化的直流微电网双向直流变换器反步滑模控制[J]. 电力系统保护与控制, 2018, 46(2): 43-49.
Wang Baohua, Jiang Li. Backstepping sliding mode control based on exact feedback linearization for bi-directional DC converter in DC microgrid[J]. Power System Protection and Control, 2018, 46(2): 43-49.
[8] 刘宁宁, 曹炜, 赵晋斌. 直流微电网的一种增量式下垂控制方法[J]. 电力系统保护与控制, 2018, 46(8): 24-30.
Liu Ningning, Cao Wei, Zhao Jinbin. An incremental droop control method for DC micro-grid[J]. Power System Protection and Control, 2018, 46(8): 24-30.
[9] Michon M, Duarte J L, Hendrix M, et al. A three-port bi-directional converter for hybrid fuel cell systems[C]// IEEE Annual Power Electronics Specialists Con- ference, Aachen, Germany, 2004: 4736-4742.
[10] Tao Haimin, Kotsopoulos A, Duarte J L, et al. Transformer-coupled multiport ZVS bidirectional DC-DC converter with wide input range[J]. IEEE Transactions on Power Electronics, 2008, 23(2): 771- 781.
[11] Zhao Chuanhong, Round S D, Kolar J W. An isolated three-port bidirectional DC-DC converter with decoupled power flow management[J]. IEEE Transactions on Power Electronics, 2008, 23(5): 2443-2453.
[12] Wang Yifeng, Han Fuqiang, Yang Liang, et al. A three-port bidirectional multi-element resonant con- verter with decoupled power flow management for hybrid energy storage systems[J]. IEEE Access, 2018, 6(1): 61331-61341.
[13] 杨旭, 王卫, 王盼宝, 等. 基于串联谐振网络的三端口DC/DC变换器解耦方法[J]. 电网技术, 2017, 41(2): 478-485.
Yang Xu, Wang Wei, Wang Panbao, et al. Decoupling method of series resonance based three-port DC/DC converter[J]. Power System Technology, 2017, 41(2): 478-485.
[14] Phattanasak M, Gavagsaz-Ghoachani R, Martin J, et al. Control of a hybrid energy source comprising a fuel cell and two storage devices using isolated three-port bidirectional DC-DC converters[J]. IEEE Transactions on Industry Applications, 2015, 51(1): 491-497.
[15] Kim S Y, Song H, Nam K. Idling port isolation control of three-port bidirectional converter for EVs[J]. IEEE Transactions on Power Electronics, 2012, 27(5): 2495-2506.
[16] Zhao Chuanhong, Kolar J W. A novel three-phase three-port UPS employing a single high-frequency isolation transformer[C]//IEEE Annual Power Elec- tronics Specialists Conference, Aachen, Germany, 2004: 4135-4141.
[17] Cortes P, Kazmierkowski M P, Kennel R M, et al. Predictive control in power electronics and drives[J]. IEEE Transactions on Industrial Electronics, 2008, 55(12): 4312-4324.
[18] 梅杨, 陈丽莎, 黄伟超, 等. 交错并联Buck-Boost变换器模型预测控制方法[J]. 电气传动, 2017, 47(7): 32-36.
Mei Yang, Chen Lisha, Huang Weichao, et al. Model predictive control method for interleaved parallel Buck-Boost converter[J]. Electric Drive, 2017, 47(7): 32-36
[19] 梅杨, 陈丽莎, 黄伟超, 等. 级联式双向DC-DC变换器的优化控制方法[J]. 电工技术学报, 2017, 32(19): 153-159.
Mei Yang, Chen Lisha, Huang Weichao, et al. Opti- mized control method of cascaded bi-directional DC-DC converters[J]. Transactions of China Electro- technical Society, 2017, 32(19): 153-159.
[20] 安峰, 宋文胜, 杨柯欣. 电力电子变压器的双有源全桥DC-DC变换器模型预测控制及其功率均衡方法[J]. 中国电机工程学报, 2018, 38(13): 3921-3929.
An Feng, Song Wensheng, Yang Kexin. Model predictive control and power balance scheme of dual- active-bridge DC-DC converters in power electronic transformer[J]. Proceedings of the CSEE, 2018, 38(13): 3921-3929.
[21] An Feng, Song Wensheng, Yang Kexin, et al. Improved dynamic performance of dual active bridge DC-DC converters using MPC scheme[J]. IET Power Electronics, 2018, 11(11): 1756-1765.
[22] Bai Hua, Mi C, Wang Chongwu, et al. The dynamic model and hybrid phase-shift control of a dual-active- bridge converter[C]//Annual Conference of IEEE Industrial Electronics, Orlando, USA, 2008: 2840- 2845.
[23] Saeed J, Hasan A. Unit prediction horizon binary search-based model predictive control of full-bridge DC-DC converter[J]. IEEE Transactions on Control Systems Technology, 2018, 26(2): 463-474.
[24] 贾志东, 姜久春, 程龙, 等. 适用于Boost变换器的自适应模型预测控制算法[J]. 中国电机工程学报, 2018, 38(19): 5838-5845.
Jia Zhidong, Jiang Jiuchun, Cheng Long, et al. An adaptive model predictive control for DC-DC Boost converters[J]. Proceedings of the CSEE, 2018, 38(19): 5838-5845.
[25] 肖智明, 陈启宏, 张立炎. 电动汽车双向DC-DC变换器约束模型预测控制研究[J]. 电工技术学报, 2018, 33(增刊2): 489-498.
Xiao Zhiming, Chen Qihong, Zhang Liyan. Con- strained model predictive control for bidirectional DC-DC converter of electric vehicles[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(S2): 489-498.
[26] 黄珺, 王跃, 李卓强, 等. 基于三重移相控制的双主动全桥直流变换器优化调制策略[J]. 中国电机工程学报, 2016, 36(6): 1658-1666.
Huang Jun, Wang Yue, Li Zhuoqiang, et al. Opti- mized modulation scheme of dual active bridge DC-DC converter based on triple-phase-shift control[J]. Proceedings of the CSEE, 2016, 36(6): 1658-1666.
[27] 王伟, 张晶涛, 柴天佑. PID参数先进整定方法综述[J]. 自动化学报, 2000, 26(3): 247-255.
Wang Wei, Zhang Jingtao, Chai Tianyou. A survey of advanced PID parameter tuning methods[J]. Acta Automatica Sinica, 2000, 26(3): 247-255.
Model Predictive Control of Three-Port Isolated Bidirectional DC-DC Converter
Abstract In order to improve the dynamic performance of the three-port isolated bidirectional DC-DC converter in DC micro-grid, a model predictive control (MPC) strategy is proposed for the triple-active bridge (TAB) DC-DC converter. Considering the control targets of each port of TAB converter, the discretization prediction model of TAB converter is established based on phase-shifting control and average model, and the predictive controller is designed by optimal solution of MPC problem to realize the decoupling control effect among ports. The influence of system parameter deviation of MPC strategy is further analyzed, and the MPC control scheme of TAB converter that suppresses steady-state error is designed. The TAB prototype is built based on the dual processor control core of TMS320F28335+FPGA_XC6SLX16. The experimental results have verified that the proposed method is effective, and has faster dynamic characteristics and port power decoupling operation capability.
keywords：DC micro-grid, three-port DC-DC converter, phase-shifting control, average model, model predictive control
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.191169
国家重点研发计划资助项目（2017YFB0903300）。
收稿日期 2019-09-12
改稿日期 2019-12-09
年 珩 男，1978年生，教授，博士生导师，研究方向为新能源技术、交直流混合供电等。E-mail: nianheng@zju.edu.cn（通信作者）
叶余桦 男，1996年生，硕士研究生，研究方向为新能源技术、交直流混合供电等。E-mail: yeyuhua@zju.edu.cn
（编辑 陈 诚）