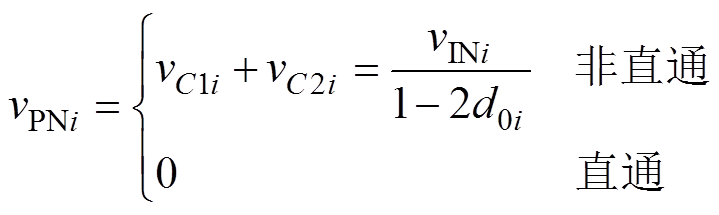（1）式中，d0i（i=1, 2,…, N）为子模块直通占空比，即直通时间与开关周期的比值；vPNi、vINi分别为第i个子模块的直流链电压及电源输入电压。如无特别说明，后文中vPNi皆指代非直通状态下的值。
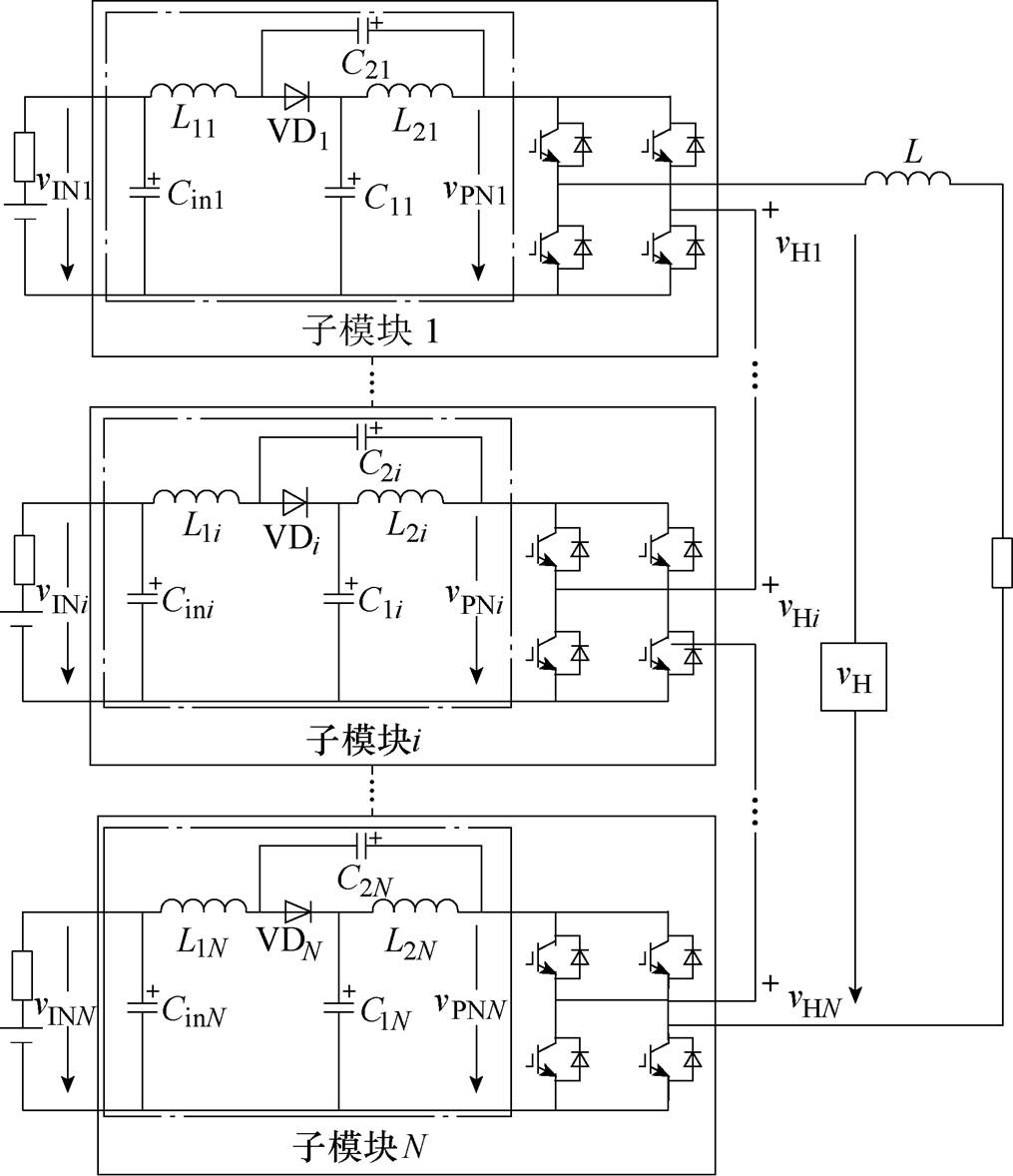
图1 单相QZS-CHI拓扑结构
Fig.1 Topology of a single-phase QZS-CHI
摘要 准Z源级联H桥逆变器（QZS-CHI）在分布式发电中具有广阔的应用前景。传统调制方法的直通加入过程会使开关频率倍增，进而导致开关损耗较大。该文提出一种多调制波移相正弦脉宽调制方法，将直通量植入开关切换时刻，可有效降低损耗。由于直通占空比与调制比存在约束关系，会对输出电平数造成影响，分析了QZS-CHI的输出电平数与调制比、模块数、直通占空比的关系。通过搭建级联6模块QZS-CHI的仿真模型及试验样机，验证开环条件下调制方法和输出电平分析的正确性，实验结果表明，新提出的调制方法最大效率可达96.64%，相比传统调制方法，可提升1.71%的效率点。
关键词：准Z源 级联多电平逆变器 调制 输出电压 多模块
准Z源逆变器（Quasi-Z-Source Inverter, QZSI）是一种新型的逆变器拓扑，该结构在传统电压源型逆变器（Voltage Source Inverter, VSI）的电源输出端及H桥输入之间耦合了由电感、电容、二极管组成的无源阻抗网络，用以替代传统两级式电压源逆变器前级DC-DC变流器[1-4]。QZSI最大的特点在于允许H桥同一桥臂上下两管同时导通，称为直通状态（shoot-through state），并利用该状态储能，泵升直流链电压。与传统VSI相比，QZSI可在单极结构实现升降压功能，且可完全免疫由于电磁干扰造成的桥臂短路问题以及避免死区时间加入带来的输出波形畸变。而与两级式VSI相比，QZSI具有更少的功率变换级数和开关数量，可一定程度地提高系统效率，降低系统成本。基于上述优点，QZSI在风力/光伏发电[5]、混合动力汽车[6-7]、交流调速[8-9]、燃料电池系统[10]等场合得到了应用与发展。
将准Z源阻抗网络耦合到传统级联H桥变流器的H桥与直流输入电源之间，可构成准Z源级联H桥逆变器（Quasi-Z-Source Cascaded H-bridge Inverter, QZS-CHI），将其应用于分布式光伏发电系统中是近年来一个新的研究思路[10-11]，具有诸多优点。例如，QZS-CHI利用准Z源网络进行储能升压，无需额外增加DC-DC环节，可在光伏输入电压大幅度变化时保持模块直流链电压恒定，有利于降低开关应力裕量及实现分布式的最大功率点跟踪功能[12]；采用模块化的设计，可根据光伏系统设计要求进行组合，实现串联式无变压器并网；独特的直通状态可提高系统抗干扰能力，增强可靠性。
由于QZS-CHI耦合了准Z源及级联H桥变流器的特征，其调制方式需同时考虑直通植入与多电平形成。文献[13-14]提出了简单直通植入与移相正弦脉宽调制相结合的调制方法，具有原理及实现简单的优点；但该调制方法增加了额外的开关频率，将导致模块变流器效率降低，且通过物理电路实现时需添加额外的逻辑门元件。文献[15]采用锯齿波（非等腰三角波）进行调制，直通量植入时不会增加开关频率；但由于锯齿波调制下的脉冲波总有一个沿的导通或关断时刻不受误差信号控制，将会影响系统动态性能。文献[16-18]提出在传统空间矢量调制中引入直通零矢量调制QZS-CHI，可解决传统调制方法带来的频率倍增问题；但空间矢量数会随模块数增多变得尤为庞大，使得该方法难以实现。此外，由于QZS-CHI模块是基于对开关管零状态的复用（直通过程）来实现单级系统升压和逆变功能，因此模块输入电压、直流链电压与系统整体输出电压具有强耦合关系[1, 11]，会出现互相制约的情况。有关QZS-CHI的输出电压特性以及其对系统设计的影响尚待进一步研究。
本文重点关注准Z源级联H桥逆变器调制方法的实现，通过分析变流器的运行原则，提出了一种多调制波移相正弦脉宽调制方法，该方法将直通量植入到开关切换时刻，不会额外增加开关频率，且实现方法简单，可扩展至任意模块QZS-CHI中。接着根据调制比约束关系，分析了变流器的输出电压特性。最后通过仿真及实验验证了相关方法及理论。
单相QZS-CHI的拓扑结构如图1所示，逆变系统由N个独立供电电源、N个变流子模块、滤波器L以及单相交流电网组成。其中，变流子模块由准Z源阻抗网络与H桥串联组成，使得由其级联形成的QZS-CHI兼具准Z源逆变器与传统级联H桥逆变器的特点。
对如图1所示的某一子模块，稳态时存在直通与非直通两种工作状态。直通状态下H桥同一桥臂上下两个开关管同时导通，电源向准Z源网络储能，抬升直流链电压。非直通状态下H桥按照正常调制下的开关序列动作，进行DC-AC变换。根据伏秒/安秒平衡原理，当电路处于稳态时[1]，可推导出
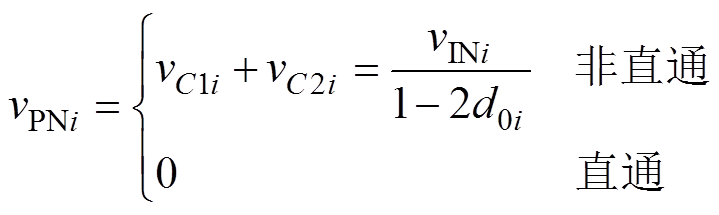（1）式中，d0i（i=1, 2,…, N）为子模块直通占空比，即直通时间与开关周期的比值；vPNi、vINi分别为第i个子模块的直流链电压及电源输入电压。如无特别说明，后文中vPNi皆指代非直通状态下的值。
图1 单相QZS-CHI拓扑结构
Fig.1 Topology of a single-phase QZS-CHI
由于子模块的直通状态发生在原始开关状态的零状态内，直通状态对H桥的有效输出不造成影响，因此，QZS-CHI电网侧的输出合成电压vH为N个串联子模块输出电压之和，即
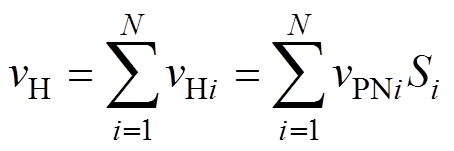（2）式中，vHi为第i个变流子模块的输出电压；Si
{-1, 0, 1}为第i个模块的开关函数。
以两模块QZS-CHI为例，假设所有模块的直流链电压相等且都为VPN。输出合成电压vH可以有±2VPN、±VPN、0共5个电平。
图2给出vH为VPN时的两种可能工作状态。图2a中，S1k={1, 0, 0, 1}，S2k={0, 1, 0, 1}，k=1, 2,…,4。模块1、2都处于非直通状态，其输出电压分别为VPN、0，因此总的合成电压vH为VPN，该工作状态与传统级联H桥逆变器相同。图2b中，S1k={1, 0, 0, 1}，S2k={1, 1, 1, 1}（采用传统调制方法，详见第2.1小节），根据开关状态，输出电流流经模块2的四个开关管，准Z源二极管截止，直通储能的电流同样流经模块2的4个开关管，模块2的输出电压为0，总合成电压vH仍然为VPN。
因此，只要直通状态植入到原始开关零状态（使vHi为零的开关状态）中，则直通植入对逆变器的交流侧输出不造成任何影响。
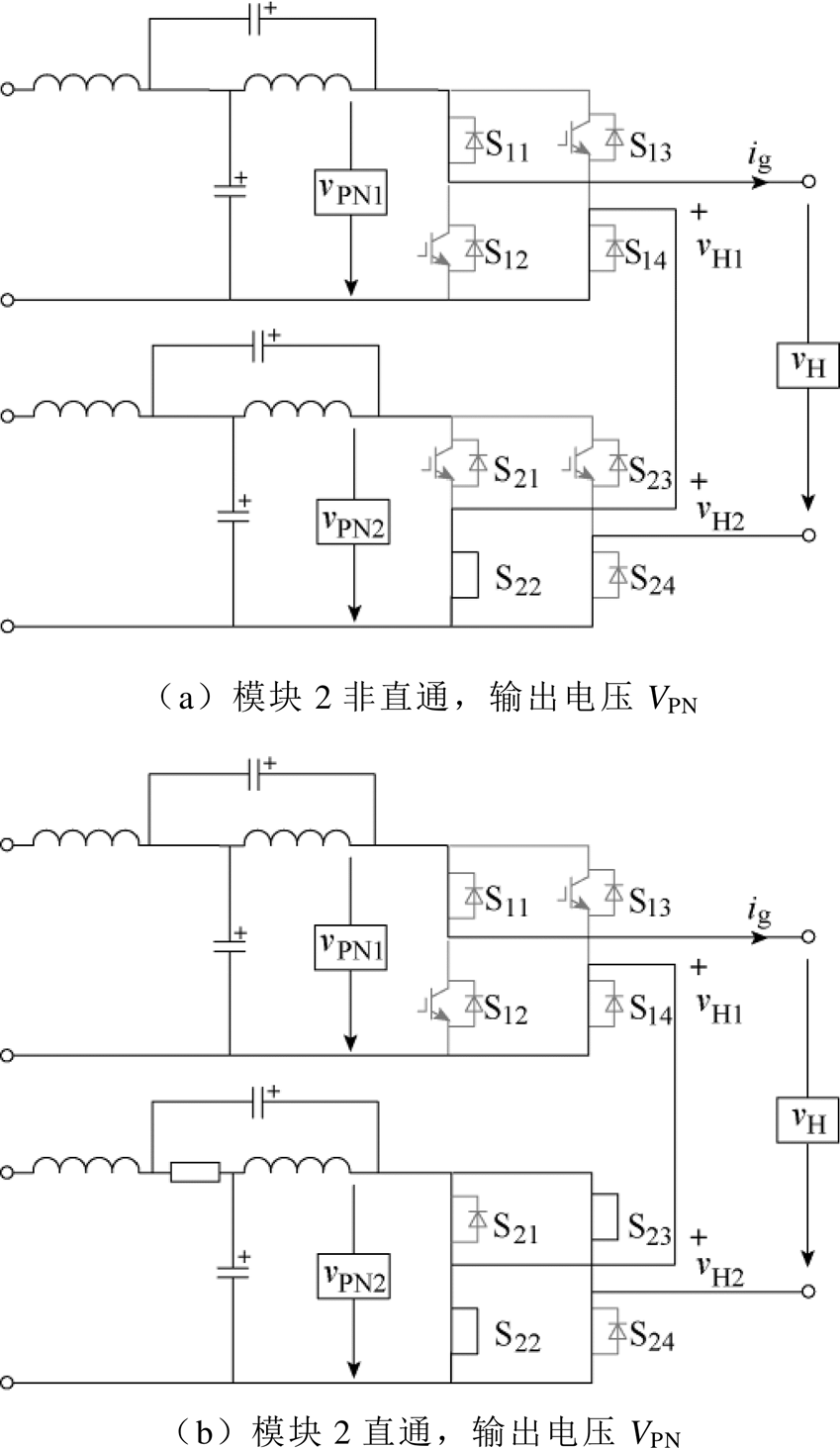
图2 两模块QZS-CHI的某一运行状态分析
Fig.2 Operating states analysis of two modules QZS-CHI
根据QZS-CHI的工作原理可知，其调制需同时考虑直通植入与多电平形成。图3给出了传统QZS- CHI调制方法，该方法由传统简单升压直通植入方法与传统移相正弦脉宽调制（Sinusoidal Pulse Width Modulation, SPWM）组合构成。
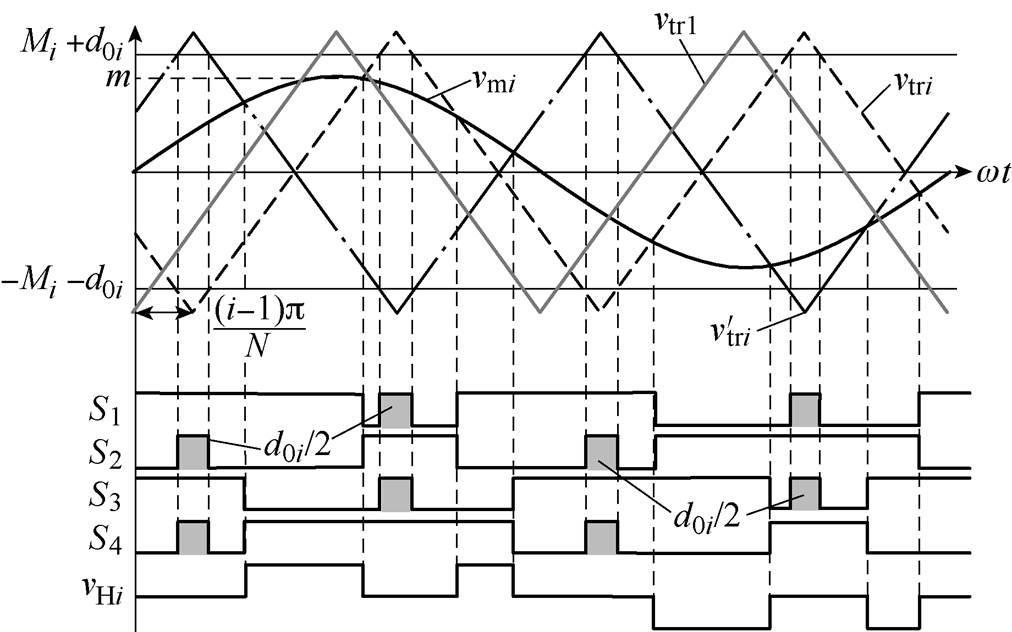
图3 传统QZS-CHI调制方法
Fig.3 Traditional modulation method of QZS-CHI
图3中，vtr1为子模块1的三角载波，假设其初始相位为零。vtri、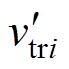
为子模块i的三角载波，其相位互差180°。mi为子模块i的调制波，且mi= Misin(wt)，Mi为调制比，为原始调制波幅值与三角载波幅值的比值。d0i，S1～S4分别为模块i的直通占空比和开关信号，vtri与vtr1的相位差为
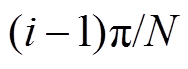，即模块间三角载波相位互差
。
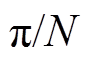传统QZS-CHI调制方法是在多电平移相调制基础上，通过简单升压（simple boost）方法植入直通量。图3中，当mi＞vtri时，S1输出为高，S2为低；当mi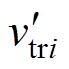＞时，S4输出为高，S3为低。考虑直通植入，当vtri、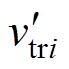＞mi+d0i或vtri、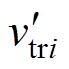＜-mi-d0i时，S1～S4输出都强制为高，也即在一个开关周期共植入了d0i的直通量。该直通植入发生在开关零状态，因此对vHi的输出不产生影响，但该方法的直通植入使开关频率倍增，将导致开关损耗增加。
为克服传统QZS-CHI调制方法开关频率倍增的缺陷，本文提出新的适用于多模块QZS-CHI的多调制波移相正弦脉宽调制（Multi-modulation Wave- forms Phase Shift SPWM, MWPS-SPWM）方法，调制原理如图4所示。
图4 多调制波移相正弦脉宽调制方法
Fig.4 Proposed MWPS-SPWM method
图4中，原始调制波mi被拆分为4个新的调制波vmS1～vmS4，分别对应4个开关管的开关信号S1～S4。根据mi的正负极性，各调制波可分段表示为
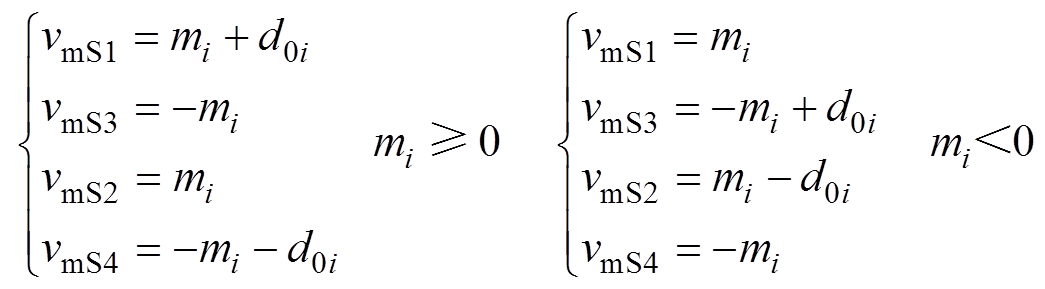（3）当vmSk＞vtri时（k=1, 3），Sk输出为高，否则为低；当vmSk＞vtri时（k=2, 4），Sk输出为低，否则为高。
当原始调制波mi＞0且S1、S4对应的开关管同时导通时，模块输出电压vHi=+vPNi。与传统移相正弦脉宽调制（Phase Shift-SPWM, PS-SPWM）相比，由于S1对应调制波上移了d0i，驱动信号S1将延迟d0i/4关断，并提前d0i/4开通。会造成同一桥臂S1、S2对应的开关管在该区域内同时导通，也即植入了d0i/2的直通量。同理，S4对应调制波的下移使S4、S3在S4延迟关断，提前导通区域内直通，并植入d0i/2的直通量。因此，一个开关周期的直通植入量为d0i。由图4可见，直通植入同样发生在开关零状态，直通植入对原始调制波调制下的vHi输出波形不造成任何影响。调制波mi＜0时，分析与前述相似。
综上，MWPS-SPWM的实质是对模块原始调制波进行上下平移，实现直通量植入，模块间的移相调制与传统多电平移相调制相同。
当忽略直通占空比（d0i=0）时，传统QZS-CHI调制方法等同于MWPS-SPWM。此时S1、S2对应的调制波相同，S3、S4对应的调制波相同且与前者相差180°。三角载波互差180°与调制波互差180°形成的开关波形相同，假设各QZS-CHI模块的直流链电压相等，调制比相同，各模块在MWPS-SPWM下的电压如图5所示。图5中，vtr1、vtri分别为模块1、i的三角载波，与v'tr1、v'tri相位互差180°，vtr1、vtri相位互差(i-1)p/N。调制波最大值Mi与三角载波分别相交于qi1、qi2。
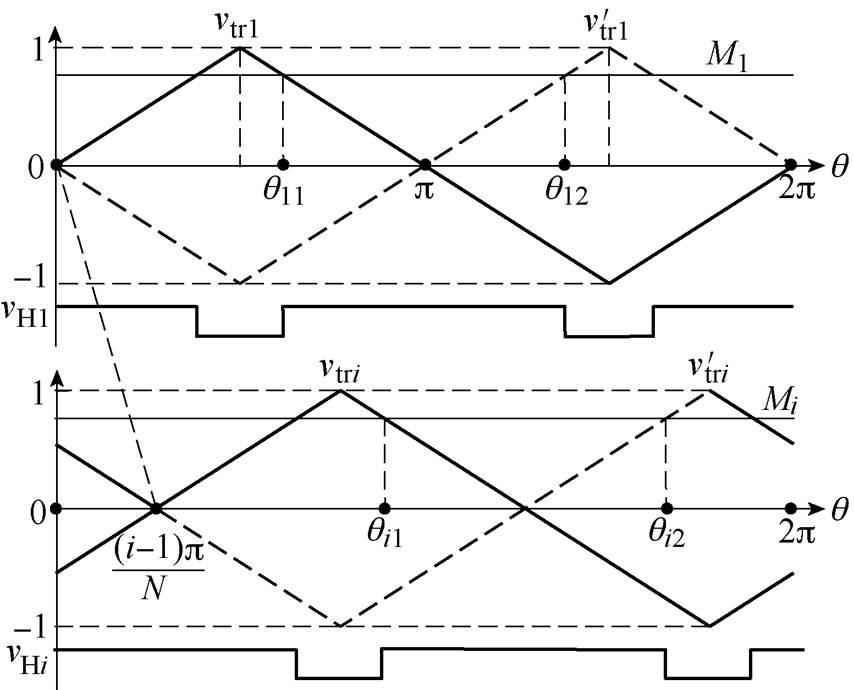
图5 MWPS-SPWM下模块输出波形
Fig.5 Output waveforms using MWPS-SPWM
根据调制原则可知，模块1在q11、q12区间输出为高电平VPN。以q =p/2为参考点，随着三角载波往右移相，高电平随之往右移动，也即qi1、qi2增大。根据图5，应用三角形相似定理，可以得出
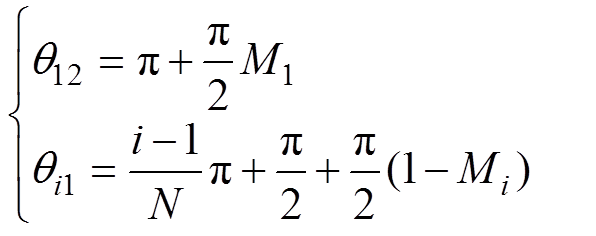（4）式中，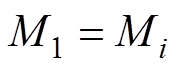
。
若所有模块移相之后的高电平都在[p/2, 3p/2]区间内，则级联模块输出的最大电压为NVPN，电平数为2N+1。要使至少有i个模块高电平在该区间内，则级联模块输出电压最大值至少为iVPN，电平数至少为2i+1。得出后者结论，需满足模块i的高电平起始点qi1小于模块1的高电平结束点q12，即
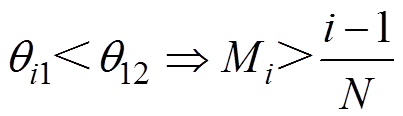（5）因此可以得出，调制比Mi与级联逆变器输出电平数K存在如下关系
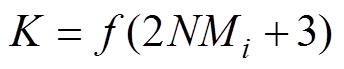（6）
式中，f (x)为向下舍入到奇数函数。由式（6）可知，随着调制比降低，级联H桥的输出电平数也相应减少。当采用MWPS-SPWM或传统调制时，调制波与直通占空比共同调制三角载波。为保证直通植入对开关有效状态不产生影响，应满足
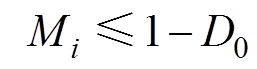（7）式中，D0为各直通占空比的最大值（限幅值），一般情况下所有模块具有相同的D0。可以发现，直通占空比对调制比的约束是QZS-CHI区别于传统CHBI的重要特征。结合式（6）和式（7）可得QZS-CHI输出电压vH的电平数K的最大值为
（8）
式（8）体现了QZS-CHI系统中直通植入对输出电平数最大值的影响：当0≤D0＜1/N时，Kmax= 2N+1；当1/N≤D0＜2/N时，Kmax降低为2N-1，以此类推。值得注意的是，式（8）只确定了QZS-CHI电平数的最大值限制，其实际输出电压的电平数仍需按照当前的Mi，根据式（6）确定。
图6给出了D0=0.25时，QZS-CHI的输出电平数K与调制比Mi、模块数N的关系。当N=2时，最大输出电平数可达到5，等于2N+1；而当N=6时，由于直通占空比限制了调制比的最大值，其最大输出电平数降为11，小于2N+1。由图6也可以看出，QZS-CHI的级联模块数越多，受直通占空比影响而限制的最大输出电平数越多。
为验证开环条件下样机工作状态、调制方法的正确性，仿真与实验搭建了级联6模块QZS-CHI系统。表1给出了元器件及系统参数取值。
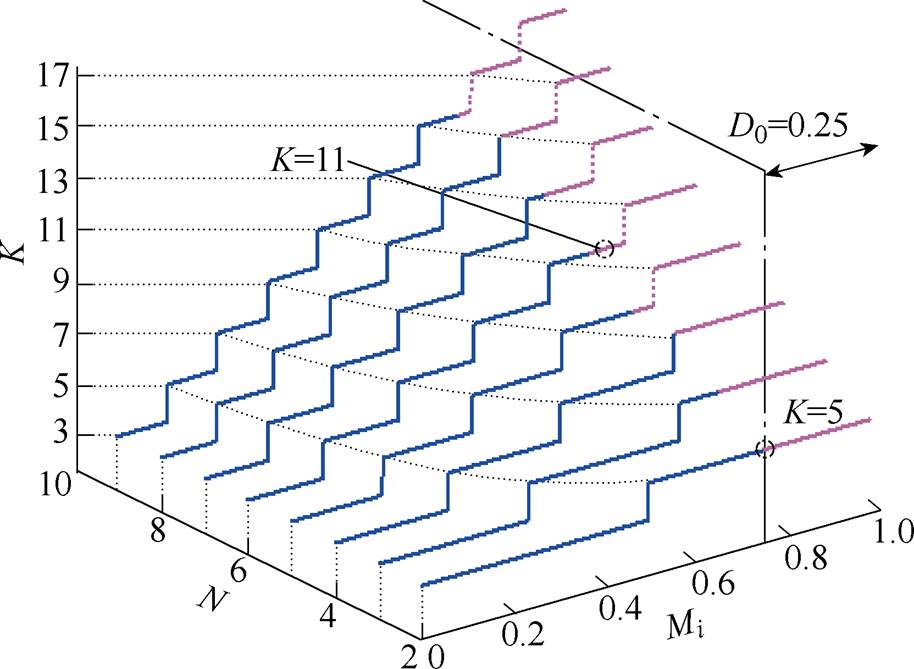
图6 电平数与调制比、模块数、直通占空比关系
Fig.6 The relationship between level, modulation ratio, module number and shoot-through duty ratio
表1 级联6模块QZS-CHI的元器件及系统参数
Tab.1 Components parameters and system parameters of cascaded 6-module QZS-CHI
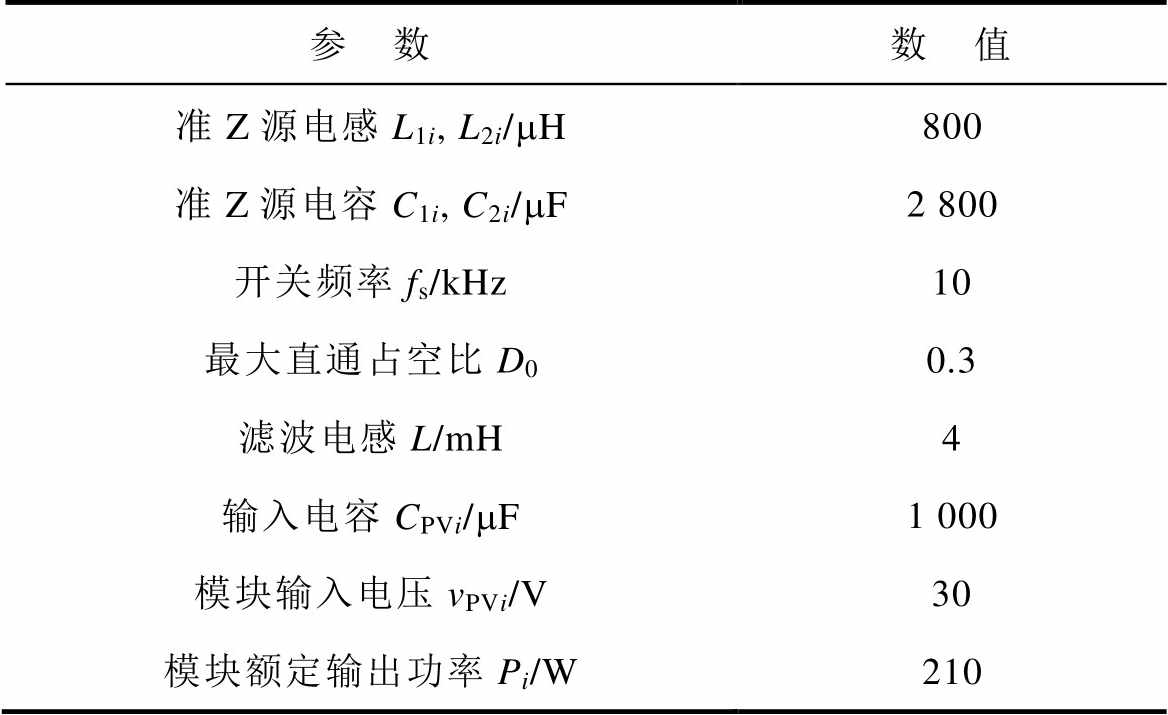
参 数数 值 准Z源电感L1i, L2i/mH800 准Z源电容C1i, C2i/mF2 800 开关频率fs/kHz10 最大直通占空比D00.3 滤波电感L/mH4 输入电容CPVi/mF1 000 模块输入电压vPVi/V30 模块额定输出功率Pi/W210
设定所有QZS-CHI模块都有：d0i=0.2，Mi=0.8。图7给出了调制波mi＞0时某一子模块采用MWPS- SPWM与传统调制下的开关及输出电压仿真波形。
图7a中，由于调制波的上下平移，导致同一桥臂上下两管存在直通状态，该直通状态下，直流链电压为零，一个开关周期内共有4次直通状态出现。可以发现，直通植入发生在原始开关零状态（S1,3=0，S2,4=1），因此直通植入对逆变器正常输出不造成影响。图7b中，直通信号通过与原始开关信号相或的方式植入，开关管频率加倍。直通植入时直流链电压为零，一个开关周期内共有两次直通状态。同理，直通状态发生在原始开关信号零状态下，对输出波形不造成影响。调制波mi＜0时的开关及输出电压波形与图8类似。
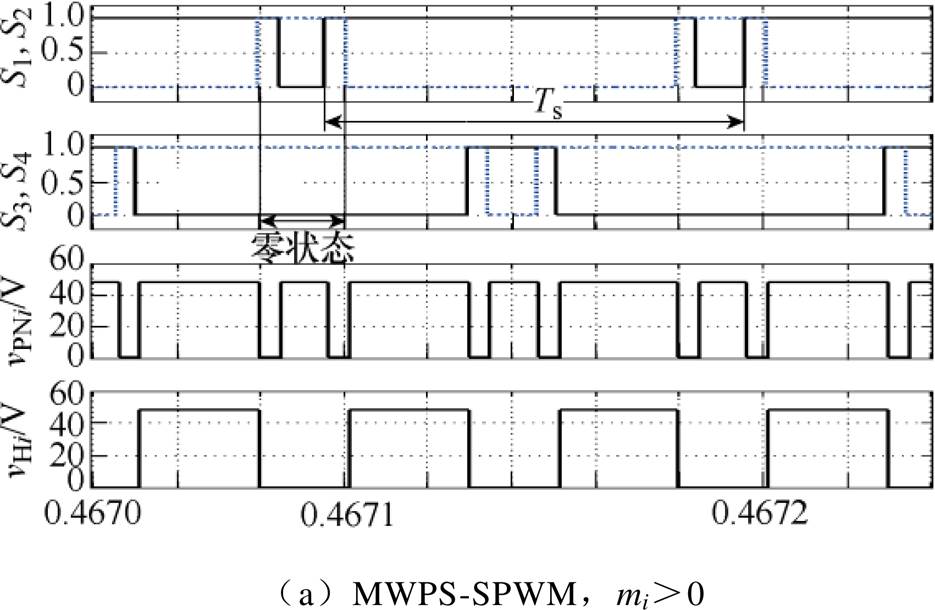
图7 开关及输出电压仿真波形
Fig.7 Simulation waveforms of switch firing pulse and output voltages
图8a给出了某一子模块在MWPS-SPWM下开关管的开关信号S3、S4的驱动波形、桥臂输出电压vHi以及直流链电压vPNi的波形。S4的延迟关断、提前开启使同一桥臂上下两管同时导通而植入直通量，此时vHi、vPNi都为零。由图可知，开关频率为10kHz，MWPS-SPWM在直通植入时没有额外增加开关频率。图8b给出了在传统QZS-CHI调制方法下开关管的开关信号S3、S4的驱动波形、桥臂输出电压vHi以及直流链电压vPNi的波形。可以发现，传统调制方法增加了开关频率，因此会增加模块损耗。
为验证MWPS-SPWM较传统QZS-CHI调制的优越性，对QZS-CHI模块在两种调制方式下的效率进行实验对比，如图9所示，可以发现，MWPS- SPWM最大可提升1.71%的效率点，且模块最大效率可达96.64%。
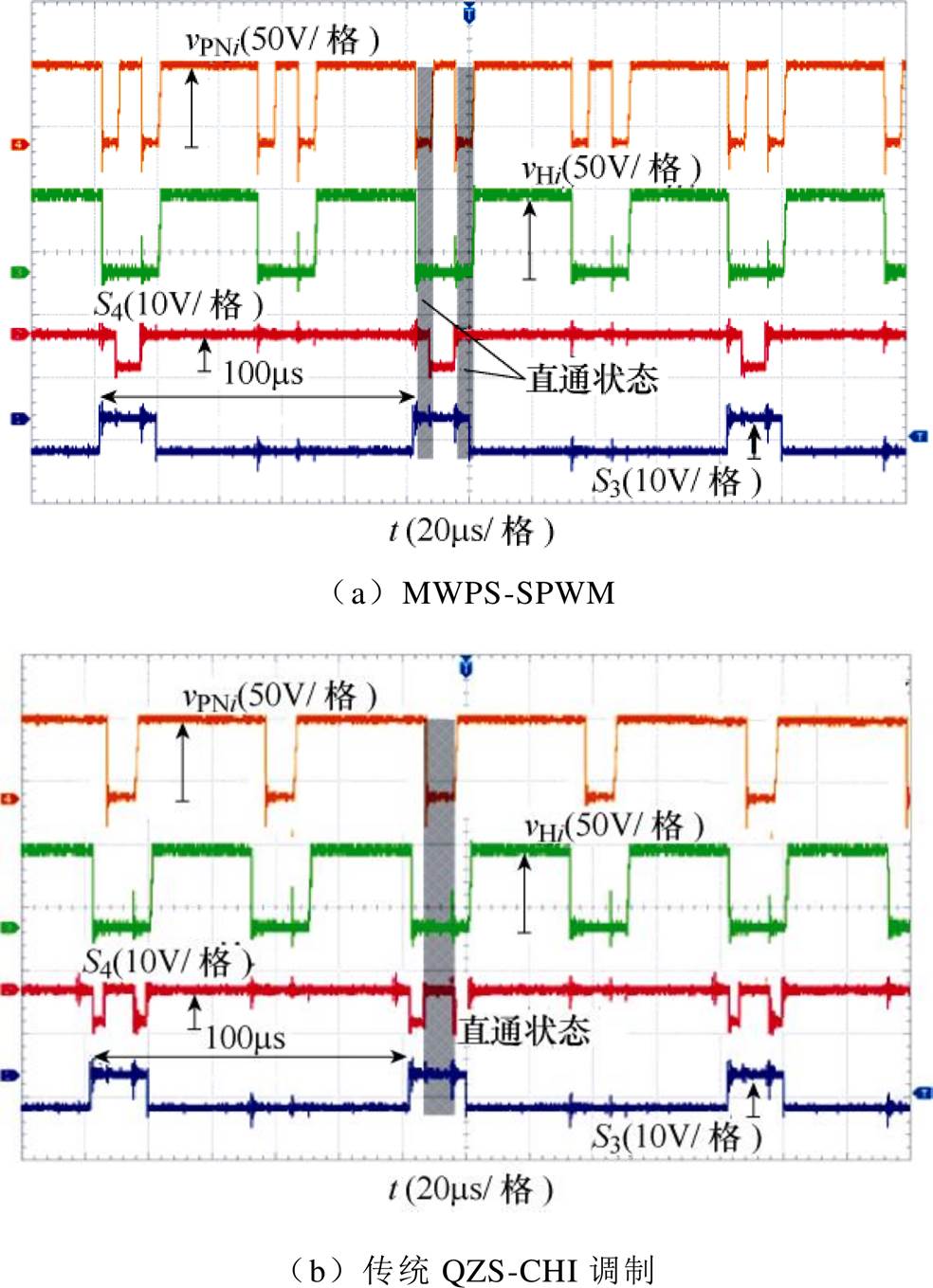
图8 开关及输出电压实验波形
Fig.8 Experimental waveforms of switch firing pulse and output voltages
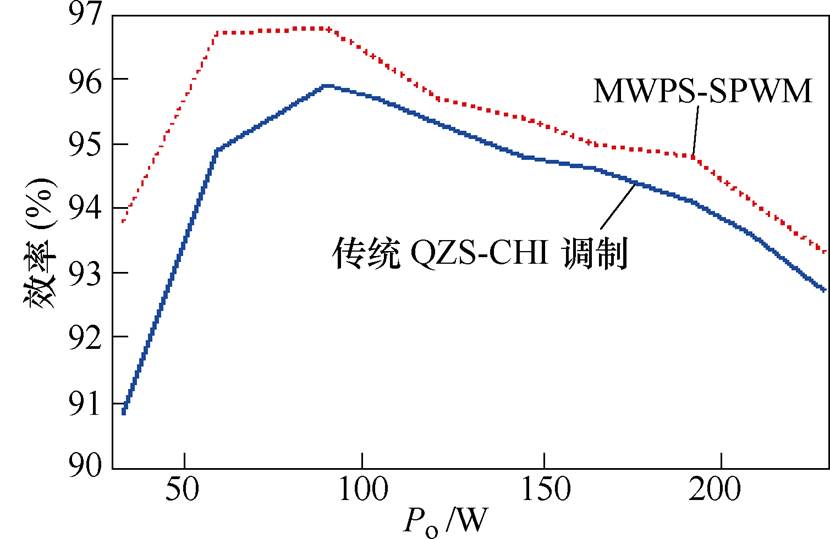
图9 QZS-CHI模块在两种调制方法下的效率对比
Fig.9 Efficiency comparison of a single module of QZS-CHI under the two modulation methods
为验证MWPS-SPWM方法形成多电平的有效性及QZS-CHI的输出电压特性分析，搭建了6模块QZS-CHI仿真及实验模型。图10给出了不同调制比、直通占空比条件下的开环仿真结果。其中，图10a对应的仿真条件为：调制比Mi=0.9，直通占空比d0i=0.1，输入电压vPVi=30V。仿真结果显示，直流链电压vPNi=37.2V，升压比vPN/vPV≈1.25。满足QZS-CHI稳态运行关系式。级联模块数N=6，输出电平数K=13，输出电压最大值约为225V，满足式（6）的相关分析。图10b对应的仿真条件为：调制比Mi=0.8，直通占空比d0i=0.2。输入电压（约30V）与直流链电压（约49.5V）依然满足QZS-CHI稳态运行关系式，QZS-CHI输出电压电平数K=11，输出电压最大值约为250V，依然满足式（6）。
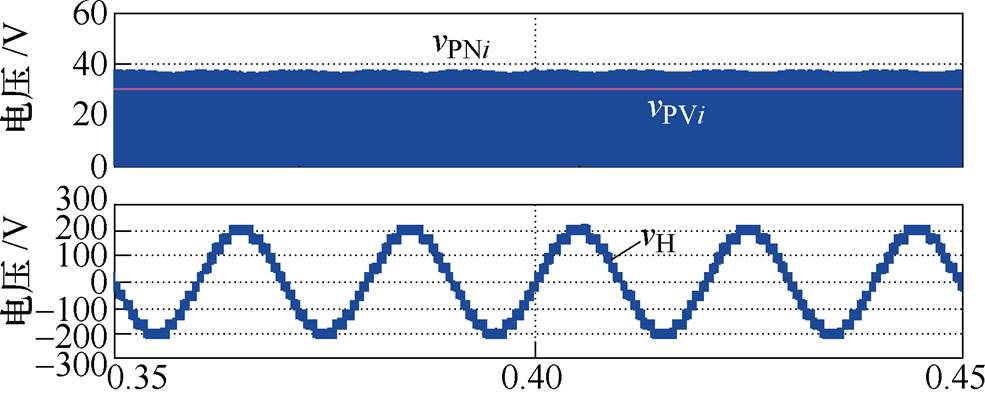
（a）仿真条件：Mi=0.9，d0i=0.1，vPVi=30V
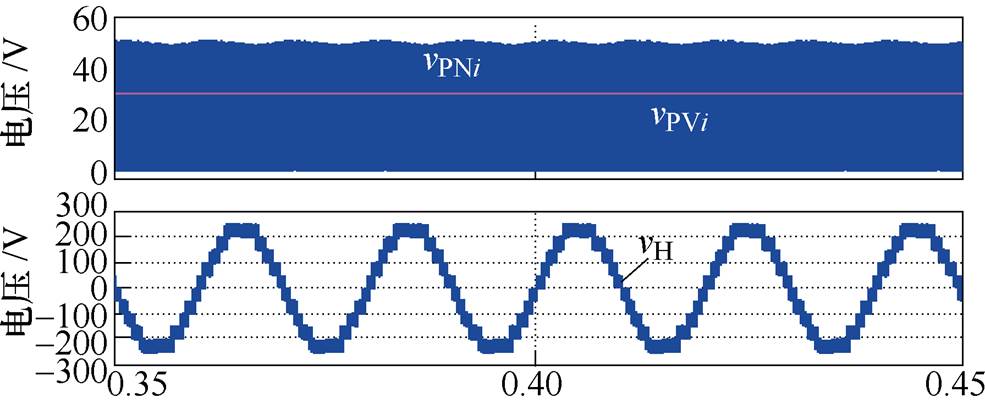
（b）仿真条件：Mi=0.8，d0i=0.2，vPVi=30V
图10 不同条件6模块QZS-CHI的输出波形仿真结果
Fig.10 Simulation results of 6-module QZS-CHI under different conditions
在图10的两组仿真对比中，都有Mi=1-d0i。因此，所得的电平数即为其可最大输出的电平数。对于6模块级联逆变器，其理想最大输出电平数为13。因此从仿真结果可以发现，在QZS-CHI系统中，由于直通占空比的加入，输出最大电平数会受到约束，且直通占空比越大，最大输出电平数越小。此外还可以看出，QZS-CHI的输出多电平波形良好，验证了MWPS-SPWM方法的有效性。
图11给出了开环控制下6模块级联QZS-CHI的关键实验波形。实验时取各模块调制比Mi=0.8，直通占空比d0i=0.2，实际电路参数与仿真一致。实验中某一模块的输入电压vPV约为30V，直流链电压vPN约为50V，级联系统输出电压vH为十一电平，最大值约250V，且负载电压vL为正弦波。实验结果满足电平数与调制比、模块数、直通占空比的关系推论，且与图10b仿真结果相符。
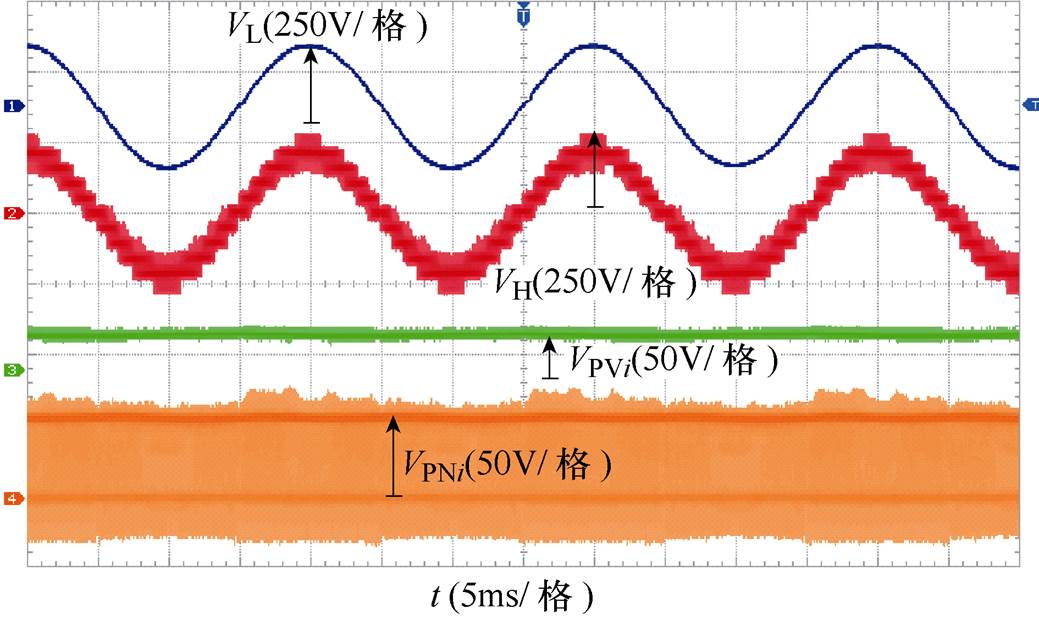
图11 开环级联6模块QZS-CHI的实验波形
Fig.11 Experimental waveforms of 6-module QZS-CHI in open-loop control
本文提出了用于QZS-CHI的MWPS-SPWM方法，通过对模块原始调制波进行上下平移形成拆分的直通量，并叠加至原开关零状态中。与传统方法相比，该调制方式无需额外增加开关频率，可有效提高系统效率，且便于扩展至多模块QZS-CHI中。此外，分析了QZS-CHI输出电平数与调制比、模块数、直通占空比的关系，QZS-CHI的级联模块数越多，受直通占空比影响而限制的最大输出电平数越多。本文通过搭建6模块QZS-CHI仿真模型及实验样机，验证了相关的理论及分析。
参考文献
[1] 李媛, 彭方正. Z源/准Z源逆变器在光伏并网系统中的电容电压恒压控制策略[J]. 电工技术学报, 2011, 26(5): 62-69.
Li Yuan, Peng Fangzheng. Constant capacitor voltage control strategy for Z-source/quasi-Z-source inverter in grid-connected photovoltaic systems[J]. Transa- ctions of China Electrotechnical Society, 2011, 26(5): 62-69.
[2] 杜春水, 刘强, 郭文君, 等. 准Z源级联多电平逆变器单元间功率平衡控制[J]. 电机与控制学报, 2019, 23(8): 19-27.
Du Chunshui, Liu Qiang, Guo Wenjun, et al. Power balance control strategy for quasi-Z-source cascaded multilevel inverter units[J]. Electric Machines and Control, 2019, 23(8): 19-27.
[3] Yuan Li, Shuai Jiang, Cintron-Rivera J G, et al. Modeling and control of quasi-Z-source inverter for distributed generation applications[J]. IEEE Transa- ctions on Industrial Electronics, 2013, 60(4): 1532- 1541.
[4] 蔡春伟, 曲延滨, 盛况. 准Z源逆变器的暂态建模与分析[J]. 电机与控制学报, 2011, 15(10): 7-13.
Cai Chunwei, Qu Yanbin, Sheng Kuang. Transient modeling and analysis of quasi-Z-source-inverter[J]. Electric Machines and Control, 2011, 15(10): 7-13.
[5] 董帅, 张千帆, 王睿, 等. SVPWM控制时双向Z源逆变器电容电压纹波分析[J]. 电工技术学报, 2017, 32(24): 107-114.
Dong Shuai, Zhang Qianfan, Wang Rui, et al. Analysis of capacitor voltage ripple for bi-directional Z-source inverters based on SVPWM[J]. Transactions of China Electrotechnical Society, 2017, 32(24): 107-114.
[6] 胡斯登, 梁梓鹏, 范栋琦, 等. 基于Z源变换器的电动汽车超级电容-电池混合储能系统[J]. 电工技术学报, 2017, 32(8): 247-255.
Hu Sideng, Liang Zipeng, Fan Dongqi, et al. Imple- mentation of Z-source converter for ultracapacitor- battery hybrid energy storage system for electric vehicle[J]. Transactions of China Electrotechnical Society, 2017, 32(8): 247-255.
[7] Guo Feng, Fu Lixing, Lin C H, et al. Development of an 85kW bidirectional quasi-Z-source inverter with DC-link feed-forward compensation for electric vehicle applications[J]. IEEE Transactions on Power Elec- tronics, 2013, 28(12): 5477-5488.
[8] 薛必翠, 丁新平, 张承慧, 等. 准Z源逆变器交流调速系统及部分PAM/PWM控制策略[J]. 电工技术学报, 2012, 27(10): 142-149.
Xue Bicui, Ding Xinping, Zhang Chenghui, et al. Quasi-Z-source inverter adjustable speed drives system and its partly PAM/PWM control strategy[J]. Transactions of China Electrotechnical Society, 2012, 27(10): 142-149.
[9] 吴昊坤, 黄科元, 吕维, 等. 用于高速永磁电机的Z源逆变器直流链电压控制策略[J]. 电工技术学报, 2019, 34(1): 1-10.
Wu Haokun, Huang Keyuan, Lü Wei, et al. Z-source inverter DC-link voltage control strategy for high speed permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 1-10.
[10] Zhang Yun, Shi Jilong, Zhou Lei, et al. Wide input- voltage range Boost three-level DC-DC converter with quasi-Z source for fuel cell vehicles[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 6728-6738.
[11] 程启明, 李涛, 程尹曼, 等. 基于受控耗散Hamiltonian系统模型的光伏准Z源T型三电平并网逆变器控制策略[J]. 电工技术学报, 2019, 34(8): 1718-1727.
Cheng Qiming, Li Tao, Cheng Yinman, et al. Control strategy of PV quasi-Z-source T-type three-level inverter based on port controlled Hamiltonian with dissipation model[J]. Transactions of China Electro- technical Society, 2019, 34(8): 1718-1727.
[12] Abu-Rub H, Iqbal A, Ahmed S M, et al. Quasi-Z- source inverter-based photovoltaic generation system with maximum power tracking control using ANFIS[J]. IEEE Transactions on Sustainable Energy, 2013, 4(1): 11-20.
[13] Sun Dongsen, Ge Baoming, Yan Xingyu, et al. Modeling, impedance design, and efficiency analysis of quasi-Z source module in cascaded multilevel photovoltaic power system[J]. IEEE Transactions on Industrial Electronics, 2015, 61(11): 6108-6117.
[14] Liang Weihua, Liu Yushan, Ge Baoming, et al. Double-line-frequency ripple model, analysis & impedance design for energy stored single-phase quasi-Z source photovoltaic system[J]. IEEE Transa- ctions on Industrial Electronics, 2017, 65(4): 3198- 3209.
[15] Zhou Yan, Liu Liming, Li Hui. A high-performance photo- voltaic module-integrated converter (MIC) based on cascaded quasi-Z-source inverters (qZSI) using eGaN FETs[J]. IEEE Transactions on Power Electronics, 2013, 28(6): 2727-2738.
[16] 孙东森. 储能型Quasi-Z源级联多电平光伏逆变器研究[D]. 北京: 北京交通大学, 2013.
[17] Liu Yushan, Ge Baoming, Abu-Rub H, et al. Over- view of space vector modulations for three-phase- source/quasi-Z-source inverters[J]. IEEE Transa- ctions on Power Electronics, 2014, 29(4): 2098-2108.
[18] 屈艾文, 陈道炼, 苏倩. 三相准Z源并网逆变器的简单升压改进空间矢量调制策略[J]. 电工技术学报, 2018, 33(4): 826-836.
Qu Aiwen, Chen Daolian, Su Qian. Simple Boost modified space vector modulation strategy for three-phase quasi-Z-source grid-connected inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 826-836.
A Multi-Modulation Waveform Phase-Shift Sinusoidal Pulse Width Modulation Method of QZS-CHI and Its Output Voltage Analysis
Abstract Quasi-Z-source cascaded H-bridge inverters (QZS-CHI) have broad application prospects in distributed generation. In the conventional modulation method, the insertion of the shoot-through state doubles the switching frequency, resulting in large switching loss. In this paper, a multi-modulation waveform phase-shifting SPWM method is proposed by inserting the shoot-through state into the switching moment, which can effectively reduce the switching loss. Since the shoot-through duty ratio is constrained by the modulation ratio, the level of the output voltage is affected. The relations of the output voltage level with the modulation ratio, the number of modules and the shoot-through duty ratio are analyzed in this paper. By constructing the simulation model and test prototype of the cascaded 6-module QZS-CHI, the modulation method and the output level analysis under open-loop conditions are verified. The experimental results show that the maximum efficiency of the proposed modulation method can reach 96.64%, which is 1.71% higher than that of the traditional modulation method.
keywords：Quasi-Z-source, cascaded multilevel inverters, modulation, output voltage, multi- module
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.190911
收稿日期2019-07-18
改稿日期 2019-09-17
王 剑 男，1993年生，硕士，工程师，研究方向为高电压与绝缘技术。E-mail: jianwang16@foxmail.com（通信作者）
张 芮 男，1992年生，硕士，工程师，研究方向为电力电子技术。E-mail: zhangrui_cq@foxmail.com
（编辑 崔文静）