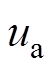 、
、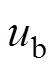 、
、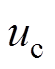 ,三相电压在静止坐标系上的瞬时值和其所对应的空间矢量U如图1所示。图1中,空间矢量U以角速度
,三相电压在静止坐标系上的瞬时值和其所对应的空间矢量U如图1所示。图1中,空间矢量U以角速度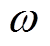 逆时针方向旋转;空间矢量U在a、b、c轴上的投影ua、ub、uc,仅表示电网三相电压瞬时值的大小;旋转的空间矢量U与静止坐标系a轴的夹角
逆时针方向旋转;空间矢量U在a、b、c轴上的投影ua、ub、uc,仅表示电网三相电压瞬时值的大小;旋转的空间矢量U与静止坐标系a轴的夹角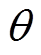 为电网电压的实时相位,锁相环的目标就是要确定相位
为电网电压的实时相位,锁相环的目标就是要确定相位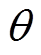 的大小,SRF-PLL的输出即为此角度。
的大小,SRF-PLL的输出即为此角度。摘要 准确快速地获取电网基波正序电压的相位信息,是实现并网变流器精确控制的前提。然而当电网出现异常时,传统的闭环锁相方法动态响应时间较长,难以满足快速响应的控制需求。为此提出一种基于三相电压空间矢量的开环锁相方法,该方法首先通过过零检测得到电网的频率;然后利用离散傅里叶级数滤除电网电压中的谐波与噪声,并得到与基波电压相互正交的电压信号;在此基础上采用对称分量法提取电压正序分量;最后根据电压空间矢量计算基波正序电压的实时相位。同时为了应对电网电压突变时过零检测出现的异常频率,提出一种改进的过零检测算法,可有效应对电网电压异常时的频率检测。所提出的锁相方法无需参数设计且结构简单、响应速度快,在异常电网环境下具有较强的鲁棒性,仿真和实验结果验证了该方法的有效性和可行性。
关键词:开环锁相 空间矢量 离散傅里叶级数 对称分量法 过零检测
随着新能源发电、远距离输电及电能质量治理等应用的快速发展,电力电子变流器在电力系统中的渗透率不断提高[1]。而快速准确地检测电网基波正序电压的相位信息,是实现电力电子变流器同步并网,并进行精确的电流和功率控制的前提[2-3]。现有的相位检测方法有很多种,大致可以分为闭环锁相环[4-5]和开环锁相环[6]两类。
闭环锁相环通过反馈控制来实现相位的检测,主要包含鉴相器、环路滤波器、压控振荡器三个部分[5]。基于同步参考坐标系的闭环锁相环(Synchronous Reference Frame-Phase Locked Loop, SRF-PLL)[7]由于结构简单、检测精度高等优点,被广泛应用于三相并网变流器中,但当电网出现不平衡或谐波畸变时,这类锁相环的输出存在一定程度的相位波动,无法为变流器的控制提供可靠的参考信号[8-9]。为此,诸多文献在SRF-PLL的基础上提出了不同的改进方案,包括基于双同步坐标系的锁相环[10]、基于对称分量法的锁相环[11]、基于双二阶广义积分器的锁相环[12]、基于复数滤波器的锁相环[13]和基于延时信号消除法的锁相环[14]等,这些改进的锁相环本质上是在SRF-PLL的基础上增加了电压基波分量提取的环节,在非理想电网条件下均能取得一定的效果。然而,闭环锁相环在控制回路中几乎都采用了PI控制器[5],锁相环的动态响应速度取决于控制器的调节时间,现有闭环锁相环响应时间均过长,相位或频率突变时响应时间甚至都超过了3个工频周期[15],同时在复杂电网条件下,PI控制器的参数很难设计[16],难以满足锁相环准确、快速响应的要求。
为了解决闭环锁相环动态响应速度慢、参数难以设计的问题,不少文献提出了各类开环锁相的方案。文献[6, 17-18]采用固定角频率的滤波器提取电网电压的基波正序分量,并设计了相应的校正环节修正频率波动时的稳态相位误差,但当频率出现偏移且电网电压中存在谐波和负序分量时,上述方法都不能有效消除谐波和负序电压对输出锁相相位的影响。文献[19-20]针对单相变流器的应用提出了相应的开环锁相方案,所提出的方法也无法消除频率偏移时电网电压中谐波的影响,且受滤波器延时的影响,扰动下锁相的动态响应时间超过了1个周期。文献[21-22]先得到电网的频率和相对相位差,然后在相对相位差的基础上叠加频率的积分得到电网实时相位,该方法的相位检测精度主要依靠电网频率的准确测量,一旦电网存在扰动导致检测频率出现扰动,该方法所输出的相位则容易出现较大的稳态误差。文献[23]采用有限长单位冲激响应(Finite Impulse Response, FIR)滤波器提取电网电压基波正序分量计算相位,并通过滑动平均滤波器补偿相位的偏差,两个滤波器的总延时超过了一个周波,锁相的动态响应时间偏长。文献[16]提出的方法可以将锁相响应时间控制在一个工频周期之内,但锁相的结构相对复杂,不利于工程实施。另有一些文献为开环锁相设计了较为复杂的滤波算法,如最小二乘法[24]、卡尔曼滤波器[25]等,这些方案在异常电网条件下能实现较好的锁相效果,但算法复杂、难以在数字处理器中实现,这里不再详细介绍。
针对以上所提到的问题,为实现电网基波正序电压的快速准确锁相,本文提出了一种基于三相电压空间矢量的开环锁相方案,同时为应对复杂电网环境,基于傅里叶级数设计了一种结构简单的电网基波正序电压提取方案,仿真和实验验证了所提方案的有效性和可行性。
对于一个三相系统,其所有的物理量都可以用一个旋转的矢量在三相静止坐标系上的投影来表示,这个用以表示三相物理量的矢量称之为空间矢量。假设电网电压理想对称,其瞬时值分别为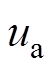 、
、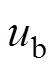 、
、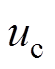 ,三相电压在静止坐标系上的瞬时值和其所对应的空间矢量U如图1所示。图1中,空间矢量U以角速度
,三相电压在静止坐标系上的瞬时值和其所对应的空间矢量U如图1所示。图1中,空间矢量U以角速度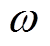 逆时针方向旋转;空间矢量U在a、b、c轴上的投影ua、ub、uc,仅表示电网三相电压瞬时值的大小;旋转的空间矢量U与静止坐标系a轴的夹角
逆时针方向旋转;空间矢量U在a、b、c轴上的投影ua、ub、uc,仅表示电网三相电压瞬时值的大小;旋转的空间矢量U与静止坐标系a轴的夹角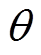 为电网电压的实时相位,锁相环的目标就是要确定相位
为电网电压的实时相位,锁相环的目标就是要确定相位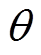 的大小,SRF-PLL的输出即为此角度。
的大小,SRF-PLL的输出即为此角度。
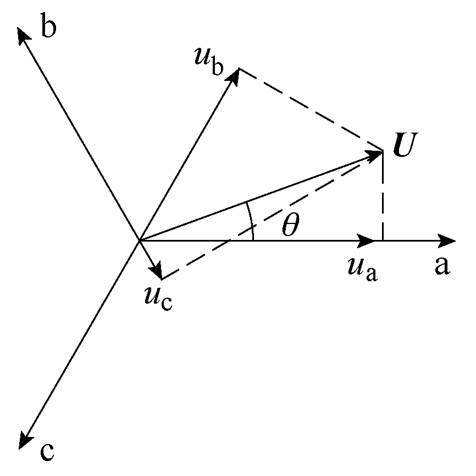
图1 三相电压与空间矢量的关系
Fig.1 Relation between three-phase voltage and space vector
由于在任意时刻,三相电压所对应的空间矢量的位置都可以通过电网电压瞬时值唯一确定,因此相位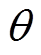 也可通过电压的瞬时值求取。根据空间矢量和三相电压之间的关系可以得到
也可通过电压的瞬时值求取。根据空间矢量和三相电压之间的关系可以得到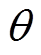 的大小为
的大小为
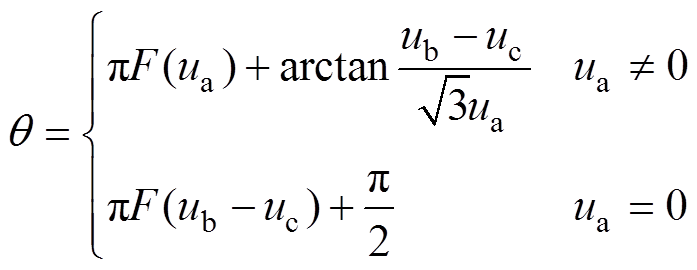 (1)
(1)式中,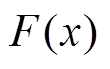 为阶跃函数,具体描述为
为阶跃函数,具体描述为
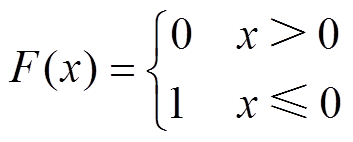 (2)
(2)
在理想电网条件下,通过式(1)可以瞬间得到电网电压的实时相位,从而可以显著提高锁相的速度。得到准确相位后,通过旋转变换等方式可轻松得到电网电压的幅值信息。
前述的锁相技术考虑的是理想电网条件,但实际的电网不可避免地存在谐波、不平衡和频率偏移等工况,而式(1)的相位计算由于消除了闭环环节,对非理想电网较为敏感,谐波和噪声等都会使锁相相位产生畸变,因此如何从电网电压中提取基波正序分量成为锁相的关键一环,下文将进行详细介绍。
目前有很多种方法从畸变的电压中提取基波分量,其中基于离散傅里叶级数的基波提取方法不仅具有较强的滤波特性,而且原理简单、抗干扰能力强,在实际应用中较为广泛[18, 21, 26],因此本文采用该方法滤除电网电压中的谐波分量。
电力系统中的电压波形均是半波对称的,即不含偶次谐波,则电网任意一相的电压可以表征为
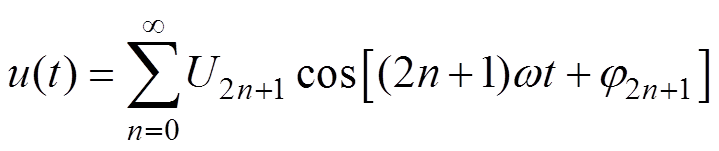 (3)
(3)式中,U和j 分别为基波电压的幅值和初始相位; 和
和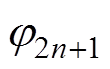 为谐波电压的幅值和初始相位(n= 1,…)。则式(3)的电压信号傅里叶级数的基波分量为
为谐波电压的幅值和初始相位(n= 1,…)。则式(3)的电压信号傅里叶级数的基波分量为
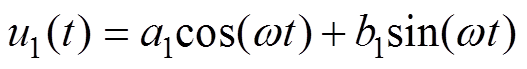 (4)
(4)
式中,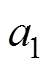 和
和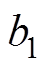 为基波分量的系数,稳态时为固定值,其具体表达式分别为
为基波分量的系数,稳态时为固定值,其具体表达式分别为
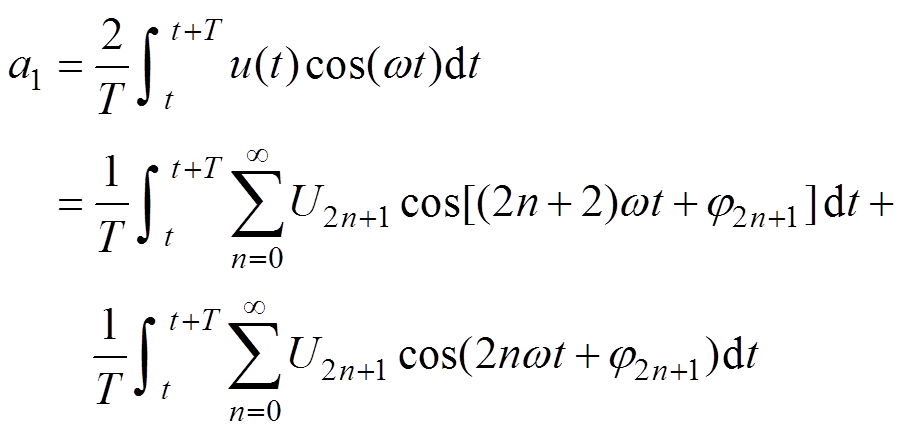 (5)
(5)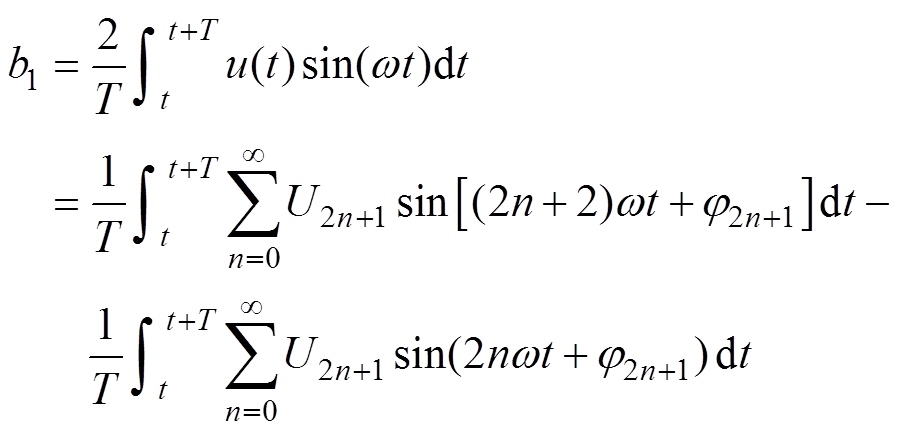 (6)
(6)
式中,T为基波周期。式(5)和式(6)被积函数中的交流成分在一个周期的积分之后均为零,注意到被积函数中的交流量的频率均为基波成分的偶数倍,其在半个周期的积分即可变为零。因此可将积分的时间窗口从一个周期变为半个周期,加快基波提取的速度,即
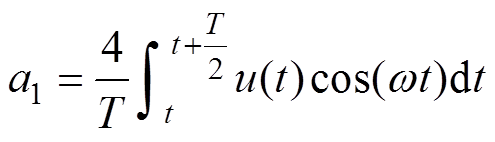 (7)
(7) (8)
(8)
对式(4)、式(7)、式(8)离散化可以得到离散傅里叶级数的迭代计算公式为
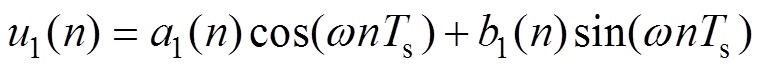 (9)
(9)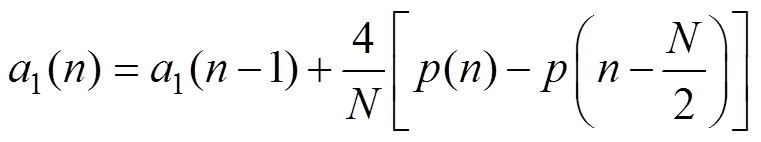 (10)
(10)
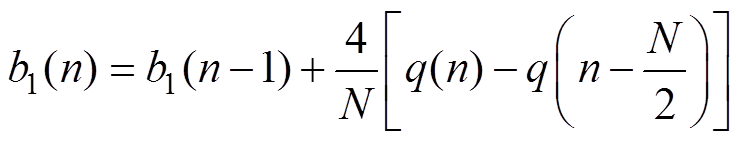 (11)
(11)
式中,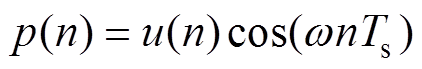 ;
;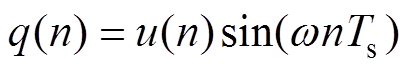 ;
; ,Ts为采样周期。以上离散傅里叶级数在每个计算周期只需要进行几次加法运算和乘法运算,没有复杂的算法,不会占用太多的处理器资源。
,Ts为采样周期。以上离散傅里叶级数在每个计算周期只需要进行几次加法运算和乘法运算,没有复杂的算法,不会占用太多的处理器资源。
通过离散傅里叶级数可以有效滤除电网电压中的谐波和噪声,但是无法消除电压三相不平衡所带来的影响,因此还需要将正序分量从不平衡电压中分解出来。本文采用经典的对称分量法来提取正序电压分量。
忽略零序分量,电压中正序分量计算公式为
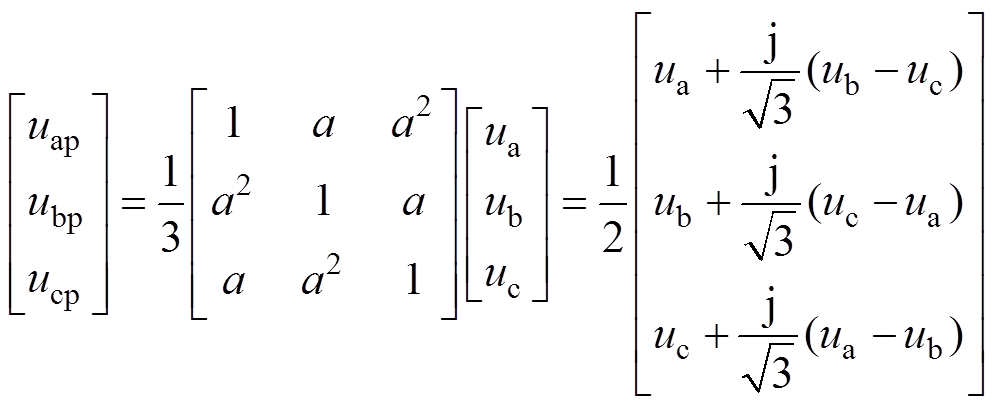 (12)
(12)式中,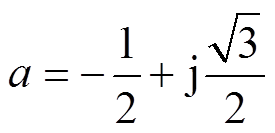 。
。
式(12)中包含虚部,复变量中虚部相对于实部有90°偏移特性,因此为了实现上述正序分量的分解运算,需要对电压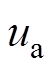 、
、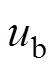 、
、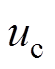 进行90°偏移,从而构造虚拟的正交信号。目前常用的正交信号构造方法主要有延时法、求导法、二阶广义积分器法和全通滤波器法等[27],但以上方法要么存在谐波放大的问题,要么实现起来较为复杂,同时以上方法均会在原始信号的基础上引入一定的延时,不利于锁相环的快速准确响应。
进行90°偏移,从而构造虚拟的正交信号。目前常用的正交信号构造方法主要有延时法、求导法、二阶广义积分器法和全通滤波器法等[27],但以上方法要么存在谐波放大的问题,要么实现起来较为复杂,同时以上方法均会在原始信号的基础上引入一定的延时,不利于锁相环的快速准确响应。
2.1节提到利用傅里叶级数滤除系统电压中的谐波,如式(4)所示,则对式(4)进行改造即可简单地构造出正交信号,且正交信号与原始信号保持同步,不会引入额外的延时。用符号v表示与电压u相互正交的信号,则电压u1(t)的正交信号为
 (13)
(13)与式(9)类似,其离散化表达为
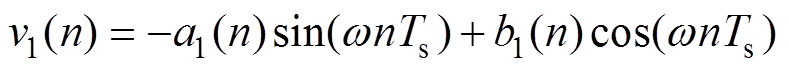 (14)
(14)
结合式(9)、式(12)和式(14),电压的基波正序分量可以表示为
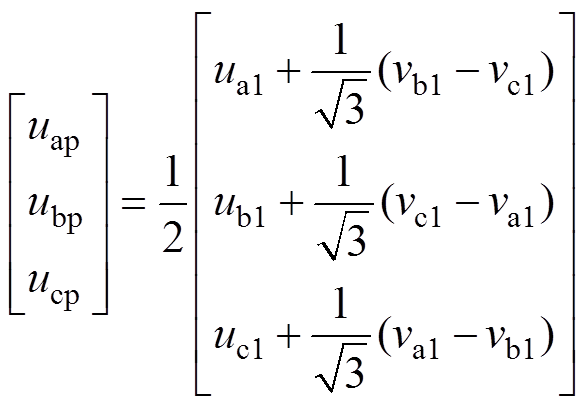 (15)
(15)前述的利用傅里叶级数滤除谐波和构造正交信号,均需要控制系统提供标准的基波正弦信号以供计算。当电网电压的频率偏离基准频率时,如果傅里叶级数仍然按照基准频率进行计算,则无法有效滤除谐波,且输出信号的相位会产生误差,导致本文所提出的方法不能准确锁相,因此频率信息的获取对整个开环锁相系统来说十分关键。
频率检测有多种方法,其中过零检测法因其简单易行、快速稳定等优点得到了广泛使用[16, 18, 21]。但当电网的相位出现突变时,过零检测方法得到的频率会出现异常偏高或异常偏低的情况,影响傅里叶级数的输出。为此,本文对过零检测算法进行了改进,提高了过零检测应对谐波和相位突变的能力,具体算法流程如图2所示。
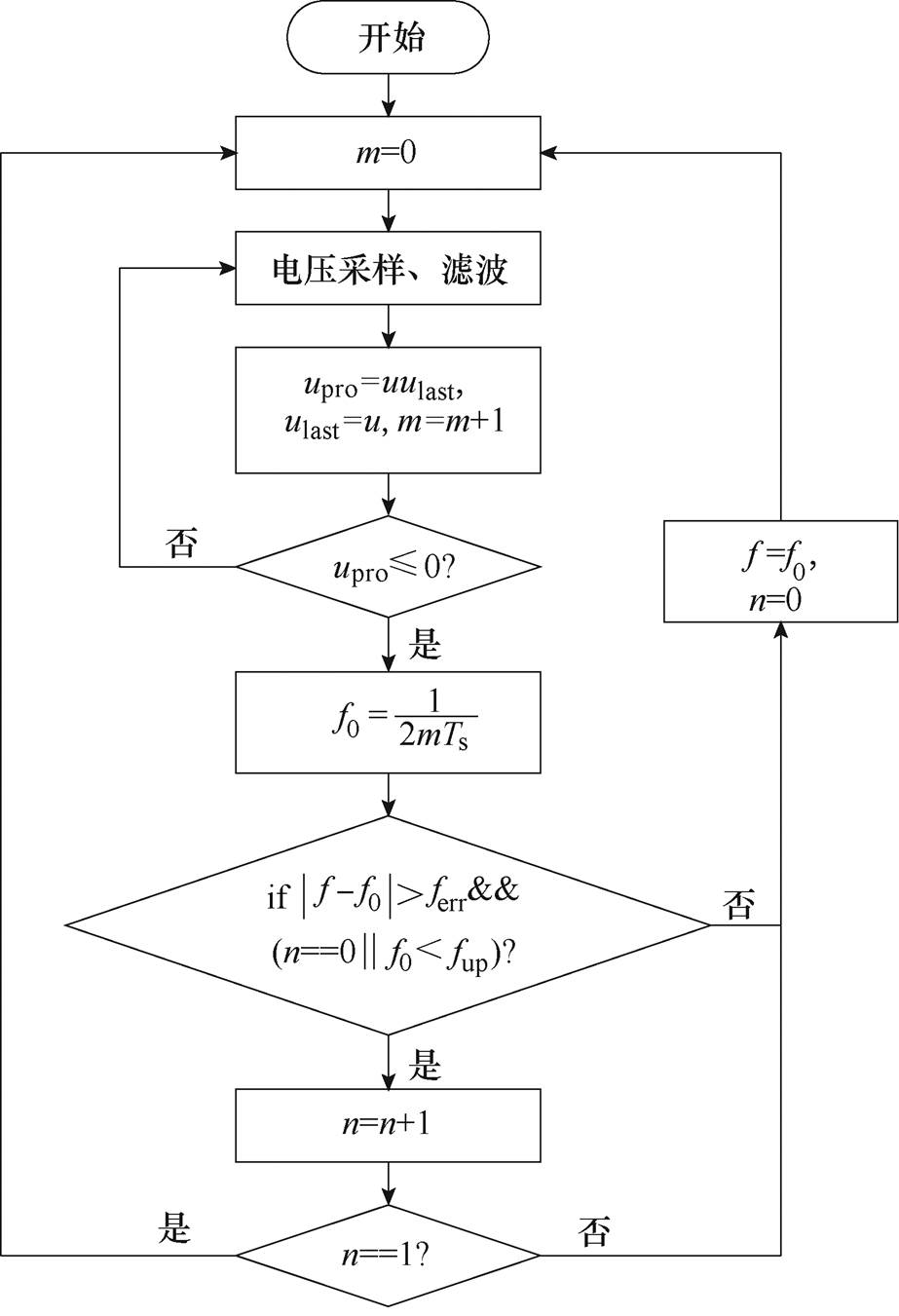
图2 过零检测算法流程
Fig.2 Algorithm of zero-crossing detection
图2中,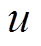 为采样的任意相电压,ulast为上个采样周期的电压,upro为
为采样的任意相电压,ulast为上个采样周期的电压,upro为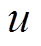 与ulast的乘积;
与ulast的乘积;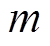 为计算周期的计数,主要用于频率的计算;f0为每个过零点计算出的频率,f为算法最终输出的频率,fup为设置的频率上限,ferr为允许的频率偏差;n用于异常频率的检测。算法的主要思想是将过零点计算出的频率与上一个过零点计算的频率进行比较,如果频率偏差在一定的范围内,则接受这个过零点的频率,如果偏差过大,则输出上一个过零点的频率,并等待下一个过零点频率的计算。考虑到电压过零点检测存在误差而导致的频率波动,频率偏差ferr的大小应该根据实际情况折中选取。ferr越大,电网稳态运行时因为电压过零点采样误差所导致的频率抖动会越大;ferr越小,电网稳态运行时检测到的频率越准确,但当电网电压出现扰动时,检测算法将无法有效识别异常的频率跳变。综合考虑本文选取
为计算周期的计数,主要用于频率的计算;f0为每个过零点计算出的频率,f为算法最终输出的频率,fup为设置的频率上限,ferr为允许的频率偏差;n用于异常频率的检测。算法的主要思想是将过零点计算出的频率与上一个过零点计算的频率进行比较,如果频率偏差在一定的范围内,则接受这个过零点的频率,如果偏差过大,则输出上一个过零点的频率,并等待下一个过零点频率的计算。考虑到电压过零点检测存在误差而导致的频率波动,频率偏差ferr的大小应该根据实际情况折中选取。ferr越大,电网稳态运行时因为电压过零点采样误差所导致的频率抖动会越大;ferr越小,电网稳态运行时检测到的频率越准确,但当电网电压出现扰动时,检测算法将无法有效识别异常的频率跳变。综合考虑本文选取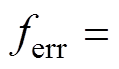
 。电压信号在进行过零检测之前需要先经过一个低通滤波器,可以粗略滤除电压中的谐波和高频噪声,有效地防止谐波和噪声引起的多个过零点的问题,而设置低通滤波器仅会给电压信号带来一点延时,不影响频率检测的精度。以上过零检测算法能够应对大部分电网电压突变情况下的异常频率。
。电压信号在进行过零检测之前需要先经过一个低通滤波器,可以粗略滤除电压中的谐波和高频噪声,有效地防止谐波和噪声引起的多个过零点的问题,而设置低通滤波器仅会给电压信号带来一点延时,不影响频率检测的精度。以上过零检测算法能够应对大部分电网电压突变情况下的异常频率。
图3为本文所提出的开环锁相方法的总体框图。采样的电网电压先经过一个低通滤波器,滤除谐波分量,再利用图2所示的过零检测算法得到电网频率,然后将检测到的频率输入到离散傅里叶级数中,用以提取电网电压中的基波分量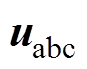 和与其相互正交的电压信号
和与其相互正交的电压信号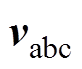 。在此基础上通过对称分量法分离出电压中的正序分量,最后再利用式(1)的方法计算电压的实时相位。由于离散傅里叶级数提取基波需要半个周期的延时,在电网频率固定的条件下,该方法可以在半个周期内准确获取电网相位,考虑到频率的波动,在最极端的情况下该方法也能在1.5个周期内准确锁相。而且整个锁相过程只需要进行简单的数学运算,无需参数设计,因此适用于任何环境下的电网,具有较强的鲁棒性。
。在此基础上通过对称分量法分离出电压中的正序分量,最后再利用式(1)的方法计算电压的实时相位。由于离散傅里叶级数提取基波需要半个周期的延时,在电网频率固定的条件下,该方法可以在半个周期内准确获取电网相位,考虑到频率的波动,在最极端的情况下该方法也能在1.5个周期内准确锁相。而且整个锁相过程只需要进行简单的数学运算,无需参数设计,因此适用于任何环境下的电网,具有较强的鲁棒性。
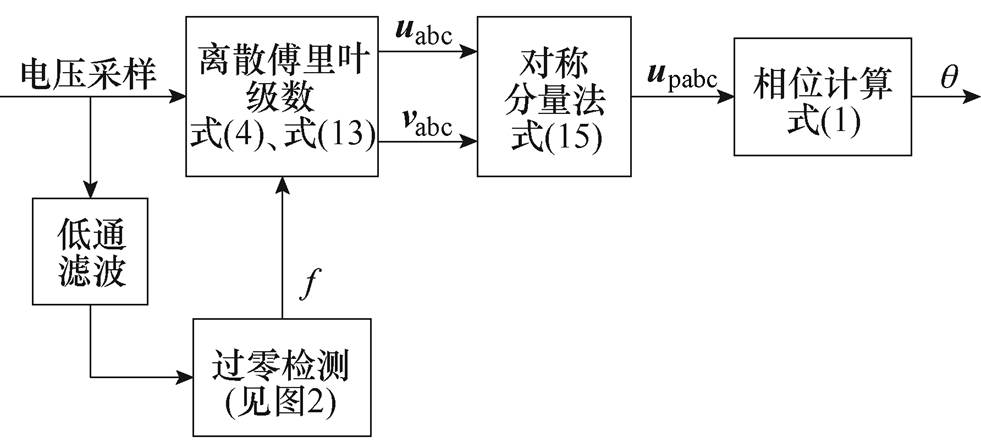
图3 开环锁相总体框图
Fig.3 Diagram of proposed open-loop phase-locked
为了验证本文方法的有效性,将所提出的锁相方法与目前性能较好的闭环锁相方法,如基于级联延时信号消除法的锁相环[14](Cascaded Delayed Signal Cancellation PLL, CDSC-PLL)和开环锁相方法,如增强型开环锁相[17](Enhanced version of the True Open-Loop Synchronization, ETOLS)进行对比,并在Matlab/Simulink上搭建仿真模型进行分析。闭环锁相环CDSC-PLL控制器采用PI控制,比例系数为0.4,积分系数为20。图3中,滤波器采用最简单的一阶低通滤波器,截止频率为250Hz。为了检验锁相环的动态效果,设计了六种运行工况见表1,用以模拟电网正常运行、谐波畸变、不对称、频率突变、相位突变和综合故障的情况。
表1 不同运行工况下的电网电压参数
Tab.1 Voltage parameters under different conditions
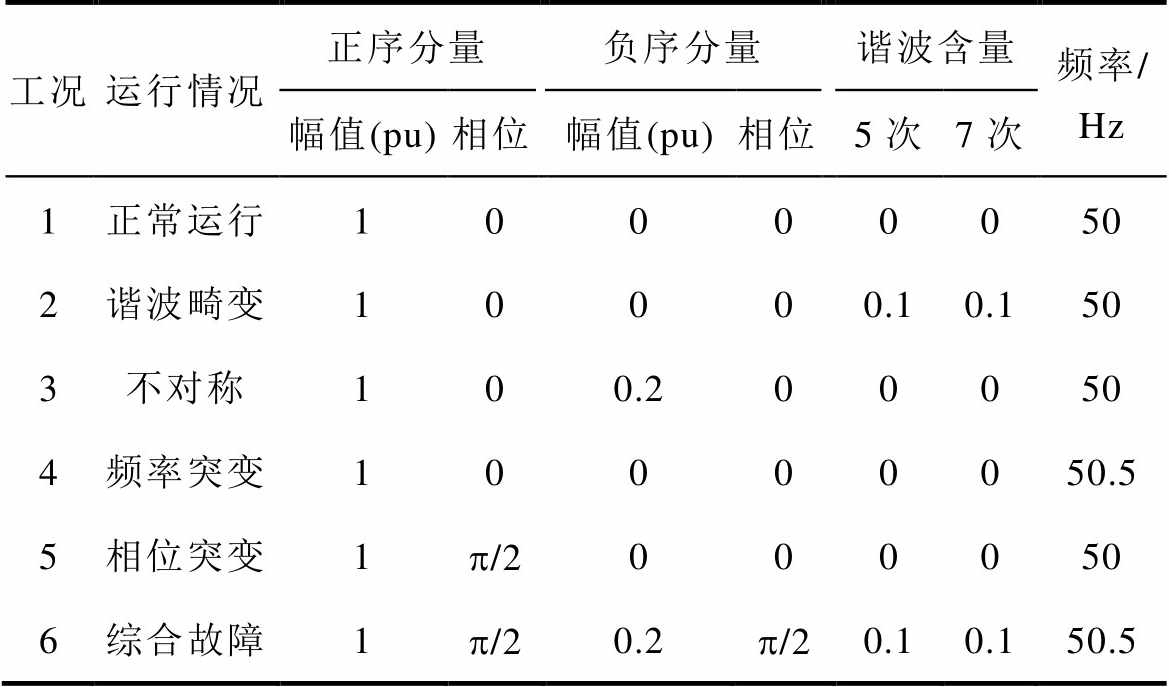
工况运行情况正序分量负序分量谐波含量频率/ Hz 幅值(pu)相位幅值(pu)相位5次7次 1正常运行10000050 2谐波畸变10000.10.150 3不对称100.200050 4频率突变10000050.5 5相位突变1p/2000050 6综合故障1p/20.2p/20.10.150.5
图4为电网从工况1切换到工况2的仿真结果,即电网电压突加谐波下的电网电压波形和三种锁相环输出相位与基准相位的误差波形。当电网电压出现畸变时,三种锁相环的相位误差都出现了不同程度的波动,其中本文所提出的开环锁相方法在半个周期内,相位误差即可恢复到零,ETOLS的响应时间约19ms,而CDSC-PLL响应时间超过了两个周期。由于ETOLS中存在微分环节,对谐波较为敏感,因此动态过程中相位误差的波动较大。虽然本文所提的开环锁相方法相位误差幅值要比闭环锁相方法大,但误差在1.5°以内,且恢复较快,对电力电子装置的控制影响不大。同时5次谐波和7次谐波的叠加,导致电网电压波形存在多个过零点,从仿真的波形看,采用图2的过零检测算法得到的频率未出现异常的突变,说明该算法可以有效应对电网电压畸变时的频率检测。
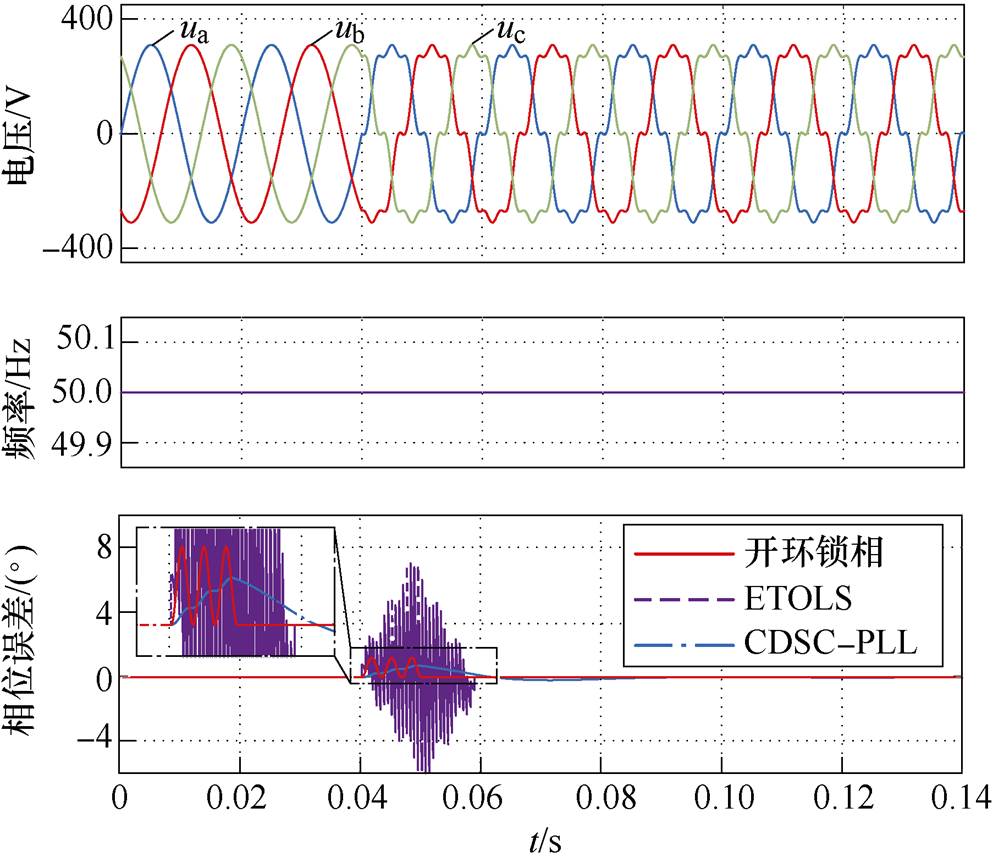
图4 谐波畸变时的锁相结果
Fig.4 Phase-locked results of harmonic distortion
图5为电网电压中突加负序分量的不对称运行时的锁相结果。由于负序电压的注入,电网各相电压出现了轻微相位跳变,此时离散傅里叶级数提取出的电压基波分量在半个周波内会存在一定误差,这直接体现在锁相相位的波动上,如图5开环锁相的波形所示,半个周期之后相位误差恢复为零。对应的ETOLS 和CDSC-PLL响应速度均较慢,动态性能不如本文所提出的锁相方法。

图5 不对称运行时的锁相结果
Fig.5 Phase-locked results of asymmetric
考虑到电网允许的供电频率偏差为±0.5Hz,仿真中模拟了电网频率突变的极限工况,图6为电网频率从50Hz突变到50.5Hz的锁相结果。过零检测算法通常需要0.5~1个周期的响应时间,电网频率突变后检测到的第一个频率值虽然与实际频率不一致,但在算法允许的范围内。因此此算法将该频率作为正常频率输出,为傅里叶级数提取的基波提供基准信号。半个周期之后,开环锁相的相位误差达到一个暂态的稳定值,但由于傅里叶级数的计算频率与实际频率不一致,此时稳定的相位误差并不为零,该误差的大小与两个频率值的偏差大小相关。直到过零检测得到电网实际频率半个周期之后,开环锁相输出相位与实际相位的误差才恢复到零,从图1中可以看出,整个相位捕获过程耗时大约为23ms。与此同时,ETOLS锁相时间约为19ms,而CDSC-PLL需要大约3个周期才能获取电网准确相位,且相位误差幅值比本文所提出的开环锁相方法大。不过三种锁相方法的相位误差均在2°以内,即频率的突变对相位的影响相对较小。

图6 频率突变时的锁相结果
Fig.6 Phase-locked results of frequency change
图7为电网电压从工况1切换到工况4,即电网电压相位突变下的锁相结果。在相位突变的瞬间,三种锁相方法的相位误差均达到了最大值p/2,此误差大小与电网电压相位突变的大小相同。从仿真结果可以看出,开环锁相方法的相位误差在相位突变后平稳地恢复到零,整个过程耗时约半个周期,对应的ETOLS需要19ms,而CDSC-PLL需要3个周期左右才能达到稳定。
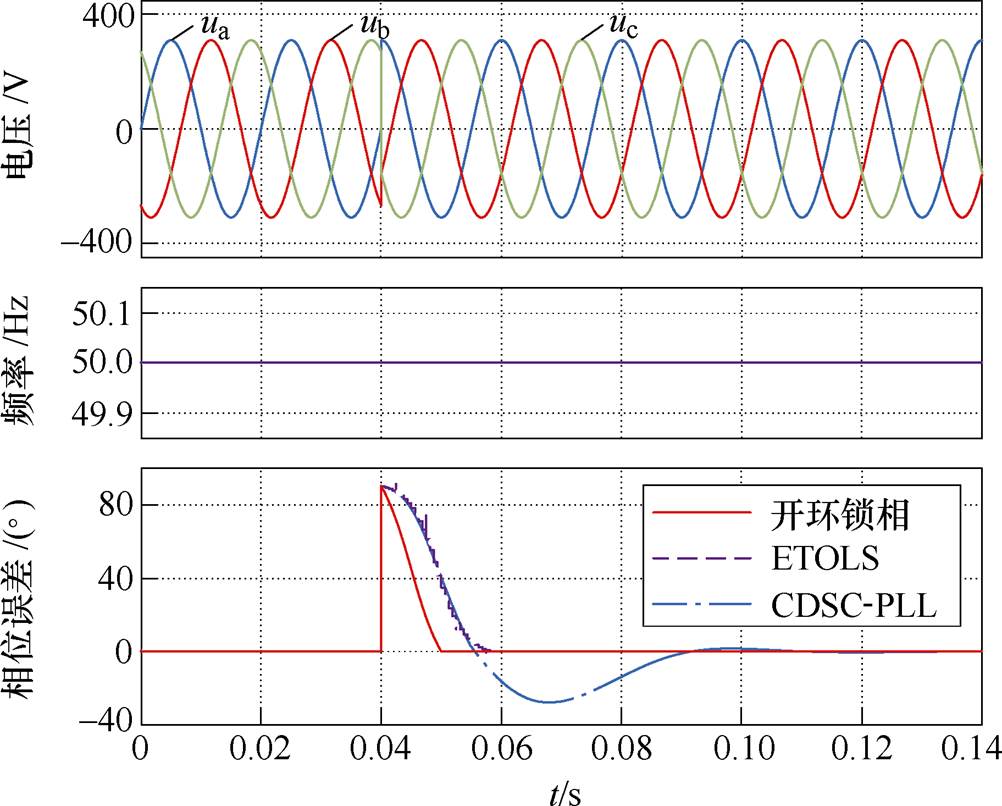
图7 相位突变时的锁相结果
Fig.7 Phase-locked results of phase change
图8为电网电压从工况1切换到工况5时的锁相结果,即电网电压同时出现谐波、不平衡、相位突变以及频率突变。可以看出,本文提出的开环锁相方法在极端电网条件下依然能快速准确获取电网相位。图中,过零检测算法耗时约15ms,由于频率的误差对相位误差的影响不大,因此图8中显示的锁相时间仅约10ms,但实际上相位误差恢复到零大约在检测出实际频率的半个周波之后,即准确锁相需要约25ms。与此同时,ETOLS的动态响应速度与本文所提的方法相当,但平均误差较大;而闭环锁相方法CDSC-PLL需要3个周波相位误差才达到零,本文所提出的锁相方法与之相比响应速度至少提升了两倍以上。
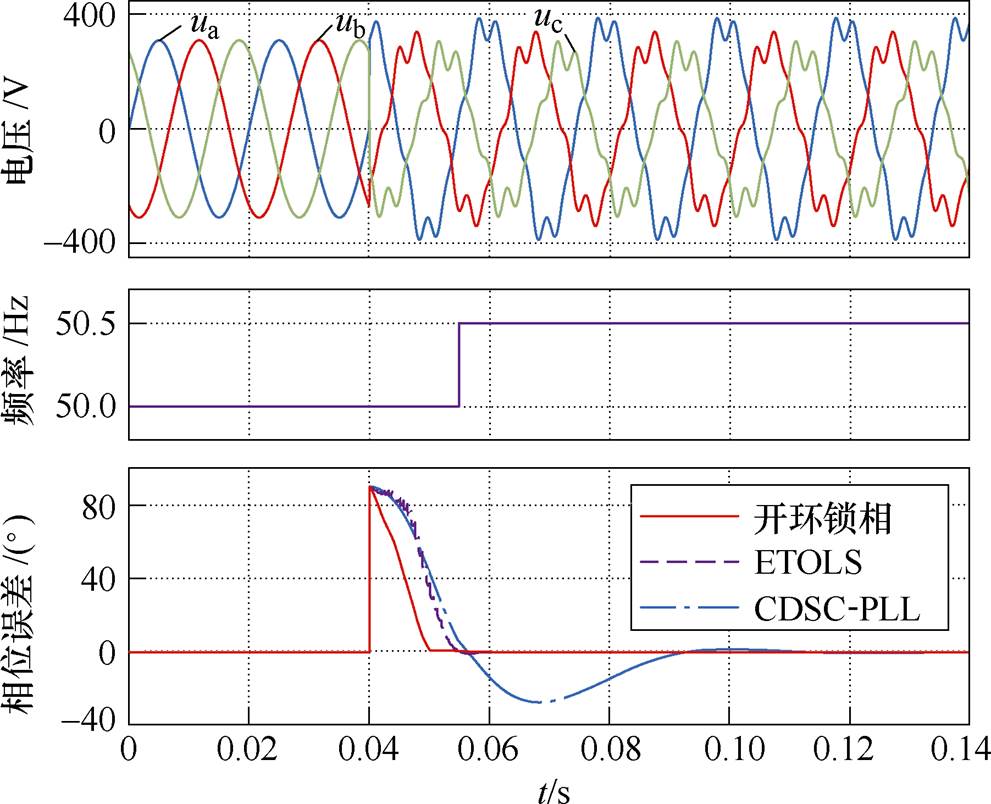
图8 非理想电网下的锁相结果
Fig.8 Phase-locked results of non-ideal grid
以上仿真结果表明,本文所提出的开环锁相方法与文献中的开环锁相方法ETOLS和闭环锁相方法CDSC-PLL相比,都具有明显的优势,更适用于复杂电网环境下的电网锁相。
实验采用Altera公司的Cyclone IV系列FPGA作为控制器,具体型号为EP4CE6E22I7。考虑到过零检测输出的频率精度与电压信号采样频率相关,采样频率越高,电压的频率检测精度越高,而高的采样频率并不会给FPGA的运行带来负担,因此实验时电压的采样频率设为50kHz。电网信号由RTLAB模拟输出,电网各种异常工况同样见表1。FPGA计算出的频率和相位信息由控制板上的D-A转换电路输出。
图9和图10分别为电网电压突加谐波和负序分量下的电网电压波形和锁相输出相位波形,图中的电压为电网线电压uab和ubc。当电网出现谐波和不平衡工况时,锁相输出的相位未见有明显变化,即该方法在谐波和不平衡工况下响应速度较快,同时过零检测算法的输出也不受谐波和不平衡的影响。
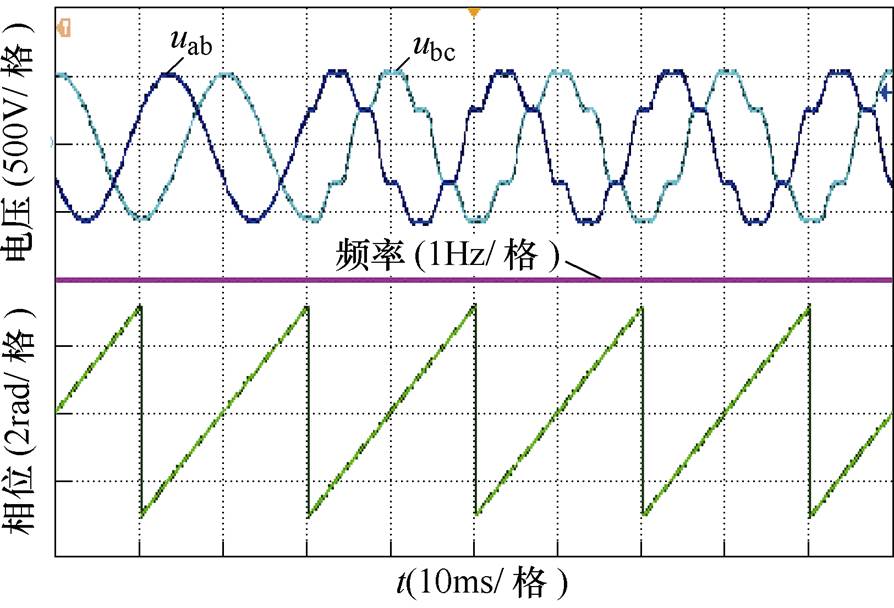
图9 谐波畸变时的实验结果
Fig.9 Experimental results of harmonic distortion
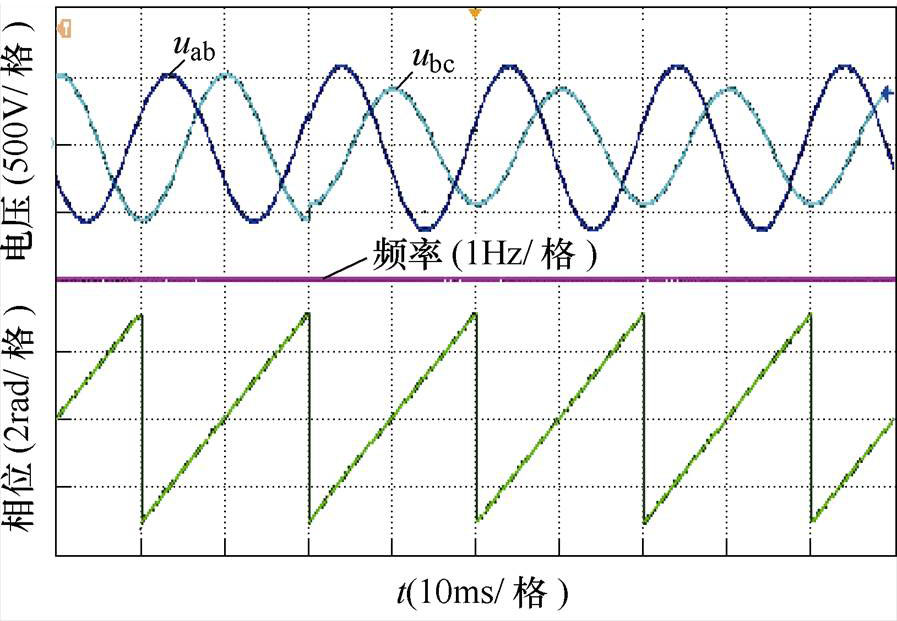
图10 不对称运行时的实验结果
Fig.10 Experimental results of asymmetric
图11为电网电压频率从50Hz突变到50.5Hz的实验结果。与图6所示的仿真结果类似,输出的频率波形都存在一个中间频率,频率检测大约耗时17ms,同时频率突变的过程中,锁相得到的相位波形未见明显改变,锁相效果较好。图12为电网电压相位突变p/2的实验波形,在相位产生突变后,锁相输出的相位波形存在明显的调节过程,该过程平滑且迅速,经过大约10ms达到准确的相位输出。
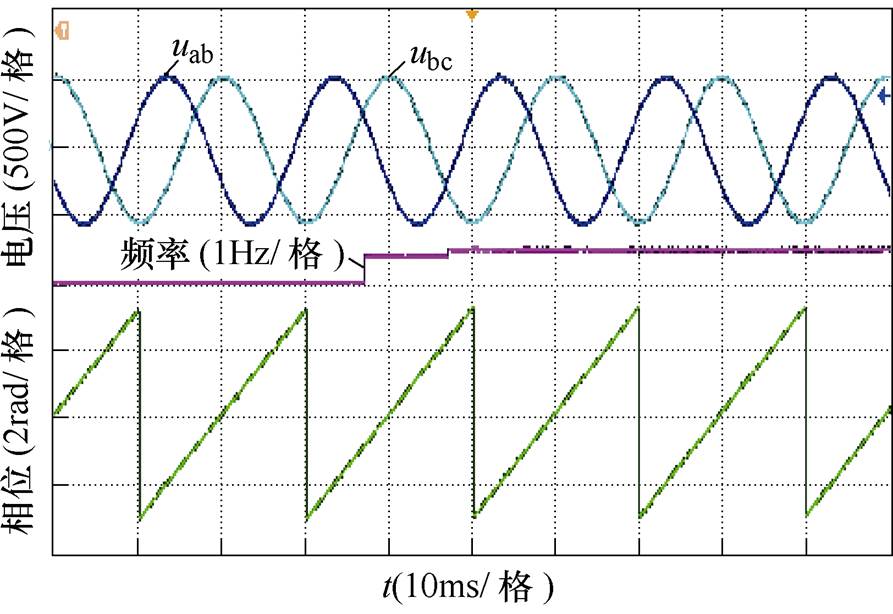
图11 频率突变时的实验结果
Fig.11 Experimental results of frequency change
图13为电网电压从工况1切换到工况6时的实验结果,过零检测算法耗时约15ms,由于频率误差对相位的影响较小,图中的相位波形大约在10ms左右就达到了准确的输出。
以上实验结果表明,本文所提出的锁相方法在各种异常电网工况下均能准确快速地计算出电网相位,具有较好的锁相效果。
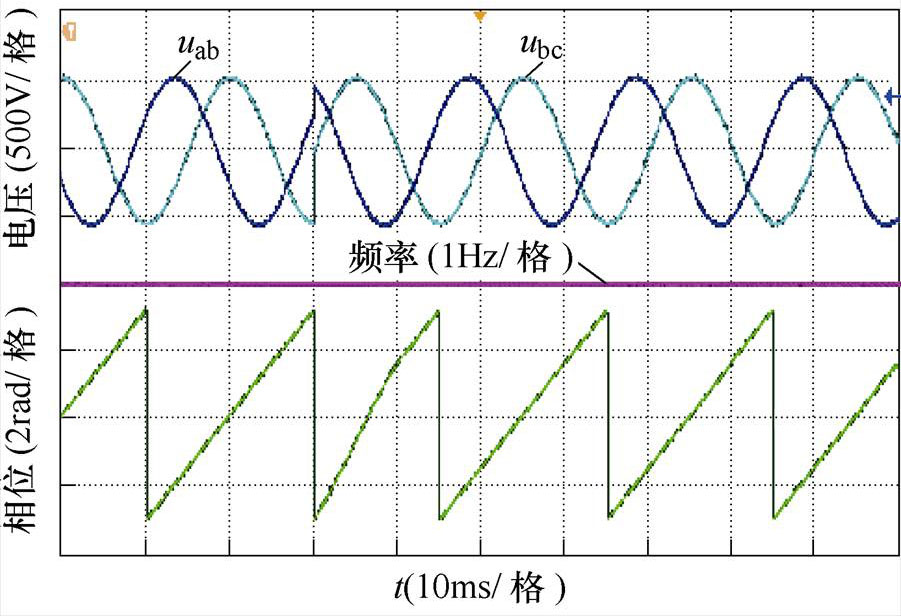
图12 相位突变时的实验结果
Fig.12 Experimental results of phase change
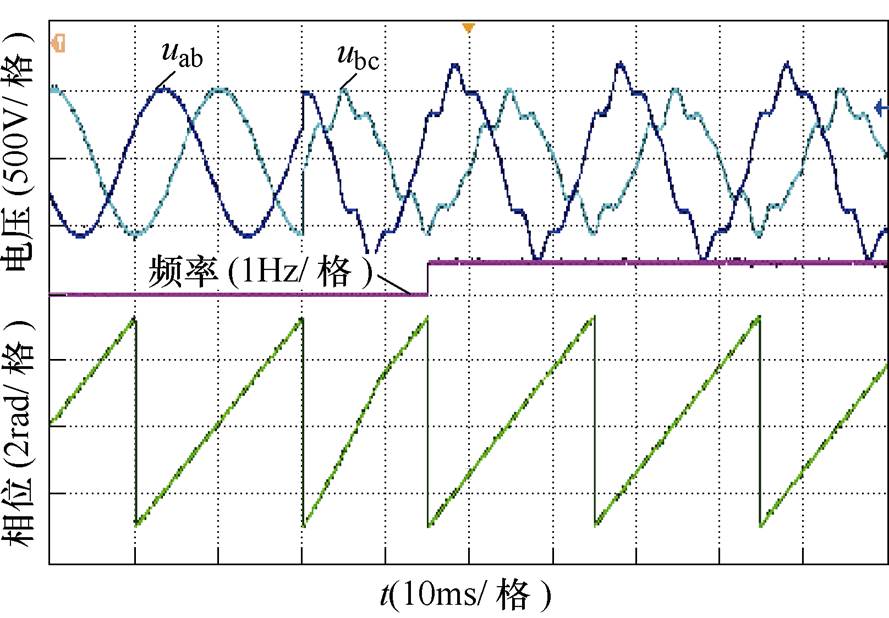
图13 非理想电网下的实验结果
Fig.13 Experimental results of non-ideal grid
为快速准确获取电网基波正序电压的相位,本文提出了一种结构简单的开环锁相方法。
1)基于三相电压空间矢量,提出电压相位的开环计算方法,在理想条件下,该方法可以无延时得到电网实时相位。
2)考虑非理想电网,采用离散傅里叶级数提取电网电压的基波分量,同时利用傅里叶级数对基波分量进行90°相移,在此基础上利用对称分量法分离出正序电压。当电网频率固定时,所采用滤波方案可以在半个周期之内提取出基波正序电压。
3)针对电网频率的变化,改进了现有的过零检测算法,使其在电网电压突变时能快速准确检测出电网频率,而不出现频率的异常跳变。
4)所提出的开环锁相方法实现简单,响应速度较快,可以应用于各种异常的电网工况,具有较强的鲁棒性,仿真和实验结果证明了该方法的有效性和优越性。
参考文献
[1] 肖湘宁, 廖坤玉, 唐松浩, 等. 配电网电力电子化的发展和超高次谐波新问题[J]. 电工技术学报, 2018, 33(4): 707-720.
Xiao Xiangning, Liao Kunyu, Tang Songhao, et al. Development of power-electronized distribution grids and the new supraharmonics issues[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 707- 720.
[2] Blaabjerg F, Teodorescu R, Liserre M, et al. Overview of control and grid synchronization for distributed power generation systems[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1398-1409.
[3] 曾正, 邵伟华, 刘清阳, 等. 并网逆变器数字锁相环的数学物理本质分析[J]. 电工技术学报, 2018, 33(4): 808-816.
Zeng Zheng, Shao Weihua, Liu Qingyang, et al. Mathematical and physical fundaments of digital phase-locked loop for grid-connected inverters[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 808-816.
[4] 郭磊, 王丹, 刁亮, 等. 针对电网不平衡与谐波的锁相环改进设计[J]. 电工技术学报, 2018, 33(6): 1390-1399.
Guo Lei, Wang Dan, Diao Liang, et al. A modified design of phase-locked loop for unbalanced and distorted grid voltage conditions[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1390- 1399.
[5] Golestan S, Guerrero J, Vasquez J. Three-phase PLLs: a review of recent advances[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 1894-1907.
[6] Freijedo F D, Dovalgandoy J, Lopez O, et al. A generic open-loop algorithm for three-phase grid voltage/current synchronization with particular refer- ence to phase, frequency, and amplitude estimation[J]. IEEE Transactions on Power Electronics, 2009, 24(1): 94-107.
[7] Chung S K. A phase tracking system for three phase utility interface inverters[J]. IEEE Transactions on Power Electronics, 2000, 15(3): 431-438.
[8] Liu Baoquan, Zhuo Fang, Zhu Yixin, et al. A three- phase PLL algorithm based on signal reforming under distorted grid conditions[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 5272-5283.
[9] Karimi-Ghartemani M, Iravani M R. A method for synchronization of power electronic converters in polluted and variable-frequency environments[J]. IEEE Transactions on Power Systems, 2004, 19(3): 1263-1270.
[10] Rodriguez P, Pou J, Bergas J, et al. Decoupled double synchronous reference frame PLL for power con- verters control[J]. IEEE Transactions on Power Electronics, 2007, 22(3): 1078-1078.
[11] Yazdani D, Mojiri M, Bakhshai A, et al. A fast and accurate synchronization technique for extraction of symmetrical components[J]. IEEE Transactions on Power Electronics, 2009, 24(3): 674-684.
[12] Rodriguez P, Teodorescu R, Candela I, et al. New positive-sequence voltage detector for grid synchro- nization of power converters under faulty grid conditions[C]//Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 2006: 1-7.
[13] 回楠木, 王大志, 李云路. 基于复变陷波器的并网锁相环直流偏移消除方法[J]. 电工技术学报, 2018, 33(24): 263-272.
Hui Nanmu, Wang Dazhi, Li Yunlu. DC-offset elimination method for grid-connected phase-locked loop based on complex notch filter[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 263- 272.
[14] Wang Yifei, Li Yunwei. Three-phase cascaded delayed signal cancellation PLL for fast selective harmonic detection[J]. IEEE Transactions on Indu- strial Electronics, 2013, 60(4): 1452-1463.
[15] Golestan S, Guerrero J M, Vasquez J C. Single-phase PLLs: a review of recent advances[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(12): 9013-9030.
[16] 熊连松, 卓放, 刘小康, 等. 不对称电网同步相位的快速开环捕获方法研究[J]. 中国电机工程学报, 2015, 35(22): 5682-5691.
Xiong Liansong, Zhuo Fang, Liu Xiaokang, et al. Research on fast phase synchronization scheme for three-phase unbalanced power system[J]. Proceedings of the CSEE, 2015, 35(22): 5682-5691.
[17] Golestan S, Vidal A, Yepes A G, et al. A true open- loop synchronization technique[J]. IEEE Transa- ctions on Industrial Informatics, 2016, 12(3): 1093- 1103.
[18] Baradarani F, Zadeh M R D, Zamani M A. A phase- angle estimation method for synchronization of grid- connected power-electronic converters[J]. IEEE Transactions on Power Delivery, 2015, 30(2): 827- 835.
[19] Golestan S, Guerrero J M, Vasquez J C. An open- loop grid synchronization approach for single-phase applications[J]. IEEE Transactions on Power Electro- nics, 2018, 33(7): 5548-5555.
[20] Xiao Furong, Dong Lei, Li Li, et al. A novel open- loop frequency estimation method for single-phase grid synchronization under distorted conditions[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 1287-1297.
[21] Lee K J, Lee J P, Shin D, et al. A novel grid synchro- nization PLL method based on adaptive low-pass notch filter for grid-connected PCS[J]. IEEE Transa- ctions on Industrial Electronics, 2014, 61(1): 292- 301.
[22] Nwobu C J, Nakiganda A M, Zhang L. Grid voltage synchronization for unbalanced voltages using the energy operator[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 1415-1424.
[23] Roncero S P, Garcia X T, Torres A P, et al. Fun- damental positive- and negative-sequence estimator for grid synchronization under highly disturbed operating conditions[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 3733-3746.
[24] Ramos C J, Martins A P, Carvalho A S. Frequency and phase-angle estimation using ordinary least squares[J]. IEEE Transactions on Industrial Electro- nics, 2015, 62(9): 5677-5688.
[25] Bagheri A, Mardaneh M, Rajaei A H, et al. Detection of grid voltage fundamental and harmonic com- ponents using Kalman filter and generalized averaging method[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1064-1073.
[26] 肖勇, 赵伟, 黄松岭. 基于离散傅里叶级数的非同步采样下谐波功率测量算法[J]. 电工技术学报, 2018, 33(7): 1570-1578.
Xiao Yong, Zhao Wei, Huang Songling. Harmonic power measurement algorithm based on discrete Fourier series in asynchronous sampling[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(7): 1570-1578.
[27] Monfared M, Golestan S, Guerrero J M. Analysis, design, and experimental verification of a synchro- nous reference frame voltage control for single-phase inverters[J]. IEEE Transactions on Industrial Elec- tronics, 2014, 61(1): 258-269.
An Open-Loop Phase-Locked Method Based on Three-Phase Voltage Space Vector
Abstract Accurate and fast phase acquisition for fundamental positive-sequence components is the premise for precise control of grid-connected converters. However, when the power grid is abnormal, the traditional closed-loop phase-locked method has a slow dynamic response, which is difficult to meet the control requirements of fast response. For this reason, an open-loop phase-locked method based on three-phase voltage space vector is proposed. In the method, the frequency of power grid is obtained by zero-crossing detection, the harmonic and noise in the grid voltage are filtered by discrete Fourier series, and the voltage signal orthogonal to the fundamental voltage is obtained. On this basis, the symmetric component method is used to extract the positive sequence component of voltage. Finally, the phase of fundamental positive-sequence voltage is calculated based on voltage space vector. At the same time, an improved zero-crossing detection algorithm is proposed to deal with the abnormal frequency when the voltage of power grid changes abruptly, which can effectively detect the frequency of abnormal grid voltage. The proposed phase-locked method does not require parameter design, and has a simple structure and fast response speed. It has strong robustness in abnormal grid environment. The simulation and experimental results verify the effectiveness and feasibility of the proposed method.
keywords:Open-loop phase-locked, space vector, discrete Fourier series, symmetric component method, zero-crossing detection
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.190922
国家重点研发计划(2016YFB0900400)和智能电网联合基金(U1866601)资助项目。
收稿日期 2019-07-25
改稿日期 2019-12-06
余 攀 男,1995年生,博士研究生,研究方向为大功率电力电子技术。E-mail: pyu@whu.edu.cn(通信作者)
盛万兴 男,1965年生,教授级高工,博士生导师,研究方向为配电网运行与控制、分布式发电和微电网关键技术等。E-mail: wxsheng@epri.sgcc.com.cn
(编辑 陈 诚)