 (1)
(1)摘要 减振降噪是电抗器在制作和应用过程中需要考虑的重要因素,但目前的减振方法多集中在被动减振方面,无法从根源上减小电磁振动。该文针对串联电抗器提出一种基于谐波注入的主动减振方法。首先,根据串联电抗器的振动加速度与其输入功率变化率的正比例关系推导出功率变化率与输入电流的关系,由于电抗器中注入谐波会改变其输入电流的波形,所以提出通过增加反向奇数次谐波激励来降低电抗器的功率变化率,从而抑制电抗器的振动,并利用遗传算法计算出最优的谐波注入量。然后,建立串联电抗器的电磁-机械耦合模型,基于有限元法计算电抗器铁心的电磁振动,对比分析得到注入谐波后串联电抗器的平均减振效果为12.90%。最后,搭建串联电抗器振动实验平台,得到注入谐波后电抗器的振动加速度平均幅值减小为12.75%,验证了仿真结果的正确性。通过仿真与实验证明了该方法对电抗器有很好的减振效果。
关键词:串联电抗器 电磁振动 功率变化率 谐波注入 减振
串联电抗器具有限制短路电流和抑制谐波的作用,能够保证电力系统安全稳定的运行[1-2]。为防止铁心饱和,产生更大的电感值,会在电抗器铁心饼之间设置多段气隙,铁心气隙两端周期性变化的麦克斯韦电磁力使电抗器铁心发生变形,产生振动,这种振动不仅造成噪声污染,而且还会导致电抗器紧固件松动,加速构件老化,影响电抗器的使用寿命[3-6]。因此,如何降低电抗器的振动噪声逐渐成为国内外学者研究的重点。
电抗器的振动及减振是电抗器制作和应用过程中需要考虑的关键因素。目前,电抗器的减振措施主要集中在隔振与噪声屏蔽等方面,徐征宇等为电抗器设计了多层隔/吸声复合结构的隔声装置来减小噪声污染[7]。T. Ishikawa等设计了一种新型三角型电抗器,通过分散电磁力达到减振的效果[8]。Gao Yanhui等提出高硬度气隙介质材料对铁心节点振动受力的影响,并通过数值计算确定了气隙介质材料的最佳硬度[9-10]。常晨等研究了螺杆预紧力对电抗器振动的影响,并得出随着预紧力的增加,电抗器的振动呈下降趋势,在预紧力达到一定程度时振动加速度的变化量开始减弱的结论[11]。Zhu Lihua等提出利用柔性高磁导率软磁复合材料填充铁心接缝,采用疏导易流的方式来降低铁心的电磁噪声[12]。赵路娜等用负超磁致伸缩材料填充电抗器铁心气隙,利用负超磁致伸缩材料在磁场作用下产生负形变的特性来抵消电抗器原有的机械形变[13-14]。
但目前的这些减振方法多集中在被动减振方面,无法从根源上减小电磁振动。本文提出一种主动减振方法,首先根据串联电抗器的振动加速度与其输入功率变化率的正比例关系,提出通过增加谐波激励来减小电抗器铁心表面的振动加速度,并通过遗传算法计算出最优的谐波注入量;然后建立串联电抗器的电磁-机械耦合模型,用数值方法计算谐波注入前和谐波注入后电抗器铁心的振动加速度;最后通过实验验证了仿真分析的正确性。本文工作对电抗器减振研究具有指导意义。
文献[15]针对开关磁阻电机提出了一种将功率时间导数作为机电系统的输入,并利用卷积理论计算定子表面振动加速度的预测方法。得出磁场在未饱和之前,振动加速度与功率变化率峰值成正比。串联电抗器的磁场工作在线性部分,且其振动主要由铁心气隙处的麦克斯韦电磁力引起,因此串联电抗器的振动加速度与其输入功率变化率也具有一定的正比例关系,即
 (1)
(1)串联电抗器由交流电流激励,为得到电抗器的输入功率变化率与激励电流的关系,根据功率平衡方程
 (2)
(2)
当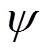 工作在线性部分时,有
工作在线性部分时,有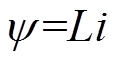 ,则式(2)可写为
,则式(2)可写为

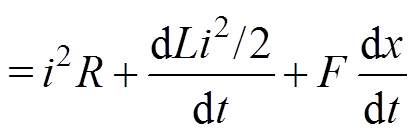 (3)
(3)
式中,x为气隙长度;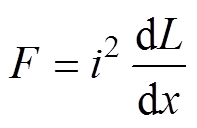 为电磁力。由式(3)可知,外界输入功率主要分布在导线损耗功率、磁场中储存的电磁功率和电抗器振动的机械功率三个方面。在电抗器运行过程中,铜导线损耗的功率与电抗器振动的机械功率相对于输入的功率很小,所以输入的功率大部分都转换成磁场中储存的电磁功率,则式(3)可简化为
为电磁力。由式(3)可知,外界输入功率主要分布在导线损耗功率、磁场中储存的电磁功率和电抗器振动的机械功率三个方面。在电抗器运行过程中,铜导线损耗的功率与电抗器振动的机械功率相对于输入的功率很小,所以输入的功率大部分都转换成磁场中储存的电磁功率,则式(3)可简化为
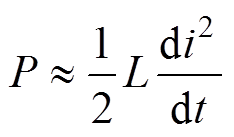 (4)
(4)则
 (5)
(5)
令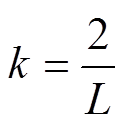 ,得
,得
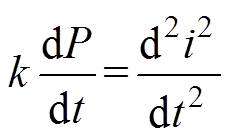 (6)
(6)根据式(1)、式(6)得
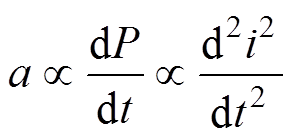 (7)
(7)
因此,如果使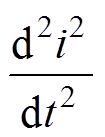 减小,则电抗器的输入功率变化率
减小,则电抗器的输入功率变化率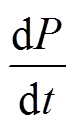 降低,则电抗器的振动加速度
降低,则电抗器的振动加速度 也会降低。
也会降低。
电抗器中注入谐波会改变其输入电流的波形,其功率变化率波形也会发生改变。因此适当地在电抗器中注入谐波会降低电抗器输入功率的变化率,进而降低其振动加速度。本文提出在基波激励的基础上叠加3次和5次反向谐波激励的方法来达到减小串联电抗器振动加速度的目的。所施加的激励电流为
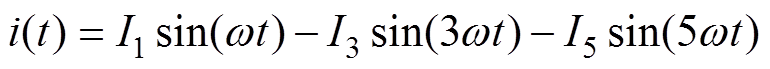 (8)
(8)式中,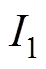 为基波激励电流的峰值;
为基波激励电流的峰值;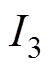 和
和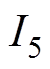 分别为3次和5次谐波激励电流的峰值;
分别为3次和5次谐波激励电流的峰值;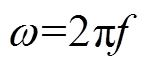 ,
,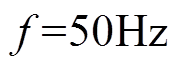 。
。
遗传算法是一种通过模拟自然进化过程搜索最优解的方法。该方法采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则[16]。
根据第1.1节所述,为了降低电抗器的电磁振动,要求叠加谐波激励时电抗器的功率变化率要小于只有基波激励时的功率变化率,即应该寻找使输入功率变化率峰值达到最小时的谐波注入量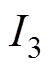 和
和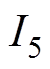 。本文所选串联电抗器的激励电流为20A,即
。本文所选串联电抗器的激励电流为20A,即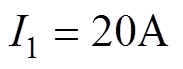 。根据式(6)、式(8),可令
。根据式(6)、式(8),可令
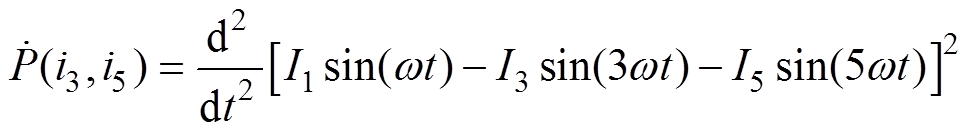 (9)
(9)得出串联电抗器注入谐波激励最优化数学模型为
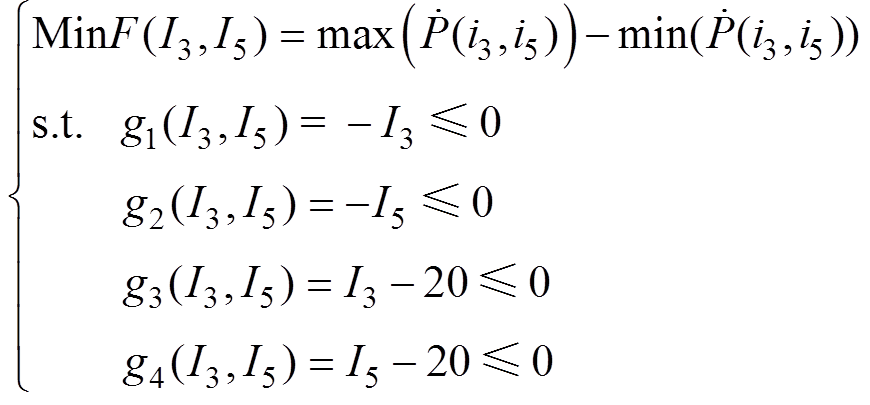 (10)
(10)
式中,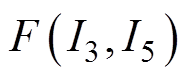 为目标函数式;
为目标函数式;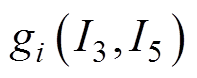
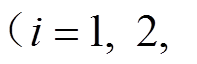
 为约束条件;预设的迭代次数为1 000次,最终得到的具有最大适应度的
为约束条件;预设的迭代次数为1 000次,最终得到的具有最大适应度的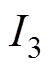 、
、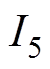 作为最优解输出。经计算最优解为
作为最优解输出。经计算最优解为 ,
,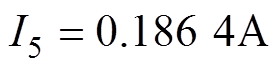 ,3次和5次谐波注入量分别只占基波激励的0.143 5%和0.932 0%,此时功率变化率正负峰值之差最小,为
,3次和5次谐波注入量分别只占基波激励的0.143 5%和0.932 0%,此时功率变化率正负峰值之差最小,为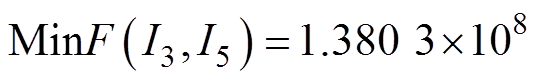 。因为3次、5次谐波注入量相对于基波主激励非常小,所以可忽略其对电抗器的影响。
。因为3次、5次谐波注入量相对于基波主激励非常小,所以可忽略其对电抗器的影响。
注入谐波后的功率变化率采集电路如图1所示,电阻R和电感L模拟了电抗器绕组的内在阻抗,可通过改变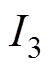 和
和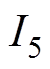 的峰值来调节谐波的注入量。
的峰值来调节谐波的注入量。
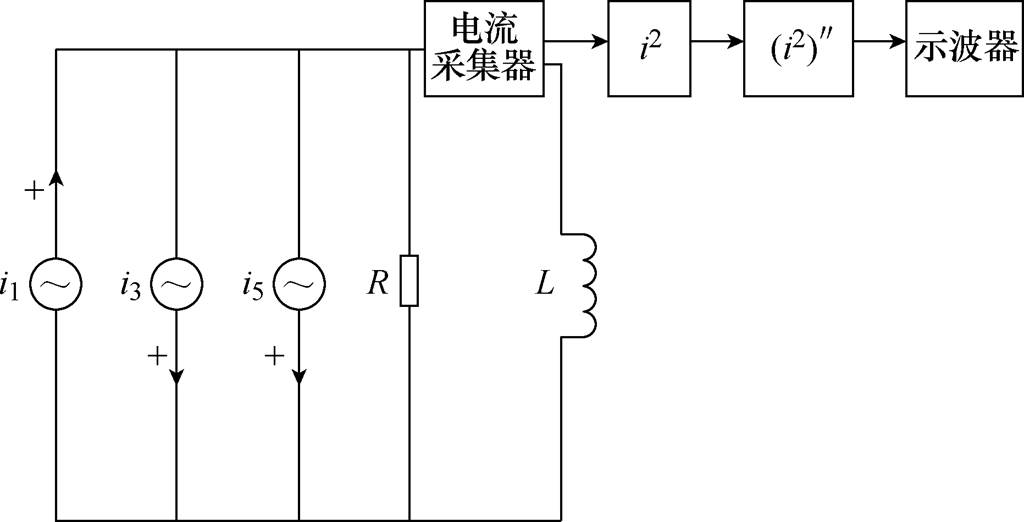
图1 功率变化率采集电路
Fig.1 Power change rate acquisition circuit diagram
将最优的3次和5次谐波注入量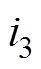 和
和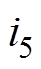 输入功率变化率电路,分别得到基波及注入谐波激励时的功率变化率,如图2所示。
输入功率变化率电路,分别得到基波及注入谐波激励时的功率变化率,如图2所示。
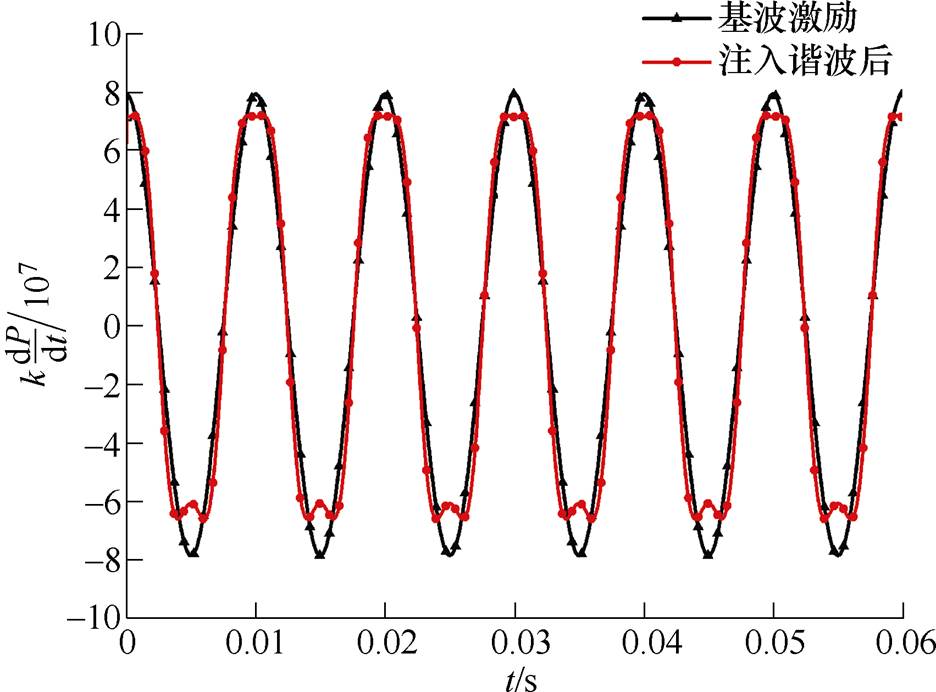
图2 基波及注入谐波激励时的功率变化率
Fig.2 Power change rate curves when fundamental wave and injected harmonic excitation
由图2可知,电抗器输入功率变化率曲线为正弦波形,周期为0.01s,注入谐波后其波形负峰值处出现小的凹槽。基波激励时,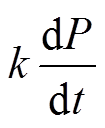 的峰值是
的峰值是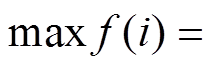
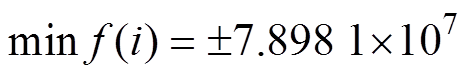 ,注入谐波后
,注入谐波后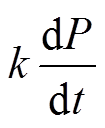 的正负峰值分别为
的正负峰值分别为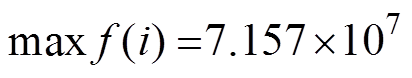 、
、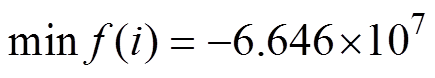 ,注入谐波后电抗器的输入功率变化率的平均幅值减小12.62%。
,注入谐波后电抗器的输入功率变化率的平均幅值减小12.62%。
为准确计算注入谐波前后电抗器的振动特性,本文建立电抗器铁心的磁-机械耦合模型,根据有限元法对电抗器铁心注入谐波前后振动特性进行 分析。
铁心系统的总能量包括磁场能、电流位能、应变能、麦克斯韦力所做的功。其能量泛函可表示为
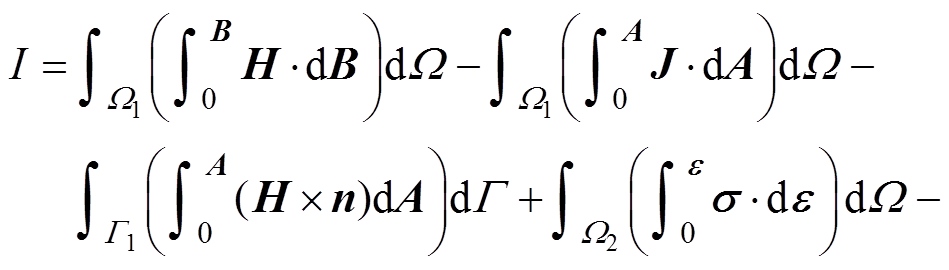
 (11)
(11)
式中,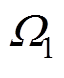 、
、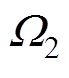 分别为电磁场和机械场的分析域;
分别为电磁场和机械场的分析域;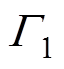 、
、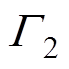 分别为磁场和机械场的边界;
分别为磁场和机械场的边界;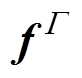 、
、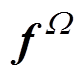 分别为机械场的外表面力密度和外体积力密度;B为磁通密度;H为磁场强度;
分别为机械场的外表面力密度和外体积力密度;B为磁通密度;H为磁场强度;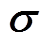 、
、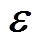 、
、 分别为应力、应变张量、振动位移;J为电流密度;A为矢量磁位。
分别为应力、应变张量、振动位移;J为电流密度;A为矢量磁位。
将泛函的变分问题转化为多元函数求极值的问题。泛函求取极值的条件为
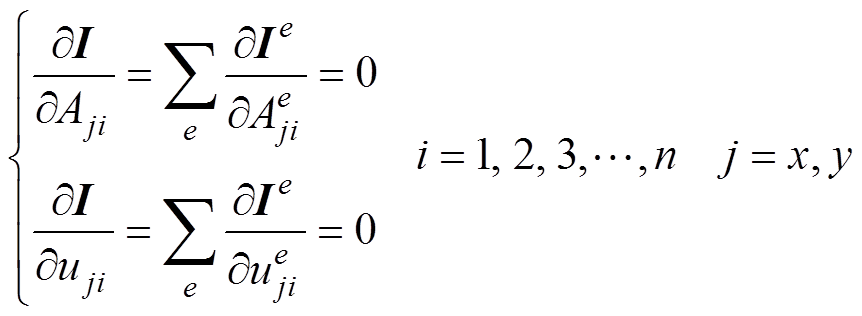 (12)
(12)式中,x、y为坐标轴方向。
由此形成的整体的有限元离散方程为
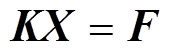 (13)
(13)式中,K为磁-机械刚度矩阵系数;X为矢量磁位A与振动位移u组成的位置列矩阵;F为由电流密度J、外表面力密度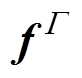 和外体积力密度
和外体积力密度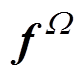 组成的列矩阵。通过求解该矩阵方程即可求得节点矢量磁位A和振动位移u,进而求得磁通密度和振动加速度分布。
组成的列矩阵。通过求解该矩阵方程即可求得节点矢量磁位A和振动位移u,进而求得磁通密度和振动加速度分布。
建立电抗器的几何模型,本文采用三柱铁心结构,并忽略机械构件对本体振动的影响。电抗器铁心及绕组的结构及尺寸如图3所示。
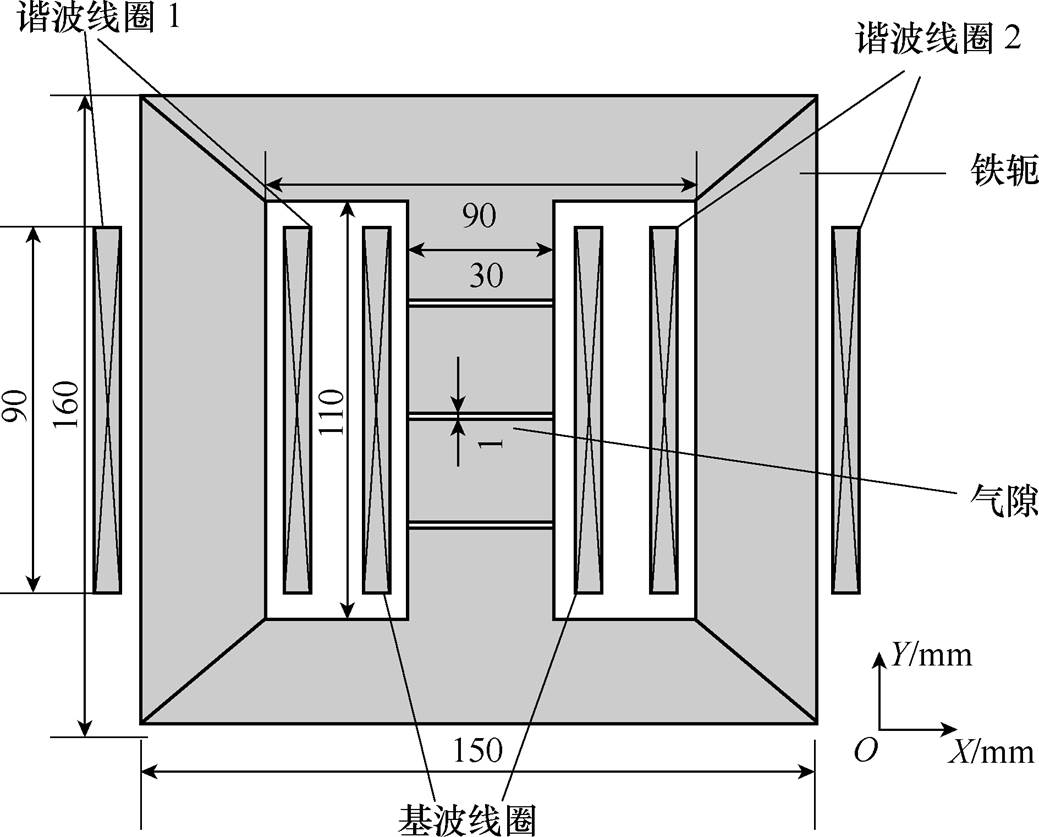
图3 串联电抗器的结构及尺寸
Fig.3 Structure and size of series reactor
中间铁心柱上缠绕的是基波激励绕组,两个谐波激励绕组分别缠绕在左右两个铁心柱周围,基波绕组与谐波绕组匝数均为31匝。将1.2节计算出的最优的等效谐波注入量I3和I5通入谐波绕组,计算注入谐波前后电抗器铁心的振动情况。
电抗器的电磁振动与其磁通密度和铁心的应力分布密切相关。经计算,得到基波激励与叠加谐波激励的电抗器在t =0.065s时的铁心磁场与应力分布分别如图4和图5所示。
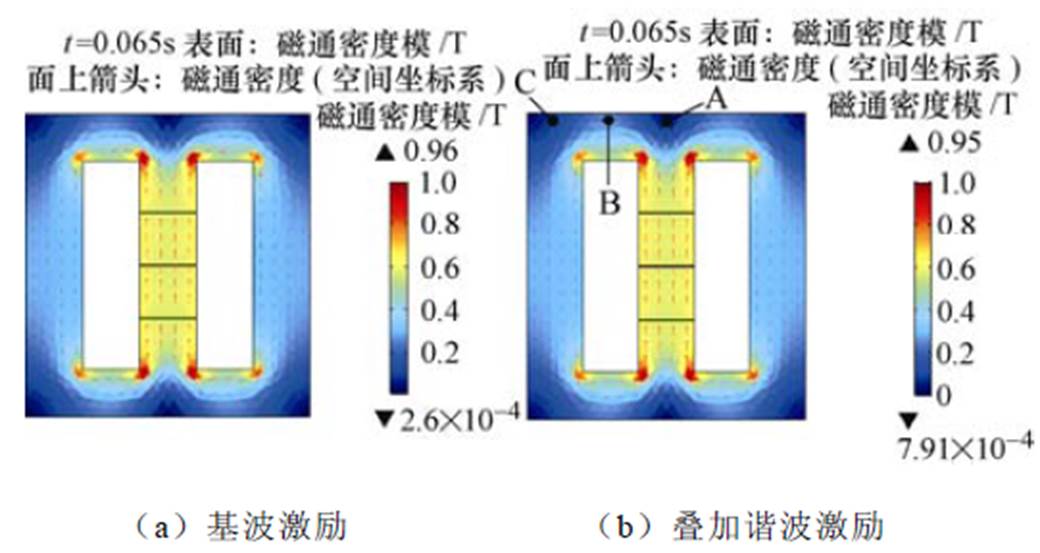
图4 t =0.065s时刻电抗器铁心磁场强度分布
Fig.4 Distribution of magnetic field strength of reactor core at t =0.065s
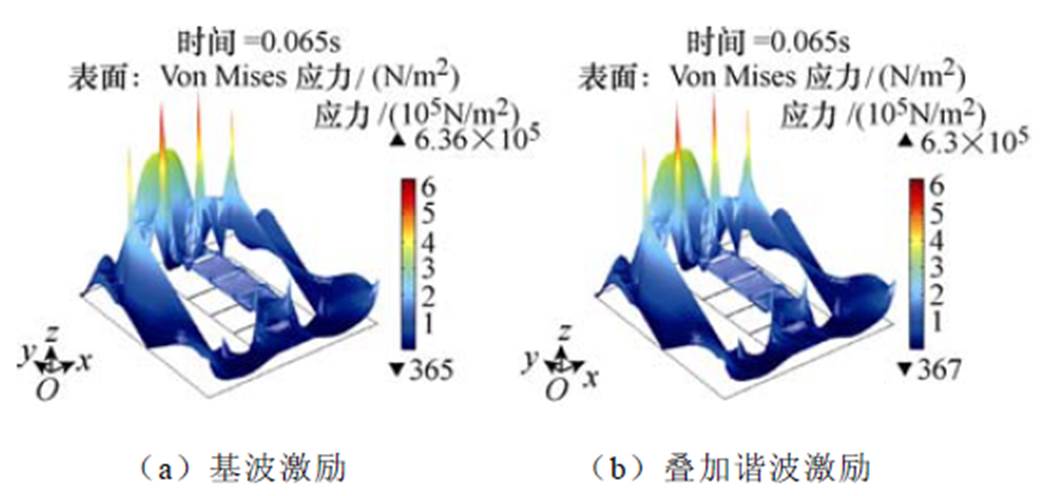
图5 t =0.065s时刻电抗器铁心应力分布
Fig.5 Stress distribution of reactor core at t =0.065s
根据图4可知,磁场密度在铁心中柱及拐角处分布较为集中,在铁心拐角处磁通密度最大为0.96T,注入谐波后最大磁通密度略微减小为0.95T,因此谐波的注入对电抗器的电感值几乎没有影响。根据图5可知,应力主要集中在气隙处、拐角处以及铁心上表面,铁心内部应力形成这种分布特性主要是由于铁心的气隙结构造成的,叠加谐波激励后铁心最大应力有所减小。
由于电抗器气隙及铁心外有线圈及绝缘材料包围,实验时无法对其气隙与拐角处的振动加速度进行测量。为保证实验与仿真的测试点相同,根据电抗器铁心的左右几何结构对称以及励磁条件对称等特性对电抗器铁心中柱上方的测试点A、铁轭上方的测试点B、铁心左柱上方的测试点C的振动加速度进行测量,三点位置如图4b所示。图6分别给出了A、B、C三点基波激励与注入谐波后电抗器铁心的振动加速度的对比曲线。
从图6可以明显看出,注入谐波后电抗器铁心表面振动加速度波形的峰值处出现凹槽,这正与电抗器注入谐波后的功率变化率曲线(见图2)相对应。同时,注入谐波后电抗器铁心表面振动加速度均有了明显的减小。为了反映加速度曲线整体的变化情况,用加速度曲线峰-峰值app来表示电抗器铁心的振动幅度,即

图6 基波与注入谐波激励时的振动加速度曲线
Fig.6 Vibration and acceleration curves of fundamental wave and injected harmonic excitation
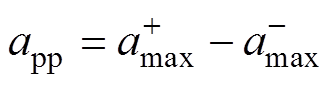 (14)
(14)式中,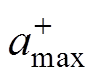 、
、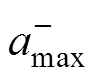 分别为加速度曲线在一个周期内的最大值和最小值。根据此计算方法得到注入谐波前后的加速度曲线峰-峰值,对比结果见表1。
分别为加速度曲线在一个周期内的最大值和最小值。根据此计算方法得到注入谐波前后的加速度曲线峰-峰值,对比结果见表1。
表1 加速度平均幅值对比
Tab.1 Acceleration average amplitude comparison

参数点A加速度平均振幅/(m/s2)点B加速度平均振幅/(m/s2)点C加速度平均振幅/(m/s2) 基波激励0.090 50.063 20.016 8 注入谐波后0.078 80.055 20.014 6 减振效果(%)12.9312.6613.10
根据对比情况可知,注入谐波后的电抗器A、B、C三点的综合平均减振效果为12.90%,这也说明了注入谐波的主动减振方法是可行的。
为了验证理论分析的正确性,本文对串联电抗器在基波与注入最优谐波量两种激励方式下进行了振动对比实验测试,振动测试系统实验如图7所示。谐波发生器与两个谐波绕组串联提供谐波激励,同时调节谐波激励电流的输出相位,使其与通入基波绕组的电流的相位相同。
为保证实验条件与仿真条件相一致,利用振动加速度传感器对电抗器上的A、B、C三点进行测量,测试点位置如图4b所示。图8给出了基波激励与注入谐波后电抗器的振动加速度随时间变化的对比曲线。
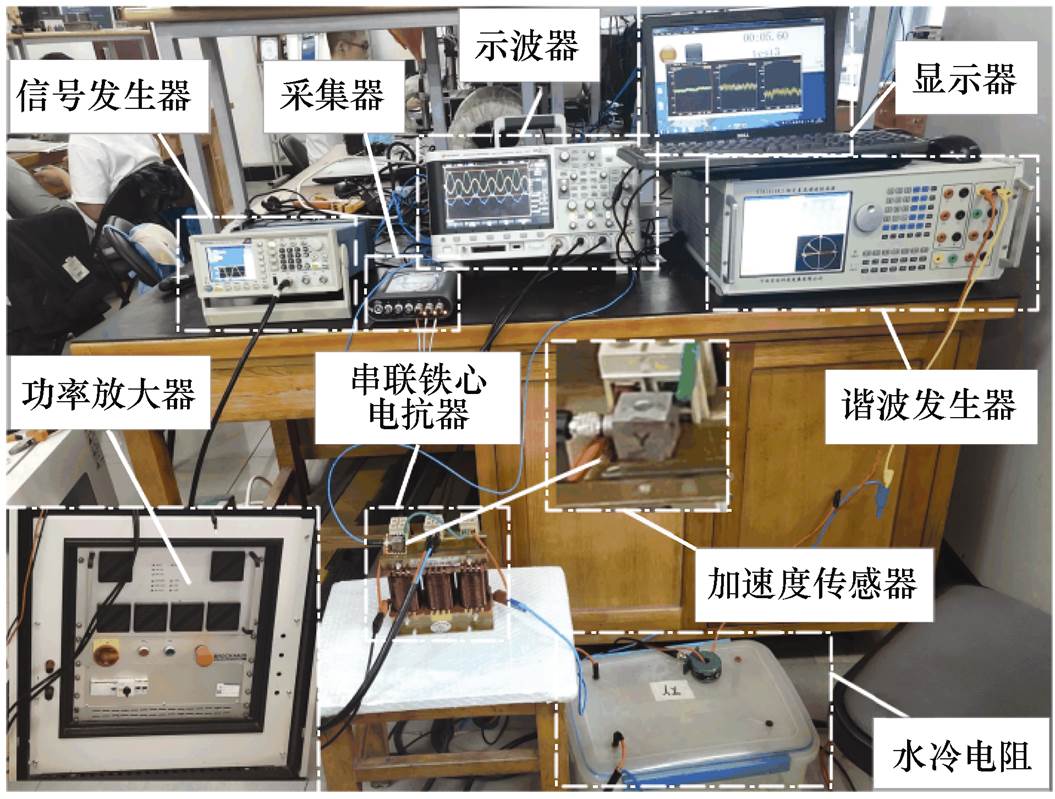
图7 串联电抗器振动实验
Fig.7 Series reactor vibration experiment diagram
对比仿真和实验测试结果,实验测得的振动加速度波形不是严格的正弦波形,且实验测得的振动加速度幅值要稍大于仿真的加速度幅值,这主要是由于实测振动加速度不仅包含电磁振动加速度,还包括了机械振动、仪器的安装和固定等各种因素对振动加速度的影响。从总体来看,测量结果与仿真结果的波形趋势基本一致。注入谐波后,电抗器铁心表面振动加速度的平均幅值减小12.75%。
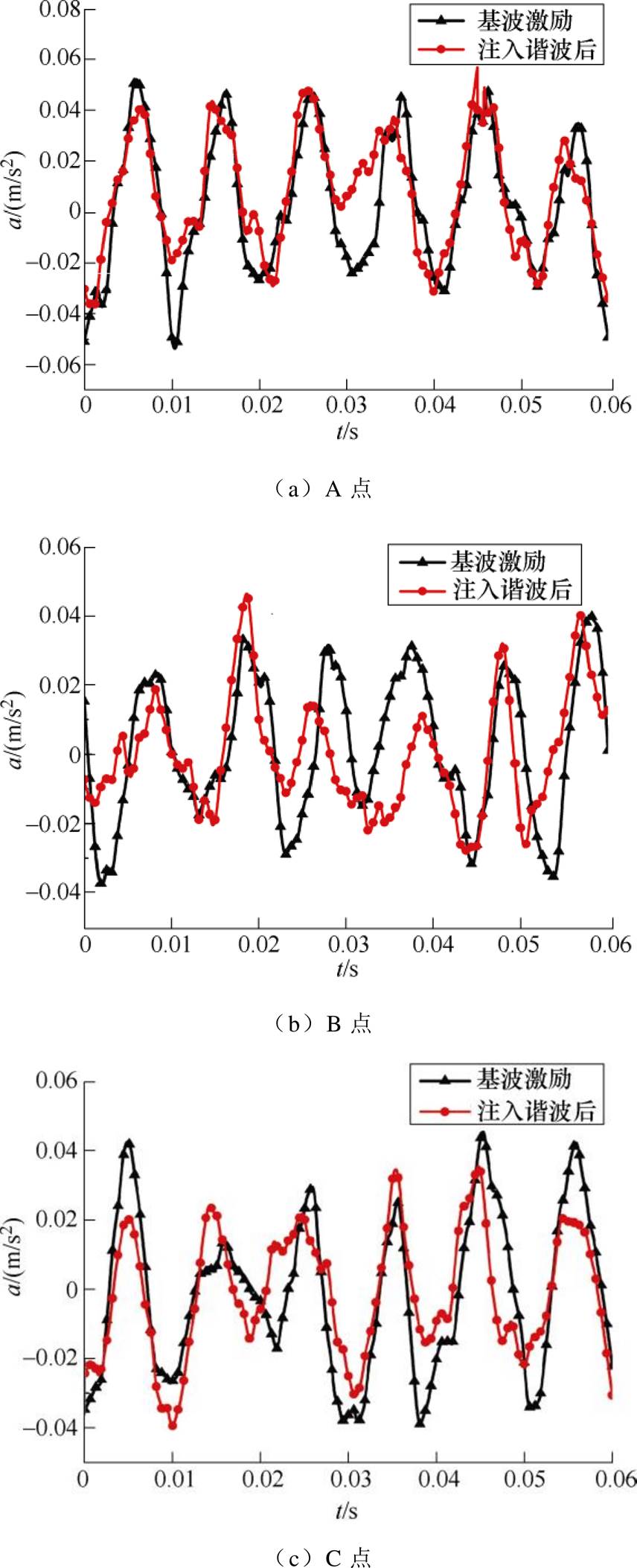
图8 基波与注入谐波激励时的振动加速度对比曲线
Fig.8 Vibration and acceleration curves of fundamental wave and injected harmonic excitation
为了更好地分析注入谐波后对各频率振动加速度的影响,对实验数据进行频谱分析如图9所示。可以看出,100Hz为主要振动频率,注入谐波后主频振动均有减小,虽然有的频率振动加速度幅值增大,但是从整体来看注入谐波后,电抗器的振动加速度是减小的。
综上所述,此实验结果有效地验证了理论分析的正确性,即注入谐波的主动减振方法是可行的。
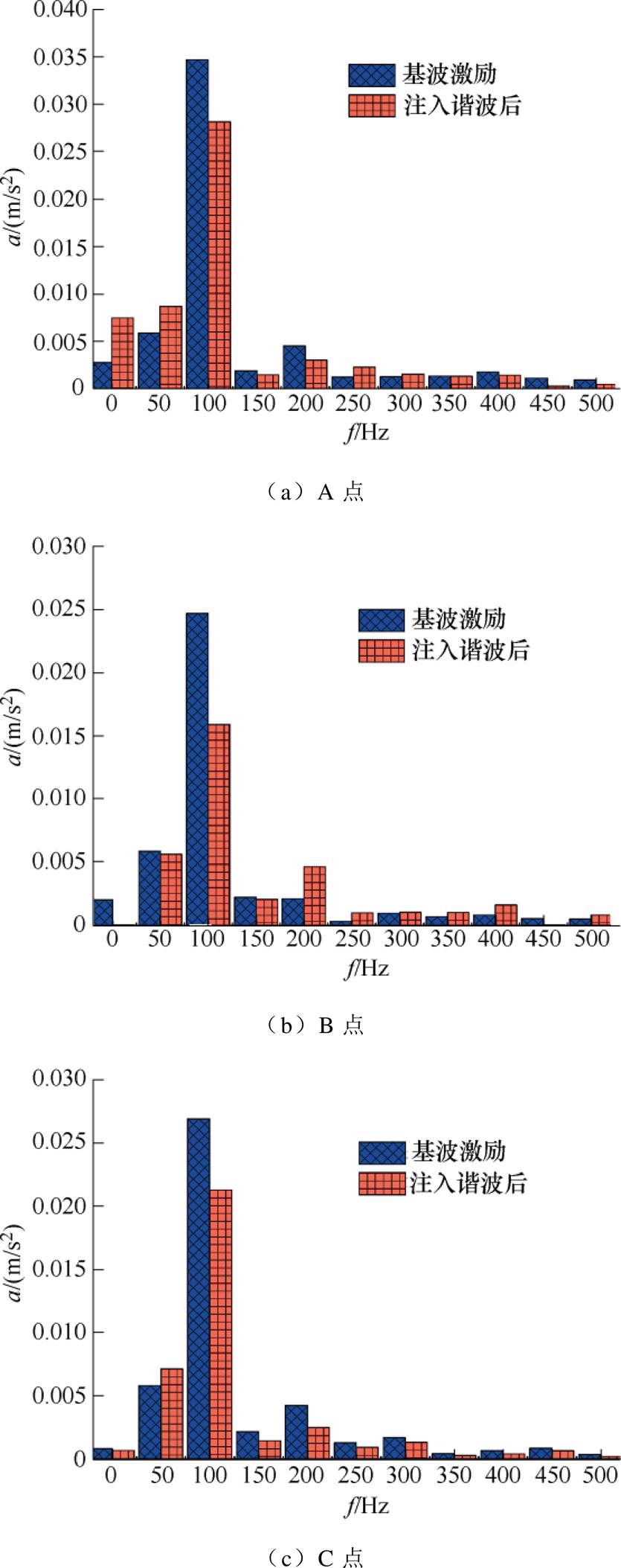
图9 振动加速度的频谱分析
Fig.9 Spectrum analysis of vibration acceleration
电抗器的振动问题一直制约着电抗器的发展和应用。目前的减振措施主要为被动减振,无法从根源上减小电磁振动。因此,本文提出一种基于谐波注入的主动减振方法。
1)根据串联电抗器的振动加速度与其输入功率变化率的正比例关系提出通过增加3次和5次谐波激励来减小电抗器的输入功率变化率,进而减小电抗器铁心的振动加速度。并通过遗传算法计算出最优的谐波注入量为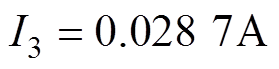 ,
,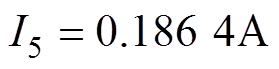 。
。
2)建立串联电抗器的电磁-机械耦合模型,用数值方法计算电抗器铁心的振动加速度。得出注入谐波后,在t =0.065s时刻,电抗器铁心磁通密度略微减小,铁心应力集中分布在气隙处、拐角处以及铁心上表面,最大应力减小,且电抗器的振动加速度明显减小,平均减振效果为12.90%。
3)搭建串联电抗器振动实验平台,得到注入谐波后电抗器的减振效果为12.75%,验证了仿真结果的正确性,证明该方法对电抗器的减振降噪有很好的效果。
参考文献
[1] 周明, 曹炜, 陈文涛, 等. 串联电抗器对电力系统短路电流特性影响的研究[J]. 电力系统保护与控制, 2017, 45(11): 147-153.
Zhou Ming, Cao Wei, Chen Wentao, et al. Study on influence of series reactor on power system short-circuit current characteristics[J]. Power System Protection and Control, 2017, 45(11): 147-153.
[2] 张鹏宁, 李琳, 程志光, 等. 并联电抗器与变压器模型铁心振动仿真与试验对比[J]. 电工技术学报, 2018, 33(22): 5273-5281.
Zhang Pengning, Li Lin, Cheng Zhiguang, et al. Vibration simulation and experiment comparison of shunt reactor and transformer model core[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(22): 5273-5281.
[3] Yan Rongge, Gao Xu, Zhu Lihua, et al. Research on three- dimensional stress distribution of reactor core[J]. IEEE Transactions on Applied Supercondu- ctivity, 2016, 26(4): 1-4.
[4] 张鹏宁, 李琳, 聂京凯, 等. 考虑铁心磁致伸缩与绕组受力的高压并联电抗器振动研究[J]. 电工技术学报, 2018, 33(13): 3130-3139.
Zhang Pengning, Li Lin, Nie Jingkai, et al. Study on the vibration of high voltage shunt reactor con- sidering of magnetostriction and winding force[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3130-3139.
[5] 祝丽花, 王斌, 刘松, 等. 不同负载对干式变压器电磁振动的影响分析[J]. 电工技术学报, 2018, 33(7): 1599-1606.
Zhu Lihua, Wang Bin, Liu Song, et al. Research on electromagnetic vibration of dry type transformer under different types of load[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1599- 1606.
[6] 胡静竹, 刘涤尘, 廖清芬, 等. 基于有限元法的变压器电磁振动噪声分析[J]. 电工技术学报, 2016, 31(15): 81-88.
Hu Jingzhu, Liu Dichen, Liao Qingfen, et al. Analysis of transformer electromagnetic vibration noise based on finite element method[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 81-88.
[7] 徐征宇, 李金忠, 葛栋, 等. 特高压并联电抗器高性能隔声装置研制[J]. 高电压技术, 2018, 44(7): 2276-2283.
Xu Zhengyu, Li Jinzhong, Ge Dong, et al. Deve- lopment of high performance sound insulation device for UHV shunt reactor[J]. High Voltage Engineering, 2018, 44(7): 2276-2283.
[8] Ishikawa T, Sugiyama H, Baba E, et al. Reactor vibration analysis in consideration of coupling between the magnetic field and vibration[J]. Industry Applications Conference, 2004, 2(5): 872-877.
[9] Gao Yanhui, Nagata M, Muramatsu K, et al. Noise reduction of a three-phase reactor by optimization of gaps between cores considering electromagnetism and magnetostriction[J]. IEEE Transactions on Magnetics, 2011, 47(10): 2772-2775.
[10] Gao Yanhui, Muramatsu K, Hatim M J, et al. Design of a reactor driven by inverter power supply to reduce the noise considering electromagnetism and magneto- striction[J]. IEEE Transactions on Magnetics, 2010, 46(6): 2179-2182.
[11] 常晨, 刘兰荣, 卢美林, 等. 并联电抗器等效模型的振动噪声特性试验研究[J]. 电气技术, 2019, 20(2): 37-47.
Chang Chen, Liu Lanrong, Lu Meilin, et al. Investigates the characteristics of vibration and noisebased on the equivalent model to shunt reactor[J]. Electrical Engineering, 2019, 20(2): 37-47.
[12] Zhu Lihua, Yang Qingxin, Yan Rongge, et al. Numerical computation for a new way to reduce vibration and noise due to magnetostriction and magnetic forces of transformer cores[J]. Journal of Applied Physics, 2013, 113(17): 17A333.
[13] 闫荣格, 赵路娜, 贲彤, 等. 70基于负超磁致伸缩效应电抗器减振新方法的研究[J]. 振动与冲击, 2018, 37(19): 254-258.
Yan Rongge, Zhao Luna, Ben Tong, et al. A new vibration reduction method for reactors using NGMM[J]. Journal of Vibration and Shock, 2018, 37(19): 254-258.
[14] Yan Rongge, Liu Weiying, Wu Yuechao, et al. Reactor vibration reduction based on giant magneto- strictive materials[J]. AIP Advances, 2017, 7(5): 056677.
[15] Castano Sanchez S, Bilgin B, Lin J, et al. Radial forces and vibration analysis in an external-rotor switched reluctance machine[J]. IET Electric Power Applications, 2016, 11(2): 252-259.
[16] 肖曦, 许青松, 王雅婷, 等. 基于遗传算法的内埋式永磁同步电机参数辨识方法[J]. 电工技术学报, 2014, 29(3): 21-26.
Xiao Xi, Xu Qingsong, Wang Yating, et al. Parameter identification of interior permanent magnet synchronous motors based on genetic algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 21-26.
Research on Vibration Reduction of Series Reactor Based on Harmonic Injection
Abstract Vibration and noise reduction are important factors that need to be considered during the production and application of reactors. However, most of the current damping methods focus on passive vibration reduction, which cannot reduce the electromagnetic vibration from the root causes. Therefore, an active vibration reduction method based on harmonic injection is proposed for the series reactor. Firstly, according to the positive proportional relationship between the vibration acceleration of the series reactor and the change rate of input power, the relationship between the change rate of power and the input current was deduced. Because the input harmonics in the reactor could change the waveform of the input current, it was proposed to reduce the change rate of power of the reactor by increasing the reverse odd harmonic excitation, thereby suppressing the vibration of the reactor. The optimal harmonic injection amount was calculated by genetic algorithm. Then, the electromagnetic- mechanical coupling model of the series reactor was established, and the electromagnetic vibration of the core of the reactor was calculated based on the finite element method. The comprehensive average damping effect of the series reactor after harmonic injection is 12.90%. Finally, the vibration test platform of series reactor was built. The damping effect of the reactor after harmonic injection is 12.75%, which verifies the correctness of the simulation results. The simulation and experiment show that the method has a good effect on the vibration reduction of the reactor.
keywords:Series reactor, electromagnetic vibration, change rate of power, harmonic injection, vibration reduction
中图分类号:TM47
DOI: 10.19595/j.cnki.1000-6753.tces.190807
收稿日期2019-07-02
改稿日期 2019-08-28
国家自然科学基金资助项目(51777054)。
闫荣格 女,1969年生,教授,博士生导师,研究方向为电工理论与新技术。E-mail: yanrg@hebut.edu.cn(通信作者)
赵文月 女,1991年生,硕士研究生,研究方向为电工理论与新技术。E-mail: 1205887741@qq.com
(编辑 崔文静)