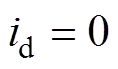 ,则定子矢量方向与永磁体磁场方向在空间上正交的。电磁推力方程为
,则定子矢量方向与永磁体磁场方向在空间上正交的。电磁推力方程为摘要 针对永磁直线同步电动机(PMLSM)伺服系统中易受不确定性因素影响的问题,该文提出一种自适应加加速度控制(AJC)方法。首先建立含有不确定性的PMLSM伺服系统动态方程。然后,通过模型前馈控制补偿系统的参数不确定性所产生的模型误差,提高系统的响应速度。最后,采用AJC抑制系统中外部扰动、非线性摩擦力等不确定性因素,自适应律使鲁棒增益收敛于有界范围内,提高系统的鲁棒性;AJC的输出信号积分后形成了反馈控制律,削弱了控制律中开关函数激励未建模动态引起的高频谐振,保证了控制信号的稳定性和连续性。系统实验结果表明,该控制方法能够产生平稳的控制信号,明显地提高系统的控制性能,减小跟踪误差,避免高频振荡,进而改善PMLSM伺服系统的控制精度。
关键词:永磁直线同步电动机 不确定性 自适应加加速度控制 鲁棒性
永磁直线同步电动机(Permanent Magnet Linear Synchronous Motor, PMLSM)取消了滚珠丝杠等机械传动环节,具有结构简单、推力平稳、定位精确、响应快速等优点[1]。因此,PMLSM广泛应用于工业机器人、XY平台、数控机床等高精密制造工业[2-3]。然而,伺服系统存在外部扰动、非线性摩擦、参数变化、未建模动态等不确定性因素将严重影响系统性能[4-5]。因此,必须采用具有较强鲁棒性的控制方法,以实现伺服系统稳定、快速的控制要求。
为解决不确定性因素对系统的影响,许多学者提出不同的方案对其进行补偿。文献[6]提出一种参数自适应律对扰动模型进行估计,并补偿非线性摩擦,但模型估计参数可能无法收敛。文献[7]通过自适应鲁棒控制方法对含不确定性因素的系统进行控制,然而该方法只能保证跟踪误差的有界收敛,跟踪性能可能受到影响。文献[8]提出一种自适应神经网络控制技术,但是神经网络的学习速度较慢,导致误差不能快速收敛。文献[9]通过滑模控制(Sliding Mode Control, SMC)抑制系统的不确定性,然而滑模控制中不连续控制效果产生的抖振问题并未完全解决,并可能激励未建模动态产生高频振荡[10]。由于未建模动态的激励与控制信号的加加速度相关,文献[11]提出RISE(robust integral of the sign of the error)反馈控制方法,将加加速度与控制信号的鲁棒项相关联,加加速度控制的输出信号积分后间接形成系统的反馈控制律。该方法可以产生连续的控制效果,实现了优异的控制性能。然而鲁棒增益过大将影响系统的稳定性。
为此,本文提出一种自适应加加速度控制(Adaptive Jerk Control, AJC)方法解决PMLSM伺服系统的不确定性问题。模型前馈控制用以补偿系统的参数不确定性;同时,AJC削弱了伺服系统中外部扰动、非线性摩擦、未建模动态等不确定性因素的影响,并且该方法间接产生连续、平稳的反馈控制律避免了高频振荡;AJC中的指数型自适应律使鲁棒增益快速地收敛,提高了系统的控制精度。最后通过实验验证了所提出的控制方案能够有效减小跟踪误差,满足PMLSM伺服系统的控制要求。
PMLSM采用磁场定向控制,令d轴电流分量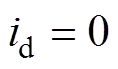 ,则定子矢量方向与永磁体磁场方向在空间上正交的。电磁推力方程为
,则定子矢量方向与永磁体磁场方向在空间上正交的。电磁推力方程为
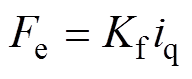 (1)
(1)式中,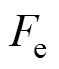 为电磁推力;
为电磁推力;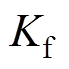 为电磁推力常数;
为电磁推力常数;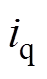 为
为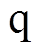 轴电流。机械运动方程为
轴电流。机械运动方程为
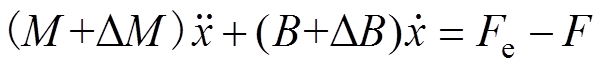 (2)
(2)
式中,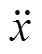 为动子加速度;
为动子加速度;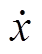 为动子速度;
为动子速度;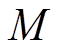 为动子总质量;
为动子总质量;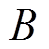 为黏滞摩擦因数;
为黏滞摩擦因数;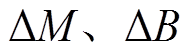 分别为
分别为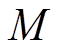 与
与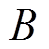 参数变化的不确定量;
参数变化的不确定量;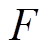 为包括外部扰动、摩擦力、未建模动态等扰动。
为包括外部扰动、摩擦力、未建模动态等扰动。
根据式(1)和式(2)得到PMLSM的动态方程为
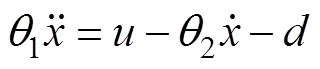 (3)
(3)式中,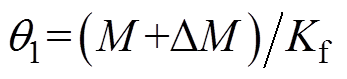 ;
;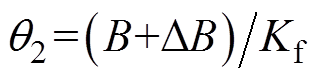 ;d=F/Kf;伺服系统的控制律为u=iq。
;d=F/Kf;伺服系统的控制律为u=iq。
为确保PMLSM伺服系统的精确位置跟踪,避免高频振荡,控制信号应该平稳、连续;同时,在含有参数变化、外部扰动等不确定性的情况下控制信号应具有快速的动态响应。为兼顾稳定性与快速性,设计一种AJC方法。PMLSM的AJC系统框图如图1所示。
定义滤波误差向量为
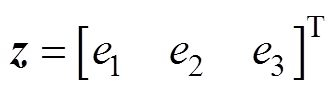 (4)
(4)其中
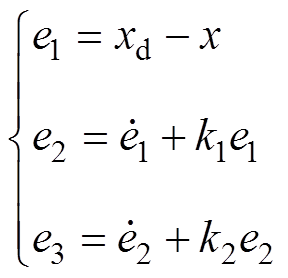 (5)
(5)
式中,xd为参考位置;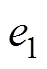 为位置跟踪误差;k1、k2为反馈增益,
为位置跟踪误差;k1、k2为反馈增益,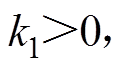
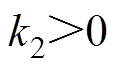 。与传统鲁棒控制不同,引入滤波误差可获得额外的设计自由度。将式(4)代入式(3)得
。与传统鲁棒控制不同,引入滤波误差可获得额外的设计自由度。将式(4)代入式(3)得
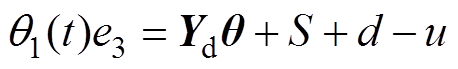 (6)
(6)式中,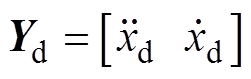 为参考位置向量;q 为系统参数向量,
为参考位置向量;q 为系统参数向量,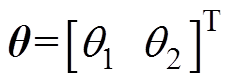 ;S为参考模型与实际模型之间动力学方程的误差,即
;S为参考模型与实际模型之间动力学方程的误差,即
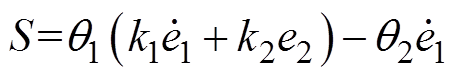 (7)
(7)
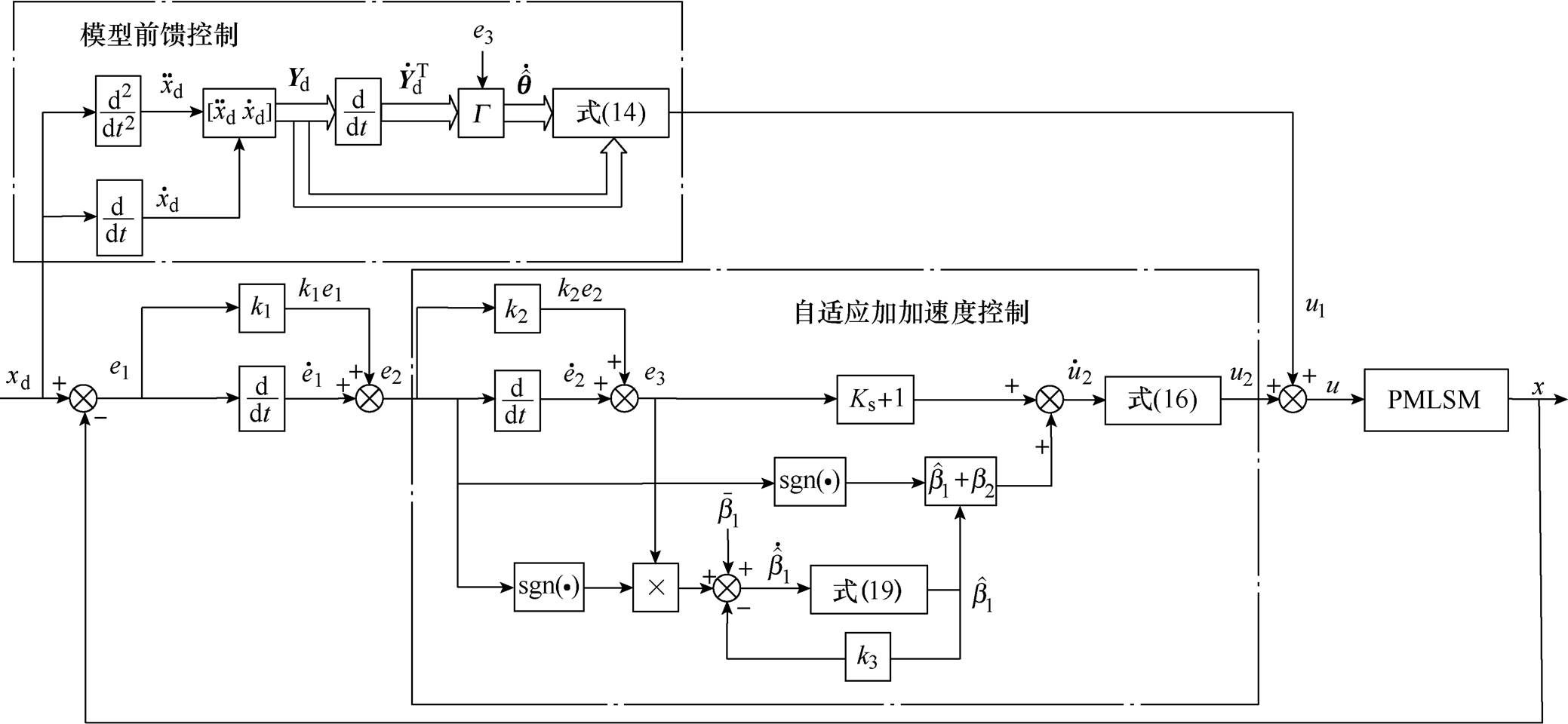
图1 PMLSM的AJC系统框图
Fig.1 Block diagram of AJC system for PMLSM
因此,根据式(6)提出一种RISE反馈控制方法,PMLSM伺服系统的控制律为
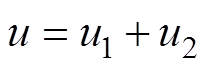 (8)
(8)式中,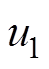 为基于模型的前馈控制律,通过参数自适应实现模型补偿,表示为
为基于模型的前馈控制律,通过参数自适应实现模型补偿,表示为
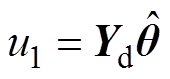 (9)
(9)
式中,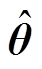 为系统参数向量的估计值;
为系统参数向量的估计值;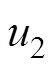 为反馈控制律,当系统存在外部扰动、摩擦力等不确定性时以确保闭环系统的稳定性。这种二自由度的控制结构减小了u1、u2之间的相互影响,便于调整控制器增益。
为反馈控制律,当系统存在外部扰动、摩擦力等不确定性时以确保闭环系统的稳定性。这种二自由度的控制结构减小了u1、u2之间的相互影响,便于调整控制器增益。
为保证反馈控制律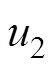 的连续性,则加加速度控制律
的连续性,则加加速度控制律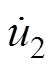 应该是有界的。因此,式(6)求导得
应该是有界的。因此,式(6)求导得
 (10)
(10)式中,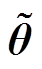 为系统的参数估计误差向量,
为系统的参数估计误差向量,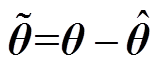 ;
;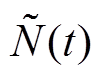 与
与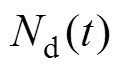 为不可测项,表示为
为不可测项,表示为
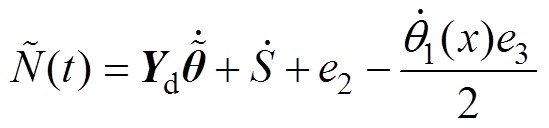 (11)
(11)
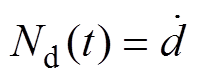 (12)
(12)采用基于梯度的自适应律对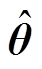 进行更新
进行更新
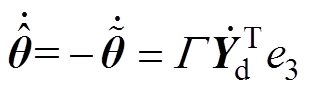 (13)
(13)
式中,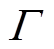 为正常数。由式(13)得到前馈控制律
为正常数。由式(13)得到前馈控制律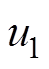 为
为
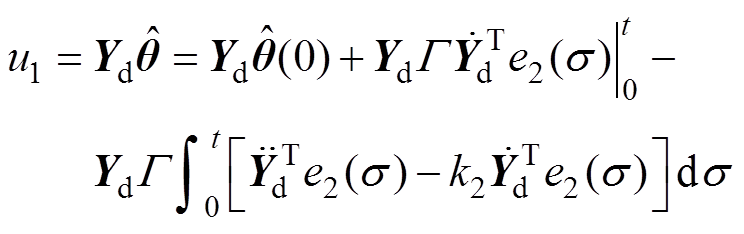 (14)
(14)设计自适应加加速度控制律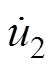 为
为
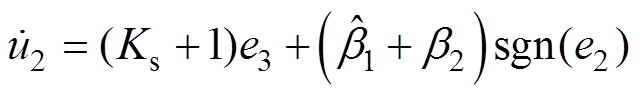 (15)
(15)式中,Ks为常数,Ks>0;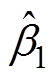 为自适应鲁棒增益;
为自适应鲁棒增益;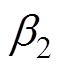 为固定鲁棒增益,并且
为固定鲁棒增益,并且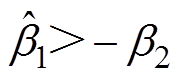 ,
,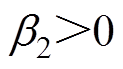 。因此反馈控制律
。因此反馈控制律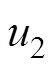 为
为
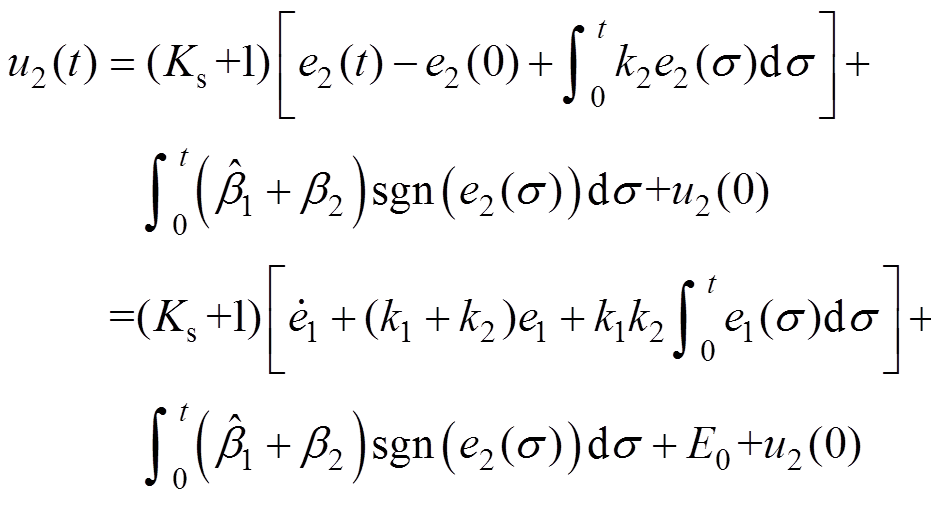 (16)
(16)
式中,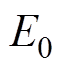 为初始条件产生的误差,即
为初始条件产生的误差,即
 (17)
(17)为避免鲁棒增益过大而产生的高频谐振,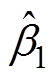 设计为
设计为
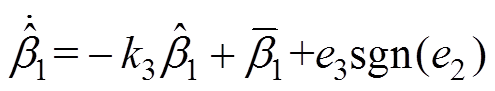 (18)
(18)
式中,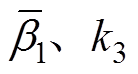 为正常数。令
为正常数。令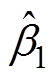 以指数方式收敛至
以指数方式收敛至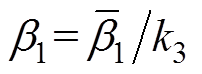 ,则
,则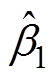 表示为
表示为
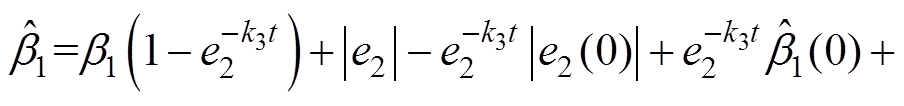
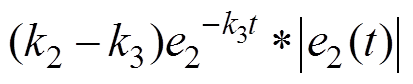 (19)
(19)
式中,“*”表示卷积运算。
由于d为二阶连续可导函数,由中值定理[12]得
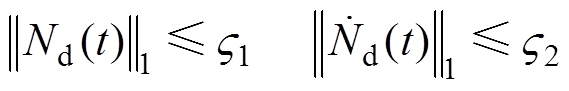 (20)
(20)式中,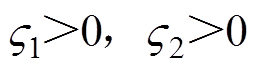 。因为
。因为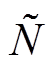 连续,则
连续,则
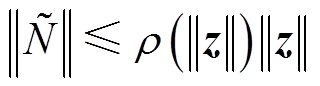 (21)
(21)
式中,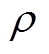 为非负递减函数。
为非负递减函数。
当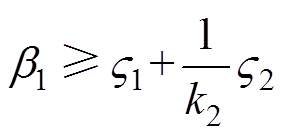 且
且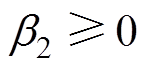 时,定义
时,定义
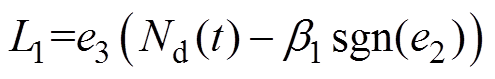 (22)
(22)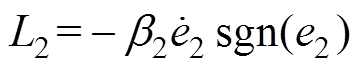 (23)
(23)
并且
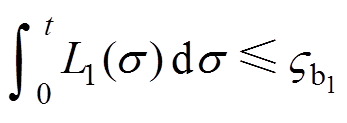 (24)
(24)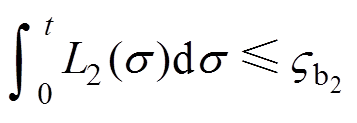 (25)
(25)
式中,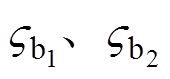 为正常数。由式(24)和式(25)得
为正常数。由式(24)和式(25)得
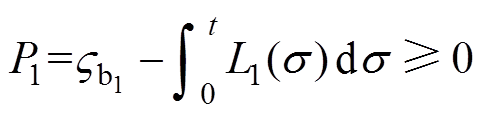 (26)
(26)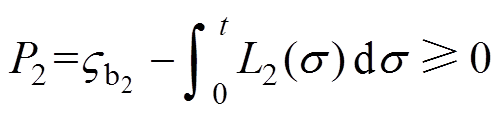 (27)
(27)
令
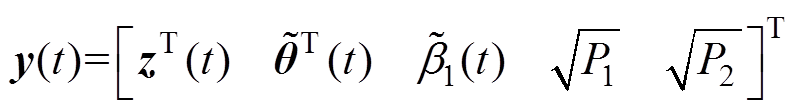 (28)
(28)选择Lyapunov函数
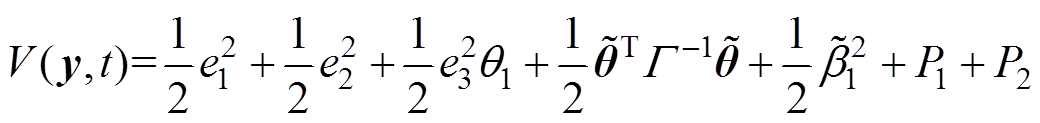 (29)
(29)
式中,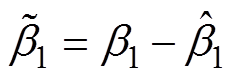 。因为
。因为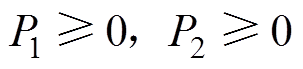 ,则
,则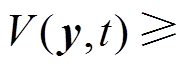 0,并且
0,并且
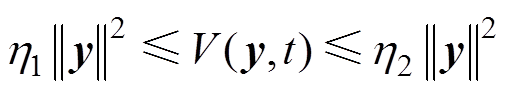 (30)
(30)式中,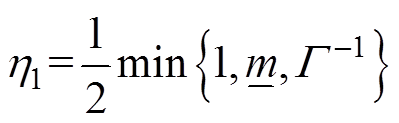 ,
,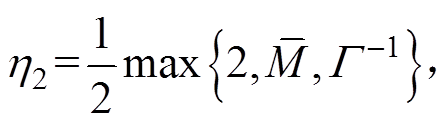
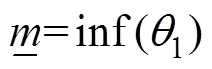 ,
, 。
。
对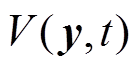 求导,得
求导,得
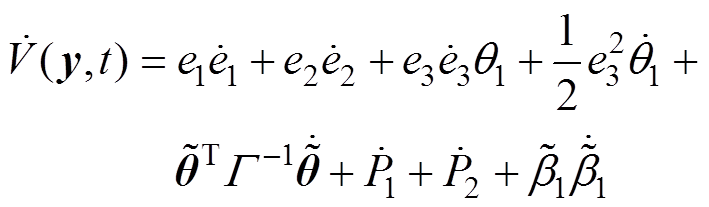 (31)
(31)将式(4)、式(10)、式(13)、式(15)、式(26)、式(27)代入式(31),得
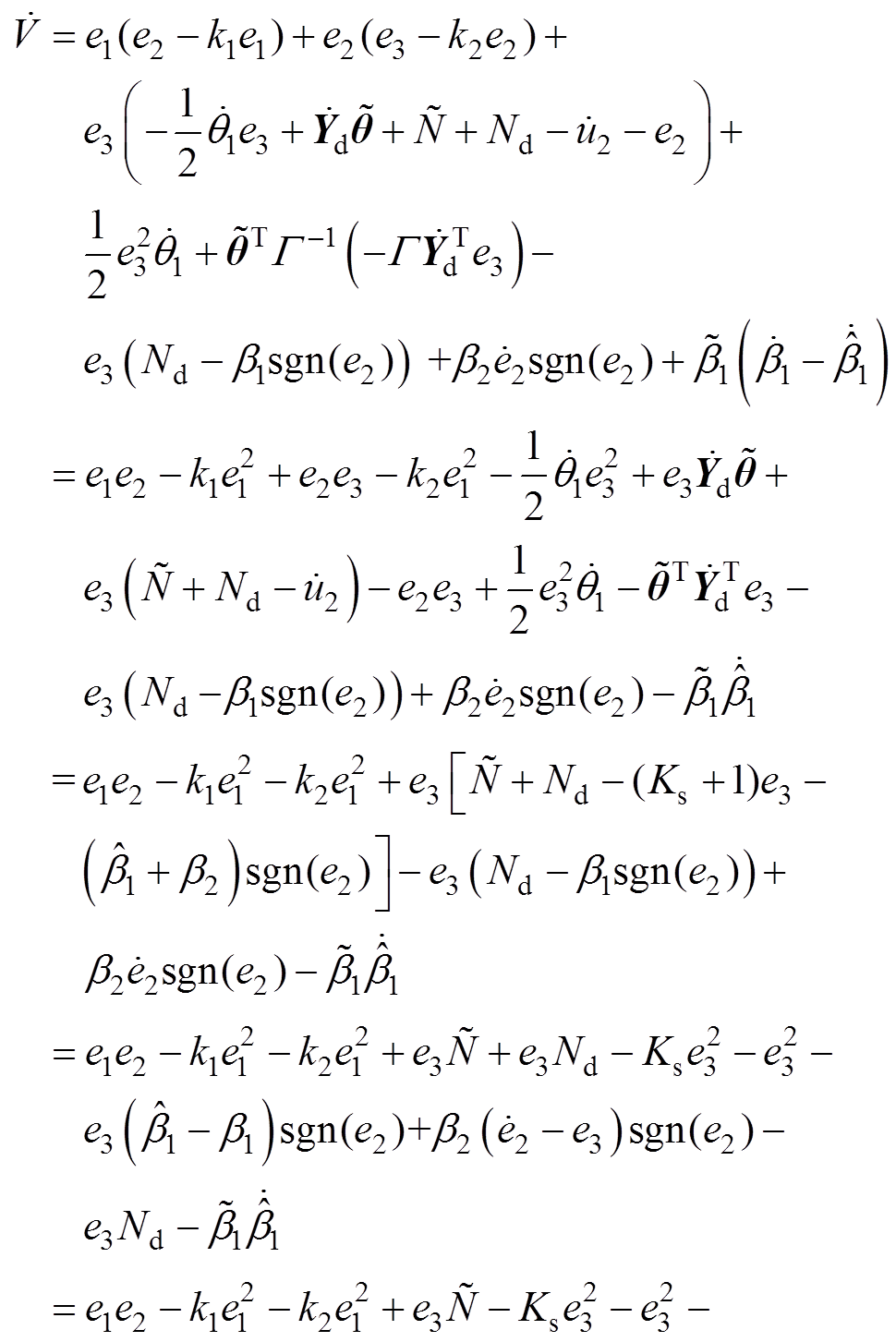
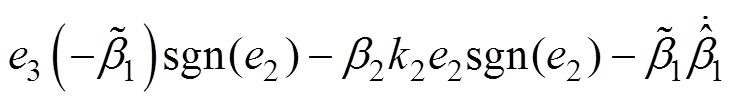 (32)
(32)因为
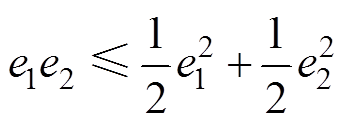 (33)
(33)
将式(33)代入式(32),并结合式(21),得

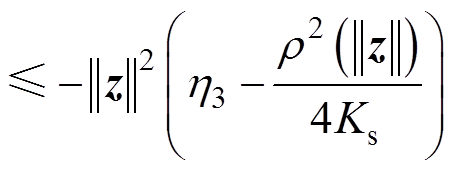 (34)
(34)
式中,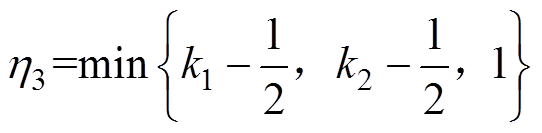 ,
,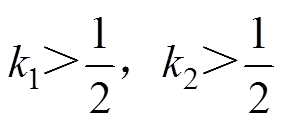 。令
。令
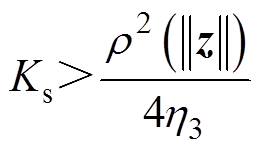 (35)
(35)则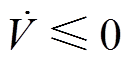 。根据Barbalat引理,当
。根据Barbalat引理,当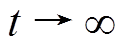 时,
时,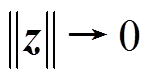 ,
,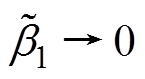 。从而保证了系统的稳定性。
。从而保证了系统的稳定性。
实验中选择型号为TMS320 F2812A的DSP作为控制算法核心,对PMLSM伺服系统进行实验研究,其硬件结构如图2所示。实验装置主要包括PMLSM、PC+DSP运算控制单元、IPM主回路功率变换单元、动子电流检测单元和直线光栅尺位置检测单元等。
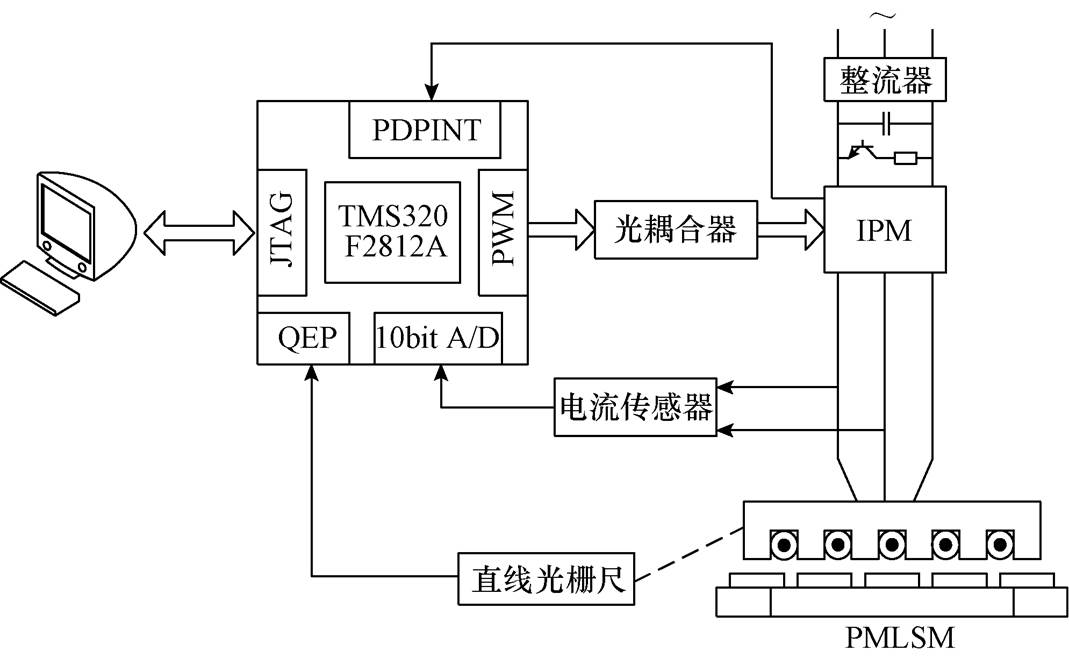
图2 基于DSP的PMLSM伺服系统硬件结构
Fig.2 Hardware structure diagram of PMLSM servo system based on DSP
为了验证本文所提出的控制方案的有效性,对系统实验进行了对比分析。PMLSM的参数为: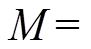
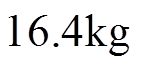 ,Kf=50.7N/A,B=8.0N·s/m。系统分别采用SMC与AJC进行实验。针对不同输入指令,反复调整控制器参数。SMC控制律设计为
,Kf=50.7N/A,B=8.0N·s/m。系统分别采用SMC与AJC进行实验。针对不同输入指令,反复调整控制器参数。SMC控制律设计为
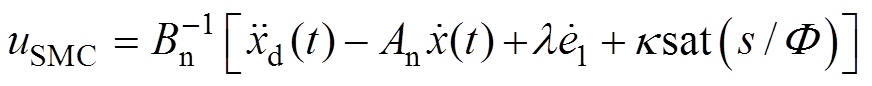 (36)
(36)
式中,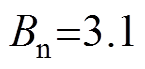 ,
,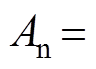
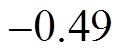 ,
,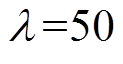 ,
,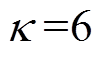 ,
,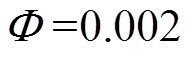 ,
,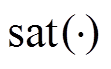 为饱和函数。AJC中相关参数选择为:
为饱和函数。AJC中相关参数选择为: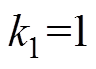 ,
,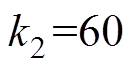 ,
,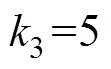 ,
,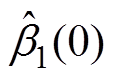 =0.6,
=0.6,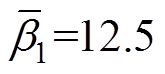 ,
,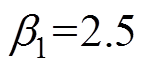 ,
,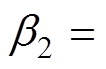
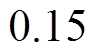 ,
,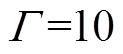 ,
,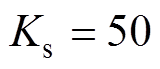 。
。
电机空载起动,并对伺服系统输入幅值为1mm的阶跃信号,待系统稳定运行之后,于第2s时在电机动子上突加50N的外部负载,观察系统的运行情况,实验结果如图3所示。由图3a和图3b可见,两种控制方法的位置跟踪误差都能较快地收敛至零附近,跟踪性能较好;当外加扰动时,SMC产生的最大跟踪误差为7.2mm,AJC产生的最大跟踪误差为4mm,表明AJC具有较强的鲁棒性;当系统处于稳态时,SMC产生的跟踪误差约为-1.5~1.4mm,AJC产生的跟踪误差约为-0.6~0.7mm。图3c和图3d为两种控制方法的控制律曲线。在电机起动时,SMC系统控制律处于-1.2~1.4之间变化,稳态时控制律约为-0.8~1.15;AJC系统控制律在初始时刻的变化范围约为-0.4~0.95,并最终稳定在0.93~1.03。图3e表明,自适应鲁棒增益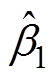 能够最终收敛于
能够最终收敛于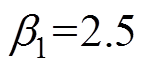 ,证明了自适应律的收敛性。因此,当系统输入阶跃信号并外加扰动的情况下,AJC能够产生更加稳定的控制信号,从而保证系统具有较强的鲁棒性能。
,证明了自适应律的收敛性。因此,当系统输入阶跃信号并外加扰动的情况下,AJC能够产生更加稳定的控制信号,从而保证系统具有较强的鲁棒性能。


图3 阶跃信号的实验结果
Fig3 Experimental results of step signal
为了进一步验证AJC的性能,对系统输入幅值为1mm、频率为2Hz的正弦信号,实验结果如图4所示。图4a和图4b中,SMC产生的最大跟踪误差约为-3.7mm,稳态时跟踪误差保持在-1.3~1.1mm;AJC产生的最大跟踪误差约为2mm,稳态时跟踪误差保持在-0.6~0.6mm。当系统处于稳定状态时,SMC系统控制律在-0.2~0.2之间波动,AJC系统控制律稳定在-0.09~0.09范围内,如图4c和图4da所示。图4e中的自适应鲁棒增益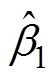 最终收敛在2.5附近。因此,当系统输入正弦信号时,AJC能够产生更平稳、连续的控制信号,跟踪误差较小,跟踪性能较好。
最终收敛在2.5附近。因此,当系统输入正弦信号时,AJC能够产生更平稳、连续的控制信号,跟踪误差较小,跟踪性能较好。

图4 正弦信号的实验结果
Fig.4 Experimental results of sinusoidal signal
为考察参数变化对系统的影响,输入幅值为1mm、频率为2Hz的正弦信号并设置电机参数为:M=32.8kg,实验结果如图5所示。由图可见,SMC产生的最大跟踪误差约为-8mm,稳态时跟踪误差保持在-2.3~2.1mm;AJC产生的最大跟踪误差约为3.5mm,稳态时跟踪误差保持在-0.9~1mm。对比图5a和图5b发现,参数的改变对SMC系统产生了较大的影响,尤其在电机的起动时刻。当系统处于稳定状态时,SMC系统控制律在1.8~3之间变动,AJC系统控制律稳定在1.9~2.5范围内,如图5c和图5d所示。因此,AJC能够较好地抑制参数变化对系统的影响。

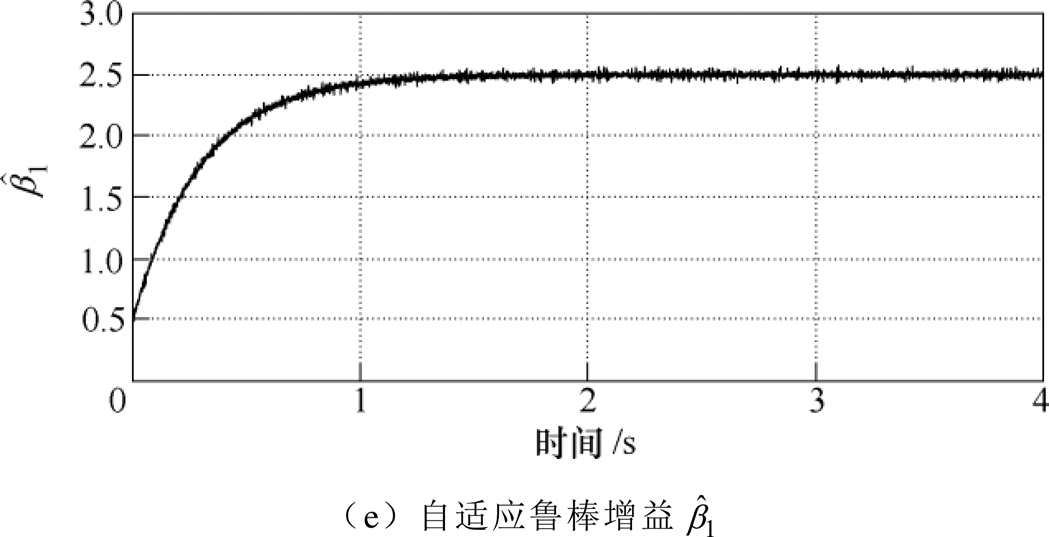
图5 变参数的实验结果
Fig.5 Experimental results of varying parameter
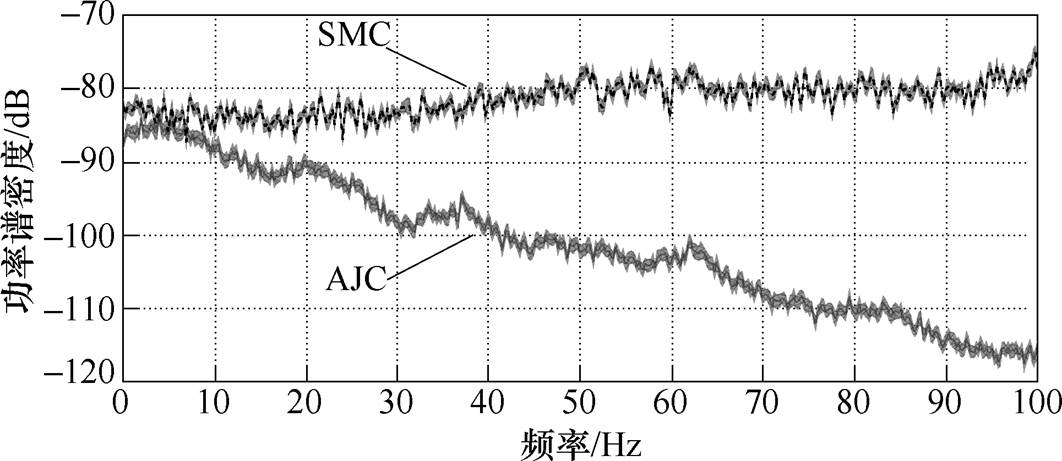
图6 速度跟踪误差的功率谱密度
Fig.6 Power spectral density of velocity tracking error
对图4中AJC系统速度跟踪误差进行Welch功率谱密度分析,结果如图6所示。阴影区域表示95%的置信区间。由图6可见,在高频处SMC的功率谱密度较大,因为开关函数和较大的鲁棒增益使得SMC产生抖振现象,影响系统的跟踪性能;而AJC的速度误差集中在0~20Hz,在高频处功率谱密度逐渐衰减,表明AJC产生的连续控制信号不会激励未建模动态中的高阶项,避免了高频振荡。
为实现PMLSM伺服系统的高精度、高速度的控制要求,考虑外部扰动、参数变化、非线性摩擦力、未建模动态等不确定性对系统的影响,提出了一种基于自适应加加速度控制器的RISE反馈控制方案。利用模型前馈控制补偿参数变化不确定性产生的模型误差;AJC形成平稳、连续的控制信号,自适应律保证了鲁棒增益的收敛性,提高系统的控制精度。实验结果表明,所采用的控制方案有效地抑制了系统的不确定性,并产生了更稳定的控制信号,显著地减小了跟踪误差。
参考文献
[1] Lu Qinfen, Mei Weihu. Recent development of linear machine topologies and applications[J]. CES Transa- ctions on Electrical Machines and Systems, 2018, 2(1): 65-72.
[2] 原浩,赵希梅. 基于积分滑模的永磁直线同步电动机直接推力控制[J]. 电工技术学报, 2019, 34(3): 39-44.
Yuan Hao, Zhao Ximei. Direct thrust force control based on integral sliding mode for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 39-44.
[3] 吴勇慷, 赵希梅. 基于函数链径向基神经网络的PMLSM自适应反推控制[J]. 电工技术学报, 2018, 33(17): 4044-4051.
Wu Yongkang, Zhao Ximei. Adaptive backstepping control based on functional link radial basis function neural network for PMLSM[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4044-4051.
[4] 智淑亚, 吴洪兵. 数控进给伺服系统摩擦补偿控制仿真[J]. 沈阳工业大学学报, 2019, 41(4): 361-365.
Zhi Shuya, Wu Hongbing. Simulation of friction compensation control of NC feed servo system[J]. Journal of Shenyang University of Technology, 2019, 41(4): 361-365.
[5] 王丽梅, 张宗雪. H型精密运动平台交叉耦合模糊PID同步控制[J]. 沈阳工业大学学报, 2018, 40(1): 1-5.
Wang Limei, Zhang Zongxue. Cross-coupled fuzzy PID synchronous control for H-type precision motion platform[J]. Journal of Shenyang University of Technology, 2018, 40(1): 1-5.
[6] Chen Zhen, Yao Bin, Wang Qingfeng. Accurate motion control of linear motors with adaptive robust compensation of nonlinear electromagnetic field effect[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(3): 1122-1129.
[7] Hu Chuxiong, Yao Bin, Wang Qingfeng. Performance- oriented adaptive robust control of a class of nonlinear systems preceded by unknown dead zone with comparative experimental results[J]. IEEE/ ASME Transactions on Mechatronics, 2013, 18(1): 178-189.
[8] Ting Chen-Sheng,Lieu Jyun-Fan, Liu Chun-Shan, et al. An adaptive FNN control design of PMLSM in stationary reference frame[J]. Journal of Control Auto- mation & Electrical Systems, 2016, 27(4): 391-405.
[9] Chen Kun Yung. Sliding mode minimum-energy control for a mechatronic motor-table system[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(3): 1122-1129.
[10] 赵希梅, 金鸿雁. 基于Elman神经网络的永磁直线同步电机互补滑模控制[J]. 电工技术学报, 2018, 33(5): 973-979.
Zhao Ximei, Jin Hongyan. Complementary sliding mode control for permanent magnet linear syn- chronous motor based on Elman neural network[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 973-979.
[11] Yao Jianyong, Deng Wenxiang, Jiao Zongxia. RISE- based adaptive control of hydraulic systems with asymptotic tracking[J]. IEEE Transactions on Auto- mation Science & Engineering, 2015, 3(14): 1524- 1531.
[12] Xian Bin, Dawson D M, Marcio de Queiroz, et al. A continuous asymptotic tracking control strategy for uncertain nonlinear systems[J]. IEEE Transactions on Automatic Control, 2004, 49(7): 1206-1211.
Adaptive Jerk Control for Permanent Magnet Linear Synchronous Motor Servo System
Abstract An adaptive jerk control (AJC) scheme was proposed in view of the susceptibility of uncertainty factors in the permanent magnet linear synchronous motor (PMLSM) servo system. Firstly, the dynamic of the PMLSM servo system with uncertainties was established. Then, the model-based feedforward control was used to compensate for the dynamic error caused by parametric uncertainties, and the response speed of the system was improved. Moreover, AJC was adopted to suppress the uncertainties such as external disturbance and nonlinear friction in the system. Robust gain was convergent following an adaptive law in a bounded range and the robustness of the system was enhanced. The output signal of AJC was integrated to form the feedback control law, which weakened the high frequency resonance caused by unmodeled dynamics of the switching function excitation, ensuring the stability and continuity of the control signal. The experimental results indicate that the control method can generate a smooth control signal and the control performance of the system is improved significantly. The tracking error is reduced and high frequency oscillation is successfully avoided. The control precision of the PMLSM servo system is more accurate.
keywords:Permanent magnet linear synchronous motor, uncertainty, adaptive jerk control, robustness
中图分类号:TP273; TM351
DOI: 10.19595/j.cnki.1000-6753.tces.190675
辽宁省自然科学基金计划重点项目(20170540677)和辽宁省教育厅科学技术研究项目(LQGD2017025)资助。
收稿日期2019-06-05
改稿日期 2019-09-29
原 浩 男,1992年生,博士研究生,研究方向为直线伺服、智能控制等。E-mail: yuanhao_sut@163.com
赵希梅 女,1979年生,教授,博士生导师,研究方向为电机控制、机器人控制、智能控制等。E-mail: zhaoxm_sut@163.com(通信作者)
(编辑 赵 鹏)