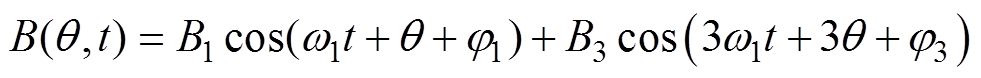 (1)
(1)摘要 针对采用3次谐波注入的非正弦供电多相感应电机,该文提出一种基于等效电路与分布磁路法的稳态性能迭代计算方法,对3次谐波注入参数对于电机稳态性能的影响规律进行定量分析。结果表明,当3次谐波注入满足气隙磁通密度中3次谐波与基波“峰谷相对”,且3次谐波磁通密度幅值为基波的1/6时,谐波注入对电机稳态性能的优化效果达到最佳。以某型45kW十五相感应电机为对象进行计算与实验验证,结果表明,在气隙磁通密度最大值和电流有效值不变的情况下,采用3次谐波注入时的基波电压与输出功率相对无注入情况最大可提升约13%。
关键词:多相感应电机 稳态性能 3次谐波注入 分布磁路法
感应电机具有结构简单、运行可靠、维修方便等固有优点,近年来随着感应电机多相化设计与变频驱动技术的发展,多相感应电机的容量与转矩密度不断提高。多相大容量感应电机兼具高功率密度和高可靠性的特点,能满足舰船综合电力推进系统等领域对推进电机的特殊要求,具有广泛的应用前景[1]。
电机多相化设计消除了传统三相电机内部的5、7次等有害谐波磁动势,因此可以采用利用率更高的集中整距绕组,并结合非正弦供电方式,有效改善铁心材料利用率,提高电机转矩密度[2-3]。非正弦供电的基本原理是在定子电流中注入特定的谐波分量,谐波电流产生的谐波磁动势使气隙磁通密度波形更接近理想“方波”,磁动势在气隙磁通密度最大值,即铁心齿部饱和程度不变的情况下非正弦供电对应气隙磁通密度基波分量,在传统正弦供电的基础上进一步增大,从而实现了铁心材料更充分的利用,有助于提高电机转矩密度等性能指标。
多相感应电机非正弦供电方式的影响机理与控制实现的相关研究得到了国内外学者的广泛关注[4-7],其中本项目组针对此类电机的特殊电磁问题开展了一系列研究,前期工作成果包括参数计算、数学建模与磁动势分析等[8-13],为完整分析非正弦供电方式影响提供了理论基础。文献[14]针对非正弦供电多相感应电机的稳态性能分析方法开展了相关研究,以气隙磁动势波形“峰谷相对”为目标,计算了最优气隙磁动势对应的3次谐波注入所需的电压电流参数。然而,多相感应电机非正弦供电的根本目标为实现气隙磁通密度波形的精确控制,目前研究中均以端口电压或气隙磁动势波形最优为出发点,但在漏抗参数和铁心饱和的影响下,无法保证气隙磁通密度波形达到最优,同时分析中谐波注入参数一般设定为理想值,没有考虑不同3次谐波注入的幅值、相位参数对多相感应电机性能的影响规律,相关研究尚待进一步深入。
本文以非正弦供电多相感应电机为研究对象,提出一种基于非正弦气隙磁通密度的多相感应电机稳态性能计算方法,并对3次谐波注入的幅值和相位参数对于电机稳态性能的影响规律进行定量分析。首先以电机非正弦气隙磁通密度波形为基本出发点,在保证气隙最大磁通密度,即铁心齿部饱和程度不变的情况下,给出了3次谐波磁通密度在不同幅值、相位的情况下,气隙磁通密度基波分量变化规律,从理论角度分析了3次谐波注入对于电机性能的优化效果;进一步以基波及3次谐波等效电路为基础,并以气隙磁通密度波形为出发点,给出了非正弦供电感应电机稳态性能迭代计算方法;最终以一型45kW十五相感应电机为例,通过理论计算与实验验证,得到不同3次谐波注入参数对电机稳态性能的影响规律。
电机定子电流内部注入3次谐波会产生对应的3次谐波磁动势,从而使气隙磁通密度波形叠加3次谐波分量。取定子静止坐标系,忽略3次以上的谐波,基波与3次谐波叠加情况下的电机气隙磁通密度分布为
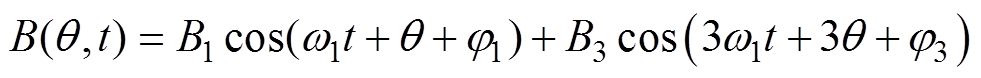 (1)
(1)式中,w1为定子基波频率;q 为电角度;j1为基波气隙磁通密度相位;j3为3次谐波气隙磁通密度相位;B1为基波气隙磁通密度幅值;B3为3次谐波气隙磁通密度幅值。
在正弦气隙磁通密度中叠加3次谐波之后,磁通密度波形会出现明显变化。例如基波与3次谐波磁通密度相位关系满足“峰谷相对”时,气隙磁通密度波形如图1a所示,其形状近似于方波,此时基波磁通密度幅值大于磁通密度最大值,而当基波与3次谐波磁通密度相位关系满足“峰峰相对”时,气隙磁通密度波形如图1b所示,为尖顶波,此时基波磁通密度幅值小于气隙磁通密度最大值。
为定量评价谐波注入对于气隙磁通密度波形的优化效果,定义基波磁通密度与气隙磁通密度最大值的比值k1max=B1/Bmax。在保证气隙磁通密度最大值不变的条件下,可控制3次谐波注入参数,使气隙磁通密度波形尽量接近理想方波,提高气隙基波磁通密度幅值,则k1max越大,3次谐波注入对磁通密度波形的优化效果越好。

图1 基波与3次谐波叠加磁通密度波形
Fig.1 Superimposed magnetic density waveforms for fundamental and 3-order harmonic
根据式(1)可知,3次谐波注入幅值与相位是影响其优化效果的主要参数,定义3次谐波磁通密度与基波磁通密度的幅值比值k31=B3/B1,相位差j31=j3-3j1,利用理想气隙磁通密度波形,分析不同注入幅值与相位对于基波磁通密度的影响,结果如图2所示。
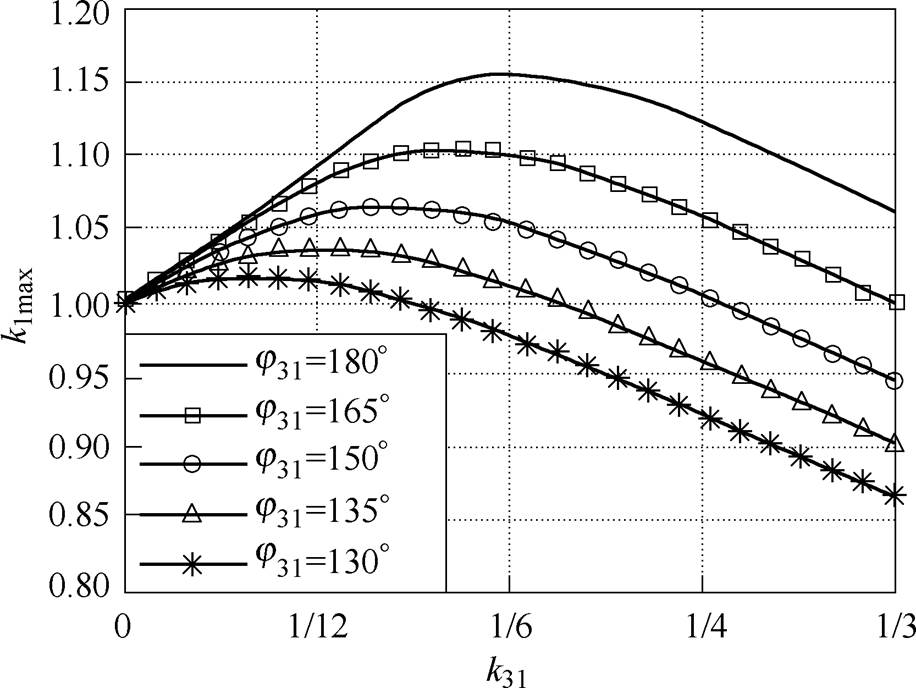
图2 3次谐波磁通密度的幅值与相位对气隙磁通密度的影响
Fig.2 Influence of amplitude and phase of 3-order harmonic magnetic density on magnetic density waveforms
首先考虑相位关系,根据图2,基波与3次谐波气隙磁通密度满足“峰谷相对”关系,即j31=180°时,气隙磁通密度波形出现对称的“削顶”,气隙磁通密度优化效果达到最大。其次考虑幅值关系,k31= 1/6时,达到k1max最大值,基波磁通密度提升比例最大为1.15。而若基波与3次谐波气隙磁通密度的幅值比例不满足1/6,或者相位关系偏移“峰谷相对”,基波磁通密度的优化效果出现明显降低,尤其在注入比例或者偏移角度较大时,k1max会低于1,此时基波磁通密度反而低于无注入工况。
理论上,3次谐波注入对于基波气隙磁通密度的优化效果可以达到15%,而在实际电机应用中,由于电机轭部饱和等非理想因素的影响,3次谐波注入对电机功率等参数优化效果一般会略低于理论 值[5]。因此,为准确计算3次谐波注入对电机稳态性能的影响,必须同时考虑谐波注入与电机铁心饱和等因素的影响,建立基于气隙磁通密度波形的感应电机稳态性能计算方法。
电机稳态性能分析中,可认为结构数据与基本运行参数为已知量,同时为保证电机安全运行,电机所能承受的最大电流与最大齿部磁负荷不应超过其额定值。因此,对比分析3次谐波注入对电机性能的影响规律,应保持气隙磁通密度最大值与输入电流总有效值与无注入工况相同,且不超过额定值。
为确定3次谐波注入幅值与相位参数对于电机性能的影响,稳态性能分析以气隙磁通密度为出发点,为便于分析,根据式(1),定义复数参数a31来表示气隙磁通密度波形中基波与3次谐波磁通密度的幅值与相位关系,有
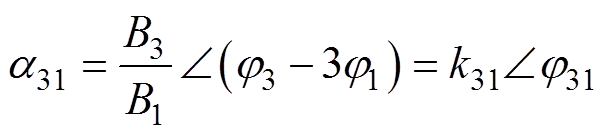 (2)
(2)综上所述,输入条件参数主要包括:①电机转速设定值n;②输入电流总有效值目标值IRMS_0; ③气隙磁通密度最大值设定值Bd max_0;④3次谐波注入的幅值相位关系复参数设定值a31_0。
等效电路为分析感应电机稳态性能的重要工具,感应电机的基波、3次谐波“T形”等效电路如图3所示。根据式(1),基波电流产生基波磁通密度的转速为w1,3次谐波电流产生3次谐波磁通密度的转速也为w1,即基波与3次谐波磁通密度保持同方向同速旋转[8],因此由转差率定义,得出基波等效电路中的转差率与3次谐波等效电路中的转差率相等,设为s。
图3所示的等效电路当中,R11、R13为基波、3次谐波定子电阻,X11、X13为基波、3次谐波定子漏抗,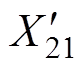 、
、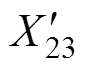 为基波、3次谐波转子漏抗折算值,
为基波、3次谐波转子漏抗折算值,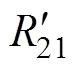 、
、 为基波、3次谐波转子电阻折算值。上述参数中,定子电阻在基波与3次谐波等效电路中相等,而3次谐波定子漏抗与基波定子漏抗并不相同,其计算过程详见文献[10]。基波等效电路中转子参数计算在现有参考文献中已有成熟方法[15],3次谐波下的转子导条电阻、槽漏抗等参数计算方法与基波情况相同,转子参数的绕组折算关系也相同,但需要考虑以下两点差异:一是笼型转子端环电阻折算至导条电阻时,因基波电流与3次谐波电流相位关系不同使得折算公式不一样;二是由于基波引起的高次谐波与3次谐波引起的高次谐波不同导致转子谐波漏抗不相等[11]。
为基波、3次谐波转子电阻折算值。上述参数中,定子电阻在基波与3次谐波等效电路中相等,而3次谐波定子漏抗与基波定子漏抗并不相同,其计算过程详见文献[10]。基波等效电路中转子参数计算在现有参考文献中已有成熟方法[15],3次谐波下的转子导条电阻、槽漏抗等参数计算方法与基波情况相同,转子参数的绕组折算关系也相同,但需要考虑以下两点差异:一是笼型转子端环电阻折算至导条电阻时,因基波电流与3次谐波电流相位关系不同使得折算公式不一样;二是由于基波引起的高次谐波与3次谐波引起的高次谐波不同导致转子谐波漏抗不相等[11]。
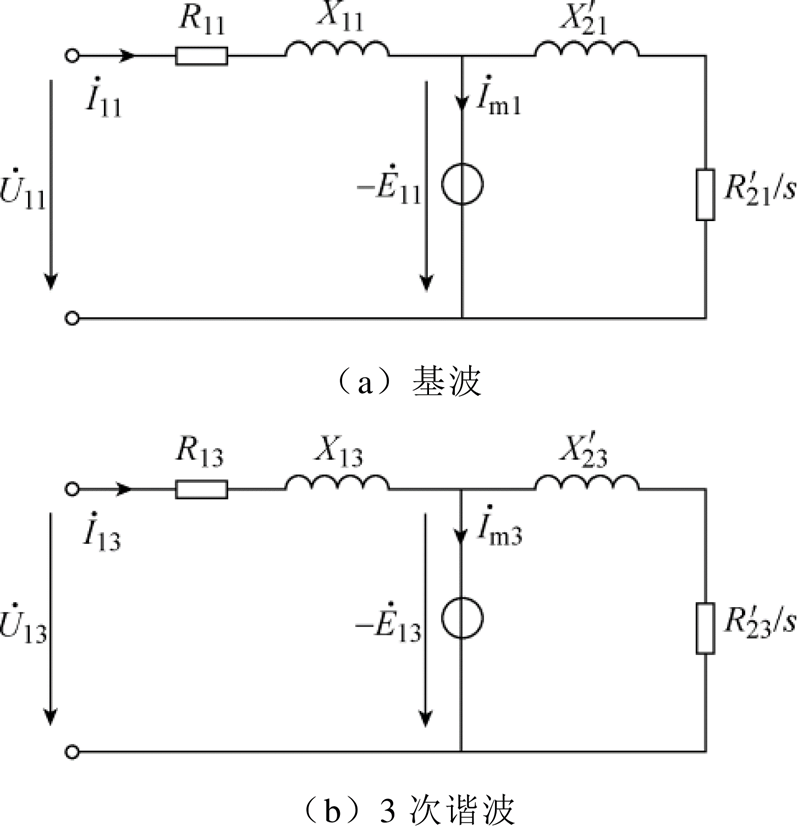
图3 感应电机等效电路
Fig.3 Equivalent circuits of induction motor
电机铁心饱和等因素会导致基波、3次谐波的感应电动势与励磁电流之间存在耦合,因此等效电路中的励磁电路不再采用传统的励磁电抗参数,而采用流控电压源表示。
以基波与3次谐波等效电路为基础,建立以气隙波形为出发点的稳态性能计算方法,计算中共涉及三层迭代,从内向外依次为:① 3次谐波励磁电流相量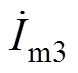 迭代;②基波励磁电流幅值Im1迭代;③转差率s迭代。
迭代;②基波励磁电流幅值Im1迭代;③转差率s迭代。
最外层转差率与传统三相感应电机稳态性能迭代计算方法类似,但由于迭代出发点为气隙磁通密度波形,不是常规的端口电压等,中间层迭代和内层迭代与传统方法存在明显区别。
2.3.1 3次谐波励磁电流相量迭代
稳态性能计算的最内层迭代以3次谐波励磁电流相量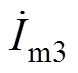 为自变量,通过调整变量
为自变量,通过调整变量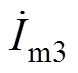 ,使气隙磁密波形的3次谐波与基波磁通密度的幅值与相位关系满足设定要求,即式(2)定义的a13参数与设定值a13_0相等。
,使气隙磁密波形的3次谐波与基波磁通密度的幅值与相位关系满足设定要求,即式(2)定义的a13参数与设定值a13_0相等。
内层迭代中,基波励磁电流大小Im1视为已知,令基波励磁相量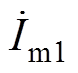 的相位为0°,即
的相位为0°,即
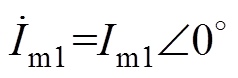 (3)
(3)根据基波与3次谐波励磁电流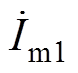 、
、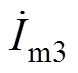 ,进行磁路计算得到气隙磁通密度波形,经傅里叶分解得到基波、3次谐波磁通密度的幅值与相位,进一步根据式(2)计算得到复数参数a31。
,进行磁路计算得到气隙磁通密度波形,经傅里叶分解得到基波、3次谐波磁通密度的幅值与相位,进一步根据式(2)计算得到复数参数a31。
内层迭代的基础为磁路计算。传统磁路计算基于正弦假设,无法应用于非正弦场合,而有限元法等数值方法计算量大,运算速度慢,无法满足方案设计阶段的多方案分析对比的需要。本文内层迭代采用分布磁路法进行磁路计算,该方法从基波与3次谐波励磁电流所产生的合成磁动势出发,以周向分块为处理关键,通过迭代计算得到沿圆周各节点气隙磁通密度,并由傅里叶分解得到基波磁通密度和3次谐波磁通密度。该方法可以充分考虑非正弦供电与磁路饱和的影响,同时计算效率优于有限元等数值方法,本文所涉及的分布磁路法具体过程可参考文献[8, 14]。
内层迭代的收敛条件为参数a31与设定值a31_0的误差小于允许值ea,即
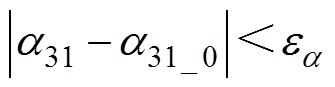 (4)
(4)若收敛条件不满足,需要对3次谐波励磁电流相量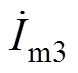 进行修正,在此采用复数域牛顿迭代法。定义迭代目标参数a31为
进行修正,在此采用复数域牛顿迭代法。定义迭代目标参数a31为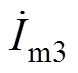 的函数,即
的函数,即
 (5)
(5)
采用牛顿迭代法,迭代变量修正值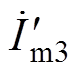 为
为
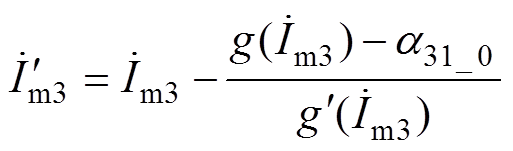 (6)
(6)式中,导数 在运算中为隐含形式,一般难以解析求解,可以采用局部离散差分进行近似,即
在运算中为隐含形式,一般难以解析求解,可以采用局部离散差分进行近似,即
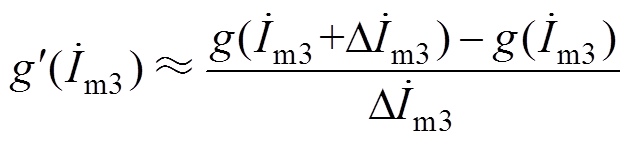 (7)
(7)
式中,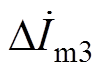 为足够小的复数量,可根据迭代速度要求进行取值。
为足够小的复数量,可根据迭代速度要求进行取值。
上述内层迭代过程以分布磁路法为基础,可以确定满足基波与3次谐波磁通密度幅值与相位相对关系的3次谐波励磁电流相量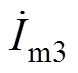 ,即确定了基波与3次谐波励磁电流的幅值与相位关系,并得到相应情况下铁心各部分磁通密度,为后续的分析计算提供了基础。
,即确定了基波与3次谐波励磁电流的幅值与相位关系,并得到相应情况下铁心各部分磁通密度,为后续的分析计算提供了基础。
稳态性能计算的内层迭代流程如图4所示。
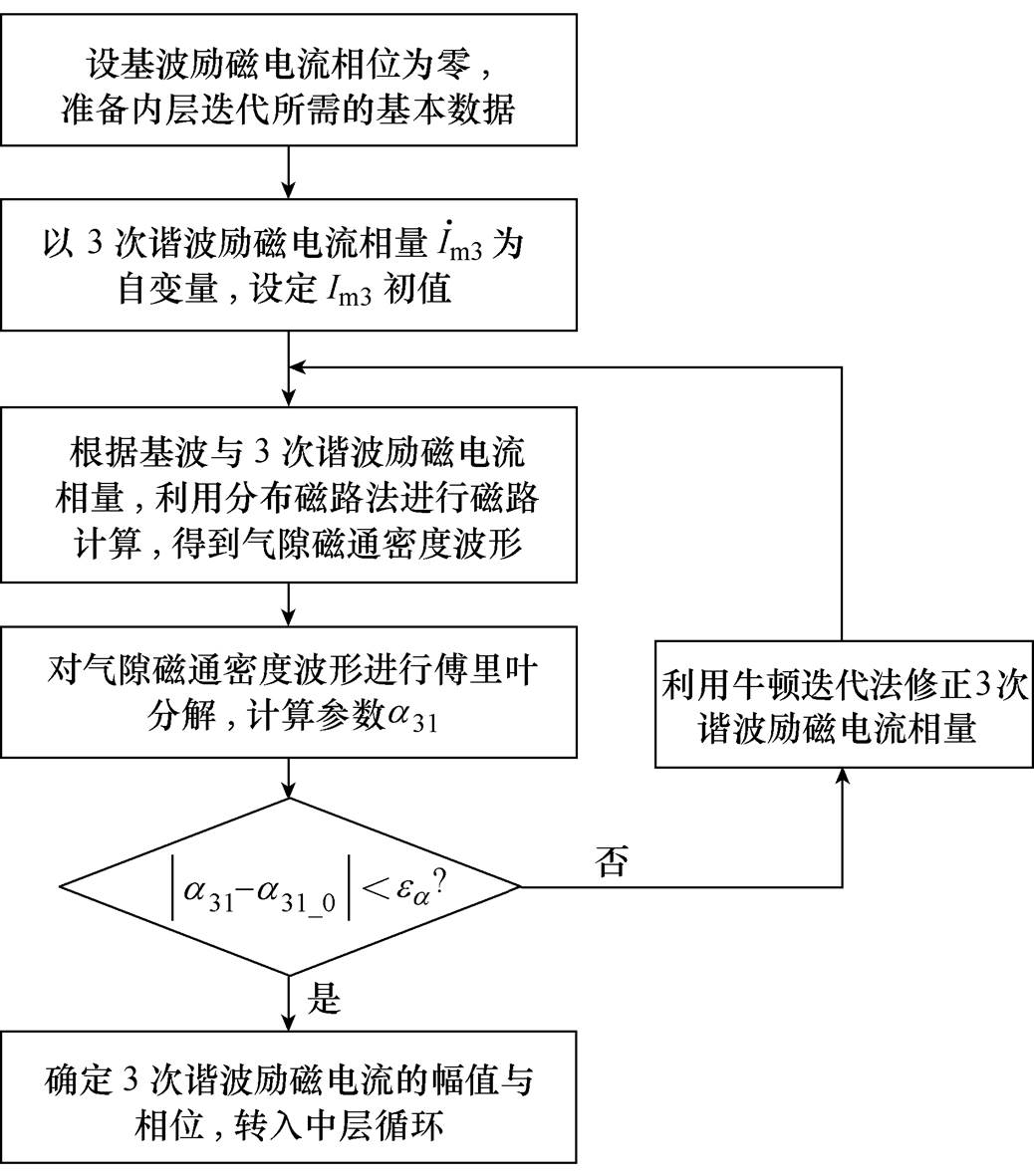
图4 内层迭代流程
Fig.4 Inner layer iterative flow char
2.3.2 基波励磁电流迭代
稳态性能计算的中间层迭代以励磁电流大小Im1为自变量,迭代目标为使气隙磁通密度波形的最大值Bd max与设定输入值Bd max_0相同。
内层迭代的收敛条件是Bd max与Bd max_0的误差小于允许值eB,即
 (8)
(8)若收敛条件不满足,则对Im1进行修正,修正公式为
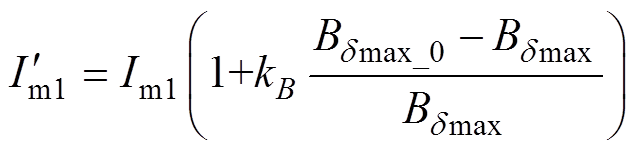 (9)
(9)
式中,kB为经验系数,可在0.05~1间取值,取大值可能发散,取小值迭代次数增多,具体取值时要权衡考虑。
稳态性能计算的中间层迭代流程如图5所示。
2.3.3 转差率迭代
稳态性能计算的最外层的迭代变量为转差率s,迭代目标为使电机输入电流总有效值IRMS达到设定值IRMS_0。根据内层与中层迭代结果,定子基波、3 次谐波相电流为
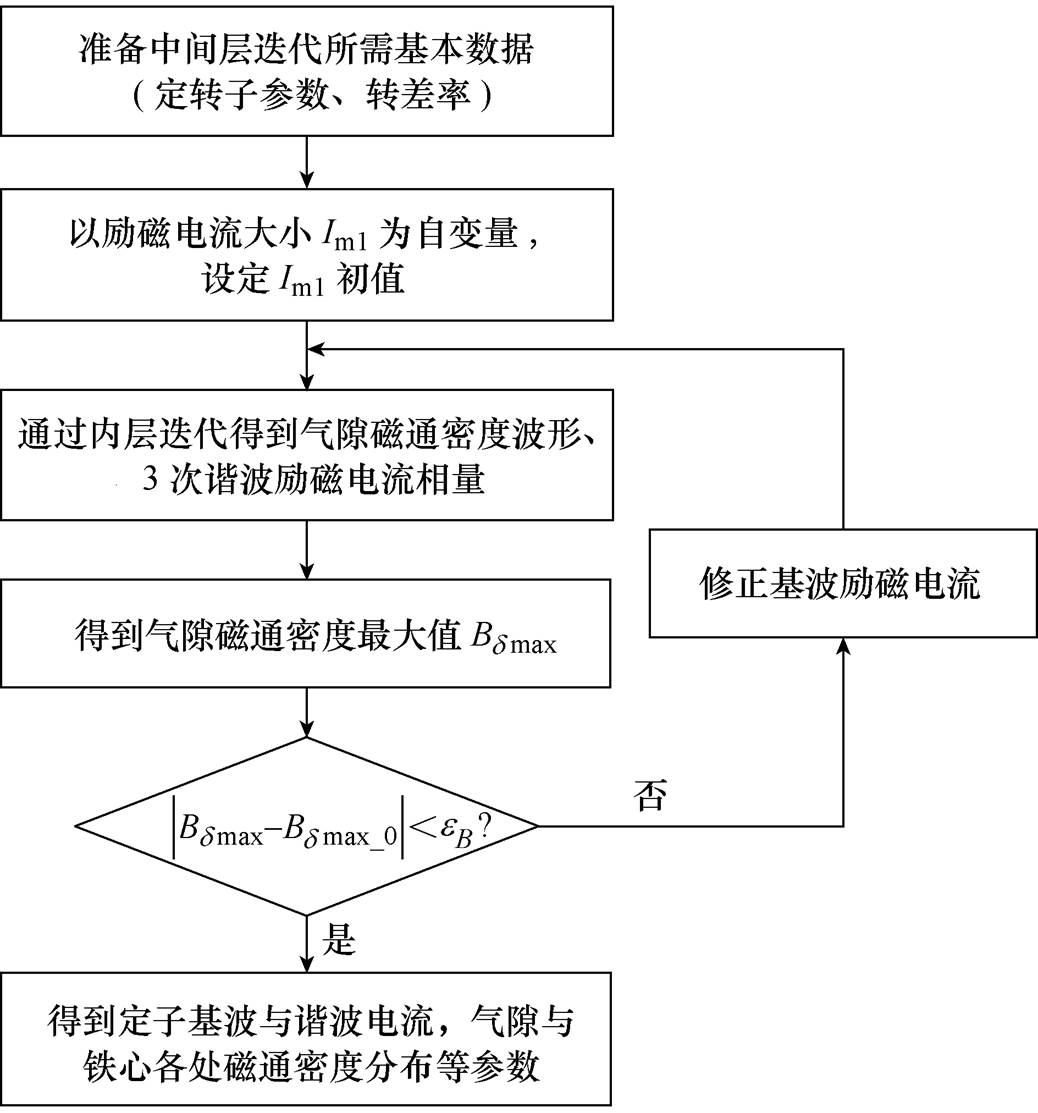
图5 中层迭代流程
Fig.5 Middle layer iterative flow chart
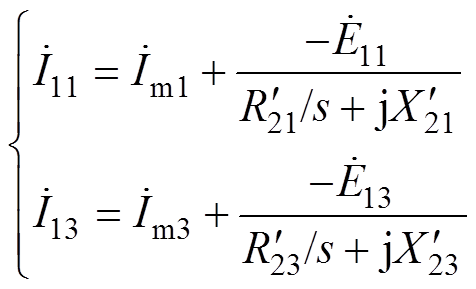 (10)
(10)不考虑3次以上谐波,IRMS为
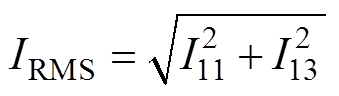 (11)
(11)
内层迭代的收敛条件是IRMS与IRMS_0的误差小于允许值eI,即
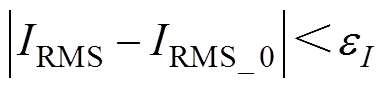 (12)
(12)若收敛条件不满足,则对Im1进行修正,公式为
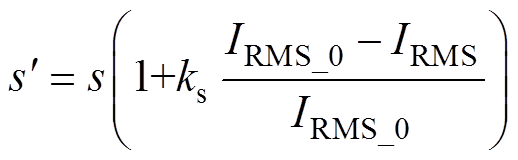 (13)
(13)
式中,ks为经验系数,取值方法与中间层迭代中的系数kB相同。
稳态性能计算的外层迭代流程如图6所示。
根据基波与3次谐波等效电路,定子电压基波、3次谐波相量为
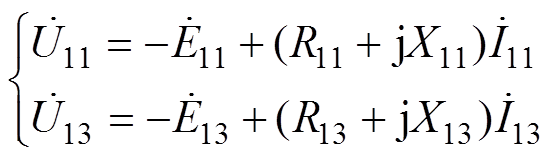 (14)
(14)基波、3次谐波输入功率为
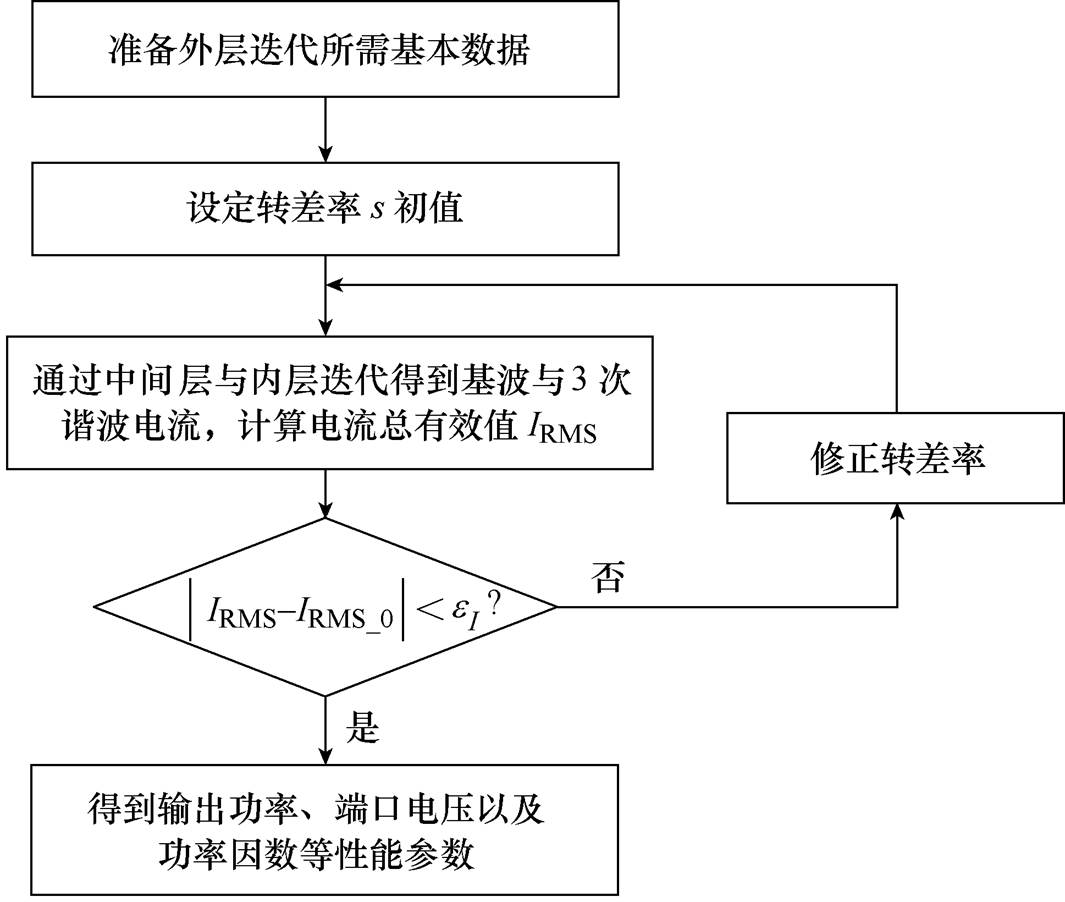
图6 外层迭代流程
Fig.6 Outer layer iterative flow char
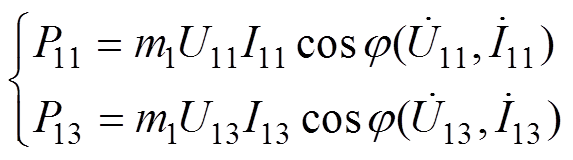 (15)
(15)总输出功率为
 (16)
(16)
式中,pCu11、pCu13为基波、3次谐波定子铜耗;pCu21、pCu23为基波、3次谐波转子铜耗;pmec为机械损耗;pad为杂散损耗。上述损耗计算方面均采用常规方法,具体计算公式可参考文献[15]。pFe为铁耗,传统铁耗计算公式仅能考虑基频,在非正弦供电情况下不适用,本文铁耗计算采用文献[16]给出的铁耗计算模型。
综合上述三层迭代计算结果,最终可以得到在给定气隙磁通密度最大值、电流总有效值以及规定谐波注入参数情况下的电机输出功率、效率以及电压电流等稳态性能参数。针对不同3次谐波注入参数重复上述迭代计算过程,可得到谐波参数对稳态参数的影响规律。
本文以某45kW十五相感应电机为分析对象,对不同3次谐波注入参数对电机稳态性能的影响进行计算分析。表1给出了该样机在无3次谐波注入情况下的主要额定参数。
针对45kW十五相感应电机,以无3次谐波注入的额定工况为基准,气隙磁通密度最大值(约0.76T)与电流有效值(约26.6A)保持不变。不同注入幅值与相位对于电机基波电压的影响如图7所示。首先考虑相位的影响,与图2的规律类似,基波与3次谐波气隙磁通密度满足“峰谷相对”关系,即j31=180°时,基波电压提升效果最为明显。其次考虑幅值影响,在“峰谷相对”的情况下,当3次谐波磁密幅值为基波的1/6,即k31=1/6时,基波电压提升优化效果达到最大值,最大基波电压达到158.4V,相对无注入情况下的140V,优化效果达到13.14%。
表1 某45kW十五相感应电机主要参数
Tab.1 The main parameters of 45kW 15-phase induction motor

参 数数 值 额定功率P/kW45 相数m15 极对数p2 额定转速n/(r/min)600 定子相电压U1/V140 定子外径D1/mm560 定子内径Di1/mm350.2 铁心结构长度l/mm230 气隙长度g/mm0.9 定子槽数Z160 转子槽数Z238
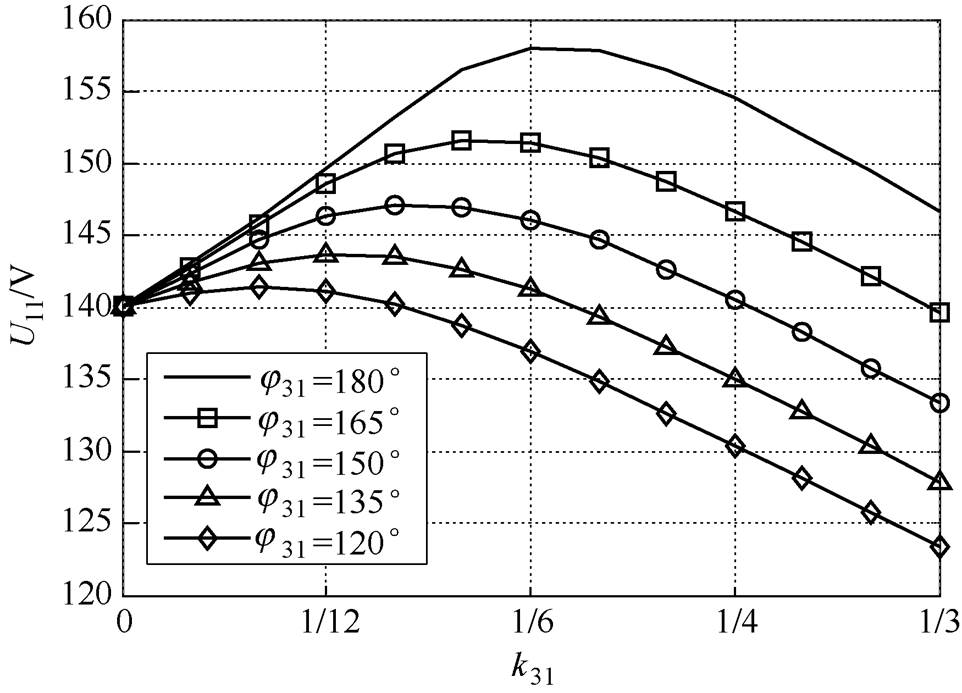
图7 3次谐波磁通密度的幅值与相位对基波电压的影响
Fig.7 Influence of amplitude and phase of 3-order harmonic magnetic density on fundamental voltage
而若基波与3次谐波气隙磁通密度的比例不满足1/6,或者相位关系偏移“峰谷相对”,则基波电压的优化效果出现明显降低,甚至低于无注入情况,此时3次谐波注入对于电机性能存在负面影响。
进一步分析不同3次谐波注入参数对于输出功率的影响,计算结果如图8所示。首先考虑相位的影响,图7与图2的规律类似,当基波与3次谐波气隙磁通密度满足“峰谷相对”关系,即j31=180°时,输出功率的提升效果最为明显。其次考虑幅值影响,在“峰谷相对”的情况下,当3次谐波磁密幅值为基波的1/6,即k31=1/6时,功率输入提升优化效果达到最大值,最大输出功率达到50.9kW,相对无注入情况下,其优化效果达到13.11%。
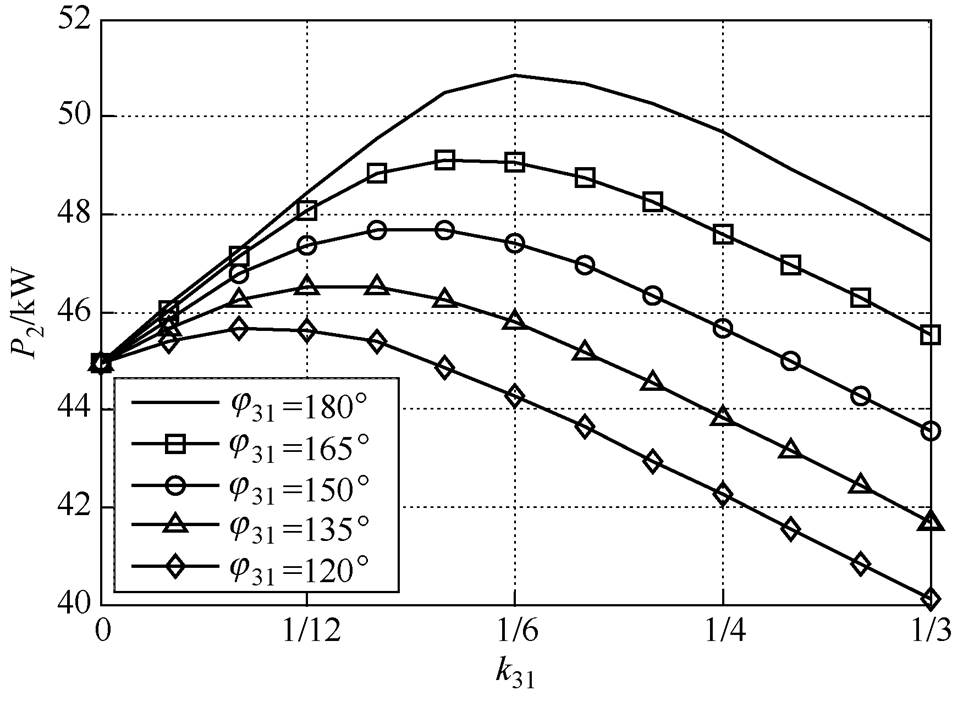
图8 3次谐波磁通密度的幅值与相位对输出功率的影响规律
Fig.8 Influence of amplitude and phase of 3-order harmonic magnetic density on output power
而若基波与3次谐波气隙磁通密度的注入比例不满足1/6,或者相位关系偏移“峰谷相对”,则输出功率的优化效果出现明显降低,甚至低于无注入情况,此时3次谐波注入对于电机性能存在负面影响。
综上所述,针对45kW十五相感应电机,保持气隙磁通密度最大值和电流总有效值不变的情况下,3次谐波气隙磁通密度相位满足“峰谷相对”,同时3次谐波磁通密度幅值为基波磁通密度的1/6时,3次谐波注入对电机性能的效果达到最优,基波电压与输出功率可提升13%。若不满足上述幅值相位关系,则3次谐波注入对于电机稳态性能的优化效果将明显降低,甚至出现负面作用。
利用45kW十五相感应电机,对3次谐波注入对于电机稳态性能影响规律进行实验验证。45kW十五相感应电机实验系统如图9所示,实验过程中,非正弦供电电源通过专用十五相变频器经PWM得到,使用的十五相变频驱动系统如图10所示。
实验中,保持转速为额定600r/min,同时维持气隙磁通密度最大值和电流有效值与无注入额定工况相同,分别根据图7、图8中无3次谐波注入与最优3次谐波注入比例工况进行稳态运行实验,实验中得定子电压与电流波形如图11所示,其中电压波形为PWM波,图11中,i为定子电流,u1为定子电压,u11为定子电压基波分量,u13为定子电压3次谐波分量。

图9 某型45kW十五相感应电机
Fig.9 45kW 15-phase induction motor

图10 45kW十五相感应电机变频驱动系统
Fig.10 Variable frequency drive system of 45kW 15-phase induction motor
实验中45kW十五相感应电机的定子表面布置有探测线圈,线圈跨距设定为一个极距。电机运行时,气隙磁通密度会在探测线圈上产生感应电动势,因此根据探测线圈的感应电动势的实验波形,可以反推出气隙磁通密度波形,得到基波与3次谐波气隙磁通密度的实验值。在上文提到的最优3次谐波注入工况下,探测线圈的感应电动势的实验波形如图12所示。
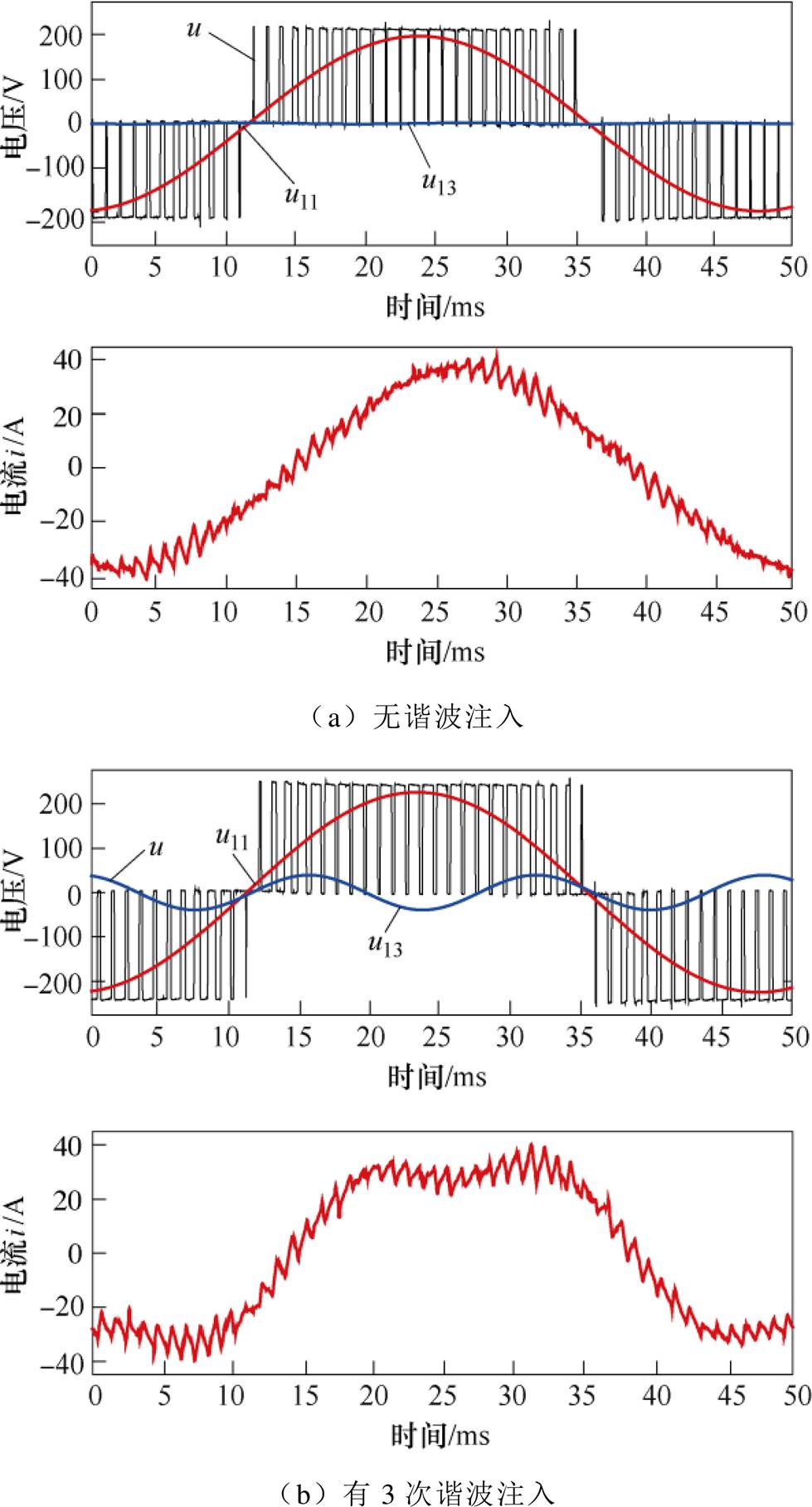
图11 45kW十五相感应电机电压电流波形
Fig.11 Experimental voltage and current waveforms of the 45kW 15-phase induction motor
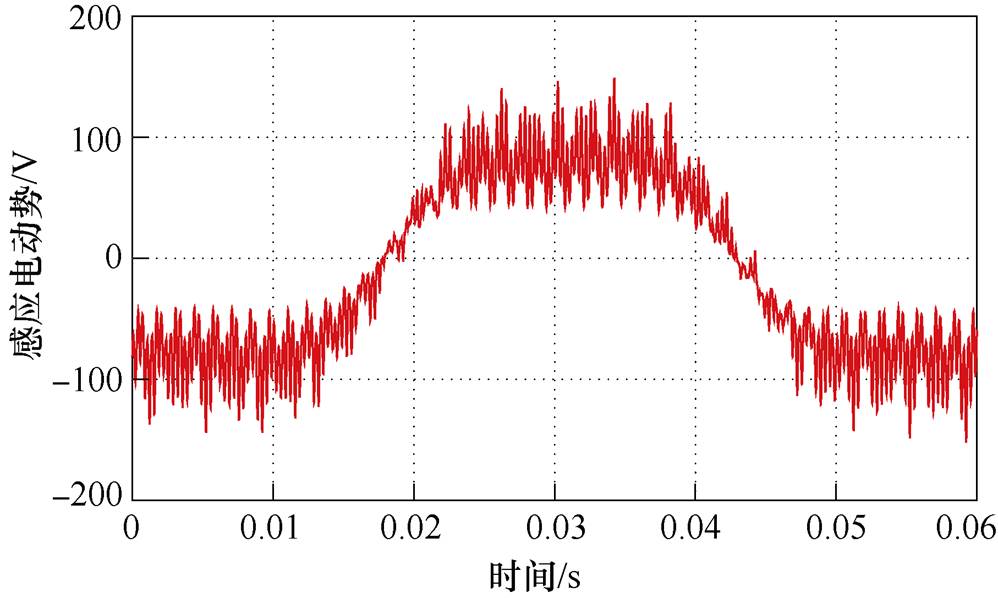
图12 探测线圈感应电动势波形
Fig.12 Experimental induced voltage waveform of the detection coil
根据图12给出的探测线圈感应电动势波形,可以反推得到气隙磁通密度波形,进而通过傅里叶分解得到基波与3次谐波气隙磁通密度幅值与相位。表2给出了最优3次谐波注入工况下基波与3次谐波气隙磁通密度幅值与相位理论值与实验值的对比,两者吻合较好,此时气隙磁通密度波形满足基波与3次谐波“峰谷相对”,同时3次谐波幅值约为基波的1/6,证明3次谐波注入后的气隙磁通密度波形达到最优。
进一步对于实验所得的电压电流波形进行傅里叶分解,得到主要稳态参数的实验结果,并与本文提出方法的计算结果进行对比,结果见表3,其中基波与3次谐波电压的相位差j31_U=j3_U-3j1_U,j3_U、j1_U分别为基波与3次谐波电压的相位,基波与3次谐波电流的相位差j31_I的计算方法与j31_U类似。对比可见,主要稳态参数的计算结果与实验值吻合较好,相对无注入情况,3次谐波注入使电机基波电压与输出功率提升约13%,验证了本文分析结论的有效性。
表2 基波与3次谐波磁通密度的幅值与相位
Tab.2 Amplitude and phase of fundamental and 3-order harmonic magnetic density

数值参数 B1/TB3/TB3/B1φ31/(°) 计算值0.880 70.146 80.166 7180 实验值0.877 20.1450.165 3181.1 误差(%)-0.40-1.23-0.840.61
表3 计算值与实验值对比
Tab.3 The comparison between calculation and experimental results
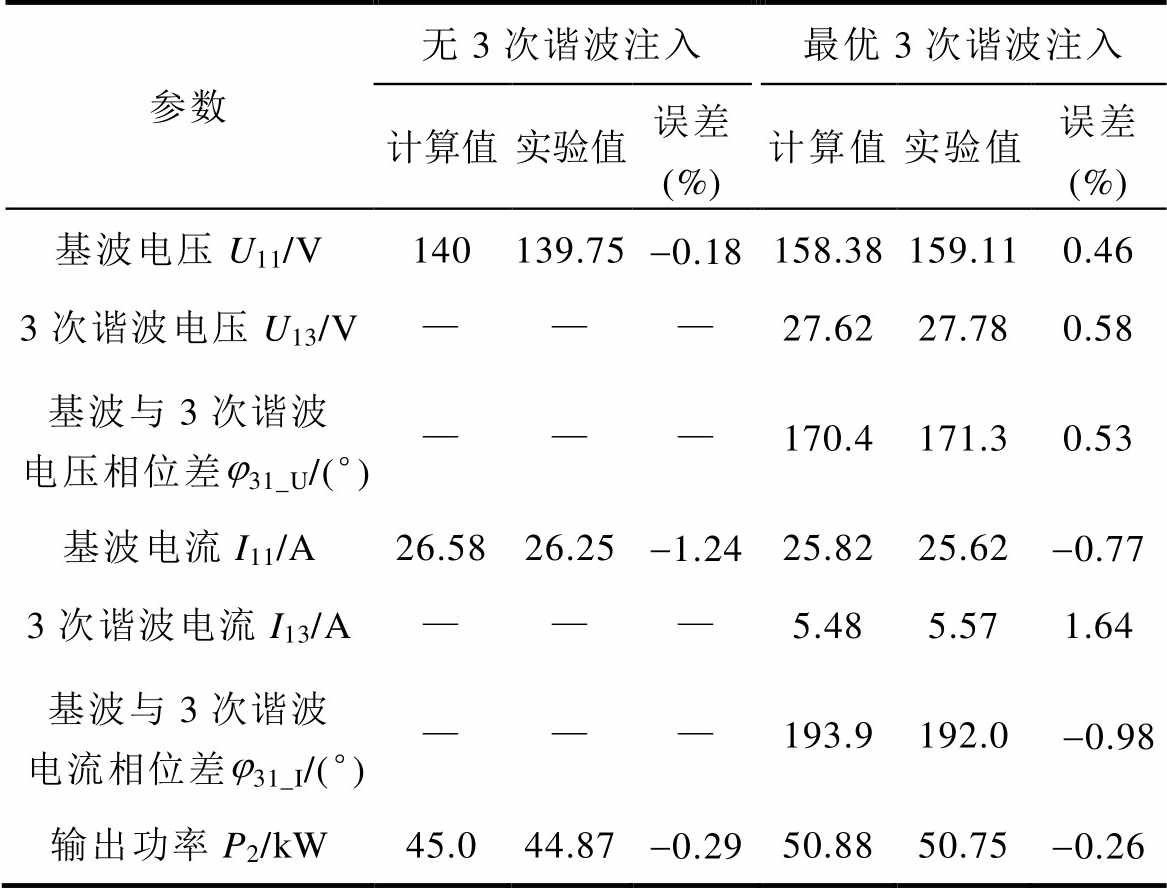
参数无3次谐波注入最优3次谐波注入 计算值实验值误差 (%)计算值实验值误差 (%) 基波电压U11/V140139.75-0.18158.38159.110.46 3次谐波电压U13/V———27.6227.780.58 基波与3次谐波电压相位差j31_U/(°)———170.4171.30.53 基波电流I11/A26.5826.25-1.2425.8225.62-0.77 3次谐波电流I13/A———5.485.571.64 基波与3次谐波电流相位差j31_I/(°)———193.9192.0 -0.98 输出功率P2/kW45.044.87-0.2950.8850.75-0.26
本文以非正弦供电多相感应电机为对象,采用基于稳态等效电路与分布磁路法的稳态性能迭代计算方法,对3次谐波注入参数对于电机稳态性能的影响规律进行定量分析。所提出的稳态性能迭代计算方法以气隙磁通密度波形为基本出发点,同时为保证3次谐波磁通密度不同幅值、相位参数与设定值相同,内层迭代以复数形式的3次谐波励磁电流相量为迭代变量,并采用牛顿迭代法进行迭代,最终通过三层迭代得到非正弦供电多相感应电机的稳态性能计算结果。
气隙磁通密度中的3次谐波与基波的幅值相位关系是影响电机稳态性能的关键因素,3次谐波气隙磁通密度相位满足“峰谷相对”,同时3次谐波磁通密度幅值为基波磁通密度的1/6时,3次谐波注入的优化效果达到最优。理论上,注入后气隙基波磁通密度相对无注入工况最大可以提升15%,实际电机受铁心饱和等因素影响,性能提升幅度应略低于理论值,在气隙磁通密度最大值和电流总有效值不变的情况下,某型45kW十五相感应电机应用3次谐波注入,基波电压与输出功率最大可提升约13%。
若气隙磁通密度波形中3次谐波与基波不满足最优的幅值相位关系,则3次谐波注入对于电机稳态性能的优化效果将明显降低,甚至出现负面影响。因此,若多相反应电机采用3次谐波注入供电,需要对谐波电压电流进行精准控制,以充分发挥注入3次谐波对电机性能的优化效果。
参考文献
[1] Levi E, Bojoi R, Profumo F, et al. Multiphase induction motor drives-a technology status review[J]. IET Electric Power Applications, 2007, 1(4): 489- 516.
[2] Abdel-Khalik A S, Masoud M I, Williams B W. Improved flux pattern with third harmonic injection for multiphase induction machines[J]. IEEE Transa- ctions on Power Electronics, 2012, 27(3): 1563-1578.
[3] 刘东, 黄进, 康敏, 等. 多相感应电机的非正弦供电技术[J]. 中国电机工程学报, 2011, 31(12): 84-89.
Liu Dong, Huang Jin, Kang Min, et al. Non- sinusoidal voltage fed multiphase induction motors[J]. Proceedings of the CSEE, 2011, 31(12): 84-89.
[4] Xu H, Toliyat H A, Petersen L J. Five-phase induction motor drives with DSP-based control system[J]. IEEE Transactions on Power Electronics, 2002, 17(4): 524-533.
[5] Abdel-Khalik A S, Masoud M I, Ahmed S, et al. Effect of current harmonic injection on constant rotor volume multiphase induction machine stators: a comparative study[J]. IEEE Transactions on Industry Applications, 2012, 48(6): 2002-2013.
[6] 陈林. 十五相感应电机定子绕组多相开路的稳态特性[J]. 电工技术学报, 2004, 19(11): 14-19.
Chen Lin. Steady state performance of a 15-phase induction machine with multiphase stator windings open circuited[J]. Transactions of China Electro- technical Society, 2004, 19(11): 14-19.
[7] 朱鹏, 乔鸣忠, 张晓锋, 等. 3次谐波电流注入对五相感应电机系统运行性能影响分析[J]. 电工技术学报, 2016, 31(20): 102-110.
Zhu Peng, Qiao Mingzhong, Zhang Xiaofeng, et al. The effects of third harmoic current injection on operration performance of five-phase induction motor[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 102-110.
[8] 王东, 吴新振, 马伟明, 等. 非正弦供电十五相感应电机磁路计算方法[J]. 中国电机工程学报, 2009, 29(12): 58-64.
Wang Dong, Wu Xinzhen, Ma Weiming, et al. Magnetic circuit calculation of fifteen-phase indu- ction motor with non-sinusoidal supply[J]. Pro- ceedings of the CSEE, 2009, 29(12): 58-64.
[9] 康敏, 于文娟, 孔武斌. 非正弦供电下的五相感应电机弱磁优化控制策略[J]. 电机与控制学报, 2018, 22(8): 89-97.
Kang Min, Yu Wenjuan, Kong Wubin. Field weakening optimum control strategies with non- sinusoidal power supply for five-phase induction motor[J]. Electric Machines and Control, 2018, 22(8): 89-97.
[10] 孔武斌, 于文娟, 王征宇, 等. 电动汽车用多相电机电流控制策略比较[J]. 电机与控制学报, 2019, 23(1): 9-18.
Kong Wubin, Yu Wenjuan, Wang Zhengyu, et al. Comparison of control strategies based on multiphase motor for electric vehicle[J]. Electric Machines and Control, 2019, 23(1): 9-18.
[11] 王东, 马伟明, 郭云珺, 等. 基于非正弦供电方式的多相感应电动机建模[J]. 电工技术学报, 2010, 25(2): 6-14.
Wang Dong, Ma Weiming, Guo Yunjun, et al. Modelling of multiphase induction motor with non- sinusoidal supply[J]. Transactions of China Electro- technical Society, 2010, 25(2): 6-14.
[12] 朱鹏, 乔鸣忠, 于飞, 等. 基于磁动势平衡分析的多相感应电机容错控制[J]. 电工技术学报, 2019, 34(增刊1): 62-69.
Zhu Peng, Qiao Mingzhong, Yu Fei, et al. Tolerant control for multi-phase induction motor based on magnetmotive force balance analysis[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 62-69.
[13] 郑晓钦, 王东, 刘海涛, 等. 十五相感应推进电机切套减额运行转矩计算[J]. 电工技术学报, 2019, 34(1): 58-65.
Zheng Xiaoqin, Wang Dong, Liu Haitao, et al. Torque calculation of fifteen-phase induction motor with different sets of winding derated operation[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 58-65.
[14] 王东, 吴新振, 程思为, 等. 非正弦供电多相感应电机稳态性能分析[J]. 中国科学: 技术科学, 2015(3): 322-329.
Wang Dong, Wu Xinzhen, Cheng Siwei, et al. Steady state performance analysis of multi-phase induction motor with non-sinusoidal supply[J]. Science China: Technological Sciences, 2015(3): 322-329.
[15] 付丰礼, 唐孝镐. 异步电动机设计手册[M]. 北京: 机械工业出版社, 2002.
[16] 陈俊全. 软磁材料电磁特性模拟与应用研究[D]. 武汉: 海军工程大学, 2013.
Steady-State Performance Analysis of Multiphase Induction Motor with Third-Order Harmonic Injection
Abstract For the multi-phase induction motor with non-sinusoidal supply, an iterative method based on equivalent circuit and distributed magnetic circuit method is proposed in this paper. In the case of the 3-order harmonic injection, the steady-state performance indexes are calculated, and the quantitative relationship between 3-order harmonic injection parameters and steady state performance indexes is obtained and analyzed. The results show that the 3-order harmonic injection has the best effect on the optimization of the steady-state performance indexes of the motor, when the 3-order harmonic and fundamental component of the air-gap magnetic density satisfies the relative positional relationship of “peak-to-valley” and the amplitude ratio equals 1/6. The 3-order harmonic injection is implemented on a 45kW fifteen-phase induction motor. As the maximum value of air-gap magnetic density and current effective value remain constant, the experimental results show that the fundamental voltage and the output power can be increased by about 13% in comparison to the non-harmonic condition.
keywords:Multiphase induction motor, steady-state performance, third-order harmonic injection, distributed magnetic circuit method
中图分类号:TM343
DOI: 10.19595/j.cnki.1000-6753.tces.190858
国家自然科学基金重大项目(51690181),国家自然科学基金青年基金项目(5180702)和湖北省自然科学基金面上项目(2019CFB607)资助。
收稿日期2019-07-16
改稿日期 2019-09-17
孟繁庆 男,1991年生,博士研究生,研究方向为多相感应电机性能分析及优化设计。E-mail: mfq_nue@163.com
王 东 男,1978年生,教授,博士生导师,研究方向为电力推进与独立电源系统。E-mail: wangdongl@vip.sina.com(通信作者)
(编辑 赵 鹏)