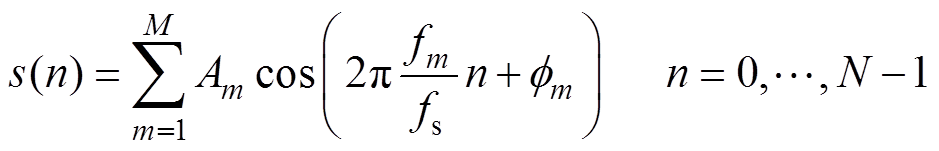 (1)
(1)摘要 针对多频率短时波动周期情况,提出基于全泄漏频谱抑制的多点插值离散傅里叶变换(DFT)校正方法。首先,利用最大旁瓣衰减窗频谱线性比例递推特性,将其他频率分量的频谱泄漏干扰以泰勒级数多项式等效近似,结合被测频率的负频谱泄漏分量建立全泄漏频谱参数模型;然后,根据谐波频谱泄漏的近似精度建立多谱线方程组,通过精确求解得到最大旁瓣衰减窗下的多谱线频率插值校正通用解析表达式;最后,采用最小二乘法得到幅值和相位的有效估计。多重仿真和实验测试结果表明,在噪声和等量级的其他频率泄漏干扰下,当被测频率低至1.5个频率分辨率时,算法依然保持具有很高的校正精度。
关键词:短时波动周期 全泄漏 多点插值离散傅里叶变换 频谱参数模型
在电能质量分析、谐波电能计量和电网同步实时监测等大量应用中,广泛采用基于离散傅里叶变换(Discrete Fourier Transform, DFT)的频谱分析方法进行电力信号处理。然而,伴随电力电子开关器件等非线性设备在电力系统中的大量应用,无处不在的谐波和间谐波等多频率分量干扰及暂态扰动过程,使得在有限时长窗口下直接采用DFT的测量精度出现严重偏差[1-3]。时域采样信号窗长限制及对 应频域的离散等间隔采样导致的频谱泄漏和栅栏效应[4-7],是其误差的两个主要来源。常用解决方法是采用时间窗函数信号加权和插值离散傅里叶变换(Interpolated DFT, IpDFT)校正来抑制频谱泄漏及消除栅栏效应。
频谱泄漏来自于两个方面:实信号经DFT后对应的共轭负频率分量;其他频次对应的正负频率分量[8-11]。当采样窗口内信号波动周期(Cycles in Record, CiR)较大时,对应各正负频率分量的离散谱线间隔较远,窗函数频谱旁瓣快速衰减特性使得泄漏干扰量级较小可以忽略不计,以致对应于待测真实频率附近的离散峰值谱线近似满足单频解析信号模型[12]。进一步的修正可根据不同时间窗函数,采用非线性拟合的离散谱线插值校正方法[13-14],消除栅栏效应带来的参数估计偏差。
然而,当采样窗口内信号CiR数量较低时,DFT频谱共轭对称特性使得负频率频谱短泄漏分量急剧增大[15-17]。另一方面,在多频率短时CiR情况下,各频次对应的DFT离散谱线间隔变小,也使得来自其他频率分量长程频谱泄漏干扰不可忽略[18],进而导致基于单频解析信号模型的非线性拟合方法失效,插值校正的估计误差已无法满足精度要求。
短时CiR频谱泄漏问题已引起国内外学者的高度关注,并开展了大量研究。一方面,针对实信号仅含单一频率,在短时CiR情况下计及负频率泄漏干扰的IpDFT及其解析方法已取得了有效进展。文献[19]使用迭代过程去除共轭负频率的频谱泄漏干扰,提出了基于精确相位谱模型的两点IpDFT。文献[20]考虑实信号经Hanning窗加权DFT后,利用对应正频率主瓣范围内的三条峰值谱线,通过线性近似Hanning窗频谱特性,首次以矩阵解析方式得到了明确的频率估计公式。文献[21]提出了通用多点加权插值离散傅里叶变换(Multipoint Weighted Interpolations of DFT, MWIDFT)算法,在Hanning窗加权DFT矩阵解析方法基础上,将其应用于任意H阶最大旁瓣衰减窗加权DFT下的频率估计。文献[22]针对上述矩阵解析方式的通用频谱插值方法,就高斯白噪声及含谐波时信号频率估计的准确度,通过推导估计方均误差(Mean Square Error, MSE)理论表达式,并以仿真方法与Cramer-Rao下界有关的统计特性进行了验证,结果表明在短时CiR情况下计及共轭负频率频谱泄漏的MWIDFT性能明显优于传统三点IpDFT。基于矩阵解析方式的改进IpDFT已应用于电力系统中低频间谐波快速检测[23],但所设定的频谱模型是建立在基波频率同步采样基础之上,即仍未考虑来自于其他频次的泄漏干扰分量。
另一方面,加窗离散采样信号经DFT计算后对应离散频率分布的不确定,以及窗函数频谱旁瓣衰减的非线性特性,使得完全消除其他频率分量所带来的谱泄漏干扰(特别是短时CiR情况)尤为困难。文献[24]通过推导并分解通用余弦窗频谱公式,发现使其具有非线性变化的有理多项式部分在主瓣范围以外的频谱具有一致单调特性,进而以加权多项式近似所有的泄漏分量,建立对应频率的复数谱等效模型,得到了高达6阶的频率估计公式。然而,该方法没有就离散窗频谱旁瓣衰减特性与多项式近似的内在关联,进行严格的数学证明。更为重要的是,将对应于负频率的频谱泄漏分量以多项式近似,势必降低插值方法的估计精度。
为此,针对短时CiR情况下频谱泄漏干扰导致IpDFT校正失准的问题,提出了基于全泄漏频谱模型的多点插值方法,可以有效提高多频率短时CiR情况下基于IpDFT的信号参数估计精度。
假设N点离散均匀采样实信号s(n)由M个频率分量组成,即
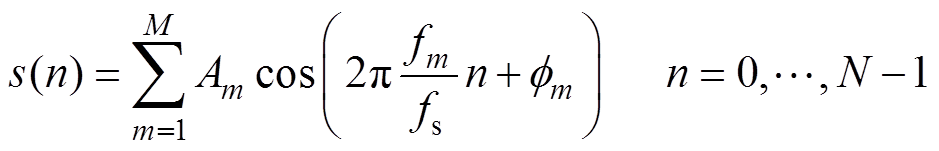 (1)
(1)式中,fs为采样频率;fm、Am和fm分别为对应频率分量的频率、幅值和初始相位。则加窗DFT为
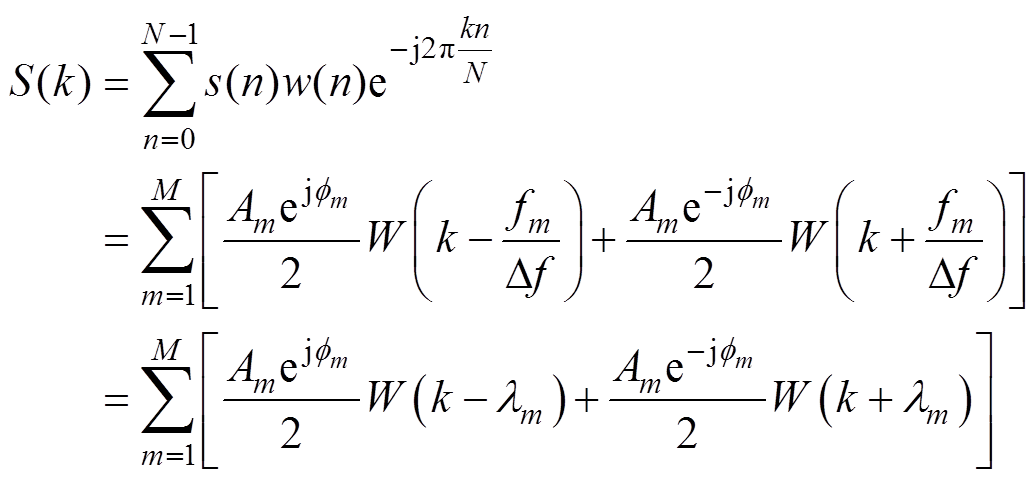 (2)
(2)
式中,k=0, 1,…, N,fm/fs=lm/N=(lm+vm)/N表示频域归一化频率;lm时域中表示对应被测频率fm的CiR个数,频域中则表示fm在频谱中所处位置;lm= [lm]ÎZ表示四舍五入取整,由频率分辨率Df=fs/N可知,余数vm的取值范围为[-0.5,0.5)。H项(H≥2)对称余弦窗函数定义为
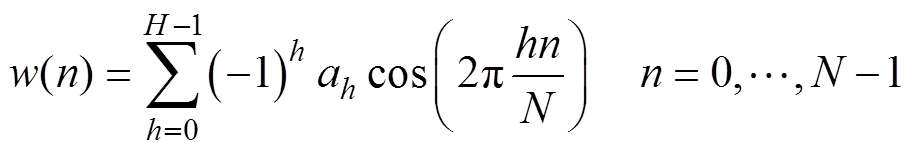 (3)
(3)式中,ah为加权系数。对应频谱函数为
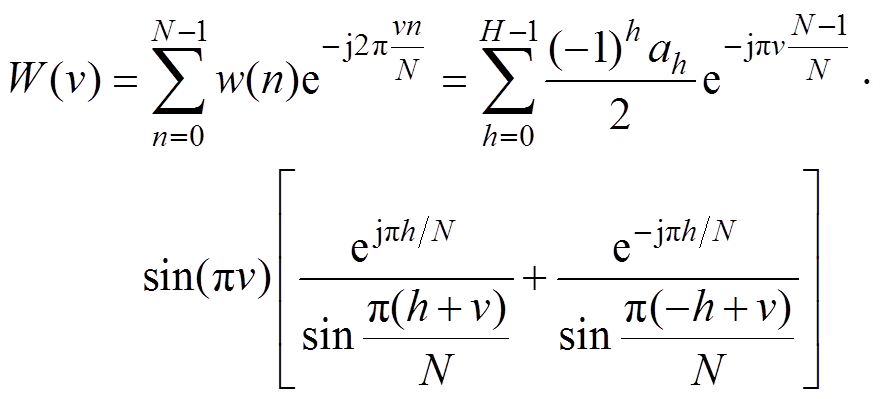 (4)
(4)
数学上单频实信号可以分解为正、负频率复解析信号之和,则从频谱角度可将式(2)包含的2M项视为以时间窗频谱函数W加权的独立频谱分量。即对于待测归一化频率lm=lm+vm,式(2)中局部离散峰值谱线S(lm)可改写为
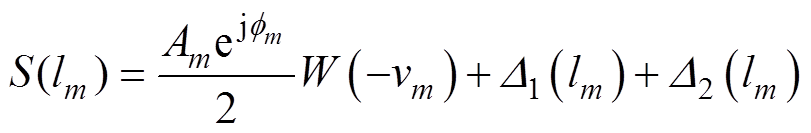 (5)
(5)式中,D1为被测频率对应的负频谱泄漏干扰分量;D2为其他频率的正负频谱泄漏干扰分量。在余弦窗函数频谱旁瓣快速衰减特性下,上述频谱泄漏分量随着其参数值lm的增加而快速减小,使得位于正频率主瓣范围内的局部峰值谱线S(lm)在量级上满足|S(lm)|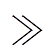 (|D1(lm), D2(lm)|),即等效为单频解析信号模型S(lm)@0.5AmW(-vm)exp(jfm)。基于经典三点IpDFT方法,利用幅值比的反函数
(|D1(lm), D2(lm)|),即等效为单频解析信号模型S(lm)@0.5AmW(-vm)exp(jfm)。基于经典三点IpDFT方法,利用幅值比的反函数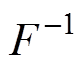 解析可得到对应频率非整余数部分vm的估计为
解析可得到对应频率非整余数部分vm的估计为
 (6)
(6)
在单频解析信号模型假设前提下,式(6)估计的相对误差[17]为
 (7)
(7)式(7)表明,当信号样本的CiR整数部分lm很小且vm不接近零时,相对估计误差显著增大。
进一步计及负频率频谱分量干扰D1时,S(lm)等效为双频解析信号模型,即
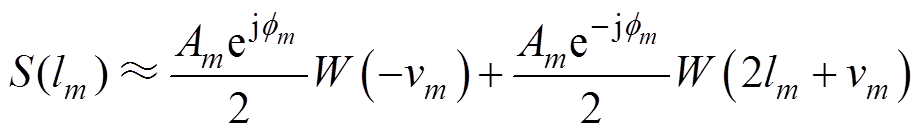 (8)
(8)利用正负频率频谱分量相关性,采用解析谱线方程组得到lm的估计值。在考虑干扰分量D2的情况下,式(8)估计的相对误差[22]为
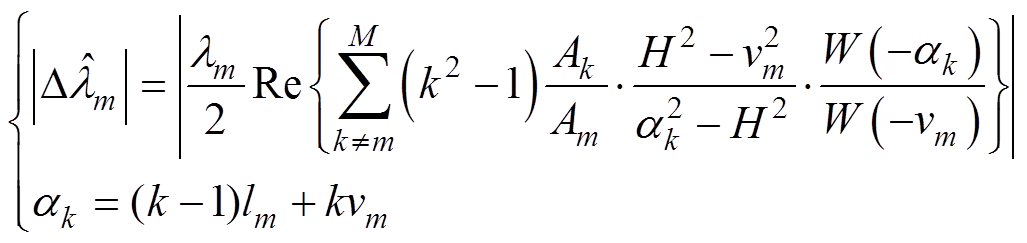 (9)
(9)
式中,对应单一频率分量影响的估计误差包络为lm的递减函数,与其幅值、频率偏移量及谱线位置有关。文献[22]仿真结果进一步显示,当CiR整数部分lm很小且vm不接近零时,量级最大的干扰频率分量与被测频率间隔越近,估计的相对误差则越大。
因此,在含有多频率分量的短时CiR情况下,有效计及上述两方面的频谱泄漏分量干扰影响,是提高谱线插值方法参数估计精度的关键。
对于通常采用的最大旁瓣衰减窗,其旁瓣渐进衰减速率为6(2H-1)dB/oct,加权系数ah满足
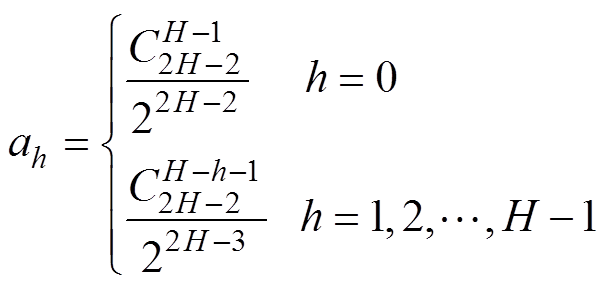 (10)
(10)式中,组合数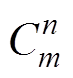 =m!/((m-n)!n!),!为阶乘运算符。当采样点数满足N
=m!/((m-n)!n!),!为阶乘运算符。当采样点数满足N 1且N
1且N |v|时,式(4)所示的最大旁瓣衰减窗频谱可以近似[23]为
|v|时,式(4)所示的最大旁瓣衰减窗频谱可以近似[23]为
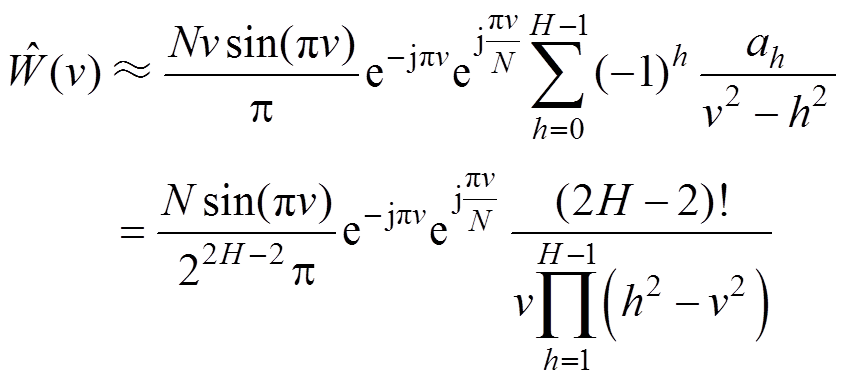 (11)
(11)
式(11)近似使得在保证其旁瓣一致渐进衰减特性及精度要求的前提下,当LÎN+时最大旁瓣衰减窗的频谱具有两个重要的线性比例递推特性,即
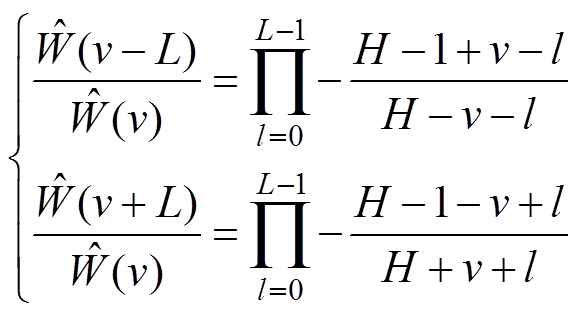 (12)
(12)明显地,式(12)右侧累积绝对值具有一致快速衰减特性。最大旁瓣衰减窗频谱近似特性如图1所示(选择H=2的Hanning窗,主瓣带宽为2,包含2H-1=3根谱线),表明随着l逐渐增大(即各频率分量对应离散谱线间隔L增加),来自其他频率的加权频谱泄漏分量D1和D2对被测真实频率附近的离散峰值谱线干扰呈级数减小。
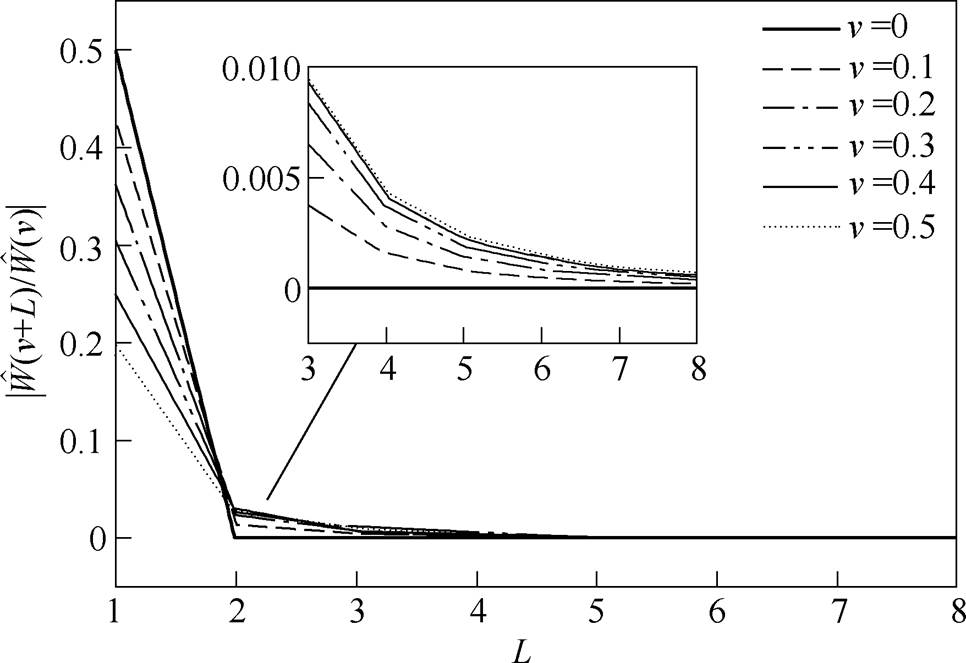
图1 最大旁瓣衰减窗频谱近似特性
Fig.1 The approximate spectral characteristics of maximum sidelobe decay windows
进一步将式(12)右侧分别以泰勒级数展开表示为
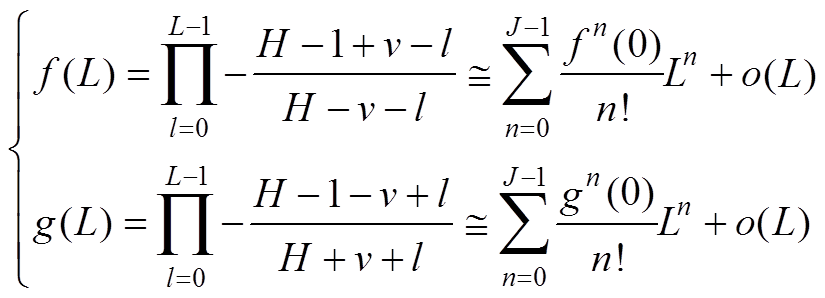 (13)
(13)式中,阶数J用以控制近似精度,满足J∈N+。
不失一般性,假设信号s(n)含有2个频率分量f1和f2,且f1<f2,离散频谱局部最大值分别处于第l1和l2根谱线,则对应l1谱线的DFT为
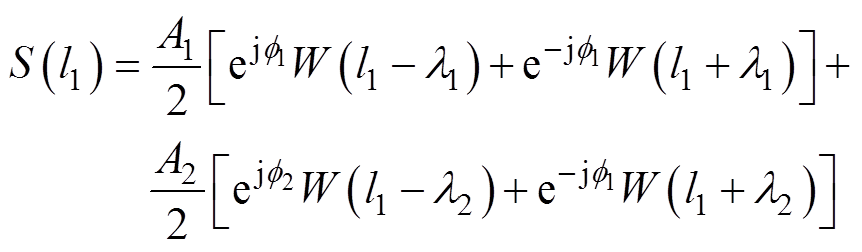 (14)
(14)利用频谱函数W正负对称特性及式(13),式(14)第二大部分(中括号内)为f2所对应的正负频率W加权旁瓣衰减分量,可分别近似为
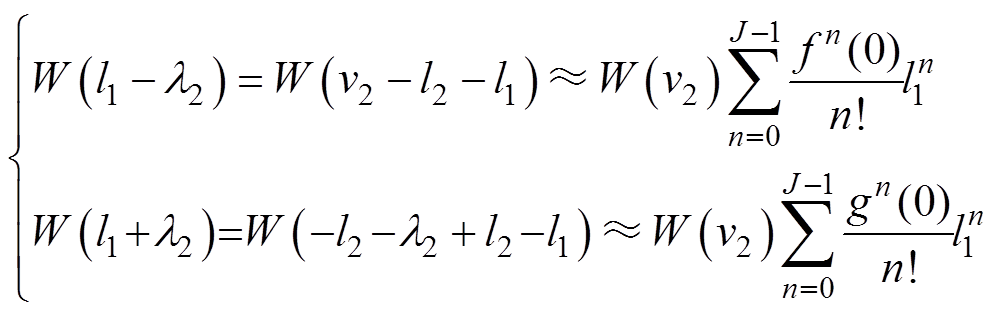 (15)
(15)
将式(15)代入式(14)可得
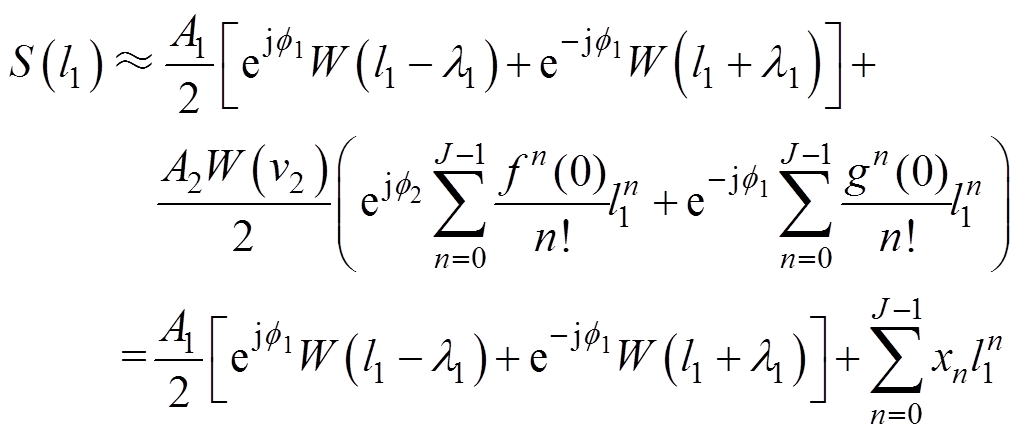 (16)
(16)式(16)为考虑全泄漏干扰的频谱近似等效模型。明显地,该模型不仅考虑了共轭负频率的频谱泄漏分量,而且在其他频率分量参数未知前提下使得其频谱泄漏干扰得以有效参数化,且与被测频率谱线位置l1的级数线性相关。
为得到式(16)所示方程中含有的J+3个未知变量:A1、f1、l1和x0~xJ-1,则在频率f1对应主瓣中心及其附近,选择kp-1、kp、kp+1、…、kp+J+1共J+3根离散谱线构建方程组,以矩阵形式表示为
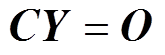 (17)
(17)式中,C=[C1C2],Y=[Y1Y2]T,对应分别为
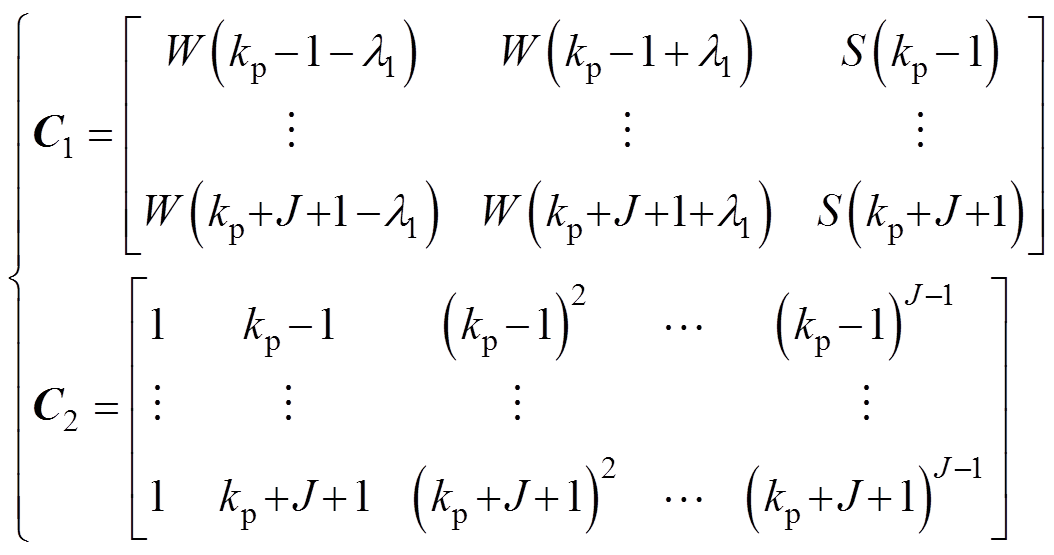 (18)
(18)
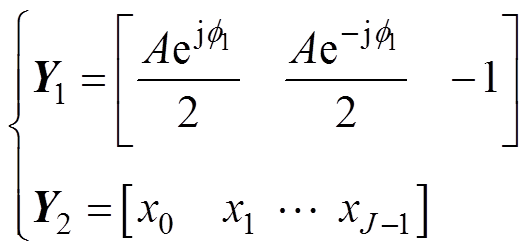 (19)
(19)根据线性代数中的克莱姆法则,非零解的存在要求齐次线性方程组系数矩阵的行列式为零,即|C|=0。此时方程|C|=0中仅有l1为未知变量,进而可得该方程的解(具体解析过程见附录)为
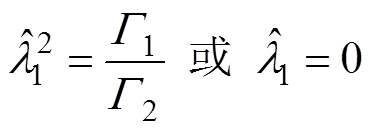 (20)
(20)
其中
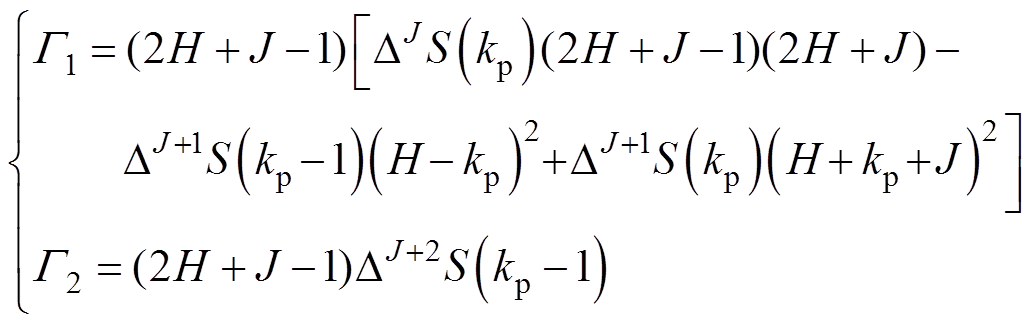
 (21)
(21)式中,符号DJ表示J阶前向差分,有
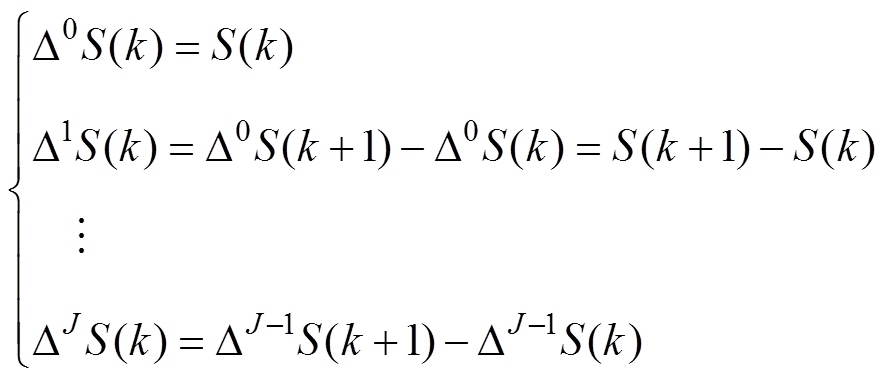 (22)
(22)
值得注意的是,将来自其他频率的频谱泄漏进行模型化的上述解析方法,其本质可以理解为抑制或减少泄漏干扰。即在极限情况下,当L增大到一定程度时,来自谐波分量的频谱泄漏干扰急剧减小,可以忽略不计(即J=0)。经验证,在这种情况下式(20)通用解析解仍然适用,此时校正方法及解析解等效于文献[6]提出的通用MWIDFT。
根据式(16)的全泄漏频谱近似等效模型,在频率估计基础上进行幅值和相位估计,分别进行如下等效(简约起见,忽略下标)
 (23)
(23)则式(16)实部和虚部分别对应为
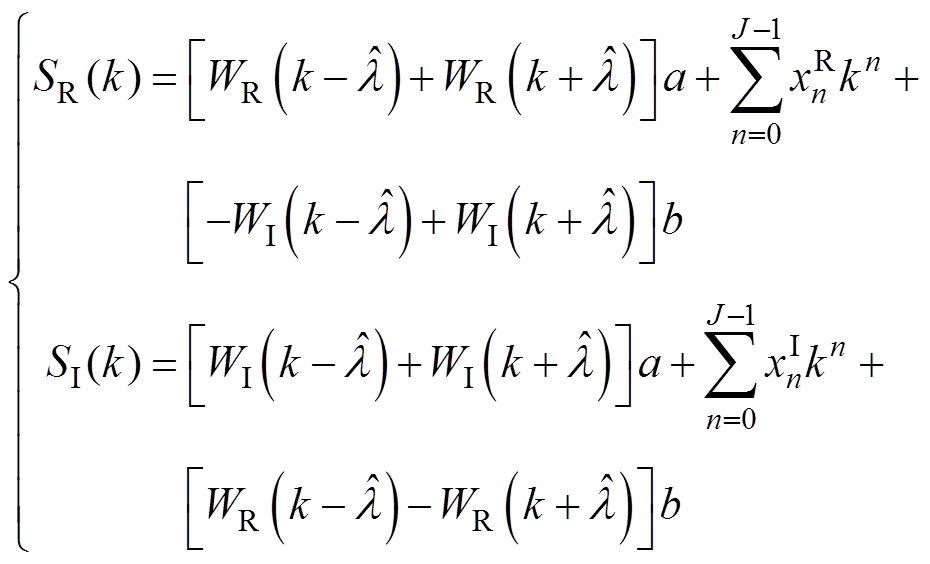 (24)
(24)
选择与前述一致的J+3根谱线,联立形成方程组为
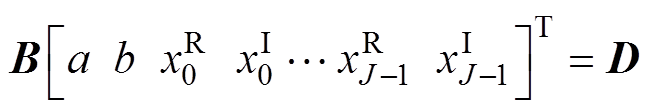 (25)
(25)系数矩阵B和D具体表达式见附录,根据最小二乘法可得解为
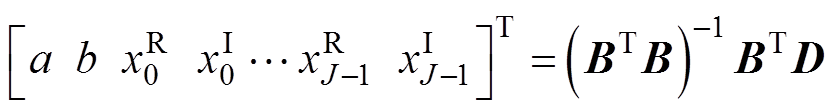 (26)
(26)
则幅值和相位估计分别为
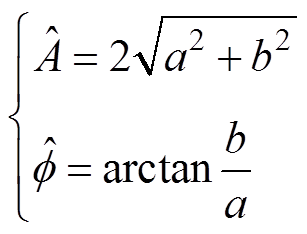 (27)
(27)根据式(20)和式(21)可知,解析解与离散采样参数(N/fs)无关,因此固定频率分辨率Df=fs/N= 1Hz,重点考察H和J的选择对算法误差精度影响。为使来自负频率和其他频率的频谱泄漏分量在量级上具有可对比性,设置仿真信号包含两个幅值相等的频率分量。被测低频分量f1=3.5Df,初始相位f1= 0°;高频干扰分量f2以步长0.001Df从7Df~13.5Df逐渐变化,对应每个频率点的初始相位f2以步长 0.5°从0°~180°变化。
对每一个仿真信号进行加窗DFT计算,进而选择相应的J+3根离散谱线,根据式(20)和式(21)进行频率估计。则对应于不同频谱泄漏近似的多项式阶数J,被测低频分量f1估计的相对误差df1在不同H下随着频率分量f2的变化趋势如图2所示。此处相对误差df1定义为
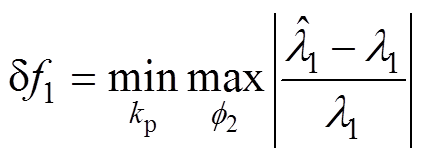 (28)
(28)
图2 f1=3.5Df时频率估计相对误差
Fig.2 Relative errors of frequency estimation at f1=3.5Df
图2中,Dl=(f2-f1)/Df。根据图2结果可知:①算法在加窗抑制旁瓣泄漏基础上,将来自频率f2的频谱泄漏干扰计入插值解析过程,整体上随着多项式阶数J的增加,对频率f2的频谱泄漏干扰近似精度越高,进而可以有效地提高频率校正精度(局部相反情况的原因在于解析谱线组包含了对应f2的主瓣谱线);②随着频率f2逐渐增大,其频谱泄漏干扰分量逐渐减小,整体上使得相对估计误差df1急剧减小,其中局部最大值对应于f2=(k+0.5)Df(此时其频谱泄漏分量最大),而局部最小值对应于f2= kDf(此时对于f2因相关同步采样而不存在频谱泄漏),即本文算法采用的全泄漏等效模型准确计及了负频率的泄漏干扰。因此即便在频率f2的频谱泄漏干扰未知前提下,依然能够有效地确保被测低频率的校正估计具有非常高的稳定性和准确度。
为更好地阐释第②点,以含有低频次谐波分量的电力信号为例。设定采样频率fs=2 000Hz,采样点数N=300,则此时对应基波分量f0=50Hz的波动周期l =7.5,即基波分量存在恒定的长程泄漏;而被测低频次谐波分量fi的频率则以步长0.001Hz从0.025~25Hz逐渐变化;两个分量的幅值都设置为1,初始相位都设置为0°。固定近似多项式阶数J=2,同时采用文献[3]中基于复数谱等效模型的解析方法进行频率校正估计,其解析解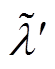 为
为
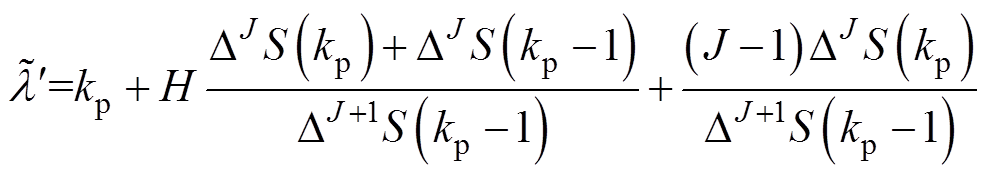 (29)
(29)进而与式(20)解析解的误差比对结果如图3所示。
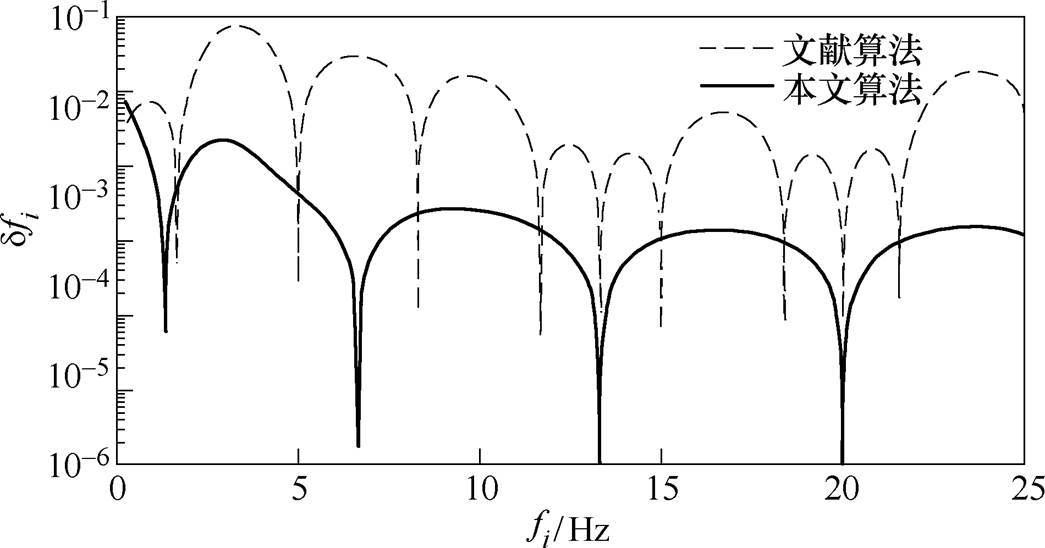
图3 f2=7.5Df时f1估计相对误差
Fig.3 Relative errors of f1 estimation at f2=7.5Df
从图3可明显看出,在基波分量恒定泄漏干扰的情况下,准确计及负频率频谱的本文算法较文献[3]中将所有泄漏分量统一以多项式近似的方法具有明显优势;同时也进一步印证了前述仿真第②点关于本文算法在低频率校正估计中稳定性的结论。
为验证算法幅值和相位估计的有效性,依然按照4.1节设置仿真信号,而被测低频分量f1的初始相位设定为0.5°。在频率估计基础上,根据式(24)~式(27)采用Hanning窗进行幅值和相位估计,对应误差分别定义为
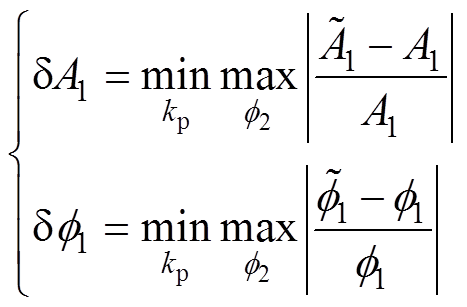 (30)
(30)以常用比值校正法作为参考进行性能比对,在f2整个变化范围内,dA1和df1随着频率分量f2的变化趋势如图4所示。
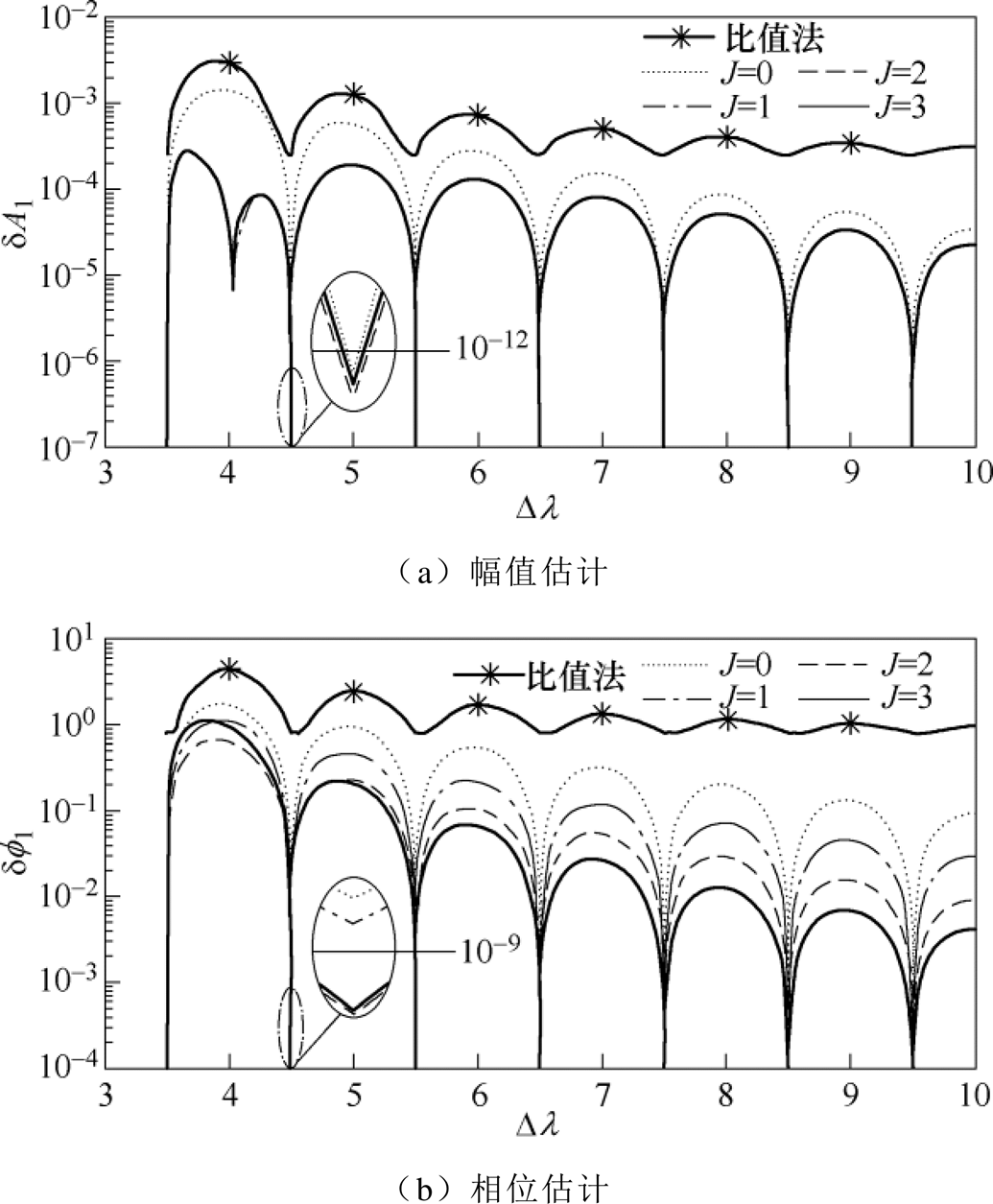
图4 幅值和相位估计相对误差
Fig.4 Relative errors of amplitude and phase estimation
对比图4和图2可知,本文算法频率估计精度对幅值和相位的估计有决定性影响,其整体变化趋势与频率估计一致,相较于比值校正法在精度上具有明显优势。而对于比值校正法,其设定的单频解析信号模型忽略了全部的频谱泄漏干扰,而仿真信号中对应负频率频谱泄漏分量保持不变,使得误差无法随着频率f2频谱泄漏干扰减小而快速减小,如图4中,在f2=kDf时其误差保持恒定大小。
为进一步评估算法在高斯白噪声情况下的估计准确度,在保持其他参数与4.2节一致前提下,信号中加入信噪比(Signal to Noise Ratio, SNR)为30~90dB的高斯随机白噪声,对应频率估计平均绝对误差(Mean Absolute Error, MAE)定义为
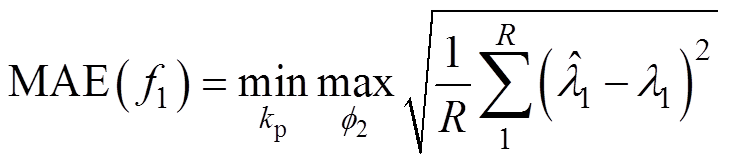 (31)
(31)重复次数R设定为10 000,则当J=1时不同SNR下频率f1估计MAE如图5所示。

图5 不同SNR下频率估计平均绝对误差
Fig.5 Errors of frequency estimation MAE under different SNR
从图5可看出,算法在噪声情况下性能较为稳健,特别是当SNR>50dB时估计误差逐渐趋于稳定,其极大值已经非常接近于无噪声时的精度。而对于精度更高的频谱泄漏多项式近似,以图5中f2= 7.5Df频点为例,在信噪比30~90dB内对比J=0, 1, 2的局部最大误差,显然随着近似精度提高参数估计误差水平将更低。不同J下频率估计误差如图6所示。
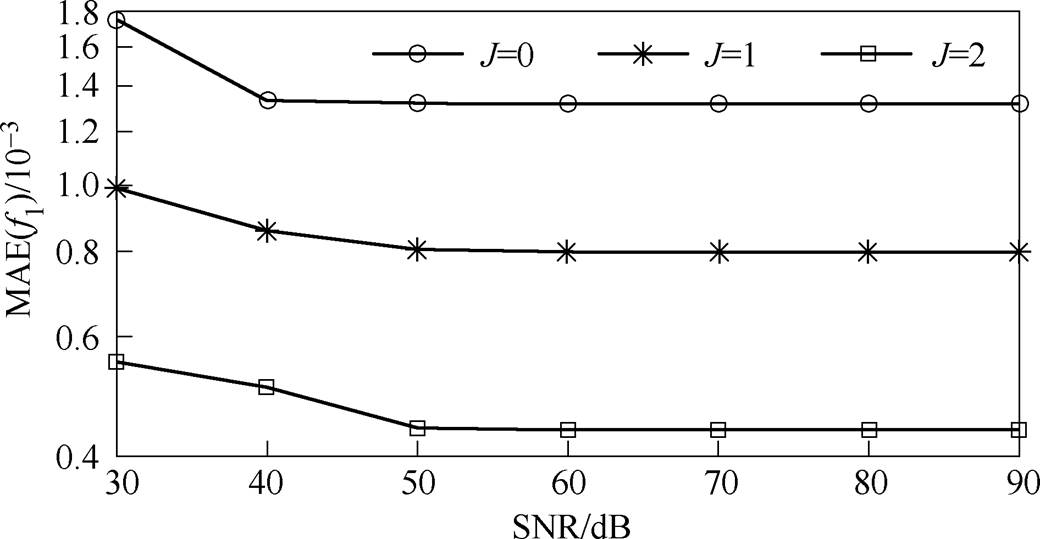
图6 不同J下频率估计误差
Fig.6 Errors of frequency estimation under different J
实验验证测试平台如图7所示,功率信号源采用精度为0.05级DK-56B1三相交直流指示仪表检定装置,采用24bit的IOtech数据记录仪进行信号采集,采样频率设定为100kHz。

图7 实验验证测试平台
Fig.7 Experimental verification test platform
鉴于信号源的单通道输出单一信号频率范围限定为[35, 70]Hz,因此采用双通道采集,经过抽取采样后合并构成测试信号。此处仍固定f2=7.5Df,测试f1为1.5Df、2.5Df、3.5Df时(见图2所示的相对局部误差最大频率点)在Hanning窗下的算法性能。其中,通过移动采样起始点改变对应频点的初始相位f1和f2,以期最大限度地找到泄漏干扰对算法性能的影响。限于篇幅,图8仅示出f1=3.5Df时的测试结果,而在f1和f2变化范围内,对应f1为1.5Df、2.5Df的局部极限相对误差df1见表1。
据图8和表1结果显示,算法性能测试结果与图2所示仿真分析结果保持一致,即在等量恒定频谱泄漏干扰情况下,得益于计及负频率泄漏干扰的参数近似等效模型,所提算法在短时CiR下的超低频校正性能依然稳健,在f1=1.5Df时极限最大误差仍能维持在10-3量级左右。
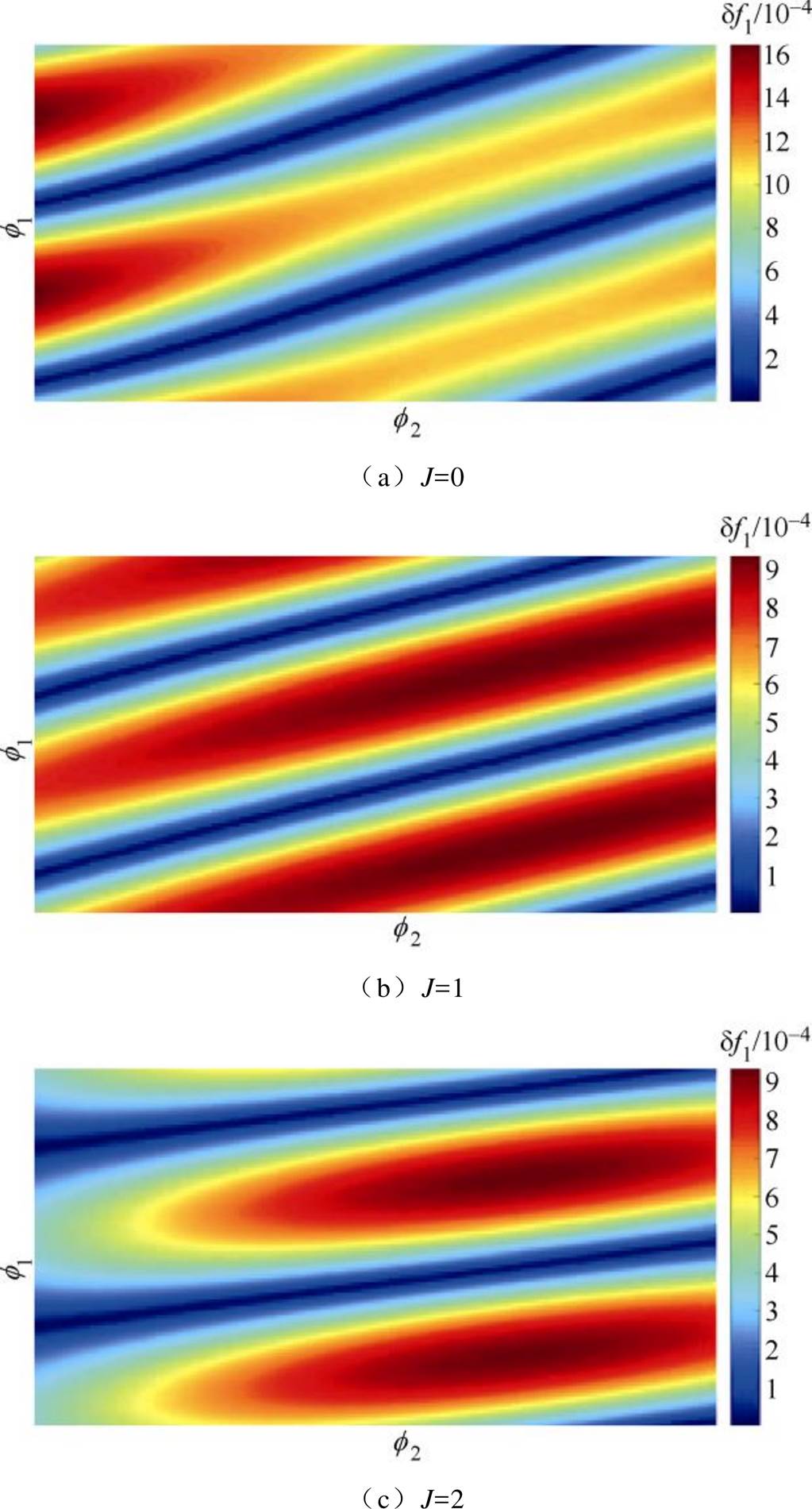
图8 f1=3.5Df时的测试结果
Fig.8 Test results at f1=3.5Df
表1 f1=1.5Df、2.5Df时的极限误差
Tab.1 Limit errors at f1 is 1.5Df and 2.5Df

误差f1/HzJ=0J=1J=2 max(df1)1.5Df4.1028×10-31.476×10-31.809×10-3 2.5Df4.015×10-39.459×10-47.659×10-4 min(df1)1.5Df6.238×10-91.081×10-94.820×10-10 2.5Df3.962×10-101.328×10-104.772×10-10
以某电力机车实测电流信号作为算法实际应用的样本,实测信号及其频谱如图9所示。电铁电流信号如图9a所示,其局部放大如图9b所示。显然作为一种具有暂态特征且包含多频率分量的信号,在如图9b中局部段需进行短时截断,以保证信号窗口内保持相对稳态。
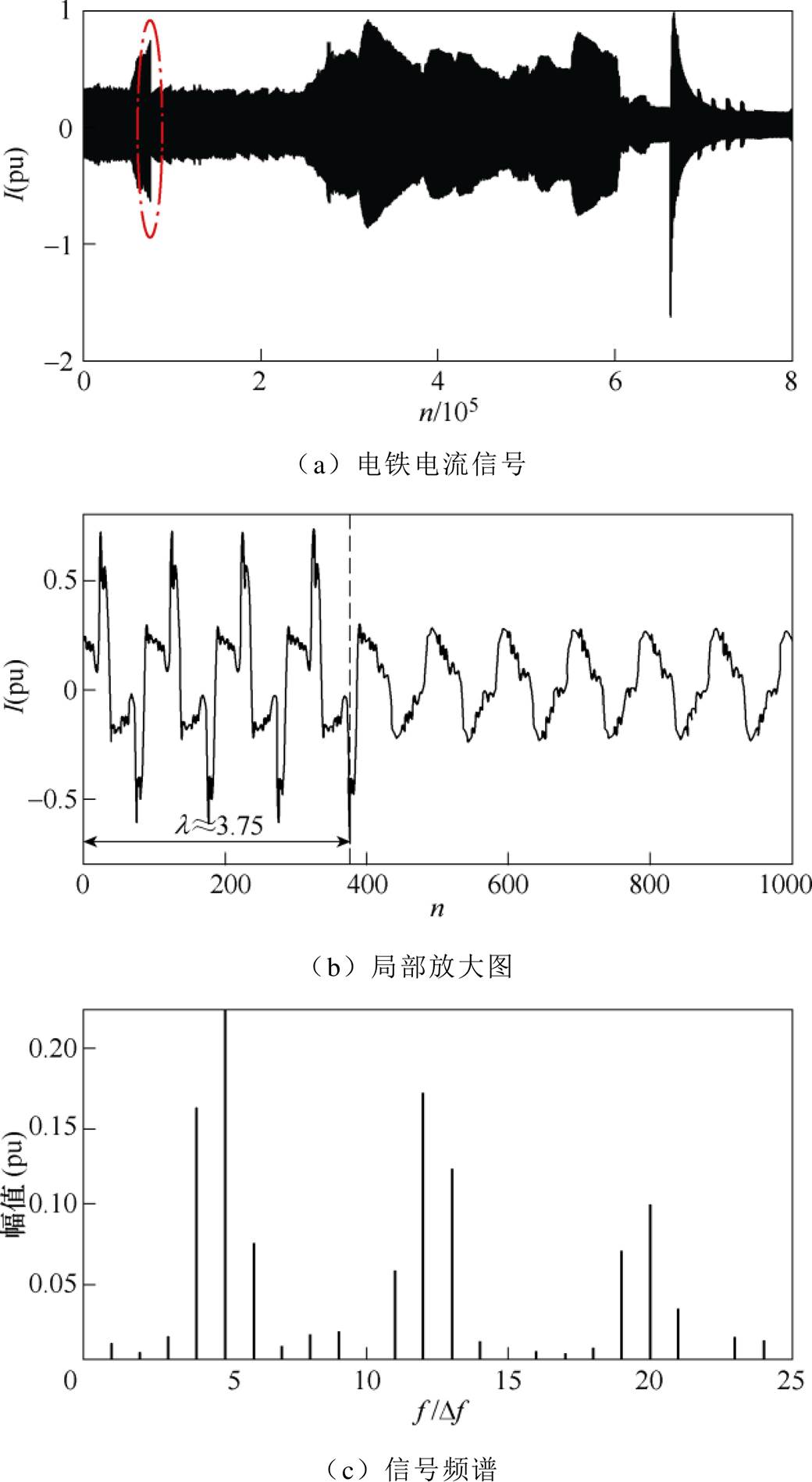
图9 实测信号及其频谱
Fig.9 Measured signal and spectra
如图9b所示,左侧截断窗口含有约3.75个基波周期,右侧含有约6.25个基波周期。以左侧数据段为例,采用Hanning窗(H=2)进行加窗插值处理,信号频谱如图9c所示。对于基波分量而言,其负频率和近邻谐波的频谱泄漏干扰已然不能忽略,若直接传统插值DFT势必存在严重测量误差,由此采用本文算法、文献[21, 24]中算法进行处理。需注意的是,本文算法和文献[21]需依次从低频向高频逐渐测量,且此处都采用J=1近似多项式模型。由于此信号为实测信号,仅以信号重构残差作为算法评定标准,三种算法的重构残差依次为:4.314 720´ 10-5、1.456 691´10-4和2.515 562´10-4,明显看出本文算法保持一定精度优势。
针对多频率短时CiR情况,本文将来自其他频率的频谱泄漏干扰有效参数化,解决了其他频率分量参数未知前提下其频谱泄漏无法量化的问题;进而基于所建立的全泄漏等效模型推导得出了明确的插值解析公式,打破了以往加窗插值算法仅限于单频解析信号的局限性。
多重仿真分析和实验验证结果显示:一方面算法通过准确计及负频率泄漏干扰,在等量级其他泄漏及噪声干扰下能够确保被测频率低至1.5Df时性能保持稳定;另一方面算法通过提升其他频谱泄漏多项式近似精度,能够进一步降低其他泄漏对插值谱线干扰,进而确保在干扰频率间距低至3个分辨率时被测频率参数估计依然具有很高的精度。
由于时间窗频谱主瓣宽度的限定,文中仅采用了最高达3阶的多项式,因而对于更高阶的最小旁瓣衰减窗,在更为密集的频谱干扰下的插值校正有待进一步研究。
1. 方程求解
J=1时,方程|C|=0表示为(简单起见,忽略下标)
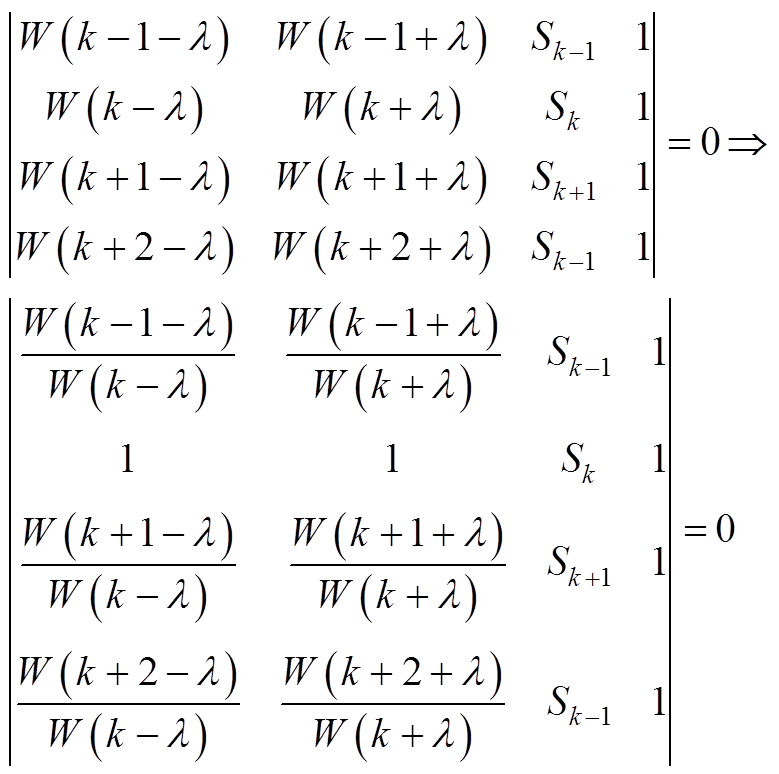 (A1)
(A1)根据式(12)窗函数频谱间的比例性质,式(A1)可化简为
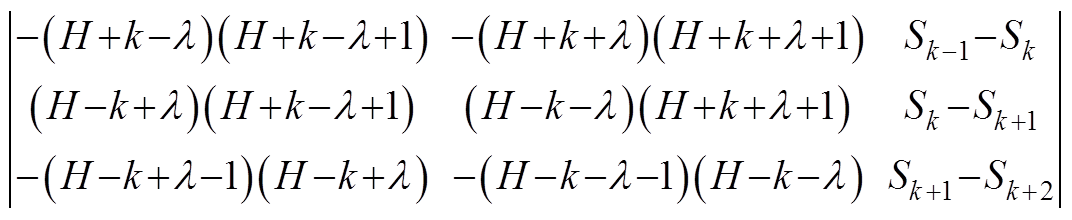
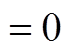 (A2)
(A2)令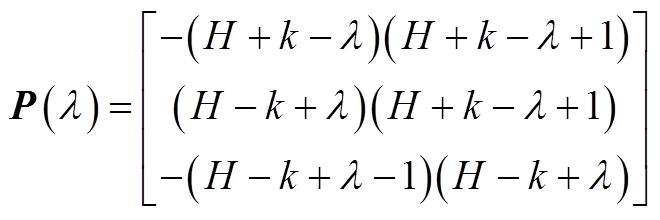

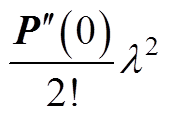 ,
,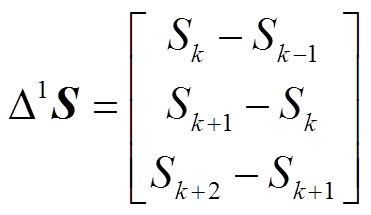 ,则式(A2)改写为
,则式(A2)改写为
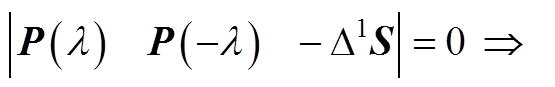

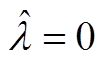 或
或 (A3)
(A3)
其中
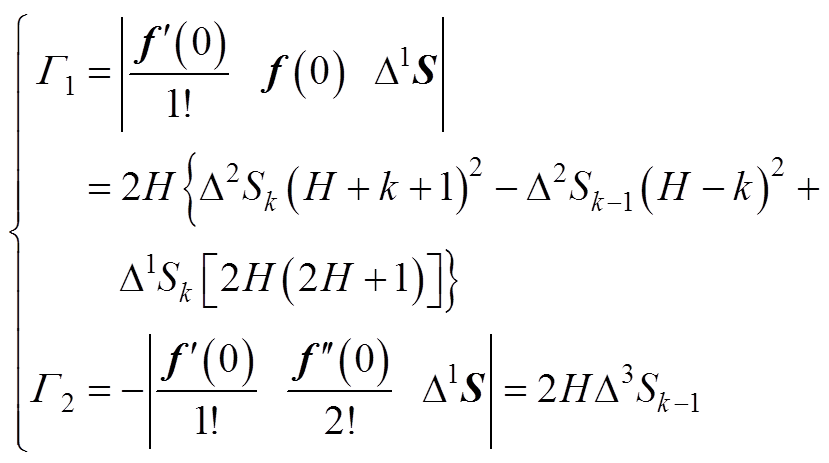 (A4)
(A4)进一步采用上述方法,同理可得,当J=2, 3, 4,…时的方程解。根据前述得到的解析公式,递推可得J>1时的通用解析解为
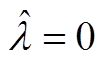 或
或
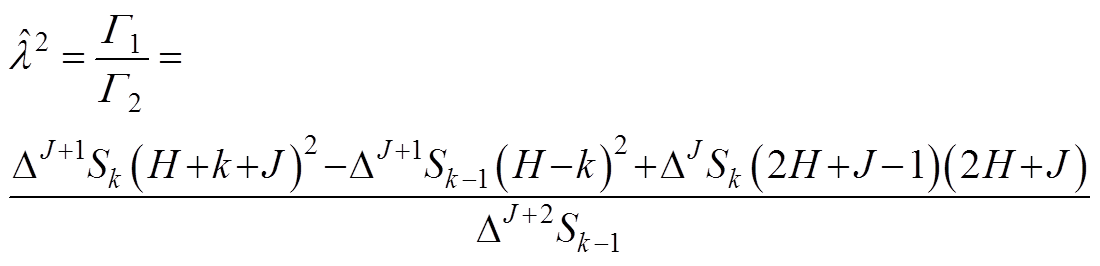 (A5)
(A5)2. 系数矩阵

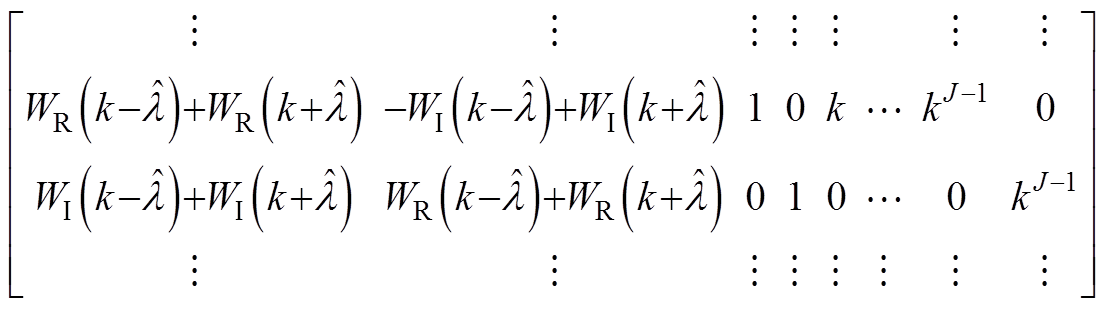
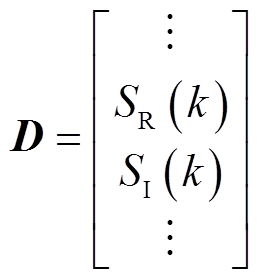 (A6)
(A6)
参考文献
[1] 王保帅, 肖霞. 一种用于谐波分析的高精度多谱线插值算法[J]. 电工技术学报, 2017, 32(15): 22-31.
Wang Baoshuai, Xiao Xia. A high accuracy multi spectrum-line interpolation algorithm for harmonic analysis[J]. Transactions of China Electrotechnical Society, 2017, 32(15): 22-31.
[2] Swanson D C. Precision spectral peak frequency measurement using a window leakage ratio function[J]. Mechanical Systems and Signal Processing, 2015, 54: 1-15.
[3] Romano P, Paolone M. Enhanced interpolated-DFT for synchrophasor estimation in FPGAs: theory, implementation, and validation of a PMU proto- type[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(12): 2824-2836.
[4] 吴超凡, 陈隆道. 应用于电力谐波分析的改进相位差校正法[J]. 电工技术学报, 2017, 32(7): 158-164.
Wu Chaofan, Chen Longdao. Improved phase differ- ence correction method applied to power harmonic analysis[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 158-164.
[5] Diao R, Meng Q. Frequency estimation by iterative interpolation based on leakage compensation[J]. Measurement, 2015, 59(1): 44-50.
[6] Belega D, Petri D. Frequency estimation by two- or three-point interpolated fourier algorithms based on cosine windows[J]. Signal Processing, 2015, 117: 115-125.
[7] Belega D, Petri D, Dallet D. Impact of harmonics on the interpolated DFT frequency estimator[J]. Mecha- nical Systems and Signal Processing, 2016, 66: 349- 360.
[8] Liguori C, Paolillo A, Pignotti A. Estimation of signal parameters in the frequency domain in the presence of harmonic interference: a comparative analysis[J]. IEEE Transactions on Instrumentation and Measurement, 2006, 55(2): 562-569.
[9] 牛鹏辉, 涂亚庆, 张海涛. 一种实正弦信号的短时频率估计新方法[J]. 电子测量与仪器学报, 2007, 21(6): 40-44.
Niu Penghui, Tu Yaqing, Zhang Haitao. New method of short-time frequency estimation for real signal[J]. Journal of Electronic Measurement and Instrument, 2007, 21(6): 40-44.
[10] Belega D, Dallet D. Multifrequency signal analysis by Interpolated DFT method with maximum sidelobe decay windows[J]. Measurement, 2009, 42(3): 420- 426.
[11] Luo Jiufei, Xie Zhijiang, Xie Ming. Interpolated DFT algorithms with zero padding for classic windows[J]. Mechanical Systems and Signal Processing, 2016, 70-71: 1011-1025.
[12] 毛育文, 涂亚庆, 张海涛, 等. 计及负频率影响的频谱分析方法及研究进展[J]. 电测与仪表, 2011, 48(5): 27-32.
Mao Yuwen, Tu Yaqing, Zhang Haitao, et al. Advances and trends in spectrum analysis metho- dology with negative frequency contribution[J]. Electrical Measurement & Instrumentation, 2011, 48(5): 27-32.
[13] 曾金芳, 滕召胜, 唐求. 自卷积检测方法及其在离散频谱校正中的应用[J]. 中国电机工程学报, 2014, 34(28): 4976-4982.
Zeng Jinfang, Teng Zhaosheng, Tang Qiu. Self- convolution detection method and its application in discrete spectrum correction[J]. Proceedings of the CSEE, 2014, 34(28): 4976-4982.
[14] 张俊敏, 刘开培, 汪立, 等. 基于主瓣宽度多谱线插值的高精度快速谐波分析算法[J]. 电工技术学报, 2018, 33(增刊1): 121-128.
Zhang Junmin, Liu Kaipei, Wang Li, et al. A precise and rapid algorithm for harmonic analysis based on multi-spectrum-line in main lobe width interpolation FFT[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 121-128.
[15] Candan C. A method for fine resolution frequency estimation from three DFT samples[J]. IEEE Signal Processing Letters, 2011, 18(6): 351-354.
[16] 陈奎孚, 王建立, 张森文. 短记录加汉宁窗的频谱校正[J]. 振动与冲击, 2008, 27(4): 49-51.
Chen Kuifu, Wang Jianli, Zhang Senwen. Spectrum correction for short records weighted by a hanning window[J]. Journal of Vibration and Shock, 2008, 27(4): 49-51.
[17] Belega D, Petri D, Dallet D. Frequency estimation of a sinusoidal signal via a three-point interpolated DFT method with high image component interference rejection capability[J]. Digital Signal Processing, 2014, 24: 162-169.
[18] 陈奎孚, 张森文, 郭幸福. 消除负频率影响的频谱校正[J]. 机械强度, 2004, 26(1): 25-28.
Chen Kuifu, Zhang Senwen, Guo Xingfu. Spectrum rectifying with negative frequency contribution eliminating[J]. Journal of Mechanical Strength, 2004, 26(1): 25-28.
[19] Aboutanios E, Mulgrew B. Iterative frequency estimation by interpolation on Fourier coefficients[J]. IEEE Transactions on Signal Processing, 2005, 53(4): 1237-1242.
[20] Chen Kuifu, Cao Xu, Li Yangfeng. Sine wave fitting to short records initialized with the frequency retrieved from Hanning windowed FFT spectrum[J]. Measurement, 2009, 42(1): 127-135.
[21] Borkowski J, Kania D, Mroczka J. Interpolated-DFT- based fast and accurate frequency estimation for the control of power[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 7026-7034.
[22] Belega D, Petri D. Effect of noise and harmonics on sine-wave frequency estimation by interpolated DFT algorithms based on few observed cycles[J]. Signal Processing, 2017, 140: 207-218.
[23] 王泽, 杨洪耕, 王佳兴, 等. 消除负频率影响的低频间谐波快速检测方法[J]. 电力自动化设备, 2015, 35(3): 140-145.
Wang Ze, Yang Honggeng, Wang Jiaxing, et al. Rapid low-frequency interharmonic detection with negative-frequency elimination[J]. Electric Power Automation Equipment, 2015, 35(3): 140-145.
[24] Chen Kuifu, Jiang Jingtao, Crowsen S. Against the long-range spectral leakage of the cosine window family[J]. Computer Physics Communications, 2009, 180(6): 904-911.
Multipoint Interpolated Discrete Fourier Transform Correction Method Considering Total Leakage Effect
Abstract A multipoint interpolated DFT correction method based on total spectral leakage suppression is proposed for the short cycles in record (CiR) of multi-frequency signal. Firstly, the spectral leakage from other frequency components is equivalently approximated to a Taylor series polynomial by the linear proportional recursive property of the maximum sidelobe decay Windows (MSDW) spectrum. The spectral parametric model of total spectral leakage is then established combined with the negative leakage component of the measured frequency. Furthermore, the corresponding equations of multipoint spectral lines are established according to the approximate order of the spectral leakage, and then the general analytical formula of multipoint frequency interpolation correction under the MSDW is derived. Finally, the least squares (LS) method is used to obtain an accurate estimation of the amplitude and phase. Multiple simulation and experimental test show that the algorithm still has high correction accuracy when the measured frequency is as low as 1.5 frequency resolutions under noise and other frequency leakage interference of equal magnitude.
keywords:Short cycles in record, total spectral leakage, multipoint interpolated discrete Fourier transform, spectral parametric model
中图分类号:TM935
DOI: 10.19595/j.cnki.1000-6753.tces.190883
国家重点研发计划课题(2018YFC0406904)和重庆市重点产业共性关键技术创新专项(重点研发项目)(CSTC2017ZDCY-ZDYFX0045)资助项目。
收稿日期 2019-07-17
改稿日期 2019-11-25
杨 超 男,1986年生,博士研究生,研究方向为数字信号处理及其在电能计量和电能质量分析中的深度应用。E-mail: 328383369@qq.com
付志红 男,1966年生,博士,教授,博士生导师,主要研究方向为电能质量分析与电能计量、电力电子、电磁探测技术等。E-mail: fuzhihong@cqu.edu.cn(通信作者)
(编辑 陈 诚)